Development of a New Pre- and Post-Processing Tool (SADAPT-TRAN) for Nonlinear Mixed-Effects Modeling in S-ADAPT

Abstract

Mechanistic modeling greatly benefits from automated pre- and post-processing of model code and modeling results. While S-ADAPT provides many state-of-the-art parametric population estimation methods, its pre- and post-processing capabilities are limited. Our objective was to develop a fully automated, open-source pre- and post-processor for nonlinear mixed-effects modeling in S-ADAPT. We developed a new translator tool (SADAPT-TRAN) based on Perl scripts. These scripts (a) automatically translate the core model components into robust Fortran code, (b) perform extensive mutual error checks across all input files and the raw dataset, (c) extend the options of the Monte Carlo Parametric Expectation Maximization (MC-PEM) algorithm, and (d) improve the numerical robustness of the model code. The post-processing scripts automatically summarize the results of one or multiple models as tables and, by generating problem specific R scripts, provide an extended series of standard and covariate-stratified diagnostic plots. The SADAPT-TRAN package substantially improved the efficiency to specify, debug, and evaluate models and enhanced the flexibility of using the MC-PEM algorithm for parallelized estimation in S-ADAPT. The parameter variability model can take any combination of normally, log-normally, or logistically distributed parameters and the SADAPT-TRAN package can automatically generate the Fortran code required to specify between occasion variability. Extended estimation features are available to avoid local minima, estimate means with negligible variances, and estimate variances for fixed means. The SADAPT-TRAN package significantly facilitated model development in S-ADAPT, reduced model specification errors, and provided useful error messages for beginner and advanced users. This benefit was greatest for complex mechanistic models.

Electronic supplementary material

The online version of this article (doi:10.1208/s12248-011-9257-x) contains supplementary material, which is available to authorized users.

INTRODUCTION

Developing and estimating mechanistic models of biological, pharmacological, and biochemical processes using nonlinear mixed-effects modeling is one of the most challenging problems. Successful application of such modeling usually requires in depth understanding of the physiology, pharmacology, biochemistry, related biological processes, and experimental techniques as well as advanced statistical, numerical, and programming skills. It is desirable to take away as much of the technical burden from a modeler as possible, since the main task for mechanistic model building is a meaningful translation of biology into robust mathematical models in agreement with the available mechanistic knowledge from literature. The latter represents the unique contribution an expert modeler provides in the biomedical field.

The true variability of almost every biological process makes estimation of such mechanistic models very demanding. To optimally describe such systems, estimate model parameters, and make meaningful inferences from model predictions, biological variability should be incorporated in the model, estimated, and used during stochastic simulations (often called Monte Carlo simulations). Nonlinear mixed-effects modeling can account for this biological variability, but requires significant technical skills.

Specification of nonlinear mixed-effects models greatly benefits from translator tools converting the model equations, estimation settings, and initial parameter estimates into the final model code that is compiled and executed. Such pre-processing translators have been developed for nonlinear mixed-effects modeling in other software packages such as NONMEM® 7 (NM-TRAN; 1), Monolix (MLXTRAN; 2), and WinBUGS (PKBugs; 3,4), for example. A variety of post-processing tools to summarize and plot modeling results and perform extended model diagnostics are available for NONMEM® (5,6), Monolix (2), and the USC-PACK (7,8), for example.

The S-ADAPT package (9) provides essentially all relevant parametric nonlinear mixed-effects modeling algorithms, including gradient search methods such as the first-order conditional estimation method (FOCE) and the Laplace method, as well as the Monte Carlo Parametric Expectation Maximization (MC-PEM), Stochastic Approximation EM (SAEM), and Markov Chain Monte Carlo (MCMC) algorithm. While S-ADAPT provides a large variety of estimation options for these algorithms, it offers limited pre- and post-processing capabilities. To better enable scientists to develop mechanistic models via nonlinear mixed-effects modeling, we identified the following pre- and post-processing steps as critical to improve the modeling process: (1) efficient, free software tools to translate model code into Fortran and to debug model code and raw datasets, (2) automated methods to improve numerical stability of Fortran code, and (3) automated post-processing tools to generate summary tables and diagnostic plots for one or multiple models.

Our first objective was to develop a state-of-the-art translator and debugger (SADAPT-TRAN)1 for model code and raw datasets that are translated into Fortran. This translator should automatically implement an extended set of parameter settings in the Fortran code to allow efficient customization of the MC-PEM algorithm in S-ADAPT. As second objective, we developed a fully automated post-processor for preparation of single and multiple model summary tables and diagnostic plots. This paper focuses on S-ADAPT as a powerful, highly customizable, free, and open-source package for nonlinear mixed-effects modeling.

MATERIALS AND METHODS

We carefully observed and analyzed the difficulties and inefficiencies faced by students and scientists with diverse backgrounds and the full range of experience levels in nonlinear mixed-effects modeling over several years to identify critical steps which benefit from support by automation and debugging.

Design and Functionality of SADAPT-TRAN

Data Flow

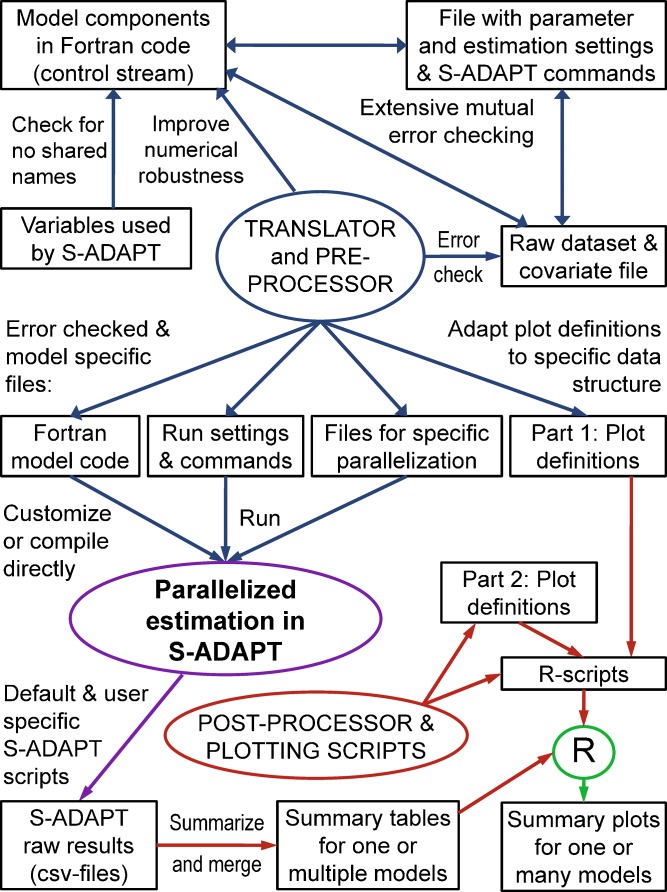
Figure 1 shows the interactions between the new SADAPT-TRAN Perl scripts, S-ADAPT (including a Fortran compiler), and R. The user has to provide the core model components as simplified Fortran code and a csv file with initial parameter estimates, covariate names, and commands for the estimation algorithm (“parameter settings file”). The processes shown in Fig. 1 can be invoked individually as well as in the aggregate using single SADAPT-TRAN commands. The new Perl scripts were developed to perform extensive, mutual error checks between all input files. Variable names used in a model are compared to the reserved variable names used by S-ADAPT to assure no overlap. The consistency of all variable names is checked within each file and within the raw dataset. Based on the guidance from the error messages provided by SADAPT-TRAN, beginners with no or very little experience in nonlinear mixed-effects modeling could (semi-)independently build and debug raw datasets and model code by adapting control streams and parameter settings files from templates. This knowledge could be conveyed to beginners within a 1.5-day workshop.

Fig. 1.

Flowchart for model code, raw data, results, and plots as implemented in the translator, pre-processor, and post-processor scripts of SADAPT-TRAN that interact with S-ADAPT for nonlinear mixed-effects modeling and R for plotting. Programs and scripts are shown in circles, data files as boxes, and error checks or operations as arrows. Blue arrows denote operations by the SADAPT-TRAN translator and pre-processor, purple arrow denotes operations by S-ADAPT, dark red arrows denote operations by the post-processor and plotting scripts, and the green arrow refers to R

The SADAPT-TRAN pre-processor checks for every variable on the right side of an equal sign whether this variable is a specified model parameter or covariate, a global variable defined in an appropriate subroutine, or a previously defined variable within the same subroutine. The pre-processor accounts for the hierarchy of subroutines and (global) variables. It seeks to prevent errors that are due to the inappropriate use of variables that change continuously over time (such as plasma concentration). This check is performed in all subroutines that are reserved for time-independent variables.

Numerical Consistency

The MC-PEM algorithm integrates over a wide parameter range to approximate the true log-likelihood. This requires numerically robust Fortran code due to evaluation of extreme parameter values. Extremely low values for clearance, for example, can cause negligible concentrations that may ultimately lead to failure of the differential equation solver.

Numerically stable Fortran code tends to be even more important for the EM algorithm than for gradient search methods, as extreme parameter values are sometimes evaluated during the first iterations of covariate effect estimation by the EM algorithm. The SADAPT-TRAN package offers several methods to optimize code: (1) automatic translation of user code into double precision format (i.e., converting numbers into double precision format, use of DEXP instead of EXP, and of DLOG instead of LOG), (2) automated limitation of arguments to the DEXP and DLOG function, (3) automated tests against extremely small variances for residual error and between subject variability (BSV), (4) user settings to set limits for random model parameters (P type in S-ADAPT) and covariate effect modified parameters (PC-type) either during all or only during the first n iterations, and (5) user prompts due to potentially unstable code such as a concentration raised to the power of a Hill coefficient.

The functionalities for code optimization included in the SADAPT-TRAN package can be readily extended with increasing user experience and be made available to the user community. To improve the availability of diagnostic data during estimation, the SADAPT-TRAN package generates model specific Fortran code to print the parameter names along with their means and coefficients of variation (or standard deviations) on the screen at the end of each iteration. These parameters are printed before parameter means (set to 1) or variances (averaged over occasions) are potentially modified to estimate between occasion variability (BOV), for example. This allows users to check the assumptions of the BOV estimation and to identify certain problems during the estimation.

Parallelized Estimation

The SADAPT-TRAN package uses the parallelized implementation of the MC-PEM algorithm in S-ADAPT to accelerate estimation times. The maximum efficiency of the parallelization increases with the number of subjects, network speed, and with model complexity.

Fully Automated Diagnostic Plots

The SADAPT-TRAN package identifies and stores the structure of the raw data, covariates, and model parameters in the first plot definition file (Fig. 1). This information supports subsequent generation of summary tables and plots. The second plot definition file is prepared while summarizing the S-ADAPT results tables that are saved as csv files from the S-ADAPT table system.

To support rapid identification of covariate effects, the SADAPT-TRAN package categorizes each covariate into a default value of six categories, if there are more than six unique levels of a covariate. Continuous covariate plots are additionally provided. Standard diagnostic plots and normalized prediction distribution errors (available in S-ADAPT version 1.57) with different symbols for data points belonging to specific covariate levels are automatically generated. The user may customize the default axis labels, units, color scheme, and various other plotting options based on a plot settings text file that can be copied and re-used throughout the current project. Knowledge of R code by the user is not required, but will allow further customization of the R scripts.

To support plotting of fitted profiles vs. time for sparse data, SADAPT-TRAN can optionally utilize the S-ADAPT feature to provide 1,000 simulated predictions per patient and dependent variable. These predictions are summarized in a csv file for plotting.

Structure of Variance–Covariance Matrix

The structure of the variance–covariance (var–cov) matrix can be specified as major diagonal, block diagonal, or full matrix. Future versions will implement banded diagonal matrices. Outside SADAPT-TRAN these specifications require extensive and error-prone Fortran coding.

Parameter Variability Model

The default transformations available in SADAPT-TRAN are the log-normal, normal, and logistic transformations (with user-defined limits). The specified transformations are implemented in the Fortran code without further user input and any combination of transformations can be chosen for model parameters. The user may specify customized transformations in the Fortran code by editing two lines per parameter. The summary results and plots for logistically transformed parameters are provided both on transformed and untransformed scale to accelerate interpretation and communication of model results.

Between Occasion Variability

Coding BOV in raw Fortran code is cumbersome and error-prone. We implemented an automated feature in SADAPT-TRAN that generates Fortran code to specify BOV for any combination of model parameters. The user has to specify the maximum number of occasions, name of the variable defining an occasion, and initial variance for each BOV term. The BOV feature recognizes logistically transformed parameters and specifies BOV on the transformed scale. Models with different numbers of occasions in different subjects can be coded in SADAPT-TRAN, if the user specifies the maximum number of occasions in the dataset as number of occasions in the parameter settings file.

Extended Settings to Customize the MC-PEM Algorithm

Updating of population means and of the var–cov matrix via the MC-PEM algorithm from one iteration to the next requires calculation of conditional means and conditional var–cov matrices from each subject. Therefore, a population mean parameter can only be optimized (“moved”) during the estimation, if it has an associated BSV. In NONMEM® terms, this means one has to estimate an “OMEGA” for every “THETA” (except for THETAs for covariate effects). Covariate effect parameters are updated at the end of each MC-PEM iteration in a separate step in S-ADAPT.

Variance Burn Feature to Prevent Convergence to Local Minima

The MC-PEM algorithm usually converges rapidly and shrinks variances quickly (often within five to ten iterations) from a large initial variance to the final variance estimate. The search space of the MC-PEM algorithm depends on the size of these variances, and population means for a parameter with small variance can only move slowly, i.e., only a short distance per iteration, compared to parameters with a large variance. Consequently, the MC-PEM algorithm may converge towards a local minimum, if variances are reduced too rapidly.

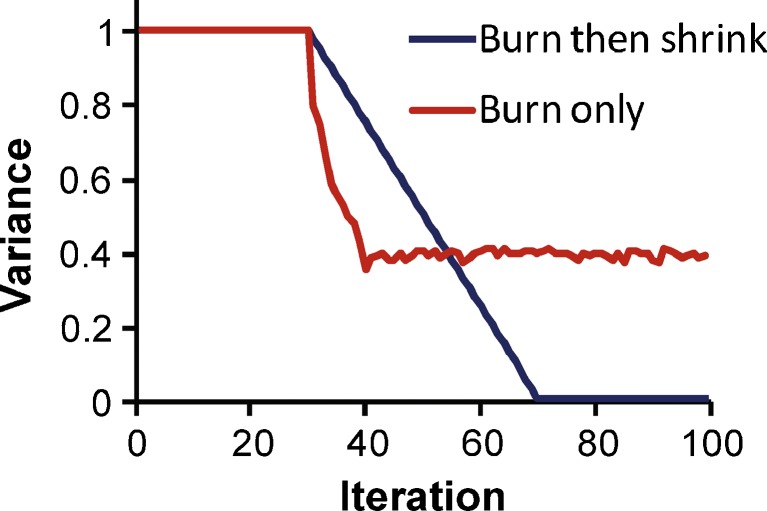
The variance burn feature automatically generates the Fortran code to modify the variances at the end of each of the first 30 iterations, for example. Thereby the variances are kept artificially large and constant (e.g., at a %CV of 100% or 200% for a log-normally distributed parameter, Fig. 2) during a specified number of iterations. This Fortran code is automatically included in the POPFINAL subroutine where the S-ADAPT package offers access to the estimated population means and to the elements of the var–cov matrix at the end of each iteration. The variance burn phase allows the user to obtain a global view on the parameter estimates with a large search space for all (or for specific) parameters. This is primarily intended to improve the population mean estimates and to prevent convergence to local minima. If the variance of a parameter is modified in such a way, SADAPT-TRAN automatically provides the Fortran code to set all covariances for this parameter to zero for the respective iteration. This prevents crashes of the estimator due to non-positive semi-definite var–cov matrices.

Fig. 2.

Application of a variance burn phase to prevent convergence of the MC-PEM algorithm to a local minimum and of a variance burn then shrink phase to estimate a population mean with small or negligible final variance

The variance burn phase is in part comparable to a burn-in phase in a Bayesian Markov chain Monte Carlo analysis. The parameter estimates directly at the end of the variance burn phase in S-ADAPT (Fig. 2) are however not assumed to be the final solution, since the variances are still manually specified at that point. After the end of the variance burn phase, the estimates for the between subject variances are optimized by the MC-PEM algorithm.

In addition, the S-ADAPT package provides extended functionality to choose the type (dfran setting) and adapt the width of the envelope function (gefficiency, gamma_min, and gamma_max) that is used for sampling. This S-ADAPT functionality is fully available in SADAPT-TRAN.

Variance Burn then Shrink Phase

An extended version of the variance burn feature can be applied to estimate a population mean with negligible variability. During the first 30 iterations, for example, variance is kept large to allow the population mean to move quickly (Fig. 2). During the subsequent variance shrinking phase, the variance is gradually shrunk from its initial to its final value over 40 iterations (iterations 31 to 70, Fig. 2), for example. Then the variance is fixed to a small final value for subsequent iterations. A final variance of 0.0225 (15% CV) or 0.01 (10% CV) will allow the population mean to move in response to other model parameters changing after iteration 70 (Fig. 2). A final variance of 0.0001 or smaller essentially prevents a population mean from moving.

Parameters with Fixed Mean and Estimated Variance

We implemented a feature in SADAPT-TRAN which allows the user to fix a population mean either during all iterations or during the first n iterations, but to estimate the associated BSV. This feature may be used to estimate between subject variability for extent of bioavailability of an oral dose under the assumption that the mean F is fixed to a known value or to one.

RESULTS

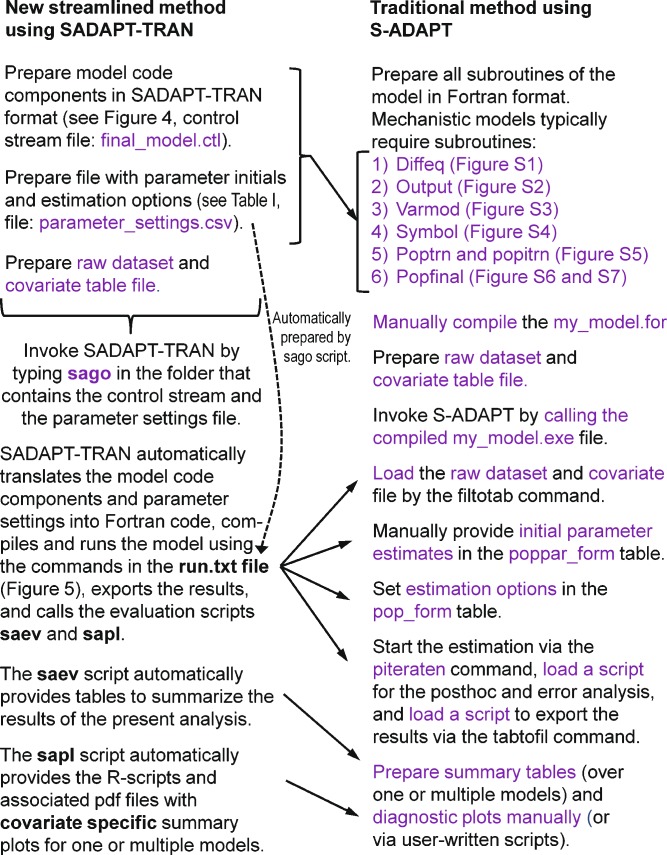
The translator and extensive bi-directional error checking capabilities of the model definition, parameter settings, and raw data files (Fig. 1) by SADAPT-TRAN greatly reduced model specification and Fortran coding errors. A population PK/PD modeling analysis using the streamlined SADAPT-TRAN process (Fig. 3) requires specification of the control stream (Fig. 4) and the parameter settings file (Table I) and preparation of the raw dataset and covariate table file (if applicable). All subsequent processes in Fig. 3 are invoked automatically by the sago command in the SADAPT-TRAN package. The respective counterparts of a traditional population PK/PD analysis in S-ADAPT are shown on the right side of Fig. 3. The run.txt file is prepared by the sago script and contains all the commands that need to be entered manually or by a user-written text file in the traditional S-ADAPT analysis. After exporting the results as csv files from the S-ADAPT system, the sago script automatically launches the saev (evaluation script creating summary tables) and the sapl script creating covariate specific diagnostic plots. The saev and sapl scripts can either summarize the results of one or of multiple models. These scripts have been applied successfully to summarize up to 1,000 models simultaneously.

Fig. 3.

Steps of a population PK/PD modeling analysis using the streamlined procedure with SADAPT-TRAN compared to the traditional procedure in S-ADAPT. The text in purple describes steps that require user input

Fig. 4.

Complete model code in SADAPT-TRAN format for a one compartment PK model with zero-order infusion [R(1)] combined with indirect response model I

Table I.

Parameter Settings File to Specify the Parameter Initials and Parameter Settings, Covariate Names, Estimation Options, and Estimation Commands

#PNAME	PMEAN	PCOV	PTYPE	PBLOCK	PTRANSF	PLOW	PHIGH	VARINI	VARBURN	VARNIT	VARIT	PBOUNDL	PBOUNDH
CL	5	1	P	1	L			1	30
V1	30	1	P	1	L			1	30
Tout12	10	1	P	2	L			1	30
Imax	0.7	4	P	2	O	0	1	4	30
BASE	15	1	P	2	L			1	30
IC50	10	1	P	2	L			1	30
HILL	1	1	P	2	L			1	30	0.01	40	0.1	20
SDin	1	.	V
SDsl	1	.	V
PDin	1	.	V
PDsl	1	.	V
COVARIATES
RUN_SETTINGS
NFILE	1CMT_PK_with_IDR_1
VERS	1
mdelete <NFILE>_*
DATAFILE	../Data/SA_Example_03_PKPD.csv
COVFILE	../Data/Covariates.csv
BEOFILE	beo.txt
NPOPITER	150
GEFFICIENCY	0.6
PMETHOD	4
NPOP	100
NPOPC	1000
NDELPAR	15
ATOL	5
RTOL	5
gamma_min	0.05
gamma_max	20
beosetup
RUN_COMMANDS
piteraten
?finish.txt
stop

COVARIATES None for this model. External scripts like the commands in the finish.txt file can be included via a “?” sign

PNAME parameter name, PMEAN initial mean, PCOV initial variance, PTYPE parameter type (P = mean with variability, V = residual error parameter), PBLOCK number of block in the variance covariance matrix, PTRANSF parameter transformation type (L = log-normal, O = logistic, N = normal), PLOW lower bound of logistically transformed variable (default = 0), upper bound of logistically transformed variable (default = 1), VARINI initial variance during the variance burn phase, VARBURN number of iterations of the variance burn phase, VARNIT variance after the variance shrink phase, VARIT number of steps in the variance shrink phase, PBOUNDL lower bound for the individual values of a P type parameter, PBOUNDH upper bound for the individual values of a P type parameter, RUN_SETTINGS estimation settings that are called once at the beginning of the estimation (please see S-ADAPT manual for explanation of variables), RUN_COMMANDS sequence of commands to be executed by the S-ADAPT command window

We present an example below including the steps required to specify a population PK/PD model and perform a population PK/PD analysis. A one compartment PK model with zero-order input combined with indirect response model 1 in SADAPT-TRAN is used as example, since this model is relatively simple and still illustrates most of the capabilities and benefits of SADAPT-TRAN. An SADAPT-TRAN model is defined by two files, the model control stream (Fig. 4; a ctl file) and a parameter settings table (Table I; a csv file). Figure 4 shows the complete model code to specify this model in SADAPT-TRAN format. Table I contains the initial parameter values, covariate names (none for this model), estimation options (RUN_SETTINGS), and estimation commands (RUN_COMMANDS).

The code components in the ctl file are split into different blocks that get translated into specific sections of subroutines according to the template.for Fortran file that resides in the SADAPT_TRAN_FOOTPRINT subfolder. Typically, a mechanistic model contains the following components: differential equations (DIFFEQ subroutine), initial conditions and output equations (OUTPUT subroutine), covariate effect relationships (POPMOD subroutine; not present in this example), residual error model (VARMOD subroutine), and code to customize the MC-PEM algorithm (POPFINAL subroutine). These and other subroutines are summarized below. The SADAPT-TRAN package defines all these subroutines fully automatically based on the control stream and the parameter settings file (i.e., Fig. 4 and Table I get translated into Figs. S1 to S7).

DIFFEQ Subroutine

The differential equation block ($DIFFEQ_DIF, supplement Fig. S1) defines the core components of this model, including the equation for the drug concentration in the central compartment (DC1) that determines the inhibition term (INH):

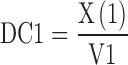1

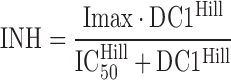2

The Imax is the maximum extent of inhibition, IC₅₀ is the drug concentration causing 50% of Imax, and Hill is the Hill coefficient. The INH term is subject to an if-condition in the model code (Fig. 3) to improve numerical robustness, since drug concentrations may become a very small negative number (e.g., −1E-300) at late times due to rounding errors. The SADAPT-TRAN package would return an error message, in case this if-condition was missing. The differential equations for the amount of drug in the central compartment [X(1)] and for the PD response [X(2)] are:

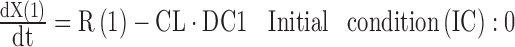3

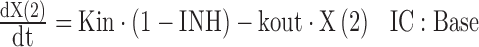4

The R(1) defines the time-delimited zero-order infusion rate, CL drug clearance, Kin the zero-order input rate of response, and kout the first-order loss rate constant for the response. Base is the baseline response. The SADAPT-TRAN package converts the code in the $DIFFEQ_DIF block into double precision format and supplements the code by the double precision variable definition statements and the common blocks at the beginning of the DIFFEQ subroutine in S-ADAPT format (Fig. S1).

OUTPUT Subroutine

The OUTPUT subroutine (Fig. S2) includes three main components: a definition of global variables ($OUTPUT_GLB), initial conditions ($OUTPUT_ICS, the default initial condition is zero), and output equation(s) ($OUTPUT_EQN). These three components are combined and translated into the OUTPUT subroutine (Fig. S2). The SADAPT-TRAN package assigns the parameter names to the correct element of the P vector and makes these model parameters available as global variables in a common block. After this definition, the logistic transformation equation for Imax is included. While the variable Tr_Imax is on transformed scale and can range from minus infinity to plus infinity, the Imax variable takes values between 0 and 1. Then the global variables kout and kin are defined and made available in a common block.

The SADAPT-TRAN package automatically implements limits for the argument of an EXP function (maximum argument value of 40) and of the LOG function (minimum argument value 1E-15) to improve the numerical stability of the code. The EXP function is automatically converted to a DEXP function and the LOG function to DLOG. The remainder of the OUTPUT subroutine specifies the initial condition for X(2) as well as the output equations.

VARMOD Subroutine

The varmod equation block ($VARMOD_EQN, Fig. 4) defines the residual error models for each dependent variable. This code gets translated into the VARMOD subroutine (Fig. S3) by SADAPT-TRAN.

SYMBOL, POPTRN, and POPITRN Subroutines

The SYMBOL subroutine (Fig. S4) defines the parameter symbols. The POPTRN and POPITRN subroutines define the forward and reverse transformation of parameters (Fig. S5). Parameters 1 to 3 and 5 to 7 are log-normally distributed, parameter 4 (Tr_Imax) is normally distributed on transformed scale, and parameters 8 to 11 are residual error parameters. In S-ADAPT, these subroutines have to be specified by the user, whereas SADAPT-TRAN automatically generates the Fortran code for these three subroutines based on the parameter settings file.

POPFINAL Subroutine

The POPFINAL subroutine is generated automatically by SADAPT-TRAN based on information in the parameter settings file. Parts of this subroutine are shown in Fig. S6. The initial code (Fig. S6, part A) creates a printout of parameter values on the screen during each iteration. The subsequent code defines a variance burn phase over the first 30 iterations for parameter CL and a variance burn then shrink phase for the Hill coefficient over 30 (burn) + 40 (shrink) iterations. The last part of the code defines the structure of the var–cov matrix for CL.

The present model contains no model parameter with BOV. In order to enable inclusion of BOV for one or multiple model parameters (which may be specified in the parameter settings file), the SADAPT-TRAN package automatically provides the associated Fortran code to specify BOV in the POPFINAL subroutine as shown in Fig. S7.

Estimation Options, Estimation Commands, and Parallelization

The SADAPT-TRAN package translates the initial parameter estimates, estimation options, and estimation commands (Table I) into the run.txt file (Figure 5). The commands in this file load the raw dataset and the covariate file (if present) into S-ADAPT, set the initial parameter estimates and estimation options, initialize the Beowulf cluster for parallelized estimation (via file beo.txt), start the estimation by the piteraten command, perform the post hoc and error analysis, and export the results as csv files by the finish.txt script. In a traditional S-ADAPT analysis, a user can define this sequence of commands in a text file and include it in the S-ADAPT analysis. However, significant manual editing is required to define such a file. The SADAPT-TRAN package generates this file automatically. Figure 6 shows the contents of the finish.txt and Figure 7 lists the commands in the beo.txt file and the content of the first four lines of the beo table file for parallelization on a single computer.

Fig. 5.

Command file (run.txt) to define the run-name (NFILE), delete all preexisting files, load the raw dataset and the covariate file, set the estimation options, initialize the Beowulf cluster for parallelized estimation, define the initial means, initial variances and parameter types, and include the estimation commands

Fig. 6.

Command file (finish.txt) for calculation of standard errors, population predictions, individual prediction (post hoc analysis), correlations, and export of results

Fig. 7.

Command file (beo.txt) for setting up a parallelized analysis using the Beowulf system and content of the first four lines of the beo table (beo.csv file)

Summary Tables and Plots

The SADAPT-TRAN package automatically provides tables with parameter values for one or multiple models rounded to three (default) significant figures. Additional tables with the individual parameter values from the post hoc analysis as well as the conditional means and conditional var–cov matrix for each subject are provided. These tables contain logistically transformed parameters such as Imax both on transformed and on untransformed scale. One summary table contains the population means, square root of the estimated variances, and the most extreme correlation in the var–cov matrix. Another summary table contains the estimated parameter values, their standard errors, and the most extreme correlations from the uncertainty matrix (varc Table in S-ADAPT).

Summary plots are automatically generated by SADAPT-TRAN for all dependent variables. The plotting script (sapl) recognizes the model specific covariates provided in the covariate table and in the dataset and provides the diagnostic plots listed in Table II both with and without stratification for covariates. The user can specify the names and units of the dependent variables and customize various other settings for the diagnostic plots via a text file that is read by the sago script. Importantly, with S-ADAPT 1.57, the WRES plot contains the normalized prediction distribution errors (NPDE) that are plotted with or without stratification by covariates. The automated NPDE plot is very useful to assess the predictive performance of a model in general and specifically for different values of covariates.

Table II.

Summary of Plots (Generated via R scripts) Automatically Provided for One or Multiple Models by SADAPT-TRAN as pdf Files

No.	File name	Description
1	ITER_Convergence_plots.pdf	Convergence plots for the objective function, population means, variances, and covariances for all iterations.
2	ITER_Convergence_plots_final.pdf	Same as (1) for iteration 31 (customizable) to the last iteration.
3	DV_vs_IPRED__or__PRED.pdf a	Observations vs. individual or population fits on linear–linear or on log–log scale for all dependent variables
4	Individual_Fit_Plots_Multiple_Models.pdf	Multi-panel plot for the individual curve fits and observations plotted vs. time. Plots are provided on linear and semi-logarithmic scale for the full time course and for the first 6 h (customizable).
5	Population_Fit_Plots_Multiple_Models.pdf	Same as (4) with population fits instead of individual fits.
6	Individual_Fit_Plots_Multiple_Models__DVID_top_bottom.pdf	Multi-panel plot for the individual curve fits and observations plotted vs. time: for each subject, all dependent variables are plotted from top to bottom on the same time scale.
7	HOC_Continuous_covariate_plots.pdf	Multi-panel scatterplot for parameter values plotted vs. continuous covariate values (one covariate at a time).
8	HOC_Categorical_covariate_plots.pdf	Multi-panel notched box plot for parameter values plotted vs. categorical covariate values (default: six categories). Continuous covariates are categorized by default into six groups.
9	WRES_plots.pdf a	Weighted residuals plotted vs. time or vs. the values of the respective dependent variable. For S-ADAPT version 1.57, these plots can be customized to contain the normalized prediction distribution errors (NPDE).
10	iWRES_plots.pdf a	Individual weighted residuals plotted vs. time or vs. the values of the respective dependent variable

^aIf covariates are present, this plot is provided also as a multi-panel figure with each level of a categorical or categorized covariate representing one panel. Additionally, this plot is provided as a single panel figure with different symbols for each level of a categorical or categorized covariate. No user input is required to generate these covariate-stratified plots

DISCUSSION

The S-ADAPT package presents a powerful tool for parametric population PK/PD modeling, provides essentially every relevant parametric algorithm for nonlinear mixed-effects modeling, and allows the user to specify a large variety of estimation options. Models can contain both continuous and categorical data for estimation and simulation in S-ADAPT as described for non-normally distributed observations in the S-ADAPT manual. However, S-ADAPT provides limited pre- and post-processing capabilities.

We recognized a unique chance to build a translator, debugger, and fully automated post-processor for S-ADAPT to benefit both teaching and research purposes. This benefit is greatest for mechanistic models that may contain 20 and more random model parameters (10–27), as the likelihood for model specification errors increases with model complexity. The bi-directional and hierarchical error checks of the SADAPT-TRAN pre-processor (Fig. 1) supported development and debugging of (large) mechanistic models and datasets. Additionally, on-the-fly availability of the current parameter estimates at the end of each iteration (created by the Fortran code in Fig. S6, part A) allows immediate identification of some estimation problems.

During the SADAPT-TRAN project, it became clear that the pre- and post-processor scripts interact synergistically. The pre-processor (sago script) and the first post-processor (saev script) provide helpful information on the parameter names and types, covariate names, and the structure of the dataset that is used to customize the plots created by the second post-processor (sapl script). Therefore, it was beneficial to develop the entire SADAPT-TRAN package. Users of traditional S-ADAPT may choose to only use the SADAPT-TRAN pre-processor without the post-processor.

This package does not restrict the functionality of S-ADAPT and can be applied to a large variety of estimation methods available in S-ADAPT (9). The user can incorporate user-defined Fortran subroutines. While the present version of SADAPT-TRAN applies to S-ADAPT, the SADAPT-TRAN functionality (Figs. 1 and 3) can be readily extended to other packages for nonlinear mixed-effects modeling.

By default, SADAPT-TRAN provides the objective function of the last iteration as well as the average objective function during the last ten iterations. If one wishes to improve the quality of the approximation of the objective function, the user may specify a large number of Monte Carlo samples during the last 15 iterations, for example. This can be specified by use of the piterater command (see S-ADAPT manual; 9) in the run commands section of the parameter settings file (Table I). In this section, the user can specify any sequence of commands and include user-written S-ADAPT scripts. This may include changes to the estimation algorithm and switches between different estimation algorithms. The user could, for example, export the results from different estimation methods using different version numbers of the S-ADAPT analysis.

With the availability of EM algorithms, it became apparent that parameter specific customization of the estimation allows the user to enhance the flexibility of EM algorithms. Estimation packages such as NONMEM® only allow the user to specify a lower bound, initial estimate, and upper bound for a parameter. While these three arguments are reasonably packaged in a text file, we chose to specify parameter specific arguments in a table (csv file) in SADAPT-TRAN, since there are currently up to 22 arguments (Table I) to be stored for each parameter in SADAPT-TRAN. We anticipate that it will be beneficial to define these arguments specifically for each parameter or for groups of parameters (e.g., for PK and PD parameters). This number of arguments will increase, as future SADAPT-TRAN versions will allow specifying hyper-prior information for three-stage hierarchical analyses with prior information in S-ADAPT.

Among the extended features in SADAPT-TRAN are the abilities (a) to fix a population mean for all or for the first n iterations, (b) to estimate a population mean with negligible variance, and (c) to implement a variance burn phase with large and constant variances during the first 30 iterations, for example. While the logic behind the implementation of these features in Fortran code is straightforward, specifying these features or defining BOV requires approximately 0.5 to 1 pages of Fortran code per parameter and feature. Defining the correct indices for parameter numbers to implement these features is an error-prone process, if it is coded manually. The SADAPT-TRAN package releases the user from this burden.

The ability to fix a population mean during the first n iterations may be particularly helpful, if one estimates a PK/PD model and has reasonable prior guesses on the PK parameters, but limited information on PD parameter estimates. In this case, one may wish to fix the population means of the PK parameters during the first n iterations before estimating all parameters simultaneously. It may also be beneficial to fix a Hill coefficient during the first 30 iterations, for example, and let this parameter float after iteration 30. In our experience, an EM algorithm may have difficulties estimating a Hill coefficient, if this parameter moved to extreme values above ten, for example, during the first 20 iterations, while the estimator is making coarse jumps of the other parameter values. Finally, users may wish to fix the mean apparent bioavailability after an oral dose to one and estimate the BSV of extent of bioavailability.

The MC-PEM algorithm requires variability of model parameters to update their population mean. Therefore, such variability has to be included for a model parameter at least during some iterations of the estimation. To estimate population means with no (or negligible) BSV, the variance burn then shrink feature was implemented specifically for each parameter in SADAPT-TRAN. The proposed variance burn and variance burn then shrink capabilities of SADAPT-TRAN were inspired by the simulated annealing work presented by Chee Ng (American Conference on Pharmacometrics, Mashantucket, CT, 2009) and also by the recommendations on estimating parameter means with negligible variances described in the S-ADAPT (9) and Monolix (2) manuals. The variance burn then shrink feature can be implemented in SADAPT-TRAN with a linearly decreasing variance (Fig. 2) for any combination of parameters and iterations. We prefer keeping a small variance (e.g., 10% or 15% CV) after the shrink phase to allow the population mean to continue to move, if needed (Fig. 2). In our experience, this is a useful function to estimate a population mean with negligible BSV using the MC-PEM algorithm. More systematic studies would be beneficial to optimize the variance shrink conditions.

The S-ADAPT package provides advanced internal functionality to adjust the width of the envelope function that is used to draw random samples for Monte Carlo integration. As described by Chee Ng (American Conference on Pharmacometrics, Mashantucket, CT, 2009), the MC-PEM algorithm tends to shrink variances rather rapidly during the first iterations. This may result in convergence to local minima, since the search space of the MC-PEM algorithm depends on the size of the BSV. Therefore, a simple additional procedure was implemented to manually fix the BSV at large values during the first n iterations (Fig. 2). We empirically found that a variance burn phase with 30 to 40 iterations provides a good compromise between improving initial parameter means and not overly prolonging the total estimation time. If a user has already good initial estimates for a model, it may be helpful to estimate the model with and without a variance burn phase, since overly large variances (100% CV and more) during the first iterations may entail large jumps of population means during the variance burn phase. Overall, the variance burn phase is meant to provide a global initial view on the parameter estimates and improve the initial population means. This phase is followed by a refined search by the importance sampling version of the MC-PEM algorithm.

CONCLUSIONS

The pre- and post-processing and debugging capabilities of the SADAPT-TRAN package greatly facilitated model building and evaluation in S-ADAPT for beginners and experts. For a basic mechanistic model, the new streamlined process in SADAPT-TRAN required 17 lines of model equations (Fig. 4), 11 lines for model parameters, three project specific settings in the parameter settings file (Table I), and a single command to launch SADAPT-TRAN, run the population PK/PD analysis, and prepare summary tables and plots. In a traditional S-ADAPT analysis, the same process would have required the user to provide about ten pages of model specific Fortran code and estimation commands (Figs. S1–S6 and Figs. 5–7) and manually prepare the summary tables and diagnostic plots. The SADAPT-TRAN package provides functionality to customize the MC-PEM algorithm for specific or all model parameters, avoid local minima, estimate population means with negligible BSV, or estimate a BSV for a fixed population mean. This package holds great promise to make the powerful capabilities of parallelized nonlinear mixed-effects modeling in S-ADAPT efficiently available to a broader user community as a free, open-source research and teaching tool.

Electronic Supplementary Materials

Below is the link to the electronic supplementary material.