Prediction-Corrected Visual Predictive Checks for Diagnosing Nonlinear Mixed-Effects Models

Abstract

Informative diagnostic tools are vital to the development of useful mixed-effects models. The Visual Predictive Check (VPC) is a popular tool for evaluating the performance of population PK and PKPD models. Ideally, a VPC will diagnose both the fixed and random effects in a mixed-effects model. In many cases, this can be done by comparing different percentiles of the observed data to percentiles of simulated data, generally grouped together within bins of an independent variable. However, the diagnostic value of a VPC can be hampered by binning across a large variability in dose and/or influential covariates. VPCs can also be misleading if applied to data following adaptive designs such as dose adjustments. The prediction-corrected VPC (pcVPC) offers a solution to these problems while retaining the visual interpretation of the traditional VPC. In a pcVPC, the variability coming from binning across independent variables is removed by normalizing the observed and simulated dependent variable based on the typical population prediction for the median independent variable in the bin. The principal benefit with the pcVPC has been explored by application to both simulated and real examples of PK and PKPD models. The investigated examples demonstrate that pcVPCs have an enhanced ability to diagnose model misspecification especially with respect to random effects models in a range of situations. The pcVPC was in contrast to traditional VPCs shown to be readily applicable to data from studies with a priori and/or a posteriori dose adaptations.

Electronic supplementary material

The online version of this article (doi:10.1208/s12248-011-9255-z) contains supplementary material, which is available to authorized users.

INTRODUCTION

Population pharmacokinetic (PK) and pharmacodynamic (PD) models are used increasingly in pharmaceutical research (1). In order to generate reliable conclusions and predictions, good diagnostic tools to evaluate the predictive performance of the models are vital (2). There are many kinds of diagnostic tools applicable to mixed-effects models (2). Since the mid-90s, simulation-based diagnostic principles have grown in popularity (3), and an especially popular diagnostic tool is the so-called Visual Predictive Check (VPC; 4–6). The popularity of VPCs can be attributed to two main advantages of the approach: [1] the principle behind the diagnostic is simple and easily communicated to both modelers and other modeling stakeholders, and [2] by the retention of the original time-course profile and the y-axis units, the VPC graphs are illustrated on a relevant and easily appreciated scale which can be powerful in guiding the modeler to the origin of a potential model misspecification.

The principle of the VPC is to assess graphically whether simulations from a model of interest are able to reproduce both the central trend and variability in the observed data, when plotted versus an independent variable (typically time). A VPC is based on multiple simulations with the model of interest and the design structure of the observed data (i.e., dosing, timing, and number of samples). Percentiles of the simulated data are compared to the corresponding percentiles of the observed data. The percentiles are calculated either for each unique value of the independent (x-axis) variable or for a bin across the independent variable. Typically, the median and 2.5th and 97.5th percentiles are presented. The interpercentile range between the outer percentiles of all the simulated data is often referred to as a prediction interval. Different widths of the prediction intervals can be assessed depending on the objective and the sample size of the original data (e.g., 5th to 95th percentile ⇒ 90% interpercentile range). The fact that VPCs are created by simulations of a large number of replicates of the original dataset design can be utilized to improve the interpretability of the VPC. By calculating the percentiles of interest for each of the simulated replicates of the original dataset design, a nonparametric confidence interval can be generated for the predicted percentiles (5). The size of the confidence intervals acts as a reference to better judge what is likely to be a true deviation between observations and model predictions. This is thought to make the interpretation of VPCs less subjective.

Ideally, a VPC will diagnose both the fixed and random effects in a mixed-effects model. In many cases, this can be done by comparing different percentiles of the observed data to percentiles of simulated data. Whenever the predictions within a bin differ largely due to different values of other independent variables (e.g., dose, covariates), the diagnosis may be hampered or misleading. In such cases, only a part of the variability observed in a traditional VPC will be caused by the random effects. Apart from making it difficult to use these VPCs to diagnose the random effects, this can also lower the power of detecting a model misspecification in the structural model. When a priori or a posteriori dose adaptation has been performed to achieve a certain target concentration, a traditional VPC can be completely uninformative. These shortcomings of the traditional VPCs have been highlighted before (5,7,8). Prediction-corrected VPC (pcVPC) offers a solution to these problems while retaining the visual interpretation of the traditional VPC.

In a pcVPC, the variability coming from variations in independent variables within a single bin is removed by normalizing the observed and simulated dependent variable based on the typical population prediction. In a very simple case of linear pharmacokinetics, with a fixed sampling schedule that is identical for all subjects and a model without any covariate relationships, this would be equivalent to performing a VPC based on dose-normalized plasma concentrations. However, many mixed-effects models are far more complicated, and prediction correction offers a general solution to the problem. In addition, normalization may be done with respect to the typical population prediction as well as to the typical population variability, accounting for different expected variability within individuals within one independent variable bin of a VPC. This is the basis for a prediction- and variability-corrected VPC (pvcVPC).

This manuscript primarily aims to introduce the concept of prediction and variability correction in VPCs and highlight situations when a pcVPC and/or a pvcVPC could add significant diagnostic value over a traditional VPC.

MATERIALS AND METHODS

VPC

In this work, VPCs were constructed based on 1,000 simulated replicates of the original dataset design. Binning on the independent variable was in the cases of a fixed sampling design carried out such that there was a single bin for each protocol time point (Example 1, 2, and 5). In the cases of data with variability in sampling times between subjects, sampling schedule binning was performed to maintain approximately the same amount of observations in each bin. Statistics were calculated in the same manner for the observed and all simulated datasets. For each dataset and in each bin, the median-dependent variable (DV) value was calculated. Out of the 1,000 median values for each bin originating from the model simulations, a nonparametric 95% confidence interval was calculated (the 2.5th and 97.5th percentile). Similar to the median, other percentiles of the data were presented with an observed value and a 95% confidence interval based on the simulated datasets. The percentile presented in each example was dependent on the size of the original dataset. Typically, the 2.5th and 97.5th percentiles of the datasets were depicted, corresponding to a 95% prediction interval, but in examples with fewer observations (Example 1, 3, and 4), a 90% interpercentile range (5th and 95th percentiles) was instead utilized. In the case of binning across more than a single unique value for the independent variable (x-variable), the width of each bin was made obvious in the graphs by the width of the square-formed confidence intervals.

pcVPC

pcVPCs differ from traditional VPCs in that the dependent variable has been subject to prediction correction before the statistics are calculated. Prediction correction aims to correct for the differences within a bin coming from independent variables (time, dose, and other covariate values) in the model and hence more clearly diagnose model misspecifications both in fixed and random effects. The normalization is done with respect to the median prediction for each bin across the independent variable (see Eq. 1). If the typical model prediction (PRED) has a lower boundary that is different from 0 (e.g., relative change from baseline has −100% as a lower boundary), the correction can adjust for this (lb_ij in Eq. 1). It is important to notice that the lower bound is from the typical model prediction and not the dependent variable which could be lower than the lower boundary for the typical model prediction (e.g., due to random effects). In mixed-effects modeling, it is common practice to log-transform the dependent variable (natural logarithm) and fit the log-transformed observations to achieve increased numerical stability (9). In the case of a log-transformed dependent variable, the transformation needs to be adjusted (see Eq. 2). A log-transformed dependent variable with a lower boundary different from zero needs to be transformed to the normal scale before a correct prediction correction can be performed.

Prediction correction (PRED correction) for dependent variable, Y_ij, with lower bound, lb_ij:

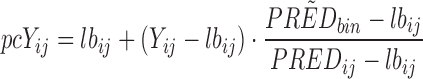1

Prediction correction (PRED correction) for log-transformed dependent variable, ln(Y_ij):

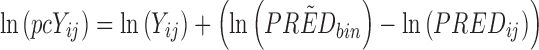2

Y_ij = observation or prediction for the ith individual and jth time point, pcY_ij = prediction-corrected observation or prediction, PRED_ij = typical population prediction for the ith individual and jth time point, and 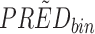= median of typical population predictions for the specific bin of independent variables.

pvcVPC

By normalizing the dependent variable to the median population prediction as well as to the typical variability Eq. 3 of each bin, pvcVPCs may be constructed. Many factors will cause the expected relative variability to differ between observations even after prediction correction. Predictions rely to different extents on the parameters in a model and hence are affected to a different extent by the between-subject/occasion variability in these parameters. Another reason for nonconstant relative variability is if any other residual error model but a strictly proportional model is used.

Variability correction (VAR correction) for prediction corrected dependent variable, pcY_ij, with standard deviation, sd(pcY_ij):

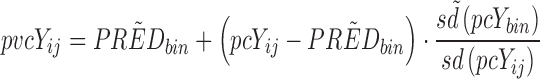3

pcY_ij = prediction-corrected observation or prediction for the ith individual and jth time point, 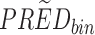= median of typical population predictions for the specific bin of independent variables, sd(pcY_ij) = standard deviation of simulated pcY_ij, and 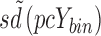= median sd(pcY_ij) for the specific bin of independent variables.

Examples

Five different examples were investigated in order to highlight different situations when pcVPC/pvcVPC can add significant value as a model diagnostic. The examples were simulated hypothetical examples (Example 1, 2, and 5) as well as applications to real data (Example 3 and 4). Example 1 is supposed to illustrate the improved ability to diagnose misspecified random effects with pcVPC compared to VPCs in case of large variability in independent variable such as dose and influential covariates. Example 2, 3, and 5 demonstrate the advantages with pcVPC in application to data following adaptive dose adjustments. In Example 4, the possibility to create informative pcVPCs with other independent variables than time on the x-axis was explored.

Example 1. Single Ascending Dose Study

A simulated example of a single ascending dose (SAD) study with a very wide dose range (10,000-fold dose range) to illustrate the principle of pcVPC for diagnosing random effects misspecification across several small dose cohorts was made. The simulated study included 10 dose levels (0.1–1,000 mg) with plasma concentration data from five subjects per dose level (i.e., in total 50 subjects). Data were simulated from a one-compartment PK model with first-order absorption and saturable elimination (Vmax = 40 mg/h, Km = 300 mg, V = 25 L, Ka = 1.5 h⁻¹). Allometric scaling was applied to Vmax, and volume of distribution (V), remaining between-subject variability (BSV), was assumed to be log-normally distributed and uncorrelated for all parameters (Vmax = 30%, Km = 20%, V = 20%, Ka = 20%, expressed as % CV). Body weight for the 50 subjects was simulated with a log-normal distribution, mean 70 kg, 25% CV, truncated at 40 and 140 kg.

A proportional residual error of 20% was assumed for the simulations. Model parameters were estimated based on three models: [1] the true model, [2] a model that assumed no allometric scaling, and [3] a model assumed no allometric scaling but with characterized correlation between Vmax and V. A fourth model, with BSV for all parameters assumed to be twice as high as the true value, was also investigated. VPCs and pcVPCs were created for all four models.

Example 2. Simulated A Posteriori Dose Adaptation (Therapeutic Drug Monitoring)

An example was constructed to illustrate the conceptual benefit with pcVPC over a traditional VPC in application to observations following adaptive dosing. Data were simulated based on an intravenous bolus dose and a one-compartment model (CL = 8.66 L/h, V = 100 L) with a log normally distributed between-subject variability (BSV_CL = 50%, BSV_V = 30%, Correlation = 90%) and a proportional residual error model (20%). The dosing was based on a fixed starting dose for all subjects (10,000 U) and a posteriori dose adaptation, mimicking therapeutic drug monitoring (TDM), based on trough concentration monitoring and dosing every 24 h. A dose adjustment schedule with the target trough of a 12.5 U/L was implemented.

Example 3. Tacrolimus in Pediatric Hematopoietic Stem Cell Transplant Recipients

A published model and dataset from a study of tacrolimus in pediatric hematopoietic stem cell transplant recipients (8) was applied as a real life example of the benefit with pcVPC in case of adaptive dosing. The study included both a priori and a posteriori dose adaptation, and the model included multiple influential covariates. The dose adaptations were not performed according to any well-documented dosing algorithm, and simulation-based model diagnostics had previously not been considered in the original publication. Simulations for the VPC, pcVPC, and pvcVPC were performed with the published model and data (8).

Example 4. Moxonidine Effect on Noradrenaline Plasma Concentrations

A model and dataset for noradrenaline (NA) following moxonidine treatment in patients with congestive heart failure (10) was used as an example. The example was intended to illustrate how pcVPC improve the opportunities for investigating the predictive properties across different independent variables (x-axis). A nonfinal model, not including a concentration-dependent symptomatic effect of moxonidine on NA, but only a moxonidine effect on disease progression, was compared to the final published model. VPCs, pcVPCs, and pvcVPCs were created for the nonfinal model and the published model (10). Separate plots were created with time-after-first-dose, time-after-dose, or predicted plasma concentration as the independent variable presented on the x-axis. Plots were also created for NA relative to baseline as a complement to nonnormalized NA concentration.

Example 5. Adjusted Infusion Rate

The example was designed to illustrate the potential benefits of pcVPC over VPC using simulated dose adjustments with application to data from studies with adaptive dosing. A hypothetical example was constructed where a loading dose was given followed by a 12-h constant infusion. The infusion rate was altered based on the observed concentrations to achieve the target concentration of 10 units. Data were simulated with a one-compartment model featuring autoinduction of CL. A simple one-compartment model without autoinduction was fitted to the data. VPCs were created based on both the realized design and simulations with the same dose alteration algorithm as in the original simulations. A pcVPC and a pvcVPC were constructed using only the realized design.

Software

All model fitting and simulations were performed with NONMEM version 6.2 (11), run on a Linux cluster with a Red Hat 9 operating system using OpenMosix and a G77 Fortran compiler. PsN version 3.2.7 (12–14) was used for automatization of NONMEM runs and postprocessing of NONMEM output. Computations for VPCs, pcVPCs, and pvcVPCs were all generated with the PsN tool “vpc.” Graphical presentation of VPC results was done with the Xpose package, version 4.2.1 (14,15), run using R version 2.10.1 (16).

RESULTS

Example 1. SAD Study

VPC for the four investigated models looked approximately similar without any clear indication of a model misspecification. Figure 1 demonstrates how the VPC indicates no model misspecification for the model without allometric scaling but how the pcVPC indicates an over prediction of the fifth percentile. The model misspecification in the model with twice the true BSV for all model parameters was clearly identified with the pcVPC but not with the traditional VPC (plots presented in Online Supplementary Material). Neither VPCs nor pcVPC indicated any important misspecification for the true model or the model without allometric scaling but with BSV correlation between Vmax and V estimated (results not shown). These results suggest that the model misspecification indicated in the pcVPC of Fig. 1 primarily comes from not characterizing the correlation between Vmax and V (induced by common dependence on body weight).

Fig. 1.

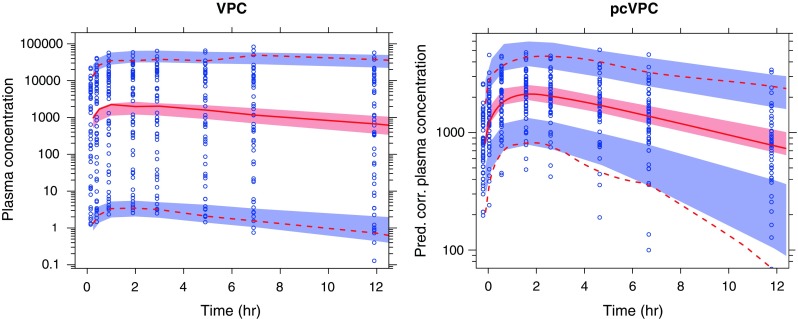
A simulated example of a SAD study with a 10,000-fold dose range and nonlinear pharmacokinetics. The diagnosed model lacked any form of estimated correlation between Vmax and volume of distribution (neither a common covariate nor estimated BSV correlation). The solid red line represents the median observed plasma concentration (nanogram per liter; prediction-corrected plasma concentration in the pcVPC to the right), and the semitransparent red field represents a simulation-based 95% confidence interval for the median. The observed 5% and 95% percentiles are presented with dashed red lines, and the 95% confidence intervals for the corresponding model predicted percentiles are shown as semitransparent blue fields. The observed plasma concentrations (prediction corrected in the pcVPC) are represented by blue circles

Example 2. Simulated A Posteriori Dose Adaptation (TDM)

Figure 2 illustrates the conceptual benefit of pcVPC in application to data following dose adaptations correlated to the dependent variable. The observed data in the VPC show decreasing concentration variability with time due to dose adaptations. In contrast, the model-predicted interpercentile range increased since simulations based on the realized design do not maintain any correlation between dose alterations and the previous observed concentration. The pcVPC corrects for the dose adjustments and correctly indicates no discrepancy between the observations and the model prediction.

Fig. 2.

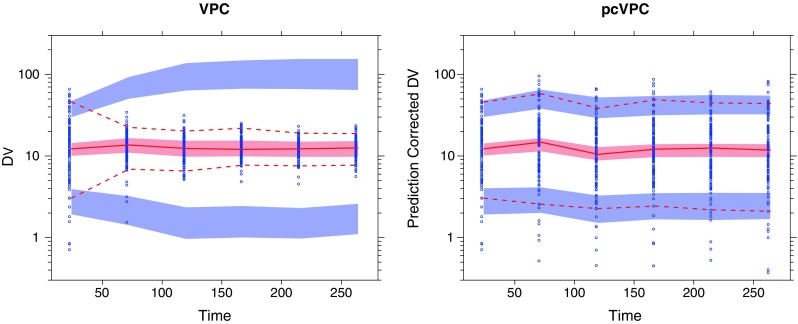
Example with a posteriori dose adaptation (TDM) based on observed trough plasma concentration (units per liter) monitoring over time. Traditional VPC (left) and pcVPC (right), with 95% interpercentile range, for the true model applied to a simulated dataset. Graphical interpretation as in Fig. 1

Example 3. Tacrolimus in Pediatric Hematopoietic Stem Cell Transplant Recipients

The VPC in Fig. 3 indicates an overprediction of between-subject variability. The corresponding pcVPC however indicates no such misspecification. This discrepancy is analogous to Example 2 and is most likely due to a similar correlation between the dependent variable and dose adjustment. A pvcVPC created for the same dataset (not presented) resulted in no principal difference to the presented pcVPC.

Fig. 3.

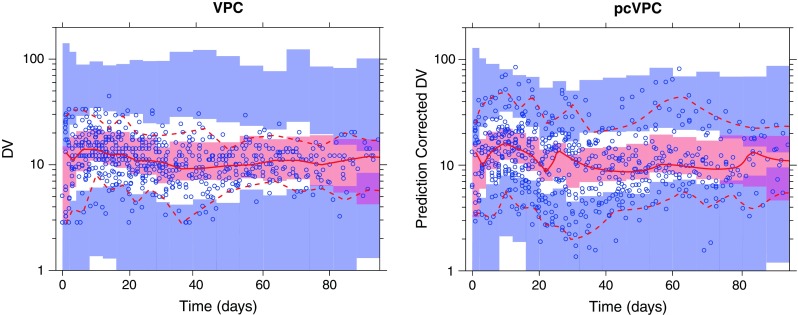
Simulation-based diagnostic plots for tacrolimus plasma concentration (nanogram per milliliter) versus time (days). Traditional VPC (left) and pcVPC (right), with 90% interpercentile range, for the final published model (8). Graphical interpretation as in Fig. 1

Example 4. Moxonidine Effect on NA Plasma Concentrations

In the upper panel of Fig. 4a, VPCs for NA plasma concentration versus study time are presented for moxonidine- and placebo-treated subjects. The VPCs are created with a prefinal model with a nonconcentration-dependent treatment effect on disease progression. No clear tendency toward model misspecifications can be detected from these plots (observed percentiles generally covered by the model-based confidence intervals). However, a large portion of the variability in these plots can be attributed to variability in baseline NA. The lower panel of Fig. 4 shows VPCs with NA relative to baseline on the y-axis. This makes model misspecification to appear more clearly: a tendency toward underpredicted NA at the predose sample (first bin of each observation period) can be observed in this plot. To visualize this misspecification, it would be a good idea to generate a VPC for NA relative to baseline vs. time-after-dose. With a traditional VPC, such a plot would be hard to interpret due to the long-term disease progression. With a pcVPC, long-term disease progression well described by the model will be corrected for if the plot is created with time-after-dose as the independent variable. Such a pcVPC is presented in the upper left hand corner of Fig. 4b (only the moxonidine cohort presented). This plot clearly points to a time-after-dose-related model misspecification. The hypothesis that this was due to lack of a concentration-dependent symptomatic effect on NA concentrations was further explored with a pcVPC with predicted moxonidine concentration (predictions based on a published PK model (10)) on the x-axis (upper left corner of Fig. 4b). The lower panel of Fig. 4b includes corresponding pcVPCs after including a moxonidine concentration-dependent symptomatic effect in the model. These pcVPCs demonstrate good predictive behavior across both time-after-dose and moxonidine concentration. The evaluated pvcVPCs were found to be only marginally different from the pcVPCs.

Fig. 4.

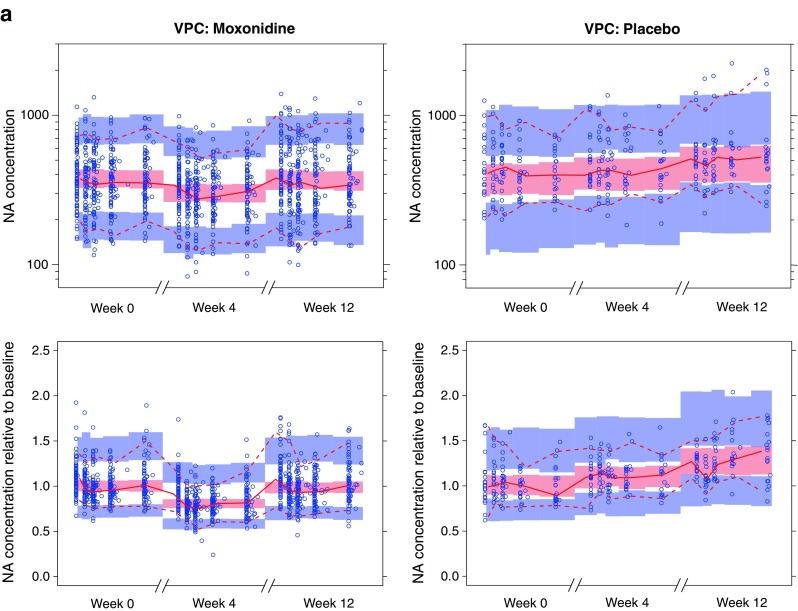
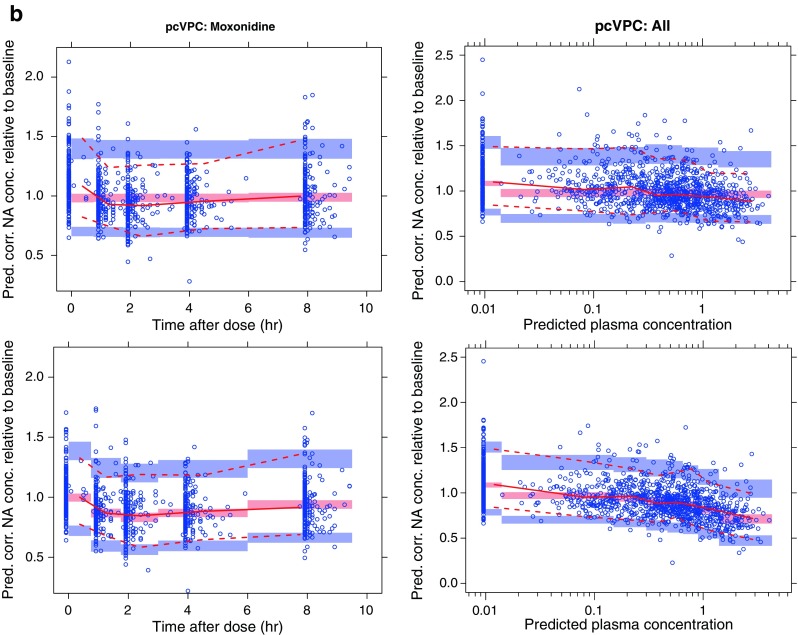
a VPCs (90% PI) for noradrenaline (NA) concentration (nanogram per liter) following moxonidine (left) or placebo (right) treatment. The plots in the upper row depict noradrenaline concentration (nanogram per liter) versus time, and the lower row depicts noradrenaline concentration over individual baseline estimate versus time. Time is presented on a broken x-axis with between 0 and 10 h after dose for the first dose and doses following 4 and 12 weeks of moxonidine treatment. Simulations are performed with a nonfinal model with nonconcentration-dependent treatment effect on disease progression. b pcVPCs (90% PI) for NA concentration (nanogram per liter) relative to individual baseline estimate. pcVPCs in the two upper plots are generated using the same nonfinal model that was used for the VPCs in Fig. 4a. The two bottom row pcVPCs are generated with a model including also a concentration-dependent symptomatic effect of moxonidine

Example 5. Adjusted Infusion Rate

A hypothetical example featuring a loading dose followed by a constant infusion was altered based on the observed concentrations to achieve the target concentration of 10 units. The example was designed to illustrate the potential benefits of pcVPC over VPC created with simulated dose adjustments according to the same algorithm that was used in the original study. The true underlying model is a one-compartment model with autoinduction of CL (Fig. 5). A simple one-compartment model without autoinduction was fitted to the data. The left hand VPC has been simulated using the same dose alteration algorithm as in the original study. The pcVPC (right) has been simulated using only the realized design. Both VPCs indicate some sort of model misspecification. The left hand VPC primarily indicates a higher model-predicted variability at times later than 2 h. The pcVPC more clearly points toward the true model misspecification by demonstrating an underprediction at early time points and an overprediction at late time points.

Fig. 5.

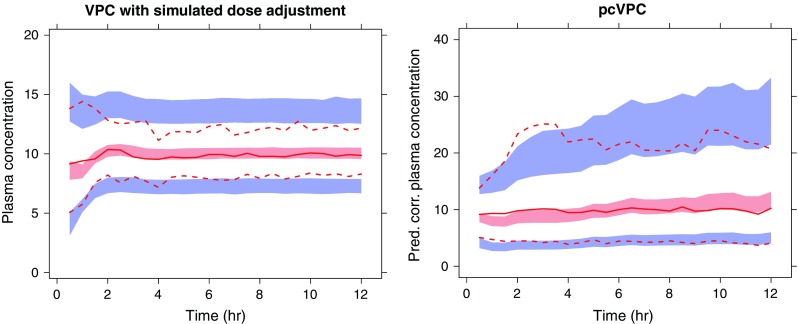
A simulated example where a loading dose was given followed by a constant infusion. The infusion rate was altered to achieve the target concentration of 10 units. The true underlying model is a one-compartment model with autoinduction of CL. A simple one-compartment model without autoinduction has been fitted to the data. The left hand VPC has been simulated using the same dose alteration algorithm as in the original study. The pcVPC (right) have been simulated using only the realized design. Outer percentiles (dashed red lines) are 2.5% and 97.5% (95% interpercentile range), the semitransparent blue fields are the corresponding model-based confidence intervals, the solid red line represents the observed median, and the semitransparent red field represents the corresponding model-based confidence interval. The actual observations are not plotted in this picture

DISCUSSION

A good PK/PD modeler always knows that even the most sophisticated model is an approximation of the truth. This insight is manifested in a quotation of George Edward Pelham Box (1987; 17): “Remember that all models are wrong; the practical question is how wrong do they have to be to not be useful.” To assess if the model is good enough to be useful for a particular purpose should be the goal of all model evaluation. The traditional VPC may fail to evaluate adequately a model's predictive performance when the expected value or expected variability in observations within a bin differs due to variations in predictors such as time, dose, or covariate values. The pcVPC and pvcVPC are designed to address such shortcomings of the traditional VPC and hence act as a valuable addition to the PK/PD modeler's diagnostic toolbox.

Example 1 illustrates how a pcVPC can aid in diagnosing random effects misspecification when a large portion of the variability comes from well-characterized relations to independent variables, in this case dose. If the example had featured linear PK, the same kind of advantage could have been achieved by creating a VPC for dose-normalized plasma concentrations. Stratifying for dose would not have been a good alternative in this case since five subjects in each dose cohort are far too few to generate an informative VPC especially for diagnosing between-subject variability. The use of pcVPC methodology reduces the need for stratification, but stratification can still be a useful tool in pinpointing specific aspects of a models predictive ability. Prediction correction will, just like dose-normalizing concentration, transform the original scale of observations and predictions. This may have the drawback of making the y-axis scale less intuitive.

Applying traditional VPCs to data following dose adjustments correlated to the dependent variable can be deceiving. This is demonstrated both for a simulated example (Example 2) and a real life example of data following TDM dose adjustments (Example 3). The issue arises from the fact that TDM dose adjustments and the observed dependent variable are inherently correlated. Such correlations can sometimes be due to indirect effects and can be less obvious. Dose adjustment may be done based on the adverse events that occur in a dose/concentration-dependent manner. This is a phenomenon that occurs not only in studies including TDM but also in all clinical studies with possibilities for dose adjustments based on an individual response. Including a dose adjustment algorithm in the simulations has been suggested as a means of maintaining the correlations between the dependent variable and the dose adjustments. However, the dose adjustments in studies do not always follow a well-established algorithm and are sometimes done based on observations that are not part of the dataset available for modeling. This can make it hard to develop a dose adjustment algorithm that accurately mimics real life dose adjustments. Furthermore, even when a reliable dose adjustment algorithm is present, simulation results can be deceiving. Example 5 illustrates how VPCs based on simulated dose adjustments can have less diagnostic value than a pcVPC based on the realized design. In a previously presented conference poster (18), it has also been shown how VPCs based on simulated dose adjustments can be completely insensitive to misspecified random effects. More information can be gained from such simulations if attention also is given to comparing the observed and simulated dose adjustment patterns. If such a comparison had been performed for Example 5, it would have revealed that the observed doses increased with time to maintain steady plasma concentrations whereas no such increase would have been seen in the simulations.

VPCs are traditionally constructed with an independent variable related to time after first observation on the x-axis. Of course, other independent variables could also be used to explore different aspects of the predictive performance of a model (19). In this manuscript, we constructed pcVPCs with other independent variables on the x-axis; in Fig. 4b, pcVPC plots with time-after-dose and predicted concentration on the x-axis are presented in a way that would not have been informative with a traditional VPC. Example 4 also illustrates how removing well-characterized baseline variability can improve the diagnostic power of a pcVPC. These plots can be created by normalizing for either the observed baseline value or the estimated baseline (the true individual baseline for the simulations). In the moxonidine example, normalizing for the observed baseline value was not an attractive alternative since some subjects lacked a baseline sample for NA. The authors would like to emphasize that the baseline normalization is only beneficial for diagnostic purposes. It has previously been shown that there are important advantages with estimating a baseline parameter rather than modeling baseline-normalized data (20).

Theoretically, normalizing for the expected variability (variability correction) in addition to normalizing for prediction should improve the diagnostic power of a VPC plot. The potential advantage with variability correction should be dependent on how large differences there are in expected variability between observations in a specific bin. In the examples investigated in this manuscript, pvcVPCs have not shown any important diagnostic advantage over pcVPCs. This might be due to a similar expected variability for most observations in the same bin.

Ways to handle data censored due to limit of detection in VPCs have previously been suggested (6,21). These approaches are not directly applicable to pcVPCs and pvcVPCs since the observations lose their rank order after prediction and variability correction. Observations censored due to limit of detection will therefore need to be handled in the same way as previously suggested for drop-out censoring of observations (22). This approach is based on omitting censored observations (e.g., BQL) in a similar manner for both the observed and simulated datasets before calculating the VPC statistics. In this case, the interpretation of the pcVPC/pvcVPC for the continuous observations will be heavily dependent on an accurate prediction of the data censoring. Therefore, diagnostics ensuring accurate prediction of censoring frequency (e.g., percentage of observation below LLOQ) versus the independent variable will be important before assessing the pcVPC/pvcVPC for the continuous observations.

The VPC and pcVPC statistics presented in this article were created with the software PsN (12,14) in conjunction with NONMEM (11). The output from PsN was graphically presented with the R package Xpose (16). However, similar plots can to the author's knowledge also be created with the nonlinear mixed-effects modeling software MONOLIX (version 3.2; 23).

The Visual Predictive Extended Residuals (VIPER) has recently been suggested to have better statistical properties than other available visual diagnostics and allow for an easier and less subjective interpretation of whether the model is “true” or not (24). With VIPER, all observations for one individual are reduced to a single, informative, data point, selected to carry the information about model fit. This is a potential drawback since it reduces the information content and likely hampers the graphical interpretation. It has been put forward as a major advantage with VIPER that it is an exact test, and that a strict rule of decision to accept a model or not can be applied. Even though this might sound appealing, it is primarily a theoretical advantage and of limited value. The only case where we actually have the true model is with simulated data. With real data, we never have a true model since even the most sophisticated model is a simplification of reality. Hence, if a diagnostic test results in the answer that the model should be rejected because it is “not the true model,” we learn nothing that we did not already know. The important thing to diagnose is if the model is good enough for a particular purpose, and if not, in what way the model needs to be improved. The ability of VIPER plots to answer these questions in application realistic examples has yet to be demonstrated. A similar lack of demonstrated practical usage goes for the recently suggested Global Uniform Distance (GUD) diagnostic (25). More documentation is available for normalized prediction distribution errors (npde) that is a residual-like type of diagnostic that can be plotted against any independent variable (26). Comets et al. recently suggested presenting npde diagnostic plots with observed percentiles and predicted confidence intervals (prediction bands) similar to the way that VPC are presented in this article (27). The de-correlation applied to npde diagnostics should theoretically avoid the inflated type 1 error with repeated observations per individuals that is seen in VPCs with confidence intervals (24). This advantage needs to be weighed against the less intuitive interpretation of the npde plots, compared to a VPC or a pcVPC, and that it is harder to assess whether an indicated deviation is clinically relevant or not. Most importantly, one diagnostic tool does not rule out using another one. The best practice most likely lies in using a wide toolbox of diagnostics, rather than one single universal test to decide whether a model is fit for purpose or not.

CONCLUSION

pcVPCs were shown to be a more informative diagnostic tool than traditional VPCs for a number of real and realistic examples. More informative diagnostic tools for assessing mixed-effects models facilitates the development of more predictive models and hence result in better possibilities for model-based decision making.

Electronic Supplementary Materials

Below is the link to the electronic supplementary material.