Head-repositioning does not reduce the reproducibility of fMRI activation in a block-design motor task

Abstract

It is hypothesized that, based upon partial volume effects and spatial nonuniformities of the scanning environment, repositioning a subject’s head inside the head coil between separate functional MRI scans will reduce the reproducibility of fMRI activation compared to a series of functional runs where the subject’s head remains in the same position. Nine subjects underwent fMRI scanning where they performed a sequential, oppositional finger-tapping task. The first five runs were conducted with the subject’s head remaining stable inside the head coil. Following this, four more runs were collected after the subject removed and replaced his/her head inside the head coil before each run. The coefficient of variation was calculated for four metrics: the distance from the anterior commisure to the center of mass of sensorimotor activation, maximum t-statistic, activation volume, and average percent signal change. These values were compared for five head-stabilization runs and five head-repositioning runs. Voxelwise intraclass correlation coefficients were also calculated to assess the spatial distribution of sources of variance. Interestingly, head repositioning was not seen to significantly affect the reproducibility of fMRI activation (p < 0.01). In addition, the threshold level affected the reproducibility of activation volume and percent signal change.

Introduction

Blood oxygenation-level-dependent (BOLD) functional magnetic resonance imaging (fMRI) is a powerful neuroimaging technique that is beginning to see clinical applications (Hennig et al., 2003). Functional MRI has been used clinically for pre-surgical mapping of motor and language functions. It has also been used to study mild cognitive impairment, Alzheimer’s disease, dementia, schizophrenia, depression, anxiety disorders, stroke, Parkinson’s disease, and multiple sclerosis (Rombouts et al., 2007). Functional MRI also has the potential to be used as a biomarker for clinical trials of drugs and medical devices treating neurological diseases or disorders.

Bennett and Miller (2010) reviewed the literature on reproducibility studies in fMRI. Four reasons why test-retest reliability is a concern include generalizable results, longitudinal assessment for clinical studies, evidentiary applications, and the concordance of results among collaborative institutions. For fMRI to be used in clinical settings, it is important to understand the reproducibility of activation metrics. Ideal reproducibility represents the ability to achieve activation patterns that match in location, significance, spatial extent, and signal magnitude in subsequent fMRI runs. Alternatively, each of these quantities may vary in their degree of reproducibility. Different amounts of signal and noise in separate runs will lead to lower reproducibility of activation patterns, reducing the clinical relevance of fMRI.

Methods to assess variability

One method to assess reproducibility is to calculate the coefficient of variation (CV). This normalized measure of dispersion is calculated as the standard deviation divided by the mean. The coefficient of variation is a dimensionless value that allows comparisons between quantities of different means or different units. One advantage of the CV is that it can be applied to many clinically meaningful metrics of fMRI activation, such as activation volume or percent signal change. The CV of these quantities can then be compared with one another to determine relative reproducibility. However, multiple measurements are required to achieve a good estimation of the CV. Additional disadvantages of the CV include a poor ability to assess relative error when the measured values are small and the underlying assumption of normality for the measurements when estimating the mean and standard deviation.

A more standard method of examining reproducibility is to calculate the intraclass correlation coefficient (ICC) (Shrout and Fleiss, 1979). The ICC is calculated using an analysis of variance (ANOVA) framework. It is defined as the ratio of the variance of a variable of interest divided by the total variance. Shrout and Fleiss (1979) devised six forms of the ICC depending on the type of ANOVA used and whether the effects are fixed or random. The ICC can be applied on a voxelwise basis to the fit coefficients resulting from a multiple linear regression analysis. For example, voxelwise ICC ratios with different variance components in the numerator (e.g., between-session variance, between-subject variance, etc.) can help identify the spatial distribution and contribution of such variance to the total variance present in the data. A disadvantage is that a study with high intersubject variability can lead to different ICC values compared to a study with low intersubject variability (Bennett and Miller, 2010).

Sources of variability

Sources of variability for fMRI studies can be divided into four main categories: 1) physiological noise, 2) scanner noise, 3) cognitive effects, and 4) head motion. Krer et al. (2001a) showed that physiological noise becomes the dominant source of noise at field strengths of 3 T and above. Physiological noise includes cardiac and respiratory fluctuations and changes in neurophysiology (cerebral blood volume (CBV), cerebral blood flow (CBF), and cerebral metabolism of oxygen (CMRO₂)) (Krer et al., 2001b). Chemical influences on the BOLD response, such as the caffeine effect (Laurienti et al., 2002), can also contribute to physiological noise. Scanner noise includes thermal noise, such as temperature-dependent fluctuations, and system noise, such as static field inhomogeneities, instabilities in the gradient fields, loading effects in the transmit and receive coils, and scanner drift (Huettel et al., 2004). Cognitive effects include varying levels of alertness, differing strategies applied to the task, non-task-related BOLD fluctuations, and learning effects. Motion includes both stimulus-correlated motion and stimulus-uncorrelated motion, the first being a more difficult confounding factor during the analysis.

Methods exist to partially account for several of these sources of variability in fMRI data. Cardiac and respiratory fluctuations can be measured and subtracted from the measured time series (Glover et al., 2000). Scanner noise can be monitored through the use of quality control measures (Friedman and Glover, 2006). Adequate instructions and training could potentially minimize cognitive effects and motion-induced noise.

One source of variability that has not been previously studied is the effect of head repositioning on the reproducibility of fMRI activation. Repositioning the head between functional runs is likely to contribute to variations in scanner-induced distortions and partial volume effects, both of which could lead to changes in fMRI activation. Although this variability is not caused by temporal fluctuations in the MR signal, it can be argued that this variability is related to scanner noise due to imperfections in the scanning environment. Previous papers (McGonigle et al., 2000; Raemaekers et al., 2007) have suggested that head-repositioning is a likely source of variability of fMRI activation in longitudinal studies. To the best of our knowledge, no systematic study has yet evaluated if head-repositioning represents a significant source of variability. Obtaining empirical evidence that head-repositioning does not reduce the reproducibility of fMRI activation would be important, as it would allow researchers to avoid discarding data from subjects that need a break in the middle of a long scanning session, a problem likely to occur in clinical settings. Having certainty that combining data from before and after the break adds no significant undesired variability would save researchers time, money, and data.

Partial volume effects, i.e. the averaging of gray matter, white matter, and cerebrospinal fluid (CSF) inside a voxel, results in voxel intensities that are a summation of different tissue types. Early studies showed the effect on fMRI of changing spatial resolution (Frahm et al., 1993; Thompson et al., 1994). Hyde et al. (2001) demonstrated that cubic voxels of dimension 1.5 × 1.5 × 1.5 mm³ were ideal to avoid partial volume effects due to the tortuosity of gray matter and to match the anatomy of microcirculation inside the gray matter. Voxels much larger than this are more likely to suffer from partial volume effects. Any movement of the head will change the fractions of different tissue types inside each voxel. Functional MRI studies performed with two different head positions are likely to be composed of voxels with different contributions of gray matter, white matter, and CSF, leading to varying strengths of intensity in voxels exhibiting a BOLD response. Based on this knowledge, it is hypothesized that partial volume effects will reduce the reproducibility of fMRI studies performed with different head positions versus fMRI studies performed with identical head positions.

Spatial variations in magnetic field inhomogeneities, gradient fields, and head coil performance all contribute to variation in signal intensity for the same material being imaged in different locations (Huettel et al., 2004). Inhomogeneities in the static magnetic field lead to geometric distortions and signal loss (Haacke et al., 1999). Nonlinearities in the magnetic gradient fields can lead to distortions as well (Haacke et al., 1999). Problems with the x- and y- gradients lead to compressed or skewed images. Problems with the z-gradient can lead to thinner or thicker slices yielding weaker or stronger signal intensity. When using a birdcage radiofrequency (RF) coil, the B₁ distribution is strongly dependent on the dielectric properties of the tissue being imaged (Alecci et al., 2001). In the radial dimension, the B₁ field is highest near the center of the coil and decreases slowly with distance from the center. In the longitudinal axis, the B₁ field is highest in the center of the coil and decreases dramatically with distance from the center. Functional MRI scans acquired with the subject’s head in the center of the head coil will give different intensity profiles compared to scans acquired with the head placed off center, especially if displaced along the longitudinal axis. Intensity normalization should reduce variability in fMRI activation caused by B₁ variation, but it may not completely eliminate it.

Problems caused by spatial variations in magnetic field inhomogeneities, gradient fields, and head coil performance can be alleviated by using high order shimming, newer gradients, and newer head coils, but this may not be enough to overcome changes in noise levels. It is hypothesized that repositioning the subject’s head inside the head coil will lead to nonlinear spatial displacements of signal intensity and noise due to spatial non-uniformities in the scanning environment, leading to a reduction in the reproducibility of fMRI activation metrics.

Both partial volume effects and spatial non-uniformities in the scanning environment should contribute complex changes in signal and noise when acquiring fMRI data when the subject’s head is imaged in different positions. Our test hypothesis was that head-repositioning should cause a decrease in the reproducibility of fMRI activation across runs compared to runs where the head remains stabilized.

Materials and Methods

Subjects

Nine healthy subjects (five men, four women, aged 43 ± 11.0 years) were recruited from the local community. These subjects were assessed by the Edinburgh handedness inventory (Oldfield, 1971) to be strongly right-handed. All volunteers were scanned under a protocol approved by the National Institutes of Health (NIH) Internal Review Board (IRB).

Experimental design

Subjects were asked to perform a sequential, oppositional finger-tapping task alternating between both hands. At the beginning of each functional run, subjects were told to tap each of their four fingers to their thumb on the right hand in succession and repeat at a rate that was constant, fast, and comfortable. Every 12 s, an auditory cue (the word “switch”) told the subjects to switch hands. Subjects were visually monitored for performance. From a visual perspective, subjects appeared to maintain a constant finger-tapping rate. After each run, subjects were asked if they were able to perform the task well.

Fifteen blocks of 12 s each resulted in exactly three minutes of finger-tapping. This task was expected to produce a robust activation in the primary sensorimotor cortex (SMC). The right and left motor cortices were expected to have opposite activation patterns due to the alternating design of the task. The supplementary motor area (SMA) was not expected to be seen in the resulting activation maps, as it would be active during the entire run and therefore lacked a contrasting state of rest.

Data acquisition

Data were acquired on a Philips Achieva 3.0 T scanner (Philips Medical Systems, Best, Netherlands) using a 6-channel receive-array radiofrequency (RF) head coil. Subjects were instructed not to move while inside the scanner. Small cushions were used to comfortably secure the subject’s head inside the head coil. After a survey scan, a magnetization-prepared rapid gradient echo (MPRAGE) scan (TR/TE/FA = 9.894 ms/4.60ms/8°, FOV = 240 mm, number of slices = 140, slice thickness = 1 mm) was acquired to obtain a high spatial resolution, T₁-weighted image of the brain. Next, nine echo planar imaging (EPI) runs (TR/TE/FA = 2000 ms/35 ms/90°, matrix = 64×64, FOV = 256 mm, number of slices = 32, slice thickness = 4 mm) were acquired. The scanner automatically discarded the first two acquisitions to allow the equilibration of magnetization. Thirty-two axial slices were acquired to cover most of the brain, focusing on the superior part. The resulting voxels were isotropic. Given that smaller voxels are expected to exhibit smaller partial volume effects (Hyde et al. 2001), we believe that the use of 4 4 4 mm³ voxels represents a conservative approach to the issue under investigation, as it represents a “worse case scenario.”

The finger-tapping tasks were performed during the EPI sequences. The subject was instructed to stay still inside the scanner and to not move his/her head or body during the task. These first five runs were designated the head-stabilization runs because the subject’s head was stabilized in one place for all five runs.

Next, the scanner operator entered the magnet room, retracted the table from the scanner, and slid the head coil away from the subject’s head. The subject was told to sit up for a minute and then lie back down. The head coil was slid over the subject’s head, and the table was advanced back into the scanner. Small cushions were again used to secure the subject’s head comfortably. Four new functional runs were acquired after repositioning the subject’s head each time in this manner. These four new runs plus the final run of the head-stabilization runs were designated the head-repositioning runs because the subject’s head was positioned separately for all five runs.

Data analysis

MR images were exported from the Philips scanner as NIFTI files. Data were analyzed using AFNI (Cox, 1996), R (R Foundation for Statistical Computing, Vienna, Austria), locally written programs in MATLAB (The Mathworks, Inc, Natick, MA), and Microsoft Excel (2003).

The MPRAGE image volume was skull-stripped and warped to the coordinates of Talairach space (Talairach and Tournoux, 1988). Next, the first image volume of each EPI run was aligned to the skull-stripped MPRAGE image volume in subject space using a python script in AFNI (align_epi_anat.py). This script uses a weighted local Pearson coefficient to align a T₂*-weighted image volume to a T₁-weighted image volume (Saad et al., 2009). Alignment results were visually inspected. If corrections were needed, spatial shifts were manually applied prior to rerunning the alignment script.

Motion

The EPI runs underwent a six-parameter, rigid-body volume registration routine (Cox and Jesmanowicz, 1997) to correct for any small motion that occurred during the runs. The first image volume, which had been aligned to the skull-stripped MPRAGE, was used as the base image volume. To assess motion during the runs, the maximum intra-run shifts were calculated for roll, pitch, yaw, superior-inferior translation, left-right translation, and posterior-anterior translation.

An assessment was made of the inter-run motion for the head-stabilization runs and the head-repositioning runs. The first image volume in each unregistered run was aligned to the first image volume of the subsequent run. This volume registration process yielded six motion parameters (roll, pitch, yaw, inferior-superior translation, right-left translation, and anterior-posterior translation) for each inter-run registration. For each of the nine subjects, we calculated four sets of inter-run motion parameters for both the head-stabilization runs and the head-repositioning runs. The absolute values of the inter-run motion parameters were averaged across both the head-stabilization runs and the head-repositioning runs for all subjects to assess the relative amount of inter-run motion.

Activation

Prior to statistical analysis, the voxel intensities of each EPI run were normalized by dividing each voxel value by the mean of its time-series and multiplying by 100. Brain masks were also applied to ignore voxels outside the brain. Spatial smoothing was not applied, as this post-processing technique would reduce any partial volume effects caused by head-repositioning.

Two rectangular stimulus waveforms, representing the right-handed and left-handed finger-tapping tasks, were convolved with a standard gamma-variate function (Cohen, 1997) to yield two BOLD response waveforms.

A multiple linear regression analysis was performed on the volume-registered, normalized EPI data sets. The baseline was fit to a second-order polynomial to account for the mean as well as any linear or quadratic trend. The six motion parameter files resulting from volume registration were used as covariates in the regression. One regression analysis was performed using the right-handed BOLD response waveform as the parameter of interest, while a second regression analysis was performed using the left-handed BOLD response waveform as the parameter of interest. Regression analysis was performed using a restricted maximum likelihood (REML) estimation of the temporal autocorrelation structure to account for temporal autocorrelations (using the AFNI command 3dREML).

False-discovery thresholding (FDR) (Genovese et al., 2002) was applied to the fMRI activation inside the brain masks to deal with the issue of multiple comparisons. Activation thresholding was then performed using the p_FDR values derived from this technique.

Region of interest (ROI) masks were drawn around the primary sensorimotor cortex of the left and right hemispheres in Talairach space. The left hemisphere sensorimotor mask included the left precentral gyrus and left postcentral gyrus defined on a Talairach atlas (48.786 cm³). The right hemisphere sensorimotor mask included the right precentral gyrus and right postcentral gyrus defined on a Talairach atlas (49.094 cm³). These masks were then warped to subject space using the reverse of the transform used to warp the subject’s MPRAGE image volume to Talairach space. The ROIs were then resampled to the EPI spatial resolution. The ROI masks were applied to the activation maps after FDR thresholding to isolate activation in the left and right primary SMC.

fMRI activation metrics

fMRI experiments produce large amounts of data that need to be summarized for reporting and discussion purposes. Entire data sets are commonly summarized in terms of a few activation metrics. The criterion for selection of the reproducibility metrics used in this study was: (1) wide acceptance in the reproducibility literature, so comparisons across studies were possible, (2) clear interpretation to minimize ambiguity, and (3) complementariness so that among all of the metrics we could perform a sound evaluation of the potential effects of head repositioning on the reproducibility of fMRI activation. The fMRI activation metrics we calculated were the distance from the anterior commisure (AC) to the center of mass of sensorimotor activation (CoM) (i.e., location), the maximum t-statistic (i.e., significance), the activation volume (i.e., spatial extent), and the average percent signal change (i.e., magnitude).

After calculating the fMRI activation metrics for each subject, we computed the mean and standard deviation of these metrics across subjects. In addition, we calculated s_w, the within-subject standard deviation (Bland and Altman, 1996; Zandbelt et al., 2008), which is defined as:

$$s_w=\sqrt{\frac{{\displaystyle \sum _{i=1}^n}{\sigma }_i^2}{n}},$$

where ${\sigma }_i^2$ is the variance for subject i and n is the total number of subjects. We then divided s_w by the mean of the associated activation metric to find the percentage of the mean for each within-subject standard deviation.

CV analysis

To assess the variability of each fMRI activation metric across a set of five runs, we calculated the coefficient of variation (CV),

$$CV=\frac{\sigma }{\mu },$$

where μ represents the mean of the metric and σ represents the standard deviation. The coefficient of variation ranges from 0, meaning no variability, to higher positive values, indicating increased variability. The CV was calculated at five different activation thresholds (p_FDR < 10⁻², 10⁻³, 10⁻⁴, 10⁻⁵, 10⁻⁶). This analysis was done separately for left and right hemisphere activation for both the head-stabilization runs and the head-repositioning runs.

The metric of average percent signal change for each run was an average of the percent signal change for every activated voxel inside the ROI for that run. For this reason, the error was propagated using standard error propagation techniques. I.e., the error for the average percent signal change of one set of runs was calculated using the formula:

$${\sigma }^{\prime }=\frac{1}{n}\sqrt{\sum _n{{\sigma }_n}^2},$$

where σ_n is the standard deviation of the average percent signal change for each run.

ICC analysis

Voxelwise intraclass correlation coefficients (ICC) were calculated for the group of subjects. Separate analyses were performed for the head-stabilization runs and the head-repositioning runs. Before running the voxelwise ICC analysis, the maps of fit coefficients for each run of each subject were warped to Talairach space. The ICC for the between-subject variance can be defined as:

$${\mathit{ICC}}_{\mathit{Subj}}=\frac{{{\sigma }_{\mathit{Subj}}}^2}{{{\sigma }_{\mathit{Subj}}}^2+{{\sigma }_{\mathit{Scan}}}^2+{{\sigma }_{\mathit{resd}}}^2},$$

while the ICC for the between-scan variance can be defined as:

$${\mathit{ICC}}_{\mathit{Scan}}=\frac{{{\sigma }_{\mathit{Scan}}}^2}{{{\sigma }_{\mathit{Subj}}}^2+{{\sigma }_{\mathit{Scan}}}^2+{{\sigma }_{\mathit{resd}}}^2}.$$

The denominator is a sum of the total variance caused by the subjects (σ_Subj ²), the scans (σ_Scan²), and unknown sources (σ_resd²). These variance components were estimated in a two-crossed-random-effect model via restricted maximum likelihood (REML) method using the AFNI program 3dICC_REML (http://afni.nimh.nih.gov/sscc/gangc/ICC_REML.html). The ICC ratios calculated in this way are equivalent to ICC(2,1) as explained by Shrout and Fleiss (1979). The ICC analysis was applied to the fit coefficients resulting from the multiple linear regression analysis of the contrast of right-handed finger tapping to left-handed finger tapping. (Computation of the ICC on the left to right contrast would have been identical.) A high ICC value (e.g., close to 1) means that the effect being tested (e.g., subject or scan) accounts for much of the variance. A low ICC value means that the effect being tested accounts for little or none of the variance. Resulting voxelwise ICC maps were overlaid onto a Talairach atlas brain.

Results

Motion

Fig. 1 shows four box and whiskers plots made using the inter-run motion parameters. The inter-run rotation parameters for the head-stabilization runs had mean values of 0.2°, 0.4°, and 0.2° for roll, pitch, and yaw, respectively (Fig. 1A). The inter-run rotation parameters for the head-repositioning runs had mean values of 1.7°, 1.7°, and 1.6° for roll, pitch, and yaw, respectively (Fig. 1B). The inter-run translation parameters for the head-stabilization runs had mean values of 0.3 mm, 0.2 mm, and 0.3 mm for inferior-superior, right-left, and anterior-posterior, respectively (Fig,. 1C). The inter-run translation parameters for the head-repositioning runs had mean values of 6.7 mm, 1.7 mm, and 2.0 mm for inferior-superior, right-left, and anterior-posterior, respectively (Fig. 1D). For voxels that were 4 4 4 mm³, the inter-run motion parameters suggest that the head-repositioning runs should suffer from partial volume effects more severely than the head-stabilization runs.

Figure 1.

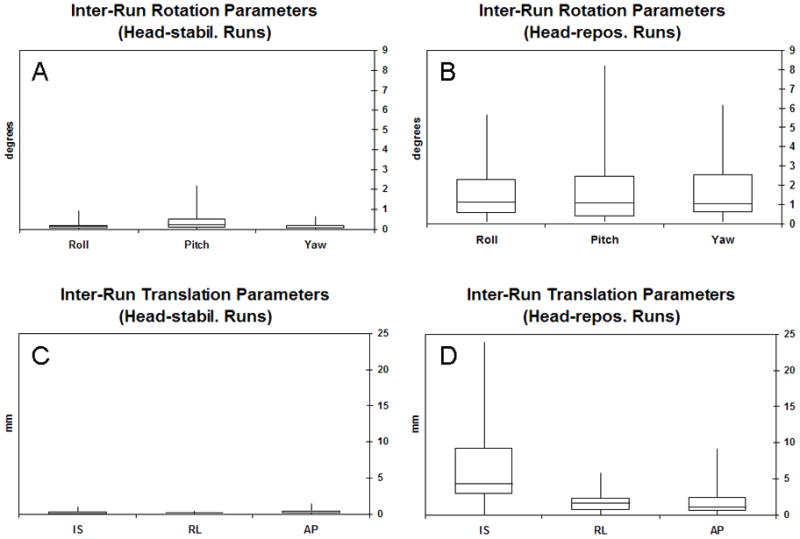
Box and whiskers plots for (A) inter-run rotation parameters for the head-stabilization runs, (B) inter-run rotation parameters for the head-repositioning runs, (C) inter-run translation parameters for the head-stabilization runs, and (D) inter-run rotation parameters for the head-repositioning runs.

An F-test was performed to test the equality of the variances of the inter-run motion parameters between the head-stabilization runs and the head-repositioning runs. For all six motion parameters, the variances for the head-repositioning runs were significantly greater (p < 10⁻¹¹) than the variances for the head-stabilization runs.

Intra-run motion was also evaluated by examining the motion parameters resulting from the volume registration process. For each subject, the maximum intra-run shift averaged across runs was less than 1.5° or 1.5 mm, suggesting that intra-run motion was not a problem for this group of subjects.

Activation

A summary of left-hemisphere fMRI activation at a threshold of p_FDR < 0.01 is shown in Table 1. The mean and standard deviation values for the four fMRI activation metrics are shown for all nine subjects. These values were then averaged across subjects. Also shown is s_w, the within-subject standard deviation. For the head-stabilization runs, the percentage of the mean for s_w was 1% (distance from AC to CoM), 13% (max t-statistic), 24% (activation volume), and 29% (average percent signal change). For the head-repositioning runs, the percentage of the mean for s_w was 1% (distance from AC to CoM), 14% (max t-statistic), 22% (activation volume), and 27% (average percent signal change). No large difference was noted for these values between the head-stabilization runs and the head-repositioning runs.

Table 1.

Runs 1–5, Left Hemisphere, Threshold: pFDR < 0.01
	Distance from AC to CoM (mm)			Maximum t-statistic			Activation Volume (μL)			Average PSC (%)
Subject	Mean	SD	(%)	Mean	SD	(%)	Mean	SD	(%)	Mean	SD	(%)
Subject 1	65.69	0.44	0.67%	10.22	1.40	14%	7040.00	1193.05	17%	1.80	0.46	26%
Subject 2	60.76	0.33	0.55%	9.80	0.84	9%	3200.00	1291.15	40%	2.33	0.45	19%
Subject 3	65.97	0.20	0.31%	13.39	1.52	11%	3980.80	442.02	11%	1.97	0.52	26%
Subject 4	67.03	0.44	0.66%	11.35	1.37	12%	4569.60	930.31	20%	2.86	0.92	32%
Subject 5	67.84	0.29	0.42%	11.94	1.07	9%	5491.20	2055.69	37%	2.01	0.52	26%
Subject 6	60.26	0.60	1.00%	10.91	2.66	24%	3340.80	1210.43	36%	2.91	0.99	34%
Subject 7	64.67	0.15	0.23%	13.69	2.09	15%	5888.00	779.91	13%	2.03	0.58	28%
Subject 8	67.45	0.50	0.74%	10.18	0.68	7%	2688.00	256.00	10%	2.85	0.73	26%
Subject 9	62.86	0.33	0.52%	11.37	0.82	7%	4505.60	435.48	10%	1.81	0.47	26%
Average	64.72	0.37 (SD)	1%	11.43	1.38 (SD)	12%	4522.67	954.89 (SD)	22%	2.29	0.63 (SD)	27%
		0.39 (sw)	1%		1.51 (sw)	13%		1090.65 (sw)	24%		0.66 (sw)	29%

Runs 5–9, Left Hemisphere, Threshold: pFDR < 0.01
	Distance from AC to CoM (mm)			Maximum t-statistic			Activation Volume (μL)			Average PSC (%)
Subject	Mean	SD	(%)	Mean	SD	(%)	Mean	SD	(%)	Mean	SD	(%)
Subject 1	65.74	0.26	0.78%	10.50	0.52	5%	5913.60	912.53	15%	1.90	0.58	31%
Subject 2	60.74	0.35	0.57%	9.31	2.41	26%	2726.40	1531.06	56%	2.51	0.45	18%
Subject 3	66.05	0.21	0.31%	11.24	0.65	6%	3980.80	451.19	11%	2.08	0.54	26%
Subject 4	66.94	0.48	0.72%	12.66	2.07	16%	4979.20	1084.61	22%	2.70	0.84	31%
Subject 5	67.89	0.30	0.44%	10.78	1.39	13%	6387.20	1084.61	17%	1.93	0.47	24%
Subject 6	60.48	0.40	0.67%	13.49	1.54	11%	4723.20	667.26	14%	2.78	0.89	32%
Subject 7	64.84	0.45	0.69%	12.56	1.14	9%	5299.20	1026.40	19%	2.05	0.48	24%
Subject 8	67.61	0.25	0.37%	10.19	2.09	21%	2483.20	683.93	28%	3.15	0.83	26%
Subject 9	62.94	0.24	0.39%	9.68	1.02	11%	3724.80	1076.08	29%	2.04	0.41	20%
Average	64.80	0.33 (SD)	1%	11.16	1.43 (SD)	13%	4468.62	946.41 (SD)	24%	2.35	0.61 (SD)	26%
		0.34 (sw)	1%		1.56 (sw)	14%		992.06 (sw)	22%		0.63 (sw)	27%

Next, we investigated whether run order had any effect on the fMRI activation metrics. For each subject, a t-test was performed to compare the means of the fMRI activation metrics for the head-stabilization runs (runs 1–5) and the head-repositioning runs (runs 5–9) for activation thresholded at p_FDR < 0.01. For all four metrics and all nine subjects, a total of four cases showed a significant difference (p < 0.05). However, there was no pattern for these differences. For one subject, the distance from AC to CoM was greater for runs 1–5, for two subjects, runs 1–5 had a higher maximum t-statistic, and for another subject, runs 5–9 had a larger activation volume. These results show that, while the order of runs may have had a significant effect in some cases, there was no consistent effect on the data.

CV analysis

We calculated the coefficient of variation (CV) at five different thresholds (p_FDR < 10⁻², 10⁻³, 10⁻⁴, 10⁻⁵, 10⁻⁶) for the four fMRI activation metrics described previously. Results were then averaged across subjects. For brevity’s sake, results shown in Table 2 and described below were calculated for a threshold of p_FDR < 10⁻². The CV for activation volume and average percent signal change are plotted over a range of thresholds in Figs. 2 and 3. Because the range of thresholds covered various powers of ten, data are plotted across the − log(p_FDR) along the abscissa. In this case, a threshold of p_FDR = 10⁻² is represented by − log(10⁻²) or 2. Data are plotted separately for the head-stabilization runs and the head-repositioning runs. Fig. 2 shows results for the left hemisphere, i.e. the dominant hemisphere, while Fig. 3 shows results for the right hemisphere.

Table 2.

Coefficient of variation (CV) for the four metrics tested at a threshold of p_FDR < 0.01

Runs	Hemisphere	Distance from AC to CoM	Maximum t-statistic	Activation Volume	Average Percent Signal Change
Head-stabil.	Left	0.01 ± 0.00	0.12 ± 0.05	0.22 ± 0.13	0.27 ± 0.04
	Right	0.01 ± 0.00	0.15 ± 0.05	0.24 ± 0.14	0.29 ± 0.06
Head-repos.	Left	0.01 ± 0.00	0.13 ± 0.07	0.17 ± 0.05	0.26 ± 0.05
	Right	0.01 ± 0.00	0.16 ± 0.07	0.19 ± 0.09	0.27 ± 0.05

Figure 2.

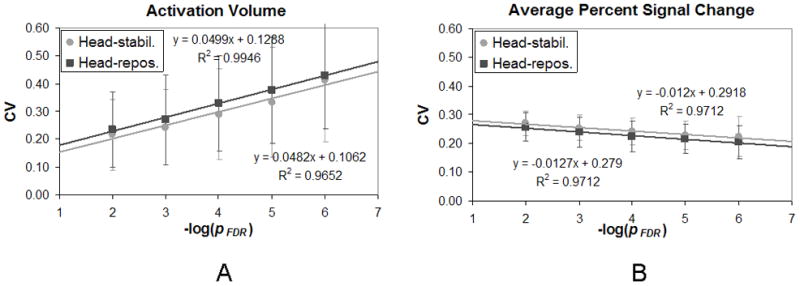
The coefficient of variation (CV) is plotted against the −log of the p_FDR threshold in the left hemisphere for (A) activation volume, and (B) percent signal change. Circles represent the head-stabilization runs while squares represent the head-repositioning runs. (Error bars represent standard deviation.)

Figure 3.

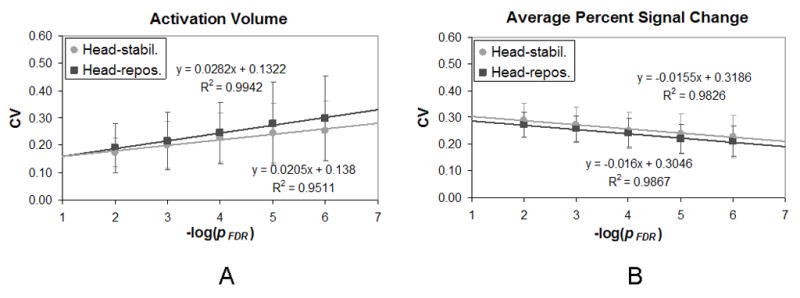
The coefficient of variation (CV) is plotted against the −log of the p_FDR threshold in the right hemisphere for (A) activation volume, and (B) percent signal change. Circles represent the head-stabilization runs while squares represent the head-repositioning runs. (Error bars represent standard deviation.)

The mean CV for location (CV_loc) was equal to 0.01 ± 0.00 for all four cases at a threshold of p_FDR < 0.01 (Table 2). A paired t-test revealed that there was no significant difference between the CV_loc for the head-stabilization runs and the CV_loc for the head-repositioning runs in either hemisphere. Moreover, the CV_loc did not change appreciably as the threshold was increased.

The mean CV for maximum t-statistic (CV_maxt) varied from 0.12 ± 0.05 to 0.16 ± 0.07 at a threshold of p_FDR < 0.01 (Table 2). A paired t-test revealed that there was no significant difference between the CV_maxt for the head-stabilization runs and the CV_maxt for the head-repositioning runs in either hemisphere. The CV_maxt, of course, remained constant as the threshold was increased.

The mean CV for activation volume (CV_vol) varied from 0.17 ± 0.05 to 0.24 ± 0.14 at a threshold of p_FDR < 0.01 (Table 2). A paired t-test revealed that there was no significant difference between the CV_vol for the head-stabilization runs and the CV_vol for the head-repositioning runs in either hemisphere. In addition, the CV_vol appeared to increase linearly as the −log(p_FDR) increased (Figs. 2A and 3A). Paired two-sample t-tests were performed to see if the CV_vol was significantly different between the thresholds of p_FDR < 10⁻² and p_FDR < 10⁻⁶. In both the left and right hemispheres, there was a significant difference in the CV_vol between these two thresholds for both the head-stabilization runs and the head-repositioning runs (p < 0.01). These findings indicated that increasing the severity of the threshold increased the CV_vol and thus reduced the reproducibility of activation volume across runs.

The mean CV for average percent signal change (CV_psc) varied from 0.27 ± 0.04 to 0.29 ± 0.06 at a threshold of p_FDR < 0.01 (Table 2). A paired t-test revealed that there was no significant difference between the CV_psc for the head-stabilization runs and the CV_psc for the head-repositioning runs in either hemisphere. In addition, the CV_psc appeared to decrease linearly as the −log(p_FDR) increased (Figs. 2B and 3B). Paired two-sample t-tests were performed to see if the CV_psc was significantly different between the thresholds of p_FDR < 10⁻² and p_FDR < 10⁻⁶. In the both the left and right hemispheres, there was a significant difference in the CV_psc between these two thresholds for both the head-stabilization runs and the head-repositioning runs (p < 0.01). These findings indicated that increasing the severity of the threshold decreased the CV_psc and thus increased the reproducibility of percent signal change across runs.

ICC analysis

Maps of voxelwise ICC values overlaid on a Talairach atlas brain are shown in Fig. 4. The maps of ICC_Subj for the head-stabilization runs (Fig. 4A) appear very similar to the ICC_Subj maps for the head-repositioning runs (Fig. 4B). Both sets of maps appear to have high ICC_Subj values (>0.8) in cortices connected to motor function: left and right primary sensorimotor cortex (SMC), supplementary motor area (SMA), left and right insula, and left and right cerebellum. The rest of the voxels in the brain have values < 0.2. These data indicated that the subject effect was largely responsible for the variance observed in these cortical areas.

Figure 4.

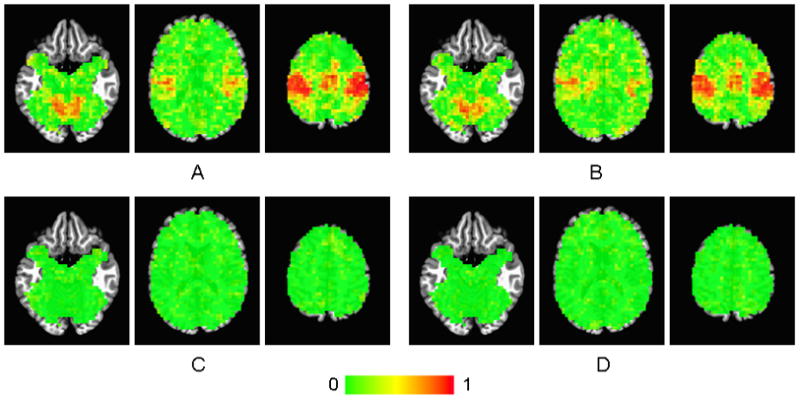
Maps of (A) ICC_Subj for the head-stabilization runs, (B) ICC_Subj for the head-repositioning runs, (C) ICC_Scan for the head-stabilization runs, and (D) ICC_Scan for the head-repositioning runs. The right side of the brain is on the right side of the image.

A scatter plot was made plotting the ICC_Subj values of the head-stabilization runs versus the ICC_Subj values of the head-repositioning runs inside the brain mask (using values above 0.01) (Fig. 5). The fitted slope was 0.85, indicating that the head-repositioning ICC_Subj values were on average slightly less than the head-stabilization ICC_Subj values.

Figure 5.

A scatter plot between ICC_Subj for the head-stabilization runs and ICC_Subj for the head-repositioning runs. The fitted slope is slightly skewed due to a bulk of voxels with low ICC values.

Maps of voxelwise ICC_Scan for the head-stabilization runs (Fig. 4C) appear very similar to the ICC_Scan maps for the head-repositioning runs (Fig. 4D). Both sets of ICC maps appear to have low ICC values (< 0.2) throughout the brain. These data indicated that the scan effect did not contribute much to the variance of the fMRI data.

Discussion

Effect of head-repositioning

Previous studies (McGonigle et al., 2000; Raemaekers et al., 2007) have suggested that head-repositioning is a source of variability in longitudinal fMRI studies. We hypothesized that partial volume effects and spatial non-uniformities in the scanner environment would reduce the reproducibility of fMRI activation metrics for a set of runs acquired with head repositioning compared to a set of runs without head repositioning. In the past, these assumptions have discouraged fMRI researchers from letting subjects leave the scanner during the middle of a scanning session. Alternatively, researchers may have decided to discard data if a subject needed a break during the middle of a session. Discarding data wastes time, money, and effort. Our results show that, in the case of a block-design motor task, there is no need to discard fMRI data if the subject needs to be temporarily removed from the scanner. This finding gives researchers more confidence in using fMRI data when subjects need to leave the scanner in the middle of a session. Furthermore, our finding allows researchers to proceed with long scanning sessions by giving the subject breaks within the session, reducing subject fatigue and potentially improving fMRI results.

Importance of volume registration

One caveat that must be issued before implementing this strategy is that a volume registration method capable of large corrections was required to align the whole brain EPI image volumes to a whole brain structural image – in our case, an MPRAGE. We used a recently developed python script in AFNI (align_epi_anat.py) to align the first image volume of each EPI run to the MPRAGE. This method allowed us to correct for the inter-run motion that occurred due to head-repositioning. Saad et al. (2009) showed that the use of a weighted local Pearson correlation cost function performed superiorly to other cost functions used in traditional registration methods used by software packages like AFNI (Cox, 1996; Cox and Jesmanowicz, 1997), FSL (Jenkinson and Smith, 2001), and SPM (Collignon et al., 1995). If partial brain acquisitions are acquired or if a pulse sequence besides EPI is used for the functional run, the alignment method used may not be sufficiently powerful to correct for inter-run head-repositioning. In this case, an additional whole-brain sequence like an MPRAGE may be needed to accompany the functional runs acquired during each sub-session. An appropriate volume registration method should be fully explored before applying the results of the current study.

Limitations

Using the first five runs as the head stabilization runs and the last five runs as the head-repositioning runs for each subject might be problematic if learning or adaptation effects were present. However, the simple motor task was unlikely to produce any learning effects, as all subjects were able to perform the task easily. Nevertheless, investigating four fMRI activation metrics in all nine subjects revealed four out of 36 cases that showed a significant difference (p < 0.05) between runs 1–5 and runs 5–9. However, there was no pattern for these differences. If this experiment were to be repeated with a cognitive task, where learning effects would be expected, it would be advisable to randomize the ordering of the head-stabilization runs and the head-repositioning runs for different subjects.

Although subjects were visually monitored to make sure they complied with the task, it is possible that subjects altered their finger-tapping rate across runs. This variable rate in finger-tapping would have added variability to the fMRI activation metrics across runs. However, a certain amount of task variability is guaranteed for fMRI studies. Our study showed that any potential, additional variability in fMRI activation metrics caused by head-repositioning was insignificant compared to variability caused by other factors, such as task performance variability.

The sample size of five runs might also be too small to notice a difference in the reproducibility between the two sets of runs. A larger set of runs gathered for both cases would have produced a higher statistical power for detecting any difference. However, if differences in reproducibility cannot be seen after comparing two sets of five runs, any difference that might still exist is likely to be negligible.

Our study analyzed fMRI activation in a block-design motor task. Block-design tasks are known for having strong detection power, but weak ability to estimate hemodynamic time courses (Birn et al., 2002). It is unclear if event-related designs, which are better at estimation, would show more variability in the time courses of BOLD responses over runs acquired with head-repositioning.

The finger-tapping motor task is used quite often in fMRI studies, as it produces a very robust response in a large cortical representation in the sensorimotor cortex. It is unclear if other types of stimuli or tasks would yield the same results as the present study. Partial volume effects and spatial nonuniformities in the scanning environment are expected to have the same effect on different areas of the brain. It is possible that the low attention to the motor task produced the dominant source of variability in fMRI activation over the different runs. A cognitive task that requires increased attention may show a higher amount of reproducibility. Conversely, the robust signal change in the motor cortex may have reduced the variability of fMRI activation. Cognitive tasks show smaller percent signal changes, which might make them more susceptible to variability caused by physiological noise. Therefore, it is uncertain if the results of this study can be extended to activation in other cortices of the brain. Future research would be needed to answer this question.

We removed our subjects from the scanner for one minute before repositioning and rescanning them. If a longer duration (hours or days) was used in between fMRI scans, then changes beyond partial volume effects, such as cognitive and neurophysiological changes, would be expected. It is unclear, however, what time frame would be necessary for the cognitive and neurophysiological changes to induce significant differences in fMRI activation.

Implications for clinical studies

Although we only scanned subjects in single sessions, we gathered reproducibility results on four fMRI activation metrics across runs within a session. Beyond the issue of head-repositioning, our analysis is useful for understanding the relevance of these four metrics vis-à-vis the clinical significance of fMRI activation.

We found that the distance from the AC to the CoM of activation was the most reproducible metric (see Table 2). This distance was used as a scalar proxy for location, as one cannot calculate the variance of a position in a 3-axis coordinate system. Previous studies (Rombouts et al., 1998; Waldvogel et al., 2000) have shown that the location of fMRI activation is highly reproducible across sessions, agreeing with our results. One flaw with our method is that the distance calculated is highly dependent on the origin chosen. Nevertheless, this quantity of distance never varied more than 2 mm for a given subject, which showed a high degree of reproducibility and matched results from a previous study (Rombouts et al., 1998). Since this variability is smaller than the dimension of the voxel used (4 mm on a side), our results confirmed that the location of fMRI activation was highly reproducible across runs within a session.

We chose to evaluate the reproducibility of the maximum t-statistic across runs. The range of the CV_maxt was found to be fairly low (12% to 16% of the mean), suggesting that the maximum t-statistic was a fairly reproducible quantity within a scanning session.

The CV for activation volume (CV_vol) ranged from 17% to 24% of the mean within a session. Early studies also showed that activation volume is not very reproducible across runs or sessions (Rombouts et al., 1997; Rombouts et al, 1998; Cohen and Dubois, 1999; McGonigle et al., 2000; Waldvogel et al., 2000). Our results agree that fMRI activation volume is not a very reproducible metric, even across runs within a session. Therefore, it may not be advisable to use activation volume as a metric in clinical studies. Furthermore, the CV_vol was found to increase linearly as the −log(p_FDR) of the threshold increased. These data revealed that activation volume became even less reproducible at higher thresholds.

The CV for average percent signal change (CV_psc) varied from 26% to 29% of the mean, revealing a low reproducibility. The CV_psc decreased linearly as the −log(p_FDR) of the threshold increased. However, increasing the threshold lowers the sensitivity, so it may not be advisable to use average percent signal change as a metric in clinical studies, even at high thresholds.

Conclusions

We showed that head-repositioning did not reduce the reproducibility of fMRI activation of a block-design motor task within a scanning session, contrary to our original hypothesis. Coefficients of variation were calculated for the distance from the anterior commisure to the center of mass of activation, the maximum t-statistic, the activation volume, and the average percent signal change. The CV for each of these metrics was not significantly different when comparing the head-stabilization runs and the head-repositioning runs. Furthermore, voxelwise ICC maps computed for each of these cases appeared similar.

Analysis of the four fMRI activation metrics revealed that the distance from the AC to the CoM of motor cortex activation was very reproducible. The other three metrics, maximum t-statistic, activation volume, and average percent signal change, were less reproducible, having CV values between 0.12 ± 0.05 and 0.29 ± 0.06 (12% to 29% of the mean). As the severity of the threshold was increased, the reproducibility of activation volume decreased significantly, while the reproducibility of average percent signal change increased significantly.

As fMRI is applied in clinical settings, it is important to understand the reproducibility of the activation maps acquired with this technology. It is also important to know what experimental factors contribute to variability. This study suggests that head-repositioning does not reduce the reproducibility of fMRI activation. Furthermore, we evaluated and compared the reproducibility of four activation metrics from a clinical perspective. We believe that this type of analysis can help to determine the clinical relevance of future fMRI studies.