Low-Income Students and the Socioeconomic Composition of Public High Schools

Abstract

Increasing constraints placed on race-based school diversification have shifted attention to socioeconomic desegregation. Although past research suggests that socioeconomic desegregation can produce heightened achievement, the “frog pond” perspective points to potential problems with socioeconomic desegregation in nonachievement domains. Such problems are important in their own right, and they may also chip away at the magnitude of potential achievement benefits. In this article, I report conducted propensity score analyses and robustness calculations on a sample of public high schools in the National Longitudinal Study of Adolescent Health. As the proportion of the student body with middle- or high-income parents increased, low-income students progressed less far in math and science. Moreover, as the proportion of the student body with middle- or high-income or college-educated parents increased, low-income students experienced more psychosocial problems. Such patterns were often more pronounced among African American and Latino students. These findings suggest curricular and social psychological mechanisms of oft-noted frog pond effects in schools and extend the frog pond framework beyond achievement itself to demographic statuses (e.g., race/ethnicity and SES) perceptually linked to achievement. In terms of policy, these findings indicate that socioeconomic desegregation plans should also attend to equity in course enrollments and the social integration of students more generally.

The common school philosophy contends that democratic societies should educate children from diverse groups under one roof (Cremin 1980). For years, this philosophy has been symbolized by efforts to end racial segregation in public education in the United States. In light of recent court challenges, however, this era of “official” racial desegregation may be drawing to a close (Orfield and Eaton 1996; U.S. Supreme Court 2007). In response, common school advocates often promote socioeconomic desegregation as a means to reduce the socioeconomic stratification of U.S. education and as a back-end way to reduce racial stratification. These efforts have intuitive appeal, empirical support (e.g., findings that poor youths’ test scores are higher in middle-class schools), and a sense of timeliness (Kahlenberg 2001). Still, potential vulnerabilities could, if left unaddressed, undercut their ultimate payoff.

This study examines socioeconomic desegregation by delving into three such vulnerabilities. First, the “frog pond” perspective highlights the negative consequences of being evaluated by relative standing in a group regardless of group composition (Marsh 1987; Marsh and Hau 2003). It suggests that poor students may face greater competition for scholastic credentials and more risks for stigmatization in middle-class schools than in schools with similar peers. These disadvantages are problematic in their own right, and they could very well reduce the magnitude of the achievement gains poor students might accrue in middle-class schools. Second, given the possibility of a “double disadvantage,” these side effects might be more pronounced for poor minority youth (Crosnoe 2005), undermining claims that socioeconomic desegregation can pick-up some goals of defunct racial balancing plans. Third, because of the dearth of experimental data and the many factors confounded with school composition effects on students (Morgan 2001; Reardon, Yun, and Kurlaender 2006), special emphasis must be placed on strengthening causal inference. In this study, therefore, I draw on the National Longitudinal Study of Adolescent Health (Add Health) to analyze the degree to which low-income students’ psychosocial adjustment and enrollment in advanced coursework decreases as the proportion of their public schools’ student body with college-educated, middle- or high-income parents increases. My analyses pay special attention to whether such differences are robust to selection effects. Moreover, I explore these patterns and their implications for historically disadvantaged racial/ethnic groups.

THE SEGREGATION OF U.S. SCHOOLS

Early educational pioneers argued that common schools promote meritocratic mobility, economic productivity, civic participation, and social cohesion (Cremin 1980). In contrast to this philosophy, the United States has a history of racial exclusion in public education. Although progress has been made on this front since Brown vs. Board of Education, race-based desegregation has been fraught with conflict and increasingly challenged in courts (Clotfelter, Ladd, and Vigdor 2005; Coleman, Kelly, and Moore 1976; Logan, Oakley, and Stowell 2008; Reardon, Yun, and Eitle 2001; Wells et al. 2008). The culmination of this trend was Parents Involved, the 2007 Supreme Court decision ending the recognition of racial balance in schools as a compelling state interest. Even before this decision, however, the contentiousness surrounding desegregation was leading to support for race-neutral alternatives. Many looked to socioeconomic desegregation, for example, in which socioeconomic status (SES) replaces race as the standard for managing the composition of schools.

SES plans have two motivations. The first is the potential for school composition to serve as a policy lever in efforts to address socioeconomic disparities in education. Schools have an established history as targets of policy intervention. Moreover, school composition is more straightforward to manipulate, at least within districts, than are other contextual factors such as school climate (Alexander, Entwisle, and Olson 2007; Arum 2000; Coleman and Hoffer 1987). For these reasons, efforts to move low-income students into middle-class schools have gained support. In theory, doing so would expose such students to peers with vocabularies and engagement patterns that support learning. It would also grant underprivileged children access to better organized classrooms with low turnover and more higher-order instruction. Furthermore, such schools often have more involved, informed parents who form networks of social capital, raise non-state financial support, and produce higher standards of performance and accountability (Kahlenberg 2001). Evidence of positive associations between students’test scores and the aggregate SES of their schoolmates, especially from analyses of the National Longitudinal Education Study (NELS), supports this contention (Chubb and Moe 1990; Gamoran 1996; Lee, Smith, and Croninger 1997; Rumberger and Palardy 2005; Rusk and Mosley 1996; Sui-Chu and Willms 1996).

The second motivation is that SES plans could offer a politically palatable way to achieve some aims of racial desegregation. Because socioeconomic disparities in school enrollment and achievement underlie corresponding racial disparities, socioeconomic desegregation should theoretically have the greatest impact on low-income minority students, many of whom would move into middle-class, White schools. In this way, a consequence of official socioeconomic desegregation could be unofficial racial desegregation, reducing both kinds of disparities (Coleman et al. 1966; Kahlenberg 2001; Plank 2000; Rothstein 2004).

Until recently, the most prominent SES plans have been in Wake County (North Carolina), La Crosse (Wisconsin), Cambridge (Massachusetts), and San Francisco (Flinspach and Banks 2005; Kahlenberg 2001; Plank 2000). In the wake of Parents Involved, which highlighted SES plans as a race-neutral approach to school integration, new plans are taking shape in Texas, Kentucky, and other states (Bazelon 2008). Despite the political expedience of this movement, some caution is in order. Below, I delve into two issues that may qualify the promise of SES plans to achieve common schools: (1) the potential for the achievement gains of such plans to obscure nonachievement risks and (2) the possibility that socioeconomic desegregation may not effectively “replace” racial desegregation.

HIDDEN RISKS

Because of the primacy of achievement in policy evaluation, the empirical base for socioeconomic desegregation focuses heavily on test scores. A thorough assessment, however, should consider multiple domains. Indeed, social theory and the history of racial desegregation both suggest that SES plans may pose unintended risks in domains of student functioning other than achievement.

The frog pond perspective, a variant of social comparison theories, contends that students evaluate themselves relative to those in their specific contexts, often regardless of how that context “ranks” in the larger world. In this way, a context offering objective advantages might also bring some subjective risks. To use the colloquial metaphor, a frog will feel like a bigger deal in a small pond than in a large pond (Bassis 1977; Marsh and Hau 2003). Sociologists have extended this concept to include others’ views of the self, not just self-views (Espenshade, Hale, and Chung 2005).

Applying the frog pond framework to socioeconomic desegregation suggests that low-income students’ curricular and social positions may be more vulnerable as the aggregate SES levels of their schools rise. First, if valued commodities are limited, such students are at a competitive disadvantage in high-SES schools (Mayer 2002). In all schools, course offerings and slots in offered courses are finite. Furthermore, students are evaluated relative to each other, with only so many As to go around (Powell, Farrar, and Cohen 1985; Schneider and Stevenson 1999). Because high-SES students are typically better prepared for high school, enjoy greater standing with school personnel, and have parents who know more about how to work the system (Alexander et al. 2007; Lareau 2004), low-income students face fiercer competition for coursework and grades—both tangible markers of progress to colleges and employers—as the number of high-SES students in a school rises. This pattern is seen among racial minority youth in diverse schools (Kelly 2009; Mickelson 2001).

Second, students’ identities develop as they are judged by others in school and use others as a standard of comparison (McFarland and Pals 2005). Because SES is an evaluative marker in diverse settings, poverty is more likely to be a social liability in a school where it is rare than one in which it is well-represented. Indeed, a socioeconomic mismatch is a recipe for spoiled identity (i.e., a stigmatized trait overwhelms a person’s identity and raises the risk of marginalization [Goffman 1963]). Negative self-perceptions and emotional distress are common outcomes of this experience (Link and Phelan 2001). Again, this pattern has been documented for minority youth, whose self-esteem and sense of social belonging tend to decline as the proportion of Whites in their schools increases (Cohen and Lotan 1997; Goldsmith 2004; Johnson, Crosnoe, and Elder 2001). This pattern also applies to low-income youth outside school. For example, mixed-method evaluations of Moving To Opportunity, an experiment in which poor families moved to middle-class neighborhoods, reveal some negative behavioral effects for adolescent boys traceable to self- and other-perceptions that they do not fit into their new, seemingly improved, environments (Clampet-Lundquist et al. 2006; Kling, Liebman, and Katz 2007).

Socioeconomic desegregation could mean that moving into a rich pond exposes poor frogs to real risks to curricular and psychosocial status that have implications for status attainment, health, and well-being over time (Roeser and Eccles 2000; Schneider and Stevenson 1999). This theoretical conclusion suggests a testable hypothesis. Specifically, low-income students in higher SES public schools should persist less far in math and science, receive lower grades, and have more psychosocial problems than their counterparts in lower SES schools.

At first glance, the frog pond hypothesis seems to contradict past evidence on test scoregains related to school SES. Higher SES schools likely provide higher-quality instruction, materials, and learning support to low-income students, even if students take lower-level classes and encounter more psychosocial problems than they would in other schools. If so, higher SES schools would offer tangible benefits to low-income youth that raise test scores but also put an artificial threshold on their coursework and grades. This threshold effect would chip away at the testing gains or create a separate kind of disadvantage even if test scores are not affected.

Consider two similar low-income students who enroll in different science classes because of their school location—student A in Physical Science in a high-SES school and student B in Biology in a low-SES school. Student B has a valued credential that student A does not. Yet, student A might learn more if the high-SES school offers better instruction, course content, and scholastic modeling in its science classes, regardless of level, than the low-SES school. The ideal situation for a low-income student would be a mixture of the two scenarios: taking the higher-level class that is more likely in the low-SES school but with the learning resources available in the high-SES school. Any support for the frog pond hypothesis will thus qualify past reports of the test score gains of low-income students in higher SES schools.

OTHER POINTS OF CONSIDERATION

Although important, hidden frog pond risks are not the only concerns that must be raised when assessing socioeconomic desegregation. Three other issues warrant attention.

First, school SES can be conceptualized multiple ways. Theoretical and methodological concerns favor parent education. The emerging consensus posits parent education as a real source of social capital in schools, and years of schooling and degrees allow more stable discrete categorization than does income, which is volatile (Crosnoe and Huston 2007; Lareau 2004). Practical policy concerns, however, favor family income because tax records are easier to verify than a lack of education credentials (Kahlenberg 2001). I hypothesize that parent education levels will matter more to frog pond effects in schools. Yet, given the fact that most SES plans rely on income criteria, I use school income as a comparative benchmark.

Second, if factors selecting low-income students into schools shape their general functioning, apparent school effects may actually be spurious (Schofield 1995). Because few SES plans have experimental designs, they do not provide sufficient leverage to attribute cause. For example, the Wake County data yield different results depending on the methods used (Flinspach and Banks 2005; Hoxby and Weingarth 2005). Although many NELS studies have longitudinal designs that control numerous confounds (Rumberger and Palardy 2005), additional steps can be taken to bolster causal inference.

By using propensity score weighting (Hirano and Imbens 2001), I address two sets of measurable selection factors suggested by past research (Furstenberg et al. 1999; Hoxby and Weingarth 2005; Morgan 2001). The first taps student behaviors and traits that could qualify for a school move or trigger school recruitment (e.g., cognitive ability and athletic status). The second taps the statuses and resources that help low-income parents navigate children through the system (e.g., marital status and parental involvement). I apply additional methods to quantify the robustness of results to confounds, such as genetics and district-level regulations, that are not measured in national data (Frank 2000).

Third, one argument for SES plans is that they may achieve some of the goals of racial desegregation. Yet, recent studies conclude that the between- versus within-district nature of racial segregation means that SES plans would likely have only small effects on the overall racial segregation of schools (Chaplin 2002; Reardon et al. 2006). Another question is whether SES plans would have different effects by race. For example, low-income minority students may face a double disadvantage that reduces the positive effects and amplifies the negative effects of school reforms that focus on only one demographic status (Crosnoe 2005). Past research finds more racial differences in school composition effects on psychosocial outcomes than on test scores (Johnson et al. 2001; Rumberger and Palardy 2006). If such a double disadvantage does exist, then the replacement argument for SES plans would be further undermined.

Following these concerns, this study examines the hypothesis that the links between school socioeconomic composition and low-income students’outcomes will be more pronounced in minority groups. I expand the usual White versus African American comparison to the growing Latino population; I also take the overall racial composition of schools into account.

METHODS

Data Source

In 1994, Add Health began as a nationally representative sample of 7th to 12th graders (http://www.cpc.unc.edu/addhealth). In the first stage, randomly selected high schools from a stratified sampling frame were matched to a set of feeder middle schools selected with a probability proportional to their student contribution to the high school. Nearly all students in these 132 schools completed the In-School Survey, a questionnaire designed to create an adolescent sampling frame. Of these 90,118 students, a representative subgroup selected evenly across high school–feeder school pairs participated in the Wave I In-Home Interview in 1995 (N = 20,745). Wave I respondents were followed up without the Wave I high school seniors in 1996 (Wave II, N = 14,738) and with them from 2001 to 2002 (Wave III, N = 15, 197). The Adolescent Health and Academic Achievement project (AHAA) collected official transcripts from the last school attended by 91 percent of Wave III respondents (http://www.prc.utexas.edu/ahaa/).

The analytic sample for this study consists of 1,119 low-income (defined below) 9th to 11th graders in public high schools. Of the 1,342 low-income public high school students in Wave I not included in this sample, I dropped 25 percent because Add Health did not follow up Wave I seniors at Wave II, which merely shifted the representativeness of the sample to a narrower grade range. I dropped the remaining cases for being Wave I non-seniors who left the sample by Wave II (30 percent) or Wave III (45 percent). Such longitudinal attrition does bias the sample (see Table 1), but Add Health’s cross-wave sampling weights correct this bias. Only 57 of the 72 Add Health public high schools contain any low-income students. Of these, 47 are represented in the analytic sample; two are dropped because they had no sampling weights calculated, and eight dropped because they did not allow the In-School Survey or had small within-school Wave I samples (which complicates measuring school SES).

Table 1.

Sample Comparisons

	Mean (SD)
	Sample 1a	Sample 2b
Gender (female)	.52	.54
	(.50)	(.50)
Age	16.94	16.71
	(1.23)	(1.16)
White	.31	.32
	(.46)	(.47)
Parent Education	2.22	2.28
	(1.09)	(1.13)
Family Structure (two-parent)	.36	.40
	(.48)	(.49)
N	2,533	1,119

^aSample 1 includes all low-income students in the Wave I sample who were enrolled in a public high school.

^bSample 2 includes all low-income public school 9th to 11th graders who participated in all three In-Home Interviews.

Main Study Variables

Low-income status

I compare Wave I parent reports of household rosters and total income in the past year to the U.S. Census poverty thresholds. Following school lunch guidelines and research conventions (Capps et al. 2005), I label families with incomes below 185 percent of the 1994 poverty line for their household size as low-income. For example, the poverty threshold for a family of four in 1994 was $15,141. I therefore identify any student from a family of four with a parent-reported income of $28,011 or lower as low-income. Given evidence of the confounding role of family wealth in income disparities in education, especially across races (Yeung and Conley 2007), the lack of information on wealth in Add Health should be viewed as a limitation of this study.

School socioeconomic composition

To assess how the outcomes of low-income students vary as a function of school socioeconomic composition, I measure the proportion of middle- and upper-class students in each school. Given that the methodologies of this study require a treatment group, I convert these school-level proportions into a set of meaningful categories. For the first task, the In-School Survey had a census-like structure for each school, which allows for the aggregation of data across all respondents in a school. Because college education is a qualitative breakpoint in SES, I collapse student responses on a multipoint scale of parents’ educational attainment to create a binary marker (1 = at least one parent is a four-year college graduate) and then average it within schools to measure the proportion of students with college-educated parents. Income data are only available at Wave I, a representative sample of each school. Without meaningful breakpoints, categorizing the income measure is not straightforward. After testing both extant policy thresholds and common econometric strategies, I settled on incomes exceeding 300 percent of the poverty line for household size as the middle-class threshold. This binary income marker has the largest overlap with the parent education marker (in terms of classifying cases as middle to upper class). For the second task, I reviewed several different strategies for breaking down the school-level proportions into groups. The strategy that best balances cell sizes with meaningfulness identifies three types of schools. In the high-SES schools, at least 40 percent of parents exceed the education and income thresholds. In the low-SES schools, less than 20 percent of parents do so. Schools in which 20 to 40 percent of parents exceed these thresholds make up the middle category.

The average low-income student attended a high school in which a quarter of students had at least one college-educated parent or a family income exceeding 300 percent of the poverty line for their household size (see Table 2). For both school income and parent education, 20 to 40 percent is the modal category. Table 3 provides a cross-tabulation of the two school SES dummy variables. As would be expected, students cluster on the diagonal, with some mismatches at the margins. The exception is that more students from the first parent education category are in the second family income category than in the first (204 versus 185).

Table 2.

Descriptive Statistics for Selected Study Variables

	Mean (SD)	Percent
High School Characteristics
Mean % of student body in students’ schools from families at 300+% poverty line	.26
	(.14)
% of sample in schools with < 20% of student body from middle/high-income families		36.25
% of sample in schools with 20 to 40% of student body from middle/high-income families		44.92
% of sample in schools with > 40% of student body from middle/high-income families		18.83
Mean % of student body in students’ schools with college-educated parents	.26
	(.10)
% of sample in schools with < 20% of student body with college-educated parents		24.23
% of sample in schools with 20 to 40% of student body with college-educated parents		66.54
% of sample in schools with > 40% of student body with college-educated parents		9.23
Student Academic Indicators
Final math course level	5.35
	(1.86)
Final science course level	3.96
	(1.24)
Final grade point average	2.22
	(.83)
Student Psychosocial Indicators
Negative self-image (Wave II)	1.86
	(.60)
Perceived social isolation (Wave II)	1.91
	(.73)
Depression (Wave II)	8.20
	(6.11)

Note: N = 1,119 low-income students in public schools. The academic indicators represent end-of-school outcomes from four-year school transcripts, which could occur anywhere between 0 to 2 years prior to Wave II, depending on whether the student was in 11th, 10th, or 9th grade in Wave I.

Table 3.

Cross-Tabulation of Two School SES Typologies (N = 1,073)

	Proportion College-Educated Parents
	< 20%	20 to 40%	> 40%
Proportion Middle- or High-Income Parents
< 20%	185	67	8
20 to 40%	204	386	124
> 40%	0	29	70

Academic indicators

AHAA transcripts provide three end-of-school progress markers. Two coursework measures tap students’ locations in the curricular hierarchy, exposure to challenging work, and ability to meet college requirements (National Center for Education Statistics [NCES] 2003). Grade point average (GPA)—a widely recognized marker of school success that factors into college enrollment and labor market entry—taps students’ ability to meet teachers’ expectations for appropriate behaviors and attitudes and the effort they exert to meet these expectations (Lee et al.1997; Rosenbaum 2001). AHAA coursework measures exploit the standardized hierarchical nature of math and science in secondary education. Based on the taxonomy for all NCES data sets (Schneider, Swanson, and Riegle-Crumb 1998; Stevenson, Schiller, and Schneider 1994), Classification of Secondary School Courses codes are assigned to each class on a transcript and then collapsed into primary categories (see Table 4). Values denote the highest level reached before graduating or dropping out. Although course sequences are ordered hierarchical categories, they are generally studied as continuous outcomes (Riegle-Crumb, Farkas, and Muller 2006). AHAA also includes a comprehensive GPA ranging from 0 to 4, created by averaging transcript-reported grades across all classes and semesters. Referring back to Table 2, low-income students typically earned Bs and Cs and completed Geometry and Biology I by the end of high school. Not only are these coursework levels a point below the levels of all Wave I students (not shown), they indicate that the average low-income student did not reach the curricular thresholds (Algebra II, Chemistry) that best predict college enrollment (Adelman 1999).

Table 4.

Categories in Math and Science Coursework Sequences

Math	Course	Science	Course
0	No Math	0	No Science
1	Remedial	1	Basic
2	General	2	General/Earth Science
3	Pre-algebra	3	Biology I
4	Algebra I	4	Chemistry I
5	Geometry	5	Advanced Science (e.g., Biology II)
6	Algebra II	6	Physics
7	Advanced Math (e.g., Statistics)
8	Pre-calculus/Trigonometry
9	Calculus

Psychosocial indicators

Based on past Add Health research (Crosnoe 2006; Resnick et al. 1997), I created three psychosocial constructs. First, students rated agreement (1 = strongly agree, 5 = strongly disagree) with four items on self-worth: “you have a lot of good qualities,” “you have a lot to be proud of,” “you feel that you are doing everything just right,” and “you like yourself the way you are.” The average of responses measures negative self-image (α = .79). Second, I reverse coded a self-rating of social acceptance (1 to 5) to measure perceived isolation in the school. Third, Add Health includes a modified version of the Center for Epidemiological Studies Depression Scale (Radloff and Locke 1986), in which students reported how often they experienced 15 symptoms of depression, such as loneliness, ranging from 0 (never or rarely) to 3 (most or all of the time). The sum of these responses measures depression (α = .86). Recall that the transcript measures tap end-of-school outcomes. The Wave II psychosocial indicators came at the end of high school for Wave I 11th graders, a year before the end for Wave I 10th graders, and two years before the end for Wave I 9th graders. According to the Wave II means in Table 1, low-income students generally had good absolute levels of psychosocial functioning. Still, they look relatively worse than all Wave I respondents (not shown).

Race/ethnicity

Dummy variables capture the biggest racial/ethnic demarcations in the sample: 32 percent White, 30 percent African American, 29 percent Latino, and 9 percent Other. I also aggregate In-School Survey data into a continuous measure (M = 60.55, SD =33.73) of the proportion of students in each school who were members of non-White racial/ethnic groups.

Plan of Analyses

To deal with selection issues, I combine propensity score weighting with robustness calculations (Frank and Sykes 2008). Propensity scores represent the conditional probability of receiving a treatment given observable characteristics selecting individuals into treatment (Rosenbaum and Rubin 1983). Here, enrollment in a medium- or high-SES school is the treatment, enrollment in a low-SES school the control. Using psmatch in STATA, I estimated logistic regressions that predict membership in the school SES categories by variables tapping the two focal selection processes (student traits and parent statuses/resources), as well as gender (to account for scholastic and athletic differences between boys and girls [Crosnoe 2006]), mean GPA of in-school peers (in case school SES effects are driven by peer achievement [Hoxby and Weingarth 2005]), and 9th grade academic indicators and Wave I psychosocial indicators (because of feedback between school SES and outcomes). Table A1 in the Appendix has descriptions of all propensity variables. The predicted probabilities generated from these models—the propensity scores—measure the characteristics of the average low-income student in treatment schools in order to identify similar low-income students in control schools.

Table A1.

Descriptions of Variables Used to Make Propensity Scores

Variable	Description
Gender	1 = female (54 percent), 0 = male.
Immigrant generation	Dummy variables, based on self-report, for first generation (foreign-born, 16 percent), second generation (U.S.-born with at least one foreign-born parent, 17 percent), third generation (U.S.-born with U.S.-born parents, 66 percent).
Measured ability	Scores, in percentiles, on an abridged version of the Peabody Picture Vocabulary Test (M = 37.75, SD = 26.12).
Diagnosed learning disability	1 = parent reported that student had been diagnosed with a learning disability (e.g., dyslexia) by a professional (11 percent), 0 = no such diagnosis.
Athletic participation	1 = student reported participation in at least one school sport program (32 percent), 0 = no such participation.
Extracurricular activity participation	1 = student reported membership in at least one school extracurricular activity (36 percent), 0 = no such participation.
Students’ educational aspirations	Students reported, on a scale of 1 to 5, how much they wanted to go to college (M = 4.21, SD = 1.21).
Prior negative self-image	Wave I version of negative self-image (see Main Study Variables section) (M = 1.94, SD = .80).
Prior perceived social rejection	Wave I version of perceived social rejection (see Main Study Variables section) (M = 1.96, SD = .81).
Prior depression	Wave I version of depression (see Main Study Variables section) (M = 8.44, SD = 6.48).
Math course level (9th grade)	9th grade version of final math coursework level (see Main Study Variables section) (M = 2.15, SD = 1.32).
Science course level (9th grade)	9th grade version of final science coursework level (see Main Study Variables section) (M = .97, SD = .79).
Overall grade point average (9th grade)	9th grade version of final GPA (see Main Study Variables section) (M = 2.27, SD = .91).
Parent education	See Main Study Variables section.
Family income	See Main Study Variables section (except continuous measure used).
Family structure	Dummy variables, based on parent and adolescent reported household rosters, for two biological parent (40 percent), single parent (35 percent), stepfamily (17 percent), and other (7 percent).
Parents’ educational aspirations	Parents reported, on a scale of 1 to 3, how disappointed they would be if student did not go to college (M = 2.31, SD = .75).
Parental involvement in education	Students reported whether, in the past month, their mothers had talked with them about grades or school or worked with them on a school project. These items were summed, and then the same procedure was followed for fathers. The final construct is the mean of the maternal and paternal constructs (α = .88) if information is not missing for both parents; otherwise, the score for the non-missing parent serves as the value (M = 1.24, SD = .89).
Parent-adolescent closeness	Student assessments of the degree to which they felt close to their fathers, felt that their fathers were warm, felt that they communicated well with their fathers, and were satisfied with their relationships with fathers (responses range from 1 to 5). These responses were averaged and the same procedure was followed for mothers. The final construct is the mean of the maternal and paternal constructs (α = .88) if information is not missing for both parents; otherwise, the score for the non-missing parent serves as the value (M = 4.21, SD = .68).
Home language use	1 = adolescent reported that language other than English was primary language spoken at home (23 percent), 0 = English was primary language.
Chose community for schools	At Wave I, parents reported that good schools were the reason they lived in their current neighborhood (47 percent).
Friends’ academic achievement	Mean GPA (0 to 4) of all friends nominated by the respondent in the In-School Survey. Over a third of the sample is missing on this measure for a variety of reasons. Wave I values were imputed when available, otherwise the sample mean was imputed with a binary marker of missingness/imputation used as a covariate (M = 2.68, SD = .42).

Note: All variables measured at Wave I (which could correspond to 9th, 10th, or 11th grade). The transcript measures were measured at 9th grade, which could have been the same time as Wave I or one to two years prior to Wave I.

Such propensity scores are typically used for matched comparisons, that is, comparing outcomes for treatment and control cases with the same propensity score and, therefore, the same likelihood of being in the treatment. Using propensity scores as model weights is a variation on matching that is more efficient and does not require unmatchable cases to be excluded (Hirano, Imbens, and Ridder 2003; Morgan and Harding 2006). With this technique, outcomes are regressed on the treatment variable in a model weighted by propensity scores, which over- or undercounts control cases in the sample depending on their propensity to be in the treatment group. Another bonus of this strategy is that it facilitates the explicit estimation of focal covariates alongside and in interaction with the treatment effect.

To illustrate this approach, consider depression in schools with high parent education. First, because the propensity score represents the predicted probability of enrollment in a high parent education school (treatment) compared with a low parent education school (control), the sample must be reduced to students in these two types of schools only. Second, the propensity score must be transformed into a modeling weight. The equation for doing so is the following: w(t,x) = t + (1 − t)/[1 − e(x)], where e(x) is the propensity score, t is treatment status, and x refers to the covariates (Hirano and Imbens 2001). The resulting weight captures the treatment effect on the treated. Third, I regressed Wave II depression on the marker for high parent education schools (the treatment) in a multilevel model with the propensity score as a modeling weight. Because the weight captures the treatment effect on the treated, doing so weights any low-income students in the high parent education school at 1 and weights any low-income students in the low parent education schools according to their value on the weight. This regression compares the depression of students in high and low parent education schools, overcounting the students in low parent education schools who have the same personal and family characteristics as the students in high parent education schools (Frank and Sykes 2008). Fourth, I enter the race/ethnicity measures (student and school) into this model as covariates.¹

Propensity scores only account for identifiable, measurable confounds. As a complement, robustness indices address problems related to unknown, or at least unmeasured, confounds. For example, the Impact Threshold for Confounding Variables (ITCV) does not control for the impact of unmeasured confounds on a focal association, but rather quantifies how powerful they must be to negate causal inference for that association. In a sense, it estimates a confidence interval for the inference (for original formulation, see Frank 2000; for applications, see Augustine, Cavanagh, and Crosnoe forthcoming; Cheng, Martin, and Werum 2007). The equation is the following: r_x,y − r^#_x,y / 1 − r^#_x,y, where r^#_x,y = t / SQRT[(n − q − 1) + t²], t is the critical t-value, n is the sample size, and q is the number of model parameters. The value identifies the minimum product of the correlation between predictor and confound and the correlation between outcome and confound (r_x,cv × r_{y, cv}) needed to reduce the focal association to nonsignificance. If the actual (if unknown) product of the two correlations exceeds this threshold, then controlling for that unobserved confound (if it could be observed) would likely alter the causal inference. Alternatively, if it is smaller, then confidence is gained. In this study, I calculated the ITCV for any significant school SES coefficient in a weighted regression. In all cases, the propensity score is partialed out of the focal correlation between predictor and outcome (r_{x,y|propensity} score).

This two-step procedure accounts for theoretically identifiable confounds that could be measured in Add Health and then gauges the degree to which the omission of any theoretically identifiable confounds that could not be measured in Add Health, or any unknown confounds, might impact the results. Although this process does not establish causality, it does improve confidence in causal inference about the impact of school enrollment on student outcomes.

RESULTS

Public High Schools of Varying Socioeconomic Composition

Table 5 presents school- and student-level cell sizes for the school SES categories. Although small, these cell sizes encompass a high degree of internal variation within and across categories. Moreover, the categories differ from each other on both levels. For example, a majority of the 10 low family income schools and nine low parent education schools had concentrated minority populations (over 40 percent of the full student body). These schools also tended to be located in urban areas. By contrast, the majority of high family income and high parent education schools had minority populations of less than 40 percent and were located in suburbs. As another example, the proportion of low-income minority students decreased across each school SES category. Notably, the dropout rate for low-income students (and for all Add Health students, not shown in table) does not differ significantly across the school categories.

Table 5.

Breakdown of Two School SES Typologies

	Proportion Middle- or High-Income Parents			Proportion College-Educated Parents
	< 20%	20 to 40%	> 40%	< 20%	20 to 40%	> 40%
School-Level
Total number of schools in category	10	20	17	9	24	14
Concentrated minority school	8a	9ab	2b	6a	10ab	3b
Urban	5	6	2	4	6	3
Suburban	4b	11ab	14a	3b	15a	11ab
Rural	1	3	1	2	3	0
Student-Level
Total number of students in category	389	482	202	260	714	99
White	42c	157b	142a	75b	223b	43a
African American	171a	127b	22c	123a	168b	29b
Latino	161a	129b	24c	53b	234a	27b
Other race/ethnicity	15b	69a	14b	9b	79a	10ab
Dropout	38	55	25	34	80	4

Note: N = 1,073 (students), 47 (schools). A concentrated minority school had 40 percent or more of the student body from racial/ethnic minority groups. Within same row under same school SES typology, Ns with different subscripts differed significantly according to one-way anova. For the school-level comparisons, statistical significance is measured at p < .10. For student-level comparisons, it is measured at p < .05. For school- and student-level variables, the column sums do not equal the total number of schools in the category for three reasons. First, concentrated minority schools could have been urban, suburban, or rural. Second, the number of schools with a 0 on the binary concentrated minority school variable is not presented, although it can be inferred from what is presented. Third, dropouts could come from any racial/ethnic group.

Although these descriptive analyses suggest that the small number of public high schools in Add Health can support an investigation of school socioeconomic composition, I should note that the case coverage is thin in places. For example, only two of the high income schools and three of the high parent education schools had concentrated minority student bodies. Moreover, fewer than 20 low-income students attended each of these schools. Although Add Health is the best available data set for examining the kinds of questions posed in this study, it is far from ideal. Looking at the results that follow, we should keep this note of caution in mind.

Proportion of Students in School with Middle- or High-Income Parents

The first dimension of school SES is the proportion of students whose parents had middle or high incomes. Table 6 presents the results from regressions for six outcomes predicted by enrollment in medium family income schools (20 to 40 percent of the student body had parents with middle or high incomes) relative to low family income schools (less than 20 percent), with the 202 students in high family income schools (over 40 percent) dropped from the analyses. Table 7 presents the results for the same models comparing the low-income students in high and low family income schools, with the 482 students in medium family income schools dropped.

Table 6.

Unweighted and Weighted Results for Academic and Psychosocial Indicators, Comparing Students in Schools with Less than 20 Percent Middle- or High-Income Parents with Counterparts in Schools with 20 to 40 Percent Middle- or High-Income Parents

	Final Math Course Level			Final Science Course Level			Final Grade Point Average
	1	2	3	1	2	3	1	2	3
20 to 40 percent middle-     or high-income school	−.25	−.44	−.81	−.45***	−.40**	.13	.25*	.05	−.28
	(.24)	(.24)	(.60)	(.10)	(.15)	(.30)	(.10)	(.16)	(.32)
School minority     representation		–.001	–.002		.003	.003		−.002	−.003
		(.004)	(.004)		(.003)	(.003)		(.003)	(.003)
African American		.08	−.08		.09	.37		−.10	–.28
		(.29)	(.47)		(.17)	(.27)		(.11)	(.20)
Latino		–.19	–.37		–.03	–.27		–.11	–.27
		(.33)	(.51)		(.19)	(.25)		(.12)	(.20)
School income ×     African American			.35			−.63			.42
			(.61)			(.33)			(.26)
School income ×     Latino			.48			−.71*			.36
			(.71)			(.30)			(.32)

	Negative Self-Image			Perceived Social Isolation			Depression
	1	2	3	1	2	3	1	2	3
20 to 40 percent middle-     or high-income school	.15*	.03	−.20	.08	−.01	−.16	.33	.40	−2.32*
	(.07)	(.09)	(.12)	(.08)	(.10)	(.10)	(.49)	(.50)	(1.04)
School minority     representation		−.001**	−.002		−.001	.00		.001	−.002
		(.002)	(.001)		(.002)	(.002)		(.01)	(.01)
African American		−.23**	.30***		−.12	−.16		−.43	−1.62
		(.07)	(.09)		(.08)	(.09)		(1.10)	(1.19)
Latino		.03	−.08		−.03	.09		−1.00	−2.15
		(.09)	(.12)		(.08)	(.09)		(1.13)	(1.23)
School income ×     African American			−.16			.08			2.97*
			(.13)			(.10)			(1.44)
School income ×     Latino			.33*			.20*			3.17**
			(.14)			(.10)			(1.21)

Note: N = 863 (self-image, social isolation, GPA), 862 (depression), 846 (math), 851 (science). White is the reference for race/ethnicity dummy variables and interactions. Other race/ethnicity is also included but not shown in the table. For each outcome, Models 2 and 3 are weighted by the transformed propensity score.

^*p < .05;

^**p < .01;

^***p < .001.

Table 7.

Unweighted and Weighted Results for Academic and Psychosocial Indicators, Comparing Students in Schools with Less than 20 Percent Middle- or High-Income Parents with Counterparts in Schools with Over 40 Percent Middle- or High-Income Parents

	Final Math Course Level			Final Science Course Level			Final Grade Point Average
	1	2	3	1	2	3	1	2	3
Over 40 percent middle-     or high-income school	−.61**	−1.07*	−.95	−.58***	−.01	.08	.12	−.28	−.33
	(.20)	(.51)	(.57)	(.15)	(.34)	(.37)	(.12)	(.44)	(.45)
School minority     representation		−.01	−.01		.01	.01		–.01	–.005
		(.01)	(.01)		(.01)	(.01)		(.01)	(.006)
African American		−.31	.20		.25	.35		−.13	−.17
		(.33)	(.32)		(.16)	(.19)		(.12)	(.15)
Latino		−.37	−.28		.00	.07		−.18	−.26
		(.50)	(.40)		(.19)	(.22)		(.16)	(.21)
School income ×     African American			–.97*			–.44			–.12
			(.46)			(.25)			(.28)
School income ×     Latino			.18			–.08			.20
			(.68)			(.26)			(.31)

	Negative Self-Image			Perceived Social Isolation			Depression
	1	2	3	1	2	3	1	2	3
Over 40 percent middle-     or high-income school	.12*	–.22*	–.34***	.14	–.09	–.16	–.93	–1.99	–2.73*
	(.06)	(.10)	(.09)	(.08)	(.16)	(.14)	(.55)	(1.10)	(1.24)
School minority     representation		–.004***	–.004**		–.002	–.002		–.01	–.01
		(.001)	(.001)		(.003)	(.003)		(.02)	(.02)
African American		–.18*	.31***		– .12:	–.19		–.49	–1.24
		(.08)	.07		(12)	(.13)		(1.01)	(1.25)
Latino		.07	–01		0.2	.00		–.34	–.85
		(.09)	(.11)		(.12)	(.15)		(1.59)	(2.21)
School income ×     African American			.63***			.33*			2.90
			(.11)			(.16)			(1.88)
School income ×     Latino			.04			–.08			.41
			(.16)			(.17)			(2.29)

Note: N = 591 (self-image, social isolation), 590 (depression), 581 (math, GPA), 578 (science, GPA). White is the reference for race/ethnicity dummy variables and interactions. Other race/ethnicity is also included but not shown in the table. For each outcome, Models 2 and 3 are weighted by the transformed propensity score.

^*p < .05;

^**p < .01;

^***p < .001.

For each outcome in both tables, Model 1 provides the unweighted results from the regression in which the focal school income category is the sole predictor. Compared with low-income students in low family income schools, those in medium and high family income schools reached lower levels of math and science and reported more negative self-images and feelings of isolation (only high family income schools for math and isolation and only marginally significant at p < .10 for isolation). At the same time, they made better grades (medium only) and reported fewer depressive symptoms (high only and only marginally significant).

To assess the robustness of these results to observable confounds, I generated propensity scores that index the probability of being in a medium or high family income school relative to a low family income school. Although many of the measured factors do not predict school enrollment, some do, especially family income itself, parents’ college aspirations for students, and student cognitive ability. I then transformed the predicted probabilities for each school SES category into weights. Model 2 in each table presents the results of the weighted regressions, which also include student and school racial/ethnic factors as covariates. Only four school effects from Model 1 persist. Low-income students reached significantly lower levels of science in medium (versus low) family income schools and marginally lower levels of math (Table 6). The effect sizes equal about a half course level for each subject, representing a quarter and a third of a standard deviation in these variables, respectively. This math disadvantage is even bigger in high family income schools (Table 7)—a full course level representing over half a standard deviation effect size. The students in the high (versus low) family income schools also had more negative self-images (one-third of a standard deviation) after weighting.

Next, I assess how robust the four significant coefficients in the weighted models are to unmeasured confounds. The largest ITCV (.14) is for the medium family income school coefficient in the science model. Controlling for some unobserved confound would reduce this coefficient to nonsignificance as long as the confound is correlated with both enrollment in a medium family income school (r_xc) and science level (r_yc) at .37 or higher. Inspection of numerous Add Health measures reveals none that are correlated with both at this magnitude. The ITCV values for the school coefficients in the math models are more moderate: .04 (r_xc × r_yc = .20 × .20) for medium family income schools and .07 (r_xc × r_yc = .26 × .26) for high family income schools. Still, this threshold is too high for any inspected variable in Add Health to meet. The ITCV for the high family income school coefficient in the self-image model (less than .01), however, is too small to offer any confidence that it would be robust if a full set of confounds could be controlled.

Finally, Model 3 (for each outcome) includes interactions between the school marker and the race/ethnicity dummy variables, controlling for school racial/ethnic composition and weighted by the propensity score. I interpret significant interactions by graphing the predicted values of the outcome for White, African American, and Latino students in each school type, holding school minority representation to its sample mean. Enrollment in medium family income schools interacts significantly with at least one race/ethnicity category to predict science course-work and all three psychosocial outcomes (see Table 6).

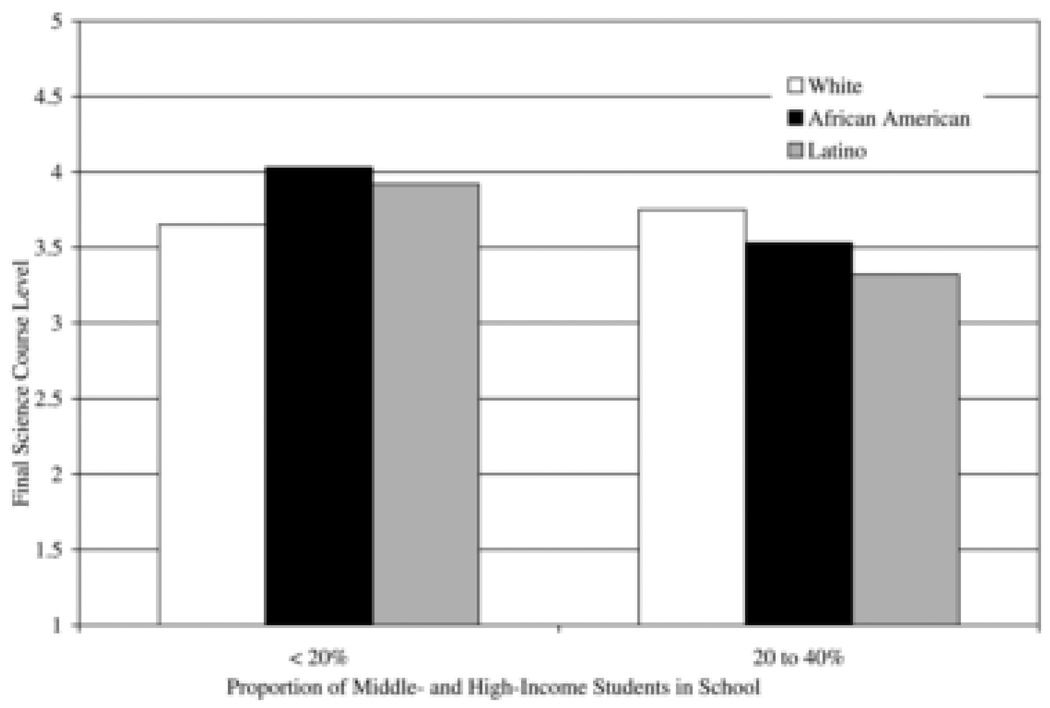
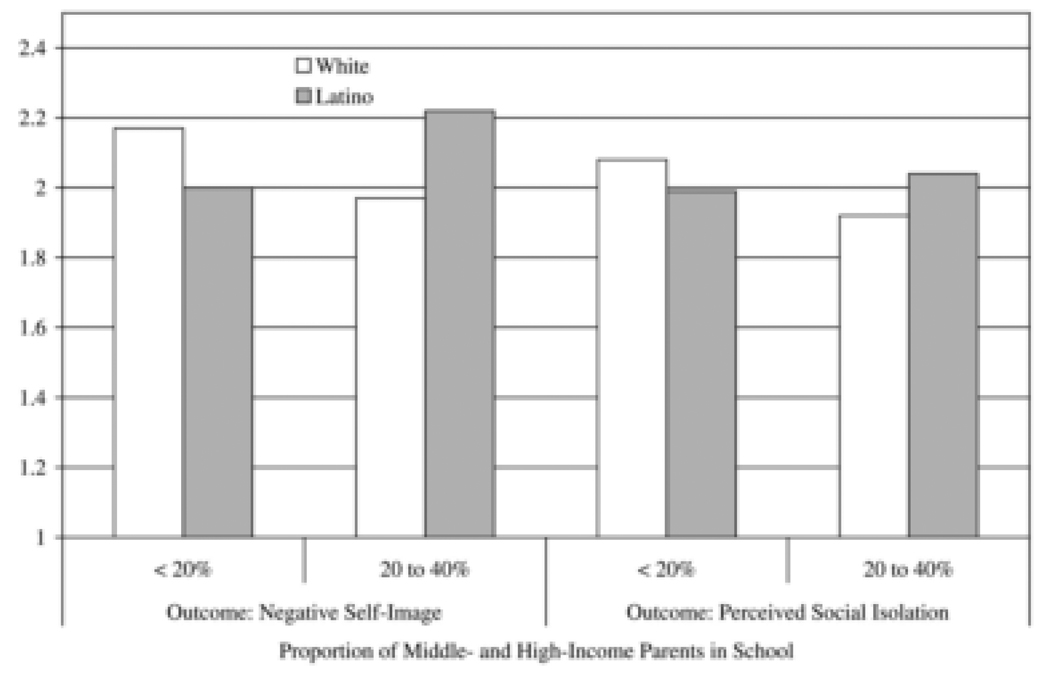
As depicted in Figure 1, the previously reported decrease in science course level associated with attending a medium (versus low) family income school holds for African American and Latino youth (although the interaction for African American narrowly misses statistical significance). Indeed, the differences between the two black bars represent a half course level (4.03 versus 3.53), and the differences between the two gray bars represent almost two-thirds of a course level (3.92 versus 3.32). White students actually post a slight nonsignificant increase in course level in the medium family income schools (3.75), compared with the low family income schools (3.65). Turning to Figure 2, White students’ scores on negative self-image and perceived isolation are lower in medium family income schools (versus low). The differences between the white bars represent 33 percent of a standard deviation for self-image (2.17 to 1.97) and 22 percent of a standard deviation for social isolation (2.08 to 1.92). Latino students’ scores, however, are higher in such schools (22 and 10 percent effect sizes, respectively). The same pattern holds for the two significant interactions in Model 3, for depression, in Table 6.

Figure 1.

Weighted Comparisons of Science Course Level between Schools Differing in Proportion of Middle- and High-Income Parents, by Race/Ethnicity

Figure 2.

Weighted Comparisons of Psychosocial Indicators between Schools Differing in Proportion of Middle- and High-Income Parents, by Race/Ethnicity

In Table 7, enrollment in high (versus low) family income schools interacts with African American status to predict four outcomes. The previously reported negative association between such enrollment and math coursework is especially pronounced for African American students. Indeed, their cross-school difference equals two full course levels. They also demonstrate a similar, albeit smaller and marginally significant, disadvantage in science coursework that is not seen in the general sample. Finally, African American students are the only group in which negative self-images and perceptions of social isolation are more pronounced in high family income schools than in low family income schools. The ITCV for both is higher in the African American subsample than in the full analytic sample.

In summary, when low-income students differed in academic and psychosocial functioning across schools, those in medium and high family income schools usually looked worse. The selection of low-income students into different school types accounts for some of these apparent school effects. Accounting for such selection, the general pattern is that low-income students had lower coursework levels in medium and high family income schools and greater perceptions of social isolation in high family income schools. Focusing on racial/ethnic differences reveals more evidence for the hypothesis of this study. For example, low-income Latinos demonstrated disadvantages across most outcomes in medium (versus low) family income schools, and African American students experienced disadvantages in at least half the outcomes in medium and high family income schools. Whites’ disadvantages were limited to math, and they often demonstrated psychosocial advantages in medium and high family income schools.

Proportion of Students in School with College-Educated Parents

The second dimension of school SES is the proportion of students with at least one parent who graduated from college (see Table 8). First, in unweighted regressions (Model 1), we see that low-income students in medium and high parent education schools made better grades than those in low parent education schools, but they also had more negative self-images and perceived themselves to be more socially isolated (isolation effect only marginally significant in Comparison 2). Second, in the logistic models that generated the propensity scores (not shown), parent education itself, nativity, student cognitive ability, and parents’ selection of neighborhood for school quality are the strongest of the few factors that significantly predict enrollment in either medium or high parent education schools. Weighting with the transformed propensity scores (Model 2) eliminates the initial school differences in GPA and negative self-image, but it leaves the initial school difference in social isolation unchanged. Additionally, weighting reveals a new pattern of greater depression in medium (versus low) parent education schools. Third, the school parent education coefficients have moderate ITCV values only for the social isolation models (ITCV = .03, r_xc × r_yc = .17 × .17, for both medium and high family income schools). Fourth, the parent education school markers do not interact with any race/ethnicity dummy variables in any model (not shown).

Table 8.

Unweighted and Weighted Results for Academic and Psychosocial Indicators, Comparing Students in Schools with Less than 20 Percent College-Educated Parents with Counterparts in Schools with 20 to 40 percent and Over 40 Percent College-Educated Parents

	Final Math Level		Final Science Level		Final Grade Point Average		Negative Self-image		Perceived Social Isolation		Depression
	1	2	1	2	1	2	1	2	1	2	1	2
Comparison 1
20 to 40 percent college-educated school	−.30	−.38	−.05	−.02	.23*	.09	.16**	.09	.22***	.19***	.37	1.00**
	(.24)	(.25)	(.17)	(.17)	(.16)	(.09)	(.06)	(.07)	(.05)	(.05)	(.48)	(.34)
School minority representation		.01		.01		−.001		.001		.002		.02
		(.005)		(.003)		(.002)		(.001)		(.001)		(.01)
African American		.06		.13		−.12		−.22		−.13*		.06
		(.29)		(.13)		(.11)		(.13)		(.06)		(.70)
Latino		−.21		−.10		−.11		−.06		−.11		−1.13
		(.33)		(.19)		(.11)		(.15)		(.06)		(.89)
Comparison 2
Over 40 percent college-educated school	−.27	−.41	−.13	−.17	27*	.08	.14	.05	.22**	.22**	.40	1.14
	(.25)	(.38)	(.21)	(.26)	(.11)	(.15)	(.08)	(.08)	(.08)	(.10)	(.95)	(.87)
School minority representation		.00		.00		−.003		−.001		.00		.02
		(.01)		(.004)		(.003)		(.001)		(.002)		(.01)
African American		.33		.28		−.15		.15		−.13		−.02
		(.34)		(.20)		(.18)		(.16)		(.10)		(.95)
Latino		.11		.06		−.13		.06		.01		.07
		(.42)		(.24)		(.20)		(.18)		(.02)		(1.13)

Note: N (Comparison 1) = 969 (self-image, social isolation, GPA), 968 (depression), 958 (math), 957 (science, GPA); N (Comparison 2) = 350 (self-image, social isolation, depression), 944 (math, science), 346 (GPA). White is the reference for race/ethnicity dummy variables and interactions. Other race/ethnicity is also included but not shown in the table. For each outcome, Model 2 is weighted by the transformed propensity score.

^*p <.05;

^**p <.01;

^***p <.001.

In summary, low-income students of all races/ethnicities appear to have more psychosocial problems in medium and high parent education schools than in low parent education schools, but causal inference is adequate for only the social isolation results. The hypothesized risks of attending schools with larger proportions of students with college-educated parents is confined to only one domain, albeit consistently across racial/ethnic groups.

CONCLUSIONS

The nascency of socioeconomic desegregation offers a ground-level opportunity to get it right by learning from social theory and drawing lessons from the much longer history of racial desegregation. This study attempts just that. The findings fall into three categories.

First, in all instances in which low-income students in higher SES schools demonstrated causally robust differences from low-income students in lower SES schools, the difference indicates a disadvantage for the former. These curricular and psychosocial risks seem to be at odds with the consistent findings of achievement gains for low-income students in middle-class schools (Rumberger and Palardy 2005). Both advanced coursework and social belongingness have well-documented associations with achievement, so low-income students should achieve less in higher SES schools if, as this study indicates, they take lower-level math and science and feel more isolated. Yet no extant evidence suggests this is the case. Because Add Health has no test data, I could not delve into this paradox. One theoretical explanation is what I call “lost gains.” Specifically, some portion of the overall achievement gains to be realized by socioeconomic desegregation is lost to unintended side effects. The end result might be a net positive for achievement that could actually have been bigger. Consider a low-income girl attending a predominantly middle-class school. She likely faces greater competition for slots in advanced courses and for social recognition, and, therefore, ends her science career at Chemistry I and feels socially isolated. At the same time, she is likely exposed to higher-quality instruction, institutional resources, and information flows than had she taken Chemistry II and felt a greater sense of belonging in a lower SES school. As long as the advantages outweigh the disadvantages, she should post achievement gains. She would likely post bigger gains, however, if she received the intended advantages without the unintended disadvantages.

Second, the risks of attending higher SES schools tend to be more common and pronounced for racial/ethnic minorities, and are occasionally confined to them as well. In fact, Whites were the only group of low-income students to demonstrate any benefits. Latino students, on the other hand, saw consistent patterns of curricular and psychosocial disadvantages in medium family income schools. African American students experienced disadvantages in medium and high family income schools. Further analyses (not presented) indicate that psychosocial disadvantages were more prevalent in higher SES schools with low minority representations. To the extent that low-income students face nonachievement risks in higher SES schools, low-income minority students (especially those in predominantly White higher SES schools) are the most vulnerable. The lost gains phenomenon might be particularly acute among these students.

Third, the relative curricular and psychosocial disadvantages of low-income students attending high-SES schools are more prevalent, pronounced, and racially variable when measuring school SES in terms of family income, rather than parent education. Indeed, only one psychosocial indicator fits the risk pattern in medium or high parent education schools, and I find no racial/ethnic differences in such schools. Contrary to expectations, the nonachievement risks of socioeconomic desegregation could be more of a problem in income-based desegregation plans. If schoolwide networks of social capital and information offer the kind of informal inputs that promote academic (if not social) integration across diverse groups in a school (Coleman and Hoffer 1987), then perhaps rates of parent education in a school do more to capture these networks.

Of course, the analyses generating such results have some limitations. Consequently, future researchers must determine the degree to which these findings hold up to greater scrutiny across measurement and analytic approaches. The two biggest areas for improvement concern school SES measurement and causality.

Because of the propensity score framework, I had to measure school SES categorically, which ignores some variation in school composition. At the same time, because of sparse cell sizes at the high end of the school SES distributions, the cutoff for high-SES schools falls below a majority of the student body. Even at the middle and low end of the distribution, case coverage is often sparse (as described in the Results section). These problems are functions of Add Health’s design, which targeted large in-school samples from a small number of schools. Other national data sets (e.g., NELS) collect smaller in-school samples from more schools. The former strategy allows a more accurate rendering of school SES based on the responses of all or most students in the school. The latter, however, allows much broader categorization of school SES. To correct many of the school measurement problems of this study without sacrificing many of its advantages, some new data source will need to be created. Coupling this study’s findings with findings from other data sets will inform such future data collections. For now, I can only present findings with appropriate notes of caution.

Furthermore, although this study improves upon basic regression strategies that are the norm in this line of research, much more can be done to promote causal inference. The inputs in the propensity scores had to be measured contemporaneously with high school enrollment, even though some factors (e.g., sports participation) might have caused and been caused by students’ enrollment in certain schools. Furthermore, robustness indices gauge the degree of confidence in causal inference, but, unlike instrumental variable analysis (Gennetian, Magnuson, and Morris 2008), they do not estimate causal impact. They also give no insight into what the important unobserved confounds were. Still, even if all such limitations are corrected, causality cannot be established without experimental designs. Consequently, this kind of research should be seen as a necessary first step in assessing the impact of socioeconomic desegregation, providing preliminary answers to guide and tailor future experimental investigations.

These limitations must be corrected in the future. If the basic results of this study hold across future studies employing other techniques with newer or better data, then some theoretical conclusions and policy recommendations would be in order.

Theoretically, the orienting perspective of this study was the frog pond framework. This framework primarily concerns students’ academic evaluations relative to the overall academic level of their schools. I built on this framework in key ways. Following the lead of contemporary scholars (e.g., Espenshade et al. 2005), this study views academic evaluations of the self as a theoretical mediator between school composition and student outcomes and couples it with another meditational pathway through others’ evaluations. In other words, how students do academically is a function of how they view themselves and how others evaluate them relative to the academic skills and performance of their peers. This study also includes psychosocial outcomes (not just academic) as a frog pond product. Just as education credentials set up students for socioeconomic attainment, psychosocial states set them up for mental health trajectories and relationship formation. Thus, the outcome set of the frog pond effect should not be so narrow.

Perhaps most importantly, this study builds on some of the earliest frog pond studies (e.g., Trowbridge 1970) by viewing demographic statuses linked to achievement, not achievement itself, as the trigger for the comparison processes at the heart of the frog pond phenomenon. Findings from this approach suggest that students, parents, and school personnel use SES as a marker of academic ability (and social worth) when evaluating students. As a result, lower SES students are at greater competitive disadvantage in the curricular regimes and social markets of higher SES schools because their SES can label them as academically or socially inferior to their peers. Students are less differentiated by SES in lower SES schools, so SES becomes less important in social and self evaluations and the stratifying processes that arise from them.

When integrated into the broader scope of frog pond research (Marsh and Hau 2003), the results of this study suggest that frog pond effects are likely to occur in schools where resources are finite and people have to find ways to make decisions about who gets a resource. Past research highlights grades as a more common frog pond outcome than test scores. Conceivably, all students can make the same test score. In the absence of rampant grade inflation, however, teachers likely spread students across the grade scale, so that anything that signals competence to a teacher can have a stratifying effect. Similarly, this study finds more frog pond effects for coursework than for psychosocial outcomes.

With a few exceptions, schools can only accommodate so much demand for a class. In most cases, the finite number of slots generates direct comparisons among students as a means of allocating slots. Psychosocial adjustment is, for the most part, not finite. While only a limited number of students can win school-sponsored popularity contests (e.g., homecoming court), all students could plausibly have a large group of friends or romantic partners. The importance of scarce resources is also linked to the composition of schools. If students in a school are differentiated on many dimensions, the factors that appear to co-occur with academic performance become more critical to evaluation. We would thus expect general frog pond effects on official academic credentials and, to a lesser extent, student feelings of social worth in schools with differentiated curricula and rigid social hierarchies. These general frog pond effects would contribute to demographic and structural inequalities in schools that also have diverse student bodies. Importantly, these theoretical conclusions are not limited to schools. They forecast inequalities in any social institution in which diverse groups jockey for position in an environment that links performance with some demographic status (e.g., men who are more competitive for advancement in female-typed careers than in traditionally male fields [Williams 1992]).

To the extent that such theoretical conclusions are valid, they suggest that policy action should focus on reducing “scarcity” in diverse schools. For example, common curricula—everyone in a grade takes Algebra even if different levels are offered—seem to promote more equitable distributions of achievement in schools (Lee et al. 1997). At the same time, expanding extracurricular activities in schools may facilitate more equitable patterns of social integration and status. Negative psychosocial outcomes are reduced when students are given multiple activity venues to make friendships with similar others, pursue self-affirmation, and gain recognition. Even when scarcity cannot be reduced, schools can take active curricular and pedagogical steps to reduce status hierarchies that arise in diverse settings and become associated with perceptions of ability. Small group instruction techniques, for instance, have been shown to achieve this aim (Cohen and Lotan 1997).

Moving beyond general education policy, the findings of this study can—if verified in the future—inform socioeconomic desegregation more specifically. Achieving statistical representation in schools is not enough. Desegregation efforts must attend to the social integration of lower SES students, as well as their distribution across classes.

In theory, basing desegregation on parent education rather than income, which appears to pose more risks, especially to minorities, may also be a good strategy. Yet, most SES plans rely on income criteria because school districts can require tax returns to document income. While diplomas and school records can document whether parents reached a certain educational status, documenting that parents have not reached an educational threshold (making their children eligible for a higher SES school) is virtually impossible. If these results hold, then the development of methods to incorporate parent education into socioeconomic desegregation plans—despite the practical obstacles—would be a worthy enterprise. Of course, such plans might entail some psychosocial risks, but these risks would be similar across racial/ethnic groups. Finally, in light of extant evidence that socioeconomic desegregation may not produce major changes in school racial segregation (Reardon et al. 2006), the findings of heightened risks for minority students call for caution in one (but not the only) selling point of SES plans. Additional efforts are likely needed to replicate the aims of racial desegregation.

Biography

Robert Crosnoe is Associate Professor of Sociology and a faculty associate in the Population Research Center at the University of Texas at Austin. His main field of interest is the life course and human development, with a special emphasis on social psychological approaches to education and how they can illuminate socioeconomic and immigration-related inequalities. His current work focuses on the role of general developmental processes, including health and social relationships, in the educational experiences of Mexican-origin children and of children and adolescents from socioeconomically disadvantaged families.