Application of a Real-Time, Calculable Limiting Form of the Renyi Entropy for Molecular Imaging of Tumors

Abstract

Previously, we reported new methods for ultrasound signal characterization using entropy, H_f; a generalized entropy, the Renyi entropy, I_f(r); and a limiting form of Renyi entropy suitable for real-time calculation, I_f,∞. All of these quantities demonstrated significantly more sensitivity to subtle changes in scattering architecture than energy-based methods in certain settings. In this study, the real-time calculable limit of the Renyi entropy, I_f,∞, is applied for the imaging of angiogenic murine neovasculature in a breast cancer xenograft using a targeted contrast agent. It is shown that this approach may be used to detect reliably the accumulation of targeted nanoparticles at five minutes post-injection in this in vivo model.

I. Introduction

In previous work, we have described the use of a targeted nanoscale contrast agent for use with MRI, X-ray and ultrasound. In this application, α_vβ₃-targeted perfluorocarbon core nanoparticles are injected into the blood stream where they circulate and accumulate at angiogenic sites that are associated with advancing fronts of growing tumors. The geometry of this angiogenic neovasculature is highly convoluted, and the targeting sites sparse, so that the accumulating nanoparticles never comprise a planar “specular” reflector. Consequently, a scheme capable of sub-resolution sensitivity is required for their detection.

Sub-resolution detection has a long history and has typically been based on statistical signal processing using Gaussian, Rayleigh, or Rician statistics [1]–[8]. The technique we investigate in this study utilizes an approach formulated with a significantly different underlying mathematical structure [9]. It is based on the use of various forms of entropy analysis for the detection of perfluorocarbon nanoparticles targeted to tumor neovasculature [10]–[13]. These quantities are computed using a density function determined by each individual radiofrequency (RF) A-line considered as a noise-free (or nearly so) measurable function [14]. All measurable functions, not just noise functions, have mathematically well-defined distributions (for they are all “random” variables), which may be used to compute any one of several entropies. We have found that the use of these novel information-theoretic receivers is often advantageous for overcoming certain challenges related to acoustic characterization of sparse collections of nanoparticles. The physically robust liquid perfluorocarbon nanoparticles are intrinsically weak individual scatterers in the clinical ultrasound frequency range due to their small size and nongaseous nature, and are typically targeted to physiologic features at interfaces having inherent impedance mismatches (e.g. vessel walls). In addition, the epitopes to which they are targeted may be sparsely located in the accessible vasculature. Entropy techniques are well-suited to detecting small changes in the shape of the backscattered RF waveforms which may be masked by other strongly scattering features when using typical energy-based analyses. The end goal is to enable detection of nanoparticles accumulating at epitopes of interest in the least amount of time after administration, with a view towards demonstrating sensitivity to smaller quantities of contrast agent, thereby potentially reducing patient discomfort and increasing clinical throughput.

The in vivo studies in which we have utilized these techniques typically entail intravenous injection of nanoparticles that are targeted to angiogenic markers present in cancerous or precancerous tissue. The tumor site is monitored ultrasonically as the contrast agent circulates, and backscattered RF waveforms are acquired at specific time points for entropy analysis. Initial studies showed that a limiting form, H_f, of the Shannon entropy, H_S, enabled detection of nanoparticle accumulation at 30 minutes post-injection in a mouse model of squamous metaplasia [11]. Subsequent work demonstrated that a generalized form of entropy, the Renyi entropy I_f(r), could be used to distinguish backscatter differences from the previously acquired data at only 15 minutes post-injection [12]. I_f(r), where r may be thought of as a reciprocal “temperature” in the statistical mechanics sense, is defined for all r < 2; the improved detection results were obtained with r = 1.99.

Although the computational effort to obtain these results precluded clinical application with currently available equipment, the study raised the possibility of further sensitivity improvements by using values of r closer to the limiting value of 2, where I_f(r) approaches infinity. Further work based on this limiting form, labeled I_f,∞, confirmed its utility for rapid detection of nanoparticle targeting in the same animal model [13]. Moreover, the implementation of the algorithm used to compute I_f,∞ was much less computationally intensive, having an operation count lower than that used to produce the signal envelope (currently the standard for real-time ultrasonic imaging display), thus demonstrating its suitability for implementation in a real-time imaging system. As this technique is based on a “moving window” analysis of digitized RF (which requires some sacrifice in spatial resolution), clinical implementation of entropy detection would probably follow the same approach currently employed in color Doppler or strain-rate imaging modalities, in which the conventional B-mode image is overlaid with a color-coded mapping; a B-mode/entropy image could be constructed in a similar fashion.

We now present new data acquired from a murine tumor model injected with nanoparticles targeted to the α_vβ₃ integrin, a marker for angiogenesis. Ultrasonic data are acquired on a finer time scale (every 5 minutes over the course of 1 hour) to further delineate the efficacy of entropy analysis for both sensitive and specific detection of nanoparticle accumulation in and around the tumor capsule. The results of this analysis are compared, using various statistical criteria, with corresponding conventional energy-based measures applied to the same data.

II. Approach

All entropy results in this study were obtained using

$$I_{f,\infty }=log\left[\sum _{\{t_k\mid f^{\prime }(t_k)=0\}}\frac{1}{\mid {f^{\prime }}^{\prime }(t_k)\mid }\right],$$ (1)

which is derived from an asymptotic analysis of the Renyi entropy I_f(r → 2) as described previously [13]. In this application, f(t) refers to an individual RF waveform, f′(t) and f″(t) are its first and second derivatives with respect to time, and t_k is the time at which the k^th extremum occurs. Previous studies have shown that this quantity (i.e., I_f,∞, as well as I_f(r), and H_f, which is a generalization of I_f(r)) can be more sensitive to subtle changes in scattering architecture than more commonly used energy-based measures [11]–[13]. We base our current study exclusively on I_f,∞, since this quantity is calculable in real-time as described previously [13].

III. Materials and Methods

A. Animal Model

The study was performed according to an approved animal protocol and in compliance with guidelines of the Washington University institutional animal care and use committee.

Human MDA435 cancer cells were implanted in the inguinal fat pad of fifteen athymic nude mice between 19 and 20 days prior to acquisition of data. After the this period of tumor growth, five of these animals were injected with α_vβ₃-targeted nanoparticles, five were injected with nontargeted nanoparticles and five were injected with saline.

Prior to imaging, each mouse was pre-anesthesitized with a ketamine/xylazine cocktail, and injected subsequently through the tail vein with either 30 μL of α_vβ₃-targeted nanoparticle emulsion, 30 μL of non-targeted nanoparticle emulsion, or 30 μL of saline (equivalent to a whole body dose of 1.0 mL/kg; the preparation and properties of these emulsions have been described previously, [12], [13]). The mouse was then placed on a heated platform maintained at 37°C, and anesthesia was administered continually with isoflurane gas through a nose cone. Post-injection, ultrasound data were acquired at 5 minute intervals for 1 hour. After the ultrasound data were collected, the mouse was euthanized and the tumor was excised for histological staining.

B. Ultrasonic Data Acquisition

A schematic of the experimental setup is shown in Fig. 1. RF data were acquired with a research ultrasound system (Vevo 660, Visualsonics, Toronto, Canada) having analog and sync ports to permit digitization. Tumors were located and imaged with a 35 MHz single element probe, and the RF data corresponding to single frames were stored for off-line analysis. Each frame consisted of 384 lines of 2048 twelve-bit words acquired at a sampling rate of 200 MHz using a CompuScope 12400 digitizer card (GaGe Applied Technologies, Lockport, IL) in a controller PC. Each frame corresponded spatially to a region 1.5 cm wide and 0.8 cm deep. At the bottom left of Fig. 1 is a conventionally formed image from one of the mice used in our study. Also shown in this figure is a representative histological section extracted from an example mouse model. Visible in the section is an area of skin, below which is a thin angiogenic layer identified by immunohistochemical staining, and below that, a portion of the tumor capsule. The close proximity of neovasculature to the skin-transducer interface is one of the primary obstacles that must be overcome by any quantitative detection scheme intended to determine the extent of this region.

Fig. 1.

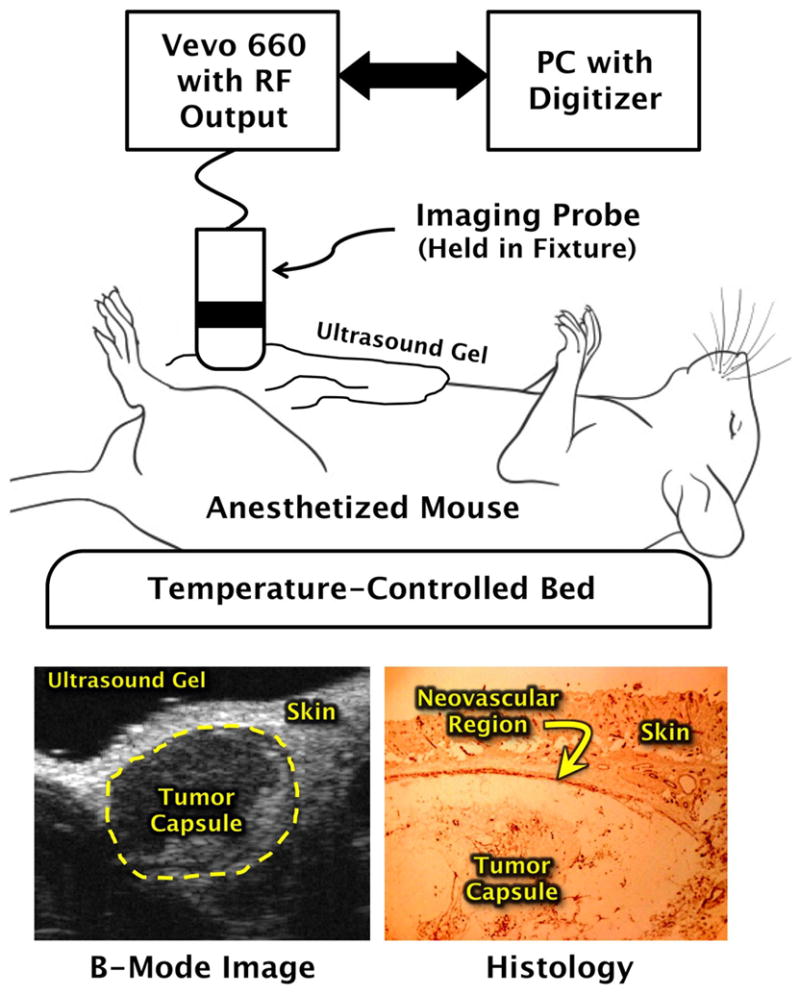
Schematic diagram of the equipment used to acquire in vivo backscattered RF data. Bottom panels show example B-mode ultrasound image of tumor (left), and a stained histologic section of a tumor indicating portions where α_vβ₃-targeted nanoparticles nanoparticles could adhere.

C. Ultrasonic Image Preparation and Processing

Since the real-time entropy depends on the second derivative of the raw data, a potentially noise-enhancing process, all RF data were lowpass-filtered in the frequency domain as a first step in data analysis. This was accomplished by multiplying the Fourier transform of each RF line by the filter function, F(f),

$$F(f)=\frac{1}{2}(1.0+tanh[a(f_{\text{c}}-f)])$$ (2)

where a = 0.25 and f_c = 36 MHz. The cutoff frequency f_c was chosen to correspond to the typical upper limit of the meaningful bandwidth of the backscattered signal from within the tumors after being attenuated by overlying tissue. The function F(f) has the shape of a smoothed rectangular window whose passband drops off near f_c. The coefficient a governs the sharpness of this transition. This function was chosen as a gate function since it is infinitely differentiable. We have investigated other window functions (e.g., various pole number Butterworth filters) and find that all perform in a roughly equivalent way. The use of other types of noise suppression, such as the application of smoothing splines to the input RF waveforms, is an active area of research in our laboratory whose impact is currently being assessed.

After filtering, each of the 384 RF lines in the frame was first up-sampled from 2048 to 4096 points, using a cubic spline fit to the original data set in order to improve the stability of the entropy algorithms. A by-product of this “order N″ (where N is the number of sample points) algorithm is simultaneous output of a corresponding array of second derivative values of the fit function [15]. Next, a moving window analysis was performed on the second derivative data set, using Eq. (1) to compute I_f,∞, by translating a rectangular window (256 points long, 0.64 μs) in 0.08 μs steps (32 points), resulting in 121 window positions within the output data set. For comparison, an analogous procedure was performed on the same data using a conventional imaging metric, based on the logarithm of the signal energy (log[E_f]).

Grayscale images formed from the processed data were subjected to an image-histogram based analysis to quantify levels of enhancement, beginning with computation of the normalized probability density function (PDF) of the image sequence (i.e., 0, 5, …, 60 minute images). The PDF was then integrated to obtain the cumulative distribution function (CDF) of the image sequence. The pixel values corresponding to the lower 2%, 4%, …, 98% of the CDF were then used to segment each image in the sequence into two regions corresponding to “enhanced” and “unenhanced” tissue. The mean value of pixels in the “enhanced” region was computed for each image in the sequence as a function of time post-injection. Beyond the initial selection of the imaging plane and digitization window, no user-drawn regions of interest were utilized in the image analysis, all digitized signals were included.

IV. Results and Discussion

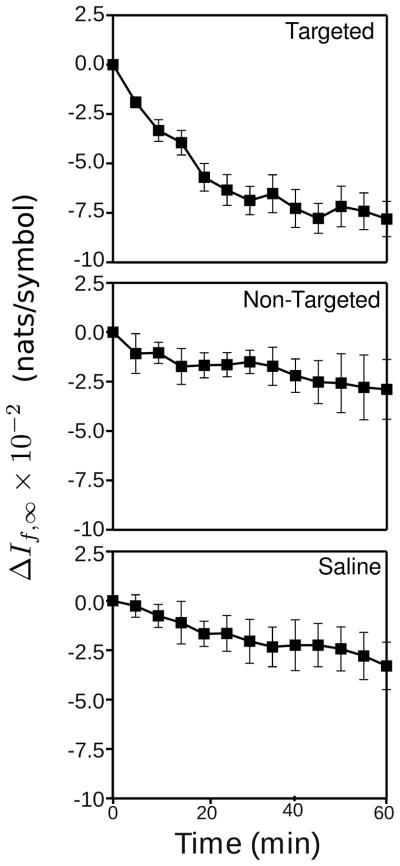
Fig. 2 shows the average change in I_f,∞ (relative to the first observation point, which was typically acquired within 1 minute of nanoparticle injection) for the animals used in this study labeled in each plot by group. Error bars are also shown at each time time point. These plots were obtained using the I_f,∞ image segmented by setting the CDF threshold to include only the bottom 30% of I_f,∞ pixel values. In the top panel is the plot for the animals injected with α_vβ₃-targeted nanoparticles, which decreases as a function of time. The downward trend is less evident for both the non-targeted and saline control groups. It should be noted that the trend for decreasing I_f,∞ values with time is opposite to what has been reported in a different model of cancer growth, the K14-HPV16 precancerous mouse ear analyzed with a variety of information-theoretic metrics [11]–[13]. Although it is not clear what effect the difference in tissue type might produce, we note that there is substantially more attenuation associated with ultrasound backscattered from the thicker and deeper tissue regions of the solid tumors described here than with the very thin ears of the previous studies. Although not reported here, we have observed that altering the spectral content of the input waveforms via filtering or other means can change the direction of the temporal trends seen in I_f,∞ from negative to positive, or vice versa; however, the differences between targeted and control groups are typically preserved, and it is these differences that are important for reliable detection of accumulating nanoparticles.

Fig. 2.

Plots of the average change in I_f,∞ with time for each group in this study, obtained by segmenting the I_f,∞ images by setting the CDF threshold to include only the lowest 30% of pixel values.

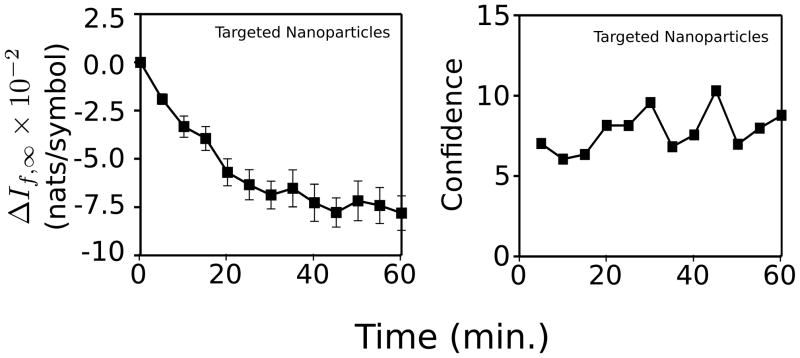
The average plot for the group injected with α_vβ₃-targeted nanoparticles is reproduced on the left side of Fig. 3. The right-hand side of the figure shows a plot of the corresponding ratio of the mean value to standard error for each time point. For the purposes of detecting a change from the baseline value, it is actually this ratio that is important. To shorten subsequent discussion of our results we will define this ratio, labeled the “confidence,” [16] c:

$$\mathbf{c}=\frac{\mid \mathit{mean}\mid }{\mathit{standard}\mathit{error}}.$$ (3)

Fig. 3.

Left: average time-course of ΔI_f,∞ images obtained from MDA435-implanted mice injected with α_vβ₃-targeted nanoparticles (same data as shown in top right of Fig. (2)). Right: corresponding c values. These data were obtained for the CDF-threshold set to include the lower 30% of pixel values in the I_f,∞ from each of the images in each group.

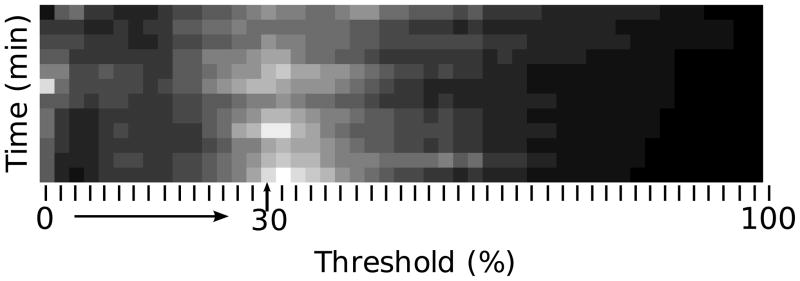
As stated above, the analysis shown in Fig. 3 was performed for all even CDF-thresholds between 0 to 98%. A summary of all resulting confidence values for mice injected with α_vβ₃-targeted nanoparticles group is depicted as a gray-scale image in Fig. 4. The grayscale value in the image corresponds to the value of c, with brighter pixels signifying greater values of c. As the image shows, the greatest confidence values are obtained for a range of CDF-thresholds between roughly 2% and 50%. For reference, the column corresponding to the CDF-threshold of 30% that was discussed in Fig. 3 is indicated by an arrow and label.

Fig. 4.

Confidence values, c, plotted as a function of time and CDF threshold for tumor-implanted mice injected with α_vβ₃-targeted nanoparticles.

The I_f,∞ confidence images for all groups studied are shown in grayscale format in the top left half of Fig. 5. In the top right of the figure, identical images are shown, but with the overlay of a threshold mask to display only confidence values greater than 2.0; all other values have been colored red. The gray pixels represent the time/analysis-threshold combinations which are statistically significant by the “two sigma” criterion. This threshold was chosen since it represents a common standard for statistical analysis, (i.e., 95% confidence interval). In the bottom half of the figure are shown the corresponding images for the log[E_f] receiver. For the conventions used in this study, the portion of the image selected by the segmentation increases as the analysis threshold is increased, so that at the 2% threshold very little of the image is selected for analysis, while at 98% nearly all of the image is included. We note that the areas in the panels for the I_f,∞ receiver for the group injected with α_vβ₃-targeted nanoparticles is somewhat larger than for the log[E_f] panel for the same group, indicating a broader range of analysis thresholds that imply the presence of targeted nanoparticles accumlating. This indicates that according to the “two sigma” criterion, the I_f,∞ receiver produces “true positives” over a broader range of analysis thresholds than does the log[E_f] receiver and is potentially a more robust statistic. Additionally, the total gray area in the control group panels (corresponding to targeted nanoparticle and saline injection) is less in the I_f,∞ panels than in the log[E_f] panels, indicating a smaller number of “false” positives are produced by the I_f,∞ receiver.

Fig. 5.

Top left: a comparison of the confidence images for the I_f,∞ receiver, like that shown in Fig. (4), for all groups in our study. Top right: same data, but with all confidence values below 2 shown in red. Bottom left a comparison of the confidence images for the log[E_f] receiver. Bottom right: same data, with all confidence values below 2 shown in red.

It is possible to formulate the detection problem in ways other than the “two sigma” criterion. One of these is shown in Fig. 6, where we have adjusted the thresholds of the confidence images to the minimum value required to eliminate “false” positives in the receiver outputs in the two control groups. For the I_f,∞ receiver, this requires setting c = 6.92, for log[E_f], c = 9.55. As in Fig. 5, the gray pixels represent those time/analysis-threshold combinations at which statistical significance (by the “no false positive” criterion) is observed. We note that by this criterion the gray region is again larger for the I_f,∞ receiver than it is for the log[E_f] receiver. Additionally, the presence of gray pixels in the top row of the I_f,∞ confidence image indicates that detection of accumulating nanoparticles occurs within 5 minutes of particle injection (again, with no false positives), whereas the energy-based receiver registers a significant change only after 10 minutes of nanoparticle introduction. However, we point out that by both criteria we are able to successfully detect accumulation of targeted nanoparticles using either receiver.

Fig. 6.

A comparison of the confidence images, c, like that shown in Fig. 5, (top) for I_f,∞ images with s = 6.92, and log[E_f], images with c = 9.55. These thresholds were chosen as the minimum which produced no “false positives” in either of the control groups when analyzed by these signal receivers.

V. Conclusion

Although both I_f,∞ and log[E_f] are able to distinguish between the group injected with α_vβ₃-targeted nanoparticles and all other controls, and Fig. 5 and Fig. 6 suggest that the entropy receiver may be more robust, much work remains to be done to demonstrate clinical utility. One encouraging fact is the ability to select operating parameters to preclude any “false” negatives from being detected within the treated group. Given that the spatial distribution of scatterers is likely to be significantly different between the control groups and the group injected with targeted nanoparticles, with nanoparticles in this group being concentrated in the advancing front of the tumor, it is possible that frequency filtering of the RF waveforms might be optimized for input to the I_f,∞ receiver by high-pass filtering. In addition, utilization of a smoothing spline in place of the non-smoothing spline used in this study may yield improvements in the noise immunity of the I_f,∞ receiver. These algorithms are being actively investigated in our group at this time.