Individual Muscle Contributions to Push and Recovery Subtasks during Wheelchair Propulsion

Abstract

Manual wheelchair propulsion places considerable physical demand on the upper extremity and is one of the primary activities associated with the high prevalence of upper extremity overuse injuries and pain among wheelchair users. As a result, recent effort has focused on determining how various propulsion techniques influence upper extremity demand during wheelchair propulsion. However, an important prerequisite for identifying the relationships between propulsion techniques and upper extremity demand is to understand how individual muscles contribute to the mechanical energetics of wheelchair propulsion. Therefore, the purpose of this study was to use a forward dynamics simulation of wheelchair propulsion to quantify how individual muscles deliver, absorb and/or transfer mechanical power during propulsion. The analysis showed that muscles contribute to either push (i.e. deliver mechanical power to the handrim) or recovery (i.e. reposition the arm) subtasks, with the shoulder flexors being the primary contributors to the push and the shoulder extensors being the primary contributors to the recovery. In addition, significant activity from the shoulder muscles was required during the transition between push and recovery, which resulted in increased co-contraction and upper extremity demand. Thus, strengthening the shoulder flexors and promoting propulsion techniques that improve transition mechanics have much potential to reduce upper extremity demand and improve rehabilitation outcomes.

1. Introduction

Nearly 70% of manual wheelchair users will likely experience upper extremity (UE) pain or overuse injury at some point in their lifetime (Finley and Rodgers, 2004). One of the main activities that contribute to the development of UE pathology is wheelchair propulsion. Specifically, the rate and magnitude of the propulsive force has been associated with symptoms of UE pathology (Boninger et al., 1999; Gellman et al., 1988; Mercer et al., 2006). To help alleviate the detrimental effects of propulsive force on UE health, recent efforts have been devoted to investigating how different propulsion techniques influence UE demand during propulsion (e.g., de Groot et al., 2008; de Groot et al., 2002; Lenton et al., 2009). However, an important prerequisite for understanding the relationships between propulsion technique and UE demand is to identify how individual muscles function to contribute to the flow of mechanical power throughout the stroke.

Previous studies have analyzed excitation timing from UE electromyography (EMG) throughout the stroke to broadly classify muscles as having either a push phase (i.e., region of hand-handrim contact) or recovery phase (i.e., region without hand-handrim contact) function (Mulroy et al., 2004; Tries, 1989). Others have used inverse dynamics to determine the flow of joint power between the trunk, arm and hand/handrim during propulsion (Guo et al., 2006; Guo et al., 2003). They showed that mechanical power generated at the shoulder and trunk was delivered to the arm and handrim during the push phase and then absorbed from the arm during the recovery phase as a result of trunk and shoulder extension. These results suggest that shoulder muscles play an important role in both mechanical power generation and arm recovery. However, no study has identified individual muscle contributions to the mechanical energetics of wheelchair propulsion, which would provide insight into how individual muscles work in synergy to satisfy the mechanical demands of wheelchair propulsion.

The purpose of this study was to use a representative forward dynamics simulation of wheelchair propulsion that emulates group-averaged wheelchair mechanics to determine how individual muscles deliver, absorb and/or transfer mechanical power during the task. This understanding has important implications for designing training techniques that help reduce UE muscle demand during propulsion and improve rehabilitation outcomes.

2. Methods

Experimental Data

Experimental data were collected from 12 experienced wheelchair users who had full UE function without pain and were capable of continuous wheelchair propulsion for 5 minutes (Table 1). After providing informed consent, data were collected using previously described procedures (Rankin et al., 2010). Briefly, participants propelled their wheelchair on a motor-driven treadmill at their self-selected overground speed for thirty seconds, during which trunk and right side UE kinematics, 3D handrim kinetics, and shoulder and elbow EMG data were collected. Ten consecutive strokes were analyzed from each subject, with each stroke beginning when a discernable tangential force was applied to the handrim. Push and recovery phase data for each stroke were normalized using cubic spline interpolation and averaged for each subject. Mean subject data were then averaged across subjects to create representative biomechanical and muscle excitation profiles.

Table 1.

Individual and group average subject characteristics and propulsion data

	Subject Characteristics						Propulsion Characteristics
Subject	Gender	Injury	Age (yrs)	Height (cm)	Mass (kg)	Time From Injury (yrs)	Stroke Time (s)	Push Time (s)	Push Speed (m/s)
1	M	T-8	37.1	172.7	75.6	14.1	1.18	0.47	1.13
2	M	T11-T12	25.6	177.8	62.3	3.6	1.05	0.36	1.08
3	M	T8	26.4	182.9	86.9	2.2	1.05	0.40	1.07
4	F	L4-L5	24.4	162.6	48.4	24.4	1.88	0.45	0.99
5	M	Spinal lipoma	23.1	167.6	44.8	3.4	1.19	0.29	1.61
6	M	T4	27.7	180.3	76.5	3.6	1.09	0.28	1.39
7	M	L1	46.5	182.9	80.0	17.1	1.28	0.48	1.14
8	M	T11-T12	38.5	185.4	69.6	21.9	1.19	0.33	1.25
9	M	C6-C7	41.1	177.8	71.4	22.9	1.16	0.52	0.96
10	M	L-1	38.0	180.3	75.2	7.3	1.11	0.47	0.83
11	M	T-10	42.1	157.5	74.7	43.1	1.37	0.52	1.16
12	F	Cerebral Palsy	24.1	149.9	51.4	24.1	0.84	0.30	0.71
Average			32.9	173.1	68.1	15.6	1.20	0.41	1.11

Musculoskeletal Model

An UE musculoskeletal model based on the work of Holzbaur et al. (2005) was developed using SIMM (Musculographics, Inc., Santa Rosa, CA, USA) and used to create a wheelchair propulsion simulation. The model is described in detail in Rankin at al. (2010). Briefly, the model consisted of segments representing the trunk and right side upper arm, forearm and hand. Shoulder movement was defined using a set of Euler rotations (Y,X,Y′) based on International Society of Biomechanics recommendations (Wu et al., 2005), representing plane of elevation, elevation angle (thoracohumeral angle) and internal-external (axial) rotation. In addition, a scapulohumeral rhythm was defined using regression equations based on cadaver data (de Groot and Brand, 2001). Elbow flexion-extension and forearm pronation-supination were represented by two additional rotations. Trunk lean was prescribed to match the experimental data and hand translation was constrained to follow the circular handrim path during the push phase. The wrist joint was fixed in the anatomical position and non-sagittal trunk motion was not modeled. Model equations-of-motion were generated using SD/FAST (PTC., Needham, MA, USA).

Twenty-six Hill-type musculotendon actuators, governed by intrinsic muscle force-length-velocity relationships (Zajac, 1989), were used to represent the major muscles crossing the shoulder and elbow joints (Table 2). Polynomial regression equations based on original model definitions (Holzbaur et al., 2005) were used to describe musculotendon length and moment arm paths, with maximum differences less than 10% (Rankin et al., 2010). Each actuator received a distinct excitation signal except the three actuators representing the latissimus dorsi, the two actuators representing the sternal pectoralis major and the two actuators representing the anconeus and lateral triceps brachii. Muscles in each of these groups received the same excitation signal. Excitation-activation dynamics were modeled using a first-order differential equation (Raasch et al., 1997) with muscle-specific time constants (Happee and Van der Helm, 1995; Winters and Stark, 1988). Muscle force was calculated based on the current muscle state (length, velocity, activation) at each time step (Zajac, 1989).

Table 2.

Upper extremity muscle definitions and group abbreviations. Muscles were grouped based on a combination of anatomical location and muscle function (identified from the segment power analysis).

Muscle	Origin	Insertion
ADELT
Anterior Deltoid	Clavicle	Humerus
MDELT
Middle Deltoid	Scapula	Humerus
PDELT
Posterior Deltoid	Scapula	Humerus
PECM
Pectoralis Major, clavicular head	Clavicle	Humerus
Pectoralis Major, sternal head 1	Thorax	Humerus
Pectoralis Major, sternal head 2	Thorax	Humerus
Corachobrachialis	Scapula	Humerus
LAT
Teres Major	Scapula	Humerus
Lattissimus Dorsi 1	Thorax	Humerus
Lattissimus Dorsi 2	Thorax	Humerus
Lattissimus Dorsi 3	Thorax	Humerus
SUBSC
Subscapularis	Scapula	Humerus
INFSP
Infraspinatus	Scapula	Humerus
TMIN
Teres Minor	Scapula	Humerus
SUPSP
Supraspinatus	Scapula	Humerus
BRD
Brachoradialis	Humerus	Radius
Brachialis	Humerus	Ulna
BIC
Biceps Brachii, short head	Scapula	Radius
Biceps Brachii, long head	Scapula	Radius
TRIlat
Anconeus	Humerus	Ulna
Triceps Brachii, Lateral	Humerus	Ulna
Triceps Brachii, Medial	Humerus	Ulna
TRIlong
Triceps Brachii, Long Head	Scapula	Ulna
SUP
Supinator	Ulna	Radius
PT
Pronator Quadratus	Ulna	Radius
Pronator Teres	Humerus	Radius

Dynamic Optimization

A global optimization algorithm (simulated annealing, Goffe et al., 1994) was used to identify muscle excitation patterns that minimized differences between the simulation and group-averaged experimental propulsion data using an optimal tracking cost function (Neptune et al., 2001). Quantities included in the cost function were the three shoulder angles, elbow flexion-extension and forearm rotation angles, and the 3D handrim forces. The simulation handrim forces were determined using SD/FAST.

Neural excitation patterns were defined using a linear sum of four parameterized Henning patterns, defined by twelve parameters and given by the equation:

$$\sum _{i=1}^4{u}_i(t)=\left\{\begin{array}{cc}\frac{m_i}{2}\left[1-\mathit{cos}\left(\frac{2\pi (t-a_i)}{b_i-a_i}\right)\right],& a_i\le t\le b_i\\ 0,& \mathit{Otherwise}\end{array}\right\}$$

where u_i is the excitation value of Henning pattern i at time t and m_i, a_i and b_i represent the magnitude, onset parameters and offset parameters, respectively. The twenty-two excitation signals resulted in 264 total parameters to be optimized. To assure that the solution produced excitation patterns similar to the experimental data, the average EMG data were used to constrain muscle excitation onset and offset timing. Muscles without available EMG data had unconstrained excitation timing.

Segment Power Analysis

A segment power analysis (Fregly and Zajac, 1996) was performed to identify individual muscle contributions to body segment mechanical energetics over the entire stroke, which uses individual muscle power data to quantify how a muscle generates (absorbs) instantaneous mechanical power to (from) each body segment at every time-step over the stroke. Positive (negative) segment power indicates that the muscle accelerates (decelerates) the segment in the direction of its motion. Individual muscle contributions to net trunk rotation and handrim push power were also determined. Since muscle power is a scalar, this allowed individual contributions to the upper arm, forearm and hand segments to be combined into a single arm power value. Then each muscle’s biomechanical function was determined by its power contribution to the push (handrim power generation) and recovery (arm relocation) subtasks.

3. Results

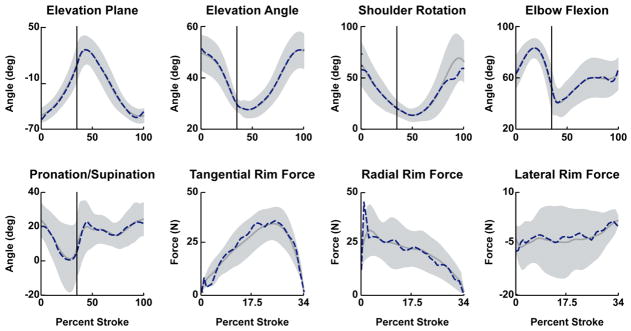
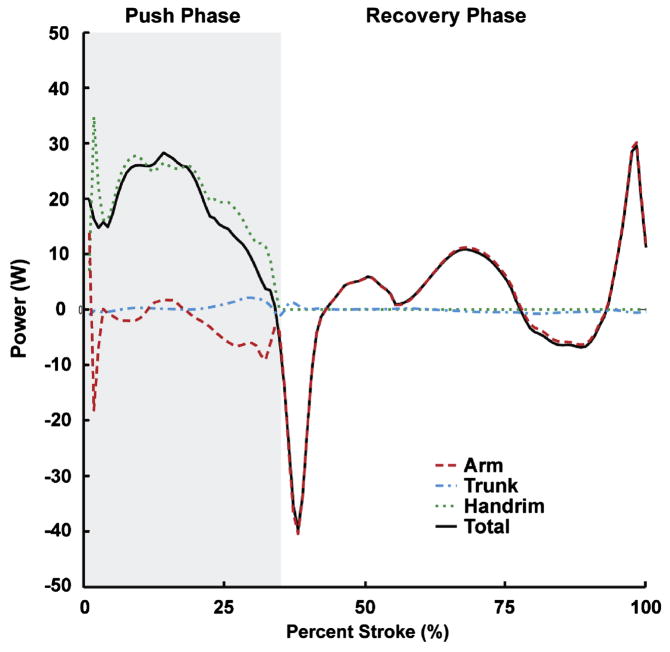
The dynamic optimization produced a simulation that closely emulated the group-averaged experimental data with average joint kinematic and handrim force differences of 2.0 degrees and 2.39 N, respectively, which were well within one standard deviation of the experimental data (12.3 degrees and 8.3 N, Table 3, Fig. 1). Net positive power was delivered to the handrim over the entire push phase (Fig. 2; dotted line positive). The majority of the power was delivered directly to the handrim (Fig. 2; dotted and solid lines similar), although some power was transferred from the arm to the handrim during the second half of the push phase (Fig. 2; dashed line negative, dotted line > solid line at ~21–34% stroke). During the recovery phase, muscle contributions to arm power alternated between absorption and delivery (Fig. 2; sign of dashed line alternates) in order to reposition the arm for the subsequent push. Overall, the trunk did not provide or remove much power from the system (Fig. 2; dash-dot line ~0).

Table 3.

Average differences between experimental and simulated kinematics and handrim forces. The simulation differences were within one standard deviation (1SD) of the experimental data

	Simulation Difference	Experimental Variability (1SD)
Shoulder Elevation Angle (deg)	0.3	14.4
Shoulder Plane of Elevation (deg)	1.7	6.0
Shoulder Internal-External Rotation (deg)	5.5	15.4
Elbow Flexion-Extension (deg)	1.0	12.5
Forearm Pronation-Supination (deg)	1.4	13.1
All Joints (deg)	2.0	12.3
Tangential Handrim Force (N)	2.27	7.74
Radial Handrim Force (N)	3.75	9.42
Lateral Handrim Force (N)	1.14	7.82
All Forces (N)	2.39	8.33

Figure 1.

Comparisons between the experimental and simulation kinematics and handrim kinetic data. Average experimental and simulation values are represented by solid and dashed lines, respectively. Shaded regions represent ±1SD of the experimental data.

Figure 2.

Net contributions to segment power during the push and recovery phases. Individual segment powers were combined into four groups for analysis: Arm (upper arm, forearm and hand segments, dashed line), Trunk (trunk, scapula and clavicle, dash-dot line), Handrim (external handrim power, dotted line) and Total (sum of all segments, solid line). A positive (negative) value indicates power was delivered to (absorbed from) the corresponding body segments.

Push Phase Subtask

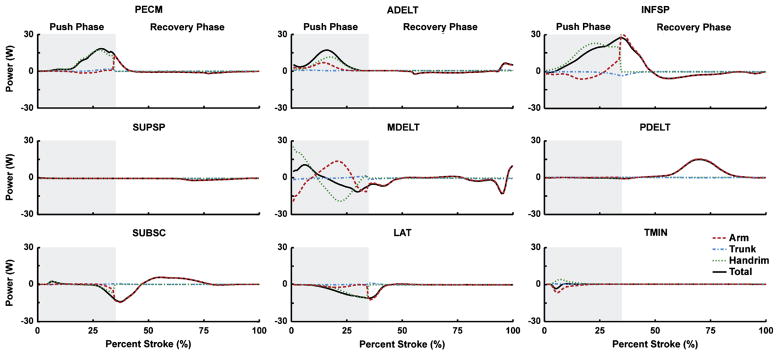
Of the shoulder muscles, the middle deltoid (Table 2, MDELT) was the primary contributor to total mechanical power during the initial third (0–11% stroke) of the push phase (Fig. 3; positive solid line), primarily by transferring energy from the arm (Fig. 3; dashed line negative, dotted line > solid line). Subsequently, the pectoralis major group (Table 2, PECM), anterior deltoid (ADELT) and infraspinatus (INFSP) generated the majority of total mechanical power but varied in their relative contributions to arm and handrim power. While PECM delivered power primarily to the handrim, ADELT delivered power to both the handrim and arm (Fig. 3; dotted and dashed lines). INFSP transferred power from the arm to the handrim in addition to generating power directly to the handrim (Fig. 3; dotted > solid line, dashed line negative). Teres minor (TMIN) also transferred power in a similar manner to the INFSP during early push; however, power contributions were small (Fig. 3). At the end of the push phase (30–34% stroke), the middle deltoid (MDELT), SUBSC and latissimus dorsii group (Table 2, LAT) absorbed power (Fig. 3; negative solid lines).

Figure 3.

Shoulder muscle contributions to segment power during the push and recovery subtasks. Individual segment powers were combined into four groups for analysis: Arm (upper arm, forearm and hand segments, dashed line), Trunk (trunk, scapula and clavicle, dash-dot line), Handrim (external handrim power, dotted line) and Total (sum of all segments, solid line). A positive (negative) value indicates power was delivered to (absorbed from) the corresponding body segments.

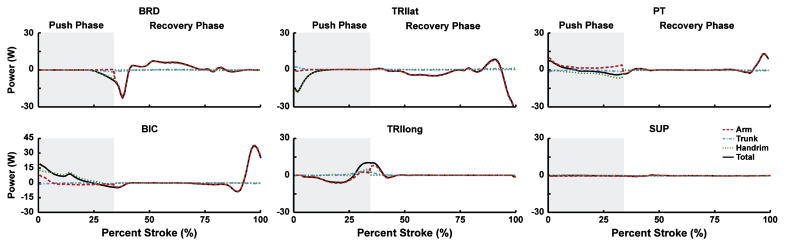
The biceps brachii (Table 2; BIC) delivered power to the handrim over the initial two-thirds of the push phase, with power contributions similar in magnitude to the shoulder muscles (Fig. 4; dotted line). At the end of the push phase, both BIC and the uniarticular elbow flexors (Table 2; BRD) absorbed power (Fig. 4; solid lines negative). Conversely, the long head of the triceps (TRIlong) first absorbed and then delivered power (Fig. 4; solid line). The uniarticular elbow extensors (Table 2; TRIlat) absorbed handrim power during the initial third of the push phase (Fig. 4). The pronator teres group (Table 2; PT) primarily transferred power between the handrim and arm (Fig. 4; dotted and dashed lines have opposite signs) instead of directly generating or absorbing power during the push phase (Fig. 4; solid line near 0).

Figure 4.

Elbow and forearm muscle contributions to segment power during the propulsion and recovery subtasks. Individual segment powers were combined into four groups for analysis: Arm (upper arm, forearm and hand segments, dashed line), Trunk (trunk, scapula and clavicle, dash-dot line), Handrim (external handrim power, dotted line) and Total (sum of all segments, solid line). A positive (negative) value indicates power was delivered to (absorbed from) the corresponding body segments. Note the change in vertical scale for BIC.

Recovery Phase Subtask

During the recovery phase, muscles systematically alternated between delivering and absorbing arm power to retract the arm (Fig. 5; dotted line), with most muscles falling into one of two groups. The first group, consisting of the shoulder extensors (Table 2; MDELT, PDELT, LAT), elbow flexors (BIC, BRD) and SUBSC absorbed power from the arm at the beginning of the recovery phase (Figs. 3, 4; dashed line at ~35–44% stroke). BRD, PDELT and SUBSC then acted to deliver arm power during the middle of recovery (45–78% stroke). Towards the end of recovery (>78% stroke), MDELT and BIC acted to first absorb and then deliver arm power (Figs. 3, 4; dashed line). The second group, consisting of the shoulder flexors (Table 2; ADELT, PECM), INFSP and elbow extensors (TRIlat, TRIlong) initially delivered a small amount of power to the arm and then absorbed power during most of the recovery phase (Figs. 3, 4; dashed line). Towards the end of recovery, TRIlat absorbed and ADELT generated arm power. The most distal arm muscles (PT, SUP) generated little power during recovery, except for PT delivering marginal power to the arm near the end of recovery (Fig. 4). If active, muscles switched from (to) power absorption to (from) generation when hand movement direction changed (Fig. 5).

Figure 5.

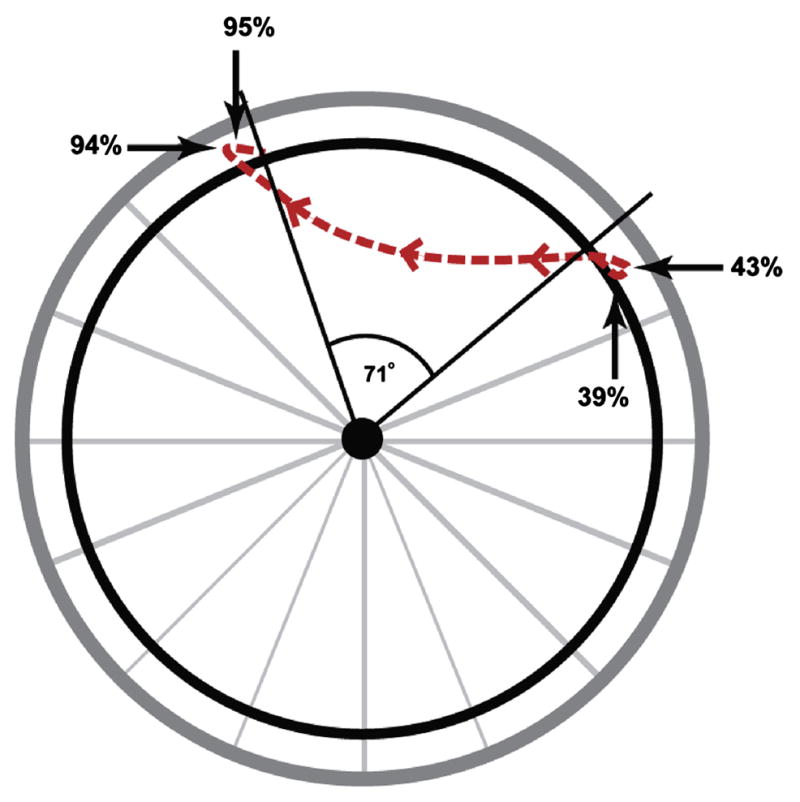
Motion of the hand during the entire stroke taken from the wheelchair propulsion simulation, which represents the average experimental propulsion data. During the push phase, the hand was in contact with the handrim (stroke angle of 71 degrees). During recovery, the hand followed the path indicated by the dotted line, with four changes in hand direction. These changes occurred in the anterior-posterior direction at 43 and 94 percent stroke and in the superior-inferior direction at 39 and 95 percent stroke.

4. Discussion

The goal of this study was to identify individual muscle function by determining how each muscle delivers, absorbs and/or transfers mechanical power to achieve wheelchair propulsion. Consistent with previous studies that found a division of labor between push and recovery phases, muscles generally functioned to either deliver power to the handrim or reposition the arm (Gutierrez et al., 2005; Lin et al., 2004; Mulroy et al., 1996; Veeger et al., 2002).

Push Phase Energetics

Net push phase arm power was consistent with the results of Guo et al. (2003, 2006), who performed a joint-level power flow analysis using an inverse dynamics model, with upper limb power systematically decreasing to a peak negative value (i.e., power absorption) near the transition point between push and recovery phases (Fig. 2; dotted line). Similarly, the simulation agreed with previous studies in which net handrim power was found to be positive throughout the push phase (Dallmeijer et al., 1998; Guo et al., 2006; Guo et al., 2003; Kwarciak et al., 2009), indicating that power is provided to the handrim throughout the push to propel the wheelchair forward (Fig. 2; dotted line). Unlike the findings of Guo et al. (2003, 2006), net power contributions from trunk lean were minor (Fig. 2; dash-dot line near 0), which may be attributed to the different study populations. Guo et al. (2003, 2006) used healthy subjects that generally have greater trunk excursions than individuals with spinal cord injury, which would result in the body providing more power during the push (Rodgers et al., 2003).

ADELT, PECM and INFSP were the primary contributors to mechanical power during the push phase, which was consistent with the large shoulder flexion moments and powers found by others (Koontz et al., 2002; Kulig et al., 1998; Morrow et al., 2010; Rodgers et al., 2003; Sabick et al., 2004) and suggests that wheelchair users likely select arm configurations that allow the shoulder flexors to function as the primary actuators during the push phase. All three muscle groups had similar trends in power generation, with peak power output occurring near the middle to end of the push phase (Fig. 3), consistent with muscle power estimates from quasi-static analyses during two different wheelchair propulsion conditions (Bregman et al., 2009). Most notable was INFSP, which contributed more handrim power than any other muscle during the push phase. However, as a rotator cuff muscle, INFSP is also responsible for helping stabilize the glenohumeral joint. Because of its dual roles of handrim power generation and joint stabilization, INFSP generates large forces and shoulder flexion moments (Lin et al., 2004; Veeger et al., 2002) during propulsion and may be highly susceptible to fatigue.

At the end of the push phase, both shoulder flexors and extensor were active (Fig. 3). This muscle co-contraction is necessary to reverse the direction of arm movement once the hand releases the handrim. At this time the wheelchair user must transition between the push and recovery subtasks, which require activity from muscles with antagonistic functions. Muscles that deliver handrim power during the push phase (PECM, INFSP) also accelerate the arm forward after release (see Recovery Phase Energetics below), a function counterproductive to the need to reduce the kinetic energy of the arm (i.e., to retract and elevate the hand during recovery, Guo et al., 2003). However, these muscles continue to deliver power for a short time after handrim release during muscle deactivation. Similarly, LAT and MDELT, which assist in recovery, are excited during the transition region to have sufficient activation time for generating force to absorb arm power and slow down forward hand movement. Combined with the force acting on the arm from the handrim, MDELT will act to elevate the humerus within the glenohumeral joint and create a condition requiring increased joint stabilization from antagonistic muscles to prevent humeral subluxation. Both PECM and INFSP help stabilize this joint, but these groups also provide much of the handrim power and are susceptible to fatigue. Therefore, demand for other muscles (e.g., TMIN, SUBSC) to provide joint stabilization may increase, which could explain the high prevalence of shoulder injuries in wheelchair users (up to 70%, Curtis et al., 1999; Gellman et al., 1988). Thus, propulsion techniques that improve transition mechanics may have a significant influence on UE demand and improve rehabilitation outcomes.

Both BIC and TRIlong were active during the majority of the push phase, with BIC delivering power directly to the handrim during the first half and TRIlong delivering power during the second half of the push (Fig. 4). Previous modeling studies have found the elbow joint moment to systematically switch from flexion to extension during the push (Price et al., 2007; Richter, 2001; Veeger et al., 1991), which is likely due to a transition from elbow flexor to elbow extensor muscle power generation (Bregman et al., 2009). The observed functions of BIC and TRIlong as providers of handrim power support the need for a flexor-extensor pattern, as BIC and TRIlong are best suited to generate handrim power at the beginning and end of the push phase, respectively. Although both groups had major roles in handrim power generation, the prevalence of elbow injury in wheelchair users is much lower (~16%, Sie et al., 1992). This may be the result of lower co-contraction, a shorter duration of elbow muscle activity and/or the greater inherent stability of the elbow joint. PT, a distal muscle, did not directly deliver or absorb power but acted to transfer energy between the arm and handrim (Fig. 3). This function is similar to that performed by the distal ankle muscles during bicycle pedaling, which act to transfer power from the leg to the crank (Neptune et al., 2000; Raasch et al., 1997).

Recovery Phase Energetics

Repositioning the arm in preparation for the subsequent push is a complex task, with muscles required to 1) absorb power to decelerate the forward movement of the arm, 2) deliver power to accelerate the arm posteriorly, 3) again absorb power to decelerate the arm and 4) again deliver power to accelerate the arm anteriorly in preparation for handrim contact during the subsequent push (Figs. 2, 5). In addition, the arm must achieve sufficient clearance from the handrim during recovery.

Both LAT and SUBSC helped reposition the hand during the initial recovery phase by absorbing power (i.e., decelerate the arm). SUBSC and PDELT then delivered power to accelerate the arm posterior (Fig. 3). In contrast, PECM and INFSP functioned to accelerate the arm forward during the initial recovery phase (Fig. 3; dotted lines). With the exception of ADELT, which functioned to provide power to the arm at the end of recovery (~> 75% stroke), the shoulder muscles were less active at the end of recovery. Low shoulder activity during this region was consistent with Price et al. (2007) who found that shoulder joint power during recovery was near zero during the end of the recovery phase (Fig. 3). Instead, most of the arm power was delivered by PT and BIC (Fig. 4). Some co-contraction also occurred at the elbow during the end of recovery (Fig. 4; BIC, TRIlong) suggesting that this period requires a large amount of elbow stabilization in preparation for contact with the handrim. Overall, the reduced roles of the shoulder muscles suggest that the recovery phase places less demand on the shoulder and rehabilitation outcomes may be improved by focusing on the push phase.

There are some potential limitations to this study. First, trunk movement outside the sagittal plane was not included and only the right arm was used in the simulation, which was based on the assumption that wheelchair propulsion is a symmetric movement. Although previous work has shown that wheelchair mechanics may be asymmetric (Hurd et al., 2008), the majority of wheelchair users have kinematic symmetry (Goosey-Tolfrey and Kirk, 2003) and differences in muscle function are likely to be small. Trunk contributions to propulsion energetics were small in this study, suggesting that out-of-plane trunk movement may have little influence on the study results. However, users do incorporate a wide range of propulsion techniques (Boninger et al., 2002; Dubowsky et al., 2009) and future studies investigating the influence of different propulsion techniques on muscle function should be performed. Also, to reduce simulation complexity, the wrist was fixed in the anatomical position and fingers were not modeled. Because a closed loop exists between the trunk and handrim, wrist movement can influence elbow and shoulder kinematics and may play a role in distal muscle function. However, the simulation in this study replicated well actual experimental shoulder and elbow joint kinematics, which limits the influence a fixed wrist would have on other joints. Previous studies have also shown wrist moments to be much lower than those at the other joints, with a primary function of power transfer instead of generation/absorption (Guo et al., 2006; Guo et al., 2003; Robertson et al., 1996; Sabick et al., 2004). Finally, a treadmill was used to collect the experimental data, which may not replicate normal propulsion. However, recent work has shown that the major characteristics of treadmill propulsion are similar to those observed overground (Kwarciak et al., 2010).

5. Conclusion

During wheelchair propulsion, muscles generally contribute to either push or recovery subtasks, with muscle co-contraction occurring during the transitions. The shoulder muscles (PECM, INFSP) appear to be particularly susceptible to fatigue and injury due to the dual roles of handrim power generation and glenohumeral joint stability and strength training focused on these muscles may improve rehabilitation outcomes. However, care should be taken to maintain muscle balance to avoid the development of additional musculoskeletal injuries. During the transition, elevated shoulder activity will create additional demand for glenohumeral joint stability, which may contribute to the shoulder pain and injuries experienced by wheelchair users. Thus, the transition region also may be an important focus area when developing rehabilitation and propulsion techniques aimed at reducing shoulder injuries. The modeling and simulation framework used in this study provided insight into how individual muscles contribute to the mechanical energetics of wheelchair propulsion and should prove useful in future studies that seek to understand how these contributions change when specific muscles lose their ability to generate force due to lack of neural drive (e.g., from spinal cord injuries) or muscle weakness (e.g., due to aging effects).