Constructing semantic representations from a gradually-changing representation of temporal context

Abstract

Computational models of semantic memory exploit information about cooccurrences of words in naturally-occurring text to extract information about the meaning of the words that are present in the language. Such models implicitly specify a representation of temporal context. Depending on the model, words are said to have occurred in the same context if they are presented within a moving window, within the same sentence or within the same document. The temporal context model (TCM), a specific quantitative specification of temporal context has proved useful in the study of episodic memory. The predictive temporal context model (pTCM) uses the same definition of temporal context to generate semantic memory representations. Taken together pTCM and TCM may prove to be part of a general model of declarative memory.

The importance of temporal context in learning the meaning of words has long been central to our understanding of the acquisition of word meaning. Contemporary computational models of semantic memory exploit this basic idea. However, the definitions of temporal context they use are contradictory with one another and often not theoretically motivated. For instance, in the BEAGLE model (Jones & Mewhort, 2007), the semantic representation of a word is the weighted average of all other word vectors that were presented in the same sentence as the word. In BEAGLE temporal context is operationalized as being constant within a sentence but changing completely between sentences. That is, words within the same sentence are in the same temporal context, but words in adjacent sentences are in completely different temporal contexts. Similarly, in LSA and the topic model (Landauer & Dumais, 1997; Griffiths, Steyvers, & Tenenbaum, 2007), a word×document matrix is the starting point for the calculations. This implies a representation of temporal context that is constant within a document, but that changes completely between documents.¹ Both of these approaches, BEAGLE and LSA and the topic model, share the assumption that temporal context is a categorical variable but differ in the time scale associated with the rate of change of temporal context. The fact that temporal context is only implicitly defined by these (and related) models makes the task of comparing the models, which vary on a number of other dimensions as well, considerably more diffcult.

The basic strategy of the research program described here is to use an explicit representation of temporal context inherited from work on episodic memory as a starting point for developing a computational semantic model. We will first briefly describe temporal context as defined by the temporal context model (TCM, Howard & Kahana, 2002; Howard, Fotedar, Datey, & Hasselmo, 2005; Sederberg, Howard, & Kahana, 2008). We will then describe how retrieval of temporal context can function to efficiently extract relationships between stimuli. Next, we describe the predictive temporal context model (pTCM, Shankar, Jagadisan, & Howard, 2009) as a solution for how to efficiently extract the meanings of words embedded in natural sequences. We then present evidence that pTCM can provide a useful description of information extracted from natural text. We close by describing several significant challenges that remain.

Temporal context in episodic memory

The initial goal of TCM was to account for the recency and contiguity effects observed in episodic recall tasks. The recency effect refers to the finding that, all other things being equal, memory is better for more recently experienced information. The contiguity effect refers to the finding that, all other things being equal, items experienced close together in time become associated such that when one comes to mind it tends to bring the other to mind as well. The contiguity effect has been extensively studied in episodic recall tasks, where it exhibits a characteristic asymmetry (see Kahana, Howard, & Polyn, 2008, for a review). Somewhat surprisingly, the contiguity effect, like the recency effect, persists over relatively long time scales, extending at least hundreds of seconds (Howard, Youker, & Venkatadass, 2008). Similarly, the contiguity effect is observed in the very earliest stages of immediate free recall (Howard, Venkatadass, Norman, & Kahana, 2007), a prediction unique to TCM among models of the recency effect.

Table 1 summarizes verbally the assumptions that constitute TCM. In TCM episodic recall proceeds by cuing with the current state of a distributed representation of temporal context. This state of context changes gradually over time. Studied items are activated by a context cue to the extent that it overlaps with the state of context when they were studied. The recency effect results from the combination of these two properties. After study of a list, items presented more recently in time were encoded in states of context that more strongly resemble the probe context. The concept that a gradually-changing memory signal contributes to forgetting is not unique to TCM, but has a long history in the mathematical psychology of learning and memory (e.g., Estes, 1955; Anderson & Bower, 1972, see also Mensink & Raaijmakers, 1988; Murdock, 1997; Brown, Neath, & Chater, 2007). TCM builds on these models, but makes the additional assumption that contextual drift is caused by the items themselves. This assumption enables the model to account for the contiguity effect in episodic memory (Howard & Kahana, 2002; Howard, Kahana, & Wingfield, 2006; Sederberg et al., 2008; Polyn, Norman, & Kahana, 2009a). Because the input to the context vector is caused by items, repetition of an item causes the state of context to change to a state similar to that during study of the neighbors of the original presentation repeated item, resulting in a contiguity effect. A further assumption of TCM is that repeated items can recover or retrieve their study context. That is, they can cause the context state to be partially reset to the state prior to the previous presentation of the repeated item.

Table 1.

Principles of operation of the temporal context model (TCM).

Temporal context changes gradually over time. Items are cued by a state of context to the extent it overlaps with their encoding context. Presentation of items causes a change in the state of context. Repeated/recalled items can recover the state of context in which they were previously studied.

An example may make this more concrete. Suppose that the model is presented with a list of words that includes the sequence … ABSENCE, HOLLOW, PUPIL, RIVER, DARLING … The temporal context in which PUPIL is encoded includes input caused by HOLLOW, and, to a lesser extent because it was further in the past, input caused by ABSENCE. Similarly, the temporal context in which each of the other items was encoded is composed of the input caused by the preceding items, weighted by their recency. If the context immediately after presentation of this sequence is used as a cue, DARLING would be most strongly activated because it’s encoding context is most similar to the cue context. In this way the model accounts for the recency effect. The model accounts for contiguity as well. Suppose that PUPIL is repeated at some later time, and it successfully recovers its encoding context. Then, the context cue recovered by PUPIL provides a better cue for RIVER than for DARLING because the encoding context for RIVER did not drift as far from PUPIL. Similarly, recovery of PUPIL’s encoding context makes a more effective cue for HOLLOW than ABSENCE for the same reason. In this way, the model accounts for the contiguity effect in both the forward and backward directions.²

The ability of items to recover their prior contextual states endows TCM with a number of important properties. For instance, the backward association manifest in the contiguity effect depends on the ability of items to recover their prior temporal contexts. Similiarly, because the prior state of context includes input caused by the items that preceded the initial presentation of the repeated item, recovering this state results in a mixing of the input patterns caused by items on the basis of their contiguity. This property can be exploited to describe effects in relational memory, as we shall see shortly. A more formal description of TCM follows. Readers who wish to avoid a mathematical description may choose to skip this subsection.

Formal description of TCM

We will deviate from some of the details (and notation) used in previous papers in order to create as much consistency as possible with the development of the semantic memory model used here. In the discussion that follows we will assume, unless otherwise noted, that the subject studies an extremely long list without repetitions of items. The state of temporal context at time step i, t_i, is a result of the previous state of context and an input pattern t^IN, caused by the item presented at time step i:

$${\mathbf{t}}_i=\rho {\mathbf{t}}_{i-1}+(1-\rho ){\mathbf{t}}_i^{IN},$$ (1)

where ρ is a scalar less than one. We assume that the input vectors are chosen such that the sum of their components is unity. Under these conditions, the sum of the components of t is also unity. Equation 1 implements the assumption that context changes gradually over time; all other things being equal, the state of temporal context at time step i resembles the previous state of context more than other states more distant in the past. Temporal context changes gradually as more (unique) items are successively presented.

We use an outer product matrix associating contexts to items to enable items to be activated by a contextual cue. During study, items are encoded in their temporal context. The matrix M is updated such that the change in M is given by:

$$\mathrm{\Delta }\mathbf{M}={\mathbf{f}}_i{\mathbf{t}}_{i-1}^{\prime },$$ (2)

where f_i is the vector associated with item i and the prime reflects the transpose. In order to recall an item, the matrix M is multiplied from the right with the current state of context. Equation 2 results in the property that each item f_i is activated to the extent that its study context overlaps with the context used as a cue.

It remains to describe the properties of the t^IN vectors. The input pattern t^IN caused by an item is composed of a fixed component that does not change across repetitions of an item over the time scale of a laboratory memory experiment that we will refer to as f and a changing component we will refer to as h. Each f_i and each h_i are caused by the item presented at time step i and depend only on the identity of that item and its previous history. The f vectors for each item are fixed throughout the simulation. If item α is presented at time step i, then

$${\mathbf{t}}_i^{IN}=(1-\gamma ){\mathbf{f}}_{\alpha }+\gamma {\widehat{\mathbf{h}}}_{\alpha }.$$ (3)

The hat in the second term indicates that h is normalized prior to entering this expression. We fix the f_αs to be unit vectors that serve as the bases for the t space. With learning, h_α changes from one presentation of item f_α to another according to

$$\mathrm{\Delta }{\mathbf{h}}_{\alpha }={\mathbf{t}}_{i-1}.$$ (4)

The function of h is to enable items to recover the temporal context in which they were studied. This implements property 4.

Relational memory, retrieved context and the hippocampus

Consider the case of a repeated item that recovers its study context when it is repeated. This means that the input caused by this item is not consistent across its two presentations. The change in the input patterns with repetitions has wide-reaching implications. The mixing of input patterns creates the ability for the model to describe associations between items that do not actually co-occur. Consider the case in which the subject learns a pair of items A-B and then much later learns B-C. If contextual retrieval takes place (i.e., if γ is nonzero), then during learning of A-B, the input pattern caused by B comes to include the temporal context that preceded it. This state of context includes information contributed by item A. As a consequence, during learning of B-C, the input pattern caused by B includes information about A. This means that the encoding context for C includes “parts of” A, even though A and C were not presented close together in time.

In fact, such transitive associations among items that have not been presented close together in time are observed (e.g. Bunsey & Eichenbaum, 1996; Slamecka, 1976; Howard, Jing, Rao, Provyn, & Datey, 2009). For instance, Howard et al. (2009) taught human subjects a long list of paired-associates with overlapping pairs. That is, subjects learned a list of thirty five pairs of the form A-B, B-C, C-D … presented in a random order for a total of twelve presentations each. During a final free recall session, subjects were asked to recall all the items from all the pairs in the order they came to mind. If a subject had just recalled a double-function word from the list, the next word they recalled would tend to come from a nearby pair, even if it was not from the same pair as the just-recalled word. For example, if the subject had just recalled B, the next word that came to mind would be more likely be D than E. In other words, subjects showed behavioral evidence for transitive associations between items across pairs that fell off as a function of the number of links in the chain between items. It is as if the subjects were able to integrate the pairs into a common global memory structure. Howard et al. (2009) demonstrated that TCM provides a good description of this behavior.

Although transitive associations actually make paired associate learning more difficult (see especially Provyn, Sliwinski, & Howard, 2007), they provide an extremely useful computational function in allowing the model to infer relationships between items that are not explicitly instructed. That is, the model does not have to be explicitly instructed that A and C “go together.” A successful model of semantic memory needs to be able to place tens of thousands of symbols in the proper relation to one another. If each of those relations needed to be explicitly instructed, the number of presentations necessary would be extremely large. Moreover, the model does not need to make a priori assumptions about the possible structure present in the learning set (Tenenbaum, Griffiths, & Kemp, 2006; Kemp & Tenenbaum, 2009). This is possible because retrieved context “spreads” along the links in the chain such that the representation at the end of training reflects the topology of the pairs it was trained on. Note that this functionality depends on a training set in which relationships can be directly inferred from contiguity.

The function of contextual retrieval in TCM is in some sense analogous to the function of dimensional reduction in LSA and the topic model. To ilustrate this, Figure 1 shows results for TCM, LSA and the topic model trained on a “corpus” that consisted of a set of “documents” each of which contained a single double function pair.³ That is, document 1 consisted of the words A and B, document 2 consisted of the words B and C and so on. Each panel shows the similarity of the representation of each word to each other word. Transitive associations can be seen by the shading among pairs of items that did not co-occur. TCM, LSA (with two dimensions) and the topic model (with two topics) all build transitive associations that bridge across pairs. Interestingly, LSA only exhibits transitive associations if the number of dimensions retained is less than the number possible. That is, if all seven dimensions were retained for LSA, the model does not exhibit across-pair associations. Rather it only makes similar words that occur in the same document. Similar results are observed for the topic model with seven topics (one for each document). It should be noted that HAL and BEAGLE also illustrate transitive associations, although this is not attributable to dimensional reduction in those models.

Figure 1. The temporal context model (TCM), a model of episodic recall based on contextual overlap, and computational models of semantic memory both predict transitive associations.

In all three panels, the figure shows the similarity of the representation of each item in a double function list of paired associates after training. a. Retrieved temporal context as defined by TCM shows transitive associations. The shading of each square codes for the similarity of the temporal context vector retrieved by the corresponding pair of items after ten trials of learning on the corresponding double function list. Vector similarity was assessed using the inner product. High values of the inner product are shaded dark. b. A representation generated using Latent Semantic Analysis (Landauer & Dumais, 1997) shows transitive associations. A singular value decomposition was computed for an item-context matrix corresponding to training on a double function list of pairs. Two dimensions were retained. Similarity of each pair of vectors was assessed using the cosine of the angle between them. High values of cosine are dark. c. The topic model (Griffiths, Steyvers, & Tenenbaum, 2007) was trained on a set of contexts simulating presentation of a double function list. The simulation used two topics and α = 0.1 and β = 0.1 (see Griffiths, Steyvers & Tenenbaum, 2007 for details). The similarity between each pair of items was estimated by comparing the Kullback-Leibler divergence of the distribution over topics induced by each item. Small values of divergence, corresponding to high similarity, are dark.

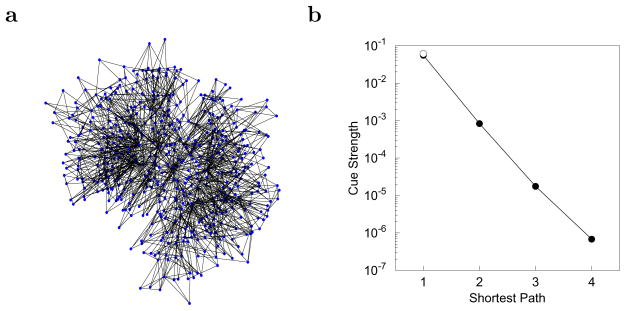
Contextual retrieval enables the development of a representation of the items that reflects their global co-occurrence structure. For instance, suppose that we train the model on a set of overlapping pairs A-B, B-C … Z-A, with the pairs presented in a random order and each pair completely isolated from the others. After training, the input caused by B will resemble the input caused by C more than the input caused by D. Similarly, the input caused by B will resemble the input caused by D more than that caused by E and so on. Retrieved temporal context enables TCM to place the input vectors caused by each item in the proper global relationship to each other. Rao and Howard (2008) showed that TCM with retrieved context can not only learn a one-dimensional topology, the ring, but also a two-dimensional topology in which items form a sheet, and more realistic topologies corresponding to naturally-occurring language. Figure 2a shows a miniature version of a small-world network (Watts & Strogatz, 1998; Strogatz, 2001) used to train the model. The network was generated with 10,000 nodes (500 are shown in Figure 2a) with connectivity comparable to that of the English language, as estimated by the network analysis of WordNet performed by Steyvers and Tenenbaum (2005). We trained TCM on pairs chosen by selecting nodes connected by an edge of the graph. Figure 2b shows the cue strength between items ⁴ as a function of the length of the shortest path between them in the network. Note that pairs with a value of shortest path greater than one were never presented together during training. Nonetheless, the model correctly decribes the distances among items from remote areas of the network. Further, this behavior depends on contextual retrieval—the cue strength is zero for remote items if contextual retrieval does not take place (open symbols).

Figure 2. Contextual retrieval enables the extraction of global structure from isolated episodes.

a. Miniature example of a small-world network with connectivity chosen according to the structure of English as estimated by Steyvers & Tenenbaum (2005). b. The cue strength between pairs chosen from the small-world network are shown as a function of the shortest path between the items. Filled symbols show TCM with contextual retrieval. The open symbol shows the value for TCM without contextual retrieval. Only one point is shown for the model without contextual retrieval because the cue strength is zero for items not presented as part of the same pair.

pTCM: Learning Structure by Predicting the Future

We have seen that contextual retrieval enables TCM to discover latent structure from presentation of isolated stimulus events and integrate them into a global representation. We have also seen that the model can learn complex topologies believed to underlie natural language. This seems like it might be sufficient to construct a model of semantic structure. Our initial strategy was to take TCM as just described and present it with a very long sequence of natural language and evaluate the model’s behavior. As it turns out, this is a deeply theoretically unsatisfactory model.⁵ The reason turns out to be that, unlike the artificial examples explored above, proximity in natural language is not a strong proxy for similarity.

Consider the meaning we would learn for a novel word presented in the following sentence “The baker reached into the oven and pulled out the FLOOB.” What is the meaning of FLOOB? In TCM, the representation of FLOOB would be updated to include information from the preceding context; i.e., FLOOB would become similar to the representation of “out,” “pulled,” “oven,” “baker,” etc. While it is reasonable to infer that a FLOOB has something to do with those words, it is not at all the case that FLOOB is synonymous with the preceding context. If it were, it would be redundant and there would be no purpose to use the word FLOOB in that context. A much more natural way do describe the meaning of FLOOB would be to make FLOOB similar to the words that would have fit into that temporal context, for instance “cake” or “bread.”

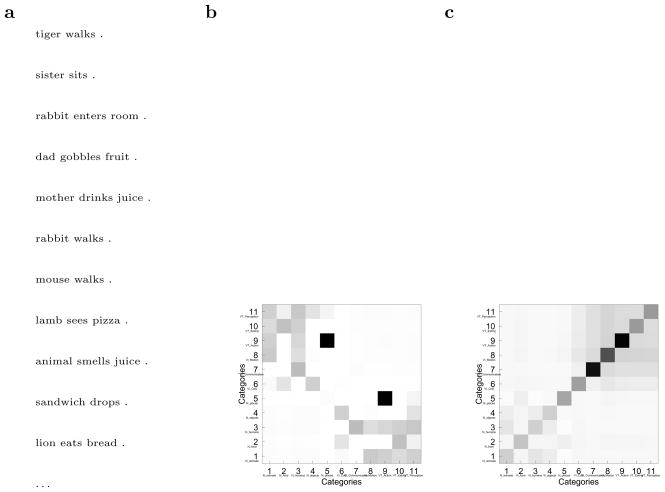
Figure 3 illustrates this problem more concretely. We trained TCM with a set of sentences generated by the simple language generator program (SLG, Rohde, 1999) using a simple grammar previously used in a connectionist simulation of language acquisition (Borovsky & Elman, 2006). The SLG generated a set of sentences from words drawn from several categories of nouns (e.g., animals, people) and verbs (e.g., perception, action) subject to both syntactic and semantic constraints (examples can be found in Figure 3a). Figure 3b reflects the semantic space generated from TCM. More explicitly, we calculated ${{\mathbf{t}}_{\alpha }^{IN}}^{\prime }{\mathbf{t}}_{\beta }^{IN}$ between different words and aggregated the results according to their category relationships. As shown by Figure 3, words become similar to the words that precede them; because the sentences all have either a N-V-N or a N-V structure, nouns become similar to verbs and vice versa.

Figure 3. pTCM as a model of semantic learning.

a. Sample sentences generated by the simple language generator. b-c. Similarity between the representations of words belonging to each category of the simple language. Dark boxes correspond to high similarity. The similarity between each word and itself is excluded from this plot. b. Category structure for TCM after being trained on sentences sampled from the simple language. c. Same as b, but for pTCM. Unlike the standard version of TCM, pTCM has learned an appropriate category structure from the simple language.

The predictive temporal context model (pTCM, Shankar et al., 2009) builds on the framework of TCM (Table 2). Just like TCM, it uses a representation of temporal context that changes gradually over time. Similarly, context is used to cue items and the input to context is caused by items. However, in pTCM, the context is used as a cue not only when items are to be recalled, but also at each time step to create a prediction about what will happen next (Property 2, Table 2). The semantic representation of an item is composed of the prediction vectors in which the word is experienced over time. This semantic representation for each word becomes part of the input to the temporal vector that the word causes when it is presented. A more formal definition follows in the next subsection. This subsection can be ommitted by the reader not interested in the mathematical details of the model’s operation. Before this, we briefly demonstrate that the adjustments present in pTCM enable us to solve the problem of learning semantic representations from sequentially-organized materials.

Table 2.

Principles of operation of the predictive temporal context model (pTCM). Compare to Table 1.

Temporal context changes gradually over time. Items are cued by a state of context to the extent it overlaps with their encoding context; cuing at each time step of learning yields a prediction. Presentation of items causes a change in the state of context. Repeated/recalled items can recover the state of context in which they were previously studied. The semantic representation of an item is composed of the prediction vectors that obtained when it was presented.

Figure 3c shows the results of the simulation with the SLG conducted with pTCM. In pTCM, the representations of words become similar to other words from the same category (dark boxes along the diagonal). To the extent that there is residual similarity across categories, it respects the part of speech of the words. For instance, the shaded box in the upper right of Figure 3c reflects the fact that verbs are more similar to other verbs than they are to nouns. This ability to simultaneously capture syntactic and semantic roles is common to the simple recurrent network (Elman, 1990) and the syntagmatic-paradigmatic model (Dennis, 2004, 2005).

Formal description of pTCM

Let us describe the process of computing the prediction vector and exploiting this information to develop a semantic representation more formally. The prediction vector at time step i, p_i, is calculated using

$${\mathbf{p}}_i=\mathbf{M}{\mathbf{t}}_i,.$$ (5)

where M differs from the matrix in Eq. 2 by virtue of being row-normalized. The vector p_i can be thought of as the prediction for what item will be presented at time step i + 1. It has been proven that for bigram languages this prediction can be perfect (Shankar et al., 2009).

Each word α in the language is associated with a semantic representation s_α that is built up from the prediction vectors available when the item is presented. If word α is presented at time step i, then s_α is updated such that the change in s_a is given by:

$$\mathrm{\Delta }{\mathbf{s}}_{\alpha }={\mathbf{p}}_{i-1}.$$ (6)

Finally, the semantic vector contributes to the input pattern (t^IN) to context when the corresponding item is presented. If item α is presented at time step i, then the cortical part of the input pattern ${\mathbf{t}}_i^{IN}$ (see Eq. 3) is given by

$${\mathbf{c}}_i=(1-\phi ){\mathbf{f}}_{\alpha }+\phi {\mathbf{s}}_{\alpha }$$ (7)

where f_α is a fixed vector orthonormal for each item and φ is a parameter that controls the degree to which the semantic representation enters context. Because our focus in this paper is on the learning of semantic representations, we will assume that recovery of a prior context states does not take place (i.e., γ = 0 in Eq. 3) throughout the remainder of this paper.

Shankar et al. (2009) demonstrated several useful results regarding the behavior of pTCM using toy languages (even simpler than the SLG) to be able to quantitatively compare the model’s behavior to the generating function of the language. One key finding is that φ enables the model to generalize across items that have similar roles in the language in much the same way that γ enables TCM to generalize across contiguity relations among items. In addition, Shankar et al. (2009) derived an expression that enables one to calculate the steady state behavior of the model in a much more computationally efficient way. In pTCM, calculation of the p vector at each time step requires a matrix multiplication. Hence pTCM is much more computationally intensive than TCM. The expression for the steady state behavior of the model exploits the somewhat surprising fact that at asymptote the semantic representations can be calculated just with knowledge of M. Similarly, at asymptote, the steady state, M can be calculated directly if the semantic representations are known.

Shankar et al. (2009) proved that this steady state aproximation precisely describes the simulation model’s behavior with a sufficiently long training set and also closely approximated the simulation model’s behavior with shorter training sequences. An important point to note is that pTCM is history-dependent. That is, the effect of being trained on a particular sequence early in training is different from the effect of being trained on the same sequence later in training. If the model is being used to estimate a language with a constant generating function, this property is a nuisance. The approximation can be thought of as the “history-independent” model that would result from averaging over all possible sequences that could lead to the same initial estimate of M.

pTCM as a model of natural language processing

The foregoing results suggest that pTCM ought to be able to learn semantic structure from natural language. In order to test this, we trained pTCM on the TASA corpus and examined the model’s behavior on a synonym test and a free association test. Because of the size of the corpus, it was not practical to run the entire simulation model. Instead, we used the history-independent steady state approximation of the simulation model (Shankar et al., 2009).

Simulation Methods

In order to test the applicability of the model to real-life language acquisition, we trained pTCM on a widely-used corpus of the English language—the Touchstone Applied Science Associates (TASA) college level corpus. The TASA corpus contains about 11 million words across 37,000 documents and 93,000 unique words. To preprocess the corpus, we stripped it of punctuation, numbers, very frequent and commonly occurring words (including function words like ‘a’, ‘the’, etc.), and words that occurred in fewer than three documents and fewer then 10 times in the whole corpus. This resulted in a reduced corpus of about 5 million tokens and 48,000 unique words. The individual documents or paragraphs in the corpus were treated as independent, i.e., the context vector did not evolve across paragraphs. The sentence separators, on the other hand, were treated as being equivalent to distractor tasks, and ρ was changed transiently during the transition from one sentence to the next, assuming a value of ρ_D between sentences.

The computation time for the steady-state approximation was sped up further by writing a parallel sparse implementation using the message passing interface (MPI) library in C++. Throughout the simulations described here, we set the sparsity threshold to 10⁻⁵. However, the amount of time required to run the approximation on a dual Xeon quadcore (3.16 GHz) machine with 8 Gb of RAM made it impractical to evaluate the model many times with varying parameters. To reduce the processing time further, we collapsed a large number of low-frequency words remaining in the preprocessed tokens into a single token. This token was treated differently from the others in that it did not have an entry in M or a semantic representation |s〉. The effect of our treatment was such that when this special token was encountered in the corpus, the context vector was multiplied by ρ, but no other action was taken. After reducing the number of words to 10,152 in this way, calculating the model on the corpus with a single set of parameters took about 16 hours.

We evaluated the model parameters based on the model’s ability to describe the semantic structure of English. For this, we assembled a pool of cue words such that

1. Each word was normed in the USF free association database (Nelson, McEvoy, & Schreiber, 2004).

2. Each word was present in our reduced corpus.

3. Each word had a synonym as evaluated by WordNet.

4. Each word’s first associate was present in our reduced corpus.

5. Each word’s first listed synonym was present in our reduced corpus.

There were 1040 such words. These had 591 unique synonyms and 583 unique first associates. In order to evaluate the models’ ability to describe performance on the synonym test in a fair manner, it was necessary to find a nonparametric measure of the degree to which the model captures the structure of the space. Let us arbitrarily separate the synonym pairs into cues and targets for expository purposes. For each cue, we calculated the inner product of the semantic representation of each of the targets to that cue and retained the rank of the cue’s target relative to the set of all targets. Ties were addressed by taking the mean rank of the values tied with that of the target. The distribution of ranks was retained and the mean log rank on the synonym test was minimized. The results presented in this paper are based on the parameters for which the mean log rank is minimal. An analogous procedure, wherein the mean log rank on the free association test is minimized, can be adopted to evaluate the model’s parameters based on the models’ performance on the free association test. In this paper, we do not report results from these parameters. We computed ranks for pTCM using two measures of similarity between word α and β. One measure, which we refer to as the pTCM free associate strength, is constructed by taking the cortical input for item α, multiplying it by the context-to-item matrix and measuring the degree to which word β is present in the output ⁶. This is analogous to presenting item α, allowing it to provide input to the state of temporal context, and seeing to what extent β is predicted. The other method compares the similarity of the cortical input of α to the cortical input of β.⁷ We refer to this latter measure as the pTCM vector space model.

The time necessary to compute pTCM on the corpus precluded a thorough search of the parameter space. We adopted the strategy of attempting to search the parameter space retaining 3000 dimensions, then evaluating the best-fitting parameters for the model retaining 10,152 dimensions. We used a downhill simplex algorithm to minimize performance on a variety of synonym tests; these ultimately did not completely converge to a solution and we took the most satisfactory solution that was available. We evaluated the simulation model with the same parameters and 3000 dimensions. However, optimization of the simulation model was not practical and we only report results from the approximation.

In order to compare pTCM to a version of LSA trained on the same inputs, we computed an LSA solution on the reduced corpus. This corpus did not include the stop words, short words and extremely infrequent words omitted at the parsing stage, but did include the words collapsed into a single string. We varied the number of dimensions retained in steps of fifty to find the value that resulted in the best performance (as measured by mean rank) on our synonym test. This value was 800. One might argue that our use of an impoverished version of LSA is somewhat unfair to that method—unlike pTCM, LSA is not subject to computational limitations that make it impractical to run on the entire corpus. For this reason, we also calculated results for LSA calculated on the entire corpus with 300 dimensions. This calculation was done with the same in-house LSA implementation we used to compute the reduced corpus. The results of this calculation were checked against the SEMMOD package (Stone, Dennis, & Kwantes, 2008).

Results

The best-fitting value of ρ, .68, was much greater than zero, indicating that multiple preceding content words contributed to the model’s estimate of temporal context. The value of ρ_D describing the rate of contextual drift across sentence boundaries was also much greater than zero indicating that information across sentence boundaries contributed positively to model performance. Critically, the best-fitting value of φ, .41, was greater than zero, indicating that the ability to generalize across experiences was important to the model’s performance. We found that a broad variety of values of φ yielded roughly similar ranks on the synonym test as long as the value of φ did not approach zero or one, at which point performance fell off dramatically.

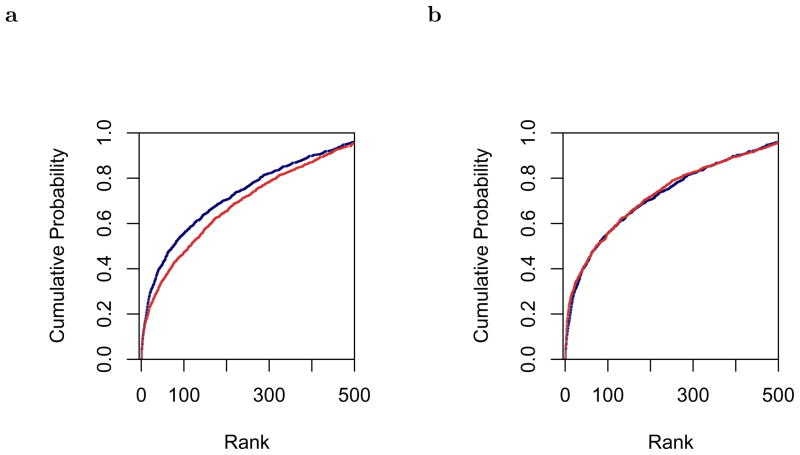
Figure 4a shows the cumulative distribution of ranks for the pTCM vector space model (dark blue) and LSA (light red) when both are trained on the reduced corpus. The graph gives the cumulative probability that the similarity of the cue word’s synonym obtained a given rank relative to the other targets. Good performance is reflected as a large number of low ranks, which means that the cumulative probability increases at low ranks. Put another way, good performance is manifest as a higher line in Figure 4a. As can be seen from Figure 4a, the distribution of ranks generated by the pTCM vector space model for synonyms was robustly lower than the ranks generated by LSA when they were both trained on the reduced corpus. Figure 4 compares performance on the synonym test for the pTCM vector space model trained on the reduced corpus (dark blue) to LSA trained on the entire corpus (light red). Although the performance of the two models appears very similar, it can be established statistically that LSA trained on the entire corpus outperforms pTCM trained on the reduced corpus. For instance, the rank on the synonym test was lower for LSA trained on the entire corpus for 551 synonyms whereas pTCM trained on the reduced corpus only produced a lower rank for 461 synonyms (p < .005 by the binomial distribution; there were 28 ties). The results of the analysis of the synonym test indicate that pTCM trained on the reduced corpus (approximately 10,000 unique words) outperforms LSA trained on the same corpus, and comparable, although slightly worse, to LSA when it was trained on the entire corpus (approximately 100,000 unique words).

Figure 4.

pTCM’s vector space model performs comparably to LSA on a synonym test. A set of 1040 synonym pairs was assembled. For each model, we calculated the similarity between a word and its synonym and expressed that as a rank relative to all the other words’ synonyms. Low ranks indicate the model is doing well at placing words with similar meanings in similar locations. a. Cumulative probability distribution of the rank of the synonym for the pTCM vector space model (dark blue) and LSA trained on the same words (light red). The higher curve indicates a larger proportion of low ranks, and thus better model performance. pTCM shows a marked improvement over LSA trained on the same words. b. Same as a, but comparing pTCM trained on the reduced corpus (dark blue) to LSA trained on the entire corpus (light red). Despite the fact that pTCM only had detailed information about 10,000 words (as opposed to 93,000 for LSA), there are relatively modest differences between the performance of pTCM and LSA.

Performance by pTCM on the synonym test was moderately correlated with performance by LSA. The correlation across pairs between the rank assigned to synonyms by pTCM and by LSA trained on the reduced corpus was .56. The correlation between pTCM and LSA trained on the entire corpus was .69. However, both of these numbers were reliably less than the correlation between LSA trained on the reduced corpus and LSA trained on the entire corpus, .74. Note that although this comparison led to the highest correlation, it also corresponded to the largest difference in performance.

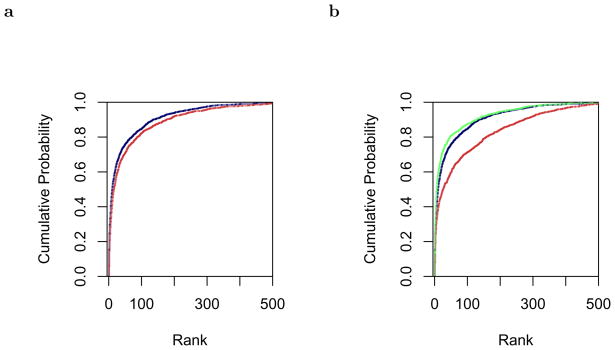
We obtained comparable results for the free associate test. First, Figure 5a shows the cumulative probability functions for the distribution of ranks of the first free associates for the pTCM vector space model (light red) and the pTCM free associate model in which the semantic representation of the cue item is used to predict the subsequent item (dark blue). There is a strong advantage for the pTCM free associate model over the pTCM vector space model in modeling free associates. Figure 5b shows the cumulative probility distribution for the pTCM free associate model trained on the reduced corpus (dark blue), LSA trained on the reduced corpus (light red) and LSA trained on the entire corpus (lighter green). As with the comparison with the synonym test, pTCM produced reliably lower ranks than LSA when they were both trained with the reduced corpus. As with the synonym test, when LSA is trained on the entire corpus, there is a small but reliable advantage over pTCM trained on the reduced corpus. For instance, the rank of the first free associate was lower for LSA trained on the entire corpus for 551 cues whereas pTCM trained on the reduced corpus only produced a lower rank for 388 cues (p < .001 by the binomial distribution; there were 101 ties).

Figure 5.

Performance on free association norms. Similarity ratings were evaluated for a list of 1040 words paired with their strongest associates. The strength of the relationship between the prime and its first associate was calculated and turned into a rank relative to the first associates of the other primes. Cumulative probability distributions of ranks are shown. Lower ranks reflect better model performance, meaning that higher curves reflect better model performance. a. The cumulative probability distribution of ranks of the first associates for the pTCM “recall” model (dark blue) and the pTCM vector space model (light red). For the pTCM recall model, the semantic representation of the cue item was used as a cue via the context-to-item matrix. The activation of each target was used to generate its rank. The vector space model simply uses the inner product of the semantic representation of items to generate similarity values. b. Cumulative probability distributions of ranks for the pTCM recall model (dark blue), LSA trained on the same words (light red) and LSA trained on the entire corpus (lighter green). pTCM trained on the reduced corpus shows dramatic improvement over LSA when it was trained on the same words. LSA trained on the entire corpus shows a modest improvement over pTCM trained on the reduced corpus.

On the free associate test, the pTCM free associate model was only moderately correlated with LSA and with the pTCM vector space model, and the pTCM vector space model was more strongly correlated with LSA trained on the entire corpus. The correlation across pairs of the rank assigned by the pTCM free associate model to the first free associate to the rank assigned by the pTCM vector space model was .48. The correlations between the pTCM free associate model and LSA trained on the reduced and entire corpus were also moderate, both r = .49. Interestingly, the correlation between the ranks assigned by the pTCM vector space model and LSA trained on the entire corpus were reliably higher, .68, and also higher than the correlation between LSA trained on the entire corpus and LSA trained on the reduced corpus, .64.

There are several conclusions that can be reached from these analyses. First, the two measures derived from pTCM, the vector space similarity and free associate strength, produce in general different results. In particular, the vector space model was inferior at modeling human free associate performance (Figure 5a). For both the synonym and free associate test, pTCM produced a dramatic advantage over LSA when both methods were trained on the reduced corpus. When LSA was trained on all the words in the corpus, approximately 100,000 unique words, it produced superior results to pTCM trained on about 10,000 unique words. It is tempting to assume that if pTCM were also provided more information by means of training it on the entire corpus it would dramatically outperform LSA. While this is a possibility, it is possible that information about low-frequency words would provide a source of noise that would actually reduce pTCM’s performance.

Nonetheless, there are clearly qualitative differences between what is being responded to by the different pTCM measures and LSA. Table 3 shows the nearest neighbors of the word BAKER for the pTCM vector space model, the pTCM free associate model and LSA trained on the entire corpus. Several results can be obtained from examination of Table 3. First, the pTCM vector space model has exclusively identified proper names, with an emphasis on last names (e.g., QUIMBY, FRITS, and WIGGLE all appear as last names in the TASA corpus). The vector space model ultimately rates as similar words that occur in similar contexts. In the TASA corpus, proper names often occur in similar roles in descriptions of conversations, as well as in the context of first names.

Table 3.

Nearest neighbors to the word “baker” using various measures of semantic similarity.

pTCM vector space	pTCM free associate	LSA
quimby	helper	gaslight
frits	tennessee	pastry
wiggle	cindy	holmes
liza	peel	sherlock
roberts	shoemaker	kendrick
rogers	cooper	passersby
miyo	loaf	sirhan
mandy	rotten	richard
frances	lazy	cakes
cass	shop	tarts
handing	baked	humphrey
pooh	blacksmith	wallace
jed	cakes	dough
gregory	onion	hubert
nicky	dough	irwin
oswald	novels	daley
zaphod	baking	assasinations
pippi	huddled	begrimed
gran	batter	leavened

The first column shows the nearest neighbors in the pTCM semantic space. The second column shows the free associates of “baker” using pTCM. The third column shows the LSA nearest neighbors with pseudodoc weighting from lsa.colorado.edu with words that appeared in the corpus less than or equal to three times removed. The highest ranking word for all three measures was baker, which has been removed from this table.

The pTCM free associate measure of BAKER generates words with a variety of origins that can be understood from examination of the TASA corpus. For instance, the presence of TENNESSEE in this list is due to several passages that discuss former Senator Howard Baker of Tennessee. The presence of CINDY in the list is attributable to a single passage in which a student (Cindy) has a conversation with her teacher (Mr. Baker). A majority of the entries for BAKER are related to the baking profession (e.g., LOAF, SHOP, BAKED). In most cases, the pTCM free associate measure produces words that appear in close proximity to BAKER in the corpus.

In contrast, LSA’s responses are grouped according to several broad themes that occur in the corpus. One easily identifiable theme are words related to the profession of baking (e.g., PASTRY, CAKES, TARTS, DOUGH). The documents describing former Senator Howard Baker give rise to several near-neighbors that are related to politics and news in the late sixties and early seventies (e.g., SIRHAN, HUMPHREY, WALLACE, DALEY, ASSASINATIONS). In addition, multiple LSA near-neighbors are related to passages describing the fictional detective Sherlock Holmes (e.g., GASLIGHT, HOLMES, SHERLOCK, BEGRIMED), who lived on Baker Street in London.

Although these measures provide comparable performance on synonym tests (Figure 4b) and free associate tests (Figure 5b), Table 3 suggests that the measures accomplish this level of performance by responding to different sources of information. Examination of Table 3 relects the fact that LSA responds to thematic information available at the level of the document. The vector space model of pTCM responds by rating words that are preceded by similar temporal contexts as similar to one another. The pTCM free associate measure rates as similar words that occur in close temporal proximity to one another. The fact that these different sources of information lead to similar performance suggests the possibility that these measures could be combined to provide a metric more useful than any one of the measures taken in isolation.

General Discussion

Previous work on TCM demonstrated that gradually-changing temporal context can provide a good account of recency and contiguity effects observed in episodic memory (Howard & Kahana, 2002; Howard, Youker, & Venkatadass, 2008; Sederberg et al., 2008; Polyn et al., 2009a). Here we discuss efforts to construct a model of semantic memory within the same framework. Contextual learning enables generalization across multiple experiences that lack overlapping elements placing stimuli into the correct global arrangement (Howard et al., 2009; Rao & Howard, 2008). The predictive temporal context model (pTCM Shankar et al., 2009) enables generalization to take place in sequentially-organized materials, such as natural language. We then showed several demonstrations that pTCM can be applied to natural language by training the model on a reduced version of the TASA corpus. pTCM dramatically outperformed LSA trained on the same reduced corpus and produced results close, although statistically inferior, to those of LSA trained on the entire corpus.

The point of this excercise was not to claim that pTCM is of superior practical utility than LSA, or other computational models of semantic memory at this time. At present, the computational demands of pTCM and the necessity of fitting multiple parameters make it unwieldy for many applications. However, because of its tight coupling with a successful model of episodic recall, it has theoretical advantages over other existing computational semantic memory models. The fact that a common description of temporal context can be used as a core concept of both a model of episodic memory performance and a model of semantic memory acquisition suggest that these concepts can form the basis of a common account of all of declarative memory. pTCM may be uniquely suited for describing the process of learning and memory retrieval that combines both semantic and episodic information.

Where is pTCM in the space of computational models of semantic learning?

A natural question to ask is how pTCM relates to extant computational models of semantic memory. Here we briefly discuss the commonalities and differences between pTCM and several widely-used models.

HAL

The hyperspace analogue to language (HAL Lund & Burgess, 1996) model uses a semantic representation that codes each word as the vector of counts of other words in the language appeared in a moving context window with that word. This is somewhat analogous to a linearly-decaying temporal context. There are numerous similarities between HAL and pTCM. These include the fact that more recent words within a document contribute more strongly to the meaning of a word (this property is not shared with LSA or the topic model). In HAL, a word recovers the set of words that occurred nearby it during learning—a process not dissimilar to retrieval of temporal context. This property enables HAL, along with the other models considered here, to account for transitive associations among items that did not co-occur in the corpus.

One of the differences between HAL and pTCM is that the range over which temporal context is defined in pTCM can quite long in pTCM—many prior words can contribute to the context. Although it remains to be seen how the “tail” of this distribution contributes to the semantic representations obtained from natural language, it is worth noting that the best-fitting parameters obtained here indicate that performance was optimal when many prior items contributed. A quick calculation reveals that in our natural language simulations as many as 27 prior items could have contributed to the context vector before passing under the sparsity threshold with the parameters used.⁸ This difference between HAL and pTCM is perhaps analogous to the distinction between buffer models of short-term memory (e.g. Atkinson & Shiffrin, 1968; Raaijmakers & Shiffrin, 1980) and TCM in understanding episodic free recall. There, the primary advantage of gradually-changing temporal context over buffers with finite range is that temporal context can provide a more natural account of recency and contiguity accounts that extend over multiple time scales (see Usher, Davelaar, Haarmann, & Goshen-Gottstein, 2008; Howard, Kahana, & Sederberg, 2008; Kahana, Sederberg, & Howard, 2008; Sederberg et al., 2008, for a thorough discussion of the relationship between TCM and buffer models). The other major point of distinction between HAL and pTCM is that in HAL there is no generalization across word meaning during learning.

BEAGLE

In BEAGLE (Jones, Kintsch, & Mewhort, 2006; Jones & Mewhort, 2007), each word is intially assigned a random vector of some length (Jones & Mewhort, 2007 used vectors of dimension 2048). During learning, an item, or semantic, representation and an order representation is aggregated for each word. This distinction between item and order information, as well as much of the mathematical machinery of BEAGLE, is inherited from the TODAM model of episodic memory tasks (Murdock, 1982, 1997). In BEAGLE, the semantic representation is formed by summing the vectors of the other words that co-occur in the same sentence. The order representation is used by constructing an N-gram convolution between successive words.

pTCM has many commonalities with BEAGLE. BEAGLE’s contextual representation can be understood as analogous to the average prior context in which an item is presented (i.e., it is similar to h if it were averaged over all prior presentations of the item). If it were possible to set γ to zero during learning, but non-zero during retrieval, the h that would result would be very similar to the context representation in BEAGLE. In both models, there is a natural model of free association that emerges—in BEAGLE this is taken from the order representation used to support the cued recall task (Murdock, 1982). There are however, important differences. As discussed above, context in pTCM changes continuously and persists across sentence boundaries, allowing for long-range contingencies between words.⁹ In contrast, BEAGLE stops at sentence boundaries. The major difference between the models is that in pTCM the representation of a word that is used to make subsequent predictions changes during learning. BEAGLE relies on statistical averaging of the initial word vectors to build up the representations. In pTCM, the changing semantic representation of a word contributes to the temporal context vector, so that all of the information that has been learned up to that point can be brought to bear in making a prediction and thus updating the representation of the other items in the language. This may result in more robust generalization during learning.

LSA

Latent semantic analysis (LSA Landauer & Dumais, 1997) has set a standard for computational models of semantic knowledge for more than a decade. It has been successful in a broad range of applied settings and has shed considerable light on the basis of knowledge formation in a theoretical sense. Although the end-state of learning in pTCM and LSA are similar to some extent (e.g., Figure 4b), pTCM and LSA are conceptually very different.

pTCM is a learning model in which information is gradually built up over experience. In contrast, the algorithm of LSA requires that all experience be accessible prior to calculating the semantic representation. LSA is consistent with a representation of temporal context that changes abruptly between documents but does not change at all within a document. The parameters of pTCM are sufficiently flexible to approximate a very-slowly changing context vector by setting ρ ≃ 1 and ρ_D = 1. The best-fitting parameters were far from these values, suggesting that the there are meaningful changes in temporal context within a document. As mentioned previously, although a vector space can be extracted from pTCM, this is not the only, or even necessarily the best, representation of meaning possible within pTCM. The free associate measure is not subject to the constraints of a vector space. For instance, the associative strength between two words is asymmetric and can violate the triangle inequality. With all these differences in mind, it is remarkable that the end-state of pTCM is as similar to that of LSA as it is.

The topic model

The probabilistic topic model (Griffiths et al., 2007), like LSA, starts with a word-by-document co-occurrence model. It makes the assumption that the words in a document are sampled from mixtures across a latent variable referred to as a topic. The model constructs a prior on the degree of mixing of topics in a given document, then estimates the probability of sampling a word given each topic using latent Dirichlet allocation (Blei, Ng, & Jordan, 2003). The distribution of words across topics gives an estimate of their meaning.

Many of the points of contrast between pTCM and the topic model are the same as those with LSA: the construction of topics makes the assumption that meaning does not change within a document, the topics calculation is taken after study of the entire corpus. Both pTCM and the topic model have a natural account of retrieval from memory, although in pTCM’s case this is embedded more strongly in a model of episodic retrieval. The primary advantage of the topic model over pTCM is its natural treatment of polysemy, which does not currently have an analogue in pTCM.

The syntagmatic-paradigmatic model

The syntagmatic paradigmatic model (SP Dennis, 2004, 2005) attempts to automatically extract knowledge from naturally-occurring text by using training exemplars to mutually satisfy syntagmatic and paradigmatic constraints. Syntagmatic association are formed between words that occur in series in language—for instance RUN and FAST. In contrast, paradigmatic associations are formed between words that have similar meaning—or that fulfill similar roles in language—e.g., RUN and WALK. SP utilizes both types of associations to model the generation of language. In pTCM, paradigmatic associations are analogous to those constructed using the vector space representation. Paradigmatic associates are words that fit into similar contextual roles and thus have similar semantic representations in pTCM. Syntagmatic associates also have an analogue in pTCM. Given a semantic representation of an item α, when multiplied by M, this gives the set of items that are predicted to follow α based on experience with the corpus (see Table 3). A single matrix, however, cannot capture the rich syntactic structure of English as may be possible with the SP model.

Does pTCM provide additional insight into the neural basis of memory?

One of the strengths of TCM as a model of episodic memory is the existence of a linking hypothesis between the structures of the model and physical processes that take place in the medial temporal lobe of the brain (Howard et al., 2005). This linking hypothesis has led to predictions about the behavior of brain states that have been confirmed with measurements from neural ensembles (Manns, Howard, & Eichenbaum, 2007). The confirmation of these neurophysiological predictions, coupled with the confirmation of numerous behavioral predictions (Schwartz, Howard, Jing, & Kahana, 2005; Howard et al., 2007; Howard, Youker, & Venkatadass, 2008; Unsworth, 2008; Howard et al., 2009; Polyn et al., 2009a; Polyn, Norman, & Kahana, 2009b) make TCM a strong model of episodic recall. Although our understanding of pTCM is at a much earlier stage, it is possible that the extenstion to pTCM will enhance the set of neural phenomena that can be addressed in a common cognitive framework.

Because pTCM is a superset of TCM (compare Table 1 with Table 2), a linking hypothesis between pTCM and the brain shares many of the same contact points—the context vector should reside in extrahippocampal medial temporal lobe (MTL) regions, especially the entorhinal cortex (see Polyn & Kahana, 2008, for a different hypothesis) and the hippocampus should be responsible for the recovery of temporal context. There are two unique predictions of pTCM. One is that the semantic representation of items should come to reflect the temporal contexts in which they are experienced. The second is that the brain uses the current state of temporal context to generate a prediction about what will happen next.

There is neurophysiological evidence that suggests both of these predictions hold. Neurons in area TE of the monkey inferotemporal cortex, a region one synapse away from the MTL, respond to high-level visual stimuli during and following their presentation in a way that is not dependent on their coarse physical properties (Miyashita & Chang, 1988). Remarkably, neurons that respond to a particular stimulus are also more likely to respond to other stimuli that are repeatedly experienced close together in time (Miyashita, 1988) or as members of a bidirectionally presented pair of stimuli that predict one another (Sakai & Miyashita, 1991). Because the neurons are responding to an arbitrary temporal pairing of the stimuli rather than any physical property they have, these findings are as one would expect if the neurons were coding a semantic representation constructed from prediction vectors. This pair-coding phenomenon has been observed both in TE and perirhinal cortex (Erickson, Jagadeesh, & R., 2000; Messinger, Squire, Zola, & Albright, 2001; Naya, Yoshida, & Miyashita, 2003), an extrahippocampal medial temporal lobe region one synapse from the entorhinal cortex. The pair-coding phenomenon also depends on feedback from the medial temporal lobe (Naya et al., 2003; Higuchi & Miyashita, 1996). Both of these properties are as one would expect if the change in the neurons’ responsiveness with experience depended on a prediction generated by a temporal context vector residing in extrahippocampal medial temporal lobe, especially the entorhinal cortex.

The other large-scale prediction of pTCM, that the brain generates a prediction about subsequent stimuli based on the current state of temporal context, may also have a neurophysiological analog. The N400 is a negative potential observed most prominently when subjects are perceiving words that are semantically incongruous (Kutas & Hillyard, 1980), i.e., “The baker reached into the oven and pulled out the BOAT.” The N400 is observed to the extent that a word is not well-predicted by its preceding semantic context (Bentin, McCarthy, & Wood, 1985; Berkum, Hagoort, & Brown, 1999; Federmeier, 2007). Notably, the prediction can be generated both by proximate words (Bentin et al., 1985) and more remote semantic context (Berkum et al., 1999), suggesting that the prediction is generated across multiple time scales at once. These findings suggest that the N400 could reflect a mismatch between a prediction generated from a temporal context vector and a presented stimulus.

The identification of these ERPs with the mismatch between a prediction vector and the presented stimulus may facilitate development of another strong link between the mathematical framework of pTCM and MTL physiology. The N400 has a large generator in extrahippocampal MTL cortical regions (McCarthy, Nobre, Bentin, & Spencer, 1995). The N400 may be understood, at least in part, as a modulation of ongoing oscillatory activity in the MTL (Fell et al., 2004). While we do not wish to claim that the MTL generator is the sole source of the scalp ERP, presentation of a stimulus that is poorly-predicted by its semantic context apparently has a profound effect on human MTL physiology. Moreover, the N400 in the anterior MTL to a studied stimulus predicts whether that stimulus will subsequently be recalled (Fernandez, Effern, Grunwald, et al., 1999, similar effects are also recorded at the scalp, see Paller & Wagner, 2002 for a review). The involvement of the N400 in the MTL in both integration with semantic context and episodic memory encoding could eventually lead to a number of interesting constraints on a physical model of declarative memory.

Episodic memory and semantic memory

We have shown that it is possible to build a model of semantic memory acquisition in the same framework occupied by a model of episodic memory. This framework leads to predictions about a tight coupling between episodic and semantic memory that we have not yet explored. For instance, in the simulations of natural language using pTCM we did not allow contextual recovery, a process we believe to be an essential aspect of episodic memory (Howard et al., 2005; Sederberg, Miller, Kahana, & Howard, accepted pending minor revision), to take place. One challenge of this future work is to specify the conditions under which episodic recovery succeeds. One intriguing possibility is that words that are poorly predicted by their study context are bound effectively to that context such that they can recover the context in the future. Another challenge is to determine which context is recovered by a word that is experienced multiple times. On the one hand, the function of episodic memory as recall of a specific event situated in a specific spatiotemporal context is defeated if all prior contexts in which a word has been experienced contribute to the context it recovers. On the other hand, simulations of learning double-function lists within a particular experiment suggest a gradual change in the temporal context recovered by an item, reflecting multiple study events in the same experiment (Howard et al., 2009). It is possible that these simulations mistake recovery of temporal context for the buildup of a prediction vector such as that utilized here. These distinctions may be teased apart by future experimentation.

The specific integration of semantic memory into the TCM framework offered by pTCM potentially places strong constraints on TCM as a model of episodic recall. Since the earliest treatments of TCM, the input caused by an item when it is initially presented is to be understood as reflecting its prior history. In more recent treatments of TCM, a distinction is made between the preexperimental context-to-item matrix and the newly-learned part of the context-to-item matrix which encodes information about the study items’ encoding context (Sederberg et al., 2008; Polyn et al., 2009a). Polyn et al. (2009a) used the preexperimental matrix to carry information about semantic relationships among words which was sufficient to account for the existence of semantic clustering in free recall. In the context of modeling episodic memory, pTCM may be understood as a method to intialize the values of the preexperimental context-to-item matrix and the input patterns caused by items when they are initially presented. Taken together, the two models reflect a shared hypothesis about the interaction between semantic and episodic factors on memory retrieval.