THE ROLE OF MASS BALANCE EQUATIONS IN GROWTH MECHANICS ILLUSTRATED IN SURFACE AND VOLUME DISSOLUTION

Abstract

Growth mechanics problems require the solution of mass balance equations that include supply terms and account for mass exchanges among constituents of a mixture. Though growth may often be accompanied by a variety of concomitant phenomena that increase modeling complexity, such as solid matrix deformation, evolving traction-free configurations, cell division, active cell contraction, etc., it is important to distinguish these accompanying phenomena from the fundamental growth process that consists of deposition or removal of mass from the solid matrix. Therefore the objective of the current study is to present a canonical problem of growth, namely dissolution of a rigid solid matrix in a solvent. This problem illustrates a case of negative growth (loss of mass) of the solid, in a mixture framework that includes three species: a solid, a solvent and a solute, where the solute is the product of the solid dissolution. By analyzing both volumetric and surface dissolution, the two fundamental modes of growth are investigated within the unified framework of mixture theory.

1. Introduction

In the mathematical framework of continuum growth theories two fundamental modes of growth are recognized: Volumetric or interstitial growth; and surface or appositional growth. In volumetric growth solid mass is deposited at locations inside a porous body, whereas in surface growth solid mass is deposited on the boundary of a body.

A consensus on modeling volumetric and surface growth has been slow to emerge. For volumetric growth, a common approach based on the principles advanced by Skalak et al. [1] has been to model the total deformation of a solid as the combination of the effects of growth and loading [2]. Thus, in the kinematic analysis of a continuum, the deformation gradient is given by F = F_e · F_g, where F_g and F_e represent the deformation from growth and loading, respectively [2]. Volumetric growth has also been modeled using only a mass supply term in the equation of conservation of mass [3].

For surface growth, Skalak et al. [1, 4] proposed to define a vector growth rate G on a surface experiencing mass deposition, which may have components both normal and tangential to the interface, whose growth velocity is given by V_G. Other investigators have similarly proposed to incorporate a mass flux vector M on the boundary surface of a material region, in the formulation of the axiom of balance of mass [5].

In our own approach [6], and in accordance with many authors [7, 8, 9, 10, 11], we have advocated using the framework of mixture theory [12, 13, 14] to model volumetric and surface growth because this framework has established the foundations for the formulation of mass exchanges among various mixture constituents, as would occur in growth processes, using the axiom of balance of mass. In mixture theory, solid mass deposition (or removal) represents a mass exchange between solvated species and the solid. In volumetric growth, solutes transport through a porous solid matrix and may deposit onto the porous lattice at points within the body. In surface growth, solutes present in a bathing solution may deposit onto the surface of the body, producing an evolving or moving boundary surface.

The conventional approach for formulating the axiom of mass balance in integral form over a control volume or material region yields the statement of mass balance in differential form needed for volumetric growth [15]. Furthermore, when accounting for singular interfaces in a material region, where certain variables may suffer a jump, the resulting jump condition from the statement of balance of mass [16] produces the governing equation for surface growth [6]. Therefore, mixture theory provides a uniform framework for modeling volumetric and surface growth.

In recent studies, several applications of volumetric growth in biological tissues have been demonstrated using this mixture theory framework. For example, the synthesis and deposition of multiple solid matrix species (such as muscle, elastin, and collagen; [8]), or charged molecular species (such as proteoglycan molecules; [17]) onto the extracellular matrix of a porous-hydrated connective tissue (such as the aortic wall) has been analyzed from this approach. The possibility that multiple generations of mass deposition from growth may assume different reference configurations was similarly investigated [18, 19]. These analyses addressed the influence of growth on alterations in tissue residual stresses. Tissue growth by cell division was similarly analyzed, where cell division was modeled as the growth of intracellular solute and solid species by uptake from the extracellular environment, resulting in a concomitant osmotic gradient driving water into the cell, thereby doubling the cell size in the synthesis phase accompanying cell division (mitosis) [17].

These applications of mixture theory to biological tissue growth have demonstrated the remarkable range of problems that may be tackled with this approach. However, it may also be argued that these sophisticated applications may have obscured the simplicity of the basic principles of growth mechanics from the axiom of mass balance, by addressing multiple mechanisms simultaneously (such as intracellular and extracellular osmotic effects, or multigenerational growth of constitutents with distinct reference configurations).

Therefore the objective of the current study is to present a canonical problem of growth, namely dissolution of a rigid solid matrix in a solvent. This problem illustrates a case of negative growth (loss of mass) of the solid, in a mixture framework that includes three species: a solid, a solvent and a solute, where the solute is the product of the solid dissolution. By analyzing both volumetric and surface dissolution, the two fundamental modes of growth are investigated within the unified framework of mixture theory. Though dissolution does not represent a dominant mechanism of growth in biological tissues, the relative simplicity of this problem may serve as an easier introduction to the application of mixture theory to biological tissue growth. Furthermore, in tissue engineering applications, modeling volumetric dissolution of a porous scaffold may be highly relevant [20, 21]; in drug delivery applications, modeling of surface dissolution of a pill or tablet may be similarly useful [22, 23].

2. Balance of Mass

The fundamental governing equation for mass deposition or removal is based on the axiom of mass balance. For interstitial growth, the differential form of this equation in a spatial frame is given by [15, 16]

$$\frac{\partial {\rho }^{\alpha }}{\partial t}+\nabla \cdot \left({\rho }^{\alpha }{\mathbf{v}}^{\alpha }\right)={\widehat{\rho }}^{\alpha }$$ (2.1)

where ρ^α is the apparent density of constituent α in the mixture;¹v^α is the velocity of that constituent, and ${\widehat{\rho }}^{\alpha }$ is the volume density of mass supply from interstitial growth (with units of mass of α per volume of the mixture in the current configuration, per time). The mass supply ${\widehat{\rho }}^{\alpha }$ is also a function of the state variables in a problem, where the functional dependence must be provided by a constitutive relation, as addressed below. To satisfy the balance of mass for the mixture as a whole [12, 15], the mass supply terms are constrained according to

$$\sum _{\alpha }{\widehat{\rho }}^{\alpha }=0$$ (2.2)

where the summation is taken over all constituents of the mixture. This relation states that mass gains by the products of a reaction must be at the expense of mass losses by the reactants.

The equivalent balance of mass relation for surface growth on a singular interface is given by [6, 16]

$$\left[\left[{\rho }^{\alpha }({\mathbf{v}}^{\alpha }-{\mathbf{v}}_{\Gamma })\right]\right]\cdot \mathbf{n}=-{\stackrel{‒}{\rho }}^{\alpha }$$ (2.3)

where Γ represents the singular surface on which growth occurs, v_Γ is the velocity of Γ, n is the unit normal on Γ whose direction defines the orientation of the interface (Figure 2.1), and ${\stackrel{‒}{\rho }}^{\alpha }$ is the area density of mass supply from surface growth (with units of mass of α per area of Γ in the current configuration, per time). The double-bracket notation represents the jump in value of its argument across the interface Γ; for the convention adopted here,

$$\left[\left[f\right]\right]\equiv f_{+}-f_{-}$$ (2.4)

where f₊ and f_– represent the respective values of f in V⁺ and V^–, such that n represents the outward normal to the V⁺ side (Figure 2.1). The surface mass supply terms are also functions of the state variables in a problem, to be defined by constitutive relations, and must similarly satisfy the constraint

$$\sum _{\alpha }{\stackrel{‒}{\rho }}^{\alpha }=0$$ (2.5)

Figure 2.1.

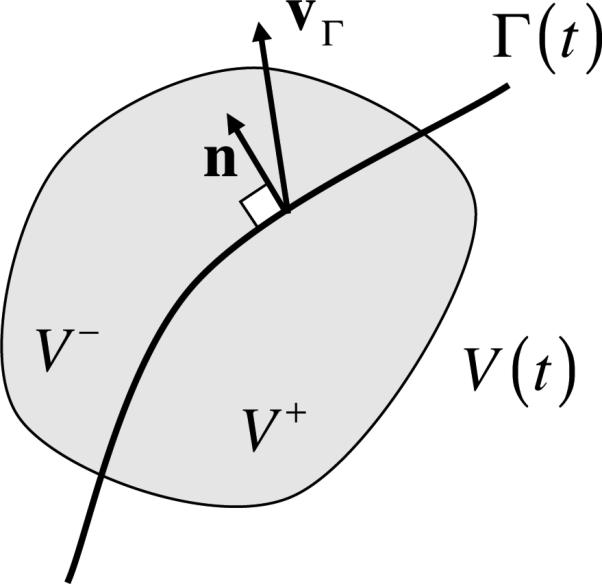
A singular interface Γ (t) separates a region V (t) into subregions V⁺ and V^–. v_Γ is the velocity of Γ and n is the unit outward normal to the ’+’ side.

3. Canonical Problems of Dissolution

Consider a canonical problem of dissolution where the mixture consists at most of a solid that can dissolve (α = s), a solvent in which it can dissolve (α = w), and a solute which is the product of the dissolution (α = u). There are two domains that need to be considered in this canonical problem: The body $\mathcal{B}$ which is dissolving and the external bath ${\mathcal{B}}_{\ast }$ in which it is dissolving, with Γ representing the interface between these two domains (Figure 3.1). ${\mathcal{B}}_{\ast }$ contains, at most, two constituents (α = w, u) and all variables associated with the external bath are denoted with a subscripted asterisk. If the body $\mathcal{B}$ is porous, it is represented by a mixture of up to three constituents (α = s, w, u); if it is non-porous, it contains only one constituent (α = s).²

Figure 3.1.

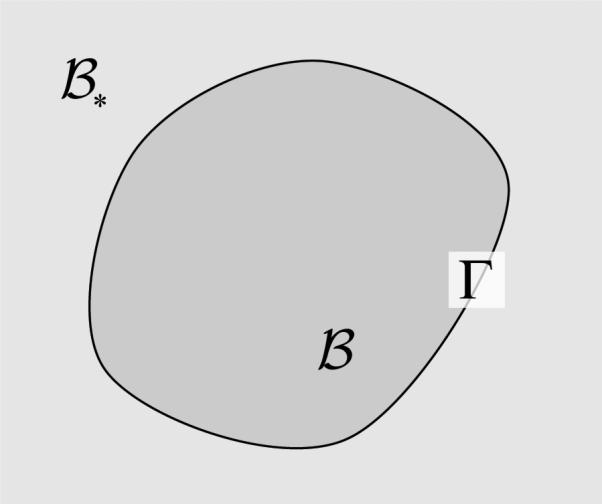
In a dissolution problem, $\mathcal{B}$ represents the dissolving body, ${\mathcal{B}}_{\ast }$ represents the bath in which the body dissolves, and Γ is the evolving interface between $\mathcal{B}$ and ${\mathcal{B}}_{\ast }$.

Note that for the problem of dissolution, the singular interface Γ is defined on the solid boundary surface of $\mathcal{B}$.³ This definition implies that (v_Γ – v^s) · n represents the surface growth velocity, directed along n.

For simplicity, the canonical problems considered here assume that the solid constituent of $\mathcal{B}$ undergoes negligible deformations. It is thus treated as a rigid solid whose motion consists at most of a rigid body rotation and translation. In a quasi-static analysis (when inertia terms are neglected), there is no loss of generality in assuming that the solid is stationary,

$${\mathbf{v}}^s=0$$ (3.1)

Another advantage of modeling the solid as rigid is that there is no longer a need to distinguish between changes in solid apparent density resulting from growth versus loading (an important topic in growth mechanics, addressed in greater detail elsewhere; 6, 17, 19). Thus, in this canonical problem, changes in ρ^s only occur as a result of growth.

For a non-porous body, the only mechanism of dissolution is by surface dissolution, since solvent can only be in contact with the outer boundary of the body. Therefore, a canonical problem representative of this case will be considered first, followed by a canonical problem of volume dissolution of a porous body.

3.1. Surface Dissolution of a non-Porous Body

When applied to each of the three constituents meeting on Γ, the jump condition of Eq.(2.3) produces

$${\rho }^{\alpha }({\mathbf{v}}^{\alpha }-{\mathbf{v}}_{\Gamma })\cdot \mathbf{n}-{\rho }_{\ast }^{\alpha }({\mathbf{v}}_{\ast }^{\alpha }-{\mathbf{v}}_{\Gamma })\cdot \mathbf{n}=-{\stackrel{‒}{\rho }}^{\alpha }\alpha =s,w,u$$ (3.2)

where ρ^α and v^α refer to the density and velocity in $\mathcal{B}$, whereas ${\rho }_{\ast }^{\alpha }$ and ${\mathbf{v}}_{\ast }^{\alpha }$ refer to those quantities in the bath ${\mathcal{B}}_{\ast }$. In the case of surface dissolution, since there is no reaction producing or removing solvent on Γ, it follows that ${\stackrel{‒}{\rho }}^w=0$, so that ${\stackrel{‒}{\rho }}^s+{\stackrel{‒}{\rho }}^u=0$ according to Eq.(2.5). Since the solid is non-porous, its apparent density is constant and equal to the true density⁴ of the solid species, thus ${\rho }^s={\rho }_T^s$. Furthermore, ${\rho }_{\ast }^s=0$ since there is no solid in ${\mathcal{B}}_{\ast }$, and ρ^w = ρ^u = 0 since there is neither solvent nor solute in a non-porous body $\mathcal{B}$. Combining all these relations produces

$$\begin{array}{cc}\hfill {\rho }_T^s({\mathbf{v}}^s-{\mathbf{v}}_{\Gamma })\cdot \mathbf{n}& =-{\stackrel{‒}{\rho }}^s\hfill \\ \hfill {\rho }_{\ast }^w({\mathbf{v}}_{\ast }^w-{\mathbf{v}}_{\Gamma })\cdot \mathbf{n}& =0\text{on}\Gamma \hfill \\ \hfill -{\rho }_{\ast }^u({\mathbf{v}}_{\ast }^u-{\mathbf{v}}_{\Gamma })\cdot \mathbf{n}& ={\stackrel{‒}{\rho }}^s\hfill \end{array}$$ (3.3)

When using Eq.(3.1) these jump conditions further simplify to

$$\begin{array}{cc}\hfill {\mathbf{v}}_{\Gamma }\cdot \mathbf{n}& =\frac{{\stackrel{‒}{\rho }}^s}{{\rho }_T^s}\hfill \\ \hfill {\mathbf{v}}_{\ast }^w\cdot \mathbf{n}& =\frac{{\stackrel{‒}{\rho }}^s}{{\rho }_T^s}\text{on}\Gamma \hfill \\ \hfill {\mathbf{v}}_{\ast }^u\cdot \mathbf{n}& ={\stackrel{‒}{\rho }}^s\left(\frac{1}{{\rho }_T^s}-\frac{1}{{\rho }_{\ast }^u}\right)\hfill \end{array}$$ (3.4)

The first of these jump conditions provides a direct relation for determining the surface growth velocity component normal to Γ from the rate of mass loss on the boundary. In a dissolution problem, since the solid is losing mass, ${\stackrel{‒}{\rho }}^s$ is a negative quantity so that v_Γ · n points inward (along –n) as expected. Since ${\rho }^s={\rho }_T^s$ is constant, loss of mass occurs entirely by the shedding of material from the surface and is manifested in the motion of Γ relative to the body as the solid dissolves.

The remaining jump conditions in Eq.(3.4) are needed for the boundary value problem describing the motion of the solvent and the solute concentration in the bath ${\mathcal{B}}_{\ast }$. Evidently, from the second relation in Eq.(3.4), the solvent must move inward as the solid dissolves. The governing equations for this boundary value problem are obtained by combining the balance of mass relations of Eq.(2.1) (using ${\widehat{\rho }}_{\ast }^w={\widehat{\rho }}_{\ast }^u=0$ in the bath) with the equations of balance of linear momentum, along with requisite constitutive assumptions, as illustrated in Section 3.3 below.

To complete these equations, a constitutive relation is needed for ${\stackrel{‒}{\rho }}^s$. For example, a relation in the form of the standard Noyes-Whitney constitutive equation for dissolution [24] may be adopted,

$${\stackrel{‒}{\rho }}^s=\stackrel{‒}{h}({\rho }_{\ast }^u-{\rho }_0^u)$$ (3.5)

where h̄ is a material coefficient (positive, with units of length per time) that provides a measure of the rate of material volume removal per area, and ${\rho }_0^u$ is a material coefficient (positive, with units of mass per volume) representing the saturation limit for the solubility of u in solvent w (${\rho }_0^u\ge {\rho }_{\ast }^u$). In general, in order to solve for v_Γ · n from the first relation in Eq.(3.4), a solution for ${\rho }_{\ast }^u$ from the boundary value problem is needed.

Example 1. In the special case when the volume of the bath ${\mathcal{B}}_{\ast }$ is much larger than that of the body $\mathcal{B}$ and the bath is well stirred, the solute concentration may be negligible relative to the saturation limit, so that

$${\stackrel{‒}{\rho }}^s\approx -\stackrel{‒}{h}{\rho }_0^u\text{when}{\rho }_{\ast }^u\ll {\rho }_0^u$$ (3.6)

This limiting case makes it possible to analyze the dissolution of $\mathcal{B}$ without solving the solute diffusion problem in the bath. Consider a spherical non-porous bead of radius r dissolving in a much larger, well-stirred bath. For this geometry it follows that v_Γ · n = dr/dt. Using the relations of Eq.(3.4)₁ and Eq.(3.6) produces

$$\frac{dr}{dt}=-\frac{{\rho }_0^u}{{\rho }_T^s}\stackrel{‒}{h}$$ (3.7)

and since h̄, ${\rho }_0^u$ and ${\rho }_T^s$ are constant in this problem, it follows that the bead radius decreases at a constant rate,

$$r\left(t\right)=r_0-\frac{{\rho }_0^u}{{\rho }_T^s}\stackrel{‒}{h}t$$ (3.8)

where r₀ = r (0) is the initial bead radius. Therefore, the time needed for complete dissolution under these well-stirred conditions is

$$t_f=\frac{{\rho }_T^s}{{\rho }_0^u}\frac{r_0}{\stackrel{‒}{h}}$$ (3.9)

At any time t in the interval 0 ≤ t ≤ t_f, the mass of the bead is

$$M\left(t\right)=M_0{\left(1-\frac{{\rho }_0^u}{{\rho }_T^s}\frac{\stackrel{‒}{h}}{r_0}t\right)}^3$$ (3.10)

where $M_0={\rho }_T^{s}4\pi r_0^3∕3$ is the initial mass of the bead.

3.2. Volume Dissolution of Porous Solid

In a porous solid the solvent interacts with the solid skeleton, producing surface dissolution at a microscopic level, which is manifested by a decrease in the apparent density ρ^s at the macroscopic level (the level of a representative volume element of the porous structure, Figure 3.2). Therefore, this alteration in ρ^s represents a mechanism of volume dissolution. Since there is no reaction producing or removing solvent (${\widehat{\rho }}^w=0$), the loss of solid is balanced by the production of solute, and ${\widehat{\rho }}^s+{\widehat{\rho }}^u=0$ according to Eq.(2.2). Thus, when also considering the solid to be rigid and stationary, the mass balance relations (2.1) for the three constituents of the mixture reduce to

$$\begin{array}{cc}\hfill \frac{\partial {\rho }^s}{\partial t}& ={\widehat{\rho }}^s\hfill \\ \hfill \frac{\partial {\rho }^w}{\partial t}+\nabla \cdot \left({\rho }^w{\mathbf{v}}^w\right)& =0\hfill \\ \hfill \frac{\partial {\rho }^u}{\partial t}+\nabla \cdot \left({\rho }^u{\mathbf{v}}^u\right)& =-{\widehat{\rho }}^s\hfill \end{array}$$ (3.11)

In a spatial frame, the solution for ρ^s is obtained by integrating the first of these relations to produce

$${\rho }^s(\mathbf{x},t)={\rho }^s(\mathbf{x},t_0)+{\int }_{t_0}^t{\widehat{\rho }}^s(\mathbf{x},\tau )d\tau$$ (3.12)

where ${\widehat{\rho }}^s$ must be given by a constitutive relation which is a function of state variables, such as ρ^s, ρ^w and ρ^u.

Figure 3.2.

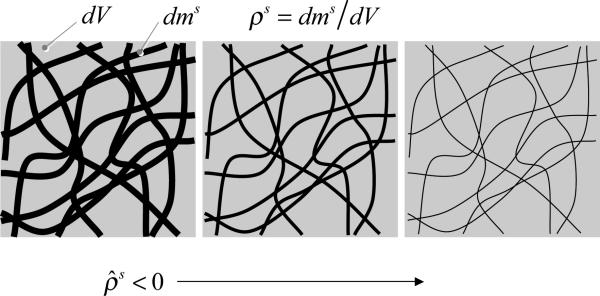
Volume dissolution (${\widehat{\rho }}^s<0$) may be viewed as a macroscopic manifestation of surface dissolution at the microscopic level. In this illustration, struts of a solid scaffold in a representative elemental volume dV are shown to become progressively thinner (left to right) as they dissolve. In the absence of deformation (constant dV), the loss of solid mass dm^s produces a decrease in apparent solid density ρ^s.

The apparent density of any constitutent may be expressed as ${\rho }^{\alpha }={\phi }^{\alpha }{\rho }_T^{\alpha }$, where φ^α is the volume fraction of α.⁵ If each of the constituents is considered intrinsically incompressible, then ${\rho }_T^{\alpha }$ is invariant in time and space. This assumption may be combined with the mixture saturation condition (the absence of voids), Σ_α φ^α = 1, and the mass balance relations of Eq.(3.11), to produce a balance of mass for the mixture,

$$\nabla \cdot \left(\frac{{\rho }^w}{{\rho }_T^w}{\mathbf{v}}^w+\frac{{\rho }^u}{{\rho }_T^u}{\mathbf{v}}^u\right)={\widehat{\rho }}^s\left(\frac{1}{{\rho }_T^s}-\frac{1}{{\rho }_T^u}\right)$$ (3.13)

This equation expresses the fact that a difference between the true densities of the solid and its solubilized form (${\rho }_T^s\ne {\rho }_T^u$) can lead to a net change in the mixture volume as dissolution (${\widehat{\rho }}^s<0$) takes place.⁶ Conversely, if ${\rho }_T^s={\rho }_T^u$, the solute occupies the same volume as the solid from which it dissolves, producing no net change in mixture volume as dissolution progresses.

In the chemistry of solutions, solute concentrations are usually expressed as the solute mass per volume of the solution (solvent + solute). In mixture theory however, ρ^u represents the mass of solute per volume of the mixture (solution + solid). Therefore, when adopting constitutive relations derived from chemistry, the solute apparent density should be renormalized according to ${\rho }^u∕(1-{\phi }^s)={\rho }_T^s{\rho }^u∕({\rho }_T^s-{\rho }^s)$ to produce a mass concentration on a solution-volume basis, since 1 – φ^s = φ^w + φ^u represents the volume fraction of the solution.⁷ For example, if a constitutive relation in the form of the Noyes-Whitney equation [24] is adopted for volume dissolution, then

$${\widehat{\rho }}^s=\widehat{h}\left(\frac{{\rho }_T^s}{{\rho }_T^s-{\rho }^s}{\rho }^u-{\rho }_0^u\right)$$ (3.14)

where ĥ is a material coefficient (positive, with units of reciprocal time) that represents the rate of material volume removal per volume, and ${\rho }_0^u$ is the saturation concentration in free solution (no solid), as also used in Eq.(3.5).

Example 2. In general, the equations presented above are insufficient to solve for all the unknowns (ρ^s,ρ^u, ρ^w, v^w, and v^u), because the motion of the solute and solvent (via permeation, diffusion, osmosis, etc.) must be additionally described by equations of balance of momentum. However, in the special case when ${\rho }_T^s={\rho }_T^u$, no net volume change occurs in the mixture during dissolution according to Eq.(3.13), and it is easy to verify that this equation may be satisfied by letting the solvent and solute be stationary,

$${\mathbf{v}}^w={\mathbf{v}}^u=0$$ (3.15)

and the apparent densities ρ^s, ρ^u and ρ^w be homogenenous. It follows from Eq.(3.11) that

$$\frac{d}{dt}({\rho }^s+{\rho }^u)=0$$ (3.16)

and

$$\frac{d{\rho }^u}{dt}=-{\widehat{\rho }}^s$$ (3.17)

Using the initial conditions ${\rho }^s={\rho }_0^s$ and ρ^u = 0 at t = 0, Eq.(3.16) may be integrated to produce

$${\rho }^s+{\rho }^u={\rho }_0^s$$ (3.18)

In this expression, ${\rho }_0^s$ is a measure of the initial solid mass content (${\rho }_0^s∕{\rho }_T^s\equiv {\phi }_0^s$ is the initial solid volume fraction); upon complete dissolution ρ^s reduces to zero and ρ^u increases to ${\rho }_0^s$. Substituting Eq.(3.18) into Eq.(3.14) and the resulting expression into Eq.(3.17) produces a non-linear ordinary differential equation for ρ^s,

$$\frac{d{\rho }^s}{dt}=\widehat{h}\left(\frac{{\rho }_0^s-{\rho }^s}{{\rho }_T^s-{\rho }^s}{\rho }_T^s-{\rho }_0^u\right)$$ (3.19)

with the initial condition ${\rho }^s={\rho }_0^s$ at t = 0. A closed-form solution for this equation is not readily available, though the steady-state response (dρ^s/dt = 0) is given by

$${\rho }^s=\{\begin{array}{cc}\frac{{\rho }_0^s-{\rho }_0^u}{{\rho }_T^s-{\rho }_0^u}{\rho }_T^s\hfill & {\rho }_0^s\ge {\rho }_0^u\hfill \\ 0\hfill & {\rho }_0^s<{\rho }_0^u\hfill \end{array}\phantom{\}}\text{at steady state}$$ (3.20)

The first case reflects the outcome when the interstitial fluid saturates with solute before complete dissolution of the solid can occur, whereas the second case represents complete dissolution of the solid.

A numerical solution of (3.19) is straightforward, however there are two limiting cases that produce a linearized form of this equation. First, if the saturation concentration is small compared to the initial solid content (${\rho }_0^u\ll {\rho }_0^s$), only a small fraction of the solid can dissolve (${\rho }_T^s-{\rho }^s\approx {\rho }_T^s-{\rho }_0^s$) so that

$$\frac{d{\rho }^s}{dt}\approx \widehat{h}\left(\frac{{\rho }_0^s-{\rho }^s}{{\rho }_T^s-{\rho }_0^s}{\rho }_T^s-{\rho }_0^u\right)$$ (3.21)

and, assuming that ĥ is constant, the solution is given by

$${\rho }^s\approx {\rho }_0^s-\left(1-\frac{{\rho }_0^s}{{\rho }_T^s}\right){\rho }_0^u\left[1-\exp \left(-\frac{{\rho }_T^s}{{\rho }_T^s-{\rho }_0^s}\widehat{h}t\right)\right]$$ (3.22)

This solution shows that the dissolution process decreases the solid content at an exponential rate and steady state is achieved asymptotically with increasing time.

Second, if the initial solid content is very small (${\rho }_0^s\ll {\rho }_T^s$), then ${\rho }^s\ll {\rho }_T^s$ at all times and (3.19) reduces to

$$\frac{d{\rho }^s}{dt}\approx \widehat{h}({\rho }_0^s-{\rho }^s-{\rho }_0^u)$$ (3.23)

producing

$${\rho }^s\approx {\rho }_0^s-{\rho }_0^u\left(1-e^{-\widehat{h}t}\right)$$ (3.24)

There are two possible outcomes in this scenario. If ${\rho }_0^s\ge {\rho }_0^u$, the solid cannot dissolve completely because the solution saturates, and the steady-state response is achieved asymptotically with time, as shown in (3.24). However, if ${\rho }_0^s<{\rho }_0^u$, the solid dissolves completely (ρ^s = 0) in a finite amount of time,

$$t_f\approx -\frac{1}{\widehat{h}}\ln \left(1-\frac{{\rho }_0^s}{{\rho }_0^u}\right),{\rho }_0^s<{\rho }_0^u$$ (3.25)

and, consistent with Eq.(3.18), the solute concentration at t_f rises to ${\rho }^u={\rho }_0^s$.

3.3. Combined Mechanisms of Surface and Volume Dissolution

In a porous solid, both surface and volume dissolution are expected to occur simultaneously. Surface dissolution will cause the boundary Γ to recede with a normal velocity component (v_Γ – v^s)·n, while volume dissolution will cause a reduction in the solid apparent density ρ^s. The statements of balance of mass, Eq.(2.1), and the mixture balance of mass in the case of intrinsically incompressible constituents, Eq.(3.13), must hold in $\mathcal{B}$,

$$\begin{array}{cc}\hfill \frac{\partial {\rho }^s}{\partial t}=& {\widehat{\rho }}^s\hfill \\ \hfill \frac{\partial {\rho }^w}{\partial t}+\nabla \cdot \left({\rho }^w{\mathbf{v}}^w\right)=& 0\hfill \\ \hfill \frac{\partial {\rho }^u}{\partial t}+\nabla \cdot \left({\rho }^u{\mathbf{v}}^u\right)=& -{\widehat{\rho }}^s\hfill \\ \hfill \nabla \cdot \left(\frac{{\rho }^w}{{\rho }_T^w}{\mathbf{v}}^w+\frac{{\rho }^u}{{\rho }_T^u}{\mathbf{v}}^u\right)=& {\widehat{\rho }}^s\left(\frac{1}{{\rho }_T^s}-\frac{1}{{\rho }_T^u}\right)\hfill \end{array}$$ (3.26)

and ${\mathcal{B}}_{\ast }$,

$$\begin{array}{cc}\hfill \frac{\partial {\rho }_{\ast }^w}{\partial t}+\nabla \cdot \left({\rho }_{\ast }^w{\mathbf{v}}_{\ast }^w\right)=& 0\hfill \\ \hfill \frac{\partial {\rho }_{\ast }^u}{\partial t}+\nabla \cdot \left({\rho }_{\ast }^u{\mathbf{v}}_{\ast }^u\right)=& 0\hfill \\ \hfill \nabla \cdot \left(\frac{{\rho }_{\ast }^w}{{\rho }_T^w}{\mathbf{v}}_{\ast }^w+\frac{{\rho }_{\ast }^u}{{\rho }_T^u}{\mathbf{v}}_{\ast }^u\right)=& 0\hfill \end{array}$$ (3.27)

These equations are formulated under the simplifying assumption that the porous solid is rigid and stationary, Eq.(3.1).

Since $\mathcal{B}$ is porous, the jump conditions on the balance of mass for each constituent across Γ, Eq.(3.2), produce more general relations than in Eq.(3.4),

$$\begin{array}{cc}\hfill {\mathbf{v}}_{\Gamma }\cdot \mathbf{n}=& \frac{{\stackrel{‒}{\rho }}^s}{{\rho }^s}\hfill \\ \hfill ({\rho }^w{\mathbf{v}}^w-{\rho }_{\ast }^w{\mathbf{v}}_{\ast }^w)\cdot \mathbf{n}=& ({\rho }^w-{\rho }_{\ast }^w)\frac{{\stackrel{‒}{\rho }}^s}{{\rho }^s}\text{on}\Gamma \hfill \\ \hfill ({\rho }^u{\mathbf{v}}^u-{\rho }_{\ast }^u{\mathbf{v}}_{\ast }^u)\cdot \mathbf{n}=& {\stackrel{‒}{\rho }}^s\left(1+\frac{{\rho }^u-{\rho }_{\ast }^u}{{\rho }^s}\right)\hfill \end{array}$$ (3.28)

Constitutive relations are needed for the solid mass supply terms, as given for example in Eqs.(3.5) and (3.14).

To solve for all these unknowns it is necessary to also include the equations of balance of momentum for the fluid constituents (solvent + solute). (The balance of momentum for α = s is not needed since the solid is assumed rigid and stationary.) Under quasi-static and isothermal conditions, in the absence of external body forces, when viscous stresses in each constituent are neglected, and when all constituents are uncharged, the balance of momentum reduces to

$$-{\rho }^{\alpha }\nabla \left(\frac{p}{{\rho }_T^{\alpha }}+{\mu }^{\alpha }\right)+{\widehat{\mathbf{p}}}_d^{\alpha }=0,\alpha =w,u$$ (3.29)

where p is the fluid pressure, μ^α is the chemical potential of α (with units of energy per mass), and ${\widehat{\mathrm{p}}}_d^{\alpha }$ is the dissipative part of the momentum supply to α from all other constituents in the mixture (e.g., the frictional drag exerted on α by the other constituents, with units of force per volume) [6, 25, 26]. The corresponding jump conditions on Γ are given by

$$\left[\left[\frac{p}{{\rho }_T^{\alpha }}+{\mu }^{\alpha }\right]\right]=0,\alpha =w,u$$ (3.30)

Constitutive relations are needed for μ^α and ${\widehat{\mathrm{p}}}_d^{\alpha }$, which relate them to the state variables in this problem. In general, since dissolution of a solid may produce non-dilute (and thus, non-ideal) solutions, and since the transport properties within the porous solid (solute diffusivity, solvent permeability) may be significantly altered by dissolution, the formulation of constitutive relations that remain valid over the entire span of the dissolution process may be highly specific to the nature of the solid, solvent and solute for a particular problem and must be guided by experimental validation.

To illustrate this type of constitutive formulation, consider the case where the solution remains dilute (${\rho }^u∕{\rho }_T^u\ll 1$) and ideal during the entire process of dissolution as would occur, for example, when solute diffusion or solvent convection carries solute away significantly faster than the rate at which it is produced by dissolution. Also consider that the porous solid imparts isotropic transport properties (diffusivity and permeability) and that the dissolution process does not alter this material symmetry. Finally, assume that the mass exchange from dissolution has a negligible contribution to the momentum supply between constituents [6]. Under these constitutive assumptions, the momentum balance equations produce the following relations in $\mathcal{B}$,

$$\begin{array}{cc}\hfill \frac{{\rho }^w}{{\rho }_T^w}\left[\nabla p-\frac{R\theta }{M^u}\nabla \left(\frac{{\rho }_T^s}{{\rho }_T^s-{\rho }^s}{\rho }^u\right)\right]-\frac{R\theta }{M^u}\frac{{\rho }^u}{D_0^u}({\mathbf{v}}^u-{\mathbf{v}}^w)+\frac{1}{k}{\left(\frac{{\rho }^w}{{\rho }_T^w}\right)}^2{\mathbf{v}}^w=& 0\hfill \\ \hfill ({\rho }_T^s-{\rho }^s)\nabla \left(\frac{{\rho }^u}{{\rho }_T^s-{\rho }^s}\right)+{\rho }^u\left(\frac{1}{D^u}{\mathbf{v}}^u-\frac{1}{D_0^u}{\mathbf{v}}^w\right)=& 0\hfill \end{array}$$ (3.31)

where R is the universal gas constant and θ is the absolute temperature. M^u is the solute molecular weight, D^u is its diffusivity in the mixture (solid+solution), $D_0^u$ is its diffusivity in free solution (no solid), and k is the solvent hydraulic permeability in the porous solid. For dilute solutions $D_0^u$ and D^u may be considered independent of solute concentration. While $D_0^u$ may be constant, a constitutive relation is needed to relate D^u to ρ^s such that

$$\underset{{\rho }^s\to 0}{\lim }{D}^u=D_0^u$$ (3.32)

to account for the effect of dissolution on diffusivity through the porous solid matrix. Similarly, a constitutive relation is needed to relate k to ρ^s such that

$$\underset{{\rho }^s\to 0}{\lim }\frac{1}{k}=0$$ (3.33)

to reflect the fact that, following complete dissolution of the solid, there will be no frictional interaction between solid and solvent.

The governing equations within ${\mathcal{B}}_{\ast }$ may thus be reduced from Eq.(3.34) by letting ${\rho }_{\ast }^s=0$ and recognizing that ${\rho }_{\ast }^w∕{\rho }_T^w\approx 1$ in a dilute solution,

$$\begin{array}{cc}\hfill \nabla p_{\ast }=& 0\hfill \\ \hfill \nabla {\rho }_{\ast }^u+\frac{{\rho }_{\ast }^u}{D_0^u}({\mathbf{v}}_{\ast }^u-{\mathbf{v}}_{\ast }^w)=& 0\hfill \end{array}$$ (3.34)

It may be noted that the second of these equations is Fick's law of diffusion. For dilute solutions, the jump conditions of Eq.(3.30) further reduce to

$$\begin{array}{cc}\hfill p=p_{\ast }& \hfill \\ \hfill & \hfill \text{on}\Gamma \\ \hfill \frac{{\rho }_T^s}{{\rho }_T^s-{\rho }^s}{\rho }^u={\rho }_{\ast }^u& \hfill \end{array}$$ (3.35)

In general, the solution to these coupled, nonlinear partial differential equations needs to be obtained numerically. A numerical scheme for solving these equations must account for the time-evolution of the interface Γ. No simple canonical solution is offered here.

4. Discussion

The objective of this study was to illustrate the concept of growth mechanics in the physically meaningful problem of dissolution, without the need to model phenomena that often accompany growth processes and increase the modeling complexity. Thus, whereas many growth problems in biomechanics are concerned with the effects of loading versus growth on solid deformation, and the need to account for evolving traction-free configurations of a growing body, these specific issues were set aside in the current study by modeling the solid as rigid and stationary. This simplifying assumption naturally shifted the focus of the growth analysis back to the fundamental principle that growth is governed by the axiom of mass balance.

A fundamental principle emphasized in this study is that growth is embodied in the mass supply term of the mass balance equations, ${\widehat{\rho }}^{\alpha }$ in Eq.(2.1) or ${\stackrel{‒}{\rho }}^{\alpha }$ in Eq.(2.3), and that these supply terms can only exist if there is more than one constituent in a mixture to allow for mass exchanges, as implied by Eqs.(2.2) and (2.5). Therefore, the natural framework for describing growth mechanics is the theory of mixtures. Since growth represents mass exchanges with the solid matrix of a body, interstitial growth can occur only if the body is porous-permeable to the constituents that bind to, or get released from, the solid matrix in the growth process. In contrast, appositional growth can occur even if the solid is non-porous.

Dissolution is a process of negative growth since it implies loss of mass from the solid matrix. In the examples illustrated in this study, it was thus assumed that ${\widehat{\rho }}^s<0$, or ${\stackrel{‒}{\rho }}^s<0$, for the purpose of describing representative responses. However, positive growth (${\widehat{\rho }}^s>0$ or ${\stackrel{‒}{\rho }}^s>0$) could have been assumed just as easily, with no alteration in the governing equations. Thus, the surface growth of stalactites and stalagmites by the deposition of soluble minerals onto the underlying impermeable substrate could have easily been used as an alternative illustration, where the assumption of a rigid stationary solid would have been most reasonable. Alternatively, one could also use the governing equations presented in this study to describe the interstitial growth of collagen matrix (synthesized by fibroblasts or chondrocytes), under the simplifying assumption that solid matrix deformation is negligible and that all the amino-acids needed for producing collagen may be lumped into a single solute α = u.

In general, the mass balance equations are not sufficient to completely model growth problems, since momentum balance equations are also needed to describe mass transport, Eq.(3.29). In the canonical problems solved above, simplifying assumptions were adopted to provide trivial solutions to these equations, and help maintain the focus on the importance of mass balance equations in growth analyses. When momentum balance equations are included, additional modeling complexities arise with regard to the formulation of various constitutive relations that become relevant in growth problems, such as the evolution of transport properties with loss or gain of solid mass, as suggested by the constraints of Eqs.(3.32)-(3.33). Entire studies may have to be devoted to these subjects in the future, therefore no specific examples were illustrated here.

In summary, growth problems require the solution of mass balance equations that include supply terms and account for mass exchanges among constituents of a mixture. The statement of the axiom of mass balance may be formulated over a control volume, producing the equations for interstitial growth, or over a singular interface, producing the equations for appositional growth. Though growth may often be accompanied by a variety of concomitant phenomena that increase modeling complexity, such as solid matrix deformation, evolving traction-free configurations, cell division, active cell contraction, etc., it is important to distinguish these accompanying phenomena from the fundamental growth process that consists of deposition or removal of mass from the solid matrix.