Abstract
The number of individual items that can be maintained in working memory is limited. One solution to this problem is to store representations of ensembles that contain summary information about large numbers of items (e.g., the approximate number or cumulative area of a group of many items). Here we explored the developmental origins of ensemble representations by asking whether infants represent ensembles, and if so, how many at one time. We habituated 9-month old infants to arrays containing 2, 3, or 4 spatially intermixed colored subsets of dots, then asked whether they detected a numerical change to one of the subsets or to the superset of all dots. Experiment Series 1 showed that infants detected a numerical change to one of the subsets when the array contained 2 subsets, but not 3 or 4 subsets. Experiment Series 2 showed that infants detected a change to the superset of all dots no matter how many subsets were presented. Experiment 3 showed that infants represented both the approximate number and the cumulative surface area of these ensembles. Our results suggest that infants, like adults (Halberda, Sires & Feigenson, 2006), can store quantitative information about 2 subsets plus the superset: a total of 3 ensembles. This converges with the known limit on the number of individual objects infants and adults can store, and suggests that, throughout development, an ensemble functions much like an individual object for working memory.
Keywords: Working memory, ensemble, objects, development, infants, number
Memory for multiple visual ensembles in infancy
All cognitive processes face limits on how many items can be represented and on how much information can be processed in parallel. Research has revealed that for attention and memory, representations of objects appear to be privileged (e.g., Scholl, 2001), and adults appear able to represent information from no more than 3 or 4 objects at one time (Alvarez & Cavanagh, 2004; Broadbent, 1975; Cowan, 2001; Jiang, Olson, & Chun, 2000; Luck & Vogel, 1997; Sperling, 1960; Y. Xu, 2002; Y. Xu & Chun, 2006). This surprising limit also is observed in infants (Barner, Thalwitz, Wood, Yang, & Carey, 2007; Feigenson & Carey, 2003, 2005; Feigenson, Carey, & Hauser, 2002; Ross-Sheehy, Oakes, & Luck, 2003). For example, both adults and infants detect changes to briefly presented scenes containing 1, 2, or 3 objects, but fail to detect those same changes when more objects are present.
This limit on the number of items that can be attended and stored in working memory poses a processing problem-- How can we successfully operate in a world full of objects when we can only represent 3 or 4 of them at once? One solution to this problem is to store representations of ensembles that contain summary information about large numbers of items (e.g., the approximate number or cumulative area of a group of many items). In this paper we show that this solution is available starting in infancy, and that the constraints that shape adults’ processing of ensembles are also seen in infants. Specifically, we show: 1) that infants can represent the approximate number and the approximate cumulative surface area of items in an ensemble of dots, where the ensemble contains too many objects to attend and remember individually, and 2) that infants can maintain representations of three such ensembles at once, convergent with the number of individual objects they can represent. In this sense, the experiments we report here highlight a paradox: cognition is both strictly constrained and, at the same time, highly flexible. It is strictly constrained to represent information from no more than 3 individual items at once, yet it is flexible enough that either an individual object or an ensemble of many objects can function as an item for attention and working memory. This flexibility appears to have origins early in development.
Representing individual objects
Several lines of research suggest that ‘individual object’ is an important unit of representation for adults. For example, Luck & Vogel (1997) suggested that working memory is limited by the number of discrete objects to be remembered rather than by the total information load imposed by the objects (e.g., the total number of features present). In a change-detection task in which observers saw 2 sequentially flashed arrays and then reported whether any items in the array had changed, adults detected a change to arrays containing 4 objects, each with 4 features (16 features total) as easily as to arrays containing 4 objects, each with 1 feature (4 features total). This suggests that the primary representational unit of adults’ working memory in the change detection task is something like object, rather than object feature.
Research examining adults’ tracking abilities also suggests a critical role for objects. In their influential object-file theory, Kahneman, Treisman, & Gibbs (1992) suggested that representations of individual objects function as basic units for tracking entities through space and time. These “object file” representations are defined by spatiotemporal information and do not necessarily contain any featural information. Features such as color, shape, or category membership can be misrepresented or even altogether absent from a representation; the object representation can be maintained as long as the object maintains a coherent spatiotemporal history. Similarly, Pylyshyn’s FINST model (1989) posits an early stage of attentional processing in which objects are tracked purely on the basis of their spatiotemporal history, without regard to featural information. A key aspect of both the object-file and the FINST frameworks is that representing the existence of an individual object is privileged over representing object features.
A third source of evidence for the importance of objects comes from multiple-object tracking (MOT) studies. Observers in these studies successfully track moving visual stimuli when those stimuli behave in ways consistent with principles of object-hood, such as deleting and accreting along a leading edge when moving past an occluder (Scholl & Pylyshyn, 1999). However, observers fail to track otherwise identical stimuli when those stimuli explode into or implode out of existence (Scholl & Pylyshyn, 1999), or when they move in a noncohesive and nonrigid manner (vanMarle & Scholl, 2003).1 These MOT studies reveal that the mechanisms that support tracking of moving items are sensitive to the degree to which those items behave like real-world objects.
The above studies reveal that individual object is an important representational unit for attention and memory. This is true from early in development. Despite early claims that infants fail to store persisting object representations (Piaget, 1954), several decades of work have since shown that infants indeed can represent objects in working memory. Like adults, infants rely primarily on spatiotemporal information to track unified objects, as opposed to tracking individual object features (F. Xu & Carey, 1996). Furthermore, infants, like adults, have expectations about objects’ behavior that do not extend to non-objects (Cheries, Mitroff, Wynn, & Scholl, 2008; Chiang & Wynn, 2000; Huntley-Fenner, Carey, & Solimando, 2002; Rosenberg & Carey, submitted). For example, 5-month old infants detect the unexpected appearance or disappearance of an object from behind an occluder (e.g., Wynn, 1992). But when the same event involves the appearance or disappearance of a pile of blocks or a pour of sand (i.e., a collection or a non-solid object), infants fail to notice the change (Chiang & Wynn, 2000; Huntley-Fenner et al., 2002). This shows that, infants, like adults, are sensitive to the distinction between objects and non-objects when storing representations of occluded entities.
Adults and infants also show similar constraints on the number of individual object representations they can store in working memory. Whereas early discussions of working memory capacity suggested that adults were limited to remembering “7, plus or minus 2 items” (Miller, 1956), more recent evidence has revised this estimate to just 3 or 4 items (Alvarez & Cavanagh, 2004; Broadbent, 1975; Cowan, 2001; Luck & Vogel, 1997; Song & Jiang, 2006; Sperling, 1960; Y. Xu, 2002; Y. Xu & Chun, 2006). For example, in the change detection task described earlier, Luck & Vogel (1997) found that adults easily detected changes to visual arrays containing 1 – 4 objects, whereas performance rapidly deteriorated with arrays containing more than 4. Strikingly, this 3–4 item limit is also observed early in development across a variety of methodologies. In a modified visual change-detection paradigm, 10-month old infants detected featural changes to arrays containing 2, 3, or 4 individual objects, but failed with arrays containing 6 (Ross-Sheehy, Oakes, & Luck, 2003). In a manual search paradigm, 12- to 14- month old infants successfully remembered the hiding of 1, 2, or 3 individual objects in an opaque box, but failed when 4 objects were hidden (Barner et al., 2007; Feigenson & Carey, 2003; 2005).
Both adults (Alvarez & Cavanagh, 2004; Broadbent, 1975; Cowan, 2001; Luck & Vogel, 1997; Song & Jiang, 2006; Sperling, 1960; Y. Xu, 2002; Y. Xu & Chun, 2006) and infants (Ross-Sheehy et al., 2003) exhibit the 3–4 item limit in tasks using very short retention delays that are consistent with the use of visual short-term memory (VSTM). Infants also exhibit this limit in tasks with longer retention delays that are more consistent with the use of a modality-neutral working memory store (Barner et al., 2007; Feigenson & Carey, 2003; 2005). An analogy between the longer delays used in many infant studies and the surprisingly long persistence of object-file representations in adult vision has been noted (Noles, Scholl & Mitroff, 2005), further extending the convergence of infant and adult performance. Across multiple paradigms and multiple timescales, these results suggests that both adults and infants store no more than 3 or 4 individual objects in working memory at a time.
Representing ensembles
Despite the apparent importance of individual object as a unit for cognitive processing, many studies demonstrate that this is not the only type of entity that adults can attend and maintain in working memory. Adults also can represent arrays that contain vastly more items than working memory can store individually. This has been shown by studies that first present observers with arrays containing large numbers of items, then query them about statistical features of the array such as the total number of items (Halberda, Sires, & Feigenson, 2006), mean size of items (Ariely, 2001; Chong & Treisman, 2003, 2005; Chong, Joo, Emmanouil & Treisman, 2008; Im & Chong, 2009), average orientation of items (Parkes, Lund, Angelucci, Solomon & Morgan, 2001), density (Ross & Burr, 2010), and center of mass of the array (Alvarez & Oliva, 2008). For example, adults can estimate that an array contains “about 50” dots. They can do so without verbally counting and with brief exposure times that preclude serial attention to each individual dot in the array (e.g., Barth, Kanwisher, & Spelke, 2003; Izard & Dehaene, 2007; Moyer & Landauer, 1967; Pica, Lemer, Izard, & Dehaene, 2004). Because the number of individual items in these arrays greatly exceeds the 3–4 item limit on the number of individual objects that can be remembered at any given time, and because observers typically have to produce numerical estimates or compare quantities after a stimulus is no longer perceptually available, it appears that working memory must be able to store representations of collections, or ensembles of items, in addition to storing representations of individual objects.
However, representing ensembles comes at a cost. Whereas individual object representations are precise enough to support comparisons of the exact number of items in a scene, ensemble representations are inherently imprecise (Alvarez & Oliva, 2008; Feigenson, Dehaene, & Spelke, 2004). Adults performing rapid nonverbal enumeration produce numerical estimates that are approximately correct, but that exhibit a signature error pattern. This error is a linear function of the numerosity of the target array, such that larger quantities are represented less precisely than smaller quantities (e.g., Dehaene, 1997; Gallistel & Gelman, 2000; Moyer & Landauer, 1967; Whalen, Gallistel, & Gelman, 1999). One way of describing this imprecision is by measuring the finest numerical discrimination that observers can reliably make. For typically developing adults in industrialized cultures, this ratio is between 7:8 and 9:10 (Barth et al., 2003; Halberda & Feigenson, 2008; Pica et al., 2004). Note that if observers had been able to store in working memory precise representations of all of the individual objects in the scene, this ratio limit on discrimination would not be expected (for example, if adults are allowed to serially verbally count items, they can easily distinguish 19 items from 20 items). Therefore, the hallmark noisiness of ensemble representations distinguishes them from representations of individual objects (see Feigenson et al., 2004 for a review).
The expansion of information processing afforded by ensemble representations (e.g., representing “approximately 50 dots” rather than only up to 3 individual dots) would be even greater if observers were able to store multiple ensembles in parallel, just as they can store multiple individual objects in parallel. The ability to maintain multiple ensemble representations also would allow for the performance of computations over ensembles (e.g., computing which array is more numerous, or which array has the greater total area). Recent work suggests that adults can do just this, and that they rely on multiple ensemble representations to verify quantifier phrases like “most of these dots are blue” and “there is more green paint than yellow paint,” (Pietroski, Lidz, Hunter & Halberda, 2008; Lidz, Pietroski, Hunter & Halberda, in press). Furthermore, just as adults are constrained to storing representations of 3 individual objects in working memory, they are similarly constrained to storing representations of 3 ensembles of items in working memory (Feigenson, 2008; Halberda et al., 2006). Because these results directly motivate the current work, we describe them in detail here.
Halberda and colleagues (2006) asked whether adults can represent multiple ensembles in parallel. Observers saw arrays containing varying numbers of colored dot subsets (from 1 to 6 subsets). For example, an array could contain 21 red dots (1 color subset), or could contain 8 yellow dots and 12 cyan dots (2 color subsets), or could contain 2 red, 14 yellow, 5 cyan, 8 green, and 3 blue dots (5 color subsets). After seeing the array for 500ms, observers had to estimate either the total number of dots in the array (i.e., the superset of all dots), or the number of just one particular colored subset (e.g., just the red dots). Adults successfully estimated the number of items in a subset when either one or two colored subsets had been shown. But with arrays containing 3–6 color subsets, the error in their numerical estimates increased significantly. Importantly, when asked about the superset of all dots in the array, participants’ responses showed the signature error pattern of the approximate system and their responses were unaffected by the number of color subsets presented. This suggested that adults always successfully represented the superset, even when the subsets comprising this superset were not themselves represented.
These results suggest that adults can form representations of multiple ensembles and can store these in working memory. However, adults are limited to storing 3 ensemble representations at a time—in the task by Halberda et al. (2006), these included two color subsets and the superset of all dots. These results have since been extended to a task in which stimuli were presented sequentially rather than simultaneously. Adult observers engaged in verbal shadowing (to block counting) as they watched large numbers of several different types of objects being hidden rapidly one at a time in two buckets. They then had to report which bucket contained more items of a given type. Each item appeared for approximately 1 second and the presentation of the entire sequence lasted upwards of 40 seconds in some conditions. Observers made successful numerical comparisons between the two locations when 1, 2, or 3 object types had been hidden at each location, but failed with larger numbers of types, regardless of the total number of individual objects comprising those ensembles (Feigenson, 2008). That adults enumerated up to 3 temporally intermixed ensembles supports the view that the 3-ensemble limit originates in working memory rather than in visual attention. What is particularly striking about the findings of Halberda et al. (2006) and Feigenson (2008) is the similarity between the 3-ensemble limit and the 3-object limit demonstrated in the previous studies of attention and working memory reviewed earlier. This similarity suggests that an ensemble may function similarly to an individual object.
If an ensemble of multiple objects can function as an individual for memory (Feigenson, 2008; Halberda et al, 2006), the question arises as to how an observer determines which ensembles to treat as individuals (or put another way, how does one pick out an ensemble?). The criteria that determine which items comprise an ensemble (e.g., the blue dots, all the dots, just the big blue dots) must be specified and the ensemble must be attended prior to storing information about it in memory. This parallels a similar point concerning how individual objects come to be represented in working memory (Vogel, Woodman, & Luck, 2006). In the study by Halberda and colleagues (2006) in which observers saw spatially intermixed ensembles of colored dots, the results suggested that it was not left to chance which ensembles would be prioritized for attention and memory. Adults attended individual subsets as defined by color, and always appeared to attend and remember the superset of all items, irrespective of the number of colors in the display.
Here we investigated the origins of ensemble representations of by presenting infants with arrays similar to those shown to adults. Our objectives were to ask 1) whether infants spontaneously segment a scene into ensembles without training or guidance, 2) whether infants have limits in ensemble processing similar to adults (e.g., representing a maximum of 3 ensembles), and 3) whether infants display biases and prioritizing in processing multiple ensembles similar to those of adults (e.g., representing the superset of all items along with 1 or more subsets). Answering these questions goes beyond merely demonstrating that infants represent ensembles. Along with studies on adults, the developmental approach we take here can begin to reveal the origins of ensemble processing and its possible indepedence from explicit strategy use. For example, if ensembles function as individuals from early in development, this would suggest that parsing ensembles is a fundamental representational ability, rather than a learned strategy to overcome object-based attention and working memory limitations. And if infants prioritize the superset of all items without training or experience gained through multiple trials, this would suggest that this prioritization derives from basic information-processing constraints, rather than top-down guidance.
Can infants represent multiple ensembles?
Representations of ensembles appear to be used in the first year of life. Previous research reveals that infants, like adults, can represent the numerosity of a collection containing many more than 3–4 individual objects—for example, 6-month old infants can discriminate arrays of 8 dots from arrays of 16 (F. Xu & Spelke, 2000). Like those of adults, infants’ ensemble representations are imprecise. Six-month old infants require a 1:2 ratio between quantities to support successful discrimination: although they successfully discriminate 8 from 16 dots, they fail to discriminate 8 from 12. The precision of infants’ numerical representations increases over the course of development. Nine-month old infants successfully discriminate numerosities differing by the 2:3 ratio with which 6-month olds fail (Lipton & Spelke, 2003; F. Xu & Spelke, 2000), and older children succeed with still finer ratios (Halberda & Feigenson, 2008).
However, it remains unclear whether infants can represent the approximate numerosity of more than one ensemble at once, and if so, how many enumerations they can perform. Five-month old infants who were habituated to 2 groups of moving dots (with group membership defined by common motion) dishabituated when shown 4 groups, and vice versa (Wynn, Bloom, & Chiang, 2002). But exactly what information infants represented in this task is not known, because the authors did not ask whether infants had represented any summary information (such as approximate numerosity) about the ensembles. Therefore the results are inconclusive as to whether infants represented the moving stimuli as ensembles at all—instead they might have been led by Gestalt grouping principles to perceive each group as a single object (i.e., to perceive 2 large objects rather than 2 ensembles). Evidence that infants represented ensembles as opposed to individual objects would come from a demonstration that they represented, for example, the approximate number of items contained within each ensemble.
More compelling evidence that infants might represent more than one ensemble at a time comes from their performance with numerical ratios. McCrink & Wynn (2007) found that 6-month old infants successfully abstracted a ratio relationship between two spatially intermixed groups of colored dots, and then dishabituated to a change in this ratio. For example, infants habituated to arrays in which blue dots outnumbered yellow dots by 4:1 dishabituated when this ratio changed to 2:1. However, these infants may have discarded information about the approximate numerosity of each ensemble (i.e., approximately how many blue dots and approximately how many yellow dots were present), and instead only maintained a single representation of the ratio between the two. In McCrink and Wynn’s design, the absolute number of blue and yellow dots changed from trial to trial and only the ratio between the two ensembles remained constant. This may have invited infants to store the ratio in memory and to discard information about the absolute number of items that instantiated this ratio. In such a context, infants might fail to differentiate an array containing 10 blue and 5 yellow dots from an array containing 40 blue and 20 yellow dots, because both instantiate a 2:1 ratio of blue to yellow dots. Therefore, it remains open whether 1) infants can store multiple ensembles in memory, and 2) infants deploy this ability consistent with the prioritization and limitations that have been demonstrated in adults (i.e., always prioritize the superset, and only store up to 3 ensembles at once).
The Current Experiments
Here we asked three questions about infants’ ability to represent ensembles. First, we asked whether infants can store multiple ensemble representations simultaneously, as adults can (Feigenson, 2008; Halberda et al., 2006). Specifically, in Experiments 1a, 1b, and 1c we asked whether infants store ensemble representations of multiple subsets when presented with arrays containing 2 subsets (i.e., red and yellow dots, such that the number of colored subsets—2-- was below the 3-item limit of object-based working memory capacity), 3 subsets (such that the number of colored subsets equaled the limit of object-based capacity) and 4 subsets (such that the number of colored subsets was greater than the limit of object-based capacity). Second, in Experiments 2a, 2b and 2c we asked whether infants, like adults, show privileged representation of the superset of all items when presented with arrays containing 2 subsets (below capacity), 3 subsets (equal to capacity) and 4 subsets (greater than capacity). Finally, in Experiment 3 we asked whether the ability to attend and remember multiple ensembles allows infants to represent approximate cumulative area as well as approximate number. The intuitions guiding this work were that 1) infants, like adults, will represent ensembles, 2) the limits and prioritization of information that characterize infants’ ensemble representations will parallel those of adults, with infants representing the superset of all items and up to two color subsets from each array, and 3) these hallmarks of ensemble-based processing will apply irrespective of the particular ensemble feature with which infants are tested (e.g., approximate number or approximate area). Put more strongly, we hypothesize that both infants and adults automatically store multiple ensembles and multiple features from each attended ensemble, including number and area, as well as features that we did not test in the current series of experiments, such as center of mass, average orientation, average size, and direction of motion (Alvarez & Oliva, 2008; 2009; Ariely, 2001; Chong & Treisman, 2003; 2005; Chong et al., 2008; Parkes et al., 2001). For these reasons, we view the current studies as addressing general issues of ensemble representation, rather than addressing the narrower issue of number processing.
We tested 9-month old infants for two reasons. First, previous data suggest that by 9 months of age infants can maintain representations of at least two individual objects in visual working memory (Ross-Sheehy et al., 2003), thereby supporting the possibility that they might also represent at least two ensembles in working memory. Second, the acuity of 9-month olds’ approximate number representations has been well characterized (Lipton & Spelke, 2003, 2004; F. Xu & Arriaga, 2007), making it possible for us to test infants with numerical changes known to be both within and beyond their threshold of numerical acuity.
We used a habituation procedure (Fantz, 1964) to parametrically explore infants’ ability to encode and remember ensembles. We note that using habituation may draw upon a different type of memory than that previously investigated in adults’ storage of multiple ensembles. Previous investigations with adults measured representations stored in visual short-term memory (involving array presentations of less than 1 second: Halberda et al., 2006) and working memory (and possibly long-term memory, involving array presentations of dozens of seconds: Feigenson, 2008). Here we showed infants repeated presentations of visual arrays totaling approximately 100 seconds of habituation time (i.e., infants saw an average of 10 habituation trials lasting approximately 10 seconds each) prior to presenting infants with the test arrays. It is currently unknown whether this type of paradigm relies on visual working memory, amodal working memory, long-term memory, or some combination of memory systems (see Oakes & Bauer, 2007), though there is no previous literature suggesting that long-term memory should be limited to storing only 3 individual objects or 3 ensembles at once. Demonstrating which memory system is responsible for a 3-ensemble limit is not our objective. Rather, if the current procedure reveals limits on infants’ representations of multiple ensembles that are convergent with adults’ 3-ensemble limit, and if it reveals biases in infants’ prioritizing of ensembles that are convergent with adults’ prioritizing of the superset of all dots, this will argue for an early developmental origin for ensemble representations, irrespective of which particular attention and memory systems are involved.
General Method
Apparatus
Infants sat in a high chair approximately 60 cm from a computer screen that was surrounded by a green curtain. Parents sat approximately 60 cm behind infants and were instructed not to speak or direct infants’ attention throughout the experimental session. The experimenter controlled the study from behind the curtain and was not visible to infants during the experiment. A concealed video camera recorded infants’ looking behavior.
Design
Across all experiments, infants first were habituated to arrays containing a constant number of color-defined subsets, with each subset containing a constant number of dots (except for the Area Condition of Experiment 3, in which number varied and area remained constant). We presented habituation trials until infants either a) met the habituation criterion of three consecutive trial durations equaling less than 50% of the first three consecutive trial durations, or b) completed 15 habituation trials without meeting this criterion. The number of infants who met the habituation criterion across experiments was: Experiment 1a: 14/16 (average number of habituation trials = 9.6); Experiment 1b: 12/16 (average = 9.1); Experiment 1c: 12/16 (average = 9.7; Experiment 2a: 15/16 (average = 9.3); Experiment 2b: 12/16 (average = 9.9); Experiment 2c: 13/16 (average = 9.2); Experiment 3: 13/20 (average = 10.0). To ask whether our pattern of results across all experiments depended on whether infants had habituated or instead had seen all 15 habituation trials without meeting the habituation criterion, we conducted a 2 (Trial Type: Discriminable or Non-Discriminable test trials) × 3 (Test Trial Pair: 1st, 2nd, or 3rd pair) × 8 (Experiment) × 2 (Habituation Status: Habituator vs. Non-Habituator) analysis of variance (ANOVA). This revealed no significant main effect or interactions involving Habituation Status, and therefore this variable was dropped from further analysis.
We did exclude 2 infants who not only failed to habituate within the maximum of 15 trials, but who also showed looking patterns that were the reverse of those typically seen in habituation experiments: looking times that increased rather than decreased over habituation trials. This increase in looking time resulted in these two infants having ratios for the change in looking from the first three to the last three habituation trials that were 3 SDs above the mean. The mean habituation ratio for all infants was 0.37 (a ratio less than 1 reflects decreasing looking from the first three to the last three habituation trials). The habituation ratio for excluded subject 1 was 2.02, (Experiment 1b) and for excluded subject 2 was 1.29 (Experiment 2a). Finally, for inclusion in the final sample, infants’ looking times for each test trial had to fall no more than 3 SDs from the group mean. We describe the number of excluded infants in the Participants section for each experiment.
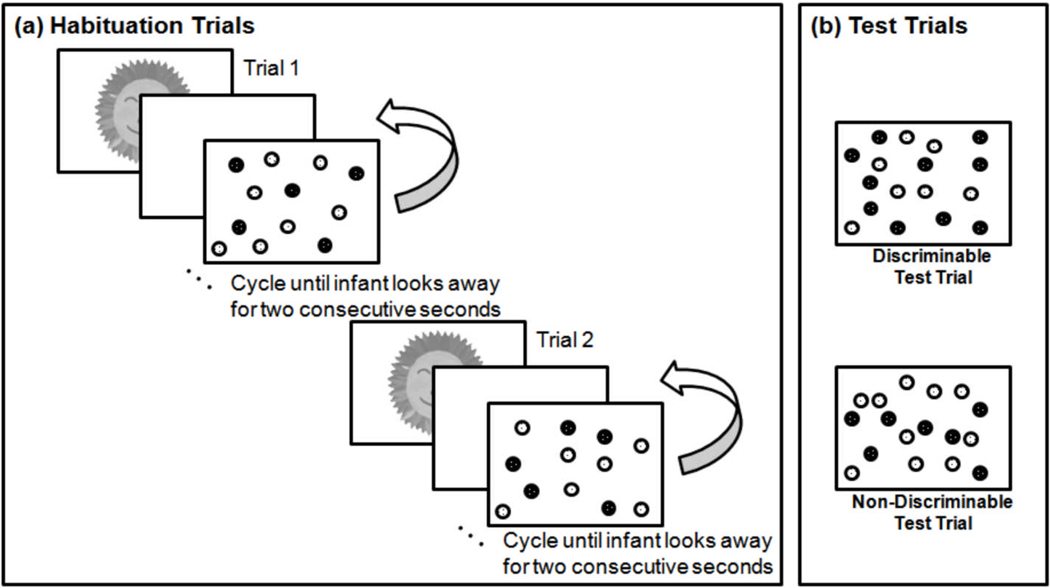
We habituated infants to arrays like that shown in Figure 1, in which multiple ensembles of dots (containing either 2, 3, or 4 subsets) were spatially intermixed, with exact dot position changing from trial to trial. Tables 1–3 report the number of dots presented in each Experiment. Dots were placed randomly within each array, except that arrays in which there was an unusually large amount of spatial grouping were not used. Following habituation, infants saw two types of test trials in alternation. In Experiment Series 1, on Discriminable test trials the number of dots in one of the subsets doubled whereas the number of dots in the other sets remained unchanged. In Experiment Series 2, on Discriminable trials the superset of all dots in the array doubled and subsets were not identifiable during test (because at test all dots turned grey). In Experiment 3, for half of the infants the number, and for the other half the total cumulative area, of one of the subsets doubled whereas the other subset remained unchanged. We chose a 1:2 ratio for the Discriminable changes across our experiments because previous experiments showed that infants younger than those tested here successfully detected a 1:2 ratio change across several different absolute numerosities when presented with a single ensemble of dots or sounds (Lipton & Spelke, 2003; F. Xu, 2003; F. Xu & Arriaga, 2007; F. Xu & Spelke, 2000). For the cumulative area changes in Experiment 3, results from a paradigm similar to ours found that 6-month-old infants required a 1:4 change in cumulative area between habituation and test in order to detect a change (Cordes & Brannon, 2008). However, preliminary results from our laboratory suggested that 9-month-old infants may have sufficient acuity to detect a 1:2 change in cumulative area with our displays (our Experiment 3 displays contained two color subsets of heterogeneous sizes, whereas the Cordes & Brannon [2008] displays contained a single set of homogeneous size). Therefore, to maintain consistency in the current experiments across number and area dimensions we showed infants a 1:2 ratio change on all Discriminable test trials, including the change in cumulative area on the Discriminable test trials for Experiment 3.
Figure 1.
(a) Schematic of two trials from the habituation phase of the Experiments. Infants saw between 6 and 15 trials over the course of habituation. (b) Schematic of two trials from the test phase. Infants saw 3 Discriminable test trials and 3 Non-Discriminable test trials in alternating order.
Table 1.
Numerical ratios presented to infants in Experiment Series 1
| Habituation | Test | ||
|---|---|---|---|
| Discriminable | Non-Discriminable | ||
| # of dots | # of dots (Habituation:Test Ratio) | ||
| Experiment 1a | |||
| Subset A | 5 | 10 (.50) | 7 (.71) |
| Subset B | 7 | 7 (1.00) | 10 (.70) |
| Superset | 12 | 17 (.71) | 17 (.71) |
| Experiment 1b | |||
| Subset A | 5 | 10 (.50) | 6 (.83) |
| Subset B | 7 | 7 (1.00) | 9 (.78) |
| Subset C | 8 | 8 (1.00) | 10 (.8) |
| Superset | 20 | 25 (.80) | 25 (.80) |
| Experiment 1c | |||
| Subset A | 5 | 10 (.50) | 6 (.83) |
| Subset B | 6 | 6 (1.00) | 8 (.75) |
| Subset C | 5 | 5 (1.00) | 6 (.83) |
| Subset D | 4 | 4 (1.00) | 5 (.80) |
| Superset | 20 | 25 (.80) | 25 (.80) |
Note. The number in parenthesis is the relationship between the habituation and test display (obtained by dividing the number of dots shown during habituation by the number of dots shown during test). The finest ratio that 9-month old infants have been shown to discriminate is 2:3 (0.66; Lipton & Spelke, 2003; Lipton & Spelke, 2004).
Table 3.
Numerosity and surface area of stimuli presented to infants in Experiment 3 (order was randomized for each infant)
| Collection A | Collection B | ||||
|---|---|---|---|---|---|
| Number Control | Number | (Surface Area) | Number | (Surface Area) | |
| Habituation Trials | |||||
| Trial A | 5 | (15) | 5 | (21) | |
| Trial B | 5 | (15) | 7 | (21) | |
| Trial C | 5 | (15) | 9 | (21) | |
| Trial D | 7 | (15) | 5 | (21) | |
| Trial E | 7 | (15) | 7 | (21) | |
| Trial F | 7 | (15) | 9 | (21) | |
| Trial G | 9 | (15) | 5 | (21) | |
| Trial H | 9 | (15) | 7 | (21) | |
| Trial I | 9 | (15) | 9 | (21) | |
| Discriminable Test Trials | |||||
| Trial A | 6 | (30) | 6 | (21) | |
| Trial B | 6 | (30) | 8 | (21) | |
| Trial C | 8 | (30) | 6 | (21) | |
| Trial D | 8 | (30) | 8 | (21) | |
| Non-Discriminable Test Trials | |||||
| Trial A | 6 | (21) | 6 | (30) | |
| Trial B | 6 | (21) | 8 | (30) | |
| Trial C | 8 | (21) | 6 | (30) | |
| Trial D | 8 | (21) | 8 | (30) | |
| Area Control | |||||
| Habituation Trials | |||||
| Trial A | 5 | (25) | 7 | (25) | |
| Trial B | 5 | (25) | 7 | (35) | |
| Trial C | 5 | (25) | 7 | (45) | |
| Trial D | 5 | (35) | 7 | (25) | |
| Trial E | 5 | (35) | 7 | (35) | |
| Trial F | 5 | (35) | 7 | (45) | |
| Trial G | 5 | (45) | 7 | (25) | |
| Trial H | 5 | (45) | 7 | (35) | |
| Trial I | 5 | (45) | 7 | (45) | |
| Discriminable Test Trials | |||||
| Trial A | 10 | (30) | 7 | (30) | |
| Trial B | 10 | (30) | 7 | (40) | |
| Trial C | 10 | (40) | 7 | (30) | |
| Trial D | 10 | (40) | 7 | (40) | |
| Non-Discriminable Test Trials | |||||
| Trial A | 7 | (30) | 10 | (30) | |
| Trial B | 7 | (30) | 10 | (40) | |
| Trial C | 7 | (40) | 10 | (30) | |
| Trial D | 7 | (40) | 10 | (40) | |
On Non-Discriminable test trials the number of dots (or sizes of dots in Experiment 3) in all of the subsets (Experiment Series 1 & Experiment 3) or the superset (Experiment Series 2) increased by a ratio known to be non-discriminable to infants of this age (see Table 1). We relied on findings from previous experiments that infants of the same age or older than those tested here failed to discriminate 3:4 and 4:5 ratios when presented with a single group of dots or sounds (Brannon, Suanda, & Libertus, 2007; Lipton & Spelke, 2003; F. Xu & Arriaga, 2007).
Infants saw 6 test trials presented in 3 pairs. Each pair contained one Discriminable and one Non-Discriminable test trial, with Discriminable and Non-Discriminable trials shown in alternation. Whether infants saw Discriminable or Non-Discriminable test trials first was counterbalanced across infants.
Finally, we randomized the color-number pairing (or color-size pairing for Experiment 3) across infants in each Experiment such that approximately equal numbers of infants saw each color associated with each numerosity/size (e.g., in Experiment 1a approximately half the infants were habituated to arrays containing 5 red dots and 7 yellow dots, and approximately half the infants were habituated to arrays containing 7 red dots and 5 yellow dots.) Which color served as the ‘target array’ (i.e., the array that changed numerosity on Discriminable test trials) was also randomized across infants. Although no previous work suggests that any of the colors we presented would be more salient to infants than others, we wanted to ensure that any observed success or failure was not due to a uniquely noticeable color. No effect of color was found in any Experiment, thus we excluded this variable from further analsyses.
Procedure
Each trial consisted of a static array of dots shown for 700ms, followed by 50ms of blank screen (see Figure 1). This two-step sequence flashed repeatedly until infants lost interest, at which point the trial ended. The criteria we used to determine the start and stop of each trial across habituation and test were based on those commonly used across many looking time experiments, and in particular by experiments testing infants’ enumeration abilities (e.g., Brannon, Abbott, & Lutz, 2004; Brannon, Lutz, & Cordes, 2006; McCrink & Wynn, 2007; F. Xu & Spelke, 2000; F. Xu, Spelke, & Goddard, 2005; F. Xu & Arriaga, 2007). The minimum looking time for a habituation trial was 0.5 seconds and the maximum was 120 seconds, and each trial ended when infants looked away for 2 consecutive seconds. In between trials a static image of a smiling, colorful sun appeared onscreen to reorient infants’ attention and a musical song was played for as long as the sun image was visible. As soon as infants had reoriented to the screen, the experimenter pressed a key to start the next trial. For test trials, the minimum looking time was 0.5 seconds and the maximum was 60 seconds.
Each testing session was coded online by an experienced observer in the next room who was blind to the condition in which infants were being tested. The coder indicated when infants were looking at the screen by pressing a button that interfaced with software (Xhab; Pinto, 1996) that recorded looking times and computed habituation. Each session also was digitally recorded and later coded offline by two experienced observers who were blind to the condition in which infants were being tested. Inter-observer agreement on the duration of infants’ looking was calculated across all trials for all infants across all Experiments. The average correlation between the two observers was .95, and did not differ by Experiment.
Experiment Series 1: subset enumeration
In our first series of experiments we asked whether infants, like adults, can enumerate subsets of visual items from a spatially intermixed array. We then probed the limits of this ability by determining how many such subsets infants can simultaneously enumerate. Because each subset can be thought of as an ensemble, this allowed us to begin to address questions about infants’ ensemble representations.
Experiment 1a: 2 subsets
Given that no other study has shown conclusively that infants can enumerate more than one ensemble at a time, our first step was to ask whether 9-month old infants can simultaneously represent 2 ensembles in working memory.
Method
Participants
Sixteen healthy, full-term 8- to 9.5-month old infants participated (11 females; age range: 8 months, 3 days to 9 months, 5 days; mean age 8 months, 20 days). Fourteen additional infants were excluded from the final analysis (3 for parental interference, 8 for fussiness, and 3 for looking more than 3 SDs from the group mean on one or more test trials). The large number of infants whose data could not be included likely was due to the fact that this was the first experiment we ran, and we were still adjusting non-critical aspects of our procedure (such as the amount of time we spoke to parents prior to entering the testing room). This may have led to higher rates of fussiness than our other experiments. However, the number of participant exclusions we report here is not unusual for looking time experiments with infants; a recent metaanalysis of participant exclusion across over one hundred infant looking time studies found that between 0 and 62% of infants failed to complete a testing session due to fussiness. More importantly, the analysis found no evidence that exclusion of fussy infants systematically influenced experimental outcomes (i.e., that rates of exclusion were correlated with either positive or negative findings [Slaughter & Suddendorf, 2007]).
Stimuli and Design
We habituated infants to arrays like that shown in Figure 1, in which a subset of red dots was spatially intermixed with a subset of yellow dots. All dots were the same size. On Discriminable test trials the number of dots in one of the two subsets increased by a 1:2 ratio (i.e., the numerosity of the target subset changed from 5 to 10 and the numerosity of the non-target 7-dot subset remained unchanged). On Non-Discriminable test trials the number of dots in both subsets increased by a 5:7 ratio. Importantly, a 5:7 ratio change has been demonstrated by previous studies to be undetectable by infants of this age (Brannon et al., 2007; Lipton & Spelke, 2003; Xu & Arriaga, 2007; Table 1).
This design ruled out the possibility that infants would respond to a difference in the total number of dots in the test arrays. The absolute numerosities of the supersets (i.e., red plus yellow dots) in the Discriminable and Non-Discriminable test arrays were identical (both contained 17 dots), thereby making these supersets equally numerically novel relative to the habituation arrays. Furthermore, the change in the numerosity of the superset between habituation and test was designed to instantiate a ratio (12:17) that infants of this age cannot yet discriminate (Lipton & Spelke, 2003; F. Xu & Arriaga, 2007). In this way, Experiment 1a was designed so that the only detectable change in numerosity occurred within one of the color subsets on the Descriminable test trials.
Results and Discussion
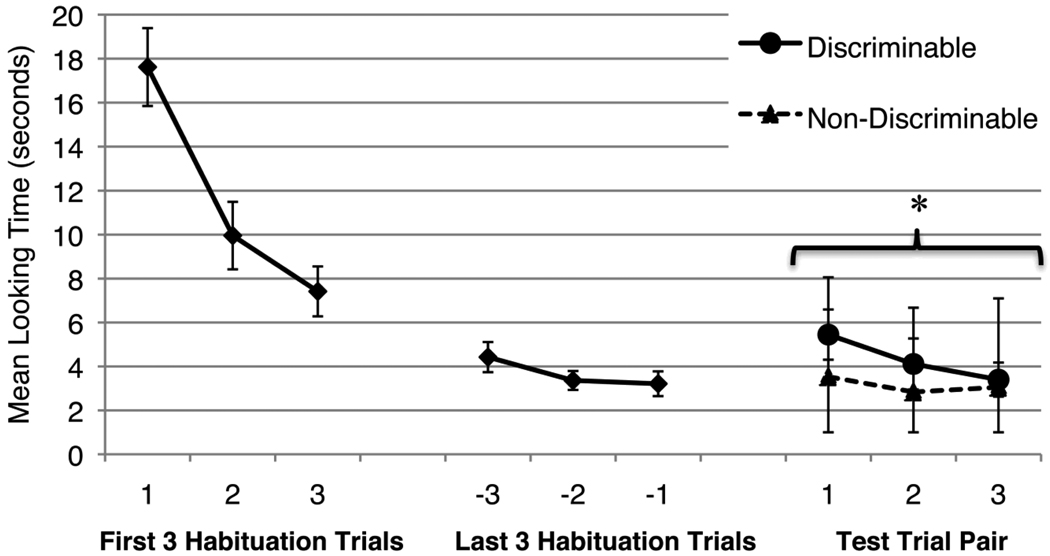
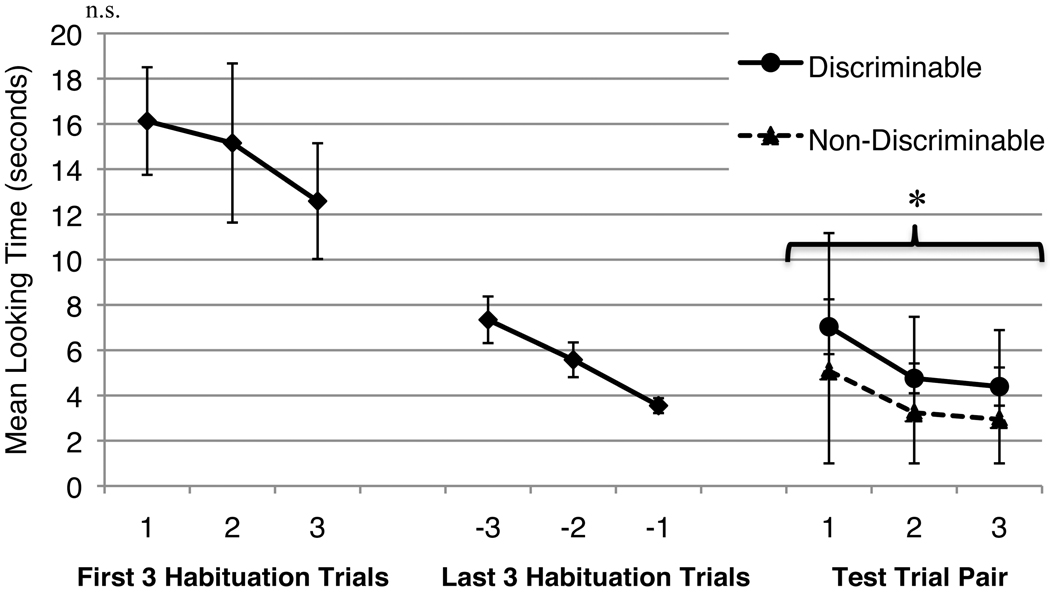
Figure 2 shows infants’ average looking across habituation and test trials. Infants’ looking times were analyzed using a 2 (Trial Type: Discriminable or Non-Discriminable) × 3 (Test Trial Pair) analysis of variance (ANOVA). This revealed a main effect of Trial Type, F (1,15) = 5.00, p < 0.05, ηp2 = 0.25, with infants looking longer at the Discriminable test arrays (M = 4.32 seconds) than the Non-Discriminable test arrays (M = 3.14 seconds). No other main effects or interactions were observed.
Figure 2.
Mean looking times in Experiment 1a. Error bars represent standard errors. The asterisk reflects a main effect of Trial Type across all 3 Test Trial Pairs.
The results of Experiment 1a extend our understanding of ensemble representation by showing that infants, like adults, can maintain representations of at least 2 ensembles in memory at once. Because infants had no way of knowing whether the red or the yellow subset was going to change from habituation to test, the group success at detecting the numerical doubling on the Discriminable test trials suggests that infants had maintained numerical information about both subsets in memory.
Experiment 1b: three subsets
Experiment 1a demonstrated that infants can maintain representations of the approximate numerosity of two subsets in working memory. These results are consistent with those of Halberda et al. (2006) and Feigenson (2008), who demonstrated the same ability in adults. Halberda and Feigenson also identified an upper limit to this ability: adults were able to store representations of 3 ensembles, just as they are able to store representations of about 3 individual objects (Alvarez & Cavanagh, 2004; Broadbent, 1975; Cowan, 2001; Jiang et al., 2000; Luck & Vogel, 1997; Sperling, 1960; Y. Xu, 2002; Y. Xu & Chun, 2006). For adults, these 3 ensembles consisted of the superset of the array, as well as 2 subsets. In order to determine the upper limit on infants’ ability to store multiple ensemble representations in memory, we next presented infants with arrays containing 3 colored subsets and asked whether they would detect a numerical change to just one of them. Based on previous findings (Halberda et al., 2006), we expected that infants would fail to enumerate 3 dot subsets from a single array. However, if infants (in contrast to adults) do not store ensemble representations of the superset of the array, they may succeed in storing 3 subset ensembles in parallel.
Method
Participants
Sixteen healthy, full-term 8- to 9.5-month old infants participated (9 females; age range: 8 months, 5 days to 9 months, 14 days; mean age 8 months, 25 days). Four additional infants were excluded from analysis (1 for parental interference, 2 for looking more than 3 SDs from the group mean on one or more test trials, and 1 for an atypical habituation pattern).
Stimuli and Design
We habituated infants to displays containing 3 colored subsets of dots (red, yellow, and blue). One of the subsets contained 8 dots, one contained 7 dots, and one contained 5 dots, for a total of 20 dots (see Table 1). On Discriminable test trials the number of dots in one of the 3 color subsets (the target subset) doubled from that shown during habituation (i.e., changed from 5 to 10). The number of dots in the other 2 color subsets remained unchanged. On Non-Discriminable test trials the number of dots in each of the 3 color subsets changed slightly from that seen during habituation (see Table 1), by an amount known not to be discriminable to infants of this age (i.e., ratio changes of 4:5, 7:9, and 5:6; Lipton & Spelke, 2003; F. Xu & Arriaga, 2007). As in Experiment 1a, this design equated the change in the superset of all dots between habituation and test across the two types of test trials (i.e., the superset changed from 20 to 25 dots on both Discriminable and Non-Discriminable trials). This 4:5 ratio is known not to be discriminable to infants of this age (Lipton & Spelke, 2003; F. Xu & Arriaga, 2007).
Results and Discussion
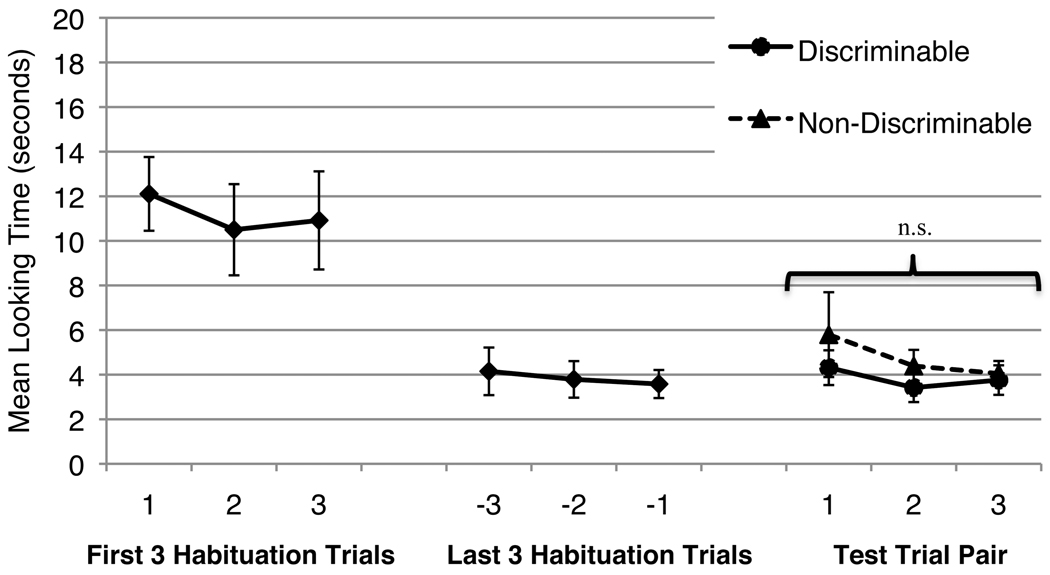
Figure 3 shows infants’ average looking across habituation and test trials. Infants’ looking times were analyzed using a 2 (Trial Type: Discriminable or Non-Discriminable) × 3 (Test Trial Pair) analysis of variance (ANOVA). There was no main effect of Trial Type F (1,15) = 2.18, p = 0.16, ηp2 = 0.13, nor any other significant main effects or interactions. Infants did not look longer at the Discriminable test arrays (M = 3.83 seconds) than at the Non-Discriminable test arrays (M = 4.74 seconds).
Figure 3.
Mean looking times in Experiment 1b. Error bars represent standard errors. The n.s. reflects a non-significant effect of Trial Type across all 3 Test Trial Pairs.
Infants showed no evidence of having maintained ensemble representations of 3 color subsets, as shown by their failure to look longer on Discriminable than Non-Discriminable test trials. Presented with three spatially intermixed ensembles of colored dots, infants did not notice when the numerosity of one of these ensembles doubled, despite their success at detecting the same 1:2 ratio change when presented with a single ensemble (Lipton & Spelke, 2003; F. Xu, 2003; F. Xu & Arriaga, 2007; F. Xu & Spelke, 2000) or with two ensembles (Experiment 1a). To confirm this apparent breakdown in infants’ memory capacity for ensembles, we asked whether infants’ ability to detect a subset change differed between Experiment 1a (2 subsets) and Experiment 1b (3 subsets). An Experiment (Experiment 1a or Experiment 1b) by Trial Type (Discriminable or Non-Discriminable test trials) ANOVA revealed an interaction F (1,31) = 6.61, p < 0.05, ηp2 = 0.18. This suggests that infants’ ability to detect a change to the numerosity of a subset depended on the number of ensembles present in the array.
Experiment 1c: four subsets
Although Experiment 1b showed that infants failed to represent three subsets concurrently, we next tested infants with arrays containing four subsets, for two reasons. First we wanted an additional experiment to confirm infants’ failure to represent more than 2 subsets. Second, in Experiment Series 2 it will be critical to test infants’ successful representation of the superset of all items in arrays with 4 color subsets (see Experiment 2c). We therefore conducted Experiment 1c allow for a comparison of infants’ representation of subsets (Experiment 1c) versus the superset (Experiment 2c) when presented with 4 color subsets. As in Experiments 1a and 1b, we tested infants’ memory capacity for multiple colored subsets of dots by changing the numerosity of one of the subsets by a discriminable amount, and asking whether infants detected the change. Based on the results of Experiment 1b, we predicted that infants would fail to detect this change.
Method
Participants
Sixteen healthy, full-term 8- to 9.5-month old infants participated (8 females; age range: 8 months, 6 days to 9 months, 13 days; mean age 8 months, 23 days). Four additional infants were excluded from analysis (1 for parental interference, 1 for fussiness, and 2 for looking more than 3 SDs from the group mean on one or more test trials).
Stimuli and Design
We habituated infants to displays containing 4 color subsets (red, yellow, blue, and magenta). Two of the subsets contained 5 dots each, one contained 6 dots, and one contained 4 dots, totalling 20 dots (see Table 1). On Discriminable trials the number of dots in one of the color subsets (the target subset) doubled from what it had been during habituation (i.e., changed from 5 to 10). The number of dots in the other subsets remained unchanged. On the Non-Discriminable trials the number of dots in each of the 4 color subsets changed slightly, by an amount known not to be discriminable to infants of this age (i.e., ratio changes of 3:4; 4:5, and two instances of 5:6). As in Experiments 1a and 1b, this design equated the change in the superset of all dots across the two types of test trials (from 20 to 25 dots in both Discriminable and Non-Discriminable trials). This 4:5 ratio is known not to be discriminable to infants of this age (Lipton & Spelke, 2003; F. Xu & Arriaga, 2007).
Results and Discussion
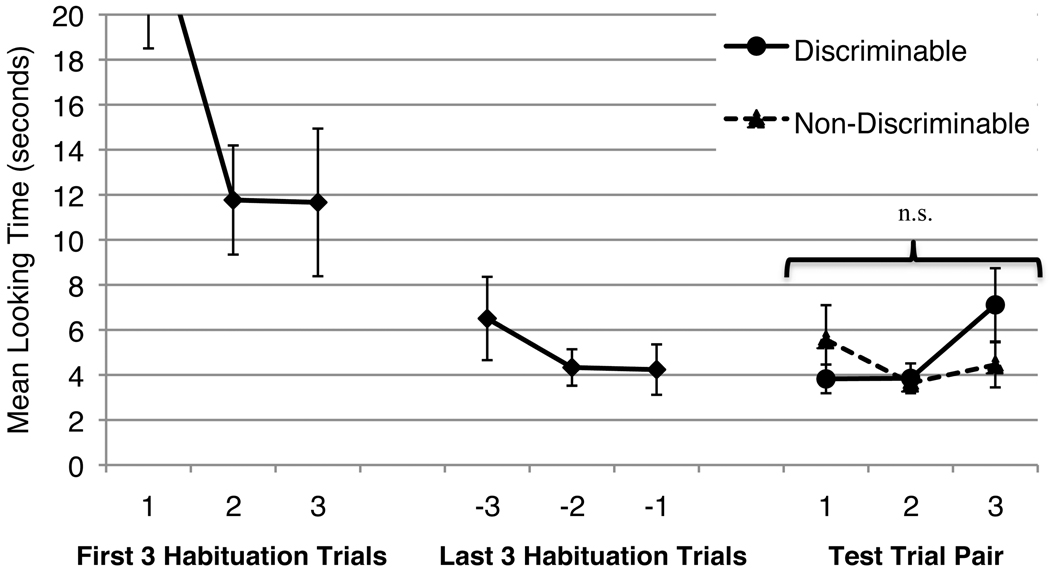
Figure 4 shows infants’ average looking across habituation and test trials. Infants’ looking times were analyzed using a 2 (Trial Type: Discriminable or Non-Discriminable) × 3 (Test Trial Pair) analysis of variance (ANOVA). This revealed no main effect of Trial Type, F (1,15) = 0.21, p = 0.65, ηp2 = 0.01, nor any other significant main effects or interactions. Infants did not look longer at the Discriminable test arrays (M = 4.93 seconds) than at the Non-Discriminable test arrays (M = 4.56 seconds).
Figure 4.
Mean looking times in Experiment 1c. Error bars represent standard errors. The mean look on the first habituation trial was 24.89 (SE ± 6.38). The n.s. reflects a non-significant effect of Trial Type across all 3 Test Trial Pairs.
Infants’ performance with 4 color subsets (Experiment 1c) did not differ from their performance with 3 subsets (Experiment 1b), as shown by an Experiment by Trial Type ANOVA that yielded no interaction between the two factors F (1,31) = 1.59, p = 0.22, ηp2 = 0.05. As predicted, infants failed to store ensemble representations of 4 color subsets in memory.
General discussion of Experiment Series 1
Experiments 1a, 1b, and 1c reveal a striking similarity in infants’ and adults’ memory for ensembles. Like adults, infants in Experiment 1a demonstrated the ability to store multiple ensemble representations in parallel. However, like adults (Halberda et al., 2006), infants in Experiments 1b and 1c were limited in the number of subsets they could simultaneously store. Recall that adults’ working memory limit for ensembles parallels their working memory limit for individual objects—adults appear limited to representing 3 ensembles at once, just as they are limited to representing 3 individual objects at once (Feigenson, 2008; Halberda et al., 2006). Notably, when tested with dot arrays much like those shown to infants in the present studies, adults stored information about the superset plus two color subsets. Furthermore, adults successfully represented the superset regardless of the number of subsets presented (Halberda et al., 2006). This prioritizination of the superset appeared to be automatic, as their reaction times and error rates to enumerate the superset suggested that they had selected, stored, and enumerated the superset as a single entity, rather than enumerating the subsets and then rapidly adding their approximate numerosities (Halberda et al., 2006).
Thus far, we have presented evidence that infants can store representations of 2 ensembles at once (Experiment 1a). Do infants also represent the superset of all items in the array? Because we did not probe infants about the numerosity of the superset of the array, and because in Experiments 1a, 1b, and 1c we designed the change in the numerosity of the superset to be non-discriminable to infants, this aspect of the degree to which infants’ memory capacity for ensembles parallels that of adults remains untested. For this reason we next asked whether infants, like adults, would respond to a change in the numerosity of the superset of all dots.
Experiment Series 2: superset enumeration
In Experiments 2a, 2b, and 2c we tested infants’ memory for the superset of the array when presented with 2 subsets (Experiment 2a), 3 subsets (Experiment 2b), and 4 subsets (Experiment 2c). If infants’ memory capacity parallels that of adults (Halberda et al, 2006), infants should succeed at discriminating a 1:2 numerical change to the superset of the array in all of these cases.
Experiment 2a: two subsets and the superset
As in Experiment 1a, we habituated infants to arrays containing spatially intermixed red and yellow dots. To ask whether infants represented the superset of all dots, on Discriminable test trials the numerosity of the superset doubled (i.e., changed by a 1:2 ratio), whereas on Non-Discriminable trials the superset changed by an amount known not to be discriminable to infants of this age (i.e., changed by a 5:7 ratio; Lipton & Spelke, 2003). To ensure that any response to the Discriminable test arrays was due to a change in numerosity of the superset, as opposed to a change in the two color subsets (as it was not possible to double the numerosity of the superset without also doubling the numerosity of at least one of the subsets), the test arrays contained grey dots only. This allowed us to conceal which dots had been members of the red versus the yellow subset.
Method
Participants
Sixteen healthy, full-term 8- to 9.5-month old infants participated (7 females; age range: 8 months, 2 days to 9 months, 12 days; mean age 8 months, 19 days). Nine additional infants were excluded from the analysis (2 for parental interference, 4 for fussiness, 2 for looking more than 3 SDs from the group mean on one or more test trials, and 1 for an abnormal habituation pattern.
Stimuli and Design
Infants were habituated to arrays containing 5 red dots intermixed with 5 yellow dots. Following habituation infants saw Discriminable and Non-Discriminable test arrays that always contained only grey dots that were of identical size to those seen during habituation. On Discriminable test trials the total number of dots onscreen doubled from what it had been during habituation (i.e., changed from 10 to 20). On Non-Discriminable test trials the total number of dots changed by a 5:7 ratio (i.e., changed from 10 to 14; see Table 2)—a ratio known not to be discriminable to infants of this age (Lipton & Spelke, 2003; F. Xu & Arriaga, 2007).
Table 2.
Numerical ratios presented to infants in Experiment Series 2
| Habituation | Test | ||
|---|---|---|---|
| Discriminable | Non-Discriminable | ||
| # of dots | # of dots (Habituation:Test Ratio) | ||
| Experiment 2a | |||
| Subset A | 5 | - | - |
| Subset B | 5 | - | - |
| Superset | 10 | 20 (.50) | 14 (.71) |
| Experiment 2b | |||
| Subset A | 8 | - | - |
| Subset B | 7 | - | - |
| Subset C | 7 | - | - |
| Superset | 22 | 44 (.50) | 31 (.71) |
| Experiment 2c | |||
| Subset A | 8 | - | - |
| Subset B | 7 | - | - |
| Subset C | 7 | - | - |
| Subset D | 8 | - | - |
| Superset | 30 | 60 (.50) | 40 (.71) |
Note. The number in parenthesis is the relationship between the habituation and test display (obtained by dividing the number of dots shown during habituation by the number of dots shown during test). The finest ratio that 9-month old infants have been shown to discriminate is 2:3 (0.66; Lipton & Spelke, 2003; Lipton & Spelke, 2004).
Results and Discussion
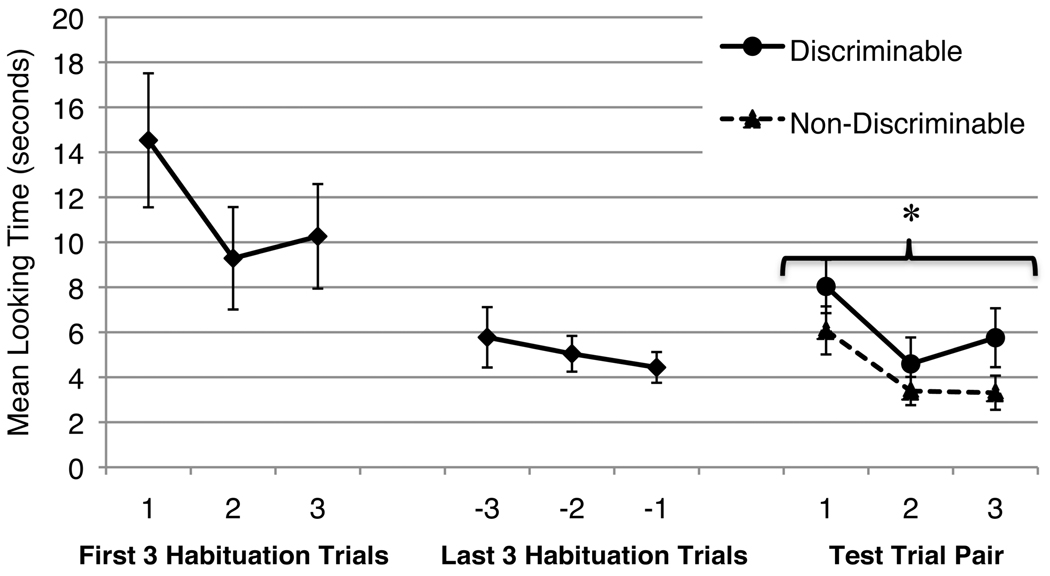
Figure 5 shows infants’ average looking across habituation and test trials. Infants’ looking times were analyzed using a 2 (Trial Type: Discriminable or Non-Discriminable) × 3 (Test Trial Pair) analysis of variance (ANOVA). This revealed a main effect of Trial Type, F (1,15) = 6.73, p < 0.05, ηp2 = 0.31. Infants looked longer at the Discriminable test arrays (M = 5.40 seconds) than at the Non-Discriminable test arrays (M = 3.76 seconds). There was also a main effect of Test Trial Pair, F (1,15) = 8.33, p < 0.01, ηp2 = 0.36, reflecting infants’ general decrease in looking across the 3 test trial pairs.
Figure 5.
Mean looking times in Experiment 2a. Error bars represent standard errors. The asterisk reflects a main effect of Trial Type across all 3 Test Trial Pairs.
The results of Experiment 2a suggest that when presented with an array containing two subsets, infants, like adults, store a representation of the superset of all items in memory. Because the habituation arrays in Experiment 1a and Experiment 2a were nearly identical, and because infants did not know during habituation whether they would be probed on a subset or on the superset of the array, the combined results of Experiments 1a and 2a suggest that infants simultaneously represented 2 subsets and the superset of the array; a total of 3 ensembles.
Experiment 2b: three subsets and the superset
As described earlier, a notable aspect of adults’ performance in memory tasks involving ensembles is that adults appear automatically to represent the superset of the array, regardless of the number of subsets presented (Halberda et al., 2006). This raises the question of whether infants also store information about the superset of an array when presented with more subsets than they can remember. To address this question, we showed infants habituation arrays containing 3 spatially intermixed subsets (like those in Experiment 1b, in which infants failed to enumerate 3 subsets), then tested them with arrays containing only grey dots.
Method
Participants
Sixteen healthy, full-term 8- to 9.5-month old infants participated (12 females; age range: 8 months, 5 days to 9 months, 12 days; mean age 8 months, 23 days). Five additional infants were excluded from the analysis (1 for parental interference, 1 for fussiness, and 3 for looking more than 3 SDs from the group mean on one or more test trials).
Stimuli and Design
Infants were habituated to arrays nearly identical to those used in Experiment 1b, containing one subset of 8 dots and two subsets of 7 dots each, totalling 22 dots. Following habituation infants saw Discriminable and Non-Discriminable test arrays that contained only grey dots. On Discriminable test trials the total number of dots doubled from what it had been during habituation (i.e., changed from 22 dots to 44 dots). On Non-Discriminable test trials the total number of dots changed by a 22:31 ratio (i.e., changed from 22 dots to 31 dots; see Table 2), a ratio known not to be discriminable to infants of this age (Lipton & Spelke, 2003; F. Xu & Arriaga, 2007).
Results and Discussion
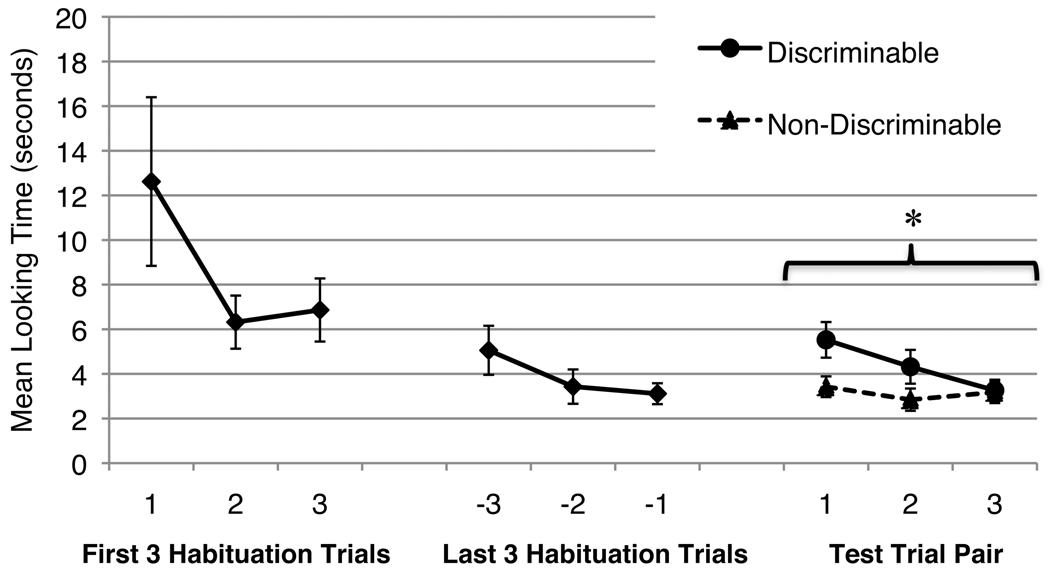
Figure 6 shows infants’ average looking across habituation and test trials. Infants’ looking times were analyzed using a 2 (Trial Type: Discriminable or Non-Discriminable) × 3 (Test Trial Pair) analysis of variance (ANOVA). This revealed a main effect of Trial Type, F (1,15) = 5.66, p < 0.05, ηp2 = 0.27. Infants looked longer at the Discriminable test arrays (M = 6.13 seconds) than at the Non-Discriminable test arrays (M = 4.26 seconds). There was also a main effect of Test Trial Pair, F (1,15) = 4.91, p < 0.05, ηp2 = .25, reflecting infants’ general decrease in looking over the three test trial pairs.
Figure 6.
Mean looking times in Experiment 2b. Error bars represent standard errors. The asterisk reflects a main effect of Trial Type across all 3 Test Trial Pairs.
Combined with Experiment 1b, Experiment 2b shows that infants represent and enumerate the superset of all items even when the array contains too many subsets to represent individually. In adults, superset representation remains robust even when the array contains far too many subsets to represent individually (6 subsets; Halberda et al., 2006). In Experiment 2c we sought to replicate this finding by presenting infants with arrays containing 4 color subsets and testing their response to a change in the superset. Experiment 2c also was critical to ruling out the possibility that infants’ success in Experiments 2a and 2b stemmed from infants separately representing the colored subsets, and later summing them to achieve a representation of the numerosity of the superset. This is a possible interpretation of Experiments 2a and 2b because in those experiments the number of subsets presented to infants was 3 or fewer, and hence never exceeded the 3-item capacity limit of working memory. By presenting infants with too many subsets to separately represent (4 subsets) and asking whether they still represent the superset, we can ask whether infants encoded and remembered the superset directly.
Experiment 2c: four subsets and the superset
Method
Participants
Sixteen healthy, full-term 8- to 9.5-month old infants participated (7 females; age range: 8 months, 8 days to 9 months, 14 days; mean age 8 months, 26 days). Thirteen additional infants were excluded from the analysis (5 for parental interference, 4 for fussiness, and 4 for looking more than 3 SDs than the group mean on one or more test trials).
Stimuli and Design
Infants were habituated to arrays containing 4 subsets, nearly identical to those in Experiment 1c: two subsets of 8 dots each and two subsets of 7 dots each, totalling 30 dots. On Discriminable test trials the total number of dots doubled from what it had been during habituation (i.e., 30 changed to 60 total dots). On Non-Discriminable test trials the total number of dots changed by a 5:7 ratio (30 changed to 42 total dots; see Table 2), a ratio known not to be discriminable to infants of this age (Lipton & Spelke, 2003; F. Xu & Arriaga, 2007).
Results and Discussion
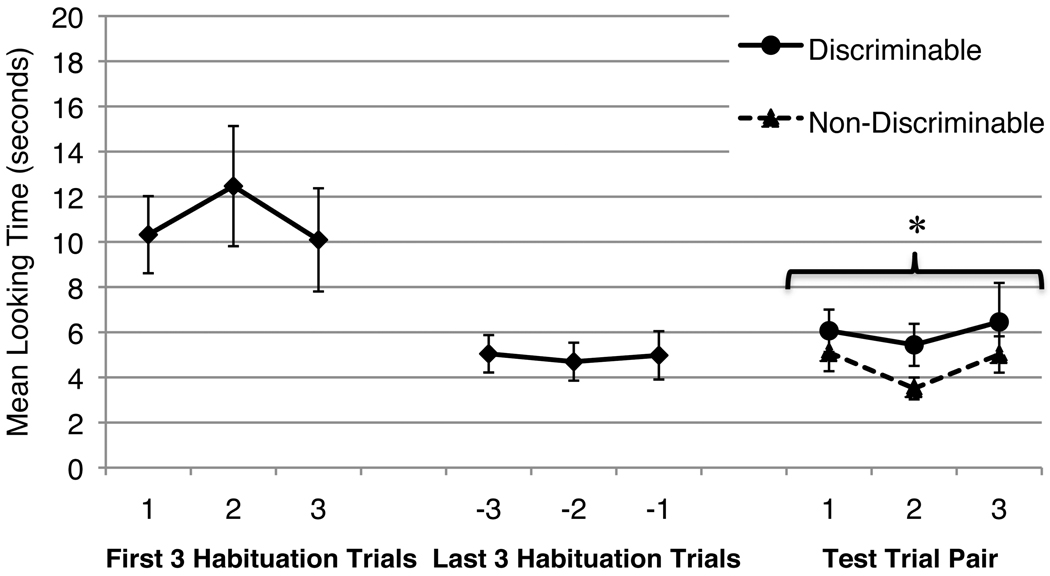
Figure 7 shows infants’ average looking across habituation and test trials. Infants’ looking times were analyzed using a 2 (Trial Type: Discriminable or Non-Discriminable) × 3 (Test Trial Pair) analysis of variance (ANOVA). This revealed a main effect of Trial Type, F (1,15) = 6.66, p < 0.05, ηp2 = 0.31. Infants looked longer at the Discriminable test arrays (M = 4.37 seconds) than at the Non-Discriminable test arrays (M = 3.15 seconds). There were no other main effects or interactions.
Figure 7.
Mean looking times in Experiment 2c. Error bars represent standard errors. The asterisk reflects a main effect of Trial Type across all 3 Test Trial Pairs.
Recall that in Experiments 1b (3 subsets) and 1c (4 subsets), infants failed to detect a numerical change to one of the color subsets in the array. In Experiments 2b (3 subsets) and 2c (4 subsets), the habituation arrays shown to infants were nearly identical to those in Experiments 1b and 1c, yet infants responded to a numerical change to the superset. To ask whether changing the superset instead of a subset significantly affected infants’ performance, we conducted a 2 (Condition: Subset change or Superset change) × 2 (Trial Type: Discriminable or Non-Discriminable) × 2 (Number of Subsets: 3 or 4) ANOVA. This yielded an interaction between Condition and Trial Type, F (1,60) = 6.98, p < .01, ηp2 = 0.10, and no other significant effects. Infants in Experiments 2b and 2c, who saw the superset of all dots change, looked longer at Discriminable than Non-Discriminable test trials. In contrast, infants in Experiments 1b and 1c, who saw one color subset change, showed no preference.
General Discussion of Experiment Series 2
Experiment Series 2 reveals another striking similarity between infants’ and adults’ memory for ensembles. Like adults, infants in Experiments 2a, 2b, and 2c successfully represented the superset of the array even when the number of subsets exceeded their memory capacity. Because infants had no way of knowing during habituation that the superset of all dots would double on Discriminable test trials (as opposed to one of the subsets doubling, as in Experiment Series 1), their longer looking on Discriminable test trials suggests that they had automatically encoded the numerosity of the superset regardless of the number of subsets present. Based on these results, it appears that for infants, just as for adults (Halberda et al., 2006), an ensemble reprensentation of the superset occupies one “slot” in memory, leaving two remaining slots available by which to represent subsets (N.B. the notion of “slot” here is used simply for illustration, and is not meant to imply a commitment to a particular model of working memory storage).
Our experiments were designed to rule out several alternative explanations for infants’ success. First, our design ruled out the possibility that infants summed the numerosities of the subsets rather than representing the superset directly. Not only does infants’ failure to represent the numerosity of 3 and 4 subsets in Experiments 1b and 1c suggest that infants could not have summed the necessary subsets, but Experiment 2c shows that infants represented the superset even when presented with a number of subsets that exceeded their 3-item working memory capacity. Second, our design rules out that the pattern of observed performance simply reflected a preference to look at arrays with greater numbers of dots during test, ignoring the habituation displays. Although it is true that in Experiment Series 2 the Discriminable test arrays always contained more total dots than the Non-Disciminable test arrays, the numerical difference between the Discriminable and Non-Discriminable test arrays is known to be too small to be consistently detected by infants of this age (i.e., the ratio of Discriminable to Non-Discriminable was 20:14 in Exp 2a, 44:31 in Exp 2b, and 60:42 in Exp 2c). At 9 months, infants require at least a 2:3 ratio to detect a numerical difference between two arrays (Xu & Arriaga, 2007). Only in Experiment 2c was the ratio difference between the Discriminable and Non-Discriminable test trials nearing this value leaving this account unable to explain infants’ success in Experiments 2a and 2b. Therefore, it appears that infants must have represented the numerosity of the superset of dots during habituation, and compared this to the numerosities displayed during test trials. Infants were able to do this regardless of the number of subsets presented.
One other possible concern is that the total number of dots in the array (i.e., the number of dots in the superset) was larger in Experiments 1b and 1c than in Experiment 1a (i.e., during habituation there were 12 dots in Experiment 1a, 20 in Experiment 1b, and 20 in Experiment 1c). This raises the possibility that infants failed to detect numerical changes to the subsets in Experiments 1b and 1c because they were overwhelmed by the total number of dots onscreen, rather than because they were limited to representing 3 ensembles in memory. However, two findings argue against this interpretation. First, in previous studies, infants younger than those tested here successfully discriminated a change to a single group containing even larger numbers of dots (i.e., 32 dots in the studies by F. Xu et al., 2005), and successfully abstracted ratios from arrays containing up to 50 dots (McCrink & Wynn, 2007). Second, and perhaps more convincingly, infants succeeded at enumerating the superset of all dots in Experiments 2b and 2c, both of which involved test arrays with larger total numerosities than those with which infants failed in Experiments 1b and 1c (i.e., during habituation there were 22 dots in Experiment 2b and 30 dots in Experiment 2c). In this way, infants’ success in Experiments 2b and 2c enrich our understanding of their failure in Experiments 1b and 1c.
Finally, we note that throughout Experiments Series 1 and 2, the size of the individual dots comprising the ensembles remained constant throughout habituation and test trials. As such, numerosity was confounded with cumulative surface area and other measures of continuous extent (e.g., cumulative circumference, luminance). It therefore is possible that infants in Experiment 1a and Experiments 2a, 2b, and 2c were responding to a change in the total continous extent of one of the ensembles rather than to a change in its numerosity. Indeed, recent work suggests that adults represent multiple different quantitative features when shown visual arrays like those used in the present experiments. Adults represent the average numerosity of ensembles (Halberda et al 2006, Ross & Burr, 2010), mean size of the items comprising ensembles (Ariely, 2001; Chong & Treisman, 2003, 2005; Chong et al., 2008), average orientation of items in ensembles (Parkes et al, 2001), density of ensembles (Ross & Burr, 2010), and the average location of ensembles (Alvarez & Oliva, 2008), and adults can represent multiple features from a single ensemble (e.g., average size and average orientation; Emmanouil & Treisman, 2008). These findings raise the possibility that infants, too, might represent multiple quantitative features of an attended ensemble. Previous work has found that infants respond to changes in numerosity when continuous extent is controlled (e.g., Brannon et. al. 2004, Cordes & Brannon, 2008, Lipton & Spelke, 2003, F. Xu & Spelke, 2000; F. Xu, et al., 2005), and respond to changes in continuous extent when number is controlled (Cordes & Brannon, 2008; Feigenson, Carey, & Spelke, 2002; Clearfield & Mix, 1999). Furthermore, both infants (Cordes & Brannon, 2009) and adults (Hurewitz, Gelman, & Schnitzer, 2006) appear able to represent both number and continuous extent simultaneously.
Regardless of whether infants in the present expriments were responding on the basis of number or area, the implications for attention and memory remain the same. In order to represent either of these quantitative features, the ensemble itself had to be attended and maintained in memory. Our results show that infants can attend and remember multiple ensembles at once, and that like adults, infants prioritize storage of the superset. When the number of subsets shown exceeds infants’ memory capacity, our framework predicts that neither number nor area is represented for the subsets. But when the number of ensembles present is within the capacity of working memory, we predict that infants can represent either number or area.
Experiment 3: number vs. area in infants’ ensemble representations
We tested this prediction in Experiment 3, in which we asked whether infants represent approximate number (in displays controlled for cumulative area) and approximate area (in displays controlled for number) of two ensemble subsets. We focused on approximate number and approximate cumulative area because these are features that have been well studied in previous investigations of infants’ visual representations.
We presented infants with arrays containing two colored subsets (like those in Experiments 1a and 2a). For half of the infants we controlled for cumulative surface area and asked whether infants would respond to a change in the numerosity of one of the subsets. For the other half of infants we controlled for number and asked whether infants would respond to a change in cumulative surface area of one of the subsets.
Method
Participants
Twenty healthy full-term 8- to 9.5-month old infants participated (11 females; age range: 8 months, 3 days to 9 months, 14 days; mean age 8 months, 21 days). Three additional infants were excluded from analysis (2 for parental interference and 1 for fussiness).
Stimuli and Design
Infants were habituated to displays similar to those in Experiment 1a. We randomly assigned infants to either the Number or the Surface Area condition. Infants in the Number condition saw arrays in which the numerosity of each of the two subsets remained constant across habituation, whereas the cumulative surface area of the subsets varied from trial to trial. This was designed to make it more difficult for infants to form a stable representation of surface area during habituation, thereby increasing the likelihood that they would attend to number. At test, surface area was controlled such that the Discriminable and Non-Discriminable arrays were equally novel in terms of the cumulative surface area of the two subsets. As such, the numerical doubling of the target subset on the Discriminable test trials was the only feature that differentiated Discriminable from Non-Discriminable arrays (and importantly, the target subset doubled in number, but not in cumulative area).
Infants in the Surface Area condition saw arrays in which the cumulative surface area of each of the two subsets remained constant across habituation, whereas the total number of dots in each subset varied from trial to trial. This was designed to make it more difficult for infants to form a stable representation of number during habituation, thereby increasing the likelihood that they would attend to area. At test, number was controlled such that the Discriminable and Non-Discriminable arrays were equally novel in terms of the numerosity of the two ensembles. The doubling of the cumulative area of the target subset on the Discriminable test trials was the only feature that differentiated the two trial types (and importantly, the target subset doubled in area, but not in number).
Stimuli and Design: Number Condition
In the Number Condition, the number of dots comprising each color subset remained constant across habituation trials whereas the cumulative surface area of both color subsets varied. There were 3 possible cumulative surface areas for each subset: 25 cm2, 35 cm2, and 45 cm2. These 3 surface area values were crossed for the red and yellow subsets (e.g, for arrays containing 25 cm2 of red dots there were 3 pairings: one with 25 cm2 of yellow dots, one with 35 cm2 of yellow dots, and one with 45 cm2 of yellow dots), creating a total of 9 possible habituation arrays. During habituation infants saw these 9 arrays in random order without replacement. If infants required more than 9 trials to habituate, additional arrays were randomly chosen from these original 9. Finally, individual dot size varied both within a single habituation array and across habituation arrays to dissuade responses based on this factor.
At test infants were shown novel arrays. As in Experiment 1a, infants saw Discriminable test trials in which the numerosity of the 5-dot collection changed to 10, and the numerosity of the 7-dot collection remained unchanged. These alternated with Non-Discriminable test trials in which the numerosity of the 5-dot collection changed to 7, and the numerosity of the 7-dot collection changed to 10 (both ratios known not to be discriminable to infants of this age; see Table 3). Unlike in Experiment 1a, for both Discriminable and Non-Discriminable trials the two subsets shown at test always had novel cumulative surface areas (either 30 cm2 or 40 cm2) that were chosen to be equidistant from the average cumulative surface area seen during habituation (35 cm2). As such, the Discriminable and Non-Discriminable test trials were equally novel in terms of area. There were 4 possible arrangements of surface area. One had a red subset surface area of 30 cm2 paired with a yellow subset surface area of 30 cm2. The second had a red subset surface area of 30 cm2 paired with a yellow subset surface area of 40 cm2. The third had a red subset surface area of 40 cm2 paired with a yellow subset surface area of 40 cm2. And the fourth had a red subset surface area of 40 cm2 paired with a yellow subset surface area of 30 cm2. Each infant saw 3 of these 4 possible surface area arrangements (chosen randomly), paired with a doubling of numerosity (Discriminable test trials), as well as 3 of the 4 possible surface area arrangements paired with a non-discriminable change in numerosity (Non-Discriminable test trials). Because changes in cumulative surface area were controlled for, any preference to look more on the Discriminable test trials would suggest a response to number.
Stimuli and Design: Area Condition
Infants in the Area condition saw similar displays, except that the cumulative surface area of the dots comprising each color subset remained constant across habituation trials whereas the numerosity of both color subsets varied. There were 3 possible numerosities for each subset during habituation: 5, 7, and 9. These 3 numerosities were crossed for the red and yellow subsets (e.g, for arrays containing 5 red dots there were 3 pairings: one with 5 yellow dots, one with 7 yellow dots, and one with 9 yellow dots), creating a total of 9 possible habituation arrays. As in the Number Condition, during habituation infants saw these 9 arrays in random order without replacement. Finally, individual dot size varied both within a single habituation array and across habituation arrays to dissuade responses based on this factor. If infants required more than 9 trials to habituate, additional arrays were randomly chosen from these original 9.
At test infants were shown novel arrays. These contained Discriminable test trials in which the cumulative surface area of one subset changed from 15 cm2 to 30 cm2, and the cumulative surface area of the other subset remained unchanged. These alternated with Non-Discriminable test trials in which the cumulative surface area of one subset changed from 15 cm2 to 21 cm2, and the cumulative surface area of the other subset changed from 21 cm2 to 30 cm2 (both ratios which are known not to be discriminable to infants of this age; see Table 3). Unlike in Experiment 1a, for both Discriminable and Non-Discriminable trials the two subsets shown at test always had novel numerosities (either 6 or 8) that were chosen to be equidistant from the average numerosity seen during habituation (7). As such, the Discriminable and Non-Discriminable test trials were equally numerically novel. There were 4 possible arrangements of numerosity. One had a red subset numerosity of 6 paired with a yellow subset numerosity of 6. The second had a red subset numerosity of 6 paired with a yellow subset numerosity of 8. The third had a red subset numerosity of 8 paired with a yellow subset numerosity of 6. And the fourth had a red subset numerosity of 8 paired with a yellow subset numerosity of 8. Each infant saw 3 of these 4 possible numerosity arrangements (randomly chosen), paired with a doubling of surface area (Discriminable test trials), as well as 3 of the 4 possible numerosity arrangements paired with a non-discriminable change in surface area (Non-Discriminable test trials). Because changes in numerosity were controlled for, any preference to look more on the Discriminable test trials would suggest a response to cumulative surface area.
Results and Discussion
Figure 8 shows infants’ average looking across habituation and test trials. Infants’ looking times were analyzed using a 2 (Condition: Number or Area) × 2 (Trial Type: Discriminable or Non-Discriminable) × 3 (Test Trial Pair) analysis of variance (ANOVA). This revealed a main effect of Trial Type, F (1,18) = 4.79, p < 0.05, ηp2 = 0.21. Infants looked longer at the Discriminable test arrays (M = 5.47 seconds) than at the Non-Discriminable test arrays (M = 4.10 seconds). Imporantly, there was no significant effect of Condition, F (1,18) = .089, p = 0.77, ηp2 = 0.01, nor a Condition×Trial Type interaction, F (1,18) = .01, p = 0.91, ηp2 = 0.001. Infants looked longer at the Discriminable test arrays than the Non-Discriminable test arrays whether they were in the Number Condition (Discriminable mean looking = 5.67 seconds, Non-Discriminable mean looking = 4.20 seconds) or in the Area Condition (Discriminable mean looking = 5.28 seconds, Non-Discriminable mean looking = 4.01 seconds) suggesting that infants were able to rely upon either cumulative surface area or numerosity changes to notice a change at test.
Figure 8.
Mean looking times in Experiment 3. Error bars represent standard errors. The asterisk reflects a main effect of Trial Type across all 3 Test Trial Pairs.
These results suggest that infants can represent either the discrete numerosity or the continuous surface area of an ensemble. Because infants in Experiment 3 had no way of knowing during habituation whether the red subset or the yellow subset was going to change (in numerosity or in surface area), their success in both the Number and Area Conditions implies that they represented the numerosity or the cumulative surface area of at least two ensembles simultaneously. This result is consistent with studies showing that adults presented with a single ensemble can represent a variety of summary features (Ariely, 2001; Alvarez & Oliva, 2008; Chong & Treisman, 2003, 2005; Emmanouil & Treisman, 2008; Halberda et al, 2006).
The results of Experiment 3 raise several questions for further exploration. The first is whether infants in Experiment 3 represented the numerosity and the cumulative area of the superset of all dots, in addition to the numerosity and area of the two subsets. Based on the results of Experiment Series 2, we predict that infants would succeed if tested with the superset using displays similar to those in Experiment 3. A second question is whether infants in Experiment Series 1 and 2 were responding to changes in numerosity, in cumulative surface area or in both. Although Experiment 3 cannot answer this question, it does show that infants are capable of responding to changes in either of these quantitative features (see also Cordes & Brannon, 2008; 2009). In Experiment 3, we designed the stimuli in order to make it more likely that infants would represent either number (in the Number Condition) or surface area (in the Area Condition). We did this by holding one quantitative feature constant across habituation trials while varying the other, in order to direct infants’ attention to the feature of interest. It remains unknown whether this manipulation was actually required for infants’ success. One way to test this would be to show infants identical habituation sequences, and then to test half of the infants with a change in numerosity (with surface area controlled) and the other half of infants with a change in surface area (with numerosity controlled). Success at this would demonstrate simultaneous representation of numerosity and surface area for multiple ensembles. Given infants’ successful representation of both number and area in arrays with only one ensemble (Cordes & Brannon, 2009), we think it likely that infants also would represent both number and area when shown multiple ensembles. However, we note that research suggests that infants have a more precise representation of approximate number than of approximate cumulative area (Cordes & Brannon, 2008; 2009).
General Discussion
Together, the present experiments comprise the first investigation of infants’ ability to store multiple representations of ensembles in memory. Previous studies have found that both infants and adults can represent up to 3 individual objects in working memory (adults: Alvarez & Cavanagh, 2004; Broadbent, 1975; Cowan, 2001; Jiang et al., 2000; Luck & Vogel, 1997; Song & Jiang, 2006; Sperling, 1960; Y. Xu, 2002; Y. Xu & Chun, 2006; infants: Barner et al., 2007; Feigenson, 2005; Feigenson & Carey, 2003, 2005; Feigenson et al., 2002; Feigenson & Halberda, 2004; Ross-Sheehy et al., 2003). For adults the number of non-object ensembles that can be remembered is also 3 (Feigenson, 2008; Halberda et al., 2006), suggesting that the 3-item limit of working memory is not restricted to objects but rather applies more broadly to various types of individual entities.
Here we asked whether untrained, pre-verbal infants also can represent multiple ensembles, and if so whether the limit on this ability would converge with the limit on infants’ ability to represent individual objects. Experiment Series 1 showed that infants, like adults, can store representations of 2 subsets from a single array, where the subsets were distinctively colored collections of spatially intermixed dots. However, infants failed to remember 3 or 4 such subsets, convergent with the performance of adults with similar displays (Halberda et al, 2006). Experiment Series 2 suggests that infants, like adults, automatically encode the superset of the array (i.e., the total number of dots across all subsets), even when the number of subsets presented exceeds working memory capacity. Finally, Experiment 3 suggests that memory representations of ensembles can support infants’ computations of either approximate number or or approximate cumulative area. Hence, the experiments we report here offer evidence of striking parallels in processing by infants and adults.
Of course, the above conclusions require ruling out other potential explanations for the observed pattern of infants’ success and failure. One such concern is that perhaps infants failed to enumerate subsets when 3 or 4 color subsets were presented not because of constraints on the number of ensembles that could be maintained in memory, but rather because increasing the number of colors in the display made it harder for infants to attentively select subsets on the basis of color. The color values we used were very similar to those used in the displays of Halberda et al (2006). Halberda and colleagues found that when adults were told which color would be queried prior to display onset, they performed just as well at selecting and enumerating a color subset in displays containing 4, 5, or 6 colors as they did with displays containing 2 or 3 colors. That selection based on color was quite easy for adults with these multi-colored displays argues against the interpretation that selection of color subsets was more difficult in Experiments 1b and 1c than in the other experiments. In addition, one previous experiment with infants provides more direct evidence for this conclusion. In that experiment, 10-month old infants saw arrays contanining either 3 or 6 differently colored squares, briefly flashed. When given a pre-cue to attend to a particular square, infants succeeded at detecting a subsequent change to that square’s color. This was true for both 3- and 6-square arrays. However, without the pre-cue infants only detected a change to the 3-square arrays (Ross-Sheehy et al., 2003). The finding that infants can direct attention to specific items within a 6-object array suggests that infants, like adults, can perform efficient selection even when presented with numbers of colors that exceed working memory capacity (Ross-Sheehy, 2005). Based on these previous findings, we suggest that infants performed like adults with the displays in our experiments: although selection from 3- and 4-color subsets was possible, performance deteriorated because the capacity limit of working memory had been exceeded.
Perhaps the most striking issue raised by our present results with infants, and by previous results with adults (Feigenson, 2008; Halberda et al., 2006), is the question of how working memory can be limited to storing up to 3 individual objects in parallel (e.g., Luck & Vogel, 1997), and yet, under different circumstances, can store not just one but multiple ensemble representations, each containing many more than 3 objects. Our answer to this puzzle is that each ensemble functions as an individual entity for visual attention and working memory. Support for this suggestion is two-fold. First, the agreement between the object-based limit of working memory capacity and the ensemble-based limit demonstrated here suggests a common storage constraint. As we noted earlier, both infants and adults have been shown to remember at most 3 or 4 individual objects in paradigms that measure working memory capacity. Here we found that infants can remember 3 ensembles. The agreement in these limits suggests that an ensemble takes up roughly the same amount of storage space in working memory as a single object, despite the fact that it contains multiple items. The suggestion that representing an ensemble does not require separately representing each of its components is not without precedent. At least one existing model of enumeration suggests that rather than separately individuating and then counting each item in an array, an approximate number representation is generated by collapsing across an un-individuated continuous representation of the entire array (Dehaene & Changeux, 1993). In this model, a topographical mental map represents the location of all items in the array, and a series of numerosity detectors then sums activations across all of the detected locations. Different numbers are thereby represented as continuous distributions of neural activation, with no individually represented component items. Although the feasibility of implementing this model in early vision remains an open question, recent empirical results lend support to this type of model. As described earlier, adult observers can accurately report summary information about an array, such as the average size of the items (Ariely, 2001; Chong & Treisman, 2003, 2005), their approximate number (Halberda et al., 2006), or their average spatial location (Alvarez & Oliva, 2008), while at the same time performing at or near chance at reporting information about any particular individual item in the array.
A second piece of evidence that supports our suggestion that an ensemble functions as an individual for visual attention and working memory is infants’ success at remembering ensembles, each containing many more than 3 items, in the face of their failure to remember more than 3 or 4 individual objects in similar paradigms. Ross-Sheehy and colleagues (2003) presented 10-month-old infants with arrays of 1, 2, 3, 4, or 6 different colored squares. An array of squares was visible for 500ms, disappeared for 250ms, was again visible for 500ms, and so on. On some sequences, the color of each square in the array remained constant from flash to flash. On other sequences, the color of just one of the squares changed (which square changed its color was random from one flash to the next). The question was whether infants would remember the colors of all of the squares in the array, and detect when any one of them had changed. Success was indicated by longer looking to the changing array relative to the non-changing array that contained the same number of squares. Ross-Sheehy and colleagues found that 10-month-old infants succeeded at remembering the color of 1, 2, 3, and perhaps 4 individual objects, but failed with 6 objects.2 This reveals that when more than 4 objects were present, and the task required attention and memory for each object, infants failed to remember the colors of each individual object. Therefore, if infants in our task had attempted to represent each dot in the array as an individual object, they would have failed to enumerate the red and the yellow dots because, as Ross-Sheehy et al. (2003) demonstrate, with arrays containing more than 4 dots infants would have failed to remember whether or not a particular dot was red or yellow.
A possible solution to this problem, and the solution that we favor, is that all of the dots within a particular subset (e.g., all of the yellow dots in the array) were selected in parallel as a single ensemble collection, and this ensemble then functioned as an individual for visual attention and working memory. After segmentation, approximate number could be encoded into memory as a feature of the ensemble by a parallel enumeration system (Allik & Tuulmets, 1991; Dehaene & Changeux, 1993). If an ensemble did not function as a single individual for visual attention and working memory, it is difficult to see how infants could have enumerated even one color subset (given the failure to represent the color of individual squares in the studies by Ross-Sheehy et al. [2003]), and it would be a mystery why the limit on the number of ensembles that can be enumerated turns out to be three, convergent with the limit for remembering individual items.
If an item is successfully maintained in memory, how much information is represented about that item? In the case of individual objects, some studies suggest that the answer depends on how many items are being maintained. For example, Alvarez & Cavanagh (2004) found that the number of items remembered by adults depended on whether those items were simple (like colored squares) or complex (like Chinese characters; see also Eng, Chen, & Jiang, 2005; Wilken & Ma, 2004; Y. Xu & Chun, 2006; Zosh & Feigenson, submitted). Although the existence of this type of tradeoff between memory capacity and memory resolution is controversial (see Awh, Barton, & Vogel, 2007; Bays & Husain, 2008; Scolari, Vogel, & Awh, 2008; Zhang & Luck, 2008), the question arises whether representations of ensembles might also be subject to such a tradeoff. Does maintaining representations of larger numbers of ensembles lead to coarser representations? One way to ask this using the current paradigm would be to manipulate the ratio change shown to infants. In all of the experiments reported here we asked whether infants detected a 1:2 change, which is known to be easily discriminable to 9-month old infants (Lipton & Spelke, 2003; Xu & Spelke, 2000). Might infants succeed at detecting an even finer-grained change (e.g., 2:3) when maintaining a representation of 1 or 2 ensembles, but not 3 ensembles? Furthermore, is a capacity-resolution tradeoff evident in adults’ representations of ensembles? These questions remain ripe for future testing.
In conclusion, our present findings suggest that ensemble representations function as individuals for visual attention and working memory, and that they do so across the lifespan, or at least by 9 months of age. The 3-ensemble limit we identified converges with the limit on the number of individual objects that can be attended and maintained. This convergence suggests that although working memory may be limited to storing up to 3 objects at one time, it is also flexible enough to store 3 ensembles, each containing summary information, for many more than 3 objects at a time. Thus we suggest that one of the hallmarks of working memory—its capacity limit—is moderated by a surprising degree of representational flexibility that is in place from early in development.
Acknowledgments
We thank Rachel Austin, Catia Cividini, Bernice Chiang, Jaeeun Chung, Alexandra Cork, Kelli Hill, Jennifer Jimenez, Catherine Juravich, Katherine Muenks, Andrea Stevenson, Allison Wessell, Mariko Moher, and Katherine Young for their help in data collection and coding. This work was supported by National Institutes of Health (NIH) grant NIH R01 HD057258 to L.F. and J.H. and a James S. McDonnell Foundation Scholar Award to L.F.
This work was completed as a portion of the dissertation of J.M.Z.
Footnotes
Publisher's Disclaimer: The following manuscript is the final accepted manuscript. It has not been subjected to the final copyediting, fact-checking, and proofreading required for formal publication. It is not the definitive, publisher-authenticated version. The American Psychological Association and its Council of Editors disclaim any responsibility or liabilities for errors or omissions of this manuscript version, any version derived from this manuscript by NIH, or other third parties. The published version is available at www.apa.org/pubs/journals/xge
Early studies using MOT also suggested that such object tracking was capacity-limited, in that only 3–4 objects could be tracked at once (Pylyshyn & Storm, 1988). However, more recent investigations suggest that attentive tracking may instead be resource-limited, as performance depends on factors such as the speed at which objects move (Alvarez & Franconeri, 2007) and their degree of crowding (Franconeri, Jonathan, & Scimeca, 2010).
As with similar studies with adults (e.g., Luck & Vogel, 1997), the statistical success on 4-object trials could result from storing only three of the four objects in memory, and recognizing a change on an average of three-fourths of all of the flickering arrays across the duration of the experiment. Thus, the 4-object success is consistent with infants storing at least 3 and perhaps 4 objects in memory.
Contributor Information
Jennifer M. Zosh, Department of Human Development & Family Studies, The Pennsylvania State University, Brandywine
Justin Halberda, Department of Psychological and Brain Sciences, Johns Hopkins University.
Lisa Feigenson, Department of Psychological and Brain Sciences, Johns Hopkins University.
References
- Allik J, Tuulmets T. Occupancy Model of Perceived Numerosity. Perception & Psychophysics. 1991;49(4):303–314. doi: 10.3758/bf03205986. [DOI] [PubMed] [Google Scholar]
- Alvarez GA, Cavanagh P. The Capacity of Visual Short-Term Memory Is Set Both by Visual Information Load and by Number of Objects. Psychological Science. 2004;15(2):106–111. doi: 10.1111/j.0963-7214.2004.01502006.x. [DOI] [PubMed] [Google Scholar]
- Alvarez GA, Franconeri SL. How many objects can you track? Evidence for a resource-limited attentive tracking mechanism. Journal of Vision. 2007;7(13):1, 10. doi: 10.1167/7.13.14. 14. [DOI] [PubMed] [Google Scholar]
- Alvarez GA, Oliva A. The representation of simple ensemble visual features outside the focus of attention. Psychological Science. 2008;19(4):392–398. doi: 10.1111/j.1467-9280.2008.02098.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alvarez GA, Oliva A. Spatial ensemble statistics are efficient codes that can be represented with reduced attention. Proceedings of the National Academy of Sciences of the United States of America. 2009;106(18):7345–7350. doi: 10.1073/pnas.0808981106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ariely D. Seeing sets: representation by statistical properties. Psychological Science. 2001;12(2):157–162. doi: 10.1111/1467-9280.00327. [DOI] [PubMed] [Google Scholar]
- Awh E, Barton B, Vogel EK. Visual working memory represents a fixed number of items, regardless of complexity. Psychological Science. 2007;18:622–628. doi: 10.1111/j.1467-9280.2007.01949.x. [DOI] [PubMed] [Google Scholar]
- Barner D, Thalwitz D, Wood J, Yang SJ, Carey S. On the relation between the acquisition of singular-plural morpho-syntax and the conceptual distinction between one and more than one. Developmental Science. 2007;10(3):365–373. doi: 10.1111/j.1467-7687.2007.00591.x. [DOI] [PubMed] [Google Scholar]
- Barth H, Kanwisher N, Spelke ES. The construction of large number representations in adults. Cognition. 2003;86(3):201–221. doi: 10.1016/s0010-0277(02)00178-6. [DOI] [PubMed] [Google Scholar]
- Bays PM, Husain H. Dynamic shifts of limited working memory resources in human vision. Science. 2008;321:851–854. doi: 10.1126/science.1158023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brannon EM, Abbott S, Lutz DJ. Number bias for the discrimination of large visual sets in infancy. Cognition. 2004;93(2):59–68. doi: 10.1016/j.cognition.2004.01.004. [DOI] [PubMed] [Google Scholar]
- Brannon EM, Lutz D, Cordes S. The development of area discrimination and its implications for number representation in infancy. Developmental Science. 2006;9(6):59–64. doi: 10.1111/j.1467-7687.2006.00530.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brannon EM, Suanda S, Libertus K. Temporal discrimination increases in precision over development and parallels the development of numerosity discrimination. Developmental Science. 2007;10(6):770–777. doi: 10.1111/j.1467-7687.2007.00635.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Broadbent DE. The magic number seven after fifteen years. In: Kennedy A, Wilkes A, editors. Studies in Long-Term Memory. John Wiley & Sons; 1975. pp. 3–18. [Google Scholar]
- Cheries EW, Mitroff SR, Wynn K, Scholl BJ. Cohesion as a constraint on object persistence in infancy. Developmental Science. 2008;11(3):427–432. doi: 10.1111/j.1467-7687.2008.00687.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chiang WC, Wynn K. Infants' tracking of objects and collections. Cognition. 2000;77(3):169–195. doi: 10.1016/s0010-0277(00)00091-3. [DOI] [PubMed] [Google Scholar]
- Chong SC, Treisman A. Representation of statistical properties. Vision Research. 2003;43(4):393–404. doi: 10.1016/s0042-6989(02)00596-5. [DOI] [PubMed] [Google Scholar]
- Chong SC, Treisman A. Statistical processing: computing the average size in perceptual groups. Vision Research. 2005;45(7):891–900. doi: 10.1016/j.visres.2004.10.004. [DOI] [PubMed] [Google Scholar]
- Chong SC, Joo SJ, Emmanouil T-A, Treisman A. Statistical processing: Not so implausible after all. Perception and Psychophysics. 2008;70(7):1327–1334. doi: 10.3758/PP.70.7.1327. [DOI] [PubMed] [Google Scholar]
- Clearfield MW, Mix KS. Number versus contour length in infants' discrimination of small visual sets. Psychological Science. 1999;10(5):408–411. [Google Scholar]
- Cordes S, Brannon EM. The difficulties of representing continuous extent in infancy: Using number is just easier. Child Development. 2008;79(2):476–489. doi: 10.1111/j.1467-8624.2007.01137.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cordes S, Brannon EM. The relative salience of discrete and continuous quantity in young infants. Developmental Science. 2009;12(3):453–463. doi: 10.1111/j.1467-7687.2008.00781.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cowan N. The magical number 4 in short-term memory: A reconsideration of mental storage capacity. Behavioral and Brain Sciences. 2001;24(1):87–114. doi: 10.1017/s0140525x01003922. [DOI] [PubMed] [Google Scholar]
- Dehaene S. Number Sense: How the Mind Creates Mathematics. Oxford University Press; 1997. The adult number line; pp. 64–88. [Google Scholar]
- Dehaene S, Changeux J-P. Development of elementary numerical abilities: A neuronal model. Journal of Cognitive Neuroscience. 1993;5(4):390–407. doi: 10.1162/jocn.1993.5.4.390. [DOI] [PubMed] [Google Scholar]
- Eng HY, Chen D, Jiang Y. Visual working memory for simple and complex visual stimuli. Psychonomic Bulletin and Review. 2005;12:1127–1133. doi: 10.3758/bf03206454. [DOI] [PubMed] [Google Scholar]
- Emmanouil TA, Treisman A. Dividing attention across feature dimensions in statistical processing of perceptual groups. Perception & Psychophysics. 2008;70(6):946–954. doi: 10.3758/pp.70.6.946. [DOI] [PubMed] [Google Scholar]
- Fantz RL. Visual Experience in infants: Decreased attention to familiar patterns relative to novel ones. Science. 1964;146:668–670. doi: 10.1126/science.146.3644.668. [DOI] [PubMed] [Google Scholar]
- Feigenson L. A double-dissociation in infants' representations of object arrays. Cognition. 2005;95(3):B37–B48. doi: 10.1016/j.cognition.2004.07.006. [DOI] [PubMed] [Google Scholar]
- Feigenson L. Parallel non-verbal enumeration is constrained by a set-based limit. Cognition. 2008;107:1–18. doi: 10.1016/j.cognition.2007.07.006. [DOI] [PubMed] [Google Scholar]
- Feigenson L, Carey S. Tracking individuals via object-files: evidence from infants' manual search. Developmental Science. 2003;6(5):568–584. [Google Scholar]
- Feigenson L, Carey S. On the limits of infants' quantification of small object arrays. Cognition. 2005;97(3):295–313. doi: 10.1016/j.cognition.2004.09.010. [DOI] [PubMed] [Google Scholar]
- Feigenson L, Carey S, Hauser M. The Representations Underlying Infants' Choice of More: Object Files Versus Analog Magnitudes. Psychological Science. 2002;13(2):150–156. doi: 10.1111/1467-9280.00427. [DOI] [PubMed] [Google Scholar]
- Feigenson L, Carey S, Spelke ES. Infants' discrimination of number vs. continuous extent. Cognitive Psychology. 2002;44:33–66. doi: 10.1006/cogp.2001.0760. [DOI] [PubMed] [Google Scholar]
- Feigenson L, Dehaene S, Spelke ES. Core systems of number. Trends in Cognitive Sciences. 2004;8(7):307–314. doi: 10.1016/j.tics.2004.05.002. [DOI] [PubMed] [Google Scholar]
- Feigenson L, Halberda J. Infants chunk object arrays into sets of individuals. Cognition. 2004;91(2):173–190. doi: 10.1016/j.cognition.2003.09.003. [DOI] [PubMed] [Google Scholar]
- Franconeri SL, Jonathan SV, Scimeca JM. Tracking multiple objects is limited only by object spacing, not by speed, time, or capacity. Psychological Science. 2010 doi: 10.1177/0956797610373935. in press. [DOI] [PubMed] [Google Scholar]
- Gallistel CR, Gelman R. Non-verbal numerical cognition: from reals to integers. Trends in Cognitive Sciences. 2000;4(2):59–65. doi: 10.1016/s1364-6613(99)01424-2. [DOI] [PubMed] [Google Scholar]
- Halberda J, Feigenson L. Developmental change in the acuity of the "Number sense": The approximate number system in 3-, 4-, 5-, and 6-year-olds and adults. Developmental Psychology. 2008;44(5):1457–1465. doi: 10.1037/a0012682. [DOI] [PubMed] [Google Scholar]
- Halberda J, Sires SF, Feigenson L. Multiple spatially overlapping sets can be enumerated in parallel. Psychological Science. 2006;17(7):572–576. doi: 10.1111/j.1467-9280.2006.01746.x. [DOI] [PubMed] [Google Scholar]
- Huntley-Fenner G, Carey S, Solimando A. Objects are individuals but stuff doesn't count: perceived rigidity and cohesiveness influence infants' representations of small groups of discrete entities. Cognition. 2002;85(3):203–221. doi: 10.1016/s0010-0277(02)00088-4. [DOI] [PubMed] [Google Scholar]
- Hurewitz F, Gelman R, Schnitzer B. Sometimes area counts more than number. Proceedings of the National Academy of Sciences. 2006;103(51):19599–19604. doi: 10.1073/pnas.0609485103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Im HY, Chong SC. Computation of mean size is based on perceived size. Attention, Perception & Psychophysics. 2009;71(2):375–384. doi: 10.3758/APP.71.2.375. [DOI] [PubMed] [Google Scholar]
- Izard V, Dehaene S. Calibrating the mental number line. Cognition. 2007 doi: 10.1016/j.cognition.2007.06.004. [DOI] [PubMed] [Google Scholar]
- Jiang Y, Olson IR, Chun MM. Organization of visual short-term memory. Journal of Experimental Psychology. 2000;26(3):683–702. doi: 10.1037//0278-7393.26.3.683. [DOI] [PubMed] [Google Scholar]
- Kahneman D, Treisman A, Gibbs BJ. The reviewing of object files: object-specific integration of information. Cognitive Psychology. 1992;24(2):175–219. doi: 10.1016/0010-0285(92)90007-o. [DOI] [PubMed] [Google Scholar]
- Lidz J, Pietroski P, Hunter T, Halberda J. Interface transparency and the psychosemantics of most. Natural Language Semantics. (in press) [Google Scholar]
- Lipton JS, Spelke ES. Origins of number sense: Large-number discrimination in human Infants. Psychological Science. 2003;14(5):396–401. doi: 10.1111/1467-9280.01453. [DOI] [PubMed] [Google Scholar]
- Lipton JS, Spelke ES. Discrimination of Large and Small Numerosities by Human Infants. Infancy. 2004;5(3):271–290. [Google Scholar]
- Luck SJ, Vogel EK. The capacity of visual working memory for features and conjunctions. Nature. 1997;390(6657):279–281. doi: 10.1038/36846. [DOI] [PubMed] [Google Scholar]
- McCrink K, Wynn K. Ratio abstraction by 6-month-old infants. Psychological Science. 2007;18(8):740–745. doi: 10.1111/j.1467-9280.2007.01969.x. [DOI] [PubMed] [Google Scholar]
- Miller GA. The magical number seven, plus or minus two: Some limitations on our capacity for processing information. The Psychological Review. 1956;63(2):81–97. [PubMed] [Google Scholar]
- Moyer RS, Landauer TK. Time required for Judgements of Numerical Inequality. Nature. 1967;215(5109):1519–1520. doi: 10.1038/2151519a0. [DOI] [PubMed] [Google Scholar]
- Noles N, Scholl BJ, Mitroff SR. The persistence of object-file representations. Perception & Psychophysics. 2005;67(2):324–334. doi: 10.3758/bf03206495. [DOI] [PubMed] [Google Scholar]
- Oakes L, Bauer P, editors. Short- and Long-term Memory in Early Childhood: Taking the First Steps Toward Remembering. New York: Oxford University Press; 2007. [Google Scholar]
- Parkes L, Lund J, Angelucci A, Solomon JA, Morgan MJ. Compulsory averaging of crowded orientation signals in human vision. Nature Neuroscience. 2001;4:739–744. doi: 10.1038/89532. [DOI] [PubMed] [Google Scholar]
- Pietroski P, Lidz J, Hunter T, Halberda J. The meaning of most: Semantics, numerosity and psychology. Mind & Language. 2009;24(5):554–585. [Google Scholar]
- Piaget J. The origins of intelligence in children. New York: International University Press; 1954. [Google Scholar]
- Pica P, Lemer C, Izard V, Dehaene S. Exact and approximate arithmetic in an Amazonian indigene group. Science. 2004;306(5695):499–503. doi: 10.1126/science.1102085. [DOI] [PubMed] [Google Scholar]
- Pinto JP. Palo Alto, CA: 1996. XHAB (version 6.5): Experimental control software for MS-DOS [computer software] [Google Scholar]
- Pylyshyn Z. The Role of Location Indexes in Spatial Perception - a Sketch of the Finst Spatial-Index Model. Cognition. 1989;32(1):65–97. doi: 10.1016/0010-0277(89)90014-0. [DOI] [PubMed] [Google Scholar]
- Pylyshyn ZW, Storm RW. Tracking multiple independent targets: evidence for a parallel tracking mechanism. Spatial Vision. 1988;3(3):179–197. doi: 10.1163/156856888x00122. [DOI] [PubMed] [Google Scholar]
- Rosenberg R, Carey S. Towards a cohesive account of non-cohesion: Not all entities are equal in infants' physical world. (submitted) [Google Scholar]
- Ross J, Burr DC. Vision senses number directly. Journal of Vision. 2010;10(2):1–8. doi: 10.1167/10.2.10. [DOI] [PubMed] [Google Scholar]
- Ross-Sheehy S. Attentional modulation of infant visual short-term memory (Doctoral dissertation) 2005. [Google Scholar]
- Ross-Sheehy S, Oakes LM, Luck SJ. The development of visual short-term memory capacity in infants. Child Development. 2003;74(6):1807–1822. doi: 10.1046/j.1467-8624.2003.00639.x. [DOI] [PubMed] [Google Scholar]
- Scholl BJ. Objects and attention: the state of the art. Cognition. 2001;80:1–46. doi: 10.1016/s0010-0277(00)00152-9. [DOI] [PubMed] [Google Scholar]
- Scholl BJ, Pylyshyn ZW. Tracking multiple items through occlusion: clues to visual objecthood. Cognitive Psychology. 1999;38(2):259–290. doi: 10.1006/cogp.1998.0698. [DOI] [PubMed] [Google Scholar]
- Scolari M, Vogel EK, Awh E. Perceptual expertise enhances the resolution but not the number of representations in working memory. Psychonomic Bulletin and Review. 2008;15:215–222. doi: 10.3758/pbr.15.1.215. [DOI] [PubMed] [Google Scholar]
- Slaughter V, Suddendorf T. Participant loss due to "fussiness" in infant visual paradigms: A review of the last 20 years. Infant Behavior & Development. 2007;30:505–514. doi: 10.1016/j.infbeh.2006.12.006. [DOI] [PubMed] [Google Scholar]
- Song J-H, Jiang Y. Visual working memory for simple and complex features: An fMRI study. NeuroImage. 2006;30(3):963–972. doi: 10.1016/j.neuroimage.2005.10.006. [DOI] [PubMed] [Google Scholar]
- Sperling G. The information available in brief visual presentations. Psychological Monographs. 1960;74(11):1–29. [Google Scholar]
- vanMarle K, Scholl BJ. Attentive tracking of objects versus substances. Psychological Science. 2003;14(5):498–504. doi: 10.1111/1467-9280.03451. [DOI] [PubMed] [Google Scholar]
- Vogel EK, Woodman GF, Luck SJ. The time course of consolidation in visual working memory. Journal of Experimental Psychology: Human Perception and Performance. 2006;32(6):1436–1451. doi: 10.1037/0096-1523.32.6.1436. [DOI] [PubMed] [Google Scholar]
- Whalen J, Gallistel CR, Gelman R. Nonverbal counting in humans: The psychophysics of number representation. Psychological Science. 1999;10(2):130–137. [Google Scholar]
- Wilken P, Ma WJ. A detection theory account of change detection. Journal of Vision. 2004;4:1120–1135. doi: 10.1167/4.12.11. [DOI] [PubMed] [Google Scholar]
- Wynn K. Addition and subtraction by human infants. Nature. 1992;358(6389):749–750. doi: 10.1038/358749a0. [DOI] [PubMed] [Google Scholar]
- Wynn K, Bloom P, Chiang WC. Enumeration of collective entities by 5-month-old infants. Cognition. 2002;83(3):B55–B62. doi: 10.1016/s0010-0277(02)00008-2. [DOI] [PubMed] [Google Scholar]
- Xu F. Numerosity discrimination in infants: Evidence for two systems of representations. Cognition. 2003;89(1):B15–B25. doi: 10.1016/s0010-0277(03)00050-7. [DOI] [PubMed] [Google Scholar]
- Xu F, Arriaga RI. Number discrimination in 10-month-old infants. British Journal of Developmental Psychology. 2007;25:103–108. [Google Scholar]
- Xu F, Carey S. Infants' metaphysics: The case of numerical identity. Cognitive Psychology. 1996;30(2):111–153. doi: 10.1006/cogp.1996.0005. [DOI] [PubMed] [Google Scholar]
- Xu F, Spelke ES. Large number discrimination in 6-month-old infants. Cognition. 2000;74(1):B1–B11. doi: 10.1016/s0010-0277(99)00066-9. [DOI] [PubMed] [Google Scholar]
- Xu F, Spelke ES, Goddard S. Number sense in human infants. Developmental Science. 2005;8(1):88–101. doi: 10.1111/j.1467-7687.2005.00395.x. [DOI] [PubMed] [Google Scholar]
- Xu Y. Limitations of object-based feature encoding in visual short-term memory. Journal of Experimental Psychology: Human Perception and Performance. 2002;28(2):458–468. doi: 10.1037//0096-1523.28.2.458. [DOI] [PubMed] [Google Scholar]
- Xu Y, Chun MM. Dissociable neural mechanisms supporting visual short-term memory for objects. Nature. 2006;440(7080):91–95. doi: 10.1038/nature04262. [DOI] [PubMed] [Google Scholar]
- Zhang W, Luck SJ. Discrete fixed-resolution representations in visual working memory. Nature. 2008;453(7192):233–235. doi: 10.1038/nature06860. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zosh JM, Feigenson L. A capacity-resolution tradeoff in infant working memory. (submitted) [Google Scholar]