Discriminant analysis of longitudinal cortical thickness changes in Alzheimer’s disease using dynamic and network features

Abstract

Neuroimage measures from magnetic resonance (MR) imaging, such as cortical thickness, have been playing an increasingly important role in searching for bio-markers of Alzheimer’s disease (AD). Recent studies show that, AD, mild cognitive impairment (MCI) and normal control (NC) can be distinguished with relatively high accuracy using the baseline cortical thickness. With the increasing availability of large longitudinal datasets, it also becomes possible to study the longitudinal changes of cortical thickness and their correlation with the development of pathology in AD. In this study, the longitudinal cortical thickness changes of 152 subjects from four clinical groups (AD, NC, Progressive-MCI and Stable-MCI) selected from Alzheimer’s Disease Neuroimaging Initiative (ADNI) are measured by our recently-developed 4D (spatial+temporal) thickness measuring algorithm. It is found that the four clinical groups demonstrate very similar spatial distribution of GM loss on cortex. To fully utilizing the longitudinal information and better discriminate the subjects from four groups, especially between Stable-MCI and Progressive-MCI, three different categories of features are extracted for each subject, i.e., (1) static cortical thickness measures computed from the baseline and endline, (2) cortex thinning dynamics, such as the thinning speed (mm/year) and the thinning ratio (endline/baseline), and (3) network features computed from the brain network constructed based on the correlation between the longitudinal thickness changes of different ROIs. By combining the complementary information provided by features from all three different categories, two classifiers are trained to diagnose AD and to predict the conversion to AD in MCI subjects, respectively. In the leave-one-out cross-validation, the proposed method can distinguish AD patients from NC at an accuracy of 96.1%, and can detect 81.7% (AUC=0.875) of the MCI converters at 6-months ahead of their conversions to AD. Also, by analyzing the brain network built via longitudinal cortical thickness changes, a significant decrease (P<0.02) of the network clustering coefficient (associated with the development of AD pathology) is found in the Progressive-MCI group, which indicates the degenerated wiring efficiency of the brain network due to AD. More interestingly, the decreasing of network clustering coefficient of the olfactory cortex region was also found in the AD patients, which suggests the olfactory dysfunction. Although the smell identification test is not performed in ADNI, this finding is consistent with other AD-related olfactory studies.

1. Introduction

Alzheimer’s Disease (AD) is the most common cause of dementia. With the incidence rate doubling every 5 years after the age of 65, AD poses significant medical, social and socioeconomic challenges. Due to the fact that the cortical atrophy associated with AD can be detected in vivo using MRI, neuroimaging measures have been playing an increasingly important role in searching for bio-markers of AD that can be used for early diagnosis, progression monitoring and also therapy responses measure. Recent studies have focused on individuals with mild cognitive impairment (MCI), a concept used to describe a high-risk ‘pre-dementia’ state (the prodromal stage of Alzheimer’s disease (Dubois et al., 2007)), in which a deterioration of cognitive skills can be measured while the ability to manage tasks of daily living remains intact (Petersen et al., 1999; Petersen, 2004). According to epidemiological studies, each year 6~25% of subjects with MCI eventually convert to clinical AD, which is a markedly higher annual rate of conversion than that observed in normal elderly control population, which is around 1% (Petersen, 2001). However, MCI is a heterogeneous group. There have been approaches to more precisely define different MCI clinical presentations (Petersen, 2004). When individuals have impairments in domains other than memory it is classified as non-amnestic single- or multiple-domain MCI and these individuals are believed to be more likely to convert to other dementias. Additionally, when memory loss is the predominant symptom, it is termed ‘amnestic’ MCI. Subjects in this subtype show greatest risk for conversion to AD in 6 years. These MCI subjects finally develop probable AD, which are referred to as Progressive-MCI (P-MCI). In contrast, some other MCI subjects do not convert to AD even after several years of follow-up, which are referred to as Stable-MCI (S-MCI). Therefore, more and more emphasis has been placed on identifying those P-MCI individuals from the MCI group. Successful identification of such individuals at an early-stage before the onset of clinical symptoms may lead to effective intervention of pharmacological treatments for AD as they become available.

It has been shown that many P-MCIs present evolving AD-like patterns of brain atrophy. Therefore, to find out how AD-induced GM atrophy spreads spatially and temporally in the brain, many longitudinal studies of normal aging or AD-degenerated cortical thinning have been conducted, in which GM volume/density are measured and analyzed within regions of interest (ROIs) or voxel-wisely (Resnick et al., 2003; Thompson et al., 2003; Toga and Thompson, 2003; Gogtay et al., 2004; Thompson et al., 2004; Chételat et al., 2005; Davatzikos et al., 2009; Desikan et al., 2009; Dickerson et al., 2009). Recently, cortical thickness is also proposed as a more stable parameter for AD diagnosis than volume/density measures, because it is a more direct measure of GM atrophy due to the cytoarchitectural feature of the GM (Regeur, 2000; Singh et al., 2006). Hence, as an alternative to volumetric measures, the assessment of thickness of the cerebral cortex has been recently proposed as a more sophisticated way to measure brain atrophy resulting from the AD neuropathological changes (Lerch et al., 2005). This measure has been proven both precise and sensitive in detecting alterations in cortical morphology (Lerch and Evans, 2005). Cortical thickness analysis has been successfully used in various studies as markers to separate AD patients from healthy controls and MCI subjects (Chételat et al., 2005; Singh et al., 2006; Du et al., 2007; Desikan et al., 2009; Hutton et al., 2009). In addition, more recently, attempts to distinguish P-MCI from S-MCI by analyzing the baseline cortical thickness have also been reported (Querbes et al., 2009).

So far, although there are plenty of longitudinal thickness studies focused on the comparative analysis between different clinical groups (Toga and Thompson, 2003; Chételat et al., 2005; Lerch et al., 2005; Thompson et al., 2004; Singh et al., 2006), research work on classification or AD conversion prediction using the longitudinal cortical thickness changes still remains scarce. Compared to the volumetric measure, the obstacles in incorporating longitudinal thickness change information into the classification largely come from the difficulties in measuring the subtle longitudinal thickness changes accurately and reliably. Comparing the thickness of cortical structures (1.2~4.5 mm) with the resolution of MR images (~1 mm), cortical structures are only a few voxels thick in the images and the possible errors in the measuring process could be considerably large. This situation becomes even worse when the thickness at different time-points are measured independently, because the expected change in GM thickness during the early stage of AD is less than 1 mm in most brain regions (Lerch et al., 2005; Singh et al., 2006), which can be easily overwhelmed by the noises. In our recently developed 4D cortical thickness measuring method (Li et al., 2010), the accuracy and the robustness of thickness measurement for longitudinal images have been significantly improved by incorporating the information from all time-points as a constraint or guidance to each other. This leads to a much higher correlation detected between the thickness measured by our method and the MMSE (Mini-Mental State Examination score (Folstein et al., 1975)) or CDR-SOB (Clinical Dementia Rating-Sum of Boxes (Morris, 1993)) scores, when compared with the common 3D measuring method.

With this 4D cortical thickness measuring method, in this study, experiments are designed to compare the thickness change patterns among four different clinical groups (AD, NC, S-MCI and P-MCI). Besides comparing the static features (such as thickness measured at each time-point), the temporal dynamic measures are also extracted, such as the thinning speed (mm/year) and thinning ratio (endline/baseline). In addition, to capture the system-level information, a brain network is first constructed based on the correlation of longitudinal cortical thickness changes between different ROIs, and then the network clustering coefficient (Rubinov and Sporns, 2009) which represents the wiring efficiency of the network is also extracted as feature in this study. Finally, we combine these three different categories of features to find 4D patterns that can be used to effectively diagnose AD or predict the MCI converters (the P-MCI patients) in MCI group.

2. Methods

2.1. Participants and inclusion criteria

The longitudinal dataset used in the preparation of this article were obtained from the ADNI database (www.adniinfo.org). The ADNI was launched in 2003 by the National Institute on Aging (NIA), the National Institute of Biomedical Imaging and Bioengineering (NIBIB), the Food and Drug Administration (FDA), private pharmaceutical companies and non-profit organizations as a $60 million, 5-year public–private partnership. The primary goal of ADNI has been to test whether serial MRI, PET, other biological markers and clinical and neuropsychological assessment can be combined to measure the progression of MCI and early AD. Determination of sensitive and specific markers of very early Alzheimer’s disease progression is intended to aid researchers and clinicians in the development of new treatments and monitor their effectiveness, as well as lessen the time and cost of clinical trials. The image acquisition parameters have been described in www.adniinfo.org. The ADNI protocol included a sagittal volumetric 3D MPRAGE with 1.25×1.25 mm in-plane spatial resolution and 1.2 mm thick sagittal slices (8° flip angle). TR and TE values of the ADNI protocol were somewhat variable, but the target values were TE ~3.9 ms and TR ~8.9 ms. In ADNI, other than 1.5T, for some subjects and time-points, MR scans of 3.0T strength field are also available. However, to be consistent between scans of different subjects and different time-points, 1.5T scans are used in this study, since they are available for more subjects and time-points.

According to ADNI clinical procedures, diagnosis of Alzheimer’s disease was made if the subject had a MMSE score between 20 and 26, a CDR score of 0.5 or 1, and met NINCDS/ADRDA (McKhann et al., 1984) criteria for probable Alzheimer’s disease. The diagnosis of single-domain amnestic MCI was made according to the revised MCI criteria (Petersen, 2004): (i) MMSE scores between 24–30; (ii) reported memory complaint; (iii) having objective memory loss measured by education adjusted scores on Wechsler Memory Scale Logical Memory II (D., 1987); (iv) a CDR of 0.5; (v) absence of significant levels of impairment in other cognitive domains, essentially preserved activities of daily living, and absence of dementia.

In this study, subjects from ADNI are included in the P-MCI group, if they satisfy the following criteria: (i) Every subject was re-scanned and re-evaluated every six months for, at least, a period of 24 months. Therefore, including baseline, each has at least 5 time-points. (ii) Each subject developed probable AD after, at least, 12 months from the baseline scan. Thus, there are at least 3 time-points before conversion. This is the minimum number of time-points needed for the calculation of dynamic features. As of Dec. 2009, when the data was downloaded, totally 39 subjects from ADNI were found to meet the above criteria and are thus included into the P-MCI group. For other three clinical groups, subjects are selected to match the demographic information in P-MCI group to have the same gender and age. Specifically, for each subject in P-MCI group, a subject with the same gender and age is sought in other group. If failed, the gender constraint is firstly relaxed, and then the age. However, in no circumstance, subjects with age difference bigger than 3 years are included. Due to the similar reason for the calculation of dynamic features, the subjects in other clinical groups are required to have at least 4 time-points. The demographic and clinical information of all the selected subjects in four groups are summarized in Table 1.

Table 1.

Descriptive demographic information of the subjects in the study.

Group	NC	S-MCI	P-MCI	AD	P – value
No. of subjects	40	36	39	37
No. and percentage of males	23 (58%)	25 (69%)	25 (64%)	23 (62%)	NS
Baseline age, mean (SD)	73.7 (6.3)	75.3 (6.9)	75.6 (7.4)	74.8 (8.0)	NS
MMSE at first visit, mean (SD)	29.4 (0.7)	26.8 (1.6)	26.5 (1.7)	23.0 (1.9)	P < 0.001*
MMSE at last visit, mean (SD)	28.8 (1.3)	25.8 (2.8)	21.1 (4.1)	13.8 (4.7)	P < 0.001
Significant decrease in MMSE	P < 0.05	P < 0.001	P < 0.001	P < 0.001
No. and percentage of ApoE4 carriers	9 (22.5%)	21 (58.3%)	28 (71.8%)	27 (72.8%)

NS: Not significant

^*Significant difference in MMSE scores, except between S-MCI and P-MCI

2.2. Image preprocessing

The preprocessing step performed in our method is a standard procedure as used in general brain image analysis, aiming to reduce image noise and remove non-brain tissues. For each image, intensity inhomogeneity is firstly corrected using the N3 algorithm (Sled et al., 1998). Many algorithms have been developed to remove non-brain tissues, such as the skull and the extra- cranial tissues, including Brain Surface Extractor (BSE) (Shattuck and Leahy, 2001) and Brain Extraction Tool (BET) (Smith, 2002). However, it is still hard to achieve good skull stripping results on every subject through automatic algorithm. For better results, we combine BSE and BET to take advantage of both algorithms, followed by a manual editing to ensure that skull removal is accurate. In order to maintain the consistency between different time-points, the above skull stripping is firstly performed on baseline scan and then applied to all rigidly-aligned follow- up scans. We note here that the common method of registering all follow-ups to the baseline may introduce bias. The main reason is that only the follow-up images are interpolated and, therefore, smoothed a little bit after registration (Yushkevich et al., 2010). In our implementation, the baseline image is first rigidly (instead of affine which will affect the accuracy of thickness measures due to the shearing transformation) registered to a standard template to introduce the similar interpolation/smoothing effect on the baseline image. After this, all follow-up images are rigidly registered to the warped baseline image.

2.3. Temporal consistent longitudinal cortical thickness measurement

To avoid getting jittery longitudinal thickness measures, in our recently developed method (Li et al., 2010), the information from all time-points are incorporated as a constraint or guidance to each other when measuring the cortical thickness. Specifically, after obtaining the 4D segmentation results using CLASSIC (Xue et al., 2006), an unbiased group-wise registration algorithm (Wu et al., 2010) is adopted to register each time-point image to a common space by iteratively constructing the group-mean image (via averaging the images from all time-points of a subject) and registering each time-point to the latest estimated group-mean image. In this way, the spatial correspondence among the scans of the same subject is established. The reason of not using the baseline as the template for registration is to avoid the possible bias which generally tends to exaggerate the longitudinal change as reported in (Yushkevich et al., 2010; Thomas et al., 2009). After performing the group-wise registration, the Jacobian determinants of the resultant deformation fields are computed to quantify the expansion or contraction caused by the deformation on each voxel. Then, in the group-mean space, the warped GM map from each time-point is multiplied by the Jacobian determinant voxel-wisely to preserve the GM volume before warping. Due to partial volume effects, limited resolution and noise in imaging, ‘buried sulci’ (part of the cortical surface hidden within the deep and narrow sulci) is often observed. This usually leads to the over estimation of the cortical thickness. To overcome this problem, a method proposed by (Hutton et al., 2008) is adopted to recover the buried sulci. In this method, starting from the initial WM map, GM layers are successively recovered to surround the WM, until the two sides meet in the middle of the buried sulci. Thus, the set of central voxels can be re-labeled as the restored CSF.

In the final step, since these GM maps have been all aligned in a standardized stereotaxic space (i.e., group-mean space), for each GM voxel in this space, the cortical thickness of each time-point can be computed as the line-integral (Aganj et al., 2009) of the underlying GM density map along a direction on which the summation of the integrals in all time-points is minimized (Li et al., 2010). In this way, the information from different time-points is fully utilized as a constraint or guidance for finding the measuring direction (which is the key factor in consistent measurement of longitudinal thickness). Due to the fact that the obtained thickness measuring direction is optimal and consistent for all time-points in the longitudinal image dataset, this 4D measurement of thickness is much more temporally consistent, robust and accurate than the conventional 3D measurement that estimates the thickness of each time-point image independently. For more details of this 4D thickness measuring method, we refer the readers to (Li et al., 2010).

After the longitudinal thickness measurement, for each subject, the obtained thickness maps of different time-points need to be mapped to a standard space (Tzourio-Mazoyer et al., 2002), in order to compare the thickness across different subjects at the corresponding location. Since all images at different time-points of each subject have been registered to the group-mean image, we just need to register the group-mean image to the template space, and then bring the obtained thickness maps of all time-points to this space by using the estimated deformation field. Finally, in order to suppress the registration errors between subjects, the mapped thickness in the template space is smoothed by a 6 mm full-width-at-half-magnitude (FWHM) Gaussian filter before across- subject comparison. In voxel-based morphometry (VBM) (Good et al., 2001), following spatial normalization, data are often smoothed using FWHM filter to improve the validity of statistical inferences and to reduce inter-individual variation or registration residual. The size of the smoothing kernal is generally chosen empirically. An often quoted ’rule of thumb’ rule of selecting the size of the smoothing kernel is that a kernel should be at least 2–3 times the voxel dimension (Jones et al., 2005). Therefore, in our study, starting from 1.5×3=4.5 mm to 9.0 mm, we test the statistical inferences of different kernel size in a interval of 0.5 mm, and finally selected the kernel size as 6 mm which gives the highest correlation between thickness measures and clinical scores (CDR).

2.4. Feature extraction

After estimating the longitudinal cortical thickness changes using the 4D measuring method, the static, dynamic and network features can be extracted as detailed below.

2.4.1. Static and dynamic features

In this study, we call the thickness measure computed from a single time-point as the static feature, since it describes a static state in the progression of GM loss or disease development. Generally, only the baseline measurements are used for cortical thickness based classification in the existing works. However, in our study, the endline (last time-point) is also used to provide the most recent information of the pathological development. Moreover, with the increasing availability of longitudinal image datasets, dynamic features that directly describe the temporal changes of cortical thickness can also be calculated to provide more information. For instance, compared with static measures, the thinning ratio defined as (1 – endline/baseline) × 100% may be a more accurate measurement of the severity of the disease. Meanwhile, a linear regression on thickness values of all time-points can also be performed voxel-wisely to find the thinning speed (mm/year). This measure gives the kinetic of the GM loss and could be more helpful in prediction of the disease development. Therefore, besides the static features (i.e., baseline and endline measures), we also calculate two dynamic features, i.e., thinning ratio and thinning speed in this study.

2.4.2. Adaptive ROIparcellation

In order to improve the robustness and reduce the dimensionality of the feature set, usually, the mean feature value computed within each ROI is used in the classification, instead of using the thickness measures on every single voxel directly. Therefore, the partition of the whole cortex into different ROIs is a very important step in the ROI-based feature extraction. Conventionally, the cortical parcellation can be achieved by mapping the anatomical labels of an atlas to each subject. However, due to the fact that the spatial distribution of thickness changes does not necessarily coincide with the anatomical partitions, the thickness changes on different voxels within a ROI could be heterogeneous. Therefore, directly averaging the feature values within each pre-defined anatomical ROI may cancel or attenuate the information contained by the features. To better reflect the spatial distribution of cortical thickness changes, we apply data-driven method (Fan et al., 2007; Davatzikos et al., 2008) to automatically parcellate the brain cortex into different ROIs.

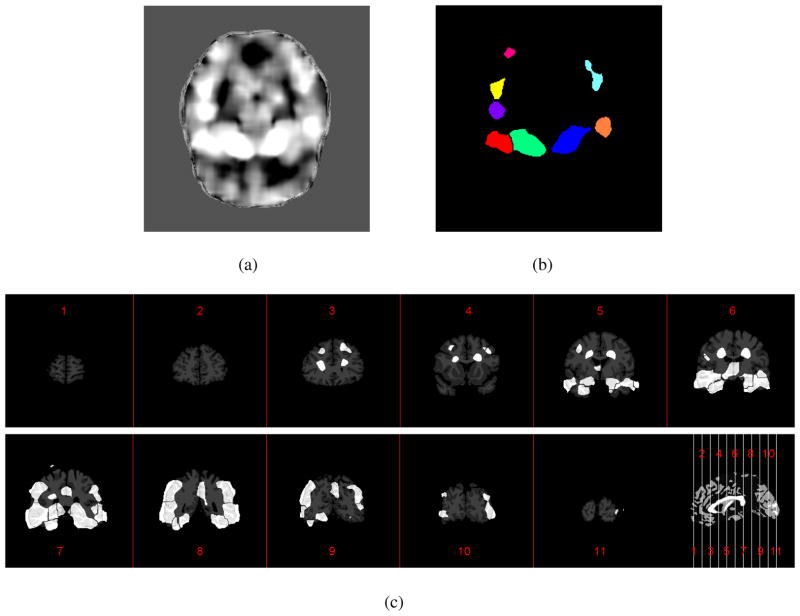
Here, we use the ROI generation for the baseline thickness as an example to explain the idea of adaptive ROI definition. First, on each voxel, across all subjects, the Pearson’s correlation between the baseline thickness and the classification labels (for instance, ‘1’ for AD and ‘0’ for NC) is computed. One axial slice of the resultant correlation map is shown in Figure 1(a) with high correlation indicating high discriminative power. As the figure shows, the voxels with relatively high correlations form many different clusters. Using the “watershed” segmentation algorithm, these clusters can be segmented and defined as ROIs shown in Figure 1(b). In this process, the small clusters with relatively low correlation are excluded in order to limit the number of ROIs, because of their low and less-reliable discriminative ability for the classification. This means that, for the purpose of classification, the obtained ROIs do not necessarily cover all the cortical regions. As an example, the final ROI partition results on baseline thickness are shown in Figure 1(c). As can be seen, most of the ROIs exist on the temporal and parahippocampal cortex area. This is consistent with the findings in (Holland et al., 2009; Desikan et al., 2009), in which these regions are also reported as the most affected by AD. In the similar manner, ROIs for endline thickness, thinning speed and thinning ratio can also be generated, respectively. After that, within each ROI, the mean value of each feature can then be computed.

Figure 1.

An example of generating the spatial-adaptive ROIs for baseline thickness. (a) Correlation map between the baseline thickness and the classification labels; (b) The ROIs obtained via watershed segmentation corresponding to (a); (c) The ROIs generated for baseline thickness shown in different coronal slices.

2.4.3. Network features

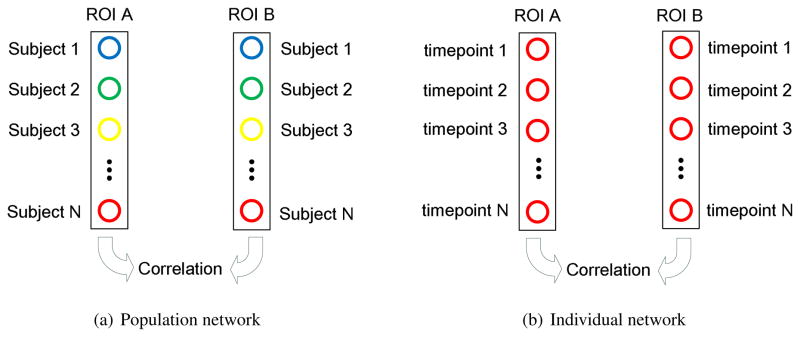
An important problem in neuroscience is how to characterize the underlying architectures of complex brain networks. Electroencephalography (EEG) (Micheloyannis et al., 2006; Stam et al., 2007) and fMRI (Egüıluz et al., 2005; Achard et al., 2006) have been used to explore the connections in brain. The brain network constructed based on these functional measures are called the functional network. More recently, structural measurements, such as cortical thickness, were also used to build the anatomical network (He et al., 2007). In this network, two areas are considered anatomically connected if they show statistically significant correlations (p < 0.01) on cortical thickness across different subjects (as shown in Figure 2(a)). The small-worldness property was also observed in this thickness-revealed network, which is consistent with the findings from the networks constructed with functional measures. Since the network constructed in this way (He et al., 2007) represents the ‘average’ connection information in a population, we refer it as the population network.

Figure 2.

Two different methods for thickness-based brain network construction. (a) In the population network, the pairwise connection between two ROIs is established, if the thickness measures from different subjects show significant correlation between these two ROIs; (b) In the individual network, the pairwise connection between two ROIs is established, if the thickness measures from different time-points of the same subject show significant correlation between these two ROIs.

As a source of higher level information, the thickness-based network information is also included in this study. However, different from the network information in a population, we need network information at individual level for the classification task. Therefore, in our study, we use a slightly different method to construct the network. Firstly, the whole brain cortex is partitioned into 90 ROIs according to the AAL atlas (Tzourio-Mazoyer et al., 2002). It should be noticed that here we do not use the spatial-adaptive ROIs (as described in Section 2.4.2) for network construction. This is because the adaptively defined ROIs may not cover all the cortical regions as shown in Figure 1. Therefore, to make the constructed network complete, the ROI partitions used for network construction are generated according to an anatomical atlas (Tzourio-Mazoyer et al., 2002). Next, for each time-point, the mean cortical thickness of each ROI is computed. After that, a pairwise ROI connection is constructed, if the longitudinal cortical thickness changes in two ROIs are statistically correlated (as shown in Figure 2(b)). Lastly, the brain network is constructed based on such connections. In this way, the constructed network represents the brain connection information of each subject. Thus, measures of this subject-specific network can be used for the classification purpose. Corresponding to the population network in (He et al., 2007), we refer our proposed network as individual network in the remaining part of this paper.

With the proposed individual network, in this study, we calculate the clustering coefficient (Rubinov and Sporns, 2009) on every ROI as the network feature, which is defined as the ratio of the number of connections between one node’s neighbors divided by the maximum possible connections between its neighbors. Intuitively, the clustering coefficient measures the local wiring efficiency of the brain network and is closely correlated to the small-worldness property of the underlying brain-network.

To summarize, for each ROI of a subject, the following five groups of features (as shown in Table 2) are extracted in our study: Baseline Thickness (BT, mm), Endline Thickness (ET, mm), Thinning Ratio (TR, %), Thinning Speed (TS, mm/year) and Clustering Coefficient (CC) of brain network. Consequently, each subject is represented by 262 longitudinal image features.

Table 2.

Features defined and extracted in the study.

Features	Static		Dynamic		Network
	Baseline Thickness(BT)	Endline Thickness(ET)	Thinning Ratio (TR)	Thinning Speed (TS)	Clustering Coefficient (CC)
Number	26	29	56	61	90

2.5. Feature selection and classifier training

In this study, as shown in Table 2, each subject has 262 features from three categories (static, dynamic and network), which give different aspects of information about a subject. Among these features, some information may be complementary and some may be redundant or overlapped. Therefore, for the best classification performance, the optimal set of the features from three different categories should contain the most comprehensive information and, at the same time, with the minimum redundancy. To achieve this, we use the mRMR (minimum redundancy maximum relevance) feature selection algorithm (Peng et al., 2005) to select the best feature subset. This filtering feature selection approach considers all features jointly and identifies a minimal set of features which jointly maximally differentiate the classes. With this feature selection method, we first train an SVM (support vector machine) nonlinear classifier to recognize the spatial-temporal thinning and the brain network changing patterns that distinguish AD from NC individuals. For the discrimination between P-MCI and S-MCI, similar approach is adopted except that only the thickness values measured 6 months ahead of AD conversion are used. Thus, the classification results actually give a short-term prediction of the conversion from MCI to AD.

3. Results

3.1. Improved accuracy in measuring the longitudinal thickness changes

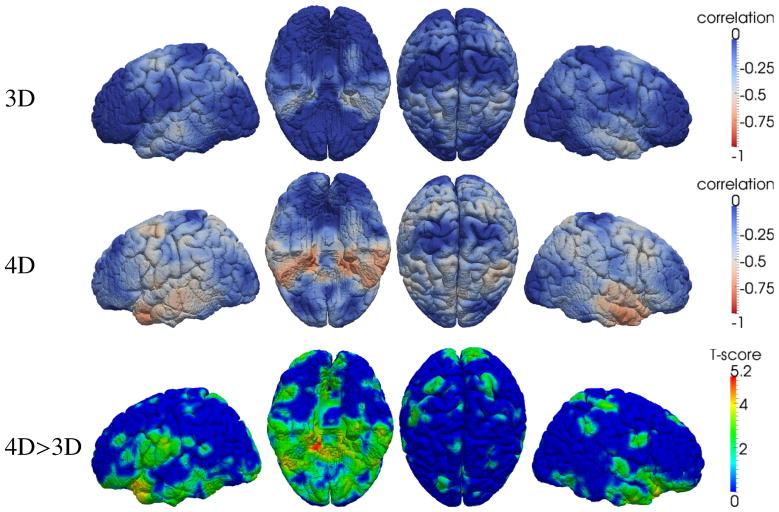
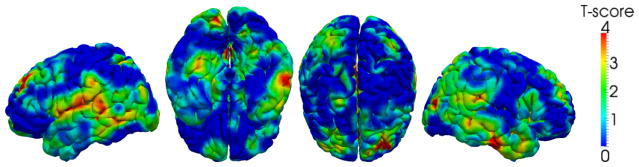
To show the improved accuracy in our temporal-consistent 4D thickness measurement, correlation between the thickness measurements and the CDR-SOB scores are computed on each subject and then averaged in the P-MCI group. The reason to choose P-MCI group is because subjects in this group have relatively large change of thickness and clinical scores. The results of the conventional 3D method (Aganj et al., 2009) and the 4D method (Li et al., 2010) are compared in Figure 3, in which much higher correlations are found between the clinical score and the 4D thickness measures. To show the significance of improvement, the T-score map indicating the places where 4D measures give statistically higher correlations is also provided. To control the multiple comparison errors, False Discovery Rate (FDR, defined as the expected proportion of false positives among all significant tests) correction is adopted. As an indirect validation for thickness measurement (Lerch and Evans, 2005; Aganj et al., 2009), the higher correlation with the clinical score indicates that the new 4D thickness measuring method provides more sensitive and accurate measurement of the longitudinal thickness changes.

Figure 3.

Average correlation between thickness and CDR-SOB scores within the P-MCI subjects (each has 5 time-points). The higher correlation implies the improved accuracy using the 4D thickness measurement (Li et al., 2010). From left to right: the left, inferior, superior and right views, respectively. The bottom shows the T-score (p < 0.05, FDR corrected) where 4D method gives significant high correlation than the 3D method.

3.2. 4D pattern of cortex thinning in different groups

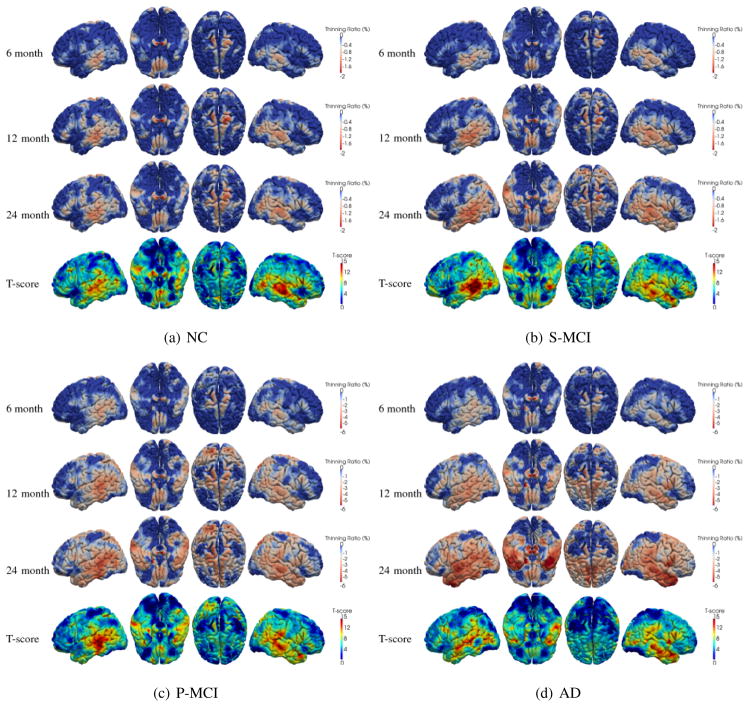
With the longitudinal thickness measured for each subject at all time-points, 4D maps of the thickness thinning ratio within each clinical group can be computed. First, in the template space (Tzourio-Mazoyer et al., 2002), for each subject the thickness thinning ratio is computed by comparing the thickness at each follow-up time-point with that at baseline. Then, by averaging the thinning ratio maps of different subjects at the corresponding time-point, the mean thinning ratio map in different clinical groups is computed. The results for NC, S-MCI, P-MCI and AD group are shown in Figures 4(a)–4(d), respectively. As the figures show, on average, four groups have very different cortical thinning ratios (NC: < 1.5%, S-MCI: <2%, P-MCI: 1 ~ 4% and AD: 2~6%, for 24 months).

Figure 4.

Cortical thinning patterns in different clinical groups. The fourth row shows the location where significant (p < 0.05, FDR corrected) cortex thinning (by comparing baseline and endline) is detected.

The similar spatial distribution of cortical thinning in all four groups also indicates that, instead of distinguishing the four groups only depends on the specific spatial patterns based on static features, adding dynamic features may give valuable complementary information for the purpose of classification, especially between P-MCI and S-MCI. Therefore, the thinning speeds of the subjects in P-MCI and S-MCI group are compared voxel-wisely by adding age and gender as confounding variables. The results are shown in Figure 5. As we can see, significant difference exists between the thinning speed of two groups. Specifically, the cortical thinning on anterior prefrontal cortex, temporal gyrus and parahippocampal area is much faster in P-MCI group than that in the S-MCI group. This indicates that adding the dynamic features may help differentiate the P-MCI subjects from S-MCI subjects.

Figure 5.

Cortical areas with higher thinning speed in P-MCI group than in S-MCI group. From left to right, T-scores (p < 0.05, FDR-corrected) are shown in left, inferior, superior and right views, respectively.

3.3. Discriminative power of different features

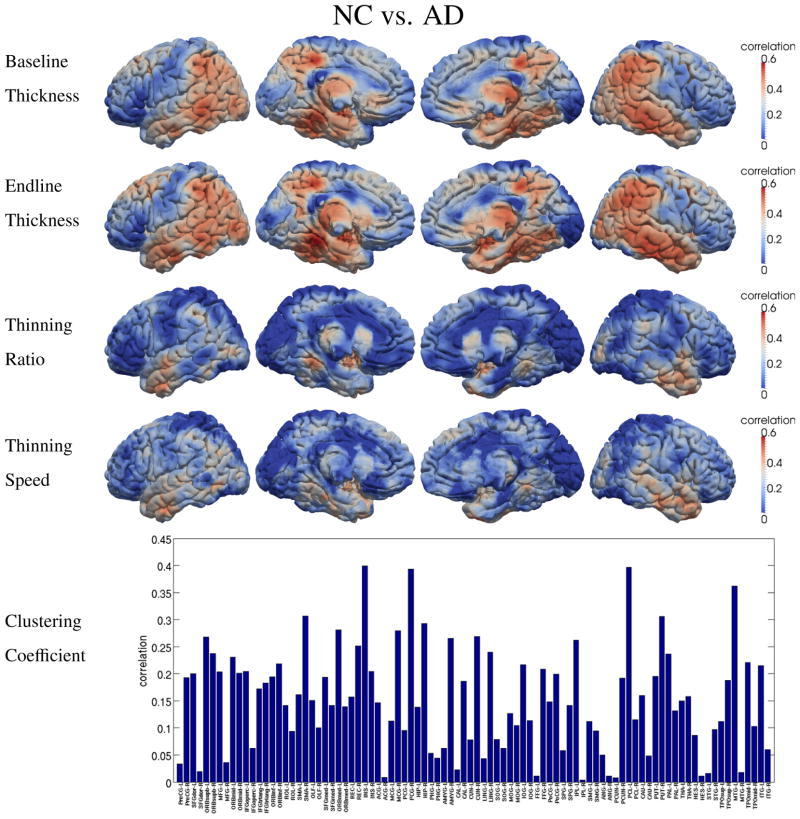
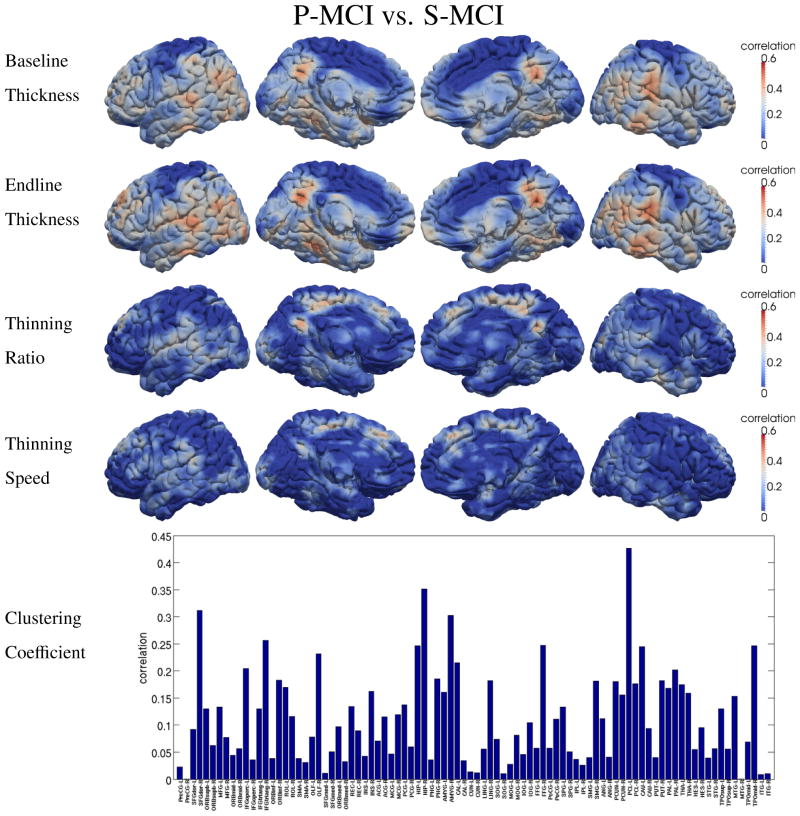
To show the discriminating power of different features, the correlation between each of the five proposed features and the classification labels is calculated for different classification tasks, i.e., AD vs. NC and P-MCI vs. S-MCI, respectively. The results are shown in Figure 6 and Figure 7, in which higher correlation suggests higher discriminative ability in the classification tasks. In both two figures, baseline and endline features show quite similar spatial patterns, although higher correlation is observed at endline. This is because these two static features carry similar information of the disease development. Since the cortical thinning process continues during the study, the GM loss becomes more severe and much easier to detect at the endline. However, when compared with the other two dynamic features, i.e., thinning ratio and thinning speed, very different spatial distributions can be observed. This is because the dynamic features carry different information about the pathology: the thinning ratio indicates the severity of the disease and the thinning speed represents the trend of degeneration. This part of information is not available in the static features and thus is complementary to the static features.

Figure 6.

Discriminative power of five different types of features in distinguishing NC and AD. High correlation indicates high discrimination power.

Figure 7.

Discriminative power of five different types of features in distinguishing P-MCI and S-MCI. High correlation indicates high discrimination power.

As high-level information, the clustering coefficient of the thickness-change-revealed brain network also shows relatively high correlations with the classification labels, as indicated by the bottom figures in Figure 6 and Figure 7. Not surprisingly, parahippocampal cortex, temporal lobe and supramarginal gyrus are found among the regions with high correlations, since relatively high GM loss was also detected in these regions.

It may be noticed that dynamic and network features both show relatively low correlation to the classification labels, when compared with static features. One possible reason is that these features rely on multiple time-points and need more complex computation, therefore they are more sensitive to noises. However, as these new features provide complementary information to the static features, by adding them, the discriminative ability of the selected features as a whole set will be improved. In our classification experiments, the similar phenomenon was also observed. The performance of the classifiers has been successfully improved by adding the dynamic and network features, as we will see in details in the next section.

3.4. Thickness-based classification results

To validate the effectiveness of the proposed static, dynamic and network features for AD diagnosis and conversion prediction, three different combinations of features, i.e., static, static+dynamic and static+dynamic +network, are tested in the leave-one-out cross-validation.

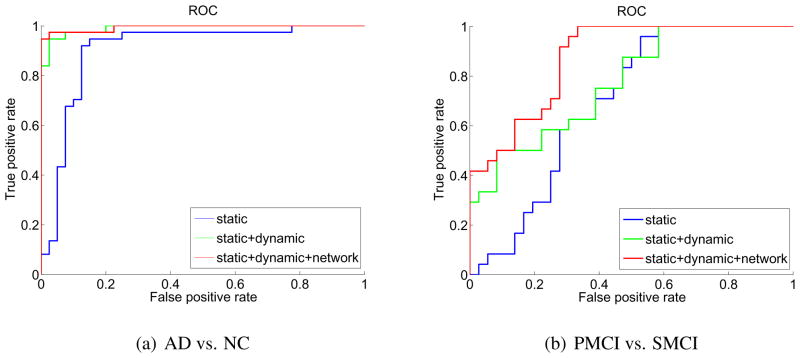
The accuracies of the two classification tasks, i.e., AD vs. NC and P-MCI vs. S-MCI, with respect to three different combinations of features are summarized in Table 3. As we can see, the more the complementary information is added (by adding more features), the higher the classification rate can be achieved. Among these three combinations of features, the static+dynamic +network combination gives the best results. For AD and NC classification, the accuracy reaches as high as 96.1%, in which adding the dynamic features contributes the most of the improvement. More importantly, for classification between P-MCI and S-MCI, the classification rate is improved from 76.7% to 81.7%. This means that we can achieve a higher accuracy in the prediction of MCI-to-AD conversion. For more information about the performance of the classifiers, the Receiver Operation Curves (ROC) of different classifiers with different feature combinations are also provided in Figure 8.

Table 3.

Comparisons of the classification accuracy of three different combinations of features.

Group	Static	Static+Dynamic	Static+Dynamic+Network
AD vs. NORMAL	89.6%	94.8% (p < 0.0001)	96.1% (p < 0.002)
P-MCI vs. S-MCI	76.7%	80.3% (p < 0.0001)	81.7% (p < 0.003)

The p-value shows the significance of improvement by comparing with the static method.

Figure 8.

Receiver Operation Curve (ROC) of different feature combinations.

3.5. Discriminative features selected for classification

By adding the complementary information (provided by dynamic and network features) into the thickness-based AD diagnosis and prediction of the MCI to AD conversion, the classification accuracy is improved significantly. Therefore, it is interesting to analyze the optimal features selected by the classifier. Table 4 lists the optimal features selected to best discriminate between AD and NC, and also between P-MCI and S-MCI. The “order” in the table does not represent the importance of a feature individually, because the mRMR feature selection algorithm (Peng et al., 2005) considers the relationship between all the features to favor the complementary and avoid redundancy. Intuitively, these orders only mean that, if only one feature is used for classification, the feature with order “1” should be selected. Then, if two features are considered, the order “2” feature should be included, because the combination of these two features has the best performance, compared with any other two-feature combinations. In other words, every newly added feature in the table contains some complementary information to the existing ones, until no more complementary information can be found. For instance, for distinguishing AD and NC, it is found that the combination of 7 features (listed in Table 4(a)) gives the best accuracy and adding more features will not help any more. As we can see, features from all three categories (static, dynamic and network) are selected, since they provide complementary information. As expected, more dynamic features (4 out of 6) are selected for the discrimination of P-MCI and S-MCI. In contrast, for the discrimination of AD and NC, more static features (3 out of 7) are selected, whereas only two dynamic features are chosen. The selection of network features shows very interesting results. For the diagnosis of AD, the clustering coefficient on olfactory is selected as the second feature. This result is consistent with the findings in other non-imaging-based studies focusing on the association between AD and olfactory dysfunction (Koss et al., 1988; Talamo et al., 1989; Murphy et al., 1990; McCaffrey et al., 2000; Wesson et al., 2010b).

Table 4.

The selected optimal feature set for two classification tasks.

(a) AD vs. NC
Order	Feature	Regions
1	Endline Thickness	Parahippocampal Left (PHG-L) Fusiform Left (FFG-L)
2	Clustering Coefficient	Olfactory Left (OLF-L)
3	Thinning Speed	Temporal Inferior Right (ITG-R)
4	Endline Thickness	Precentral Right (PreCG-R) Frontal Middle Right (MFG-R)
5	Clustering Coefficient	Cuneus Right (CUN-R)
6	Endline Thickness	Supra Marginal Left (SMG-L) Temporal Supra Left (STG-L)
7	Thinning Speed	Temporal Middle Right (MTG-R) Temporal Inferior Right (ITG-R)

(b) P-MCI vs. S-MCI
Order	Feature	Regions
1	Baseline Thickness	Supra Marginal Left (SMG-L) Angular Left (ANG-L) Parietal Inferior Left (IPL-L)
2	Thinning Speed	Postcentral Left (PoCG-L)
3	Thinning Ratio	Temporal Middle Left (MTG-L)
4	Clustering Coefficient	Fusiform Left (FFG-L)
5	Thinning Speed	Paracentral Lobule Left (PCL-L)
6	Thinning Speed	Temporal Middle Right (MTG-R) Temporal Supra Right (STG-R)

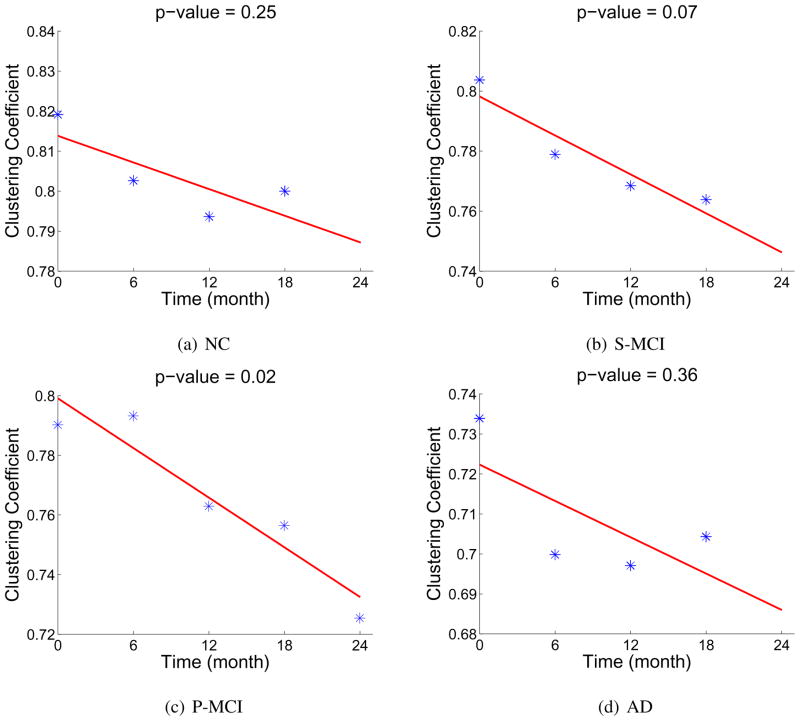
3.6. Decreased network clustering efficiency in P-MCI group

As described in Section 2.4.3, for the purpose of classification, the subject-specific brain network is constructed for providing additional information for classification. On the other hand, it will also be interesting to investigate the general longitudinal network changes in a population. For this purpose, we also construct such population network (He et al., 2007) on each time-point within the 4 clinical groups. Especially, by comparing the networks at different time-points in the P-MCI group, we can find the longitudinal changes of brain network associated with the progression of AD. In our study, significant decrease of the clustering coefficient of the brain network is observed in the P-MCI group (see Figure 9(c)), which shows the degenerated small-worldness in the brain network caused by AD. This indicates that, with the development of AD, not only the localized GM loss can be observed, but also on a larger scale the brain connections between different regions are degenerated. Similar decreases of the clustering coefficient are also observed in S-MCI and AD group, but not significant. In the NC group, with a much smaller scale, such decrease is also observed.

Figure 9.

Decrease of the average clustering coefficient (on 90 nodes) observed in 4 clinical groups.

4. Discussion

4.1. Similar spatial patterns of cortical thinning in four clinical groups

Based on the measured longitudinal thickness changes within four different clinical groups, we first explore the possibility of finding different spatial patterns of cortical thinning to differentiate the four clinical groups. The similar idea has been used to differentiate AD and frontotemporal dementia (Duet al., 2007). However, in our study, by comparing the spatial pattern of cortical thinning in different groups (shown in Figure 4), it is found that the spatial pattern of GM loss associated with the AD-related pathology is similar to the pattern observed in normal aging. Specifically, parahippocampal cortex, middle/inferior temporal gyrus, supramarginal gyrus, angular gyrus and superior frontal gyrus (consistent with the findings in (Sowell et al., 2004; Desikan et al., 2009; Holland et al., 2009)) are the regions in which relatively higher thinning ratios are detected in all four groups. This indicates that, regarding the cortex atrophy, the pathological development of AD can be viewed as an ‘accelerated’ process of normal aging, because the AD-related GM loss has the similar spatial distribution as that in normal aging, but at a much higher speed. The answer to the question regarding why this thinning process stops (at least temporarily) in the S-MCI group could be very helpful in the effort of finding effective intervention of pharmacological treatments of AD. Although the thinning ratio and thinning speed are different in all four groups, the anatomical areas where the cortical thinning is observed are mainly temporal lobe and around parahippocampal region. As expected, the thinning speed is relatively higher in P-MCI group than in S-MCI and NC group. The highest thinning speed is observed in AD group. To summarize the observed atrophy patterns in the sequence of time-points, the first area in which the thinning is observed is the supramarginal gyrus, angular gyrus and posterior superior/middle temporal gyrus. Then, the cortex thinning spreads, within the temporal lobe, from posterior to anterior, to fusiform gyrus and temporal pole. The highest thinning ratio is observed on parahippocampal cortex. The thinning speed becomes even higher in subjects with probable AD (the AD group). These findings are consistent with the results in (Thompson et al., 2003; Gogtay et al., 2004; Thompson et al., 2004; Lerch et al., 2005; Singh et al., 2006; Julkunen et al., 2009).

Our finding that four groups share a common spatial pattern of thickness change is also supported by the results from other two related studies (Querbes et al., 2009; Davatzikos et al., 2009). In both studies, a classifier was first trained to distinguish AD and NC by learning the different pattern of changes in either GM density (Davatzikos et al., 2009) or cortical thickness (Querbes et al., 2009). After that, in both studies, the trained classifier was applied to the subjects in MCI group. The output score of the classifier, which is continuous before thresholding, was used as a measure of severity of the AD-like brain change. The effectiveness of this AD measure was then validated by the experiments, in which high correlations were observed between MMSE scores and this classifier-generated scores (Davatzikos et al., 2009). In addition, in NC group, this AD vs. NC classification score was also found to be highly correlated to the age. Both the above two related studies show that the brain change patterns are similar in different groups but with different magnitudes.

4.2. Complementary information provided by the dynamic and network features

In order to find the biomarker which can differentiate P-MCI from S-MCI for the prediction of the conversion from MCI to AD, two dynamic measures, i.e., the thinning ratio (related to the severity of AD) and the thinning speed (related to AD’s development speed), are proposed in our study. In Figure 5, the thinning speed is found significantly higher in P-MCI group than in S- MCI group, mainly on supramarginal gyrus, inferior parietal lobule and right inferior temporal gyrus. To demonstrate the ability of these features in the discrimination of P-MCI and S-MCI, the correlations between these features and the classification labels are shown in Figure 7. Relatively high correlations are observed on paracentral lobule, precuneus, lingual, inferior/middle temporal, parahippocampal and entorhinal cortex, respectively. The proposed network feature (clustering coefficient) represents high-level information revealed by longitudinal thickness changes. Among the anatomical regions found with high correlation between network features and classification labels (as shown in Figure 6 and Figure 7), the GM loss is also observed in some of these regions, such as fusiform and mid temporal pole. However, no significant GM loss was found in other regions, such as supplementary motor area, superior frontal and paracentral lobule. This can be explained as that, since network features measure the wiring efficiency of the brain network, the degeneration of one cortical region may also affect the network property of other regions (which connect to the degenerated regions). Therefore, the network features are more global than the local GM loss features and thus give additional information.

4.3. Network degeneration around olfactory gyrus

It has been noticed that Alzheimer’s disease often results in impaired olfactory perceptual acuity (Koss et al., 1988; Talamo et al., 1989; Murphy et al., 1990; Doty, 2001). Due to this fact, the olfactory deficit was used to discriminate AD from major depression (McCaffrey et al., 2000) and even proposed as a potential biomarker for early-stage AD diagnosis (Wesson et al., 2010b). More recent pathological study also suggests the correlation between olfactory dysfunction and AD (Wesson et al., 2010a). Recently, MR image study (Frisoni et al., 2009) also reported reduced density in the orbitofrontal olfactory cortex in the earliest stages of the AD. In our study, although we did not detect significant atrophy in olfactory gyrus by directly using the thickness information provided by either static or dynamic features. However, by adding the high-level network information, the clustering coefficient from the olfactory gyrus is selected as the second feature in Table 4 for discriminating AD from NC. One explanation to this finding is that, the olfactory deficit observed in AD probably can be caused by either the degeneration of the olfactory gyrus itself, or by the dysfunction of information transmission channel (connecting to the olfactory gyrus). This finding also indicates the effectiveness of the network features in differentiating AD from NC.

5. Conclusion

By using our longitudinal cortical thickness measurement method, we first compared the spatial pattern of cortical thinning in four clinical groups. It is found that a similar pattern of GM loss is shared among all clinical groups. At the same time, thinning dynamics, such as the thinning speed and the thinning ratio, give complementary information in distinguishing the four groups, especially between S-MCI and P-MCI. In addition to the features directly based on the thickness measures, brain network is also constructed to extract high-level connectivity information, by analyzing the correlation of longitudinal thickness changes between different ROIs. Combining the complementary information provided by features from all three different categories (static, dynamic and network), the classification accuracy between AD and NC, as well as the accuracy in predicting the MCI-to-AD conversion, are both improved. The analysis of brain network changes also shows significant decrease of the clustering coefficient associated with AD development in P- MCI group. In addition, the decreased network wiring efficiency around the olfactory cortex may suggest the olfactory dysfunction in AD which is consistent with many other AD-related olfactory research with smell identification test.

Beside the interesting findings with substantial clinical implications, this study also has some limitations. First, we used linear cortex thinning model in the study. Within a relative short period of time (24 month) and a limited number of scans (at most 5 time-points), constant thinning speed may be a reasonable simplification. In the future study, if longitudinal information of more time-points becomes available, more sophisticated thinning model could be investigated. Second, for the prediction of AD-conversion in MCI group, the validation was made according to the diagnosis obtained in the following 6 months. However, after 6 months, it is possible that some S-MCI subjects may convert to probable AD. Therefore, for have more accurate evaluation about the cortical thickness based prediction, the results should be re-visited when more longitudinal information become available. Third, the clustering coefficient, a network measure used in this study, is defined as ‘the ratio of the number of connections between one node’s neighbors divided by the maximum possible connections between its neighbors’, which means only the neighbors are included. Recently, another network measure, ‘communicability’, was proposed by (Crofts et al., 2010). In the definition of this measure, not only the local direct connections but also the long distance indirect connections are also taken into account. In the future study, such more advanced network measures could be applied. Lastly, due to the fact that the ADNI study is primarily concerned with developing imaging measures and biomarkers for incipient AD, the appropriate subtype of MCI (amnestic-MCI) which likely represents prodromal AD is emphasized. Because of this, the MCI population of ADNI is very amnestic and may not reflect the true distributions of different subtypes of MCI in the whole population.