Feasibility of Neural Stimulation With Floating-Light-Activated Microelectrical Stimulators

Abstract

Neural microstimulation is becoming a powerful tool for the restoration of impaired functions in the central nervous system. Microelectrode arrays with fine wire interconnects have traditionally been used in the development of these neural prosthetic devices. However, these interconnects are usually the most vulnerable part of the neuroprosthetic implant that can eventually cause the device to fail. In this paper, we investigate the feasibility of floating-light-activated microelectrical stimulators (FLAMES) for wireless neural stimulation. A computer model was developed to simulate the micro stimulators for typical requirements of neural activation in the human white and gray matters. First, the photon densities due to a circular laser beam were simulated in the neural tissue at near-infrared (NIR) wavelengths. Temperature elevation in the tissue was calculated and the laser power was retrospectively adjusted to 325 and 250 mW/cm² in the gray and white matters, respectively, to limit ΔT to 0.5 °C. Total device area of the FLAMES increased with all parameters considered but decreased with the output voltage. We conclude that the number of series photodiodes in the device can be used as a free parameter to minimize the device size. The results suggest that floating, optically activated stimulators are feasible at submillimeter sizes for the activation of the brain cortex or the spinal cord.

I. Introduction

Electrical stimulation is currently used as a treatment method in a number of disorders of the central and peripheral nervous system and is being investigated for new applications [1]-[5]. Many of these applications demand very localized activation of the neural tissue to produce functional results particularly in the central nervous system (CNS). In order to achieve this high spatial selectivity, microelectrodes with penetrating shanks have been developed [6]-[8]. In these electrode designs, electric current is delivered to the array through a bundle of fine, flexible wires. However, these interconnects are usually the most vulnerable part of the neural implant that can eventually cause the devise to fail [9].

An attractive way of eliminating the interconnects is to transfer the electrical stimulus to the electrode wirelessly. In that case, the electrode becomes a floating device mechanically and electrically. Getting rid of the interconnects would improve device longevity by solving the wire breakage problem [9]. The tethering forces due to interconnects, which is the primary source of chronic tissue reaction [10], [11], would be eliminated. With no wires attached, the electrode would float and move along the neural tissue as it experiences translational and rotational displacements.

Our group is pursuing a novel floating microstimulator design that uses optical means for energy transfer [12]-[14]. In the envisioned paradigm, the microstimulator, essentially a semiconductor photodiode, is implanted into the neural tissue at the targeted site of the CNS, typically a few millimeters below the pial surface. The laser source and control electronics are implanted at a distant site (e.g., the subclavicular area) that is most convenient for transcutaneous charging of batteries and programming of the pulse parameters using radio-frequency (RF) telemetry. Multimode optical fiber is used to transfer the laser pulses near the microstimulator to activate it. The tip of the optical fiber is located just above the microstimulator, but outside the dura matter, possibly inserted through a hole into the skull or vertebrae. Therefore, the envisioned distance that the laser beam has to travel is only in the order of a few millimeters into the neural tissue above the microstimulator.

Since the stimulator does not have any active circuitry that requires continuous power for storing the stimulus current or controlling its waveform parameters, the device can be made in the submillimeter range. This study is motivated by the fact that if these small devices can activate sufficiently large volumes of neural tissue that can generate physiological responses of functional significance, this approach can become a powerful tool for improving longevity and functionality of many neural prosthetic applications by eliminating the wire interconnects. A light-activated microstimulator with a fiber-optic tail was reported recently by another group [15]. This design apparently does not intend to address the tethering problems of interconnects, but the implant longevity can be improved significantly because the wire connections are replaced by optical fiber.

To investigate the feasibility of the FLAMES approach, we first question how small can a floating stimulator be made without requiring extremely high levels of current for neural activation. That is, a floating stimulator is, by definition, a bipolar device since anode and cathode will be placed on the same substrate close to each other. The device output voltage will be shorted out by the decreasing access resistance of the conductive medium as the contacts approach each other. Finite-element analysis was employed to answer this question [13]. Computer simulations showed that the bipolar electrode voltage on a floating stimulator decreases only 20% when the intercontact distance is reduced from infinity to three times the size of the contacts. This suggests that the size of the stimulator as well as the contacts can be in the submillimeter range without losing much stimulation strength.

There are several other issues that need to be addressed for the optimization of floating microstimulators: 1) Can a sufficient number of photons be transmitted to a microstimulator implanted in depths of the white or gray matter to generate the currents needed without causing excessive temperature elevations near the surface? 2) Can the materials currently used for neural electrode contacts provide sufficient charge injection capacity (CIC) for microscale floating stimulators? 3) Does the output voltage play a role in determining the device size? and 4) Is the choice of substrate material, such as gallium arsenide (GaAs) and silicon (Si), critical?

We address all four questions in this paper with computer simulations as the first step toward implementation of this approach. The first question deals with Monte Carlo simulations of photon penetration into neural tissue in combination with an analytical heat-transfer model for inhomogeneous media. Then, the photon densities (fluence) predicted by this software are entered into a Matlab code that calculates the device parameters using a model based on the electrical equivalent of photodiodes. Matlab code then calculates the device dimensions for varying input parameters and for some typical neural stimulation applications. Finally, the volume of activation is predicted for these applications using an analytical model for a mammalian axon in a volume conductor [16].

II. Methods

A. Monte Carlo Simulations of Photon Penetration

Public domain software was utilized for Monte Carlo simulations [17] that calculated the probabilistic locations of a large number of photons on a 3-D grid as they propagated inside the tissue. An infinitely narrow photon beam was vertically transported down to infinitely wide multilayered tissue. Each layer was described by the refractive index, the absorption coefficient (μ_a), the scattering coefficient (μ_s), the anisotropy factor (g), and the thickness of the layer. As the light travels in the tissue, its intensity decreases due to absorption and scattering. Some of the incident light also reflects back at the surface of entry. Some of the photons exit the tissue slab through the other side (transmittance). The simulation software keeps a score of the photon densities inside the tissue (fluence) and on each side of the medium (reflectance and transmittance).

The photon densities for a finite-size light beam were computed by convolving the beam profile with the photon densities simulated for the infinitely narrow beam. A flat, circular intensity profile was assumed for the beam. Typical values for the absorption coefficient (0.47 cm⁻¹, [18]), scattering coefficient (51 cm⁻¹, [18]), anisotropy factor (g =0.9), and the refractive index (1.38), [19] of human gray matter were adopted from the literature for all simulations unless indicated otherwise. In order to simulate human white matter, only the absorption (0.64 cm⁻¹) [18] and scattering coefficients (265 cm⁻¹) [18] were adjusted.

B. Temperature Elevation Due to NIR Exposure

The temperature increase in the neural tissue was calculated based on the fluence values predicted by the Monte Carlo simulations and a 3-D analytical heat-transfer model developed in Matlab. The fluence values were first multiplied with the absorption coefficient to find the heat distribution in the medium. The photon beam entered this cylindrical volume from its top surface and produced a fluence profile that was axially symmetric (Fig. 1). Next, the temperature elevations were computed due to photons absorbed in the volume by using a steady-state heat-transfer model. Briefly, each voxel in the volume (40 × 40 × 40 μm³) was treated as a point heat source, located in the center of the voxel, that had an intensity proportional to the number of photons absorbed in the voxel. Temperature elevation at any point in a homogeneous medium due to a point heat source is given by

$$\Delta T=\frac{Q}{4\pi kr}$$ (1)

where Q is the point heat source (W), k is the thermal conductivity (0.57 and 0.5 W · m⁻¹ ·° C⁻¹ for gray and white matters [20]), and r is the distance from the source. The medium above the neural tissue was assumed to be air (k= 0.003 W · m⁻¹ ·° C⁻¹). In order to account for this inhomogeneity, fictitious heat sources of equal distance from the top border were imagined by using an analogy to current sources in inhomogeneous media [21]. The imaginary sources were scaled to account for the difference in the thermal conductivity coefficients of neural tissue and air. Treating a finite-size voxel as a point source introduced a small error at the nearest grid points to the voxel. The error was negligible after adding the temperature contributions from all other voxels in the medium. Simulations were repeated for gray and white matter and the maximum temperature increases in the medium were noted. The maximum incident light power was calculated retrospectively to keep the maximum temperature in the tissue below 0.5°C, a critical value at which changes in neuronal excitability become evident [22]. These exposure levels were used in the remaining simulations. Laser energy transferred to the tissue was considered as a constant heat source here because the pulse intervals employed in neural stimulation are much smaller compared to the thermal time constant of a volume of tissue that is a few cubic millimeters, which is in the order of several seconds.

Fig. 1.

The 3-D model geometry used in the heat-transfer model for calculations of temperature rise due to the absorption of the NIR light beam.

C. Electrical Model of the Device

A passive device that converts the light energy into electric current with maximum efficiency is essentially a PIN photodiode. A photodiode can be modeled as an ideal diode in parallel to a current source as shown in Fig. 2(b). The parallel resistor represents the leakage current that flows regardless of the voltage polarity. The I-V relation of a photodiode was modeled by using the classical equation

$$I_{\mathrm{diode}}=I_{\mathrm{sat}}\left(e^{-(q{V}_{\mathrm{diode}}∕kTf)}-1\right)-I_{ph}$$ (2)

where I_sat is the reverse saturation current; q is the electronic charge; k is Boltzmann’s constant; T is the temperature (°K); f is the ideality factor for practical photodiodes; and I_ph is the current generated by the incident photons, which is the light power received by the photodiode times its responsivity (R). The values adopted for these parameters are as follows (for Si and GaAs, respectively). R = 0.25, 0.5 A/W; f = 1.2, 1.5; I_sat = 10⁻⁹, 10⁻⁹ A/cm²; K = 1.38 × 10⁻²³ J/K; q = 1.6 × 10⁻¹⁹ C; T = 310 K (body temperature).

Fig. 2.

Electrical model of the FLAMES, which includes the photodiodes, the interface with the tissue at the contacts, and the tissue impedance (B). The drawing on top shows the arrangement of the photodiode active area and the contacts on the wafer (A). The aspect ratio of the top surface is 1:5.

For the remainder of this paper, we will use the parameters adopted from the literature that are typical for Si and GaAs photodiodes as practical choices. Therefore, the emphasis will be on the minimization of overall device dimensions and not on the design of individual photodiodes. Our main objective is to demonstrate how external parameters demanded by certain applications effect the overall device size and search if there are any optimal points in the parameter space. Multiple diodes in series were simulated in order to increase the output voltage. All photodiodes in series were assumed to receive the same intensity of light and generate the same current.

The parallel resistance to the diodes was ignored in the simulations due to its negligible effect on the results. Nevertheless, a parallel resistor will be included in the prototype device to ensure a discharge path for the double-charge layer capacitors of the contacts during the off periods of the current.

The middle dash box in Fig. 2(b) contains the electrical equivalent of the electrode-electrolyte interface. The electrode impedance is best simulated using a frequency-dependent capacitor or a constant phase element [23] to account for the nonideal capacitive behavior of the electrochemical double layer. In our simulation, we assumed an ideal capacitor and an infinite parallel resistance, because different recipes used in fabrication of these surfaces introduce several times larger variations into the capacitor value itself than variations due to its nonideal behavior as a function of frequency. We assumed a capacitor value that can give a charge injection capacity (CIC) of 1 mC/cm² within the voltage limits of the water window. This CIC can be achieved with materials such as titanium nitride (TiN) [24], iridium oxide (IrOx) [25], or PEDOT [26], [27]. The last one is more suitable for this application to achieve the assumed CIC without the need for dc bias. The water window was taken as 1 V for the anodic and cathodic directions [24], [27]. The tissue is simulated as a pure resistive load that consisted of twice the access resistance; one for each contact.

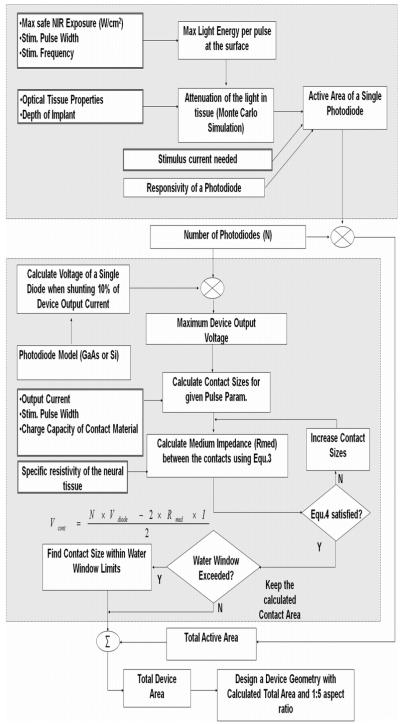
D. Calculations of Device Area

Photodiodes and the contacts are envisioned on the same side of the fabrication wafer where each device will be diced into a rectangle of a 1:5 aspect ratio [to make the intercontact distance three times the size of the contacts, Fig. 2(a)]. Fig. 3 depicts the flowchart for the calculation of total device area, which mainly consists of the active areas of the photodiodes to receive the light energy, and the two contacts for delivering the current into the tissue. Minimizing the device top surface area is equivalent to minimizing the device size because the minimum height is primarily dictated by the strength of the substrate material rather than the thickness of the PIN diode structure. The boxes with double-lined frames indicate input parameters that are to be chosen according to the requirements of a specific application. The large box with gray filling on top demarcates the calculation steps for the active area of a single photodiode. The active area is a function of the light energy that is available at the tissue surface, the attenuation encountered by the time it gets to the device, and the efficiency by which the photons are converted into electron-hole pairs in the photodiode. The laser energy for each pulse is found by dividing the maximum safe exposure value for the continuous beam by the pulse frequency. Then, the peak power is elevated proportionally to deliver this energy within 0.2 ms of pulse duration. The selection of pulse duration is based on the neural prosthetic applications shown in Table I.

Fig. 3.

Matlab flow diagram for the calculation of the FLAMES surface area. Boxes with thicker-line frames indicate the input parameters chosen according to the application.

TABLE I.

Flames Device Dimensions Estimated for Two Different Neural Prosthetic Applications in Humans. Simulation Results for GaAs (Bottom) and Si (Top) Devices are Separated by a Dash Line

Human Application		Stimulus Parameters			Simulation Results
Implant Site in Humans	Implant Depth	Reference	Current (μA)	Pulse Width/ Freq.	N	Total Active Area (μm2)	Total Contac t Area (μm2)	Device Dimension L × W (μm2)	Charge Density (μC/cm2)	Activation Distance (μm) for Fibers of 1 / or 7μm
Human Visual Cortex	2mm of gray matter	Schmidt et al., 1996 (human)	25	0.2ms/ 200Hz	4	5,440	3,674	213×43	272	66/66
					4	2,720	2,251	158×31	444	64/60
Spinal Cord Ventral Horn Motoneurons in L4	1.5mm white + 1.0mm gray	Tai et al., 2003 (cat)	100	0.2ms/ 40Hz	7	30,324	14,830	475×95	270	98/134
					7	15,162	9,122	348×70	438	100/120
		Mushahwar et al, 2006 (cat study)	150*	0.2ms/ 50Hz	7	56,861	31,560	665×133	190	112/212
					7	28,434	19,060	487×98	315	120/188
		Saigal et al., 2004 (cat study)	200#	0.2ms/ 25Hz	10	54,150	26,050	633×127	307	140/254
					10	27,080	16,350	466×93	489	146/226

^*at ~ 30 N Tetanic Force

^#Stepping on a Treadmill). N is the Number of Series Photodiodes in the Device

The second large gray box shows the calculation steps for the contact areas. The device output voltage is equal to the sum of the potentials across the electrode-electrolyte interface at each contact and the voltage across the medium. The current flowing through the parallel diodes [Fig. 2(b)] will be determined by the output voltage according to the diode (2). A maximum of 10% of the output current is allowed to flow through the diodes in the simulations by adjusting the contact sizes as will be described.

For a given device current and contact CIC, the contact area determines the voltage that will develop across the electrode-electrolyte interface for the anode and the cathode. The contact size also determines the access resistance for each contact [R_med in (3)] which, in turn, defines the voltage across the medium when multiplied by the current (4). The access impedance for a circular electrode at the border of a semi-infinite medium is given as [28]

$$R_{\text{access}}=\frac{\rho }{4r}$$ (3)

where ρ is the specific resistivity of the medium (Ωcm), and r is the radius of a circular electrode. The impedance of a square electrode is about 5.5% less than a circular one with the same area, as calculated numerically using finite-element analysis [13]. This effect of contact shape as well as the decrease in R_med due to a short separation between contacts were factored into the simulations. The total medium impedance is twice the value calculated by (3), since the cathode and anode each has its own access resistance, less [Author: “minus” instead of “less”?] a 20% decrease [13].

Finally, if the calculated value of the contact voltage (V_cont) is larger than the water window, the contact size is increased proportionally to keep the voltage just within the limits. Forcing the contact sizes to a larger value, however, reduces the device output voltage, because of a decrease in R_med.

In (4), either the medium voltage (2×R_med×I) or the contact voltages may become dominant depending on the interplay between the specific resistivity of the medium (ρ) and the CIC of the material chosen for the contacts, respectively. Here, the contact area is decreased iteratively until the total voltage reaches up to a value where 10% of the output current (I) is flowing through the parallel diodes according to (2). The total voltage across N series diodes is equal to the voltage across the medium plus the two contacts, as formulated

$$V_{\text{out}}=N\times V_{\mathrm{diode}}=2\times R_{\text{med}}\times I+2\times V_{\mathrm{cont}}.$$ (4)

III. Results

A. Temperature Elevation Due to NIR Exposure

First, we studied the temperature elevations due to the absorption of NIR light by the neural tissue (Fig. 4). It was found that the laser beam power had to be set to 325 and 250 mW/cm² in the gray and white matters, respectively, in order to limit the maximum temperature at 0.5 °C inside the tissue. The temperature profile is different than the photon density profile due to the dissipation of heat through the medium. The maximum temperature elevations are observed not at the surface but at about 1200 μm (gray) and 700 μm (white) below the surface. Also, the fluence values are larger inside the tissue than the surface. Photons entering the medium may reflect back after scattering a few times just below the surface, but the ones that are able to penetrate more stay around longer before they are finally absorbed. This elevates the photon density inside the medium. The selection of a large beam size may be necessary to maximize the photon density at deeper layers of the tissue (simulations are not shown). We have chosen a beam radius of 2 mm for all simulations in this paper.

Fig. 4.

NIR fluence (W/cm²) inside the (a) gray and (c) white matters due to a 2-mm radius NIR beam and the resulting temperature elevations in tissue (B for gray and D for white). Fluence data are color-coded in the logarithmic scale. The NIR light beam is aimed from top to the center of the volume. Due to cylindrical symmetry, the plots show the fluence and temperature distributions only in one-half of a cross section.

B. Device Size as a Function of Application-Specific Variables

The effects of four application-specific variables and an independent variable were investigated on the active and contact areas as well as the output voltage of the microstimulator. The application-specific variables are the device-output current (I), the implantation depth of the stimulator (Depth), the medium-specific resistivity (ρ), and the tissue type (white versus gray). The independent variable is the number of series photodiodes in the device (N). Other parameters were fixed at typical values for the stimulation of the CNS (f = 50 Hz and PW = 200 μs) unless specified otherwise.

The active PN junction area of a single GaAs photodiode is plotted as a function of implant depth and the device current in Fig. 5. The active area increases exponentially with implant depth because of an exponential decrease in the number of photons available. The dependence of the active area on the device output current is almost a linear line. The photodiode active area is independent of medium resistivity per se but varies with the tissue type because of scattering and absorption (not shown).

Fig. 5.

Active area for a single GaAs photodiode as a function of output current and implantation depth into human gray matter.

In Fig. 6, the combined area for the anodic and cathodic contacts is plotted as a function of current, medium resistivity, implant depth, and N, varying only one parameter at a time. Contact sizes increase exponentially as a function of current [Fig. 6(a)]. As the current increases, the voltage across the medium increases and leaves a smaller voltage window for the contacts (V_contact) since the total voltage is limited by the voltage output generated by the photodiodes [N × V_diode in (4)]. The contacts need to be made larger in order to achieve the same total charge within a smaller voltage window across the double-charge layer. The rise in the contact area is an exponential rather than a linear line because increasing current also demands a larger total charge from the contacts.

Fig. 6.

Total contact area (anode+cathode) as a function of: (a) Output current (Depth = 3 mm, ρ = 500 Ωcm, N = 6). (b) Medium-specific impedance (Depth = 3 mm, I = 50 μA, N = 6). (c) Implantation depth (I = 50 μA, ρ = 500 Ωcm [29], N = 6). (d) The number of photodiodes in a device (N). Only one parameter is varied in each plot while the others are fixed at values shown in parentheses.

Medium-specific impedance (ρ) has a very similar effect on the contact area as shown in Fig. 6(b). Implantation depth would not have any effect on the contact area if the diode characteristics were independent of it [Fig. 6(c)]. However, we imposed a condition that a maximum of 10% of the device output current should flow through the PN junction of the photodiodes at the end of the pulse duration. For deeper implants, the active area increases as discussed before [Fig. 5]. This increases the saturation current (I_sat) of the diodes since I_sat is proportional to the active area. As a result, the voltage across each diode decreases for 10% of the output current, according to (2), again leaving a smaller voltage window for the contacts. Therefore, the contact area has to increase slowly as plotted in Fig. 6(c) with implantation depth to accommodate this decrease in the contact voltage. The last plot in Fig. 6 indicates that the contact areas decrease exponentially by the number of photodiodes in the device. This is because the allowed contact voltage increases quickly with additional diodes in series (4). Larger contact voltages (within the water window) allow smaller contact areas for the same total charge.

Total device area, which is equal to the sum of the active and the two contact areas, is shown in Fig. 7 as a function of three parameters. Dominated by the active area, the total device area increases exponentially by the device current in Fig. 7(a).

Fig. 7.

Total device area (active areas plus contact areas) as a function of: (a) output current, (b) medium-specific resistivity, and (c) implantation depth. Fixed parameters are the same as in the Fig. 6 legend.

Sincee the active areas are independent of the medium impedance, the plot in Fig. 7(b) is a reflection of the exponential increase of the contact sizes as a function of medium-specific resistance in Fig. 6(b). Implant depth has a marginal effect on the contacts [shown in Fig. 6(c)] but a major impact on the active area of the photodiodes (Fig. 5). Thus, the combined plot in Fig. 7(c) is again dominated by the active area, when all of the other parameters are fixed.

Total area calculations for Si photodiodes are similar in appearance to those of GaAs, but are about twice higher in value. The active areas are doubled due to lower efficiency of Si at NIR wavelengths (R = 0.25 versus 0.5). The larger saturation current of Si diodes causes the output to be shunted at lower voltages by the PN junction. As a result of smaller output voltage, the contact areas turn out to be also larger for Si devices.

The data in Fig. 7 are plotted in a different way in Fig. 8 to demonstrate that the total device area can be minimized by proper selection of N. The depth of implant increases from 0.5 to 3 mm in each panel shown in different colors. The left column simulates human gray matter and the right column simulates human white matter. The optimum N value that minimizes the total area changes depending on the other three parameters considered; the implantation depth, the output current, and the tissue type. The rise on the left side of each plot is due to the large contact area needed for small N, as shown in Fig. 6(d). The ramp toward the right in each plot is a result of the linear dependence of the active area on N. The slope, however, changes as a function of implantation depth. As the current is increasing from 25 μA (top row) to 50 μA (middle row) and then to 75 μA (bottom row), both arms at extreme values of N are rising in each figure. Nevertheless, the effect of the current on the contact area is stronger, hence the optimum number of diodes shifts toward the right as the left arms of the plots move up faster. On the other hand, the change from gray matter to white matter is more substantial. These plots suggest that minimum device size strongly depends on all three parameters (i.e., the current, the tissue type (which also means medium-specific resistance), and the implantation depth).

Fig. 8.

Total device area as a function of N. The output current increases from top to bottom (25, 50, and 75 μA). Medium-specific resistances are representative of the gray (500 Ωcm) and white matters (longitudinal and transverse resistivity 300 Ωcm and 1200 Ωcm [30]), left and right columns, respectively. Implantation depths are as indicated in the first plot.

The voltage that develops across the medium, which is essentially the stimulation voltage, is studied in Fig. 9. The voltage increases sharply with current first and then soars. The plot would be linear if the contact size is kept constant while the current is increasing, since the medium impedance (access resistance) is defined by the contact size. However, the contact area has to be made larger as the current is increasing because the voltage across the contact capacitance is limited by the water window. The larger contact area, in turn, reduces the medium impedance between the contacts, hence the voltage across the medium [V_med in (4). Thus, the combined effect is that the medium voltage does not increase linearly by current.

Fig. 9.

Device output voltage as a function of: (a) output current, (b) medium-specific impedance, (c) implantation depth, and (d) the number of photodiodes in a device. Fixed parameters for each plot are the same as in the Fig. 6 legend.

The effect of the medium-specific impedance is similar to that of the device current on the output voltage [Fig. 9(b)]. The output voltage soars up to around 4.8 V and 3.7 V (GaAs and Si, respectively) for the largest medium impedance and the number of diodes considered (N = 6). Contrary to its effect on the contact area [in Fig. 6(c)], increasing implantation depth slightly reduces the output voltage [Fig. 9(c)]. The underlying mechanism, however, is the same as in Fig. 6(c). For deeper implants, the active area increases and the saturation current of the diodes (I_sat) increases as well.

This, in turn, reduces the voltage across each diode (2) and the overall device output voltage (4). As expected, the output voltage increases almost linearly with the number of diodes [Fig. 9(d)] when all other parameters are fixed. The GaAs plot saturates at N = 7 due to the limitation of the contact voltage by the water window. For N <7, the minimum contact size that satisfies (3) and (4) produces a contact voltage that is always less than 1 V. For N ≥7, however, the contact voltage exceeds the water window and the contact size has to be increased until the voltage is reduced back to 1 V. In this case, the left side of (4) is truncated at a voltage less than the total diode voltage rated for 10% of output current. A similar effect is observed with Si for N >10 (not shown).

C. Application of Practical Examples

Finally, device dimensions are estimated according to the requirements of two neural prosthetic applications as practical examples (Table I). Stimulation parameters for the human visual cortex (as an aid to blind subjects) were taken from Schmidt et al. [1]. Assuming an implantation depth of 2 mm for the targeted structures, the optimum number of GaAs or Si phodiodes was found as 4 with a total device surface area of 4971 and 9114 μm² respectively. The stimulation of ventral horn neurons of the lumbosacral cord as a method of restoring locomotion was considered for the second application. Since there are no human data, we adopted the spinal-cord microstimulation parameters from cat studies. The depth of ventral horn neurons was estimated as 2.5 mm (1.5 mm of white and 1.0 mm of gray matter) from the dorsolateral funicular pial surface at the level of L4 in the human [31]. Three different sets of stimulation parameters were tested based on the experience of three groups. The optimum number of diodes varied between 7 and 10 depending on stimulation parameters and the semiconductor type used. Device dimensions (L×W) for an aspect ratio of 5:1 are also shown in Table I. GaAs devices, in general, are smaller. The device thickness (height) is limited only by the mechanical strength of the semiconductor material. The next column shows the injected charge density of the contacts for an optimized device geometry in each case. The fact that the CIC values do not reach the limit of 1 mC/cm² indicates that the water window did not limit the output voltage for this optimum number of diodes.

We also computed the maximum distance for activation of a myelinated nerve fiber that is running parallel above the top surface of the device, based on the formulation developed by Warman et al. [16]. This model produces a driving function along the fiber considering not only the spatial second derivative of the extracellular field but also the contributions of the currents flowing into five neighboring nodes on each side of the central node. The threshold value is predicted from the intracellular strength-duration curve for the neuron and the peak of the driving function. We used the chronaxie time and rheobase given in this model for the mammalian axon (30 μs and 3.85 mA/cm²). Fig. 10 shows the driving function in the vertical plane running longitudinally (y axis) in the center of the microstimulator where z = 0 corresponds to the top surface. The driving function has a positive peak above the cathode and a negative peak above the anode. The black ring around the positive peak shows the threshold for activation. There are small positive and negative peaks with black rings on each side. This is due to the contributions from the adjacent nodes when they line up with the contacts. Any fiber falling into the black rings will be activated. The maximum distance along the z-axis from the top surface of the stimulator is calculated and entered into the last column of Table I for each device.

Fig. 10.

Driving function according to [16] for the FLAMES in the last row of Table I for a 7-μm myelinated mammalian axon fiber running parallel along the device above its top surface. The black belt shows the threshold of activation (i.e., axons placed inside this line will be activated).

Two extreme values for the fiber size were considered:, 1 and 7 μm, based on a report by Terao et al. [32] where they studied the diameter of the myelinated fibers in the human corticospinal tract and found that most of the fibers fall into the range of 1–7.28 μm. The activation distances are quite similar for both fiber sizes when the device size is comparable to the intermodal distance of the 1-μm fiber. However, the 7-μm fiber can be activated at much larger distances with larger devices. As a general rule, the activation distance does not vary much depending on the semiconductor type (i.e., device size) for the same output current. In one case, the activation distance is larger for the smaller fiber. This exception occurs due to misalignment of the nodes of Ranvier with the contact locations.

IV. Discussion

A. Device Size

Our simulations show that minimum device sizes that can generate functionally useful stimuli depend on a number of parameters. Overall, the results suggest that submillimeter size FLAMES are feasible for implantation depths that are sufficient for a number of neural prosthetic application in the human cortex and the spinal cord.

Another important conclusion is that the device size can be minimized by optimizing the number of photodiodes, which essentially determines the maximum output voltage. The optimum number of photodiodes varies with all of the parameters considered; implantation depth, tissue type, and device current. The optimum number of diodes (N) is a reflection of the fact that increasing the output voltage helps to reduce the device size. These N values could be smaller if the CIC of the contact material were larger. The fabrication of several GaAs diodes vertically poses a technical challenge although planar organization of multiple Si diodes would not be very difficult. The total device areas shown in Table I do not include the surface area needed to incorporate a parallel resistance for discharging the interface capacitances during off cycles. This resistor can consume a significant percentage of the total area for devices with small output currents where the resistor value is in the mega-ohm range. The actual device sizes may deviate from our simulation results because of large errors of margin inherent to the microfabrication process. Moreover, the optical tissue properties reported in the literature vary in a large range.

B. GaAs versus Si

GaAs photodiodes are recommended over Si ones because of smaller device sizes, which is primarily due to GaAs’s higher quantum efficiency at NIR wavelengths, and second, GaAs photodiodes can reach larger output voltages before the PN junction begins shunting the output voltage. This is due to smaller saturation currents that can be achieved with GaAs. The larger output voltage, in turn, allows smaller contacts and smaller devices.

C. Charge Injection Capacity

The CIC of the material used for the device contacts is a critical parameter that strongly impacts the contact sizes especially for small N [Fig. 6(d)]. Novel materials that exceed the CIC of 1 mC/cm² can reduce the device dimensions substantially from the values reported here. Both titanium nitride [24] and iridium oxide [25] are reportedly capable of providing these injection rates, particularly if a bias voltage is applied to the contact in the case of iridium oxide. The biasing option was not recommended here since it would complicate the device design with additional active circuitry. PEDOT provides similarly high CIC without the need for a bias voltage [26].

The charge per pulse values considered in Table I range between 5–40 nC, which are comparable to threshold charges for subretinal (7–50 nC in the rabbit and pig [33] and 1.6 nC in isolated chicken retina [34]) and for epiretinal (7 nC in amphibian [35]) stimulation. Electrode sizes range from 10–100 μm in these reports, which are also comparable to the ones in Table I (~ the device width). The threshold currents/charges may vary substantially depending on how far the targeted neural structures are located. Palanker et al. [36] predicted that the threshold for activating a cell of 10-μm size at a distance half the size of a monopolar electrode would be about 550–620 μC/cm². The threshold for a larger cell or a bypassing axon would be smaller. As a comparison, the charge densities in Table I vary from 190 μC/cm² to 489 μC/cm². Snow et al. reported that 400 μC/cm² is sufficient for stimulation in the spinal cord [37].

D. Laser Exposure and Heating Effect

The safe level of NIR exposure is given only for the skin and retina by the recently updated American National Standards for Safe Use of Lasers (ANSI Z136.1-2007). Using the tables in this publication, the maximum permissible exposure (MPE) was calculated as 400 mW/cm² on the skin at a wavelength of 830 nm.

For the neural tissue, we used a temperature increase of 0.5°C as a limiting factor in our simulations, which predicted slightly lower thresholds for NIR exposure (325 and 250 mW/cm² for gray and white). Our simulations did not account for blood circulation or the effect of metabolism. Without NIR exposure, the metabolism and the heat dissipating effect of the blood circulation should balance each other and stabilize the brain temperature around 37 °C. Some of the additional heat generated by the NIR exposure should be dissipated away by blood circulation, which was responsible for a temperature decrease of about 0.15 °C in a simulation where the heating effect of the electrode current was studied for deep brain stimulation [38]. Therefore, the temperature elevation in the real neural tissue should not exceed the 0.5 °C level predicted here when all factors are considered. The temperature elevation will remain within 0.5 °C only as long as multiple sites are not activated simultaneously in a small area.

It should be noted that the peak power is much higher when the energy is delivered in a pulsed fashion even though the total energy per second is below the calculated safety limit. The energy is delivered in concentrated packages during each pulse. The thermal time constant of neural tissue, which is a function of heated volume, is much longer than the interpulse intervals considered here for neural stimulation (<40 ms). Therefore, we assumed that the instantaneous temperature rises are averaged out by this capacitive effect in the tissue. The beam profile is also critical to keep the temperatures below a certain limit in the neural tissue while delivering sufficient energy to activate the microstimulators. A Gaussian profile circular beam, for instance, would have a peak of 1/(2πσ²) times the total power of the source, where σ is the value where the Gaussian intensity profile drops down to 1/e² of its peak in the 2-D plane. For small diameter beam sizes, the profile can be very peaky and, therefore, easily induces large temperature elevations in the center of the beam. We adopted a flat profile circular beam, which can be obtained with the use of optical microlenses, to avoid the spatial peak effect.

The laser beam size is an important factor in the FLAMES approach. In the envisioned paradigm, the laser source will be fixed to a bone; however, the devices will be moving in and out of focus with the movements of the CNS inside the dura. The sensitivity to motion can be reduced by increasing the beam size. Fig. 4(a) and (c) suggests that photon density does not change much for horizontal displacements of the source that are in the same order as the beam radius. The tradeoff is that a larger tissue volume will be radiated by a larger beam.

Optical properties of tissue play an important role in the FLAMES design. NIR light can penetrate more easily into neural tissue than the visible light. Scattering is the dominant form of interaction with the neural tissue at NIR wavelengths. Gray matter has a lower scattering coefficient than the white matter and, as a result, NIR light penetrates more readily into the gray matter. A significantly larger device area is required to collect sufficient light photons for similar implantation depths in the white matter. The reportedly higher specific resistivities [34] of the white matter also increase the device contact areas.

E. Future Studies

The activation distances shown in Table I vary between 60 and 254 μm, depending on the fiber size and the device output current. A number of potential applications can be conceived for the FLAMES with these volumes of activation. Stimulation of the visual cortex and intraspinal stimulation are only two examples considered here.

Retinal prostheses that are being developed in several labs across the world [34], [40]-[43] use photodiode arrays to activate retinal cells in a way similar to the approach pursued in this paper. Biostability of these photodiode arrays was tested for subretinal implants in vivo [42]. The Si–oxide passivation layer of the chips was dissolved in 6–12 months and the underlying Si was corroded. Biocompatibility and in vivo stability of potential coating materials need to be investigated for the FLAMES as well. A delivery method for the implantation of FLAMES into the targeted regions in the spinal cord and the brain cortex is also being investigated in our laboratory. Future goals include fabrication and testing of optimized device geometries in animal models.

V. Conclusion

The most significant conclusion of this study is that optically activated neural stimulators are feasible for implantation depths of a few millimeters without causing ΔT larger than 0.5 °C in the medium and keeping the device size to under a millimeter. Any technique that can enhance the penetration of light energy through neural tissue or maximize the transfer of charges from the stimulator into the medium will be instrumental for achieving smaller device sizes. A critical design parameter for achieving smaller device dimensions is the CIC of the contact materials.

A floating, wireless stimulator with micrometer dimensions can be an important step toward the realization of many neural prosthetic ideas that require the stimulation of neural tissue in the most mobile parts of the nervous system, such as the spinal cord. The spinal cord experiences substantial translational and rotational displacements that make chronic implantation of microwire electrodes nearly impossible. The implantation of a sufficient number of FLAMES in the visual cortex for a visual prosthesis may prove to be challenging at the end. In the spinal cord, however, a few channels of stimulation are sufficient to restore function as demonstrated in some studies [2]-[4].

Biography

Ammar Abdo (S’09) received the B.S. degree in biomedical engineering from the Hashemite University, [Author: Please provide city] Jordan, in 2004 and the M.Sc. degree in biomedical engineering from the New Jersey Institute of Technology, Newark, in 2007, where he is currently pursuing the Ph.D. degree in biomedical engineering.

His research interests include developing microstimulators for neural stimulation applications.

Mesut Sahin (M’95–SM’06) received the B.S. degree in electrical engineering from Istanbul Technical University, Istanbul, Turkey, in 1986 and the M.S. and Ph.D. degrees in biomedical engineering from Case Western Reserve University, Cleveland, OH, in 1993 and 1998, respectively.

He was an R&D Engineer in the telecommunication industry from 1987 to 1990 in Istanbul. He received a scholarship from the Turkish Ministry of Education to support his graduate education in the U.S. in 1990. After receiving the Ph.D. degree, he continued his training as a Postdoctoral Research Associate in studies related to functional electrical stimulation in obstructive sleep apnea. He joined Louisiana Tech University, Ruston, as an Assistant Professor of Biomedical Engineering in 2001. He has been on the faculty of Biomedical Engineering at New Jersey Institute of Technology, Newark, since 2005 and became Associate Professor in 2009. He has authored many peer-reviewed publications. His research interests include floating-ight-activated microstimulators, as well as spinal-cord-computer and brain-computer interfaces.

Prof. Sahin received a Whitaker Award from Louisiana Tech University to continue his work on spinal-cord computer interfaces. He received a postdoctoral grant from the Christopher Reeve Paralysis Foundation in 1999 to study the signals from the descending tracts of the spinal cord as a means of interfacing with the central nervous system.