Spectral Regularization Algorithms for Learning Large Incomplete Matrices

Abstract

We use convex relaxation techniques to provide a sequence of regularized low-rank solutions for large-scale matrix completion problems. Using the nuclear norm as a regularizer, we provide a simple and very efficient convex algorithm for minimizing the reconstruction error subject to a bound on the nuclear norm. Our algorithm Soft-Impute iteratively replaces the missing elements with those obtained from a soft-thresholded SVD. With warm starts this allows us to efficiently compute an entire regularization path of solutions on a grid of values of the regularization parameter. The computationally intensive part of our algorithm is in computing a low-rank SVD of a dense matrix. Exploiting the problem structure, we show that the task can be performed with a complexity linear in the matrix dimensions. Our semidefinite-programming algorithm is readily scalable to large matrices: for example it can obtain a rank-80 approximation of a 10⁶ × 10⁶ incomplete matrix with 10⁵ observed entries in 2.5 hours, and can fit a rank 40 approximation to the full Netflix training set in 6.6 hours. Our methods show very good performance both in training and test error when compared to other competitive state-of-the art techniques.

1. Introduction

In many applications measured data can be represented in a matrix X_m×n, for which only a relatively small number of entries are observed. The problem is to “complete” the matrix based on the observed entries, and has been dubbed the matrix completion problem [CCS08, CR08, RFP07, CT09, KOM09, RS05]. The “Netflix” competition (e.g. [SN07]) is a popular example, where the data is the basis for a recommender system. The rows correspond to viewers and the columns to movies, with the entry X_ij being the rating ∈ {1,…,5} by viewer i for movie j. There are 480K viewers and 18K movies, and hence 8.6 billion (8.6 × 10⁹) potential entries. However, on average each viewer rates about 200 movies, so only 1.2% or 10⁸ entries are observed. The task is to predict the ratings that viewers would give to movies they have not yet rated.

These problems can be phrased as learning an unknown parameter (a matrix Z_m×n) with very high dimensionality, based on very few observations. In order for such inference to be meaningful, we assume that the parameter Z lies in a much lower dimensional manifold. In this paper, as is relevant in many real life applications, we assume that Z can be well represented by a matrix of low rank, i.e. Z ≈ V_m×kGk×n, where k ≪ min(n, m). In this recommender-system example, low rank structure suggests that movies can be grouped into a small number of “genres”, with G_ℓj the relative score for movie j in genre ℓ. Viewer i on the other hand has an affinity V_iℓ for genre ℓ, and hence the modeled score for viewer i on movie j is the sum ${\displaystyle {\sum }_{\ell =1}^k{V}_{i\ell }{G}_{\ell j}}$ of genre affinities times genre scores. Typically we view the observed entries in X as the corresponding entries from Z contaminated with noise.

Recently [CR08, CT09, KOM09] showed theoretically that under certain assumptions on the entries of the matrix, locations, and proportion of unobserved entries, the true underlying matrix can be recovered within very high accuracy. [SAJ05] studied generalization error bounds for learning low-rank matrices.

For a matrix X_m×n let Ω ⊂ {1,…,m} × {1,…,n} denote the indices of observed entries. We consider the following optimization problem:

$$\begin{array}{ll}\hfill \text{minimize}& \text{rank}(Z)\hfill \\ \hfill \text{subject to}& {\displaystyle \sum _{(i,j)\in \mathrm{\Omega }}{(X_{ij}-Z_{ij})}^2\le \delta ,}\hfill \end{array}$$ (1)

where δ ≥ 0 is a regularization parameter controlling the tolerance in training error. The rank constraint in (1) makes the problem for general Ω combinatorially hard [SJ03]. For a fully-observed X on the other hand, the solution is given by a truncated singular value decomposition (SVD) of X. The following seemingly small modification to (1),

$$\begin{array}{ll}\hfill \text{minimize}& {\Vert Z\Vert }_{*}\hfill \\ \hfill \text{subject to}& {\displaystyle \sum _{(i,j)\in \mathrm{\Omega }}{(X_{ij}-Z_{ij})}^2\le \delta ,}\hfill \end{array}$$ (2)

makes the problem convex [Faz02]. Here ‖Z‖_* is the nuclear norm, or the sum of the singular values of Z. Under many situations the nuclear norm is an effective convex relaxation to the rank constraint [Faz02, CR08, CT09, RFP07]. Optimization of (2) is a semi-definite programming problem [BV04, Faz02] and can be solved efficiently for small problems, using modern convex optimization software like SeDuMi and SDPT3. However, since these algorithms are based on second order methods [LV08], they can become prohibitively expensive if the dimensions of the matrix get large [CCS08]. Equivalently we can reformulate (2) in Lagrange form

$$\underset{\mathrm{Z}}{\text{minimize}}\frac{1}{2}{\displaystyle \sum _{(i,j)\in \mathrm{\Omega }}{(X_{ij}-Z_{ij})}^2+\lambda {\Vert Z\Vert }_{*}.}$$ (3)

Here λ ≥ 0 is a regularization parameter controlling the nuclear norm of the minimizer Ẑ_λ of (3); there is a 1-1 mapping between δ ≥ 0 and λ ≥ 0 over their active domains.

In this paper we propose an algorithm Soft-Impute for the nuclear norm regularized least-squares problem (3) that scales to large problems with m, n ≈ 10⁵–10⁶ with around 10⁴–10⁵ or more observed entries. At every iteration Soft-Impute decreases the value of the objective function towards its minimum, and at the same time gets closer to the set of optimal solutions of the problem 2. We study the convergence properties of this algorithm and discuss how it can be extended to other more sophisticated forms of spectral regularization.

To summarize some performance results¹:

• We obtain a rank-11 solution to (2) for a problem of size (5 × 10⁵) × (5 × 10⁵) and |Ω| = 10⁴ observed entries in under 11 minutes.

• For the same sized matrix with |Ω| = 10⁵ we obtain a rank-52 solution in under 80 minutes.

• For a 10⁶ × 10⁶ sized matrix with |Ω| = 10⁵ a rank-80 solution is obtained in approximately 2.5 hours.

• We fit a rank-40 solution for the Netflix data in 6.6 hours. Here there are 10⁸ observed entries in a matrix with 4.8 × 10⁵ rows and 1.8 × 10⁴ columns. A rank 60 solution takes 9.7 hours.

The paper is organized as follows. In Section 2, we discuss related work and provide some context for this paper. In Section 3 we introduce the Soft-Impute algorithm and study its convergence properties. The computational aspects of the algorithm are described in Section 4, and Section 5 discusses how nuclear norm regularization can be generalized to more aggressive and general types of spectral regularization. Section 6 describes post-processing of “selectors” and initialization. We discuss simulations and experimental studies in Section 7 and application to the Netflix data in Section 8.

2. Context and related work

[CT09, CCS08, CR08] consider the criterion

$$\begin{array}{ll}\hfill \text{minimize}& {\Vert Z\Vert }_{*}\hfill \\ \hfill \text{subject to}& Z_{ij}=X_{ij},\forall (i,j)\in \mathrm{\Omega }\hfill \end{array}$$ (4)

With δ = 0, the criterion (1) is equivalent to (4), in that it requires the training error to be zero. Cai et. al. [CCS08] propose a first-order singular-value-thresholding algorithm SVT scalable to large matrices for the problem (4). They comment on the problem (2) with δ > 0, but dismiss it as being computationally prohibitive for large problems.

We believe that (4) will almost always be too rigid and will result in overfitting. If minimization of prediction error is an important goal, then the optimal solution Z* will typically lie somewhere in the interior of the path (Figures 1,2,3), indexed by δ.

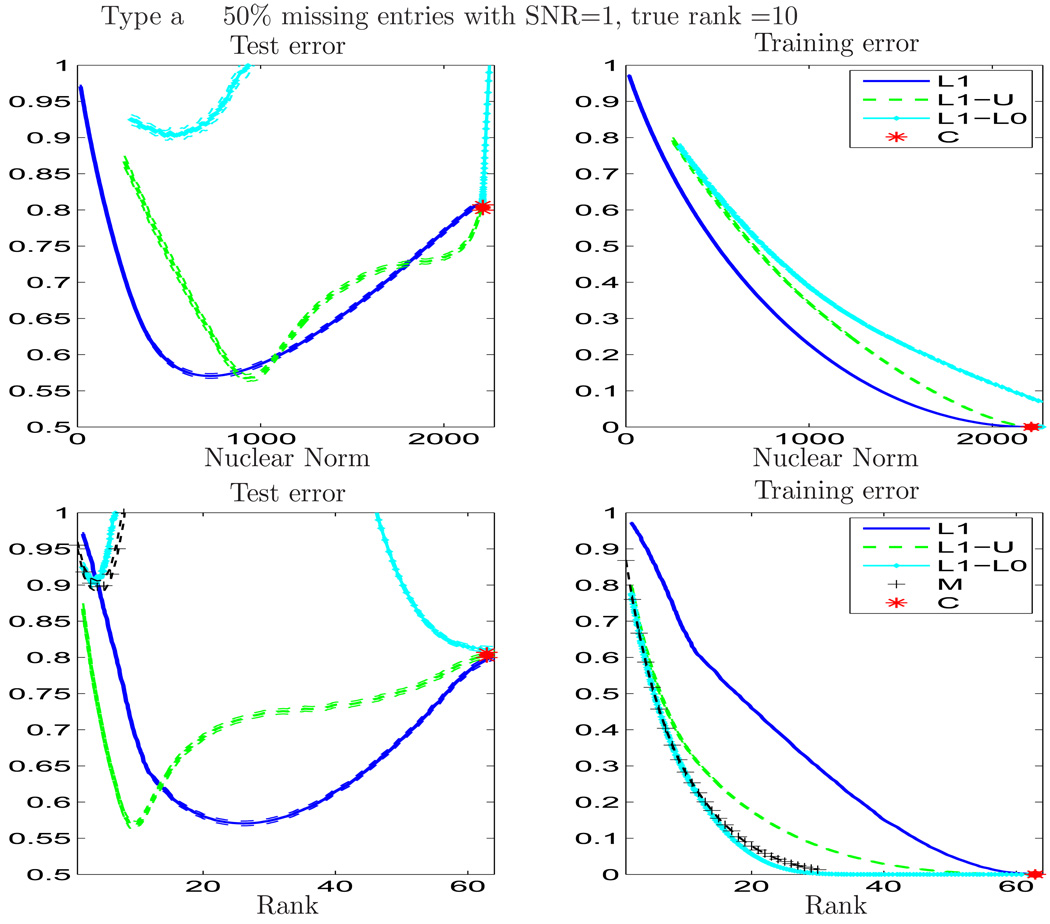
Figure 1.

L1: solution for Soft-Impute; L1-U: Post processing after Soft-Impute; L1-L0 Hard-Impute applied to L1-U; C : SVT algorithm; M: OptSpace algorithm. Both Soft-Impute and Pp-SI perform well (prediction error) in the presence of noise. The latter estimates the actual rank of the matrix. Both the Pp-SI and Hard-Impute perform better than Soft-Impute in training error for the same rank or nuclear norm. Hard-Impute and OptSpace perform poorly in prediction error. SVT algorithm does very poorly in prediction error, confirming our claim that (4) causes overfitting — it recovers a matrix with high nuclear norm and rank > 60 where the true rank is only 10. Values of test error larger than one are not shown in the figure. OptSpace is evaluated for a series of ranks ≤ 30.

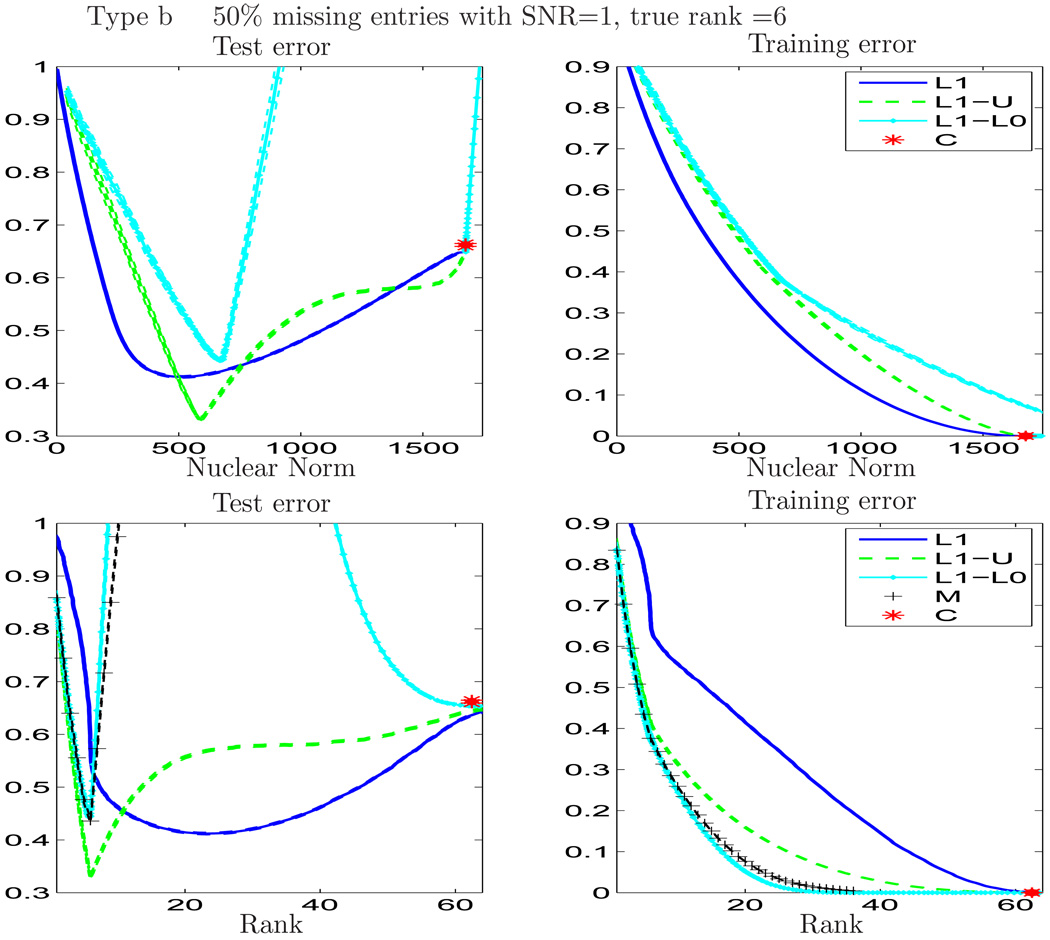
Figure 2.

Pp-SI does the best in prediction error, closely followed by Soft-Impute. Both Hard-Impute, OptSpace have poor prediction error apart from near the true rank of the matrix ie 6 where they show reasonable performance. SVT algorithm does very poorly in prediction error — it recovers a matrix with high nuclear norm and rank > 60 where the true rank is only 6. OptSpace is evaluated for a series of ranks ≤ 35.

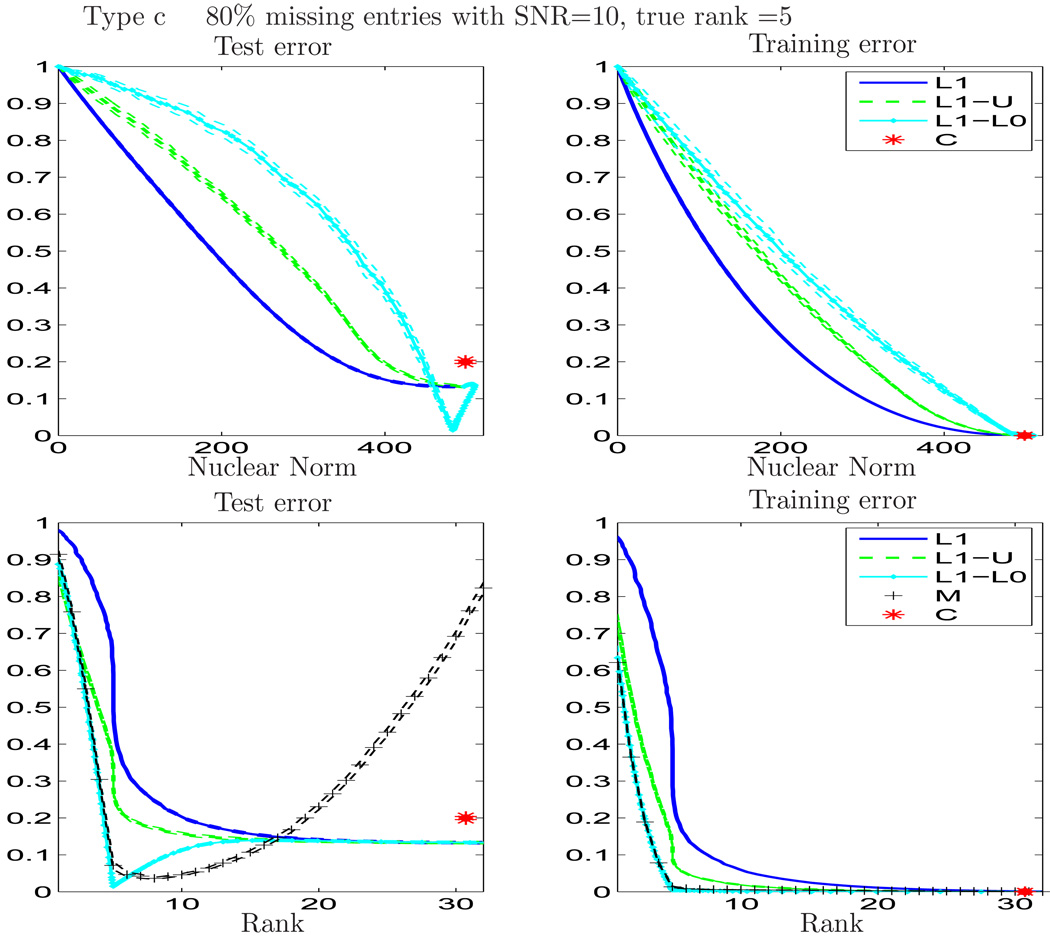
Figure 3.

When the noise is low, Hard-Impute can improve its performance. It gets the correct rank whereas OptSpace overestimates it. Hard-Impute performs the best here wrt prediction error, followed by OptSpace. The latter does better than Soft-Impute. The noise here is low, still the SVT recovers a matrix with high rank approximately 30 and has poor prediction error as well. The test error of the SVT is found to be different from the limiting solution of Soft-Impute, though the former is allowed to run for 1000 iterations for convergence. This suggests that for small fluctuations of the objective criteria (11,2) around the minima the estimated “optimal solution” is not robust.

In this paper we provide an algorithm for computing solutions of (2) on a grid of δ values, based on warm restarts. The algorithm is inspired by Hastie et al.’s SVD- impute [HTS⁺99, TCS⁺01], and is very different from the proximal forward-backward splitting method of [CCS08, CW05] as well as the Bregman iterative method proposed in [MGC09]. The latter is motivated by an analogous algorithm used for the ℓ₁ penalized least-squares problem. All these algorithms [CCS08, CW05, MGC09] require the specification of a step size, and can be quite sensitive to the chosen value. Our algorithm does not require a step-size, or any such parameter.

In [MGC09] the SVD step becomes prohibitive, so randomized algorithms are used in the computation. Our algorithm Soft-Impute also requires an SVD computation at every iteration, but by exploiting the problem structure, can easily handle matrices of dimensions much larger than those in [MGC09]. At each iteration the non-sparse matrix has the structure:

$$Y=Y_{SP}(\text{Spare})+Y_{LR}(\text{Low Rank})$$ (5)

In (5) Y_SP has the same sparsity structure as the observed X, and Y_LR has the rank r ≪ m, n of the estimated Z. For large scale problems, we use iterative methods based on Lanczos bidiagonalization with partial re-orthogonalization (as in the PROPACK algorithm [Lar98]), for computing the first r singular vectors/values of Y. Due to the specific structure of (5), multiplication by Y and Y′ can both be achieved in a cost-efficient way. More precisely, in the sparse + low-rank situation, the computationally burdensome work in computing the SVD is of an order that depends linearly on the matrix dimensions — O((m + n)r) + O(|Ω|). In our experimental studies we find that our algorithm converges in very few iterations; with warm-starts the entire regularization path can be computed very efficiently along a dense series of values for δ.

Although the nuclear norm is motivated here as a convex relaxation to a rank constraint, we believe in many situations it will outperform the rank-restricted estimator. This is supported by our experimental studies and explored in [SAJ05, RS05]. We draw the natural analogy with model selection in linear regression, and compare best-subset regression (ℓ₀ regularization) with the lasso (ℓ₁ regularization) [Tib96, THF09]. There too the ℓ₁ penalty can be viewed as a convex relaxation of the ℓ₀ penalty. But in many situations with moderate sparsity, the lasso will outperform best subset in terms of prediction accuracy [Fri08, THF09]. By shrinking the parameters in the model (and hence reducing their variance), the lasso permits more parameters to be included. The nuclear norm is the ℓ₁ penalty in matrix completion, as compared to the ℓ₀ rank. By shrinking the singular values, we allow more dimensions to be included without incurring undue estimation variance.

Another class of techniques used in collaborative filtering problems are close in spirit to (2). These are known as maximum margin factorization methods, and use a factor model for the matrix Z [SRJ05]. Let Z = UV′ where U_m×r and V_n×r (U, V are not orthogonal), and consider the following problem

$$\begin{array}{cc}\underset{U,V}{\text{minimize}}& {\displaystyle \sum _{(i,j)\in \mathrm{\Omega }}{(X_{ij}-{(UV\prime )}_{ij})}^2+\lambda ({\Vert U\Vert }_F^2+{\Vert V\Vert }_F^2).}\end{array}$$ (6)

It turns out that (6) is equivalent to (3), since

$${\Vert Z\Vert }_{*}=\underset{U,V:Z=UV\prime }{\text{minimize}}\frac{1}{2}({\Vert U\Vert }_F^2+{\Vert V\Vert }_F^2)$$ (7)

This problem formulation and related optimization methods have been explored by [SRJ05, RS05, TPNT09]. A very similar formulation is studied in [KOM09]. However (6) is a non-convex optimization problem in (U, V). It has been observed empirically and theoretically [BM05, RS05] that bi-convex methods used in the optimization of (6) get stuck in suboptimal local minima if the rank r is small. For a large number of factors r and large dimensions m, n the computational cost may be quite high [RS05]. Moreover the factors (U, V) are not orthogonal, and if this is required, additional computations are required [O(r(m + n) + r³)].

Our criterion (3), on the other hand, is convex in Z for every value of λ (and hence rank r) and it outputs the solution Ẑ in the form of its SVD, implying that the “factors” U, V are already orthogonal. Additionally the formulation (6) has two different tuning parameters r and λ, both of which are related to the rank or spectral properties of the matrices U, V. Our formulation has only one tuning parameter λ. The presence of two tuning parameters is problematic:

• It results in a significant increase in computational burden, since for every given value of r, one needs to compute an entire system of solutions by varying λ.

• In practice when neither the optimal values of r and λ are known, a two-dimensional search (eg by cross validation) is required to select suitable values.

3. Algorithm and Convergence analysis

3.1 Notation

We adopt the notation of [CCS08]. Define a matrix P_Ω(Y) (with dimension n × m)

$$P_{\mathrm{\Omega }}(Y)(i,j)=\{\begin{array}{ll}{Y}_{ij}\hfill & \text{if}(i,j)\in \mathrm{\Omega }\hfill \\ 0\hfill & \text{if}(i,j)\notin \mathrm{\Omega },\hfill \end{array}$$ (8)

which is a projection of the matrix Y_m×n onto the observed entries. In the same spirit, define the complementary projection $P_{\mathrm{\Omega }}^{\perp }(Y)$ via $P_{\mathrm{\Omega }}^{\perp }(Y)+P_{\mathrm{\Omega }}(Y)=Y$. Using (8) we can rewrite Σ_(i,j)∈Ω (X_ij – Z_ij)² as ${\Vert P_{\mathrm{\Omega }}(X)-P_{\mathrm{\Omega }}(Z)\Vert }_F^2$.

3.2 Nuclear norm regularization

We present the following lemma, given in [CCS08], which forms a basic ingredient in our algorithm.

Lemma 1. Suppose the matrix W_m×n has rank r. The solution to the optimization problem

$$\begin{array}{cc}\underset{Z}{\text{minimize}}& \frac{1}{2}{\Vert W-Z\Vert }_F^2+\lambda {\Vert Z\Vert }_{*}\end{array}$$ (9)

is given by Ẑ = S_λ(W) where

$$\begin{array}{ccc}{\mathbf{S}}_{\lambda }(W)\equiv U{D}_{\lambda }V\prime & \mathit{\text{\hspace{1em}with\hspace{1em}}}& D_{\lambda }=\text{diag}[{(d_1-\lambda )}_{+},\dots ,{(d_r-\lambda )}_{+}],\end{array}$$ (10)

UDV′ is the SVD of W, D = diag [d₁,…,d_r], and t₊ = max(t, 0).

The notation S_λ(W) refers to soft-thresholding [DJKP95]. Lemma 1 appears in [CCS08, MGC09] where the proof utilizes the sub-gradient characterization of the nuclear norm. In Appendix A.1 we present an entirely different proof, which can be extended in a relatively straightforward way to other complicated forms of spectral regularization discussed in Section 5. Our proof is followed by a remark that covers these more general cases.

3.3 Algorithm

Using the notation in 3.1, we rewrite (3)

$$\begin{array}{cc}\underset{Z}{\text{minimize}}& \frac{1}{2}{\Vert P_{\mathrm{\Omega }}(X)-P_{\mathrm{\Omega }}\Vert }_F^2+\lambda {\Vert Z\Vert }_{*}.\end{array}$$ (11)

Let $f_{\lambda }(Z)=\frac{1}{2}{\Vert P_{\mathrm{\Omega }}(X)-P_{\mathrm{\Omega }}(Z)\Vert }_F^2+\lambda {\Vert Z\Vert }_{*}$ denote the objective in (11).

We now present Algorithm 1—Soft-Impute—for computing a series of solutions to (11) for different values of λ using warm starts.

Algorithm 1 Soft-Impute

Initialize Zold = 0 and create a decreasing grid Λ of values λ1 > … > λK. For every fixed λ = λ1, λ2,… ∈ Λ iterate till convergence: Compute $Z^{\text{new}}\leftarrow {\mathbf{S}}_{\lambda }(P_{\mathrm{\Omega }}(X)+P_{\mathrm{\Omega }}^{\perp }(Z^{\text{old}}))$ If $\frac{{\Vert Z^{\text{new}}-Z^{\text{old}}\Vert }_F^2}{{\Vert Z^{\text{old}}\Vert }_F^2}<\in$ go to step 2d. Assign Zold ← Znew and go to step 2a. Assign Ẑλ ← Znew and go to step 2. Output the sequence of solutions Ẑλ1,…,ẐλK.

The algorithm repeatedly replaces the missing entries with the current guess, and then updates the guess by solving (9). Figures 1, 2 and 3 show some examples of solutions using Soft-Impute (blue curves). We see test and training error in the top rows as a function of the nuclear norm, obtained from a grid of values Λ. These error curves show a smooth and very competitive performance.

3.4 Convergence analysis

In this section we study the convergence properties of Algorithm 1. We prove that Soft-Impute converges to the solution to (11). It is an iterative algorithm that produces a sequence of solutions for which the criterion decreases to the optimal solution with every iteration. This aspect is absent in many first order convex minimization algorithms [Boy08]. In addition the successive iterates get closer to the optimal set of solutions of the problem 2. Unlike many other competitive first-order methods [CCS08, CW05, MGC09], Soft-Impute does not involve the choice of any step-size. Most importantly our algorithm is readily scalable for solving large scale semidefinite programming problems (2,11) as will be explained later in Section 4.

For an arbitrary matrix Z͂, define

$$Q_{\lambda }(Z|\tilde{Z})=\frac{1}{2}{\Vert P_{\mathrm{\Omega }}(X)+P_{\mathrm{\Omega }}^{\perp }(\tilde{Z})-Z\Vert }_F^2+\lambda {\Vert Z\Vert }_{*},$$ (12)

a surrogate of the objective function f_λ(z). Note that f_λ (Z͂) = Q_λ (Z͂|Z͂) for any Z͂

Lemma 2. For every fixed λ ≥ 0, define a sequence $Z_{\lambda }^k$ by

$$Z_{\lambda }^{k+1}=\text{arg}\underset{Z}{\text{min}}{Q}_{\lambda }(Z|Z_{\lambda }^k)$$ (13)

with any starting point $Z_{\lambda }^0$. The sequence $Z_{\lambda }^k$ satisfies

$$f_{\lambda }(Z_{\lambda }^{k+1})\le Q_{\lambda }(Z_{\lambda }^{k+1}|Z_{\lambda }^k)\le f_{\lambda }(Z_{\lambda }^k)$$ (14)

Proof. Note that

$$Z_{\lambda }^{k+1}={\mathbf{S}}_{\lambda }(P_{\mathrm{\Omega }}(X)+P_{\mathrm{\Omega }}^{\perp }(Z_{\lambda }^k))$$ (15)

by Lemma 1 and the definition (12) of $Q_{\lambda }(Z|Z_{\lambda }^k)$.

$$\begin{array}{lll}{f}_{\lambda }(Z_{\lambda }^k)\hfill & =\hfill & Q_{\lambda }(Z_{\lambda }^k|Z_{\lambda }^k)\hfill \\ \hfill & =\hfill & \frac{1}{2}{\Vert P_{\mathrm{\Omega }}(X)+P_{\mathrm{\Omega }}^{\perp }(Z_{\lambda }^k)-Z_{\lambda }^k\Vert }_F^2+\lambda {\Vert Z_{\lambda }^k\Vert }_{*}\hfill \\ \hfill & \ge \hfill & \underset{Z}{\text{min}}\frac{1}{2}\left\{{\Vert P_{\mathrm{\Omega }}(X)+P_{\mathrm{\Omega }}^{\perp }(Z_{\lambda }^k)-Z\Vert }_F^2\right\}+\lambda {\Vert Z\Vert }_{*}\hfill \\ \hfill & =\hfill & Q_{\lambda }(Z_{\lambda }^{k+1}|Z_{\lambda }^k)\hfill \\ \hfill & =\hfill & \frac{1}{2}{\Vert \left\{P_{\mathrm{\Omega }}(X)-P_{\mathrm{\Omega }}(X_{\lambda }^{k+1})\right\}+\left\{P_{\mathrm{\Omega }}^{\perp }(Z_{\lambda }^k)-P_{\mathrm{\Omega }}^{\perp }(Z_{\lambda }^{k+1})\right\}\Vert }_F^2+\lambda {\Vert Z_{\lambda }^{k+1}\Vert }_{*}\hfill \\ \hfill & =\hfill & \frac{1}{2}\left\{{\Vert P_{\mathrm{\Omega }}(X)-P_{\mathrm{\Omega }}(Z_{\lambda }^{k+1})\Vert }_F^2+{\Vert P_{\mathrm{\Omega }}^{\perp }(Z_{\lambda }^k)-P_{\mathrm{\Omega }}^{\perp }(Z_{\lambda }^{k+1})\Vert }_F^2\right\}+\lambda {\Vert Z_{\lambda }^{k+1}\Vert }_{*}\hfill \end{array}$$ (16)

$$\begin{array}{ll}\ge \hfill & \frac{1}{2}{\Vert P_{\mathrm{\Omega }}(X)-P_{\mathrm{\Omega }}(Z_{\lambda }^{k+1})\Vert }_F^2+\lambda {\Vert Z_{\lambda }^{k+1}\Vert }_{*}\hfill \\ =\hfill & Q_{\lambda }(Z_{\lambda }^{k+1}|Z_{\lambda }^{k+1})\hfill \\ =\hfill & f(Z_{\lambda }^{k+1})\hfill \end{array}$$ (17)

Lemma 3. The nuclear norm shrinkage operator S_λ(·) satisfies the following for any W₁, W₂ (with matching dimensions)

$${\Vert {\mathbf{S}}_{\lambda }(W_1)-{\mathbf{S}}_{\lambda }(W_2)\Vert }_F^2\le {\Vert W_1-W_2\Vert }_F^2$$ (18)

In particular this implies that S_λ (W) is a continuous map in W.

Lemma 3 is proved in [MGC09]; their proof is complex and based on trace inequalities. We give a concise proof in Appendix A.2.

Lemma 4. The successive differences ${\Vert Z_{\lambda }^k-Z_{\lambda }^{k-1}\Vert }_F^2$ of the sequence $Z_{\lambda }^k$ are monotone decreasing:

$${\Vert Z_{\lambda }^{k+1}-Z_{\lambda }^k\Vert }_F^2\le {\Vert Z_{\lambda }^k-Z_{\lambda }^{k-1}\Vert }_F^2\forall k$$ (19)

Moreover the difference sequence converges to zero. That is

$$Z_{\lambda }^{k+1}-Z_{\lambda }^k\to 0\mathit{\text{ as }}k\to \infty$$

The proof of Lemma 4 is given in Appendix A.3.

Lemma 5. Every limit point of the sequence $Z_{\lambda }^k$ defined in Lemma 2 is a stationary point of

$$\frac{1}{2}{\Vert P_{\mathrm{\Omega }}(X)-P_{\mathrm{\Omega }}(Z)\Vert }_F^2+\lambda {\Vert Z\Vert }_{*}$$ (20)

Hence it is a solution to the fixed point equation

$$Z={\mathbf{S}}_{\lambda }(P_{\mathrm{\Omega }}(X)+P_{\mathrm{\Omega }}^{\perp }(Z))$$ (21)

The proof of Lemma 5 is given in Appendix A.4.

Theorem 1. The sequence $Z_{\lambda }^k$ defined in Lemma 2 converges to a limit $Z_{\lambda }^{\infty }$ that solves

$$\begin{array}{cc}\underset{Z}{\text{minimize}}& \frac{1}{2}{\Vert P_{\mathrm{\Omega }}(X)-P_{\mathrm{\Omega }}(Z)\Vert }_F^2+\lambda {\Vert Z\Vert }_{*}\end{array}$$ (22)

Proof. It suffices to prove that $Z_{\lambda }^k$ converges; the theorem then follows from Lemma 5.

Let Ẑ_λ be a limit point of the sequence $Z_{\lambda }^k$. There exists a subsequence m_k such that $Z_{\lambda }^{m_k}\to {\widehat{Z}}_{\lambda }$. By Lemma 5, Ẑ_λ solves the problem (22) and satisfies the fixed point equation (21).

Hence

$$\begin{array}{lll}{\Vert {\widehat{Z}}_{\lambda }-Z_{\lambda }^k\Vert }_F^2\hfill & =\hfill & {\Vert {\mathbf{S}}_{\lambda }(P_{\mathrm{\Omega }}(X)+P_{\mathrm{\Omega }}^{\perp }({\widehat{Z}}_{\lambda }))-{\mathbf{S}}_{\lambda }(P_{\mathrm{\Omega }}(X)+P_{\mathrm{\Omega }}^{\perp }(Z_{\lambda }^{k-1}))\Vert }_F^2\hfill \\ \hfill & \le \hfill & {\Vert (P_{\mathrm{\Omega }}(X)+P_{\mathrm{\Omega }}^{\perp }({\widehat{Z}}_{\lambda }))-(P_{\mathrm{\Omega }}(X)+P_{\mathrm{\Omega }}^{\perp }(Z_{\lambda }^{k-1}))\Vert }_F^2\hfill \\ \hfill & =\hfill & {\Vert P_{\mathrm{\Omega }}^{\perp }({\widehat{Z}}_{\lambda }-Z_{\lambda }^{k-1})\Vert }_F^2\hfill \end{array}$$ (23)

$$\begin{array}{cc}\le & {\Vert {\widehat{Z}}_{\lambda }-Z_{\lambda }^{k-1}\Vert }_F^2\end{array}$$ (24)

In (23) two substitutions were made; the left one using (21) in Lemma 5, the right one using (15). Inequality (24) implies that the sequence ${\Vert {\widehat{Z}}_{\lambda }-Z_{\lambda }^{k-1}\Vert }_F^2$ converges as k → ∞. To show the convergence of the sequence $Z_{\lambda }^k$ it suffices to prove that the sequence ${\widehat{Z}}_{\lambda }-Z_{\lambda }^k$ converges to zero. We prove this by contradiction.

Suppose the sequence $Z_{\lambda }^k$ has another limit point $Z_{\lambda }^{+}\ne {\widehat{Z}}_{\lambda }$. Then ${\widehat{Z}}_{\lambda }-Z_{\lambda }^k$ has two distinct limit points 0 and $Z_{\lambda }^{+}-{\widehat{Z}}_{\lambda }\ne 0$. This contradicts the convergence of the sequence ${\Vert {\widehat{Z}}_{\lambda }-Z_{\lambda }^{k-1}\Vert }_F^2$. Hence the sequence $Z_{\lambda }^k$ converges to ${\widehat{Z}}_{\lambda }:=Z_{\lambda }^{\infty }$.

The inequality in (24) implies that at every iteration $Z_{\lambda }^k$ gets closer to an optimal solution for the problem (22)². This property holds in addition to the decrease of the objective function (Lemma 2) at every iteration. This is a very nice property of the algorithm and is in general absent in many first order methods such as projected sub-gradient minimization [Boy08].

4. Computation

The computationally demanding part of Algorithm 1 is in ${\mathbf{S}}_{\lambda }(P_{\mathrm{\Omega }}(X)+P_{\mathrm{\Omega }}^{\perp }(Z_{\lambda }^k))$. This requires calculating a low-rank SVD of a matrix, since the underlying model assumption is that rank(Z) ≪ min{m, n}. In Algorithm 1, for fixed λ, the entire sequence of matrices $Z_{\lambda }^k$ have explicit low-rank representations of the form $U_k{D}_k{V}_k^{\prime }$ corresponding to ${\mathbf{S}}_{\lambda }(P_{\mathrm{\Omega }}(X)+P_{\mathrm{\Omega }}^{\perp }(Z_{\lambda }^{k-1}))$

In addition, observe that $P_{\mathrm{\Omega }}(X)+P_{\mathrm{\Omega }}^{\perp }(Z_{\lambda }^k)$ can be rewritten as

$$\begin{array}{ccccc}{P}_{\mathrm{\Omega }}(X)+P_{\mathrm{\Omega }}^{\perp }(Z_{\lambda }^k)& =& \left\{P_{\mathrm{\Omega }}(X)-P_{\mathrm{\Omega }}(Z_{\lambda }^k)\right\}& +& Z_{\lambda }^k\\ & =& \mathit{\text{Sparse}}& +& \mathit{\text{Low Rank}}\end{array}$$ (25)

In the numerical linear algebra literature, there are very efficient direct matrix factorization methods for calculating the SVD of matrices of moderate size (at most a few thousand). When the matrix is sparse, larger problems can be solved but the computational cost depends heavily upon the sparsity structure of the matrix. In general however, for large matrices one has to resort to indirect iterative methods for calculating the leading singular vectors/values of a matrix. There is a lot research in numerical linear algebra for developing sophisticated algorithms for this purpose. In this paper we will use the PROPACK algorithm [Lar, Lar98] because of its low storage requirements, effective flop count and its well documented MATLAB version. The algorithm for calculating the truncated SVD for a matrix W (say), becomes efficient if multiplication operations Wb₁ and W′b₂ (with b₁ ∈ ℜⁿ, b₂ ∈ ℜ^m) can be done with minimal cost.

Algorithm Soft-Impute requires repeated computation of a truncated SVD for a matrix W with structure as in (25). Note that in (25) the term $P_{\mathrm{\Omega }}(Z_{\lambda }^k)$ can be computed in O(|Ω|r) flops using only the required outer products (i.e. our algorithm does not compute the matrix explicitly).

The cost of computing the truncated SVD will depend upon the cost in the operations Wb₁ and W′b₂ (which are equal). For the sparse part these multiplications cost O(|Ω|). Although it costs O(|Ω|r) to create the matrix $P_{\mathrm{\Omega }}(Z_{\lambda }^k)$, this is used for each of the r such multiplications (which also cost O(|Ω|r)), so we need not include that cost here. The LowRank part costs O((m + n)r) for the multiplication by b₁. Hence the cost is O(|Ω|) + O((m + n)r) per vector multiplication.

For the reconstruction problem to be theoretically meaningful in the sense of [CT09] we require that |Ω| ≈ nr · poly(log n). In practice often |Ω| is very small. Hence introducing the Low Rank part does not add any further complexity in the multiplication by W and W′. So the dominant cost in calculating the truncated SVD in our algorithm is O(|Ω|). The SVT algorithm [CCS08] for exact matrix completion (4) involves calculating the SVD of a sparse matrix with cost O(|Ω|). This implies that the computational cost of our algorithm and that of [CCS08] is the same. This order computation does not include the number of iterations required for convergence. In our experimental studies we use warm-starts for efficiently computing the entire regularization path. We find that our algorithm converges in a few iterations. Since the true rank of the matrix r ≪ min {m, n}, the computational cost of evaluating the truncated SVD (with rank ≈ r) is linear in matrix dimensions. This justifies the large-scale computational feasibility of our algorithm.

The PROPACK package does not allow one to request (and hence compute) only the singular values larger than a threshold λ — one has to specify the number in advance. So once all the computed singular values fall above the current threshold λ, our algorithm increases the number to be computed until the smallest is smaller than λ. In large scale problems, we put an absolute limit on the maximum number.

5. Generalized spectral regularization: from soft to hard-thresholding

In Section 1 we discussed the role of the nuclear norm as a convex surrogate for the rank of a matrix, and drew the analogy with lasso regression versus best-subset selection. We argued that in many problems ℓ₁ regularization gives better prediction accuracy [ZY06]. However, if the underlying model is very sparse, then the lasso with its uniform shrinkage can overestimate the number of non-zero coefficients [Fri08]. It can also produce highly shrunk and hence biased estimates of the coefficients.

Consider again the problem

$$\underset{\text{rank}(Z)=k}{\text{minimize}}{\Vert P_{\mathrm{\Omega }}(X)-P_{\mathrm{\Omega }}(Z)\Vert }_F^2,$$ (26)

a rephrasing of (1). This best rank-k solution also solves

$$\text{minimize}\frac{1}{2}{\Vert P_{\mathrm{\Omega }}(X)-P_{\mathrm{\Omega }}(Z)\Vert }_F^2+\lambda {\displaystyle \sum _{j}I({\gamma }_j(Z)>0),}$$ (27)

where γ_j(Z) is the jth singular value of Z, and for a suitable choice of λ that produces a solution with rank k.

The “fully observed” matrix version of the above problem is given by the ℓ₀ version of (9) as follows:

$$\underset{Z}{\text{min}}\frac{1}{2}{\Vert W-Z\Vert }_F^2+\lambda {\Vert Z\Vert }_0$$ (28)

where ‖Z‖₀ = rank(Z). The solution of (28) is given by a reduced-rank SVD of W; for every λ there is a corresponding q = q(λ) number of singular-values to be retained in the SVD decomposition. Problem 28 is non-convex in W but its global minimizer can be evaluated. As in (10) the thresholding operator resulting from (28) is

$${\mathbf{S}}_{\lambda }^H(W)=U{D}_{q}V\prime \text{\hspace{1em}where\hspace{1em}}{D}_q=\text{diag}(d_1,\dots ,d_q,0,\dots ,0)$$ (29)

Similar to Soft-Impute (Algorithm 1), we present below Hard-Impute (Algorithm 2) for the ℓ₀ penalty.

In penalized regression there have been recent developments directed towards “bridging” the gap between the ℓ₁ and ℓ₀ penalties [Fri08, FL01, Zha07]. This is done via using concave penalties that are a better surrogate (in the sense of approximating the penalty) to ℓ₀ over the ℓ₁. They also produce less biased estimates than those produced by the ℓ₁ penalized solutions. When the underlying model is very sparse they often perform very well [Fri08, FL01, Zha07], and often enjoy superior prediction accuracy when compared to softer penalties like ℓ₁. These methods still shrink, but are less aggressive than the best-subset selection.

By analogy, we propose using a more sophisticated version of spectral regularization. This goes beyond nuclear norm regularization by using slightly more aggressive penalties that bridge the gap between ℓ₁ (nuclear norm) and ℓ₀ (rank constraint). We propose minimizing

$$f_{\mathbf{p},\lambda }(Z)=\frac{1}{2}{\Vert P_{\mathrm{\Omega }}(X)-P_{\mathrm{\Omega }}(Z)\Vert }_F^2+\lambda {\displaystyle \sum _j\mathbf{p}({\gamma }_j(Z);\mu )}$$ (30)

Algorithm 2 Hard-Impute

Create a decreasing grid Λ of values λ1 > … > λK. Initialize Z̃λk k = 1,…,K (see Section 6). For every fixed λ = λ1, λ2,… ∈ Λ iterate till convergence: Initialize Zold ← Z̃λ. Compute $Z^{\text{new}}\leftarrow {\mathbf{S}}_{\lambda }^H(P_{\mathrm{\Omega }}(X)+P_{\mathrm{\Omega }}^{\perp }(Z^{\text{old}}))$ If $\frac{{\Vert Z^{\text{new}}-Z^{\text{old}}\Vert }_F^2}{{Z^{\text{old}}\Vert }_F^2}<\in$, go to step 2e. Assign Zold ← Znew and go to step 2a. Assign ẐH,λ ← Znew. Output the sequence of solutions ẐH, λ1, …, ẐH, λK.

where p(|t|;µ) is concave in |t|. The parameter µ ∈ [µ_inf, µ_sup] controls the degree of concavity. We may think of p(|t|; µ_inf) = |t| (ℓ₁ penalty) on one end and p(|t|; µ_sup) = ‖t‖₀ (ℓ₀ penalty) on the other. In particular for the ℓ₀ penalty denote f_p,λ (Z) by f_H,λ (Z) for “hard” thresholding. See [Fri08, FL01, Zha07] for examples of such penalties.

In Remark 1 in Appendix A.1 we argue how the proof can be modified for general types of spectral regularization. Hence for minimizing the objective (30) we will look at the analogous version of (9), (28) which is

$$\underset{Z}{\text{min}}\frac{1}{2}{\Vert W-Z\Vert }_F^2+\lambda {\displaystyle \sum _j\mathbf{p}({\gamma }_j(Z);\mu )}$$ (31)

The solution is given by a thresholded SVD of W:

$${\mathbf{S}}_{\lambda }^{\mathbf{p}}(W)=U{D}_{\mathbf{p},\lambda }V\prime$$ (32)

Where D_p,λ is a entry-wise thresholding of the diagonal entries of the matrix D consisting of singular values of the matrix W. The exact form of the thresholding depends upon the form of the penalty function p(·;·), as discussed in Remark 1. Algorithm 1 and Algorithm 2 can be modified for the penalty p(·;µ) by using a more general thresholding function ${\mathbf{S}}_{\lambda }^{\mathrm{p}}(·)$ in Step 2b. The corresponding step becomes:

$$Z^{\text{new}}\leftarrow {\mathbf{S}}_{\lambda }^p(P_{\mathrm{\Omega }}(X)+P_{\mathrm{\Omega }}^{\perp }(Z^{\text{old}}))$$

However these types of spectral regularization make the criterion (30) non-convex and hence it becomes difficult to optimize globally.

6. Post-processing of “selectors” and initialization

Because the ℓ₁ norm regularizes by shrinking the singular values, the number of singular values retained (through cross-validation, say) may exceed the actual rank of the matrix. In such cases it is reasonable to undo the shrinkage of the chosen models, which might permit a lower-rank solution.

If Z_λ is the solution to (11), then its post-processed version $Z_{\lambda }^u$ obtained by “unshrinking” the eigen-values of the matrix Z_λ is obtained by

$$\begin{array}{lll}\alpha \hfill & =\hfill & \underset{{\alpha }_i\ge 0,i=1,\dots ,r_{\lambda }}{\text{arg min}}\Vert P_{\mathrm{\Omega }}(X)-{\displaystyle \sum _{i=1}^{r_{\lambda }}{\alpha }_i{P}_{\mathrm{\Omega }}(u_i{v}_i^{\prime })}{\Vert }^2\hfill \\ Z_{\lambda }^u\hfill & =\hfill & U{D}_{\alpha }V\prime ,\hfill \end{array}$$ (33)

where D_α = diag(α₁,…,α_rλ). Here r_λ is the rank of Z_λ and Z_λ = UD_λV′ is its SVD. The estimation in (33) can be done via ordinary least squares, which is feasible because of the sparsity of $P_{\mathrm{\Omega }}(u_i{v\prime }_i)$ and that r_λ is small.³ If the least squares solutions α do not meet the positivity constraints, then the negative sign can be absorbed into the corresponding singular vector.

Rather than estimating a diagonal matrix D_α as above, one can insert a matrix M_rλ×rλ between U and V above to obtain better training error for the same rank [KOM09]. Hence given U, V (each of rank r_λ) from the Soft-Impute algorithm, we solve

$$\begin{array}{l}\widehat{M}=\underset{M}{\text{arg min}}\Vert P_{\mathrm{\Omega }}(X)-P_{\mathrm{\Omega }}(UMV\prime ){\Vert }^2\hfill \\ {\widehat{Z}}_{\lambda }=U\widehat{M}V\prime \hfill \end{array}$$ (34)

The objective function in (34) is the Frobenius norm of an affine function of M and hence can be optimized very efficiently. Scalability issues pertaining to the optimization problem (34) can be handled fairly efficiently via conjugate gradients. Criterion (34) will definitely lead to a decrease in training error as that attained by Ẑ = U D_λ V′ for the same rank and is potentially an attractive proposal for the original problem (1). However this heuristic cannot be caste as a (jointly) convex problem in (U, M, V). In addition, this requires the estimation of up to $r_{\lambda }^2$ parameters, and has the potential for overfitting. In this paper we report experiments based on (33).

In many simulated examples we have observed that this post-processing step gives a good estimate of the underlying true rank of the matrix (based on prediction error). Since fixed points of Algorithm 2 correspond to local minima of the function (30), well-chosen warm starts Ẑ_λ are helpful. A reasonable prescription for warms-starts is the nuclear norm solution via (Soft-Impute), or the post processed version (33). The latter appears to significantly speed up convergence for Hard-Impute. This observation is based on our simulation studies.

7. Simulation Studies

In this section we study the training and test errors achieved by the estimated matrix by our proposed algorithms and those by [CCS08, KOM09]. The Reconstruction algorithm (OptSpace) described in [KOM09] considers criterion (1) (in presence of noise). It writes Z = USV′ (which need not correspond to the SVD). For every fixed rank r it uses a two-stage minimization procedure: firstly on S and then on U, V (in a Grassmann Manifold) for computing a rank-r decomposition Ẑ = ÛŜV̂′ It uses a suitable starting point obtained by performing a sparse SVD on a clean version of the observed matrix P_Ω(X). This is similar to the formulation of Maximum Margin Factorization (MMF) (6) as outlined in Section 1, without the Frobenius norm regularization on the components U, V.

To summarize, we look at the performance of the following methods:

• (a) Soft-Impute (algorithm 1); (b) Pp-SI Post-processing on the output of Algorithm 1, (c) Hard-Impute (Algorithm 2) starting with the output of (b).

• SVT algorithm by [CCS08]

• OptSpace reconstruction algorithm by [KOM09]

In all our simulation studies we took the underlying model as $Z_{m\times n}=U_{m\times r}{V}_{r\times n}^{\prime }$ + noise; where U and V are random matrices with standard normal Gaussian entries, and noise is i.i.d. Gaussian. Ω is uniformly random over the indices of the matrix with p% percent of missing entries. These are the models under which the coherence conditions hold true for the matrix completion problem to be meaningful as pointed out in [CT09, KOM09]. The signal to noise ratio for the model and the test-error (standardized) are defined as

$$\text{SNR}=\sqrt{\frac{\text{var}(UV\prime )}{\text{var}(\text{noise})}};\text{testerror}=\frac{{\Vert P_{\mathrm{\Omega }}^{\perp }(UV\prime -\widehat{Z})\Vert }_F^2}{{\Vert P_{\mathrm{\Omega }}^{\perp }(UV\prime )\Vert }_F^2}$$ (35)

Training error (standardized) is defined as ${\Vert P_{\mathrm{\Omega }}(Z-\widehat{Z})\Vert }_F^2/{\Vert P_{\mathrm{\Omega }}(Z)\Vert }_F^2$— the fraction of the error explained on the observed entries by the estimate relative to a zero estimate.

In Figures 1,2,3 results corresponding to the training and test errors are shown for all algorithms mentioned above — nuclear norm and rank— in three problem instances. The results displayed in the figures are averaged over 50 simulations. Since OptSpace only uses rank, it is excluded from the left panels. In all examples (m, n) = (100, 100). SNR, true rank and percentage of missing entries are indicated in the figures. There is a unique correspondence between λ and nuclear norm. The plots vs the rank indicate how effective the nuclear norm is as a rank approximation — that is whether it recovers the true rank while minimizing prediction error.

For SVT we use the MATLAB implementation of the algorithm downloaded from the second author’s [CCS08] webpage. For OptSpace we use the MATLAB implementation of the algorithm as obtained from the third author’s webpage [KOM09].

7.1 Observations

In Type a, the SNR= 1, fifty percent of entries are missing and the true underlying rank is ten. The performances of Pp-SI and Soft-Impute are clearly better than the rest. The solution of SVT recovers a matrix with a rank much larger than the true rank. The SVT also has very poor prediction error, suggesting once again that exactly fitting the training data is far too rigid. Soft-Impute recovers an optimal rank (corresponding to the minima of the test error curve) which is larger than the true rank of the matrix, but the prediction error is very competitive. Pp-SI estimates the right rank of the matrix based on the minima of the prediction error curve. This seems to be the only algorithm to do so in this example. Both Hard-Impute and OptSpace perform very poorly in test error. This is a high noise situation, so the Hard-Impute is too aggressive in selecting the singular vectors from the observed entries and hence ends up reaching a very sub-optimal subspace. The training errors of Pp-SI and Hard-Impute are smaller than that achieved by the Soft-Impute solution for a fixed rank along the regularization path. This is expected by the very method of construction. However this deteriorates the test error performance of the Hard-Impute, at the same rank. The nuclear norm may not give very good training error at a certain rank (in the sense it has strong competitors), but this trade off is compensated in the better prediction error it achieves. Though the nuclear norm is a surrogate of rank it eventually turns out to be a good regularization method. Hence it should not be merely seen as a rank approximation technique. Such a phenomenon is observed in the context of penalized linear regression as well. It is seen that the lasso, a convex surrogate of ℓ₀ penalty produces parsimonious models with good prediction error in a wide variety of situations — and is indeed a good model building method.

In Type b, the SNR = 1, fifty percent of entries are missing and the true underlying rank is six. OptSpace performs poorly in test error. Hard-Impute performs worse than the Pp-SI and Soft-Impute, but is pretty competitive near the true rank of the matrix. In this example however the Pp-SI is the best in test error and nails the right rank of the matrix. Based on the above two example we observe that in high noise models Hard-Impute and OptSpace behave very similarly.

In Type-c the SNR= 10, the noise is relatively small as compared to the other two cases. The true underlying rank is 5, but the proportion of missing entries is much higher around eighty percent. Test errors of both Pp-SI and Soft-Impute are found to decrease till a large nuclear norm after which they become roughly the same, suggesting no further impact of regularization. OptSpace performs well in this example getting a sharp minima at the true rank of the matrix. This good behavior of the latter as compared to the previous two instances is because the SNR is very high. Hard-Impute however shows the best performance in this example. The better performance of both OptSpace and Hard-Impute over Soft-Impute is because the true underlying rank of the matrix is very small. This is reminiscent of better predictive performance of best-subset or concave penalized regression over lasso in set-ups where the underlying model is very sparse [Fri08].

In addition we performed some large scale simulations in Table 1 for our algorithm in different problem sizes. The problem dimensions, SNR and time in seconds are reported. All computations are done in MATLAB and the MATLAB implementation of PROPACK is used.

Table 1.

Performance of the Soft-Impute on different problem instances. Effective rank is the rank of the recovered matrix at value of λ for (11). Convergence criterion is taken as “fraction of improvement of objective value” less than 10⁻⁴. All implementations are done in MATLAB including the MATLAB implementation of PROPACK on a Intel Xeon Linux 3GHz processor. Timings (in seconds) are to be interpreted keeping the MATLAB implementation in mind.

(m, n)	|Ω|	true rank	SNR	effective rank	time(s)
(3 × 104, 104)	104	15	1	(13, 47, 80)	(41.9, 124.7, 305.8)
(105, 105)	104	15	10	(5, 14, 32, 62)	(37, 74.5, 199.8, 653)
(105, 105)	105	15	10	(18, 80)	(202, 1840)
(5 × 105, 5 × 105)	104	15	10	11	628.14
(5 × 105, 5 × 105)	105	15	1	(3, 11, 52)	(341.9, 823.4, 4810.75)
(106, 106)	105	15	1	80	8906

8. Application to Netflix data

In this section we report briefly on the application of our proposed methods to the Netflix movie prediction contest. The training data consists of the ratings of 17,770 movies by 480,189 Netflix customers. The data matrix is extremely sparse, with 100,480,507 or 1% of the entries observed. The task is to predict the unseen ratings for a qualifying set and a test set of about 1.4 million ratings each, with the true ratings in these datasets held in secret by Netflix. A probe set of about 1.4 million ratings is distributed to participants, for calibration purposes. The movies and customers in the qualifying, test and probe sets are all subsets of those in the training set.

The ratings are integers from 1 (poor) to 5 (best). Netflix’s own algorithm has an RMSE of 0.9525 and the contest goal is to improve this by 10%, or an RMSE of 0.8572. The contest has been going for almost 3 years, and the leaders have recently passed the 10% improvement threshold and may soon be awarded the grand prize. Many of the leading algorithms use the SVD as a starting point, refining it and combining it with other approaches. Computation of the SVD on such a large problem is prohibitive, and many researchers resort to approximations such as subsampling (see e.g. [RMH07]). Here we demonstrate that our spectral regularization algorithm can be applied to entire Netflix training set (the Probe dataset has been left outside the training set) with a reasonable computation time.

We removed the movie and customer means, and then applied Hard-Impute with varying ranks. The results are shown in Table 2.

Table 2.

Results of applying Hard-Impute to the Netflix data. The computations were done on a Intel Xeon Linux 3GHz processor; timings are reported based on MAT-LAB implementations of PROPACK and our algorithm. RMSE is the root mean squared error over the probe set. “train error” is the proportion of error on the observed dataset achieved by our estimator relative to the zero estimator.

rank	time (hrs)	train error	RMSE
20	3.3	0.217	0.986
30	5.8	0.203	0.977
40	6.6	0.194	0.965
60	9.7	0.181	0.966

These results are not meant to be competitive with the best results obtained by the leading groups, but rather just demonstrate the feasibility of applying Hard-Impute to such a large dataset. In addition, it may be mentioned here that the objective criterion as in Algorithm 1 or Algorithm 2 is known to have optimal generalization error or reconstruction error under the assumption that the structure of missing-ness is approximately uniform [CT09, SAJ05, CR08, KOM09]. This assumption is definitely not true for the Netflix data due to the high imbalance in the degree of missingness. The results shown above are without any sophisticated rounding schemes to bring the predictions within [1, 5]. As we saw in the simulated examples, for small SNR Hard-Impute performs pretty poorly in prediction error as compared to Soft-Impute; the Netflix data is likely to be very noisy. These provide some explanations for the RMSE values obtained in our results and suggest possible directions for modifications and improvements to achieve further improvements in prediction error.

Appendix A. Appendix

A.1 Proof of Lemma 1

Proof. Let $Z={\tilde{U}}_{m\times n}{\tilde{D}}_{n\times n}{\tilde{V}\prime }_{n\times n}$ be the SVD of Z. Assume WLOG m ≥ n. We will explicitly evaluate the closed form solution of the problem (9).

$$\frac{1}{2}{\Vert Z-W\Vert }_F^2+\lambda {\Vert Z\Vert }_{*}=\frac{1}{2}\left\{{\Vert Z\Vert }_F^2-2{\displaystyle \sum _{i=1}^n{\tilde{d}}_i{\tilde{u}}_i^{\prime }W{\tilde{v}}_i+{\displaystyle \sum _{i=1}^n{\tilde{d}}_i^2}}\right\}+\lambda {\displaystyle \sum _{i=1}^n{\tilde{d}}_i}$$ (36)

where

$$\tilde{D}=\text{diag}\left[{\tilde{d}}_1,\dots ,{\tilde{d}}_n\right],\tilde{U}=[{\tilde{u}}_1,\dots ,{\tilde{u}}_n],\tilde{V}=[{\tilde{v}}_1,\dots ,{\tilde{v}}_n]$$ (37)

Minimizing (36) is equivalent to minimizing

$$-2{\displaystyle \sum _{i=1}^n{\tilde{d}}_i{\tilde{u}}_i^{\prime }W{\tilde{v}}_i+{\displaystyle \sum _{i=1}^n{\tilde{d}}_i^2}}+{\displaystyle \sum _{i=1}^{n}2\lambda }{\tilde{d}}_i;\text{wrt}({\tilde{u}}_1,{\tilde{v}}_1,{\tilde{d}}_1),i=1,\dots ,n$$

under the constraints U͂′U͂ = I_n, V͂′V͂ = I_n and d͂_i ≥ 0∀_i

Observe the above is equivalent to minimizing (wrt U͂, V͂) the function Q(U͂, V͂)

$$Q(\tilde{U},\tilde{V})=\underset{\tilde{D}\ge 0}{\text{min}}\frac{1}{2}\left\{-2{\displaystyle \sum _{i=1}^n{\tilde{d}}_i{\tilde{u}}_i^{\prime }W{\tilde{v}}_i+{\displaystyle \sum _{i=1}^n{\tilde{d}}_i^2}}\right\}+\lambda {\displaystyle \sum _{i=1}^n{\tilde{d}}_i}$$ (38)

Since the objective to be minimized wrt D͂ (38) is separable in d͂_i, i = 1, …, n it suffices to minimize it wrt each d_i separately.

The problem

$$\underset{{\widehat{d}}_i\ge 0}{\text{minimize}}\frac{1}{2}\left\{-2{\widehat{d}}_i{\tilde{u}}_i^{\prime }W{\tilde{v}}_i+{\tilde{d}}_i^2\right\}+\lambda {\tilde{d}}_i$$ (39)

can be solved looking at the stationary conditions of the function using its sub-gradient [Boy08]. The solution of the above problem is given by $S_{\lambda }({\tilde{u}}_i^{\prime }W{\tilde{v}}_i)={({\tilde{u}}_i^{\prime }W{\tilde{v}}_i-\lambda )}_{+}$ the soft-thresholding of ${\tilde{u}}_i^{\prime }W{\tilde{v}}_i$⁴. More generally the soft-thresholding operator [FHHT07, THF09] is given by S_λ(x) = sgn(x)(|x| − λ)₊. See [FHHT07] for more elaborate discussions on how the soft-thresholding operator arises in univariate penalized least-squares problems with the ℓ₁ penalization.

Plugging the values of optimal d͂_i, i = 1, …, n; obtained from (39) in (38) we get

$$Q(\tilde{U},\tilde{V})=\frac{1}{2}\left\{{\Vert Z\Vert }_F^2-2{\displaystyle \sum _{i=1}^n{({\tilde{u}}_i^{\prime }W{\tilde{v}}_i-\lambda )}_{+}({\tilde{u}}_i^{\prime }W{\tilde{v}}_i-\lambda )+{({\tilde{u}}_i^{\prime }X{\tilde{v}}_i-\lambda )}_{+}^2}\right\}$$ (40)

Minimizing Q(U͂, V͂) wrt (U͂, V͂) is equivalent to maximizing

$${\displaystyle \sum _{i=1}^n\{2{({\tilde{u}}_i^{\prime }W{\tilde{v}}_i-\lambda )}_{+}({\tilde{u}}_i^{\prime }W{\tilde{v}}_i-\lambda )-{({\tilde{u}}_i^{\prime }X{\tilde{v}}_i-\lambda )}_{+}^2}\}={\displaystyle \sum _{{\tilde{u}}_i^{\prime }W{\tilde{v}}_i>\lambda }{({\tilde{u}}_i^{\prime }W{\tilde{v}}_i-\lambda )}^2}$$ (41)

It is a standard fact that for every i the problem

$$\underset{{\Vert u\Vert }_2^2\le 1,{\Vert v\Vert }_2^2\le 1}{\text{maximize}}u\prime Wv,\text{such that}u\perp \{{\widehat{u}}_1,\dots ,{\widehat{u}}_{i-1}\};v\perp \{{\widehat{v}}_1,\dots ,{\widehat{v}}_{i-1}\}$$ (42)

is solved by û_i, v̂_i the left and right singular vectors of the matrix W corresponding to its i^th largest singular value. The maximum value equals the singular value. It is easy to see that maximizing the expression to the right of (41) wrt (u_i, v_i), i = 1,…,n is equivalent to maximizing the individual terms ${\tilde{u}}_i^{\prime }W{\tilde{v}}_i$. If r(λ) denotes the number of singular values of W larger than λ then the (û_i, v̂_i), i = 1,… that maximize the expression (41) correspond to [u₁,…,u_r(λ)] and [v₁,…,v_r(λ)]; the r(λ) left and right singular vectors of W corresponding to the largest singular values. From (39) the optimal D͂ = diag [d͂₁,…,d͂_n] is given by D_λ = diag [(d₁ − λ)₊,…, (d_n − λ)₊].

Since the rank of W is r, the minimizer Ẑ of (9) is given by UD_λV′ as in (10).

Remark 1. For a more general spectral regularization of the form λ Σ_i p(γ_i(Z)) (as compared to Σ_iλγ_i(Z) used above) the optimization problem (39) will be modified accordingly. The solution of the resultant univariate minimization problem will be given by $S_{\lambda }^{\mathbf{p}}({\tilde{u}}_i^{\prime }W{\tilde{v}}_i)$ for some generalized “thresholding operator” $S_{\lambda }^{\mathbf{p}}(·)$, where

$$S_{\lambda }^{\mathbf{p}}({\tilde{u}}_i^{\prime }W{\tilde{v}}_i)=\underset{{\tilde{d}}_i\ge 0}{\text{arg min}}\frac{1}{2}\left\{-2{\tilde{d}}_i{\tilde{u}}_i^{\prime }W{\tilde{v}}_i+{\tilde{d}}_i^2\right\}+{\lambda }_{\mathbf{p}}({\tilde{d}}_i)$$ (43)

The optimization problem analogous to (40) will be

$$\underset{\tilde{U},\tilde{V}}{\text{minimize}}\frac{1}{2}\left\{{\Vert Z\Vert }_F^2-2{\displaystyle \sum _{i=1}^n{\tilde{d}}_i{\tilde{u}}_i^{\prime }W{\tilde{v}}_i+{\displaystyle \sum _{i=1}^n{\tilde{d}}_i^2}}\right\}+\lambda {\displaystyle \sum _i\mathbf{p}(}{\tilde{d}}_i)$$ (44)

where ${\widehat{d}}_i=S_{\lambda }^{\mathbf{p}}({\tilde{u}}_i^{\prime }W{\tilde{v}}_i)$, ∀_i. Any spectral function for which the above (44) is monotonically increasing in ${\tilde{u}}_i^{\prime }W{\tilde{v}}_i$ for every i can be solved by a similar argument as given in the above proof. The solution will correspond to the first few largest left and right singular vectors of the matrix W. The optimal singular values will correspond to the relevant shrinkage/threshold operator $S_{\lambda }^{\mathbf{p}}(·)$ operated on the singular values of W. In particular for the indicator function p(t) = λ1(t ≠ 0), the top few singular values (un-shrunk) and the corresponding singular vectors is the solution.

A.2 Proof of Lemma 3

This proof is based on sub-gradient characterizations ans is inspired by some techniques used in [CCS08].

Proof. From Lemma 1, we know that if Ẑ solves the problem (9), then it satisfies the sub-gradient stationary conditions:

$$0\in -(W-\widehat{Z})+\lambda \partial {\Vert \widehat{Z}\Vert }_{*}$$ (45)

S_λ(W₁) and S_λ(W₂) solve the problem (9) with W = W₁ and W = W₂ respectively hence (45) holds with W = W₁, Ẑ₁ = S_λ(W₁) and W = W₂, Ẑ₂ = S_λ(W₁).

The sub-gradients of the nuclear norm ‖Z‖_* are given by [CCS08, MGC09]

$$\partial {\Vert Z\Vert }_{*}=\{UV\prime +\omega :{\omega }_{m\times n},U\prime \omega =0,\omega V=0,{\Vert \omega \Vert }_2\le 1\}$$ (46)

where Z = U DV′ is the SVD of Z.

Let p(Ẑ_i) denote an element in ∂‖Ẑ_i‖_*. Then

$${\widehat{Z}}_i-W_i+\lambda p({\widehat{Z}}_i)=0,i=1,2.$$ (47)

The above gives

$$({\widehat{Z}}_1-{\widehat{Z}}_2)-(W_1-W_2)+\lambda (p({\widehat{Z}}_1)-p({\widehat{Z}}_2))=0$$ (48)

from which we obtain

$$\langle {\widehat{Z}}_1-{\widehat{Z}}_2,{\widehat{Z}}_1-{\widehat{Z}}_2\rangle -\langle W_1-W_2,{\widehat{Z}}_1-{\widehat{Z}}_2\rangle +\lambda \langle p({\widehat{Z}}_1)-p({\widehat{Z}}_2),{\widehat{Z}}_1-{\widehat{Z}}_2\rangle =0$$ (49)

where 〈a, b〉 = trace (a′b).

Now observe that

$$\langle p({\widehat{Z}}_1)-p({\widehat{Z}}_2),{\widehat{Z}}_1-{\widehat{Z}}_2\rangle =\langle p({\widehat{Z}}_1),{\widehat{Z}}_1\rangle -\langle p({\widehat{Z}}_1),{\widehat{Z}}_2\rangle -\langle p({\widehat{Z}}_2),{\widehat{Z}}_1\rangle +\langle p({\widehat{Z}}_2),{\widehat{Z}}_2\rangle$$ (50)

By the characterization of subgradients as in (46) and as also observed in [CCS08], we have

$$\langle p({\widehat{Z}}_i),{\widehat{Z}}_i\rangle ={\Vert {\widehat{Z}}_i\Vert }_{*}\text{and}{\Vert p({\widehat{Z}}_i)\Vert }_2\le 1,i=1,2$$

which implies

$$|\langle p({\widehat{Z}}_i),{\widehat{Z}}_j\rangle |\le {\Vert p({\widehat{Z}}_i)\Vert }_2{\Vert {\widehat{Z}}_j\Vert }_{*}\le {\Vert {\widehat{Z}}_j\Vert }_{*}\text{for}i\ne j\in \{1,2\}$$

Using the above inequalities in (50) we obtain:

$$\langle p({\widehat{Z}}_1),{\widehat{Z}}_1\rangle +\langle p({\widehat{Z}}_2),{\widehat{Z}}_2\rangle ={\Vert {\widehat{Z}}_1\Vert }_{*}+{\Vert {\widehat{Z}}_2\Vert }_{*}$$ (51)

$$-\langle p({\widehat{Z}}_1),{\widehat{Z}}_2\rangle -\langle p({\widehat{Z}}_2),{\widehat{Z}}_1\rangle \ge -{\Vert {\widehat{Z}}_2\Vert }_{*}-{\Vert {\widehat{Z}}_1\Vert }_{*}$$ (52)

Using (51),(52) we see that the r.h.s. of (50) is non-negative. Hence

$$\langle p({\widehat{Z}}_1)-\langle p({\widehat{Z}}_2),{\widehat{Z}}_1-{\widehat{Z}}_2\rangle \ge 0$$

Using the above in (48), we obtain:

$${\Vert {\widehat{Z}}_1-{\widehat{Z}}_2\Vert }_F^2=\langle {\widehat{Z}}_1-{\widehat{Z}}_2,{\widehat{Z}}_1-{\widehat{Z}}_2\rangle \le \langle W_1-W_2,{\widehat{Z}}_1-{\widehat{Z}}_2\rangle$$ (53)

Using the Cauchy-Schwarz Inequality ‖Ẑ₁ − Ẑ₂‖₂‖W₁ − W₂‖₂ ≥ 〈Ẑ₁ − Ẑ₂, W₁ − W₂〉 in (53) we get

$${\Vert {\widehat{Z}}_1-{\widehat{Z}}_2\Vert }_F^2\le \langle {\widehat{Z}}_1-{\widehat{Z}}_2,W_1-W_2\rangle \le {\Vert {\widehat{Z}}_1-{\widehat{Z}}_2\Vert }_2{\Vert W_1-W_2\Vert }_2.$$

and in particular

$${\Vert {\widehat{Z}}_1-{\widehat{Z}}_2\Vert }_F^2\le {\Vert {\widehat{Z}}_1-{\widehat{Z}}_2\Vert }_2{\Vert W_1-W_2\Vert }_2$$

which further simplifies to

$${\Vert W_1-W_2\Vert }_F^2\ge {\Vert {\widehat{Z}}_1-{\widehat{Z}}_2\Vert }_F^2={\Vert {\mathbf{S}}_{\lambda }(W_1)-{\mathbf{S}}_{\lambda }(W_2)\Vert }_F^2$$

A.3 Proof of Lemma 4

Proof. We will first show (19) by observing the following inequalities

$$\begin{array}{lll}{\Vert Z_{\lambda }^{k+1}-Z_{\lambda }^k\Vert }_F^2\hfill & =\hfill & {\Vert {\mathbf{S}}_{\lambda }(P_{\mathrm{\Omega }}(X)+P_{\mathrm{\Omega }}^{\perp }(Z_{\lambda }^k))-{\mathbf{S}}_{\lambda }(P_{\mathrm{\Omega }}(X)+P_{\mathrm{\Omega }}^{\perp }(Z_{\lambda }^{k-1}))\Vert }_F^2\hfill \\ (\text{by}\text{Lemma}3)\hfill & \le \hfill & {\Vert \left(P_{\mathrm{\Omega }}(X)+P_{\mathrm{\Omega }}^{\perp }(Z_{\lambda }^k)\right)-\left(P_{\mathrm{\Omega }}(X)+P_{\mathrm{\Omega }}^{\perp }(Z_{\lambda }^{k-1})\right)\Vert }_F^2\hfill \\ \hfill & =\hfill & {\Vert P_{\mathrm{\Omega }}^{\perp }(Z_{\lambda }^k-Z_{\lambda }^{k-1})\Vert }_F^2\hfill \end{array}$$ (54)

$$\le {\Vert Z_{\lambda }^k-Z_{\lambda }^{k-1}\Vert }_F^2$$ (55)

The above implies that the sequence $\{{\Vert Z_{\lambda }^k-Z_{\lambda }^{k-1}\Vert }_F^2\}$ converges (since it is decreasing and bounded below). We still require to show that $\{{\Vert Z_{\lambda }^k-Z_{\lambda }^{k-1}\Vert }_F^2\}$ converges to zero.

The convergence of $\{{\Vert Z_{\lambda }^k-Z_{\lambda }^{k-1}\Vert }_F^2\}$ implies that:

$${\Vert Z_{\lambda }^{k+1}-Z_{\lambda }^k\Vert }_F^2-{\Vert Z_{\lambda }^k-Z_{\lambda }^{k-1}\Vert }_F^2\to 0\text{as}k\to \infty$$

The above observation along with the inequality in (54),(55) gives

$${\Vert P_{\mathrm{\Omega }}^{\perp }(Z_{\lambda }^k-Z_{\lambda }^{k-1})\Vert }_F^2-{\Vert Z_{\lambda }^k-Z_{\lambda }^{k-1}\Vert }_F^2\to 0\Rightarrow P_{\mathrm{\Omega }}(Z_{\lambda }^k-Z_{\lambda }^{k-1})\to 0$$ (56)

as k → ∞.

Lemma 2 shows that the non-negative sequence $f_{\lambda }(Z_{\lambda }^k)$ is decreasing in k. So as k → ∞ the sequence $f_{\lambda }(Z_{\lambda }^k)$ converges. Furthermore from (16),(17) we have

$$Q_{\lambda }(Z_{\lambda }^{k+1}|Z_{\lambda }^k)-Q_{\lambda }(Z_{\lambda }^{k+1}|Z_{\lambda }^{k+1})\to 0\text{as}k\to \infty$$

which implies that

$${\Vert P_{\mathrm{\Omega }}^{\perp }(Z_{\lambda }^k)-P_{\mathrm{\Omega }}^{\perp }(Z_{\lambda }^{k+1})\Vert }_F^2\to 0\text{as}k\to \infty$$

The above along with (56) gives

$$Z_{\lambda }^k-Z_{\lambda }^{k-1}\to 0\text{as}k\to \infty$$

This completes the proof.

A.4 Proof of Lemma 5

Proof. The sub-gradients of the nuclear norm ‖Z‖_* are given by

$$\partial {\Vert Z\Vert }_{*}=\{UV\prime +W:W_{m\times n},U\prime W=0,WV=0,{\Vert W\Vert }_2\le 1\}$$ (57)

where Z = U DV′ is the SVD of Z. Since $Z_{\lambda }^k$ minimizes $Q_{\lambda }(Z|Z_{\lambda }^{k-1})$, it satisfies:

$$0\in -(P_{\mathrm{\Omega }}(X)+P_{\mathrm{\Omega }}^{\perp }(Z_{\lambda }^{k-1})-Z_{\lambda }^k)+\partial {\Vert Z_{\lambda }^k\Vert }_{*}\forall k$$ (58)

Suppose Z* is a limit point of the sequence $Z_{\lambda }^k$. Then there exists a subsequence {n_k} ⊂ {1, 2, …} such that $Z_{\lambda }^{n_k}\to Z^{*}$ as k → ∞.

By Lemma 4 this subsequence $Z_{\lambda }^{n_k}$ satisfies

$$Z_{\lambda }^{n_k}-Z_{\lambda }^{n_k-1}\to 0$$

implying

$$P_{\mathrm{\Omega }}^{\perp }(Z_{\lambda }^{n_k-1})-Z_{\lambda }^{n_k}\to P_{\mathrm{\Omega }}^{\perp }(Z_{\lambda }^{*})-Z_{\lambda }^{*}=-P_{\mathrm{\Omega }}(Z^{*})$$

Hence,

$$(P_{\mathrm{\Omega }}(X)+P_{\mathrm{\Omega }}^{\perp }(Z_{\lambda }^{n_k-1})-Z_{\lambda }^{n_k})\to (P_{\mathrm{\Omega }}(X)-P_{\mathrm{\Omega }}(Z_{\lambda }^{*})).$$ (59)

For every k, a sub-gradient $p(Z_{\lambda }^k)\in \partial {\Vert Z_{\lambda }^k\Vert }_{*}$ corresponds to a tuple (u_k, v_k, w_k) satisfying the properties of the set $\partial {\Vert Z_{\lambda }^k\Vert }_{*}$ (57).

Consider $p(Z_{\lambda }^{n_k})$ along the sub-sequence n_k. As n_k → ∞, $Z_{\lambda }^{n_k}\to Z_{\lambda }^{*}$. Let

$$Z_{\lambda }^{n_k}=u_{n_k}{D}_{n_k}{v}_{n_k}^{\prime },Z^{*}=u_{\infty }D*v_{\infty }^{\prime }$$

denote the SVD’s. The product of the singular vectors converge $u_{n_k}^{\prime }{v}_{n_k}\to u_{\infty }^{\prime }{v}_{\infty }$. Furthermore due to boundedness (passing on to a further subsequence if necessary) w_nk → w_∞. The limit $u_{\infty }{u}_{\infty }^{\prime }+w_{\infty }$ clearly satisfies the criterion of being a sub-gradient of Z*. Hence this limit corresponds to $p(Z_{\lambda }^{*})\in \partial {\Vert Z_{\lambda }^{*}\Vert }_{*}$.

Furthermore from (58), (59), passing on to the limits along the subsequence n_k we have

$$\mathbf{0}\in -(P_{\mathrm{\Omega }}(X)-P_{\mathrm{\Omega }}(Z_{\lambda }^{*}))+\partial {\Vert Z_{\lambda }^{*}\Vert }_{*}$$ (60)

Hence the limit point $Z_{\lambda }^{*}$ is a stationary point of f_λ(Z).

We shall now prove (21). We know that for every n_k

$$Z_{\lambda }^{n_k}={\mathbf{S}}_{\lambda }(P_{\mathrm{\Omega }}(X)+P_{\mathrm{\Omega }}^{\perp }(Z_{\lambda }^{n_k-1}))$$ (61)

From Lemma 4 we know $Z_{\lambda }^{n_k}-Z_{\lambda }^{n_k-1}\to 0$. This observation along with the continuity of S_λ(·) gives

$${\mathbf{S}}_{\lambda }(P_{\mathrm{\Omega }}(X)+P_{\mathrm{\Omega }}^{\perp }(Z_{\lambda }^{n_k-1}))\to {\mathbf{S}}_{\lambda }(P_{\mathrm{\Omega }}(X)+P_{\mathrm{\Omega }}^{\perp }(Z_{\lambda }^{*}))$$

Thus passing over to the limits on both sides of (61) we get

$$Z_{\lambda }^{*}={\mathbf{S}}_{\lambda }(P_{\mathrm{\Omega }}(X)+P_{\mathrm{\Omega }}^{\perp }(Z_{\lambda }^{*}))$$

therefore completing the proof.