On the difference between negative damping and eigenmode synchronization as two phonation onset mechanisms

Abstract

Negative damping and eigenmode synchronization as two different mechanisms of phonation onset are distinguished. Although both mechanisms lead to a favorable phase relationship between the flow pressure and the vocal fold motion as required for a net energy transfer into the vocal folds, the underlying mechanisms for this favorable phase relationship are different. The negative damping mechanism relies on glottal aerodynamics or acoustics to establish before onset and maintain after onset the favorable phase relationship, and therefore has minimum requirements on vocal fold geometry and biomechanics. A single degree-of-freedom vocal fold model is all that is needed for self-oscillation in the presence of a negative damping mechanism. In contrast, the mechanism of eigenmode synchronization critically depends on the geometrical and biomechanical properties of the vocal folds (at least 2-degrees-of-freedom are required), and has little requirement on the glottal aerodynamics other than flow separation. The favorable phase relation is established once synchronization occurs, regardless of the phase relationship imposed by glottal aerodynamics before onset. Unlike that of the negative damping mechanism, initiation of eigenmode synchronization requires neither a velocity-dependent flow pressure nor an alternating convergent-divergent glottis. The clinical implications of the distinctions between these two mechanisms are discussed.

INTRODUCTION

According to the myoelastic-aerodynamic theory of voice production (Van Den Berg, 1958), vocal fold vibration results from the combined effect of a negative Bernoulli pressure during the open phase of the glottal cycle and a subglottal pressure buildup during glottal closure. However, as pointed out by Ishizaka (1981) and Titze (1988), the theory is inadequate in explaining how energy is transferred from the airflow to the vocal folds to sustain vibration. According to Bernoulli’s equation, the airflow pressure would always be 90° out of phase with vocal fold surface velocity, resulting in no net energy transfer from the airflow to the vocal folds over one cycle of vibration. Thus, Bernoulli pressure alone does not provide a mechanism for energy transfer from airflow to the vocal folds.

Titze (1988) argued that a driving force asymmetry between the opening and closing phases of one oscillation cycle is crucial for a net energy transfer from airflow into the vocal folds and the initiation of phonation. He further argued that such driving pressure asymmetry can be achieved by either an inertive vocal tract loading or a glottis with alternating convergent and divergent profiles as induced by surface wave propagation along the medial surface. Both two conditions led to a negative damping term in the resulting governing equation of Titze’s surface wave model (1988), and phonation onset occurred when the combined negative damping was large enough to overcome the positive structural damping of the vocal folds.

Although the surface wave motion induces a negative damping term in Titze’s equivalent single degree-of-freedom (DOF) model, it results from eigenmode synchronization (also called coupled-mode flutter in engineering literature); a mechanism that is fundamentally different from negative damping. As we will show below, the negative damping mechanism relies on glottal aerodynamics or acoustics to establish before onset and maintain after onset the favorable phase relationship required for net energy transfer, and therefore has minimum requirements on vocal fold geometry and biomechanics. A single-DOF vocal fold model is all that is needed for self-oscillation in the presence of a negative damping mechanism. In contrast, the mechanism of eigenmode synchronization critically depends on the geometrical and biomechanical properties of the vocal folds (at least 2-DOFs are required), and has little requirements on glottal aerodynamics other than flow separation (Zhang, 2008). The favorable phase relation is established once synchronization occurs, regardless of the phase relationship imposed by glottal flow before onset. Unlike that of the negative damping mechanism, initiation of eigenmode synchronization requires neither a velocity-dependent flow pressure nor an alternating convergent-divergent glottis (Ishizaka, 1981; Zhang et al., 2007).

NEGATIVE DAMPING

To illustrate the difference between the two mechanisms, let us first consider the destabilizing mechanism in a single-DOF system,

$$\stackrel{\mathrm{··}}{y}+\frac{c_{\mathrm{vf}}}{m_{\mathrm{vf}}}\stackrel{·}{y}+\frac{k_{\mathrm{vf}}}{m_{\mathrm{vf}}}y=\frac{f}{m_{\mathrm{vf}}},$$ (1)

where m_vf, c_vf, and k_vf are the mass, damping, and stiffness of the single-mass vocal fold model, y is the displacement of the single-mass vocal fold, and f is the force due to intraglottal flow pressure acting on the vocal fold model. As we are concerned about system dynamics around phonation onset, the driving flow pressure is linearized around the appropriate mean state and only linear terms are retained. This also allows us to further decompose the flow pressure into three terms that are proportional to vocal fold acceleration (flow-induced mass), velocity (flow-induced damping), and displacement (flow-induced stiffness), respectively (for details refer to Zhang et al., 2007),

$$f=m_{\mathrm{f}}\stackrel{\mathrm{··}}{y}+c_{\mathrm{f}}\stackrel{·}{y}+k_{\mathrm{f}}y.$$ (2)

Substitution of Eq. 2 into Eq. 1 yields,

$$\stackrel{\mathrm{··}}{y}+\frac{c}{m}\stackrel{·}{y}+\frac{k}{m}y=0,$$ (3)

where m = m_vf − m_f is the total mass, c = c_vf − c_f is the total damping, and k = k_vf − k_f is the total stiffness. The stability of Eq. 3 can be investigated by solving it as an eigenvalue problem and examining its corresponding eigenvalues. An eigenvalue with a positive real part (or growth rate) indicates that positive net energy is transferred into the corresponding eigenmode so that the eigenmode is linearly unstable and its amplitude will grow with time. Therefore, phonation onset occurs when the real part of one eigenvalue first becomes positive with increasing subglottal pressure. The phonation onset frequency is then given by the imaginary part of the eigenvalue, whereas the vibratory pattern is determined by the corresponding eigenvector.

The eigenvalues of Eq. 3 are

$$\lambda =\frac{-c}{2m}\pm \sqrt{\frac{c^2}{4m^2}-\frac{k}{m}}.$$ (4)

Considering the small density ratio between air and vocal folds, the total mass m can be assumed to be always positive. Thus, destabilization in a single-DOF system occurs as long as the total damping becomes negative (c = c_vf − c_f < 0), i.e., the real part of the eigenvalue in Eq. 4 becomes positive [Fig. 1a]. For a non-zero-frequency instability, the magnitude of total damping also has to be small so that c² − 4mk < 0, at which condition the eigenvalue in Eq. 4 has a non-zero imaginary part (i.e., non-zero phonation frequency). Note that the flow-induced stiffness k_f in this case does not affect the total damping c, and thus has no effect on the onset threshold. Therefore, negative damping due to a velocity-dependent driving force is the only onset mechanism in a single-DOF system.

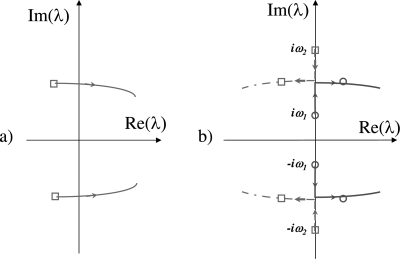
Figure 1.

(Color online) The eigenvalue movement in the complex plane as the system moves toward instability. (a) The single eigenmode of a single-DOF system is destabilized by an increasing negative damping; the arrow indicates direction of eigenvalue movement with decreasing (more negative) total damping; (b) with increasing subglottal pressure, two eigenmodes (denoted by circle and square) of a 2-DOF system gradually approach each other and eventually synchronize. Further increase in subglottal pressure causes one eigenmode (denoted by the circle) to leave the imaginary axis into the right half plane and become destabilized; the arrow indicates direction of eigenvalue movement as the subglottal pressure is increased.

An important feature of negative damping is that the energy transfer, or the phase relationship between flow pressure and surface velocity, is critically dependent on glottal aerodynamics or acoustics (Table TABLE I.). This mechanism has essentially no requirement on vocal fold geometry and biomechanics so that even a single-DOF system is able to self-oscillate in the presence of negative damping. Examples of flow-induced negative damping include acoustical coupling to an inertive vocal tract (Flanagan and Landgraf, 1968; Titze, 1988) or a compliant subglottal system (Zhang et al., 2006), the presence of a flow boundary layer (Miles, 1957), and a velocity-dependent moving flow separation point (Howe and McGowan, 2010).

Table 1.

Comparison between negative damping and eigenmode synchronization as two phonation onset mechanisms. P₁ and P₂ (V₁ and V₂) denote the flow pressure (vocal fold surface velocity) associated with the two synchronizing eigenmodes. The integration is performed along the vocal fold surface.

	Negative damping	Eigenmode synchronization
Complex-plane representation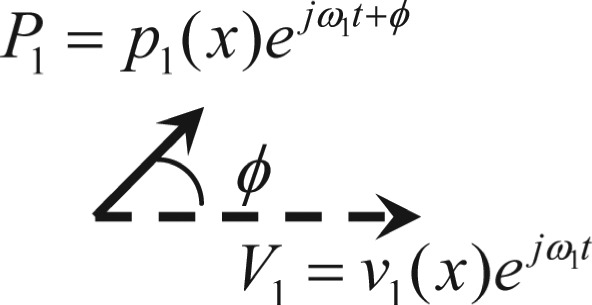
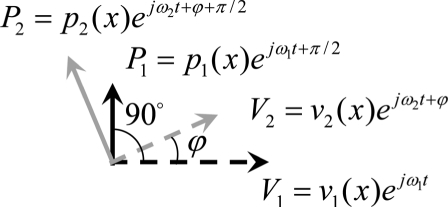Favorable phase relationship	Directly imposed by glottal aerodynamics or acoustics $\varphi \ne \frac{\pi }{2}$	Provided by synchronizing two vocal fold modes to the same frequency but different phases (ϕ ≠ 0, ω1 = ω2, a12 ≠ a21)
Flow pressure	velocity-dependent	Displacement-dependent, no need to be velocity-dependent
Dominant physics	Glottal aerodynamics or acoustics	Vocal fold geometry and biomechanics
Energy transfer	Same-mode energy transfer $E=\frac{1}{2}\cos \phi \int p_1{v}_{1}dx\ne 0$	Cross-mode energy transfer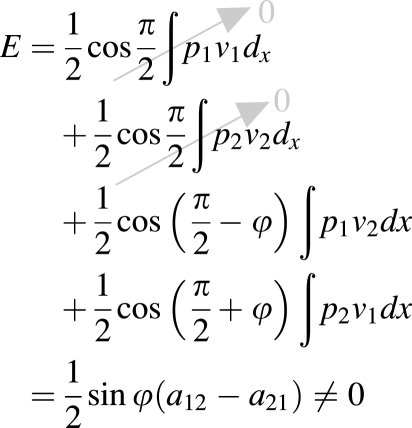

EIGENMODE SYNCHRONIZATION

In contrast, eigenmode synchronization requires at least 2-DOFs and is highly influenced by vocal fold geometry and biomechanics. Let us now consider a 2-DOF dynamical system. The negative damping mechanism still applies in a 2-DOF system. To avoid instability due to negative damping and to focus on the eigenmode synchronization mechanism due to a velocity-independent flow pressure, we will for the time being neglect the damping term (both structural and flow-induced damping) and consider a driving force with only a displacement-dependent term (i.e., flow-induced stiffness term),

$$\begin{array}{ccc}\hfill \stackrel{\mathrm{··}}{q}+\left[\begin{array}{cc}\hfill {\omega }_1^2\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\omega }_2^2\hfill \end{array}\right]q=K_{\mathrm{f}}q,& \hfill & \hfill \end{array}$$ (5)

where ω₁ and ω₂ are the two natural frequencies of the 2-DOF vocal fold structure, q is the generalized coordinate vector, and K_f is the flow-induced stiffness matrix. Zhang (2010) showed that the flow-induced stiffness is proportional to the subglottal pressure P_s so that Eq. 5 can be rewritten as,

$$\begin{array}{ccc}\hfill \stackrel{\mathrm{··}}{q}+\left[\begin{array}{cc}\hfill {\omega }_1^2\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\omega }_2^2\hfill \end{array}\right]q=P_s\left[\begin{array}{cc}\hfill a_{11}\hfill & \hfill a_{12}\hfill \\ \hfill a_{21}\hfill & \hfill a_{22}\hfill \end{array}\right]q.& \hfill & \hfill \end{array}$$ (6)

The matrix elements a_ij quantify the spatial similarity between the flow pressure induced by the ith eigenmode and the vocal fold motion of the jth eigenmode along the vocal fold surface [see their definition in Eq. 7 of Zhang, 2010]. In other words, they quantify the cross-mode energy transfer efficiency between the ith and jth eigenmodes, if the two modes have the same frequency and thus are able to interact with each other. The eigenvalues of Eq. 6 are,

$${\lambda }^2=\frac{-[({\omega }_1^2-P_s{a}_{11})+({\omega }_2^2-P_s{a}_{22})]\pm \sqrt{\Delta }}{2}$$ (7)

where

$$\Delta =[({\omega }_1^2-P_s{a}_{11})-({\omega }_2^2-P_s{a}_{22})]{}^2+4P_s^2{a}_{12}{a}_{21}.$$ (8)

For P_s = 0 (i.e., without airflow), the eigenvalues (±jω₁ and ±jω₂) all lie on the imaginary axis in the complex plane [Fig. 1b]. When the flow-induced stiffness K_f satisfies certain conditions (a₁₂a₂₁ < 0, for details refer to Zhang, 2010) Eq. 7 shows that, with increasing subglottal pressure P_s, the eigenvalues gradually approach each other, and eventually merge into one eigenvalue when Δ = 0. Further increases in subglottal pressure would cause one of the eigenvalues to leave the imaginary axis into the right half complex plane with a positive real part and a non-zero imaginary part, indicating the onset of a non-zero-frequency instability [Fig. 1b; also see Fig. 5 in Zhang et al., 2007].

To understand how the velocity-independent flow-induced stiffness transfers energy from airflow into the vocal folds during eigenmode synchronization, it is helpful to note the following two features of the coupled system. First, once synchronized to the same frequency, the flow pressure induced by one mode can then interact with the surface velocity of the other mode. Although the flow pressure and the surface velocity of the same mode are 90° out of phase, synchronization of the two modes at a non-zero phase (ϕ ≠ 0 in Table TABLE I.) allows the flow pressure of one mode to be partially in phase with the surface velocity of the other mode (Table TABLE I.). Second, due to flow separation, the two synchronizing modes differ in capability of inducing a flow pressure that is spatially similar to the motion of the other mode (Zhang, 2008, 2010). For example, in Zhang et al. (2007), the intraglottal pressure induced by the third eigenmode (which captured mainly an out-of-phase medial-lateral motion) was spatially similar to the second eigenmode (which captured mainly an in-phase medial-lateral motion), whereas the pressure induced by the second mode was much less similar to the motion of the third mode. This leads to a difference in energy transfer efficiency [as quantified by the off-diagonal matrix elements a_ij in Eq. 6] between the two cross-mode interactions of the two synchronizing modes [i.e., a₁₂ ≠ a₂₁ in Eq. 6], and ensures a non-zero net energy transfer from airflow into the vocal folds over one oscillation cycle (Table TABLE I.). Note that, this condition is automatically satisfied as the two efficiencies are required to have opposite sign so that a₁₂a₂₁ < 0 if eigenmode synchronization were to occur at all.

Note that the eigenmode synchronization and the resulting energy transfer as discussed above are induced by a flow-induced stiffness term alone. In other words, Eq. 7 shows that onset can be induced by a velocity-independent driving force (i.e., the flow pressure depends only on vocal fold displacement). This contrasts with the single DOF system in which a velocity-dependent driving force (negative damping) is required for onset.

DISCUSSION

It is now obvious that a negative Bernoulli pressure is not a critical requirement in either one of the two mechanisms. Being proportional to vocal fold displacement, the negative Bernoulli pressure is not a negative damping and does not directly provide the required phase relationship between flow pressure and surface velocity. For eigenmode synchronization, energy transfer depends on the characteristics of the flow-induced stiffness matrix, which is determined primarily by vocal fold properties, rather than whether the intraglottal pressure is positive or negative during a certain phase of the oscillation cycle.

Although eigenmode synchronization leads to a time-varying glottal geometry, an alternating convergent-divergent glottal geometry is not essential to the initiation of self-sustained vocal fold oscillation. Theoretically, the glottis can maintain a convergent or divergent profile during the entire oscillation cycle and yet still self-oscillate. This was confirmed by experiments using physical vocal fold models which had a divergent shape during most portion of the oscillation cycle (Zhang et al., 2006). In fact, if an alternating convergent-divergent glottal geometry is a necessary condition for phonation onset, this would suggest that phonation onset is only possible when the glottal channel is uniform. This is because the uniform glottis is the only geometry that is able to alternately change from convergent, uniform, to divergent over one oscillation cycle when subjected to disturbances of infinitely small amplitude. Fortunately, this is not the case, as simulations have shown that phonation onset is possible for a glottis with either convergent or divergent prephonatory geometry.

Is it possible to reduce a 2-DOF system to a single-DOF system while still preserving the eigenmode synchronization mechanism? In general, this is not possible because the phase relationship between the two synchronizing modes is a dynamic variable of the coupled system and is often unknown a priori. Previous studies (Ishizaka, 1988; Berry et al., 1994, 2001; Zhang et al., 2007) showed that such phase relationship varied with both subglottal pressure and vocal fold properties. When a 2-DOF system is reduced to single-DOF and only one eigenmode is retained, such phase relation between the synchronizing modes can no longer be calculated and has to be either modeled or arbitrarily specified, which often leads to distortion of the eigenmode synchronization process. For example, such order reduction was attempted by Titze (1988) by imposing a constant phase relationship (through a constant surface wave velocity) between the two synchronizing eigenmodes (the upper and lower margins of the medial surface oscillate in-phase in one mode, and out of phase in the other mode). Because of this prescribed rather than calculated phase relationship, the eigenmode synchronization process, the resulting vibratory pattern, and their dependence on vocal fold geometry and biomechanics cannot be studied in the surface wave model. Specifically, the mucosal wave speed or the phase delay in motion along the vocal fold surface, which was used as an independent control parameter in Titze’s (1988) surface wave model, has been shown to be spatially dependent and depends on both vocal fold geometry and biomechanics (Boessenecker et al., 2007; Zhang, 2009). Because of this dependence of mucosal wave speed on vocal fold properties, the effects of the geometrical and material properties of the vocal fold (e.g., prephonatory glottal configuration, medial surface thickness, body or cover stiffness, etc.) on phonation cannot be properly investigated using the surface wave model.

Another aspect of the reduction problem concerns the reduction of a continuum vocal fold model to a 2-DOF vocal fold model, e.g., the two-mass model. An infinite number of eigenmodes exist in continuum models. As a result, eigenmode synchronization in continuum models may be influenced by other eigenmodes that are not actively involved in the synchronization process (Zhang et al., 2007; Zhang, 2010). Furthermore, more than one pair of eigenmodes can be simultaneously synchronized by the glottal flow, and, depending on the specific phonatory conditions (e.g., vocal fold geometry and stiffness), phonation onset may occur as a different pair of eigenmodes is synchronized and destabilized (Zhang, 2009). Consequently, the vibratory pattern may change abruptly due to even slight changes in either vocal fold geometry or biomechanical properties (Tokuda et al., 2007). This possibility of vocal fold vibration at a different eigenmode makes it difficult to estimate model parameters of the two-mass model if the model is expected to be valid across a variety of phonatory regimes without re-estimating model parameters for each regime.

CONCLUSION

In summary, although for both mechanisms the energy transfer is caused by a favorable phase relationship between the flow pressure and vocal fold motion, the underlying mechanisms for this favorable phase relationship are different (Table TABLE I.). For negative-damping-induced onset, the favorable phase relationship is directly provided by glottal aerodynamics (e.g., the moving flow separation point in Howe and McGowan, 2010, or coupling to acoustics). Thus the glottal flow should be accurately modeled. For eigenmode synchronization, the favorable phase relation is established by synchronizing two modes at the same frequency but different phases, regardless of the flow pressure–surface motion phase relationship imposed by glottal aerodynamics before onset. As vocal fold geometry and biomechanics critically determine the synchronization process and energy transfer (Zhang, 2010), they need to be accurately represented. Low-order vocal fold models such as the one-mass and two-mass models are inadequate in completely capturing the physics of eigenmode synchronization.

Clinically, if the negative damping can be shown to be the dominant mechanism of phonation onset, clinical intervention methods should then be designed to modify the specific aerodynamic or acoustic mechanism that determines the phase relationship between the flow pressure and the surface motion, e.g., by shaping the subglottal or supraglottal airway to achieve a favorable acoustic impedance condition or a better moving pattern of the flow separation point, or reducing vocal fold damping (if possible). For phonation induced primarily by eigenmode synchronization, surgical intervention should then be aimed to facilitate early occurrence of mode synchronization by modifying the geometrical and biomechanical properties of the vocal folds (e.g., using laryngeal implants inserted into the vocal fold body or cover layer) to decrease the frequency spacing and enhance coupling between eigenmodes that may be potentially synchronized and destabilized (Zhang, 2010).

Considering that humans have much less direct control of glottal aerodynamics, the fact that humans are capable of producing a large variety of voice types through vocal fold posturing seems to suggest that eigenmode synchronization is the primary mechanism of phonation onset in normal phonation. Although confirmed by Zhang et al. (2007) using a simplified glottal flow model, this dominant role of eigenmode synchronization still remains to be verified by experiments under different laryngeal conditions. On the other hand, even in the case when eigenmode synchronization dominates different negative damping mechanisms may interact and affect the synchronization process. For example, Zhang et al. (2007) showed that the flow-induced damping may interfere with the eigenmode synchronization process and affect phonation threshold. For large vibration amplitudes, the eigenmode synchronization will cause the glottal shape to alternately change from convergent, uniform, to divergent thereby introducing a velocity-dependent driving pressure associated with moving flow separation point (Howe and McGowan, 2010). The extent to which these different negative damping mechanisms affect eigenmode synchronization needs to be investigated in future studies.