Assessment of accuracy of the structure-factor-size-estimator method in determining red blood cell aggregate size from ultrasound spectral backscatter coefficient

Abstract

A computer simulation study to produce ultrasonic backscatter coefficients (BSCs) from red blood cell (RBC) clusters is discussed. The simulation algorithm is suitable for generating non-overlapping, isotropic, and fairly identical RBC clusters. RBCs were stacked following the hexagonal close packing (HCP) structure to form a compact spherical aggregate. Such an aggregate was repeated and placed randomly under non-overlapping condition in the three-dimensional space to mimic an aggregated blood sample. BSCs were computed between 750 KHz and 200 MHz for samples of various cluster sizes at different hematocrits. Magnitudes of BSCs increased with mean aggregate sizes at low frequencies (<20 MHz). The accuracy of the structure-factor-size-estimator (SFSE) method in determining mean aggregate size and packing factor was also examined. A good correlation (R² ≥ 0.94) between the mean size of aggregates predicted by the SFSE and true size was found for each hematocrit. This study shows that for spherical aggregates there exists a region for each hematocrit where SFSE works most accurately. Typically, error of SFSE in estimating mean cluster size was <20% for dimensions between 14 and 17 μm at 40% hematocrit. This study suggests that the theoretical framework of SFSE is valid under the assumption of isotropic aggregates.

INTRODUCTION

Some ultrasonic tissue characterization techniques generally consider frequency dependent information of backscatter echoes to quantify tissue structural properties, such as the size, acoustic impedance, number density of scattering particles, etc. This approach has been successfully used for the characterization of the eye,1, 2 liver,3 kidney,4 prostate,5 breast tissues6 and also to monitor cell apoptosis in order to evaluate the efficacy of cancer therapies.7 Blood has also been characterized by employing this technique.8 The main purpose of ultrasonic characterization of blood is to assess the level of red blood cell (RBC) aggregation, which is a surrogate marker of inflammation.9 Readers may refer to Fig. 5 of Ref. 10 and Fig. 1 of Ref. 11 to see microscopic images of RBC aggregation and to illustrate how non-aggregated RBCs form clusters with time under different pro-aggregating conditions. An enhanced level of RBC aggregation is a pathological state and is associated with many circulatory diseases such as deep venous thrombosis, atherosclerosis, and diabetes mellitus. The ultrasonic backscatter technique has the potential to provide a method for non-invasive determination of RBC cluster size, consequently allowing one to address the role of RBC aggregation in the processes of such diseases.

Yu and Cloutier10 recently proposed a parametric form of backscatter coefficient (BSC). They arrived at that mathematical form by using a second order Taylor series expansion of the structure factor and thus obtained two physically relevant parameters of aggregation: The mean diameter of aggregates D and the packing factor W. The packing factor is related to the volume ratio of RBCs known as the hematocrit (H), and is sensitive to the spatial arrangement of scatterers.12, 13 The parameter D estimates how many cells are attached as an aggregate. They used the parametric form of the BSC to analyze experimental data in vitro and obtained sound rheological results.11 The method is referred as the structure-factor-size-estimator (SFSE). Franceschini et al.14 further developed this model to incorporate attenuation effects of intervening tissues between the probe and the blood flow with the objective of providing a method applicable to in vivo situations. It was shown in that work that simultaneous evaluation of D, W, and of the attenuation coefficient of the intervening tissue layers could be obtained but the validation of the SFSE has been so far conducted only experimentally. However, the experimental assessment of accuracy of SFSE in determining the mean size of aggregates by optical means was possible only at a low hematocrit (6%), since RBCs are not visible with a microscope at a normal physiological hematocrit of typically 35%–55%.10

The aim of the work presented here is to describe a simple and rapid method to simulate randomly distributed compact RBC clusters in order to evaluate the accuracy of the SFSE method. The cells were assumed to be arranged in a spherical cluster in such a way so that a hexagonal close packing (HCP) structure was obtained. Note that this scheme provides the highest packing density [i.e., fractional volume occupied by spheres and also referred as the hematocrit (H)] that is about 0.74 for spheres.15 Such an aggregate was repeated and placed randomly under non-overlapping condition in the three-dimensional (3D) space to mimic aggregated blood samples. The ensemble average of the BSC was determined by simulation from the samples comprising non-overlapping, isotropic, and fairly identical spherical RBC aggregates. Consequently, cluster size dependent ultrasound backscatter properties were studied. The accuracy of the SFSE method in estimating the mean cluster size was accomplished by comparing estimated results (using SFSE) and actual cluster sizes (determined by using the coordinates of cells attached to the clusters, known from the simulations) at hematocrits from 0.20 to 0.40, which is not possible experimentally by optical means. A low hematocrit of 0.20 is a condition that can be encountered in severe anemia. As far as the authors are aware, the approach described here has never been employed to generate RBC aggregates as well as to study ultrasound backscatter from a collection of such aggregates.

The paper is organized in the following way. In Sec. 2 we discuss the theoretical models describing ultrasonic backscatter by a collection of erythrocytes. Section 3 illustrates the simulation method. Results are presented in Sec. 4. Quality of our results in the light of experimental observations is discussed in Sec. 5 followed by a summary in Sec. 6.

THEORETICAL MODEL

The backscattering cross-section per unit volume or the BSC for the scattering of an incident plane wave with wave vector $\overrightarrow{k}$ by an ensemble of particles of uniform size can be cast in terms of the Percus–Yevick packing factor (W_PY), as described in Chapter 5 of Ref. 8,

$${\chi }_b(-2\overrightarrow{k})={\mathit{mW}}_{\mathit{PY}}{\sigma }_b(-2\overrightarrow{k}),$$ (1)

where m is the number density of particles and it is related to the hematocrit (H) as m = H∕V_s. Here, V_s denotes the volume of an equivalent sphere of a RBC, which is a good model of the backscattering cross-section ${\sigma }_b(-2\overrightarrow{k})$ (less than 5% error) below 18 MHz.16 The subscript b here indicates backscattering. The Percus–Yevick packing factor (W_PY) for spatially random distribution of hard spherical particles with equal radii can be expressed as8

$$W_{\mathit{PY}}=\frac{(1-H){}^4}{(1+2H){}^2}.$$ (2)

The analytical expression of the backscattering cross-section for the scattering of an incident plane wave by a weak spherical scatterer of radius a can be derived by using the Born approximation and it is given by17

$$\begin{array}{cc}\multicolumn{1}{c}{{\sigma }_b(-2\overrightarrow{k})}& =\frac{1}{16{\pi }^2}{V}_s^2{k}^4{(\frac{{\kappa }_e-\kappa }{\kappa }-\frac{{\rho }_e-\rho }{{\rho }_e})}^2\hfill \\ \multicolumn{1}{c}{}& \mathrm{\hspace{1em}\hspace{1em}\hspace{1em}}\times {\left(3\frac{\mathit{sin}2\mathit{ka}-2\mathit{ka}\mathit{cos}2\mathit{ka}}{(2\mathit{ka}){}^3}\right)}^2.\hfill & \mathrm{}\hfill \end{array}$$ (3)

Here, κ and ρ indicate the adiabatic compressibility and density of the surrounding medium (blood plasma), respectively. The same quantities for the RBC scatterer are given by κ_e and ρ_e. Equation (1) is valid in the low frequency range and was observed to provide a good fit to experimental data for the backscattering of non-aggregated RBCs when probed at 7.5 MHz.18

On the other hand, the resultant backscatter signal from a collection of identical particles can be obtained by using the linear superposition principle for signals backscattered by individual particles. The corresponding BSC for a collection of particles can be written as19, 20

$$\begin{array}{cc}\multicolumn{1}{c}{{\chi }_b(-2\overrightarrow{k})}& =m〈\frac{1}{N}{|\sum _{n=1}^N\mathit{exp}(i2\overrightarrow{k}•{\overrightarrow{r}}_n)|}^2〉{\sigma }_b(-2\overrightarrow{k})\hfill \\ \multicolumn{1}{c}{}& =\mathit{mS}(-2\overrightarrow{k}){\sigma }_b(-2\overrightarrow{k}),\hfill & \mathrm{}\hfill \end{array}$$ (4)

where $S(-2\overrightarrow{k})$ is the structure factor of the medium and dictates how backscatter would vary with the spatial organization of particles. The symbol ⟨⟩ represents the ensemble average. The position vector ${\overrightarrow{r}}_n$ defines the center of the nth spherical scatterer in space and N is the total number of scatterers within the scattering volume (mentioned as the region of interest later in this article). In general, the structure factor of a medium containing particles distributed in the 3D space can be determined from the 3D Fourier transform of the spatial distribution of particles (see the Appendix of Refs. 13, 21). However, if the direction of the interrogating wave coincides with an axis of the coordinate system of the region of interest (ROI), then Eq. (4) reduces to one dimensional form and therefore computation of structure factor becomes trivial. In this work, Eq. (4) was computed for samples composed of randomly distributed 3D RBC clusters which were isotropic and fairly similar in size. Accordingly, cluster size dependent backscatter was examined.

Recently, Yu and Cloutier10 used a second order Taylor series expansion of the structure factor to obtain two physically relevant parameters, namely W and D. The parameter D was computed from the mean radius of gyration (R_g) of the aggregates. With this expansion Eq. (4) reduces to,

$${\chi }_b(-2\overrightarrow{k})=m(W-4k^2{R}_g^2){\sigma }_b(-2\overrightarrow{k}).$$ (5)

The radius (R_sp) of a homogeneous spherical object is related to its radius of gyration as $R_{\mathrm{sp}}=\sqrt{5∕3}{R}_g$ and thus the mean size of aggregates in terms of number of RBCs could be presented as, D = R_sp∕a. Yu and Cloutier used Eq. (5) to fit measured backscatter data corresponding to different RBC aggregation levels and the technique was referred to the SFSE method. In the present study, we also employed Eq. (5) to fit simulated frequency dependent BSC curves obtained by computing Eq. (4) for different samples with various clustering conditions. This enabled us to examine cluster size dependent ultrasound backscatter by RBCs as well as to assess the SFSE method by comparing the mean cluster size from simulated aggregates to that predicted by the said method from simulated BSC.

SIMULATION METHOD

Simulation of spatial distributions of aggregated RBCs

Different approaches to simulate compact RBC aggregates have been explored. For example, RBC clusters could be generated by allowing particles to interact via a Morse type potential and then by evolving the system through random positioning of cells.19 However, this technique is computationally intensive and can only produce random lose packing (RLP) configurations of particles with packing fractions of 0.60 ± 0.02 in three dimensions.22 Moreover, previously only 5.5 dB enhancement of BSC was found at 7.5 MHz at the highest aggregating condition at H = 0.40 using this technique19 and that is on the lower side compared to experimentally measured values. Alternatively, one can rely on algorithms to construct random close packing (RCP) configurations23, 24 that are expected to increase BSC. Jodrey and Tory24 developed this algorithm to generate RCP of equal spheres from a random distribution of points. In that study, each point is the center of an inner and an outer sphere. RCP configuration was achieved by slowly shrinking the outer diameter and by eliminating overlapping of outer spheres. The procedure was terminated when two diameters became on the same order. The implementation of such RCP algorithms is not straightforward, they are computationally intensive and also the attainable packing fraction (0.64 ± 0.02) of particles is still limited.

On the other hand, a highest packing density (0.74) can be obtained by using regular packing schemes such as HCP or cubic close packing (CCP).15 As mentioned earlier, it is expected that significant enhancement of BSC would be possible by using HCP of cells. In the current study, we followed this scheme to form an aggregate. The generation of such structure is simple and fast because cells have to be placed only at some defined locations. Such an aggregate prototype could be repeated and placed randomly in the 3D space to generate a tissue realization consisting of non-overlapping, isotropic, and fairly identical RBC clusters.

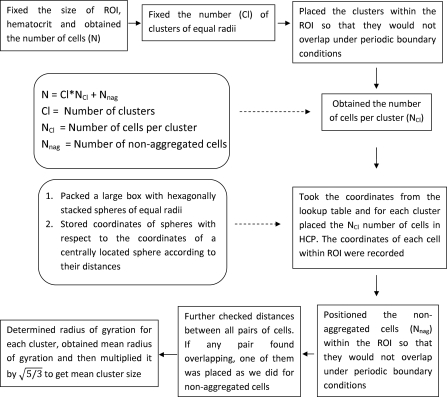
Initially, spatial locations of centers of the clusters of identical size were chosen randomly within the ROI under the condition that they would not overlap. The term “region of interest” is used to refer to the scattering volume. The periodic boundary conditions were imposed during this process. That means the clusters at the boundaries of the ROI would not overlap with the others at the opposite boundaries and thus removed the edge effect. The total number (fixed by the size of the ROI and the hematocrit) of cells was equally divided (truncated to the nearest lower integer value) into these clusters and the cells were stacked by following a HCP structure for each cluster.

To accomplish this (see Fig. 1), at the beginning (in order to pack cells in HCP structure) a large number of spheres (arbitrarily chosen) representing RBCs were packed within a box. They were stacked in such a way that they formed a HCP structure.15 After that, the coordinates of the centers of spheres with respect to the center of a sphere located at the central region of the box were recorded according to their distances and stored in a lookup table. The next step was to take the coordinates of the required number of RBC mimicking spheres from the lookup table. Accordingly, spheres were stacked with respect to the center of a cluster and thus the HCP structure was obtained for each cluster. Note that the lookup table provided the coordinates of the spheres with respect to the center of the cluster. However, to compute Eq. (4) one needed to know the position coordinates of the centers of those spheres with respect to the origin of the ROI. This could be easily obtained by summing the coordinates of the centers of those spheres and that of the cluster center. Similarly, spheres were stacked with respect to other cluster centers and also their coordinates with respect to the origin of the ROI were determined. The remaining spheres (those did not belonging to any cluster and behaving as disaggregated RBCs) were placed spatially at random in the ROI maintaining non-overlapping condition under periodic boundary conditions with the existing spheres. Further, an additional step was conducted to find overlapping pairs of cells. If they were found, then a new coordinate under non-overlapping condition was assigned for one of them. In this case too periodic boundary conditions were imposed while checking the non-overlapping condition of that cell with the others. In this way, spatial organization of spheres (most of them were included within clusters and others were randomly distributed spatially in the ROI) mimicking a tissue sample was obtained.

Figure 1.

Flow chart illustrating simulation steps to generate spherical clusters with HCP of red blood cells.

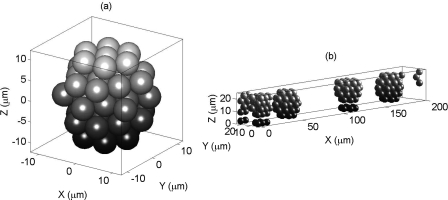
Figure 2a presents an arrangement of 51 spheres or RBCs in HCP forming a spherical 3D cluster. A realization of an aggregated blood tissue is shown in Fig. 2b. As an example and for clarity of the figure, a smaller ROI (200 × 20 × 20 μm³) occupied by the RBCs at 14% hematocrit is displayed. Note that the BSC curves shown in the later sections were computed for a ROI of 1000 × 125 × 125 μm³. Figure 2b contains four non-overlapping, identical, and randomly placed RBC clusters and each cluster is composed of 51 RBCs. These clusters maintained periodic boundary conditions. That means if a portion of a cluster crossed a boundary wall, then that portion appeared at the opposite side. The effects of periodic boundary conditions can be observed at least for two (1st and 3rd) clusters, as shown in Fig. 2b, and thus some portions of those clusters appeared at the opposite sides.

Figure 2.

(a) An arrangement of 51 spheres (representing RBCs) in HCP configuration forming a RBC cluster. (b) It shows a simulated aggregated blood tissue sample containing four clusters where each cluster is composed of 51 spheres. The non-overlapping clusters are randomly placed in the ROI under periodic boundary conditions. For clarity, a smaller ROI at a lower hematocrit (H ≈ 14%) is shown.

The radius of gyration (R_g) of a cluster of that tissue sample was computed by using the distances of the constituent spheres with respect to the center of the cluster as,

$$R_g=\sqrt{\frac{3}{5}{a}^2+\frac{1}{n_c}\sum _{j=1}^{n_c}{r}_j^2},$$ (6)

where n_c is the total number of spheres forming a cluster and r_j is the distance of the center of the jth sphere from the cluster center. This was done for each cluster associated with a tissue realization and accordingly the mean radius of gyration (⟨R_g⟩) of clusters was obtained. The mean size (R_sim) of clusters was then determined by multiplying the average radius of gyration with a factor $\sqrt{5∕3}$ (i.e., $R_{\mathrm{sim}}=\sqrt{5∕3}⟨R_g⟩$). Note that the non-aggregated RBCs were not taken into account during this estimation. Figure 1 summarizes this procedure through a flow chart diagram. The computed numerical value of R_sim acted as a gold standard and further used to assess accuracy of the SFSE.

Computation of a simulated BSC curve

As mentioned earlier, the size of the ROI was fixed to 1000 × 125 × 125 μm³. The simulated backscatter measurements were carried out for the scattering of incident plane waves propagating along the longest dimension of the ROI and that was considered as the x axis in this case. The length of the ROI along the x axis was sufficiently large and therefore provided good resolution in the frequency domain. However, much smaller dimensions were used along the two other lateral directions. This was done to restrict the volume of the ROI, the number of RBCs, and the computational time. The number of particles for this size of ROI was 35 919, 53 879, and 71 839 at 20%, 30%, and 40% hematocrits, respectively. Further, collections of particles were distributed randomly within the ROI, and the Fourier transformation of the spatial organization of particles was computed for those particles to generate a BSC curve for the propagation of waves along the x axis only. Therefore, spectral characteristics were dependent upon the spatial organization of cells within the ROI along the direction of propagation of waves and were not affected by the periodic boundary conditions (which were used to generate spatial arrangements of cells). The spectral characteristics would be affected only if multiple ROIs attached together along that direction would have been considered.

The radius of the equivalent sphere of a RBC was fixed to 2.75 μm, corresponding to a typical RBC volume of 87 μm³. The numerical values of density and compressibility of a RBC were assigned as ρ_e = 1.092 g∕cm³ and κ_e = 34.1 × 10⁻¹² cm²∕dyne, respectively.18 The same quantities for the ambient medium (plasma) were chosen as ρ = 1.005 g∕cm³ and κ = 44.3 × 10⁻¹² cm²∕dyne, respectively.18 For each sample, the cluster size frequency dependent BSC was obtained by evaluating Eq. (4) and a mean curve was determined from 250 different tissue realizations.

Fitting of a simulated mean BSC curve with the SFSE

The final step was to fit the simulated mean BSC curve with the SFSE between 5 MHz and the frequency corresponding to the first minimum of that curve on a log–log scale. The mean BSC curve generally exhibited minima at multiple frequencies depending upon the mean cluster size associated with that sample. The parameters W and R_sp were obtained by optimizing Eq. (5) and the simulated BSC curve. The optimization was carried out by using the “fminsearch” function of matlab 7.8.0.347 (R2009a). The estimated mean size (R_sp) of aggregates was then compared to the actual mean size (R_sim) obtained from the simulation to examine the accuracy of the SFSE method. This procedure was carried out at three hematocrit levels for different cluster sizes.

RESULTS

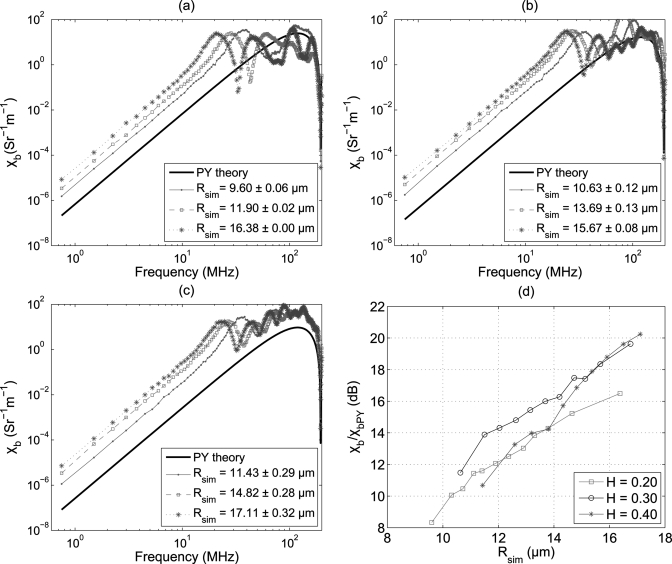
Figures 3a, 3b, 3c demonstrate variations of the BSC at some clustering conditions for three hematocrits over a large frequency range [750 KHz–200 MHz, computed using Eq. (4)]. The simulated clusters were tightly packed by the cells leaving small numbers of cells as non-aggregated cells. For example, for a sample simulated realization at 0.20 hematocrit [R_sim = 9.60 ± 0.06 μm in Fig. 3a], 98.37% RBCs of the total number of cells formed aggregates and remaining 1.63% cells were distributed randomly in space. In another case at 0.40 hematocrit [R_sim = 17.11 ± 0.32 μm, Fig. 3c] these numbers were 92.28% and 7.72%, respectively. The mean radius of simulated 3D isotropic clusters is presented in the legend denoting the corresponding aggregation level for each sample. BSC predicted by the Percus–Yevick (PY) packing theory is also shown for comparison. The PY theory describes backscatter properties of non-aggregated RBCs in the low frequency regime (1–30 MHz typically), where ka < π∕10.8 It was expected that PY results would not match with the simulated BSC curves because aggregated RBCs cannot be considered as spatially random distribution of spheres with equal radii and therefore the PY model is not valid for aggregated samples. It may also be noticed from Fig. 3 that BSC between 750 KHz and the frequency corresponding to the first maximum, increased as the cluster size increased for all samples. Moreover, the first minimum (or the first maximum) appeared at a lower frequency for a sample containing aggregates than that of the non-aggregated blood. For example, the first minimum in Fig. 3a occurred at about 195 MHz for the Percus–Yevick curve but it appeared at nearly 60 MHz for the first sample with simulated mean aggregate size of R_sim = 9.60 ± 0.06 μm. Note that the position of the first minimum is a signature of the size of the scattering objects (either individual cells or clumps composed of collection of cells).25 For any hematocrits, the first minimum appeared at lower frequencies as bigger aggregates were simulated.

Figure 3.

(Color online) (a) Variations of the BSC with interrogating frequency at different simulated mean cluster sizes for H = 0.20. The black line corresponds to BSC predicted by the Percus–Yevick packing theory. (b) Same as (a) but for H = 0.30. (c) Same as (a) but for H = 0.40. (d) Increase of BSC with respect to that of the Percus–Yevick packing theory in decibel with cluster size at 7.5 MHz. Variations at three hematocrits are shown.

Figure 3d illustrates how the BSC measured at 7.5 MHz (normalized by that of the PY theory and expressed in decibel) varies with the cluster size. It is evident from the figure that BSC increased as the mean size of clusters increased26 and it is true for all hematocrits. Further, the relative increase of BSC with respect to that of the Percus–Yevick packing theory for a particular cluster size is always higher at H = 0.30 than that of H = 0.20. For instance, at R_sim ≈ 12.0 μm the relative increase of BSC is about 12 dB for H = 0.20 but it is nearly 14 dB at H = 0.30. However, for H = 0.40, the relative increase is comparable to that of H = 0.20 up to R_sim ≈ 14.0 μm and is similar to that of H = 0.30 beyond R_sim ≈ 15.0 μm. Additionally, although we did not present it graphically, we observed that spectral slopes on a log–log scale between 1 and 10 MHz remained around 4 (Rayleigh scattering regime) for all samples at all three hematocrits.

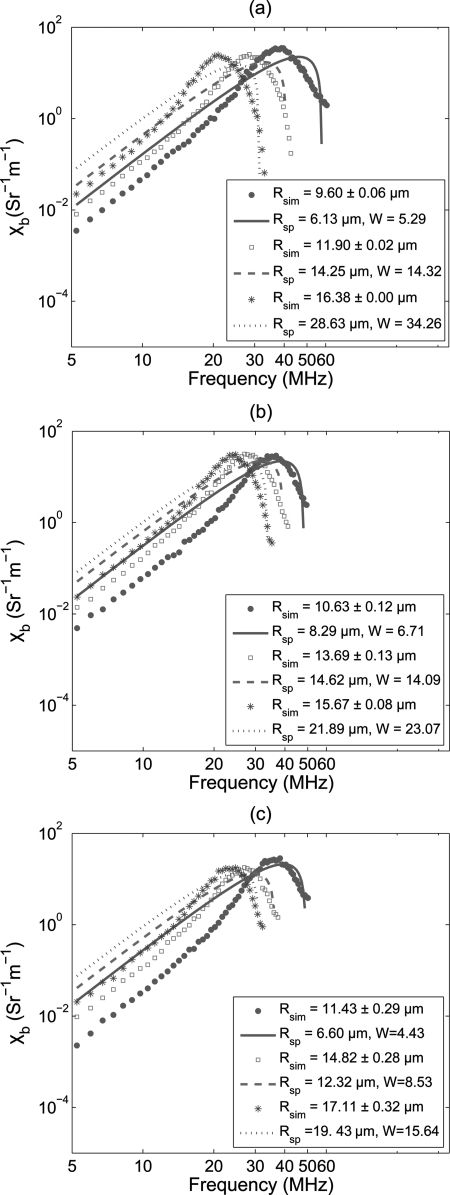
Figure 4a displays simulated frequency dependent BSC curves fitted with the SFSE method for the same clustering conditions described in Fig. 3a. The estimated values of R_sp and W are presented in the legend. It is clear from the figure that the second order expansion of the structure factor is insufficient to model the complex behavior of BSC. Indeed, some disagreements between the simulated and fitted SFSE curves are present, especially in the low frequency range, where each fitted curve over-estimates the BSC. Figures 4b, 4c demonstrate fittings of the BSC curves with SFSE, for H = 0.30 and 0.40, respectively. Fitting characteristics are similar to that of Fig. 4a.

Figure 4.

(Color online) (a) BSC curves fitted with the SFSE model at different clustering conditions at H = 0.20. Both R_sp and W estimated by the SFSE method are given in the legend. (b) Same as (a) but for H = 0.30. (c) Same as (a) but for H = 0.40.

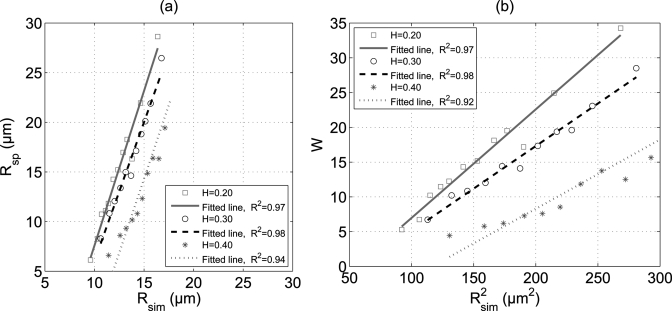
To assess the accuracy of the SFSE method, we have plotted [see Fig. 5a] the estimated values of R_sp as a function of R_sim for all three hematocrits. The linear regression lines are also shown in the figure. Although the SFSE model did not provide good fittings of the simulated BSCs, still excellent correlations (R² ≥ 0.94) were found between estimated and true cluster sizes for each hematocrit. Furthermore, it can be seen that for each hematocrit there is a region where the SFSE method works at its best. For example, error associated with the prediction of the SFSE method is less than 20% when the mean size of aggregates varies between 14 and 17 μm at 40% hematocrit. However, below this range SFSE underestimates the aggregate size but above this range it overestimates the size, especially at the lower hematocrits. The variation of W with square of R_sim is shown in Fig. 5b for all hematocrits. It is evident that W and R_sim follow a quadratic relationship. Straight line fits were also obtained by using the least square fitting technique and good correlations (R² ≥ 0.92) were found between W and ${\mathrm{R}}_{\mathrm{sim}}^2$ for each hematocrit.

Figure 5.

(Color online) (a) Comparison of estimated aggregate size with actual aggregate size at three hematocrits (H = 0.20, 0.30, and 0.40). (b) Plot of W as a function of square of the actual aggregate size at different hematocrits.

DISCUSSIONS

The scheme discussed in this paper is based on a phenomenological approach to simulate RBC clusters. It did not consider realistic interactions between the cells. It is a simple method because cells within a cluster were stacked in a particular way to form the HCP structure and provided tightly packed aggregates. This is also a fast method to generate tissue realizations mimicking aggregated erythrocyte samples because RBCs can be located at only defined positions. For example, at 40% hematocrit it took about 42 s in a remote computer cluster to generate a tissue configuration consisting of aggregates with a mean radius of 17.11 ± 0.32 μm. Similarly, for another sample (with a mean aggregate radius of 12.59 ± 0.29 μm) at that hematocrit, approximately 72 s was required to generate each configuration with the same computing platform. In this case the number of clusters was higher because it contained smaller aggregates than the previous one. Thus, the execution time was slightly more since it was needed to assign coordinates for more number of cluster centers at non-overlapping condition.

In this study, we found that BSC increased as the cluster size increased. For instance, nearly 17 dB enhancement of BSC at H = 0.40 was measured at 7.5 MHz frequency for the biggest cluster size (with mean radius of 17.11 ± 0.32 μm) with respect to that of non-aggregating blood [see Fig. 3d]. This observation is in accordance with previous experimental works. For example, Yuan and Shung27 estimated approximately 15 dB increase of BSC at 7.5 MHz for porcine whole blood when the shear rate was decreased from 22 to 2 s⁻¹. Note that a reduction in shear rate promoted aggregation and consequently cluster size increased. The numerical values associated with the enhancement of BSC presented in this study confirmed the fact that the simulated aggregate sizes were in the same range to that of experiments. Also, the numerical values of the spectral slope that we computed remained around 4 within the 1–10 MHz frequency band, where the BSC curves exhibited linear variations with frequency on a log–log scale for all samples.

In addition to that, this was the first attempt to examine the accuracy of SFSE by using simulated backscatter signals from samples containing non-overlapping, isotropic, and fairly identical 3D clusters mimicking RBC aggregates (normally compact aggregates instead of rouleaux are formed in vivo under pathological conditions). This study provided us a way to compare predicted cluster sizes with that of simulations. We observed excellent correlations (R² ≥ 0.94) between estimated and true cluster sizes for all hematocrits and also that the packing factor W maintained a quadratic relationship with the mean radius of aggregates (see Fig. 5). These findings are consistent with experimental results reported in Ref. 10. In that work, the mean sizes of RBC aggregates were determined from direct optical microscopy measurements for blood samples with 6% hematocrit at different time points of aggregation. In case of the ultrasonic method, the mean sizes were estimated with the SFSE from estimated backscattered spectra at 6% hematocrit. A good correlation (R² ≥ 0.76) was found between optical and ultrasonic methods. As introduced earlier, this comparison was not carried out at typical human hematocrits (20%–55%) because it is almost impossible to get non-overlapping clusters for image processing.

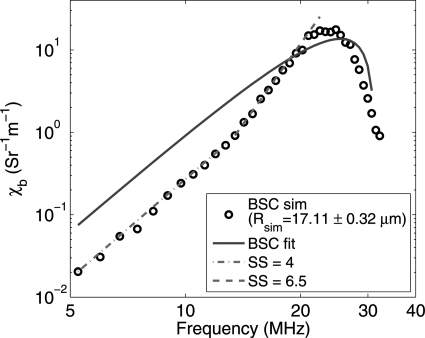
The SFSE model quite satisfactorily fit to experimental BSC curves in Ref. 10, but in the present work we did not observe much agreement between fitted curves and simulated BSC data points (see Fig. 4). As an example, we are highlighting this behavior in Fig. 6. In this figure, a simulated BSC curve (corresponding to R_sim = 17.11 ± 0.32 μm and H = 0.40) and the fitted SFSE curve are shown. Note that the spectral slope for the simulated curve is around 4 in the frequency band of 5–13 MHz but it is about 6.5 between 13 and 25 MHz. This is suggesting that the SFSE method cannot consider changes in spectral slope in the frequency bandwidth, where spectral slope remains positive. It may be noted that spectral slopes superior to 4 at low frequencies could also be observed in the experiments performed by Yu and Cloutier (see Fig. 4 in Ref. 10). Also, as discussed in Chapter 4 of Ref. 8 on the basis of a Gaussian correlation model and experimental evidences, spectral slopes greater than 4 might appear for dense media in the low frequency range. With simulations, we may have emphasized spectral slopes above 4 because we did not consider attenuation of waves, which is more important at higher frequencies. In addition to that, spectral slopes above 4 could be observed maybe because we did not consider poly-disperse clusters. In general, for poly-disperse clusters, the maxima and minima locations of BSC are different for different clusters and thus a relatively smoother BSC curve can be obtained.28

Figure 6.

(Color online) Illustration of changes in spectral slope for a simulated BSC curve.

Although we did not observe good fits of the simulated BSC curves with the SFSE, the estimations of SFSE were in good agreement with some cluster size ranges. The results suggest that there lies a region where the SFSE method works at its best for each hematocrit. At 40% hematocrit, error associated with the prediction of SFSE in determining the cluster size was within 20% when mean aggregate sizes remained within 14–17 μm. Franceschini et al.14 also mentioned in their paper that SFSE worked well for blood samples when mean radii of clusters were ≤13.90 μm for a Couette flow experiment and ≤10.02 μm for a tube flow experiment. They reached this conclusion by inspecting behaviors of correlation coefficients (BSC versus frequency of SFSE fittings). The upper limit of validity of the SFSE, as found from the current study, was also in the same range but we did not observe good performance of the SFSE for clusters with mean radii <14 μm. One possible reason for this discrepancy is that in simulations we dealt with tightly packed clusters but in reality clusters would not be that tight because of the presence of electrostatic repulsive potential. This potential would not allow cells to come very close to each other and thus would encourage forming loosely packed clusters, unless inflammatory related diseases are present to promote the formation of compact clusters. In other words, SFSE may work more accurately over a larger range for loosely packed clusters than tightly packed clusters.

As described earlier, the SFSE model has been derived by using a Taylor series expansion and retaining terms up to the second order. Therefore, contributions from the higher order terms have been neglected and that might explain the suboptimum fittings of BSC curves for some RBC clustering examples. Also, in this study, we modeled individual biconcave RBCs as spheres and studied BSC between 750 KHz and 200 MHz. The impact of modeling a RBC by a sphere on the frequency dependence of the backscatter cross-section has been studied and errors are introduced at frequencies above 18 MHz, typically.16 The impact of this simplification on BSC and SFSE determinations of W and R_sp in the case of aggregating cells is unknown and still needs to be explored.

CONCLUSIONS

A simulation algorithm suitable for generating non-overlapping, isotropic, and fairly identical RBC aggregates was presented. The RBCs considered as homogeneous spheres were assumed to follow a HCP structure to form compact spherical aggregates. Note that a very high packing density ≈0.74 for spheres can be achieved for this packing scheme. Such an aggregate prototype was repeated and placed randomly under non-overlapping condition in the 3D space to mimic aggregated blood samples. The method is simple, fast, and easy to implement. The frequency dependent BSCs were computed for samples with varying mean cluster sizes at different hematocrits. Consequently, cluster size dependent backscatter and efficacy of the SFSE method in determining the mean aggregate size were examined.

It was found that the BSC increased as the mean aggregate size increased and this was true for all hematocrits. For example, at H = 0.40, BSC increased from approximately 10 to 20 dB compared to that of non-aggregated blood sample at 7.5 MHz when the mean cluster size varied from 11.5 to 17 μm. Overall, 8 dB enhancements of BSC were observed for the other two hematocrits (H = 0.20 and 0.30) from lowest to highest cluster sizes considered in this study [see Fig. 3d], at the same interrogating frequency. Although the SFSE did not provide good fits to the simulated BSC curves, still excellent correlations (R² ≥ 0.94) between predicted (using the SFSE method) and true (known from simulations) mean size of aggregates were found for each hematocrit. The second estimated parameter W exhibited a quadratic relationship with mean size (R_sim) of RBC aggregates for each hematocrit and in this case good correlation coefficients (R² ≥ 0.92) were also computed. In future, it would be interesting to incorporate real interactions between cells to form both isotropic (strong adhesive energy simulating pathological inflammatory conditions) and anisotropic (normal condition) clusters. Another interesting study might be to evaluate the performance of the Gaussian form factor model4 to extract size information from backscatter spectra and compare that with SFSE prediction.