Modeling subharmonic response from contrast microbubbles as a function of ambient static pressure

Abstract

Variation of subharmonic response from contrast microbubbles with ambient pressure is numerically investigated for non-invasive monitoring of organ-level blood pressure. Previously, several contrast microbubbles both in vitro and in vivo registered approximately linear (5–15 dB) subharmonic response reduction with 188 mm Hg change in ambient pressure. In contrast, simulated subharmonic response from a single microbubble is seen here to either increase or decrease with ambient pressure. This is shown using the code BUBBLESIM for encapsulated microbubbles, and then the underlying dynamics is investigated using a free bubble model. The ratio of the excitation frequency to the natural frequency of the bubble is the determining parameter—increasing ambient pressure increases natural frequency thereby changing this ratio. For frequency ratio below a lower critical value, increasing ambient pressure monotonically decreases subharmonic response. Above an upper critical value of the same ratio, increasing ambient pressure increases subharmonic response; in between, the subharmonic variation is non-monotonic. The precise values of frequency ratio for these three different trends depend on bubble radius and excitation amplitude. The modeled increase or decrease of subharmonic with ambient pressure, when one happens, is approximately linear only for certain range of excitation levels. Possible reasons for discrepancies between model and previous experiments are discussed.

INTRODUCTION

Encapsulated microbubbles (diameter <10 μm) can signifi cantly improve the quality of diagnostic ultrasound images.1, 2, 3 They also produce strong second harmonic (i.e., response at frequency 2f when excited at f)4 and subharmonic response (response at f ∕ 2)5, 6, 7 that are harnessed in harmonic8 and subharmonic imaging.9, 10, 11, 12 Subharmonic response from contrast microbubbles has been proposed as a possible means for estimating organ-level local blood pressure, leveraging the dependence of subharmonic response on ambient pressure.13, 14 Commercial contrast agents showed 5–15 dB decrease with ∼25 kPa (= 188 mm Hg) ambient pressure variation both in vitro and in vivo.14, 15, 16, 17 Andersen and Jensen18 recently simulated subharmonic response decrease with ambient pressure from the contrast agents Levovist (Schering AG, Berlin, Germany) and Sonazoid (GE Healthcare, Oslo, Norway) using the bubble dynamics code BUBBLESIM.19 Here, we report a detailed numerical investigation of the subharmonic response of microbubbles to show that as per single bubble dynamics, subharmonic response may either decrease or increase with ambient pressure depending on other parameters, and explain the underlying physics.

Local organ-level pressure information can help to determine the state of health and to diagnose several diseases related to heart and vascular system, e.g., portal hypertension.20, 21 The current technique of inserting manometer-tipped catheter is invasive. On the other hand, currently available non-invasive procedure using Doppler ultrasound has been reported to be non-reproducible.22, 23 The idea of using scattering properties of microbubbles for non-invasive pressure estimation has been around for over three decades.13, 24 Fairbank and Scully25 first proposed using air bubbles for cardiac pressure measurements. They showed theoretically and then verified experimentally that the resonance frequency of an air-bubble shifts with ambient pressure change in water. However, accurate pressure measurement using shift in resonance required producing more uniform and smaller (<10 μm) microbubbles. Later workers26, 27, 28 tried to improve upon this idea; however, rapid dissolution of free air bubbles—a micron radius air bubble dissolves in 20 ms29, 30, 31—prevented its practical implementation. Since the development of stable encapsulated ultrasound contrast microbubbles in the 1990s, they are again being considered for pressure estimation. Bouakaz et al.32 used low-frequency high-amplitude ultrasound pulses to destroy the encapsulation of contrast microbubbles, and generated free bubbles at the region of interest. Then, they investigated ambient pressure dependent dissolution time of these free bubbles for local blood pressure estimation and reported a sensitivity of 50 mm Hg. Brayman et al.33 found that transmission through air based contrast agent Albunex drastically reduced with ambient pressure increase due to the bubble destruction. Intrinsic limitations in sensitivity of these techniques prevented their clinical implementation.

Shi et al.13 experimentally found the subharmonic component—in contrast to the fundamental and second harmonic components—from Levovist to be strongly dependent on ambient pressure. With a 2 MHz excitation frequency and 0.39 MPa excitation pressure, they reported a 9.9 dB linear reduction in the peak amplitude of the subharmonic component for a 24.8 kPa rise in ambient pressure. The same group later verified this observation with other contrast agents—reduction of 10.1 dB for Optison (GE Healthcare, Princeton, NJ), 11.03 dB for Definity (Lantheus Imaging, N. Billerica, MA), 12.2 dB for PRC-1 (Zhifuxian, Xinqiao Hospital, the Third Military Medical University, Chongqing, China), and 13.3 dB for Sonazoid.15 Note that the results were a cumulative effect of the entire bubble distribution of a contrast agent. Adam et al.16 experimentally investigated the sensitivity of Optison with cyclic as well as static pressure variation specifically at a frequency of 4 MHz. They found an 8 dB reduction in subharmonic response with 40–140 mm Hg increase in ambient pressure. Andersen and Jensen17 measured subharmonic response from SonoVue (Bracco, Milano, Italy) as a function of increasing and decreasing ambient pressure at 0.485 and 0.5 MPa and 4 MHz; the response has a high level of scatter, but the ratio of subharmonic to fundamental showed a linear decrease. On the other hand, a recent experimental study found that the subharmonic response from a phospholipid-coated contrast microbubble (similar to BR14 or Sono Vue) increased by 28.9 dB for 180 mm Hg increase of ambient pressure at a very small acoustic excitation level of 50 kPa,34 possibly because of buckling of the encapsulation. However, they also reported a 9.6 dB decrease in subharmonic response at higher excitation pressure of 400 kPa for the same ambient pressure increase.

Intuitively, one would expect that an increase in the ambient pressure would decrease the bubble size and inhibit the oscillation of a microbubble and, therefore, would result in a reduced subharmonic response (as well as a reduction in the overall echo level). The experimental results (except for those by Frinking et al.34) described above seem to indicate the same. However, in this paper, we will use mathematical models of bubble dynamics to show that the above physical intuition is partially misleading. In fact, we show below that the determining parameter of the subharmonic response is the ratio of the excitation frequency to the resonance frequency. Changing the ambient pressure changes the resonance frequency and, thereby, the frequency ratio. For different acoustic excitation pressure levels, changing ambient pressure can either increase or decrease the subharmonic response depending on this ratio. For some range of parameters, the variation is far more complicated. This behavior is clearly at odds with the experimental observations mentioned above, and warrants further modifications of the existing models. However, developing better models requires that we understand the predictions of existing models.

As mentioned earlier, Andersen and Jensen18 used bubble dynamics code BUBBLESIM to show a reduction of the subharmonic response with pressure variation. The code is based on a modified version of the classical bubble dynamics equation and uses a linear viscoelastic shell model. For the two contrast agents, Levovist and Sonazoid, they used mean radius to be 3.0 and 3.2 μm, respectively, along with the material properties previously reported.35 In the following text, we show that the BUBBLESIM code predicts both increasing and decreasing subharmonic responses with ambient pressure for the same contrast agents depending on frequency. The previous conclusion was obtained based on a study with single excitation frequency values—2.06 MHz for Levovist and 2.46 MHz for Sonazoid. Here, we observe the other responses simply by broadening the simulation to other excitation frequencies. We note that currently there are many models of encapsulated microbubbles by various research groups,36, 37, 38 including our own.39, 40, 41 However, we feel that none of these models enjoys unambiguous validity for describing the complete dynamics of a contrast microbubble. Therefore, we use the well established model for a free bubble to understand and explain the model dynamics of subharmonic response and its dependence on ambient pressure here. We will indicate the behaviors of encapsulated microbubbles, where appropriate. Note that nonlinear oscillation of free bubbles has been investigated using perturbation methods. It showed that there exits a threshold acoustic excitation level for subharmonic response from bubbles. The threshold is minimum when the excitation frequency is twice the natural frequency of the bubble,42, 43, 44 a fact we would find critical for the results below. There has also been numerical investigation of the Rayleigh–Plesset equation of bubble dynamics showing subharmonic oscillations. However, most of the numerical investigations are directed toward radial dynamics,45 not the scattered pressure response, which is of interest for pressure estimation.

In the following text, we first provide the mathematical formulation and numerics. We then provide simulation results from BUBBLESIM and Rayleigh–Plesset equation for a free bubble. Finally, we summarize our findings.

MATHEMATICAL FORMULATION AND NUMERICAL SOLUTION

Encapsulated bubble dynamics

To simulate the dynamics of an encapsulated microbubble and compare with the numerical investigations of Andersen and Jensen,18 we use the BUBBLESIM code. It is a variation of the Rayleigh–Plesset equation. It assumes the encapsulation to be a linear viscoelastic layer of finite thickness and possessing a bulk viscosity and elasticity. The model was developed by Hoff et al.19 based on an earlier model proposed by Church.36 Details of the model can be found in these references.

Free bubble dynamics

After showing the behavior of encapsulated contrast microbubbles using BUBBLESIM, we choose to explain the model dynamics by concentrating on free bubble oscillations. This is described by the Rayleigh–Plesset equation,

$$\rho \left(R\ddot{R}+\frac{3}{2}{\dot{R}}^2\right)=P_G-\frac{2\gamma }{R}-4\mu \frac{\dot{R}}{R}-\left(p_{\text{atm}}+p_{\text{ov}}\right)+p_A(t)-\frac{R}{c}\frac{d{P}_G}{dt},$$ (1)

where R is the spherical bubble radius, $\stackrel{·}{R}$ and $\stackrel{\mathrm{··}}{R}$ are first and second order time derivative of the bubble radius R, ρ is liquid density, μ is liquid viscosity, γ is gas–liquid interfacial tension, p_atm is the atmospheric pressure, p_ov is over-pressure, p_A is the excitation pressure with amplitude P_A, and c is sound velocity in liquid. Note that the last term in (1) is a compressibility term added to the classical Rayleigh–Plesset equation. In contrast to other compressible form of the bubble dynamics equations (e.g., Herring, Keller-Miksis, Gilmore; see Refs. 46, 47 for a review) this one remains stable for high Mach numbers.48 We assume that the gas content of the bubble does not change (neglect gas diffusion). The gas pressure P_G inside is given by the polytropic law

$$P_{\mathrm{G}}=P_{\mathrm{G}0}{\left(\frac{R_0}{R}\right)}^{3k},$$ (2)

where R₀ is the initial bubble radius, P_G0 is the initial gas pressure and k is the polytropic exponent. Incorporating Eq. (2) in Eq. (1), we get

$$\begin{array}{cc}\multicolumn{1}{c}{\rho (R\stackrel{\mathrm{··}}{R}+\frac{3}{2}{\stackrel{·}{R}}^2)}& =P_{{\mathrm{G}}_0}{\left(\frac{R_0}{R}\right)}^{3k}(1-\frac{3k\stackrel{·}{R}}{c})-\frac{2\gamma }{R}-4\mu \frac{\stackrel{·}{R}}{R}\hfill \\ \multicolumn{1}{c}{}& \hspace{0.5em}-(p_{\mathrm{atm}}+p_{\mathrm{ov}})+p_{\mathrm{A}}.\hfill \end{array}$$ (3)

Equation (3) is solved using a stiff solver (ODE15s) in matlab^® (Mathworks Inc., Natick, MA) with initial conditions $R=R_0$ and $\stackrel{·}{R}=0$. The pressure P_s (t) scattered by a bubble is41

$$P_S(r,t)=\rho \frac{R}{r}(2{\stackrel{·}{R}}^2+R\stackrel{\mathrm{··}}{R}).$$ (4)

We use fast Fourier transform (FFT) routine of matlab to obtain the power spectrum. For the FFT, we only use the part of the simulation where transients have subsided. We use the peak values corresponding to the different frequencies (i.e., fundamental or different harmonic) in contrast to an integrated value around the peak used in a previous Ref. 18. We use ρ = 1000 kg∕m³, μ = 0.001 kg∕ms, γ = 0.072 N∕m, k = 1.07 (adiabatic process value for C₄F₁₀; note that it is quite close to the isothermal limit k = 1), and c = 1485 m∕s. Note that with the inclusion of the compressibility effects in Eq. (3), radiation damping along with viscous damping is included in the free bubble model. Damping has been shown to increase the threshold for subharmonic generation, and extreme reduction of overall damping in presence of encapsulation for contrast microbubbles was surmised to give rise to extremely low threshold for subharmonic generation.7

Change in initial bubble radius with ambient pressure

Change in the ambient pressure statically changes the contrast microbubble radius. Previous modeling study18 of change in subharmonic response with pressure did not account for static radius change (but see Ref. 34). It has been argued that high gas compressibility allows microbubbles to change shape substantially in response to the changing hydrostatic pressure which leads to pressure dependent scattered response.13 At static condition ($\stackrel{\mathrm{··}}{R}=0$ and $\stackrel{·}{R}=0$) the pressure inside a microbubble is higher than the ambient pressure. For zero-over-pressure (indicated by the superscript 0), we get

$$P_{{\mathrm{G}}_0}^0=p_{\mathrm{atm}}+\frac{2\gamma }{R_0^0},$$ (5)

where $R_0^0$ is the static bubble radius under zero-over-pressure, i.e., atmospheric pressure. In fact, the higher gas pressure inside results in a higher concentration inside the bubble that drives the dissolution process of a free bubble in tens of milliseconds.29 The encapsulation of surface active molecules reduces the surface tension and hinders gas permeation thus ensuring their stability.30 Furthermore, we have recently shown that the surface elasticity provides additional mechanism of stabilization.49, 50 Therefore, for such a microbubble, the time scale of gas diffusion is far larger, and one can assume that the bubble content to remain constant initially (∼10 min), but sufficiently large over-pressure would destroy bubbles in the long run.16 Here, therefore, although we consider a free bubble case, we assume gas content to be constant. It can arguably be more appropriate for an actual encapsulated contrast microbubble except when over-pressure leads to substantial gas diffusion or partial destruction. Increasing ambient pressure (i.e., applying over-pressure) leads to the condition:

$$P_{{\mathrm{G}}_0}=p_{\mathrm{atm}}+p_{\mathrm{ov}}+\frac{2\gamma }{R_0}.$$ (6)

Using an expression that embodies the gas law (2), we obtain from Eqs. (5) and (6)

$$p_{\mathrm{atm}}+p_{\mathrm{ov}}+\frac{2\gamma }{R_0}=(p_{\mathrm{atm}}+\frac{2\gamma }{R_0^0}){\left(\frac{R_0^0}{R_0}\right)}^{3k},$$ (7)

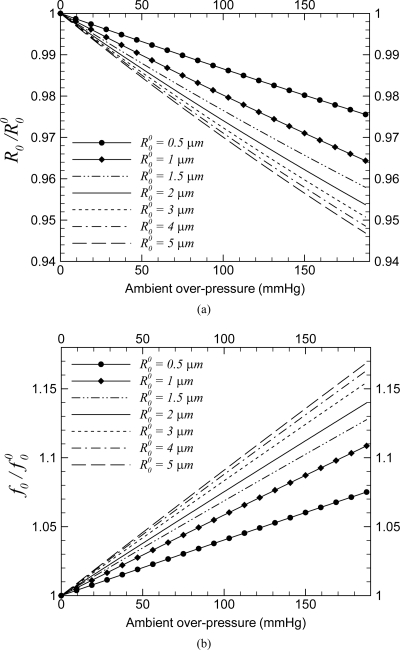
which can be solved to find the initial radius R₀ at the ambient static pressure p_amb = p_atm + p_ov. We plot in Fig. 1a initial bubble size R₀ for different bubble sizes $R_0^0$ under zero-over-pressure. For a pressure range from 0 to 186 mm Hg (typical of blood pressure in the human body), and microbubbles of static radius 0.5 − 5 μm, radius changes by a maximum of only ∼6%, as was also shown previously by similar calculation.51 With an encapsulation, additional stiffness leads to an even smaller radius change.

Figure 1.

(a) Fractional change in initial radius of a free bubble due to change in ambient pressure and (b) fractional change in linear resonance frequency due to change in ambient pressure.

On the other hand, note that the linear resonance frequency f₀ of a bubble

$$f_0=\frac{1}{2\pi R_0}\sqrt{\frac{1}{\rho }(3{\mathit{kp}}_{\mathrm{amb}}+\frac{2\gamma }{R_0}(3k-1))}$$ (8)

depends both on ambient pressure and radius. We note that the resonance frequency is determined by a ratio between the “spring” and the “mass” terms. In the above equation, the second term inside the square root derives from the interfacial stresses—in this case of free bubbles due to the surface tension. For other encapsulation models, this term is suitably modified as, e.g., in Eq. (9) below. We plot the change in resonance frequency for different $R_0^0$ in Fig. 1b, where $f_0^0$ is the linear resonance frequency for no ambient over-pressure $(f_0^0\equiv f_0@p_{\mathrm{ov}}=0)$. It is important to note that although the bubble radius change for typical blood pressure variation is not large compared to the oscillatory change under excitation, the change in linear resonance frequency f₀ with the ambient pressure, we see below, is substantial to critically affect the dynamics of subharmonic response.

RESULTS AND DISCUSSION

Simulation of subharmonic response from contrast microbubbles using BUBBLESIM

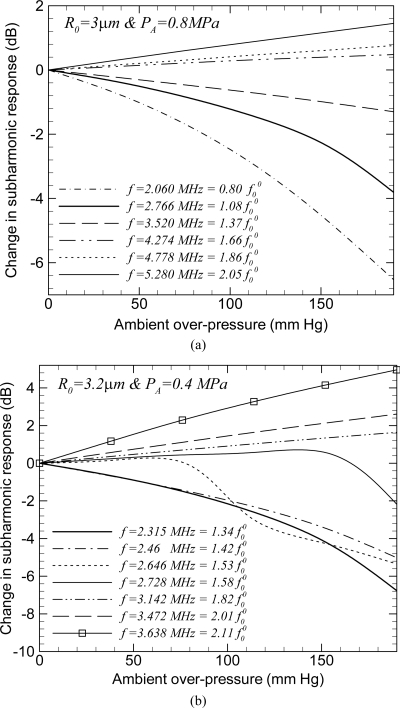
Andersen and Jensen18 have simulated dynamics of contrast agents Levovist and Sonazoid to show that subharmonic response registered decreases (2–16 dB for Levovist and 4–30 dB for Sonazoid depending on number of cycles 10–256 in the exciting pulse), with an increase of over-pressure from 0 to 25 kPa. For Levovist, they used a mean radius of 3 μm and 2.06 MHz for the frequency of excitation. We use the same code with the same radius R₀ = 3 μm (without accounting for any static radius change due to over-pressure change) to plot subharmonic change with over-pressure, i.e., increase in ambient pressure over the atmospheric pressure, for different excitation frequency f [Fig. 2a]. We have taken care to see that we reproduce the curves reported in the above reference. We use a rectangular excitation pulse of 32 cycles at 0.8 MPa. The resonance frequency of an encapsulated bubble for the model of encapsulation used in BUBBLESIM is19

$$f_0=\frac{1}{2\pi R_0}\sqrt{\frac{1}{\rho }(3{\mathit{kp}}_{\mathrm{amb}}+12G_s\frac{d_{\mathrm{se}}}{R_0})}.$$ (9)

G_s is the shear modulus of the encapsulation material and d_se is the thickness of the encapsulation. Properties for the Levovist and Sonazoid (see below) encapsulations are given in Ref. 18 (their Table II). At zero-over-pressure (p_amb = p_atm), for Levovist $f_0^0=2.57\mathrm{MHz}$. Therefore, in Fig. 2a, the curve for f = 2.06 MHz $(0.80f_0^0)$ is a reproduction of the subharmonic response decrease, as given in Ref. 18. Note that for other excitation frequencies, cases with $f<1.6f_0^0$ shows a reduction with ambient pressure increase. However, for higher excitation frequencies $f\ge 1.7f_0^0$, the subharmonic response increases with the ambient pressure. Therefore, the increase or decrease of the subharmonic response on ambient pressure as per BUBBLESIM depends on the operating frequency. As mentioned before, the subharmonic response increase with the increasing over-pressure has not been reported in experiments at these excitation levels.

Figure 2.

Change in the subharmonic response of mono-dispersed contrast microbubbles with a 32-cycle rectangular driving pulse for (a) Levovist (R₀ = 3 μm and P_A = 0.8 MPa) and (b) Sonazoid (R₀ = 3.2 μm and P_A = 0.4 MPa) as per BUBBLESIM.

For Sonazoid, Andersen and Jensen18 used mean radius of 3.2 μm and simulated at 2.46 MHz. Equation (8) gives the resonance frequency to be $f_0^0=1.727\mathrm{MHz}$. In Fig. 2b, we plot the change in the subharmonic response from Sonazoid as a function of over-pressure for 0.4 MPa 32 cycle pulse with varying excitation frequency. The case for $f=2.46\mathrm{MHz}(f=1.42f_0^0)$ corresponds to the case presented in the aforementioned reference. Similar to the Levovist case, the change in subharmonic could be either a decrease or an increase depending on the excitation frequency. In fact, even a non-monotonic variation of subharmonic component is seen for excitation frequency in the range $1.5f_0^0\le f<1.7f_0^0$ in Fig. 2b. Once again, we note that such variation has not been reported in experiments. Below this excitation frequency range, subharmonic response decreases with increasing over-pressure, and for f ≥ 1.7 f₀ it increases. In the rest of the article here, we adopt the well established model of a free bubble to understand the underlying dynamics of increase or decrease of subharmonic response with over-pressure. It avoids the complicacy with a particular choice of encapsulation model.

Effects of ambient pressure on the subharmonic scattering from a free microbubble

As mentioned before, in the following, we numerically solve the free bubble dynamics Equation (3) using MATLAB to find the scattered pressure (4) and thereby the power spectrum. We account for the effect of over-pressure change on the bubble radius using Eq. (7) to find the initial bubble radius R₀ for a given $R_0^0$.

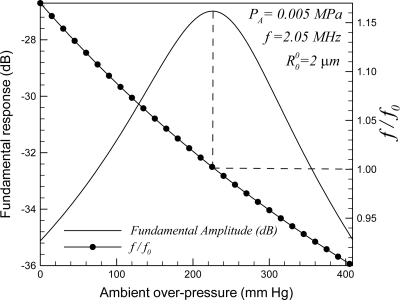
First we plot the fundamental scattered response from a free bubble of radius 2 μm at 2.05 MHz excitation frequency and 0.005 MPa excitation pressure in Fig. 3. As mentioned before, increasing ambient pressure increases the resonance frequency f₀ as also shown in Fig. 3; consequently f ∕ f₀ monotonically decreases. And therefore, at this low acoustic excitation, the fundamental response resembles the classical response function of a harmonic oscillator. As long as f ∕ f₀ > 1, increase in the ambient pressure drives the system toward resonance leading to an increasing fundamental response. But for f ∕ f₀ < 1, ambient pressure increase has the opposite effect of decreasing the response. Near the resonance, the response first increases and then decreases with the increasing ambient pressure. This behavior of the fundamental response motivates us to investigate the subharmonic response in terms of effects of ambient pressure on the resonance frequency.

Figure 3.

Variation of fundamental response of a 2 μm free microbubble with ambient over-pressure and normalized excitation frequency f ∕ f₀.

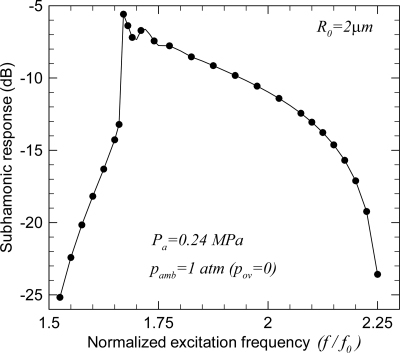
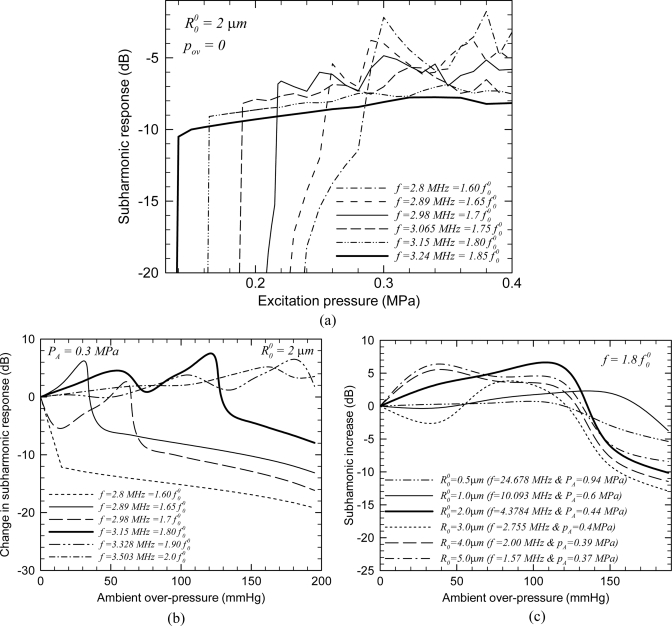
Unlike fundamental response, subharmonic response from a bubble, at a fixed excitation frequency, occurs only in a narrow range of excitation pressure—there is no or little subharmonic component below a threshold level of excitation pressure,42 and above a high value of excitation pressure, the scattered pressure is chaotic and a clear subharmonic peak above the background spectrum is lost. The range of excitation pressure for subharmonic generation is different at different excitation frequencies. It is well known that bubbles are most susceptible to subharmonic oscillations when driven at excitation frequency close to twice the linear resonance frequency.43, 45 One would, therefore, expect that the subharmonic scattering would be maximum for an excitation frequency near twice the resonance frequency. Figure 4 plots subharmonic response for a 2 μm radius free bubble at one atmosphere ambient pressure (p_ov = 0) and 0.24 MPa excitation pressure to show that as the normalized excitation frequency increases, it first increases in the range f ∕ f₀ < 1.6, reaches a maximum around f ∕ f₀ ≈ 1.65 to decrease thereafter for f ∕ f₀ > 1.8. Note that the maximum occurs at frequency ratio < 2; such a shift in maximum toward lower frequency ratio was also found for subharmonic component of radius–time curve obtained numerically.45 In the range 1.6 ≤ f ∕ f₀ ≤ 1.8, subharmonic component exists but shows non-smooth variation. With the increasing excitation level, the bubble response for a particular order of resonance leans toward lower frequency with a jump phenomenon45 which can be seen here as well.

Figure 4.

Variation of the subharmonic response of a 2 μm radius free bubble with normalized excitation frequency f ∕ f₀.

Although here the excitation frequency, rather than the ambient pressure was changed, this figure proves crucial to understand the dependence of subharmonic on the ambient pressure. We argue that the changing ambient pressure changes the normalized frequency f ∕ f₀ and depending on the range of normalized frequency achieved, one can get three different behaviors of subharmonic with ambient pressure variation. Accordingly, we consider three different ranges of excitation frequencies. Because the resonance frequency changes with ambient pressure, ranges are defined with excitation frequency normalized by the resonance frequency $f_0^0$ at zero-over-pressure (i.e., at P_amb = P_atm).

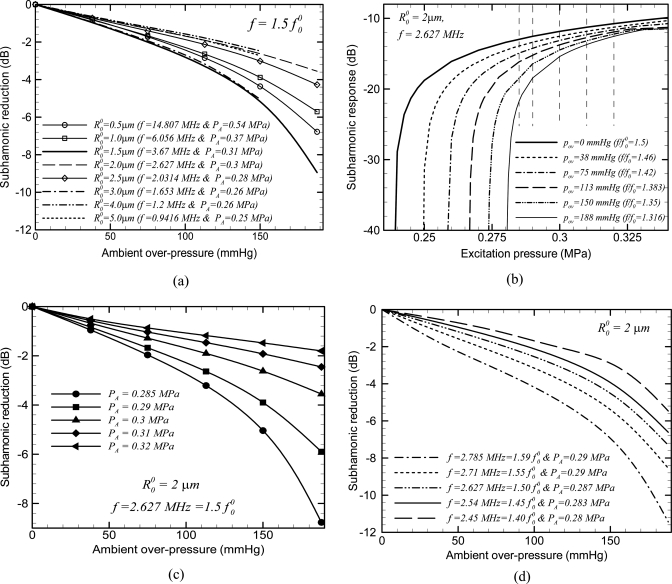
Case 1$(1.4f_0^0\le f<1.6f_0^0)$: Based on our findings from Fig. 4, for $f<1.6f_0^0$, we expect a decrease in subharmonic response with the increasing over-pressure due to reduction in f ∕ f₀. In Fig. 5a, we plot the variation in the subharmonic response with over-pressure for different bubble sizes $(R_0^0=0.5-5\mu \mathrm{m})$. For each of these bubbles, the resonance frequency $f_0^0$ at the zero-over-pressure is different. Therefore, for each of them, we choose an exciting frequency f such that $f=1.5f_0^0$. For each bubble radius, as expected, the subharmonic amplitude decreases with the increasing ambient pressure. We choose different excitation pressure amplitude for each bubble radius to ensure subharmonic generation in the range of ambient pressure variation considered; for each bubble radius, threshold excitation level for subharmonic generation is different. For larger bubbles $(R_0^0>2.5\mu \mathrm{m})$, the reduction in f ∕ f₀ with increase in ambient pressure takes f ∕ f₀ farther from minimum threshold of subharmonic generation (f ∕ f₀ = 2). Therefore, the subharmonic response was not seen for larger bubbles at higher values of ambient pressure in the considered range.

Figure 5.

Variation of subharmonic response (a) with ambient over-pressure for free bubbles of radius $R_0^0=0\mathrm{.}5\mathrm{,}1\mathrm{,}1\mathrm{.}5\mathrm{,}2\mathrm{,}2\mathrm{.}5\mathrm{,}3\mathrm{,}4$, and $5\mu \mathrm{m}$ at respective excitation frequencies such that $f=1.5f_0^0$, (b) with excitation pressure for a free bubble of $R_0^0=2\mu \mathrm{m}$ at $f=2.627\mathrm{MHz}=1.5f_0^0$, (c) with ambient pressure for a free bubble of $R_0^0=2\mu \mathrm{m}$ at fixed excitation frequency $(f=2.627\mathrm{MHz}=1.5f_0^0)$ and different excitation pressures, and (d) with the ambient pressure for a free bubble of $R_0^0=2\mu \mathrm{m}$ at different excitation frequencies.

The reduction in subharmonic amplitude at $f=1.5f_0^0$ [Fig. 5a] can be better understood by Fig. 5b, where we plot the variation in the subharmonic response as a function of the excitation pressure for a 2 μm radius bubble at a fixed excitation frequency of f = 2.63 MHz $(=1.5f_0^0)$ for different over-pressures. The plot clearly shows the phenomenon of threshold for subharmonic generation in that for each case, if and only if the excitation pressure reaches over a critical excitation level, one sees considerable subharmonic signal. As the over-pressure P_ov increases, the linear resonance frequency increases [see Eq. (8)] and, therefore, the normalized excitation frequency f ∕ f₀ decreases. For the range considered (i.e., near $f=1.5f_0^0$) reduction in f ∕ f₀ pushes it away from its supposed value of 2 for minimum excitation threshold. The increased threshold for subharmonic generation can clearly be seen in Fig. 5b. Also note that when one considers a particular excitation level ]indicated by the dashed lines in Fig. 5b] the subharmonic response decreases monotonically with the increasing over-pressure at this excitation pressure. Furthermore, note that the magnitude of subharmonic reduction at a fixed excitation frequency depends on the excitation pressure. To understand this dependence, we plot the reduction in the subharmonic response as a function of ambient pressure for the same bubble (radius 2 μm) and at the same excitation frequency of 2.63 MHz $(f=1.5f_0^0)$ but for different excitation pressures in Fig. 5c. For this case, one sees from Fig. 5b, that the excitation pressure has to be greater than 0.28 MPa (threshold at P_ov = 188 mm Hg) for ensuring subharmonic generation. At 0.285 MPa excitation pressure, one sees approximately 9 dB reduction in subharmonic response for the increase in ambient pressure from 0 to 188 mm Hg. Previous measurement indicated a linear decrease of subharmonic (dB) with ambient pressure variation.15, 16 Here we note that the reduction level decreases with the increasing excitation pressure. Above 0.3 MPa excitation pressure, the reduction for the entire range of pressure variation is small (< 5 dB) and variation is almost linear. However, for lower acoustic excitation levels, subharmonic generation is quite weak at higher ambient pressures and, therefore, one sees sharp nonlinear increase in the subharmonic reduction at the high end.

Although we choose $f=1.5f_0^0$ to show our simulation results, monotonic reduction in subharmonic response is seen at other frequencies as long as $1.4f_0^0\le f<1.6f_0^0$. The range is particular to the radius $R_0^0=2\mu \mathrm{m}$. For any zero-over-pressure bubble radius, the range is defined by an upper value corresponding to the excitation frequency of maximum subharmonic response, and a lower value which is above the fundamental resonance. For $f<1.4f_0^0$, with increase in P_ov, f ∕ f₀ reduces far away from 1.6 and approaches 1 (fundamental resonance) which leads to an increase in the subharmonic response. In Fig. 5d, we find monotonic reduction in the subharmonic response with over-pressure increase for different excitation frequencies in the range $1.4f_0^0\le f<1.6f_0^0$. The acoustic pressure amplitude for each excitation frequency is chosen to be above the threshold for subharmonic generation.

Case 2$(1.6f_0^0\le f<2.1f_0^0)$: In this range, Fig. 4 indicates a more complex variation of subharmonic with normalized frequency and, therefore, we expect a similar behavior with ambient pressure. We first plot the subharmonic response with the excitation pressure for a free bubble of radius 2 μm, at different excitation frequencies and zero-over-pressure (i.e., at atmospheric pressure) in Fig. 6a. As expected, the threshold for subharmonic generation decreases as the excitation frequency approaches twice the linear resonance frequency7, 42 and the peak subharmonic response occurs at excitation frequency close to $~1.6f_0^0$ similar to what is found in Fig. 3. However, more significant to note was the non-monotonic variation of the subharmonic response with the excitation pressure in the saturation zone for excitation frequencies as $1.6f_0^0\le f\le 1.8f_0^0$. Such chaotic variation in subharmonic response leads to the non-monotonic variation of subharmonic amplitude with ambient over-pressure. This is shown in Fig. 6b for a free bubble of the same radius at different excitation frequencies $(1.6f_0^0<f\le 2.0f_0^0)$, where the excitation level was chosen to be 0.3 MPa. In Fig. 6c, we show that the non-monotonic variation happens for other bubble radii $(R_0^0=0.5-5\mu \mathrm{m})$. We choose the excitation frequency such that $f=1.8f_0^0$, and the excitation levels are also chosen to ensure that it is above the threshold for subharmonic generation.

Figure 6.

Variation of subharmonic response (a) with excitation pressure for a free bubble of $R_0^0=2\mu \mathrm{m}$ at different excitation frequencies and zero ambient over-pressure, (b) with ambient over-pressure for a free bubble of $R_0^0=2\mu \mathrm{m}$ at different excitation frequencies and P_A = 0.3 MPa, and (c) with ambient over-pressure for free bubbles of radius $R_0^0=1,2,3,4$, and $5\mu \mathrm{m}$ at excitation frequencies such that $f=1.8f_0^0$.

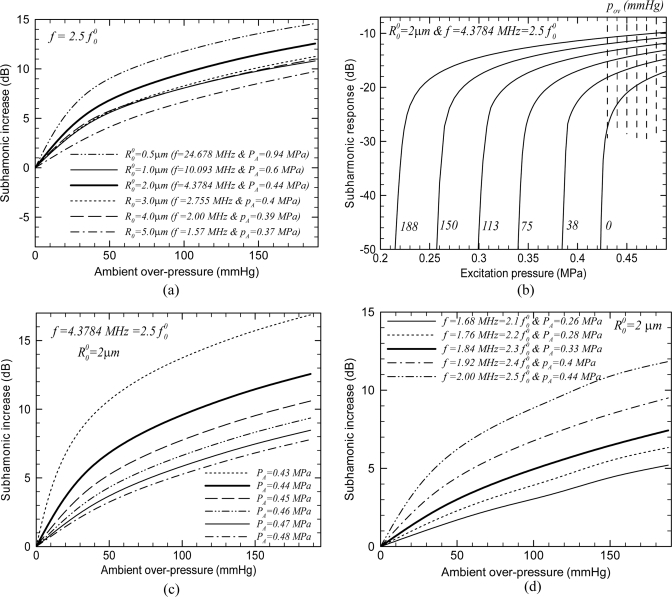
Case 3$(f\ge 2.1f_0^0)$): In this section, we explore monotonic increase of subharmonic with the increasing over-pressure following the result in Fig. 4 that shows that subharmonic increases with decreasing f ∕ f₀ for f ∕ f₀ > 2. The presentation mimics the one for case 1. Figure 7a plots the variation of subharmonic response for different bubble radii (0.5–5 μm) at excitation frequencies for each bubble such that $f=2.5f_0^0$. For each case, the subharmonic monotonically increases with the increase in over-pressure. Once again, the excitation level for each pressure is chosen to ensure subharmonic generation, i.e., the level is above the subharmonic generation threshold. Note that the increase in subharmonic amplitude is of comparable magnitude to that of the reduction in subharmonic at $f=1.5f_0^0$. As seen before, to further investigate the monotonic increase, Fig. 7b plots subharmonic as a function of increasing excitation pressure for a bubble of radius 2 μm at various over-pressures. The excitation frequency is chosen to be $f=4.38\mathrm{MHz}=2.5f_0^0$ for each over-pressure value. Note the subharmonic threshold phenomenon as in Fig. 5b. However, the curves for different over-pressures are now stacked in an order opposite to the one in Fig. 5b—increasing over-pressure decreases threshold for subharmonic generation. With increase in the ambient over-pressure, f ∕ f₀ decreases and approaches two which results in: (1) decreased threshold for subharmonic generation and (2) higher amplitude of subharmonic component at a fixed excitation. These two variations together, at fixed excitation pressure, results in a monotonic increase in subharmonic amplitude with increasing over-pressure p_ov, as indicated by the dashed lines at different excitation levels. This is shown in Fig. 7c, where the simulation is done for the exactly same bubble radius and excitation frequency. From Fig. 7b, one notes that above 0.43 MPa excitation, each over-pressure case registers subharmonic component. Therefore, in Fig. 7c, we consider excitation levels above this value. Following previous observations of a linear variation of experimentally measured subharmonic response with over-pressure, we note that for the lowest two excitation levels (0.43 and 0.44 MPa) the subharmonic increase can be considered approximately linear above 70 mm Hg of over-pressure. For higher values of excitation levels, the increase is almost linear in the entire range of over-pressure increase.

Figure 7.

Variation of subharmonic response (a) with ambient over-pressure for free bubbles of radius $R_0^0=0\mathrm{.}5\mathrm{,}1\mathrm{,}1\mathrm{.}5\mathrm{,}2\mathrm{,}2\mathrm{.}5\mathrm{,}3\mathrm{,}4$, and $5\mu \mathrm{m}$ at excitation frequencies such that $f=2.5f_0^0$, (b) with excitation pressure for a free bubble of $R_0^0=2\mu \mathrm{m}$ at $f=4.3784\mathrm{MHz}\mathrm{=}2.5f_0^0$, (c) with ambient pressure for a free bubble of $R_0^0=2\mu \mathrm{m}$ at fixed excitation frequency $(f=4.3784\mathrm{MHz}\mathrm{=}2.5f_0^0)$ and different excitation pressures, and (d) with ambient pressure for a free bubble of $R_0^0=2\mu \mathrm{m}$ at different excitation frequencies.

Finally, in Fig. 7d, we show that the case of monotonic increase happens for other excitation frequencies as well. The excitation pressure at each frequency is chosen to be above the threshold excitation at that frequency. Increasing over-pressure increases the resonance frequency f₀ taking the normalized frequency progressively closer to the value 2. The subharmonic response therefore increases with increasing over-pressure. We note that most previous experiments recorded a decrease of subharmonic with the increasing over-pressure. The only case of subharmonic increase observed with ambient pressure increase is at a much lower excitation level of 50 kPa. These authors observed a cross-over of behavior at the excitation pressure of 350 kPa; below this excitation level, subharmonic response increased with increasing over-pressure, and above it subharmonic response decreased with increasing over-pressure.34

SUMMARY

We numerically investigated the subharmonic response of encapsulated contrast microbubbles for its use in non-invasive local blood pressure estimation. Experimentally, several contrast microbubbles registered substantial (5–15 dB) reduction in the subharmonic response with the ambient pressure increase of 180 mm Hg.14, 15, 17, 34 A recent numerical simulation used BUBBLESIM code to show that subharmonic response from contrast agents Levovist and Sonazoid decreases with ambient pressure.18 However, we show that for the same contrast agents (same radius and material properties), the same code predicts that subharmonic response can either monotonically increase or decrease or show more complex non-monotonic behavior with ambient pressure. This result is obtained when excitation frequencies other than the single values investigated in that paper are applied. The behavior therefore really depends on the frequency of excitation. The excitation frequencies (2–5 MHz) chosen here to show this are within the clinical range. We delineate the frequency ranges where these three different behaviors are seen. Although two of them—non-monotonic behavior and monotonic increase in the subharmonic response with the over-pressure increase—have not been observed experimentally, one can explain these model behaviors.

Because of the lack of a uniformly valid model of encapsulated contrast microbubbles, we choose then the well established free bubble model to explain the underlying physics of this behavior of the subharmonic response with the ambient pressure. We show that the determining parameter is the ratio f ∕ f₀ of excitation frequency to the natural frequency of the bubble. This is natural in view of the well known threshold phenomenon of subharmonic generation42, 43—the subharmonic response occurs above a threshold excitation level, and the threshold is minimum at an excitation frequency which is twice the natural frequency. Correspondingly, we find that the subharmonic response is maximum near this exciting frequency. The subharmonic response increases when 1.4 < f ∕ f₀ < 1.6, reaching a maximum for f ∕ f₀ ∼ 1.6 and then decreasing for higher value of the ratio. The maximum at f ∕ f₀ ∼ 1.6 is consistent with previous observation that with increasing excitation level, echo maximum shifts to frequency lower than two.45 Changing ambient pressure increases resonance frequency, thereby decreasing this ratio. However, how that affects the subharmonic depends on in which range the ratio is changing. If ambient pressure increase leads to f ∕ f₀ approaching the aforementioned value corresponding to the maximum subharmonic, then the subharmonic response increases in the process. On the other hand, if ambient pressure increase leads to this ratio moving away from the value, the subharmonic decreases. Near the value corresponding to the maximum subharmonic, ambient pressure increase gives rise to a complex non-monotonic variation in subharmonic response. We have shown that the phenomenon—three different behaviors—is quite robust and happens at different frequency of excitations and amplitudes and bubble radii. The precise values of the frequency ratio that define the ranges for the three different behaviors depend on bubble radius and excitation amplitude.

We also show that the subharmonic response at a frequency occurs in a narrow range of excitation pressure delimited by a threshold excitation value and an upper limit beyond which the oscillation becomes more chaotic marked by a broad power spectrum with much diminished and less distinctive subharmonic peak. Previous experimental investigations observed linear variation in the subharmonic response with over-pressure. Following that, we see here that the simulated monotonic increase or decrease of subharmonic with the ambient pressure increase, when one happens, is approximately linear only for certain range of excitation pressure, away from the subharmonic generation threshold, and well within the saturation zone.

We argue that in view of the above, the physical intuition—that a contrast microbubble quickly responds to an ambient pressure increase by decreasing its size and oscillation, thereby resulting in less scattered response—is partially misleading. The maximum change in the bubble radius with ambient pressure is around 6% and possibly even less for an encapsulated microbubble (however, note that for bubbles close to its buckling radius, the rate of radius decrease with further over-pressure increase could be more (see Fig. 3 in Ref. 34); buckling is not considered here). On the other hand, the changing ambient pressure changes the natural frequency of a bubble, which determines the increase or decrease of acoustic response of a microbubble. However, experimental observations to date have failed to report any increase (except at very low excitation level34), indicating possibly other mechanisms that is not accounted for in the analytical model considered here.

We now consider the effects neglected here that might explain the discrepancies between the experiment and theory. Note that experimental observations are aggregate results of contribution from an entire bubble distribution, each bubble in the distribution having a different resonance frequency. At a particular frequency of excitation, change in the ambient pressure would increase the subharmonic response for some of them and decrease in others. The relative contribution of each bubble size depends on its relative number, as well as its strength of variation giving rise to a composite effect that can still be a net decreasing subharmonic response with ambient pressure. We have neglected gas diffusion and partial or complete dissolution of bubbles in response to over-pressure increase, and considered constant gas content of a bubble. Although contrast agent encapsulation stabilizes a bubble by hindering gas permeation, and decreasing the effective surface tension,30, 49, 50 over-pressure would enhance gas permeation. Indeed Adam et al.,16 while reporting subharmonic reduction with ambient pressure for contrast agent Optison, also indicated bubble dissolution with ambient pressure increase. Authors also report a time lag of 50–70 s before the correlation between ambient pressure increase and subharmonic reduction is established. The time scale is substantially larger than the oscillation period of a bubble and, therefore, likely results from the change in bubble population triggered by gas diffusion. Sufficient bubble dissolution can indeed result in reduction of subharmonic response. Finally, our results here are obtained for a particular model of contrast microbubble implemented in BUBBLESIM following a recent modeling study, and then the free bubble model (to explain the basic dynamics). Note that the qualitative behavior of the subharmonic response as a function of the ambient pressure, which is the main focus of this work, remains the same for both the free bubble model and the encapsulated bubble model used in BUBBLESIM. This further justifies the use of the free bubble model here to explore the underlying physics. However, we note that there are physics not addressed in BUBBLESIM which are important to both qualitatively and quantitatively model bubble response. BUBBLESIM assumes a linear viscoelastic constitutive equation for the encapsulation material and a finite thickness.19 Although this one as most existing encapsulation models incorporates the basic physics of increased stiffness (and thereby higher resonance frequency) and damping due to the shell, recent studies have indicated the importance of encapsulation buckling or strain softening38 in describing nonlinear oscillation, specifically subharmonic response.41 One needs to investigate encapsulation models that incorporate these effects, and such effort is currently underway.