Michaelis–Menten speeds up tau-leaping under a wide range of conditions

Abstract

This paper examines the benefits of Michaelis–Menten model reduction techniques in stochastic tau-leaping simulations. Results show that although the conditions for the validity of the reductions for tau-leaping remain the same as those for the stochastic simulation algorithm (SSA), the reductions result in a substantial speed-up for tau-leaping under a different range of conditions than they do for SSA. The reason of this discrepancy is that the time steps for SSA and for tau-leaping are determined by different properties of system dynamics.

INTRODUCTION

Biochemical systems typically involve complex networks with many reactions and many molecular species. While studying such systems, reduced models can not only benefit simulation speed but also aid in the understanding of complex models. The Michaelis–Menten (M–M) approximation^{1, 2} of enzyme–substrate reactions, which replaces the set of three reactions

$$E+S\underset{c_2}{\overset{c_1}{\rightleftharpoons }}ES\stackrel{c_3}{\to }E+P,$$ (1)

with the single reaction

$$S\stackrel{c}{\to }P,$$ (2)

is a widely used model reduction technique for ordinary differential equation (ODE) chemical kinetics models, and has been the subject of refinements over the years.^{3, 4, 5}

Recent studies have shown that the M–M approximation can also benefit the simulation of stochastic chemical kinetics models. With regard to the use of the M–M approximation in the stochastic simulation algorithm (SSA),⁶ Rao and Arkin⁷ derived a stochastic M–M approximation from the quasi-steady-state assumption (QSSA); and Mastny et al.⁸ verified the QSSA using perturbation analysis. Gillespie et al.⁹ examined the validity of the same abridgment for a similar but simpler reaction set

$$S_1\underset{c_2}{\overset{c_1}{\rightleftharpoons }}{S}_2\stackrel{c_3}{\to }{S}_3,$$ (3)

abridged to

$$S_{12}\stackrel{c}{\to }{S}_3.$$ (4)

They showed that the abridgment is valid for SSA under four sets of conditions, and that for only one of these cases does it result in a substantial speed-up for SSA. Sanft et al.¹⁰ extended the analysis to the M–M approximation and obtained similar results.

However, little attention has been paid to the abridgment when it is used in the context of tau-leaping. The tau-leaping algorithm¹¹ is an approximate strategy to accelerate SSA simulations. This paper examines the conditions for validity and for speed-up of the abridgment applied to both reaction set 3 and reaction set 1 in the context of tau-leaping, and shows that the abridgment results in a substantial speed-up for tau-leaping under a different range of conditions than is the case for SSA.

BACKGROUND

Consider a well-stirred chemical reaction system with n molecular species S₁, …, S_n and m reaction channels R₁, …, R_m. Let x_i(t) denote the population of species S_i at time t, and x(t)=(x₁(t)^{,...,x_n(t))T} the state vector of the system at time t. Let each reaction R_j be characterized by its propensity function a_j(x) and stoichiometry vector ν_j: the probability that one R_j reaction will occur in the next infinitesimal time interval [t, t + dt), given x(t)=x, is a_j(x)dt, and the change to the system's state vector induced by one R_j reaction is ν_j. Then the dynamics of the whole system can be described by the chemical master equation.¹² The SSA is an exact method to numerically solve the chemical master equation by simulating a large number of trajectories of the system.

The tau-leaping algorithm is an approximate method to accelerate SSA. Instead of simulating one reaction at a time, tau-leaping steps the system by a selected time interval, τ, during which many reactions may fire. The idea is that if the propensity functions are nearly constant during the interval, the number of times that each reaction fires can be approximated by a Poisson random number P(a_j(x)τ). Then the state of the system can be advanced by the formula

$$\mathbf{x}(t+\tau )\approx \mathbf{x}\left(t\right)+\sum _{j=1}^m\mathcal{P}\left(a_j\left(\mathbf{x}\right)\tau \right){\nu }_j.$$ (5)

The requirement that the propensities are nearly constant during the time interval [t, t + τ] is called the leap condition: for some ε ≪ 1,

$$|{\Delta }_{\tau }{a}_j\left(\mathbf{x}\right)∕a_j\left(\mathbf{x}\right)|\le \varepsilon ,\text{forall}j=1,...,m.$$ (6)

The step size τ is dictated by the need to satisfy the leap condition.

It is easy to see that the tau-selection strategy is crucial to the accuracy and speed of tau-leaping simulations. Several strategies have been proposed. The most widely used strategy for mass action reactions is due to Cao et al.¹³ In that strategy, the leap condition is written in terms of the changes in species populations rather than the changes in propensities, and the expression for τ is given by

$$\tau =\underset{i}{\min }\left\{\frac{\max \left\{\varepsilon x_i∕g_i,1\right\}}{\left|{\sum }_j{\nu }_{ij}{a}_j\left(x\right)\right|},\frac{\max {\left\{\varepsilon x_i∕g_i,1\right\}}^2}{\left|{\sum }_j{\nu }_{ij}^2{a}_j\left(x\right)\right|}\right\},$$ (7)

where ε ≪ 1 is the preset accuracy control parameter, ν_ij are the stoichiometric terms, and g_i is the highest order of reaction in which species S_i appears as a reactant. (For further details, see Ref. 13.)

RESULTS

Abridgment of reaction set 3: Conditions for validity

Both SSA and tau-leaping are based on the same assumption that the dynamics of the chemical reaction system is governed by the propensity functions as defined above. In the case of the unimolecular reaction R₃ in reaction set 3, given the population x₂ of species S₂, the probability for reaction R₃ to fire in the next infinitesimal time dt is given by the product of the corresponding propensity function a₃ and dt: a₃dt = c₃x₂dt. Gillespie et al.⁹ showed that this condition is mathematically equivalent to the following condition: in the absence of competing reactions, the time to the next firing of reaction R₃ is an exponential random variable with mean 1∕(c₃x₂). Therefore, the validity condition of the abridgment is that the time to the next firing of reaction R₃ (the event of a S₃ molecule being generated) must be approximately an exponential random variable with mean 1∕a_a(x₁₂), where x₁₂ = x₁ + x₂ and a_a(x₁₂) is the propensity function of the abridged reaction. Note that a_a is a function of x₁₂ = x₁ + x₂, rather than a₃ being a function of x₂. Since both SSA and tau-leaping share the same assumption above of how the system dynamics is governed by propensity functions, this validity condition for the abridgment holds for both SSA and tau-leaping. The additional assumption in tau-leaping that the propensity functions are nearly constant during each time step does not affect the validity condition.

For reaction system 3, Gillespie et al.⁹ showed that the validity condition can be satisfied if and only if

$$\left(\frac{c_1}{c_1+c_2+c_3}\right)\left(\frac{c_3}{c_1+c_2+c_3}\right)\ll 1,$$ (8)

which is satisfied if and only if at least one of the four conditions holds:

$$\begin{array}{c}\hfill c_2\gg c_1,\end{array}$$ (9a)

$$\begin{array}{c}\hfill c_3\gg c_1,\end{array}$$ (9b)

$$\begin{array}{c}\hfill c_1\gg c_3,\end{array}$$ (9c)

$$\begin{array}{c}\hfill c_2\gg c_3,\end{array}$$ (9d)

and the propensity function of the abridged model is given by

$$a_a\left(x_{12}\right)=\frac{c_1{c}_3{x}_{12}}{c_1+c_2+c_3},$$ (10)

where x₁₂ = x₁ + x₂.

Because SSA and tau-leaping share the same validity condition, 8 is also the condition for the validity of the abridgment for tau-leaping, and the propensity function is given by Eq. 10.

Abridgment of reaction set 3: Conditions for speed-up

Gillespie et al.⁹ also showed that under only one condition will the abridgment speed up the SSA simulation significantly: c₂ ≫ c₃. This is because the SSA simulates every reaction event of the system; thus the speed of an SSA simulation is determined by the number of reaction firings. When c₂ ≫ c₃, many fewer reaction firings take place in the abridged system than in the original system.

For tau-leaping, since the speed of the simulation is determined by the size of the leap step τ, we must re-examine the conditions for speed-up. The leap condition 7 requires that all propensity functions remain almost constant during a time step. Thus, the time step of tau-leaping is restricted by how fast the propensity functions change and is implicitly restricted by how fast the populations of the reactants change. The key to a significant acceleration of tau-leaping simulation by abridgment is to remove the intermediate highly reactive species with the following properties:

• 1Their populations change rapidly, thus the step size of tau-leaping is restricted by those species.
• 2The distributions of their populations remain almost constant for a much longer time than their populations do, thus the average values of the corresponding propensity functions over time during this new longer step can be approximated by the expectations of those propensity functions over the distributions.

For the abridgment of reaction set 3 to reaction set 4, the conditions for validity of the abridgment are given in Eqs. 8 or 9. To examine the extent of speed-up, we compare the time step τ_f of the full model 3 with the time step τ_a of the abridged model 4 under different conditions in the Appendix. Several interesting conclusions can be summarized from the analysis:

• 1The abridgment always speeds up tau-leaping, as shown in A9, A18.
• 2The conditions corresponding to a substantial speed-up from the abridgment for both tau-leaping and SSA are compared in Table 1. The condition εx₁₂ ≫ 1 is assumed in all the conditions for tau-leaping, as this is the situation where tau-leaping is advantageous over SSA. It is easy to see that for most situations (except for when c₂ ≫ c₃), tau-leaping simulation benefits from the abridgment under a wider range of conditions than is the case for SSA simulation.

Table 1.

Conditions for a substantial speed-up from the abridgment, for tau-leaping and SSA, applied to reaction set 3.

	c2≫̸︀c3
	c2 ≫ c1	c3 ≫ c1	c1 ≫ c3	c2 ≫ c3
Tau-leaping	$x_{12}\ll {\displaystyle \frac{2{(c_2+c_3)}^3}{\varepsilon c_1^2{c}_3}}$		$\left\{\begin{array}{c}\hfill x_{12}\gg \frac{1}{\varepsilon },\mathrm{if}{c}_2\gg c_1\\ \hfill \frac{c_3}{2\varepsilon c_2}\ll x_{12}\ll \frac{2c_1^2}{\varepsilon c_2{c}_3},\mathrm{if}{c}_2\ll c_3\\ \hfill x_{12}\ll \frac{2c_1^2}{\varepsilon c_2{c}_3},\mathrm{otherwise}\end{array}\right.$	c2 ≫ c1 or $x_{12}\ll {\displaystyle \frac{2c_1^2}{\varepsilon c_2{c}_3}}$
SSA	∅			x12 > 0

Abridgment of enzyme-substrate system

For the enzyme–substrate system 1, Sanft et al.¹⁰ showed that the condition for validity of the stochastic M–M approximation is the same as that of the deterministic case,³ namely,

$$E_T\ll S_0+K_m,$$ (11)

where E_T = E(t) + ES(t), S₀ = S(0), and K_m = (c₂ + c₃)∕c₁. The propensity function of the abridged system is also the same as the deterministic M–M rate:

$$a\left(\mathbf{x}\right)\approx \frac{V_{\text{max}}S}{K_m+S},$$ (12)

where V_max=c₃E_T. And, under only one condition will the abridgment speed up the SSA simulation significantly: c₂ ≫ c₃.

Applying the same arguments in Sec. 3A, the condition for validity and the stochastic M–M rate are the same for tau-leaping as for SSA.

On the other hand, for tau-leaping, the abridged system is no longer a mass-action system. However, it is easy to see that the propensity function 12 depends on the population of S, and

$$\frac{{\Delta }_{\tau }a}{a}=\frac{K_m{\Delta }_{\tau }S}{(K_m+S-{\Delta }_{\tau }S)S}<\frac{{\Delta }_{\tau }S}{S}.$$ (13)

Thus the τ selection strategy in Eq. 7 with g = 1 can be used to calculate the tau-leaping step size of the abridged system:

$${\tau }_a=\frac{\varepsilon S}{V_{\text{max}}S∕(K_m+S)}=\frac{\varepsilon (K_m+S)}{V_{\text{max}}}.$$ (14)

To calculate the characteristic tau-leaping step size of the original system, we can make use of the corresponding ODE results as estimates of the expected populations:

$$\begin{array}{cc}\hfill \overline{E}& \approx \frac{E_T{K}_m}{K_m+S},\hfill \end{array}$$ (15a)

$$\begin{array}{cc}\hfill \overline{ES}& \approx \frac{E_{T}S}{K_m+S}.\hfill \end{array}$$ (15b)

Applying the τ selection strategy 7, we can easily see that τ_f < τ_a by examining the contribution to τ of the change in S. Then by examining the contribution to τ of the changes in E and ES, we have

$${\tau }_f<\frac{\max {\left\{\varepsilon \min \left\{\overline{E},\overline{ES}\right\},1\right\}}^2}{c_{1}S\overline{E}+(c_2+c_3)\overline{ES}}.$$ (16)

When $\varepsilon \overline{E}\le 1$ or $\varepsilon \overline{ES}\le 1$, which is equivalent to

$$\min \left\{K_m,S\right\}\le \frac{K_m+S}{\varepsilon E_T},$$ (17)

we obtain

$${\tau }_f<\frac{1}{c_{1}S\overline{E}+(c_2+c_3)\overline{ES}}=\frac{K_m+S}{2(c_2+c_3)E_{T}S},$$ (18)

$$\frac{{\tau }_f}{{\tau }_a}<\frac{c_3}{2(c_2+c_3)\varepsilon S}.$$ (19)

Again, we are only interested in the case εS ≫ 1, where tau-leaping is advantageous over SSA. In this case, τ_f ≪ τ_a, and the speed gain grows as c₂∕c₃ increases. Note that since K_m + S ≫ E_T and ε ≪ 1, condition 17 is actually a very loose condition.

When $\varepsilon \overline{E}>1$ and $\varepsilon \overline{ES}>1$, which is equivalent to

$$\min \left\{K_m,S\right\}>\frac{K_m+S}{\varepsilon E_T},$$ (20)

we obtain

$${\tau }_f<\frac{{\varepsilon }^2{E}_T\min {\left\{K_m,S\right\}}^2}{2(c_2+c_3)S(K_m+S)},$$ (21)

$$\begin{array}{ccc}\hfill \frac{{\tau }_f}{{\tau }_a}& & <\frac{\varepsilon E_T^2{c}_3\min {\left\{K_m,S\right\}}^2}{2(c_2+c_3)S{(K_m+S)}^2}\hfill \\ & & =\frac{c_3}{2(c_2+c_3)}\frac{1}{\varepsilon S}{\left(\frac{\varepsilon E_T\min \left\{K_m,S\right\}}{K_m+S}\right)}^2.\hfill \end{array}$$ (22)

The condition for the abridgment to gain a substantial speed-up in this case is given by

$$\frac{c_3}{2(c_2+c_3)}\frac{1}{\varepsilon S}\ll {\left(\frac{K_m+S}{\varepsilon E_T\min \left\{K_m,S\right\}}\right)}^2.$$ (23)

Either $S\gg \varepsilon E_T^2$, or c₂ ≫ c₃ and $S\ll ̸︀\varepsilon E_T^2$, or if the values of K_m and S are widely separated will there be a large speed-up.

The conditions corresponding to a substantial speed-up from the M–M abridgment for both tau-leaping and SSA are compared in Table 2. It is easily seen that the M–M abridgment yields a significant speed-up for tau-leaping under a different range of conditions than it does for SSA, for the enzyme–substrate system.

Table 2.

Conditions for a substantial speed-up from the M–M abridgment, for tau-leaping and SSA, applied to the enzyme–substrate system 1.

	c2≫̸︀c3	c2 ≫ c3
Tau-leaping	$S\gg \varepsilon E_T^2$ or ${\displaystyle {\left(\frac{K_m+S}{\min \left\{K_m,S\right\}}\right)}^2\gg \frac{\varepsilon E_T^2}{S}}$	$S\ll ̸︀\varepsilon E_T^2$ or ${\displaystyle {\left(\frac{K_m+S}{\min \left\{K_m,S\right\}}\right)}^2\gg \frac{c_3\varepsilon E_T^2}{c_{2}S}}$
SSA	∅	S > 0

NUMERICAL EXAMPLES

Based on the analysis in Sec. 3, we tested and timed the abridgment to different reaction systems under different conditions using the adaptive tau-leaping code in STOCHKIT 2.0.¹⁴ The tests were carried on a personal computer with an Intel Core 2 Quad Q9300 2.5 GHz central processing unit and 4 GB RAM.

Speed-up of reaction set 3

For the abridgment of reaction set 3, we choose two sets of parameters to show the different speed-up behavior of SSA and tau-leaping. Parameter set I was chosen as follows: c₁ = 1, c₂ = 100, c₃ = 100. This corresponds to the condition c₂ + c₃ ≫ c₁. To show how condition A16 factors into the speed-up, we set x₂(0) = x₃(0) = 0, and varied x₁(0) = x₁₂(0). The simulation time and speed-up of SSA and tau-leaping under different initial conditions or to the different system end time t_end, all with 10 000 runs, is shown in Table 3. ε was set to 0.01 in the τ selection. We can see from the table that: (a) the speed-up gain of SSA from the abridgment does not change as the initial condition changes. This agrees with the results of Gillispie et al.⁹ because the speed-up gain of SSA is determined solely by the c₂∕c₃ ratio; (b) tau-leaping gains a considerable speed-up when condition A16 is satisfied; and (c) the speed-up of tau-leaping is not large when condition A16 is not satisfied, but if t_end is large enough the system will go into the region of condition A16 eventually and tau-leaping will benefit substantially from the abridgment. All of these results agree with the analysis.

Table 3.

Simulation time and speed-up of SSA and tau-leaping under different initial conditions, for parameter set I, applied to reaction set 3.

		SSA			Tau-leaping
x1(0)	tend	Original(s)	Abridged(s)	Speed-up	Original (s)	Abridged (s)	Speed-up
1 × 105	1	58	9	6	50	1	50
1 × 106	1	650	110	6	5	1	5
1 × 107	1	5800	900	6	3	1	3
1 × 106	10	1660	290	6	220	2	110

Parameter set II was chosen so that c₁ ≫ c₃ ≫ c₂ to illustrate the only case for which tau-leaping would not gain a substantial speed-up, regardless of the system end time t_end. The speed-up of tau-leaping under different initial conditions or to different t_end is shown in Table 4. The other parameters and values are set to: c₁ = 100, c₂ = 0.01, c₃ = 1, x₂(0) = x₃(0) = 0, ε = 0.01. Noting that c₃∕(2εc₂) = 5000 and $2c_1^2∕\left(\varepsilon c_2{c}_3\right)=2\times {10}^8$, we can see that the results are consistent with condition A26: tau-leaping will benefit substantially from the abridgment when $c_3∕\left(2\varepsilon c_2\right)\ll x_{12}\ll 2c_1^2∕\left(\varepsilon c_2{c}_3\right)$. A quick test of SSA shows that the speed-up for SSA under this set of parameters is between 3 and 4. Tau-leaping benefits from the abridgment more significantly than SSA when condition A26 is satisfied.

Table 4.

Speed-up of tau-leaping (abridged system vs original system) for different initial conditions or system end times, for parameter set II, applied to reaction set 3.

x1(0)	1 × 104	1 × 106	1 × 108
tend=1	4	20	3
tend=10	3	17	34

Speed-up of enzyme–substrate system

For the abridgment of enzyme–substrate system 1, we chose three sets of parameters and initial conditions to show the different speed-up behavior of SSA and tau-leaping:

• 1c₁ = 1, c₂ = 10, c₃ = 10, S(0) = 1 × 10⁵, E(0) = 100, ES(0) = P(0) = 0, t_end=10. This set corresponds to the condition c₂≫̸︀c₃ and $S\gg \varepsilon E_T^2$. According to the analysis, only tau-leaping should be able to gain a substantial speed-up from the abridgment;
• 2c₁ = 1, c₂ = 100, c₃ = 1, S(0) = 1 × 10⁵, E(0) = 100, ES(0) = P(0) = 0, t_end=10. This set corresponds to the condition c₂ ≫ c₃ and $S\gg \varepsilon E_T^2$. Under this condition, both SSA and tau-leaping should be able to gain a substantial speed-up; and
• 3c₁ = 1, c₂ = 1 × 10¹⁰, c₃ = 1 × 10⁸, S(0) = 1 × 10¹⁰, E(0) = 1 × 10⁸, ES(0) = P(0) = 0, t_end=1×10⁻¹². This set corresponds to the condition that c₂ ≫ c₃ holds but neither Eq. 17 nor Eq. 23 holds. The analysis suggests that only SSA should be able to gain a substantial speed-up from the abridgment.

The simulation time and speed-up of SSA and tau-leaping under different parameters and initial conditions, all with 10 000 runs, are shown in Table 5. It is easy to see that the results agree with the analysis.

Table 5.

Simulation time and speed-up of SSA and tau-leaping under different parameters and initial conditions, applied to enzyme–substrate system 1.

	SSA			Tau-leaping
Parameters set	Original (s)	Abridged (s)	Speed-up	Original (s)	Abridged (s)	Speed-up
I	28	8	4	39	0.08	488
II	139	0.8	174	221	0.02	1105
III	695	3	232	0.03	0.02	2

Accuracy of the M–M abridgment

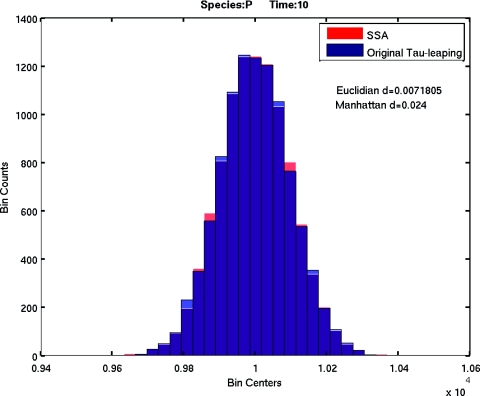
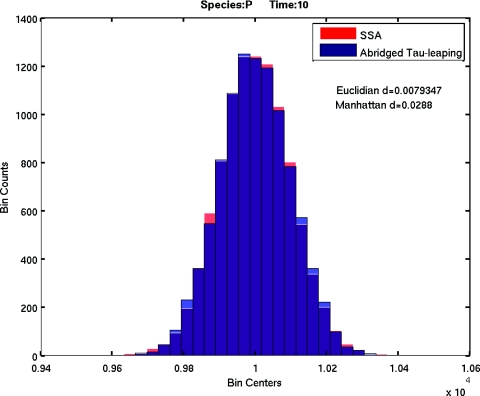
Next, we tested the accuracy of the M–M abridgment for tau-leaping. We chose an enyzme substrate reaction set with the following set of parameters: c₁ = 1, c₂ = 10, c₃ = 10. Initial conditions were set to S(0) = 10⁵, E(0) = 100, ES(0) = P(0) = 0. The system end time was set to 10. Thus, the validity condition for the M–M approximation 11 will be satisfied all the time. The baseline is the histogram of product P at the system end time of 10 000 SSA simulations of the original enzyme substrate model. 10 000 tau-leaping simulations were performed for both the original model and the abridged M–M model. The comparison of the histograms of the product P for both SSA simulation and tau-leaping simulation of the original model is shown in Fig. 1, while the comparison of the histograms of P for SSA simulation and tau-leaping simulation of the abridged model is shown in Fig. 2. The Euclidian distance and Manhattan distance in the figures are respectively L² norm and L¹ norm of the histogram distance:¹⁵ suppose X and Y are two groups of samples with N samples in X and M samples in Y, and all the sample values are bounded in the interval I=[x_min,x_max). Let L=x_max−x_min. Divide the interval I into K subintervals I_i=[x_min+(i−1)L∕K,x_min+iL∕K). Then the histogram distance is given by

$$D_K(X,Y)=\sum _{i=1}^K\left|\frac{{\sum }_{j=1}^N\chi (x_j,I_i)}{N}-\frac{{\sum }_{j=1}^M\chi (y_j,I_i)}{M}\right|,$$ (24)

where the characteristic function χ(x, I_i) is defined as

$$\chi (x,I_i)=\left\{\begin{array}{cc}\hfill 1,& \hfill \text{if}x\in I_i\text{,}\\ \hfill 0,& \hfill \text{otherwise.}\end{array}\right.$$ (25)

The histogram distance results show that the M–M abridgment is accurate and valid under this condition. Different conditions are also tested and all of them show that the M–M abridgment is valid when the validity condition 11 is satisfied.

Figure 1.

The comparison of histograms of product P at the system end time of SSA simulation and tau-leaping simulation of the original model.

Figure 2.

The comparison of histograms of product P at the system end time of SSA simulation and tau-leaping simulation of the abridged model.

Circadian oscillation model

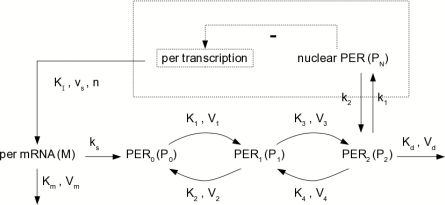
Next, we consider a more complicated model: a circadian oscillation model in the Drosophila period protein (PER).¹⁶ The scheme of the model is shown in Fig. 3. In this model, per mRNA (M) is synthesized in the nucleus and transfers to the cytosol at a maximum rate v_s. It is also degraded by an enzyme there with a maximum rate V_m and Michaelis constant K_m. The PER protein ( PER ₀) is synthesized at a rate proportional to M by a first-order rate constant k_s. The reversible phosphorylations of the PER proteins, between P₀ and P₁ and between P₁ and P₂, are governed by a set of Michaelis–Menten reactions at maximum rates V_i, with Michaelis constants K_i (i = 1, 2, 3, 4). The bisphosphorylated form P₂ is degraded by an enzyme with a maximum rate V_d and Michaelis constant K_d, and transported into the nucleus with a first-order rate constant k₁. The nuclear bisphosphorylated form of PER P_N is transported into the cytosol with a first-order rate constant k₂, while it also exerts a negative feedback on per transcription described by a Hill equation with repression threshold constant K_I and Hill coefficient n. The detailed kinetic laws, parameter values, and initial conditions can be found in Goldbeter.¹⁶

Figure 3.

Scheme of the model for circadian oscillations in PER. Six out of the ten reactions are Michaelis–Menten reactions.

To compare the results with the original M–M model to a comparable mass-action model, we converted this 5 species, 10 reaction model into a full 17 species, 22 reaction stochastic model by replacing all the 6 Michaelis–Menten reactions with enzyme–substrate reactions. The system volume was chosen to be the characteristic size of a cell nucleus, 1000 μm³. Then we varied the ratios of backward dissociation rates [c₂ in system 1] to forward dissociation rates [c₃ in system 1] of the enzyme–subsrate compounds, to see the different speed-up behavior of the Michaelis–Menten abridgment applied to SSA and tau-leaping. To simplify the problem, we took all of the six ratios (corresponding to c₂∕c₃) to be the same. The simulation time and speed-up of SSA and tau-leaping with different c₂∕c₃ ratios, all with 1000 runs and t_end=1, is shown in Table 6. The result shows that for this model, SSA will gain a large speed-up from the M–M abridgment only when c₂ ≫ c₃ is satisfied, while tau-leaping can benefit substantially from the M–M abridgment under a wider range of conditions.

Table 6.

Simulation time and speed-up of SSA and tau-leaping with different c₂∕c₃ ratios, applied to the circadian oscillation model.

	SSA			Tau-leaping
c2∕c3	Original (s)	Abridged (s)	Speed-up	Original (s)	Abridged (s)	Speed-up
0.01	1042	674	2	1271	3	424
1	1701	674	3	2103	3	701
100	78 200	674	116	83 800	3	2.8 × 104

APPENDIX: ANALYSIS OF SPEED-UP OF THE ABRIDGMENT OF REACTION SET 3

For this analysis, we assume that εx₁₂ ≫ 1, as this is the situation where tau-leaping is advantageous over SSA.

For the abridged model 4, applying the τ selection strategy 7, we get

$${\tau }_a=\frac{\varepsilon x_{12}}{c_1{c}_3{x}_{12}∕(c_1+c_2+c_3)}=\frac{\varepsilon (c_1+c_2+c_3)}{c_1{c}_3}.$$ (A1)

On the other hand, the step size τ_f of the original model 3 is restricted by the minimum of

$$\begin{array}{cc}\hfill {\tau }_{11}& =\frac{\max \left\{\varepsilon x_1,1\right\}}{\left|c_1{x}_1-c_2{x}_2\right|},\hfill \end{array}$$ (A2a)

$$\begin{array}{cc}\hfill {\tau }_{12}& =\frac{\max {\left\{\varepsilon x_1,1\right\}}^2}{\left|c_1{x}_1+c_2{x}_2\right|},\hfill \end{array}$$ (A2b)

$$\begin{array}{cc}\hfill {\tau }_{21}& =\frac{\max \left\{\varepsilon x_2,1\right\}}{\left|c_1{x}_1-(c_2+c_3)x_2\right|},\hfill \end{array}$$ (A2c)

$$\begin{array}{cc}\hfill {\tau }_{22}& =\frac{\max {\left\{\varepsilon x_2,1\right\}}^2}{\left|c_1{x}_1+(c_2+c_3)x_2\right|}.\hfill \end{array}$$ (A2d)

Since τ_f varies with x₁ and x₂, the expectations of x₁ and x₂ are used to calculate the characteristic time step of the original system. Because it is a linear system, the expectations of x₁ and x₂ are the same as the results of the corresponding ODE solutions. Let $\overline{x_1}$ and $\overline{x_2}$ denote the expectation of x₁ and x₂, and x′ = dx∕dt. Then

$$\begin{array}{cc}\hfill {\overline{x_1}}^{\prime }& =-c_1\overline{x_1}+c_2\overline{x_2},\hfill \end{array}$$ (A3a)

$$\begin{array}{cc}\hfill {\overline{x_2}}^{\prime }& =c_1\overline{x_1}-(c_2+c_3)\overline{x_2}.\hfill \end{array}$$ (A3b)

To evaluate the τ values in A2, we are concerned with the ratio r between $\overline{x_2}$ and $\overline{x_1}$:

$$\overline{x_2}=r\overline{x_1}.$$ (A4)

Substituting A4 into A3, we have

$$r^{\prime }=-c_2{r}^2+(c_1-c_2-c_3)r+c_1.$$ (A5)

Applying the QSSA (r′ = 0) and requiring that r > 0, we obtain

$$r=\frac{(c_1-c_2-c_3)+\sqrt{{(c_1-c_2-c_3)}^2+4c_1{c}_2}}{2c_2}.$$ (A6)

Now consider the different conditions under which the abridgment is valid:

• 1
  Conditions 9a or 9b: If either of these conditions holds, then c₂ + c₃ ≫ c₁, hence

  $$\begin{array}{ccc}\hfill r& =& \frac{c_1-c_2-c_3}{2c_2}\left(1-\sqrt{1+\frac{4c_1{c}_2}{{(c_1-c_2-c_3)}^2}}\right)\hfill \\ & \approx & \frac{c_1}{c_2+c_3}\ll 1.\hfill \end{array}$$ (A7)
  In this case,

  $$x_1\approx \frac{c_2+c_3}{c_1+c_2+c_3}{x}_{12}\gg x_2\approx \frac{c_1}{c_1+c_2+c_3}{x}_{12},$$ (A8)

  and εx₁ ≈ εx₁₂ ≫ 1 as assumed. Thus the τ_f is at most

  $${\tau }_{11}\approx \frac{\varepsilon (c_2+c_3)}{c_1{c}_3}<{\tau }_a.$$ (A9)

  Further calculation reveals that τ₂₁ = ∞ and τ₁₂ > τ₂₂. Thus τ_f = min {τ₁₁, τ₂₂}.

  When εx₂ ⩽ 1, we have

  $${\tau }_{22}\approx \frac{1}{2c_1{x}_1}\approx \frac{c_1+c_2+c_3}{2c_1(c_2+c_3)x_{12}},$$ (A10)

  thus (recalling that εx₁₂ ≫ 1)

  $$\frac{{\tau }_{22}}{{\tau }_a}\approx \frac{c_3}{2\varepsilon x_{12}(c_2+c_3)}\ll 1.$$ (A11)
  In this case a significant speed up is ensured. Condition εx₂ ⩽ 1 is equivalent to

  $$x_{12}\le \frac{c_1+c_2+c_3}{\varepsilon c_1}.$$ (A12)

  When εx₂ > 1, we have

  $${\tau }_{22}\approx \frac{{\varepsilon }^2{x}_{12}{c}_1}{2(c_2+c_3)(c_1+c_2+c_3)},$$ (A13)

  $$\frac{{\tau }_{22}}{{\tau }_a}\approx \frac{\varepsilon x_{12}{c}_1^2{c}_3}{2(c_2+c_3){(c_1+c_2+c_3)}^2}\approx \frac{\varepsilon x_{12}{c}_1^2{c}_3}{2{(c_2+c_3)}^3}.$$ (A14)
  To yield a substantial speed-up in this case, the following condition must be satisfied:

  $$\frac{c_1+c_2+c_3}{\varepsilon c_1}<x_{12}\ll \frac{2{(c_2+c_3)}^3}{\varepsilon c_1^2{c}_3}.$$ (A15)
  As a consequence, when c₂ + c₃ ≫ c₁, the condition for the abridgment to gain a significant speed up in tau-leaping is A12 or A15:

  $$x_{12}\ll \frac{2{(c_2+c_3)}^3}{\varepsilon c_1^2{c}_3}.$$ (A16)

  Since c₂ + c₃ ≫ c₁ and ε ≪ 1, this is actually a very loose condition. If the end time of a simulation is long enough, the simulation will always gain a large speed up when there are enough S₁ and S₂ consumed and the system goes into the region of condition A16.
• 2
  Conditions 9c or 9d: If either of these conditions holds, then c₁ + c₂ ≫ c₃, hence

  $$\begin{array}{ccc}\hfill r& =& \frac{c_1-c_2-c_3}{2c_2}+\frac{c_1+c_2+c_3}{2c_2}\hfill \\ & & \times \sqrt{1-\frac{4c_2{c}_3}{{(c_1+c_2+c_3)}^2}}\approx \frac{c_1}{c_2}.\hfill \end{array}$$ (A17)
  In this case, x₁ ≈ c₂x₁₂∕(c₁ + c₂), x₂ ≈ c₁x₁₂∕(c₁ + c₂), and the τ_f is at most

  $${\tau }_{21}\approx \frac{\varepsilon }{c_3}<{\tau }_a.$$ (A18)

  Further calculation reveals that τ₁₁ = ∞. Thus τ_f = min {τ₂₁, τ₁₂, τ₂₂}.

  If c₂ ≫ c₁, then τ₂₁ ≪ τ_a, thus τ_f < τ₁₂ ≪ τ_a.

  If c₂ ∼ c₁, then $\overline{x_2}\sim \overline{x_1}$, both εx₁ ≫ 1 and εx₂ ≫ 1 hold as assumed, thus

  $$\begin{array}{ccc}\hfill {\tau }_{22}\sim {\tau }_{12}& \approx & \frac{{\varepsilon }^2{x}_{12}{c}_2}{2c_1(c_1+c_2)}\sim \frac{{\varepsilon }^2{x}_{12}}{4c_1}\hfill \\ & =& \frac{\varepsilon x_{12}{c}_3}{4(c_1+c_2+c_3)}{\tau }_a.\hfill \end{array}$$ (A19)

  The condition to yield a substantial speed gain in this case is

  $$x_{12}\ll \frac{4(c_1+c_2+c_3)}{\varepsilon c_3};$$ (A20)

  If c₂ ≪ c₁, then $\overline{x_2}\gg \overline{x_1}$,

  $$\begin{array}{cc}\hfill {\tau }_{22}& \approx \frac{{\varepsilon }^2{x}_{12}}{2c_2+c_3},\hfill \end{array}$$ (A21)

  $$\begin{array}{cc}\hfill {\tau }_{12}& \approx \max \left\{\frac{{\varepsilon }^2{x}_{12}{c}_2}{2c_1(c_1+c_2)},\frac{c_1+c_2}{2c_1{c}_2{x}_{12}}\right\},\hfill \end{array}$$ (A22)

  whence

  $$\begin{array}{cc}\hfill \frac{{\tau }_{22}}{{\tau }_a}& \approx \frac{\varepsilon x_{12}{c}_3}{2c_2+c_3},\hfill \end{array}$$ (A23)

  $$\begin{array}{cc}\hfill \frac{{\tau }_{12}}{{\tau }_a}& \approx \max \left\{\frac{\varepsilon x_{12}{c}_2{c}_3}{2c_1^2},\frac{c_3}{2\varepsilon x_{12}{c}_2}\right\}.\hfill \end{array}$$ (A24)

  To yield a major speed-up, at least one of A23 or A24 should be much less than 1, which is equivalent to

  $$\left\{\begin{array}{cc}\hfill {\displaystyle x_{12}\ll \frac{2c_1^2}{\varepsilon c_2{c}_3},}& \hfill \text{if}{c}_2\gg c_3\text{or}{c}_2\sim c_3;\\ \hfill {\displaystyle \frac{c_3}{2\varepsilon c_2}\ll x_{12}\ll \frac{2c_1^2}{\varepsilon c_2{c}_3},}& \hfill \text{if}{c}_2\ll c_3.\end{array}\right.$$ (A25)
  Consequently, when c₁ + c₂ ≫ c₃, the condition of a substantial speed up in tau-leaping is

  $$\left\{\begin{array}{cc}\hfill {\displaystyle x_{12}\gg \frac{1}{\varepsilon },}& \hfill \text{if}{c}_2\gg c_1;\\ \hfill {\displaystyle \frac{c_3}{2\varepsilon c_2}\ll x_{12}\ll \frac{2c_1^2}{\varepsilon c_2{c}_3},}& \hfill \text{if}{c}_2\ll c_3;\\ \hfill {\displaystyle x_{12}\ll \frac{2c_1^2}{\varepsilon c_2{c}_3},}& \hfill \text{otherwise}.\end{array}\right.$$ (A26)

  Notice c₁ + c₂ ≫ c₃, this is also a very loose condition. If the end time of a simulation is long enough, the simulation can always gain a large speed up except for the case c₂ ≪ c₃ and x₁₂≫̸︀c₃∕(2ɛc₂).