Blood Vessel Deformations on Microsecond Time Scales by Ultrasonic Cavitation

Abstract

Transient interactions among ultrasound, microbubbles, and microvessels were studied using high-speed photomicrography. We observed liquid jets, vessel distention (motion outward against the surrounding tissue), and vessel invagination (motion inward toward the lumen). Contrary to current paradigms, liquid jets were directed away from the nearest vessel wall and invagination exceeded distention. These observations provide insight into the mechanics of bubble-vessel interactions, which appear to depend qualitatively upon the mechanical properties of biological tissues.

Introduction

In 1917, Rayleigh noted that a collapsing bubble can generate sufficient pressures to damage nearby surfaces [1]. For a bubble collapsing near a rigid boundary, a liquid jet can form that penetrates through the bubble and toward the boundary. Such jets have long been considered a potential source of damage to nearby surfaces [2]. While early studies of bubble-induced damage were motivated by cavitation damage to ship propellers [3], medical ultrasound has brought focus to interactions between micron-sized bubbles and viscoelastic tissues.

Recent observations of bubbles near lipid membranes [4], biological cells [5-6] or viscoelastic gels [7-8] indicate that a nearby compliant boundary can be deformed by ‘pushing’ and ‘pulling’ forces associated with volumetric bubble oscillations. Although bubbles have been observed to form jets directed away from viscoelastic surfaces under certain conditions [8], a study using cells mounted on a rigid substrate suggested that cell membranes may be disrupted by the impingement of liquid jets directed at cells [6]. Although significant in demonstrating how bubbles and viscoelastic materials interact, these previous studies were performed in vitro and do not directly address the clinical environment in which microbubbles are injected into blood vessels to provide imaging contrast for some types of diagnostic ultrasound studies, or to try to achieve therapeutic effects. In addition to possessing unknown viscoelastic properties, blood vessels also impose a volumetric confinement on bubble oscillations. Constrained within blood vessels, microbubbles excited by ultrasound not only can rupture the vessel [9], but also can affect the vascular endothelium; there is hope that the latter effect can be exploited to modify vessel permeability to enhance local drug or gene delivery [4, 10-11]. Accordingly, numerical simulations [12-16] and experiments [17-19] have sought to elucidate how bubbles and vessels interact. Based on prior work, vascular rupture in ultrasound applications has been attributed to either liquid-jet impingement or vessel distention due to ‘pushing’ forces [15, 17, 19].

Observations of bubble dynamics in vessels with surrounding tissue have been reported only once [19]. In that pioneering work, streak and strobe imaging were used; however, the transient dynamics of bubbles and vessels were not captured. Here, we used high-speed microphotography to visualize directly transient interactions between ultrasound-activated microbubbles and blood vessels within ex vivo tissue. Both bubble oscillations and vessel displacements were observed on microsecond time scales.

Experimental methods

Basic elements of the experiment are described here, while further details are included in the supplementary material [20]. Optically transparent ex vivo rat mesentery was used as a tissue model. After each rat was anesthetized, its mesentery was exposed and perfused with saline until flushed clear of blood. The mesentery and intestine were then excised. A segment of the mesentery with a rich vascular network was spread out so that its periphery was sandwiched between plates held together by magnets. The plates possessed a central, semicircular hole (3.5 cm radius) so that the targeted mesentery tissue was immediately surrounded only by saline. Next, lipid-coated perfluoropropane microbubbles were mixed with saline and injected into the mesentery segment. Green India ink was added to the saline at a volume concentration less than 3% to increase the optical contrast of vessels relative to surrounding tissues and indicate blood vessel leakage. With this approach, vessels between 10 and 100 μm in diameter were targeted for observation.

Prepared tissue samples were transferred to a water tank located on the stage of an inverted microscope with either a 40× or 60× water-immersion objective. The microscope was aligned confocally with a focused annular ultrasound transducer (H102; Sonic Concepts, Bothell, WA, USA) positioned opposite the microscope objective. Backlighting was provided by a light source coupled to an optical fiber fed through the aperture in the center of the transducer. The transducer was driven by an amplified function generator signal, resulting in single ultrasound pulses at 1 MHz that lasted about 2 μs. These pulses were measured in situ with a fiber optic hydrophone (FOPH 2000; RP Acoustics, Leutenbach, Germany) and were characterized by peak negative pressures (PNP) from 0.8–7.2 MPa, thereby representing a range from diagnostic to therapeutic levels. During each insonation, images were captured by a camera (Imacon 200; DRS Hadland, Cupertino, CA, USA) using an exposure time of 50 ns and an interframe time of 300 ns.

To address how well the experimental setup simulated the acoustic conditions of intact mesentery tissue within the body, several issues were considered. First, saline mixed with ink was injected into the target vessel in place of blood. Although blood is several times more viscous than saline, the present study involved acoustic excitation amplitudes at which the resulting bubble dynamics were controlled by the inertia of the surrounding medium rather than its viscosity. Accordingly, the presence of saline rather than blood likely did not affect test conditions significantly. In addition, it is instructive to understand test conditions outside the vessel. Mesentery tissue segments were peripherally clamped and held in saline. The limited mesentery thickness is important in that bubble dynamics may be affected by viscous dissipation in tissue surrounding the vessel [14]. The ratio of sample thickness to the diameter of the target vessel was typically greater than 1.5 and simple calculations suggest that this thickness was sufficient to capture 70% or more of the viscous effects in tissue associated with bubble motion. Lastly, it is necessary to consider the presence of a microscope objective near the target vessel. The relatively long working distances of the objectives prevented acoustic reflections from interfering with observations. Almost all images were acquired using the 40× objective (3.5 mm working distance). For this objective, reflections arrived 4.6 μs after the initial excitation pulse while the final image frame was captured at 3.9 μs. For the three observations that used the 60× objective (2 mm working distance), the reflection arrived at 2.6 μs such that it did not overlap the primary pressure pulse. Though the reflection did overlap with several of the acquired image frames, the reflected pulse was attenuated and these few observations appeared to be fully consistent with those at 40×. Further details of the test conditions are discussed in the supplementary material [20].

Results

The confinement imposed by vessels and surrounding tissue did not prevent bubbles from undergoing large volumetric oscillations that included inertial collapses. In turn, vessels deformed on the same microsecond time scale as bubble oscillations. In most cases, we observed the extent of vessel-wall invagination to be greater than the corresponding distention. This behavior is illustrated by the image sequence presented in Fig. 1a, in which bubbles respond to a 6.4 MPa PNP pulse, leading to distention (middle) and invagination (right) of the upper vessel wall. In particular, the sharp, notch-like shape of the invagination implies the presence of large mechanical strains. Another aspect of the observed interactions involves the possibility of asymmetric bubble collapses and the formation of liquid jets. In Fig. 1b, a bubble subjected to a 4.0 MPa PNP pulse distends the nearest vessel wall (middle) and subsequently forms a liquid jet (right) that penetrates through the bubble but is directed away from this wall. For 20 separate cases in which liquid jets were identifiable, the jet was always directed away from the nearest vessel wall. Despite the expectations for rigid boundaries [3], jets directed either toward or away from compliant boundaries have been reported [3, 8]. Based on our observations, the mechanical properties of vessels and the surrounding tissue (which are not well quantified) may often lead to jetting away from the vessel wall, thereby limiting the ability of impinging jets to damage vessels.

Fig. 1.

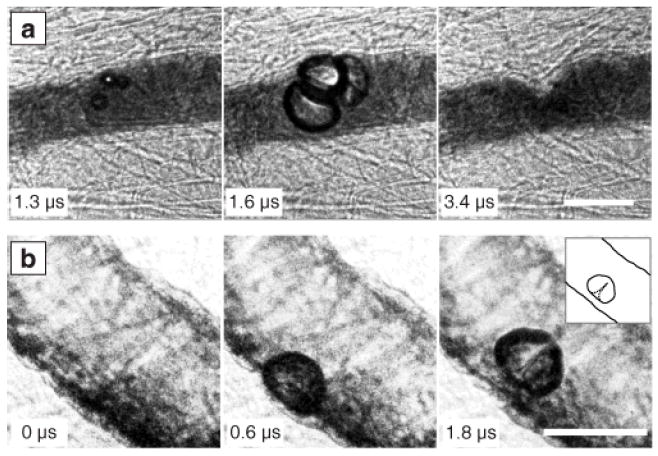
Characteristics of observed bubble-vessel interactions. (a) A group of bubbles distends the vessel wall (middle); subsequent invagination (right) appears localized and markedly larger than the distention. (b) A bubble distends the vessel wall (middle) and then forms a liquid jet directed away from this wall (right, with inset showing a sketch for clarity). Complete image sequences are shown in Movies S1 and S2 of the supplementary material [20]. In all the figures, time stamps indicate the time after arrival of the start of the ultrasound pulse, and scale bars represent 50 μm.

To study vessel deformations, image sequences of bubble-vessel interactions were captured for a range of vessel sizes (10 100 μm) and pressure amplitudes (0.8–7.2 MPa). These observations specifically include cases in which an isolated or dominant target bubble could be identified, so that the interaction between that bubble and the surrounding vessel could be analyzed. In Fig. 2, the resulting vessel deformation data are summarized, showing that invagination exceeded distention in 60 of 70 cases. Although the ratio of invagination to distention was not uniquely sensitive to pressure amplitude, larger vessel deformations did correlate with higher pressures. Based on the flow direction in the blood vessels, venules and arterioles were identified. For both venules and arterioles, invagination larger than distention was observed in most cases. However, arterioles account for 8 of the 10 observations in which invagination did not exceed distention. We speculate that arterioles and venules had different stiffnesses, thereby affecting the interaction. To illustrate different types of interaction, four cases are depicted in Fig. 3. Each interaction is characterized by three images that show respectively the vessel at its initial state, at maximum distention, and at maximum observed invagination. If the bubble filled the vessel, as in the middle frame of Fig. 3a, the subsequent invagination appeared to be circumferentially symmetric. Otherwise, distention and invagination were localized to a specific region of the vessel wall nearest the bubble. Note in Fig. 3b that the bubble translated away from the vessel wall. Although no liquid jet is visible, we would expect the direction of translation to correspond to the direction of any jetting [3, 8]. In sequences c and d, invagination is apparent even though the bubbles did not contact the vessel walls.

Fig. 2.

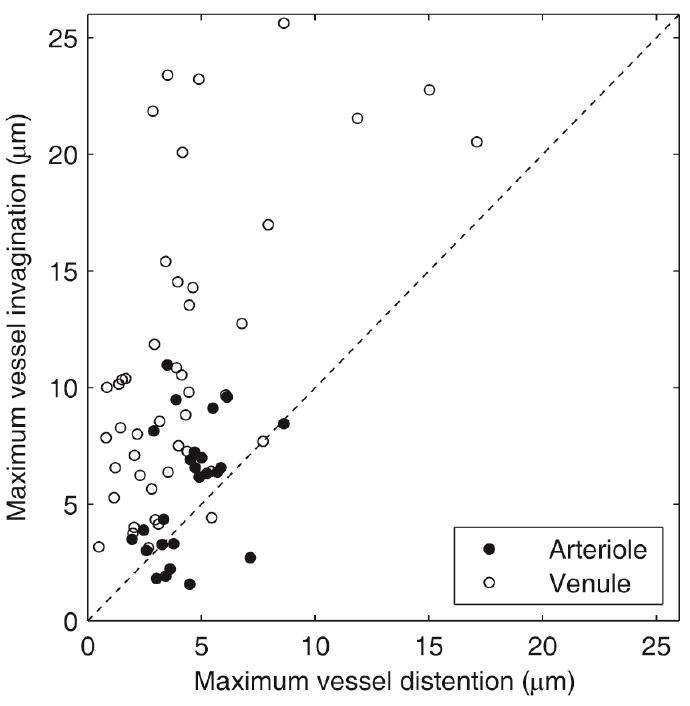
Comparison of maximum vessel invagination and distention. Each data point represents observed changes in vessel diameter for an interaction between an isolated or dominant target bubble and a vessel. Observations include microvessels with diameters between 10 and 100 μm and ultrasound pulses with peak negative pressures (PNP) between 0.8 and 7.2 MPa. In 60 out of 70 cases, the data fall above the dashed line, demonstrating that invagination typically exceeded distention.

Fig. 3.

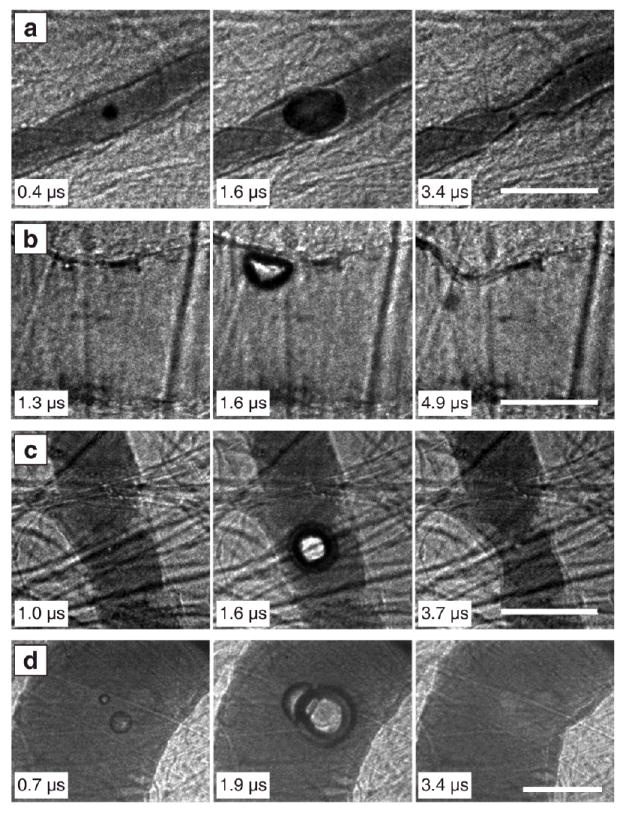
Image sequences to illustrate types of vessel invagination. In a and b, localized vessel invagination was observed when the bubble contacted the vessel wall. In c and d, the bubble did not contact the vessel wall, but still induced local vessel invagination. (a) PNP = 1.5 MPa, vessel diameter = 22 μm. (b) PNP = 4.0 MPa, vessel diameter = 71 μm. (c) PNP = 0.9 MPa, vessel diameter = 42 μm. (d) PNP = 7.2 MPa, vessel diameter = 100 μm. Complete image sequences corresponding to a–d are shown in Movies S3–S6 of the supplementary material [20].

To quantify the observed vessel displacements from Fig. 3, radial displacements of the point on the vessel wall closest to the center of the bubble were measured, and the results are plotted in Fig. 4. In each of these cases, distention was small relative to invagination. Moreover, vessel walls behaved similarly in that the average inward wall speed was around 9 m/s over the time range from 1.5–2.5 μs. Achieving such a velocity over such a short time scale implies that this response was forced rather than evoked [20]. In addition, vessels achieved their maximum invaginations after the ultrasound pulse had passed and bubble motions had mostly ceased. Finally, from other photographic sequences acquired over longer durations, we note that invaginated vessels returned to their original shapes on a time scale of milliseconds [20, see Fig. S3]. The lag of maximum invagination relative to bubble oscillations and the subsequent relaxation to the initial vessel shape imply that the vessel and surrounding tissues exhibited both viscous and elastic properties.

Fig. 4.

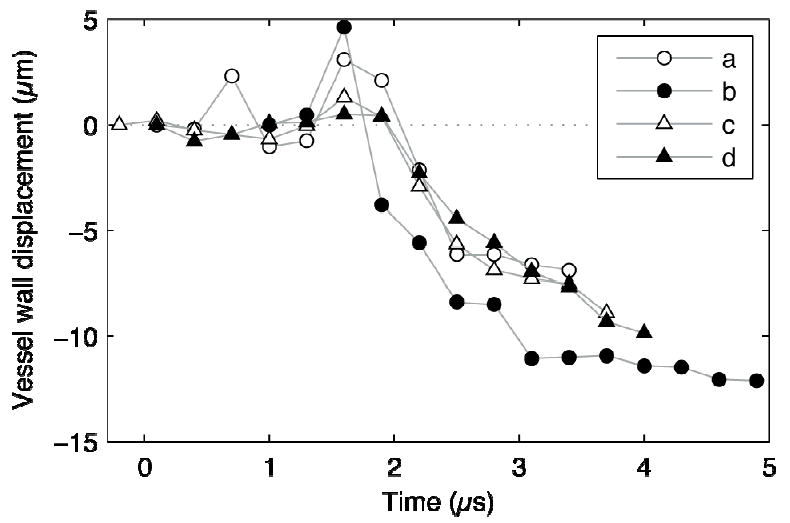
Measurements of radial displacements of the vessel wall at the point closest to the bubble for Figs. 2a–d. Each marker denotes a measurement from a single image frame. Deflections toward the lumen were defined to be negative. For each of these sequences, vessel invagination exceeded distention by a significant margin. The observed invaginations occurred after bubbles collapsed (at about 2 μs in the plot) and persisted even after bubbles rebounded.

Discussion

To physically explain jetting away from a compliant boundary, Brujan [8] notes that the boundary can store energy when distended by an expanding bubble; as the bubble collapses, rebounding of the boundary creates a short-lived pressure gradient that tends to push flow away from the boundary. If this pressure gradient is large enough, a liquid jet directed away from the boundary will form. Consistent with a pressure gradient and flow directed away from a flat boundary, we now consider a streamline that begins far away, runs along the boundary, and enters the gap between the bubble and the boundary. As the boundary rebounds and the bubble collapses, flow along this streamline converges toward the bubble and the pressure in the gap would be lower than the equilibrium pressure far away. In this way, the pressure gradient associated with the rebound of a compliant boundary not only can lead to jets directed away, but also can imply the imposition of a negative pressure in the gap between the bubble and the boundary (relative to the equilibrium pressure far away). Moreover, negative pressure changes at the boundary would tend to create invagination-type deformations. Accordingly, observations of jets directed away from the nearest vessel wall and the prominence of vessel invagination appear to be linked behaviors.

Continuing with the idea of a streamline that enters the gap between a bubble and a flat boundary, we note that integration of the momentum equation along this streamline yields a Bernoulli-type relation. If we assume a priori knowledge of the bubble’s radial dynamics and adopt simple geometric assumptions about the flow in the gap, we obtain a relation that is a modified version of the well known equation for the pressure around an unconfined, oscillating spherical bubble. This modified Bernoulli relation defines pressure in the gap, which would be “felt” by the boundary, and provides a tool for exploring how the geometry of flow confinement affects this pressure [20, see section 3]. Two types of relevant flow confinement can be identified: near-field confinement for flow restricted in a small gap between a bubble and a boundary, and far-field confinement for flow that does not spherically diverge with increasing distance from the bubble. Far-field confinement is particularly relevant when the bubble size approaches the vessel diameter and streamlines remain parallel to the vessel axis. Both types of confinement lead to higher ratios of negative to positive pressure at the boundary [20, see Fig. S5]. The ability of both near-field and far-field confinement to enhance negative pressures is consistent with the observations presented in Fig. 3, in which prominent invagination occurs for bubbles that both do and do not visibly contact the vessel walls.

Conclusions

We make two primary observations about how acoustically excited bubbles interacted with microvessels in ex vivo tissue: vessel deformations favored invagination over distention, and liquid jets formed during collapse were directed away from the nearest vessel wall. Similar qualitative behaviors have been described previously for bubbles interacting with a nearby compliant boundary; however, even qualitative characteristics of such interactions are expected to be sensitive to the mechanical properties of the boundary material [8]. Because the mechanical properties of tissue remain incompletely understood (especially for strains and strain rates relevant to medical ultrasound), our observations identify how bubbles are likely to interact with real vessels. In future work, measurement of invagination and distention will be compared to histological vessel damage to correlate potential bioeffects with mechanisms of interaction. In addition, the shape and extent of invaginations will be characterized, and subsequent relaxations will be observed. Such observations will allow estimation of the elasticity and viscosity of tissue at time and length scales relevant to acoustic cavitation.