Quantitative principal component model for skin chromophore mapping using multi-spectral images and spatial priors

Abstract

We describe a novel reconstruction algorithm based on Principal Component Analysis (PCA) applied to multi-spectral imaging data. Using numerical phantoms, based on a two layered skin model developed previously, we found analytical expressions, which convert qualitative PCA results into quantitative blood volume and oxygenation values, assuming the epidermal thickness to be known. We also evaluate the limits of accuracy of this method when the value of the epidermal thickness is not known. We show that blood volume can reliably be extracted (less than 6% error) even if the assumed thickness deviates 0.04mm from the actual value, whereas the error in blood oxygenation can be as large as 25% for the same deviation in thickness. This PCA based reconstruction was found to extract blood volume and blood oxygenation with less than 8% error, if the underlying structure is known. We then apply the method to in vivo multi-spectral images from a healthy volunteer’s lower forearm, complemented by images of the same area using Optical Coherence Tomography (OCT) for measuring the epidermal thickness. Reconstruction of the imaging results using a two layered analytical skin model was compared to PCA based reconstruction results. A point wise correlation was found, showing the proof of principle of using PCA based reconstruction for blood volume and oxygenation extraction.

1. Introduction

Assessment of the metabolic state of skin surface lesions is often desired in clinical routines as a measure for treatment outcome. Since the main absorbing components of the skin in the near-infrared spectrum are blood, melanin, lipids, and water, spatial maps of those can be obtained by near infrared diffuse multi-spectral imaging. Such concentration maps can be provided by applying an analytical, numerical, or stochastic skin model, where reconstruction is usually performed pixel by pixel. Diffuse reflectance imaging of the skin and model based image reconstruction of skin chromophores has already found its application for successfully assessing parameters for healthy and diseased skin [1–7]. However, translation into the clinic is often difficult. Few example of multi-spectral imaging have found their way into clinical routines [8,9]. The main disadvantage of these methods arises in calculating the parameters, by fitting the digitized imaging data to a model, which, dependent on the model used and the image size, can be rather computationally expensive. As a result, most methods are not capable of addressing applications where quantitative functional information is needed in real time.

In addition to the time consideration in reconstruction methods, multiple layer skin models are also structure dependent: these can vary from two to six layers [3,6,10,11] depending on the complexity of the model used. For a two layered case, the first layer describes the epidermis and the second one the dermis. In the near infrared spectrum (below 900nm), absorption and scattering properties in the epidermis are based on melanin and in the dermis on hemoglobin.

Principal Component Analysis (PCA) applied to multi-spectral images in the near-infrared has been proposed previously as an alternative tool for assessing skin chromophores [12–14]. PCA, first introduced in 1901 [15], is a statistical tool, which linearly transforms imaging data into an orthogonal coordinate system, where the axes correspond to the inherent information within the data set. One of the biggest advantages of using PCA lies in its speed of computation, which allows real-time analysis of large image sets. Applied to optical imaging, PCA has been used for noise reduction and image enhancement [16], in multi-spectral imaging data for biological cell analysis [17], and to pattern analysis for skin lesion classification [18]. Applied to RGB images, PCA was used on relative color features for unsupervised lesion classification [14,19,20].

Using PCA for extracting blood and melanin values has been described by Tsumura et al. [13], showing that skin color in digital RGB images can be described by attributing melanin and blood to the first two principal components. Fadzil et al. [21,22] applied PCA and Independent Component Analysis (ICA) to RGB imaging data for extraction of blood and melanin values in vitiligo lesions to qualitatively evaluate skin re-pigmentation progression. Our group has shown previously [12] that PCA applied to multi-spectral images from the skin in the wavelength range between 750nm and 850nm can be used for mapping blood volume and blood oxygenation, where the first eigenvector describes blood volume, the second eigenvector blood oxygenation. This description was found to qualitatively match the temporal behavior and spatial distribution of reconstruction results, using a two-layered analytical skin model. However, a subject dependent shift in the data was also observed. Since all subjects were of same ethnic origin, thus with same melanin concentration, it was hypothesized that this shift is due to epidermal thickness variations.

The aim of this paper is to explore the ability of PCA to provide quantitative blood volume and oxygenation values, which we will refer to as PCA based reconstruction. To the best of our knowledge, no previous attempt has been made for converting PCA results into actual values. We are thus investigating PCA based reconstruction of blood volume and blood oxygenation from multi-spectral images. The work is performed by introducing numerical phantoms based on an analytical two-layered skin model for photon migration in the near infrared spectrum (forward model), where the first layer describes the epidermis and the second layer the dermis. Using the forward model, we created two image sets, both with the same spatially varying blood volume and blood oxygenation distribution; in one set the epidermal thickness was maintained at a uniform value, in the second, the thickness varied from pixel to pixel (in a checkerboard manner). Each image set consisted of ten wavelength sets (evaluated at 750nm, 800nm, and 850nm), where each wavelength set corresponded to a different epidermal thickness, for the uniform image set, or thickness variation, for the variable image set. For all image sets, the melanin concentration was held constant in order to evaluate thickness variations alone. We then apply PCA on each wavelength set and show the correlation between the first eigenvector and blood volume as well as the second eigenvector and blood oxygenation, and their dependence on the epidermal thickness. Based on these correlations, we describe analytical expressions for converting values on the eigenvector 1 axis to blood volume values, as well as values on the eigenvector 2 axis to blood oxygenation values. We postulate that the accuracy of PCA based reconstruction is dependent on the epidermal thickness. To address this issue, we assume prior knowledge of the underlying skin structures imaged and we estimate the error in the two-layered model reconstruction and PCA based reconstruction if the epidermal thickness used deviates from the actual values. It is important to point out that any model could be used for creating the forward model, and that the conversion described in this paper, i.e. the PCA based reconstruction, is specific for the two-layered model case. Of course, the results will only be as precise as the model used. Based on previous work [23], we found the two-layered model to be suitable and effective for most skin conditions, but note that this model might not be applicable to every given situation or skin condition.

In order to validate the PCA based reconstruction on in vivo data, we correlate results from the two-layered model reconstruction and PCA based reconstruction. Since we show that, if melanin concentration is assumed to be known, the epidermal thickness is an important factor, we used Optical Coherence Tomography (OCT) for measuring the epidermal thickness. OCT is a powerful imaging technique [24], which provides structural information of the sample imaged with a resolution of a few micrometers. The basics and an overview of this technique can be found in references [25,26]. OCT has been applied to the skin previously and it has been shown that extraction of the epidermal thickness is possible [27–29].

We describe in vivo results from a healthy volunteer’s lower forearm, which was imaged with multi-spectral imaging as well as OCT. We then applied the two-layered reconstruction as well as PCA based reconstruction, assuming the melanin concentration to be known and taking the epidermal thickness for each pixel into account. Finally we show the quantitative match between reconstructed and PCA based reconstructed blood volume, as well as blood oxygenation. We demonstrate that knowing the underlying structures of the sample imaged is important for both two-layered model reconstruction and PCA based reconstruction. We also demonstrate that PCA based reconstruction can indeed be used as a quantitative tool for blood volume and oxygenation extraction.

2. Modeling

2.1. Analytical two-layered skin model

The skin model used for reconstruction of blood volume and oxygenation was developed, validated [23], and described previously [6,12,30,31] and will from now on be referred to as two-layered reconstruction, in comparison to PCA based reconstruction. The model is based on a two layered structure, the first one being the melanin containing epidermis, the second one being the blood containing dermis, with optical properties of the skin taken from literature values [32–34]. According to Monte Carlo Simulations [23], the thickness of the dermis could be modeled as a semi-infinite slab. The maximal depth in the dermis imaged was found to be 2mm. The generalized model can be written as:

$$I_e=S\cdot R_e{\left(\lambda \right)}^2\cdot R_d\left(\lambda \right)$$ (1)

where I_e is the wavelength (λ) dependent intensity measured in the CCD camera, S is a scaling factor, R_e(λ) the wavelength dependent reflectivity of the epidermis, and R_d(λ) the reflectivity of the dermis. The reflectivity of the epidermis, R_e(λ), is based on Lambert’s law and can be written as [32]:

$$R_e\left(\lambda \right)=e^{-{\mu }_e\cdot d}=e^{-\left(v_m\cdot 0.66\cdot {10}^{11}\cdot {\lambda }^{-3.33}\cdot d\right)}$$ (2)

with v_m the concentration of melanin, d the thickness of the epidermis and µ_e the absorption coefficient of the epidermis, which is based on the absorption of melanin. The reflectivity by the dermis, R_d(λ), which includes the absorption due to blood volume, v_db, and oxygenation, v_boxy, is based on the analytical solution of photon migration in turbid media [35] based on random walk theory and can be written as:

$$R_d\left(\lambda \right)=\frac{e^{-2\left({\mu }_d/{{\mu }^{\prime }}_s\right)}}{\sqrt{24\left({\mu }_d/{{\mu }^{\prime }}_s\right)}}.\left(1-e^{-\sqrt{24\left({\mu }_d/{{\mu }^{\prime }}_s\right)}}\right)\approx 1.06-1.45\cdot {\left({\mu }_d/{{\mu }^{\prime }}_s\right)}^{0.35},$$ (3)

$${\mu }_d=v_{db}\cdot \left[\left(1-v_{boxy}\right)\cdot {\mu }_{deoxy}+\left(v_{boxy}\right)\cdot {\mu }_{oxy}\right]$$ (4)

where µ'_s is the reduced scattering coefficient and µ_d is the absorption coefficient of the dermis, with µ_deoxy and µ_oxy being the absorption coefficients of deoxygenated and oxygenated blood respectively. It is worth noting that it has been shown previously that the thickness of the dermis can affect the reflectance results [36]. This effect is neglected in the two layered model used here.

2.2. Principal Component Analysis

Principal Component Analysis (PCA) and reasoning for applying it to multi-spectral images have been described before [12,37] and shall only be touched briefly here. PCA [15] linearly transforms the imaging data into an orthogonal coordinate system whose axes correspond to the principal components in the data, i.e., the first principal component accounts for as much variance in the data as possible and, successively, further components capture the remaining variance. Through an eigenanalysis, the principal components are determined as eigenvectors of the data set’s covariance matrix and the corresponding eigenvalues refer to the variance that is captured within each eigenvector.

For three wavelength images, PCA is performed on the collection of three-dimensional pixel vectors of the zero mean data. The three eigenvectors p₁, p₂, p₃—the principal components ordered according to the magnitude of their eigenvalues—provide the transformed data

$$Y=W^{T}X$$ (5)

where W = (p₁ p₂ p₃). Rearranging the vectors in Y into matrices yields again three 2D images. We showed previously [12] that, when applied to multi-spectral skin imaging data between 750nm and 850nm, the first eigenvector qualitatively correlates with blood volume, and the second with blood oxygenation.

2.3. Numerical phantoms – forward model

We created numerical phantoms based on the two layered skin model (Eqs. (1-4)). Those intensity images at 750nm, 800nm, and 850nm were 500 pixels x 500 pixels, with each pixel having a given unique combination of blood volume and blood oxygenation values, which vary between 0.001 and 0.5 fractional blood volume and between 0.001 and 0.99 fractional blood oxygenation, where fractional is defined as percent divided by 100. These values are covering physiologically relevant as well as extreme values. The spatial distribution of blood volume and blood oxygenation can be seen in Fig. 1 . The scaling factor, S, in Eq. (1) was held constant and set to be S = 9.26.10⁴, taken from previous in vivo imaging data calculation [6,12], where all subjects had melanin concentrations within Fitzpatrick scale 1. In order to evaluate epidermal thickness variations and not the combined effect of melanin and epidermal thickness, melanin was held constant and set to be v_m = 8%, which corresponds to a Fitzpatrick scale value of 1 [38].

Fig. 1.

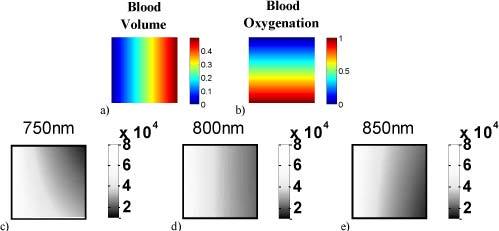
Spatial distributions of blood volume (a) and blood oxygenation (b) for the numerical phantoms. Each resulting intensity image pixel has a unique combination of those two. Resulting intensity images with epidermal thickness of d = 0.06 mm are shown for 750 nm (c), 800 nm (d), and 850 nm (e).

In order to account for the influence of the epidermis on PCA results, melanin concentration was held constant and the epidermal thickness was varied. Two different image sets were created, where the first image set consisted of 10 wavelength sets at 750nm, 800nm, 850nm each, where the difference between them lies in the epidermal thickness, which was set to constant at d = [0.02, 0.04, 0.06, 0.08, 0.10, 0.12, 0.14, 0.16, 0.18, 0.20] mm. The second image set also consisted of 10 wavelength sets, but with a spatially variable epidermal thickness within each, where the epidermal thickness was varied in a checkerboard fashion, with three different values (d₁–d₃) reported in Table 1 .

Table 1. Epidermal thickness variation within different image sets.

d1 [mm]	d2 [mm]	d3 [mm]
0.02	0.04	0.06
0.03	0.07	0.11
0.04	0.08	0.12
0.06	0.09	0.12
0.07	0.10	0.13
0.08	0.10	0.12
0.10	0.14	0.18
0.11	0.13	0.15
0.12	0.15	0.18
0.14	0.16	0.18

The second set with variable thickness is of particular importance for PCA, because of the way PCA is performed. Since PCA is applied to all pixels simultaneously (one transformation per wavelength images) rather than pixel wise, spatial variations in the epidermal thickness could therefore be evaluated. By setting the melanin concentration to a constant value and varying the epidermal thickness, we were able to evaluate, for a given melanin concentration, the combined influence of melanin times thickness (Eq. (2)), which is the total effect of the epidermis.

2.3.1. PCA on numerical phantoms

PCA was performed separately for each of the wavelength sets in the two image sets, resulting in 20 eigenvector sets of 3. The correlation between eigenvector 1 and blood volume, as well as eigenvector 2 and blood oxygenation, was then evaluated for its dependence on d.

2.3.2. PCA based reconstruction – inverse model

In order to convert the unitless PCA results into actual blood volume and blood oxygenation values, the PCA converted data was investigated for its dependence on blood volume, oxygenation, and epidermal thickness. The data projected onto eigenvector 1 was plotted against blood volume and eigenvector 2 against blood oxygenation. By curve fitting of the data, analytical expressions were found, which convert eigenvector 1 into blood volume and eigenvector 2 into blood oxygenation, both as a function of the epidermal thickness. This conversion will be referred to as ‘PCA based reconstruction’ and is described in detail in the results section.

2.3.3. Thickness dependent error analysis

The two image sets were then reanalyzed by applying the two-layered reconstruction, as well as the novel PCA based reconstruction, but making the assumption of the epidermal thickness being d = 0.06mm for all wavelength sets. This value in the inverse model has been set corresponding to a representative literature value for the lower forearm [28,39] and does not correspond to the actual thickness set in the forward model. Since the image sets have given blood volume and oxygenation values, the thickness dependent error in both reconstruction schemes could be calculated. The error was defined as true blood volume and oxygenation, minus reconstructed blood volume and oxygenation, assuming d = 0.06mm.

3. In vivo measurements

3.1. Multi-spectral and OCT instrument

Diffuse multi-spectral images as well as OCT images were acquired from the lower forearm of a healthy volunteer. The diffuse reflectance multi-spectral imaging system used in this work has been described in detail elsewhere [6] and shall only be described here briefly. Polarized light from a white light source (halogen 150W) is used for illumination of the sample. A second polarizer is placed before the detection unit, with its polarization orientation perpendicular to the incident beam polarization, thus guaranteeing diffuse reflectance measurements and removal of specular reflection [40].

Wavelength dependent images were captured by a CCD camera (Princeton Instruments CCD-612-TKB, Roper Scientific) after passing through narrow bandpass filters (750, 800, 850 nm; 40nm FWHM, CVI Laser). For calibration purposes, images from a 90% reflectance paper (Kodak) were also acquired at each image filter.

OCT provides structural information of the sample imaged with a resolution of a few micrometers. The OCT system is based on spectral domain OCT [41] and was built specifically for this project. The system is fiber based with a superluminescence diode light source (DenseLight, Singapore) emitting at λ₀ = 1300 nm with ∆λ = 130 nm and output power 24mW. The interferometer is based on a Michelson interferometer with a 50/50 fiber coupler. The beam is scanned across the sample via an x-y galvo-scanner, where the beam is focused onto the sample surface by an achromatic lens with focal length of 35 mm. Optical power on the sample was ~5mW. A variable neutral density filter was used in the reference arm in order to operate the spectrometer camera close to the saturation limit. Backscattered light from the skin is recombined with the reference arm light at the interferometer exit and detected by the spectrometer. At the spectrometer, light is collimated and directed onto a diffraction grating (Wasatch, USA) with 1100 lines/mm. The dispersed spectrum is focused by an achromatic lens of 100 mm focal length on and recorded by a 1024 element InGaAs line scan camera (Goodrich, Princeton, NJ), which results in 512 pixels in z-direction.

For in vivo measurements, the A-scan rate was set to 10 kHz (exposure time 55µs) and B-scans were acquired with 15 f/s. A paper mask, seen in Fig. 2 , was placed on the forearm. The paper mask was composed of an outer 6 cm square (pink in Fig. 2b and c) and 16 inner 1 cm squares, aligned in a grid pattern. Twelve of those squares within the mask were imaged, resulting in 12 3D data sets of 500x500x512 pixels (x-y-z direction), which correspond to 14 mm in x and y direction, and 2.5 mm in z direction. The area in x and y direction was chosen to contain part of the mask as well, in order to align the measured OCT images with multi-spectral images. Refractive index matching gel was not used, since it would have biased the multi-spectral images obtained from the same area.

Fig. 2.

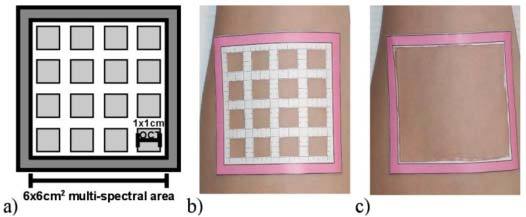
Paper mask placed on the forearm. The small squares were imaged with OCT first and the outer square was imaged with the multi-spectral imaging system. A cartoon of the mask is seen in (a), the mask on the forearm for OCT imaging in (b), and for multi-spectral imaging in (c).

After acquiring the OCT images, the inner part of the grid was removed, leaving only the outer square (Fig. 2c), which was imaged by the multi-spectral imaging system. For multi-spectral images, the upper arm was occluded by a pressure cuff with 180mmHg pressure. This amount of pressure was chosen to achieve arterial occlusion and the pressure lasted for 5min. Multi-spectral images were taken every 30 seconds before occlusion, during occlusion and for 5 minutes afterwards, resulting in 26 time points in total. Occlusion experiments were chosen as the behavior of blood volume and blood oxygenation over time is well known, which is ischemia during, and reactive hyperemia after occlusion [5,12,30,42,43].

All volunteers signed a consent form approved by the Institutional Review Board of the Eunice Kennedy Shriver National Institute of Child Health and Human Development under the protocol number 08-CH-0001.

3.2. In vivo data—skin model based and PCA based reconstruction

For in vivo calculation of blood volume and oxygenation, multi-spectral images from the occlusion experiment were used. Preprocessing of the data included spectral and spatial illumination artifact removal [6], rigid body registration for motion artifact removal, as well as curvature correction [31]. Two layered skin model reconstruction as well as PCA based reconstruction was performed, using the epidermal thickness, measured by OCT, as spatial priors. For the two-layered skin model reconstruction, melanin concentration was assumed to be known and set to v_m = 8%.

Epidermal thickness segmentation of the OCT images was performed on B-scans on linear scale. Before segmentation was performed, a moving mean-filter of 5x5 pixels was applied. The skin surface was found by moving along the z-direction, finding the first pixel larger than a user defined threshold. In order to remove outliers, pixel positions which were further away than 3 pixels from the standard deviation over the two neighboring ones on either side, were removed. For smoothing the surface, the missing points were then interpolated based on nearest neighbor interpolation. For finding the epidermis-dermis boundary, the maximum intensity value below the skin surface in z-direction was found. Again, in order to avoid outliers, pixels which were further away than 5 pixels from the standard deviation over the two neighboring ones were removed and smoothing was performed with interpolation. A refractive index of n = 1.42 [44] was used to convert optical into geometric thickness, thus obtaining the actual epidermal thickness values.

4. Results

4.1. PCA applied to numerical phantoms

PCA was performed separately for each wavelength set of the two image sets. The relationship between PCA converted data, projected onto eigenvector 1 and blood volume values, as well as eigenvector 2 and blood oxygenation values for both image sets (uniform and spatially varying epidermal thicknesses) are shown in Fig. 3 .

Fig. 3.

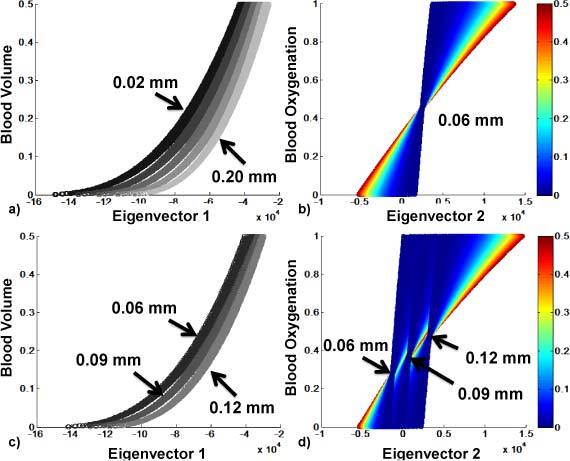
Eigenvector 1 and 2 vs. blood volume and blood oxygenation, respectively. 3a and 3b show results for the uniform thickness set; 3c and 3d for spatially varying thickness set. 3a and 3c show results color-coded with thickness d; 3b shows one wavelength set of uniform thickness of 0.06mm; 3d shows a wavelength set of varying thickness; 3b and 3d are color-coded with blood volume, showing the dependence of eigenvector 2 on blood volume as well as on thickness.

The first row of images (a-b) shows these relationships for the first image set (uniform epidermal thickness). Five of the 10 wavelength sets were used to create Fig. 3a, each gray value corresponding to a different wavelength set, thus a different epidermal thickness (d = 0.02 mm – d = 0.2 mm). Figure 3b shows eigenvector 2 projection vs. blood oxygenation for d = 0.06mm, color-coded with blood volume, where a high dependency on blood volume can be seen. The same relationships are shown in Fig. 3c and 3d for one wavelength set of the second image set with varying epidermal thickness of d = [0.06 0.09 0.12]mm. Results for eigenvector 1 (3a and 3c) show that blood volume can uniquely be extracted for a known epidermal thickness. Eigenvector 2 (3b and 3d) shows a dependency on blood volume as well as epidermal thickness. Using OCT, the epidermal thickness can be extracted. Thus, we show in the next section, that the eigenvectors can be converted into blood volume and oxygenation, assuming the epidermal thickness to be known.

4.2. PCA based reconstruction

4.2.1. PCA based reconstruction of blood volume based on eigenvector 1

Fitting of a cubic polynomial to all eigenvector 1 pixels of the spatially varying image set was performed (Curve Fitting Toolbox, Matlab, Math Works, Natick, MA). This fitting was done for a given thickness, thus for all ten thickness combinations. The conversion of eigenvector 1 into blood volume values can be seen in Eq. (6).

$$VD{B}^{*}=C_1\cdot Y_1{}^3+C_2\cdot Y_1{}^2+C_3\cdot Y_1+C_4,$$ (6)

where VDB* = (vdb₁, …, vdb_n), which is blood volume at each pixel based on PCA, Y₁ = (y_1,1, …, y_1,n), which is the projection on to eigenvector 1 at each pixel.

The coefficients (C₁ – C₄) of the cubic polynomial were found to dependent on the thickness and are given by a cubic polynomial as well, with coefficients seen in Table 2 . The magnitude of the coefficients, (as low as 10^-16) is explained by the magnitude of the eigenvector values (~10¹⁵) for a cubic polynomial. The final values thus lie between 0 and 1 (fractional percentage).

Table 2. Coefficients for cubic polynomial for C₁-C₄.

	a0	a1	a2	a3
C1	4.40x10−14	−4.13x10−15	1.63x10−15	1.04x10−16
C2	9.19x10−9	−8.74x10−10	5.95x10−10	7.95x10−11
C3	5.47x10−4	−9.05x10−5	5.50x10−5	1.65x10−5
C4	5.21	−1.67	0.27	1.05

The result of this PCA based reconstruction of blood volume can be seen in Fig. 4 . Figure 4a shows the PCA based reconstruction of blood volume applied to all 10 wavelength sets of the first image set (uniform thickness); Fig. 4b applied to the second image set (spatially varying thickness). The correlation between this calculated blood volume and real blood volume is linear, shows no longer a dependence on the thickness and makes predictions of blood volume possible with an error of less than 8% for blood volume values of 0.5.

Fig. 4.

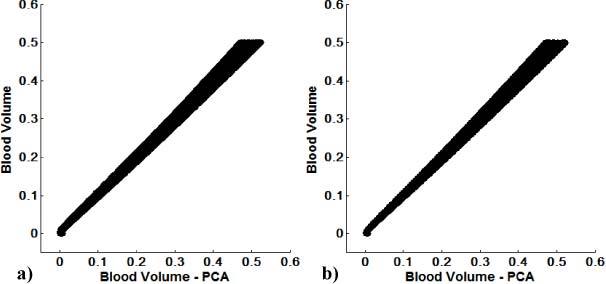
PCA based reconstruction of blood volume vs. blood volume for all uniform d (a) and spatially varying d (b) image sets. After correction, blood volume can be assessed within a maximum error of 8%, using eigenvector 1.

4.2.2. PCA based reconstruction of blood oxygenation based on eigenvector 2

PCA based reconstruction for blood oxygenation using eigenvector 2 was also evaluated by the second image set (spatially varying thickness) and then applied to the first image set (uniform thickness). It was found that eigenvector 2 is dependent on blood volume as well as on thickness. Since eigenvector 1 is also dependent on thickness, it empirically was found that a linear relationship between eigenvector 2 and blood oxygenation could be established by dividing eigenvector 2 with eigenvector 1. This linear relationship can be written as:

$$VBOX{Y}^{*}=A\cdot \frac{Y_2}{Y_1}+B$$ (7)

where VBOXY* = (vboxy₁, …, vboxy_n), which is blood oxygenation at each pixel based on PCA, Y₂ = (y_2,1, …, y_2,n), which is the projection along eigenvector 2 at each pixel, A = (a₁, …, a_n) and B = (b₁, …, b_n) are the slope and intercept, respectively. The slope A was found to be blood volume dependent and thickness independent as can be seen in Fig. 5a for the image set with spatially varying thickness vs. blood volume. After fitting against blood volume, the slope was found to be:

Fig. 5.

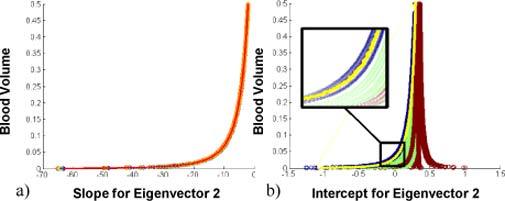
Slope and intercept of eigenvector 2. 5a. shows the slope A vs. blood volume, 5b. the intercept B vs. blood volume, where the blue curves show the smallest thickness within the wavelength set (d₁), green show d₂, red d₃.

$$A=-6.27\cdot VD{B}^{-0.35}+5.99$$ (8)

Since blood volume can be calculated based on eigenvector 1 with less than 8% error, the slope can be calculated based on eigenvector 1. The intercept B was found to be dependent on blood volume as well as the thickness. Figure 5b shows the intercept B vs. blood volume, where blue, green, and red correspond to the minimum, middle and the maximum thickness within one wavelength set. The minimum thickness in an image can be described as an outlier in the image. Since it influences the results, it can be said that PCA is sensitive to outliers in thickness within an image. The intercept for the minimum thickness, B_min, could therefore be fitted (shown in Fig. 5b – yellow) and written as:

$$B_{\min }=-S_1\cdot VD{B}^{-S_2}+S_3$$ (9)

where the coefficients S₁, S₂, S₃ can be determined through a linear dependence on thickness (Eq. (10)). This epidermal thickness dependence explains the remaining ‘widening’ of the intercept of the minimum thickness (see inset in Fig. 5b - blue). These coefficients were found to be:

$$\begin{array}{l}{S}_1=-0.22\cdot d_{\min }-0.13\\ S_2=-0.04\cdot d_{\min }-0.34\\ S_3={}_{}{}^{}0.14\cdot d_{\min }+0.47\end{array}$$ (10)

where d_min is the minimum thickness, which corresponds to d₁ in Table 1.

The relationship between the intercept for the minimum thickness, B_min, and the intercept for the remaining thicknesses D = (d₁, d₂, d₃) was found to be linear and dependent on the difference between the minimum and remaining thickness. The intercept B can thus be calculated by a linear equation with B_min, given as:

$$B=S_4\cdot B_{\min }+S_5$$ (11)

where the coefficients S₄ and S₅ can be written as:

$$S_4=-18.44\cdot \left(D-d_{\min }\right)+1.04;S_5=6.25\cdot \left(D-d_{\min }\right)-0.01$$ (12)

The resulting blood oxygenation calculation based on Eq. (7) (PCA based reconstruction) vs. blood oxygenation can be seen in Fig. 6 . Figure 6a shows PCA based reconstruction of blood oxygenation vs. real blood oxygenation for the first image set (uniform thickness), Fig. 6b for the second image set (spatially varying thickness).

Fig. 6.

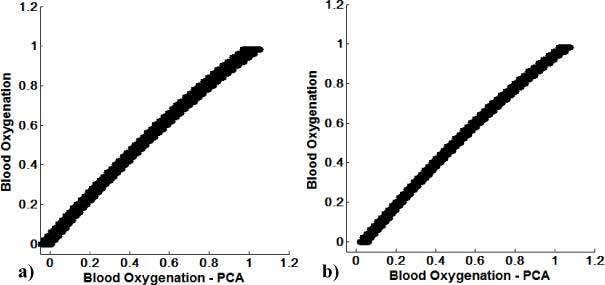
PCA based reconstruction of blood oxygenation vs. blood oxygenation for the first image set (uniform d) (a), second image set (spatially varying d) (b).

4.3. Thickness dependent error analysis

4.3.1. Epidermal thickness dependent error in two layered model reconstruction

Error analysis of two layered model reconstructed blood volume and oxygenation values for all wavelength sets of the first image set (uniform thickness) can be determined if an epidermal thickness of d = 0.06mm is assumed. The relative error is defined as the difference between the known blood volume and oxygenation values (set in the forward model) minus reconstructed ones. Results can be seen in Fig. 7 . The error in blood volume (Fig. 7a) is color-coded with blood volume values and is linearly dependent on epidermal thickness. As expected, it is zero for the image set, which has actual thickness d = 0.06mm, but as large as 15% for d = 0.20mm.

Fig. 7.

Relative error in two layered model reconstruction. A constant epidermal thickness of d = 0.06mm is assumed for calculations. The error in blood volume values is shown in (a), color-coded with blood volume. The error in blood oxygenation in dependence on blood volume is shown in (b), color-coded with blood oxygenation.

The error in blood oxygenation (Fig. 7b) is color-coded for blood oxygenation. It was found to be blood oxygenation as well as blood volume dependent and to be as large as 60% (for v_db = 4% and blood oxygenation 95%) for d = 0.20mm. The error decreases with increasing blood volume values.

4.3.2. Epidermal thickness dependent error in PCA based reconstruction

The errors in PCA based reconstruction of blood volume and blood oxygenation can be seen in Fig. 8 . The procedure was the same as for the two layered model reconstruction analysis, which was assuming d = 0.06mm at each pixel. The error analysis in PCA based reconstruction was performed separately on both image sets (uniform thickness and spatially varying). Figure 8 shows the relative error in PCA based reconstruction of blood volume and oxygenation for the first image set. Figure 8a shows the results for blood volume, where the error linearly increases with thickness. The error ranges from 3% (d = 0.02mm) to 15% (d = 0.2mm) blood volume. Figure 8b shows the error in blood oxygenation as a function of blood volume. For a given blood volume value, the error also depends on oxygenation. For larger blood volume values, this dependency decreases and thus the error in oxygenation decreases. It shall be noted that the error at d = 0.06mm is not zero, since the PCA based reconstruction has an uncertainty, as shown in Figs. 4 and 6.

Fig. 8.

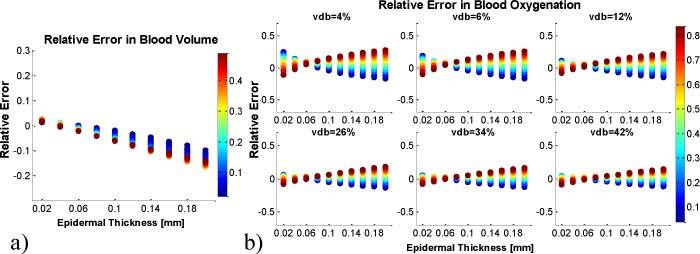
Relative error in PCA based reconstruction for the uniform epidermal thickness image set. A constant epidermal thickness of d = 0.06mm is assumed for calculations. The error in blood volume values is shown in (a), color-coded with blood volume. The error in blood oxygenation in dependence on blood volume is shown in (b), color-coded with blood oxygenation.

The relative error for the second image set (spatially varying epidermal thickness) was found to be not significantly different from the first image set (data not shown). It is important to note that the error in PCA based reconstruction is symmetric around zero, whereas the error in two layered model reconstruction is not. The error in oxygenation for the model reconstruction (Fig. 7) is therefore larger than the PCA based reconstruction error. This important finding indicates that the PCA based reconstruction is less sensitive to epidermal thickness variations.

4.4. In vivo results

The epidermal thickness was extracted based on 3D OCT image sets of the lower forearm. Figure 9a shows a representative B-scan through part of the arm in logarithmic scale with image area of 14 mm x 1.3 mm. The area of the arm is surrounded by the paper mask, which is seen at the left and right outer part of the image. The red lines indicate the surface of the skin as well as the boundary of the dermal layer. The OCT system is not artifact free and a ghost image can also be seen on top of the skin surface. A representative A-scan can be seen in Fig. 9b, plotted in linear scale. The skin surface and the epidermal-dermal boundary are indicated with the red dotted lines.

Fig. 9.

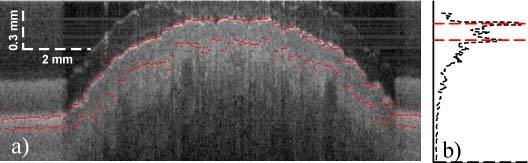
B-scan (a), A-scan (b). A typical section of the forearm is shown in a, where the red lines indicate the surface of the skin as well as the boundary to the dermal layer. A representative A-scan in linear scale is seen in b.

The average thickness of each 1 cm square can be seen in Fig. 10 , with error bars given by the standard deviation over each area. The overall thickness does not vary significantly over the 12 areas measured, with a mean thickness of 115.2µm ± 32µm. Taking pixel wise measures of epidermal thickness into account, two-layered reconstruction of blood volume and oxygenation as well as PCA based reconstruction was performed. After downsampling the OCT images to match the pixel size of multi-spectral images (400 µm x 400 µm), registration was performed. Since only a subset of the data was used, which was based on the four center 1 cm squares, the number of pixels was reduced significantly.

Fig. 10.

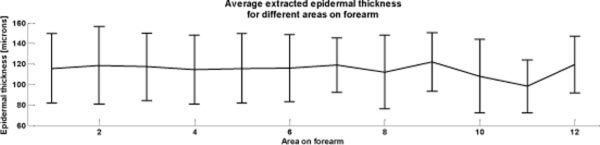
Average and standard deviation of extracted epidermal thickness over twelve 1x1cm2 areas on the forearm of a healthy volunteer.

Two-layered reconstruction of blood volume and oxygenation was performed first, which includes calculation of the scaling factor S. The found scaling factor was S = 1.24.10⁵, which is larger than the assumed one for PCA based reconstruction. For PCA based reconstruction, the scaling factor was set to S = 9.26.10⁴, which corresponds to the average value of several subjects with 300ms exposure time. Therefore, the intensity images had to be scaled to S = 9.26.10⁴ before PCA was performed. Since we have shown previously [12] that the number of pixels is important for reliable performance of PCA, data transformation with PCA was done with eigenvectors found previously on a different data set from the same subject. After PCA was performed, the PCA based reconstruction was applied.

Blood volume and oxygenation were extracted with both reconstruction methods and the comparison over time can be seen in Fig. 11 . For each time point, the average value over the entire image area was taken and data is shown with standard deviation over all pixels. Blood volume (Fig. 11a) and oxygenation (Fig. 11b) follow the expected temporal course for occlusion, which is constant for blood volume with an overshoot in blood oxygenation after occlusion (hyperemia).

Fig. 11.

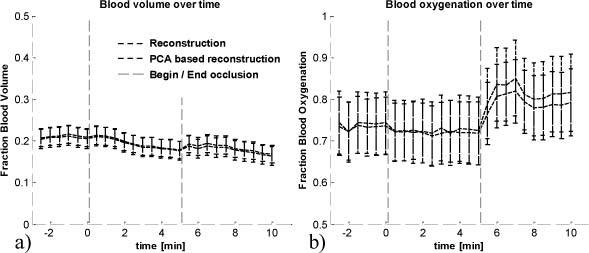
Blood volume (a) and oxygenation (b) over time, extracted with two-layered reconstruction and PCA based reconstruction. Begin and end of occlusion is indicated by the vertical lines at time t = 0min and t = 5min.

The point wise correlation between two-layered reconstruction results and PCA based reconstruction results is shown in Fig. 12 . Data was taken from all time points, before, during, and after occlusion. The correlation between reconstructed blood volume and PCA based reconstructed blood volume, seen in Fig. 12a, shows a pixel wise correspondence. The correlation between reconstructed blood oxygenation and PCA based reconstruction results is shown in Fig. 12b. The remaining error in correlation can be explained by uncertainty in extraction of the epidermal thickness.

Fig. 12.

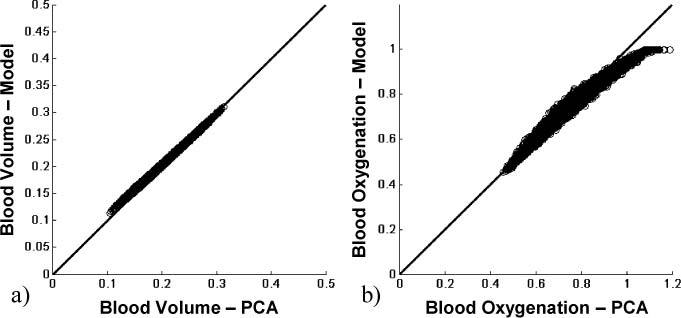
In vivo results for blood volume (a) and blood oxygenation (b), showing a pixel wise correspondence between two-layered reconstruction and PCA based reconstruction.

5. Discussion

Diffuse multi-spectral imaging in the near-infrared wavelength range has previously been used to assess blood volume and oxygenation in healthy and diseased skin [1–3,5,6,12,30,37,42,45]. These parameters are of particular interest for assessing the metabolic state of skin-lesions for treatment follow-up, since they function as a measure of angiogenic processes and metabolic state of a tumor. Generally those parameters are being assessed by fitting the intensity data to an analytical or numerical model of photon migration, with prior assumptions being made. If a two layered analytical skin model is being used, the effect of the epidermis on reflectance data is dependent on the melanin concentration as well as the epidermal thickness, whereas melanin dominates in means of light reflectance. When trying to reconstruct for melanin as well as the epidermal thickness, crosstalk between those two is dominant, leading to erroneous results. Often, the epidermal thickness is assumed to be known. If the assumption is wrong, reconstruction results will be erroneous. Quantitative reconstruction thus depends on the assumptions made.

Principal Component Analysis (PCA) has been proposed as an alternative tool for extracting information from reflectance imaging data from the skin [12,14,19–21,37,46]. The biggest advantage of PCA lies in the speed of computation, which provides information in real-time, as well as in its model independence. Tsumura et al. [13,14] extracted blood and melanin values when applying PCA to RGB imaging data. Those results were qualitative though and no attempt was done to convert the results into quantitative parameters. We have shown previously [12,37] that PCA applied to multi-spectral imaging data from the skin in the wavelength range between 750nm and 850nm can be used for blood volume and oxygenation extraction and mapping. We showed that the data projected on to the first eigenvector follows the spatial and temporal behavior of blood volume and the projection on to the second eigenvector of oxygenation. Those findings though were also qualitative.

We created multiple numerical phantoms with given melanin concentration and blood volume and blood oxygenation distributions and varied the epidermal thickness. Since PCA is performed on 2D images and thus takes spatial variations into account, the epidermal thickness was chosen to be uniform in the first image set and spatially varying in the second image set. By keeping melanin constant and varying the epidermal thickness, we were able to look at the total effect of the epidermis as well. PCA was applied to each image set of those simulations and the relationship between eigenvector 1 and blood volume as well as eigenvector 2 and blood oxygenation was being investigated (Fig. 3). We found that PCA can decouple the dependence of blood volume and oxygenation, making eigenvector 1 only blood volume and thickness dependent. Eigenvector 2 was found to be blood volume, oxygenation, and thickness dependent. Having found those dependencies and assuming prior knowledge about the underlying structure (epidermal thickness), PCA results could be converted into actual blood volume and oxygenation values (Fig. 4 and 6), resulting in a PCA based reconstruction.

For blood oxygenation calculation with this PCA based reconstruction, we found that the smallest thickness within the image becomes an important parameter. If one single pixel in the image has a thickness, which is more than 20µm smaller than the next bigger one, the error becomes significantly larger (data not shown). The reason for this dependence is that PCA is performed on 2D images, thus is dependent on spatial variation. This also means that PCA is inherently dependent on outliers. It shall be noted that this is a scenario, which is not to be expected for in vivo imaging, since it is highly unlikely to find an outlier in the epidermal thickness. Such a case could potentially only be found based on experimental errors of extracting the thickness from structural images. We further found that blood oxygenation could not reliably be extracted for blood volume values smaller than 4%. This is to be expected though, since the sensitivity is decreased for small blood volume values. For Blood volume values larger than 4%, blood oxygenation could be extracted within 10% error.

We further evaluated the error in reconstruction, using the analytical two layered model, if the epidermal thickness is not known. The error in reconstruction of blood volume and oxygenation, using a two-layered model as well as PCA based, was evaluated assuming an epidermal thickness of d = 0.06, which is a representative literature value for the lower arm [28,39]. For the two layered reconstruction, we found that the error in blood volume increases linearly with error in epidermal thickness assumption (Fig. 7a). If the difference between assumed and true value is <0.06mm, the error is moderately low (<6% blood volume). Blood volume can thus still be reconstructed within 6% error, and is therefore not very sensitive to epidermal thickness variations. In comparison, the error in oxygenation (Fig. 7b), which is not linear with thickness, can be as large as 40% if the assumed epidermal thickness varies from the real value by 0.06mm.

Using PCA based reconstruction, the error in calculations, if an epidermal thickness of d = 0.06mm is assumed, was evaluated using image sets with both, uniform and spatially varying, epidermal thickness. PCA based reconstruction showed the same trend and magnitude of errors in blood volume (Fig. 8a) as the error using reconstruction with a two layered model. The error in oxygenation was found to be smaller than for the reconstruction results, thus making PCA based reconstruction less sensitive to epidermal thickness variations. It is important to point out that the error behavior with epidermal thickness is not the same between PCA based reconstruction and two layered reconstruction. The error in oxygenation, using PCA based reconstruction, was found to be symmetric on zero, whereas the error for two layered reconstruction was increasing for all oxygenation values.

For the in vivo data validation, we used multi-spectral imaging on the skin in combination with Optical Coherence Tomography (OCT) on the same area for obtaining spatial priors. The multi-spectral images were acquired before, during, and after arterial occlusion of the upper arm. The temporal comparison between two-layered reconstruction results and PCA based reconstruction results (Fig. 11) was performed by averaging over all pixels per time point. Blood volume and oxygenation were found to follow the expected temporal course for arterial occlusion. No significant difference was found between two-layered reconstruction and PCA based reconstruction, confirming the validity of PCA based reconstruction. The average blood oxygenation values were found to not significantly decrease during occlusion. This can be explained by averaging over all pixels, which include blood vessels as well as surrounding non-vascular tissue. We were not able to isolate the blood vessels in the image, but found that the temporal behavior varies considerably between pixels and several of them showing the expected ischemic behavior.

We also showed a pixel wise correlation between two-layered model reconstructed blood volume and PCA reconstructed blood volume results, as well as a good correlation for blood oxygenation (Fig. 12). Since the majority of points lie on the 45 degree line and thus correlate point wise, the PCA based reconstruction could be validated against the two layered reconstruction algorithm. This point wise correspondence could be used for validation, since the error behavior between reconstruction and PCA based reconstruction is not identical (Fig. 7 vs. 8). Only in the case of correct epidermal thickness measures, the two values coincide. Otherwise, the data points would not lie on the 45 degree line. As explained previously, the actual blood volume and oxygenation values are dependent on the underlying two-layered skin model used for conversion. Thus, the validation shown here, demonstrates that the PCA based reconstruction is only as good as the two-layered reconstruction, but with the benefit of obtaining results in real time.

The same reasoning holds for the remaining uncertainty in oxygenation values (Fig. 12) which might be attributed to the epidermal thickness extraction. The algorithm used is based on thresholding of OCT intensity values, rather than more sophisticated methods, leading to uncertainties in extraction. This uncertainty leads to two effects, which are shifting of oxygenation values and blurring of the correlation between two-layered reconstruction and PCA based reconstruction. This effect can also explain blood oxygenation values larger than 100%, which clearly is erroneous. It shall further be noted that the scaling factor had to be calculated first by the reconstruction algorithm in order to scale the data for PCA. Since the scaling factor is related to the light illuminating the sample, this calculation is not needed if the incident light intensity is measured. Additionally it should be mentioned that the melanin content has been assumed 8% for PCA conversion. It is well known that the effect of melanin absorption on reflectance is much stronger than the epidermal thickness. Here, the melanin concentration was assumed to be known in accordance with the Fitzpatrick scale. If a wrong assumption is being made, the presented PCA conversion will yield to erroneous results. Thus, in order to further generalize the PCA results, melanin values will have to be taken into account and treated as an unknown. Since we are able to decouple the dependence of melanin and epidermal thickness (Eq. (2)) by measuring the epidermal thickness with OCT, we hypothesize that it should be possible to quantify melanin as well. We hypothesize that if more wavelengths are being taken into account, a dependence on melanin might occur in the third eigenvector. Future work will be addressing this hypothesis.

Having demonstrated the proof of principle of using PCA based reconstruction in combination with OCT to obtain quantitative blood volume and blood oxygenation values, future work will include changes in the multi-spectral setup to measure the incident light. Those technical improvements will lead to acquiring data from a greater number of healthy volunteers, as well as imaging patients with skin surface tumors. Especially for imaging skin tumors, prior knowledge of the underlying structure is important since the structural conformation often differs from healthy skin. Having a near real-time imaging tool, multiple skin lesions could be imaged and results interpreted instantly.

6. Conclusion

A novel approach of obtaining blood volume and oxygenation values using multi-spectral imaging data from skin by applying PCA has been introduced. It has been shown previously that qualitative results can be obtained and here we are showing that those results can be converted into quantitative ones, using a PCA based reconstruction algorithm. Here we created numerical phantoms based on an analytical two layered skin model with varying blood volume and oxygenation, and applied PCA. Structural changes have been investigated as well, namely changes in the epidermal thickness, and its influence on PCA results. We were able to find analytical expressions for converting the unitless data from PCA into actual blood volume and blood oxygenation values within 8% error, if melanin and the epidermal thickness are known. The error for reconstruction and PCA based reconstruction if the epidermal thickness is not known was also calculated, assuming d = 0.06mm for both image sets. This error analysis revealed that the underlying thickness has to be known, otherwise the error in blood oxygenation can be as large as 60%, for a difference of 0.14mm between actual thickness and assumed one. In order to validate the PCA based reconstruction on in vivo data, OCT and multi-spectral measurements on the lower forearm of a healthy volunteer undergoing arterial occlusion have been performed. OCT was used to extract the epidermal thickness, which was used as prior information for two-layered reconstruction and PCA based reconstruction. We showed the correspondence between two-layered reconstruction and PCA based reconstruction for spatial and temporal behavior of blood volume and oxygenation. We were able to find a linear correlation between two-layered reconstruction and PCA based reconstruction, making it possible to use PCA for quantitative assessment of blood volume and oxygenation. Since PCA can be performed in real time, it is a promising tool for clinical evaluation of skin malignancies.