Abstract
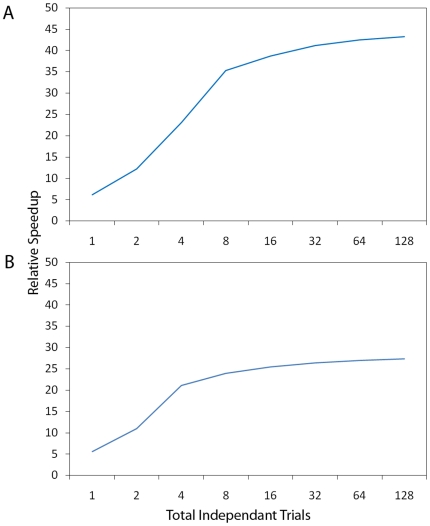
High performance computing on the Graphics Processing Unit (GPU) is an emerging field driven by the promise of high computational power at a low cost. However, GPU programming is a non-trivial task and moreover architectural limitations raise the question of whether investing effort in this direction may be worthwhile. In this work, we use GPU programming to simulate a two-layer network of Integrate-and-Fire neurons with varying degrees of recurrent connectivity and investigate its ability to learn a simplified navigation task using a policy-gradient learning rule stemming from Reinforcement Learning. The purpose of this paper is twofold. First, we want to support the use of GPUs in the field of Computational Neuroscience. Second, using GPU computing power, we investigate the conditions under which the said architecture and learning rule demonstrate best performance. Our work indicates that networks featuring strong Mexican-Hat-shaped recurrent connections in the top layer, where decision making is governed by the formation of a stable activity bump in the neural population (a “non-democratic” mechanism), achieve mediocre learning results at best. In absence of recurrent connections, where all neurons “vote” independently (“democratic”) for a decision via population vector readout, the task is generally learned better and more robustly. Our study would have been extremely difficult on a desktop computer without the use of GPU programming. We present the routines developed for this purpose and show that a speed improvement of 5x up to 42x is provided versus optimised Python code. The higher speed is achieved when we exploit the parallelism of the GPU in the search of learning parameters. This suggests that efficient GPU programming can significantly reduce the time needed for simulating networks of spiking neurons, particularly when multiple parameter configurations are investigated.
Introduction
As the bounds of single processor speed-up have reached a stringent limit, the self-fulfilling “Moores Law” dictating a doubling of computational speed roughly every 24 months can only be realised by increasing the number of processing cores on a single chip. Inevitably this has serious implications on the design of algorithms that must take into account the resultant parallel architectures (parallelisation). Similar to multi-core CPU systems, the Graphics Processing Unit (GPU) is a parallel architecture which is currently emerging as an affordable supercomputing alternative to high performance computer grids. In contrast to multi-core parallelism, the GPU architecture consists of a much larger number of simplistic vector processing units which follow a stream-like programming model [1], [2]. The availability of high quality GPU programming tool-kits such as the Compute Unified Device Architecture (CUDA) and Open Computing Language (OpenCL), has without doubt propelled GPU computing into the mainstream. Despite this, GPU programming requires careful optimisations and knowledge of the underlying architecture in order to gain notable performance speed-ups. It is therefore imperative to use only algorithms which form a good fit to GPU hardware by exploiting large amounts of fine grained parallelism when applying GPU programming to scientific problems such as the simulation of populations of biologically plausible neurons which we explore in this paper.
The purpose of this work is twofold. First, we demonstrate that GPU can be efficiently used in the context of Computational Neuroscience, as a low cost alternative to computer clusters. Second, using the GPU computing power, we study how specific network architectures of biologically plausible (spiking) neurons perform in learning an association task. More specifically, we simulate a two layer network of spiking neurons entirely on the GPU. The input layer represents the location of an artificial animal and the output layer its decision, i.e. which action to perform. We investigate two alternative architectures. In the first, the output layer has recurrent, “Mexican-Hat”-type connectivity[3]–[5], i.e. short range excitatory, long range inhibitory connections. This type of connectivity has been identified in cortex organisation [6]–[8] and offers a “plausible” neural network implementation for reading out the information (the decision) encoded in the output layer. We term this scenario “non-democratic” decision making, as the participation of the neurons in the decision is influenced by others via recurrent (lateral) connections. As a consequence, first occurring spikes can significantly affect the activity bump formation in the recurrent network. In the second architecture there are no recurrent connections. The readout of the encoded information in the output layer is done via a “population vector” [7], [9], without taking into account how this could be implemented in neural networks terms. We term this scenario “democratic” decision making, as every neuron participates in the decision without being influenced by others. Learning in both scenarios takes place by modifying the synapses between the input and the output layer according to a spike-based Reinforcement Learning rule derived from reward optimisation by gradient ascent [10]–[12], an approach that can be linked to policy gradient methods in machine learning [13], [14].
Our simulations indicate that “non-democratic” decision making, which is based on “Mexican-Hat”-type connectivity, is prone to “crosstalk” of learning when input-layer neurons are participating in the representation of multiple states. In our setup, this is due to overlapping neuronal receptive fields. We borrow the term “crosstalk” from the field of electronics in the following sense. If a neuron in the input layer is active during more than one state (network input), it can be considered as part of more than one sub-network. Synaptic changes that take place in one sub-network involving this specific neuron may affect the output of another sub-network, inducing therefore “noise” in the decision making process. The advantage of the “democratic” decision making over the “non-democratic” is that “crosstalk” tends to cancel out due to the linear nature of the population vector readout and the symmetry of the task. We further underline this argument with sets of experiments, which investigate the influence of varying the reward function and the effect of additive noise. The results of the study are presented in section Results .
The simulations presented here would have been extremely time consuming (or even virtually impossible) on a low cost desktop computer without the use of GPU programming. Our GPU simulations shows speed-ups of up to a factor of 42 compared to a serial implementation running on a Intel i7-930 quad core CPU. Our implementation is also parallel over a number of independent simulations, enabling us to produce statistically accurate results and also to perform rapid searches over various parameter configurations. This functionality has allowed us to scan vast parameter spaces demonstrating important and general differences between the two systems of “democratic” and “non-democratic” decision making. The code developed is presented in Methods together with a brief introduction to GPU Programming and a discussion of the resulting performance gain and future work.
Results
In this section, we introduce and signify the importance of the modelling problem, which is an essential element of a navigation scenario. We describe the network architecture in detail and present the simulation results for various configurations. Finally, we draw conclusions related to the performance of the learning system. More specifically, when the neurons in the output layer do not equally contribute to the decision taken, but are influencing each other via strong, non-linear dynamics, the system is more susceptible to noise and learning performance generally degrades.
The Simulation Paradigm
Action selection mechanisms are often modelled as “winner-take all” or “winner-take most” networks. Making a decision involves some kind of competition [15], [16] where the winner exhibits maximum activation and hence represents the decision whereas the losers' activity decays to a low state. These mechanisms, that are typically modelled by lateral connectivity, are not only attractive from a conceptual point of view but are scenarios worthy of exploration when building models, as they can provide simple mechanisms by which information can be sent to other neurons. Evidence of short range excitatory/long range inhibitory connectivity has been identified in cortex organisation, see for instance [6]–[8] and references therein.
Decision making [17]–[21] can be also considered in the context of Reinforcement Learning [22]–[24], where an agent explores its environment and learns to perform the right actions that bring maximal reward. Such scenarios are often incorporated in behavioural animal studies, where, for instance rodents are learning to perform specific tasks that involve spatial learning memory. One such task is the Morris water-maze[25].
A previous model [12] studied a Morris water-maze navigation scenario, similar to [26]–[30], but implementing the agent with a spiking neural network. This specific model explored “Mexican-Hat”- type lateral connectivity (MHC) as a simple “biologically plausible scenario” for reading out information and action selection. In fact, neurons do not simultaneously form excitatory and inhibitory synapses, but such a behaviour could in principle be achieved via interneurons. The MHC introduces a non-linear (non-democratic) effect in the decision making process, as all neurons are silenced by the inhibition introduced by the MHC except for a small group of neighbouring neurons which form an “activity bump”. This bump can be interpreted as corresponding to the winning action (i.e. the animal decision), suggesting a simple mechanism to extract information out of a competing group of neurons, that can be implemented easily in neural networks, without the need of additional “plugged on” read-out mechanisms.
Learning in this network model takes place by modifying the synapses via a spike-based Reinforcement Learning rule [12] derived from reward optimisation by gradient ascent [10], [11], [31]–[35], an approach that can be linked to policy gradient methods in machine learning [13], [14]. Other classes of spike-based Reinforcement Learning rules are based on Temporal-Difference (TD) learning [36]–[39], in particular actor-critic models [23], [37], [40] and on the extension of classical STDP models [41]–[43] to reward-modulated STDP rules [11], [44]–[46].
Interestingly, learning was shown to fail when MHC-based architectures were combined with the policy gradient spiking Reinforcement Learning rule derived in [10]–[12] (within the range of tested parameters). If however, we are not concerned about how the population decision is communicated between layers of neurons (and therefore do not implement MHC) but simply read out the activity via the population vector [7], [9], learning does not fail. We term this operation a“democratic decision”, because the non-linear effect of the lateral connections is absent from the process: all neurons “vote” freely without being “influenced” by other neurons and their votes are weighted by their activity (in a linear fashion) so every spike per neuron counts the same.
These findings naturally raise the following questions. Which precisely are the
conditions that favour the “democratic” decisions versus the
“non-democratic” ones? In order to answer this question, we study
the results of a similar problem but with a reduced complexity (in one
dimension) that allows a systematic parameter study via high performance GPU
simulation. Our animat (artificial animal) “lives” on a circle (1D
space) and performs the following task. We set the animat randomly to one
position on the circle (encoded as an angle from 0 to
 ). The animat then chooses a direction. At each position
there is one “correct” direction, which depends smoothly on the
position; if the animat chooses it, it will receive maximum reward. Choices
“near” the correct direction also receive some reward, according to
a reward function. This smoothness assumption with respect to the rewarded
action makes learning possible. The setting of the animat at a location and
selection of a decision constitutes a single trial. After completion of a trial
the animat is placed randomly at a new position and the task is repeated. The
problem will be fully learned if the animat chooses the correct direction at
each position in the cycle. In the simulations that follow, without loss of
generality we assume that the “correct” (maximally rewarded)
direction is the one that is equal to the initial position that the animat is
placed.
). The animat then chooses a direction. At each position
there is one “correct” direction, which depends smoothly on the
position; if the animat chooses it, it will receive maximum reward. Choices
“near” the correct direction also receive some reward, according to
a reward function. This smoothness assumption with respect to the rewarded
action makes learning possible. The setting of the animat at a location and
selection of a decision constitutes a single trial. After completion of a trial
the animat is placed randomly at a new position and the task is repeated. The
problem will be fully learned if the animat chooses the correct direction at
each position in the cycle. In the simulations that follow, without loss of
generality we assume that the “correct” (maximally rewarded)
direction is the one that is equal to the initial position that the animat is
placed.
Model Architecture
Our model architecture implements a simple two-layer network of neurons. The
cells of the input layer, which we term “Place Cells” due to the
conceptual similarity to the biological place cells discovered by O'Keefe
and Dostrovsky in 1971 [47], are arranged on a circle. Each cell has a tuning
curve with a unique preferred direction (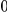 to
to
 ). Preferred directions are equally spaced on the circle.
In accordance with evidence [48], the ensemble of Place Cells codes for the position
of the animat. The output layer has a similar structure; each output cell has a
preferred direction and the population vector of the ensemble codes for the
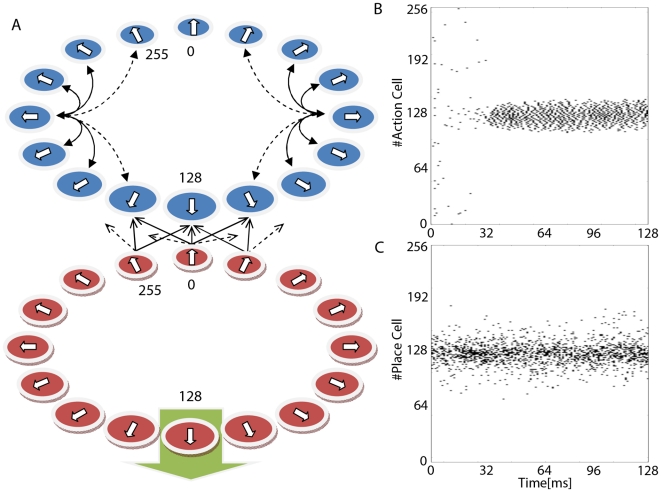
“action” the animat takes. A schematic diagram of the network is
shown in Figure 1A.
). Preferred directions are equally spaced on the circle.
In accordance with evidence [48], the ensemble of Place Cells codes for the position
of the animat. The output layer has a similar structure; each output cell has a
preferred direction and the population vector of the ensemble codes for the
“action” the animat takes. A schematic diagram of the network is
shown in Figure 1A.
Figure 1. Model Architecture.
Our animat (artificial animal) “lives” on a circle and
performs the following task. We place the animat randomly to one
position on the circle. The animat then chooses a direction, the
decision, 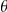 . At each
position there is one “correct” direction
. At each
position there is one “correct” direction
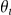 . Choices
. Choices
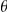 close to
the correct direction
close to
the correct direction 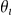 receive
some reward, according to a Gaussian reward function. This processes
(the setting of the animat at a location, selection of a decision,
receiving a reward and updating of the feed-forward weights) constitutes
a single trial. After completion of a trial the animat is placed
randomly at a new position and the task is repeated. The task will be
fully learned if the animat chooses the correct direction at each
position on the circle. A: Shows a schematic overview of our two layer
model architecture consisting of Place Cells (red) and Action Cells
(blue). Place Cells (modelled as Poisson neurons) are connected to
Action Cells (Integrate-and-Fire neurons) using an all-to-all feed
forward network (not all connections are shown). In addition Action
Cells may be interconnected via lateral Mexican hat-type connections
(not all connections are shown). The layer of Place Cells is arranged in
a ring like topology with each neuron
receive
some reward, according to a Gaussian reward function. This processes
(the setting of the animat at a location, selection of a decision,
receiving a reward and updating of the feed-forward weights) constitutes
a single trial. After completion of a trial the animat is placed
randomly at a new position and the task is repeated. The task will be
fully learned if the animat chooses the correct direction at each
position on the circle. A: Shows a schematic overview of our two layer
model architecture consisting of Place Cells (red) and Action Cells
(blue). Place Cells (modelled as Poisson neurons) are connected to
Action Cells (Integrate-and-Fire neurons) using an all-to-all feed
forward network (not all connections are shown). In addition Action
Cells may be interconnected via lateral Mexican hat-type connections
(not all connections are shown). The layer of Place Cells is arranged in
a ring like topology with each neuron 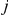 having a
preferred angle, and firing with maximum probability if the location of
the animat happens to coincide with this preferred angle. In the example
shown the animat is placed at the location that corresponds to the
preferred direction of neuron index
having a
preferred angle, and firing with maximum probability if the location of
the animat happens to coincide with this preferred angle. In the example
shown the animat is placed at the location that corresponds to the
preferred direction of neuron index 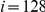 . The top
layer, also arranged in a ring topology, codes for the location the
animat will choose. B: Shows the output spike train of the Action Cells
demonstrating a bump formation around neuron
(
. The top
layer, also arranged in a ring topology, codes for the location the
animat will choose. B: Shows the output spike train of the Action Cells
demonstrating a bump formation around neuron
(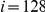 ) with a
resulting decision angle
) with a
resulting decision angle 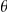 matching
the preferred angle of
matching
the preferred angle of 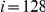 . In this
example the target angle
. In this
example the target angle 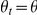 , and
therefore the animat has made the correct decision. C: Shows the spike
train of the input layer (Place Cells) when the animat is placed at the
location encoded by neuron
, and
therefore the animat has made the correct decision. C: Shows the spike
train of the input layer (Place Cells) when the animat is placed at the
location encoded by neuron 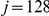 .
.
We study two variants of the same architecture, one with a recurrent Mexican-Hat connectivity (MHC) among the neurons of the output layer, and one without lateral connections. We note that in the case where MHC is present, the population vector, which decodes the decision, points very precisely at the direction that corresponds to the neuron(s) with the maximal activity. For a direct comparison, we use the population vector in both architectures to extract the decision of the output cells, though it would have being equivalent if, in the case of lateral connections, we were reading out the decision as the activity peak.
In Figure 1B we show the activity of the input layer, the Place Cells. In Figure 1C we plot the activity of the output layer (“Action Cells”) for the network with MHC. Learning is achieved by the modification of the feedforward connections from the input layer to the output layer according to a Reinforcement Learning policy gradient spiking rule [10]–[12].
Place Cells
Place Cells are modelled as Poisson neurons. The stochastic firing rate
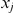 of Place Cell
of Place Cell 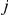 is determined
by the distance between its preferred direction
is determined
by the distance between its preferred direction
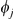 and the animat's location
and the animat's location
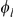 :
:
| (1) |
where the function
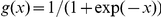 is the sigmoidal (logistic) function (the
neuron's response function),
is the sigmoidal (logistic) function (the
neuron's response function), 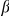 a positive
parameter that determines the steepness of the sigmoidal function,
a positive
parameter that determines the steepness of the sigmoidal function,
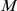 is the total number of Place Cells, and
is the total number of Place Cells, and
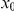 a factor that scales the maximum frequency at which
the Place Cells can fire. The purpose of
a factor that scales the maximum frequency at which
the Place Cells can fire. The purpose of 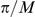 in Equation 1
is that the firing rate of neuron
in Equation 1
is that the firing rate of neuron 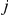 drops to half
of the maximum (
drops to half
of the maximum (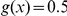 ) when the
animat is placed in between neuron
) when the
animat is placed in between neuron 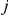 and either of
its directly neighbouring neurons
and either of
its directly neighbouring neurons 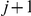 ,
,
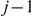 , i.e.
, i.e. 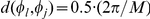 . Parameter
. Parameter
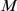 allows scaling of this property with the number of
neurons. The distance
allows scaling of this property with the number of
neurons. The distance 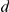 between the
two angles
between the
two angles 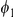 and
and
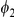 and is given by:
and is given by:
| (2) |
The neurons are Poisson for the following reason. Given the rate
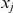 (which is constant in each trial), the spikes are
generated according to a Poisson process with intensity
(which is constant in each trial), the spikes are
generated according to a Poisson process with intensity
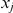 , which is equivalent to saying that all spikes are
independent with the expected number of spikes in an interval of length
, which is equivalent to saying that all spikes are
independent with the expected number of spikes in an interval of length
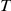 being
being 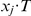 . Throughout
our simulations we use the constant values of
. Throughout
our simulations we use the constant values of
 ,
, 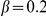 and
and
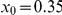 (unless otherwise stated) resulting in a maximum
firing rate of
(unless otherwise stated) resulting in a maximum
firing rate of 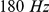 at the most
active neuron in the population.
at the most
active neuron in the population.
The parameter 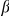 is crucial for
the system as it determines the overlap of neighbouring receptive fields of
the Place Cells. In plain words, every cell
is crucial for
the system as it determines the overlap of neighbouring receptive fields of
the Place Cells. In plain words, every cell 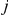 fires
maximally when the animat is at its preferred location
(
fires
maximally when the animat is at its preferred location
(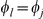 ). By making the sigmoidal function less steep
(decreasing
). By making the sigmoidal function less steep
(decreasing 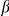 ), the neuron
will respond with a higher probability when the animat is located far away
from
), the neuron
will respond with a higher probability when the animat is located far away
from 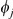 . This results in that neuron
. This results in that neuron
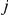 will contribute with a higher probability to the
representation of more potential locations of the animat.
will contribute with a higher probability to the
representation of more potential locations of the animat.
Action Cells
Action cells are modeled as Leaky Integrate-and-Fire units [49] with
escape noise, which are a special case of the Spike Response Model [50]. The
change in membrane potential 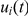 of a neuron
of a neuron
 , which receives input from Place Cell
, which receives input from Place Cell
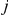 at time
at time 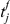 (with
(with
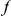 being an index on the individual spikes of neuron
being an index on the individual spikes of neuron
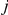 ), and input via lateral connections from Action Cell
), and input via lateral connections from Action Cell
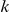 at time
at time 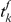 , is given
by:
, is given
by:
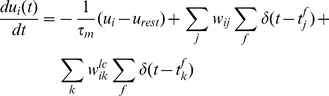 |
(3) |
where
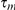 is the membrane time constant of
is the membrane time constant of
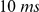 ,
, 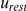 is the resting
potential of
is the resting
potential of 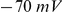 and
and
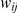 is the synaptic strength between the presynaptic
(place) cell
is the synaptic strength between the presynaptic
(place) cell 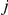 and the
postsynaptic (action) cell
and the
postsynaptic (action) cell  . Furthermore
. Furthermore
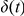 denotes the Dirac function and
denotes the Dirac function and
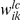 the synaptic strength of the lateral connection
between Action Cells
the synaptic strength of the lateral connection
between Action Cells  and
and
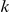 .
.
Spikes are generated with an instantaneous probability
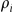 determined by an exponential function of the
form:
determined by an exponential function of the
form:
| (4) |
where
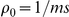 is a scaling factor of the firing rate. The
parameter
is a scaling factor of the firing rate. The
parameter 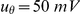 can be considered as a “soft” firing
threshold and
can be considered as a “soft” firing
threshold and 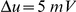 controls the
"sharpness" of the “soft” threshold, see also [50],
chapter 5.3.
controls the
"sharpness" of the “soft” threshold, see also [50],
chapter 5.3.
After a neuron fires, its membrane voltage does not return directly to the
resting potential. Instead, it increases its negative polarization even
further (known as hyperpolarizing spike afterpotential). To account for this
phenomenon, right after a spike is emitted we set the neuron's membrane
potential to  , i.e.
, i.e.
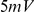 below the resting potential.
below the resting potential.
Lateral Connections
In our model, the weights of the lateral connections are determined by a
Mexican-Hat-shaped function of the distance between Action Cells
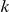 and
and  , yielding a
(fixed) synaptic strength
, yielding a
(fixed) synaptic strength 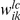 determined
by:
determined
by:
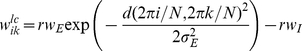 |
(5) |
where
 is the scaling of the MHC,
is the scaling of the MHC,
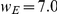 is the strength of the excitatory MHC weights,
is the strength of the excitatory MHC weights,
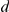 is the distance function defined in Equation 2,
is the distance function defined in Equation 2,
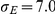 is the length scale of the MHC,
is the length scale of the MHC,
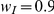 is the strength of inhibitory MHC, and
is the strength of inhibitory MHC, and
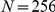 is the number of Action Cells. Parameter
is the number of Action Cells. Parameter
 takes the value of
takes the value of 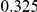 unless
otherwise stated. In Figure
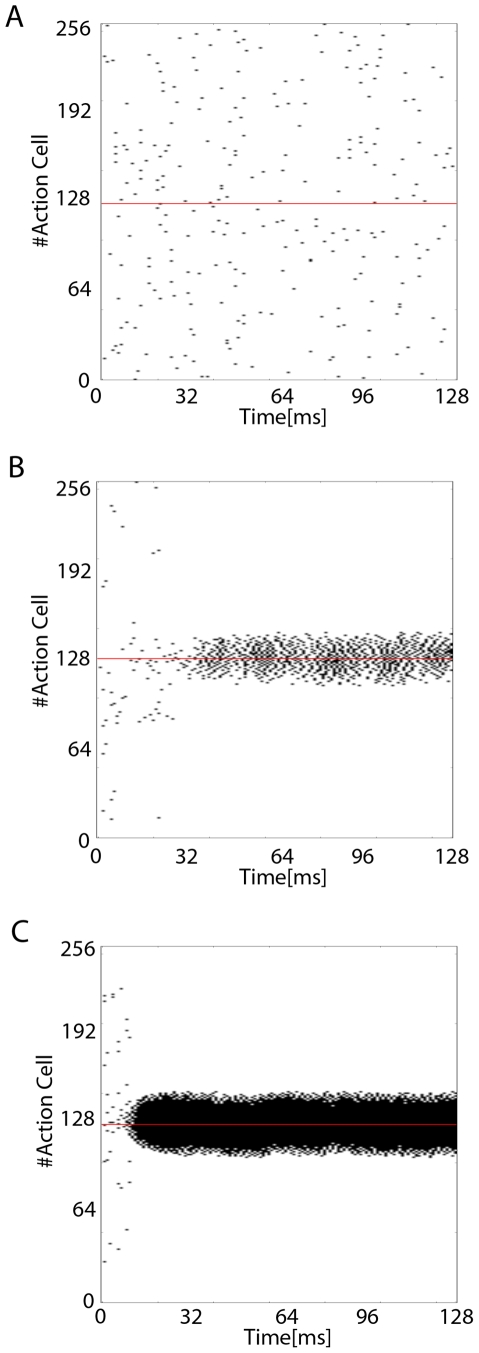
2 we plot the activity of the output layer for a system without
lateral connections (
unless
otherwise stated. In Figure
2 we plot the activity of the output layer for a system without
lateral connections (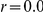 , panel A), a
system with lateral connections (
, panel A), a
system with lateral connections (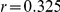 , panel B) and
a system with very strong lateral connections
(
, panel B) and
a system with very strong lateral connections
(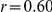 , panel C).
, panel C).
Figure 2. Lateral Connection Strength.
Figure shows the effect of varying the lateral connection strength
parameter  on the
spiking activity of the Action Cells over a period of
on the
spiking activity of the Action Cells over a period of
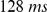 (before learning has taken place). For clarity, the figures show a
decision angle of value of
(before learning has taken place). For clarity, the figures show a
decision angle of value of  suggesting a centralised high activity around Place Cell index
suggesting a centralised high activity around Place Cell index
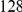 (as in
Figure 1).
A: Shows a system without lateral connections where
(as in
Figure 1).
A: Shows a system without lateral connections where
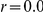 . B:
Shows a system with lateral connections where
. B:
Shows a system with lateral connections where
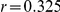 . C:
Shows a system with very strong lateral connections where
. C:
Shows a system with very strong lateral connections where
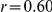 .
.
Action Selection and Reward
For each cycle of the simulation the decision angle
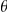 is determined from the average population vector of
the neuronal activity over the cycle time
is determined from the average population vector of
the neuronal activity over the cycle time 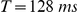 as
follows:
as
follows:
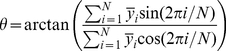 |
(6) |
where
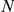 is the number of Action Cells and
is the number of Action Cells and
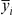 is the average neuronal activity of the Action Cell
is the average neuronal activity of the Action Cell
 over the cycle calculated as:
over the cycle calculated as:
| (7) |
with 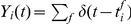 being the
entire postsynaptic spike train of the Action Cell
being the
entire postsynaptic spike train of the Action Cell
 fired at times
fired at times 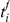 .
.
Given the decision angle, a reward is determined by the following reward function:
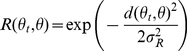 |
(8) |
where
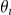 denotes the target angle,
denotes the target angle,
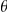 is the decision angle of the Action Cell population
as determined by Equation 6,
is the decision angle of the Action Cell population
as determined by Equation 6, 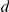 is the
distance function defined in Equation 2 and
is the
distance function defined in Equation 2 and 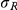 is the
standard deviation of the reward function with a default value of
is the
standard deviation of the reward function with a default value of
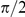 (unless specified otherwise in the text).
(unless specified otherwise in the text).
Learning Rule
Learning takes place by modifying the feedforward connections
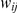 between place and Action Cells at the end of each
trial according to the following policy gradient learning rule [10]–[12]:
between place and Action Cells at the end of each
trial according to the following policy gradient learning rule [10]–[12]:
| (9) |
where  is the
learning rate,
is the
learning rate, 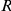 the reward
calculated from Equation 8,
the reward
calculated from Equation 8, 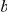 a reward
baseline and
a reward
baseline and 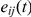 the
eligibility trace [44] defined below. The variable
the
eligibility trace [44] defined below. The variable
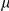 is a uniformly distributed random noise sample from
the interval
is a uniformly distributed random noise sample from
the interval 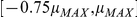 . The reward
baseline takes the value of
. The reward
baseline takes the value of 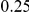 and its
presence speeds up learning for both systems.
and its
presence speeds up learning for both systems.
The eligibility trace 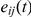 is a memory of
the previous activity of the synapse, and is calculated
as:
is a memory of
the previous activity of the synapse, and is calculated
as:
| (10) |
where
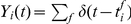 is the spike train of the postsynaptic neuron
is the spike train of the postsynaptic neuron
 ,
, 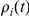 the
instantaneous probability of firing and
the
instantaneous probability of firing and 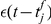 the time
course of the excitatory (or inhibitory) postsynaptic potential (EPSP or
IPSP) caused by the
the time
course of the excitatory (or inhibitory) postsynaptic potential (EPSP or
IPSP) caused by the  firing of
neuron
firing of
neuron 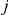 , which is modelled as:
, which is modelled as:
| (11) |
with 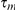 being the
membrane time constant of
being the
membrane time constant of  and
and
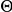 the step (Heaviside) function.
the step (Heaviside) function.
We would like to emphasise that the rule presented here can be mapped to a classical Reinforcement Learning rule in discrete time, namely the Associative Reward Inaction (ARI) [13], [16], [51], see also [12].
Analysis of System Performance
In the following section, we discuss the system performance with and without lateral connections under four different scenarios focusing on the effects of (i) varying the lateral connection strength, (ii) varying the shape of the reward function, (iii) varying the overlap of the Place Cell receptive fields and (iv) adding uniform noise onto the synaptic updates.
Performance and Lateral Connections
Our simulations show that lateral connections have a strong effect on the
performance of the animat. In Figure 2 we show a raster plot of the Action Cell spikes for
three different cases. Panel A corresponds to a system without lateral
connections (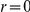 ), panel B to a
system with weak lateral connections (
), panel B to a
system with weak lateral connections (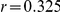 ) and panel C
for a system with strong lateral connections
(
) and panel C
for a system with strong lateral connections
(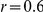 ). The strength
). The strength 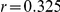 of the lateral
connections was chosen as small as possible under the constraint that the
dynamics still exhibit a pronounced activity bump (assessed visually). The
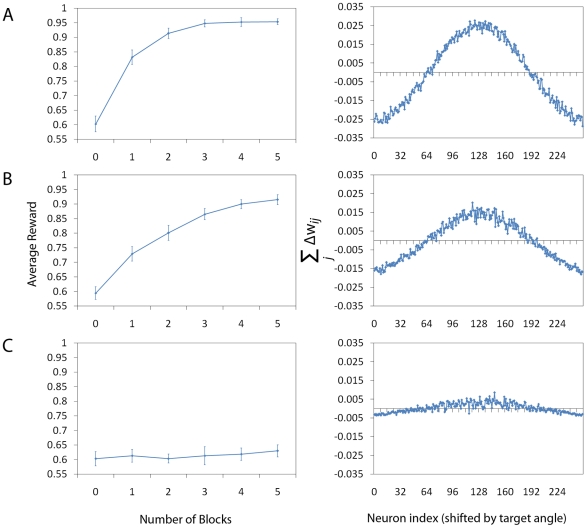
corresponding performance for these three cases is shown in Figure 3. Panels A–C
(left column) show the average performance ( = average
reward obtained) over
of the lateral
connections was chosen as small as possible under the constraint that the
dynamics still exhibit a pronounced activity bump (assessed visually). The
corresponding performance for these three cases is shown in Figure 3. Panels A–C
(left column) show the average performance ( = average
reward obtained) over 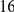 animats as a
function of the number of training blocks. Each block consists of
animats as a
function of the number of training blocks. Each block consists of
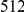 learning cycles. During these blocks, the weights
are updated at the end of each trial according to the learning rule of
Equation 9. The average reward is calculated independently from the blocks
of learning trials. Following a block of learning trials, the animat
performs
learning cycles. During these blocks, the weights
are updated at the end of each trial according to the learning rule of
Equation 9. The average reward is calculated independently from the blocks
of learning trials. Following a block of learning trials, the animat
performs 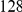 analysis trials with learning disabled, based on
which the performance of the system is evaluated (mean reward over a total
of 128x16 samples). The sole purpose of this procedure is to obtain an
accurate estimate of the performance without interference from learning.
Error bars show the standard deviation over the 16 independent animats.
Simulation parameters are reported in Table 1. Parameters for neurons are taken
from the literature, learning parameters (learning rate
analysis trials with learning disabled, based on
which the performance of the system is evaluated (mean reward over a total
of 128x16 samples). The sole purpose of this procedure is to obtain an
accurate estimate of the performance without interference from learning.
Error bars show the standard deviation over the 16 independent animats.
Simulation parameters are reported in Table 1. Parameters for neurons are taken
from the literature, learning parameters (learning rate
 , reward baseline
, reward baseline 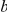 ) and overlap
of neighbouring receptive fields (
) and overlap
of neighbouring receptive fields (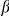 ) were jointly
optimised for each of the systems studied.
) were jointly
optimised for each of the systems studied.
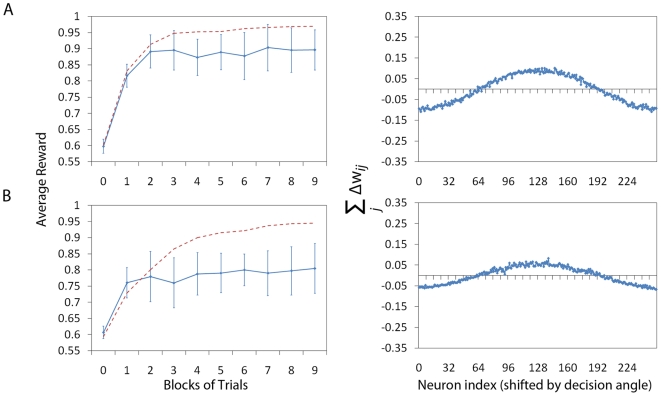
Figure 3. Analysis of System Performance.
Panels A–C (left column) show the average performance of 16
animats calculated in the following way. Every animat completes a
number of blocks of 512 trials (the number here varies from 0 to 5),
with weights being updated at the end of each trial. We term these
“blocks of learning trials”. In these figures, 0 blocks
of learning trials means that no learning has taken place. The
average reward is calculated independently from the blocks of
learning trials. Following a block of learning trials, the animat
performs of 128 independent (analysis) trials with learning being
disabled, based on which the performance of the system is evaluated
(mean reward over a total of 128x16 samples). The parameters for
systems A–C are the same as in the previous figure (i.e. A: no
lateral connections, B: lateral connections and C: very strong
lateral connections). We note that the system without lateral
connections achieves 70% of reward twice as fast as the
system with lateral connections. The system with strong lateral
connections completely fails to learn the task. We can obtain a
better understanding of the difference between the three systems by
plotting the gradient term for each case correspondingly (Panels
A–C, right column). We calculate the gradient numerically by
summing the value of the potential weight change (before learning
where the potential change is maximal)
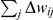 over
Place Cell index
over
Place Cell index 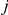 and by
shifting the index
and by
shifting the index  of the
Action Cell population so that the peak will always appear at the
middle of the graph. To achieve a smooth graph, we average over a
total of
of the
Action Cell population so that the peak will always appear at the
middle of the graph. To achieve a smooth graph, we average over a
total of 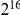 trials. We note that the gradient is larger when lateral connections
are absent.
trials. We note that the gradient is larger when lateral connections
are absent.
Table 1. Default model parameters used for producing simulation results.
| Parameter | Value | Description |
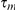
|
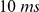
|
membrane time constant |
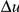
|
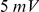
|
width of the threshold region |
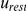
|
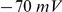
|
resting potential |
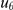
|
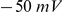
|
firing threshold |
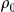
|
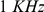
|
scaling factor of the firing rate |
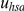
|
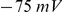
|
membrane potential after spike emission |

|
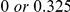
|
lateral connectivity scale |
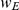
|

|
lateral connectivity excitation |
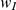
|
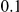
|
lateral connectivity inhibition |
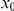
|
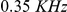
|
input activity factor |
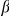
|
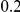
|
overlap of the receptive fields |
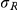
|
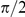
|
standard deviation of the reward function |

|
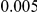
|
learning rate |
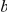
|
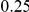
|
reward baseline |
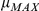
|
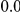
|
additive noise |
Simulation results shown in Figures 1–
7 use the above parameters
except where indicated otherwise. The value of
 is
either
is
either 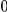 or
or
 depending on where lateral connections are present (the later
indicates that they are). The parameter
depending on where lateral connections are present (the later
indicates that they are). The parameter
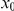 is
chosen produce an input of 180Hz. Parameters for the neuronal
model are taken from the literature. Other parameters are found
through parameter search.
is
chosen produce an input of 180Hz. Parameters for the neuronal
model are taken from the literature. Other parameters are found
through parameter search.
We note that the system without lateral connections achieves the level of
70% of the maximum reward twice as fast as the best of the systems
with lateral connections. Furthermore, the system with strong lateral
connections completely fails to learn the task. In order to obtain a better
understanding of the difference between the three systems, we plot the
“weight gradient” 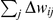 for each case
correspondingly (Figure
3, right column). We calculate this gradient numerically in the
following way. Before learning (i.e. all weights randomly initialised as
zero), we sum up the values of the potential weight changes over the index
for each case
correspondingly (Figure
3, right column). We calculate this gradient numerically in the
following way. Before learning (i.e. all weights randomly initialised as
zero), we sum up the values of the potential weight changes over the index
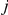 and subsequently shift the index
and subsequently shift the index
 of the Action Cell population by the respective
target angle (
of the Action Cell population by the respective
target angle (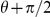 ) so that the
peak will always appear at the middle of the graph. To achieve a smooth
graph, we average over a total of
) so that the
peak will always appear at the middle of the graph. To achieve a smooth
graph, we average over a total of 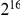 trials. We
note that the gradient and hence the information for learning the weights is
larger when lateral connections are absent. If lateral connections are
strong enough to systematically result in an activity bump, they can achieve
at best a speed almost half of the system without lateral connections. We
would like to emphasise that the learning rate was optimised for both
systems to achieve maximum performance. Increasing further the learning rate
for the MHC system would also increase the noise and result in a similar or
lower performance. This fact underlines that there is a smaller
signal-to-noise ratio in the gradient of the MHC system compared to the
system without MHC.
trials. We
note that the gradient and hence the information for learning the weights is
larger when lateral connections are absent. If lateral connections are
strong enough to systematically result in an activity bump, they can achieve
at best a speed almost half of the system without lateral connections. We
would like to emphasise that the learning rate was optimised for both
systems to achieve maximum performance. Increasing further the learning rate
for the MHC system would also increase the noise and result in a similar or
lower performance. This fact underlines that there is a smaller
signal-to-noise ratio in the gradient of the MHC system compared to the
system without MHC.
These results can be partially understood by taking into account that in systems with lateral connections, the activity bump and thus the decision settles into a location that is largely determined by the most active neurons over a short time interval at the beginning of the trial. With increasing strength of the lateral connections, this time interval becomes shorter. The neuron models considered here feature escape noise and therefore shorter time intervals result in higher relative noise levels, making systems with strong lateral connections prone to noise (i.e. activity that carries no information about the task). In Reinforcement Learning, performance is strongly affected by the Exploration/Exploitation trade-off, i.e. the percentage of choosing random actions in hope of discovering a “better way” to achieve the goal versus making choices based on the system's current knowledge. Under the conditions discussed here, we may obviously conclude that there is too much noise in systems with strong lateral MHC.
It is worth considering additional aspects that may cause degrading
performance in systems with strong lateral connections. The Place Cells have
overlapping receptive fields, meaning that one neuron participates in the
representation of different states of the system, namely those that are
close to its preferred direction. Here closeness is measured in terms of the
overlap parameter 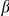 . This is a
feature of the network that allows information “diffusion”
between different learning states and speeds up learning, as simulations
(not presented here) show. However, a neuron that participates in
representing a state, say
. This is a
feature of the network that allows information “diffusion”
between different learning states and speeds up learning, as simulations
(not presented here) show. However, a neuron that participates in
representing a state, say 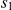 , can affect
the decision based on the weights it has learned during its participation to
another state
, can affect
the decision based on the weights it has learned during its participation to
another state 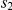 . We term this
effect “crosstalk”. This phenomenon is more likely to cancel out
when the decision of the network is based on the population vector of the
activity without lateral connections (corresponding to a linear operation)
rather than when a non-linear operation (MHC) is in place.
. We term this
effect “crosstalk”. This phenomenon is more likely to cancel out
when the decision of the network is based on the population vector of the
activity without lateral connections (corresponding to a linear operation)
rather than when a non-linear operation (MHC) is in place.
To collect evidence for this hypothesis, we perform three sets of
experiments. In the first one, we vary the shape of the reward function. By
making the reward function more sharp, we expect that synaptic weight
changes will affect a smaller number of neurons and therefore performance
may improve for a system with lateral connections. In the second one, we
explicitly increase the overlap of the response function of the Place Cell
receptive fields, ie. we increase 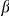 , expecting
that the system with lateral connections will perform worse. In the third
experiment, we add uniform additive noise with a positive bias to the
synaptic weight updates, with the intention of “mimicking” the
“crosstalk” effect. We expect that performance will deteriorate
for the systems with lateral connections more than that of systems without
lateral connections.
, expecting
that the system with lateral connections will perform worse. In the third
experiment, we add uniform additive noise with a positive bias to the
synaptic weight updates, with the intention of “mimicking” the
“crosstalk” effect. We expect that performance will deteriorate
for the systems with lateral connections more than that of systems without
lateral connections.
Shape of the Reward Function
We consider the effect of varying the reward function
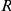 (Equation 8) by modifying the standard deviation of
the reward function
(Equation 8) by modifying the standard deviation of
the reward function 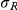 from
from
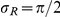 to
to 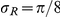 . Since our
reward is not normalised and in essence by changing
. Since our
reward is not normalised and in essence by changing
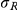 the total amount of reward changes, we introduce an
error function
the total amount of reward changes, we introduce an
error function 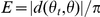 , a function of
the angle between the decision
, a function of
the angle between the decision 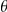 and the target
and the target
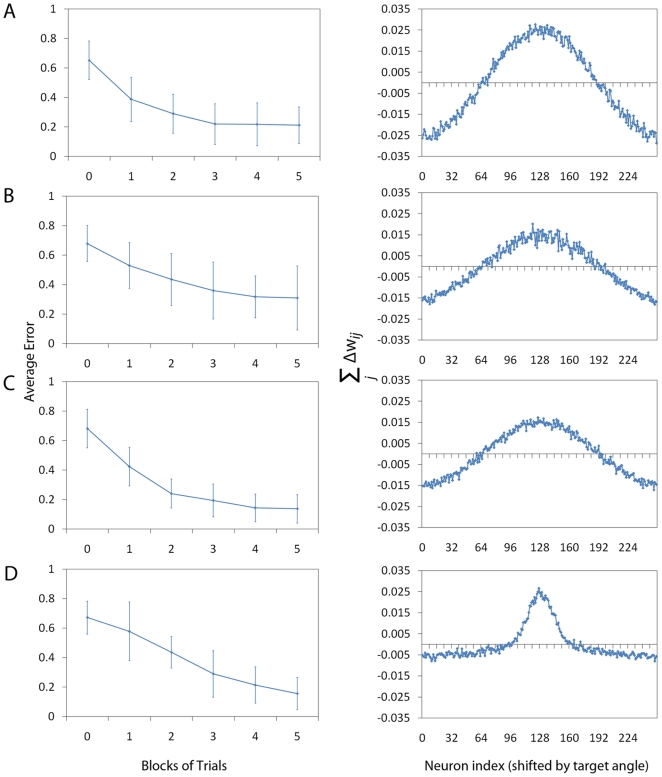
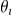 , that directly measures system performance. Figure 4 shows the effect
of the two different reward functions with respect to the learning
performance. Panels A and B show the results for configurations using the
“wide” Gaussian with parameters
, that directly measures system performance. Figure 4 shows the effect
of the two different reward functions with respect to the learning
performance. Panels A and B show the results for configurations using the
“wide” Gaussian with parameters 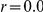 and
and
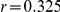 respectively. Panels C and D show the results for
configurations using the “narrow” Gaussian with parameters
respectively. Panels C and D show the results for
configurations using the “narrow” Gaussian with parameters
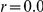 and
and 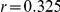 respectively.
To produce the average error graphs (left column) in the panels A–D,
we have averaged over 16 independent animats performing up to 5 blocks of
512 trials. Every point of the graph represents the average normalised error
of the system, which, similar to Figure 3, is calculated over a separate
block of 128 analysis trials (without updating the synaptic weights). Error
bars show the standard deviation over the 16 independent animats.
respectively.
To produce the average error graphs (left column) in the panels A–D,
we have averaged over 16 independent animats performing up to 5 blocks of
512 trials. Every point of the graph represents the average normalised error
of the system, which, similar to Figure 3, is calculated over a separate
block of 128 analysis trials (without updating the synaptic weights). Error
bars show the standard deviation over the 16 independent animats.
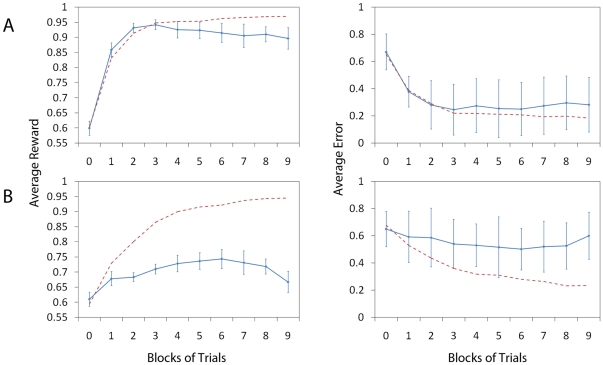
Figure 4. Reward Function Shape.
We investigate the effect of the reward function shape by changing it
from a “wide” Gaussian (Panels A and B,
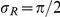 ) to a
“narrow” Gaussian (Panels C and D,
) to a
“narrow” Gaussian (Panels C and D,
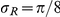 ). Here
we plot average error graphs as they provide a measurement that
allows us to compare systems with different reward functions. To
produce the average error graphs (panels A–D, left column), we
have averaged over 16 independent animats performing 5 blocks of 512
trials. Every point of the graph represents the average normalised
error of the system (i.e. the normalised absolute difference between
the target angle
). Here
we plot average error graphs as they provide a measurement that
allows us to compare systems with different reward functions. To
produce the average error graphs (panels A–D, left column), we
have averaged over 16 independent animats performing 5 blocks of 512
trials. Every point of the graph represents the average normalised
error of the system (i.e. the normalised absolute difference between
the target angle 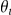 and
the decision angle
and
the decision angle 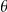 )
which, similar to Figure 3, is calculated over a separate block of 128
analysis trials (without updating the synaptic weights). Error bars
show the standard deviation over the 16 independent animats. We
observe that after 5 blocks of trials, the system corresponding to
the “wide” Gaussian reward function without lateral
connections shown in (A) has reached a lower final error than that
of the system with lateral connections (B). When a narrow Gaussian
reward is instead used, the system with lateral connections (D)
recovers this difference in final error with respect to the system
without lateral connections (C). As with the previous plot we show
(right column panels) the gradient of the system configurations
A–D by plotting the sum of the potential weight change
(calculated in the same way as previously). For clarity, plots A and
B are repeated from Figure 3. We note that when a narrow Gaussian reward is
used the system with lateral connections (D) learns over a very
narrow band close to the target angle. In contrast the profile of
the system without lateral connections (C) remains consistent with
that of the wide reward, learning across a broader range of the
population.
)
which, similar to Figure 3, is calculated over a separate block of 128
analysis trials (without updating the synaptic weights). Error bars
show the standard deviation over the 16 independent animats. We
observe that after 5 blocks of trials, the system corresponding to
the “wide” Gaussian reward function without lateral
connections shown in (A) has reached a lower final error than that
of the system with lateral connections (B). When a narrow Gaussian
reward is instead used, the system with lateral connections (D)
recovers this difference in final error with respect to the system
without lateral connections (C). As with the previous plot we show
(right column panels) the gradient of the system configurations
A–D by plotting the sum of the potential weight change
(calculated in the same way as previously). For clarity, plots A and
B are repeated from Figure 3. We note that when a narrow Gaussian reward is
used the system with lateral connections (D) learns over a very
narrow band close to the target angle. In contrast the profile of
the system without lateral connections (C) remains consistent with
that of the wide reward, learning across a broader range of the
population.
We observe that, after 5 blocks of trials, the system without lateral
connections (with the “wide” Gaussian reward function) shown in
(A) has reached a lower (final) error than that of the system with lateral
connections (B). These results are repeated from Figure 3 with a different error measure.
With a narrow Gaussian reward function, the system with lateral connections
(D) recovers this difference in final error with respect to the system
without lateral connections (C). As in Figure 3, we show (right column) the
gradient 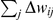 for the system configurations A–D. In summary,
systems with strong MHC learn better with more narrow reward functions,
whereas systems without MHC achieve the same performance. This is in
agreement with our “crosstalk” hypothesis.
for the system configurations A–D. In summary,
systems with strong MHC learn better with more narrow reward functions,
whereas systems without MHC achieve the same performance. This is in
agreement with our “crosstalk” hypothesis.
Overlapping Receptive Fields
We further investigate how increasing the overlap of the Place Cell receptive
fields to 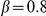 affects the simulations. A higher degree of overlap
introduces ambiguity about the position, and a lower performance is
anticipated due to the decreased signal to noise ratio in general but
nevertheless we expect that this is more observable in the system with
lateral connections than the system without.
affects the simulations. A higher degree of overlap
introduces ambiguity about the position, and a lower performance is
anticipated due to the decreased signal to noise ratio in general but
nevertheless we expect that this is more observable in the system with
lateral connections than the system without.
Figure 5 shows the
simulation results. In panel Panel A (left column) we see the average reward
for the system without lateral connections versus the blocks of learning
trials and in panel B (left column) the reward for the system with lateral
connections, again versus the blocks of learning trials. These plots are
calculated in exactly the same way as in Figure 3. The red dashed lines shows the
corresponding graphs from Figure 3 over 9 blocks of trials for a direct comparison. We can
observe that the system without lateral connections is indeed less affected
by the increase of the 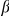 parameter than
the system with lateral connections. We also show the gradient (right column
panels) similar to Figures
3 and 4, by
plotting the sum of the potential weight change. Reduced amplitude of the
gradient corresponds to reduced performance.
parameter than
the system with lateral connections. We also show the gradient (right column
panels) similar to Figures
3 and 4, by
plotting the sum of the potential weight change. Reduced amplitude of the
gradient corresponds to reduced performance.
Figure 5. Overlapping receptive fields.
Figure shows the effect of increasing the overlap of the receptive
fields (to 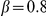 ) of
the Place Cells. Panel A shows a configuration without lateral
connections and panel B shows a configuration with lateral
connections (and corresponds to systems A and B from Figures 3 and
4). The
plots of the average reward (left column, solid line) are calculated
in exactly the same way as in Figure 3 shown over 9 blocks of
512 trials, rather than 5. The red dashed line shows the values from
Figure 3
over 9 blocks for direct comparison. We can observe that the system
without lateral connections is less affected by the increase of the
) of
the Place Cells. Panel A shows a configuration without lateral
connections and panel B shows a configuration with lateral
connections (and corresponds to systems A and B from Figures 3 and
4). The
plots of the average reward (left column, solid line) are calculated
in exactly the same way as in Figure 3 shown over 9 blocks of
512 trials, rather than 5. The red dashed line shows the values from
Figure 3
over 9 blocks for direct comparison. We can observe that the system
without lateral connections is less affected by the increase of the
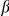 parameter than the system with lateral connections. The plots of the
gradient (right column) are produced as in Figures 3 and 4, by plotting the
sum of the potential weight change (calculated in the same way as in
previous figures).
parameter than the system with lateral connections. The plots of the
gradient (right column) are produced as in Figures 3 and 4, by plotting the
sum of the potential weight change (calculated in the same way as in
previous figures).
Additive Synaptic Noise
Finally, we heuristically mimic the effect of “crosstalk” on the
synaptic connections by adding noise with a positive bias to the weight
update rule described by equation 9. The non-zero bias is motivated by the
fact that the shape of the gradient indicates that learning takes place
mostly via positive synaptic updates. To find the appropriate parameter
regime for the noise, we have performed a parameter search over the variable
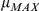 Figure 6 shows the
simulation results for
Figure 6 shows the
simulation results for 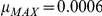 . Panels A and
B show the network performance without and with lateral connections (as in
previous figures) respectively. The plots of average reward (left column)
are calculated as in Figures
3 and 5. The
red dashed line shows the values without noise from Figure 3 (systems A and B correspond) for
direct comparison. The plots of average error (right column) are calculated
as in Figure 4. The red
dashed line shows the values without noise from Figure 4 (again, systems A and B
correspondingly). As expected, we observe that both the average reward and
average error performance measures show that the system without lateral
connections is more robust to noise added directly to the synaptic weight
updates.
. Panels A and
B show the network performance without and with lateral connections (as in
previous figures) respectively. The plots of average reward (left column)
are calculated as in Figures
3 and 5. The
red dashed line shows the values without noise from Figure 3 (systems A and B correspond) for
direct comparison. The plots of average error (right column) are calculated
as in Figure 4. The red
dashed line shows the values without noise from Figure 4 (again, systems A and B
correspondingly). As expected, we observe that both the average reward and
average error performance measures show that the system without lateral
connections is more robust to noise added directly to the synaptic weight
updates.
Figure 6. Additive Synaptic Noise.
Figure shows the effect of additive uniformly distributed synaptic
noise on the network performance by setting
 (see
Equation 9). Panels A and B show the network performance without and
with lateral connections (as in previous figures) respectively. The
plots of average reward (left column, solid line) are calculated as
in Figures 3 and
5 showing
learning curves over 9 blocks of 512 trials. The red dashed line
shows the values without noise from Figure 3 (systems A and B
correspond) for direct comparison. Similarly, the plots of average
error (right column, solid line) are calculated as in Figure 4. The red
dashed line shows the values without noise from Figure 4 (again, systems A and B
respectively). We can observe that both the average reward and
average error performance measures show that the system without
lateral connections is far more robust to noise applied directly to
the synaptic weight.
(see
Equation 9). Panels A and B show the network performance without and
with lateral connections (as in previous figures) respectively. The
plots of average reward (left column, solid line) are calculated as
in Figures 3 and
5 showing
learning curves over 9 blocks of 512 trials. The red dashed line
shows the values without noise from Figure 3 (systems A and B
correspond) for direct comparison. Similarly, the plots of average
error (right column, solid line) are calculated as in Figure 4. The red
dashed line shows the values without noise from Figure 4 (again, systems A and B
respectively). We can observe that both the average reward and
average error performance measures show that the system without
lateral connections is far more robust to noise applied directly to
the synaptic weight.
We further analyse the difference between the performance of the two systems
in Figure 7 (A: no
lateral connections, B: with lateral connections) in the following way. We
plot the eligibility trace for each case with and without an additive noise
term 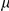 . This corresponds to
. This corresponds to 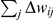 from Equation
9 for
from Equation
9 for 
 and
and 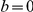 and allows us
to look at the gradient information without taking into account the shape of
the reward function. We calculate the eligibility trace
(
and allows us
to look at the gradient information without taking into account the shape of
the reward function. We calculate the eligibility trace
(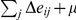 ) numerically by summing the value of the potential
eligibility trace (before learning where the potential change is maximal)
over the (input neurons) index
) numerically by summing the value of the potential
eligibility trace (before learning where the potential change is maximal)
over the (input neurons) index 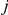 and by
shifting the index
and by
shifting the index  of the Action
Cell population so that the maximum will be at the middle of the graph.
Curves resulting from this procedure are particularly noisy when a small
number of samples is used. To smooth them out we calculate them over a total
of
of the Action
Cell population so that the maximum will be at the middle of the graph.
Curves resulting from this procedure are particularly noisy when a small
number of samples is used. To smooth them out we calculate them over a total
of  trials. The left column panels show the eligibility
trace without noise. The right column plots show the eligibility trace,
including noise (
trials. The left column panels show the eligibility
trace without noise. The right column plots show the eligibility trace,
including noise (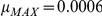 as in Figure 6). We note that
the eligibility trace of the system without lateral connections is
relatively unchanged by the effect of noise, where as the system with
lateral connections has an eligibility trace which is drastically reduced in
magnitude.
as in Figure 6). We note that
the eligibility trace of the system without lateral connections is
relatively unchanged by the effect of noise, where as the system with
lateral connections has an eligibility trace which is drastically reduced in
magnitude.
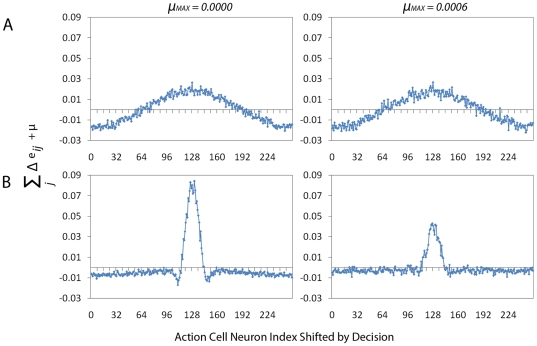
Figure 7. Noise Analysis.
To obtain a better understanding of the difference between the
performance of the two systems from Figure 6 (A: no lateral
connections, B: with lateral connections) we plotting the
eligibility trace for each case with and without an additive noise
term 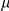 . This
corresponds to
. This
corresponds to 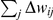 from
Equation 9 for
from
Equation 9 for 
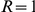 and
and 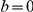 and
allows us to look at the gradient information without taking into
account the shape of reward. We calculate the eligibility trace
(
and
allows us to look at the gradient information without taking into
account the shape of reward. We calculate the eligibility trace
(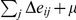 )
numerically by summing the value of the potential eligibility trace
(before learning, where the potential change is maximal) over Place
Cell index
)
numerically by summing the value of the potential eligibility trace
(before learning, where the potential change is maximal) over Place
Cell index 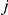 and by
shifting the index
and by
shifting the index  of the
Action Cell population so that the maximum will be at the middle of
the graph. To obtain smooth curves, we calculate this value over a
total of
of the
Action Cell population so that the maximum will be at the middle of
the graph. To obtain smooth curves, we calculate this value over a
total of 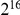 trials. The left column panels show the eligibility trace without
noise. The right column panels show the the eligibility trace,
including noise (
trials. The left column panels show the eligibility trace without
noise. The right column panels show the the eligibility trace,
including noise (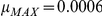 as in
Figure 6).
In both cases the same random seeds are used when generating spikes
and target angles to ensure both systems are presented with the same
information. The resulting right column figures therefore give an
indication of the effect of the noise. We note that the eligibility
trace of system without lateral connections is relatively unchanged
by the effect of noise, where as the system with lateral connections
results in an eligibility trace drastically reduced in
magnitude.
as in
Figure 6).
In both cases the same random seeds are used when generating spikes
and target angles to ensure both systems are presented with the same
information. The resulting right column figures therefore give an
indication of the effect of the noise. We note that the eligibility
trace of system without lateral connections is relatively unchanged
by the effect of noise, where as the system with lateral connections
results in an eligibility trace drastically reduced in
magnitude.
Discussion
Here, we presented a study of two spiking networks, one with lateral connections
among the neurons of the output layer (Mexican Hat-type connectivity, MHC) and one
without lateral connections. The two networks are learning a simple association
learning task, which corresponds to a simplified yet self contained version of a
full navigation problem. We use GPU programming to perform exhaustive optimisation
of the simulation parameters and to produce a set of scenarios that investigate the
learning performances of the two systems under various conditions. We conclude the
following. In systems that feature lateral MHC, which introduces a non-linear
(“non-democratic”) decision making process, the first few spikes
occurring in each trial can significantly influence the activity bump formation and
therefore the decision, see also [7]. This effect manifests itself in a low signal-to-noise
ratio in the learning rule compared to systems without lateral MHC, which was
revealed by investigating the weight “gradient”
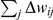 . As a result, more samples are required for MHC systems to
reliably extract the values for the synaptic weights that correspond to the
“correct” input-output relationship. In the extreme case of strong
lateral connections, the activity bump formation of the recurrent network (the
“decision”) is strongly driven by noise rather than the feed forward
input and thus no reasonable weights are learned. If lateral synaptic weights are
present, and strong enough to result in bump formation, the system can at best reach
half of the learning speed of a network without MHC.
. As a result, more samples are required for MHC systems to
reliably extract the values for the synaptic weights that correspond to the
“correct” input-output relationship. In the extreme case of strong
lateral connections, the activity bump formation of the recurrent network (the
“decision”) is strongly driven by noise rather than the feed forward
input and thus no reasonable weights are learned. If lateral synaptic weights are
present, and strong enough to result in bump formation, the system can at best reach
half of the learning speed of a network without MHC.
Furthermore, we formulated the following additional hypothesis that may partially explain the reduced learning performance in MHC systems. Our simulation results hint that systems with MHC are prone to “crosstalk” between learning trials when the state of the agent is coded with the help of neurons with opverlapping receptive fields. We borrow the term “crosstalk” from electronics to describe that a neuron participates in different “circuits” or sub-networks (consisting of connections from active input neurons to output neurons). Learning in one sub-network may lead to synaptic changes that could affect another sub-network. We identify this behaviour by performing three additional simulations:
Increasing overlap of the receptive fields (state representation),
Widening of the rewarded function and
Adding uniform noise with a positive bias to the weight vector.
In all these cases, learning is impaired for the “non-democratic”
decision making in MHC networks. This can be understood in the following way. Neuron
 (Place Cell) that participates in the representation of
state
(Place Cell) that participates in the representation of
state 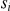 may have a weak connection to the neurons (Action Cells)
participating to the “correct” decision
may have a weak connection to the neurons (Action Cells)
participating to the “correct” decision 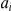 . However, it may have
a strong connection to neurons encoding a different action
. However, it may have
a strong connection to neurons encoding a different action
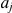 acquired during its participation to representing
acquired during its participation to representing
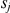 . As a consequence, when being active again during
. As a consequence, when being active again during
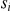 , it could bias the decision to a wrong action. This
“crosstalk” is of course also present in the system without lateral MHC.
There, however, crosstalk effects tend to cancel out due to the linear population
vector readout and the symmetry of the task. This is in contrast to MHC systems
where the crosstalk effects do not cancel out in general due to the non-linear
dynamics of the activity bump formation. This results in further reduction of the
signal-to-noise ratio of the learning rule for MHC systems, and as a consequence
learning slows down and converges to lower performances. Hence
“democratic” decision making is more robust than the
“non-democratic” alternative.
, it could bias the decision to a wrong action. This
“crosstalk” is of course also present in the system without lateral MHC.
There, however, crosstalk effects tend to cancel out due to the linear population
vector readout and the symmetry of the task. This is in contrast to MHC systems
where the crosstalk effects do not cancel out in general due to the non-linear
dynamics of the activity bump formation. This results in further reduction of the
signal-to-noise ratio of the learning rule for MHC systems, and as a consequence
learning slows down and converges to lower performances. Hence
“democratic” decision making is more robust than the
“non-democratic” alternative.
We would like to emphasise that the presence of noise in neural systems is not necessarily a curse. Though in our study noise seems to impair a network with MHC, exploration itself is an essential part of Reinforcement Learning. Moreover, noise in neural systems might be beneficial as, for instance, it prevents synchronisation and allows for fast and accurate propagation of signals, see [52]–[54].
As a final note, the study here would have been very difficult using a low cost desktop computer, without resorting to GPU programming. Not only parameter search itself can be very time consuming but producing statistically accurate results for systems with multiple sources of noise (poisson neurons, escape noise, additive noise) can be very challenging. To achieve smooth graphs, averages were often calculated over 2,048 independent trials. This was possible due to exploiting the parallelism of the GPU architecture by running multiple instances of the model in parallel. We hope that our Methods will be applicable to problems of similar nature, whenever numerous samples are required to guarantee the validity of the results.
Methods
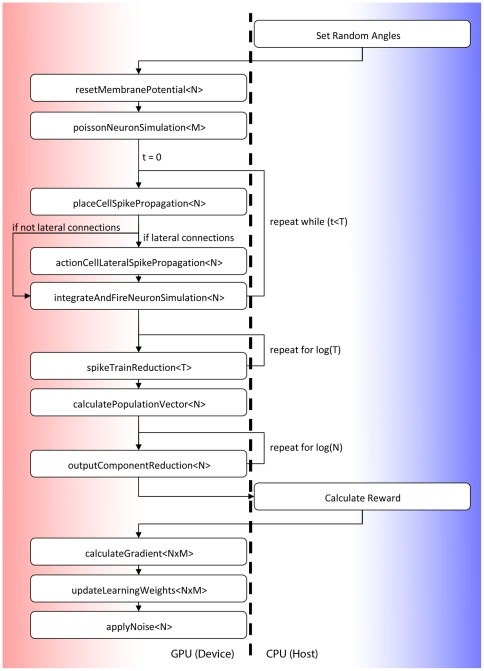
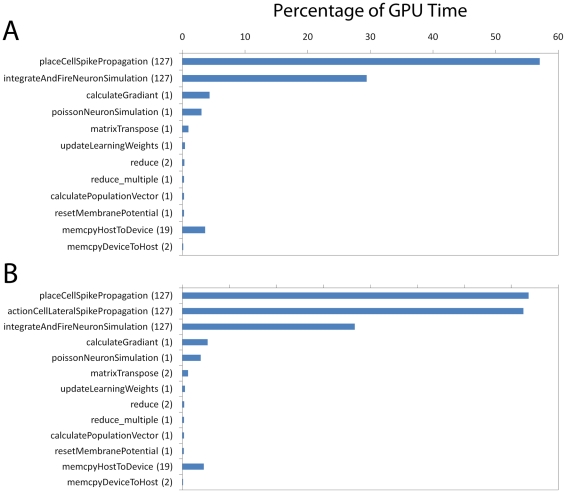
This section describes the GPU implementation of the model presented in Results and is divided in three parts. The first part introduces the CUDA programming Application Programming Interface (API) and hardware architecture. The second part describes our implementation and the third part evaluates the performance of our GPU implementation and suggests techniques which will be used in the future to further improve simulation performance. A general introduction to GPU computing and CUDA can be found at [55].
An Introduction to the GPU and CUDA
We have chosen to implement our spiking neural network on the GPU using the CUDA programming API which is described in detail in the CUDA Programming Guide [56]. The key concept within this API is the use of a special purpose function (a “kernel” function) identifying code to be run on the GPU device and which describes the behaviour of a large number of independent but functionally equivalent units of computational execution. Each independent unit of execution, more commonly referred to as a thread, can be assumed to operate simultaneously (i.e. in parallel) but on a different stream of data. This differs from traditional CPU parallelism in that the parallelism is formed through the distribution of the streams of data across processors, referred to as data parallelism, rather than of separate tasks, which are described by different functions, known as task parallelism. In Computational Neuroscience a simple conceptual example is the following. A non-recurrent population of similar neurons can be simulated using the data parallel thread paradigm as each individual neuron is described by the same functional behaviour (i.e. the kernel function) but operates in parallel using its own local stream of information which indicate, for example, the neurons membrane potential, synaptic weights, etc.
At a hardware level the CUDA architecture consists of a varying number of multiprocessors each with access to dedicated Dynamic Random Access Memory (DRAM). The DRAM is equivalent but independent from traditional memory accessed by the CPU and therefore information on the CPU (host) must be transferred to the GPU (device) memory before any execution of a kernel can take place (and vice versa once GPU execution has completed). Each multiprocessor contains an array of scalar processors, responsible for execution of the individual threads. A scalar processor is the simplest form of a processor that processes one data point at a time. Large groups of threads are split between physical multiprocessors by arranging them into smaller groups which are called thread blocks. For the sake of simplicity one can assume a simple mapping between each scalar processor and individual threads. For a more factual explanation of the reality of technical aspects such how threads are broken down into smaller executional units and how threads are interleaved on a single processors the reader is directed towards the CUDA programming Guide [56] or the book CUDA by Example [55].
Perhaps the most powerful feature of the CUDA architecture is the availability of
a small amount of user configurable shared memory cache, which is an area of
memory available on each multiprocessor considerably faster to access than main
memory, that allows simple communication between threads within the same group.
Considering the simple conceptual neuron example presented above it is not
immediately clear how this can be of any benefit. To illustrate the benefits of
the memory cache consider a matrix multiplication example where each thread is
responsible for computing an element 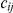 of the Matrix C
which is the product of two matrices A and B. Naively each thread may compute
of the Matrix C
which is the product of two matrices A and B. Naively each thread may compute
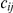 by considering the dot product of row
by considering the dot product of row
 and column
and column 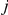 , an operation
which requires each thread to read both an entire column and row from matrices A
and B respectively. Alternatively by using the memory cache intelligently, the
total number of memory reads from the two matrices can be drastically reduced
(and performance increased substantially) by allowing each thread within a group
to calculate a single product. Each of these single products can be stored
within the cache and then used by the other threads in calculating the element
, an operation
which requires each thread to read both an entire column and row from matrices A
and B respectively. Alternatively by using the memory cache intelligently, the
total number of memory reads from the two matrices can be drastically reduced
(and performance increased substantially) by allowing each thread within a group
to calculate a single product. Each of these single products can be stored
within the cache and then used by the other threads in calculating the element
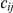 of C. The example assumes a situation where a single
block of threads is small enough to hold the single element products without
exceeding the size of the memory cache. More generally, it is advisable to
maximise the ratio of computational arithmetic to memory access, commonly
referred to as arithmetic intensity, by maximising usage of the user
configurable cache (or other similar caches which are not discussed within this
paper) which will ensure simulations attain maximum performance.
of C. The example assumes a situation where a single
block of threads is small enough to hold the single element products without
exceeding the size of the memory cache. More generally, it is advisable to
maximise the ratio of computational arithmetic to memory access, commonly
referred to as arithmetic intensity, by maximising usage of the user
configurable cache (or other similar caches which are not discussed within this
paper) which will ensure simulations attain maximum performance.
GPU programming in Neuroscience
Prior to our own work there has already been some interest in performing simulations of neuron populations on high performance architectures including GPUs. Simulations of artificial neural networks in discrete time [57], [58] present the most simplistic case where large matrix multiplication operations, known to be very efficient on the GPU, bear the brunt of the computational load. With respect to simulating more biologically plausible neuron systems operating in continuous time and where dense matrix multiplications can not be used, a notable GPU implementation is that of Bernhard and Keriven [59] which employs the technique (prior to modern CUDA and OpenCL libraries) of mapping an algorithm to graphics primitives in order to utilise GPUs. A multi-purpose spiking neural-network simulator is implemented, using a limited neighbourhood of connections between local neurons to minimise communication overhead. The Brian simulation package [60], [61] not only provides a simple syntax for specifying systems of spiking neurons within a Python Application Programming Interface (API) but also demonstrates GPU acceleration for various aspects of the simulation processes. The first use of CUDA was in the context of accelerating the automatic fitting of neuron models to electro-physiological recordings [62]. More recently [63] the same authors have turned their attention to GPU accelerated simulations of neuron dynamics, performing simulations of a number of spiking neuron models on GPUs. However, the simulation of propagation and back-propagation of spikes is not implemented on the GPU but instead it remains on the Central Processing Unit (CPU) due to the lack of inherent parallelism. An alternative configurable simulation environment for simulating spiking neurons on the GPU is proposed in [64]. Moreover, Bhuiyan et al. [65] have demonstrated the implementation of the Hodgkin Huxley and Izhikevich models of neurons on a number of parallel architectures including multi-core CPUs, the Cell Broadband Engine and the GPU. In their work, the GPU is used to perform the simulation of a single layer of neurons, whereas the simulation of the second layer of neurons and processing of spike data takes place on the host (after the data has been transferred from the GPU device). This work shows that the GPU is able to perform considerably well for the Hodgkin Huxley model, with a speed-up of over 100 times for 5.8 million neurons. This is attributed to the ratio of arithmetic work load over data transfer (also known as arithmetic intensity) which is considerably greater for the Hodgkin Huxley model than for the Izhikevich's model, for which the speed-up (only being 9.5) does not amortize the cost of communication between neurons. Aside from simulations of neuron systems using commodity (or consumer hardware), several research projects aim to perform large scale simulations of biological neuron systems using large computer clusters. The Swiss institution EPFL are currently developing highly accurate sub-neuron level simulations [66] and the IBM Almaden Research Center has simulated systems of sizes equivalent to that of the cortical system of a cat [67], both using the IBM BlueGene/L supercomputing architecture. Additionally, the Biologically Inspired Massively Parallel Architecture (BIMPA) project takes a completely new approach to brain simulation choosing to design a highly interconnected low power hardware architecture inspired by neuron interconnectivity [68]. Another similar attempt, the Fast Analog Computing with Emergent Transient States (FACETS) project resorted to dedicated analogue VLSI hardware [69]–[71] to achieve high simulation speeds and developed PyNN [72]–[77], a Python-based simulator-independent language for building neuronal network models.
Implementing our Spiking Neuron Model in CUDA
In our implementation, we discretize the model's equations using Euler's method. Conceptually the various stages of a single trial of the learning are broken down into small functional units which map directly to CUDA kernels. Figure 8 shows these various kernel functions (running on the GPU device) as well as the CPU host functions which are described individually below in more detail.
Figure 8. Simulation Flowchart.
Figure shows the simulation process of our spiking neural network model.
Steps shown on the left are broken down into CUDA kernels where the
figure in  brackets
brackets represents
the total number of threads which are invoked for each kernel (for
simplification this assumes only a single independent trial). The value
N represents the number of Action Cell neurons (256), the value M
represents the number of Place Cell neurons (256) and the value T
represents the total number of number of discrete time steps, i.e.
represents
the total number of threads which are invoked for each kernel (for
simplification this assumes only a single independent trial). The value
N represents the number of Action Cell neurons (256), the value M
represents the number of Place Cell neurons (256) and the value T
represents the total number of number of discrete time steps, i.e.
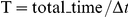 (which is
(which is
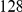 when
when
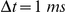 ). Steps
shown on the right indicate calculations performed on the Host CPU.
). Steps
shown on the right indicate calculations performed on the Host CPU.
While the figure refers to a simple case where only a single trial is considered, in reality we are able to perform many independent trials at once. Each of these independent trials may use a different parameter configuration or the same configuration. In addition to the main simulation loop, additional host side code is used to allocate all GPU memory in advance and seed a number of independent streams of pseudo random parallel numbers [78] which are used in spike generation and noise application. Each of the kernels described below uses a common technique called memory coalescing which describes the processes of reading sequential consecutive (in each thread) values from memory in a way which allows fewer large memory requests to be issued, improving performance.
Set Random Initial Angles
Preceding the brunt of the GPU simulation the CPU host calculates a random unique initial animat location (angle) for each trial to be performed. This is then transferred to the GPU using a CPU host to GPU device memory copy. As the number of possible initial locations is relatively small, it does not make sense to perform this operation on the GPU due to overheads associated with calling a CUDA kernel function.
Reset Membrane Potential Kernel
This CUDA kernel is responsible only for resetting the block of GPU memory
allocated to hold the N Action Cell membrane potentials from the previous
learn step's final value to  .
.
Poisson Neuron Simulation Kernel
This CUDA kernel is launched with M total threads each of which calculates
the firing rate frequency (given in Equation 1) for each of the M Place
Cells. This value is then compared to T GPU generated random numbers, where
T is the number of discrete steps in the total time period (i.e.
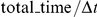 ), to output T total spike values of 0 (not fired) or
1 (fired). Conceptually it would have been possible to launch M*T
independent threads to perform this operation however the overhead of
recalculating the firing rate frequency for each thread is greater than the
overhead of performing a loop over T.
), to output T total spike values of 0 (not fired) or
1 (fired). Conceptually it would have been possible to launch M*T
independent threads to perform this operation however the overhead of
recalculating the firing rate frequency for each thread is greater than the
overhead of performing a loop over T.
Place Cell Spike Propagation Kernel
This CUDA kernel represents the first stage of the simulation loop over time
T. For each time step the kernel is launched and performs a dense matrix
vector multiplication for the Place Cell inputs at time
 and the corresponding synaptic strengths for each
Place Cell to Action Cell combination. Our implementation of the matrix
vector multiplication is based upon the technique described by [79] and uses
shared memory to cache the input spikes and an optimisation called loop
unrolling (see [56] or [55]) to perform a parallel
reduction to reduce instruction overhead.
and the corresponding synaptic strengths for each
Place Cell to Action Cell combination. Our implementation of the matrix
vector multiplication is based upon the technique described by [79] and uses
shared memory to cache the input spikes and an optimisation called loop
unrolling (see [56] or [55]) to perform a parallel
reduction to reduce instruction overhead.
Action Cell Lateral Spike Propagation Kernel
As with the “placeCellSpikePropagation” kernel, this CUDA kernel
performs a dense matrix vector multiplication for the Action Cell output
spikes from the previous time step ( ) and the
corresponding lateral cell synaptic connection weights.
) and the
corresponding lateral cell synaptic connection weights.
Integrate and Fire Neuron Simulation Kernel
This CUDA kernel launches a thread for each of the N Action Cells, each of
which updates and saves to global memory the membrane potential using the
spiking activity contributions of the Place Cell spike propagation (and the
Action Cell lateral spike propagations if the system uses lateral
connections). Following this, the kernel computes the instantaneous
probability of firing (which is output to global memory) and then using a
randomly generated number outputs a spiking value at the given discrete time
step  . For neurons which produce a spike emission, a
refractory period is applied by resetting the membrane potential to the
value
. For neurons which produce a spike emission, a
refractory period is applied by resetting the membrane potential to the
value 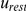 . Figure
9 shows our actual CUDA kernel code for performing this stage of
the simulation.
. Figure
9 shows our actual CUDA kernel code for performing this stage of
the simulation.
Figure 9. Spiking Simulation Kernel.
This figure shows the CUDA kernel used to perform the update of a spiking Action Cell neuron. Conceptually the kernel is relatively simple, using linear algebra style computation to update the neurons membrane potential (d_u_out) using the previous potential (d_u). The kernel also saves to the GPU Device memory the probability of firing (d_YProb) and the actual spike contribution (d_Y) of the neuron without requiring any localised caching of data. The variable index is calculated using a thread (tx) and block of thread identifiers (blockIdx.x) and represents the neuron index position within a large list of all neurons being simulated by the kernel. The value blockIdx.y indicates the independent trial number for each neuron this used to calculate the offset variables of N_offset and NT_offset which are used to ensure unique values for each neuron in each independent trial are accessed. The variable configuration_offset is similarly used to represent an index in which to look up one of the independent parameter configuration values. The corresponding function pow2mod uses bit shift operations to perform an efficient integer modulus operation where the divisor is a power of 2. The kernel function arguments are all prefixed with “d_” to indicate memory on the GPU device rather than the GPU host. The argument “seeds” is also an area of memory on the GPU device which is used to hold seeds for the parallel random number generation.
Spike Train Reduction Kernel
In order to calculate the population vector of our Action Cells we consider
the average firing rate over the total time period of
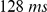 . To calculate this quantity in parallel on the GPU
we sum the number of spikes of each neuron over the total number of discrete
time steps T (i.e.
. To calculate this quantity in parallel on the GPU
we sum the number of spikes of each neuron over the total number of discrete
time steps T (i.e. 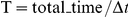 ) by performing
a parallel reduction of values over
) by performing
a parallel reduction of values over  steps. We use
the parallel reduction technique described by [80] which employs a
number of advanced optimisation techniques to obtain maximum performance.
Before this kernel operates we also perform a matrix transpose of the spike
train information Y to ensure that the reduction step is able to perform
coalesced memory reading. The additional computation proves more efficient
than performing the reduction using an uncoalesced memory access
pattern.
steps. We use
the parallel reduction technique described by [80] which employs a
number of advanced optimisation techniques to obtain maximum performance.
Before this kernel operates we also perform a matrix transpose of the spike
train information Y to ensure that the reduction step is able to perform
coalesced memory reading. The additional computation proves more efficient
than performing the reduction using an uncoalesced memory access
pattern.
Calculate Population Vector Kernel
This CUDA kernel calculates the output components of the population vector.
That is the individual terms 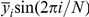 and
and
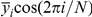 for each Action Cell
for each Action Cell  from Equation
6.
from Equation
6.
Output Component Reduction Kernel
The population vector is calculated by performing two parallel reduction
operations on the output components in order to reduce them to a pair of
single values. The same parallel reduction technique is used as in the
“spikeTrainReduction” step, however the output components of the
population vector do not need to be transposed to ensure a coalesced memory
access pattern is followed. Whilst there is a large overhead for performing
this operation with very few threads in the final
 steps this is compensated for when multiple
independent trials perform the same kernel function.
steps this is compensated for when multiple
independent trials perform the same kernel function.
Calculate Reward
The calculation of the reward function is not suitable for GPU implementation as it requires calculation of only a single value per trial. Fortunately, as the output compensates have been reduced to two single values in the previous step, the transfer of data from the device back to the host is minimal (only two values). Following the calculation of the reward function as described by Equation 8, the reward is then copied back to the device to be used in subsequent steps.
Calculate Gradient Kernel
This kernel performs the calculation of the term
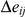 from Equation 9. Functionally this operation is a
dense matrix multiply operation based on the CUDA matrix multiplication
example from the CUDA SDK. This uses shared memory to substantially reduce
the number of global memory reads. The matrix P (the probability of firing)
is transposed to ensure coalesced memory access. Spike train Y was
transposed and stored previously (during the
“spikeTrainReduction” step).
from Equation 9. Functionally this operation is a
dense matrix multiply operation based on the CUDA matrix multiplication
example from the CUDA SDK. This uses shared memory to substantially reduce
the number of global memory reads. The matrix P (the probability of firing)
is transposed to ensure coalesced memory access. Spike train Y was
transposed and stored previously (during the
“spikeTrainReduction” step).
Update Learning Weights Kernel
This CUDA kernel performs the synaptic weight adjustment of the connections
between the Action Cells and Place Cells. They are updated using Equation 9
where the reward value and the component of the gradient for each Action
Cell  and Place Cell
and Place Cell 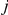 combination
are multiplied.
combination
are multiplied.
Apply Noise Kernel
This CUDA kernel is called only if the noise contribution value
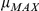 is greater than
is greater than  . The kernel
simply applies a basic linear operation to add a noise component to each
synaptic strength connection value. This is performed using M threads which
loop over the N synaptic weights. While it would be possible to perform this
with M*N independent threads (and as part of the previous step) this
would require a considerably larger number of independent random streams (a
separate stream is required also for each independent trials) which we have
found to cause the random number generation algorithm to break down (at
roughly
. The kernel
simply applies a basic linear operation to add a noise component to each
synaptic strength connection value. This is performed using M threads which
loop over the N synaptic weights. While it would be possible to perform this
with M*N independent threads (and as part of the previous step) this
would require a considerably larger number of independent random streams (a
separate stream is required also for each independent trials) which we have
found to cause the random number generation algorithm to break down (at
roughly  .
.
Simulation code and analysis scripts, developed in CUDA, are available from
ModelDB [81] at http://senselab.med.yale.edu/modeldb via accession number
136807. In the results presented here we use a time step of
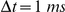 , but we have verified that our results remain
consistent when smaller time steps are used.
, but we have verified that our results remain
consistent when smaller time steps are used.
Performance Analysis and Discussion
We consider the performance of our GPU implementation by comparing its performance to that of a version of the same model implemented in Python using the BLAS enabled numpy library. This library uses natively implemented SSE vector instructions (which optimise operations carried out on groups of data) and multi-core support to accelerate linear algebra operations. Figure 10 shows the performance of the system configuration without and with lateral connections (the difference being the execution of the “actionCellLateralSpikePropagation” function). Performance is measured in relative speedup over the Python implementation by considering the difference in execution time between the two versions over the period of an entire simulation 10 blocks of 512 trials (10 blocks of 256 for the system without dynamics) including analysis of 128 trials for each of the 10 blocks. The hardware configuration used for benchmarking consists of a Intel i7-930 quad core CPU with 6 GB of RAM and a NVIDIA GTX 480 GPU. We have observed that as the number of independent trials is increased, the relative performance does also. This is not surprising as with a single independent trial the number of threads used by many of CUDA kernels is far below the number required to ensure all of the hardware multiprocessors have work to carry out. We have found that 8 independent trials to be the minimum to ensure that each of the multiprocessors will be kept busy. Beyond this number of independent trials, performance levels out for each of the two system configurations. This is useful as we have found that a minimum of 8 independent trials (we have used 16 throughout our experimentation unless otherwise stated) provides a good numeric numeric average to calculate the standard deviation of the average reward value for each learning step. For each of the simulation result obtained in Figure 10 we have used an optimal value of 256 threads per block. By ensuring we only use system wide model parameter values (i.e. N, M and T) of power two numbers we also ensure that our kernel launches fit neatly within our chosen thread block size. Whilst it would be possible to use non power of two values the decision to use them represents the best case scenario for the GPU as their is exactly the number of threads required to perform the computations.
Figure 10. Relative Performance Speedup.
Figure shows the relative performance improvement of our GPU model with respect to a similar Python implementation using numpy's BLAS implementation. Relative performance refers to the percentage increase in performance by considering the absolute timings of the two implementations over an entire simulation. The horizontal axis indicates Ind_total, that is the total number of independent trials which in this case represents independent animats (rather than animats in different configurations). A: Represents the case for our model without lateral connections. B: Represents a case with lateral connections which is the same however it includes an additional code execution to perform simulation of the lateral spike propagation.
The performance difference between the two system configurations in Figure 10 can be accounted for
by considering where the majority of GPU time is spent. Figure 11 shows where the percentage of GPU
simulation time is spent for both system configurations (without and with
lateral connections). The obvious observation is that for both systems the
majority of simulation time is spent performing the spike propagation operations
which are repeated 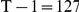 times during our
profiling observation. In the case of the system with lateral connections this
is most evident and a total of only
times during our
profiling observation. In the case of the system with lateral connections this
is most evident and a total of only 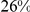 constitutes other
aspects of the simulation (in contrast with
constitutes other
aspects of the simulation (in contrast with 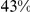 where there are no
lateral connections). As all other aspects of the system simulation are the same
it can be deduced that the calculation of spike propagations is considerably
less efficient than other aspects of our implementation. This is not surprising
as each propagation calculation is a matrix vector operation which is inherently
bound by memory operations (bandwidth) is is therefore less likely to offer the
kind of performance improvement we can observe with operations which contain a
higher percentage of arithmetic intensity (such as the
“integrateAndFireNeuronSimulation” kernel) or heavy use of shared
memory (such as the gradient calculation). As a result we must conclude that
whilst our simulation performance is considerably better when using the GPU (a
simulation without lateral connections and with 128 independent trials takes for
example almost 7 hours on the CPU when compared to 9 minutes on the GPU) that
future work must address the limitation of the matrix vector performance. In
previous work [59], which used simulated spiking neurons for pattern
recognition tasks, this has been done by considering only a small subset of feed
forward connections (based on a 2D grid layout). For more general neuron
populations using all to all feed forward connections, we propose that future
work will assess the use of a sparse vector matrix implementation which will
reduce computational load (and increase performance) by performing calculations
only where there are spikes (perhaps by reducing the matrix/vector magnitudes
using parallel reduction). Alternatively we may consider the use of an agent
based simulation framework on the GPU (such as GPU FLAME [82], [83]) which will similarly
avoid redundant computations by processing spikes as communicated messages
passed between neurons rather than through the dense matrix based mathematical
implementation presented here. The vector containing spike information is sparse
in the sense that over a single discrete time step only a small number of
neurons actually fire. As a result the matrix vector multiplications, which are
where the majority of GPU time is spent, are inefficient as they are performing
a dense calculation i.e. calculating many terms with zero values. Using a sparse
matrix vector operation would make this more efficient as would using an agent
based approach where neurons would perform computation only on spikes which were
generated.
where there are no
lateral connections). As all other aspects of the system simulation are the same
it can be deduced that the calculation of spike propagations is considerably
less efficient than other aspects of our implementation. This is not surprising
as each propagation calculation is a matrix vector operation which is inherently
bound by memory operations (bandwidth) is is therefore less likely to offer the
kind of performance improvement we can observe with operations which contain a
higher percentage of arithmetic intensity (such as the
“integrateAndFireNeuronSimulation” kernel) or heavy use of shared
memory (such as the gradient calculation). As a result we must conclude that
whilst our simulation performance is considerably better when using the GPU (a
simulation without lateral connections and with 128 independent trials takes for
example almost 7 hours on the CPU when compared to 9 minutes on the GPU) that
future work must address the limitation of the matrix vector performance. In
previous work [59], which used simulated spiking neurons for pattern
recognition tasks, this has been done by considering only a small subset of feed
forward connections (based on a 2D grid layout). For more general neuron
populations using all to all feed forward connections, we propose that future
work will assess the use of a sparse vector matrix implementation which will
reduce computational load (and increase performance) by performing calculations
only where there are spikes (perhaps by reducing the matrix/vector magnitudes
using parallel reduction). Alternatively we may consider the use of an agent
based simulation framework on the GPU (such as GPU FLAME [82], [83]) which will similarly
avoid redundant computations by processing spikes as communicated messages
passed between neurons rather than through the dense matrix based mathematical
implementation presented here. The vector containing spike information is sparse
in the sense that over a single discrete time step only a small number of
neurons actually fire. As a result the matrix vector multiplications, which are
where the majority of GPU time is spent, are inefficient as they are performing
a dense calculation i.e. calculating many terms with zero values. Using a sparse
matrix vector operation would make this more efficient as would using an agent
based approach where neurons would perform computation only on spikes which were
generated.
Figure 11. Performance Profile.
Figure shows the performance profile of our GPU implementation with
respect to where GPU time is spent during the simulation (shown as a
percentage for each GPU kernel corresponding with figure 8). The figure in brackets
next to the vertical axis label indicates the total number of times the
kernel function is called over single “learn step” with a
total time simulation period of T = 128 and
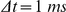 . An
additional amount of CPU time is also required however this is
negligible in the scale of the overall simulation. A: Represents the
case for our model without lateral connections. B: Represents a case
with lateral connections which is the same however it includes a kernel
function “actionCellLateralSpikePropagation” which performs
the lateral spike propagation simulation.
. An
additional amount of CPU time is also required however this is
negligible in the scale of the overall simulation. A: Represents the
case for our model without lateral connections. B: Represents a case
with lateral connections which is the same however it includes a kernel
function “actionCellLateralSpikePropagation” which performs
the lateral spike propagation simulation.
Acknowledgments
EV would like to thank Eilif Muller for bringing to her attention the use of GPU for simulations in the first place as well as a relevant reference on simulations of large-scale spiking neural networks on GPU.
Footnotes
Competing Interests: The authors have declared that no competing interests exist.
Funding: This work has been supported by the Royal Society International Joint Projects grant 2009/R4 (royalsociety.org) for EV and MG. MG acknowledges support from the Flanders Research Foundation grants G.0836.09 and G.0244.08 (www.fwo.be). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1.Gummaraju J, Rosenblum M. IEEE Computer Society. Washington, DC, USA: 2005. Stream programming on general-purpose processors. In: MICRO 38: Proceedings of the 38th annual IEEE ACM International Symposium on Microarchitecture. pp. 343–354. [Google Scholar]
- 2.Buck I, Foley T, Horn D, Sugerman J, Fatahalian K, et al. ACM. New York, NY, USA: 2004. Brook for gpus: stream computing on graphics hardware. In: SIGGRAPH ′04: ACM SIGGRAPH 2004 Papers. pp. 777–786. doi: http://doi.acm.org/10.1145/1186562.1015800. [Google Scholar]
- 3.Amari SI. Homogeneous nets of neuron-like elements. Biological Cybernetics. 1975;17:211–220. doi: 10.1007/BF00339367. [DOI] [PubMed] [Google Scholar]
- 4.Amari S. Dynamics of pattern formation in lateral-inhibition type neural fields. Biol Cybern. 1977;27:77–87. doi: 10.1007/BF00337259. [DOI] [PubMed] [Google Scholar]
- 5.Hamaguchi K, Okada M, Yamana M, Aihara K. Correlated firing in a feedforward network with mexican-hat-type connectivity. Neural Comput. 2005;17:2034–2059. doi: 10.1162/0899766054322937. [DOI] [PubMed] [Google Scholar]
- 6.Coultrip R, Granger R, Lynch G. A cortical model of winner-take-all competition via lateral inhibition. Neural Networks. 1992;5:47–54. [Google Scholar]
- 7.Spiridon M, Gerstner W. Effect of lateral connections on the accuracy of the population code for a network of spiking neurons. Network: Computation in Neural Systems. 2001;12:409–421257-272. [PubMed] [Google Scholar]
- 8.Piekniewski F. Rutkowski L, Scherer R, Tadeusiewicz R, Zadeh L, Zurada J, editors. Persistent activation blobs in spiking neural networks with mexican hat connectivity. Artifical Intelligence and Soft Computing, Springer Berlin/Heidelberg, volume 6114 of Lecture Notes in Computer Science. 2010. pp. 64–71.
- 9.Georgopoulos AP, Schwartz A, Kettner RE. Neuronal population coding of movement direction. Science. 1986;233:1416–1419. doi: 10.1126/science.3749885. [DOI] [PubMed] [Google Scholar]
- 10.Pfister JP, Toyoizumi T, Barber D, Gerstner W. Optimal spike-timing dependent plasticity for precise action potential firing in supervised learning. Neural Computation. 2006;18:1309–1339. doi: 10.1162/neco.2006.18.6.1318. [DOI] [PubMed] [Google Scholar]
- 11.Florian RV. Reinforcement learning through modulation of spike-timing-dependent synaptic plasticity. Neural Computation. 2007;19:1468–1502. doi: 10.1162/neco.2007.19.6.1468. [DOI] [PubMed] [Google Scholar]
- 12.Vasilaki E, Frémaux N, Urbanczik R, Senn W, Gerstner W. Spike-based reinforcement learning in continuous state and action space: When policy gradient methods fail. PLoS Comput Biol. 2009;5:e1000586. doi: 10.1371/journal.pcbi.1000586. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Williams R. Simple statistical gradient-following methods for connectionist reinforcement learning. Machine Learning. 1992;8:229–256. [Google Scholar]
- 14.Baxter J, Bartlett P, Weaver L. Experiments with infinite-horizon, policy- gradient estimation. Journal of Artificial Intelligence Research. 2001;15:351–381. [Google Scholar]
- 15.Wang X. The frontal lobes: development, function, and pathology; 2006. A microcircuit model of prefrontal functions: ying and yang of reverberatory neurodynamics in cognition.92 [Google Scholar]
- 16.Vasilaki E, Fusi S, Wang XJ, Senn W. Learning exible sensori-motor mappings in a complex network. Biol Cybern. 2009;100:147–158. doi: 10.1007/s00422-008-0288-z. [DOI] [PubMed] [Google Scholar]
- 17.Beierholm U, Dayan P. Pavlovian-Instrumental Interaction in “Observing Behavior”. PLoS Computational Biology. 2010;6 doi: 10.1371/journal.pcbi.1000903. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Dayan P. Goal-directed control and its antipodes. Neural Networks. 2009;22:213–219. doi: 10.1016/j.neunet.2009.03.004. [DOI] [PubMed] [Google Scholar]
- 19.Talmi D, Dayan P, Kiebel S, Frith C, Dolan R. How humans integrate the prospects of pain and reward during choice. Journal of Neuroscience. 2009;29:14617. doi: 10.1523/JNEUROSCI.2026-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Dayan P, Daw N. Decision theory, reinforcement learning, and the brain. Cognitive, Affective, & Behavioral Neuroscience. 2008;8:429. doi: 10.3758/CABN.8.4.429. [DOI] [PubMed] [Google Scholar]
- 21.Dayan P. Better than conscious; 2008. The role of value systems in decision making. pp. 51–70. [Google Scholar]
- 22.Sutton RS, Barto AG. Towards a modern theory of adaptive networks: expectation and prediction. Psychol Review. 1981;88:135–171. [PubMed] [Google Scholar]
- 23.Barto A, Sutton R, Anderson C. Neuronlike adaptive elements that can solve difficult learning and control problems. IEEE transactions on systems, man, and cybernetics. 1983;13:835–846. [Google Scholar]
- 24.Sutton R, Barto A. Time-derivative models of pavlovian reinforcement. In: Gabriel M, Moore J, editors. Learning and Computational Neuroscience: Foundations of Adaptive Networks. Cambridge: MIT-Press; 1990. pp. 497–537. [Google Scholar]
- 25.Morris R, Garrard P, Rawlins J, O′Keefe J. Place navigation impaired in rats with hippocampal lesions. Nature. 1982;297:681–683. doi: 10.1038/297681a0. [DOI] [PubMed] [Google Scholar]
- 26.Foster D, Morris R, Dayan P. Models of hippocampally dependent navigation using the temporal difference learning rule. Hippocampus. 2000;10:1–16. doi: 10.1002/(SICI)1098-1063(2000)10:1<1::AID-HIPO1>3.0.CO;2-1. [DOI] [PubMed] [Google Scholar]
- 27.Arleo A, Gerstner W. Spatial cognition and neuro-mimetic navigation: a model of hippocampal place cell activity. Biological Cybernetics. 2000;83:287–299. doi: 10.1007/s004220000171. [DOI] [PubMed] [Google Scholar]
- 28.Stroesslin T, Sheynikhovich D, Chavarriaga R, Gerstner W. Robust self-localisation and navigation based on hippocampal place cells. Neural Networks. 2005;18:1125–1140. doi: 10.1016/j.neunet.2005.08.012. [DOI] [PubMed] [Google Scholar]
- 29.Sheynikhovich D, Chavarriaga R, Strösslin T, Gerstner W. Spatial representation and navigation in a bio-inspired robot. Biomimetic Neural Learning for Intelligent Robots: Intelligent Systems, Cognitive Robotics, and Neuroscience. 2005. pp. 245–264.
- 30.Legenstein R, Wilbert N, Wiskott L. Reinforcement learning on slow features of highdimensional input streams. PLoS Comput Biol. 2010;6:e1000894. doi: 10.1371/journal.pcbi.1000894. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Seung HS. Learning in spiking neural networks by reinforcement of stochastic synaptic transmission. Neuron. 2003;40:1063–1073. doi: 10.1016/s0896-6273(03)00761-x. [DOI] [PubMed] [Google Scholar]
- 32.Xie X, Seung H. Learning in neural networks by reinforcement of irregular spiking. Physical Review E. 2004;69:41909. doi: 10.1103/PhysRevE.69.041909. [DOI] [PubMed] [Google Scholar]
- 33.Fiete I, Seung H. Gradient Learning in Spiking Neural Networks by Dynamic Perturbation of Conductances. Physical Review Letters. 2006;97:48104. doi: 10.1103/PhysRevLett.97.048104. [DOI] [PubMed] [Google Scholar]
- 34.Baras D, Meir R. Reinforcement learning, spike-time-dependent plasticity, and the bcm rule. Neural Computation. 2007;19:2245–2279. doi: 10.1162/neco.2007.19.8.2245. [DOI] [PubMed] [Google Scholar]
- 35.Friedrich J, Urbanczik R, Senn W. Learning spike-based population codes by reward and population feedback. Neural computation. 2010;22:1698–1717. doi: 10.1162/neco.2010.05-09-1010. [DOI] [PubMed] [Google Scholar]
- 36.Watkins C. Cambridge: PhD-thesis, Cambridge University; 1989. Learning from delayed rewards. [Google Scholar]
- 37.Sutton R, Barto A. MIT Press, Cambridge; 1998. Reinforcement learning. [Google Scholar]
- 38.Potjans W, Morrison A, Diesmann M. A spiking neural network model of an actor-critic learning agent. Neural Comp. 2009;21:301–339. doi: 10.1162/neco.2008.08-07-593. [DOI] [PubMed] [Google Scholar]
- 39.Di Castro D, Volkinshtein S, Meir R. Temporal difference based actor critic learning - convergence and neural implementation. NIPS. 2009;22:385–392. [Google Scholar]
- 40.Suri R, Schultz W. Temporal difference model reproduces anticipatory neural activity. Neural Computation. 2001;13:841–862. doi: 10.1162/089976601300014376. [DOI] [PubMed] [Google Scholar]
- 41.Gerstner W, Kempter R, van Hemmen JL, Wagner H. A neuronal learning rule for submillisecond temporal coding. Nature. 1996;383:76–78. doi: 10.1038/383076a0. [DOI] [PubMed] [Google Scholar]
- 42.Kempter R, Gerstner W, van Hemmen JL. Hebbian learning and spiking neurons. Phys Rev E. 1999;59:4498–4514. [Google Scholar]
- 43.Abbott LF, Nelson SB. Synaptic plasticity: Taming the beast. Nature Neuroscience. 2000;3:1178–1183. doi: 10.1038/81453. [DOI] [PubMed] [Google Scholar]
- 44.Izhikevich E. Solving the distal reward problem through linkage of stdp and dopamine signaling. Cerebral Cortex. 2007;17:2443–2452. doi: 10.1093/cercor/bhl152. [DOI] [PubMed] [Google Scholar]
- 45.Farries MA, Fairhall AL. Reinforcement Learning With Modulated Spike Timing Dependent Synaptic Plasticity. J Neurophysiol. 2007;98:3648–3665. doi: 10.1152/jn.00364.2007. [DOI] [PubMed] [Google Scholar]
- 46.Legenstein R, Pecevski D, Maass W. A learning theory for reward-modulated spiketiming-dependent plasticity with application to biofeedback. PLoS Computational Biology. 2008;4(10):e1000180. doi: 10.1371/journal.pcbi.1000180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.O′Keefe J, Dostrovsky J. The hippocampus as a spatial map. preliminary evidence from unit activity in the freely-moving rat. Brain Res. 1971;34:171–175. doi: 10.1016/0006-8993(71)90358-1. [DOI] [PubMed] [Google Scholar]
- 48.Jensen O, Lisman JE. Position Reconstruction From an Ensemble of Hippocampal Place Cells: Contribution of Theta Phase Coding. J Neurophysiol. 2000;83:2602–2609. doi: 10.1152/jn.2000.83.5.2602. [DOI] [PubMed] [Google Scholar]
- 49.Stein RB. A theoretical analysis of neuronal variability. Biophys J. 1965;5:173–194. doi: 10.1016/s0006-3495(65)86709-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Gerstner W, Kistler WK. Cambridge UK: Cambridge University Press; 2002. Spiking Neuron Models. [Google Scholar]
- 51.Barto A. Learning by statistical cooperation of self-interested neuron-like neuron elements. Human Neurobiology. 1985;4:229–256. [PubMed] [Google Scholar]
- 52.Van Rossum M. The transient precision of integrate and fire neurons: Effect of background activity and noise. Journal of Computational Neuroscience. 2001;10:303–311. doi: 10.1023/a:1011268215708. [DOI] [PubMed] [Google Scholar]
- 53.Van Rossum M, Turrigiano G, Nelson S. Fast propagation of firing rates through layered networks of noisy neurons. Journal of Neuroscience. 2002;22:1956. doi: 10.1523/JNEUROSCI.22-05-01956.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Van Rossum M, Renart A. Computation with populations codes in layered networks of integrate-and-fire neurons. Neurocomputing. 2004;58:265–270. [Google Scholar]
- 55.Sanders J, Kandrot E. Addison-Wesley; 2010. CUDA by Example: An Introduction to General-Purpose GPU Programming. [Google Scholar]
- 56.NVIDIA Corporation. NVIDIA CUDA Programming Guide 2008.
- 57.Ly DL, Paprotski V, Yen D. Technical report, University of Toronto; 2008. Neural networks on gpus: Restricted boltzmann machines. [Google Scholar]
- 58.Martnez-Zarzuela M, Daz Pernas F, Dez Higuera J, Rodrguez M. Sandoval F, Prieto A, Cabestany J, Graa M, editors. Fuzzy art neural network parallel computing on the gpu. Computational and Ambient Intelligence, Springer Berlin, Heidelberg, volume 4507 of Lecture Notes in Computer Science. 2007. pp. 463–470.
- 59.Bernhard F, Keriven R. Spiking neurons on GPUs. International Conference on Computational Science (4) 2006. pp. 236–243.
- 60.Goodman D, Brette R. Brian: a simulator for spiking neural networks in Python. Frontiers in neuroinformatics. 2008;2 doi: 10.3389/neuro.11.005.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Goodman D, Brette R. The Brian simulator. Frontiers in neuroscience. 2009;3:192. doi: 10.3389/neuro.01.026.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Cyrille R, M GDF, Jonathan P, Romain B. Automatic fitting of spiking neuron models to electrophysiological recordings. Frontiers in Neuroinformatics. 2010;4:12. doi: 10.3389/neuro.11.002.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Goodman D. Code generation: A strategy for neural network simulators. Neuroinformatics. 2010;8:183–196. doi: 10.1007/s12021-010-9082-x. [DOI] [PubMed] [Google Scholar]
- 64.Nageswaran J, Dutt N, Krichmar J, Nicolau A, Veidenbaum A. A configurable simulation environment bfor the efficient simulation of large-scale spiking neural networks on graphics processors. Neural Networks. 2009;22:791–800. doi: 10.1016/j.neunet.2009.06.028. [DOI] [PubMed] [Google Scholar]
- 65.Bhuiyan M, Pallipuram V, Smith M. Acceleration of spiking neural networks in emerging multi-core and gpu architectures. Parallel Distributed Processing, Workshops and Phd Forum (IPDPSW), 2010 IEEE International Symposium on. 2010. pp. 1–8. doi: 10.1109/IPDPSW.2010.5470899.
- 66.Markram H. The blue brain project. Nature Reviews Neuroscience. 2006;7:153–160. doi: 10.1038/nrn1848. [DOI] [PubMed] [Google Scholar]
- 67.Ananthanarayanan R, Esser SK, Simon HD, Modha DS. 1–12. New York, NY, USA: ACM; 2009. The cat is out of the bag: cortical simulations with 109 neurons, 1013 synapses. In: SC ′09: Proceedings of the Conference on High Performance Computing Networking, Storage and Analysis. doi: http://doi.acm.org/10.1145/1654059.1654124. [Google Scholar]
- 68.Furber S, Temple S. Fulcher J, Jain L, editors. Neural systems engineering. Computational Intelligence: A Compendium, Springer Berlin Heidelberg, volume 115 of Studies in Computational Intelligence. 2008. pp. 763–796.
- 69.Renaud S, Tomas J, Bornat Y, Daouzli A, Saighi S. Neuromimetic ICs with analog cores: an alternative for simulating spiking neural networks. In: Circuits and Systems, 2007. ISCAS 2007. IEEE International Symposium on. IEEE. 2007:3355–3358. [Google Scholar]
- 70.Bruederle D, Bill J, Kaplan B, Kremkow J, Meier K, et al. Simulator-Like Exploration of Cortical Network Architectures with a Mixed-Signal VLSI System. Proceedings of the 2010 IEEE International Symposium on Circuits and Systems (ISCAS 10) 2010. pp. 2784–8787.
- 71.Bill J, Schuch K, Bruederle D, Schemmel J, Maass W, et al. Compensating inhomogeneities of neuromorphic vlsi devices via short-term synaptic plasticity. Frontiers in Computational Neuroscience. 2010;4:12. doi: 10.3389/fncom.2010.00129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Davison A, Yger P, Kremkow J, Perrinet L, Muller E. PyNN: towards a universal neural simulator API in Python. BMC Neuroscience. 2007;8:P2. [Google Scholar]
- 73.Davison A, Bruederle D, Eppler J, Kremkow J, Muller E, et al. PyNN: a common interface for neuronal network simulators. Frontiers in neuroinformatics. 2008;2 doi: 10.3389/neuro.11.011.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Eppler J, Helias M, Muller E, Diesmann M, Gewaltig M. PyNEST: a convenient interface to the NEST simulator. Frontiers in neuroinformatics. 2008;2 doi: 10.3389/neuro.11.012.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Bruederle D, Mueller E, Davison A, Muller E, Schemmel J, et al. Establishing a novel modeling tool: a python-based interface for a neuromorphic hardware system. Frontiers in neuroinformatics. 2009;3 doi: 10.3389/neuro.11.017.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Davison A, Hines M, Muller E. Trends in programming languages for neuroscience simulations. Frontiers in neuroscience. 2009;3:374. doi: 10.3389/neuro.01.036.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Davison A, Muller E, Bruederle D, Kremkow J. The Neuromorphic Engineer; 2010. A common language for neuronal networks in software and hardware. [Google Scholar]
- 78.van Meel J, Arnold A, Frenkel D, Portegies Zwart S, Belleman R. Harvesting graphics power for MD simulations. Molecular Simulation. 2008;34:259–266. [Google Scholar]
- 79.Bell N, Garland M. NVIDIA Technical Report NVR-2008-004, NVIDIA Corporation; 2008. Efficient sparse matrix-vector multiplication on CUDA. [Google Scholar]
- 80.Sengupta S, Harris M, Zhang Y, Owens JD. Scan primitives for gpu computing. In: GH ′07: Proceedings of the 22nd ACM SIGGRAPH/EUROGRAPHICS symposium on Graphics hardware. Aire-la-Ville, Switzerland, Switzerland: Eurographics Association, 2007;97–106 [Google Scholar]
- 81.Hines M, Morse T, Migliore M, Carnevale N, Shepherd G. ModelDB: a database to support computational neuroscience. Journal of Computational Neuroscience. 2004;17:7–11. doi: 10.1023/B:JCNS.0000023869.22017.2e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Richmond P, Romano D. Proceedings of EUROSIS ESM 2008; 2008. A high performance framework for agent based pedestrian dynamics on gpu hardware. [Google Scholar]
- 83.Richmond P, Walker D, Coakley S, Romano D. High performance cellular level agent-based simulation with FLAME for the GPU. Briefings in bioinformatics. 2010;11:334. doi: 10.1093/bib/bbp073. [DOI] [PubMed] [Google Scholar]