Second-order Poisson Nernst-Planck solver for ion channel transport

Abstract

The Poisson Nernst-Planck (PNP) theory is a simplified continuum model for a wide variety of chemical, physical and biological applications. Its ability of providing quantitative explanation and increasingly qualitative predictions of experimental measurements has earned itself much recognition in the research community. Numerous computational algorithms have been constructed for the solution of the PNP equations. However, in the realistic ion-channel context, no second order convergent PNP algorithm has ever been reported in the literature, due to many numerical obstacles, including discontinuous coefficients, singular charges, geometric singularities, and nonlinear couplings. The present work introduces a number of numerical algorithms to overcome the abovementioned numerical challenges and constructs the first second-order convergent PNP solver in the ion-channel context. First, a Dirichlet to Neumann mapping (DNM) algorithm is designed to alleviate the charge singularity due to the protein structure. Additionally, the matched interface and boundary (MIB) method is reformulated for solving the PNP equations. The MIB method systematically enforces the interface jump conditions and achieves the second order accuracy in the presence of complex geometry and geometric singularities of molecular surfaces. Moreover, two iterative schemes are utilized to deal with the coupled nonlinear equations. Furthermore, extensive and rigorous numerical validations are carried out over a number of geometries, including a sphere, two proteins and an ion channel, to examine the numerical accuracy and convergence order of the present numerical algorithms. Finally, application is considered to a real transmembrane protein, the Gramicidin A channel protein. The performance of the proposed numerical techniques is tested against a number of factors, including mesh sizes, diffusion coefficient profiles, iterative schemes, ion concentrations, and applied voltages. Numerical predictions are compared with experimental measurements.

I Introduction

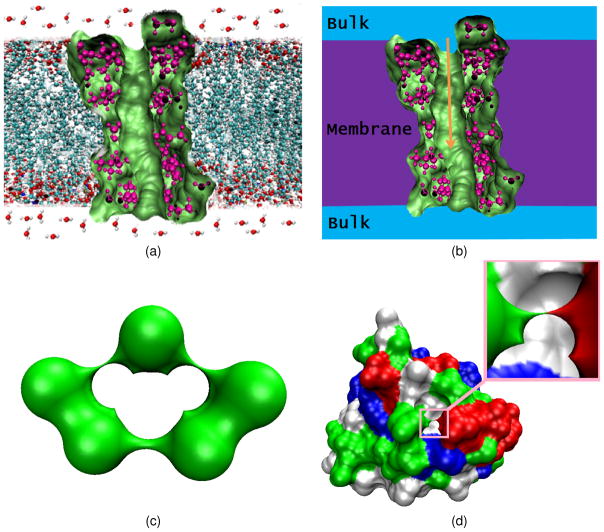
All fundamental self-sustaining processes of living organisms are based on their ability to receive, process, create and transmit signals. Although biological signals are often referred to as hormones, growth factors etc., they can be as elementary as small ions whose motions create electrostatic potentials across the cell membrane. Electrochemical transmembrane gradient induces flow of ions in and out of cells through membrane proteins.¹⁹ The membrane proteins that give rise to selective ion permeability are called ion channels. As their name implies, ion channels have pores that permit particular ions to cross the cellular membrane. Ion channels are essential to cell sustaining and control a wide variety of important physiological processes, ranging from nerve and muscle excitation, muscle contraction, action potential generation and resting, sensory transduction, cell volume and blood pressure regulation, cell proliferation, hormone secretion, fertilization, maintenance of salt and water balance, learning and memory, to programmed cell death.²¹ Typical ion channels are voltage-gated or ligand-gated. Voltage-gated ion channels open or close depending on their response to the magnitude of the voltage gradient across the plasma membrane, while ligand-gated ion channels open or close depending on the binding or interaction of ligands with ion channels. Additionally, there are ion channels that are gated by extracellular chemical signals (e.g., neurotransmitters), or by intracellular signals (e.g., second messengers).⁴² Finally, mechanical or thermal stimuli, such as force or temperature, are increasingly recognized as regulators of ion channels and impact cell structure and function. Figure 1(a) gives an illustration of a simple voltage-gated ion channel, the Gramicidin A channel.

Figure 1.

Illustrations of ion channel geometry, computational setup, and geometric singularities. (a) Gramicidin A channel; (b) Computational setup for the PNP system; (c) Geometric singularities in the molecular surface of a five-atom structure; (d) Geometric singularities in the molecular surface of protein 451c (Color map indicates the residues).

A wide range of experimental techniques and methods have been developed for investigating the structure and function of ion channels over the past few decades.²¹ For example, classical electro-physiology techniques are used to study ion channel responses to current injections. Crystallographic and nuclear magnetic resonance (NMR) spectroscopic techniques are often employed to determine the structure and/or structural features of ion channels. Genetic engineering techniques are utilized to identify the active site information of ion channels after the introduction of mutations. Pharmacological techniques are commonly used to elevate or suppress ion channel responses. Additionally, animal models usually serve as prototypes for human ion channel studies. The advances in experimental techniques have led to enormous progress in our understanding of the structure, function, dynamics and transport of ion channels.

The paramount importance and abundant experimental data have stimulated much theoretical and computational investigation in ion channels. Various theoretical and computational approaches, from fundamental to phenomenological, are also developed to understand the biological mechanism of ion channels. The most commonly used theoretical techniques in the field are stochastic models, ab initio molecular dynamics (MD),³⁷ classical molecular dynamics (MD), and continuum descriptions. Among these techniques, ab initio MD has played a crucial role in revealing the complex mechanism of molecular systems, such as chemical reactions. Due to its detailed description of electronic structure and the extremely demanding nature of coupling electronic structure to molecular motion, ab initio MD is limited to small systems at present. Classical MD utilizes empirical interaction potentials or force fields to describe molecular motions and is able to handle an entire ion channel, including ions, counterions, solvent, lipids and proteins. Unfortunately, it is still quite difficult for commonly used MD methods to run up to the time scale of ion permeation across most real channel membranes and to determine ion conductance.¹³ As a result, approaches that reduce the dimensionality of the ion channel systems are playing important roles in ion channel dynamics and transport. One of these approaches is Monte Carlo (MC) methods²⁴ which rely on repeated random sampling to compute the probability of movement of a selected set of particles. Monte Carlo approaches simulate the ion permeation across the membrane over long time-scales without having to treat all the solvent molecules explicitly. Another class of important reduced models is Brownian dynamics (BD), which is based on the stochastic equation of motions of ion particles driven by some effective potential functions. Both MC and BD approaches provide an explicit representation of ions while treat solvent and lipids as featureless dielectrics.⁴⁴ These reduced models are simpler and computationally less expensive than all-atom MD and have been some of the main workhorses in ion channel transport modeling and prediction for many years.

A further simplification in the ion representation, i.e., the so called mean-field approximation of ions, leads to a fully continuous model, Poisson Nernst-Planck (PNP) equations, in which ions are not treated as microscopic discrete entities but as continuous charge densities, see Fig. 1(b). Therefore, the PNP theory describes both the solvent and ions as continuous distributions. Consequently, there are a few limitations associated with the PNP model. It is well-known that the PNP theory neglects the finite volume effect of ion particles, which can be important for small channel pores.²⁶ Moreover, non-electrostatic interactions between ions are not accounted in the PNP model. Finally, there is a lack of the description of ionic dielectric boundary effects in the PNP theory. Nevertheless, the PNP theory incorporates realistic channel structure and discrete protein charge locations in its modeling and computation, and treats the electrostatic potential distribution, concentration and flux of ions in the system in a self-consistent manner. Consequently, the PNP theory is able to yield a good prediction of ion channel transport at a relatively small computational cost. The performance of the above mentioned MD, BD and PNP theories is compared in the theoretical prediction of ion permeation transport of the OmpF porin channel from Escherichia coli.²⁵ For a more comprehensive and general understanding of these theoretical and computational approaches, the reader is referred to the related literature.^{13, 28, 30, 31, 44}

Mathematically, the PNP equations are considerably interesting. First, they are strongly coupled and thus are nonlinear in nature. The well-posedness of the PNP system under biological setting is an interesting issue. Additionally, existence and uniqueness of the solution to the PNP system under biomolecular setting give rise to an important mathematical problem. In fact, the PNP system of equations has been analyzed mathematically to certain extent in the biological context.^{3, 4, 17} Under the assumption that the Debye length is small relative to the diameter of the narrow channel, the PNP system can be viewed as a singularly perturbed system. Liu analyzed the boundary value problem of a one-dimensional steady-state PNP system for ion flows through a narrow membrane channel by using the geometric singular perturbation theory.³⁴ Within the framework of dynamical systems, the global behavior was studied in terms of limiting fast and slow systems, and the existence and (local) uniqueness of the boundary value problem was discussed. Recently, Abaid et al.¹ investigated higher order matched asymptotic expansions of a steady-state PNP system with particular attention to the I-V curve relation of ion channels. Special structures of the zeroth order inner and outer systems make it possible to provide an explicit derivation of higher order terms in asymptotic expansions. Full scale mathematical analysis of the PNP system in the realistic biomolecular context is yet to be achieved. Due to complexity of the irregular geometry and presence of geometric singularities as shown in Fig. 1, analytic solution to the original PNP system is unfeasible. As such, numerical analysis and computer simulation are the main strategies for obtaining physically meaningful solutions to the PNP system in practical applications.

The importance of computational techniques to the numerical analysis of the PNP system cannot be overemphasized. A number of mathematical algorithms, including finite difference, finite element and finite volume methods, have been utilized in the past two decades for solving the PNP equations describing the ion transmembrane flow. A lattice relaxation algorithm in conjugation with the finite difference method was developed by Kurnikova and coauthors²⁷ to solve the PNP equations for ion transport with the three-dimensional (3D) realistic geometry of the Gramicidin A dimer. The accuracy of their method was calibrated with simple parallel plate and cylindrical pore geometries. Hollerbach et al.²² applied a spectral element method for solving the 3D PNP equations with various sensitivity analysis to determine the impact of the PNP model parameters to I-V curves. Mathur and Murthy³⁸ developed a multigrid algorithm based on an unstructured cell-centered finite volume method for solving the PNP equations. It has been shown that their methods perform well for the transport of K⁺ and Cl⁻ in a synthetic ion channel for driving voltages, surface charges, ion concentrations and channel aspect ratios ranging over several orders of magnitude. While each of the computational technique has its particular merits, a comparison of the performance of different techniques has not been performed.

Although existing PNP solvers have provided a good understanding of ion channel flows, a number of numerical challenges that may seriously affect the convergence, accuracy, and efficiency of current PNP solvers still need to be addressed. First, no second order convergent numerical algorithm has been reported for solving the nonlinear PNP equations in the literature for ion channels, to our best knowledge. The analysis of numerical convergence is very important to computational algorithms. Without such an analysis, one may not be able to determine whether it is a model deficiency or a numerical defect in case that the PNP result does not agree with experimental data. Additionally, as shown in Fig. 1(b), the protein structure provides a large number of discrete charges which are modeled as Dirac delta functions. Consequently, the solution of the Poisson equation with singular charge sources poses a computational difficulty. Efficient mathematical algorithms need to be developed for dealing with large number of singular charges. Moreover, there is a dielectric interface in the PNP system that separates the ion flow domain from the protein/lipid domain. Because of the use of discontinuous dielectric constants in these two domains, the solution of Poisson equation is non trivial. A set of interface conditions has to be carefully enforced in order to make the original PNP equations mathematically meaningful. Unfortunately, there is no report on explicit enforcement of the interface conditions in the literature for ion channel geometry. Finally, the existence of geometric singularity in the molecular surfaces of biomolecules,⁴⁵ see Figs. 1(c) and (d), severely deteriorates the chance of constructing a second order convergent numerical algorithm for the PNP equations. Image processing type of smoothing algorithms may be used to increase the regularity of the molecular surfaces, which, however, could result in 10–40% over-estimation of solvation energies and forces,⁴⁶ and make the problem mathematically less interesting. In fact, it is the combination of irregular geometry, singular charges, discontinuous dielectric coefficients and nonlinearity that makes the solution of PNP equations in the biomolecular context numerically challenging while mathematically interesting.

The solution of elliptic equations with discontinuous coefficients and singular sources has been an important problem in computational mathematics in the past few decades. Special numerical techniques have to be developed in order to achieve high-order numerical accuracy.^{2, 7, 33, 48} There is a tendency in using Cartesian grid methods for complex interface problems. One advantage of Cartesian grid methods is that there is no need to generate computational grids which avoids the cost of grid generation. Cartesian grids also enable the use of simple data structures and standard FD stencils, which simplify the computational algorithm. Moreover, many contemporary software packages, such as fast Poisson solvers, multigrid schemes, level set methods, etc., are mainly developed for Cartesian grids, and thus can be taken advantage of. On the other hand, in order to properly maintain the accuracy at the interface, additional numerical treatments are required near the interface in Cartesian grids. In 1977, Peskin pioneered the immersed boundary method (IBM)⁴¹ to address this class of elliptic interface problems. Alternative methods have also been reported in the literature, including the ghost fluid method,^{18, 35} finite-volume-based methods,⁴⁰ and integral equation methods.³⁹ A piecewise-polynomial discretization and Krylov-accelerated multigrid approach was proposed by Chen and Strain.¹⁰ A major advance in the field was due to LeVeque and Li,²⁹ who constructed a remarkable second order sharp interface scheme, the immersed interface method (IIM).^{29, 32} However, these interface techniques have not been implemented for the PNP equations in the context of realistic biomolecules, partially due to numerical challenges discussed in the last paragraph.

Recently, we have proposed a highly accurate algorithm, the matched interface and boundary (MIB) method^{50–52, 55, 56} for treating the discontinuous dielectric constants and singular sources in the complex biological geometry. Many essential ideas of the present MIB method were introduced in earlier interface schemes for solving Maxwell’s equation.⁵² The MIB method makes use of simple Cartesian grids, standard finite difference schemes, lowest order physical jump conditions and fictitious domains. While the physical jump conditions are enforced at each intersecting point of the interface and the mesh lines, the MIB method takes care of the interface condition in a systematic way. Furthermore, the MIB method has been used as a novel boundary scheme to treat various general boundary conditions in boundary value and eigenvalue problems.⁵³ The MIB is of arbitrarily high-order accuracy in principle, and sixth-order accurate MIB schemes have been constructed in 2D⁵⁶ and 3D⁵⁰ geometric settings. We have developed three generations of MIB based Poisson-Boltzmann solvers, MIBPB-I,⁵⁴ MIBPB-II,⁴⁹ and MIBPB-III.²⁰ It is worth to mention that the MIBPB-I is the first PB solver that explicitly enforces the interface conditions in the biomolecular context; however, it cannot maintain its designed second-order accuracy in the presence of molecular surface singularities,⁴⁵ i.e., cusps and self-intersecting surfaces commonly occurred in biomolecular systems as shown in Figs. 1(c) and (d). This problem was carefully addressed in the MIBPB-II by utilizing an advanced MIB technique developed by Yu et al.;⁵⁰ however, the MIBPB-II still loses its accuracy whenever the mesh size is as large as half of the smallest van der Waals radius in a protein structure, because of the interference of the interface and singular charges. To resolve this difficulty, we further developed Dirichlet to Neumann mapping approach^{12, 57} to split the singular charge part of the solution from the regular part in our MIBPB-III,²⁰ which is by far the most accurate and stable PB solver. To our knowledge, except for the MIBPB, there is no other numerical method that delivers second order accuracy in solving the Poisson-Boltzmann equation with discontinuous coefficients, singular sources and primitive geometric singularities in the biomolecular context. The MIBPB-III is a few orders of magnitude more accurate at a given mesh size and about three times faster at a given accuracy than some traditional PB solvers.^{9, 20}

The object of the present work is to construct a second-order convergent numerical method for the solution of the PNP equations in the ion-channel context. The PNP system is significantly more challenging to solve than the Poisson-Boltzmann equation for a few reasons. First, the Poisson equation in the PNP system not only inherits the full set of difficulties from the Poisson-Boltzmann equation, such as discontinuous coefficients, singular sources and geometric singularities, but also encounters additional hurdles, such as the time-varying charge density in the solvent domain. Moreover, the Nernst-Planck equation in the 3D ion-channel context is also a challenging numerical problem due to irregular geometric boundaries and possible geometric singularities, i.e., non-smooth boundaries. To our knowledge, no second-order numerical scheme has been reported in the literature for this problem with primitive geometric singularities associated with the commonly used molecular surfaces,⁴⁵ although it is fairly easy to construct second-order Nernst-Planck solvers on artificial geometries obtained by using surface smoothing techniques. Furthermore, the evaluation of the flux in the PNP system can be a problem. The flux vector may not converge or may be unstable when the boundary condition is not appropriately implemented. Finally, the coupling of two nonlinear equations needs to be carried out with care to ensure the convergence of the nonlinear iterations. All of these obstacles are overcome in the present work to come up with a second order PNP solver.

The rest of the paper is organized as follows. Section II is devoted to theoretical models and mathematical algorithms. We briefly review the PNP model and state the problem. This description also helps establishing the notation. A number of computational algorithms are presented. The Dirichlet to Neumann mapping (DNM) approach is introduced for the treatment of singular charges. We reformulate the PNP system such that the Dirac delta function in the Poisson equation can be removed by using Green’s function, which leads to an additional Neumann condition at the interface. We develop the marched interface and boundary (MIB) method for dealing with complex interfaces in the Poisson equation and complex boundaries in the Nernst-Planck equation. An iterative scheme²⁷ is applied to solve the coupled nonlinear equation system and to obtain converged solution. We validate the proposed second order PNP scheme in Section III. We first confirm the designed convergence of solving the PNP equations by a simple geometry, a sphere. While it is barely impossible to derive analytic solutions for protein structures due to the complexity of the geometry, analytical test solutions are developed in terms of keeping the original structure of the PNP system with minor modifications of the right hand side source term by adding extra components which result from the test solutions. In this way, the order of accuracy of proposed methods can be tested since the structure of the PNP system is maintained in the test solution. In Section IV, we present a detailed description of some important aspects about the application of the PNP model to realistic ion transport simulations. First, we discuss the unit conversion. The Gaussian unit system is used in our scheme. Additionally, the diffusion coefficient profiles are found to play an important role in ion concentration, electrostatic potential and ion transport. The coefficient in the bulk region is set to be the experimental measurement value, while appropriate coefficient values are used for the channel region. Moreover, iterative schemes are very important for the efficiency of the simulation. Two different iteration schemes are implemented and discussed in detail. Furthermore, the potential and concentration profiles are computed with different mesh sizes. Finally, the simulated current values are compared to experimental data. A good agreement between the simulation results and the experimental data has been achieved.

II Theoretical model and mathematical algorithm

The modeling aspect of the PNP system has been intensively discussed in the literature, including a differential geometry based multiscale formulation.⁴⁷ Since our goal is to construct a second-order PNP solver, we consider only the standard PNP equations. Various computational algorithms for the PNP system are discussed in detail. The proposed technique can be easily applied to modified versions of the PNP model.

II.A Poisson-Nernst-Planck (PNP) equations

The PNP model combines the Nernst-Planck theory description of electrodiffusion of ions in the trans-membrane channel with the Poisson theory description of the electrostatic potential whose gradient serves as a driven force of the ion motion. Consider an open domain Ω ∈ ℝ³, Ω = Ω_m ∪ Ω_s, where Ω_m represents the biomolecular region (or the ion exclusion region) and Ω_s represents the solvent region (or the ion inclusion region). We use Γ to denote the interface between these two regions, such that Γ = Ω_m ⊂ Ω_s. It is standard to use the molecular surface^43,45 as the interface Γ, although other well-tested surfaces such as minimal molecular surface^{5, 6} can be used as well. It is pointed out that whenever a smoothed surface is used for biophysical applications, extensive validation in terms of volume, surface area and solvation free energy analysis has to be performed over a large number of biomolecules.

II.A.1 The Poisson equation

The electrostatic potential Φ(r) depends on the dielectric properties of the medium, also the external voltage applied across the system, and most importantly, both the fixed charges and the mobile charges in the system. The electrostatic potential profile Φ(r) is determined by the Poisson equation

$$-\nabla ·(\epsilon (\mathbf{r})\nabla \mathrm{\Phi }(\mathbf{r}))=4\pi \sum _{\beta =1}^{N_a}{q}_q\delta (\mathbf{r}-{\mathbf{r}}_{\beta })+4\pi \sum _{\alpha =1}^{N_c}{q}_{\alpha }{C}_{\alpha }(\mathbf{r}),$$ (1)

where q_β is the (fractional) charge of the protein at position r_β(β = 1, 2, …, N_a), q_α and C_α are respectively the charge and concentration of the αth ionic species(α = 1, 2, …, N_c). Constants N_a and N_c are, respectively, the number of charged atoms in the biomolecule, and the number of ionic species in the solvent. The dielectric function ε is defined as

$$\epsilon (\mathbf{r})=\{\begin{array}{cc}{\epsilon }_m,& \mathbf{r}\in {\mathrm{\Omega }}_m,\\ {\epsilon }_s,& \mathbf{r}\in {\mathrm{\Omega }}_s,\end{array}$$ (2)

where ε_m and ε_s are the dielectric functions in the molecular and solvent regions, respectively. Normally, we choose ε_m as a constant while ε_s as a function whose values may vary from in the bulk domain to the ion channel region. Here, ε_m and ε_s can differ much from each other.

To ensure the well posedness, the Poisson equation (1) satisfies the jump conditions at the interface Γ

$$\{\begin{array}{ll}[\mathrm{\Phi }(\mathbf{r})]={\mathrm{\Phi }}^m(\mathbf{r})-{\mathrm{\Phi }}^s(\mathbf{r})=0,\hfill & \mathbf{r}\in \mathrm{\Gamma },\hfill \\ [\epsilon (\mathbf{r}){\mathrm{\Phi }}_{\text{n}}(\mathbf{r})]={\epsilon }_m\nabla {\mathrm{\Phi }}^m(\mathbf{r})·\mathbf{n}-{\epsilon }_s\nabla {\mathrm{\Phi }}^s(\mathbf{r})·\mathbf{n}=0,\hfill & \mathbf{r}\in \mathrm{\Gamma },\hfill \end{array}$$ (3)

where the superscripts in Φ^m and Φ^s indicate Φ is defined in Ω_m and Φ is defined in Ω_s, n = (n₁, n₂, n₃) is the outward normal direction of the interface. Given the geometric complexity and the low regularity of the interface, the enforcement of the jump conditions (3) is highly non-trivial with primitive molecular surfaces.

The electrostatic system satisfies the far field boundary condition, i.e., lim_r→±∞ Φ(r) = 0. However, computationally, Dirichlet and Neumann boundary conditions are practically used, i.e., Φ (r) = Φ⁰(r) is given on ∂Ω according to the applied voltage at electrodes. The Neumann boundary is used in other parts of boundaries. In fact, as long as boundaries are sufficiently far from the ion channel pore, the boundary conditions are not very important, except for the applied voltage conditions.

II.A.2 The Nernst-Planck equation

The influence of the electrostatic potential on the overall electrodiffusivity of ions can be evaluated by using the well established fundamental theory. The Nernst-Planck equation describes the rate of change of the concentration of each ion species due to the concentration flux

$$\frac{\partial C_{\alpha }(\mathbf{r})}{\partial t}=-\nabla ·{\mathbf{J}}_{\alpha }(\mathbf{r}),$$ (4)

where the concentration flux consists of ion diffusivity and electrostatic force

$${\mathbf{J}}_{\alpha }(\mathbf{r})=-D_{\alpha }(\mathbf{r})\left[\nabla C_{\alpha }(\mathbf{r})+\frac{q_{\alpha }}{{\text{k}}_{\text{B}}\text{T}}{C}_{\alpha }(\mathbf{r})\nabla \mathrm{\Phi }(\mathbf{r})\right].$$ (5)

Here Constants k_B and T are, respectively, the Boltzmann constant and the absolute temperature, D_α(r) is the spatially dependent diffusion coefficient of species α.

For the steady-state of the system, the Nernst-Planck equation in Ω^s can be written in the following form

$$\nabla ·D_{\alpha }(\mathbf{r})\left[\nabla C_{\alpha }(\mathbf{r})+\frac{q_{\alpha }}{{\text{k}}_{\text{B}}\text{T}}{C}_{\alpha }(\mathbf{r})\nabla \mathrm{\Phi }(\mathbf{r})\right]=0.$$ (6)

Physically there is no ion penetration through the interface Γ. This condition can be implemented in two different ways.^8,22 In Boundary condition I, one requires that the normal component of the flux be zero on Γ

$$-D_{\alpha }(\mathbf{r})\left[\nabla C_{\alpha }(\mathbf{r})+\frac{q_{\alpha }}{{\text{k}}_{\text{B}}\text{T}}{C}_{\alpha }(\mathbf{r})\nabla \mathrm{\Phi }(\mathbf{r})\right]·\mathbf{n}=0\text{on}\mathrm{\Gamma }.$$ (7)

In Boundary condition II, one simply requires that the flux vanishes on Γ

$$-D_{\alpha }(\mathbf{r})\left[\nabla C_{\alpha }(\mathbf{r})+\frac{q_{\alpha }}{{\text{k}}_{\text{B}}\text{T}}{C}_{\alpha }(\mathbf{r})\nabla \mathrm{\Phi }(\mathbf{r})\right]=\mathbf{0}\text{on}\mathrm{\Gamma }.$$ (8)

Obviously, the Boundary condition II is a stronger requirement. The implementation complexity for these two boundary conditions is quite different when the geometries of the underlying problem is very complex, which is the case for channel proteins.

On the boundary ∂Ω, C_α(r) = C_0α(r) is given according to the bulk concentration of each species.

Obviously, the Poisson equation (1) and the Nernst-Planck equation (6) are coupled to each other to form a closed system, which makes the PNP system strongly nonlinear. Appropriate iterative schemes are required for solving these coupled PDEs.

II.B Mathematical algorithms

In this subsection, we discuss mathematical techniques for the solution of coupled PNP equations.

II.B.1 Dirichlet to Neumann mapping (DNM) for dealing with singular charges

For the Poisson equation, the Dirac delta functions describing partial charges are involved in the source term, see Eq. (1). If this term is treated numerically with interpolation schemes to distribute the delta function at one given point to its neighboring grid points, the mesh size may be restricted and the order of accuracy may reduce.²⁰ Here we treat this term analytically by employing the Green’s function formulation.^20,57 To remove the delta function in the source term, Φ is decomposed into two parts: the regular part Φ̃(r) and the singular part Φ̄(r)

$$\mathrm{\Phi }(\mathbf{r})=\stackrel{\sim }{\mathrm{\Phi }}(\mathbf{r})+\overline{\mathrm{\Phi }}(\mathbf{r}),$$ (9)

where Φ̄(r) is defined as^{12, 20}

$$\overline{\mathrm{\Phi }}(\mathbf{r})=\{\begin{array}{ll}{\mathrm{\Phi }}^{\ast }(\mathbf{r})+{\mathrm{\Phi }}^0(\mathbf{r}),\hfill & \mathbf{r}\in {\mathrm{\Omega }}_m\hfill \\ 0,\hfill & \mathbf{r}\in {\mathrm{\Omega }}_s.\hfill \end{array}$$ (10)

Here Φ^*(r) is the Green’s function which can be given analytically

$${\mathrm{\Phi }}^{\ast }(\mathbf{r})=\sum _{\beta =1}^{N_a}\frac{q_{\beta }}{{\epsilon }_m\mid \mathbf{r}-{\mathbf{r}}_{\beta }\mid }.$$ (11)

Consequently, the unbounded part of the solution is removed from the numerical computation. The Φ⁰(r) satisfies the Laplace equation with a Dirichlet boundary condition

$$\{\begin{array}{ll}{\nabla }^2{\mathrm{\Phi }}^0(\mathbf{r})=0,\hfill & \mathbf{r}\in {\mathrm{\Omega }}_m\hfill \\ {\mathrm{\Phi }}^0(\mathbf{r})=-{\mathrm{\Phi }}^{\ast }(\mathbf{r}),\hfill & \mathbf{r}\in \mathrm{\Gamma }.\hfill \end{array}$$ (12)

This decomposition of Φ gives rise to a Poisson equation for Φ̃(r) without the singular term,

$$\{\begin{array}{ll}-\nabla ·(\epsilon \nabla \stackrel{\sim }{\mathrm{\Phi }}(\mathbf{r}))=4\pi \sum _{\alpha =1}^{N_c}{q}_{\alpha }{C}_{\alpha }(\mathbf{r})\hfill & \mathbf{r}\in \mathrm{\Omega }\hfill \\ [\stackrel{\sim }{\mathrm{\Phi }}(\mathbf{r})]=0\hfill & \mathbf{r}\in \mathrm{\Gamma }\hfill \\ [\epsilon {\stackrel{\sim }{\mathrm{\Phi }}}_{\mathbf{n}}(\mathbf{r})]={\epsilon }_m\nabla ({\mathrm{\Phi }}^{\ast }(\mathbf{r})+{\mathrm{\Phi }}^0(\mathbf{r}))·\mathbf{n}\hfill & \mathbf{r}\in \mathrm{\Gamma }\hfill \end{array}$$ (13)

Note that as a consequence, the interface jump condition in Eq. (13) is modified from the original one. Therefore, to compute the electrostatic potential, we need to solve both Eqs. (12) and (13).

II.B.2 Matched interface and boundary (MIB) method

By applying the Green’s function formulation, the resulting system, i.e., Eqs. (12), (13) and (6), is slightly different from the original PNP equations. Numerically, three equations need to be solved iteratively. While it seems to increase the computational complexity, in fact, Eq (12) only needs to be solved once since it is independent of the concentration profile, and the benefit is that one does not have to do the discretization of the delta function. In this section, the computational details for solving these equations are discussed. Here, the standard second order central finite difference scheme is adopted for the interpolation of the regular points (which are away from the interface and boundary^{20, 51}), while the interpolation for irregular points (which are close to the interface^{20, 51}) needs some efforts for different interface and boundary conditions. The matched interface and boundary (MIB) method is employed here to take care of the irregular points where the fictitious values are used and also a set of auxiliary points is involved.

Solution to the boundary value problem

To obtain Φ⁰(r), we need to solve the boundary value problem given in Eq (12). We use the standard seven-point finite difference scheme on all the regular grid points, and for irregular points, we use the interface values at the intersecting points of the mesh and the interface. Since the resulting finite difference weights of the seven-point scheme are not strictly symmetric, this treatment slightly reduces the accuracy of the scheme at the grid points close to the interface. However, we have tested that this local accuracy reduction does not affect the overall second order convergence of our scheme.²⁰ Moreover, in the discretization, care is taken to ensure the resulting matrix is nearly symmetric and almost diagonally dominant so that it can be efficiently solved by a preconditioned biconjugate gradient solver⁵¹ or other Krylov space techniques.⁹

Solution to the elliptic interface problem

To obtain Φ̃(r), we need to solve the interface problem given by Eq (13). Assuming C_α where α = 1, 2, …, N_c are known at this moment, our goal is to solve this elliptic equation with complex interface geometry. Note that in this case the interface is the surface of the protein molecule. Here the MIB method is used to enforce the jump condition along the interface by employing fictitious values and auxiliary points. It has been shown in the literature, computationally, the MIB method can handle the interface with large curvatures, deal with discontinuous coefficients of the elliptic equation and keep the overall second-order of accuracy of the numerical scheme in the presence of many irregular points.^{50, 51, 55} Furthermore, a systematic way of decomposing the 2D and 3D problems to 1D ones is developed, and it can be extended to high order schemes by using a similar idea as shown in the second-order scheme.

To discretize the equation along x direction at point (i, j, k), we use

$${(\epsilon {\stackrel{\sim }{\mathrm{\Phi }}}_x)}_x=\frac{{\epsilon }_{i+\frac{1}{2}}{\stackrel{\sim }{\mathrm{\Phi }}}_{i+1,j,k}-({\epsilon }_{i+\frac{1}{2}}+{\epsilon }_{i-\frac{1}{2}}){\stackrel{\sim }{\mathrm{\Phi }}}_{i,j,k}+{\epsilon }_{i-\frac{1}{2}}{\stackrel{\sim }{\mathrm{\Phi }}}_{i-1,j,k}}{{(\mathrm{\Delta }x)}^2},$$ (14)

where Δx is the mesh size on the x direction.

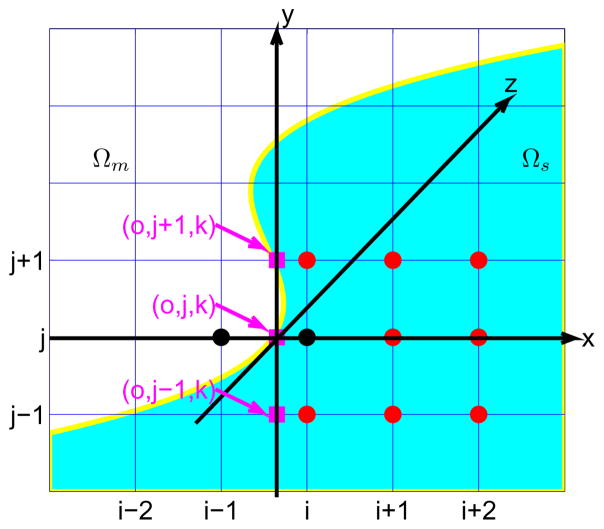
Since the solution Φ̃ may not be a smooth function across the interface, the application of this conventional finite difference scheme needs to be reconsidered for the irregular point, such as the point (i, j, k) and (i − 1, j, k) in Fig. 2, which are very close to the interface. In this context, the notation “f” is used to denote the fictitious value. For example, f_i−1,j,k denotes the fictitious value at point (i − 1, j, k) extended from domain Ω_s, while f_i,j,k denotes the fictitious value at point (i, j, k) extended from domain Ω_m. In this case, the discretization scheme would be

Figure 2.

An illustration of the geometry near the interface. The jth mesh line intersects the interface at point (0, j, k). A pair of irregular points (i − 1, j, k) and (i, j, k) are indicated by black ●, and other auxiliary points are indicated by red .

$${(\epsilon {\stackrel{\sim }{\mathrm{\Phi }}}_x)}_x{\mid }_{(i-1,j,k)}=\frac{{\epsilon }_{i-\frac{1}{2}}{f}_{i,j,k}-({\epsilon }_{i-\frac{1}{2}}+{\epsilon }_{i-\frac{3}{2}}){\stackrel{\sim }{\mathrm{\Phi }}}_{i-1,j,k}+{\epsilon }_{i-\frac{3}{2}}{\stackrel{\sim }{\mathrm{\Phi }}}_{i-2,j,k}}{{(\mathrm{\Delta }x)}^2}$$ (15)

$${(\epsilon {\stackrel{\sim }{\mathrm{\Phi }}}_x)}_x{\mid }_{(i,j,k)}=\frac{{\epsilon }_{i+\frac{1}{2}}{\stackrel{\sim }{\mathrm{\Phi }}}_{i+1,j,k}-({\epsilon }_{i+\frac{1}{2}}+{\epsilon }_{i-\frac{1}{2}}){\stackrel{\sim }{\mathrm{\Phi }}}_{i,j,k}+{\epsilon }_{i-\frac{1}{2}}{f}_{i-1,j,k}}{{(\mathrm{\Delta }x)}^2}$$ (16)

The value of f_i−1,j,k and f_i,j,k are determined by the jump conditions as shown below. First, at each intersecting point of the interface and the mesh line, we need to set up a local coordinate (ξ, η, ζ), which is related to the original reference coordinate as

$$\left[\begin{array}{c}\xi \\ \eta \\ \zeta \end{array}\right]=P·\left[\begin{array}{c}x\\ y\\ z\end{array}\right],$$ (17)

where the transformation matrix P has the form

$$P=\left[\begin{array}{ccc}sin\phi cos\theta & sin\phi sin\theta & cos\phi \\ -sin\theta & cos\theta & 0\\ -cos\phi cos\theta & -cos\phi sin\theta & sin\phi \end{array}\right].$$ (18)

Here angles are defined by the outward unit normal direction n of the interface, where n = (sin φ cos θ, sin φ sin θ, cos φ), θ and φ are the azimuth and zenith angles for n.

With this new coordinate, the jump conditions on the interface Γ can be expressed as

$$[\epsilon {\stackrel{\sim }{\mathrm{\Phi }}}_{\xi }]={\epsilon }_m(sin\phi cos\theta {\stackrel{\sim }{\mathrm{\Phi }}}_x^m+sin\phi sin\theta {\stackrel{\sim }{\mathrm{\Phi }}}_y^m+cos\phi {\stackrel{\sim }{\mathrm{\Phi }}}_z^m)-{\epsilon }_s(sin\phi cos\theta {\stackrel{\sim }{\mathrm{\Phi }}}_x^s+sin\phi sin\theta {\stackrel{\sim }{\mathrm{\Phi }}}_y^s+cos\phi {\stackrel{\sim }{\mathrm{\Phi }}}_z^s)$$ (19)

and

$$[\stackrel{\sim }{\mathrm{\Phi }}]={\stackrel{\sim }{\mathrm{\Phi }}}^m-{\stackrel{\sim }{\mathrm{\Phi }}}^s,$$ (20)

where the superscripts in Φ̃^m and Φ̃^s indicate Φ̃ is defined in Ω_m and Φ̃ is defined in Ω_s.

Then by using Eq. (19) and differentiating Eq. (20) with respect to η and ζ, one has two more jump conditions

$$\left[\begin{array}{c}[\epsilon {\stackrel{\sim }{\mathrm{\Phi }}}_{\xi }]\\ [{\stackrel{\sim }{\mathrm{\Phi }}}_{\eta }]\\ [{\stackrel{\sim }{\mathrm{\Phi }}}_{\zeta }]\end{array}\right]=\left[\begin{array}{ccc}sin\phi cos\theta & sin\phi sin\theta & cos\phi \\ -sin\theta & cos\theta & 0\\ -cos\phi cos\theta & -cos\phi sin\theta & sin\phi \end{array}\right]\left[\begin{array}{c}{\epsilon }_m{\stackrel{\sim }{\mathrm{\Phi }}}_x^m\\ {\stackrel{\sim }{\mathrm{\Phi }}}_y^m\\ {\stackrel{\sim }{\mathrm{\Phi }}}_z^m\end{array}\right]-\left[\begin{array}{ccc}sin\phi cos\theta & sin\phi sin\theta & cos\phi \\ -sin\theta & cos\theta & 0\\ -cos\phi cos\theta & -cos\phi sin\theta & sin\phi \end{array}\right]\left[\begin{array}{c}{\epsilon }_s{\stackrel{\sim }{\mathrm{\Phi }}}_x^s\\ {\stackrel{\sim }{\mathrm{\Phi }}}_y^s\\ {\stackrel{\sim }{\mathrm{\Phi }}}_z^s\end{array}\right].$$ (21)

Therefore, we have a total of four jump conditions but only two fictitious values to be determined.

In Eq. (21), there are six derivatives involved in the computation. Due to geometric constraints, some of these six derivatives may be difficult to obtain numerically. To reduce the difficulty of doing discretizations for the derivatives, two of the most difficult-to-valuate ones are determined and eliminated in our approach by utilizing jump conditions in Eq. (21). If the fictitious values are on x direction, then one of the derivatives on y direction ( ${\stackrel{\sim }{\mathrm{\Phi }}}_y^m,{\stackrel{\sim }{\mathrm{\Phi }}}_y^s$) can be eliminated. Additionally, one of the derivatives on z direction ( ${\stackrel{\sim }{\mathrm{\Phi }}}_z^m,{\stackrel{\sim }{\mathrm{\Phi }}}_z^s$) can be eliminated. The main principle of eliminating the derivatives is to keep those derivatives that are easier to evaluate, and eliminate those that are comparatively difficult to evaluate due to geometric constraints. As a result, if ${\stackrel{\sim }{\mathrm{\Phi }}}_y^m$ and ${\stackrel{\sim }{\mathrm{\Phi }}}_z^m$ are eliminated by some algebraic computation in Eq. (21), then

$$a[\epsilon {\stackrel{\sim }{\mathrm{\Phi }}}_{\xi }]+b[{\stackrel{\sim }{\mathrm{\Phi }}}_{\eta }]+c[{\stackrel{\sim }{\mathrm{\Phi }}}_{\zeta }]=d_1{\stackrel{\sim }{\mathrm{\Phi }}}_x^m+d_2{\stackrel{\sim }{\mathrm{\Phi }}}_x^s+d_3{\stackrel{\sim }{\mathrm{\Phi }}}_y^s+d_4{\stackrel{\sim }{\mathrm{\Phi }}}_z^s,$$ (22)

where the coefficients a, b, c, d₁, d₂, d₃ and d₄ are obtained through the algebraic computation while carrying out the elimination. In this paper, w_n,i, w_n,j and w_n,k are used to denote the nth order weight coefficients along x, y, or z direction evaluated at different i, j or k positions respectively. Then by using two jump conditions, Eq. (20) and the new formulated jump condition Eq. (22) on the interface Γ, we have

$$[\stackrel{\sim }{\mathrm{\Phi }}]=({\omega }_{0,i-2},{\omega }_{0,i-1},{\omega }_{0,i}){({\stackrel{\sim }{\mathrm{\Phi }}}_{i-2,j,k},{\stackrel{\sim }{\mathrm{\Phi }}}_{i-1,j,k},f_{i,j,k})}^T-({\omega }_{0,i-1},{\omega }_{0,i},{\omega }_{0,i+1}){(f_{i-1,j,k},{\stackrel{\sim }{\mathrm{\Phi }}}_{i,j,k},{\stackrel{\sim }{\mathrm{\Phi }}}_{i+1,j,k})}^T$$ (23)

$$a[\epsilon {\stackrel{\sim }{\mathrm{\Phi }}}_{\xi }]+b[{\stackrel{\sim }{\mathrm{\Phi }}}_{\eta }]+c[{\stackrel{\sim }{\mathrm{\Phi }}}_{\zeta }]=d_1({\omega }_{1,i-2},{\omega }_{1,i-1},{\omega }_{1,i}){({\stackrel{\sim }{\mathrm{\Phi }}}_{i-2,j,k},{\stackrel{\sim }{\mathrm{\Phi }}}_{i-1,j,k},f_{i,j,k})}^T+d_1({\omega }_{1,i-1},{\omega }_{1,i},{\omega }_{1,i+1}){(f_{i-1,j,k},{\stackrel{\sim }{\mathrm{\Phi }}}_{i,j,k},{\stackrel{\sim }{\mathrm{\Phi }}}_{i+1,j,k})}^T+d_3{\stackrel{\sim }{\mathrm{\Phi }}}_y^s+d_4{\stackrel{\sim }{\mathrm{\Phi }}}_z^s.$$ (24)

Since ${\stackrel{\sim }{\mathrm{\Phi }}}_y^s$ and ${\stackrel{\sim }{\mathrm{\Phi }}}_z^s$ are the derivatives that can be evaluated by using the auxiliary points, if the geometry is shown as in Fig. 2, then the red dots on the figure can be chosen to interpolate the values on the off-grid points, namely Φ̃_o,j−1,k, Φ̃_o,j,k and Φ̃_o,j+1,k. In this case the following discretization scheme can be applied

$$\begin{array}{l}{\stackrel{\sim }{\mathrm{\Phi }}}_y^s=({\omega }_{1,j-1},{\omega }_{1,j},{\omega }_{1,j+1}){({\stackrel{\sim }{\mathrm{\Phi }}}_{o,j-1,k},{\stackrel{\sim }{\mathrm{\Phi }}}_{o,j,k},{\stackrel{\sim }{\mathrm{\Phi }}}_{o,j+1,k})}^T\\ =({\omega }_{1,j-1},{\omega }_{1,j},{\omega }_{1,j+1})\left[\begin{array}{c}({\omega }_{0,i},{\omega }_{0,i+1},{\omega }_{0,i+2}){({\stackrel{\sim }{\mathrm{\Phi }}}_{i,j-1,k},{\stackrel{\sim }{\mathrm{\Phi }}}_{i+1,j-1,k},{\stackrel{\sim }{\mathrm{\Phi }}}_{i+2,j-1,k})}^T\\ ({\omega }_{0,i},{\omega }_{0,i+1},{\omega }_{0,i+2}){({\stackrel{\sim }{\mathrm{\Phi }}}_{i,j,k},{\stackrel{\sim }{\mathrm{\Phi }}}_{i+1,j,k},{\stackrel{\sim }{\mathrm{\Phi }}}_{i+2,j,k})}^T\\ ({\omega }_{0,i},{\omega }_{0,i+1},{\omega }_{0,i+2}){({\stackrel{\sim }{\mathrm{\Phi }}}_{i,j+1,k},{\stackrel{\sim }{\mathrm{\Phi }}}_{i+1,j+1,k},{\stackrel{\sim }{\mathrm{\Phi }}}_{i+2,j+1,k})}^T\end{array}\right].\end{array}$$ (25)

Assuming the geometry is the same along z direction, then we have the following expression

$${\stackrel{\sim }{\mathrm{\Phi }}}_z^s=({\omega }_{1,k-1},{\omega }_{1,k},{\omega }_{1,k+1})=\left[\begin{array}{c}({\omega }_{0,i},{\omega }_{0,i+1},{\omega }_{0,i+2}){({\stackrel{\sim }{\mathrm{\Phi }}}_{i,j,k-1},{\stackrel{\sim }{\mathrm{\Phi }}}_{i+1,j,k-1},{\stackrel{\sim }{\mathrm{\Phi }}}_{i+2,j,k-1})}^T\\ ({\omega }_{0,i},{\omega }_{0,i+1},{\omega }_{0,i+2}){({\stackrel{\sim }{\mathrm{\Phi }}}_{i,j,k},{\stackrel{\sim }{\mathrm{\Phi }}}_{i+1,j,k},{\stackrel{\sim }{\mathrm{\Phi }}}_{i+2,j,k})}^T\\ ({\omega }_{0,i},{\omega }_{0,i+1},{\omega }_{0,i+2}){({\stackrel{\sim }{\mathrm{\Phi }}}_{i,j,k+1},{\stackrel{\sim }{\mathrm{\Phi }}}_{i+1,j,k+1},{\stackrel{\sim }{\mathrm{\Phi }}}_{i+2,j,k+1})}^T\end{array}\right].$$ (26)

Let g₁ = [Φ̃], g₂ = a[εΦ̃_ξ] + b[Φ̃_η] + c[Φ̃_ζ], and plug Eq. (25) and Eq. (26) into Eq. (24), we have

$$g_2=d_1({\omega }_{1,i-2},{\omega }_{1,i-1},{\omega }_{1,i}){({\stackrel{\sim }{\mathrm{\Phi }}}_{i-2,j,k},{\stackrel{\sim }{\mathrm{\Phi }}}_{i-1,j,k},f_{i,j,k})}^T-d_2({\omega }_{1,i-1},{\omega }_{1,i},{\omega }_{1,i+1}){(f_{i-1,j,k},{\stackrel{\sim }{\mathrm{\Phi }}}_{i,j,k},{\stackrel{\sim }{\mathrm{\Phi }}}_{i+1,j,k})}^T+d_3({\omega }_{1,j-1},{\omega }_{1,j},{\omega }_{1,j+1})\left[\begin{array}{c}({\omega }_{0,i},{\omega }_{0,i+1},{\omega }_{0,i+2}){({\stackrel{\sim }{\mathrm{\Phi }}}_{i,j-1,k},{\stackrel{\sim }{\mathrm{\Phi }}}_{i+1,j-1,k},{\stackrel{\sim }{\mathrm{\Phi }}}_{i+2,j-1,k})}^T\\ ({\omega }_{0,i},{\omega }_{0,i+1},{\omega }_{0,i+2}){({\stackrel{\sim }{\mathrm{\Phi }}}_{i,j,k},{\stackrel{\sim }{\mathrm{\Phi }}}_{i+1,j,k},{\stackrel{\sim }{\mathrm{\Phi }}}_{i+2,j,k})}^T\\ ({\omega }_{0,i},{\omega }_{0,i+1},{\omega }_{0,i+2}){({\stackrel{\sim }{\mathrm{\Phi }}}_{i,j+1,k},{\stackrel{\sim }{\mathrm{\Phi }}}_{i+1,j+1,k},{\stackrel{\sim }{\mathrm{\Phi }}}_{i+2,j+1,k})}^T\end{array}\right].+d_4({\omega }_{1,k-1},{\omega }_{1,k},{\omega }_{1,k+1})\left[\begin{array}{c}({\omega }_{0,i},{\omega }_{0,i+1},{\omega }_{0,i+2}){({\stackrel{\sim }{\mathrm{\Phi }}}_{i,j,k-1},{\stackrel{\sim }{\mathrm{\Phi }}}_{i+1,j,k-1},{\stackrel{\sim }{\mathrm{\Phi }}}_{i+2,j,k-1})}^T\\ ({\omega }_{0,i},{\omega }_{0,i+1},{\omega }_{0,i+2}){({\stackrel{\sim }{\mathrm{\Phi }}}_{i,j,k},{\stackrel{\sim }{\mathrm{\Phi }}}_{i+1,j,k},{\stackrel{\sim }{\mathrm{\Phi }}}_{i+2,j,k})}^T\\ ({\omega }_{0,i},{\omega }_{0,i+1},{\omega }_{0,i+2}){({\stackrel{\sim }{\mathrm{\Phi }}}_{i,j,k+1},{\stackrel{\sim }{\mathrm{\Phi }}}_{i+1,j,k+1},{\stackrel{\sim }{\mathrm{\Phi }}}_{i+2,j,k+1})}^T\end{array}\right].$$ (27)

Reorganizing each term in Eq. (23) and Eq. (27), it forms the following small linear system

$$\left[\begin{array}{cc}{a}_{11}& a_{12}\\ a_{21}& a_{22}\end{array}\right]\left[\begin{array}{c}{f}_{i-1,j,k}\\ f_{i,j,k}\end{array}\right]=\left[\begin{array}{c}\sum _{l,m,n}{b}_{1(l,m,n)}{\stackrel{\sim }{\mathrm{\Phi }}}_{l,m,n}+g_1\\ \sum _{l,m,n}{b}_{2(l,m,n)}{\stackrel{\sim }{\mathrm{\Phi }}}_{l,m,n}+g_2\end{array}\right],$$ (28)

where a_ij and b_i(l,m,n)(i = 1, 2) are the coefficients, Φ̃_l,m,n are all the values of Φ̃ on auxiliary grid points used in the computation, i.e., Φ̃_i−1,j,k, Φ̃_i,j,k, Φ̃_i+1,j,k, Φ̃_i+2,j,k, Φ̃_i,j−1,k, Φ̃_i+1,j−1,k, Φ̃_i+2,j−1,k, Φ̃_i,j+1,k, Φ̃ _i+1,j+1,k, Φ̃_i+2,j+1,k, Φ̃_i,j,k−1, Φ̃_i+1,j,k−1, Φ̃_i+2,j,k−1, Φ̃_i,j,k+1, Φ̃_i+1,j,k+1 and Φ̃_i+2,j,k+1 in the above mentioned case.

Solving Eq. (28), then f_i−1,j,k and f_i,j,k can be written as a linear combination of Φ̃ values defined on the mesh grids and the jump condition values g₁ and g₂, that is:

$$\left[\begin{array}{c}{f}_{i-1,j,k}\\ f_{i,j,k}\end{array}\right]=\left[\begin{array}{c}\sum _{l,m,n}{p}_{1(l,m,n)}{\stackrel{\sim }{\mathrm{\Phi }}}_{l,m,n}+p_1{g}_1\\ \sum _{l,m,n}{p}_{2(l,m,n)}{\stackrel{\sim }{\mathrm{\Phi }}}_{l,m,n}+p_2{g}_2\end{array}\right],$$ (29)

where p_i(l,m,n) and p_i (i = 1, 2) are the computed coefficients. This relation can be applied to Eqs. (15) and (16) for the discretization. Here one important issue is how to choose the set of auxiliary points for the interpolation of the off-grid points. One systematic way is shown in the next section. Details on how to treat some particular cases are discussed in our earlier work.⁵¹

Solution to the mixed boundary value problem

To obtain C_α(r), we need to solve Eq (6). For simplicity, let $\lambda =\frac{q_{\alpha }}{k_{B}T}$, and the index α in C_α(r) and D_α is dropped in this section, since the same discretization scheme is used for obtaining the concentration of each ion species. Here, we present the discretization scheme by an example along x direction. To discretize the equation along x direction at point (i, j, k), we have

$${(D(C_x+\lambda C{\mathrm{\Phi }}_x))}_x=D_{i+\frac{1}{2}}\left(C_{i+1,j,k}-C_{i,j,k}+\lambda \frac{1}{2}(C_{i+1,j,k}+C_{i,j,k})({\mathrm{\Phi }}_{i+1,j,k}-{\mathrm{\Phi }}_{i,j,k})\right)\frac{1}{{(\mathrm{\Delta }x)}^2}-D_{i-\frac{1}{2}}\left(C_{i,j,k}-C_{i-1,j,k}+\lambda \frac{1}{2}(C_{i,j,k}+C_{i-1,j,k})({\mathrm{\Phi }}_{i,j,k}-{\mathrm{\Phi }}_{i-1,j,k})\right)\frac{1}{{(\mathrm{\Delta }x)}^2}$$ (30)

This conventional central finite difference scheme is adopted for all the regular points, however, the scheme needs to be modified for the irregular points according to different boundary conditions. Here we test two different kinds of boundary conditions given in Eqs. (7) and (8). The implementation details of these two different boundary conditions are discussed below.

Boundary condition I

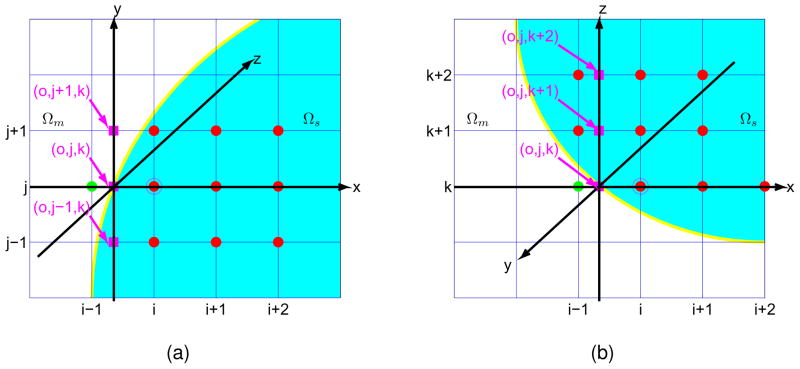
The boundary condition is given by the normal component of the flux, i.e., J · n = 0 on Γ. Consider one geometry as shown in Fig. 3, here we need to rewrite the value of f_i−1,j,k as a linear combination of the values defined inside Ω_s. That is, the solution inside the domain Ω_s is smoothly extended by using the boundary condition. The extension may vary for different boundary conditions. For the boundary condition given in Eq (7), we have the following condition at the off grid interface point (o, j, k),

Figure 3.

Sets of auxiliary points for the discretization of the derivatives. (a) Auxiliary points along y direction; (b) Auxiliary points along z direction.

$$(C_x+\lambda C{\mathrm{\Phi }}_x)n_1+(C_y+\lambda C{\mathrm{\Phi }}_y)n_2+(C_z+\lambda C{\mathrm{\Phi }}_z)n_3=0.$$ (31)

By rearranging similar terms, this equality can be rewritten as

$$C_x{n}_1+C_y{n}_2+C_z{n}_3+\lambda C({\mathrm{\Phi }}_x{n}_1+{\mathrm{\Phi }}_y{n}_2+{\mathrm{\Phi }}_z{n}_3)=0.$$ (32)

The main issue here is how to carry out the discretizations for C_y, C_z, Φ_x, Φ_y and Φ_z at (o, j, k). The following scheme is used for finding auxiliary points along y and z directions.

To discretize C_y, a set of auxiliary points are involved. A systematic way for the selection of auxiliary points is described as follows.

• Step 1): Determine the possible strategies for the discretization of the first derivative along the y direction

  • Strategy A:

    $$C_y{\mid }_{o,j,k}=({\omega }_{1,j-1},{\omega }_{1,j},{\omega }_{1,j+1}){(C_{o,j-1,k},C_{o,j,k},C_{o,j+1,k})}^T$$
  • Strategy B:

    $$C_y{\mid }_{o,j,k}=({\omega }_{1,j},{\omega }_{1,j+1},{\omega }_{1,j+2}){(C_{o,j,k},C_{o,j+1,k},C_{o,j+2,k})}^T$$
  • and Strategy C:

    $$C_y{\mid }_{o,j,k}=({\omega }_{1,j-2},{\omega }_{1,j-1},{\omega }_{1,j}){(C_{o,j-2,k},C_{o,j-1,k},C_{o,j,k})}^T$$

• Step 2): Find a possible choice for the interpolation at (o,m,k), where m = j − 2, j − 1, j,j + 1 and j + 2. For example, to interpolate C(o,j − 2, k), the following choices can be used to find the auxiliary points.

  • Choice A:

    $$C_{o,j-2,k}=({\omega }_{0,i-1},{\omega }_{0,i},{\omega }_{0,i+1}){(C_{i-1,j-2,k},C_{i,j-2,k},C_{i+1,j-2,k})}^T$$
  • Choice B:

    $$C_{o,j-2,k}=({\omega }_{0,i},{\omega }_{0,i+1},{\omega }_{0,i+2}){(C_{i,j-2,k},C_{i+1,j-2,k},C_{i+2,j-2,k})}^T$$
  • and Choice C:

    $$C_{o,j-2,k}=({\omega }_{0,i-2},{\omega }_{0,i-1},{\omega }_{0,i}){(C_{i-2,j-2,k},C_{i-1,j-2,k},C_{i,j-2,k})}^T$$

    Here one of the choices can be taken if all three points for the interpolation are all inside Ω_s; say if (i − 1,j − 2,k), (i,j − 2,k) and (i + 1, j − 2,k) are all inside Ω_s, then Choice A is taken for the interpolation of C_o,j−2,k.

• Step 3): Make the decision after 9 points are found for the interpolation, and all the choices are sorted sequentially. In fact, we prefer central schemes (Strategy A), as long as C_o,j−1,k, C_o,j,k and C_o,j+1,k, each of them can be found by one of the interpolation schemes in Choices A, B and C. Here if the geometry around point (i, j, k) is as what is shown in Fig. 3, then follow Steps 1) to 3), the red points can be used as the auxiliary points for the interpolation, and f_i−1,j,k can be written as a linear combination of the points C_i,j,k and C_i+1,j,k, in addition to red points.

Boundary condition II

The boundary condition is given by the flux component on the interface, i.e., J = 0 on Γ. Define J = (J^x, J^y, J^z), then the following discretization schemes are applied for different geometries. If (i − 1, j, k) lies outside Ω_s, while (i, j, k), (i + 1, j, k), (i + 2, j, k) are all inside Ω_s as shown in Fig. 3, then

$$\begin{array}{l}\frac{\partial J^x}{\partial x}{\mid }_{(i,j,k)}=w_{1,o}{J}_{o,j,k}^x+w_{1,i+\frac{1}{2}}{J}_{1+\frac{1}{2},j,k}^x+w_{1,i+\frac{3}{2}}{J}_{i+\frac{3}{2},j,k}^x\\ =w_{1,o}{J}_{o,j,k}^x+w_{1,i+\frac{1}{2}}(-D_{i+\frac{1}{2}})\left[\frac{C_{i+1,j,k}-C_{i,j,k}}{\mathrm{\Delta }x}+\lambda \frac{1}{2}(C_{i+1,j,k}+C_{i,j,k})\frac{{\mathrm{\Phi }}_{i+1,j,k}-{\mathrm{\Phi }}_{i,j,k}}{\mathrm{\Delta }x}\right]+w_{1,i+\frac{3}{2}}(-D_{i+\frac{3}{2}})\left[\frac{C_{i+2,j,k}-C_{i+1,j,k}}{\mathrm{\Delta }x}+\lambda \frac{1}{2}(C_{i+2,j,k}+C_{i+1,j,k})\frac{{\mathrm{\Phi }}_{i+2,j,k}-{\mathrm{\Phi }}_{i+1,j,k}}{\mathrm{\Delta }x}\right].\end{array}$$ (33)

If (i − 1, j, k) and (i + 2, j, k) lie outside Ω_s, while (i, j, k), (i + 1, j, k) are inside Ω_s, define (o′, j, k) as the interface point between (i + 1, j, k) and (i + 2, j, k), then

$$\begin{array}{l}\frac{\partial J^x}{\partial x}{\mid }_{(i,j,k)}=w_{1,o}{J}_{o,j,k}^x+w_{1,i+\frac{1}{2}}{J}_{i+\frac{1}{2},j,k}^x+w_{1,o^{\prime }}{J}_{o^{\prime },j,k}^x\\ =w_{1,o}{J}_{o,j,k}^x+w_{1,i+\frac{1}{2}}(-D_{i+\frac{1}{2}})\left[\frac{C_{i+1,j,k}-C_{i,j,k}}{\mathrm{\Delta }x}+\lambda \frac{1}{2}(C_{i+1,j,k}+C_{i,j,k})\frac{{\mathrm{\Phi }}_{i+1,j,k}-{\mathrm{\Phi }}_{i,j,k}}{\mathrm{\Delta }x}\right]+w_{1,o^{\prime }}{J}_{o^{\prime },j,k}^x.\end{array}$$ (34)

So basically the geometry around (i, j, k) is examined first and then the corresponding scheme is applied for the irregular point.

II.B.3 Iterative scheme for the coupled PNP system

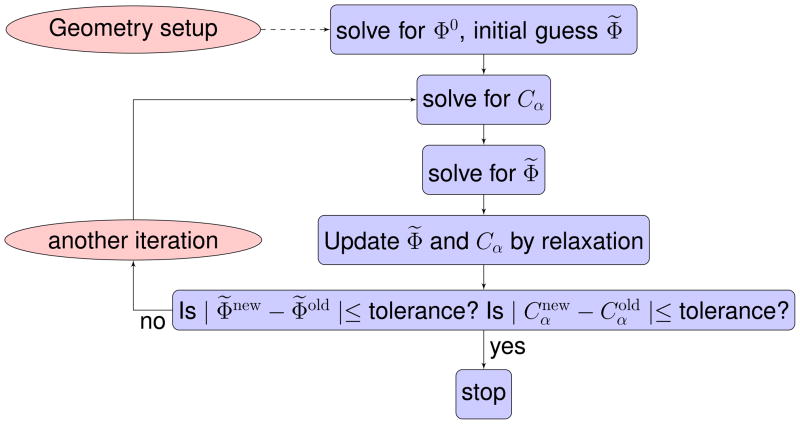
To obtain the solution for the PNP system, we start from solving Eq (12). We then solve Eqs. (13) and (6) iteratively. A flow chart of our solution procedure is given in Fig. 4. The Successive Over Relaxation (SOR)-like iterations are used to make sure that the algorithm is convergent^8,11

Figure 4.

Flowchart of the numerical implementation of solving the PNP system.

$$\{\begin{array}{l}{\mathrm{\Phi }}^{\text{new}}=w{\mathrm{\Phi }}^{\text{old}}+(1-w){\mathrm{\Phi }}^{\text{new}}\hfill \\ C_{\alpha }^{\text{new}}=w{C}_{\alpha }^{\text{old}}+(1-w)C_{\alpha }^{\text{new}}\hfill \end{array}$$ (35)

where the relaxation parameter w is selected between 0 and 2. We have noted that without the use of the SOR-like scheme, the direct iteration may not converge. A similar iterative scheme was also used in our differential geometry based solvation analysis to obtain the solution to the coupled Poisson-Boltzmann and surface evolution equations.¹¹

In this work, we also utilize the Gummel iteration,¹⁵ which is another efficient way for solving the coupled nonlinear partial different equations (PDEs). The comparison of the performance of two iterative schemes is presented in Section IV.C.

III Numerical validation

In this section, we examine the convergence order, test the accuracy and demonstrate the feasibility of the proposed PNP schemes. We design analytical solutions for the coupled PNP equations by slightly modifying the right hand source term. The numerical tests are carried out from simpler geometries to complicated biomolecular structures. To analyze the numerical performance of the proposed schemes, we use two error measurements, i.e., the maximum absolute error L_∞ and L₂ error by comparing to the exact solution

$$\begin{array}{l}{L}_{\infty }={max}_{i,j,k}\mid u(i,j,k)-u_{\text{ex}}(i,j,k)\mid \\ L_2=\sqrt{\frac{1}{N_x{N}_y{N}_z}{\sum }_{i,j,k}{(u(i,j,k)-u_{\text{ex}}(i,j,k))}^2}\end{array}$$ (36)

where u and u_ex are numerical and exact solutions, respectively. Here each linear system formed by the discretization is solved using the portable, extensible toolkit for scientific computation (PETSc), see the webpage “http://www.mcs.anl.gov/petsc/petsc-as/” for details. It is a suite of data structures and routines for the scalable (parallel) solution of scientific applications modeled by partial differential equations. For PETSc options, Incomplete LU is chosen as the pre-conditioner and the tolerance of the PETSc iterations is set to be 10⁻⁶ in all test cases. In this section, the dielectric constants ε_m = 1 and ε_s = 80 are used for the numerical tests.

III.A Analytical test solutions for the PNP system

It is difficult to find the analytic solution to the PNP system for 3D realistic geometries. To validate the proposed numerical method, we design the test solutions which mimic all the important features of the PNP system with some modifications of the jump conditions and right hand side of the equations. Specifically, the right hand side of the equations and the jump conditions are derived from the given test solutions. The test solutions are prescribed in the following form

$$\mathrm{\Phi }(\mathbf{r})=\{\begin{array}{ll}\text{cos}x\text{cos}y\text{cos}z+{\mathrm{\Phi }}^{\ast }(\mathbf{r})\hfill & \mathbf{r}\in {\mathrm{\Omega }}_m\hfill \\ -\frac{2\pi }{3{\epsilon }_s}\text{cos}x\text{cos}y\text{cos}z\hfill & \mathbf{r}\in {\mathrm{\Omega }}_s\hfill \end{array}$$ (37)

$$C_1(\mathbf{r})=\{\begin{array}{ll}0\hfill & \mathbf{r}\in {\mathrm{\Omega }}_m\hfill \\ \text{cos}x\text{cos}y\text{cos}z+1.0\hfill & \mathbf{r}\in {\mathrm{\Omega }}_s\hfill \end{array}$$ (38)

$$C_2(\mathbf{r})=\{\begin{array}{ll}0\hfill & \mathbf{r}\in {\mathrm{\Omega }}_m\hfill \\ 0.5\text{cos}x\text{cos}y\text{cos}z+1.0\hfill & \mathbf{r}\in {\mathrm{\Omega }}_s,\hfill \end{array}$$ (39)

where r = (x, y, z), and Φ^*(r) is defined as

$${\mathrm{\Phi }}^{\ast }(\mathbf{r})=\sum _{\beta =1}^{N_a}\frac{q_{\beta }}{{\epsilon }_m\sqrt{{(x-x_{\beta })}^2+{(y-y_{\beta })}^2+{(z-z_{\beta })}^2}},$$ (40)

where r_β are atomic central positions of proteins taken from the Protein Data Bank (PDB) and q_β are their corresponding partial charges. Note that these solutions can be very oscillatory when the computational domain is very large, which is the case for ion channel geometries.

Accordingly, this set of solutions satisfies the following PNP type equations

$$\{\begin{array}{ll}-\nabla ·(\epsilon (\mathbf{r})\nabla \mathrm{\Phi }(\mathbf{r}))=4\pi \sum _{\beta =1}^{N_a}\delta (\mathbf{r}-{\mathbf{r}}_{\beta })+4\pi \sum _{\alpha =1}^2{q}_{\alpha }{C}_{\alpha }(\mathbf{r})+F(\mathbf{r})\hfill & \mathbf{r}\in \mathrm{\Omega }\hfill \\ \nabla ·D_1(\mathbf{r})[\nabla C_1(\mathbf{r})+q_1{C}_1(\mathbf{r})\nabla \mathrm{\Phi }(\mathbf{r})]=F_1(\mathbf{r})\hfill & \mathbf{r}\in {\mathrm{\Omega }}_s\hfill \\ \nabla ·D_2(\mathbf{r})[\nabla C_2(\mathbf{r})+q_2{C}_2(\mathbf{r})\nabla \mathrm{\Phi }(\mathbf{r})]=F_2(\mathbf{r})\hfill & \mathbf{r}\in {\mathrm{\Omega }}_s\hfill \end{array}$$ (41)

Where q₁ = 1, q₂ = −1, D₁(r) ≡ 1 and D₂(r) ≡ 1, and

$$\{\begin{array}{l}F(\mathbf{r})=\{\begin{array}{ll}3\text{cos}x\text{cos}y\text{cos}z\hfill & \text{in}{\mathrm{\Omega }}_m\hfill \\ 0\hfill & \text{in}{\mathrm{\Omega }}_s\hfill \end{array}\hfill \\ F_1(\mathbf{r})=-3.0\text{cos}x\text{cos}y\text{cos}z+\nabla ·\left[(\text{cos}x\text{cos}y\text{cos}z+1.0)\nabla (-\frac{2\pi }{3{\epsilon }_s}\text{cos}x\text{cos}y\text{cos}z)\right]\text{in}{\mathrm{\Omega }}_s\hfill \\ F_2(\mathbf{r})=-1.5\text{cos}x\text{cos}y\text{cos}z-\nabla ·\left[(0.5\text{cos}x\text{cos}y\text{cos}z+1.0)\nabla (-\frac{2\pi }{3{\epsilon }_s}\text{cos}x\text{cos}y\text{cos}z)\right]\text{in}{\mathrm{\Omega }}_s.\hfill \end{array}$$ (42)

On the interface Γ, the jump conditions for the electrostatic potential are given by

$$\{\begin{array}{l}[\mathrm{\Phi }]=\text{cos}x\text{cos}y\text{cos}z+{\mathrm{\Phi }}^{\ast }(\mathbf{r})+\frac{2.0\pi }{3{\epsilon }_s}\text{cos}x\text{cos}y\text{cos}z\hfill \\ [\epsilon {\mathrm{\Phi }}_n]={\epsilon }_m\nabla [\text{cos}x\text{cos}y\text{cos}z+{\mathrm{\Phi }}^{\ast }(\mathbf{r})]·\mathbf{n}+{\epsilon }_s\nabla \left[\frac{2.0\pi }{3{\epsilon }_s}\text{cos}x\text{cos}y\text{cos}z\right]·\mathbf{n}.\hfill \end{array}$$ (43)

As discussed earlier, the non-flux boundary condition for the concentration can be implemented in two ways. Boundary condition I is given by

$$\{\begin{array}{l}-D_1(\nabla C_1+q_1{C}_1\nabla \mathrm{\Phi })·\mathbf{n}=-[\nabla (\text{cos}x\text{cos}y\text{cos}z+1.0)+(\text{cos}x\text{cos}y\text{cos}z+1.0)\nabla {\mathrm{\Phi }}_s]·\mathbf{n}\hfill \\ -D_2(\nabla C_2+q_2{C}_2\nabla \mathrm{\Phi })·\mathbf{n}=-[\nabla (0.5\text{cos}x\text{cos}y\text{cos}z+1.0)-(0.5\text{cos}x\text{cos}y\text{cos}z+1.0)\nabla {\mathrm{\Phi }}_s]·\mathbf{n}.\hfill \end{array}$$ (44)

For Boundary condition II, the boundary condition for the concentration flux is given by

$$\{\begin{array}{l}-D_1(\nabla C_1+q_1{C}_1\nabla \mathrm{\Phi })=-[\nabla (\text{cos}x\text{cos}y\text{cos}z+1.0)+(\text{cos}x\text{cos}y\text{cos}z+1.0)\nabla {\mathrm{\Phi }}_s]\hfill \\ -D_2(\nabla C_2+q_2{C}_2\nabla \mathrm{\Phi })=-[\nabla (0.5\text{cos}x\text{cos}y\text{cos}z+1.0)+(0.5\text{cos}x\text{cos}y\text{cos}z+1.0)\nabla {\mathrm{\Phi }}_s].\hfill \end{array}$$ (45)

In this work, we implement and compare these schemes. The preferred auxiliary point sets are used by one of the above mentioned strategies whenever possible.

III.B Numerical test on a spherical geometry

We consider a simple test geometry. The computational domain Ω is the cube which has the size of [−4, 4] × [−4, 4] × [−4, 4], and Ω_m is represented by a sphere centered at (0,0,0) with radius 2, as shown in Fig. 5. A unit positive charge is assigned to the center of the sphere. The analytical solution is given in Section III.A.

Figure 5.

An illustration of the spherical geometry.

Table 1 gives a comparison of numerical errors and convergence orders. It shows a very good second order convergence. We noted that the maximum error is recorded on the irregular point which is close to the interface. This result indicates that the proposed second-order PNP solver works very well for spherical geometry. Additionally, there is essentially little difference in accuracy and convergence between two concentration flux schemes. This is excepted because the geometry is very simple.

Table 1.

Numerical errors and orders in solving PNP equations for the spherical test case.

		Boundary condition I				Boundary condition II
	mesh size	L∞	L∞ order	L2	L2 order	L∞	L∞ order	L2	L2 order
	h = 0.2	3.17E-3	—	2.84E-4	—	3.34E-3	—	2.86E-4	—
Φ	h = 0.1	8.32E-4	1.93	7.41E-5	1.94	8.49E-4	1.98	7.52E-5	1.93
	h = 0.05	2.23E-4	1.90	2.02E-5	1.88	2.15E-4	1.98	1.91E-5	1.98
	h = 0.2	5.63E-3	—	1.80E-3	—	3.08E-3	—	9.27E-4	—
C1	h = 0.1	1.32E-3	2.09	4.32E-4	2.06	7.70E-4	2.00	2.35E-4	1.98
	h = 0.05	3.00E-4	2.14	9.49E-5	2.19	1.90E-4	2.02	5.92E-5	1.99
	h = 0.2	3.77E-3	—	1.22E-3	—	1.73E-3	—	5.08E-4	—
C2	h = 0.1	1.09E-3	1.79	3.32E-4	1.88	4.32E-4	2.00	1.29E-4	1.98
	h = 0.05	3.38E-4	1.84	9.23E-5	1.85	1.11E-4	1.96	3.27E-5	1.98

III.C Numerical test on two proteins

To further validate our new methods, we consider two complex systems, the molecular surfaces of two proteins whose coordinates are obtained from the Protein Data Bank (PDB IDs: 1uxc and 1ajj). For each protein data, to obtain a full all-atom model, all attached water molecules are cleaned and hydrogen atoms are added. Atomic van der Waals radii defining the dielectric boundary are taken from the CHARMM22 force field,³⁶ and the molecular surface is generated by the MSMS program with density 10 and probe radius 1.4 Å.⁴⁵ It is well-known that the molecular surface definition admits cusps and sharp self-intersecting surfaces, which may lead to accuracy reduction in the computation, see Fig. 1(d) for the geometric singularity of one protein structure. The partial charges for proteins are obtained by PDB2PQR software,¹⁶ and are accounted in Φ^*. The test solutions are given by Eqs. (46)–(48).

$$\mathrm{\Phi }(\mathbf{r})=\{\begin{array}{ll}\text{cos}x\text{cos}y\text{cos}z+{\mathrm{\Phi }}^{\ast }(\mathbf{r})\hfill & \mathbf{r}\in {\mathrm{\Omega }}_m\hfill \\ -\frac{0.4\pi }{3{\epsilon }_s}\text{cos}x\text{cos}y\text{cos}z\hfill & \mathbf{r}\in {\mathrm{\Omega }}_s\hfill \end{array}$$ (46)

$$C_1(\mathbf{r})=\{\begin{array}{ll}0\hfill & \mathbf{r}\in {\mathrm{\Omega }}_m\hfill \\ 0.2\text{cos}x\text{cos}y\text{cos}z+0.3\hfill & \mathbf{r}\in {\mathrm{\Omega }}_s\hfill \end{array}$$ (47)

$$C_2(\mathbf{r})=\{\begin{array}{ll}0\hfill & \mathbf{r}\in {\mathrm{\Omega }}_m\hfill \\ 0.1\text{cos}x\text{cos}y\text{cos}z+0.3\hfill & \mathbf{r}\in {\mathrm{\Omega }}_s\hfill \end{array}$$ (48)

The rest of the related quantities can be easily derived as shown in Section III.A.

From Fig. 6, one may see that the molecular surfaces of two proteins provide very irregular interface and complex geometry for the PNP system. The computational domain in each case is set to be slightly larger than the dimension of the molecular surface. Since for some of the irregular points, due to the geometry restriction, it is barely possible to use the central finite difference scheme for the discretization, there are some loss of accuracy in the L_∞ norm, as show in Tables 2 and 3, but since this accuracy reduction occurs only to a few points, the L₂ norms of both cases show very good convergent results. Due to complexity of the problem, the results shown in Tables 2 and 3 are the best for PNP equations applied to real protein structures with primitive molecular surfaces, to our knowledge.

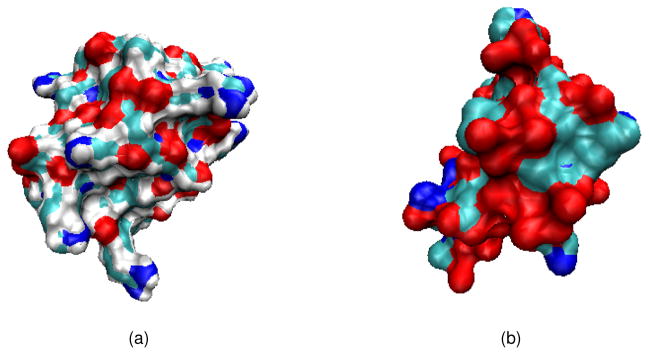
Figure 6.

Illustrations of two protein structures used in the numerical tests. The color maps indicate the residues. (a) Protein 1uxc; (b) Protein 1ajj.

Table 2.

Numerical errors in solving PNP equations for protein structure 1uxc.

		Boundary condition I				Boundary condition II
	mesh size	L∞	L∞ order	L2	L2 order	L∞	L∞ order	L2	L2 order
	h = 1.0	0.11	—	1.19E-2	—	9.98E-2	—	1.02E-2	—
Φ	h = 0.5	2.80E-2	1.97	3.08E-3	1.95	2.42E-2	2.04	2.50E-3	2.03
	h = 0.25	6.99E-3	2.00	7.97E-4	1.95	5.98E-3	2.02	6.27E-4	2.00
	h = 1.0	0.30	—	1.35E-2	—	8.07E-2	—	6.25E-3	—
C1	h = 0.5	3.83E-2	2.96	3.20E-3	2.08	1.31E-2	2.62	1.44E-3	2.12
	h = 0.25	1.24E-2	1.63	8.58E-4	1.90	2.67E-3	2.29	3.52E-4	2.03
	h = 1.0	0.11	—	8.86E-3	—	4.23E-2	—	3.47E-3	—
C2	h = 0.5	2.15E-2	2.12	2.34E-3	1.92	7.37E-3	2.52	7.67E-4	2.18
	h = 0.25	6.93E-3	1.63	5.54E-4	2.08	1.21E-3	2.61	1.84E-4	2.06

Table 3.

Numerical errors in solving PNP equations for protein structure 1ajj.

		Boundary condition I				Boundary condition II
	mesh size	L∞	L∞ order	L2	L2 order	L∞	L∞ order	L2	L2 order
	h = 1.0	0.11	—	1.20E-2	—	9.22E-2	—	8.88E-3	—
Φ	h = 0.5	2.87E-2	1.94	2.93E-3	2.03	2.35E-2	1.97	2.18E-3	2.03
	h = 0.25	7.56E-3	1.92	7.93E-4	1.89	5.94E-3	1.98	5.51E-4	1.98
	h = 1.0	0.11	—	1.25E-2	—	6.62E-2	—	5.99E-3	—
C1	h = 0.5	4.70E-2	1.23	3.12E-3	2.00	1.05E-2	2.66	1.41E-3	2.09
	h = 0.25	1.24E-2	1.92	8.61E-4	1.86	1.83E-3	2.52	3.46E-4	2.03
	h = 1.0	6.35E-2	—	8.24E-3	—	3.81E-2	—	3.28E-3	—
C2	h = 0.5	2.49E-2	1.49	2.00E-3	2.07	6.54E-3	2.54	7.53E-4	2.13
	h = 0.25	7.16E-3	1.73	5.62E-4	1.82	1.05E-3	2.64	1.82E-4	2.05

It is interesting to compare the performance of Boundary condition I and Boundary condition II. From Tables 2 and 3, it is seen that Boundary condition II gives a slightly better result in terms of absolute error and order of accuracy. One main reason is that the discretization algorithm in Boundary condition II is much simpler and fewer grid points are involved in its implementation. On the other hand, for Boundary condition I, to compute derivative values on the interface, which usually are off grid, one needs to find 18 auxiliary points in the same domain. This may not be numerically feasible for geometric singularities or in shallow regions. With the same geometry, for the Poisson equation, one can resort to a larger region since one has the choices of which derivatives are to be used, or state differently, since points in either domain Ω_m or Ω_s can be used. In contrast, for the Nernst-Planck equation, we have more limited choices since we can only use points in domain Ω_s. Therefore, we may have to compromise the order of accuracy due to the constrain of the geometry. Of course there might be other factors which may affect the result somewhat, for example the tolerance of the solver, but not very much.

III.D Numerical test on an ion channel geometry

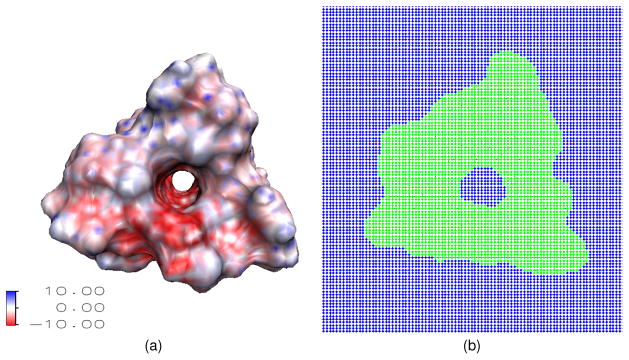
Before simulating the ion transport in real ion channels, we design one more numerical test to check the convergence and accuracy of the proposed PNP algorithm for the channel protein structure. One of the most popular ion channels used in the theoretical studies is the Gramicidin A (GA) channel (PDB code: 1MAG), see Fig. 7(a). A wide variety of theoretical models have been applied to the GA channel because it involves a relatively small number of atoms and because there are many experimental data available in the literature for this channel. The computational domain of the GA channel incorporates four different regions, i.e., the channel region, bulk region, protein region and the membrane layers, see Fig. 1(b). The structure preparation is done according to the following procedure. First, the molecular surface of the GA channel protein is generated by the MSMS program with density 10 and probe radius 1.4 Å⁴⁵ as mentioned in the previous subsection, with atomic van der Waals radii from the CHARMM22 force field.³⁶ The partial charges for each atom in the protein are obtained by using the PDB2PQR software, and are accounted in Φ^*. It is important to check that there is no breaking slice in the pore morphology. As stated in the literature, it is known that the GA channel pore region is along the z direction.⁸ Therefore, to locate channel grid points in the solvent, we sliced the surface along z direction. For each slice, the solvent region enclosed by the biomolecule is the channel pore region, and the solvent region outside the biomolecule is the bulk region. One of such slices is shown in Fig. 7(b), where the green color indicates the protein region. After all the channel pore points are located, the membrane layers are added to the geometry, see Fig. 1(b). Here a slab with the length of 24 A along z direction (from z = 9 Å to z = 33 Å) is used for the representation of implicit membrane layers. In general, the position of membrane layers has little impact to the channel transport property, because no charge is assigned to the membrane in the present work. On the other hand, it would be very important to precisely define the membrane position had membrane been doped with charges, which can be easily done.

Figure 7.

Illustrations of the Gramicidin A channel structure. (a) A 3D view of the geometric structure of Gramicidin A with surface electrostatic potential. The intensive red color inside channel pore indicated that the pore region is negatively charged, which selects positive ions; (b) A cross section in the xy plane, where green color indicates the protein region and blue color indicates the solvent region.

The exact solutions are given by Eqs. (46)–(48). Our numerical results are listed in Table 4. In general, results for Φ_s and Φ are slightly better than those of C₁ and C₂, particularly under Boundary condition I, for the reason discussed in the last subsection: It is easier to solve the Poisson equation than to solve the Nernst-Planck equation when the geometry is very complex.

Table 4.

Numerical errors in solving PNP equations for an ion channel, Gramicidin A.

		Boundary condition I				Boundary condition II
	mesh size	L∞	L∞ order	L2	L2 order	L∞	L∞ order	L2	L2 order
	h = 1.0	0.18	—	1.84E-2	—	0.14	—	1.65E-2	—
Φ	h = 0.5	3.93E-2	2.20	5.10E-3	1.85	2.72E-2	2.36	4.05E-3	2.03
	h = 0.25	1.52E-2	1.37	1.43E-3	1.83	1.52E-2	0.84	9.99E-4	2.02
	h = 1.0	0.16	—	1.11E-2	—	8.41E-2	—	6.06E-3	—
C1	h = 0.5	6.70E-2	1.26	3.62E-3	1.62	1.67E-2	2.33	1.57E-3	1.95
	h = 0.25	2.20E-2	1.61	1.27E-3	1.51	4.68E-3	1.84	3.92E-4	2.00
	h = 1.0	0.13	—	8.37E-3	—	5.54E-2	—	3.42E-3	—
C2	h = 0.5	5.18E-2	1.33	2.96E-3	1.50	1.23E-2	2.17	9.97E-4	1.78
	h = 0.25	1.83E-2	1.50	1.12E-3	1.40	3.91E-3	1.65	2.39E-4	2.06

Apparently, Boundary condition II performs better in both the accuracy and the order of the convergence, compared to Boundary condition I. This happens because the GA pore is quite narrow with a diameter of about 4 Å, consequently, it may be difficult to find all the required auxiliary points for the MIB scheme in the channel pore region and leads to accuracy reduction. Boundary condition II is more rigorous in terms of implementing physical boundary conditions. It is easier to implement and shows much better convergent rate. Numerically, it is found that Boundary condition II not only converges faster, but also provides more stable results in the flux or conductance evaluation. Because the present test involves realistic channel geometry and essentially the original PNP equations, we believe that the findings from the present test are applicable to PNP simulations. Therefore, in the following section, we make use of Boundary condition II exclusively.

IV Ion channel simulations

With the confidence built from our numerical validation given in Section III, we investigate the electrostatic and transport properties of sodium chloride in the Gramicidin A (GA) ion channel in this section. The preparation of the GA structural data has been discussed in the last section. Here, we start from the unit conversion so that the physical measurements can be compared with experimental data. Additionally, we discuss the construction of continuous diffusion coefficient profiles. Furthermore, different schemes for self-consistent iterations are examined. Finally, computational results are shown with different mesh sizes.

IV.A Unit conversion

For real physical problems, it is important to solve coupled PNP equations in one unit convention. We apply the Gaussian units shown in Table 5 for the unit conversion. ²³ Additionally, the following constant values are employed: Avagadro’s number N_A = 6.0220450 × 10²³, Boltzmann’s constant k_B = 1.3806620 × 10⁻¹⁶erg/K, and fundamental charge e_c = 4.8032424 × 10⁻¹⁰esu.

Table 5.

Gaussian units.

abbr.	unit	represents	equivalent expressions
Å	Angstroms	distance	10−8cm
l	liter	volume	cm3
molar	moles per liter	concentration	mol/l
dyn	dyne	force	esu2/cm
erg	erg	energy	dyn · cm

Define $u(\mathbf{r})=\frac{{\text{e}}_{\text{c}}\stackrel{\sim }{\mathrm{\Phi }}(\mathbf{r})}{{\text{k}}_{\text{B}}\text{T}}$, and q_α = Q_αe_c, then u(r) is the nondimensionless electrostatic potential and Q_α is the nondimensionless charge. For example, Q_K⁺ = 1 and Q_Cl⁻ = −1. Then the reformulated PNP system Eqs. (13) and (6) can be written as

$$-\nabla ·(\epsilon \nabla u)=4\pi \sum _{\alpha =1}^{N_c}\frac{Q_{\alpha }{{\text{e}}_{\text{c}}}^2}{{\text{k}}_{\text{B}}\text{T}}{C}_{\alpha }$$ (49)

$$\nabla ·D_{\alpha }(\nabla C_{\alpha }+Q_{\alpha }{C}_{\alpha }\nabla u)=0.$$ (50)

Moreover, considering that the radius information obtained for all the atoms in the protein are in units of Å, the voltage is defined in volt for the boundary condition, and concentration is given in molar, then the following unit transformations are used

$$u_{bd}=\frac{{\stackrel{\sim }{\mathrm{\Phi }}}_{bd}}{300.0}\frac{{\text{e}}_{\text{c}}}{{\text{k}}_{\text{B}}\text{T}}$$ (51)

$${\stackrel{\sim }{C}}_{bd}=\frac{C_{bd}{\text{N}}_{\text{A}}{(Å)}^2}{1000}\frac{{\text{e}}_{\text{c}}}{{\text{k}}_{\text{B}}\text{T}}.$$ (52)

Applying the unit transformations, the following PNP equations can be obtained,

$$-\nabla ·(\epsilon \nabla u)=4\pi \sum _{\alpha =1}^{N_c}{Q}_{\alpha }{\stackrel{\sim }{C}}_{\alpha }$$ (53)

$$\nabla ·D_{\alpha }(\nabla {\stackrel{\sim }{C}}_{\alpha }+Q_{\alpha }{\stackrel{\sim }{C}}_{\alpha }\nabla u)=0.$$ (54)

Equations (53) and (54) are used in our computation.

In the following computations, the dielectric constants for the protein and membrane layer are set to 2, and for the solvent, the dielectric constant is set to 80. The diffusion coefficients in the bulk region are set to their experimental values: D_K = 2.0 × 10⁻⁵cm²/s, D_Cl = 2.03 × 10⁻⁵cm²/s. Also, the same boundary condition is applied for concentrations of K⁺ and Cl⁻, which is denoted as C₀, the voltage difference on the boundary is denoted as V₀.

IV.B Diffusion coefficient profiles

From the physical point of view, the diffusion coefficients in the bulk region and the channel pore region should be different, particularly for narrow pores. In fact, for extremely narrow “dry” pores, the concept of diffusion may no longer hold. In general, the diffusion coefficient bulk region should be larger than that in the pore region, and can be obtained from the experimental measurement. While the diffusion coefficient in the channel pore region is yet to be determined. Computationally, we introduce buffering regions between the bulk and channel regions, where the diffusion coefficient is interpolated by the value between the bulk and channel regions. Here we build the diffusion coefficient function as follows

$$D(\mathbf{r})=\{\begin{array}{ll}{D}_{\text{chan}}\hfill & \mathbf{r}\in \text{Channel}\text{region}\hfill \\ D_{\text{chan}}+(D_{\text{chan}}-D_{\text{bulk}})f(\mathbf{r})\hfill & \mathbf{r}\in \text{Buffering}\text{region}\hfill \\ D_{\text{bulk}}\hfill & \mathbf{r}\in \text{Bulk}\text{region}\hfill \end{array}$$ (55)

where the function f(r) is given by

$$f(\mathbf{r})=f(z)=n{\left(\frac{z-z_{\text{chan}}}{z_{\text{bulk}}-z_{\text{chan}}}\right)}^{n+1}-(n+1){\left(\frac{z-z_{\text{chan}}}{z_{\text{bulk}}-z_{\text{chan}}}\right)}^n$$ (56)

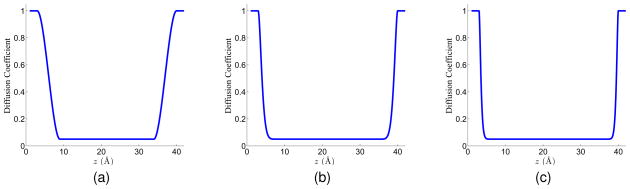
where n is an integer, n ≥ 2 and z ∈ [z_channel, z_bulk]. Here we assume that the channel structure lies along the z direction. This construction is a generalization of the diffusion profile mentioned by Hwang et al.²⁴ The advantage of using this profile is that it can make sure that D(r) is C¹ continuous so that it is differentiable in the Nernst-Planck equation. Additionally, it is a constant in the channel and bulk region, and has a continuous transition in the buffering regions. Figure 8 shows the diffusion coefficient profiles when n = 2, n = 9 and n = 19 respectively, as n increases, the length of the transition regions (where the coefficient drops from the bulk value to the channel value) becomes shorter. In these figures, the bulk coefficient is normalized to 1, and the channel coefficient is 20 times smaller than the bulk region, i.e., 0.05.

Figure 8.

Diffusion coefficient profiles defined in Eq. (55) for different n values. (a) n = 2; (b) n = 9; (c) n = 19.

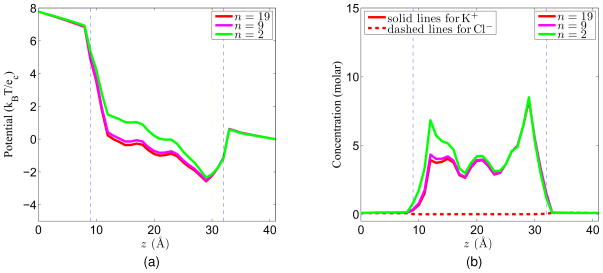
For the boundary condition, the voltage applied to the system is given by the potential difference along the z direction. Additionally, the Neumann boundary condition is used for other parts of the boundary. For the concentration, Dirichlet boundary condition is applied. For a given boundary condition(V₀ = 200mV and C₀ = 0.1molar), the potential and concentration profiles for different n values are shown in Figure 9, from which we can see that the change in diffusion coefficient profiles has an impact on the value of the potential and concentration. As n increases, since the coefficient profile does not change quite much, then the potential and concentration values only have a minor change, as shown in this figure for n = 9 and n = 19.

Figure 9.

Computational results for different n values with V₀ = 200mV and C₀ = 0.1molar. (a) Potential profiles; (b) Concentration profiles.

IV.C Convergence of self consistent iteration schemes

While SOR-like iteration is very convenient to apply for self-consistent iterations, the Gummel iteration¹⁵ is widely used in the PNP system for the self-consistent iteration particularly in semiconductor device simulations. In the semiconductor device computation, it is often assumed that one may express electron density in terms of the Fermi function when the other current density is negligible. In our case, we can linearize our system by assuming the Boltzmann distribution: ${\stackrel{\sim }{C}}_{\alpha }={\stackrel{\sim }{C}}_{0\alpha }{e}^{-\frac{q_{\alpha }}{{\text{k}}_{\text{B}}\text{T}}(\mathrm{\Phi }-{\mathrm{\Phi }}_{\alpha })}$, where C̃_0α is the bulk ion concentration. Let set $u_{\alpha }=\frac{{\text{e}}_{\text{c}}{\mathrm{\Phi }}_{\alpha }}{{\text{k}}_{\text{B}}\text{T}}$, then C̃_α = C̃_0αe^{−Q_α(u−u_α)}; thus, we have

$$\frac{\partial {\stackrel{\sim }{C}}_{\alpha }}{\partial u}={\stackrel{\sim }{C}}_{\alpha }(-Q_{\alpha }).$$

We therefore obtain the linearization

$${\stackrel{\sim }{C}}_{\alpha }^{(n+1)}={\stackrel{\sim }{C}}_{\alpha }^{(n)}+\delta {\stackrel{\sim }{C}}_{\alpha }$$ (57)

$$={\stackrel{\sim }{C}}_{\alpha }^{(n)}+\frac{\partial \stackrel{\sim }{C}}{\partial u}\delta u$$ (58)

$$={\stackrel{\sim }{C}}_{\alpha }^{(n)}+{\stackrel{\sim }{C}}_{\alpha }^{(n)}(-Q_{\alpha })(u^{(n+1)}-u^{(n)}).$$ (59)

As a consequence, the Poisson equation at the iteration level n + 1 is given by

$$-\nabla ·(\epsilon \nabla u^{(n+1)})=4\pi \sum _{\alpha =1}^{N_c}{Q}_{\alpha }{\stackrel{\sim }{C}}_{\alpha }^{(n+1)}$$ (60)

$$=4\pi \sum _{\alpha =1}^{N_c}{Q}_{\alpha }[{\stackrel{\sim }{C}}_{\alpha }^{(n)}+{\stackrel{\sim }{C}}_{\alpha }^{(n)}{Q}_{\alpha }(u^{(n+1)}-u^{(n)})]$$ (61)

$$=4\pi \sum _{\alpha =1}^{N_c}{Q}_{\alpha }{\stackrel{\sim }{C}}_{\alpha }^{(n)}-4\pi \sum _{\alpha =1}^{N_c}{Q}_{\alpha }^2{\stackrel{\sim }{C}}_{\alpha }^{(n)}(u^{(n+1)}-u^{(n)}).$$ (62)

Reorganizing the similar terms leads to

$$-\nabla ·(\epsilon \nabla u^{(n+1)})+4\pi \sum _{\alpha =1}^{N_c}{Q}_{\alpha }^2{\stackrel{\sim }{C}}_{\alpha }^{(n)}{u}^{(n+1)}=+4\pi \sum _{\alpha =1}^{N_c}{Q}_{\alpha }{\stackrel{\sim }{C}}_{\alpha }^{(n)}+4\pi \sum _{\alpha =1}^{N_c}{Q}_{\alpha }^2{\stackrel{\sim }{C}}_{\alpha }^{(n)}{u}^{(n)}.$$ (63)

Thus in Gummel iteration, Eq. (63) and Eq. (37) are solved iteratively.

To compare the efficiency of these two different iteration schemes, the iteration numbers are computed for both of them with the same boundary condition. For SOR-like iterations, the relaxation parameters for C and Φ are set to be 0.1 for the first 3 steps, and 0.3 for the following steps. Table 6 shows that for the Gummel iteration, for the same concentration boundary condition, as the voltage goes higher, it needs more iterations to reach a convergent result. Additionally, for the same potential boundary condition, as the concentration goes higher, it needs more iterations to reach a convergent result. Table 7 shows that for the SOR-like iteration scheme. It takes more iterations to reach a convergent result for higher voltage difference. However, when the voltage is fixed, the iteration number does not change too much. By comparing two tables, it shows that for a relatively lower concentration profile, the Gummel iteration is preferred, since we do not have to worry about the relaxation parameter and it converges very fast. However, for a higher concentration profile, the SOR-like scheme may converges faster than Gummel iterations if the relaxation parameters are appropriately chosen. In the present comparison, fixed relaxation parameters are used for in all SOR-like iterations (i.e., ω = 0.1 for the first three steps and then ω = 0.3 for the rest of the iterations (if not converge, then ω = 0.2 is used instead). In fact, iteration numbers can be reduced if the relaxation parameter is allowed to vary under different cases.

Table 6.

Computational results on the number of iteration steps in Gummel iterations.

measurements	V0 = 0mV	V0 = 50mV	V0 = 100mV	V0 = 150mV	V0 = 200mV
C0 = 0.1	14	18	19	20	25
C0 = 0.2	21	28	30	31	32
C0 = 0.5	35	51	55	56	56
C0 = 1.0	49	78	84	88	87
C0 = 2.0	61	113	121	125	123

Table 7.

Computational results on the number of iteration steps in SOR-like iteration.

measurements	V0 = 0mV	V0 = 50mV	V0 = 100mV	V0 = 150mV	V0 = 200mV
C0 = 0.1	43	41	39	50	54
C0 = 0.2	42	40	47	68	76
C0 = 0.5	37	37	45	74	94
C0 = 1.0	37	37	38	59	77
C0 = 2.0	43	40	38	46	54

IV.D Potential and concentration profiles for different mesh sizes

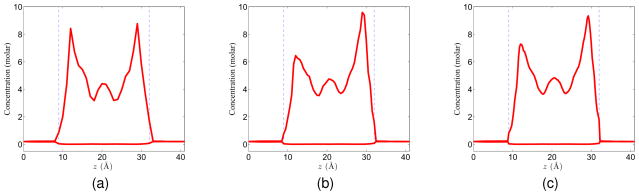
It is very often in the PNP literature that the result is obtained for given mesh size and there is no information about the convergence of one’s computational algorithm. In the present work, much attention is given to the validation and convergent investigation both with an analytical system and with the realistic system. Here, we discuss the behavior of the results under different mesh sizes. In general, a coarser mesh requires less computational time while introducing more computational error. To quantitatively examine the impact of the mesh sizes in this particular PNP application, we compute the results for three sets of mesh sizes: h = 1.0Å, h = 0.5Å and h = 0.25Å under the same given voltage and concentration boundary condition. For the geometric setup, the channel region is identified at a finer mesh, i.e., h = 0.25 Å. Then this channel pore definition is used in all mesh sizes.

For a given boundary condition(V₀ = 100mV and C₀ = 0.2molar), the potential and concentration profiles obtained under different mesh sizes are presented in Figs. 10 and 11. Essentially, our results indicate the same set of local maxima and local minima for both the potential and concentration profiles. There are only slight variations among results obtained with different meshes. However, in terms of computational time, there is a big difference. It takes around half day to finish the computation when mesh size is h = 0.25 Å on a personal computer. The electric current across the membrane pore is calculated by the expression

Figure 10.

Potential profiles on different mesh sizes with V₀ = 100mV and C₀ = 0.2molar. (a) h=1.0; (b) h=0.5; (c) h=0.25.

Figure 11.

Concentration profiles under different mesh sizes with V₀ = 100mV and C₀ = 0.2molar. (a) h = 1.0; (b) h = 0.5; (c) h = 0.25.

$$I=\sum _{\alpha =1}^{N_c}{q}_{\alpha }{\int }_{L_x,L_y}{D}_{\alpha }\left[\frac{D{C}_{\alpha }}{\partial z}+\frac{q_{\alpha }}{{\text{k}}_{\text{B}}\text{T}}{C}_{\alpha }\frac{\partial \mathrm{\Phi }}{\partial z}\right]\mathit{dxdy}.$$ (64)

The current is evaluated at each cross section inside the pore and it is found that the value is not sensitive to the location of the cross section, and the current through the middle of the pore is shown in Tab 8. While the total current also includes the accuracy for evaluating the integral in Eq. (64), current per unit area shows a clear tendency that as the mesh size goes smaller, the difference in the current value evaluated at each unit area gets smaller.

IV.E Comparison with experimental data

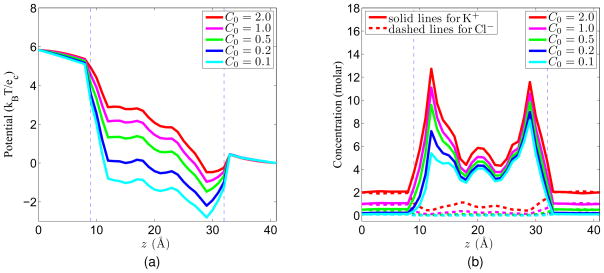
After the above tests confirm the performance of the proposed PNP algorithms, we now apply our technique to GA channel to predict the physical measurements, such as ion concentration profiles, electrostatic potential distributions and current-voltage (I-V) curves. To compare with the experimental I-V data, the potential and concentration values at V₀ = 0mV, V₀ = 50mV, V₀ = 100mV, V₀ = 150mV and V₀ = 200mV are computed for different bulk concentrations, namely C₀ = 0.1molar, C₀ = 0.2molar, C₀ = 0.5molar, C₀ = 1.0molar and C₀ = 2.0mol. Figure 12 shows the potential and concentration profiles for five different bulk concentrations while the same voltage is applied to the system (V₀ = 150mV). It is seen that higher bulk concentration elevates the potential profile, and increases the concentration in the channel pore region. Figure 13 shows the electrostatic potential and concentration profiles for five different applied voltage values, while the bulk concentration is the same (C₀ = 0.1molar). It can be seen that on the left hand side (close to higher potential), the change in the potential is larger than that in the right hand side (close to lower potential), which corresponds to a more obvious change in the concentration profile on the left.

Figure 12.

Potential and concentration profiles with V₀ = 150mV. (a) Potential profiles; (b) Concentration profiles.

Figure 13.

Potential and concentration profiles with C₀ = 0.1molar. (a) Potential profiles; (b) Concentration profiles.

It is observed that a larger diffusion coefficient is needed to match the data at a higher concentration boundary condition, while a smaller diffusion coefficient can be used to match the data at a lower concentration level. While it may not have an agreement on what is the exact value of the diffusion coefficient, we can see they are basically on the same scale, and also we can see that indeed for the sodium transport, a much smaller diffusion coefficient is used, comparing to the potassium coefficient in the channel.

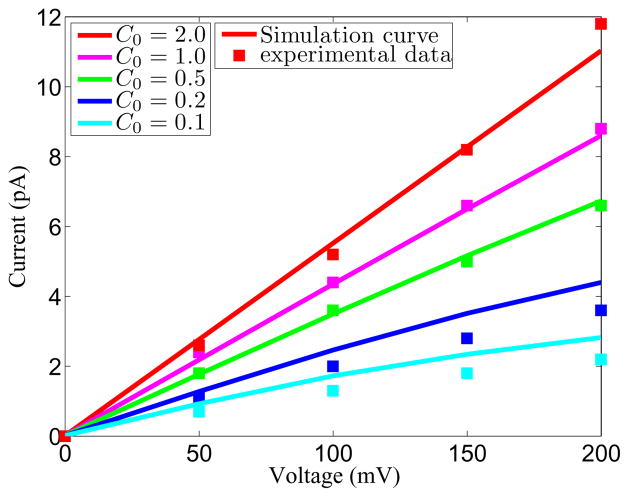
The experimental I-V plots for GA channel from Cole et al.,¹⁴ the right panel of Figure 8 in their paper is used as the reference data for the comparison. For the bulk diffusion coefficient, the experimental data are used. However, there is no experimental data available for the diffusion coefficient in the channel pore. Many different ways are use to in the literature to match experimental data. Here we use the same current value as that used in the experiment, i.e., V = 200mV to obtain the range of diffusion coefficients. We find that a diffusion coefficient which is 21 times smaller than the bulk coefficient shows a reasonable match. The comparison between the simulation data and experimental data is shown in Fig. 14. While there are some deviations between the present predictions and experimental values, overall, there is a good agreement between two sets of data. Based on our extensive validation and test of the present PNP algorithm, we have a good reason to believe that the discrepancy between the present PNP predictions and experimental data is due to the inherent limitations of the PNP theory. This aspect will be further investigated in our future work.

Figure 14.

A comparison of the simulation I-V curve and experimental data.

A comparison between the PNP prediction and experimental data¹⁴ was also presented in the literature.⁸ In their work the bulk diffusion coefficient is rescaled to make a good fitting with experimental results. However, the validity of such an approach was questioned by Hollerbach et al.²²

V Concluding remarks

The Poisson-Nernst-Planck (PNP) theory is a well-established electrodiffusion model for a wide variety of applications in chemistry, physics, nano-science and biology. In the past two decades, it has been extensively used in the ion channel analysis to compute the electrostatic and concentration profiles, as well as current-voltage (I-V) curves. Despite of a number of limitations, it is by far one of the most accepted theoretical models because of its simplicity and ability of explaining many experimental measurements. It is expected that with some modifications, the PNP based theories will play an increasingly important role in nano-bio science and technology.

Numerical analysis and application of the PNP model for ion channel dynamics and transport are enormous in the literature. However, none of previous work has ever reported numerical accuracy and convergence order analysis for realistic ion channels, to our knowledge. In fact, it is tremendously challenging to construct a second-order convergent algorithm for the PNP system in the biomolecular context due to a number of numerical obstacles. First, the Poisson equation admits a dielectric interface which separates the protein pore region and the ion domain. Since different dielectric constants are conventionally used in two domains, the discontinuous coefficients across the interface lead to interface jump conditions for the Poisson equation. There is no report of rigorous numerical enforcement of the interface jump condition in the literature for ion channels, to our knowledge. The lack of rigorous interface treatment will reduce the numerical convergence to the first order regardless what numerical method is employed. Additionally, the channel protein admits partial charges, which are usually modeled by Dirac delta functions. The introduction of unbounded delta functions further reduces the convergent order for a normal numerical method. Moreover, what might be the most devastating feature is that the channel interface is usually non-smooth, i.e., having geometric singularities,⁴⁵ due to the use of molecular surfaces. It is extremely difficult to construct the second-order algorithm over complex 3D geometric singularities. Furthermore, coupling between the Poisson equation and the Nernst-Planck equation makes the PNP system nonlinear, which significantly reduces the chance of constructing a high-order numerical scheme. It is the combination of these numerical difficulties that makes the PNP problem in the biomolecular context numerically challenging and academically attractive.

The present work constructs the first second order convergent numerical scheme for solving PNP equations for realistic ion channels with a primitive molecular surface. A number of advanced numerical techniques are introduced to the solution of the PNP system. First, we design a Dirichlet to Neumann mapping (DNM) scheme for removing the charge singularity. The resulting Poisson equation is solved without the charge source term but is subject to an extra Neumann interface condition. Additionally, we reformulate the matched interface and boundary (MIB) algorithm for solving the PNP equations with channel protein structure, interface jump condition and geometric singularities. The redesign of the MIB algorithm for the PNP system is highly non trivial although previous MIB methods and concepts reduce the present numerical difficulties. Moreover, a couple of iterative schemes are utilized to solve coupled Poisson and Nernst-Planck equations. The proposed second order PNP algorithm is extensively validated against a number of test cases, from a sphere, two proteins, to a realistic ion channel. Our results confirm the design accuracy and convergent order. Finally, numerical applications are carried out to the Gramicidin A (GA) channel protein with a wide range of ion concentrations and applied voltages. Our results are compared with experimental data. A good agreement with experimental measurements of I-V curves is achieved over a certain range of concentrations. However, there are still obvious discrepancies between the present PNP prediction and experimental measurements. Based on the extensive numerical test detailed in the present work, we attribute these discrepancies to the limitation of the PNP model. This aspect is under our investigation.

Table 8.

Computational results of electrical currents under different mesh sizes.

mesh size	h = 1.0	h = 0.5	h = 0.25
current value	2.4647	2.7114	3.0134
current per unit area	0.2465	0.2781	0.2836
CPU time (second)	249	4141	39034