Using Blur to Affect Perceived Distance and Size

Abstract

We present a probabilistic model of how viewers may use defocus blur in conjunction with other pictorial cues to estimate the absolute distances to objects in a scene. Our model explains how the pattern of blur in an image together with relative depth cues indicates the apparent scale of the image’s contents. From the model, we develop a semiautomated algorithm that applies blur to a sharply rendered image and thereby changes the apparent distance and scale of the scene’s contents. To examine the correspondence between the model/algorithm and actual viewer experience, we conducted an experiment with human viewers and compared their estimates of absolute distance to the model’s predictions. We did this for images with geometrically correct blur due to defocus and for images with commonly used approximations to the correct blur. The agreement between the experimental data and model predictions was excellent. The model predicts that some approximations should work well and that others should not. Human viewers responded to the various types of blur in much the way the model predicts. The model and algorithm allow one to manipulate blur precisely and to achieve the desired perceived scale efficiently.

1. INTRODUCTION

The pattern of blur in an image can strongly influence the perceived scale of the captured scene. For example, cinematographers working with miniature models can make scenes appear life size by using a small camera aperture, which reduces the blur variation between objects at different distances [Fielding 1985]. The opposite effect is created in a photographic manipulation known as the tilt-shift effect: A full-size scene is made to look smaller by adding blur with either a special lens or postprocessing software tools [Laforet 2007; Flickr 2009; Vishwanath 2008].

Figures 1 and 2 demonstrate the miniaturization effect. In Figure 2, the image in the upper left has been rendered sharply and to typical viewers looks like a life-size scene in San Francisco. The upper-right image has been rendered with a blur pattern consistent with a shorter focal distance, and it looks like a miniature-scale model. The two images in the lower row demonstrate how the application of a linear blur gradient can have a similar effect.

Fig. 1.

(a) Rendering a cityscape with a pinhole aperture results in no perceptible blur. The scene looks large and far away. (b) Simulating a 60m-wide aperture produces blur consistent with a shallow depth of field, making the scene appear to be a miniature model.

Original city images and data from GoogleEarth are copyright Terrametrics, SanBorn, and Google.

Fig. 2.

Upper two images: Another example of how rendering an image with a shallow depth of field can make a downtown cityscape appear to be a miniature-scale model. The left image was rendered with a pinhole camera, the right with a 60m aperture. Lower two images: Applying a blur gradient that approximates a shallow depth of field can also induce the miniaturization effect. The effects are most convincing when the images are large and viewed from a short distance.

Original city images and data from GoogleEarth are copyright Terrametrics, SanBorn, and Google. Original lake photograph is copyright Casey Held.

Clearly, blur plays a significant role for conveying a desired sense of size and distance. However, the way the visual system uses blur to estimate perceived scale is not well understood. Okatani and Deguchi [2007] have shown that additional information, such as perspective, is needed to recover scene scale. But a more detailed, perceptually-based model will provide further insight into the effective application of blur. This article presents a general probabilistic model of distance estimation from blur. From the model, we develop an algorithm for manipulating blur in images to produce the desired apparent scale. We then validate the model and algorithm with a psychophysical study. Finally, we explore potential applications.

2. BACKGROUND

2.1 Defocus Blur in Computer Graphics and Photography

The importance of generating proper depth-of-field effects in synthetic or processed imagery is well established. Special-effects practitioners often manipulate the depth of field in images to convey a desired scale [Fielding 1985]. For example, it is commonplace in cinematography to record images with small apertures to increase the depth of field. Small apertures reduce the amount of defocus blur and this sharpening causes small-scale scenes to look larger. Images created with proper defocus are also generally perceived as more realistic and more aesthetic [Hillaire et al. 2007, 2008].

Blur can also be used to direct viewers’ attention to particular parts of an image. For example, photographers and cinematographers direct viewer gaze toward a particular object by rendering that object sharp and the rest of the scene blurred [Kingslake 1992; Fielding 1985]. Eye fixations and attention are in fact drawn to regions with greater contrast and detail [Kosara et al. 2002; Cole et al. 2006; DiPaola et al. 2009]. These applications of blur may help guide users toward certain parts of an image, but our analysis suggests that the blur manipulations could also have the undesired consequence of altering perceived scale. This suggestion is consistent with another common cinematic practice where shallow depth of field is used to draw a viewer into a scene and create a feeling of intimacy between the film subjects and viewer. A shallower depth of field implies a smaller distance between the viewer and subjects which creates the impression that the viewer must be standing near the subjects.

As depth-of-field effects are used more frequently, it is important to understand how to generate them accurately and efficiently. Some of the earliest work on computer-generated imagery addressed the problem of correctly rendering images with defocus blur. Potmesil and Chakravarty [1981] presented a detailed description of depth-of-field effects, the lens geometry responsible for their creation, and how these factors impact rendering algorithms. The seminal work on distribution ray tracing by Cook and colleagues [Cook et al. 1984] discussed defocus and presented a practical method for rendering images with finite apertures. Likewise, the original REYES rendering architecture was built to accommodate a finite aperture [Cook et al. 1987]. Development of the accumulation buffer was motivated in part by the need to use hardware rendering methods to generate depth-of-field effects efficiently [Haeberli and Akeley 1990]. Kolb et al. [1995] described a method for rendering blur effects that are specific to a real lens assembly as opposed to an ideal thin lens. Similarly, Barsky [2004] investigated rendering blurred images using data measured from a specific human eye.

Even with hardware acceleration, depth-of-field effects remain relatively expensive to render. Many methods for accelerating or approximating blur due to defocus have been developed [Fearing 1995; Rokita 1996; Barsky et al. 2003a; 2003b; Mulder and van Liere 2000], and the problem of rendering such effects remains an active area of research.

Researchers in computer vision and graphics have also made use of the relationship between depth and blur radius for estimating the relative distances of objects in photographs. For example, Pentland [1987] showed that blur from defocus can be used to recover an accurate depth map of an imaged scene when particular parameters of the imaging device are known. More recently, Green and colleagues [Green et al. 2007] used multiple photographs taken with different aperture settings to compute depth maps from differences in estimated blur. Others have created depth maps of scenes using specially constructed camera apertures [Levin et al. 2007; Green et al. 2007; Moreno-Noguer et al. 2007].

2.2 Aperture and Blur

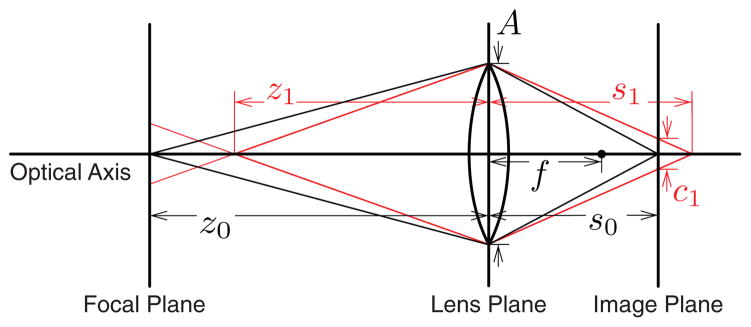
When struck by parallel rays, an ideal thin lens focuses the rays to a point on the opposite side of the lens. The distance between the lens and this point is the focal length, f. Light rays emanating from a point at some other distance z₁ in front of the lens will be focused to another point on the opposite side of the lens at distance s₁. The relationship between these distances is given by the thin-lens equation.

$$\frac{1}{s_1}+\frac{1}{z_1}=\frac{1}{f}$$ (1)

In a typical imaging device, the lens is parallel to the image plane containing the film or CCD array. If the image plane is at distance s₀ behind the lens, then light emanating from features at distance z₀ = 1/(1/f − 1/s₀) along the optical axis will be focused on that plane (Figure 3). The plane at distance z₀ is the focal plane, so z₀ is the focal distance of the device. Objects at other distances will be out of focus, and hence will generate blurred images on the image plane. We can express the amount of blur by the diameter c of the blur circle in the image plane. For an object at distance z₁, c₁ = |A(s₀/z₀)(1 − z₀/z₁)|, where A is the diameter of the aperture. It is convenient to substitute d for the relative distance z₁/z₀, yielding

Fig. 3.

Schematic of blur in a simple imaging system. z₀ is the focal distance of the device given the lens focal length, f, and the distance from thelens to the image plane, s₀. An object at distance z₁ creates a blur circle of diameter c₁, given the device aperture, A. Objects within the focal plane will be imaged in sharp focus. Objects off the focal plane will be blurred proportional to their dioptric (m⁻¹) distance from the focal plane.

$$c_1=\left|A\frac{s_0}{z_0}\left(1-\frac{1}{d}\right)\right|.$$ (2)

The depth of field is the width of the region centered around the focal plane where the blur circle radius is below the sharpness threshold, or the smallest amount of perceptible blur. Real imaging devices, like the human eye, have imperfect optics and more than one refracting element, so Eqs. (1) and (2) are not strictly correct. Later we describe those effects and show that they do not affect our analysis significantly. An important aspect of Eq. (2) is the inverse relationship between z₀ and c₁. This relationship means that the blur at a given relative distance d increases as z₀ decreases. In other words, the depth of field becomes narrower with closer focal distances. For this reason, a small scene imaged from close range generates greater blur than a scaled-up version of the same scene imaged from farther away. As explained in Section 4, it is this relationship that produces the perceived miniaturization in Figure 2.

3. ADJUSTING BLUR TO MODULATE PERCEIVED DISTANCE AND SIZE

3.1 Tilt-and-Shift Lenses and Linear Blur Gradients

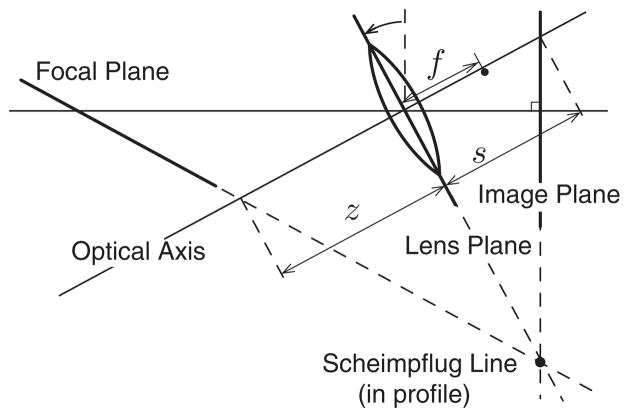
So far we have assumed that the imaging and lens planes are parallel, but useful photographic effects can be generated by slanting the two planes with respect to each other. Some cameras do so with a “tilt-and-shift” lens mount that allows the position and orientation of the lens to be changed relative to the rest of the camera [Kingslake 1992]; other cameras achieve an equivalent effect by adjusting the orientation of the filmback. Rotation of the lens relative to the image plane affects the orientation of the focal plane relative to the optical axis (Figure 4). In such cases, the image and lens planes intersect along the so-called Scheimpflug line. The focal plane also intersects those planes at the Scheimpflug line [Kingslake 1992; Okatani and Deguchi 2007]. Because the focal plane is not perpendicular to the optical axis, objects equidistant from the lens will not be blurred equally. One can take advantage of this phenomenon by tilting the lens so that an arbitrary plane in the scene is in clear focus. For example, by making the focal plane coplanar with a tabletop, one can create a photograph in which all of the items on the table are in clear focus. The opposite effect is created by tilting the lens in the opposite direction, so that only a narrow band of the tabletop is in focus. The latter technique approximates a smaller depth of field. The pattern of blur in the image is close to that produced by a slanted object plane photographed with a conventional camera at short range [Okatani and Deguchi 2007]. McCloskey and colleagues [2009] showed that the pattern of blur produced by a slanted plane is a linear gradient, with the blur and distance gradients running in the same direction. Therefore, it stands to reason that a tilt-and-shift image could be similar to a sharply rendered image treated with a linear blur gradient. Indeed, most of the tilt-and-shift examples popular today, as well as Figure 2(d), were created this way [Flickr 2009]. However, there can be large differences in the blur patterns produced by each method, and it would be useful to know whether these differences have any impact on the perception of the image.

Fig. 4.

The Scheimpflug principle. Tilt-and-shift lenses cause the orientation of the focal plane to shift and rotate relative to the image plane. As a result, the apparent depth of field in an image can be drastically changed and the photographer has greater control over which objects are in focus and which are blurred.

3.2 Comparing Blur Patterns

As previously discussed, it is often useful to make the scene depicted in an image appear bigger or smaller than it actually is. Special-effects practitioners can make a scene look bigger by recording with a small aperture or make the scene look smaller by recording with a large aperture [Fielding 1985]. Consider recording a small scene located z₀ meters away from the camera and trying to make it appear to be m times larger and located ẑ₀ = mz₀ meters away from the camera. Assume that with a camera aperture diameter of A, the apparent size matches the actual size. Then, referring to the equations we developed in Section 2.2, the amount of blur we want to have associated with a given relative distance d is given by

$$\begin{array}{l}{\widehat{c}}_1=\left|A\frac{s_0}{{\widehat{z}}_0}\left(1-\frac{1}{d}\right)\right|=\left|A\frac{s_0}{m{z}_0}\left(1-\frac{1}{d}\right)\right|\\ =\left|\left(\frac{A}{m}\right)\left(\frac{s_0}{z_0}\right)\left(1-\frac{1}{d}\right)\right|.\end{array}$$ (3)

Here we see that we can achieve the same amount of blur as encountered with a focal distance of ẑ₀ = mz₀ by shooting the scene at distance z₀ and setting the diameter of the camera aperture to  = A/m. The aperture must therefore be quite small to make a scene look much larger than it is and this limits the amount of available light, causing problems with signal-to-noise ratio, motion, and so forth. Likewise the aperture must be quite large to make the scene look much smaller than it actually is, and such large apertures might be difficult to achieve with a physical camera. Because of these limitations, it is quite attractive to be able to use a conventional camera with an aperture of convenient size and then to manipulate blur in postprocessing, possibly with blur gradients.

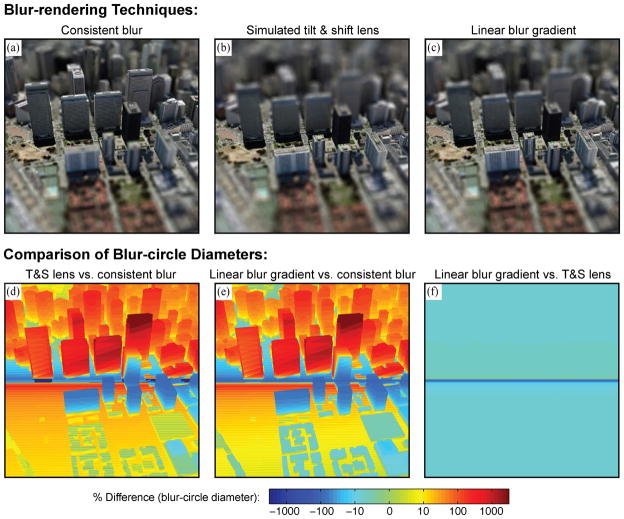
We quantified the differences in three types of blur (i.e., consistent, linear gradient, and tilt-shift) by applying them to 14 full-scale scenes of San Francisco taken from GoogleEarth (Figure 5(a) shows an example). In each image, we wanted to produce large variations in blur, as if viewed by the human eye (aperture ≈ 4.6mm) with a focal distance z₀ of only 0.06m to the center of the scene. Because the actual focal distance was 785m, being consistent with a human eye at 0.06m meant that a virtual camera with a very large aperture of 60.0m was necessary. To produce each consistent-blur image, we captured many images of the same locale from positions on a jittered grid covering a circular aperture. We translated each image to ensure that objects in the center of the scene, which were meant to be in focus, were aligned from one image to another. We then averaged these images to produce the final image. This approach is commonly used with hardware scan-conversion renderers to generate images with accurate depth-of-field effects [Haeberli and Akeley 1990]. The tilt-and-shift images were generated in a similar fashion, but with the simulated image plane slanted relative to the camera aperture. The slant angles were chosen to produce the same maximum blur magnitudes as the consistent-blur images (slant = −16.6° in Figure 5(b)). The direction of the slant (the tilt) was aligned with the distance gradient in the scenes. The distance gradient was always vertical, so the aligned blur gradient was also vertical. The maximum magnitudes of the gradients were set to the average blur magnitudes along the top and bottom of the consistent-blur images (Figure 5(c)). Thus, the histograms of blur magnitude were roughly equal across the three types of blur manipulation. For the linear blur gradients, blur was applied to the pixels by convolving them with cylindrical box kernels. A vertical blur gradient is such that all of the pixels in a given row are convolved with the same blur kernel.

Fig. 5.

Comparison of blur patterns produced by three rendering techniques: consistent blur (a), simulated tilt-and-shift lens (b), and linear blur gradient (c). The settings in (b) and (c) were chosen to equate the maximum blur-circle diameters with those in (a). The percent differences in blur-circle diameters between the images are plotted in (d), (e), and (f). Panels (d) and (e) show that the simulated tilt-and-shift lens and linear blur gradient do not closely approximate consistent blur rendering. The large differences are due to the buildings, which protrude from the ground plane. Panel (f) shows that the linear blur gradient provides essentially the same blur pattern as a simulated tilt-and-shift lens. Most of the differences in (f) are less than 7%; the only exceptions are in the band near the center, where the blur diameters are less than one pixel and not detectable in the final images.

We calculated the differences between the blur diameters produced by each rendering technique. The blur patterns in the tilt-and-shift-lens and linear-blur-gradient images were similar to each other (generally never differing by more than 7%; Figure 5(f)), but differed greatly from the pattern in the consistent-blur condition (Figure 5(c)(d)). The differences relative to consistent blur result from the buildings that protrude from the ground plane. In Section 6, we explore whether the differences affect perceived distance. This analysis was performed on all of our example images and we found that linear blur gradients do in fact yield close approximations of tilt-and-shift blur, provided that the scenes are roughly planar. This is why tilt-and-shift images and their linear-blur-gradient approximations have similarly compelling miniaturization effects.

Our next question is, why does blur affect the visual system’s estimates of distance and size? To answer this, we developed a probabilistic model of the distance information contained in image blur.

4. MODEL: BLUR AS AN ABSOLUTE DEPTH CUE

4.1 Vision Science Literature

The human eye, like other imaging systems, has a limited depth of field, so it encounters blur regularly. Blur depends partly on the distance to an object relative to where the eye is focused, so it stands to reason that it might be a useful perceptual cue to depth. The vision science literature is decidedly mixed on this issue. Some investigators have reported clear contributions of blur to depth perception [Pentland 1987; Watt et al. 2005], but others have found either no effect [Mather and Smith 2000] or qualitative effects on perceived depth ordering, but no more [Marshall et al. 1996; Mather 1996; Palmer and Brooks 2008]. This conflicts with the clear perceptual effects associated with the blur manipulation in Figure 2. A better understanding of the distance information contained in blur should yield more insight into the conditions in which it is an effective depth cue.

4.2 Probabilistic Inference of Distance from Blur

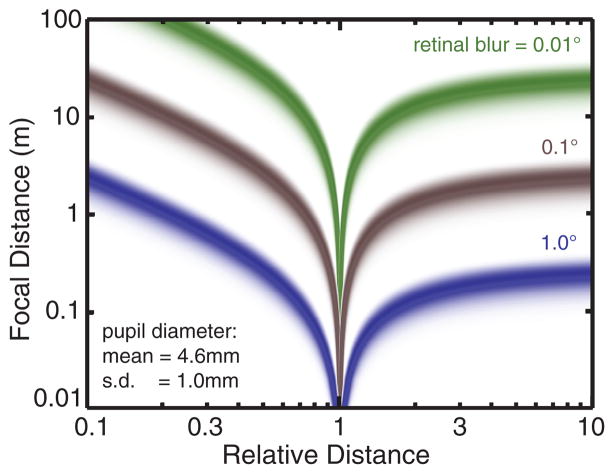
The physical relationship between camera optics and image blur can help us understand the visual system’s use of retinal-image blur. For instance, if an object is blurred, is it possible to recover its distance from the viewer? To answer this, we return to Eq. (2). Regardless of whether a photograph or a real scene is being viewed, we assume that the visual system interprets the retinal image as being produced by the optics of the eye. Now the aperture A is the diameter of a human pupil, z₀ is the distance to which the eye is focused, and d is the relative distance to the point in question. Figure 6 shows the probability of z₀ and d for a given amount of blur, assuming A is 4.6mm ± 1mm [Spring and Stiles 1948]. For each blur magnitude, infinite combinations of z₀ and d are possible. The distributions for large and small blur differ: large blur diameters are consistent with a range of short focal distances, and small diameters are consistent with a range of long distances. Nonetheless, one cannot estimate focal distance or relative distance from a given blur observation. How then does the change in perceived distance and size in Figure 2 occur?

Fig. 6.

Focal distance as a function of relative distance and retinal-image blur. Relative distance is defined as the ratio of the distance to an object and the distance to the focal plane. The three colored curves represent different amounts of image blur expressed as the diameter of the blur circle, c, in degrees. We use angular units because in these units, the image device’s focal length drops out [Kingslake 1992]. The variance in the distribution was determined by assuming that pupil diameter is Gaussian distributed with a mean of 4.6mm and standard deviation of 1mm [Spring and Stiles 1948]. For a given amount of blur, it is impossible to recover the original focal distance without knowing the relative distance. Note that as the relative distance approaches 1, the object moves closer to the focal plane. There is a singularity at a relative distance of 1 because the object is by definition completely in focus at this distance.

The images in Figure 2 contain other depth cues (i.e., linear perspective, relative size, texture gradient, etc.) that specify the relative distances among objects in the scene. Such cues are scale ambiguous, with the possible exception of familiar size (see Section 3.3.2), so they cannot directly signal the absolute distances to objects. We can, however, determine absolute distance from the combination of blur and these other cues. To do this, we employ Bayes’ Law, which prescribes how to compute the statistically optimal (i.e., lowest variance) estimate of depth from uncertain information. In the current case of estimating distance from blur and other cues, estimates should be based on the posterior distribution

$$P(z_0,d\mid c,p)=\frac{P(c\mid z_0,d)P(p\mid z_0,d)P(z_0,d)}{P(c,p)},$$ (4)

where c and p represent the observed blur and perspective, respectively. In this context, perspective refers to all pictorial cues that result from perspective projection, including the texture gradient, linear perspective, and relative size. Using a technique in Burge et al. [2010], we convert the likelihood distributions and prior on the right side of the equation into posterior distributions for the individual cues and then take the product for the optimal estimate.

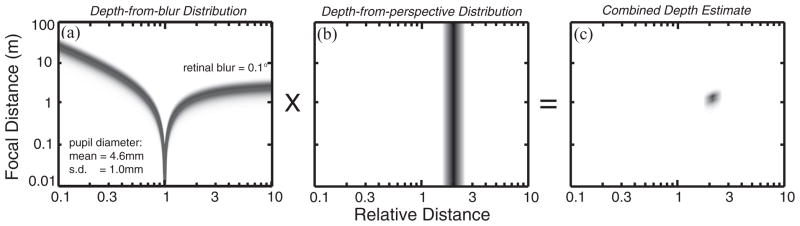
Figure 7 shows the result. The left panel illustrates the relationship between focal distance and relative distance for a given amount of blur in the retinal image, P(z_o, d|c). The middle panel shows the relationship between distance and perspective cues: P(z_o, d|p). For two objects in the scene, one at the focal distance and one at another distance, one can estimate the ratio of distances to the objects from perspective. For instance, perspective cues may reveal the slant and tilt of the ground plane, and then the position of the objects along that plane would reveal their relative distances from the observer [Sedgwick 1986]. The variance of P(z_o, d|p) depends on the reliability of the available perspective cues: lower variance when the cues are highly reliable. The right panel shows the combined distribution derived from the products of the distributions in the left and middle panels. By combining information in blur and perspective, the model can now estimate absolute distance. We use the median of the product distribution as the depth estimate.

Fig. 7.

Bayesian analysis of blur as cue to absolute distance. (a) The probability distribution P(z_o, d|c) where c is the observed blur diameter in the image (in this case, 0.1°), z₀ is the focal distance, and d is the relative distance of another point in the scene. Measuring the blur produced by an object cannot reveal the absolute or relative distance to points in the scene. (b) The probability distribution P(z_o, d|p) where p is the observed perspective. Perspective specifies the relative distance, but not the absolute distance: it is scale ambiguous. (c) The product of the distributions in (a) and (b). From this posterior distribution, the absolute and relative distances of points in the scene can be estimated.

In summary, blur by itself provides little information about relative or absolute distance, and perspective cues by themselves provide little information about absolute distance. But the two cues in combination provide useful information about both distances. This constitutes our model of how blur is used in images like Figure 2 to provide an impression of absolute distance.

4.2.1 Impact on Previous Findings

As we said earlier, vision scientists have generally concluded that blur is a weak depth cue. Three reasons have been offered for its ineffectiveness. It is useful to evaluate them in the context of the model.

1. Blur does not indicate the sign of a distance change: that is, it does not by itself specify whether an out-of-focus object is nearer or farther than an in-focus object. It is evident in Figure 6 and Eq. (2) that a given amount of blur can be caused by an object at a distance shorter or longer than the distance of the focal plane. The model in Figure 7 makes clear how the sign ambiguity can be solved. The perspective distribution is consistent with only one wing of the blur distribution, so the ambiguity is resolved by combining information from the two cues.

2. The relationship between distance and blur is dependent on pupil size. When the viewer’s pupil is small, a given amount of blur specifies a large change in distance; when the pupil is large, the same blur specifies a smaller change. There is no evidence that humans can measure their own pupil diameter, so the relationship between measured blur and specified distance is uncertain. The model shows that distance can still in principle be estimated even with uncertainty about pupil size. The uncertainty only reduces the precision of depth estimation.

3. The visual system’s ability to measure changes in retinal-image blur is limited, so small changes in blur may go undetected [Mather and Smith 2002]. Blur discrimination is not well characterized, so we have not yet built corresponding uncertainty into the model. Doing so would yield higher variance in the blur distributions in Figure 6 and the left panel of Figure 7, much like the effect of uncertainty due to pupil diameter.

Thus, the model shows how one can in principle estimate distance from blur despite uncertainties due to sign ambiguity, pupil diameter, and blur discrimination. Furthermore, this estimation does not require that the focal distance be known beforehand, that more than one image recorded with different focal distances be available, or that the camera have a specially designed aperture.

4.2.2 Perspective Cues

The model depends on the reliability of the relative-distance information provided by perspective. In an image like the urban scene in Figure 1, linear perspective specifies relative distance quite reliably, so the variance of P(z_o, d|p) is small. As a consequence, the product distribution has low variance: that is, the estimates of absolute and relative distance are quite precise. In an image of an uncarpentered scene with objects of unknown size and shape, perspective and other pictorial cues would not specify relative distance reliably, and the variance of P(z_o, d|p) would be large. In this case, the product distribution would also have high variance and the distance estimates would be rather imprecise. Thus, the ability to estimate depth from blur is quite dependent on the ability to estimate relative distance from perspective or other pictorial cues. We predict, therefore, that altering perceived size by manipulating blur will be more effective in scenes that contain rich perspective cues than it will be in scenes with weak perspective cues.

We have also assumed that perspective cues convey only relative-distance information. In fact, many images also contain the cue of familiar size, which conveys some absolute-distance information. We could incorporate this into the model by making the perspective distribution in Figure 7(b) two-dimensional with different variances horizontally and vertically. We chose not to add this feature to simplify the presentation and because we have little idea of what the relative horizontal and vertical variances would be. It is interesting to note, however, that familiar size may cause the pattern of blur to be less effective in driving perceived scale. Examples include photos with real people, although even these images can appear to be miniaturized if sufficient blur is applied appropriately.

4.2.3 Recovering Focal Distance in Practice

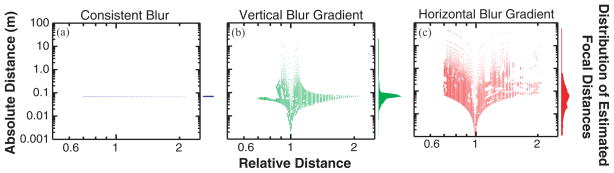
The model can be implemented to estimate the focal distance z₀ used to create a given image. First, the blur circle c₁ and relative distance d are estimated at several locations in the image. Then, assuming some values for parameters A and s₀, Eq. (2) can be used to calculate z₀. Compiling the z₀ estimates from all the example points provides a marginal distribution of estimates of the focal distance (Figure 9). The median of the marginal distribution may then be interpreted as the final estimate of z₀, with the variance of this distribution indicating the estimate’s reliability. If the blur and depth information are either difficult to measure or not properly matched, the reliability will be low, and the blur in the image will have less impact on the visual system’s estimate of the distance and size of the scene.

Fig. 9.

Determining the most likely focal distance from blur and perspective. Intended focal distance was 0.06m. Each panel plots estimated focal distance as a function of relative distance. The left, middle, and right panels show the estimates for consistent blur, vertical blur gradient, and horizontal blur gradient, respectively. The first step in the analysis is to extract the relative-distance and blur information from several points in the image. The values for each point are then used with Eq. (2) to estimate the focal distance. Each estimate is represented by a point. Then all of the focal distance estimates are accumulated to form a marginal distribution of estimates (shown on the right of each panel). The data from a consistent-blur rendering most closely matches the selected curve, resulting in extremely low variance. Though the vertical blur gradient incorrectly blurs several pixels, it is well correlated with the relative distances in the scene, so it too produces a marginal distribution with low variance. The blur applied by the horizontal gradient is mostly uncorrelated with relative distance, resulting in a marginal distribution with large variance and therefore the least reliable estimate.

5. ESTIMATING DISTANCE IN IMAGES WITH MANIPULATED BLUR

Our model predicts that the visual system estimates absolute distance by finding the focal distance that is most consistent with the blur and perspective in a given image. If the blur and perspective are consistent with one another, accurate and precise distance estimates can be obtained. We explored this notion by applying the procedure from Section 4.2.3 to images with three types of blur: (1) blur that is completely consistent with the relative distances in a scene (consistent-blur condition), (2) blur that is mostly correlated with the distances (vertical-blur-gradient condition), and (3) blur that is uncorrelated with the distances (horizontal-blur-gradient condition).

Fourteen scenes from GoogleEarth were used. Seven had a large amount of depth variation (skyscrapers) and seven had little depth variation (one- to three-story buildings). The camera was placed 500m above the ground and oriented down 35° from earth-horizontal. The average distance from the camera to the buildings in the centers of each scene was 785m.

5.1 Applying Blur Patterns

The consistent-blur rendering technique described in Section 3.2 was used. The diameters of the simulated camera apertures were 60.0, 38.3, 24.5, 15.6, and 10.0m. The unusually large apertures were needed to produce blur consistent with what a human eye with a 4.6mm pupil would receive when focused at 0.06, 0.9, 0.15, 0.23, and 0.36m, respectively. Figures 8(b) and (c) show example images with simulated 24.5m and 60m apertures. The vertical blur gradient was, as stated, aligned with the distance gradient. It was generated using the technique described in Section 3.2. Figures 8(d) and 8(e) are examples. The horizontal blur gradients employed the same blur magnitudes as the vertical gradients, but were orthogonal to the distance gradients. Figures 8(f) and 8(g) are examples.

Fig. 8.

The four types of blur used in the analysis and experiment: (a) no blur, (b) and (c) consistent blur, (d) and (e) linear vertical blur gradient, and (f) and (g) linear horizontal blur gradient. Simulated focal distances of 0.15m (b,d,f) and 0.06m (c,e,g) are shown. In approximating the blur produced by a short focal length, the consistent-blur condition produces the most accurate blur, followed by the vertical gradient, the horizontal gradient, and the no-blur condition.

Original city images and data from GoogleEarth are copyright Terrametrics, SanBorn, and Google.

5.2 Calculating Best Fits to the Image Data

To predict the viewers’ response to each type of blur, we applied the procedure in Section 4.2.3 to each image.

1. We selected pixels in image regions where blur would be most measurable, namely areas containing high contrast, by employing the Canny edge detector [Canny 1986]. The detector’s parameters were set such that it found the subjectively most salient edges. We later verified that the choice of parameters did not affect the model’s predictions.

2. Recovering relative distance and blur information:

   1. Relative distances in the scene were recovered from the video card’s z-buffer while running GoogleEarth. These recovered distances constitute the depth map. In our perceptual model, these values would be estimated using perspective information. The z-buffer, of course, yields much more accurate values than a human viewer would obtain through a perspective analysis. However, our primary purpose was to compare the predictions for the three blur types. Because the visual system’s ability to measure relative distance from perspective should affect each prediction similarly, we chose not to model it at this point. We can add such a process by employing established algorithms [Brillault-O’Mahony 1991; Coughlan and Yuille 2003].

   2. For the consistent-blur condition, the depth map was used to calculate the blur applied to each pixel. For the incorrect blur conditions, the blur for each pixel was determined by the applied gradients.

3. To model human viewers, we assumed A = 4.6mm and s₀ =17mm. We assumed no uncertainty for s₀ because an individual viewer’s eye does not vary in length from one viewing situation to another. We then used Eq. (2) to calculate z₀ for each pixel.

4. All of the estimates were combined to produce a marginal distribution of estimated focal distances. The median of the distribution was the final estimate.

The results for the example images in Figures 8(c), 8(e), and 8(g) are shown in Figure 9. The other images produced quantitatively similar results.

5.3 Predictions of the Model

First consider the images with consistent blur. Figure 9(a) shows the focal-distance estimates based on the blur and relative-distance data from the image in Figure 8(c). Because the blur was rendered correctly for the relative distances, all of the estimates indicate the intended focal distance of 0.06m. Therefore, the marginal distribution of estimates has very low variance and the final estimate is accurate and precise.

Next consider the images with an imposed vertical blur gradient. Figure 9(b) plots the blur/relative-distance data from the vertical-blur image in Figure 8(e). The focal-distance estimates now vary widely, though the majority lie close to the intended value of 0.06m. This is reflected in the marginal distribution to the right, where the median is close to the intended focal distance, but the variance is greater than in the consistent-blur case. We conclude that vertical blur gradients should influence estimates of focal distance, but in a less compelling and consistent fashion than consistent blur does. Although it is not shown here, scenes with larger depth variation produced marginal distributions with higher variance. This result makes sense because the vertical blur gradient is a poorer approximation to consistent blur as the scene becomes less planar.

Now consider the images with the imposed horizontal blur gradient. In these images, the blur is mostly uncorrelated with the relative distances in the scene, so focal-distance estimates are scattered. While the median of the marginal distribution is similar to the ones obtained with consistent blur and the vertical gradient, the variance of the distribution is much greater. The model predicts, therefore, that the horizontal gradient will have the least influence on perceived distance.

The analysis was also performed on images rendered by simulated tilt-shift lenses. The amount of tilt was chosen to reproduce the same maximum blur magnitude as the vertical blur gradients. The marginal distributions for the tilt-shift images were essentially identical to those for the vertical-blur-gradient images. This finding is consistent with the observation that linear blur gradients and tilt-shift lenses produce very similar blur magnitudes (Figure 5) and presumably similar perceptual effects.

These examples show that the model provides a useful framework for predicting the effectiveness of different types of image blur in influencing perceived distance and size. The horizontal gradient results also highlight the importance of accounting for distance variations before applying blur.

5.4 Algorithm

Our model predicts that linear blur gradients can have a strong effect on the perceived distance and size of a scene. But we used carefully chosen rendering parameters to produce the blur gradient images: the maximum blur magnitude was the same as that produced by a consistent-blur image taken at the intended focal length, and the tilt of the lens and the orientation of the gradient were perfectly aligned with the distance gradient in the scene. To simplify the application of the model to images, we developed a semiautomated algorithm that allows the user to load a sharply rendered image, indicate a desired perceived distance and size, and then apply the appropriate blur gradient to achieve that outcome.

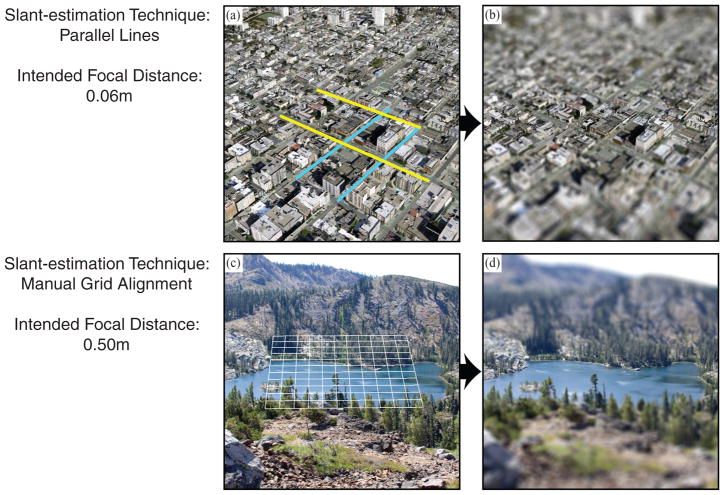
We implemented the algorithm for scenes that are approximately planar globally, but it could be extended to scenes that are only locally planar. The user first sets the desired focal distance z₀ and the viewer’s pupil diameter A. To simulate the human eye, s₀ is set to 0.017m [Larsen 1971]. Next, the slant σ and tilt τ of the planar approximation to the scene are estimated using one of two methods (slant and tilt are, respectively, the angle between the line of sight and surface normal, and the direction of the slant relative to horizontal). If the scene is carpentered, like the cityscape in Figure 11(a), we use the technique in Algorithm 1, originally described by Okatani and DeGuchi [2007]. If the scene is uncarpentered, like the landscape in Figure 11(b), then a grid is displayed over the image. The viewer uses a mouse to rotate the grid until it appears to be parallel to the scene. The orientation of the grid yields σ and τ. Parameters l and v (defined in Figure 10) are recovered from the settings (in our case, from OpenGL) that were used to render the grid on-screen. Finally, Algorithm 2 determines the amount of blur assigned to each pixel, then creates the final image.

Fig. 11.

Input and output of the semiautomated blurring algorithm. The algorithm can estimate the blur pattern required to simulate a desired focal length. It can either derive scene information from parallel lines in a scene or use manual feedback from the user on the overall orientation of the scene. (a) Two pairs of parallel lines were selected from a carpentered scene for use with the first approach. (b) The resulting image once blur was applied. Intended focal distance = 0.06m. (c) A grid was manually aligned to lie parallel to the overall scene. (d) The blurred output designed to simulate a focal distance of 0.50m.

Algorithm 1.

Determining σ and τ from Parallel Lines

prompt user to select two pairs of lines that are parallel in the original scene;

p1 = intersection of first line pair;

p2 = intersection of second line pair;

pc = center of image;

vanLine = line connecting p2 and p1;

v = sqrt(|p1y p2y + p1x p2x|);

l = distance between pc and vanLine;

σ = π/2−atan(l/v)

τ = angle between vanLine and the image’s horizontal axis;

Fig. 10.

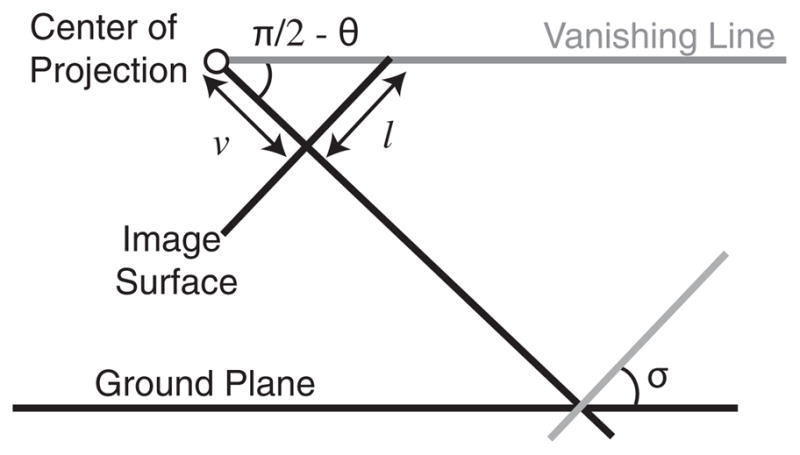
Schematic of variables pertinent to the semiautomated blurring algorithm. Here, the image surface is equivalent to the monitor surface, and v and l are in units of pixels. σ indicates the angle between the ground plane’s surface normal and the imaging system’s optical axis. Refer to Algorithm 1 for details on how each value can be calculated from an input image. (Adapted from Okatani and Deguchi [2007].)

Algorithm 2.

Calculating and Applying Blur to Image

Figure 11 shows two example images produced by our algorithm. The scene is carpentered in panel (a), so the parallel-line-selection option was employed. Panel (b) shows the output of the algorithm, with an intended focal distance of 0.06m. The scene is not carpentered in Figure 11(c), so the user aligned a grid to be parallel to the predominant orientation of the scene. The resulting blurred image in panel (c) was designed to simulate a focal distance of 0.50m.

The algorithm provides an effective means for blurring images in postprocessing, thereby changing the perceived distance and size of a scene. The semiautomated technique frees the user from the calculations needed to create nearly correct blur, and produces compelling results for images ranging from urban scenes to landscapes. Its effectiveness is supported by our model’s predictions, which in turn were validated by the following psychophysical experiment.

6. PSYCHOPHYSICAL EXPERIMENT

We examined how well the model’s predictions correspond with human distance percepts. We were interested in learning two things: (1) Do human impressions of distance accurately reflect the simulated distance when defocus blur is applied to an image, and (2) How accurately must defocus blur be rendered to effectively modulate perceived distance?

6.1 Methods

We used the previously described blur-rendering techniques to generate stimuli for the perceptual experiment: consistent blur, vertical blur gradient, and horizontal blur gradient. An additional stimulus was created by rendering each scene with no blur. The stimuli were generated from the same 14 GoogleEarth scenes on which we conducted the analysis in Section 4.4.

Each subject was unaware of the experimental hypotheses and was not an imaging specialist. They were positioned with a chin rest 45cm from a 53cm CRT and viewed the stimuli monocularly. Each stimulus was displayed for 3 seconds. Subjects were told to look around the scene in each image to get an impression of its distance and size. After each stimulus presentation, subjects entered an estimate of the distance from a marked building in the center of the scene to the camera that produced the image. There were 224 unique stimuli, and each stimulus was presented seven times in random order for a total of 1568 trials. The experiment was conducted in four sessions of about one hour each. At the end, each subject was debriefed with a series of questions, including how they formulated their responses and whether the responses were based on any particular cues in the images. If the debriefing revealed that the subject did not fully understand the task or had based his or her answers on strategies that circumvented the phenomenon being tested, his or her data were excluded.

6.2 Results

Ten subjects participated, but the data from three were discarded. Two of the discarded subjects revealed in debriefing that they had done the task by estimating their height relative to the scene from the number of floors in the pictured buildings and had converted that height into a distance. They said that some scenes ”looked really close,” but described a conversion that scaled the perceived size up to the size of a real building. The third subject revealed that she had estimated distance from the amount of blur by assuming that the camera had a fixed focal distance and therefore anything that was blurrier had to be farther away.

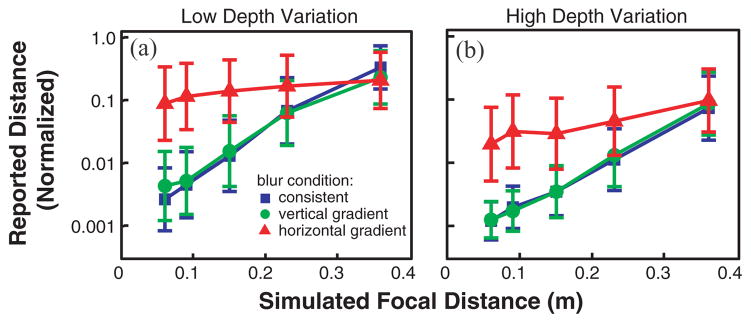
Figure 12 shows the results averaged across the seven remaining subjects, with the left and right panels for the low- and high-depth-variation images, respectively. (Individual subject data are available in the supplemental material.) The abscissas represent simulated focal distance (the focal distance used to generate the blur in the consistent-blur condition); the values for the vertical and horizontal blur gradients are those that yielded the same maximum blur magnitudes as in the consistent-blur condition. The ordinates represent the average reported distance to the marked object in the center of the scene divided by the average reported distance for the no-blur control condition. Lower values mean that the scene was seen as closer and therefore presumably smaller.

Fig. 12.

Results of the psychophysical experiment averaged across the seven subjects. Panels (a) and (b) respectively show the data when the images had low and high depth variation. The type of blur manipulation is indicated by the colors and shapes of the data points. Blue squares for consistent blur, green circles for vertical blur gradient, and red triangles for horizontal blur gradient. Error bars represent standard errors. Individual subject data are included in the supplemental material.

All subjects exhibited a statistically significant effect of blur magnitude [3-way, repeated-measures ANOVA, F(5,30) = 13.8, p < 0.00001], reporting that the marked object appeared smaller when the blur was large. The effect of magnitude was much larger in the consistent-blur and vertical-blur-gradient conditions than in the horizontal-gradient condition, so there was a significant effect of blur type [F(3,18) = 14.7, p < 0.00001]. There was a tendency for the high-depth-variation scenes to be seen as closer, but for blur magnitude to have a larger effect for the low-depth-variation scenes [F(1,6) = 2.27, p = 0.18 (not significant)].

These results show that perceived distance in human viewers is influenced by the pattern and magnitude of blur just as the model predicts. Consistent blur and aligned-linear-gradient blur (which is used in our semiautomated algorithm) yield systematic and predictable variations in perceived distance. Linear gradients that are not aligned with distance information yield a much less systematic variation in perceived distance.

7. DISCUSSION

7.1 Validity of Assumptions in the Model

Our representation of the depth information conveyed by retinal-image blur was an approximation to information in the human visual system. Here we discuss four of our simplifying assumptions.

First, we represented the eye’s optics with an ideal lens free of aberrations. Image formation by real human eyes is affected by diffraction due to the pupil, at least for pupil diameters smaller than 3mm, and is also affected by a host of higher-order aberrations including coma and spherical aberration at larger pupil diameters [Wilson et al. 2002]. Incorporating diffraction and higher-order aberrations in Figure 7(a) would have yielded greater retinal-image blur than shown for distances at or very close to the focal distance: The trough in the blur distribution would have been deeper. The model estimates absolute distance from image regions with a wide range of relative distances, not just distances near the focal plane. Therefore, if the image contains a sufficient range of relative distances, the estimates are unaffected by the simplifying assumptions about the eye’s optics.

Second, we assumed that the visual system’s capacity to estimate depth from blur is limited by the optics of retinal-image formation. In fact, changes in blur magnitude smaller than 10% are generally indiscriminable [Mather and Smith 2002]. If we included this observation, the marginal distributions in Figure 9 would have larger variance than the ones shown, but the medians (and therefore the distance estimates) would be little affected.

Third, we assumed that the eye’s optics are fixed. In fact, the optical power of the eye varies continually due to adjustments of the shape of the crystalline lens, a process called accommodation. Accommodation is effected by commands sent to the muscles that control the shape of the lens. These commands are a cue to distance, albeit a variable and weak one [Wallach and Norris 1963; Fisher and Ciuffreda 1988; Mon-Williams and Tresilian 2000]. In viewing real scenes, accommodation turns blur into a dynamic cue that may allow the visual system to glean more distance information than we have assumed. However, the inclusion of accommodation into our modeling would have had little effect because the stimuli were images presented on a flat screen at a fixed distance, so the changes in the retinal image as the eye accommodates did not mimic the changes that occur in real scenes. We intend to pursue the use of dynamic blur and accommodation using volumetric displays that yield a reasonable approximation to the relationship in real scenes (e.g., Akeley et al. [2004]).

Fourth, our model assumes that the viewer was fixating at the center of each image, which was rendered sharply. In fact, each observer was instructed to look around the entire image, resulting in unnatural patterns of blur on the retina. In natural viewing, the object of fixation is usually in focus. Inclusion of the incorrect blur patterns in the model would increase the variance, and in turn decrease the reliability, of the distance estimate.

7.2 Algorithm Effectiveness

The predictions of the model and the results of the psychophysical experiment confirmed the effectiveness of the linear blur gradients applied by our algorithm. Specifically, linear gradients and consistent blur were similarly effective at modulating perceived distance and size. Currently, the algorithm is most effective for planar scenes, and it is only useful for adding blur and making sharply focused scenes appear smaller. Further development could incorporate regional slant estimation to increase its accuracy for scenes with large distance variations, and include a sharpening algorithm to reduce blur and make small scenes appear larger.

7.3 Impact on Computer Graphics

The model we developed explains a number of phenomena in which blur does or does not affect perceived distance and scale. Some of these phenomena occur in photography, cinematography, and graphics, so the model has several useful applications.

7.3.1 Application: Natural Depth of Field

One of the main points of our analysis is that there is an appropriate relationship between the depth structure of a scene, the focal distance of the imaging device, and the observed blur in the image. From this relationship, we can determine what the depth of field would be in an image that looks natural to the human eye. Consider Eq. (2). By taking advantage of the small-angle approximation, we can express blur in angular units

$$b_1=2{tan}^{-1}\left(\frac{c_1}{2s_0}\right)\approx \frac{c_1}{s_0},$$ (5)

where b₁ is in radians. Substituting into Eq. (2), we have

$$b_1=\left|\frac{A}{z_0}\left(1-\frac{1}{d}\right)\right|,$$ (6)

which means that the diameter of the blur circle in angular units depends on the depth structure of the scene and the camera aperture and not on the camera’s focal length [Kingslake 1992].

Suppose that we want to create a photograph with the same pattern of blur that a human viewer would experience if he or she was looking at the original scene. We photograph the scene with a conventional camera and then have the viewer look at the photograph from its center of projection. The depth structure of the photographed scene is represented by z₀ and d, different d’s for different parts of the scene. We can recreate the blur pattern the viewer would experience when viewing the real scene by adjusting the camera’s aperture to the appropriate value. From Eq. (6), we simply need to set the camera’s aperture to the same diameter as the viewer’s pupil. If a viewer looks at the resulting photograph from the center of projection, the pattern of blur on the retina would be identical to the pattern created by viewing the scene itself. Additionally, the perspective information would be correct and consistent with the pattern of blur. This creates what we call “natural depth of field.” For typical indoor and outdoor scenes, the average pupil diameter of the human eye is 4.6mm (standard deviation is 1mm). Thus to create natural depth of field, one should set the camera aperture to 4.6mm, and the viewer should look at the resulting photograph with the eye at the photograph’s center of projection. We speculate that the contents of photographs with natural depth of field will have the correct apparent scale.

7.3.2 Application: Simulating Extreme Scale

We described how to manipulate blur to make small scenes look large and large scenes look small. These effects can be achieved by altering the blur pattern in postprocessing, but they can also be achieved by using cameras with small or large apertures. Specifically, if the focal distance in the actual scene is z₀, and we want to make it look like ẑ₀ where ẑ₀ = mz₀, Eq. (2) implies that the camera’s aperture should be set to A/m. In many cases, doing this is not practical because the required aperture is too restrictive. If the aperture must be quite small, the amount of light incident on the image plane per unit time is reduced, and this decreases the signal-to-noise ratio. If the aperture must be very large, it might not be feasible with a physically realizable camera. Consequently, it is very attractive to be able to adjust the blur pattern in postprocessing in order to produce the desired apparent scale.

The demonstrations we showed here made large scenes look small. Figure 8(a) shows an image that was recorded with a focal length of ~800m and a pinhole (A ≈ 0) aperture. We made the image look small in panels 8(b) and 8(c) by simulating in postprocessing focal lengths of 0.15 and 0.06m. We could have created the same images by recording the images with cameras whose aperture diameters were 24.5 and 60m, respectively, but this is clearly not feasible with a conventional camera. It is much more attractive to achieve the same effects in postprocessing, and our algorithm shows how to do this.

Our analysis also applies to the problem of making small scenes look large. If we have an image recorded with a particular aperture size, we want to reduce the blur in the image in the fashion implied by Figure 8. Our algorithm could potentially be used to determine the desired blur kernel diameter for each region of the image. However, implementation of this algorithm would require some form of deconvolution, which is prone to error [Levin et al. 2007].

7.3.3 Application: Using Other Depth Cues to Affect Perceived Scale

Besides blur, several other cues are known to affect perceived distance and scale. It is likely that using them in conjunction with blur manipulation would strengthen the effect on perceived distance and scale.

Atmospheric attenuation causes reductions in image saturation and contrast across long distances [Fry et al. 1949], and serves as the motivation for the commonly used rendering method known as depth cueing. Not surprisingly, more saturated objects tend to be perceived as nearer than less saturated objects [Egusa 1983]. In fake miniatures, the saturation of the entire image is often increased to strengthen the impression that the scene is close to the camera and small [Flickr 2009]. Conversely, a reduction in saturation helps create the impression that the scene is far away and therefore large. It is also not surprising, given the atmospheric effects, that high-contrast textures are perceived as nearer than low-contrast textures [Ichihara et al. 2007; Rohaly and Wilson 1999]. We suspect, therefore, that adjusting image contrast would also be useful in creating the desired apparent size.

In principle, the acceleration of an object due to gravity is a cue to its absolute distance and size [Saxberg 1987; Watson et al. 1992]. When an object rises and falls, the vertical acceleration in the world is constant. Thus, distant objects undergoing gravity-fed motion have slower angular acceleration across the retina than close objects. Human viewers are quite sensitive to this, but they use a heuristic in which objects generating greater retinal speed (as opposed to acceleration) are judged as nearer than objects generating slower retinal speeds [Hecht et al. 1996]. This effect has been used in cinematography for decades: practitioners display video at slower speed than the recorded speed to create the impression of large size [Bell 1924; Fielding 1985].

The accommodative state of the viewer’s eye can affect perceived distance [Wallach and Norris 1963; Fisher and Ciuffreda 1988; Mon-Williams and Tresilian 2000]. Thus, if an image is meant to depict a small scene very close to the eye, the impression of small size might be more convincing if the image is actually viewed from up close. Accommodation is, however, a weak cue to depth, so effects of actual viewing distance may be inconsistent.

7.3.4 Application: Blur and Stereo Displays

Stereo image and video production has recently gained a great deal of attention. Several studios are producing films for stereo viewing and many movie houses have installed the infrastructure for presenting these three-dimensional movies [Schiffman 2008]. Additionally, many current-generation televisions are capable of stereo display [Chinnock 2009]. It is therefore timely to consider blur rendering in stereo content.

Disparity, the cue being manipulated in stereo images, has the same fundamental geometry as blur [Schechner and Kiryati 2000]. Disparity is created by the differing vantage points of two cameras or eyes, while blur is created by the differing vantage points of different positions in one camera’s or eye’s aperture. Consider two pinhole cameras with focal lengths f. The distance from the camera apertures to the film planes is s₀, and the distance between apertures is I. The cameras are converged on an object at distance z₀ while another object is presented at z₁. The images of the object at z₀ fall in the centers of the two film planes and therefore have zero disparity. The images of the object at z₁ fall at different locations X_L and X_R creating a disparity of

$$\delta =X_L-X_R=I\left(\frac{s_0}{z_0}\right)\left(1-\frac{1}{d}\right),$$ (7)

where d = z₁/z₀ and 1/s₀ = 1/f − 1/z₀. The connection to image blur is clear if we replace the aperture A in Eq. (2) with two pinholes at its edges. Then two images of z₁ would be formed and they would be separated by c₁. From Eqs. (2) and (7), for cameras of focal lengths f,

$$c_1=(A/I)\mid \delta \mid .$$ (8)

Thus, the magnitudes of blur and disparity caused by a point in a three-dimensional scene should be proportional to one another. In human vision, the pupil diameter is roughly 1/12 the distance between the eyes [Spring and Stiles 1948], so the diameters of blur circles are generally 1/12 the magnitudes of disparities. Because the geometries underlying disparity and blur are similar, this basic relationship holds for the viewing of all real scenes.

How should the designer of stereo images and video adjust blur and disparity? Because of the similarity in the underlying geometries, the designer should make the disparity and blur patterns compatible. To produce the impression of a particular size, the designer can use the rule of thumb in Eq. (8) to make the patterns of blur and disparity both consistent with this size. To do otherwise is to create conflicting information that may adversely affect the intended impression. Two well-known phenomena in stereo images and video (i.e., the cardboard-cut-out effect [Yamanoue et al. 2000; Meesters et al. 2004; Masaoka et al. 2006] and puppet-theater effect [Yamanoue 1997; Meesters et al. 2004]) may be caused by blur-disparity mismatches.

The blur-rendering strategy should depend, however, on how people are likely to view the stereo image. Consider two cases. (1) The viewer looks at an object at one simulated distance and maintains fixation there. (2) The viewer looks around the image, changing fixation from one simulated distance to another.

In the first case, the designer would render the fixated object sharply and objects nearer and farther with the blur specified by Eq. (8). By doing so, the blur and disparity at the viewer’s eyes are matched, yielding the desired impression of three-dimensional structure. The blur rendering can guide the viewer’s eye to the intended object [Kosara et al. 2001; DiPaola et al. 2009]. This would be common for entertainment-based content.

In the second case, the rule of thumb in Eq. (8) should probably not be applied. In real scenes, the viewer who looks at a nearer or farther object converges or diverges the eyes to perceive a single image and accommodates (i.e., adjusts the eye’s focal power) to sharpen the retinal image. If the rule of thumb were applied in creating a stereo image, objects at simulated distances nearer or farther than the sharply rendered distance would be blurred. The viewer who looks nearer or farther would again converge or diverge the eyes, but the newly fixated object would be blurred on the retina no matter how the viewer accommodated, and this would yield a noticeable and annoying conflict. On the other hand, if the image was rendered sharply everywhere, the viewer would experience a sharp retinal image with each new fixation, and this outcome would probably be more desirable. This notion could be important in applications like medical imaging, where the viewer may need to look at features throughout the scene.

Thus, blur rendering in stereo images should probably be done according to the rule of thumb in Eq. (8) when the designer intends the viewer to look at one simulated distance, but should not be done that way when the viewer is likely to look at a variety of distances.

8. CONCLUSIONS AND FUTURE WORK

We showed how manipulating blur in images can make large things look small and small things look large. The strength of the effect stands in contrast with previous notions of blur as a weak depth cue. A probabilistic model shows that absolute or relative distance cannot be estimated from image blur alone, but that these distances can be estimated quite effectively in concert with other depth cues. We used this model to develop a semiautomatic algorithm for adjusting blur to produce the desired apparent scale. The results of a psychophysical experiment confirmed the validity of the model and usefulness of the algorithm.

We described how blur and stereo operate over similar domains, providing similar information about depth. A rule of thumb can be used to assure that blur and disparity specify the same three-dimensional structure. As stereo images and video become increasingly commonplace, it will be important to learn what artistic variations from the natural relationship between blur and disparity can be tolerated.

We also described how the normal relationship between blur and accommodation is disrupted in pictures. Learning more about the consequences of this disruption will be valuable to the development of advanced displays in which the normal relationship can be approximated.