Dynamic reconfiguration of human brain networks during learning

Abstract

Human learning is a complex phenomenon requiring flexibility to adapt existing brain function and precision in selecting new neurophysiological activities to drive desired behavior. These two attributes—flexibility and selection—must operate over multiple temporal scales as performance of a skill changes from being slow and challenging to being fast and automatic. Such selective adaptability is naturally provided by modular structure, which plays a critical role in evolution, development, and optimal network function. Using functional connectivity measurements of brain activity acquired from initial training through mastery of a simple motor skill, we investigate the role of modularity in human learning by identifying dynamic changes of modular organization spanning multiple temporal scales. Our results indicate that flexibility, which we measure by the allegiance of nodes to modules, in one experimental session predicts the relative amount of learning in a future session. We also develop a general statistical framework for the identification of modular architectures in evolving systems, which is broadly applicable to disciplines where network adaptability is crucial to the understanding of system performance.

The brain is a complex system, composed of many interacting parts, which dynamically adapts to a continually changing environment over multiple temporal scales. Over relatively short temporal scales, rapid adaptation and continuous evolution of those interactions or connections form the neurophysiological basis for behavioral adaptation or learning. At small spatial scales, stable neurophysiological signatures of learning have been best demonstrated in animal systems at the level of individual synapses between neurons (1–3). At a larger spatial scale, it is also well-known that specific regional changes in brain activity and effective connectivity accompany many forms of learning in humans—including the acquisition of motor skills (4, 5).

Learning-associated adaptability is thought to stem from the principle of cortical modularity (6). Modular, or nearly decomposable (7), structures are aggregates of small subsystems (modules) that can perform specific functions without perturbing the remainder of the system. Such structure provides a combination of compartmentalization and redundancy, which reduces the interdependence of components, enhances robustness, and facilitates behavioral adaptation (8, 9). Modular organization also confers evolvability on a system by reducing constraints on change (8, 10–12). Indeed, a putative relationship between modularity and adaptability in the context of human neuroscience has recently been posited (13, 14). To date, however, the existence of modularity in large-scale cortical connectivity during learning has not been tested directly.

Based on the aforementioned theoretical and empirical grounds, we hypothesized that the principle of modularity would characterize the fundamental organization of human brain functional connectivity during learning. More specifically, based on several studies relating the neural basis of modularity to the development of skilled movements (15–17), we expected that functional brain networks derived from acquisition of a simple motor skill would display modular structure over the variety of temporal scales associated with learning (18). We also hypothesized that modular structure would change dynamically during learning (4, 19), and that characteristics of such dynamics would be associated with learning success.

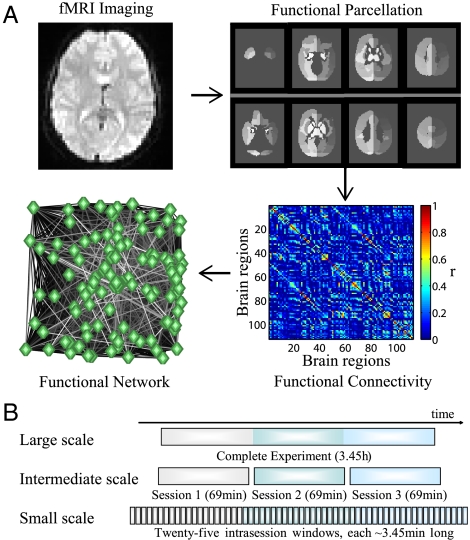
We tested these predictions using fMRI, an indirect measure of local neuronal activity (20), in healthy adult subjects during the acquisition of a simple motor learning skill composed of visually cued finger sequences. We derived low frequency (0.06–0.12 Hz) functional networks from the fMRI data by computing the temporal correlation between activity in each pair of brain regions to construct weighted graphs or whole-brain functional networks (21–23) (Fig. 1A and SI Appendix). This network framework enabled us to estimate a mathematical representation of modular or community organization, known as “network modularity,” for each individual over a range of temporal scales. We evaluated the evolution of network connectivity over time using the mathematical framework described in ref. 25, and we tested its relationship with learning. See Materials and Methods for details of the sample, experimental paradigm, and methods of analysis.

Fig. 1.

Structure of the investigation. (A) To characterize the network structure of low-frequency functional connectivity (24) at each temporal scale, we partitioned the raw fMRI data (Upper Left) from each subject’s brain into signals originating from N = 112 cortical structures, which constitute the network’s nodes (Upper Right). The functional connectivity, constituting the network edges, between two cortical structures is given by a Pearson correlation between the mean regional activity signals (Lower Right). We then statistically corrected the resulting N × N correlation matrix using a false discovery rate correction (54) to construct a subject-specific weighted functional brain network (Lower Left). (B) Schematic of the investigation that was performed over the temporal scales of days, hours, and minutes. The complete experiment, which defines the largest scale, took place over the course of three days. At the intermediate scale, we conducted further investigations of the experimental sessions that occurred on each of those three days. Finally, to examine higher-frequency temporal structure, we cut each experimental session into 25 nonoverlapping windows, each of which was a few minutes in duration.

Results

Static Modular Structure.

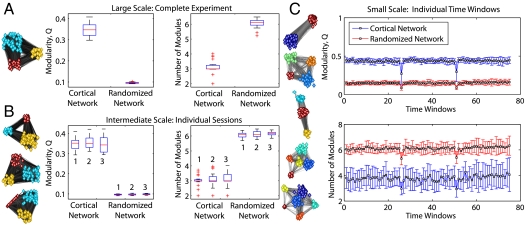
We investigated network organization over multiple temporal scales—over days, hours, and minutes—during motor learning (18, 19) (Fig. 1B). We used a diagnostic measure of the amount of network modularity in the system—the modularity index Q (See Materials and Methods for a mathematical definition). At each scale, we found Q to be larger than expected in a random network, indicating a significant segregation of the brain into distinct modules or communities (Fig. 2 A–C). The cortex is organized into fewer modules than the random network, indicating that the functional activity of the brain is significantly integrated across cortical regions. Because these results were consistent for all of the temporal scales that we examined, we concluded that the brain shows temporal scaling of functional organization, consistent with the scaling in frequency (26) and spatial (27, 28) domains previously reported. Furthermore, the temporal structure of this organization is graded in the sense that fewer modules (about three) on longer timescales (Fig. 2 A and B) are complemented by more modules (about four) on shorter timescales (Fig. 2C). This graded structure is analogous to that found in the nested modular networks of underlying brain anatomy where few modules uncovered at large spatial scales are complemented by more modules at smaller spatial scales (27).

Fig. 2.

Multiscale modular architecture. (A) Results for the modular decomposition of functional connectivity across temporal scales. (Left) The network plots show the extracted modules; different colors indicate different modules and larger separation between modules is used to visualize weaker connections between them. (A) and (B) correspond to the entire experiment and individual sessions, respectively. Boxplots show the modularity index Q (Left) and the number of modules (Right) in the brain network compared to randomized networks. See Materials and Methods for a formal definition of Q. (C) Modularity index Q and the number of modules for the cortical (blue) compared to randomized networks (red) over the 75 time windows. Error bars indicate standard deviation in the mean over subjects.

Dynamic Modular Structure.

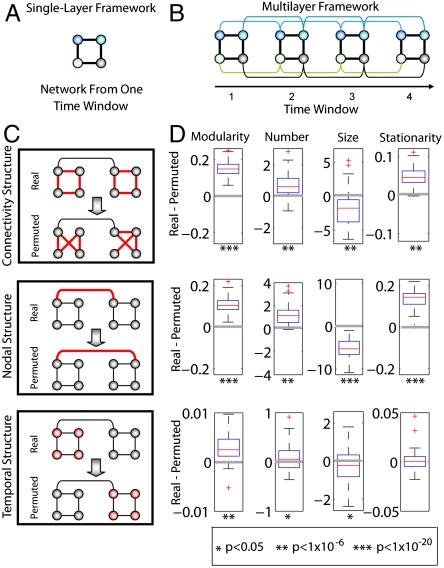
We next consider evolvability, which is most readily detected when the organism is under stress (29) or when acquiring new capacities such as during external training in our experiment. We found that the community organization of brain connectivity reconfigured adaptively over time. Using a recently developed mathematical formalism to assess the presence of dynamic network reconfigurations (25), we constructed multilayer networks in which we link the network for each time window (Fig. 3A) to the network in the time windows before and after (Fig. 3B) by connecting each node to itself in the neighboring windows. We then measured modular organization (30–32) on this linked multilayered network to find long-lasting modules (25).

Fig. 3.

Temporal dynamics of modular architecture. (A) Schematic of a toy network with four nodes and four edges in a single time window. (B) Multilayer network framework in which the networks from four time windows are linked by connecting nodes in one time window to themselves in the adjacent time windows (colored curves). (C) Statistical framework composed of a connectional null model (Top), a nodal null model (Middle), and a temporal null model (Bottom) in which intranetwork links, internetwork links, and time windows, respectively, in the real network are randomized in the permuted network. (We show all of the randomized links in red.) (D) Boxplots showing differences in modular architecture between the real and permuted networks for the connectional (Top), nodal (Middle), and temporal (Bottom) null models. We measured the structure of the network using the modularity index Q, the number of modules, the module size, and stationarity, which is defined as the mean similarity in the nodal composition of modules over consecutive time steps. Below each plot, we indicate by asterisks the significance of one-sample t-tests that assess whether the differences that we observed were significantly different from zero (gray lines): A single asterisk indicates p < .05, two asterisks indicate p < 1 × 10^-6, and three asterisks indicate p < 1 × 10^-20.

To verify the reliability of our measurements of dynamic modular architecture, we introduced three null models based on permutation testing (Fig. 3C). We found that cortical connectivity is specifically patterned, which we concluded by comparison to a “connectional” null model in which we scrambled links between nodes in each time window (33). Furthermore, cortical regions maintain these individual connectivity signatures that define community organization, which we concluded by comparison to a “nodal” null model in which we linked a node in one time window to a randomly chosen node in the previous and next time windows. Finally, we found that functional communities exhibit a smooth temporal evolution, which we identified by comparing diagnostics computed using the true multilayer network structure to those computed using a temporally permuted version (Fig. 3D). We constructed this temporal null model by randomly reordering the multilayer network layers in time.

By comparing the structure of the cortical network to those of the null models, we found that the human brain exhibited a heightened modular structure in which more modules of smaller size were discriminable as a consequence of the emergence and extinction of modules in cortical network evolution. The stationarity of communities, defined by the average correlation between partitions over consecutive time steps (34), was also higher in the human brain than in the connectional or nodal null models, indicating a smooth temporal evolution.

Learning.

Given the dynamic architecture of brain connectivity, it is interesting to ask whether the specific architecture changes with learning—either at a gross scale through an adaptation in the number or sizes of modules or at a finer scale through alterations in the nodal composition of modules. Empirically, we found no significant differences between experimental sessions in the coarse diagnostics. To quantify finer-scale architectural fluctuations, we introduced the notion of node flexibility using the network properties determined in the multilayer framework. “Flexibility” is the number of times that each node changes module allegiance, normalized by the total possible number of changes (SI Appendix). The flexibility of the network as a whole is then defined as the mean flexibility over all nodes.

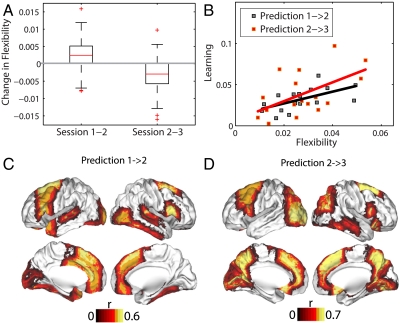
Network flexibility is a measure that captures changes in the local properties of individual network elements. We found that network flexibility changed during the learning process—first increasing and then decreasing (Fig. 4A)—demonstrating a meaningful biological process. In particular, the flexibility of a participant in one session could be used as a predictor of the amount of learning (as measured by improvement in the time required to complete the sequence of motor responses) in the following session (Fig. 4B). Regions of the brain that were most responsible for this predictive power of individual differences in learning were distributed throughout the cortex, with strong loadings in the frontal, presupplementary motor, posterior parietal, and occipital cortices (Fig. 4 C and D). We could not predict future learning capacity reliably using conventional task-related fMRI activation, supporting our conclusion that flexibility provides a useful approach for modeling system evolvability.

Fig. 4.

Flexibility and learning. (A) Boxplots showing that the increase in flexibility from experimental session 1 to session 2 was significantly greater than zero (a one-sample t-test gives the result t ≈ 6.00 with p ≈ 2 × 10^-8), and that the magnitude of the decrease in flexibility from session 2 to session 3 was significantly greater than zero (t ≈ 7.46, p ≈ 2 × 10^-11). (B) Significant predictive correlations between flexibility in session 1 and learning in session 2 (black curve, p ≈ 0.001) and between flexibility in session 2 and learning in session 3 (red curve, p ≈ 0.009). Note that relationships between learning and network flexibility in the same experimental sessions (1 and 2) were not significant; we obtained p > 0.13 using permutation tests. (C) Brain regions whose flexibility in session 1 predicted learning in session 2 (p < 0.05, uncorrected for multiple comparisons). Regions that also passed false-positive correction were the left anterior fusiform cortex and the right inferior frontal gyrus, thalamus, and nucleus accumbens. (D) Brain regions whose flexibility in session 2 predicted learning in session 3 (p < 0.05, uncorrected for multiple comparisons). Regions that also passed false-positive correction for multiple comparisons were the left intracalcarine cortex, paracingulate gyrus, precuneus, and lingual gyrus and the right superior frontal gyrus and precuneus cortex. In (C) and (D), colors indicate the Spearman correlation coefficient r between flexibility and learning.

Our results indicate that flexibility is sensitive to both intraindividual and interindividual variability. Across participants, we found that network flexibility was modulated by learning (Fig. 4A). However, we also found that each participant displayed a characteristic flexibility. The variation in flexibility over participants was larger than the variation in flexibility across sessions, as measured by the intraclass correlation coefficient: ICC ≈ 0.56, F-statistic F(17,34) ≈ 4.85, p ≈ 4 × 10^-5.

Discussion

Modularity of Functional Connectivity.

Modularity is an intuitively important property for dynamic, adaptable systems. The accompanying system decomposability provides necessary structure for complex reconfigurations. Modularity can be a property of morphology, as has been widely described in the context of evolution and development (11, 12, 29), as well as of the interconnection patterns of social, biological, and technological systems (30, 31). More pertinent to this paper, recent evidence suggests that modular organization over several spatial scales, or hierarchical modularity, also characterizes the large-scale anatomical connectivity of the human brain (27, 28), as well as the spontaneous fluctuations (35, 36) thought to stem from anatomical patterns (37). However, the putative relationship between adaptability and modular structure has not been previously explored in the context of the brain connectome.

In the present study, we have shown that the functional connectivity of the human brain during a simple learning paradigm is inhomogeneous. Instead, it is segregated into communities that can each perform unique functions. This segregation of connectivity structure manifested consistently over the scale of days, hours, and minutes, suggesting that community structure provides a generalizable framework to study the evolution of temporally distinct phenomena (12). However, it is also notable that connectivity at the shortest temporal scale displayed higher variability, perhaps reflecting the necessity for dynamic modulation of human brain function over relatively short intervals during learning (19). In light of historically strict definitions of cognitive modules as completely encapsulated structures (38), it is important to emphasize that the modules that we have uncovered remain integrated with one another by a complex pattern of weak interconnections.

Dynamic Network Evolution.

Efforts to characterize both resting state (39) and task-based large-scale connectivity of human brain structure and function (21–23) have focused almost exclusively on static representations of underlying connectivity patterns. However, both scientific intuition and recent evidence suggest that connectivity can be modulated both spontaneously (40) and by exogenous stimulation (4). The exploration of temporally evolving network architecture therefore forms a critical frontier in neuroscience.

Our exploration of dynamic community structure in an experimental paradigm that requires neurophysiological adaptability provides insight into the organizational principles supporting successful brain dynamics. Similar to social systems (34), we found that community organization changed smoothly with time, displaying coherent temporal dependence on what had gone before and what came after, a characteristic compatible with complex long-memory dynamical systems (41).

In addition to global adaptability, we found that diverse regions of the brain performed different roles within communities: Some maintain community allegiance throughout the experiment (low-flexibility nodes), and others constantly shift allegiance (high-flexibility nodes). Biologically, this network flexibility might be driven by physiological processes that facilitate the participation of cortical regions in multiple functional communities. Learning a motor skill induces changes in both the structure and connectivity of the cortex (42, 43), which is accompanied by increased excitability and decreased inhibition of neural circuitry (44–46). However, it is plausible that flexibility might also be driven by task-dependent processes that require the capacity to balance learning across subtasks. For example, the particular experiment utilized in this study demanded that subjects master the use of a response box, decoding of the stimulus, performance of precise movements, balancing of attention between stimuli, and switching between different sequences of movements.

Flexibility and Learning.

Importantly, the inherent temporal variability in network structure measured by nodal flexibility was not a stable signature of an individual’s functional organization but was instead modulated by consecutive stages of learning—first increasing and then decreasing as movement time stabilized in the later stages of learning (19). The modulation of flexibility by learning was evident not only at the group level but also in individuals. The amount of flexibility in each participant could be used to predict that participant’s learning in a following experimental session. In addition to supporting the theoretical utility of accessible but often ignored higher-order (bivariate, multivariate) statistics of brain function, this result could potentially be used to inform decisions on how and when to train individuals on new tasks depending on the current flexibility of their brain. From this work alone, however, we are unable to determine whether or not learning is the only possible modulator of flexibility. Complementary experiments could be designed to test whether flexibility is also modulated by fatigue or exogenous stimulants to increase subsequent skilled learning. We also found that interindividual variability in flexibility was larger than intraindividual variability, indicating that flexibility might be a reliable indicator of a given subject’s brain state. Consequently, our methodology could potentially be of use in predicting a given individual’s response to training or neurorehabilitation (47, 48).

Flexibility might be a network signature of a complex underlying cortical system characterized by noise (49). Such a hypothesis is bolstered by recent complementary evidence suggesting that variability in brain signals also supports mental effort in a variety of cognitive operations (50), presumably by aiding the brain in switching between different network configurations as it masters a new task. Indeed, the theoretical utility of noise in a nonlinear dynamical system like the brain (51) lies in its facilitation of transitions between network states or system functions (52) and therefore helps to delineate the system’s dynamic repertoire (53). However, despite the plausibility that network flexibility and cortical noise are related, future studies are necessary to directly test this hypothesis.

Methodological Considerations.

The construction of brain networks from continuous association matrices, such as those based on pairwise correlation or coherence, has historically been performed by applying a threshold to the data to construct a binary graph in which an edge exists if the association between the nodes it connects is above the threshold and does not exist otherwise (21–23). However, the statistical validity of that method is hampered by the need to choose an arbitrary threshold as well as by the discretization of inherently continuous edge weights. In the current work, we have instead used fully weighted networks in which connections retain their original association value unless that value was found to be insignificant (based on statistical testing employing a false discovery rate correction for multiple comparisons) (54). Future studies comparing multiple network construction techniques will be important to statistically assess the added value of weighted-edge retention in the assessment of network correlates of cognition.

Second, partitioning a set of nodes into a set of communities is nondeterministic polynomial-time hard (55) so that modularity-optimization algorithms produce many near-optimal partitions of the network (56). The number of near-optimal partitions tends to be larger for large networks, and it also tends to be larger in binary networks than in weighted ones (56). In the present paper, we study small weighted networks in which the number of near-optimal partitions is small. Nevertheless, we have systematically explored the partition landscape in our optimization of the modularity index. Accordingly, we report mean modularity estimates that our results suggest are representative (see SI Appendix). However, further work is necessary to measure common community assignments in the ensemble of partitions to identify consistently segregated groups of brain regions. Such research will aid in further exploration of the biological relevance of the detected communities.

Finally, the statistical validation of community structure in social and biological systems is complicated by several factors. For example, many investigations, especially in social systems, are hindered by their small number of instantiations. In our work, the relatively large number of subjects in conjunction with estimations of multiple networks over various temporal scales facilitated a stringent statistical assessment of community structure both in comparison to randomly connected graphs and, as we have developed for dynamic networks, to graphs where nodal identities or times were scrambled. An important future area of research will focus on the development of alternative null models that are not perfectly random but which assume increasingly biologically realistic network architectures.

Conclusion

Consistent with our hypotheses, we have identified significant modular structure in human brain function during learning over a range of temporal scales: days, hours, and minutes. Modular organization over short temporal scales changed smoothly, suggesting system adaptability. The composition of functional modules displayed temporal flexibility that was modulated by early learning, varied over individuals, and was a significant predictor of learning in subsequent experimental sessions. Furthermore, we developed and reported a general framework for the statistical validation of dynamic modular architectures in arbitrary systems. Additionally, our evidence for adaptive modular organization in global brain activity during learning provides critical insight into the dependence of system performance on underlying architecture.

Materials and Methods

Twenty-five right-handed participants (16 female, 9 male; mean age 24.25 years) volunteered with informed consent in accordance with the University of California, Santa Barbara Internal Review Board. After exclusions for task accuracy, incomplete scans, and abnormal MRI, 18 participants were retained for subsequent analysis. All participants had less than 4 years of experience with any one musical instrument, had normal vision, and had no history of neurological disease or psychiatric disorders. Participants were paid for their participation.

The experimental framework consisted of a simple motor learning task in which subjects responded to a visually cued sequence by generating responses using the four fingers of their nondominant hand on a custom response box. Participants were instructed to respond swiftly and accurately. Visual cues were presented as a series of musical notes on a pseudo-musical staff with four lines such that the top line of the staff mapped to the leftmost key depressed with the pinkie finger. Each 12-note sequence contained three notes per line, which were randomly ordered without repetition and free of regularities such as trills and runs. The number and order of sequence trials was identical for all participants. All participants completed three training sessions in a five-day period, and each session was performed inside the MRI scanner.

Recordings with fMRI were conducted using a 3.0 T Siemens Trio with a 12-channel phased-array head coil. For each functional run, a single-shot echo planar imaging sequence that is sensitive to blood oxygen level dependent (BOLD) contrast was used to acquire 33 slices (3 mm thickness) per repetition time (TR), with a TR of 2,000 ms, an echo time of 30 ms, a flip angle of 90 °, a field of view of 192 mm, and a 64 × 64 acquisition matrix. Image preprocessing was performed using the Oxford Center for Functional Magnetic Resonance Imaging of the Brain (FMRIB) Software Library (FSL), and motion correction was performed using FMRIB’s linear image registration tool. Images were high-pass filtered with a 50 s cutoff period. Spatial smoothing was performed using a kernel where full width at half maximum was 8 mm. Signals were normalized globally to account for transient fluctuations in intensity.

The whole brain is parcellated into a set of N regions of interest that correspond to the 112 cortical and subcortical structures anatomically identified in FSL’s Harvard–Oxford atlas. For each individual fMRI dataset, we estimate regional mean BOLD time series by averaging voxel time series in each of the N regions. These regional time series are then subjected to a wavelet decomposition to reconstruct wavelet coefficients in the 0.06–0.12 Hz range (scale two). We estimate the correlation or coherence A_ij between the activity of all possible pairs of regions i and j to construct N × N functional connectivity matrices A (Fig. 1A). Individual elements of A_ij are subjected to statistical testing, and the value of all elements that do not pass the false discovery rate correction for multiple comparisons are set to zero; otherwise, the values remain unchanged. The complete set of weighted network nodes is partitioned into communities by maximizing the modularity index Q (30, 31). In the simplest static case, supposing that node i is assigned to community g_i and node j is assigned to community g_j, the modularity index is defined as

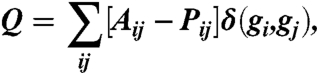[1]

where δ(g_i,g_j) = 1 if g_i = g_j and it equals 0 otherwise, and P_ij is the expected weight of the edge connecting node i and node j under a specified null model. (A more complex formula is used in the dynamic network case; see SI Appendix.) The elements of the matrix A_ij are weighted by the functional association between regions, and we thoroughly sample the distribution of partitions that provide near-optimal Q values (56). The functional connectivity is termed “modular” if the value of Q is larger than that expected from random network null models that control for both the mean and variability of connectivity.

We tested for static modular structure on the individual networks and on dynamic network structure on a multilayer network created by linking networks between time steps (25). In both cases, we assess modular organization using the modularity Q and the number of modules n. In the dynamic case, we also used two additional diagnostics to characterize modular structure: the mean module size s and the stationarity of modules ζ. We defined s to be the mean number of nodes per community over all time windows over which the community exists. We used the definition of module stationarity from ref. 34. We started by calculating the autocorrelation function U(t,t + m) of two states of the same community G(t) at m time steps apart using the formula

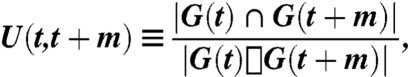[2]

where |G(t)∩G(t + m)| is the number of nodes that are members of both G(t) and G(t + m), and |G(t)∪G(t + m)| is the total number of nodes in G(t)∪G(t + m) (34). We defined t₀ to be the time at which a community is born and t^′ to be the final time step before a community is extinguished. The stationarity of a community is then

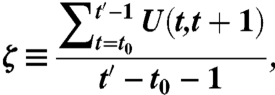[3]

which is the mean autocorrelation over consecutive time steps (34).

In principle, modular architecture might vary with learning by displaying changes in global diagnostics such as the number of modules or the modularity index Q, or by displaying more specific changes in the composition of modules. To measure changes in the composition of modules, we defined the flexibility f_i of a node to be the number of times that a node changed modular assignment throughout the session, normalized by the total number of changes that were possible (i.e., by the number of consecutive pairs of layers in the multilayer framework). We then defined the flexibility F of the entire network as the mean flexibility over all nodes in the network: .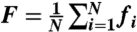

See SI Appendix for further mathematical details and methodological descriptions.