Spreading dynamics and wetting transition of cellular aggregates

Abstract

We study the spreading of spheroidal aggregates of cells, expressing a tunable level of E-cadherin molecules, on glass substrates decorated with mixed fibronectin and polyethylene glycol. We observe the contact area by optical interferometry and the profile by side-view microscopy. We find a universal law of aggregate spreading at short times, which we interpret through an analogy with the spreading of viscoelastic droplets. At long times, we observe either partial wetting or complete wetting, with a precursor film of cells spreading around the aggregate with two possible states. In strongly cohesive aggregates this film is a cellular monolayer in the liquid state, whereas in weakly cohesive aggregates, cells escape from the aggregate, forming a 2D gas. The escape of isolated cells is a physical mechanism that appears also to be present in the progression of a noninvasive tumor into a metastatic malignant carcinoma, known as the epithelial-mesenchymal transition.

Tissue spreading is a fundamental process in embryonic development (1–3), wound healing (4), and cancer invasion and propagation. A tumor is not malignant if it remains cohesive. Understanding how noninvasive tumor cells become metastatic is the most prominent challenge in current cancer research. The first step of cancer propagation (invasion) is characterized by a loss of cell adhesion associated to an increase in cell motility, followed by an entry into blood circulation (intravasation), an escape into a new tissue (extravasation), and the proliferation leading to a secondary tumor (5). The loss of cell adhesion, characteristic of aggressive metastatic cancer, is analogous to that of the epithelial-mesenchymal transition (EMT) during embryonic development (6, 7), which is a key process during gastrulation (8) or neural crest development (9). A repression of E-cadherin expression (involved in the formation of adherens junctions between cells mediated by homophilic ligation in the presence of calcium) has been reported for cells undergoing an EMT transition (10). Here we study the role of E-cadherin expression in the wetting behavior of tissues. We use as a model system cellular aggregates of variable cohesivity, spreading on glass substrates of variable adhesivity.

Spherical cellular aggregates are useful in vitro systems to study the properties of tissues. The characterization of tissue mechanics through viscosity has been debated since the pioneering work of Steinberg. He demonstrated that embryonic tissues behave like liquids and are characterized by a well-defined surface tension (11). Mixing cells of two tissues, he observed cell sorting: The tissue with the lower surface tension surrounds the tissue with a higher tension (12–14). If two aggregates are brought in contact, they coalesce to form a single, larger spheroid. The fusion of two aggregates (15, 16) leads to the determination of the capillary velocity V^∗ = γ/η, where γ is the surface tension and η is the viscosity. Compressed between two plates, aggregates behave as viscoelastic droplets. From the measurement of the force versus time, one can derive the elastic modulus at short times and the surface tension at long times (17–19). A shift from liquid to elastic behavior by increasing the tissue cohesion provided by the extracellular matrix has been recently reported (20). Cell aggregate properties have also been characterized by aspiration into a pipette (21). Above a threshold pressure, the dynamics of penetration into the pipette exhibits an elastic behavior at short time scales, and a viscous behavior at long time scales. The aspiration dynamics leads to a measurement of the surface tension γ and the viscosity η. We can conclude from these experiments that tissues are “transient” foams, and flow at long time like viscoelastic pastes.

Ryan et al. (22) analyzed the competition between cell–cell and cell–substrate adhesion on tissue spreading. Here we pursue this approach by studying quantitatively the spreading of tissues with different levels of E-cadherin. We interpret our observations in the framework of statics and dynamics of wetting (23). We have used murin sarcoma (S-180) cell lines transfected to express various levels of E-cadherin molecules at the surface of the cells (24), thereby controlling the intercellular adhesion energy. The level of E-cadherin expression is denoted by ϕ, where the most adhesive cell line is defined as ϕ = 100%. We also use cell lines with ϕ = 48% and ϕ = 21%, which express, respectively, a level of E-cadherin of 48% and 21% of the most adhesive cell line. The cell–cell adhesion energy per unit area W_CC deduced from the separation force (24) varies approximately with the square of ϕ. As the substrate, we use glass coverslips decorated with a mixture of fibronectin and PEG-poly-L-lysine (PEG-PLL). The cell–substrate adhesion occurs through the binding of integrins to fibronectin (25). Integrins are receptors that mediate attachment of a cell by specific binding with the extracellular matrix components. The fraction of fibronectin x (in number of molecules) varies from 0% to 100%, allowing the cell–substrate adhesion energy per unit area W_CS to vary in a broad range.

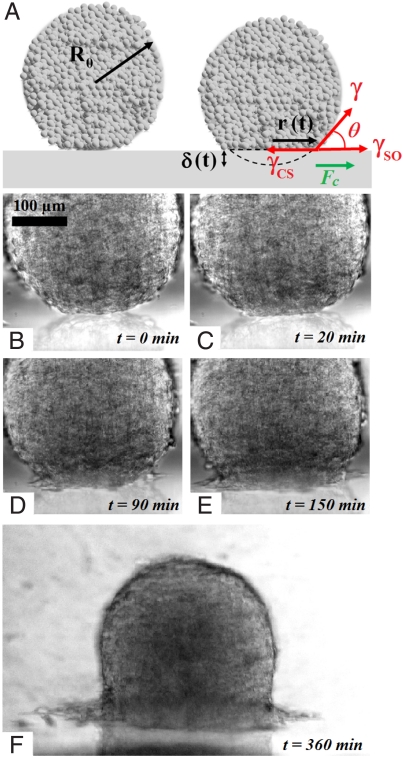
When an aggregate is put into contact with the substrate, we observe two regimes: either partial wetting where the aggregate forms at equilibrium a spherical cap, with an equilibrium contact angle; or complete wetting, where the aggregate spreads totally, surrounded by a precursor film. These two regimes are distinguished by the sign of the spreading coefficient, S = γ_SO - (γ_CS + γ), where γ_SO, γ_CS, and γ are, respectively, the substrate-medium, cell–substrate, and tissue interfacial energies shown in Fig. 1A. Introducing the cell–substrate adhesion energy per unit area W_CS, we can write γ_CS = (γ_SO + γ) - W_CS. This expresses the energy conservation when a cell–substrate interface is formed from a substrate-medium and a cell-medium interface. Similarly, W_CC can be seen as the energy gain per unit area as two cell-medium interfaces get into contact, i.e., 2γ - W_CC = 0. The spreading parameter can thus be written as S = W_CS - W_CC. If S < 0, i.e., W_CS < W_CC (“PEG-PLL-rich substrate”), the drop forms at equilibrium a spherical cap with a finite contact angle (partial wetting). If S > 0, i.e., W_CS > W_CC, the drop spreads (complete wetting) to form a wetting film consisting of a cell monolayer.

Fig. 1.

Spreading of an aggregate on a solid substrate. (A) Schematic of the spreading profile and the parameters used in the wetting model. (B–F) Different steps of the spreading of a cohesive aggregate (ϕ = 100%) on a fibronectin-coated substrate (x = 100%): (B) initial contact formation at t = 0, (C) flattening of the aggregate, (D) formation of the precursor film, and (E and F) growth and spreading of the precursor film.

In the remainder of the paper, we discuss the dynamics of spreading, which exhibits two regimes. At short times, the aggregate deforms like a viscoelastic drop (Fig. 1C). At long times, a precursor film of cells appears around the aggregate (Fig. 1D) if the fraction of fibronectin is larger than a critical value, x > x_C similarly to complete wetting observed in liquids (26). The precursor film consisting of a monolayer of cells grows and spreads around the aggregate (Fig. 1 E and F) (see also Movie S1).

Universal Early Dynamics Of Spreading

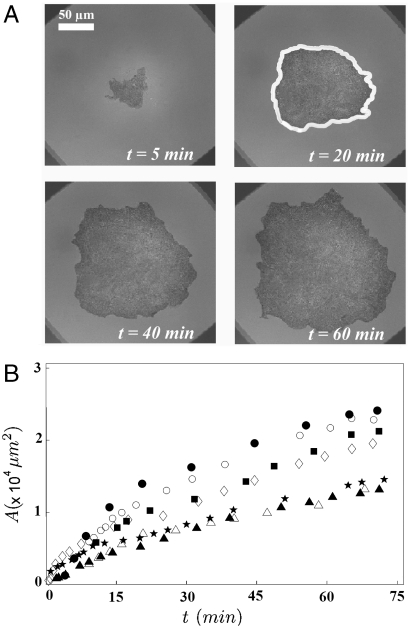
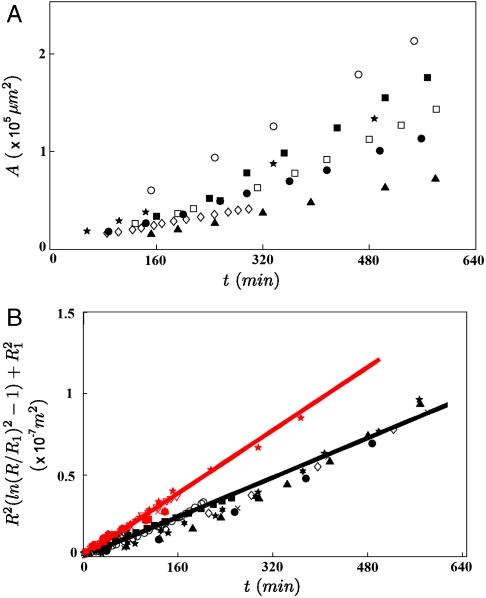
In this section, we describe the growth of the contact area of cell aggregates expressing various levels ϕ of E-cadherin deposited on a surface coated with mixed fibronectin/PEG-PLL (0% < x < 100%). We have used reflection interference contrast microscopy (RICM) to characterize the aggregate adhesion on the substrates (see Materials and Methods for details). This technique allows us to visualize adhesion patches as darker regions (27). Fig. 2 A shows snapshots of the observed contact area of a ϕ = 100% aggregate on a substrate coated with fibronectin (x = 100%). We measure the contact area by measuring the area enclosed by the contour of the dark spot shown in Fig. 2A. Fig. 2B shows the time evolution of the contact area for ϕ = 100% aggregates of various sizes. The initial time t = 0 is the time when the aggregate is deposited on the surface. The bigger the aggregates are, the faster they spread on the surface. We also notice that the time evolution of the contact area is not linear.

Fig. 2.

Early stage of spreading of an aggregate on a solid substrate. (A) Snapshots of the contact area of a ϕ = 100% aggregate (R₀ = 150 μm) on a substrate coated with fibronectin (x = 100%) observed with RICM. Contact area A is defined by the area enclosed by the white contour. (B) Contact area A of ϕ = 100% aggregates as a function of time [R₀ = 73 μm (▴); 75 μm (▵); 86 μm (★); 96 μm (◊); 102 μm (▪); 135 μm (○); and 158 μm (•)].

The early state of aggregate spreading is driven by the capillary force per unit length of the contact line (28, 29), F_c = γ cos θ + γ_SO - γ_CS = W_CS + γ(cos θ - 1), where θ is the dynamic contact angle shown in Fig. 1A. At early times, the deformation of the aggregate is small (θ ≪ 1) and F_c ∼ W_CS so that the surface energy gain per unit time 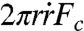can be written as 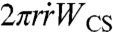, where r is the contact radius of the cap and 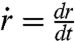. This force is balanced by the viscous dissipation. To calculate the dissipation, we treat our aggregates as a viscoelastic liquid. In this case, the flow field is imposed by the deformation field. At early times, the ball flattens out at the bottom (Fig. 1C). The volume of viscous dissipation associated to the deformation scales like r³ (30, 31). The indentation of the ball is δ ∼ r²/R₀, where R₀ is the initial radius of the aggregate and the deformation rate is 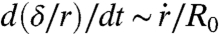. The viscous energy dissipation given by 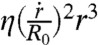, where η is the viscosity of the aggregate, is balanced by the gain of surface energy leading to

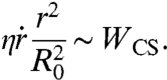[1]

After integration, we obtain

[2]

where 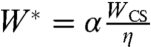is a characteristic velocity and α is a numerical coefficient. This law, first derived for the spreading of soft viscoelastic polymeric beads (32), is expected to describe the early stages of spreading for both complete and partial wetting regimes.

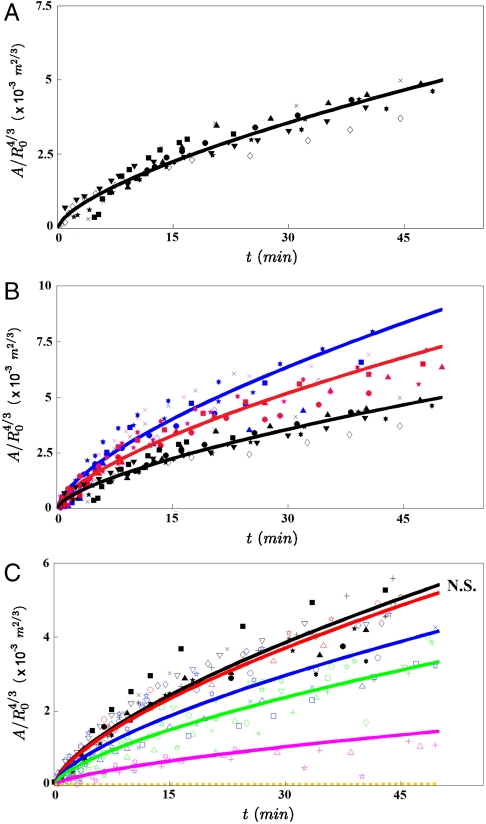
Fig. 3A represents 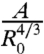versus time, where A = πr² is the contact area. Interestingly, all curves of Fig. 2B, corresponding to different aggregate radii, collapse onto the same universal law, showing that A varies with the aggregate radius as 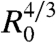and with time as t^2/3 (Fig. 3A). It is remarkable that a living system such as a cellular aggregate exhibits the same contact dynamics as soft rubber beads (32).

Fig. 3.

Role of W_CC and W_CS in the early spreading dynamics. (A) The contact area normalized by 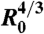, where R₀ is the initial radius of the aggregate, increases as t^2/3 (ϕ = 100%). The different symbols stand for different experiments. The solid line is the fit to our data using Eq. 2. (B) Contact area of the early stage of spreading of ϕ = 21% (blue), ϕ = 48% (red), and ϕ = 100% (black) aggregates (x = 100%). (C) Contact area of the early stage of spreading of ϕ = 100% aggregates for mixed fibronectin/PEG-PLL substrates with x = 0% (orange); 35% (magenta); 51% (green); 68% (blue); 81% (red); 100% (black). In all figures, the symbols correspond to experimental measurements, the solid lines are the fits to our data using Eq. 2, and the dashed line is an extrapolation of Eq. 2 for x = 0%. The difference between any two curves is statistically significant (P < 0.0001), except for the pair of curves labeled N.S. (not significant).

Next, we examine the role of E-cadherin expression level on the early stages of spreading. In these experiments, three E-cadherin levels were considered (ϕ = 21%, 48%, and 100%), and the surface was coated with fibronectin (x = 100%). Fig. 3B shows the contact area normalized by 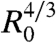for these different cell lines. The solid line is the fit to the data using Eq. 2, with W^∗ as the fitting parameter. As integrin expression level remains the same for all the cell lines and x = 100% for all cases, the adhesive energy per unit area between the cell and the substrate W_CS is considered to stay constant in all the experiments. Thus, this series of experiments allows us to compare the viscosities of the different cell lines. Table 1 shows the comparison of viscosities of cell aggregates expressing different levels of E-cadherins. Our results suggest that the aggregate viscosity increases with the level of E-cadherins. This observation is consistent with the fact that increasing the density number of E-cadherins at the surface of the cells reinforces the links between cells in the aggregate and prevents the relative motion of cells. Our discussion assumes the cell–cell adhesion not to affect the cell–substrate adhesion and therefore disregards the cross-talk between integrins and cadherins in cell adhesion, which is expected to have a weak quantitative effect on the spreading dynamics (33, 34).

Table 1.

Physical parameters derived from fitting our experimental data of early spreading (η) and of long-time spreading (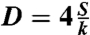) experiments

ϕ (%)	21%	48%	100%
η/η(ϕ=100%)	0.42 ± 0.03	0.57 ± 0.03	1
D(ϕ=100%)/D	gas state	0.6 ± 0.1	1

We have also examined the influence of the wettability of the substrate for a given level of E-cadherins (ϕ = 100% for all cases). We coat the substrates with a mixture of fibronectin and PEG-PLL. Specifically, we studied the cases where the percentage of fibronectin is x = 0%, 35%, 51%, 68%, 81%, and 100%. When the surface is totally coated with PEG-PLL (x = 0%), the aggregate remains perfectly spherical and does not spread. This is an example of a living droplet in zero wetting condition (35). For larger values of x (e.g., x = 35%), the aggregate starts to spread like a viscoelastic drop and the spreading stops without any precursor film of cells. For x≥51%, we observe complete wetting (S > 0). The aggregate spreads following successively the two previously described regimes: spreading like a viscoelastic drop at short times, followed by the flow of a precursor film from the aggregate at longer times. The wetting transition observed between the cases x = 35% and x = 51% indicates that the spreading coefficient S changes sign for an intermediate value of x. In all cases, we can follow the kinetics of the viscoelastic spreading at early times. Fig. 3C shows the contact area normalized by 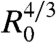for constant ϕ = 100% and a range of values of x. For each x, the value of W^∗ (Eq 2) is obtained. The same cell line is used in these experiments so that the viscosity is kept constant. Thus, this series of experiments allows us to derive W_CS as a function of the percentage of fibronectin x, shown in Table 2. For x = 81% and x = 100%, we obtain comparable values of W^∗, and the difference between the curves is not statistically significant (P > 0.05), whereas an x ≤ 68% results in limited aggregate spreading and reduces the adhesion energy W^∗. This saturation effect is attributed to the fact that for x = 81%, there is already enough fibronectin on the substrate to bind all the integrins on the cell surface due to restricted integrin clustering (36).

Table 2.

Cell–substrate adhesion energy per unit area W_CS as a function of x

x(%)	0%	35%	51%	68%	81%	100%
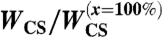	0	0.16	0.49	0.76	0.94	1

W_CS is obtained for ϕ = 100% aggregates from fitting the experimental data of the early spreading on mixed fibronectin-PEG-PLL surfaces. The maximum absolute error on the reported values is 0.03.

Precursor Films: Liquid–Gas Transition and Growth

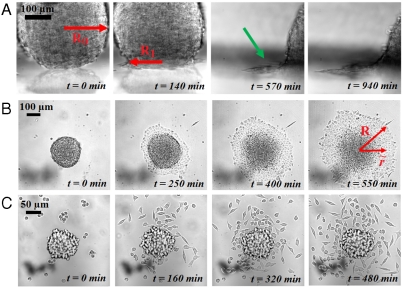
In this section we study the precursor film that forms when S > 0 (complete wetting). An aggregate with ϕ = 100% is deposited on a fibronectin-coated surface (x = 100%). After around 90 min, a monolayer of cells spreads away from the aggregate at the contact line as shown by the green arrow in Fig. 4A (side view). A similar situation is observed in the spreading of nonvolatile liquids, which exhibit terraced height profile, the height of each step being one molecule (37–39).

Fig. 4.

Growth and liquid-to-gas transition of the precursor film (x = 100%). (A) Escape of a precursor film (indicated by the green arrow) seen from the side. (B) Top view of the spreading for an aggregate with ϕ = 100% (liquid state). (C) Top view of the spreading for an aggregate with ϕ = 21% (gaseous state).

We examine the influence of E-cadherin expression on the precursor film. For ϕ = 100% (more cohesive aggregate), the film is strongly cohesive as shown in Fig. 4B (Movie S2). For the cell line with ϕ = 21% (less cohesive aggregate), the film is considerably different as shown in Fig. 4C (Movie S3). Cells escape from the aggregate to migrate individually in all directions forming a disconnected cell cloud. The dynamics of spreading of this cell cloud are governed by isolated cell motility. From a thermodynamic point of view, the precursor film is in a liquid state for the most cohesive aggregates and in a 2D gas state for the lowest E-cadherin expression. A similar behavior is observed in the complete wetting of simple liquids, where 2D liquid-to-gas phase transitions may occur in the precursor monolayer film (40). By decreasing the E-cadherin expression level, one can induce a liquid-to-gas transition in the precursor film leading to the escape of individual cells.

In the liquid state (where a collective migration is observed), we examine the kinetics of evolution of the monolayer by measuring its area (i.e., film contour) with time as shown in Fig. 4B. Fig. 5A shows the evolution of the area with time of the circular film for aggregates of various sizes with ϕ = 100%. The precursor film spreads faster for larger aggregates. In the gas state, the model based on slippage of a cell monolayer is not applicable because the spreading is governed by individual cell motility.

Fig. 5.

Spreading dynamics of the precursor film in the liquid state. (A) Area versus time of the precursor film for ϕ = 100% E-cadherin aggregates of various sizes (R₀ = 51 μm (▴); 59 μm (◊); 68 μm (•); 76 μm (★); 87 μm (□); 98 μm (▪); and 138 μm (○). (B) Experimental (markers) and theoretical (lines) evolution of the precursor film with time (Eq. 5) for ϕ = 48% (red) and ϕ = 100% (black). Note that the vertical axis has been normalized according to the model, which makes the data for different aggregate sizes collapse following a straight line, as predicted by the model.

The adhesive energy gain per unit time, which can be written as 2πSRV(R), is balanced by the dissipation in the precursor film spreading away from the aggregate. Previously, de Gennes and Cazabat have described the dynamics of growth of a stratified precursor film (38). They have included the existence of two types of flow: (i) shear with the substrate and (ii) permeation normal to the layer. The permeation flow is limited to a narrow region near the contact line, the size of which they called the permeation length, and they show that its contribution to the viscous dissipation is negligible. Thus, the viscous dissipation of the film slipping on the substrate can be written as

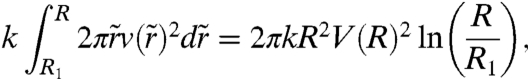[3]

where k is the friction coefficient, R₁ is the radius of the contact line, R is the radius of the precursor film, 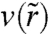is the velocity of the film at a radius 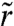, and V(R) is the velocity at the edge of the precursor film (see Fig. 4).

The spreading of the film is governed by a balance between the surface energy gain and the viscous dissipation, leading to

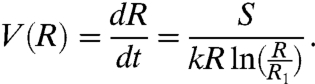[4]

After integration, we obtain

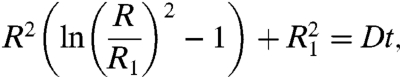[5]

where 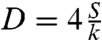can be interpreted as a diffusion coefficient of the precursor film. Experimentally, we observe that the precursor film starts at a radius R₁ ≈ 0.6R₀, where R₀ is the initial radius of the aggregate. Using R₁ = 0.6R₀, we fit our experimental data using Eq. 5 for aggregates of different sizes and two cell lines, ϕ = 48% and ϕ = 100% (Fig. 5B). Notice that the curves of Fig. 5A collapse onto the same straight line, of slope D. From the fits, we extract D_ϕ=48% = 4.0 ± 0.1 × 10^-12 m²·s^-1 and D_ϕ=100% = 2.5 ± 0.1 × 10^-12 m²·s^-1 (see Table 1). The precursor film spreads faster in the case of ϕ = 48% aggregates because S = W_CS - W_CC and 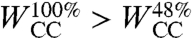, leading to 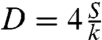larger. The spreading of the precursor film is well described by a diffusive law (Eq. 5), as for simple liquids.

Conclusion

Cell aggregates spread like drops of a simple viscous liquid, where the dissipative parameters controlling the wetting properties (viscosity and friction coefficient) depend upon cellular activity. Indeed, we observe a slowing down of the spreading dynamics by a factor of two when the temperature is decreased from 37 to 30 °C, which is considerably larger than what is observed with usual liquids (41). The wetting is governed by the spreading parameter S = W_CS - W_CC, indicating the competition between cell–substrate adhesion and cell–cell adhesion. We have observed a partial-to-complete wetting transition by tuning the cellular affinity to the substrate. The early stages of spreading are characterized by a universal law given by R ∼ t^1/3. If S > 0, the first regime is followed by a second one where a precursor film flows from the aggregate according to a diffusive law R ∼ t^1/2. A decrease in the E-cadherin expression level (i.e., W_CC), induces a 2D liquid–gas transition in the precursor film, where cells escape individually from the aggregate. The escape of cells from the aggregate resembles the epithelial-mesenchymal transition observed in metastatic tumors, also associated with a decrease of E-cadherin expression level. In addition, our model of the spreading dynamics provides estimates of physical properties of tissues. Specifically, we can estimate the variation of the viscosity η with the E-cadherin expression levels.

Materials and Methods

Cell Culture and Aggregate Preparation.

Cells were cultured at 37 °C under 95% air/ 5% CO₂ atmosphere in DMEM enriched with 10% calf serum (culture medium). Upon reaching confluency, cells were prepared for aggregation following a procedure similar to that of Ryan et al. (22). Aggregates ranging from 50 to 400 μm in diameter were obtained from 5 mL of cell suspension in CO₂-equilibrated culture medium at a concentration of 4 × 10⁵ cells per milliliters in 25-mL Erlenmeyer flasks and placed in a gyratory orbital shaker at 75 rpm at 37 °C for 22 h. The flasks were pretreated with 2% dimethylchlorosilane in chloroform to prevent adhesion of cells to the glass surface.

Preparation of Coated Glass Substrates.

Twenty-five millimeter circular glass coverslips were sonicated in ethanol for 5 min, dried at ambient temperature, and exposed to deep UV for 5 min. Fibronectin (Sigma-Aldrich) coating was performed using a 0.1 mg/mL solution of fibronectin in PBS solution (pH 7.4) for 1 h. Mixed coating of fibronectin and PEG-PLL (PLL(20)-g[3.5]-PEG(2), Surface Solution) was done by mixing at various rates a 0.1 mg/mL fibronectin in phosphate buffer solution (PBS; pH 7.4) and a 0.1 mg/mL PEG-PLL in Hepes solution (pH 7.3) for 1 h. Coverslips are then rinsed with PBS (pH 7.4).

Aggregate Spreading.

Aggregates were placed on a coated glass coverslip that forms the bottom of a cylindrical experimental chamber filled with CO₂-equilibrated culture medium maintained at 37 °C using a heating platform. To prevent evaporation, the open surface was sealed with mineral oil. Short-time spreading was observed using RICM on an inverted microscope (Zeiss Axiovert 100) equipped with a × 20 oil immersion objective (NA 0.75) and recorded with a CCD camera (CoolSnap EZ, Photometrics) at an acquisition rate of 1 frame per 30 s. Long-time spreading was observed using an inverted microscope (Zeiss Axiovert 100) equipped with a × 20 air objective (NA 0.45). To image the profile of the spreading, the aggregates were brought in contact with a vertical coated coverslip by means of a micropipette, which holds the aggregate by slight aspiration. After a few minutes, once the aggregate sticks to the vertical coverslip, the suction is removed. The spreading is then visualized on an inverted microscope (Zeiss Axiovert 100). Movies S1–S3 were recorded with a CCD camera (Luca-R, Andor) at an acquisition rate of 1 frame every 8 min. Cell viability in aggregates was checked using the Trypan blue dye exclusion test (42). After letting the aggregate spread for about 10 h, Trypan blue is added to the experimental chamber to a final concentration of 20%. The number of dead cells present at the core of the aggregate remains small and approximately constant from the time of aggregate formation to the end of the experiment, confirming that aggregates remain viable during the experiment. Contact and precursor film areas were measured by tracing the contours of the spreading aggregate, using ImageJ software (National Institutes of Health) and taking the enclosed area (Fig. 2).

Statistical Analysis.

The early stage spreading experiments were fitted according to the law 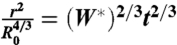using a least square method. Statistical analysis of the results was performed using a Student t test on the values of W^∗. A P value smaller than or equal to 0.0001 was considered as significant.