Multivariate analysis of maize disease resistances suggests a pleiotropic genetic basis and implicates a GST gene

Abstract

Plants are attacked by pathogens representing diverse taxonomic groups, such that genes providing multiple disease resistance (MDR) are expected to be under positive selection pressure. To address the hypothesis that naturally occurring allelic variation conditions MDR, we extended the framework of structured association mapping to allow for the analysis of correlated complex traits and the identification of pleiotropic genes. The multivariate analytical approach used here is directly applicable to any species and set of traits exhibiting correlation. From our analysis of a diverse panel of maize inbred lines, we discovered high positive genetic correlations between resistances to three globally threatening fungal diseases. The maize panel studied exhibits rapidly decaying linkage disequilibrium that generally occurs within 1 or 2 kb, which is less than the average length of a maize gene. The positive correlations therefore suggested that functional allelic variation at specific genes for MDR exists in maize. Using a multivariate test statistic, a glutathione S-transferase (GST) gene was found to be associated with modest levels of resistance to all three diseases. Resequencing analysis pinpointed the association to a histidine (basic amino acid) for aspartic acid (acidic amino acid) substitution in the encoded protein domain that defines GST substrate specificity and biochemical activity. The known functions of GSTs suggested that variability in detoxification pathways underlie natural variation in maize MDR.

The genic basis of quantitative variation in resistance to plant diseases is poorly understood. For many plant diseases, resistance conditioned by multiple genes with quantitative effects is the only type available or is the best option for developing durably resistant cultivars. Resistance conditioned by single genes with qualitative effects tends to be more easily overcome by evolving pathogen populations (1). In environments where plants are infected with multiple pathogens, multiple disease resistance (MDR) can contribute to fitness. Thus, strong artificial phenotypic selection pressure for MDR is applied in some plant breeding programs (2). Both to provide a better understanding of plant defense and to support sustainable practical efforts to sustainably reduce crop losses, it would be valuable to identify the genes that condition quantitative resistance to multiple diseases. Identification of such genes would provide insight into the evolution of pleiotropic effects and mechanisms that provide quantitative resistance and allow for more strategic deployment of resistance genes in the development of unique cultivars.

Evidence that MDR genes exist in plants includes the detection of clusters of quantitative trait loci for different diseases (3, 4) and the identification of induced gene mutations that affect plant responses to infection with different pathogens (5–7). These observations have prompted the hypothesis that there exists naturally occurring allelic variation for MDR. Indeed, positional cloning (in wheat) or silencing (in rice) of genes at quantitative trait loci has led to the recent discovery of such MDR genes (8, 9). To test the hypothesis that genes conditioning variation in MDR exist in maize, we extended a mixed model approach for structured association mapping (10) to a multivariate framework using a mapping panel developed for the dissection of complex (polygenic) traits (11). In this panel, linkage disequilibrium (LD) decays within 1,500 nucleotides in most genic regions (12). Because maize genes are physically separated by much greater distances, a significant association may be taken as evidence for a causal relationship between genic variation and trait variation if population structure is appropriately taken into account. Similarly, a genetic correlation observed between different traits can be taken as evidence that some common genes underlie the phenotypic variation in multiple traits.

We systematically characterized 253 maize inbred lines representing much of the global variation among maize inbreds in replicated field trials across multiple environments for resistance to three fungal leaf diseases of maize: (i) southern leaf blight (SLB), caused by Cochliobolus heterostrophus (Ch); (ii) gray leaf spot (GLS), caused by Cercospora zeae-maydis (Czm) and Cercospora zeina (Cz); and (iii) northern leaf blight (NLB), caused by Setosphaeria turcica (St). These are among the most damaging diseases of maize worldwide. The pathogens are in the same taxonomic class (the Dothideomycetes) and share some aspects of pathogenesis (13, 14) (Fig. S1).

For all three pathogens, infection is initiated when spores land and germinate on the leaf surface and penetrate directly either through the leaf cuticle and epidermis or stoma. One major difference is that Ch and Czm/Cz grow intercellularly in leaves during initial infection, whereas St grows intracellularly (Fig. S1). For all three fungi, hyphae ramify within the living plant mesophyll tissue, but they do so for different periods of time before causing host cell death: 2 to 3 d for Ch, approximately 3 wk for Czm/Cz, and approximately 2 wk for St. Uniquely, St invades the xylem after ramifying in the mesophyll before reinfecting the mesophyll. The three fungi are known to produce phytotoxins that can enable or enhance pathogen infection and disease development [Ch (15), Czm (16), and St (17, 18)]. Ultimately, all three fungi derive their nutrition from dead host cells and reproduce on the surface of dead tissue. Aspects of pathogenesis that are unique to each disease could require distinct host mechanisms, pathways, and genes that confer single disease resistance. In contrast, MDR may be mediated by host mechanisms that respond to shared aspects of pathogenesis.

Results and Discussion

The maize association panel used in this study is a collection of inbred lines from public breeding programs worldwide and represents substantial diversity present in maize (11, 19). In our experiments, the panel exhibited extensive variation in quantitative resistance to each of the diseases. Empirical multivariate best linear unbiased predictors (E-MBLUPs) for inbred line resistances encompassed large proportions of the scoring scales used to measure resistance: 71% for SLB, 77% for GLS, and 67% for NLB when a model that accounted for the experimental design (not including covariates or covariance structures that were used in subsequent analyses) was fit to the data. The E-MBLUP distributions were slightly skewed; highly susceptible lines in the panel were less frequent than highly resistant ones (Fig. S2). Therefore, although substantial variation in resistances existed among the inbred lines, the panel was moderately enriched with resistant inbreds, which may reflect breeders’ selection for resistance to these diseases of maize.

The mixed model restricted maximum likelihood approach to estimating random effects provides population-level estimates of covariance parameters (20). Thus, the covariances estimated in this study (Table S1) pertain to the worldwide population of public maize breeding lines. To assess the amount of trait genetic variance harbored among public maize breeding lines comparatively, trait-specific genetic variances were standardized by the maximum variance possible for each measurement scale. These comparisons demonstrated similar amounts of genetic variation in resistance to SLB, GLS, and NLB, irrespective of the model used (Table S2, compare models with the same covariates and covariance structures; covariate and covariance modeling is described below).

The large amount of genotypic variation in quantitative resistance in the panel may partially be explained by pleiotropic effects of other traits. In particular, plant maturity, measured as the number of days from planting to anthesis (DTA), has previously been found to correlate with resistance to SLB, GLS, and NLB (21). Regression analysis (SI Materials and Methods) revealed that DTA was associated with highly significant portions of variation in resistance to all three diseases. For SLB, GLS, and NLB, the median proportion of variation explained by DTA across environments was 45% (minimum = 26%, maximum = 54%), 52% (minimum = 38%, maximum = 61%), and 48% (minimum = 45%, maximum = 59%), respectively. In an attempt to characterize the levels of quantitative resistance independent of maturity effects, unless otherwise specified, all subsequent analyses included environment-specific DTA covariates in the multivariate mixed model.

The lines comprising the association panel are not all independent, because population structure and pedigree relationships exist among them. To minimize detection of spurious correlations and associations attributable to genetic nonindependence or genome-wide LD, we also incorporated large-scale population structure information (contained in a matrix, Q) and pairwise relative kinship relationships among lines (contained in a matrix, K) into the statistical model (10). In principle, this allows inference to be drawn with respect to the LD remaining at very short nucleotide distances. The matrix, Q, was incorporated as a fixed-effect covariate in the model, and, like DTA, the amount of resistance variation explained by Q was quantified by the coefficient of determination, R². Alone, Q explained a significant but smaller amount of the resistance variation than DTA: Among environments, the median R² attributable to Q for SLB, GLS, and NLB was 27% (minimum = 25%, maximum = 32%), 27% (minimum = 21%, maximum = 29%), and 25% (minimum = 13%, maximum = 30%), respectively. Population structure in the maize panel is associated with maturity (11), such that the disease resistance variation explained by Q was not independent of the variation explained by DTA; Q explained an additional 6%, 3%, and 5% of the variation in SLB, GLS, and NLB resistance, respectively, when added to the model with the DTA covariate.

Model specifications exploiting K can permit the partitioning of the total genotypic variance into its components. The additive and residual genetic variances (for inbred lines, this residual corresponds to additive epistatic variance) were estimated by simultaneously fitting the random inbred line effect with and without K in the same model (22). The proportions of genotypic variance estimated to be due to additive variance for SLB, GLS, and NLB were 95%, 100%, and 97%, respectively. This suggested that additive epistatic variance was a relatively insignificant component of the genotypic variance, which is consistent with the genetic basis inferred for other traits in maize that have been characterized using inbred lines (23, 24). The accuracy of K-based partitioning of genotypic variance has not been fully investigated; therefore, our inference should be taken with some caution.

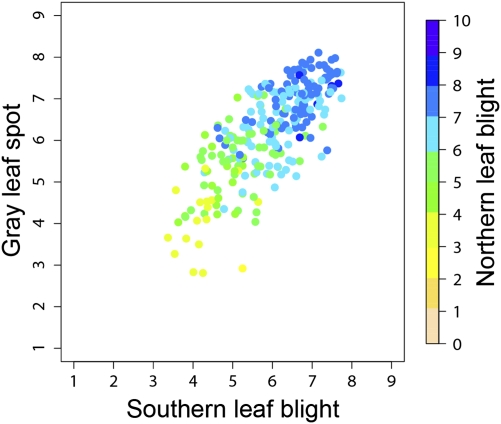
Once confounding factors (maturity, population structure, and kinship) were accounted for, genetic correlations among traits were investigated. High positive (>0.5) genetic correlations were detected between all pairwise trait combinations (Fig. 1 and Table 1). The genetic correlation coefficient between resistance to GLS and NLB (r = 0.67) was highest and ∼0.10 greater than that between either of those disease resistances and SLB (r = 0.55 and r = 0.58, respectively). The 95% confidence intervals for the estimated correlation coefficients overlapped for all trait pairs, leading us to conclude that genetic correlations did not differ substantially among trait pairs. Genetic correlations may arise from LD among alleles that affect individual traits, or they may arise from pleiotropy, whereby allelic variation affects more than one trait. Considering the panels’ characteristic low levels of LD and assuming that Q and K have adequately modeled population structure, it is suggested that pleiotropic allelic variation exists in maize for MDR. The fact that the correlations differed significantly from 1.0 suggests that MDR is conditioned by a combination of single disease resistance and MDR genes. These results support and extend those of previous studies on SLB, GLS, and NLB in which biparental populations have been examined (e.g., 21, 25).

Fig. 1.

Scatterplot of breeding values for resistance to SLB, GLS, and NLB. Each point corresponds to a different inbred line; breeding value-based inbred line ranks are available in Table S4. Axes span the full range of the measurement scales (for NLB, the transformed scale) for which resistance increases with increasing values. A color scale is used to indicate breeding values for NLB resistance.

Table 1.

Genetic correlations between resistance to SLB, GLS, and NLB estimated with a multivariate mixed model

		Covariates and covariance structures used in the model*
Trait 1	Trait 2	No Cov	DTA	DTA, Q	DTA, K	DTA, Q, K
SLB	GLS	0.83 ± 0.023	0.71 ± 0.037	0.61 ± 0.047	0.58 ± 0.051	0.55 ± 0.054
SLB	NLB	0.82 ± 0.025	0.71 ± 0.037	0.66 ± 0.044	0.59 ± 0.052	0.58 ± 0.054
NLB	GLS	0.84 ± 0.025	0.72 ± 0.038	0.67 ± 0.046	0.68 ± 0.047	0.67 ± 0.049

SEs for the estimates are shown after the ± symbol.

*The following model differences existed (all models included experimental design factors): No Cov, no covariates or covariance structure; DTA, days to anthesis; Q, population structure covariate; K, relative kinship covariance structure.

We investigated the robustness of the model-based estimates to the presence of lines in the panel that exhibited extreme DTA in the evaluation environments (SI Materials and Methods). For these lines, measurements of disease resistance may be less accurate because the timing of measurement and disease development were offset. We also examined whether genetic correlation estimates varied among population groups previously defined by Q (19). Although the correlations estimated for the tropical-subtropical population group were lower than those estimated for the entire panel or any other subgroup (Table S3), these analyses revealed that the correlations were not influenced by population structure per se. Instead, cohorts of late flowering lines (that include mostly lines of tropical-subtropical origin) were associated with lower variability in resistances and lower correlations among diseases (Table S3). Thus, the correlation estimates obtained in this study appear to be lessened by the inclusion of data from nonadapted, late-flowering, inbred lines.

The multivariate framework can be used to test for multitrait-marker associations, provided that Q and/or K can account for the panels’ genetic structure. The same gene-derived set of 858 SNP markers used to estimate K values was tested to examine whether the distribution of observed marker P values conformed to its expected uniform distribution under the multivariate null hypothesis. Indeed, with DTA, Q, and K fit in the model, the test statistic P values followed null hypothesis expectations closely, revealing that for the multivariate test, Q and K corrected for a potentially high rate of false-positive results (DTA had little impact; Fig. S3).

Each of the traits had high heritabilities (h² ± SE for SLB was 0.95 ± 0.01, h² ± SE for GLS was 0.91 ± 0.01, and h² ± SE for NLB was 0.87 ± 0.01), indicating that the majority of variation among inbred lines was attributable to genetic variation, providing good power to detect causal genes. Therefore, we proceeded to search for significant MDR associations from among the 858 SNP tests performed. These SNPs represent a mere 0.0015% of SNP sites in maize [estimated assuming a 2.5-Gb maize genome with SNPs every 44th nucleotide (26)]. Surprisingly, 3 SNP tests withstood multiple test correction at a false discovery rate of 5.0%. These SNPs were present in the following three genes: (i) a member of the glutathione S-transferase (GST) gene family (P value = 2.2 × 10⁻⁴); (ii) Tasselseed2 (Ts2), a gene associated with developmentally regulated cell death in maize (27) (P value = 1.0 × 10⁻³); and (iii) a maize-expressed sequence tag with unknown function (P value = 1.5 × 10⁻³) (Dataset S1 SNP identifiers, respectively: 4205, 3613, and 3906).

The multivariate null hypothesis is well suited to testing for pleiotropic associations. The null hypothesis states that there is no difference between the sets of trait means estimated for the groups of lines defined by the alleles at a given locus, while accounting for within- and between-trait covariances. Multivariate tests are generally expected to provide greater statistical power. Nevertheless, there are circumstances in which separate univariate tests may detect significant effects undetectable by a single multivariate test (28). It is also possible for only a subset of the traits to exhibit a significant deviation, leading to the rejection of the multivariate null hypothesis. Comparing the 95% confidence intervals for the estimated trait-specific SNP effects, we found that the SNP 3906 was significantly associated with GLS resistance only (Fig. S4). The effect of the Ts2-located SNP was significantly associated with NLB resistance only. The most significant SNP, located in the GST gene, was associated with resistance to all three pathogens. As a matter of comparison, univariate analysis resulted in an association of this GST SNP with resistance to SLB and NLB but not to GLS, suggesting that the multivariate model provided a gain in statistical power.

The GST gene was considered a plausible candidate gene for MDR based on the following evidence. First, we have previously hypothesized the role of GSTs in quantitative disease resistance (29). Second, the GST identified in this study is a member of a plant-specific clade previously implicated in defense (30). Third, using the encoded amino acid sequence of the GST gene (National Center for Biotechnology Information accession no. NP_001104994.1), a BLASTp search against the curated UniProt database revealed homologs associated with plant pathogen interactions, induction by auxin, and an array of stress responses. The related pathogenesis GST (potato Prp-1) is induced by fungal infection and has been associated with quantitative resistance to late blight caused by Phytophthora infestans (31, 32). Fourth, in rice, the GST gene family was among 4 of 145 families found to be significantly associated with quantitative trait loci for resistance to various diseases (3). Finally, the map position of the GST gene identified in this study colocalized with or immediately flanked quantitative trait loci for SLB, GLS, and NLB identified in previous studies [compare position 298 cM on chromosome 7 with quantitative trait loci (4)]. A closer examination suggested that these resistance loci were not attributable to the effect of this GST gene; based on our SNP data, each of the significantly associated GST SNPs identified in this study (above and below) was invariant among the five biparental population parents used in previous studies (33–38). Alternatively, other GST alleles that are undetectable in our study could underlie functional variation at these quantitative trait loci.

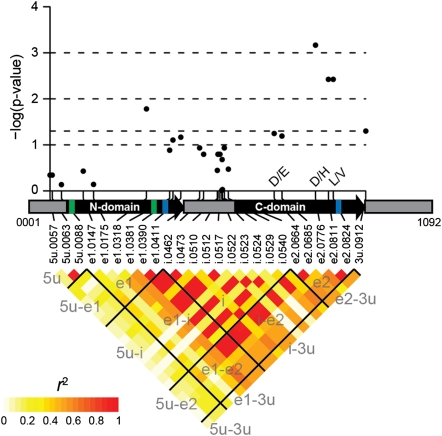
We resequenced the full-length GST gene across the panel of inbred lines. Across polymorphic sites, resequencing produced data from a minimum of 139 to a maximum of 185 of the 253 lines used in our study. Multivariate associations were detected in exonic and 3′-UTR regions of the gene at P ≤ 0.05 (without multiple test correction; Fig. 2). The originally associated SNP (e2.0685 in Fig. 2) exhibited a moderately significant P value of 0.065; the decrease in significance can be attributed to the substantial decrease in sample size (from n = 248 to n = 169) of the resequencing data. Despite lower sample sizes, three highly significant (P < 0.005) associations were detected at SNPs in LD (r² > 0.6) in the second exon of the gene (Fig. 2). The most significantly associated SNP (P = 0.00068; n = 160; e2.0776 in Fig. 2) causes a radical amino acid substitution of histidine (basic amino acid) for aspartic acid (acidic amino acid). The estimated effect of the “favorable” SNP allele at this position was modest for each disease, increasing resistance by 0.4–0.7 units on the disease resistance measurement scales (corresponding to ∼6% of the range for the scales; Fig. S4); the magnitude of these effects would be difficult but not impossible to discern visually.

Fig. 2.

Multivariate associations and LD in the GST gene. The gene structure is portrayed as gray boxes for the 5′-UTR, intron, and 3′-UTR and as black boxes with arrowheads for the two exons. The N and C domains are demarcated by thick colored lines: green for the N domain and blue for the C domain (the C domain comprises parts of both exons). The gene length (1,092 nucleotides) and positions of polymorphic sites (prefixed with “5u” for 5′-UTR, “e1” for exon 1, “i” for intron, “e2” for exon 2, and “3u” for 3′-UTR) were determined from the full-length gene sequence alignment, such that insertions among inbred lines expanded the length of the B73 reference sequence. (Upper) Multivariate test statistic results for polymorphic sites plotted as a function of physical distance. For nonsynonymous SNP substitutions, the amino acid polymorphisms are indicated by their one-letter codes. (Lower) LD r² estimates for each pair of polymorphic sites. Black lines and labels are meant to aid in visualizing LD among gene structures (e.g., “e1-i” indicates all pairwise comparisons between exon 1 and the intron).

GSTs are known for their roles in detoxifying xenobiotics and combating oxidative stress (39). These enzymes are ubiquitous among aerobic organisms, and their basic function in cellular protection is conserved across animals and plants, although GSTs exhibit a range of biochemical reactions and are involved in diverse biological functions (39, 40). In their protective role against cellular damage, GST monomers or dimers (typically homodimers) conjugate glutathione or bind directly to hydrophobic substrates, such as toxins and their incited radical chain reaction byproducts, rendering them less reactive and more water-soluble, and thus more tractable for vacuolar sequestration (40). The N-terminal domain of GST proteins is involved in the highly conserved function of binding glutathione, whereas the C-terminal domain interacts with diverse substrates and facilitates dimerization and other functions, determining GST specificity and activity. The most significant genetic associations and nonsynonymous amino acid substitution polymorphisms detected were in exon 2, which encodes the majority of the C-terminal domain (Fig. 2).

By developing a unique analytical approach for structured association mapping, we discovered high genetic correlations between resistances to three agriculturally important maize diseases. This was found in a public genetic resource with low LD in which genome-wide inference on the pleiotropic effects of individual genes may be made. The association of a GST gene with SLB, GLS, and NLB disease resistance and the identification of a specific amino acid substitution provided biological and biochemical plausibility that this member of the maize GST gene family affects MDR.

Materials and Methods

Phenotypic Analysis of SLB, GLS, and NLB Resistance.

Two hundred fifty-three maize inbred lines (Table S4) were used in this study. These lines were a subset of a larger panel (n = 302) of publicly available lines sampled from temperate and tropical breeding programs worldwide (11). Disease trials were conducted separately [plants were neither coinoculated nor coinfected (to any noticeable extent)] over a 4-y period (Table S5). Each trial was planted as a randomized complete block design with two replications. Plants were seeded at a within-row spacing of ∼15 cm and a between-row spacing of ∼75 cm. Disease resistance was measured visually on a row basis. Plant maturity was recorded as DTA (i.e., when half of the plants in a row had shed pollen).

Resistance to SLB was evaluated in five environments (Table S5). Resistance was measured using a scale ranging from 1–9 that emphasized symptoms on the ear leaf (37). All SLB trials were artificially inoculated as previously described (33). Multiple measurements ∼10 d apart were taken with a minimum of three measurements per trial. In 2003, in Homestead, FL, personnel were not available to record DTA for the rows in this experiment. In the same field, however, DTA was recorded in a neighboring experiment that included the same set of lines planted in a randomized complete block design but not inoculated with SLB. The least-square means of DTA from that experiment were used as a substitution for the unavailable DTA data. One of the replications in the 2004 experiment in Clayton, NC, was discarded because of poor plant growth.

Resistance to GLS was evaluated in three environments (Table S5). Resistance was measured in the same way as described for SLB with a minimum of three separate measurements taken per trial. In Andrews, NC, the natural occurrence of the pathogen provided consistently high disease pressure. No personnel were available to record DTA in 2004; thus, the least-square means of DTA measured in 2005 and 2006 were used as a substitution for the unavailable DTA data.

Resistance to NLB was evaluated in three environments (Table S5). Resistance was measured as the percentage of diseased leaf area on a scale of 0–100%. To give NLB resistance scores the same directionality as SLB and GLS scores, they were inverted: 0% = all leaf area infected and 100% = no leaf area infected. A minimum of three measurements were taken per trial. All NLB experiments were artificially inoculated following procedures described previously for New York (41) and North Carolina (25).

Statistical Analyses.

From the multiple disease ratings collected on each row in each disease trial, the level of resistance was calculated as the area under the disease progress curve, standardized by the total time during which measurements were taken (sAUDPC) (25). After discarding apparent recording errors based on univariate analysis of the DTA data (SI Materials and Methods), PROC GPLOT and PROC GLM of SAS software (v. 9.1.3; SAS Institute, Inc.) were used to examine the relationships between sAUDPC (dependent variable) and DTA (regressor variable) for each disease in each environment. The linear, quadratic, or cubic function of DTA that explained the most variation in sAUDPC and for which all terms were significant was used as an environment-specific function for subsequent analyses that included DTA as a covariate.

In this study, genetic association analysis relied on molecular marker-based estimates of population structure and relatedness. Estimates of population structure in this maize panel have been published previously (19). These estimates, contained in what has been referred to as a Q matrix, were probabilistic assignments of inbred lines to one of three maize subpopulations: stiff stalk (SS), non-stiff stalk (NSS), and tropical-subtropical (TS).

In addition to the population structure, finer-level pairwise relationships among lines were quantified as marker-based estimates of relative kinship. Kinship coefficients were estimated using the software SPAGeDi by the method of Ritland (42), utilizing a set of SNP markers with 85% data availability and biallelic frequencies greater than 0.05. Of the 1,089 SNP marker data downloaded from PANZEA (43), 858 fulfilled these criteria (Dataset S1). The matrix K was an n × n matrix of kinship coefficients that defined half the coefficient of the expected additive genetic covariance between each pair of individuals with diagonal elements equaled to one. Two negative pivots (eigenvalues) were present in K, resulting in a non–positive-definite genetic covariance matrix, which prevented convergence of the mixed model (described below). These were attributable to estimates of k_ij for two pairs of inbred lines, (i) NC364 and NC362 and (ii) NC336 and NC352, which were very close to the maximum theoretical value of one. Adjusting these covariances from 1.036 and 0.996, respectively, to 0.975 was required to produce a positive-definite genetic covariance matrix.

To study the genetic basis of multitrait variation, a statistical modeling approach was used to extend structured association mapping to a multivariate framework. The model was used to test fixed-effect model terms and to obtain estimates of population-level covariance parameters and E-MBLUPs for random effects. The fitted model provided estimates for ranking the collection of inbred lines comprising the association panel in terms of their additive genetic merit (i.e., breeding value) (Table S4). Covariance parameter estimates were used to calculate genetic correlations among traits and trait-specific heritabilities. A further extension of the multivariate model was used to test for multitrait-marker associations with the inclusion of an additional fixed-effect factor (i.e., SNP) in the model, as described in a subsequent section. Using ASReml v. 2 (VSN International Ltd.) (44), the following multivariate mixed model was fit to the entire sAUDPC dataset:

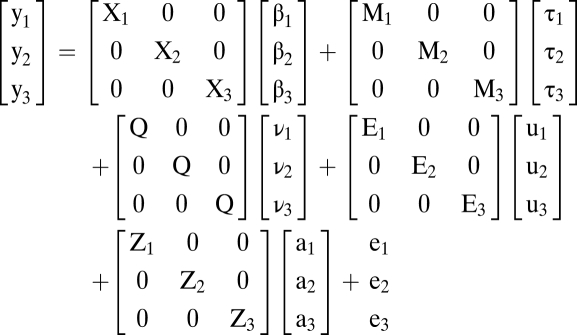where for traits i = 1–3, y_i is equal to a vector of sAUDPC observations; β_i is a vector of trait means, τ_i is a vector of fixed-effect environment-specific DTA covariates, and ν_i is a vector of fixed-effect population structure coefficients; u_i is a vector of random effects for environment, replication nested within environment, and genotypic-by-environment interaction; a_i is a vector of random genotypic effects; e_i is a vector of random residual effects; X_i, M_i, E_i, and Z_i are incidence matrices relating y_i to β_i, τ_i, u_i, and a_i, respectively; and the Q matrix is composed of independent columns (two of the three; SS and NSS) of probabilistic assignments of inbreds to population groups, relating Y_i to ν_i. The following covariance structure was assumed for genotypic effects:

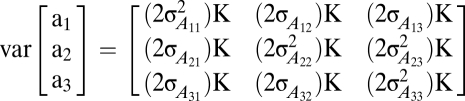where 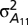is the additive genetic variance for trait 1; 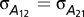is the additive genetic covariance between traits 1 and 2; 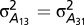is the additive genetic variance between traits 1 and 3, etc.; and K is the matrix of pairwise relative kinship coefficients. The experimental design factors and residual variances were assumed to be heterogeneous across traits but independent and identically distributed within traits. Between-trait covariances for these terms were assumed to be zero because the trait data were collected from separate trials. Initial univariate analyses of each disease-specific dataset were used to define starting values for covariance parameters (SI Materials and Methods).

Empirical multivariate best linear unbiased estimators (E-MBLUEs) were obtained for fixed effects and E-MBLUPs for random effects from the above model. When Q was present in the model, its effects were added to obtain appropriate breeding values calculated from the following linear combination:

where β_i is the overall mean for trait i = 1–3 (i.e., a constant for each trait), which was added to reflect the actual resistance value of each line on their corresponding measurement scale. ν_i was the population structure effect (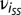, E-MBLUE for SS; 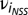, E-MBLUE for NSS), where SS_l and NSS_l are the proportional subpopulation group estimates for the lth inbred line and a_il is the E-MBLUP of the lth inbred line of the ith trait.

Functions of variance components, including heritabilities and genetic correlations as well as their SEs, were calculated using ASReml v. 2 (ref. 44, pp.170–174). Heritabilities were estimated on a line mean basis as described by Holland et al. (45).

The multivariate mixed model was used for two different purposes: (i) for making genetic inferences (e.g., estimating genetic correlations) as described above and (ii) for hypothesis testing of multitrait-marker associations. For the latter, one SNP was added at a time as a fixed-effect term to the multivariate model from above. As implemented in ASReml, a type III F-statistic was used to test the significance of each SNP locus, conditional on all other fixed-effect model terms (ref. 44, pp. 19–25). The mbf utility of ASReml v. 3 was used to automate the testing of each marker. Multitrait-marker associations were tested for the same set of SNP markers used to estimate relative kinship and for polymorphisms identified from resequencing data (below). For the multiple hypothesis tests performed in the sample of genome-wide distributed SNPs, the false discovery rate was controlled at q* = 0.05 using the method of Benjamini and Hochberg (46). For significant markers, the approximate 95% confidence interval of trait-specific allele effects was estimated as plus or minus two times the SE of prediction.

Resequencing Analysis of the GST Gene.

Four kernels from each inbred line used in this study were grown in the dark and harvested to give a total of ∼100 mg of etiolated tissue. These pooled samples were extracted in a 96-well format using the ZR-96 Plant DNA kit (D6021; Zymo Research Co.). PCR amplification and sequencing of the GST gene were accomplished in three overlapping sections using the following three primer pairs: gst23F127 5′-TCGTGCAGCCATCACTCTGTC-3′ with gst23R568 5′-CCCACTCCACCCTGATCACC-3′; gst23F510 5′-GAAGGGCGTGAAGGTGTTGG-3′ with gst23R1146 5′-AGCTCCTCGTGGGTGACGAC-3′; and gst23F1050 5′-CCGTGGGCTACCTCGACATC-3′ with gst23R1494 5′-ATTGGGCAACAGGCCAACAG-3′. The PCR mixture contained 20 μL of 1× PCR buffer, 1 M betaine, 1.5 mM MgCl₂, 200 μM dNTPs, 0.2 μM forward and reverse primer, 1 unit of New England Biolabs Taq polymerase, and ∼20 ng of genomic DNA. Thermal cycling started at 94 °C for 5 min, followed by 26 cycles at 94 °C for 30 s, 58 °C (for gst23F510/R1146) or 62 °C (for gst23F127/R568 and gst23F1050/R1494) for 45 s, and 72 °C for 80 s, with a single final extension at 72 °C for 10 min.

PCR products were quantified using E-Gel Low Range Quantitative DNA Ladder (Invitrogen) separated in 2.0% (wt/vol) agarose, and visualized by ethidium bromide fluorescence. Standardized product concentrations were sequenced by the Genomic Sciences Laboratory at North Carolina State University. A total of 1,096 sequences were analyzed from among 233 inbred lines. The software Geneious v. 5.0 (Biomatters Ltd.) was used to construct contigs for each set of sequences from the same inbred line, at which point sequencing errors were corrected to the extent possible (GenBank accession nos. JF758234--JF758466). A multiple sequence alignment of the contigs was produced using a full-length GST cDNA (NM_001111524.1) and genomic sequence (AC214483.2) of inbred line B73 from GenBank as a reference. A custom script written in the software R was used to extract polymorphism data from the multiple sequence alignment formatted for ASReml. Only polymorphic sites with minor allele presence in at least 25 individuals were used in multivariate analysis and LD estimation. The parts of Fig. 2 that include information on statistical association and LD were produced using the R program snp.plotter (47). The figure from snp.plotter was imported into Adobe Illustrator (Adobe Systems, Inc.), where the gene structure was designed based on the GST multiple sequence alignment, and other annotations were added.