Abstract
We present a lens-free optical tomographic microscope, which enables imaging a large volume of approximately 15 mm3 on a chip, with a spatial resolution of < 1 μm × < 1 μm × < 3 μm in x, y and z dimensions, respectively. In this lens-free tomography modality, the sample is placed directly on a digital sensor array with, e.g., ≤ 4 mm distance to its active area. A partially coherent light source placed approximately 70 mm away from the sensor is employed to record lens-free in-line holograms of the sample from different viewing angles. At each illumination angle, multiple subpixel shifted holograms are also recorded, which are digitally processed using a pixel superresolution technique to create a single high-resolution hologram of each angular projection of the object. These superresolved holograms are digitally reconstructed for an angular range of ± 50°, which are then back-projected to compute tomograms of the sample. In order to minimize the artifacts due to limited angular range of tilted illumination, a dual-axis tomography scheme is adopted, where the light source is rotated along two orthogonal axes. Tomographic imaging performance is quantified using microbeads of different dimensions, as well as by imaging wild-type Caenorhabditis elegans. Probing a large volume with a decent 3D spatial resolution, this lens-free optical tomography platform on a chip could provide a powerful tool for high-throughput imaging applications in, e.g., cell and developmental biology.
Keywords: computed tomography, lens-free imaging, on-chip imaging, optical microscopy, on-chip holography
Light microscopy has been an irreplaceable tool in life sciences for several centuries. The quest to resolve smaller features with better resolution and contrast has improved the capabilities of this important tool at the cost of relatively increasing its size and complexity (1). On the other hand, we have experienced the flourishing of emerging technologies such as microfluidic and lab-on-a-chip systems, which offer fast and efficient handling and processing of biological samples within highly miniaturized architectures (2–7). The optical inspection of the specimen, however, is still being performed by conventional light microscopes, which has in general several orders of magnitude size mismatch compared to the scale of the microfluidic systems. As a result, there is a clear need for alternative compact microscopy modalities toward integration with miniaturized lab-on-a-chip platforms (8).
The push for new optical microscopy modalities is not solely driven by the need for miniaturization and microfluidic integration. The fact that high resolution is achieved at the cost of significant field-of-view (FOV) reduction is another fundamental limitation of lens-based imaging. The relatively small FOV of conventional light microscopy brings additional challenges for its application to several important problems such as rare cell imaging or optical phenotyping of model organisms (9–15), where high-throughput microscopy is highly desired.
In order to provide complementary solutions to these aforementioned needs, several lens-free digital microscopy techniques (16—31) were introduced over the last few years. Along the same lines, we have recently developed an alternative lens-free imaging platform that combines high resolution and large FOV in a compact, on-chip imaging architecture (25–29). In this modality, digital in-line holograms of micro-objects are recorded on a sensor array using partially coherent illumination with unit fringe magnification such that the entire active area of the sensor serves as the imaging FOV. To overcome the resolution limitation imposed by the pixel size at the sensor, multiple subpixel shifted holograms of the sample are acquired, and pixel superresolution techniques are then applied to achieve submicron lateral resolution (29) without compromising the large FOV. As a result, a lateral imaging performance comparable to a microscope objective with a numerical aperture (NA) of approximately 0.4–0.5 is achieved over an FOV of approximately 24 mm2 (29). Relatively recently we have also extended this holographic lens-free imaging approach to opto-fluidic microscopy (OFM), providing a complementary solution to its original on-chip implementations (21–23), by using the motion of the object within the micro-channel to digitally synthesize higher resolution holograms of the object (30).
While pixel superresolution techniques in partially coherent lens-free in-line holography enable imaging with submicron lateral resolution over a large FOV, the axial resolution is unfortunately significantly lower (e.g., > 40–50 μm) as shown in Fig. S1, due to the inherently long depth-of-focus of digital in-line holography (32, 33). Accordingly, despite the fact that holographic reconstruction can be numerically focused at different depths, sectioning of planes closer than approximately 50 μm has not been feasible with lens-free wide-field holographic microscopes regardless of their detection numerical apertures (25–31). In this manuscript, this fundamental limitation will be addressed through multiangle lens-free holographic microscopy that lends itself to tomographic imaging of the samples within a large volume on a chip.
In recent years, there has also been an increased interest in optical imaging modalities that enable sectional imaging (34–48). As an example, optical projection tomography (OPT) (34), where an optically cleared specimen immersed in index-matching gel is rotated with respect to the fixed optical path of a conventional lens-based microscope, offers an isotropic resolution of approximately 10 μm in all three dimensions within an imaging volume of up to approximately 1 cm3. A modified version of OPT by using high NA objective lenses has also been implemented (35) recently to achieve submicron resolution cell imaging over a significantly reduced volume of, e.g., < 0.0005 mm3. Optical diffraction tomography (ODT) is another powerful technique where digital holography is utilized to reconstruct the 3D refractive index distribution of the specimen by changing the illumination direction (36–40), rotating the object (41), or by capturing multiple images at different wavelengths (42, 43). These tomographic systems can routinely image cells potentially achieving submicron resolution in all three dimensions. However, the trade-off between resolution and imaging volume also applies to these systems just like conventional microscopy, and high resolution is achieved at the cost of a significantly reduced imaging FOV of, e.g., < 0.04–0.2 mm2, and a depth-of-field (DOF) of < 10–20 μm, depending on the objective lens that is used.
For the same purpose, light-sheet microscopy techniques (limited to fluorescence imaging) have also been introduced that utilize a light-sheet generated by a cylindrical lens to successively illuminate selective planes within a fluorescent sample (44, 45) to create a 3D image with enhanced axial resolution. SPIM (44), for instance, achieves approximately 6 μm axial resolution in thick samples up to a few millimeters over an FOV ranging between 0.04–2 mm2, which is dictated by either the NA of the objective lens that is used or the active area of the opto-electronic sensor array. In general, these existing optical tomography platforms, as summarized above, all rely on relatively complex and bulky optical setups that are challenging to miniaturize and integrate with microfluidic systems. Therefore, an alternative tomographic microscopy platform that offers both high resolution and a large imaging volume in a compact embodiment may offer an important imaging toolset in various fields including cell and developmental biology, neuroscience, and drug discovery.
Toward this end, in this manuscript we present a unique demonstration of lens-free optical tomography, achieving < 1 μm lateral resolution together with an axial resolution of < 3 μm over a large FOV of approximately 15 mm2 as well as an extended DOF of approximately 1 mm, which could be further increased to, e.g., approximately 4 mm at the cost of reduced resolution. As a result, our lens-free optical tomography platform merges high resolution in 3D with a significantly large imaging volume, offering a 3D space-bandwidth product that is unmatched by existing optical computed tomography modalities.
In this approach, lens-free tomographic imaging is achieved by rotating a partially coherent light source with, e.g., approximately 1–10 nm spectral bandwidth, to illuminate the sample volume from multiple angles (spanning ± 50° in air), where at each illumination angle several subpixel shifted in-line projection holograms of the objects on the chip are recorded without using any lenses, lasers, or other bulky optical components (see Fig. 1). Limited spatial and temporal coherence of our hologram recording geometry brings important advantages to our reconstructed images such as reduced speckle and multiple-reflection interference noise terms. Furthermore, the unit fringe magnification in our geometry (see Fig. 1) permits recording of in-line holograms of the objects even at oblique illumination angles of, e.g., > 40°, which would not be normally feasible with conventional coherent in-line holographic imaging schemes that utilize fringe magnification, unless, e.g., the sensor-chip is also rotated along with illumination.
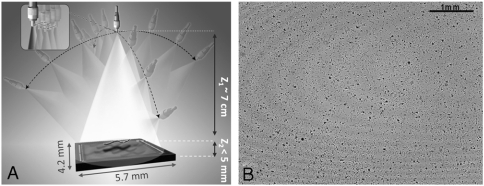
Fig. 1.
(A) Schematic diagram of the lens-free tomography setup. The sample is placed directly on the sensor array with < 5 mm distance to the active area. A partially coherent light source with spectral bandwidth of, e.g., approximately 1–10 nm, is filtered through a large aperture with diameter approximately 0.05–0.1 mm. The light source is rotated to record lens-free holograms of the micro-objects from multiple viewing angles. To digitally achieve pixel superresolution, 9 holograms are recorded, at each angle, by translating the aperture in the plane parallel to the sensor within a 3 × 3 grid with discrete shifts of < 70 μm (see the inset in A). (B) A typical full FOV (24 mm2) holographic image of 5 μm beads captured with vertical illumination.
In order to combat the limited angle artifacts in our tomograms, we have also employed a dual-axis (49, 50) tomography scheme by sequentially rotating our source in two orthogonal directions as illustrated in Fig. 1. To perform pixel superresolution and hence achieve submicron lateral resolution for each projection image, multiple lens-free in-line holograms that are subpixel shifted with respect to one another are acquired at every illumination angle (see Fig. 1). Once a set of high-resolution (HR) projection holograms (one for each illumination angle) are digitally synthesized using a pixel superresolution algorithm as shown in Fig. S2, a hybrid filtered back-projection method (51, 52) is utilized to create the final tomograms of the objects. Therefore, the superresolved projections are first digitally reconstructed (see, e.g., Fig. S3) and then back-projected to obtain volumetric images of the scattering potential of the sample.
Our results demonstrate a unique microscopy platform, where (i) optical tomographic imaging has been extended to lens-free on-chip imaging; (ii) dual-axis tomography has been applied to optical part of the electro-magnetic spectrum; and (iii) pixel superresolution techniques have been applied for optical tomographic imaging. Without the use of any lenses or coherent sources such as lasers, the presented lens-free tomographic imaging scheme achieves a spatial resolution of < 1 μm × < 1 μm × < 3 μm over a large FOV of approximately 15 mm2 and a DOF of approximately 1 mm using dual-axis tomography scheme. Lens-free projections holograms of objects within this entire volume of approximately 15 mm3 can be recorded over an angular range of ± 50°, and thereby the aforementioned resolution is maintained for a large imaging volume. We should also emphasize that this imaging volume further increases to > 48 mm3–96 mm3 at the cost of a reduction in axial resolution—i.e., approximately 3–6 μm. This decrease in resolution outside the 15 mm3 object volume is mainly due to: (i) the limited angular range of projections that can be recorded for objects that are close to the edges of the sensor or that are located at depths larger than 1 mm; and (ii) reduced signal to noise ratio (SNR) of lens-free holograms acquired at larger depth values of > 1 mm. Offering a decent spatial resolution over a large imaging volume, lens-free optical tomography could in general be quite useful for high-throughput imaging applications in, e.g., cell and developmental biology.
Results
To characterize our lens-free tomographic microscope, we performed a series of experiments using microbeads of different dimensions. Fig. 2 shows our dual-axis tomographic reconstruction results for 5 μm melamine beads (refractive index approximately 1.68, Corpuscular Inc.) distributed randomly in an approximately 50 μm-thick chamber (located at a height of z ∼ 0.8 mm from the sensor surface) filled with an optical adhesive (refractive index approximately 1.52, Norland NOA65). Image acquisition along each rotation axis takes approximately 5 min (for approximately 460 holographic frames). In this work, because we focused on the proof-of-concept, image acquisition speed was not optimized, which can in fact be significantly improved to, e.g., < 0.5 min per axis, by using a faster mechanical stage together with a higher frame rate sensor (e.g., > 10–20 fps). In order to match the FOV of the objective lens (40X, 0.65-NA) that was utilized to obtain microscope comparison images, tomograms were computed, within < 3 min using a graphics processing unit (NVidia, Geforce GTX480), only for a small region of interest cropped from a much larger FOV of approximately 24 mm2 shown in Fig. 1B. The arrows in Fig. 2 point out the beads, which are in focus at a given layer. Fig. 2 A1–A5, together with their corresponding microscope comparisons provided in Fig. 2 B1–B5 reveals that the out-of-focus beads are successfully rejected in our tomograms, and only the in-focus beads appear in the reconstructed images. To further illustrate our tomographic imaging performance, Fig. 2 A6–A8 shows a zoomed region of interest, highlighted by the blue dashed circles in Fig. 2 A3–A5, where two random beads axially overlap with a center-to-center separation of approximately 20 μm in z-direction. From these reconstruction results, it is clear that the overlapping beads are successfully resolved at their corresponding depths with minimal out-of-focus contamination from each other; and the intermediate slice shown in Fig. 2A7 has negligible spurious details, indicating successful sectioning of this axially overlapping region. These results, as validated by their corresponding microscope images shown in Fig. 2 B1–B8, demonstrate a sectional imaging ability that is beyond the reach of wide-field lens-free holographic microscopy, regardless of its detection numerical aperture or the coherence properties of its illumination (see, e.g., Fig. S1B).
Fig. 2.
Demonstrates the sectioning ability of the lens-free tomographic microscope for 5 μm beads distributed in an approximately 50 μm-thick chamber placed at z = ∼ 0.8 mm. (A1–A5) Computed tomograms, obtained with dual-axis tomography, for various planes in the chamber volume within the range -14 μm to 25 μm. (B1–B5) Microscope images (40X, 0.65NA) for the same planes shown in A1–A5. The insets in A2 and B2 show zoomed images for a bead in the corresponding tomogram and microscope image, respectively. (A6–A8 and B6–B8) Zoomed tomograms and microscope images, in order of mention, for the region highlighted by the dashed circles in A3–A5 where two beads are axially overlapping with a center-to-center separation of approximately 20 μm. While the beads are visualized with minimal contamination due to each other in their respective planes shown in A6 and A8, the tomogram of an intermediate layer between the beads shown in A7 reveals minimal spurious details, demonstrating the sectioning ability of our lens-free tomographic microscope. Scale bars for A6–A8 and B6–B8, 5 μm. The rest of the scale bars, 50 μm.
Although the results of Fig. 2 have been demonstrated over a relatively small FOV, tomograms of the entire imaging volume can be obtained by digitally combining several tomograms for different regions within the FOV that can all be calculated from the same raw holographic dataset. To demonstrate this capability, Movie S1 shows stacks of tomograms reconstructed for four different regions within the entire imaging area depicted in Fig. 1B. It should be noted that at a DOF of ≤ 1 mm, the effective FOV over which the best 3D resolution is achieved reduces to approximately 15 mm2 from 24 mm2 (which is the active area of the CMOS sensor chip) because the holograms of the objects close to edges of the sensor start to fall outside the active area at large angles of illumination. In order to evaluate whether our imaging modality suffers from aberrations and artifacts as a function of position within this large volume, we plotted the cross-sectional line profiles (along the x, y, and z dimensions) for tomograms of 5 μm beads located at various regions of interest. Fig. S4 illustrates that, as desired, these cross-sectional profiles do not vary much as a function of depth or lateral position within the volume and that the average full-width-at-half-maximum (FWHM) values of the line profiles for 5 μm bead tomograms are 4.8 μm, 4.8 μm, and 7.7 μm along x, y, and z, respectively.
To further investigate the imaging properties of our tomographic microscope, we have also imaged 2-μm diameter beads distributed within an optical adhesive, also located at a height of approximately 0.8 mm from the sensor chip. Fig. S5 A1–A3 shows the reconstructed cross-sections in x-y, y-z, and x-z planes, respectively, each cutting through the center of the bead. As revealed by the circular shape of the reconstructed bead in Fig. S5A1, our dual-axis tomography scheme eliminates the elongation artifact in the x-y plane, which is normally observed in limited angle single-axis tomography (49). On the other hand, the reconstruction of the same bead still exhibits an axial elongation due to missing projections at angles larger than ± 50° with respect to the normal of the sensor plane. Fig. 5 B1–B3 also shows cross-sectional line profiles along x, y, and z for three separate beads located at different depths. For the bead at z = -3 μm, the FWHM values for line profiles through the center are 2.3 μm, 2.2 μm, and 5.5 μm, along x, y, and z dimensions, respectively. Similar results have also been obtained with other beads located at depths z = -9 μm and z = 4 μm. Following a similar approach presented in refs. 36, 38, and 53, we also plotted in Fig. S6 the derivative of the axial line profile for the bead at z = -3 μm to estimate the resolution of our tomographic imaging platform at a height of approximately 0.8 mm from the sensor chip. The FWHM values for the line profiles of the reconstructed objects (Figs. S4 and S5), as well as their spatial derivatives (Fig. S6), suggest that an axial resolution of < 3 μm is achieved over a DOF of approximately 0.8 mm through lens-free tomographic imaging while submicron lateral resolution is maintained through pixel superresolution (29).
In addition to enabling 3D imaging of objects over a wide FOV owing to its lens-free unit-magnification geometry (Fig. 1), our platform also enjoys a significantly extended DOF compared to imaging systems where conventional microscope objectives are used. To demonstrate our large DOF, we imaged a multilayer chamber composed of 10-μm beads that has four layers stacked with approximately 1 mm separation—i.e., having a total thickness of approximately 3.3 mm. The chamber is then elevated above the sensor active area, and the furthest layer is situated approximately 4 mm away from the sensor chip. With an illumination angle spanning ± 50° in air, the entire tomographic data corresponding to an object volume of approximately 24 mm2 × 3.3 mm is acquired over approximately 10 minutes using dual-axis scanning (refer to Methods for further details). Once this raw data is acquired (which includes 9 subpixel shifted holograms at each illumination angle), separate tomograms for each depth layer are computed. These tomograms are then digitally combined into a single volumetric image, which now has a DOF of approximately 4 mm. Holographically recorded sets of projections, one of which is illustrated in Fig. S7A, comprise the entire 3D volumetric information of the thick sample, and arrows of different colors in Fig. S7 point to beads located at different layers within the multilayer chamber. One important challenge for tomographic reconstruction of such a large DOF is actually the implementation of pixel superresolution at each illumination angle. Because the raw holograms of particles/objects that are located at considerably separated depths will create different shifts, if their holograms overlap at the detector plane, blind realization of pixel superresolution will create errors for at least some of the overlapping particle holograms. To mitigate this challenge, we used a custom-designed algorithm to filter the raw holograms of different layers from each other such that pixel superresolution can be separately applied to lens-free holograms of different depth layers. More discussion on this is provided in SI Text as well as in Fig. S8. As shown in our reconstructed images (Fig. S7 B–E), an entire DOF of approximately 4 mm can be sectioned because separate tomograms calculated for a given depth range (e.g., approximately 50 μm in z) are now merged together to obtain a stack of tomograms over an extended DOF.
Next, we further quantified our reconstructed tomogram quality as a function of the depth of the object from the sensor array. For this purpose, we acquired tomograms of 4 μm diameter opaque microparticles (made of iron) at different depths—i.e., at z = 0.7 mm, 1.8 mm, 2.8 mm, and 3.8 mm from the sensor chip surface. By using the edge sharpness of the reconstructed particle tomograms (similar to refs. 36, 38, and 53), we estimated our spatial resolution in all three dimensions as a function of the particle depth, the results of which are summarized in Fig. S9. The same figure also illustrates x-y, y-z, and x-z cross-sections of the reconstructed particles that are located at different depths from the sensor chip. These results of Fig. S9 also confirm our previous conclusions that a resolution of < 1 μm × < 1 μm × < 3 μm (in x, y, and z, respectively) can be achieved up to a DOF of approximately 1 mm. As the depth reaches approximately 4 mm, the resolution of our tomograms degrades to ∼1.8 μm × ∼ 1.8 μm × < 6 μm (see Figs. S9 and S10), which is mainly due to reduced detection SNR at such larger depth values. This point will be further explored in Discussion.
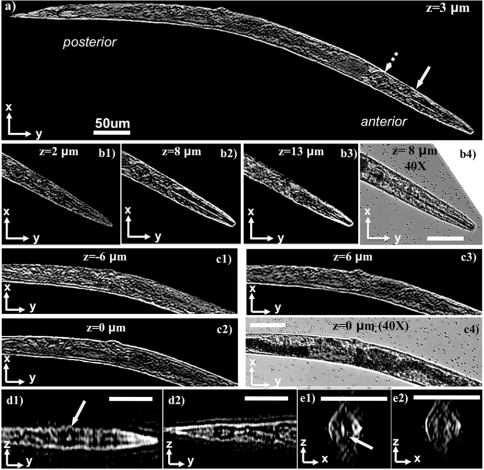
Finally, to demonstrate the performance of our lens-free tomographic microscope for applications in life sciences, we also imaged a wild-type Caenorhabditis elegans worm in L4 stage (approximately 650 μm in length) in deionized water. The worm was temporarily immobilized with 4 mM levamisole (Sigma Aldrich L9756) solution to avoid undesired motion during the image acquisition process, which took approximately 5 min. Because the worm was aligned parallel to y-axis during data acquisition, only the projections obtained by tilts along the x-axis were utilized to compute the tomograms of the worm, which took approximately 4 min using a single GPU. Fig. 3A and Fig. S11A show a slice through the whole worm corresponding to the z = 3 μm plane. The worm was observed to be slightly tilted out-of-plane with respect to the sensor surface, with its anterior elevated by approximately 8 μm. Fig. 3 B1–B3 and Fig. S11 B1–B3 show three reconstructed depth sections through the anterior region of the worm at the z = 2 μm, z = 8 μm, and z = 13 μm planes, respectively. As shown in these figures, the pharyngeal tube of the worm, which is a long cylindrical structure with < 5 μm outer diameter, is clearly visible at the z = 8 μm plane while it quickly disappears at depths away from the center of the pharynx. Fig. 3 C1–C3 and Fig. S11 C1–C3 also show the tomograms at different depths through the center and anterior regions of the same worm. Further, Fig. 3 D1, D2, E1, and E2) and Fig. S11 D1, D2, E1, and E2 show its x-z and y-z ortho-slices. In addition to these, we also show other tomographic slices of the same worm in Movie S2. In all these results, the appearance of distinct details at different sections can clearly be observed, demonstrating a significantly improved sectioning ability that is otherwise unattainable with wide-field lens-free holographic microscopy, regardless of its detection numerical aperture or coherence properties. Together with its large imaging volume, these results reveal the potential of our lens-free tomography platform for on-chip imaging and screening of optically accessible model organisms such as C. elegans and zebrafish, where high-throughput imaging is of utmost importance (9–15).
Fig. 3.
Demonstrates the application of lens-free on-chip tomography toward 3D imaging of C. elegans. (A) A tomogram for the entire worm corresponding to a plane that is 3 μm above the center of the worm. (B1–B3) Tomograms at different layers for the anterior of the worm. The pharyngeal tube of the worm, which is a long cylindrical structure with < 5 μm outer diameter, is clearly visible at z = 8 μm plane, and disappears at outer layers. (B4) A microscope image (40X, 0.65NA) for comparison. (C1–C3) Tomograms at different layers for the middle part of the worm, and a microscope image is provided in C4 for comparison. (D1 and D2) y-z ortho slices from the anterior and posterior regions of the worm, respectively. (E1 and E2) x-z ortho slices along the direction of the solid and dashed arrow in A, respectively. The 3D structure of the anterior bulb of the worm, pointed by the solid yellow arrows, can be probed by inspecting A, D1, and D3. Standard image deconvolution is applied to all the presented microscope images and tomograms to further improve their image quality as detailed in SI Text. Refer to Fig. S11 to see the raw (unfiltered) versions of these images. Movies S2 and S3 further illustrate other depth sections of the same worm. Scale bars, 50 μm.
Discussion
Our lens-free tomographic imaging system provides a unique microscopy modality that can probe a wide FOV of approximately 15 mm2 and a long DOF of approximately 1 mm at a lateral resolution of < 1 μm and an axial resolution of < 3 μm. This makes our platform especially suitable for high-throughput imaging and screening applications such as 3D model animal imaging (54). Also note that this imaging volume further increases to > 48–96 mm3 at the cost of a reduction in resolution (i.e., ∼1.2–1.8 μm × ∼ 1.2–1.8 μm × ∼ 3–6 μm in x, y, and z, respectively) as illustrated in Figs. S9 and S10.
There are several unique aspects of our lens-free incoherent holography scheme (Fig. 1) that enable achieving on-chip tomographic imaging over such a wide FOV and an extended DOF. For instance, choosing a large z1/z2 ratio of approximately 20–100 (see Fig. 1) allows holographic imaging with unit fringe magnification, which brings the large FOV to our imaging modality. The limited hologram resolution dictated by this unit magnification and the pixel size at the sensor chip is balanced by a pixel superresolution approach, which increases the lateral numerical aperture up to 0.4–0.5 without a trade-off in imaging FOV (29). The same large z1/z2 ratio also permits the use of unusually large illumination apertures (e.g., > 50 μm; see Fig. 1), which significantly simplifies the illumination end without the need for any light-coupling optics, a sensitive alignment, or a trade-off in achievable resolution (for more detailed analysis on this, refer to the appendix of ref. 25). As a result, projections are easily acquired by tilting the light source rather than having to rotate the object, which would unnecessarily complicate the setup and perturb the sample. Moreover, the simplicity of the optics and the alignment-free structure of our lens-free setup also permit straightforward implementation of dual-axis tomography.
Another unique aspect of our lens-free tomography scheme is the use of partially coherent light, both temporally and spatially. The spectral width of the illumination in our technique can be, e.g., approximately 1–10 nm with a center wavelength of, e.g., approximately 450–650 nm, which limits our coherence length to be on the order of approximately 20–350 μm. This relatively short coherence length of our technique significantly reduces two major sources of noise—i.e., the speckle and multiple-reflection interference noise terms. The latter one would especially have been a nuisance under laser illumination at oblique angles. In addition, such a limited coherence length also partially eliminates the cross-talk of different depths with each other. Such cross-interference terms are undesired and, in fact, are entirely ignored in most holographic reconstruction schemes. The same cross-interference also occurs within a given depth layer. In other words, scattering centers within the sample volume actually interfere with each other at the detector plane, which once again is a source of artifact as far as holographic reconstruction (e.g., twin-image elimination) is concerned. Our limited spatial coherence also helps us to mitigate this issue by choosing a spatial coherence diameter (e.g., < 0.5–1 mm) that is sufficiently large to record individual holograms of the objects and yet that is significantly smaller than the entire imaging FOV. This spatial coherence diameter is rather straightforward to engineer in our geometry by changing the illumination aperture (e.g., 0.05–0.1 mm) as well as by changing the distance between the source aperture and the sample volume.
The extended DOF of our platform (see, e.g., Figs. S7, S9, and S10) is a direct outcome of our lens-free holographic recording geometry, which is not restricted by the limited DOF of high NA objective lenses as utilized in some other tomography or holography schemes (36–43). Lens-free holographic recording at multiple angles enables digital reconstruction of projection images at any given depth of interest, around which tomograms can be computed. This paves the way to tomographic imaging with an extended DOF (e.g., approximately 1–4 mm) by combining such tomograms that are separately computed for different depths.
Finally, we should also discuss the limitations of this presented lens-free tomography approach. First, it is restricted to transmission geometry and therefore would be limited in performance by scattering properties of the sample volume. In other words, an extended DOF of approximately 4 mm demonstrated with our instrument should not be confused with the thickness of a continuous scattering object (such as a tissue sample) that can be optically sectioned in transmission mode. In general, determination of the 3D structure of an object from the knowledge of the scattered optical fields requires a weakly scattering object (55, 56). This assumption also forms the basis of our technique in recovering the 3D scattering potential of the objects similar to existing optical tomography platforms (34–41). Therefore, as further detailed in SI Text, the bulk of the photons incident on an object should encounter at most a single scattering event before being detected in our transmission holographic imaging geometry. Whether an object satisfies this condition depends on the scattering properties of the specimen as much as the total thickness of its connected structure (57). Our second limitation is that for weakly scattering subresolution objects, the detection SNR would limit reconstruction of their weak holograms, especially if they are located at higher depths of, e.g., > 2 mm from the sensor-chip. This also partially explains the resolution loss that is observed in Fig. S9B as the depth increases from 1 mm to 4 mm; i.e., the SNR of the acquired holograms degrade at longer depth values since the modulation depth of some of the holographic fringes start to get closer to the noise level. To combat this issue, active cooling of the detector array together with an increased illumination power (and reduced integration time) could be used to enhance the SNR and the available dynamic range of the sensor chip. On a related note, the detection SNR also partially limits the extent that pixel superresolution algorithms can digitally reduce the effective pixel size at the hologram domain. In our results, we have shown that submicron lateral resolution can be achieved by using a physical pixel size of approximately 2.2 μm under unit fringe magnification (29). To further improve our resolution, apart from using a smaller pixel size sensor chip or better detection SNR, increasing our fringe magnification (by pushing the objects closer to the source rather than the detector) is another possibility, though it does not appear promising because it would further limit the angular range that tomographic projections can be collected, as well as increase temporal and spatial coherence requirements of the source, implying an increased speckle and multiple interference noise together with a much smaller pinhole need (making it practically harder to align).
Besides reduced SNR, the resolution loss of our tomographic platform at larger depths is also related to the fact that lens-free holograms of the objects start to exit the sensor active area at large angles, further limiting the angular range that can be probed. The same is also true for objects that are located close to the edges of our imaging FOV. Fig. S10 further sheds light on this issue by calculating the achievable resolution of our platform as a function the object position within the imaging volume (refer to SI Text for details). The results of this simulation reveal that, closely following our experimental results shown in Fig. S9, the achievable axial resolution of our tomographic platform degrades from approximately 2.5 μm to approximately 5.6 μm as the depth increases from approximately 1 mm to approximately 4 mm. Further, the same simulation (Fig. S10) also indicates that the achievable 3D resolution of our platform does not significantly vary as the lateral position of the object changes within our large FOV, which is dictated by the sensor active area (approximately 24 mm2).
Another limitation of our approach is that for objects located within a microfluidic chip, uncontrolled motion of the objects within the channel during the image acquisition could degrade the achievable 3D resolution. To deal with this issue, noninvasive immobilization of the objects by using special microfluidic trap designs (58, 59) could be utilized. Another method to partially handle such uncontrolled motion of the objects during image acquisition could be digital estimation of their shifts and rotations to accordingly use these estimates in our reconstructions. A simpler 2D version of this has already been implemented in holographic opto-fluidic microscopy (HOM) (30), where the motion of the objects were utilized to synthesize superresolved holograms of the flowing sample without an external shift of the source. One final limitation of our platform we would like to mention is that fluorescent imaging over the same large object volume is rather challenging to achieve without the use of any lenses because lens-free fluorescent imaging techniques are yet limited to only ≤ 0.5 mm DOF with a much lower spatial resolution (60).
Methods
Fourier-projection theorem allows reconstructing the 3D transmission function of an object from its 2D projections along different directions (52). Accordingly, one pixel superresolved hologram for each illumination angle is digitally synthesized by utilizing multiple subpixel shifted holograms, which is followed by holographic reconstruction of all high-resolution holograms yielding lens-free projection images (see SI Text). Then, we utilize these reconstructed lens-free projection images to compute 3D tomograms of microobjects using a filtered back-projection algorithm (52). A fundamental requirement for this technique, commonly referred to as the projection assumption, is that the projection images should represent a linear summation of a certain property of the object (52), for which tomograms can be computed. While it is much easier to satisfy this condition in X-ray computed tomography due to negligible diffraction at that part of the electro-magnetic spectrum, computed tomography in the optical regime requires weakly scattering objects (34–41). Similarly, our lens-free optical tomography modality also requires that the majority of the photons experience at most a single scattering event over the volume of each stack of tomograms (57). For weakly scattering objects, together with the long depth of focus of our system (see, e.g., Fig. S1B), the scattering potential can be approximated to become additive along the direction of illumination for a tomogram slice thickness of Δz ∼ 50 μm (refer to SI Text for further discussion). Consequently, tomograms of the scattering potential of an object can be computed by applying a filtered back-projection algorithm whose inputs are the projection images calculated by holographic reconstruction of pixel superresolved lens-free holograms at each illumination angle.
Because holograms are recorded for a limited angular range of ± 50°, there is a missing region in the Fourier space of the object, commonly known as the missing wedge (49, 50). The main implication of the missing wedge is reduced axial resolution, which limits the axial resolution to a value larger than the lateral. Further, in the lateral plane, ringing artifacts are observed as well as narrowing of the point-spread function (PSF) along the direction of rotation of the illumination such that the PSF in the x-y plane becomes elliptical. For objects that are close to edges of the sensor, or that are located at a DOF > 1 mm, the angular range of projection holograms further decreases because holograms of these objects start to shift out of the active area of the sensor chip (24 mm2). As a result, the missing wedge further enlarges, leading to a decrease in achievable 3D resolution (see SI Text and Fig. S10 for further details).
In order to minimize these imaging artifacts, a dual-axis tomography scheme is implemented in this work. Projection images obtained along each tilt direction are separately back-projected to compute two sets of tomograms. These tomograms are merged in Fourier space following the numerical recipe given in ref. 49. Accordingly, the regions where both sets of tomograms have data for are averaged, while regions where only one set has useful data in its Fourier space, are filled by the data of the corresponding tomograms. As a result, the missing wedge is minimized to a missing pyramid (50), significantly reducing the aforementioned limited angle tomography artifacts as demonstrated in Results. To further reduce the artifacts outside the support of the object, we apply the mask that is utilized for digital reconstruction (25) of the vertical projection hologram to all tomograms. The missing wedge could also be iteratively filled to improve resolution and reduce artifacts (although not implemented in this manuscript) by using iterative constraint algorithms based on a priori information of the 3D support or transmission function of the object (61).
Supplementary Material
Acknowledgments.
A.O. acknowledges the support of the National Science Foundation (NSF) (CAREER Award on BioPhotonics), Office of Naval Research (Young Investigator Award), and the National Institutes of Health (NIH) Director’s New Innovator Award, DP2OD006427, from the Office of the Director, NIH. The authors also acknowledge the support of the Gates Foundation, Vodafone Americas Foundation, and the NSF BioPhotonics program (under awards 0754880 and 0930501).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission. V.N. is a guest editor invited by the Editorial Board.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1015638108/-/DCSupplemental.
References
- 1.Melton L. Imaging: The big picture. Nature. 2005;437:775–779. doi: 10.1038/437775a. [DOI] [PubMed] [Google Scholar]
- 2.Dittrich PS, Manz A. Lab-on-a-chip: microfluidics in drug discovery. Nat Rev Drug Discov. 2006;5:210–218. doi: 10.1038/nrd1985. [DOI] [PubMed] [Google Scholar]
- 3.Squires TM, Quake SR. Microfluidics: Fluid physics at the nanoliter scale Rev. Mod Phys. 2005;77:977–1026. [Google Scholar]
- 4.Whitesides G. The origins and the future of microfluidics. Nature. 2006;442:368–373. doi: 10.1038/nature05058. [DOI] [PubMed] [Google Scholar]
- 5.Haeberle S, Zengerle R. Microfluidic platforms for lab-on-a-chip applications. Lab Chip. 2007;7:1094–1110. doi: 10.1039/b706364b. [DOI] [PubMed] [Google Scholar]
- 6.Chin CD, Linder V, Sia SK. Lab-on-a-chip devices for global health: Past studies and future opportunities. Lab Chip. 2007;7:41–57. doi: 10.1039/b611455e. [DOI] [PubMed] [Google Scholar]
- 7.Chabert M, Viovy JL. Microfluidic high-throughput encapsulation and hydrodynamic self-sorting of single cells. Proc Natl Acad Sci USA. 2008;105:3191–3196. doi: 10.1073/pnas.0708321105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Oheim M. High-throughput microscopy must re-invent the microscope rather than speed up its functions. Brit J Pharmacol. 2007;152:1–4. doi: 10.1038/sj.bjp.0707348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Rohde CB, Zeng F, Gonzalez-Rubio R, Matthew A, Yanik MF. Microfluidic system for on-chip high-throughput whole-animal sorting and screening at subcellular resolution. Proc Natl Acad Sci USA. 2007;104:13891–13895. doi: 10.1073/pnas.0706513104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Chung K, Crane MM, Lu H. Automated on-chip rapid microscopy, phenotyping and sorting of C. elegans. Nat Methods. 2008;5:637–643. doi: 10.1038/nmeth.1227. [DOI] [PubMed] [Google Scholar]
- 11.Hulme SE, et al. Lifespan-on-a-chip: Microfluidic chambers for performing lifelong observation of C. elegans. Lab Chip. 2010;10:589–597. doi: 10.1039/b919265d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Sanz MA, Jong L, Tavernarakis N. Caenorhabditis elegans: A versatile platform for drug discovery. Biotechnology Journal. 2006;1:1405–1418. doi: 10.1002/biot.200600176. [DOI] [PubMed] [Google Scholar]
- 13.Kaletta T, Hengratner M. Finding function in novel targets: C. elegans as a model organism. Nat Rev Drug Discov. 2006;5:387–399. doi: 10.1038/nrd2031. [DOI] [PubMed] [Google Scholar]
- 14.Hulme SE, Shevkoplyas SS, Apfeld J, Fontana W, Whitesides GM. A microfabricated array of clamps for immobilizing and imaging C. elegans. Lab Chip. 2007;7:1515–1523. doi: 10.1039/b707861g. [DOI] [PubMed] [Google Scholar]
- 15.Kimmel CB. Stages of embryonic development of the zebrafish. Dev Dynam. 1995;203:255–310. doi: 10.1002/aja.1002030302. [DOI] [PubMed] [Google Scholar]
- 16.Xu W, Jericho MH, Meinertzhagen IA, Kreuzer HJ. Digital in-line holography for biological applications. Proc Natl Acad Sci USA. 2001;98:11301–11305. doi: 10.1073/pnas.191361398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Xu W, Jericho MH, Kreuzer HJ, Meinertzhagen IA. Tracking particles in four dimensions with in-line holographic microscopy. Opt Lett. 2003;28:164–166. doi: 10.1364/ol.28.000164. [DOI] [PubMed] [Google Scholar]
- 18.Pedrini G, Tiziani HJ. Short-coherence digital microscopy by use of a lensless holographic imaging system. Appl Optics. 2002;41:4489–4496. doi: 10.1364/ao.41.004489. [DOI] [PubMed] [Google Scholar]
- 19.Repetto L, Piano E, Pontiggia C. Lensless digital holographic microscope with light-emitting diode illumination. Opt Lett. 2004;29:1132–1134. doi: 10.1364/ol.29.001132. [DOI] [PubMed] [Google Scholar]
- 20.Garcia-Sucerquia J, Xu W, Jericho MH, Kreuzer HJ. Immersion digital in-line holographic microscopy. Opt Lett. 2006;31:1211–1213. doi: 10.1364/ol.31.001211. [DOI] [PubMed] [Google Scholar]
- 21.Heng X, et al. Optofluidic microscopy—a method for implementing a high resolution optical microscope on a chip. Lab Chip. 2006;6:1274–1276. doi: 10.1039/b604676b. [DOI] [PubMed] [Google Scholar]
- 22.Psaltis D, Quake SR, Yang C. Developing optofluidic technology through the fusion of microfluidics and optics. Nature. 2006;442:381–386. doi: 10.1038/nature05060. [DOI] [PubMed] [Google Scholar]
- 23.Lew M, Cui X, Heng X, Yang C. Interference of a four-hole aperture for on-chip quantitative two-dimensional differential phase imaging. Opt Lett. 2007;32:2963–2965. doi: 10.1364/ol.32.002963. [DOI] [PubMed] [Google Scholar]
- 24.Gopinathan U, Pedrini G, Osten W. Coherence effects in digital in-line holographic microscopy. J Opt Soc Am A. 2008;25:2459–2466. doi: 10.1364/josaa.25.002459. [DOI] [PubMed] [Google Scholar]
- 25.Mudanyali O, et al. Compact, light-weight and cost-effective microscope based on lensless incoherent holography for telemedicine applications. Lab Chip. 2010;10:1417–1428. doi: 10.1039/c000453g. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Oh C, Isikman SO, Khademhosseini B, Ozcan A. On-chip differential interference contrast microscopy using lensless digital holography. Opt Express. 2010;18:4717–4726. doi: 10.1364/OE.18.004717. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Su T, et al. Multi-angle lensless digital holography for depth resolved imaging on a chip. Opt Express. 2010;18:9690–9711. doi: 10.1364/OE.18.009690. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Seo S, et al. High-throughput lensfree blood analysis on a chip. Anal Chem. 2010;82:4621–4627. doi: 10.1021/ac1007915. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Bishara W, Su T, Coskun AF, Ozcan A. Lensfree on-chip microscopy over a wide field-of-view using pixel super-resolution. Opt Express. 2010;18:11181–11191. doi: 10.1364/OE.18.011181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Bishara W, Zhu H, Ozcan A. Holographic opto-fluidic microscopy. Opt Express. 2010;18:27499–27510. doi: 10.1364/OE.18.027499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Brady DJ, Choi K, Marks DL, Horisaki R, Lim S. Compressive holography. Opt Express. 2009;17:13040–13049. doi: 10.1364/oe.17.013040. [DOI] [PubMed] [Google Scholar]
- 32.Meng H, Hussain F. In-line recording and off-axis viewing technique for holographic particle velocimetry. Appl Optics. 1995;34:1827–1840. doi: 10.1364/AO.34.001827. [DOI] [PubMed] [Google Scholar]
- 33.Sheng J, Malkiel E, Katz J. Single beam two-views holographic particle image velocimetry. Appl Optics. 2003;42:235–250. doi: 10.1364/ao.42.000235. [DOI] [PubMed] [Google Scholar]
- 34.Sharpe J, et al. Optical projection tomography as a tool for 3d microscopy and gene expression studies. Science. 2002;296:541–545. doi: 10.1126/science.1068206. [DOI] [PubMed] [Google Scholar]
- 35.Fauver M, Seibel EJ. Three-dimensional imaging of single isolated cell nuclei using optical projection tomography. Opt Express. 2005;13:4210–4223. doi: 10.1364/opex.13.004210. [DOI] [PubMed] [Google Scholar]
- 36.Choi W, et al. Tomographic phase microscopy. Nat Methods. 2007;4:717–719. doi: 10.1038/nmeth1078. [DOI] [PubMed] [Google Scholar]
- 37.Choi W, et al. Extended depth of focus in tomographic phase microscopy using a propagation algorithm. Opt Lett. 2008;33:171–173. doi: 10.1364/ol.33.000171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Sung Y, et al. Optical diffraction tomography for high resolution live cell imaging. Opt Express. 2009;17:266–277. doi: 10.1364/oe.17.000266. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Fang-Yen C, et al. Video Rate Tomographic Phase Microscopy. J Biomed Opt. 2011;16:011005. doi: 10.1117/1.3522506. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Debailleul M, Simon B, Georges V, Haeberle O, Lauer V. Holographic microscopy and diffractive microtomography of transparent samples. Meas Sci Technol. 2008;19:074009. [Google Scholar]
- 41.Charrière F, et al. Living specimen tomography by digital holographic microscopy: Morphometry of testate amoeba. Opt Express. 2006;14:7005–7013. doi: 10.1364/oe.14.007005. [DOI] [PubMed] [Google Scholar]
- 42.Kuhn J, et al. Submicrometer tomography of cells by multiple wavelength digital holographic microscopy in reflection. Opt Lett. 2009;34:653–655. doi: 10.1364/ol.34.000653. [DOI] [PubMed] [Google Scholar]
- 43.Yu L, Kim MK. Wavelength-scanning digital interference holography for tomographic three-dimensional imaging by use of the angular spectrum method. Opt Lett. 2005;30:2092–2094. doi: 10.1364/ol.30.002092. [DOI] [PubMed] [Google Scholar]
- 44.Huisken J, et al. Optical sectioning deep inside live embryos by selective plane illumination microscopy. Science. 2004;305:1007–1009. doi: 10.1126/science.1100035. [DOI] [PubMed] [Google Scholar]
- 45.Keller PJ, Schmidt AD, Wittbrodt J, Stelzer EHK. Reconstruction of zebrafish early embryonic development by scanned light sheet microscopy. Science. 2008;322:1065–1069. doi: 10.1126/science.1162493. [DOI] [PubMed] [Google Scholar]
- 46.Jang J, Javidi B. Formation of orthoscopic three-dimensional real images in direct pickup one-step integral imaging. Opt Eng. 2003;42:1869–1870. [Google Scholar]
- 47.Haeberle O, Belkebir K, Giovaninni H, Sentenac A. Tomorgraphic diffractive microscopy: Basics, techniques and perspectives. J Mod Optic. 2010;57:686–699. [Google Scholar]
- 48.Hahn J, Lim S, Choi K, Horisaki R, Brady DJ. Video-rate compressive holographic microscopic tomography. Opt Express. 2011;19:7289–7298. doi: 10.1364/OE.19.007289. [DOI] [PubMed] [Google Scholar]
- 49.Mastronarde DN. Dual-axis tomography: An approach with alignment methods that preserve resolution. J Struct Biol. 1997;120:343–352. doi: 10.1006/jsbi.1997.3919. [DOI] [PubMed] [Google Scholar]
- 50.Arslan I, Tong JR, Midgley PA. Reducing the missing wedge: High-resolution dual axis tomography of inorganic materials. Ultramicroscopy. 2006;106:994–1000. doi: 10.1016/j.ultramic.2006.05.010. [DOI] [PubMed] [Google Scholar]
- 51.Wedberg TC, Stamnes JJ, Singer W. Comparison of the filtered backpropagation and the filtered backprojection algorithms for quantitative tomography. Appl Optics. 1995;34:6575–6581. doi: 10.1364/AO.34.006575. [DOI] [PubMed] [Google Scholar]
- 52.Radermacher M. Weighted Back-Projection Methods. Electron Tomography: Methods for Three Dimensional Visualization of Structures in the Cell. 2nd Ed. New York: Springer; 2006. pp. 245–273. [Google Scholar]
- 53.Oh WY, Bouma BE, Iftimia N, Yelin R, Tearney GJ. Spectrally-modulated full-field optical coherence microscopy for ultrahigh-resolution endoscopic imaging. Opt Express. 2006;18:8675–8684. doi: 10.1364/oe.14.008675. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Long F, Peng H, Liu X, Kim KS, Myers E. A 3D digital atlas of C. elegans and its application to single-cell analyses. Nat Methods. 2009;6:667–672. doi: 10.1038/nmeth.1366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Wolf E. Three-dimensional structure determination of semi-transparent objects from holographic data. Opt Commun. 1969;1:153–156. [Google Scholar]
- 56.Guo P, Devaney AJ. Comparison of reconstruction algorithms for optical diffraction tomography. J Opt Soc Am A. 2005;22:2338–2347. doi: 10.1364/josaa.22.002338. [DOI] [PubMed] [Google Scholar]
- 57.Ntziachristos V. Going deeper than microscopy: The optical imaging frontier in biology. Nat Methods. 2010;7:603–614. doi: 10.1038/nmeth.1483. [DOI] [PubMed] [Google Scholar]
- 58.Zeng F, Rohde CB, Yanik MF. Sub-cellular precision on-chip small-animal immobilization, multi-photon imaging and femtosecond-laser manipulation. Lab Chip. 2008;8:653–656. doi: 10.1039/b804808h. [DOI] [PubMed] [Google Scholar]
- 59.Guo XS, et al. Femtosecond laser nanoaxotomy lab-on-a-chip for in-vivo nerve regeneration studies. Nat Methods. 2008;5:531–533. doi: 10.1038/nmeth.1203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Coskun AF, Sencan I, Su TW, Ozcan A. Lensfree fluorescent on-chip imaging of transgenic Caenorhabditis elegans over an ultra-wide field-of-view. PLoS ONE. 2011;6:e15955. doi: 10.1371/journal.pone.0015955. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Verhoeven D. Limited-data computed tomography algorithms for the physical sciences. App Optics. 1993;32:3736–3654. doi: 10.1364/AO.32.003736. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.