Pitch perception beyond the traditional existence region of pitch

Abstract

Humans’ ability to recognize musical melodies is generally limited to pure-tone frequencies below 4 or 5 kHz. This limit coincides with the highest notes on modern musical instruments and is widely believed to reflect the upper limit of precise stimulus-driven spike timing in the auditory nerve. We tested the upper limits of pitch and melody perception in humans using pure and harmonic complex tones, such as those produced by the human voice and musical instruments, in melody recognition and pitch-matching tasks. We found that robust pitch perception can be elicited by harmonic complex tones with fundamental frequencies below 2 kHz, even when all of the individual harmonics are above 6 kHz—well above the currently accepted existence region of pitch and above the currently accepted limits of neural phase locking. The results suggest that the perception of musical pitch at high frequencies is not constrained by temporal phase locking in the auditory nerve but may instead stem from higher-level constraints shaped by prior exposure to harmonic sounds.

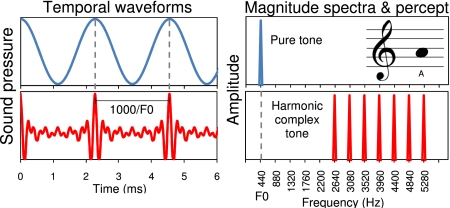
Pitch—the auditory percept related to the repetition rate of periodic sounds—plays a crucial role in music and speech (1, 2). Musical notes are defined by different pitches, which are combined to form chords (simultaneously sounded pitches) and melodies (pitch patterns over time). In speech, pitch is used to convey prosody in languages such as English as well as semantic information in tone languages such as Mandarin Chinese. Pitch can be elicited by pure tones, where the repetition rate corresponds to the tone's frequency, and harmonic complex tones, such as musical instrument sounds and voiced speech, where the repetition rate and, usually, the perceived pitch correspond to the fundamental frequency (F0) of the tone. The frequency component corresponding to the F0 does not need to be present in the sound for the corresponding pitch to be perceived, which is why this pitch is sometimes referred to as virtual pitch. Here, we use the more general expression of periodicity pitch (Fig. 1).

Fig. 1.

Schematic illustration of the relationship between acoustic periodicity and perceived pitch for pure and complex tones. A pure tone (Upper, blue) and a harmonic complex tone (Lower, red) are shown, which both produce the same pitch corresponding to the note A above middle C, as illustrated by the musical notation in Right Inset. Left shows the time waveforms with a repetition rate of 440 Hz. Right shows the tones’ spectral representations, including the fact that the complex tone does not have any energy at the fundamental frequency (F0) of 440 Hz.

The question of how pitch is perceived and coded in the auditory system has been a matter of scientific debate for well over a century (3–5). Currently, the neural coding of pitch is widely believed to rely on the precise timing of action potentials, or spikes, within the auditory nerve (6, 7). At low frequencies, spikes tend to occur at a certain phase within each cycle of a pure tone, leading to time intervals between spikes at multiples of the tone's period. In the mammals studied so far, this phenomenon of phase locking has been found to be robust for frequencies up to about 1–2 kHz and then to degrade at higher frequencies, becoming difficult to detect experimentally at frequencies between 3 and 6 kHz, depending on the species (8). Phase locking cannot be measured directly in the human auditory nerve because of the invasive nature of the measurements, but the putative upper limit of phase locking has been used to explain a number of pitch phenomena. First, our ability to recognize melodies (9–11) and musical intervals (such as the octave) (12) is severely degraded for pure tones above about 4–5 kHz, as is our ability to detect small changes in frequency (13). Second, absolute pitch—the ability of some individuals to name musical notes without reference to other notes—vanishes or becomes very weak for tones with frequencies above about 4–5 kHz (14). Third, if all of the harmonics in a complex tone are above 5 kHz, then it has been claimed that no periodicity pitch is heard at all, even if the F0 itself is below 5 kHz (15). Finally, the highest note on the grand piano (C8—4,186 Hz) and the highest notes of the highest orchestral instruments (such as piccolo) all fall in the range of 4–5 kHz. The close correspondence between the putative limit of neural phase locking and the upper limit of musical pitch has led to the widespread belief that peripheral coding constraints may have determined the upper limit of musical pitch perception and even musical instrument notes (1, 16, 17).

Contrary to current beliefs, the present experiments reveal that tones consisting of only high-frequency harmonics, all above the putative existence region of pitch, can elicit a clear periodicity pitch corresponding to the F0 and that the pitch is strong enough to support accurate melody discrimination. The results suggest that the commonly accepted limit of phase locking in the mammalian auditory nerve determines neither the upper limit of melodic pitch perception nor the upper pitch limits of musical instruments.

Results

Pitch Matching.

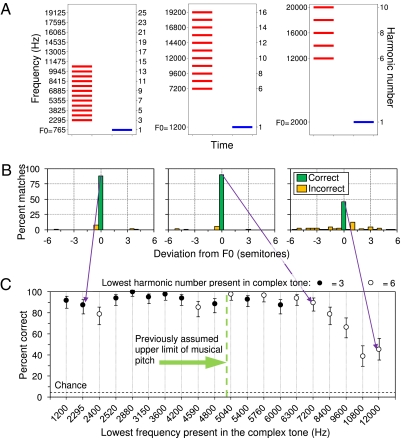
In Experiment 1, our participants were asked to adjust the frequency of a pure tone until its perceived pitch matched that of a preceding reference complex tone (Fig. 2A). The complex tones consisted of up to 12 consecutive harmonics, starting with the lowest harmonic rank of either 3 or 6. The majority of matches fell within ±0.25 semitones (or about 1.5%) of the true F0 or its octave equivalent (Fig. 2B and Fig. S1). For harmonic complex tones with components below 5 kHz, the pitch matches were accurate, in line with expectations (Fig. 2B Left). When all harmonics were above 5 kHz, the results were unexpected: all our participants showed an excellent ability to adjust the frequency of a pure tone to match the F0 of the complex tone, even though all of the harmonics were above the currently accepted 5-kHz upper limit of the existence region for periodicity pitch (Fig. 2B Center). Only when all the harmonics were above 10 kHz was some deterioration in performance observed (Fig. 2B Right). The decline in performance at very high frequencies may be due to the reduction in the number of audible harmonics; because we only screened participants for their ability to hear the stimuli up to frequencies of 16 kHz, in our highest-frequency condition, only three harmonics (12, 14, and 16 kHz) may have been audible. However, even in this condition, a clear peak in the pitch-match histogram was observed at the pure-tone frequency corresponding to the F0 of the harmonic complex or its octave equivalent.

Fig. 2.

Stimuli and results for Experiment 1 (pitch matches). (A) Schematic diagram of the stimuli used in the pitch-matching task for three sample conditions. The first stimulus in each trial was a complex tone that was fixed; the second tone was a pure tone, the frequency of which was adjusted up or down by the participants until its pitch-matched that of the complex tone. All tones were presented in a background of noise to mask possible distortion products (not included in the diagram). (B) Sample histograms from the same three sample conditions pooled across the six participants, with bin widths of 0.5 semitones. Green bars indicate matches that fell within ±0.25 semitones of the complex's F0 (or its octave equivalents) and were considered correct. Yellow bars show matches that fell outside the range considered correct when estimating performance. (C) Average percent of pitch matches that were within ±0.25 semitones of the F0 of the fixed complex tone or an octave above or below as a function of the lowest frequency present in the complex tone. Chance performance, based on a uniform distribution, corresponds to 4.17%. The lowest harmonic rank present in the complex was either three (filled circles) or six (open circles). For one-half of the conditions (10 rightmost points), the lowest frequency present in the complex tone was above 5 kHz, the previously assumed upper limit of the existence region of musical pitch (dashed green line marked by the green arrow). Error bars represent 95% confidence intervals based on the posterior distribution of the percent of correct matches across subjects.

Overall, the proportion of accurate pitch matches remained very high for many conditions in which no harmonics below 5 kHz were present (Fig. 2C); even in the highest-frequency condition tested, the average performance of 46% was significantly above the chance performance of 4% (binomial test; P < 0.0001). As shown by the confidence intervals, performance was generally more variable between participants at the higher F0s. However, no evidence for an upper limit to the existence region of pitch was found at or close to 5 kHz, which contrasts with both current beliefs and predictions based on the putative limit of phase locking in the auditory nerve.

Melody Discrimination.

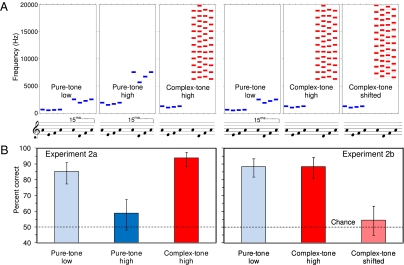
A common operational definition of pitch is that it can convey melodic information (18). Consequently, in Experiment 2a we tested whether our findings of pitch perception at high frequencies generalized to a melody discrimination task. Participants were presented with two four-note melodies, both taken from the seven-note diatonic (major) scale. The second melody had either the same notes as the first or differed in its second or third note by one scale step (Fig. 3A). A change of only one scale step ensured that an upward-going interval was never replaced by a downward-going interval (or vice versa), and therefore, the melodic contour was never reversed. In the pure-tone low condition, performance was good—the average percent-correct score was about 85% (Fig. 3B Left, light blue bar). This outcome was expected: all of the tones were well below 5 kHz and therefore, should have conveyed clear melodic information. In the pure-tone high condition, performance was much poorer, with an average percent-correct score of about 59%—close to the chance level of 50% (Fig. 3B Left, dark blue bar). Again, this result was expected based on earlier studies showing that pure-tone melody discrimination deteriorates at frequencies above about 4–5 kHz (9). The condition of most interest is the complex-tone high condition in which the second melody consisted of complex tones with F0s between 1 and 2 kHz but filtered so as to contain only harmonics above 6 kHz. Here, performance was uniformly good, with an average percent correct score of 94% (Fig. 3B Left, red bar). As indicated by 95% confidence intervals (CIs) around percent-correct scores, performance in this third condition (CI = 88–98%) was significantly better than in the second condition (CI = 48–68%) and not significantly different from performance in the first condition (CI = 78–91%). The results from this final condition show that melodic pitch information can be extracted from complex tones that contain only frequencies above 6 kHz.

Fig. 3.

Stimuli and results for experiment 2 (melody discrimination). (A) Representations of a sample melody in the conditions tested as spectrograms and in musical notation. In each condition, the first four-note melody was always comprised of pure tones. The second melody was comprised of either pure tones or filtered complex tones and was the same as the first or its second or third note was raised or lowered by one step in the diatonic scale. In this example, the second note is lowered by one step. Melody 1 in the pure-tone low condition was drawn from frequencies between 500 Hz and 1 kHz; melody 1 in the pure-tone high condition was drawn from frequencies between 1.5 and 3 kHz. In both conditions, melody 2 was transposed up by two octaves. In the complex-tone high condition, melody 1 consisted of pure tones drawn from 1 to 2 kHz, and melody 2 consisted of complex tones filtered between 7.5 and 16 kHz, with F0s between 1 and 2 kHz. The complex-tone shifted condition was the same, except that the components within each complex tone were shifted up or down by the same random amount to disrupt their harmonic relations while maintaining the same frequency spacing between components. The shift was selected for each complex tone independently from between 10% and 90% of the F0 with uniform distribution. (B) Average percentage of correct responses in the different conditions in Experiment 2 a and b. Performance in the complex-tone high condition (red bars) was good in both experiments, despite the absence of components below 6 kHz, whereas single pure tones above 6 kHz in the pure-tone high condition (dark blue bar) did not convey reliable melodic information. The poor performance in the complex-tone shifted condition (pink bar) from Experiment 2b shows that listeners were not able to reliably perceive melodic pitch using periodic temporal envelope or beating cues. Error bars represent the 95% confidence interval around the mean.

Envelope Repetition Pitch.

Is the pitch from our high-frequency complex tones elicited by the individual harmonics or by interactions between adjacent harmonics? Interactions between harmonics can lead to fluctuations in the temporal envelope at a rate corresponding to the F0—the so-called envelope repetition pitch (18–21). If our results reflected sensitivity to the temporal envelope, then they would not speak to the limit of phase locking to individual upper harmonics, because the frequency of interest would be the envelope repetition rate (1–2 kHz) rather than the frequencies of the individual components (>6 kHz). Experiment 2b tested the influence of envelope-repetition pitch by replicating conditions 1 and 3 from Experiment 2a and adding a new variant of condition 3, in which the filtered complex tone contained components that were spaced regularly apart by the F0 but were all randomly shifted in frequency by the same amount in Hertz. A useful property of these frequency-shifted complex tones is that their temporal envelope is identical to that of their harmonic counterparts, but their frequencies are no longer harmonically related (22). Thus, if the perceived pitch is based on the envelope repetition rate, then performance should be the same for the harmonic and shifted conditions. However, if the perceived pitch is based on frequency information from the individual harmonics, then the ambiguous pitches produced by the inharmonic frequency-shifted complexes should lead to poorer performance. The results from Experiment 2b indicated good performance for both of the original conditions (Fig. 3B Right, red and blue bars) but poor performance with the frequency-shifted complex tones, close to the chance level of 50% (Fig. 3B Right, pink bar). Confidence intervals for the three conditions were 82–93%, 81–94%, and 45–63%, respectively. Thus, the good performance found for harmonic complex tones with all components above 6 kHz cannot be accounted for by envelope repetition rate at the F0 or by the regular spacing of the component frequencies (23) (SI Results, Experiment 2c provides another test of envelope repetition pitch).

Discussion

The results from both the pitch-matching and melody discrimination experiments show that accurate pitch information can be conveyed by harmonics that are all above 6 kHz. The results are in direct contradiction to the widely accepted 5-kHz limit to the existence region of pitch established in early but highly influential studies (15, 24). What might explain this apparent discrepancy? There are many differences between the techniques of the earlier studies and the current one. We believe four of these may be most critical. First, the early study that tested both high F0s and high spectral regions (15) used only three consecutive harmonics, whereas our study used many (at least five, depending on the experiment and the F0). Complex tones that contain few harmonics generally produce a weaker pitch than complex tones with many harmonics (25). Therefore, the earlier study may have underestimated the ability of high-frequency harmonics to convey pitch. Second, our experiments used objective measures of performance (i.e., percent correct in a pitch-matching task and percent correct in a melody discrimination task), whereas the earlier studies were based on the more subjective measure of whether subjects believed that they could hear a periodicity pitch. Performance measures typically provide less variable and more reliable results than subjective measures, because they can be made relatively free of the influence of individual bias and criterion effects (26). Third, our tones were embedded in a noise background, whereas the tones in earlier studies were presented in quiet. We used the noise primarily to rule out the possibility that participants could detect distortion products at lower frequencies (27). However, embedding tones at levels just above masked threshold may also enhance the percept of the missing fundamental, perhaps by making the presence of the missing components more plausible, thereby encouraging perceptual filling in of the missing components and hence, the F0 (28–30). Finally, no data were provided in the early studies regarding the audibility of very high-frequency components. In our study, more than one-third of the potential participants, all of whom had clinically normal hearing, were excluded because of their high absolute thresholds at 16 kHz. It is, therefore, possible that limited audibility may have affected the early studies of the upper limit of pitch.

In physiological (31) and psychological (32) experiments on pitch it is important to ensure that distortion products are not contributing to the observed effects. To test that our background noise level was sufficient to mask any distortion products produced by the ear, we measured the distortion products elicited by a subset of the experimental stimuli. We found that the effective levels of distortion in the ear were very low [less than 20 dB sound pressure level (SPL) in all cases] and therefore, were at least 20 dB below the masked thresholds produced by our background noise (SI Results, Experiment 3).

Our results challenge the link between the upper limit of periodicity pitch and the putative limit of phase locking in the human auditory nerve. In particular, we observed a dissociation between pure tones above 6 kHz, which did not convey reliable melodic information, and those same tones when combined within a harmonic complex with an F0 (and a pitch) well below 6 kHz, which did convey reliable melodic information. The apparent dissociation may be explained in part by the possibility that the information from the multiple tones within the harmonic complex is integrated to form a more accurate representation of pitch than can be formed from a single pure tone. Previous data obtained at lower frequencies do not support this possibility: pitch discrimination thresholds for complex tones are not typically better than thresholds for pure tones (33). However, our tones were higher in frequency than those that have been used in previous studies, and it is possible that benefits of combining information across multiple frequency components are observed only at very high frequencies, where peripheral sensory limitations (e.g., poor phase locking of auditory-nerve fibers) may predominate over more central ones, ranging from neural noise in brainstem structures to higher-level constraints such as echoic memory (34). To test this possibility, we measured frequency and F0 difference limens [just noticeable differences (JNDs)] for pure and complex tones from a subset of the tones used in Experiment 2 (SI Results, Experiment 4). In contrast to earlier studies, we found discrimination thresholds that were better for the high-frequency complex tones than for the high-frequency pure tones, suggesting spectral integration of information. However, even the high-frequency pure tones produced mean JNDs of less than 1.5%—well below the 6% difference in frequency between neighboring notes in the chromatic scale. Data in the literature indicate that pitch discrimination thresholds as large as 3–5% can be sufficient for pitch interval and melody discrimination or identification (18, 20, 35, 36). Thus, performance in our melody discrimination experiments seems to have been limited not by peripheral factors (such as degraded spike-timing information in the auditory nerve at high frequencies) but by central factors occurring at or after the stage at which frequency information from different peripheral channels is combined in the CNS to estimate the pitch of complex tones. Candidate sites for the necessary neural integration range from the cochlear nucleus, where inputs from primary auditory neurons are first integrated over wide frequency regions (37), to the auditory cortex, where neural correlates of F0 and pitch and pitch strength have been identified in both human imaging studies (38–40) and neurophysiological studies in nonhuman primates (31).

If not the limits of auditory-nerve phase locking, what explains the fact that melody perception is limited to pitches below 4–5 kHz? One possibility is that melodic pitch perception is learned through repeated exposure to vocal and instrumental sounds during development and that the lack of exposure to notes higher than those found on current musical instruments results in a reduced ability to process high-F0 pitch information. Similar arguments have been explored in attempts to explain many musically related phenomena, including complex pitch perception in general and the perception of consonance or dissonance (41–43). For pitch perception, it has been argued that harmonic templates may emerge through exposure to sound (44) and that templates do not form for sounds that are not encountered in the everyday acoustic environment (45); a similar argument may apply to melodic pitch above 4–5 kHz. Indeed, recent work using EEG has suggested strong short- and long-term plasticity in pitch coding at levels as low as the auditory brainstem structures in humans (46, 47). In this way, the brainstem and/or cortical representations of pitch and pitch relations may only emerge during normal development with exposure to the appropriate sounds.

If future physiological studies were to confirm that precise spike timing in the human auditory nerve is severely degraded or absent at high frequencies, as is currently believed, then our psychophysical findings would lead to the conclusion that accurate phase locking in the auditory nerve is not necessary for complex pitch perception. This conclusion would support so-called place models of pitch perception, which rely on spatial representations of sound frequencies (i.e., tonotopy) in the cochlea (48), over time models, which rely on precise spike timing in the auditory nerve (7, 49). An earlier study suggested that spike timing information from individual harmonics was not sufficient for periodicity pitch perception (50); the current study suggests that it may not be necessary. An alternative interpretation is that phase-locked timing information in the auditory nerve can be extracted at much higher frequencies than is currently believed. This could be the case if the human auditory nerve has different response properties than those found in other mammals studied so far, or if the residual amount of phase locking at high frequencies in the human auditory nerve is similar to that in other mammals but is still sufficient to support frequency coding even at high frequencies (51–53). Distinguishing between these possibilities will require further physiological investigation of auditory-nerve properties, including the development of more direct ways to study temporal responses in the human auditory nerve.

Methods

Experiment 1: Pitch Matching.

The harmonic complex tones were generated by adding together harmonics with equal amplitudes (55 dB SPL per component). The starting phase of each harmonic was drawn randomly from a uniform distribution on each presentation. The pure tones were set to 65 dB SPL to better approximate the loudness of the complex tones. The tones were embedded in a broadband (20 Hz to 22 kHz) threshold-equalizing noise (TEN) with a level of 45 dB SPL within the estimated equivalent rectangular bandwidth (ERB_N) of the auditory filter at 1 kHz (54) to mask any possible distortion products generated by the ear (27). The tones all had a total duration of 500 ms, including 20-ms raised-cosine onset and offset ramps.

Each trial began with a 500-ms complex tone followed by a 500-ms gap and then, a 500-ms pure tone. The background noise began 300 ms before the standard tone, continued through the trial, and ended 300 ms after the end of the comparison tone. Participants were asked to adjust the frequency of the pure tone until its pitch matched that of the complex tone. The starting frequency of the pure tone was randomly selected on each block from a uniform distribution on a discrete semitone scale ±18 semitones around the F0 of the complex tone. After each trial, participants could adjust the frequency of the pure tone up or down by 4, 1, or 0.25 semitones, could elect to hear the trial at the same frequencies again, or could indicate that they were satisfied with the pitch match by using virtual buttons on a graphical user interface. Participants were encouraged to bracket the pitch of the reference complex tone by adjusting the pitch of the pure tone below and above that of the reference before making a final decision. The complex tones had F0s of 400, 765, 840, 960, 1,050, 1,200, 1,400, 1,600, 1,800, and 2,000 Hz and were comprised of up to 12 consecutive harmonics, beginning on the third or the sixth. Harmonics above 20 kHz were not generated.

Each of the six participants completed 15 matches for each combination of F0 and lowest-harmonic rank (third and sixth), resulting in a total number of matches per participant of 300 (15 matches for each of 10 F0s and two lowest-harmonic ranks). The order of presentation of the matches was randomized within each block of the 20 conditions and was different for each participant and each of the 15 repetitions. No feedback was provided to participants regarding their performance on the task.

Experiment 2: Melody Discrimination with Harmonic and Frequency-Shifted Tones.

The melody discrimination tasks involved two groups of six participants. On each trial, a four-note melody was generated from a set of eight consecutive notes from the diatonic (major) scale with equal temperament—do, re, mi, fa, sol, la, ti, and do in solfège notation with a moving do. The notes were selected randomly with uniform distribution and replacement, with the sole constraint that no three consecutive notes could be the same. The melody was presented two times. The notes in the second presentation were either unchanged (same trial) or either the second or third note of the melody was raised or lowered by one scale step (different trial). Because the change was only one scale step (either one or two semitones), it never resulted in a reversal of the melodic contour.

Participants in Experiment 2a were presented with three conditions (Fig. 3A and examples in Audios S1, S2, S3, S4, S5, and S6). Participants in Experiment 2b were presented with two of the original conditions plus a condition involving inharmonic complexes (complex-tone shifted condition). The stimuli were organized into blocks of 60 trials, consisting of 20 presentations of each condition (10 same and 10 different trials), presented in a new random order for each block. After some exposure to the low-frequency pure-tone conditions to ensure that participants understood the task and were capable of performing it, each participant completed a total of 12 blocks. The first two blocks were discarded as practice, and therefore, the reported data comprise a total of 10 blocks or 200 trials per condition per participant. Participants were informed that there would be equal numbers of same and different trials to reduce potential bias, but no trial by trial feedback on performance was provided.

The background noise was the sum of a broadband 45 dB SPL per ERB_N TEN, as in Experiment 1, and an additional 55 dB SPL per ERB_N TEN, bandpass-filtered between 20 Hz and 5.5 kHz to further exclude any possibility of audible distortion products (27). The level of the pure tones below 3 kHz was 65 dB SPL, and the level of the pure and complex tones above 6 kHz was 55 dB SPL per component before filtering. The complex tones were bandpass-filtered with corner frequencies of 7.5 and 16 kHz and spectral slopes of 30 dB/octave. This filtering ensured that tones below 6 kHz would fall below the masked threshold of the background noise and would therefore be inaudible. The starting phases of the harmonics were again selected at random from a uniform distribution. The F0s of the harmonic tones in the reference melody were between 1,000 and 2,000 Hz, and so the lowest audible harmonic ranged from the third to the sixth, depending on the F0. The inharmonic complexes were generated by shifting all of the components of the original complex up in frequency by the same amount between 10% and 90% of the F0. The size of the shift was selected randomly and uniformly from that distribution for each note independently. In this way, the spacing between each component (and hence, the envelope repetition rate) remained the same as the F0, but the tones were no longer harmonic (22).

The notes each had a total duration of 300 ms, including 10-ms raised-cosine onset and offset ramps. Within a melody, notes were separated by 200-ms gaps, producing an overall presentation rate of 2 tones/s (120 beats/min). Each melody lasted 1.8 s, and the two melodies within a trial were separated by a 700-ms gap. The background noise was gated on 200 ms before the first note of the first melody and was gated off 400 ms after the end of the final note of the second melody using 10-ms raised-cosine ramps.

Methods are described in more detail in SI Methods.