Missing value imputation in longitudinal measures of alcohol consumption

Abstract

Attrition in longitudinal studies can lead to biased results. The study is motivated by the unexpected observation that alcohol consumption decreased despite increased availability, which may be due to sample attrition of heavy drinkers. Several imputation methods have been proposed, but rarely compared in longitudinal studies of alcohol consumption. The imputation of consumption level measurements is computationally particularly challenging due to alcohol consumption being a semi‐continuous variable (dichotomous drinking status and continuous volume among drinkers), and the non‐normality of data in the continuous part. Data come from a longitudinal study in Denmark with four waves (2003–2006) and 1771 individuals at baseline. Five techniques for missing data are compared: Last value carried forward (LVCF) was used as a single, and Hotdeck, Heckman modelling, multivariate imputation by chained equations (MICE), and a Bayesian approach as multiple imputation methods. Predictive mean matching was used to account for non‐normality, where instead of imputing regression estimates, “real” observed values from similar cases are imputed. Methods were also compared by means of a simulated dataset. The simulation showed that the Bayesian approach yielded the most unbiased estimates for imputation. The finding of no increase in consumption levels despite a higher availability remained unaltered. Copyright © 2011 John Wiley & Sons, Ltd.

Introduction

The problem of missing values has been long‐standing in survey research. Although there are several textbooks (e.g. Schafer, 1997; Rubin, 1987) and software packages that address the issue [for example by imputing missing values e.g. SAS (SAS Institute Inc., 2008), Stata, (StataCorp., 2009), S‐PLUS (Insightful Corp., 2003) and R (R Development Core Team, 2007)], the problem is far from solved for particular research questions. Multiple imputation models (Rubin, 1987) have been the preferred option compared to single value imputation, as such models also deal with the uncertainty of imputed values. In longitudinal research, attrition contributes an additional source of error to the known selection biases that occur in cross‐sectional research (Twisk and de Vente, 2002). Causes of attrition in medical research often relate to drop‐outs being more ill than those with complete data (Fairclough et al., 1998; Kaciroti et al., 2009; Gunnes et al., 2009; Tang et al., 2009; Paddock and Ebener, 2009).

The present study is motivated by recent findings in alcohol research. Although there is ample evidence that restricting availability of alcohol reduces consumption levels, a recent study in the Nordic Countries points to the possibility that this may not always be the case. Despite an increase in availability due to the lowering of prices in 2003 and 2004, as well as increased European Union (EU) traveller allowances in 2004 (Grittner and Bloomfield, 2009), alcohol consumption as measured in surveys did not increase after such changes were introduced (Mäkelä et al., 2008; Grittner and Bloomfield, 2009). One reason for this surprising finding could be that particularly heavier drinkers or those who had increased consumption had dropped out of the study.

According to Carrigan et al. (2007) most standard software packages generally rely on the assumption of normally distributed multivariate data (Schafer, 1997). Even if recent work on chained regression equations has led to the incorporation of categorical, non‐normal data [e.g. multivariate imputation by chained equations (MICE) in SPLUS (van Buuren and Oudshoorn, 1999), ICE in Stata (Royston, 2005), and IVEware for SAS (Raghunathan et al., 2002)], there are still difficulties in incorporating longitudinal information into the imputation methodology of these programs.

Two aspects about population‐level alcohol consumption complicate imputation. Abstainers cannot simply be seen as consumers with zero consumption, as they differ from drinkers in many aspects (Skog and Rossow, 2006; Kerr et al., 2002), and among consumers the distribution is non‐normal (i.e. commonly right‐skewed). To take this into account, average volume of consumption among drinkers has to be modelled as a variable which is skewed and left‐censored. Therefore, two‐step models are needed that first impute whether a dropout was likely to be an abstainer. Secondly, volume of alcohol has to be imputed for those estimated to be drinkers. Several suggestions for dealing simultaneously with 0/1 (abstention) and continuous variables (consumption among consumers) exist in the literature (Olsen and Schafer, 2001; Xuefeng et al., 2009) but little research exists that compares several alternatives in a longitudinal framework (except Barnes et al., 2010) and implements techniques to deal with the non‐normal continuous part.

Although skewness can be dealt with by transformations such as logarithms, back‐transformations to the original scale (relevant for policy‐makers) are not necessarily straightforward (Duan, 1983; Skog and Rossow, 2006; Manning, 1998) and are highly sensitive to the distributional properties of the variable (i.e. the standard deviation).

Using data from a nationally representative longitudinal survey in Denmark the present study compares different approaches to impute missing values presently found in the literature. It evaluates the performance of the approaches by simulating datasets based on parameters found in the survey data where the true “missingness” mechanism is known. These approaches are:

• (1)Last value carried forward (LVCF)
• (2)Hotdeck
• (3)Heckman
• (4)Multivariate imputation by chained equations (MICE)
• (5)Bayesian inference and Markov chain Monte Carlo methods

The present study thus tries to shed light on two questions, one statistical, the other of practical relevance for policy‐making in the alcohol field:

• (a)In comparing different methods for missing value imputation in a longitudinal study, what are the differences in abstention rates and volume of alcohol consumed, when dropouts' alcohol consumption is imputed in two steps [i.e. (i) being an alcohol consumer, and (ii) the amount consumed among them]?
• (b)Can the unexpected recent finding of decreased consumption levels be explained by the differential dropout of more heavy users and/or by those who increased their alcohol consumption over the study period?

Types of missing data

Various types of missing data exist: missing completely at random (MCAR), missing at random (MAR), and missing not at random (MNAR). MCAR means that the missing data are not related to any other observed or unobserved variable. Often this assumption does not hold. If the assumption of MCAR were true, data analysis of fully observed cases would yield unbiased estimates although with lower precision. MAR means that the probability of missingness is related to observed data (e.g. socio‐demographics) but not to unobserved data; in other words missingness may differ across subgroups of the sample, but is random within these subgroups. MAR is the assumption for most imputation methods. MNAR means that the missings are related to the values in the missing variable. If MNAR is present in the data, it is complicated to impute valid values. Whether missing data are MAR or MNAR cannot be determined from the data but only by speculation. Only Heckman modelling accounts for MNAR; all other approaches which are discussed here assume MAR.

Multiple imputation

Missing data are unobserved and one cannot pretend to know the true values. Therefore single imputation methods are less appropriate because they underestimate the true variance in the data. In contrast multiple imputation methods lead to statistically more valid estimates that translate the uncertainty into the width of the confidence intervals assuming, of course, that the imputation model is correct (Kenward and Carpenter, 2007).

The typical steps to impute missing values in multiple imputation models are:

• (1)Generating plausible data values for the missing values and constructing a complete dataset.
• (2)Doing M repetitions of the first step to produce m different complete datasets.
• (3)Each of the m completed datasets will be analysed by standard statistical methods for the question of interest.
• (4)The last step is to pool the m estimates into one estimate, while combining the variation within and across the m imputed datasets (Rubin, 1987).

In this study we used multiple imputation methods for all different approaches except for LVCF where multiple imputation is not possible. Pooling of estimates was done on the basis of 10 imputed datasets.

Subjects and methods

Study design

Data come from a national survey of the Danish general population. The survey data are part of a larger study examining various effects of the tax and traveller allowance policy changes in Denmark, Sweden and Finland and details about the survey are reported elsewhere (Mäkela et al., 2008; Grittner and Bloomfield, 2009; Grittner et al., 2009).

The first of four waves was conducted in August and September 2003 before changes in availability took place, and 1771 persons, ages 16 to 69 years old, were interviewed. The cooperation rate for the 2003 (t ₀) sample was 49.6%. Respondents were re‐interviewed in 2004 (t ₁), 2005 (t ₂) and 2006 (t ₃). Over the four waves different patterns of non‐participation were possible: while some individuals participated in t ₀ only, others participated more than once or could be motivated to re‐participate after not having participated in one year (Table 1). A total of 634 persons were interviewed at all four time points.

Table 1.

Sample size and pattern of participation

Participated at	n	Percentage	t 0	t 1	t 2	t 3
t 0 only	283	16.0	X
t 0, t 1	316	17.8	X	X
t 0, t 2	79	4.5	X		X
t 0, t 3	49	2.8	X			X
t 0, t 1, t 2	238	13.4	X	X	X
t 0, t 1, t 3	59	3.3	X	X		X
t 0, t 2, t 3	113	6.4	X		X	X
All four waves	634	35.8	X	X	X	X
			1771	1247	1064	855

Measures

Respondents were first asked whether they were abstinent during the last 12 months. Alcohol consumption was measured by beverage‐specific quantity‐frequency questions. Quantity and frequency of alcohol consumption were multiplicatively combined for each beverage, converted into grams of pure ethanol and summed across beverages into VOLUME, indicating the average consumption per day. To estimate their frequency of risky single occasion drinking (RSOD) in days per year participants were also asked how often they drank alcohol to the equivalent of at least one bottle of wine, six bottles of beer or 12 small glasses of spirits. Due to non‐normality of the consumption variables FREQENCY, VOLUME and RSOD, logarithmic transformation was used to bring the distribution closer to normality.

As socio‐demographic variables participants' gender, age, education, household income, marital status, living situation (alone or not) and living in an urban or rural area were used. Household income was recoded into three categories each representing about a third of the sample. The participants' highest level of education was coded into primary or lower secondary level, upper secondary level and tertiary level (UNESCO Institute for Statistics, 1997). In all models only socio‐demographic variables at baseline were used.

Patterns of (non)participation

For the imputation of the missing values, the maximum of available information on drinking was used (Rubin, 1987). For those participating exclusively in t ₀ only this information could be used to estimate VOLUME in t _1, t ₂ or t ₃; while for those participating in t ₀, t ₁ and t ₃, the information from three measurements could be used to estimate VOLUME in t ₂. Thus for each of the three time‐points t ₁, t ₂ and t ₃ there are four different patterns for non‐participation (Table 1). For example for t ₁: a non‐participant at t ₁ could have participated (a) only at t ₀, (b) at t ₀ and t ₂, (c) at t ₀ and t ₃, or (d) at t ₀, t ₂ and t ₃.

Alcohol consumption among participants

Table 2 describes the percentage of abstainers [SOBER, 95% confidence interval (CI)] and the median, mean VOLUME (95% CI for mean) for the participants at the four time points. The percentage of abstainers is relatively low and lies between 4.0% and 5.5% (at t ₃ and t ₂, respectively). Median VOLUME (in grams of pure alcohol per day) decreased from 6.7 grams at t ₀ to 5.6 grams at t ₂ and then slightly increased by 0.3 grams at t ₃. Mean VOLUME lies between 10.8 grams and 11.9 grams (at t ₁ and t ₀, respectively). In summary, while only looking at the participants, alcohol consumption decreased over the study period but not in a linear manner.

Table 2.

Sample description: sample size, abstention rates (%) and median/mean VOLUME (pure alcohol in grams per day) among participants [95% confidence interval (CI) for means and proportions]

	Sample			SOBER	VOLUME (grams/day)
	n Participants	n Dropouts	Percentage dropouts	Percentage 95%CI	Median	Mean 95%CI
t 0	1771	0	—	5.1 4.2–6.2	6.7	11.9 11.1–12.7
t 1	1247	524	29.6	4.7 3.6–6.0	6.1	10.8 10.0–11.6
t 2	1064	707	39.9	5.5 4.3–7.1	5.6	11.6 9.9–13.3
t 3	855	916	51.7	4.0 2.9–5.5	5.9	11.0 10.0–12.1

Statistical analysis

Different approaches for missing value imputation

For every method except for LVCF we describe first the method in general and then the model for our example in detail.

LVCF

LVCF is the simplest ad hoc method. The last value was carried forward for those who dropped out. For those who could be recaptured after non‐participation, the mean VOLUME before and after the missing interval was used to estimate VOLUME (Engels and Diehr, 2003). LVCF has been criticised for several reasons (Carpenter and Kenward, 2007). It yields incorrect estimates for the variance and standard errors. The within‐subject variation is underestimated resulting in too small confidence intervals, p values and numerical problems. The strong underlying assumption is that the individual's behaviour and measurements do not change from the moment of dropout onwards or only change in a linear fashion if a missing value occurs between two measurements (Molenberghs et al., 2004). This implies that possible intervention effects are not considered. In most studies (including our survey on alcohol consumption) this assumption cannot be maintained. Particularly in the present study we expect changes in consumption levels due to increased availability of alcohol. Nevertheless we included this questionable and mostly misleading method for comparative purposes, as it is simple and is the only method not relying on distributional assumptions or regression based prediction of missing values.

Hotdeck

Introduction

Hotdeck means that a random draw from a subset of comparable cases is imputed for the missing cases. Hotdeck in contrast to “cold‐deck”, uses data for the imputation directly from the dataset with missing values whereas “cold‐deck” replaces missing values by values independent of the data set, e.g. population means. The advantage of Hotdeck is that an explicit model for the distribution of missing values is not needed and the imputations are based on observed values and will therefore not be outside the range of realistic values. Because of the simplicity of the Hotdeck approach and these desirable properties, it is a popular method of imputation, especially for large‐sample surveys where there is a large pool of data which can be used for the imputation (Siddique and Belin, 2008; Gmel, 2001).

To improve accuracy the sampling is weighted by using the propensity score of missingness (Mander and Clayton, 2003). Different methods are used for the imputation itself. Here an adapted form of the Approximate Bayesian Bootstrap method of Rubin and Schenker (1986) is used (Mander and Clayton, 2003).

Model

In the Hotdeck approach four models were used at each wave (t ₁, t ₂ and t ₃) to consider the different patterns of non‐participation. Missing values of SOBER and VOLUME were imputed in a single step by replacing the specific missing value among non‐participants by the observed values of participants who were similar on the variables SOBER, VOLUME, FREQUENCY and RSOD at all available observed waves and on the socio‐demographic variables. All models were calculated separately for men and women.

Heckman

Introduction

The Heckman method assumes a selection equation in addition to the regression equation. The selection equation estimates the probability that a dependent variable will be observed. Heckman's method accounts for MNAR (Heckman, 1979). His intention was not to create a model for missing value imputation but rather for regressions that account for non‐ignorable response mechanisms. The implemented tool in STATA is a single imputation method; however we created 10 different complete datasets by combining a multiple imputation method [predictive mean matching (PMM), see later] with the Heckman approach.

Model

To include the maximum of available information four separate models were used to estimate alcohol consumption at t ₁, t ₂ and t ₃. In the first step drinking status was estimated using a logistic model. Participants with an estimated probability to be an alcohol consumer greater than 0.5 were considered as alcohol consumers. In the second step the VOLUME was estimated with a linear model for those cases who presumably consumed alcohol in the specific wave. Abstainers (probability of being a consumer lower or equal than 0.5) were not included in this model, but were directly coded as having a VOLUME equal to zero.

In both steps the propensity to have an observed dependent variable (i.e. have participated at t_x) was regressed on SOBER and VOLUME for all available waves and socio‐demographic variables. SOBER for the non‐observed waves was estimated using the propensity to have participated, as well as SOBER and VOLUME from all available waves and age. The model to estimate VOLUME used the same variable as the models for SOBER and additionally FREQUENCY and RSOD. The models were estimated separately for women and men.

Multivariate imputation by chained equations (MICE)

Introduction

MICE is an approach that imputes data variable by variable. This means the imputation model is specified separately for each variable with missing values, while the other variables are predictors. For example, to impute missing values for variable y, first all missing values in the other variables will be filled in with randomly chosen values from these variables. Then the missing values in y are filled in using regression imputation with all other variables as predictors. The next step is to take another variable (z) with missing values and replace the previously imputed values in z using regression imputation with all other variables as predictors. This is done with all variables with missing values and is typically repeated 10 times to obtain convergence. This results in one complete dataset. The whole procedure must be repeated m times to obtain m complete datasets for multiple imputation.

The advantage of MICE is that no multivariate joint distribution assumption is necessary. MICE is very flexible in accounting for the data structure and different types of variables because the type of regression model depends on the variable being imputed. A problem might occur if the iteration procedure may not converge because the separate models are not compatible with a multivariate joint distribution (van Buuren and Oudshoorn, 1999; van Buuren, 2007).

Model

As MICE is a multivariate iterative regression model, no separate models were necessary to estimate alcohol consumption at t ₁, t ₂ and t ₃ or for different patterns of non‐participation. In the first step a logistic model was used to impute missings on SOBER at t_x using SOBER at all available waves and gender and age. (Separate models for women and men, or models using additional socio‐demographic variables led to very instable results).

For dropouts estimated to be sober at one of the waves, the missing value on VOLUME, FREQUENCY and RSOD were replaced by “0” for this specific wave. In the second step values for VOLUME were imputed with a linear regression model using SOBER (for participants observed drinking status, for dropouts estimated drinking status resulting from the first step of analyses was used), VOLUME, FREQUENCY and RSOD at all available waves and socio‐demographic variables. Abstainers at any wave were not excluded from the imputation sample as most of them were alcohol consumers at least at one of the waves.

Bayesian inference and Markov chain Monte Carlo methods (BUGS)

Introduction

This method assumes a Bayesian or full probability model, in which all quantities are treated as random variables. The imputation models were calculated with WinBUGS 1.4 (Lunn et al., 2000). BUGS stands for Bayesian inference using Gibbs sampling. The Bayesian inference focuses on the posterior distribution of the parameters and unobserved (missing) data. It is impossible to obtain inferences directly from the model by analytical evaluation. Therefore Markov Chain Monte Carlo (MCMC) methods are used to sample from the posterior distribution based on the construction of a Markov chain that has the target distribution as its stationary distribution (Spiegelhalter et al., 1999; Gilks, 1998). That means that simulated values are used for all unknown quantities and the state of the chain after a large number of steps is then used as a sample of the joint distribution. In contrast to the chained equations approach in MICE a full probability model is used where information about the distribution of the unknown parameters and the missing data is essential.

To run the model, starting values must be provided for all unobserved parameters and for the missing values. We used uninformative priors for our models. For simplicity reasons we call this method BUGS in the following text.

Model

As with the MICE approach BUGS uses one model for all observations to estimate SOBER and VOLUME for t ₁, t ₂ and t ₃. Each cycle had three steps. First the probabilities to be a consumer at t ₀, t ₁, t ₂, and t ₃ were estimated in four equations using the variable SOBER of preceding wave (except in the equation for SOBER at t ₀) and the socio‐demographic variables. Secondly, if the estimated probability was smaller than 0.5 for an individual in a specific wave, the person was considered to be an abstainer. If the estimated probability was greater than 0.5 the case was considered to be a drinker. In the third step, among drinkers, the values for VOLUME at t ₀, t ₁, t ₂ and t ₃ were estimated jointly in four equations using FREQUENCY, VOLUME and RSOD of the preceding years (except in the equation for VOLUME at t ₀), socio‐demographic variables and an individual intercept.

Models were estimated for men and women separately.

For simplicity and because FREQUENCY and RSOD were only predictors in the models, missing values on these two variables were not estimated separately but were imputed using the LVCF method.

Predictive mean matching (PMM) (Siddique and Belin, 2008)

In all models except LVCF we used predictive mean matching (PMM: Rubin, 1987; Little et al., 2008) to overcome the problem of back‐transformations. Thus, imputation models among drinkers used logarithmised VOLUME values but imputation of values did not use back‐transformations but non‐logarithmised values of donors, i.e. imputed consumption values of observed survey participants which were closest on observed values to the estimates of dropouts. All participants who had been used in the same prediction model were possible donors. Details on the implemented PMM‐method can be found in Siddique and Belin (2008).

Simulated missingness

To determine the differences between observed and imputed values of the different imputation methods, a simulated dataset was used. The basis for the simulation was the dataset from the 634 individuals who participated at all four waves. The missing data were then simulated by using sub‐samples and deleting values for SOBER and VOLUME in order to achieve the same missingness pattern as in the original dataset. Thus we tried to construct a dataset with the same percentage of missing values (30% at t ₁, 40% at t ₂, 50% at t ₃ with regard to baseline) as in the original dataset. Additionally the proportions of missing values in different subgroups which are defined by gender, age and VOLUME are comparable in the simulated dataset and in the original dataset.

Descriptive and inferential statistics

For all waves and all methods we calculated the proportion of abstainers (SOBER) (and 95% CIs), median and mean VOLUME (and 95% CIs for the mean) for dropouts as well as for the whole sample after imputation using the real data (Table 3). We also calculated the same measures for the dropouts with the simulated data (Tables 4 and 5).

Table 3.

Estimated abstention rates and estimated median/mean VOLUME (pure alcohol in grams per day, 95% CI for mean) for dropouts at t ₁, t ₂ and t ₃ and for the total sample (dropouts + participants)

		SOBER for dropouts	SOBER total	Estimated for dropouts		Total sample
		Percentage 95%CI	Percentage 95%CI	Median	Mean 95%CI	Median	Mean 95%CI
LVCF	t 1	5.3 3.7–7.6	4.9 3.9–6.0	6.6	12.4 10.3–14.6	6.3	11.3 10.4–12.1
	t 2	5.0 3.6–6.8	5.4 4.5–6.6	6.4	11.3 10.1–12.6	5.8	11.5 10.4–12.6
	t 3	5.9 4.5–7.6	5.0 4.1–6.1	5.6	11.8 10.0–13.6	5.8	11.4 10.4–12.5
Hotdeck	t 1	4.8 3.6–6.9	4.7 3.8–5.8	5.8	10.0 8.4–11.6	6.0	10.6 9.8–11.3
	t 2	5.0 3.6–6.4	5.3 4.6–6.0	5.5	11.1 8.8–13.4	5.6	11.4 10.0–12.8
	t3	3.6 2.2–5.1	3.8 3.0–4.6	5.8	10.9 9.4–12.4	5.9	10.9 10.0–11.9
Heckman	t 1	6.1 4.4–8.5	5.1 4.2–6.2	5.6	10.7 9.2–12.2	5.9	10.8 10.1–11.5
	t 2	3.4 2.3–5.0	4.7 3.8–5.8	5.2	11.0 8.4–13.5	5.5	11.4 9.9–12.8
	t 3	6.3 4.9–8.1	5.2 4.3–6.3	5.5	10.9 9.7–12.1	5.7	11.0 10.1–11.8
MICE	t 1	5.3 1.5–9.2	4.9 3.7–6.0	5.5	10.7 9.1–12.3	5.9	10.8 10.1–11.5
	t 2	4.5 0.9–8.1	5.1 3.6–6.6	5.3	10.9 8.0–13.7	5.5	11.3 9.8–12.8
	t 3	4.3 2.5–6.1	4.1 3.2–5.1	5.5	11.5 10.1–12.9	5.7	11.3 10.4–12.1
BUGS	t 1	3.3 2.6–4.0	4.2 3.8–4.7	5.7	10.4 9.2–11.7	6.1	10.7 10.0–11.4
	t 2	6.5 5.4–7.7	6.0 5.4–6.7	5.4	10.1 8.9–11.4	5.6	11.0 9.9–12.2
	t 3	4.5 3.9–5.0	4.2 3.8–4.7	5.7	10.7 9.7–11.7	5.8	10.8 10.1–11.6

Table 4.

Median/mean VOLUME and 95%CI for mean for true and estimated VOLUME for “dropouts” in the simulation (test estimated versus true values)

	t 1 (n = 188)			t 2 (n = 253)			t 3 (n = 328)
	Median	Mean 95%CI	Precision1	Median	Mean 95%CI	Precision1	Median	Mean 95%CI	Precision1
True	5.8	12.2 9.6–14.9	—	5.9	10.7 8.9–12.4	—	5.8	11.7 9.7–13.7	—
LVCF	7.7	13.7 10.3–17.2	=	6.6	10.8 9.3–12.3	=	6.5	13.2 10.1–16.4	=
Hotdeck	6.2	9.5 7.3–11.7	≠	5.5	9.2 7.3–11.1	≠	5.4	8.9 7.4–10.5	≠
Heckman	6.2	11.1 9.4–12.9	=	4.1	8.6 7.3–9.9	≠	5.3	9.1 7.9–10.3	≠
MICE	6.8	11.4 9.1–13.6	≠	6.1	13.2 7.7–18.8	≠	7.3	10.9 9.1–12.7	≠
BUGS	7.1	11.4 9.5–13.2	=	6.5	10.3 8.6–12.0	=	6.9	11.4 10.0–12.8	=

It was checked if the absolute value of the mean difference between estimated log volume and true log volume was lower than 0.6 (=) or not (≠).

Table 5.

Percentages of abstainers and 95%CI for true and estimated drinking status for “dropouts” in the simulation

	t1 (n = 188)		t2 (n = 253)		t3 (n = 328)
	Percentage 95%CI	Precisiona	Percentage 95%CI	Precisiona	Percentage 95%CI	Precisiona
True	4.3	—	4.3	—	3.7	—
	2.2–8.2		2.4–7.6		2.1–6.3
LVCF	3.2	=	2.8	=	5.2	=
	1.5–6.8		1.3–5.6		3.3–8.1
Hotdeck	4.8	≠	4.3	≠	2.9	≠
	1.3–8.3		2.2–6.4		0.6–5.2
Heckman	4.8	=	2.4	=	7.3	≠
	2.5–8.8		1.1–5.1		5.0–10.7
MICE	4.6	=	2.7	=	3.5	=
	3.1–6.1		1.0–4.4		0–7.4
BUGS	4.5	=	5.1	=	3.1	=
	3.6–5.3		3.9–6.4		2.5–3.7

^aIt was checked if more than 5% of people were misclassified (≠) compared to true value or not (=).

Using the different methods we compared mean VOLUME for the true values and the imputed values based on the simulated data only for those with missing values (“dropouts”) (Table 4). On the basis of logarithmised VOLUME we examined whether the absolute value of the mean difference was lower than 0.6 (which corresponds to 0.8 grams of pure alcohol per day). The aim was to identify the imputation method with the closest estimate for mean VOLUME and similar confidence intervals as for the true values. To test whether the bias of estimates depends on the consumption level we examined additionally abstainers and different consumption groups separately. We thus divided the group of consumers into five equal‐sized subgroups (Figure 1). We also compared rates of abstention (SOBER) among dropouts for the different methods and examined whether more than 5% of the respondents were misclassified with regard to the true drinking status (Table 5).

Figure 1.

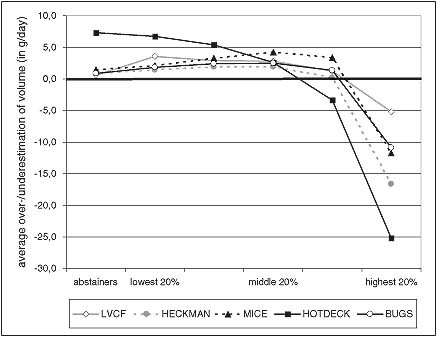
Average bias in the estimated VOLUME according to true (observed) VOLUME: abstainers and quintiles of consumers, simulated data (pooled results for t ₁, t ₂ and t ₃).

For the participants and with each imputation model after imputation of missing values we analysed time trends with linear mixed models and logarithmised VOLUME as the outcome (Table 6). We coded time as –1.5 for 2003, –0.5 for 2004, 0.5 for 2005 and 1.5 for 2006 and included a quadratic term to distinguish between linear and non‐linear time trends. We used a model with random intercept and random slope for time to allow variation between individuals with regard to general consumption level and time trends. We used Rubin's rules (Rubin, 1987) in combining estimates from the multiple imputed datasets.

Table 6.

Time trends over four time points for logarithmised VOLUME for participants and different multiple imputed datasets, random intercept and slope, beta

	n (individuals/observed)	Fixed part			Random part: variance between individuals
		Intercept	Time	Time squared	Intercept	Slope (time)	Covariance intercept and slope
Participants	1771/4937	1.88***	−0.02**	0.02**	0.97***	0.03***	0.006
LVCF	1771/7084	1.91***	−0.02**	0.01*	1.08***	0.03	0.015*
Hotdeck	1771/7084	1.88***	−0.02*	0.02*	0.57***	0.05**	−0.029**
Heckman	1771/7084	1.87***	−0.03***	0.02*	0.95***	0.02***	−0.008
MICE	1771/7084	1.87***	−0.03***	0.02*	0.95***	0.02***	0.006
BUGS	1771/7084	1.88***	−0.02***	0.02***	1.00***	0.01***	−0.003

^* p < 0.05.

^** p < 0.001.

^*** p < 0.0001.

Results

Real data

Table 3 displays estimated VOLUMES for dropouts and for the total sample (participants and non‐participants) at t ₁, t ₂ and t ₃ for the different imputation methods. Independent of the imputation approach a decrease in alcohol consumption over time can be found for the total sample when looking at all four time points (see t ₀ in Table 2). The difference between estimates of different methods for the dropouts was between 2.4 grams per day in t ₁ and 1.1 grams in t ₃ with regard to mean VOLUME.

After inclusion of imputed values, all estimates of consumption levels followed the development in consumption levels of participants only (Tables 2 and 3), namely a decrease to t ₁ and an increase from t ₁ to t ₂ and again a decrease from t ₂ to t ₃ (Table 3). In none of the models did VOLUME for the total sample in the follow‐up‐waves exceed that of t ₀. However, methods differed in imputed values. Over all three imputed waves, LVCF imputed the highest mean value for dropouts (12.4, 11.3, 11.8 grams of pure alcohol per day), whereas BUGS the lowest (10.4, 10.1, 10.7 grams of pure alcohol per day).

Abstention rates ranged between 3.3% and 6.5% for the dropouts and between 4.1% and 6.0% for the total sample with regard to all methods and all time points (Table 3). The largest difference in estimated rates of abstention for dropouts was 3.1% between BUGS (6.5%) and Heckman (3.4%) at t ₂ whereas at t ₁ Heckman estimated the highest rate of abstention (6.1%) and BUGS estimated the lowest rate (3.3%).

Table 6 displays the results from the linear regression models with random effects for participants only as well as for the imputed datasets after using different models of imputation. For all models there is a significant downward trend of VOLUME over time. All methods showed that this trend is non‐linear as indicated by the significant quadratic term for time. VOLUME decreased more in the beginning of the study than in the end. For all models the variance between individuals with regard to overall consumption levels (intercept) was significant, but models differed with regard to the extent of variation between individuals. Also the differences between individuals with regard to time trends were significant in almost all models (slope) with the exception of LVCF. There was a significant correlation between overall consumption levels and the consumption change over time only for LVCF and Hotdeck but in different directions.

Simulation

The results for the simulation are displayed in Tables 4 and 5 which show more clearly the different results: The Heckman and MICE approaches estimated an average VOLUME difference of 4.6 grams per day in t ₂ which corresponds to 1.3 litres of pure alcohol per year. For t ₁ the true value was outside the 95% CI of the Hotdeck estimate. For t ₂ this was true for the Heckman estimate. For t ₃ both Heckman and Hotdeck lead to estimates and CIs that did not include the true value. LVCF overestimated the values at all time points with a difference of 1.5 grams at t ₁ and t ₃. MICE overestimated the volume at t ₂ by 2.5 grams. All other methods underestimated VOLUME among dropouts. BUGS produced the closest estimates for t ₁ and t ₃ and a difference of 0.4 grams to the true value at t ₂. Table 4 again shows that the average bias (overestimation, underestimation) is relatively low for the BUGS estimates. This is also confirmed by the comparisons of true and estimated VOLUME measures on the individual level. The mean absolute difference between estimated logarithmised VOLUME and true logarithmised VOLUME was lower than 0.6 for BUGS and LVCF at all time points and for Heckman at t ₁.

For all approaches bias is dependent on the consumption level: consumption at low levels is overestimated while all approaches underestimate consumption for the highest quintile (Figure 1). The least underestimation among the highest 20% consumers is found for LVCF – LVCF is least affected by “regression to the mean” as it is the only method that does not rely on a regression‐approach. BUGS provides the second best estimates for high consumers.

In comparing abstention rates BUGS has the closest value at t ₁, Hotdeck at t ₂ and MICE at t ₃ (Table 5). But the picture differs at the individual level. Hotdeck misclassified more than 5% of people at all time points, Heckman only at t ₃. All other methods have misclassification rates lower than 5%.

Discussion

It is important to distinguish between the statistical and the public health implications of the present research. Different imputation methods have produced different imputed values. Hence, it seems reasonable to suggest for future studies the use of different imputation methods to gain insight into the variability of different methods, and thereby obtain an upper and lower bound of what imputation may achieve to correct for dropouts (Carpenter and Kenward, 2007).

In the present study as regards public health relevance, the conclusion would be at least two‐fold:

• (a)Consumption of respondents at follow‐up is underestimated due to non‐respondents;
• (b)None of the imputation methods would change the substantive interpretation of recent findings that the increase of alcohol availability in Denmark did not result in an increase in consumption levels.

Our simulation study showed that – besides the Bayesian approach (BUGS) – estimates of consumption levels for dropouts may result with most methods in a bias at some point in time. However, the BUGS approach like Hotdeck imputation and Heckman modelling consistently underestimated at all time points the “true values”, but the variability in underestimation/overestimation was lowest for the BUGS approach. Nevertheless it appears that none of the models, and even not those that could be estimated with more complex programs, which in turn are not easily available or easy to use, has been sufficiently capable to capture the complicated measurement of alcohol consumption, with its two estimation stages for (a) drinking status and (b) amount among drinkers. The complexity for estimating non‐response on alcohol consumption is increased by having a skewed and censored distribution among drinkers, outliers with very heavy consumption values, and also the unreliability of alcohol consumption measures which result in problems such as regression to the mean bias, and the use of transformations of measures (logarithms), back‐transformations or predictive mean matching.

In particular it appeared that all methods underestimate imputed values of the heaviest drinkers, those who are the main target of preventive actions. This bias is particularly strong for Hotdeck imputation where individuals remaining in the sample where used as donors for imputed values. Thus if the heavier drinkers in particular drop out, there may not be adequate values to be donated.

Despite all efforts at missing value imputation, we cannot rule out the possibility that the recent research findings (showing no increase in levels of consumption in Denmark while prices decreased and availability increased) may still be due to a lack of reliably and validly imputed values for heavy drinkers who are commonly more likely to drop out of survey research (Thygesen et al., 2008; Stappenbeck and Fromme, 2010). Other procedures such as parametric models using e.g. the gamma distribution for alcohol volume (Rehm et al., 2010) may have estimated an increase in alcohol use. This is, however, unlikely given that none of the models used was able to change the trend among respondents. The present study has shown that despite recent significant advances in imputation methods, the treatment of variables that are more complex, non‐normal and censored, such as volume of alcohol consumption, is not yet adequate regarding the problem of dropouts. Testing of current approaches does not unanimously reveal the best method to be used, and therefore further comparative studies using different approaches are needed. Nonetheless, the present study suggests that a Bayesian two‐stage imputation (for abstainers and volume among drinkers) to be one of the better options.

Declaration of interest statement

The authors have no competing interests.