Atomistic simulations reveal bubbles, kinks and wrinkles in supercoiled DNA

Abstract

Although DNA is frequently bent and supercoiled in the cell, much of the available information on DNA structure at the atomistic level is restricted to short linear sequences. We report atomistic molecular dynamics (MD) simulations of a series of DNA minicircles containing between 65 and 110 bp which we compare with a recent biochemical study of structural distortions in these tight DNA loops. We have observed a wealth of non-canonical DNA structures such as kinks, denaturation bubbles and wrinkled conformations that form in response to bending and torsional stress. The simulations show that bending alone is sufficient to induce the formation of kinks in circles containing only 65 bp, but we did not observe any defects in simulations of larger torsionally relaxed circles containing 110 bp over the same MD timescales. We also observed that under-winding in minicircles ranging in size from 65 to 110 bp leads to the formation of single stranded bubbles and wrinkles. These calculations are used to assess the ability of atomistic MD simulations to determine the structure of bent and supercoiled DNA.

INTRODUCTION

DNA rarely exists as a relaxed linear molecule in the cell. Eukaryotic DNA is condensed into chromatin, which is made up of units of 146 bp of DNA wrapped 1.6 times around each histone octamer to form the nucleosome complex (1). Prokaryotes store their DNA as negatively supercoiled plectonemes bound to nucleoid associated proteins (NAPs) (2). The torsional stress in a supercoiled DNA loop is distributed between untwisting and writhing, with conversion between the two being crucial for genetic regulation (2). Untwisting facilitates strand separation and generally (but not always) promotes transcription. Writhe, which requires bending, increases compaction. Local structural changes, such as bending and twisting of the DNA, are also required for the formation of many protein–DNA complexes (3,4), including the 434 repressor/operator complex (5) and the CAP–DNA complex (6). On slightly longer length scales, DNA loops containing ∼100 bp are formed by protein binding at two separate locations in regulatory complexes such as with the Lac repressor (7–10). However, due to the experimental difficulties inherent in studying the structure of supercoiled DNA at the atomic level, far less is known about bent and twisted DNA molecules than their linear counterparts. We have used molecular dynamics (MD) simulations to obtain an atomistic level description of the structure of bent and twisted DNA, which we then validate by comparison with a recent experimental study of DNA minicircles.

Small DNA loops provide an ideal experimental system for investigating torsional and bending stress in DNA. The bending stress is determined by the loop size, whereas the torsional stress is governed by the superhelical density:

The superhelical stress (σ) within a given DNA loop can be controlled by varying the linking number (Lk), where Lk is the topological quantity that defines how many times the backbone strands are wrapped around each other. Lk₀ is the linking number of a torsionally relaxed DNA molecule of a given length and is simply the number of base pairs divided by the helical repeat. Although Lk must be an integer, this is not the case for Lk₀, hence ΔLk can take non-integral values. Topoisomers are circles that differ only in their linking number. The levels of superhelical stress in bacteria such as Escherichia coli have been measured to be around σ = –0.06 (2,11), but can transiently be of far high magnitude due to transcription, which generates positive and negative supercoils in front of and behind the transcription complex, respectively (12).

There have been a number of recent experimental studies of the mechanics of DNA minicircles. To study the energy associated with bending DNA into very tight loops, Cloutier and Widom (13) measured the cyclization rates of 94 bp fragments. They measured cyclization rates 10²–10⁴-fold greater than predicted by an elastic rod model for random sequences and 10⁵-fold greater for nucleosome positioning sequences. A number of theoretical and numerical studies explained the relative ease of deformation by modifying the elastic model to include disruptions of the helical structure (14–16) and sequence effects (17). Additional experimental evidence supporting the increased flexibility of DNA has been obtained using molecular force sensors (18), fluorescence energy transfer (19) and atomic force microscopy (20). One hypothesis to explain the cyclization data was that local disruptions in the form of kinks absorb much of the curvature required to form a sharp bend. A pioneering MD study of these 94 bp circles did indeed detect two types of kinks; in type I kinks the DNA is bent between two intact base pairs, whereas in type II kinks the bend is over 3 bp and the central base pair is broken (21). However, this study used an older version of the AMBER force field, which can introduce artefacts over long simulation timescales (22). Using an updated force field kinks were only induced at a bend equivalent to that found in 45 bp circles (23). Du et al. (24) have contested the Cloutier and Widom results and set a threshold for the appearance of kinks on circles of size <84 bp (25). Similarly, a cryo-electron microscopy study of the Cloutier and Widom 94 bp circles showed an absence of kinks; their resistance to treatment with the BAL 31 endonuclease, which is thought to digest distorted DNA, also indicated that kinks are not present in this sequence (26).

To perform a systematic analysis of structural disruptions due to bending and torsional stress, Du et al. (25) constructed a series of DNA topoisomers containing between 63 bp and 205 bp and monitored their reaction with the single strand specific endonucleases BAL31 and S1. They proposed that BAL 31 is capable of digesting disruptions where base pairs remain intact, e.g. type I kinks, while S1 requires broken base pairs to digest the DNA. They found that the relaxed 63 bp loops circles were slowly digested by BAL 31, but not by the less sensitive S1 endonuclease; however, the 84 and 106 bp circles were not digested by either enzyme. They concluded that bending stress alone was sufficient to cause disruptions in 63–65 bp but not in 84 bp or 106 bp circles. The slow speed of digestion by the sensitive BAL 31 enzyme implies that these disruptions due to bending stress are relatively minor and a subsequent Monte Carlo study suggested that they occur in only a fraction of the sample (27). The results for the supercoiled minicircles were very different. The under-wound (ΔLk = −1) 63 bp circles were rapidly digested by both nucleases, indicating that the disruptions involve single-stranded regions of DNA. The ΔLk = −0.5 under-wound 100 bp loop was also digested, but the larger 200 bp ΔLk = −0.5 under-wound loop was not. These experiments set the lower limit for the levels of bending and superhelical stress required to denature DNA loops, noting that the sequences investigated were chosen so as not contain any active biological elements such as transcription initiation sites.

To identify and characterize the various disruptions caused by bending and twisting stress at the atomistic level, we have performed extensive MD simulations of a key selection of the Du et al. DNA minicircles. Focusing on the threshold required for the appearance of disruptions, we have studied different topoisomers of 65, 104 and 110 bp circles. As well as showing the nature of these DNA disruptions in atomistic detail, which is not available by any means other than computer simulation, these calculations aim to quantify the accuracy of MD calculations performed over the nanosecond timescale for measuring the response of DNA to superhelical and bending stress by directly comparing the simulations with the experimental data available.

MATERIALS AND METHODS

Choice of sequences and circle sizes

The sequences in our simulations are equivalent to those used in the experimental work of Du et al., and are provided as Supplementary Data. These sequences have an AT content close to 50%, they contain no strong intrinsic curvature (e.g. no A-tracts) and all possible 10 dinucleotides are represented in each circle. DNA disruptions are known to be extremely sensitive to twist; therefore, it is essential that the superhelical density is the same in the calculations as in the experiments. To correct for the known underestimation of relaxed DNA twist in the AMBER force field [∼33° compared to ∼34° (28)] we extended the 63 bp sequence by 2 bp and simulated 65 bp loops. Although this slightly decreased the curvature, the torsional stress is approximately zero in the simulations of the 65 bp minicircle with Lk = 6. All larger sequences were extended to correct the superhelical density in an equivalent manner.

The DNA structures were started as planar circles with the twist uniformly distributed between each base pair step (Figure 1). Repeat simulations were run with variation only in starting register (as defined below). Three 65 bp topoisomers (Lk = 5,6 and 7) were investigated; under-wound ΔLk = −1 minicircles [simulations 65A⁽⁻¹⁾ and 65B⁽⁻¹⁾], relaxed minicircles [simulations 65A⁽⁰⁾, 65B⁽⁰⁾, 65C⁽⁰⁾ and 65D⁽⁰⁾] and over-wound ΔLk = +1 minicircles [simulations 65A⁽⁺¹⁾ and 65B⁽⁺¹⁾]. Simulations of under-wound ΔLk = −0.5 (Lk = 9) 104 bp minicircles [simulations 104A^(−0.5) and 104B^(−0.5)] and relaxed (Lk = 10) 110 bp loops [simulations 110A⁽⁰⁾ and 110B⁽⁰⁾] were also performed. In addition, more strongly under-wound ΔLk = −1 and −1.5 topoisomers of the larger circles were also run [simulations 110A⁽⁻¹⁾ and 104A^(−1.5)]. A summary of the simulations and their abbreviated names can be found in Table 1.

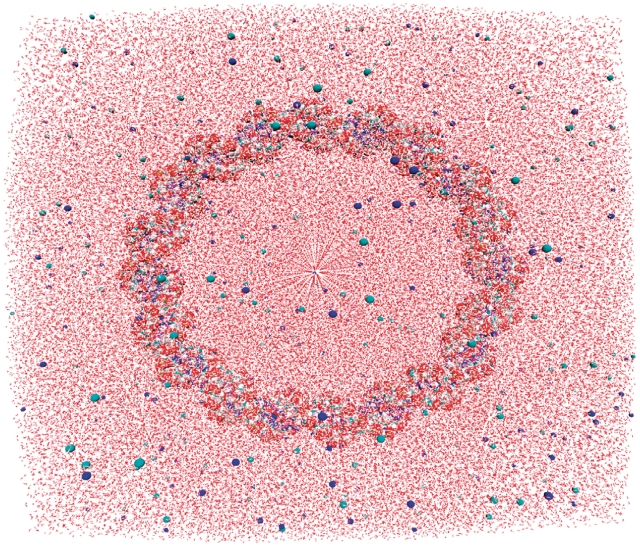
Figure 1.

An explicitly solvated starting structure (110 bp, 0.1 mol NaCl) showing the DNA and counter ions in a space filling representation.

Table 1.

A summary of the MD simulations performed and the structural disruptions that appeared

Simulation	Length (bp)	Lk (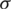)	Simulation Time (ns)	Disruptions	Digested by Endonuclease
65A(−1)	65	5 (−0.16)	55.0	Under-wound bubbles	BAL 31 and S1
65B(−1)	65	5 (−0.16)	19.6	Under-wound bubbles and wrinkle	BAL 31 and S1
65A(0)	65	6 (0.01)	57.5	None	BAL 31 slowly
65B(0)	65	6 (0.01)	52.9	Type II kink	BAL 31 slowly
65C(0)	65	6 (0.01)	51.9	Types I and II kinks	BAL 31 slowly
65D(0)	65	6 (0.01)	50.3	None	BAL 31 slowly
65A(+1)	65	7 (0.18)	58.7	Kink and bubble	NA
65B(+1)	65	7 (0.18)	18.7	Kink and bubble	NA
104A(−1.5)	104	8 (−0.16)	8.6	Under-wound bubbles and wrinkle	NA
104A(−0.5)	104	9 (−0.05)	51.3	None	BAL 31 quickly and S1 slowly
104B(−0.5)	104	9 (−0.05)	50.3	Wrinkle	BAL 31 quickly and S1 slowly
110A(−1)	110	9 (−0.10)	8.0	Under-wound kink	NA
110A(0)	110	10 (0)	52.1	None	Neither
110B(0)	110	10 (0)	50.2	None	Neither

Each simulation is named according to the number of base pairs in the minicircle and its ΔLk value (bracketed superscript), with the letter (A, B, C or D) indicating repeated simulations. The final column indicates whether the minicircles were digested by the endonucleases BAL 31 and S1 as reported by Du et al. (25).

Construction of circles and simulations protocols

Linear starting structures were built using the NUCGEN module in AMBER 10. DNA loops with a specific linking number were then constructed using an in-house program which translates and rotates the base pairs as rigid bodies into a circular arrangement (29). Sodium (Na⁺) counter ions (i.e. one per nucleotide) were added using the xLEAP module in AMBER to neutralize the system based on a coulomb potential grid. The circles were solvated with the TIP3P water model in a truncated octahedron box with a 35 Å buffer. To provide the same ionic strength as was used in the experiments, enough Na⁺ and Cl⁻ ions were randomly placed to give a salt concentration of 0.1 mol. The exact number of water molecules and ions added to solvate each structure is provided in Supplementary Table S1. All simulations were run using the AMBER 10 MD package (30). The Cornell et al. (31) PARM94 force field with PARMM99 and PARMBSC0 modifications was used throughout (22,32). The ion parameters developed recently by Cheatham et al. were employed to avoid unnatural salt crystallization (33). Minimization and heating was carried out in the multi-stage protocol developed for DNA triplexes (34) and later modified for DNA circles (29). For the production run, a constant temperature (300 K) was maintained using the Berendsen weak coupling scheme (with a coupling constant of 1 ps) and constant pressure (1 atm) by volume scaling (using a coupling constant of 0.2 ps). The long-range electrostatics interactions were treated with the particle mesh Ewald summation method. The SHAKE algorithm was used to constrain the stretching freedom of covalent bonds involving hydrogen, allowing a 2 fs time step to be used without comprising the stability of the numerical integration of the trajectory. Conformations were recorded and analysed every 1 ps. Production runs were extended to >50 ns, except where stated, in accordance with the timescale required for disruptions to appear in previous studies (21,29).

Analysis of MD trajectories

PyMOL and VMD were used to visualize the trajectories (35,36). Dihedral angles and Watson–Crick hydrogen bond distances were measured using the AMBER program PTRAJ. Hydrogen bond distances were measured between the adenine N1 and thymine H3 atoms for A:T pairs and between the guanine H1 and cytosine N3 atoms for G:C pairs. Energetic analysis was carried out using the AMBER implementation of the GB/SA method as described in our previous work (37). Base pair and base pair step parameters were determined using 3DNA (38); base pair step bending angles were defined as the angle between the 3DNA calculated base pair planes. 3DNA was also used to define the helical axis as a series of position vectors representing the base pair centres. The writhe of each snapshot was calculated by employing the directional writhe method (39) implemented using in-house code. In this method the helical axis is viewed from multiple angles and the crossover points assigned a value of −1 or +1 depending on their direction; the writhe is then the average over all possible viewing angles. We found good convergence after 10 000 randomly selected angles (Supplementary Figure S1). The writhe was also calculated by approximating the gauss integral for writhe as a summation:

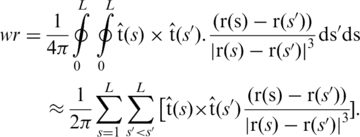r(s) defines the helical axis of length L, and tangent t(s). The two methods were found to give similar values (Supplementary Figure S2). Ion densities were calculated as spatial histograms using PTRAJ (from a trajectory rms fitted to the DNA structure), and were visualized as isodensity surfaces with VMD.

The register of the circle defines at which point along the sequence a particular face (e.g. minor groove) points towards the inside of the circle. To analyse the register, we calculated an angle that defines the direction of the minor groove in relation to the plane of the circle. Three base pair centres equally spaced along the circle define the plane. The final register is an average over multiple sets of base pair defined planes. We calculate the register to be the angle between the minor groove and the plane normal, where the minor groove direction has been obtained using 3DNA. Angles of 0–180° point in towards the centre of the circle and angles of 180–360° point outwards, with 90° showing perfect alignment between the minor groove and the inside of the circle. The starting register alignment for all simulations is provided as Supplementary Information.

RESULTS

Kinks form in torsionally relaxed 65 bp circles

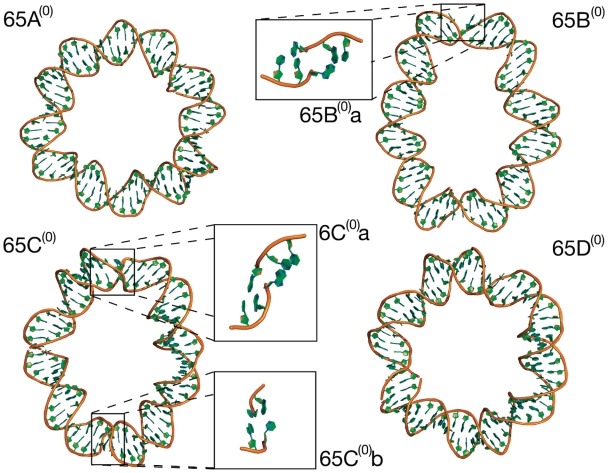
Figure 2 shows the final molecular structures obtained for the four relaxed 65 bp circle simulations. The tertiary structures remain planar and non-writhed but the circles display varying degrees of ellipticity, which indicates the formation of DNA kinks in response to the bending stress. Where there are no structural disruptions [circles 65A⁽⁰⁾ and 65D⁽⁰⁾] the loops most closely resemble circles. Kinks can be visually identified in cases 65B⁽⁰⁾ and 65C⁽⁰⁾ as short regions of high curvature. These have been highlighted and enlarged in Figure 2. The kinks distort the loops into ellipses by introducing non-continuous curvature. The appearance of disruptions is stochastic in that the number of kinks and their locations are different in otherwise equivalent simulations: 65B⁽⁰⁾ kinks once, 65C⁽⁰⁾ kinks twice (at opposite points in the loop), whereas 65A⁽⁰⁾ and 65D⁽⁰⁾ do not contain any kinks after 50 ns of MD.

Figure 2.

Final frame (>50 ns MD) molecular structures of the four torsionally relaxed 65 bp simulations. In simulations 65A⁽⁰⁾ and 65D⁽⁰⁾ the secondary structure remains intact and they closely resemble circles. Loops 65B⁽⁰⁾ and 65C⁽⁰⁾ deform into an elliptical shape due to kinks; in both 65B⁽⁰⁾ and 65C⁽⁰⁾ type II kinks occur [65B⁽⁰⁾a and 65C⁽⁰⁾a] and additionally in 65C⁽⁰⁾ a type I kink [65C⁽⁰⁾b].

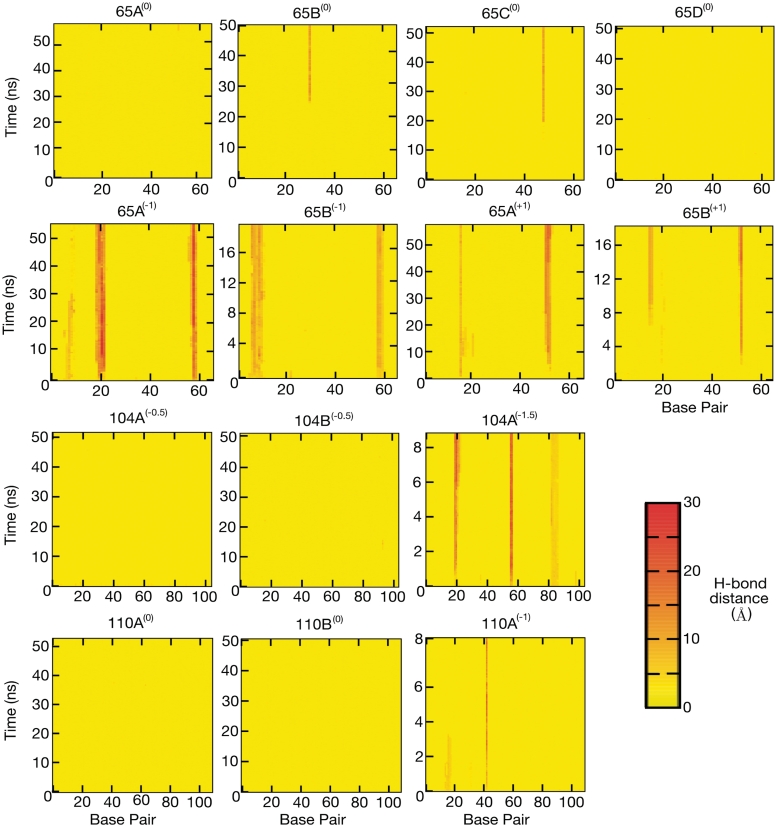
To determine whether these disruptions contain single-stranded regions, we measured the hydrogen bond distances between complementary base pairs, as shown in Figure 3. Simulations 65A⁽⁰⁾ and 65D⁽⁰⁾ remain intact while a single broken base pair develops in simulations 65B⁽⁰⁾ and 65C⁽⁰⁾. The broken bases appear after ∼25 ns in circle 65B⁽⁰⁾ and after ∼20 ns in circle 65C⁽⁰⁾, and remain until the end of the simulation (>50 ns). Both are associated with visually identifiable kinks. However, there is no evidence for a second broken base in circle 65C⁽⁰⁾, even though two kinks can be visually identified.

Figure 3.

2D colour plots showing the Watson–Crick base pair hydrogen bond distances. (Row 1) The torsionally relaxed 65 bp loops. In two out of four simulations a single base pair break occurs that is associated with a type II kink. (Row 2) Under [65A⁽⁻¹⁾ and 65B⁽⁻¹⁾] and over [65A⁽⁺¹⁾ and 65B⁽⁺¹⁾] wound 65 bp loops. In all simulations severe denaturation develops in localised regions. (Row 3) 104 bp loops. Only in the more severely under-wound loop [104A^(−1.5)] does denaturation occur. (Row 4) 110 bp loops. Denaturation develops in the under-wound loop [110A⁽⁻¹⁾].

To characterize these kinks in more detail, the base pair and base step parameters were calculated. The denatured base pair observed in simulation 65B⁽⁰⁾ is equivalent to the type II kink described by Lankas et al.; it contains a sharp bend over three consecutive base pairs of sequence d(CTA) with the central T:A base pair broken. The central pair has large propeller twist allowing the separated bases to remain stacked with opposite strands (corresponding 5′-end). The bend is dominated by large negative roll (Table 2). One of the two kinks observed in simulation 65C⁽⁰⁾ is also type II, whereas the second corresponds to a type I kink previously observed by Lankas et al. The type I kinks occurs between the two intact base pairs d(GC) and is again dominated by large negative roll. The type II kinks are associated with an increased ion density flanking the denatured DNA base, as shown in Supplementary Figure S3. Table 2 summarizes the disruptions and gives details of their sequence and curvature.

Table 2.

The sequence motifs associated with each defect

Simulation	Disruption type	Sequence	Bend	Roll
65A(−1)	Bubble	GCTATC
65A(−1)	Bubble	AGGTG
65B(−1)	Bubble	GTGCAAT
65B(−1)	Bubble	GATAT
65B(−1)	Wrinkle	T C_T T_A T
65B(0)	Type II kink	CTA	80°	−76°
65C(0)	Type II kink	CAA	85°	−81°
65C(0)	Type I kink	GC	95°	−92°
65A(+1)	Bubble	CAATG
65A(+1)	Type II kink	CAA	67°	−64°
65B(+1)	Bubble	TATC
65B(+1)	Type II kink (Bubble)	GGTG	108°	−102°
104A(−1.5)	Bubble	CGAACAA
104A(−1.5)	Bubble	TATC
104A(−1.5)	Wrinkle	C A_G G
104B(−0.5)	Wrinkle	T C_A_G G
110A(−1)	Type II kink	TCG	114°

For defects involving broken base pairs, the identity of the intact base pair either side of the denatured region is also provided. For wrinkled sequences the under-wound steps have been indicated by underlining. Bending and roll angles are listed for the kink defects where appropriate.

Bending in all three kinks is dominated by negative roll; the minor groove closes and the major groove opens. Therefore, only when the minor groove is on the inside of the circle (i.e. a register of 90°) does the appearance of a kink absorb the greatest fraction of the circles curvature. Supplementary Figure S4 shows the register of the three kinks and indicates where they develop. The kink register was calculated as the average between intact base pairs on each side of the disruption. Initially, the register exhibits large fluctuations, but the kinks always form when the register is close to 90°. Once formed, the kinks stabilize not only their own register but also of all other base pairs in the circle, as reported previously by Lankas et al. We do not expect the likelihood of defect formation to depend on the initial register of the circles for these random sequences. If, for example, the minicircles contained phased A-tract sequences, which are associated with a directional DNA curvature, then the register of the circles would be expected to be important. For the simulations, we have performed kink formation is observed to be independent of the starting register. For example, while 65A⁽⁰⁾ forms no defects, 65C⁽⁰⁾ (which starts with a register difference of only 33°) forms kinks. Simulations 65D⁽⁰⁾ and 65B⁽⁰⁾ start with a register difference of approximately one-half helical turn from these two, but only 33° apart from each other. Despite the small difference in starting register 65B⁽⁰⁾ develops a kink while 65D⁽⁰⁾ does not.

Structural disruptions occur in all supercoiled 65 bp circles

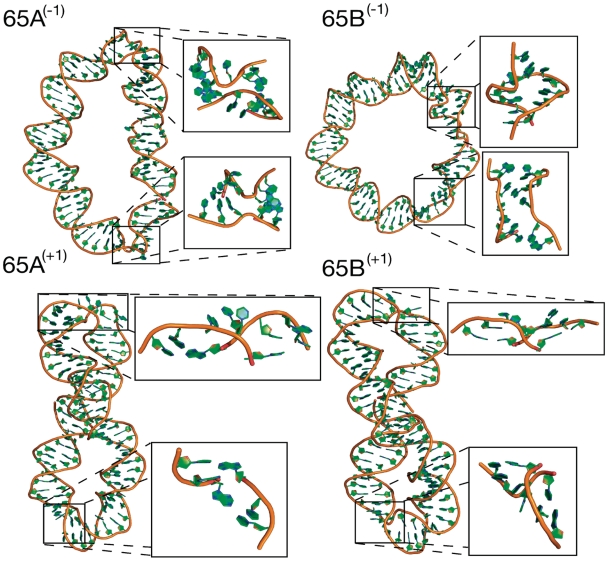
Unlike the stochastic nature of kink formation, structural deformations appear right from the start of each simulation for all the supercoiled 65bp circles. The final structures obtained from the two under [65A⁽⁻¹⁾ and 65B⁽⁻¹⁾] and two over-wound [65A⁽⁺¹⁾ and 65B⁽⁺¹⁾] DNA circle simulations are shown in Figure 4. There is a distinct difference in the global structures of the two topoisomers. The under-wound loops are strongly elliptical but remain planar and do not writhe. Conversely, the over-wound loops buckle into plectonemes, converting twist into writhe and relieving torsional stress. This asymmetry in the writhe of over and under-wound DNA has been previously observed both in single molecule experiments and in MD simulations (29,40,41). Additionally the buckling of the over-wound loop has been predicted theoretically (16). Although we have considered three topoisomers, only two were produced experimentally by the Du et al. method, which were identified as the relaxed and ΔLk = −1 topologies. The average energies of the simulations, calculated after 5 ns of equilibration, do indeed show that the over-wound structure is slightly less favourable (Supplementary Table S2). This analysis is, however, approximate as it assumes firstly that the production of topoisomers is under thermodynamic control, but also that the entropy change associated with over and under-winding is the same. Even though it was not detected experimentally, we have simulated the over-wound topoisomer to further investigate the asymmetry between over and under-wound DNA.

Figure 4.

Molecular structures showing the final frame of the MD simulations of the under-wound [65A⁽⁻¹⁾ and 65B⁽⁻¹⁾] and over-wound [65A⁽⁺¹⁾ and 65B⁽⁺¹⁾] 65 bp loops. Under-wound loops denature over multiple consecutive base pairs in two separate regions. Both over-wound loops develop one type II kink and another more severely denatured region which is similar to a type II kink but with additional broken base pairs.

Positively supercoiled 65 bp circles writhe and denature

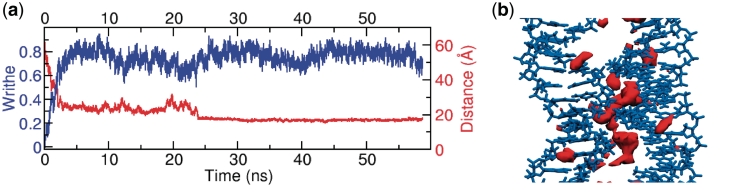
The transition of the over-wound loop from a planar circle to a plectoneme is clearly observed in the development of its writhe, as shown in Figure 5. The starting structure is circular and the writhe is initially zero. As the simulation proceeds, the writhe steadily increases over 5 ns to 0.8 as the circle folds into a figure of eight. Necessarily, two initially opposite segments of the DNA are brought into close contact (∼19Å) to form the right-handed crossover strand in which the backbone of one segment slots into the minor groove of the second (Figure 5). Such close right-handed crossover configurations have been observed in crystallographic and atomistically simulated structures of two separate strands but only in the presence of divalent cations (42,43). This particular type of backbone–minor groove interaction seen here has also been proposed as a Holliday junction model (44). We hypothesize that in these simulations supercoiling has provided a driving force that allows the two segments to adopt this configuration in the presence of monovalent ions. Figure 5 shows the isodensity surface for sodium counterions and indicates that there is a higher density of positive counterions stabilising the crossing points. The isodensity surface of the counterions in the whole writhed loop is shown in Supplementary Figure S5.

Figure 5.

(a) The writhe of the over wound 65 bp loop [65A⁽⁺¹⁾] increases from zero to around 0.75 as the circle to plectoneme transformation takes place (blue). As the writhe increases the two base pairs, 40 and 61 are brought into close contact as they form the crossover necessary to create the plectoneme (red). The distance shown is measured between the centre of masses of the two base pairs. (b) A representative molecular structure of the two strands forming a crossover taken from the MD simulation. Isodensity surface of Na⁺ counterions is shown in red. The ion density is shown at 120 ions per ų, as calculated over the final 25 ns (25 000 snapshots) of simulation 65A⁽⁺¹⁾.

The Watson and Crick hydrogen bond distances shown in Figure 3 indicate that there is considerable denaturation of the DNA in both the under and over-wound loops. For the over-wound structures, adopting a supercoiled plectoneme requires two highly bent regions to form the apices. It is here that the broken base pairs appear. In both of the two over-wound circles each apex has broken base pairs. The single broken base pair in 65A⁽⁺¹⁾ is at the centre of a type II kink (Table 2). A type II kink also occurs in 65B⁽⁺¹⁾ but then develops into a bubble when a neighbouring base pair breaks. As in the case of the relaxed 65 bp topoisomers, all kinks occur in a motif where the central broken base pair is an A:T pair. Where multiple consecutive base pairs are broken the denatured regions resemble type II kinks with additional unpaired bases (sequences provided in Table 2); they have high curvature and an unpaired base remains stacked with the 5′-end. The denatured regions appear in the over-wound circles only as writhing occurs, and therefore appear to be a consequence of the tight bending at the apices. As with the type II kinks, it is only, with one exception, A:T base pairs that have broken hydrogen bonds.

Negatively supercoiled 65 bp circles form bubbles and wrinkles

In contrast, the under-wound loops do not writhe but instead relieve torsional stress by denaturation. The experiments by Du et al. found that these minicircles were quickly digested by both of the single-strand-specific endonucleases S1 and BAL 31, suggesting that these circles should indeed contain bubbles of denatured DNA. At the start of the simulations multiple consecutive base pairs break at two separate points in circle 65A⁽⁻¹⁾ and 65B⁽⁻¹⁾ (Figure 3). Although there appears a preference for the A:T base pairs to denature, the torsional stress in this topoisomer is sufficiently large to also denature G:C pairs (Table 2). The formation of these severe disruptions allows the double helical structure to locally unwind and thus relieve torsional stress in the rest of the loop. The intact base pairs of simulation 65A⁽⁻¹⁾ start with a twist of 27.7°. When denaturation bubbles form, these absorb the unwinding stress, and the average twist of intact base pairs increases to 30.6° +/−1.1. In addition, these denatured bubbles display increased bending flexibility resulting in high curvature and producing an elliptical tertiary structure (Figure 4). Similarly to the type II kinks observed in the torsionally relaxed simulations, the denaturation bubbles are associated with increased sodium counterion density (Supplementary Figure S6).

As well as forming kinks and denaturation bubbles, these supercoiled circles also wrinkle to relieve superhelical stress. In simulation 65B⁽⁻¹⁾, one base step with negative twist appears immediately and a second after 10 ns (Supplementary Figure S7). They are separated by a step with normal positive twist (Supplementary Figure S7), giving the DNA a ‘wrinkled’ appearance. All of the base pairs involved maintain their hydrogen bonds showing this to be an alternative to denaturation for the relief of torsional stress. The negative twist is coupled to high anti-χ dihedral angles (Supplementary Figure S8), which is a rotation about the glycosyl bond joining the sugar to the base. In the high anti-conformation observed here the sugar rotates ∼90° so that it is perpendicular to the helical axis. This combined with changes in the backbone dihedral angles, primarily the ε and ζ angles, produces the left-handed DNA steps (Supplementary Figure S9). This novel structural distortion is described in greater detail for the 104 bp minicircle and in the ‘Discussion’ section.

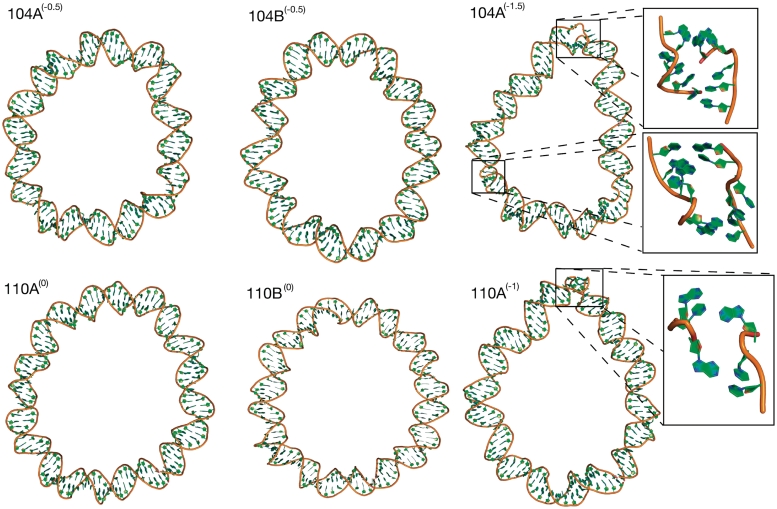
The 104 bp loops wrinkle but the relaxed 110 bp loops remain circular

The structures of the under-wound 104 bp circles with ΔLk = −0.5 and the relaxed 110 bp circles are shown in Figure 6. The hydrogen bonding distances are plotted in Figure 3. No broken base pairs develop in either the torsionally relaxed 110 bp or the 104 bp ΔLk = −0.5 circles. All simulations of the 110 bp loops remain circular and show no anomalous base step or base pair parameters that would indicate structural distortion. This simulation result compares favourably with the experiments of Du et al., who did not detect any digestion of this circle by the single-strand-specific endonucleases S1 or BAL 31.

Figure 6.

Molecular structures of the 104 bp loops showing denaturation occuring when ΔLk increases from −0.5 [104A^(−0.5) and 104B^(−0.5)] to –1.5 [104A^(−1.5)]. The torsionally relaxed 110 bp loops remain intact [110A⁽⁰⁾ and 110B⁽⁰⁾] while the under-wound loop denatures [110A⁽⁻¹⁾].

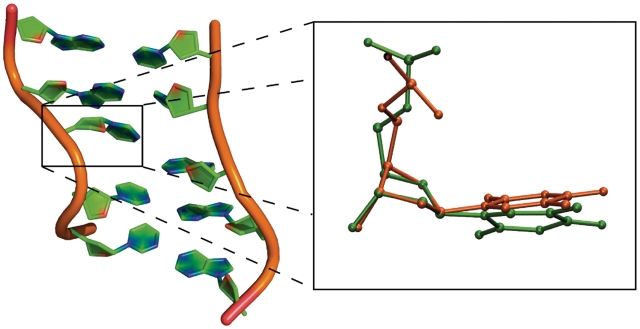
One simulation [104A^(−0.5)] of the 104 bp ΔLk = −0.5 minicircle similarly shows no structural distortions. However, analysis of the step parameters during the second simulation [104B^(−0.5)] shows the transient formation of an under-wound ‘wrinkled’ region (Supplementary Figure S10) after 12 ns that persists for 19 ns. In this region, two consecutive base pair steps unwind primarily through a change in the glycosyl bond χ dihedral angles from the anti- to the high anti-conformation (Supplementary Figure S11). This highly unusual 90° sugar rotation has been observed in the crystal structure of the junction between two Z-DNA helices (45). The overlay of the thymine base from the crystal structure with a thymine base in the wrinkled region of the simulated DNA in Figure 7 shows that there is a strong similarity in the conformation of the DNA at this base step. The backbone dihedral angles are also perturbed to accommodate the unwinding in the wrinkle, as shown in Supplementary Figure S12. There is ∼90° rotation of the ε and ∼180° rotation of the ζ dihedral angles in the two bases (96 and 115) associated with the high anti-χ conformation. While novel DNA structures predicted with empirical force fields should always be treated with caution, the crystallographic data does provide evidence that such a conformation is possible (45), and a database search shows that a number of DNA crystal structures exist with the high anti-χ conformation (46).

Figure 7.

A representative molecular structure of a DNA wrinkle taken from the under-wound region of the 104 bp Lk 9 circle [simulation 104B^(−0.5)] (left) and the overlay of the thymine base (orange) in the experimental crystal structure of the z–z junction (PDB: 3IRQ) and the thymine base (green) in the wrinkle (right). The RMSD between the two bases is 0.60Å.

Highly under-wound 104 and 110 bp loops wrinkle and denature

Although not produced experimentally by Du et al., additional simulations of a 110 bp ΔLk = −1 circle [simulation 110A⁽⁻¹⁾] and a 104 bp ΔLk = −1.5 circle [simulation 104A^(−1.5)] were performed to demonstrate that sufficient under-winding causes denaturation in these larger DNA minicircles as well as in circles only 65 bp in size. The distorted final structures of these torsionally stressed larger circles are shown in Figure 6. In the 110 bp circle, analysis of the hydrogen bonds (Figure 3) shows a single permanent broken base pair which resembles an under-wound type II kink (Table 2). The simulations shows that when this base pair breaks, the reduction in twist emerges first, followed by the high bending angle, suggesting that kink formation occurs in response to the torsional stress. More severe disruptions are observed in the 104 bp ΔLk = −1.5 circle as a result of the higher torsional stress (Figure 3). Two denaturation bubbles consisting of multiple consecutive broken base pairs are observed in separate regions of the circle (Table 2). They form untwisted bubbles that are similar in structure to those observed in the under-wound 65 bp loops. Additionally, there is an under-wound wrinkled region over 2 bp where the hydrogen bonds remain intact (Supplementary Figure S13), but there is a substantial change in the glcosyl bond χ angle and backbone dihedral angles (Supplementary Figures S14 and S15) which is similar in structure to that observed in simulations 65B⁽⁻¹⁾ and 104B^(−0.5).

DISCUSSION

We have performed a series of MD simulations to investigate the atomistic structure of minicircle DNA, which cannot be directly determined experimentally. We have then quantitatively compared the simulations with the biochemical study by Du et al. (25), which used endonucleases to probe DNA minicircles for structural disruptions. The simulations reveal three distinct types of structural distorsions in highly bent and supercoiled minicircle DNA; the types I and II kinks originally described by Lankas et al., denaturation bubbles containing between 2 and 5 broken DNA bases, and DNA wrinkles where local untwisting causes a reversal of helicity in 1–2 bp steps.

By comparing the calculations with existing experimental data, we have assessed the accuracy of atomistic simulations of supercoiled DNA performed over the 50 ns timescales accessible with our current computational resources. In agreement with the experiments, the simulations show that bending stress alone is sufficient to induce kinking in torsionally relaxed 65 bp loops. These kinks are localized, and involve the breaking of only a single base pair at most. This is consistent with the slow digestion of relaxed 63 bp topoisomers by BAL 31 (which is thought to digest local disruptions), but not the less sensitive S1 endonuclease (which is thought to require larger regions of single stranded DNA). Du et al. reported that the 63 bp ΔLk = −1 circle is quickly digested by both endonucleases in the experiments; accordingly we observe that denaturation bubbles containing 3–5 bp of single-stranded DNA form in the 65 bp under-wound loop. Du et al. found that loops larger than 100 bp were only digested by endonucleases when negatively supercoiled. In agreement, we observe no structural distortions in the simulations of torsionally relaxed 110 bp circles. The negatively supercoiled 104 bp ΔLk = −0.5 minicircle wrinkles reversibly but does not form kinks or bubbles in the simulations. Experimentally, the equivalent topoisomer is quickly digested by the sensitive BAL 31, but only slowly by the S1 nuclease.

DNA structures with the unusual glycosyl bond rotation observed in the ‘wrinkled’ DNA deformations have been previously proposed (47,48). In what is called ‘the side-by-side’ model they are used to explain how a periodic reversal of DNA helicity could be possible (47). The term ‘wrinkle’ was originally used to describe small sequence dependent deformations of the regular double helix which gave the duplex a wrinkled structure (49). Although we use it to describe larger deformations, since the helicity of the double helix is locally reversed, this term is particularly appropriate for describing the wrinkled appearance of the DNA disruptions seen in the simulations.

The full range of non-canonical DNA structures which act as substrates for these enzymes is unknown. Both enzymes have been shown to cleave B–Z junctions (50,51), mutagenic DNA lesions (52,53) and the loop regions of DNA hairpins (54); however, these structures generally involve large structural distortions such as extruded base pairs. It is therefore reasonable to assume that denaturation bubbles should be digested by both enzymes, and potentially that type II kinks, which involve a single broken base pair, should be digested only by the most sensitive BAL 31 nuclease. The idea that type I kinks and wrinkles, which contain no broken base pairs, might be targets for either endonuclease is more speculative.

The connection between the digestion of the 104 bp ΔLk = −0.5 minicircles by BAL 31 and the appearance of wrinkles in the corresponding simulation can therefore be interpreted in a number of ways. First, it is possible that the appearance of wrinkles is an artefact of the current force field; if this error were corrected the DNA would adopt a more conventional strategy to reduce superhelical stress such as denaturation, leading to a direct agreement with the experimental observations. However, there is at least one example of this type of backbone conformation in the X-ray crystal structure database (45). A second possibility is that wrinkle formation is a real process, and that the DNA structure formed is an endonuclease substrate. A third possibility is that wrinkles are real, but are an on-pathway intermediate to a much more slowly formed denatured state that is digested by endonucleases, but that we do not observe in the simulations due to the timescales involved. Alternatively, wrinkle formation might be an off-pathway intermediate to a separate endonuclease sensitive denatured state that forms too slowly to be captured in a nanosecond time frame.

We conclude that the 50 ns MD simulations provide a good description of the DNA minicircles at high levels of bending (as in 65 bp circles) and torsional stress (σ = −0.1). For lower superhelical densities (σ = −0.05), although we do indeed observe structural distortions, we cannot be as confident that these are responsible for the endonuclease digestion observed experimentally. As the levels of superhelical stress are reduced, the corresponding structural changes in the DNA become more difficult to observe in the short simulation timescales available.

What is clear from both the simulations and the biochemical experiments is that supercoiled minicircle DNA is surprisingly rich in different types of non-canonical DNA structures, adding support to the emerging view that DNA has a far greater repertoire of structural motifs than was originally thought. New experimental methods to trap and identify these new structural motifs would therefore be very valuable. In addition, it will be necessary to construct a standardized terminology for stress-induced structural defects in DNA, such as already exists to describe defects in crystalline materials (56). As DNA bending and supercoiling are ubiquitous in biology, it is possible that such structural distortions are important in DNA recognition by binding proteins and ultimately in genetic control.

FUNDING

Funding for open access charge: UK Engineering and Physical Sciences Research Council (Doctoral Training Centre Studentship to J.S.M.).

Conflict of interest statement. None declared.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.