Optimal mix of screening and contact tracing for endemic diseases

Abstract

Two common means of controlling infectious diseases are screening and contact tracing. Which should be used, and when? We consider the problem of determining the cheapest mix of screening and contact tracing necessary to achieve a desired endemic prevalence of a disease or to identify a specified number of cases. We perform a partial equilibrium analysis of small-scale interventions, assuming that prevalence is unaffected by the intervention; we develop a full equilibrium analysis where we compare the long-term cost of various combinations of screening and contact tracing needed to achieve a given equilibrium prevalence; and we solve the problem of minimizing the total costs of identifying and treating disease cases plus the cost of untreated disease cases. Our analysis provides several insights. First, contact tracing is only cost effective when prevalence is below a threshold value. This threshold depends on the relative cost per case found by screening versus contact tracing. Second, for a given contact tracing policy, the screening rate needed to achieve a given prevalence or identify a specified number of cases is a decreasing function of disease prevalence. As prevalence increases above the threshold (and contact tracing is discontinued), the screening rate jumps discontinuously to a higher level. Third, these qualitative results hold when we consider unchanged or changed prevalence, and short-term or long-term costs.

1 Introduction

Screening and contact tracing are two common means of controlling infectious diseases. Which is used depends on the disease and the context or region. For example, contact tracing (also known as partner notification) is routine for tuberculosis (TB) in the general population of low-prevalence countries. TB screening is often performed in higher prevalence contexts such as prisons and nursing homes.

Blanket screening for disease is uncommon. However, routine screening (either mandatory or recommended) for some diseases is performed in immigrants and high-risk groups. For example, immigrants are screened for TB and human immunodeficiency virus (HIV) in the US and Canada. The Centers for Disease Control and Prevention (CDC) recommend annual TB skin tests for prison employees and long-term inmates (CDC, 1996). TB screening is also commonly required for school employees and health care workers (CDC, 1993b). For pregnant women in the US, the CDC recommends screening for syphilis, Hepatitis B, chlamydia, gonorrhea, and Hepatitis C for those at high risk, and also recommends that pregnant women be offered an HIV test (CDC, 2002).

Contact tracing practice varies among diseases. In the US, health departments are legally required to perform contact tracing for all TB index cases (CDC, 2000). The CDC recommends routine contact tracing for HIV in the US (CDC, 2002), although it is not mandatory; often individuals testing positive for HIV do not want their partners informed for fear of discrimination (Pealer and Peterman, 2003). In Sweden, partner notification of HIV status is mandatory (Cowan et al., 1996). For STDs other than HIV, contact tracing has been practiced for decades (since the 19th century in Sweden and the UK and since the early 20th century in the US, for example) although it is not always routine (Cowan et al., 1996; Clarke, 1998). In one study cited in Clarke (1998), only 7–16% of chlamydia cases were referred for contact tracing.

A number of empirical studies of the cost effectiveness of contact tracing have been carried out. These include studies of TB (Dasgupta et al., 2000; Macintyre et al., 2000), HIV (Varghese et al., 1999; Cohen et al., 2004), and other STDs including chlamydia (Howell et al., 1997) and syphilis (Oxman and Doyle, 1996). For example, Oxman and Doyle (1996) performed an empirical study to compare the benefits of screening and contact tracing for early stage syphilis in Multnomah County, Oregon. The authors looked at the costs of screening and contact tracing, the number of infected individuals found by contact tracing, and the number of infected individuals found by screening (including walk-ins, who see a practitioner for symptoms, and individuals found by random screening). They determined that the average cost of finding an infected individual was slightly lower among the screened individuals than among those found by contact tracing.

Some authors have developed detailed simulation models of the effectiveness of contact tracing. For example, Kretzschmar et al. (2004) and Porco et al. (2004) looked at the efficacy of contact tracing and ring vaccination to control a smallpox outbreak. Other authors (e.g., Müller et al. (2000) and Huerta and Tsimring (2002)) have developed theoretical models to evaluate the effectiveness of contact tracing. For example, Huerta and Tsimring (2002) used a stochastic network model to derive mean-field ordinary differential equations that describe epidemic quantities of interest, such as the number of individuals who are infected, susceptible, traced, and removed. None of these models examines the cost effectiveness of contact tracing. Closest to our approach is the multiple compartment gonorrhea transmission model of Hethcote and Yorke (1984). The authors compare the efficacy of different control strategies including contact tracing but do not model their costs.

The goal of our analysis is to determine the cheapest mix of screening and contact tracing necessary to achieve a desired endemic prevalence of a disease or to identify a specified number of cases. We present a mathematical framework for this problem. We perform a partial equilibrium analysis of small-scale interventions, assuming that prevalence is unaffected by the intervention, and then develop a full equilibrium analysis where we compare the long-term cost of various combinations of screening and contact tracing needed to achieve a given equilibrium prevalence. We also solve the problem of minimizing the total costs of screening, contact tracing, and treated and untreated disease cases.

2 Framework

In this section we present our mathematical framework. All notation is summarized in Table 1. We consider an infectious disease that is endemic in a population of size N consisting of S susceptible people and I infected people (N = S + I). We let p:= I/N denote the prevalence of the disease in this population. We assume that the modeled population includes only those people who can get the disease (for example, for STDs the population would not include young children).

Table 1.

Summary of Notation

	Decision Variables
λ	per capita screening rate
δ	1 if contact tracing is performed, 0 otherwise
	Optimal Policy
( ${\lambda }_U^{\ast },{\delta }_U^{\ast }$)	optimal policy for the case of unchanged prevalence
( ${\lambda }_L^{\ast },{\delta }_L^{\ast }$)	optimal policy for the case of changed prevalence, and minimization of long-term cost
( ${\lambda }_T^{\ast },{\delta }_T^{\ast }$)	optimal policy for the case of changed prevalence, and minimization of total cost
	Costs
C(λ, δ; p)	total annual per capita cost of screening policy λ and contact tracing policy δ
CS	initial cost per person screened
CfS	cost of followup screening for a false positive
Ct	cost of confirmatory tests, counseling, and treating a single case of disease identified via screening or walk-in
CT	contact tracing cost per index case
	Other Notation
I	number of infected individuals in the population
S	number of susceptible individuals in the population
N	population size, N = I + S
p	prevalence, p = I/N
f(p, λ, δ)	rate of change in prevalence
β	sufficient contact rate
γ	fraction of incident cases who are walk-ins (who see a health practitioner for symptoms)
η	per capita exogenous rate of new infections (from sources external to the population)
KT	number of secondary cases per index case found by contact tracing
μ1	per capita natural death rate in the population
μ2	per capita untreated recovery rate from the disease
μ	per capita exit rate from infected population due to death or recovery, μ = μ1 + μ2
walk-ins(I)	annual rate of walk-ins
ω(p)	per capita walk-in rate, ω(p) = walk-ins(pN)/N
n	number of new cases to be found per year
α	cost per year of one infection
r	discount rate used to discount future costs
stp	true positive rate of initial screening
sfp	false positive rate of initial screening

We describe the dynamics of the disease using a standard random mixing model with susceptible and infected individuals, S → I (see, for example, Bailey (1975)). We assume that immunity to the disease does not exist (neither a vaccine nor previous infection provides immunity). This is reasonable for HIV, TB, and many STDs. We also assume a constant population size: the number of people entering the susceptible subgroup equals the number of people treated plus any who die in either the susceptible or infected subgroups. The assumption of a constant population size is realistic if relatively few people die of the disease.

Base Case

We first consider a base case in which there is no screening or contact tracing. New cases are identified via “walk-ins”; these are patients who see a health practitioner for symptoms. The change in prevalence at any point in time is described by the following set of differential equations:

$$\begin{array}{l}\stackrel{.}{S}=-[\beta SI/N+\eta S]-{\mu }_{1}S+{\mu }_{2}I+\text{walk}-\text{ins}(I)+{\mu }_{1}N\\ \stackrel{.}{I}=+[\beta SI/N+\eta S]-{\mu }_{1}I-{\mu }_{2}I-\text{walk}-\text{ins}(I).\end{array}$$ (1)

The bracketed term represents the incidence of new cases: β is the sufficient contact rate and ηS the annual rate at which susceptible individuals in the population become infected via exogenous sources. This could be due, for example, to international travel of susceptible people who come back infected. Assuming net immigration is zero, the ηS term could also account for the arrival of infected immigrants. We assume that the per capita death rate in the population is μ₁ and the (untreated) recovery rate from the disease is μ₂. Note that the rate of entry into the population μ₁N equals the total death rate μ₁(S + I). For diseases such HIV with no natural recovery, we can set μ₂ = 0; for diseases such as TB where natural recovery can occur, we set μ₂ > 0. In this system of equations, (infected) walk-ins arrive at an annual rate, walk-ins(I), that depends on the number of infected individuals. (We state all rates in annual terms, but any time unit could be used.)

We can rewrite the system of equations (1) as a single differential equation (since N = S + I), which we express in terms of prevalence, p:= I/N:

$$\stackrel{.}{p}=[\beta p(1-p)+\eta (1-p)]-\mu p-\omega (p).$$ (2)

In equation (2), the term ω(p):= walk-ins(I)/N denotes the per capita rate of walk-ins; and μ:= μ₁ + μ₂ so that μp is the reduction in prevalence due to deaths or recovery of infected individuals. For the remainder of our analysis, the fundamental quantity we examine is the per capita prevalence p. (Absolute numbers of infected and susceptible individuals can be readily calculated from this quantity.)

We model the annual rate of walk-ins as a fraction, γ, of the incidence of new cases:

$$\omega (p):=\gamma (1-p)[\beta p+\eta ].$$ (3)

We assume that γ < 1; not all infected individuals seek treatment. Modeling the effect of walk-ins in this way is an approximation since in reality there is some delay between the time an individual becomes infected, develops symptoms, and is then treated or removed from the population. The yearly cost per capita to identify and treat new cases is

$$\omega (p)C_t$$ (4)

where C_t is the cost of confirmatory tests, counseling, and treatment for a single case of disease.

Screening and Contact Tracing

We consider two interventions to identify (and subsequently treat) new cases: screening and contact tracing. We assume that screening can perfectly discriminate between infected and uninfected individuals; this is a reasonable assumption if screening comprises a battery of tests that taken together have near perfect sensitivity and specificity. Below we extend the model to allow for imperfect screening. We assume that screening occurs at an annual rate of λN people per year and finds infected individuals at a per capita annual rate of λp. We assume that the baseline cost per person screened is C_S. This does not include the cost of confirmatory tests, treatment, or counseling for those who test positive.

Contact tracing, if implemented, is performed for all walk-ins and infected screened individuals; these are the index cases. We model the presence or absence of contact tracing as a binary variable, δ, that takes value 1 if contact tracing is present and 0 otherwise. We assume that the mean number of additional infected individuals per index case found via contact tracing is K_T, and that the total cost of finding, testing, and treating these K_T individuals is C_T. We assume that the cost per infected person found and treated via contact tracing is greater than the usual treatment cost: thus, C_T/K_T > C_t.

With (perfect) screening and contact tracing, the cost function becomes

$$C(\lambda ,\delta ;p):=\omega (p)C_t+\lambda (C_S+C_{t}p)+\delta C_T({\lambda }_p+\omega (p)),$$ (5)

and the rate of change in prevalence is given by

$$\stackrel{.}{p}=f(p,\lambda ,\delta ):=(1-p)[\beta p+\eta ]-\mu p-(1+\delta K_T)({\lambda }_p+\omega (p)).$$ (6)

We model imperfect screening by assuming that an imperfect initial test is followed by a perfect (more expensive) test for those who initially test positive. Then screening policy λ finds λs_tpp infected individuals, where s_tp is the sensitivity (true positive rate) of the test; and yields positive initial tests for λs_fp (1 − p) uninfected individuals, where s_fp is the false positive rate of the test. The cost of confirmatory tests for individuals with true positive tests is already included in the treatment cost C_t. We assume that the cost of followup screening tests for an individual with a false positive test is C_fS. With these assumptions, equations (5) and (6) become

$$C(\lambda ,\delta ;p):=\omega (p)C_t+\lambda (C_S+C_t{s}_{\text{tp}}p+C_{\text{fS}}{s}_{\text{fp}}(1-p))+\delta C_T(\lambda s_{\text{tp}}p+\omega (p)),$$ (7)

$$\stackrel{.}{p}=f(p,\lambda ,\delta ):=(1-p)[\beta p+\eta ]-\mu p-(1+\delta K_T)(\lambda s_{\text{tp}}p+\omega (p)).$$ (8)

Note that for a given endemic prevalence p there are only two steady-state policies, that is, policies that remain the same for all time: (λ = λ₀, δ = 0) and (λ = λ₁, δ = 1). Thus, to determine a minimum cost steady-state policy, we determine the optimal screening level with and without contact tracing and then compare the costs of the two policies.

We now consider three different formulations of the problem: one in which screening and contact tracing do not change the disease prevalence (Section 3); one in which screening and contact tracing do change the disease prevalence, and the goal is to minimize long-term annual cost of maintaining a specified equilibrium prevalence (Section 4); and one in which screening and contact tracing change the disease prevalence, and the goal is to determine the level of control (and thus the associated equilibrium disease prevalence) that minimizes the total costs of screening, contact tracing, and disease (Section 5). We assume in the first formulation (Section 3) that the population is large enough and prevalence is low enough such that the disease control efforts do not change the disease prevalence; this might be the case, for example, if the disease is endemic (e.g., chlamydia) and the budget for disease control is low. The second formulation (Section 4) could reflect a situation in which the budget is high enough to reduce disease prevalence and the public health department takes a long-term perspective, aiming to minimize only the long-term costs of control. The third formulation (Section 5) could reflect the situation in which the budget is high enough to reduce disease prevalence and the health department takes a shorter-term perspective.

3 Unchanged prevalence

Suppose that screening and contact tracing have a small enough effect that the disease prevalence p remains (essentially) the same. Then the problem of determining the optimal mix of screening versus contact tracing can be viewed as one of finding and treating a specified number of cases per year at minimum cost. Building on equations (7) and (8), let $C_U^{\ast }(n;p)$ be the minimum cost of finding and treating at least n cases per year when the prevalence is p. We assume that n > Nω(p): we want to find more infected individuals than just the walk-ins. In one year at prevalence p we find N(1 + δK_T)(λs_tpp + ω(p)) cases with screening rate λ and contact tracing policy δ. The minimum cost is then given by

$$\begin{array}{l}{C}_U^{\ast }(n;p):=\underset{\delta ,\lambda }{min}C(\lambda ,\delta ;p)\\ s.t.N(1+\delta K_T)(\lambda s_{\text{tp}}p+\omega (p))\ge n\\ \lambda \ge 0,\delta \in \{0,1\}.\end{array}$$ (9)

Let ( ${\lambda }_U^{\ast }(n;p),{\delta }_U^{\ast }(n;p)$) denote the optimal policy. Since the constraint is linear in λ and the objective function is increasing in λ, we obtain

$${\lambda }_U^{\ast }(n;p)=\frac{1}{{\mathit{Nps}}_{\text{tp}}}{\left[\frac{n}{1+{\delta }_U^{\ast }(n;p)K_T}-N\omega (p)\right]}^{+}$$ (10)

where [x]⁺:= max(x, 0) is the positive part operator. When the bracketed term in equation (10) is negative, then we find more than n cases just by treating the walk-ins (and their contacts if δ = 1). Because we wish to focus on the trade-off between screening and contact tracing we assume that we want to find more cases than just the walk-ins and their contacts; thus, we henceforth assume that n ≥ Nω(p)(1 + K_T).

Substituting (10) into (9), we obtain

$$C_U^{\ast }(n;p)=\frac{1}{{\mathit{Nps}}_{\text{tp}}}\left[n\frac{C_S+C_t{s}_{\text{tp}}p+C_{\text{fS}}{s}_{\text{fp}}(1-p)+{ps}_{\text{tp}}{\delta }_U^{\ast }(n;p)C_T}{1+{\delta }_U^{\ast }(n;p)K_T}-N\omega (p)(C_S+C_{\text{fS}}{s}_{\text{fp}}(1-p))\right].$$ (11)

Comparing $C_U^{\ast }(n;p)$ for δ = 0 and δ = 1 we find that the optimal policy for contact tracing is

$${\delta }_U^{\ast }(n;p)=\{\begin{array}{ll}1\hfill & \text{if}p<\frac{C_S+C_{\text{fS}}{s}_{\text{fp}}}{s_{\text{tp}}{C}_T/K_T+C_{\text{fS}}{s}_{\text{fp}}-C_t{s}_{\text{tp}}},\hfill \\ 0\hfill & \text{otherwise}.\hfill \end{array}$$ (12)

These expressions simplify in the case of perfect screening (the terms with s_fp> drop out). For example, the condition in (12) becomes $p<\frac{C_S}{C_T/K_T-C_t}$.

From (12), we see that contact tracing is optimal when the prevalence is below a threshold, regardless of the number of cases we want to find. This is not unexpected: threshold results have been found when comparing various combinations of screening, testing, and vaccination strategies for other diseases, e.g., Hutton et al. (2007); Rubió (1997); Owens et al. (1996).

The contact tracing threshold is a positive quantity because of our assumption that C_T/K_T >C_t. We denote this threshold prevalence by P′. In the case of perfect screening, C_S/P′ = C_T/K_T − C_t, meaning intuitively that at prevalence P′ the marginal cost of finding an additional case via screening, C_S/P′, equals the average cost of finding a new case via contact tracing, C_T/K_T − C_t (we subtract C_t because C_T includes the cost of treating infected contacts while we are interested only in the cost of finding them).

From (10), we see that the optimal screening rate increases with the number of cases to be found (n). The optimal screening rate decreases if contact tracing (δ) is implemented. Additionally, the optimal screening rate decreases as the walk-in rate (ω(p)) increases.

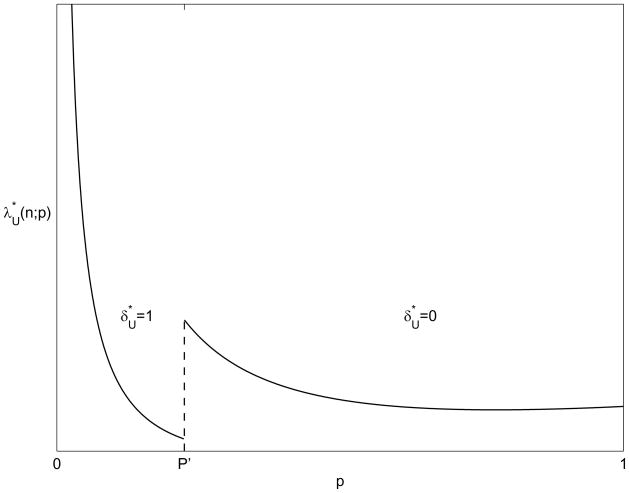
Figure 1 shows schematically how the optimal amount of screening needed to identify n cases varies with the endemic disease prevalence. This figure, and all subsequent figures in this paper, use the following parameter values: s_tp = 1, K_T = 1.5, γ = 0.1, β = 0.15, η = 0.01, μ = 0.05, s_fp = 0, C_fS = 50, C_t = 200, C_S = 15, C_T = 400, n = 10, and N = 1000. We note that with other parameter values, all figures remain qualitatively similar to those shown. When the prevalence is below P′, contact tracing is used, and the optimal screening level decreases as prevalence increases. At the threshold P′, contact tracing is discontinued, and the optimal level of screening jumps discontinuously to a higher level. For prevalence above P′, the optimal screening rate decreases in proportion to 1/p. Eventually, as p gets large enough, the optimal screening rate begins to increase slightly. This is because the number of walk-ins, Nω(p), decreases due to saturation (note the p(1 − p) term in ω (p)).

Figure 1.

Optimal levels of screening and contact tracing to find n cases as a function of existing endemic disease prevalence p, assuming that prevalence is unchanged by screening and contact tracing

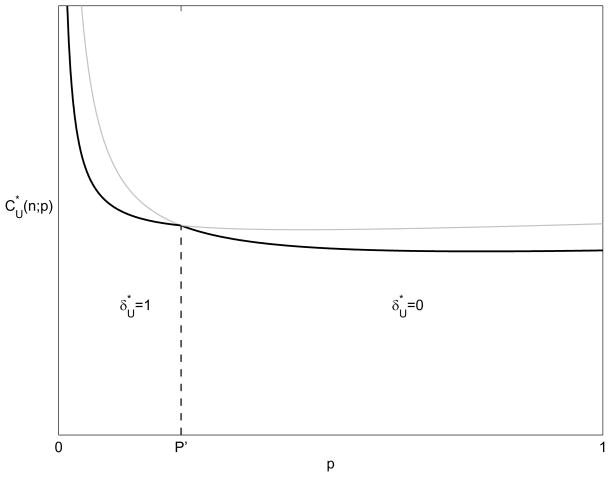
Figure 2 shows the cost of the optimal screening policy (11), with and without contact tracing. These costs are to find a fixed number, n, of infected individuals and therefore decrease with p (except for very high prevalences). The cost decreases with higher prevalence because there are more walk-ins (except for very high prevalences where the disease saturates the population) and more infected individuals, and therefore less screening is needed to find the n individuals. The cost of the optimal screening and contact tracing policy is the lower envelope of the two curves. We observe that, as prevalence increases, screening becomes more effective, and the marginal cost per infected found, $\partial C_U^{\ast }/\partial n$, decreases:

$$\frac{\partial C_U^{\ast }(n;p)}{\partial p\partial n}=\frac{-1}{p^2}\frac{C_S+C_{\text{fS}}{s}_{\text{fp}}}{1+{\delta }_U^{\ast }(n;p)K_T}\frac{1}{{Ns}_{\text{tp}}}.$$ (13)

Figure 2.

Minimum cost to find n cases as a function of existing endemic disease prevalence p, assuming that prevalence is unchanged by screening and contact tracing

4 Minimizing Long-term Costs

Under the assumptions of our model (8), if the same policy (λ, δ) is used for an extended period, then prevalence p(t) will converge to some steady-state value, P ≤ P₀. Here P₀ is the saturation prevalence with neither screening nor contact tracing. Long-term disease control costs — that is, ignoring transition costs — are determined by the steady-state prevalence, P, that is achieved. Hence it is useful to determine for each steady-state prevalence P ≤ P₀ the cheapest policy that maintains that prevalence, and the cost of that policy. We write this problem as:

$$\begin{array}{l}{C}_L^{\ast }(P):=\underset{\delta ,\lambda }{min}C(\lambda ,\delta ;p)\\ s.t.\stackrel{.}{p}(t)=0,p(t)=P\le P_0\forall t\\ \lambda \ge 0,\delta \in \{0,1\}\forall t.\end{array}$$ (14)

Substituting (8) into (14) yields

$$\begin{array}{l}{C}_L^{\ast }(P):=\underset{\delta ,\lambda }{min}C(\lambda ,\delta ;P)\\ s.t.0=(1-P)[\beta P+\eta ]-\mu P-(1+\delta K_T)(\lambda s_{\text{tp}}P+\omega (P))\\ \lambda \ge 0,\delta \in \{0,1\}.\end{array}$$ (15)

The value of P₀, obtained by substituting δ = 0 and λ = 0 into the constraint of (15) and choosing the larger solution, is

$$P_0=\frac{1}{2}-\frac{\eta }{2\beta }-\frac{\mu }{2\beta (1-\gamma )}+\sqrt{{\left(\frac{1}{2}-\frac{\eta }{2\beta }-\frac{\mu }{2\beta (1-\gamma )}\right)}^2+\frac{\eta }{\beta }}$$ (16)

which equals $1-\frac{\mu }{\beta (1-\gamma )}$ if η = 0.

To optimize (14) we compare the two steady-state policies, (λ = λ₀, δ = 0) and (λ = λ₁, δ = 1), for an endemic prevalence of P. Using analysis similar to that in Section 3, we solve for λ in the constraint of (15):

$${\lambda }_L^{\ast }(P)=\frac{1}{{Ps}_{\text{tp}}}\left[\frac{\beta P(1-P)+\eta (1-P)-\mu P}{1+{\delta }_L^{\ast }(P)K_T}-\omega (P)\right],$$ (17)

which can be expressed as

$${\lambda }_L^{\ast }(P)=\frac{1}{{Ps}_{\text{tp}}}\frac{(1-\gamma (1+{\delta }_L^{\ast }(P)K_T))[\beta P(1-P)+\eta (1-P)]-\mu P}{1+{\delta }_L^{\ast }(P)K_T}.$$ (18)

The numerator in (18) is the number of new cases each year that we need to find to maintain disease prevalence P (incident cases minus walk-ins and deaths). We divide by 1 + δK_T to determine the equivalent number of index cases, and by Ps_tp to determine the number of people we need to screen. As expected, the numerator (and hence ${\lambda }_L^{\ast }$) is nonnegative for P ≤ P₀ (where P₀ is given by (16)). Substituting (17) into (7) we obtain

$$C_L^{\ast }(P)=\omega (P)(C_t+{\delta }_L^{\ast }(P)C_T)+\left[\frac{\beta P(1-P)+\eta (1-P)-\mu P}{1+{\delta }_L^{\ast }(P)K_T}-\omega (P)\right]\frac{C_S+C_t{s}_{\text{tp}}P+C_{\text{fS}}{s}_{\text{fp}}(1-P)}{{Ps}_{\text{tp}}}.$$ (19)

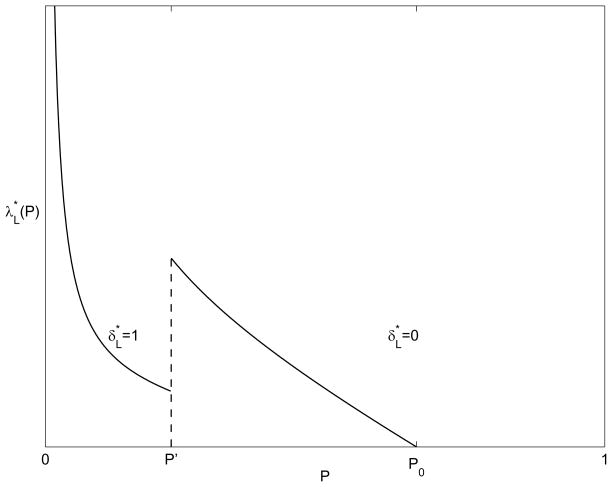
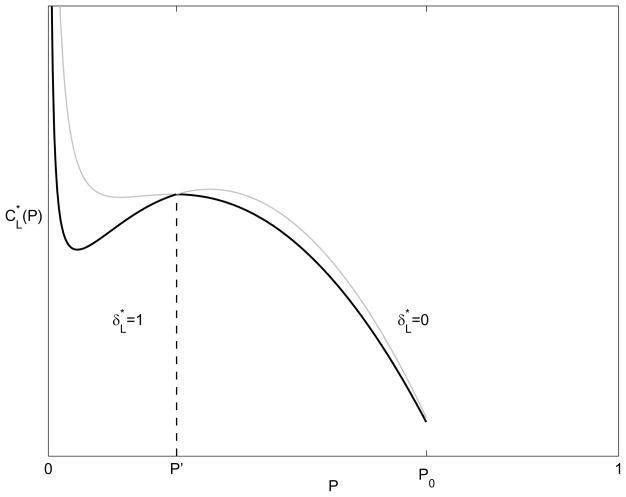
Figure 3 shows the optimal screening rate as a function of the desired endemic disease prevalence, P, and Figure 4 shows the associated cost. The shape of the cost function in Figure 4 can be explained as follows. The cost function, (7) (upon which (19) is based), contains two counteracting terms: the rate of walk-ins, ω(p), and the screening costs λp. The walk-in rate is quadratic in p, increasing for small prevalence and decreasing near saturation. So for a constant screening level λ, costs tend to rise at small prevalences and then decrease later. However, in the long-term cost setting, the optimal screening level, ${\lambda }_L^{\ast }(P)$, varies with prevalence, (18). If there were no infections from outside the population (η = 0) then the optimal screening level ${\lambda }_L^{\ast }(P)$ would be linear in prevalence and the cost would remain quadratic in P (first increasing and then decreasing). For η > 0, however, costs change in proportion to 1/P for very low prevalence because the η(1 − P)/(Ps_tp) term dominates. Thus, costs decrease sharply for very small P. Beyond some value of P (the local minimum between 0 and P′ in Figure 4) the impact of outside infections, η, is negligible and the cost behaves quadratically in P (first increasing and then decreasing).

Figure 3.

Optimal screening level ${\lambda }_L^{\ast }$ and contact tracing policy ${\delta }_L^{\ast }$ as a function of the desired endemic disease prevalence P, when the goal is to minimize long-term cost

Figure 4.

Minimum long-term cost as a function of the desired endemic disease prevalence P

Comparing $C_L^{\ast }$ for δ = 0 and δ = 1 we find that the optimal policy for contact tracing is

$${\delta }_L^{\ast }(P)=\{\begin{array}{ll}1\hfill & \text{if}P<\frac{C_S+C_{\text{fS}}{s}_{\text{fp}}}{s_{\text{tp}}{C}_T/K_T+C_{\text{fS}}{s}_{\text{fp}}-C_t{s}_{\text{tp}}},\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}$$ (20)

just as in Section 3 in the unchanged prevalence setting. (There is a second unphysical P > P₀ where the costs, $C_L^{\ast }$, in (19) are the same with and without contact tracing.)

5 Minimizing Total Costs

In the previous sections, we assumed that the disease prevalence was specified exogenously: either it was unchanged by screening and contact tracing (Section 3) or the long-term prevalence was specified and the goal was to determine the control policy to achieve that prevalence at minimum cost (Section 4). In this section we consider the problem of determining the control policy that minimizes the total cost of screening, contact tracing, and (treated and untreated) disease. The solution to this problem specifies not only the optimal screening and contact tracing policy, but also the cost-minimizing level of disease prevalence.

The cost function (7) includes the costs of screening, contact tracing, and treating identified cases of disease. To assign a cost to untreated disease cases (i.e., disease prevalence), we introduce a parameter α, which we define as the cost per year of one infection. To estimate α, we can apply concepts from cost-benefit analysis (Gold et al., 1996) and multiply the monetary value of one year of healthy life by the quality decrement associated with infection. For example, if a year of healthy life is worth $50,000 (Owens, 1998) and the quality adjustment for infection is 0.9 (thus, the quality decrement is 0.1 healthy years lost per year of life with infection), then we would estimate α as $5,000.

We state the problem as follows: given that the current prevalence is p₀, what is the best infinite-horizon dynamic policy (λ(t), δ(t)) that minimizes the total cost of screening, contact tracing, and disease, while never allowing prevalence to increase? We assume a discount rate r, and use equation (8) as the state equation. We also assume a bound on the resources available at any point in time. This bound could reflect budget constraints or physical limits on the number of people who can be screened annually. Specifically, we assume a bound of the form λ(t) ≤ λ̄ where λ̄ is some constant. We note that it should not be hard to extend the analysis to a more general bound R(p(t), λ(t), δ(t)) ≤ B where R(·) is an increasing function of λ. We write the optimal control problem as:

$$\begin{array}{l}{C}_T^{\ast }(p_0,\alpha ):=\underset{p(t),\delta (t),\lambda (t)}{min}{\int }_0^{\infty }{e}^{-rt}[C(\lambda (t),\delta (t);p(t))+\alpha p(t)]\text{d}t\\ s.t.p(0)=p_0,\stackrel{.}{p}(t)=f(p(t),\lambda (t),\delta (t))\forall t\\ \stackrel{.}{p}(t)\le 0,\lambda (t)\le \overline{\lambda }\forall t\\ 0\le \lambda (t),\delta (t)\in \{0,1\}\forall t.\end{array}$$ (21)

This control problem seeks to minimize the discounted per capita cost of finding and treating disease, ${\int }_0^{\infty }{e}^{-rt}C(·)$, plus the discounted per capita cost of (unidentified) untreated disease, ${\int }_0^{\infty }{e}^{-rt}\alpha p(t)$. We observe that as the level of disease control increases, the cost ${\int }_0^{\infty }{e}^{-rt}C(·)$ increases and the cost ${\int }_0^{\infty }{e}^{-rt}\alpha p(t)$ decreases. Thus, the optimal level of disease control is such that the marginal cost of additional case detection equals the marginal cost of case non-detection.

Out optimal control problem is autonomous and the optimal trajectory has no time dependence: if an optimal trajectory associated with initial prevalence x has prevalence and policy $(p^{\ast }(·;x),{\lambda }_T^{\ast }(·;x),{\delta }_T^{\ast }(·;x))=\overrightarrow{g}(·)$, then then for any t the function s ↦ g(s + t) gives an optimal prevalence and policy ( $p^{\ast }(·;g(t)),{\lambda }_T^{\ast }(·;g(t)),{\delta }_T^{\ast }(·;g(t))$) associated with initial prevalence g(t). This can be seen by decomposing our optimal control problem (21) for t > 0,

$$\begin{array}{l}{C}_T^{\ast }(p_0,\alpha ):=\underset{\begin{array}{c}p(s),\delta (s),\lambda (s)\\ s\le t\end{array}}{min}{C}_T^{\ast }(p(t),\alpha )+{\int }_0^t{e}^{-rs}[C(\lambda (s),\delta (s);p(s))+\alpha p(s)]\text{d}s\\ s.t.p(0)=p_0,\stackrel{.}{p}(s)=f(p(s),\lambda (s),\delta (s))\forall s\le t\\ \stackrel{.}{p}(s)\le 0,\lambda (s)\le \overline{\lambda }\forall s\le t\\ 0\le \lambda (s),\delta (s)\in \{0,1\}\forall s\le t.\end{array}$$ (22)

This means that the optimal policy ( ${\lambda }_T^{\ast }(p;\alpha ),{\delta }_T^{\ast }(p;\alpha )$) depends only on the current prevalence.

By the Pontryagin maximum principle, the optimal screening policy ${\lambda }_T^{\ast }(t)$ minimizes the Hamiltonian (with Lagrange multiplier φ) at every point along the optimal trajectory p*(t):

for all t, ${\lambda }_T^{\ast }(t)\in arg\underset{\lambda }{min}H(p^{\ast }(t),{\phi }^{\ast }(t),\lambda ,t)$,

where

$$H(p,\phi ,\lambda ,t):=e^{-rt}[C(\lambda ,{\delta }_T^{\ast }(p;\alpha );p)+\alpha p]+\phi f(p,\lambda ,{\delta }_T^{\ast }(p;\alpha )).$$ (23)

Since the Hamiltonian H(·) at any time t is linear in λ (see (7) and (8)), it follows that the optimal control will be bang-bang: ${\lambda }_T^{\ast }(t)$ is either at its minimal level, λ(p; α) or at its maximal level, λ̄. Due to the constraint ṗ = f(p, λ, δ) ≤ 0 and the fact that f(·) is decreasing in λ, the minimal level is

$$\underset{\_}{\lambda }(p;\alpha )=\frac{1}{{ps}_{\text{tp}}}\left[\frac{\beta p(1-p)+\eta (1-p)-\mu p}{1+{\delta }_T^{\ast }(p;\alpha )K_T}-\omega (p)\right].$$ (24)

Let (α):= {p: λ(p; α) ≤ λ̄} be the feasible set of prevalences: those prevalences for which there exists some screening level satisfying both constraints. This set consists of one or two intervals: note the shape of Figure 3 and the similarity of λ(·; α) to ${\lambda }_L^{\ast }(·)$. We assume the initial prevalence is feasible, p₀ ∈ (α), as otherwise (21) has no solution.

Since our problem is autonomous, the optimal contact tracing policy is the indicator function, ${\delta }_T^{\ast }(p;\alpha )={\mathbf{1}}_{A(\alpha )}(p)$, of some set A(α). Using a calculation similar to those in the previous sections, for any screening level we can find a smaller screening level that decreases prevalence at the same rate when combined with contact tracing: we can find λ̄₁(p) ≤ λ̄ and λ₁(p; α) ≤ λ(p; α) such that f(p, λ̄₁(p), 1) = f (p, λ̄, 0) and f(p, λ₁(p; α), 1) = f (p, λ(p; α), 0). In either case, the screening level with contact tracing is cheaper for prevalences p ∈ [0, P′): C(p, λ̄₁(p), 1) < C(p, λ̄, 0) and C(p, λ₁(p; α), 1) < C(p, λ(p; α), 0). Hence it is optimal to contact trace when prevalence is below a threshold, [0, P′) ⊆ A(α).

The above considerations show that it is optimal to screen at the maximal rate, λ̄, until prevalence reaches some level p₁ at time t₁ and then to remain at prevalence p₁. We can separate the costs of such a trajectory into the long-term costs of remaining at prevalence p₁,

$$\frac{C_L^{\ast }(p_1)+\alpha p_1}{r}={\int }_0^{\infty }{e}^{-rt}[C_L(p_1)+\alpha p_1]\text{d}t,$$ (25)

and the transition costs associated with changing the prevalence from p₀ to p₁,

$$J(p_0,p_1,\alpha )={\int }_0^{t_1}{e}^{-rt}[C(\overline{\lambda },{\mathbf{1}}_{A(\alpha )}(p);p(t))-C_L(p_1)+\alpha (p(t)-p_1)]\text{d}t\stackrel{.}{p}(t)=f(p(t),\overline{\lambda },{\mathbf{1}}_{A(\alpha )}(p)),p(0)=p_0,p(t_1)=p_1.$$ (26)

The total cost is their sum, $J(p_0,p_1,\alpha )+(C_L^{\ast }(p_1)+\alpha p_1)/r$, and given A(α), our problem is then to choose the p₁ that minimizes the total cost:

$$C_T^{\ast }(p_0,\alpha )=\underset{p_1\le p_0}{min}J(p_0,p_1,\alpha )+(C_L^{\ast }(p_1)+\alpha p_1)/r.$$ (27)

We write $p_1^{\ast }(p_0;\alpha )$ for the value of p₁ that achieves the optimum. Note that as we discount less, r → 0, only the long-term costs matter; that is $p_1^{\ast }(p_0;\alpha )\in arg{min}_{p\le p_0}{C}_L(p)+\alpha p$. Additionally, as we constrain λ more (i.e., decrease λ̄), then $p_1^{\ast }$ cannot decrease (a proof is in the appendix).

When the screening rate is unbounded (λ̄ = ∞), our analytic tools go further because the optimal policy decreases prevalence in a single instantaneous jump at the beginning. In this case, all prevalences are feasible, (α) = [0, ∞); the optimal contact tracing policy is the same as in the previous sections, A(α) = [0, P′); and J(·) is given by

$$J(p_0,p_1,\alpha )=\frac{C_t{s}_{\text{tp}}-C_{\text{fS}}{s}_{\text{fp}}+{\delta }_T^{\ast }(p_0)s_{\text{tp}}{C}_T}{(1+{\delta }_T^{\ast }(p_0)K_T)s_{\text{tp}}}(p_0-p_1)+\frac{C_S+C_{\text{fS}}{s}_{\text{fp}}}{(1+{\delta }_T^{\ast }(p_0)K_T)s_{\text{tp}}}log\frac{p_0}{p_1},$$ (28)

when p₀ and p₁ are on the same side of P′, the threshold prevalence for contact tracing. Equation (28) is derived in the appendix. If p₀ and p₁ are on opposite sides of P′, p₁ < P′ < p₀, then we calculate the transition cost as the cost of reducing prevalence (instantaneously) from p₀ to P′ (with no contact tracing) plus the cost of reducing prevalence (instantaneously) from P′ to p₁ (with contact tracing): J(p₀, P′, α) + J(P′, p₁, α) where δ = 0 in the J(p₀, P′, α) term and δ = 1 in the J(P′, p₁, α) term.

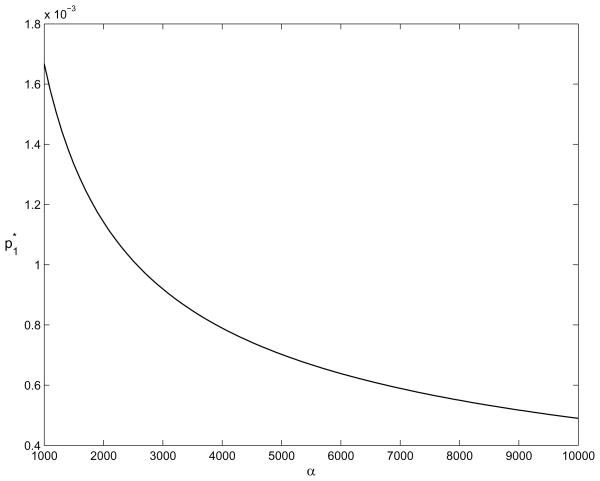
For the example problem worked out in the previous two sections, with the additional parameters r = 0.05 and λ̄ = ∞, Figure 5 shows the value of $p_1^{\ast }$ as a function of α, assuming that the constraint p₁ ≤ p₀ is not binding. The optimal solution to this problem with the constraint p₁ ≤ p₀ (thus the solution the general control problem (21)) is the smaller of p₀ and the value shown in the figure. Figure 5 illustrates the relationship between $p_1^{\ast }$ and α: as the cost of untreated disease increases, the optimal long-term prevalence decreases – which means that the optimal level of disease control (screening and contact tracing) increases.

Figure 5.

The value of $p_1^{\ast }$ as a function of α, assuming that the constraint p₁ ≤ p₀ is not binding

6 Discussion

We have developed a model to determine the cheapest mix of screening and contact tracing for control of an endemic disease. We considered three cases: 1) the population is large enough (and screening and contact tracing identify a small enough number of cases) such that disease prevalence is unchanged; 2) disease prevalence is reduced and the goal is to minimize long-term cost of control to achieve a specified prevalence; 3) disease prevalence is reduced and the goal is to minimize the total cost of identifying and treating disease plus the cost of untreated disease.

In all three cases, contact tracing is optimal only when disease prevalence is below a threshold value. When prevalence is above the threshold, enough disease cases are found per person screened that the cost per case identified via screening is less than the cost per case identified via contact tracing. When prevalence is below the threshold, mass screening becomes relatively more expensive per case identified compared to contact tracing, and contact tracing becomes part of the minimum cost solution. Additionally, when prevalence increases above the threshold and contact tracing is discontinued, the optimal of level of screening increases discontinuously to substitute for the contact tracing and thus maintain the desired degree of epidemic control.

We can apply our framework (in particular equation (12) or (20)) using data for several infectious diseases to estimate an implied value for the contact tracing threshold, P′. For simplicity we assume perfect screening: s_tp = 1 and s_fp = 0. For HIV we estimate C_S = $2.50 (Sanders et al., 2005), C_t = $175, 000 (Varghese et al., 1999), C_T = K_T (C_t +$439) (Varghese et al., 1999), and K_T = 0.12 (Varghese et al., 1999; Golden, 2002). These values imply a threshold prevalence of P′ = 0.6%. In the US, overall HIV prevalence is less than 0.4% (CDC, 2003), so our analysis suggests that contact tracing for HIV in the US makes sense except in high-prevalence areas. For syphilis we estimate C_S = $2.88 (Oxman and Doyle, 1996), C_t = $9.50 (Howell et al., 1997), C_T = $83.51 (Oxman and Doyle, 1996; Howell et al., 1997), and K_T = 1 (Oxman and Doyle, 1996), implying a threshold prevalence of P′ = 4%. This is well above the prevalence one might expect (e.g., ~ 0.05%, (CDC, 1993a)) suggesting that contact tracing for syphilis in the US makes economic sense. For TB, we estimate C_S = $5, C_t = $10, 000 (Rose, 1998), C_T = $200 + K_T C_t (Marchand et al., 1999), and K_T = 3 (Dasgupta et al., 2000), implying a threshold prevalence for contact tracing of P′ = 8%. Again, this suggests that TB contact tracing policies in the US make sense. Following similar reasoning, our analyses indicate that for diseases where the prevalence is high — such as TB in India or HIV in sub-Saharan Africa — contact tracing does not make economic sense.

In the first two formulations we presented, equilibrium disease prevalence is specified exogenously, whereas in the third formulation, the cost-minimizing equilibrium disease prevalence is found as part of the solution to the optimal control problem. This latter formulation has the advantage that it finds the best policy that satisfies the cost-effectiveness criterion implicitly given by the parameter α: the optimal level of disease control is such that the marginal cost of incremental disease control (the cost to find and treat additional disease cases) equals the marginal cost of non-control (the cost associated with undetected disease cases). Such a formulation could be particularly helpful to public health officials who may have to allocate a fixed total amount of funding across programs for the control of a number of infectious diseases. Use of the cost-effectiveness parameter α ensures that the amount of money spent to control a given disease (as determined by solving the optimal control problem) is commensurate with the value of controlling that disease.

Our work has several limitations. We based our analysis on a very simple compartmental model with random mixing. If the infectious disease is known to spread non-randomly (for example, through a contact network), then contact tracing could be more cost effective than assumed in our analysis. If it is possible to identify high-risk individuals or individuals who are centrally located in the contact network, then tracing the contacts of those individuals will (on average) cost less per case identified than will tracing the contacts of randomly selected index cases.

We assumed that the costs of screening and contact tracing were linear in the number of individuals screened and contacts traced. If these costs are nonlinear, such cost functions could readily be incorporated into our analysis. We assumed no delays in identifying new cases via walk-ins, screening, and contact tracing, and we did not include demographic or risk factors such as age, gender, or risk behaviors. For contact tracing, our analysis considered only the expected number of new cases identified per index case. Further research could explore the robustness of our results with more sophisticated models that (partially) lift these limitations, perhaps using simulation and network modeling.

Although simple, our analysis provides several insights. First, contact tracing is only cost effective when prevalence is below a threshold value. This threshold depends on the relative cost per case found by screening versus contact tracing. Second, for a given contact tracing policy (e.g., δ = 1), the screening rate needed to achieve a given prevalence or identify a specified number of cases is a decreasing function of disease prevalence. As prevalence increases above the threshold (and contact tracing is discontinued), the screening rate jumps discontinuously to a higher level. Third, these qualitative results hold when we consider unchanged or changed prevalence, and short-term or long-term costs.

Appendix

Here we justify our claim that $p_1^{\ast }$ is a nonincreasing function of λ̄.

Lemma

Consider control problem A where λ̄ = λ̄_A and problem B where λ̄ = λ̄_B ≤ λ̄_A. Then there exists solutions $p_A^{\ast }(t)$ and $p_B^{\ast }(t)$ ending up at $p_{1A}^{\ast }$ and $p_{1B}^{\ast }$ respectively such that $p_{1A}^{\ast }\le p_{1B}^{\ast }$.

Proof

Suppose by contradiction there exist two control problems A and B where $p_{1A}^{\ast }>p_{1B}^{\ast }$. Now modify the control problems so that $p_0=p_{1A}^{\ast }$. Then $p_A^{\ast }(t)=p_{1A}^{\ast }$ is an optimal solution of problem A due to the autonomous nature of the control problem. Since A is a relaxation of B, the cost of $p_A^{\ast }(·)$ is (weakly) less than the optimal cost of problem B. Hence $p_B^{\ast }(t)=p_A^{\ast }(t)=p_{1A}^{\ast }$ is also an optimal solution of problem B. In this solution $p_{1A}=p_{1B}^{\ast }$, a contradiction.

We now derive equation (28). Let $\mathrm{\Lambda }(t)={\int }_0^t\lambda (s)\text{d}s$. We perform a change of variables to write p as a function of Λ:

$$p^{\prime }(\mathrm{\Lambda })=\stackrel{.}{p}\frac{\text{d}t}{\text{d}\mathrm{\Lambda }}=f(p,\frac{\text{d}\mathrm{\Lambda }}{\text{d}t},\delta )\frac{\text{d}t}{\text{d}\mathrm{\Lambda }}$$ (29)

$$=(1-p)[\beta p+\eta ](1-\gamma (1+\delta K_T))\frac{\text{d}t}{\text{d}\mathrm{\Lambda }}-(1+\delta K_T)s_{\text{tp}}p.$$ (30)

For massive screening in very short times, Λ(t) is discontinuous and hence λ (t) is a Dirac delta function and $\frac{\text{d}t}{\text{d}\mathrm{\Lambda }}=0$ so

$$p^{\prime }(\mathrm{\Lambda })=-(1+\delta K_T)s_{\text{tp}}p(\mathrm{\Lambda })$$ (31)

$$p(\mathrm{\Lambda })=p_0{e}^{-\mathrm{\Lambda }{s}_{\text{tp}}(1+\delta K_T)}$$ (32)

where p(0) = p₀. Hence the number screened to reach prevalence p₁ solves p(Λ) = p₁:

$$\mathrm{\Lambda }=\frac{log{p}_0-log{p}_1}{(1+\delta K_T)s_{\text{tp}}}.$$ (33)

For costs we have a similar differential equation,

$$C^{\prime }(\mathrm{\Lambda })=C_S+C_t{s}_{\text{tp}}p(\mathrm{\Lambda })+C_{\text{fS}}{s}_{\text{fp}}(1-p(\mathrm{\Lambda }))+\delta C_T{s}_{\text{tp}}p(\mathrm{\Lambda }).$$ (34)

We substitute (32) and then solve the differential equation with the initial condition C(0) = 0:

$$C(\mathrm{\Lambda })=\frac{C_t{s}_{\text{tp}}-C_{\text{fS}}{s}_{\text{fp}}+\delta s_{\text{tp}}{C}_T}{(1+\delta K_T)s_{\text{tp}}}{p}_0(1-e^{-\mathrm{\Lambda }{s}_{\text{tp}}(1+\delta K_T)})+(C_S+C_{\text{fS}}{s}_{\text{fp}})\mathrm{\Lambda }.$$ (35)

Substituting in (33), we arrive at our conclusion.