Validation for 2D/3D registration II: The comparison of intensity- and gradient-based merit functions using a new gold standard data set

Abstract

Purpose:

A new gold standard data set for validation of 2D/3D registration based on a porcine cadaver head with attached fiducial markers was presented in the first part of this article. The advantage of this new phantom is the large amount of soft tissue, which simulates realistic conditions for registration. This article tests the performance of intensity- and gradient-based algorithms for 2D/3D registration using the new phantom data set.

Methods:

Intensity-based methods with four merit functions, namely, cross correlation, rank correlation, correlation ratio, and mutual information (MI), and two gradient-based algorithms, the backprojection gradient-based (BGB) registration method and the reconstruction gradient-based (RGB) registration method, were compared. Four volumes consisting of CBCT with two fields of view, 64 slice multidetector CT, and magnetic resonance-T1 weighted images were registered to a pair of kV x-ray images and a pair of MV images. A standardized evaluation methodology was employed. Targets were evenly spread over the volumes and 250 starting positions of the 3D volumes with initial displacements of up to 25 mm from the gold standard position were calculated. After the registration, the displacement from the gold standard was retrieved and the root mean square (RMS), mean, and standard deviation mean target registration errors (mTREs) over 250 registrations were derived. Additionally, the following merit properties were computed: Accuracy, capture range, number of minima, risk of nonconvergence, and distinctiveness of optimum for better comparison of the robustness of each merit.

Results:

Among the merit functions used for the intensity-based method, MI reached the best accuracy with an RMS mTRE down to 1.30 mm. Furthermore, it was the only merit function that could accurately register the CT to the kV x rays with the presence of tissue deformation. As for the gradient-based methods, BGB and RGB methods achieved subvoxel accuracy (RMS mTRE down to 0.56 and 0.70 mm, respectively). Overall, gradient-based similarity measures were found to be substantially more accurate than intensity-based methods and could cope with soft tissue deformation and enabled also accurate registrations of the MR-T1 volume to the kV x-ray image.

Conclusions:

In this article, the authors demonstrate the usefulness of a new phantom image data set for the evaluation of 2D/3D registration methods, which featured soft tissue deformation. The author’s evaluation shows that gradient-based methods are more accurate than intensity-based methods, especially when soft tissue deformation is present. However, the current nonoptimized implementations make them prohibitively slow for practical applications. On the other hand, the speed of the intensity-based method renders these more suitable for clinical use, while the accuracy is still competitive.

I. INTRODUCTION

In modern health care, medical imaging has become the technique of choice for patient treatment planning to reduce the invasiveness of either a surgical intervention or a radiotherapy treatment. However, the patient position in the treatment room might not be directly comparable to the orientation of the preinterventional images. The patient anatomy might also have changed in the time lapse between planning and treatment. For instance, the patient might have lost weight or a tumor might have shrunk in the case of radiotherapy. One or more intrainterventional 2D projective images are then usually acquired and a spatial transformation between the 2D images and the 3D preinterventional images is calculated in order to map the planning situation to the actual conditions. It is then possible to adapt the treatment planning if necessary or in the case of minimally invasive interventions display the actual position of the surgeon’s instruments relative to the planned trajectory and thereby avoid critical anatomical structures. Such a mapping between 2D and 3D images is referred to as 2D/3D image registration.

A variety of different 2D/3D registration methods were proposed in the past. The methods can be classified according to a number of criteria.¹ For 2D/3D registration, the classification according to image dimensionality and nature of registration basis is the most reasonable and unambiguous. The image dimensionality criterion is defined by the strategies to achieve spatial correspondence of images. In the case of 2D/3D registration, the 2D and 3D image information (image intensity or features) have to be brought in spatial correspondence, which can be achieved by three different strategies: Projection, backprojection, or reconstruction.¹ On the other hand, 2D/3D registration methods can also be classified according to the nature of registration basis, which yields extrinsic, intrinsic, and non-image-based methods. In this paper, we are only concerned with the intrinsic 2D/3D registration methods that rely solely on images of patient anatomy to achieve registration. The intrinsic methods can be further divided into three classes: Feature-based, intensity-based, and gradient-based methods.¹ Feature-based 2D/3D registration methods determine the transformation that minimizes the distances between 2D features of the intrainterventional image(s) and the corresponding 3D features, extracted from the preinterventional image or a model of the image.^2-5 On the other hand, intensity-based 2D/3D registrations rely solely on the information contained in voxels and pixels of 3D and 2D images, respectively. In contrast to feature-based methods, instead of the distance, the similarity measure, calculated using pixelwise comparison, defines the correspondence between 2D intrainterventional and 3D preinterventional images.^6-10 Finally, gradient-based methods use a direct relationship between 2D and 3D gradient vectors computed from 2D and 3D images, respectively, to achieve registration.^11-13 Each of these classes of methods can be further divided according to the strategy to achieve spatial correspondence discussed earlier. By far the most popular and reported group of 2D/3D registration methods are the intensity-based methods. They use the projection strategy based on simulated x-ray projection images called digitally reconstructed radiographs (DRRs).^6-10,14,15

2D/3D registration was applied in various medical fields like radiotherapy,^8,10,16 radiosurgery,⁹ orthopedic surgery,^12,17,18 interventional radiology,^3,19 and kinematic analysis.^20,21 To demonstrate the validity of a 2D/3D registration method for clinical use, a rigorous evaluation experiment must be performed. However, due to different applications, data sets, validation metrics, failure criteria, and implementation details, the results obtained from evaluation studies are not directly comparable. Furthermore, as sharing of image data sets in the research community is almost non-existent, additional comparison studies with other registration methods are not possible. To enable objective evaluation and comparison of different registration methods, publicly available standardized evaluation methodologies with image data sets, corresponding reference registrations, evaluation criteria, evaluation metric, and evaluation protocol are required. In the field of 2D/3D registration, two such standardized evaluation methodologies were proposed in the past.^22,23 Both featured a spine bone phantom with little soft tissues attached. Most recently, a new standardized evaluation methodology based on the Visible Human data set was presented. The data set features real 3D CT images of the spine and pelvis regions and synthetic 2D images, depicting soft tissues and outliers.²⁴ Although they represent valuable contributions to the field and enable standardized evaluation and comparison studies, the clinical realism is captured only to a limited extent.

In order to overcome the limitations of the precited evaluation data sets, we proposed a new gold standard image data set using a porcine head with attached fiducial markers,²⁵ which is described in the first part of this paper. The image data set features x-ray, CBCT, CT, and MR images acquired using the latest generation of medical imaging equipment for diagnostic radiology and image-guided radiation therapy. In this paper, the new data set was used to compare the performance of several intensity- and gradient-based 2D/3D registration methods.

II. MATERIALS AND METHODS

II.A. Merit functions

In this paper, six merit functions were compared. The first four merits belong to the group of the so-called intensity-based merit functions. In this case, a simulated x-ray image—a DRR—is derived from a CT volume by simulating the attenuation of virtual x rays. The DRR image is then compared to the x-ray image by means of a merit function (or similarity measure). Translational and rotational parameters (t_x,t_y, t_z,ω_x,ω_y,ω_z) yielding the rigid position of the volume T are iteratively generated by the optimizer in order to find the transformation of the volume for which the rendered DRR best matches the x-ray image. In this evaluation, four computationally efficient merit functions were used: Cross-correlation (CC),⁶ mutual information (MI),²⁶ correlation ratio (CR),²⁷ and rank correlation (RC).¹⁰ The last two measures belong to the group of the so-called gradient-based merit functions. These methods are based on the fact that rays emanating from the x-ray source that point to edges in the x-ray images are tangent to the surfaces of distinct anatomical structures. Intensity gradients calculated from the 2D images are put into correspondence with the gradient field from the 3D image. In this paper, the methods presented by Tomaževič et al.,¹¹ the backprojection gradient-based (BGB), and rather recently by Markelj et al.,¹³ the reconstruction gradient-based (RGB), were used. Since all methods were already described in literature, readers are referred to precited publications and to the review written by Markelj et al.¹ for additional information on the merit functions.

II.B. Standardized evaluation methodology

In order to assess the accuracy of 2D/3D registration methods, we followed the methodology proposed by van de Kraats et al.²³ Thereby, the mean target registration error (mTRE) metric, which is the mean of the distances between target points transformed by the ground truth and by the transformation obtained with the registration method, was used.^28,29 Points spread evenly over the volumes were used as targets. We used 454, 362, 405, 366, 372, and 366 target points for the CBCT big field of view (FOV), CBCT small FOV, CT, MR-T1, MR-T2, and MR-PD images, respectively. The starting positions were offsets of the gold standard position composed of three translational and three rotational parameters resulting in mTREs from 0 to 25 mm with a step of 1 mm. Ten starting positions were computed for each 1 mm mTRE interval, resulting in 250 starting positions altogether. We chose to report the accuracy by using only registrations with an accuracy better than a manually determined failure threshold of 5 mm and also by using all the registrations. The final accuracy was given as the root mean square (RMS), the mean, the standard deviation, and the median of the mTRE values after the registration. If a failure criterion was used, success rate, defined as the portion of successful against all registrations, was also computed to demonstrate the reliability of a method in reference to the chosen failure threshold. In order to further test the robustness of the merit functions, we computed the following properties introduced by Skerl et al.:³⁰ Accuracy (ACC), capture range, number of minima (NOM), risk of nonconvergence (RON), and distinctiveness of optimum (DO). However, in this way, the robustness cannot be completely evaluated for the RGB method. This is due to a mechanism of establishing correspondences along normals to anatomical structures using the RANSAC algorithm, which enables a more reliable and robust registration that is used in addition to the optimization of the similarity measure. Therefore, although the similarity measure of the RGB method may not be very robust by itself, the method can be nevertheless be very reliable due to the aforementioned mechanism. We also followed the protocol from Skerl et al.³⁰ for the sampling of the parametrical space. Since the 2D/3D registration methods must be adapted to the time and resource constraint in a clinical environment, the execution times of the methods were also reported.

II.C. Image data sets, image preprocessing, and masks

The comparison study of the 2D/3D registration methods was performed using the data set of the porcine head phantom. This data set consists of CBCT big FOV, CBCT small FOV, CT, MR-T1, MR-T2, and MR-PD 3D images and two pairs of kV and MV images taken from the lateral (LAT) and anterior-posterior (AP) views. The CBCT volumes and the x-ray pairs were acquired with a LINAC system. As none of the evaluated methods yielded useful results for the registration of MR-T2 and MR-PD images to x-ray images, these registrations were not included in the paper. The registrations were performed using the kV and then the MV image pairs. Since the LINAC system is regularly calibrated, the transformation matrix from the LAT view to the AP view of the x-ray images can be determined entirely by the system parameters, i.e., by the isocenter to flat panel distances and rotation of 90° from one to the other view.

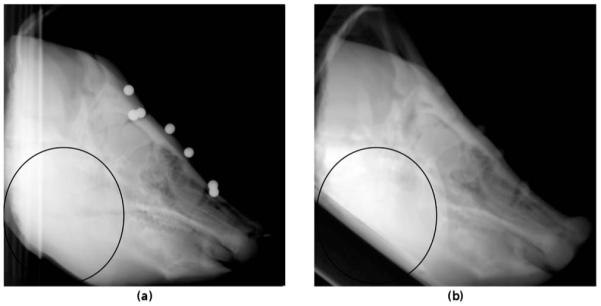
As the porcine head phantom features a significant amount of soft tissue, which is also deformed between the acquisition of the kV and MV x-ray and CBCT images and the acquisition of CT and MR images, we defined a centered circular region of interest (ROI) with a diameter of 200 pixels on the x-ray images. The ROI avoids deformed soft tissue anatomical regions [Figs. 1(a) and 1(b)]. Using a ROI is a common approach in rigid 2D/3D registration to initialize and speed up the registration.^6,8,31-34 However, in this study, it was used primarily to evaluate the robustness of the 2D/3D registration methods to the soft tissue deformation by performing registration experiments with and without the use of the ROI.

Fig. 1.

kV x-ray images with the ROI for LAT (a) and AP (b) views and the corresponding masks for LAT (c) and AP (d) views. Pixels in white were used to compute the merit functions and the intensity gradients of the 2D image.

Another encountered problem was the visibility of markers used to achieve the ground truth registration. To prevent registration bias, special masks were used to avoid the region of the markers while computing the merit functions for the intensity-based method or calculating the intensity gradients of the 2D image and the 3D gradient field of image intensity gradients for the gradient-based methods. The masks used in 2D images are shown in Figs. 1(c) and 1(d).

The implementation of the intensity-based method also required the intensities of the CT volume to be scaled to grayscale values in the range of 0–255 and windowed in order to have similar image content between DRRs and x-ray images,³⁵ while the x-ray images were resampled to an isotropic resolution of 1 mm. Only the intensities above a threshold value were used to render the DRR image. For the CBCT images, threshold values of 30 and 25 for the registrations with kV and MV images were used, respectively, while for the CT images, threshold values of 50 and 30 for the registrations with kV and MV images were used, respectively. For the MR images, no threshold was applied. The DRRs are generated using the ray-casting algorithm implemented on the graphical processing unit (GPU).³⁶ The bounding structures of the objects in the volume were refined using the cuberille algorithm.³⁷ Using this approach, a DRR from a volume size of 326×326×330 can be rendered in as low as 20 ms on an NVIDIA Quadro FX 570M graphics card with 512 MB video memory.³⁶

To calculate the 3D gradient field of image intensity gradients with high gradient magnitudes for the gradient-based methods, a Gaussian filter with a standard deviation of 0.5 mm for the CT and CBCT images and 1 mm for the MR images was used. The lower and the upper thresholds t_l and t_u of the 3D Canny filter were set as given in Table I. In the preprocessing step of the 2D images, the size of the Gaussian filter was set to 1 mm for the CT, CBCT big FOV, and MR-T1 images, and 0.5 mm for the CBCT small FOV image. The RGB method required also the size of the distance weighting parameter σ_d, which was set to 15 mm for the CT and CBCT images and to 10 mm for the MR images.

Table I.

Lower and upper thresholds t_l and t_u of the 3D Canny filter applied to extract the 3D gradient field for the gradient-based methods for different 3D modalities.

3D modality	tl	tu
CBCT big FOV	0.022	0.066
CBCT small FOV	0.02	0.06
CT	0.11	0.33
MT-T1	0.10	0.30

II.D. Software and hardware

The program used for intensity-based 2D/3D registration was developed in C++ using gcc 4.3 under Ubuntu 9.10. The minimizer chosen for the optimization was the NEUWOA software proposed recently by Powell.³⁸ The GPU parts were programed through OpenGL interface and Cg language. The program was run on a standard personal computer equipped with an Intel Core 2 Duo CPU of 3 GHz each and an NVIDIA GeForce 8800 GTS series graphics card with 640 MB RAM.

The software for the gradient-based methods was developed in C++ under MICROSOFT WINDOWS XP and was not optimized for speed. For both gradient-based methods, the original Powell optimizer was used.³⁹ The experiments were performed on an Intel Core 2 Duo, 2.13 GHz computer without the aid of a graphics card.

III. RESULTS

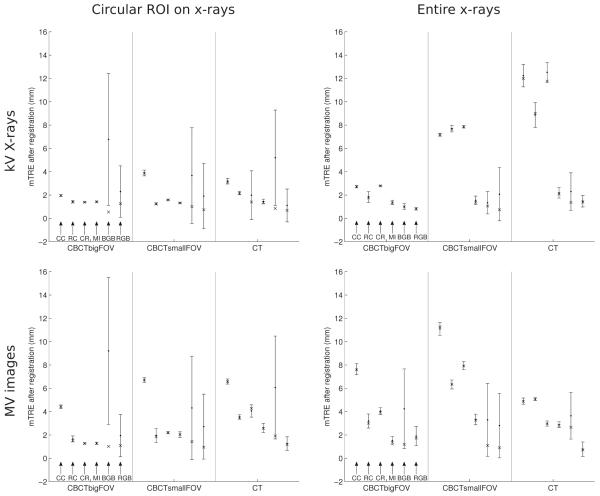
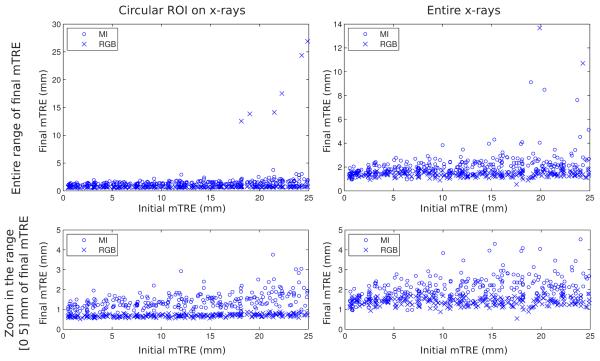
As defined in Sec. II B, the accuracy of the 2D/3D registration methods was calculated by using only registrations below a predefined failure threshold of 5 mm and also by using all the registrations. The results obtained by using a failure threshold are given in Table II as RMS mTRE values and success rates, while the results using all the registrations are given Table III as mean and standard deviation mTRE values. The results considering all the registrations are also given as plots of mean, standard deviation, and median mTREs in Fig. 3 to indicate the distribution of the registration errors. The registration results for the MR-T1 image were not included in Fig. 3 since the substantially larger mTREs would make the results of the CBCT and CT images very hard to read and interpret. The merit function properties ACC, capture range, NOM, RON, and DO are given in Table IV. Figure 4 finally presents individual registration results for the CT volume obtained with MI and RGB merit functions with the kV x-ray images with and without a ROI.

Table II.

RMS mTREs and success rates for different 3D modalities and kV and MV x-ray images with and without a ROI for the intensity-based method using four different merit functions (CC, RC, CR, and MI) and the gradient-based BGB and RGB methods. Only registrations below a failure threshold of 5 mm were considered for the calculation of accuracy. NA indicates that no successful registrations according to the failure criterion exist. The best results are typeset in bold.

3D image	X ray	ROI	mTRE: RMS (mm)						Success rate (%)
			CC	RC	CR	MI	BGB	RGB	CC	RC	CR	MI	BGB	RGB
CBCT big FOV	kV		1.97	1.46	1.40	1.43	0.56	1.30	100	100	100	100	69.6	93.2
			2.73	1.80	2.79	1.42	0.99	0.85	100	99.6	100	100	99.6	100
	MV		4.40	1.74	1.28	1.30	0.99	1.28	96.8	100	100	100	63.6	95.2
			4.95	3.11	4.00	1.61	1.17	1.72	0.4	98	97.2	99.2	79.6	98.4
CBCT small FOV	kV		3.88	1.27	1.59	1.33	1.01	0.84	97.6	100	100	100	87.6	94.4
			NA	NA	NA	1.57	1.07	0.76	0	0	0	98.8	97.6	92
	MV		NA	1.99	2.22	2.05	1.44	0.96	0	99.2	100	99.6	87.6	90
			NA	4.69	NA	3.24	1.10	0.94	0	2.8	0	94	88.0	89.2
CT	kV		3.20	2.19	1.67	1.50	0.82	0.70	99.2	100	98.8	100	74.8	97.6
			NA	4.62	NA	2.19	1.63	1.41	0	1.2	0	98.4	93.2	99.2
	MV		NA	3.55	3.83	2.65	1.89	1.20	0	99.6	82.4	98.4	77.6	99.6
			4.57	4.86	3.00	2.92	2.77	0.71	60	39.2	99.6	100	92.4	99.6
MR-T1	kV		NA	NA	3.93	NA	2.05	1.35	0	0	4	0	56.0	43.2
			NA	NA	NA	NA	2.96	3.51	0	0	0	0	22.4	21.2
	MV		NA	NA	NA	NA	NA	NA	0	0	0	0	0	0
			NA	NA	NA	NA	NA	NA	0	0	0	0	0	0

Table III.

Mean (MEAN) and standard deviation (STD) mTREs for different 3D modalities and kV and MV x-ray images with and without a ROI for the intensity-based method using four different merit functions (CC, RC, CR, and MI) and the gradient-based BGB and RGB methods. All registrations were considered for the calculation of accuracy. The best results for the CBCT and the CT images are typeset in bold.

3D image	X ray	ROI	mTRE: MEAN±STD (mm)
			CC	RC	CR	MI	BGB	RGB
CBCT big FOV	kV		1.96±0.14	1.44±0.23	1.40 ± 0.07	1.42±0.12	6.77±11.29	2.30±4.42
			2.72±0.21	1.84±0.93	2.78±0.10	1.37±0.36	1.02±0.51	0.82±0.20
	MV		4.42±0.31	1.66±0.52	1.28 ± 0.11	1.29±0.18	9.21±12.61	1.95±3.63
			7.63±0.94	3.20±1.21	4.04±0.59	1.51±0.72	4.25±6.83	1.90±1.64
CBCT small FOV	kV		3.89±0.5	1.26±0.18	1.59±0.09	1.33±0.10	3.67±8.18	1.91±5.59
			7.17±0.26	7.69±0.57	7.85±0.20	1.55±0.74	1.34±1.91	2.07±4.56
	MV		6.72±0.42	1.95±1.22	2.21±0.17	2.03±0.48	4.32±8.86	2.72±5.57
			11.09±1.08	6.33±0.77	7.94±0.68	3.33±0.91	3.30±6.23	2.81±5.53
CT	kV		3.19±0.48	2.17±0.30	1.99±4.19	1.44±0.41	5.2±8.18	1.11±2.82
			12.24±1.92	8.86±2.12	12.52±1.70	2.20±0.92	2.30±3.22	1.48±0.99
	MV		6.58±0.43	3.54±0.38	4.06±1.05	2.60±0.77	6.07±8.82	1.26±1.16
			4.90±0.52	5.07±0.24	2.98±0.45	2.88±0.51	3.65±4	0.78±1.24
MR-T1	kV		45.97±4.74	35.48±9.63	14.5±10.76	16.93±8.40	7.88±8.50	7.38±7.22
			11.70±0.28	14.77±0.68	11.21±0.31	7.58±0.99	17.35±16.11	22.51±30.56
	MV		51.47±3.55	39.49±6.32	17.43±12.98	15.46±6.66	14.65±10.83	12.02±6.37
			11±5.70	13.86±0.76	7.94±2.73	8.31±1.28	17.39±10.60	20.44±13.66

Fig. 3.

Plots of mean, standard deviation, and median mTREs of registrations of CBCT big FOV, CBCT small FOV, and CT images to kV and MV x-ray images with and without a ROI for the intensity-based method using four different merit functions (CC, RC, CR, and MI) and the gradient-based BGB and RGB methods. All registrations were considered for the calculation of accuracy statistics.

Table IV.

ACC, capture range, NOM, RON, and DO for different 3D modalities and kV and MV x-ray images with and without a ROI for the intensity-based method using four different merit functions (CC, RC, CR, and MI) and the gradient-based BGB and RGB methods. The best results in a column for each properties are typeset in bold.

		CBCT big FOV				CBCT small FOV				CT				MR-T1
		kV		MV		kV		MV		kV		MV		kV		MV
ROI
ACC	CC	1.14	1.15	1.24	2.87	1.31	2.42	1.61	3.31	0.93	3.65	1.79	2.62	18.99	4.64	17.33	4.82
	RC	0.95	0.74	0.60	1.97	0.94	2.20	0.62	2.24	1.01	2.11	2.29	3.90	22.49	4.61	17.70	8.93
	CR	0.94	1.07	0.81	1.98	0.93	2.36	1.34	2.52	0.59	3.88	1.37	2.08	2.03	2.87	4.15	5.54
	MI	0.91	0.68	0.68	0.58	0.88	0.68	0.83	0.86	0.57	0.64	0.91	1.70	6.20	1.88	5.94	5.60
	BGB	0.11	0.22	0.27	0.75	0.49	0.44	0.75	0.66	0.34	0.14	1.13	0.98	0.41	0.62	3.12	3.86
	RGB	0.46	0.16	0.51	0.45	0.40	0.43	0.58	0.66	0.34	0.14	0.48	0.20	0.58	0.66	4.48	2.77
Capture range	CC	62.57	79.20	42.77	79.20	63.18	78	61.62	78	51.83	9.78	50.86	0.98	0.72	1.44	0.72	1.44
	RC	28.51	14.26	34.06	0.79	39.78	78	10.14	68.64	44.99	0.98	18.58	0.98	0.72	0.72	0.72	0.72
	CR	33.26	79.20	26.14	67.32	33.54	78	26.52	58.50	29.34	0.98	0.98	0.98	0.72	72	0.72	0.72
	MI	25.34	56.23	34.06	0.79	37.44	24.96	0.78	1.56	25.43	53.79	0.98	0.98	0.72	0.72	0.72	0.72
	BGB	6.34	26.14	4.75	5.54	7.02	10.92	7.05	6.24	7.82	8.80	0.98	1.96	3.60	1.44	0.72	0.72
	RGB	6.34	22.97	7.13	14.26	5.46	7.80	6.24	6.24	6.85	8.80	7.82	7.82	3.60	1.44	0.72	0.72
NOM	CC	5	0	1	0	1	0	8	0	15	4	15	5	213	1	198	4
	RC	87	55	46	57	20	0	13	2	32	15	79	30	222	5	192	12
	CR	46	0	56	5	31	0	26	9	59	19	68	48	194	0	153	35
	MI	267	20	269	113	195	43	248	104	400	99	424	333	802	51	849	237
	BGB	742	142	680	646	972	573	986	910	926	428	823	729	941	915	824	927
	RGB	570	87	366	277	959	483	642	583	776	287	563	411	706	788	666	747
RON	CC	0.5	0	0	0	0	0	0.4	0	25.8	1.6	35.4	13.1	820	0	375.7	0
	RC	20.7	9.8	31.3	19.2	3.4	0	1.9	0.2	23	7.4	40.4	17.5	1178	0.4	411.6	0.7
	CR	3.7	0	9.8	0.2	4.7	0	9.6	0.3	32.7	7.3	33.8	29	44.5	0	37.9	2.9
	MI	481	1.4	65.5	30	24.6	6.36	57.7	22.5	144.4	20.20	22.5	14.3	80.7	8.6	681.5	75.8
	BGB	1138	32.3	3909	1606	77.3	211	2622	1537	1041	179	1821	1190	2765	4536	4638	5256
	RGB	701	26.2	408	230	1039	227	642	473	700	145	482	309	1902	4223	2541	4915
DO	CC	5.3	6.5	5.4	4.3	5.6	6.9	5.2	4.5	4.6	5.4	4.9	3.5	2.6	6.6	3.8	5.8
	RC	5	6	5.7	5.4	5.7	6.8	5.7	5.4	4.8	5.3	5.2	5.1	0.6	6.1	4.1	6.2
	CR	3.1	7.9	2.8	4.3	3.1	8.3	3	4.6	2.4	6.2	2.4	4.0	1.7	7.3	1.1	3.0
	MI	9.3	10.1	9.1	9.1	9	9.7	9	9.3	8	7.8	7.9	7.3	5.3	9.7	6.3	9.9
	BGB	10.2	10.6	6.5	7.5	10.3	10.9	8.3	9	7.9	8.8	5.7	7.5	9.9	8.4	3.5	2.3
	RGB	10.7	10.6	10.5	10.4	10.6	11.1	10.8	10.6	8	8.8	7.9	9	9.2	8.9	5.8	6.1

Fig. 4.

Plots of individual registration results of CT volume obtained with MI (circle) and RGB merit functions (cross) with the kV x-ray images with (left column) and without (right column) a ROI. The top row shows the individual results over the entire range of the final mTRE, the bottom row shows a zoom of the top plots in the range of 0–5 mm of the final mTRE.

The results obtained for the accuracy and reliability can be grouped according to the level of difficulty to perform a registration. For the present porcine image data set, such distinction is provided by the 3D images used for the registration. The least challenging registration is expected between the CBCT and the x-ray images. For this group of registrations, the intensities of the 3D and 2D images have a strong relationship due to the use of the same imaging equipment and imaging physics, although different x-ray energies are used, especially for the MV images. Furthermore, no soft tissue deformation exists between the 3D and 2D images since the porcine head was in the same position for the CBCT and x-ray acquisitions. Therefore, the x-ray images with and without the ROI should not have a great effect on the registration results. A more difficult registration can be expected between the CT and the x-ray images where the physical process of the image acquisition remains the same, although different photon energies and imaging devices with different detector characteristics are used. However, in this case, significant soft tissue deformation exists between the 2D and 3D images (Fig. 2). The registrations of the x-ray images with a ROI focus on the region with little or no tissue deformation and should therefore give better registration results concerning accuracy as well as reliability than the registrations with the entire x-ray images. Finally, the registrations performed between the MR-T1 and the x-ray images are the most challenging since in this case a multimodal registration must be performed. In addition, soft tissue deformation between the 3D and 2D images is also present. Better registration results should be obtained when a ROI is applied on the x-ray images.

Fig. 2.

kV x-ray in the LAT view (a) and a DRR generated from the CT volume at the gold standard position (b). The black ellipse highlights the differences between the x-ray and the DRR image due to the deformation of the soft tissue of the jaw and the positioning of the phantom during imaging with different imaging devices.

The registration results for the intensity-based method in Tables II-IV and Fig. 3 reflect the grouping according to the difficulty of registration. The best results were obtained with the CBCT images, especially when ROIs were used on the x-ray images, while accuracy was worse for the registrations with the CT images. It is clear from Table IV that overall ACC and capture range of intensity-based measures were lower with the CT than with CBCT images, while the NOM and RON were significantly higher, meaning a better robustness of the merits with CBCT images. Overall, the registration with the CBCT big FOV gave the best performance since it is the only volume that could be accurately registered by all merit functions when the entire x-ray images are considered. As known from the literature, the intensity-based method cannot deal with multimodal registrations like MR-T1 image to x-ray image registrations. For MR-T1 image, the amount of successful registrations were 0% (except for CR, which showed a very low rate (4%)), and the similarity properties were poor for this image (Table IV). In this evaluation, MI was the best merit function regarding the accuracy. If results obtained with the CBCT big FOV image are not considered, it was also the only merit function that provided accurate results when a ROI was not applied to the x-ray images. The accuracies for the successful registrations (given as the RMS of mTRE) with the kV images were between 1.33 and 2.19 mm, while the MV-based registrations gave accuracies between 1.30 and 3.24 mm (Table II). However, from Table IV, the capture range was globally the lowest of the intensity-based measures with highest NOM and RON. MI was the most accurate but least robust of the intensity-based merit functions. Good overall results could be observed for the CR and RC merit functions, which performed well in all registration experiments using kV and MV x-ray images with a ROI. In the experiments using these images, the accuracies of successful registrations for the CR merit function were between 1.40 and 1.67 mm and between 1.28 and 3.83 mm, respectively, while for the RC merit function, the accuracies of successful registrations were between 1.27 and 2.19 mm and between 1.74 and 3.55 mm, respectively (Table II). CR showed higher capture range and lower NOM and RON, revealing a better robustness than RC merit. CC gave reliable results only for registrations with the kV x-ray images using a ROI, except when registrations were performed with the CBCT big FOV images. The CC kV-based registrations with a ROI resulted in accuracies of successful registrations between 1.97 and 3.88 mm (Table II). However, it was the most robust merit with the highest capture range, lowest NOM, and RON. In Table IV, it can be observed that for registration of CBCT images with entire kV x-ray images, the CC, RC, and CR similarity measures had excellent convergence properties according to capture range, NOM, and RON parameters, while at the same time the registration results were very poor (Table II). This is also true for CR similarity measure and the registration of MR-T1 volume to the entire kV x-ray images. This is due to the fact that capture range, NOM, and RON parameters are determined in relation to the maximum of the lines of the sampled space (cf. Ref. 30), which was, in these cases, away from the gold standard and therefore lead to poor registration results.

The gradient-based methods performed very accurately for the CBCT big FOV, CBCT small FOV, and CT images. As expected from the literature,¹³ the RGB method gave the more reliable results (Fig. 3), while the accuracies of successful registrations of the two gradient-based methods were overall similar, except for the registration of CT to MV x-ray images without a ROI. For the BGB and RGB methods, the registrations with the kV images led to accuracies of successful registrations between 0.56 and 1.63 mm and between 0.70 and 1.41 mm, respectively, while the accuracies of successful registrations with the MV images were between 0.99 and 2.77 mm and between 0.71 and 1.72 mm, respectively. The overall accuracies given in Table III exhibited larger differences between the methods due to the smaller robustness of the BGB method. The introduction of the ROI in the x-ray images improved the accuracy of the BGB method, but not the RBG method, accuracies of which were not significantly affected by the deformations of the soft tissue. The gradient-based methods enabled also accurate multimodal MR-T1 image to kV x-ray image registrations with accuracies of successful registrations ranging from 1.35 to 2.05 mm when ROI was applied and from 2.96 to 3.51 mm when the entire x-ray images were used. However, for multimodal registrations, the reliability was significantly reduced (Tables II and III) with the rate of successful registration falling down to 22.4% and 21.2% for BGB and RGB methods, respectively. Table IV also demonstrated that the similarity measure of the RGB method was globally more robust than that of the BGB method. The capture ranges were overall similar, but for the BGB similarity measure, the NOM and RON parameters were always better (except for CBCT small FOV and kV images), while the DO parameter was worse than in the case of the RGB similarity measure.

If considering the results of the intensity-based registrations and gradient-based methods, putting aside results with MR-T1 images, Table IV showed a better robustness for the intensity-based registrations with a capture range up to 79.20 against 26.14 at best for gradient-based methods and lower NOM and RON. However, the gradient-based methods were always more accurate with ACC down to 0.11 against 0.68 at best for intensity-based method and they featured better DO and mTRE statistics (Tables II and III and Figs. 3 and 4). The differences in accuracy were emphasized for the CT to x-ray registrations, where the accuracy of successful registrations between CT and kV x-ray images for the intensity-based methods was approximately 1.50 mm at best, while the accuracy of the gradient-based method was always below 1.63 mm (Table II).

The results of the time requirements for computing a registration in Table V exhibit a significant advantage of the intensity-based method over the gradient-based methods. While the mean time to compute an intensity-based registration using a GPU was between 1.21 and 8.21 s, the gradient-based methods required between 45 and 100 s and between 63 and 214 s for the BGB and RGB methods, respectively. Although similar hardware was used to perform the registrations, one could argue that these results are not directly comparable since the speedup of intensity-based methods received a lot of attention over the past years and numerous approaches to this end were proposed,^8,15,40-42 some of which were applied to speed up the intensity-based method used in this paper. Furthermore, as fast DRR generation is also a research topic of other research communities, a lot of effort was put into software and hardware solutions to make it as fast as possible. On the other hand, only a handful of gradient-based methods were proposed,^11-13 none of which focused on the speed of the registration. Gradient-based methods used in this paper could be accelerated in a number of ways, for instance, by optimal coding and by the parallelization of finding the point-to-point geometrical correspondences to mention just two. Nevertheless, due to current state-of-the-art implementations of the intensity-based methods, the presumption that the intensity-based methods are time consuming due to the DRR generation must be reconsidered as their execution approaches real time.^27,43

Table V.

Registration times for different 3D modalities and kV and MV x-ray images with and without a ROI for the intensity-based method using four different merit functions (CC, RC, CR, and MI) and the gradient-based BGB and RGB methods. The best results are typeset in bold.

3D image	X ray	ROI used	Registration time (s)
			CC	RC	CR	MI	BGB	RGB
CBCT big FOV	kV		2.20	2.27	2.57	2.14	65	67
			5.46	5.85	5.69	5.21	69	207
	MV		1.48	1.52	1.81	1.41	45	63
			2.30	2.31	2.57	2.13	46	129
CBCT small FOV	kV		1.96	2.10	2.31	1.84	50	78
			4.51	4.96	4.93	4.40	67	81.5
	MV		1.29	1.35	1.49	1.21	45	74
			2.00	1.95	2.11	1.68	48	123
CT	kV		2.22	2.39	2.76	2.17	71	79
			8.21	8.01	7.64	5.70	96	199
	MV		1.61	1.64	1.78	1.53	52	73
			2.38	2.46	2.60	2.08	60	133
MR-T1	kV		2.93	2.55	2.71	2.03	100	100
			4.63	5.10	4.99	4.37	77	214
	MV		1.71	1.61	1.76	1.30	73	98
			2.33	2.01	2.60	1.83	60	143

IV. DISCUSSION

Image registration is an important enabling technology of image-guided interventions that provides image guidance by bringing the preintervention data and intraintervention data into the same coordinate frame.^44,45 However, integration of medical image registration into larger medical systems affects the clinical decision making process. Therefore, before any registration algorithm can be used in the medical theater, a rigorous performance assessment process, typically using a gold standard data set, must be performed to satisfy several requirements. The most important are those that concern accuracy, reliability, robustness, computation time, and invasiveness of intraoperative data acquisition.^46-49

In this paper, intensity- and gradient-based methods for 2D/3D registration were compared using a new gold standard data set, which was devised using a porcine head with attached fiducial markers. An intrinsic feature of the phantom presented is the fact that it contains a considerable amount of soft tissue and mobile skeletal structures (mainly the surprisingly large mandible). From a histogram of the minimum enclosing cuboid of the cadaver specimen in the CT scan, one can see that 31% of the volume is soft tissue within a range of −750–100 HU, whereas the remaining voxels in a range of 100–2272 HU only comprise 20.5% of the tissue. This can be explained by the considerable amount of musculature, fat, and salivary gland tissue in the neck and mandible region and the small intracranial volume. Therefore, we conclude that the phantom cannot be compared to a human skull, but is more similar in terms of tissue composition and mobility to anatomical regions like the human pelvis. In conclusion, the phantom is closer to a realistic clinical situation than previously available phantoms made of sections of the spine^22,23 and the data set based on the images from Visible Human project.²⁴ Moreover, the data set encompassed images of various modalities with state-of-the-art imaging devices. Therefore, the porcine head phantom allowed the comparison of the merit functions in a more complex situation which underlined the strength and weakness of each method.

The evaluation study of the intensity-based methods showed MI as the more accurate but less robust merit function, while CR proved very reliable and accurate with kV as well as MV x-ray images when a ROI was used and therefore when no significant soft tissue deformation was present between the 3D and 2D images. RC performed very similar to CR, while CC performed well only for registrations using kV x-ray images with a ROI. In this evaluation, the merit functions gave results that are in agreement with their theoretical limitations.^6,10,50,51 CC performed well only when an approximately linear relationship existed between the intensities of images undergoing registration, while CR and RC methods, designed to be more robust to the differences in the distribution of image intensities, extended their performance to registrations of MV x-ray images, however, met their limitation when soft tissue deformation was introduced in the 3D image. Finally, MI seems to have overcome the difficulty of the sparse histogram population known from the literature,^6,26,51 due to the large size of the specimen and the registration using two views, and performed reasonably well also for registrations of CT to kV and MV x-ray images with and without the ROI. An interesting thing to note is also that the intensity-based registration gave the best overall performance for the registrations using CBCT big FOV images, which outperformed registrations with the CBCT small FOV images, e.g., when the entire x-ray images were used for registration (Tables II and III).

The evaluation of the gradient-based methods has shown high accuracy to soft tissue deformation. This is especially true for the RGB method, which achieved similar registration accuracy regardless of the presence of the soft tissue deformations. The BGB method, on the other hand, exhibited more accuracy than intensity-based registration using MI, although it was significantly less robust (Table IV). The gradient methods performed especially well for the registration of the CT to kV as well as MV x-ray images. Furthermore, when registrations failures occurred, large mTRE standard deviations demonstrate large registration errors, which enable straightforward identification of misregistration (cf. registrations of CBCT big FOV images to kV and MV x-ray images using a ROI in Fig. 3).

The comparison study performed with the proposed gold standard data set and the standardized evaluation methodology between the intensity- and gradient-based 2D/3D registration methods is the second such study in literature we are aware of. The first was performed by van de Kraats et al.,²³ although on a smaller scale. They used only one merit function for the intensity-based method and compared it to the BGB gradient-based method. Furthermore, only kV x-ray images were used, although experiments using only one x-ray image were also performed. When using two x-ray images, they found the gradient-based method more accurate than the intensity-based method. The present study confirmed their conclusions. An important advantage of gradient over the intensity-based methods is also that accurate registrations with the MR-T1 images can be obtained (Table II). However, the gradient-based methods are not without its flaws. First, the gradient similarity measures demonstrated less robustness in the sense that they are more sensitive to the increase in the number of local minima when the initial displacement is increased. Then, while in the evaluation performed by van de Kraats et al.²³ the BGB gradient-based method was faster than the intensity-based method, our evaluation has shown that a state-of-the-art implementation of the intensity-based method using the GPU significantly outperforms the BGB and especially the RGB gradient-based methods in terms of the speed of registration. Furthermore, the intensity-based method is far better suited for the registration of a 3D image to a single x-ray image, where an accurate and reliable registration can be obtained,^3,6,10,42 which is not the case for the gradient-based methods.²³ However, the reported differences between the two groups of methods are also due to the specific implementations of methods used in our evaluation. While the intensity-based method was designed for intrafractional tumor position monitoring during radiotherapy,^10,52 the gradient-based methods used in this paper were not designed for a specific application. Therefore, the implementations of the intensity-based method focused on speed, while the implementations of the gradient-based methods focused more on the accuracy.

V. CONCLUSIONS

A comparison study between the intensity-based registration method with four different merit functions and two different gradient-based methods using two x-ray views was conducted. A new clinically realistic gold standard image data set with the standardized evaluation methodology that features kV and MV x-ray images and CBCT, CT, MR-T1, MR-T2, and MR-PD images of a porcine cadaver head phantom with all relevant soft tissue was used.

Concerning the intensity-based methods, MI similarity measure exhibited the best accuracy and enabled registrations of CBCT and CT images to kV as well as MV x-ray images even when soft tissue deformations between CT and x-ray images were present. However, MI was also the less robust intensity-based merit with lower capture range and higher NOM and RON. CR and RC also enabled registrations of CBCT and CT to kV and MV images, but failed when soft tissue deformations were introduced. Finally, CC enabled only registrations with kV x-ray images with no deformations. As shown in other studies,^13,23 both gradient-based methods outperformed the intensity-based method in terms of accuracy and enabled also MR-T1 to x-ray registration. Although the similarity measure used by the RGB methods was less robust, the mechanism of establishing correspondences along normals to anatomical structures using the RANSAC algorithm nevertheless enabled reliable and robust registration. However, the RGB method is very time consuming and requires at least two x-ray images.

To the best of our knowledge, this is the largest comparison study of intensity- and gradient-based methods and the first evaluation study of the gradient-based methods with the MV x-ray images in literature. Due to acquisition of image data set with state-of-the-art radiotherapy equipment, the results of the study are of special interest for image-guided radiotherapy applications, although valuable also for image-guided surgery, radiosurgery, and interventional radiology.