Tachycardia-induced early afterdepolarizations: insights into potential ionic mechanisms from computer simulations

Abstract

Although early afterdepolarizations (EADs) are classically thought to occur at slow heart rates, mounting evidence suggests that EADs may also occur at rapid heart rates produced by tachyarrhythmias, due to Ca overload of the sarcoplasmic reticulum (SR) leading to spontaneous SR Ca release. We hypothesized that the mechanism of tachycardia-induced EADs depends on the spatial and temporal morphology of spontaneous SR Ca release, and tested this hypothesis in computer simulations using a ventricular action potential mathematical model. Using two previously suggested spontaneous release morphologies, we found two distinct tachycardia-induced EAD mechanisms: one mechanistically similar to bradycardia-induced EADs, the other to delayed afterdepolarizations (DADs).

1. Introduction

Life-threatening cardiac arrhythmias, resulting from abnormal electrical activity in tissue, have been the subject of numerous clinical, physiological, and computational studies. The propagation of electrical excitation in tissue is determined in many respects by processes in individual cells. In particular, the appearance of cellular early afterdepolarizations (EADs) and delayed afterdepolarizations (DADs) are though to exert great influence on electrical behavior at the tissue level. EADs induced by rapid pacing rates, such as those rates associated with ventricular tachycardia, may facilitate the development of more pathological arrhythmias, such as torsades des pointes or ventricular fibrillation.

EADs have classically been described as occurring during bradycardia, under conditions of reduced repolarization reserve caused by drugs [1–3], ion channel mutations [4, 5], remodeling of ion channels [6], or electrolyte abnormalities such as hypokalemia [7]. These bradycardia-induced EADs are generally thought to be due to reduced repolarization reserve allowing regenerative reactivation of the L-type Ca current (I_Ca,L) in a voltage (V) window within which partial activation and incomplete inactivation of I_Ca,L overlap [8]. As I_Ca,L reactivates and initiates the EAD upstroke, it secondarily causes a corresponding cytosolic Ca (Ca_i) aftertransient just after the EAD upstroke, mediated by I_Ca,L–gated Ca-induced Ca release (CICR) from the sarcoplasmic reticulum (SR). In this case, the EAD upstroke occurs before the Ca_i aftertransient. EADs of this type have been termed early EADs [9], since they tend to occur during the plateau phase of the action potential (AP).

However, EADs have also been observed at rapid heart rates (tachycardia), both in experiments [10] and computer simulations [11–13]. Experimental evidence has suggested [14, 15] that these EADs may be generated by spontaneous (i.e. non-I_Ca,L gated) release of Ca from the SR occurring during the repolarization phase. In this mechanism, the Ca_i aftertransient occurs first due to SR and cytoplasmic Ca overload triggering spontaneous release, which secondarily triggers the corresponding EAD upstroke by activating inward Ca-sensitive currents to produce a transient inward current (I_ti). This is similar to the classic mechanism of DADs, but with spontaneous release occurring during systole (repolarization) instead of diastole [16]. EADs of this type have been termed late EADs [9], since they tend to occur during late repolarization phase, with a lower takeoff potential than early EADs.

Spontaneous SR Ca release is caused by local SR Ca release events that propagate through the cytoplasm as Ca waves [17, 18], suggesting that different patterns of local release may facilitate different global spontaneous release morphology and timing. We hypothesize that the mechanism of tachycardia-induced EADs may depend on the spatial and temporal patterns of spontaneous release waves.

To test this hypothesis, we performed computer simulation of the ventricular AP using a mathematical model [19]. In this model, spontaneous SR Ca release is represented using a modified Hodgkin-Huxley type equation for gating processes. The parameters responsible for spontaneous release kinetics, amplitude, and timing in the AP cycle can be modified to produce a spectrum of patterns. We studied two different patterns, which correspond to two physiologically plausible situations. The first is a low peak amplitude, long duration spontaneous release event [19] that represents spontaneous release initiated at a single site which then propagates slowly through the remainder of the cell. The second is a high amplitude, short duration spontaneous release event [20] that represents spontaneous release initiated near-simultaneously at multiple sites, so that the Ca waves originating at each site rapidly fuse together, abbreviating the duration and increasing the summated amplitude of global Ca release transient.

We found that the mechanism of tachycardia-induced EADs depended on the spontaneous release characteristics. We observed two types of tachycardia-induced EADs, one produced by each spontaneous release pattern, when our model was altered to simulate long QT 1 (LQT1) syndrome. One type of tachycardia-induced EAD, mechanistically similar to early EADs, was associated with the low amplitude, long duration spontaneous release starting during late diastole just before the AP upstroke. The other type, mechanistically similar to late EADs, was caused by the high amplitude, short duration spontaneous release occurring during systole.

We compare these mechanisms to experimental findings and discuss their possible relationships to long QT syndromes (LQTS), as well as to catecholaminergic polymorphic ventricular tachycardia (CPVT) syndromes. Our results provide insights into the potential ionic mechanisms governing the interplay between spontaneous release, DADs and EADs, which may have important implications for the initiation [21] and perpetuation [11–13] of tachyarrhythmias in cardiac tissue.

2. Methods

In the present study, we utilized the Chudin model of the guinea pig ventricular AP [19]. An AP model does not consider the spatially distributed properties of a real cardiac myocyte, instead averaging cell-wide characteristics. The Chudin model incorporates several properties of Ca dynamics that have been observed in physiological experiments: graded CICR gated by I_Ca,L [22], prevention of complete SR depletion during normal CICR [23], accumulation of Ca in the cytosol (Ca_i) and Ca in the junctional SR (Ca_jsr) during high-frequency stimulation [24], and spontaneous release (denoted in the model as the Ca²⁺ ion flux J_spon) dependent on Ca overload concentrations in both the SR and cytosol [25]. This model has since been modified [26] to reproduce Ca alternans by reformulating CICR as a time dependent process with a steep dependence on Ca_jsr (see Shiferaw et al. [27]), while leaving unchanged the above mentioned Ca dynamics properties (for details see Appendix).

The Chudin model was chosen because it can reproduce different J_spon wave morphologies, such as those suggested in previous simulations [19, 20], by modifying J_spon parameter values. The equation for J_spon in the Chudin model is:

$$J_{\mathit{spon}}=G_{\mathit{spon}}p({Ca}_{\mathit{jsr}}-{Ca}_i)$$ (Eq. 1)

G_spon = 60 ms⁻¹ is the spontaneous release channel conductance. The gate variable p can be considered the probability of J_spon occurrence. It is described by a Hodgkin-Huxley type differential equation, though dependent on Ca_i and Ca_jsr rather than V. Ca_jsr-Ca_i, the Ca²⁺ gradient between the JSR and cytosol, is the chemical driving force.

The differential equation describing the gate variable p is:

$$\frac{dp}{dt}=\frac{p_{\infty }-p}{{\tau }_p}$$ (Eq. 2)

$${\tau }_p={\tau }_1+{\tau }_2(1-p_{\infty })$$ (Eq. 3)

τ_p, the time constant of variable p, effectively determines the duration of a J_spon event. If τ_p is increased (by increasing parameters τ₁ and τ₂), the duration of J_spon events also increases. p_∞, the steady state value of p, is a bilinear approximation of a Hodgkin-Huxley type sigmoidal function of two variables (Ca_i and Ca_jsr), explicitly defined by the following equation (and illustrated in Fig. 1A):

$$p_{\infty }=\{\begin{array}{ll}0,\hfill & if\mathit{region}I\hfill \\ \frac{{Ca}_{\mathit{jsr}}-K1}{K3-K1},\hfill & if\mathit{region}II(a)\hfill \\ \left(\frac{{Ca}_i-K2}{K4-K2}\right)\left(\frac{{Ca}_{\mathit{jsr}}-K1}{K3-K1}\right),\hfill & if\mathit{region}II(b)\hfill \\ \frac{{Ca}_i-K2}{K4-K2},\hfill & if\mathit{region}II(c)\hfill \\ 1,\hfill & if\mathit{region}\mathit{III}\hfill \end{array}$$ (Eq. 4)

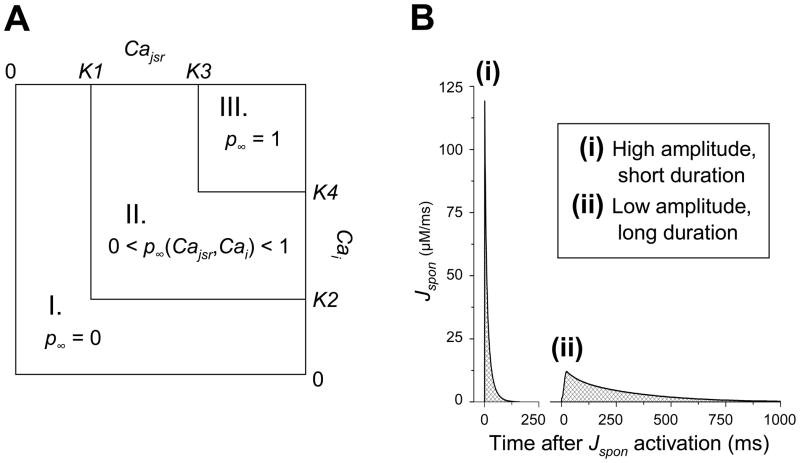
Fig. 1.

Spontaneous release (J_spon) formulation. (A) Calculation of p_∞, the steady state of the J_spon gate variable p, as a function of Ca_jsr and Ca_i. In region I (Ca_jsr < K1 or Ca_i < K2), p_∞ = 0. In region II (Ca_jsr > K1, Ca_i > K2, and either Ca_jsr < K3 or Ca_i < K4), p_∞ is a linear function of Ca_jsr and Ca_i. In region III (Ca_jsr > K3 and Ca_i > K4), p_∞ = 1. (B) Sample traces of J_spon activations (elicited via high-frequency stimulation) for two different sets of J_spon parameter values. One set (ii) yields low amplitude, long duration J_spon events. The other set (i) yields high amplitude (via reduction of K3-K1 and K4-K2), short duration (via reduction of τ_p) J_spon events. The total Ca released from the SR (crosshatched region) is relatively equal for both morphologies.

If either Ca_jsr or Ca_i are below the lower thresholds set by parameters K1 and K2, respectively, then p_∞ = 0 (see Fig. 1 A, region I). If both Ca_jsr and Ca_i exceed the lower thresholds K1 and K2, but either fails to exceed the upper threshold set by parameters K3 and K4, respectively, then p_∞ is approximated by a linear function of Ca_jsr and Ca_i (see Fig. 1 A, region II). If both Ca_jsr and Ca_i exceed the upper thresholds K3 and K4, then p_∞ = 1 (see Fig. 1 A, region III).

K1 and K2 are the threshold for a J_spon event to occur. The J_spon threshold effectively determines the timing of the onset of J_spon events in the AP cycle. During phase 3 and 4 of a normal AP, Ca_jsr is increasing and Ca_i is decreasing. Thus, to make J_spon start earlier in the AP cycle, K1 (the Ca_jsr threshold) should be decreased and K2 (the Ca_i threshold) should be increased. Table 1 presents the two pairs of K1 and K2 values used in the present study: one pair that leads to J_spon events starting during diastole (temporally outside the AP) and the other that leads to J_spon events during systole (during the AP).

Table 1.

Timing of the J_spon onset in the AP cycle for different J_spon thresholds.

K1 (mM)	K2 (μM)	Timing of Jspon onset
0.65	0.7	Diastole
0.58	1.12	Systole

The differences (K3-K1) and (K4-K2) effectively determine the amplitude of a J_spon event. If either of the differences are reduced (either by increasing the lower thresholds K1 and K2, or decreasing the upper thresholds K3 and K4), then the slope of the p_∞ function and p_∞ itself are increased, leading to higher-amplitude J_spon events.

A desired J_spon morphology can be obtained by setting the desired duration (choosing the appropriate value of τ_p) and amplitude (choosing appropriate values of K3-K1 and K4-K2). Table 2 describes the J_spon morphology for two different sets of parameter values used in the AP model for the present study. The first set of parameter values produces relatively low amplitude, long duration J_spon events (see Fig. 1 Bii), as in [19]. In the second set of parameter values, τ_p is an order of magnitude smaller than in the original, while the differences (K3-K1) and (K4-K2) are at least an order of magnitude larger. Thus, it produces high amplitude, short duration J_spon events (see Fig. 1 Bi), as in [20]. The total Ca in an average release was conserved between morphologies.

Table 2.

J_spon morphology for two different sets of parameter values.

K3 - K1 (mM)	K4 - K2 (μM)	τp (ms)	Jspon morphology
0.5	0.6	20 + 200(1 − p∞)	Low amplitude, long duration
0.0003	0.08	20(1 − p∞)	High amplitude, short duration

By first selecting the timing of the J_spon onset in the AP cycle from Table 1 (setting the values of K1 and K2), and then selecting a J_spon morphology from Table 2 (setting the values of τ_p, K3, and K4), we obtained four different J_spon events to study: low amplitude, long duration J_spon during diastole; low amplitude, long duration J_spon during systole; high amplitude, short duration J_spon during diastole; and high amplitude, short duration J_spon during systole.

The appearance of EADs under conditions of tachycardia in the Chudin AP model was contingent on several factors. The AP model itself needed to be altered to simulate LQT1, which was accomplished by reducing the slow component of the delayed rectifier K current (I_Ks) by 54%. This reduces outward current during repolarization, reducing repolarization reserve and prolonging AP duration (APD). With this modification, we induced J_spon and EADs by rapid pacing, applying an external stimulus at a high frequency (6.25 Hz, or basic cycle length 160 ms, similar to the rapid pacing rates experienced by individual cells during tachyarrhythmias) to induce Ca accumulation in the cytosol and SR and leading to the appearance of J_spon. The train of periodic stimuli was stopped when dV/dt became positive during repolarization (indicating a potential EAD). Otherwise, the next stimulus would be large enough to elicit a new AP that would overwhelm the potential EAD.

Computer simulations were performed on a desktop computer. The ordinary differential equations were numerically integrated using an explicit Euler method. The time step was dynamically adaptive to rapid changes in V, varying between 0.005 and 0.1 ms. Reducing the time step to 0.0005 ms did not significantly alter the results.

3. Results

3.1 Rapid pacing induces spontaneous release

Pacing the AP model at a rapid rate causes accumulation of both Ca_i and Ca_jsr. Eventually, Ca_i and Ca_jsr reach overload conditions, triggering J_spon. The number of paced beats necessary to cause the first J_spon event depends primarily on the pacing rate; faster rates cause faster Ca accumulation and hence J_spon occurs sooner. J_spon temporarily drains Ca_jsr, but accumulation resumes with subsequent paced beats and J_spon continues to occur with a period that depends primarily on the pacing rate. J_spon influences the AP by increasing Ca_i and altering Ca-sensitive membrane currents such as I_Ca,L, I_NaCaX and I_ns,Ca. As we will show, the induction of EADs by J_spon is determined by the J_spon morphology and timing of the J_spon onset in the AP cycle.

3.2 “Early” EADs caused by a low amplitude, long duration J_spon during diastole

When the AP model with the low amplitude, long duration J_spon during diastole (see Methods and Tables 1 and 2) is paced at a rate of 160 ms, J_spon occurs after approximately 2.4 s (see Fig. 2 A, trace of J_spon). The J_spon onset starts in late diastole just before the start of the new AP cycle (see Fig. 2 A, vertical dotted line labeled “J_spon onset” illustrates relative timing of J_spon onset and AP upstroke). J_spon continues through the AP, augmenting the Ca_i transient (see Fig. 2 A, compare the results with J_spon, solid trace, and the results with J_spon manually prevented, dashed trace). Increased Ca_i potentiates Ca-sensitive inward repolarization currents such as I_NaCaX and the Ca-activated nonselective cation current (I_ns,Ca), reducing repolarization reserve enough to produce an overt EAD (see Fig. 2 A, trace of V). If the diastolic J_spon is manually prevented, no EAD occurs (see Fig. 2 A, dashed traces).

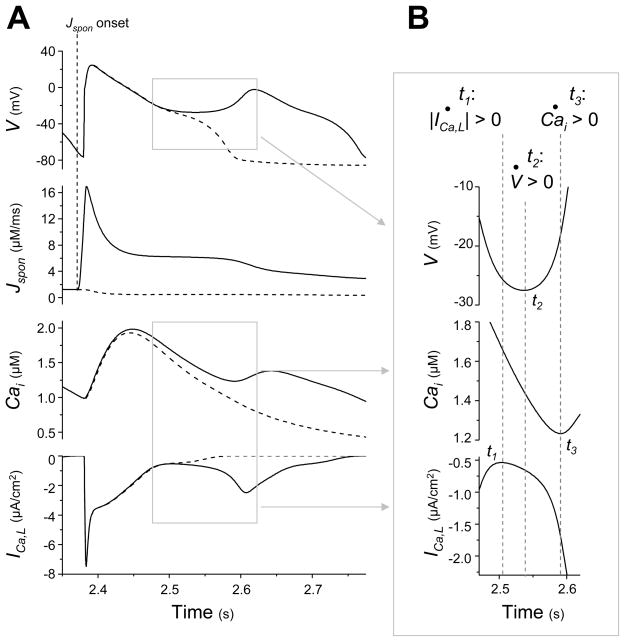
Fig. 2.

A low amplitude, long duration J_spon event starting during late diastole causes an I_Ca,L-induced (“early”) EAD. (A) Traces of V, J_spon, Ca_i, and I_Ca,L in time during a tachycardia-induced EAD in an AP model with the low amplitude, long duration J_spon (solid lines). After stimulating the AP model at a rate of 160 ms for approximately 2.4 s, a large J_spon activation starts in late diastole 8 ms before the next paced AP (vertical dotted line labeled “J_spon onset” indicates start of J_spon). An EAD occurs during the repolarization phase of the ensuing AP (t ≈ 2.6 s), approximately 170 ms after the J_spon onset. A Ca_i aftertransient and I_Ca,L reactivation are observed in conjunction with the EAD. J_spon is small but nonzero during the EAD itself. Dashed traces show the result of preventing the large J_spon activation by setting p_∞ = 0 just before it would otherwise occur. (B) Enlargement of the traces in (A) during EAD upstroke, illuminating the exact sequence of events. Time derivatives are denoted with dots (i.e., dV/dt = V̇). Slow I_Ca,L reactivation (indicated by d(|I_Ca,L|)/dt > 0) occurs first, at time t₁. The window current increases inward current and reverses repolarization, inducing the V upstroke beginning at time t₂ (indicated by dV/dt > 0). The increasing V has a positive feedback effect on I_Ca,L, causing rapid reactivation and driving a Ca_i upstroke (indicated by d(Ca_i)/dt > 0) at time t₃.

To determine which current carries the depolarizing charge of the EAD upstroke, we examine the rate of change of the membrane ionic currents immediately before the EAD upstroke (Table 3, row İ_i,EAD). The candidate currents are all those reducing repolarization reserve during this time, either increasing inward currents or decreasing outward currents. In either case, the rate of change will be negative, since convention dictates inward currents as negative and outward currents as positive. Four such currents reduce repolarization reserve immediately before the EAD upstroke: increasing inward current I_Ca,L and decreasing outward currents I_Ks, I_Kr (the rapid component of the delayed rectifier K current), and I_p(Ca) (the sarcolemmal Ca²⁺ pump current). These candidates can be narrowed down by comparing their rates of change to the rates of change they exhibit during the same phase of repolarization of an AP without an EAD (Table 3, row İ_{i, noEAD}). Of the four, only I_Ca,L is reducing repolarization reserve more in the EAD case than in the case with no EAD, indicated by the negative value in row İ_i,EAD; − İ_{i, noEAD} of Table 3. Therefore, we conclude I_Ca,L is the current responsible for the EAD upstroke (as in early EADs). I_NaCaX and I_ns,Ca are not causing the EAD upstroke themselves, though they are producing inward current during that time (Table 3, row İ_i,EAD). Rather, sustained J_spon through the AP potentiates I_NaCaX and I_ns,Ca, contributing to the initial delay of repolarization that then allows I_Ca,L reactivation to cause the EAD upstroke.

Table 3.

Ionic currents responsible for low amplitude, long duration J_spon-induced EAD upstroke. Three calculations of the average rate of change of membrane ionic currents, İ_i (μA/(cm² × s) ), over a 35 ms interval: immediately before the EAD upstroke (İ_i,EAD), during the same phase of repolarization of an AP without an EAD (İ_{i, noEAD}), and the difference between the first two cases (İ_i,EAD − İ_{i, noEAD}).

	İNa	İCa,L	İKr	İKs	İNaCaX	İns,Ca	İp(Ca)	İV
İi,EAD	0	−2.9	−3.1	−2.7	2.0	1.4	−0.9	1.8
İi, noEAD	0	6.6	−5.4	−6.6	−1.6	−5.6	−1.2	16.9
İi,EAD − İi, noEAD	0	−9.5	2.3	3.9	3.6	7.0	0.3	−15.1

Examining the EAD closely (see Fig. 2 B) confirms the role of I_Ca,L as depolarizing charge carrier and determines the relative timing of the EAD upstroke and Ca_i aftertransient. At time t = 2.500 s, we find that V is decreasing (dV/dt < 0), the Ca_i transient is declining (d(Ca_i)/dt < 0), and I_Ca,L is decreasing (d(|I_Ca,L|)/dt < 0), indicating normal repolarization. We then find that I_Ca,L reactivation (d(|I_Ca,L|)/dt > 0) occurs at time t₁ = 2.505 s, the EAD upstroke (dV/dt > 0) occurs next at time t₂ = 2.538 s, and the Ca_i aftertransient (d(Ca_i)/dt > 0) occurs last at time t₃ = 2.593 s. Suppressing I_Ca,L reactivation, by manually enforcing a monotonic decrease of |I_Ca,L| beginning at t = 2.500 s, eliminates the EAD and Ca_i aftertransient.

The underlying cause of the I_Ca,L reactivation is the disparity of the time constants for the activation gate variable, d, and the inactivation gate variable, f, as described by Zeng et al. [28]. During repolarization of an AP with no EAD, the I_Ca,L current decreases to 0 as d decreases to 0, closing the activation gate. Meanwhile, f increases to represent recovery from inactivation. When the balance of the currents is altered via J_spon and amplified inward Ca-sensitive currents, the AP temporarily enters a long plateau region where V is virtually constant. Since the time constant of d is approximately 50 times faster than the time constant of f for this range of V, d approaches its steady value much faster. V has become virtually constant and so d becomes virtually constant, but f continues to increase since it is slower to reach its steady state. Hence, the product df begins to increase and I_Ca,L reactivation occurs.

Low amplitude, long duration J_spon occurring during systole or early diastole causes neither EADs nor DADs (as shown later in Fig. 4). The ensuing AP is too delayed for J_spon to affect repolarization reserve and produce I_Ca,L reactivation, and the low amplitude does not release Ca²⁺ fast enough to cause a Ca_i aftertransient via I_ti. Instead, repolarization proceeds as normal.

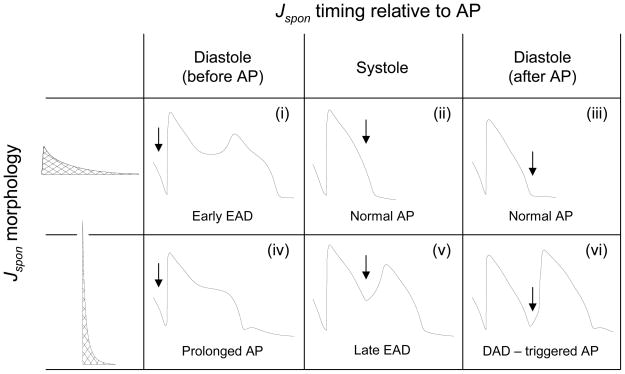
Fig. 4.

Effect of J_spon parameter values and timing of the J_spon onset in the AP cycle on AP morphology. Table shows representative V traces for the two J_spon morphologies (low amplitude/long duration versus high amplitude/short duration) and three different times of J_spon onset relative to the final paced AP (starting in diastole just before the AP, in systole, and in diastole just after the AP). Arrow indicates exact time J_spon onset begins. For the low amplitude/long duration case, J_spon in diastole just before the AP can cause an early EAD (i), as in Fig. 2. J_spon in systole or in diastole just after the AP has no effect on the AP (ii,iii). For the high amplitude/short duration case, J_spon in diastole just before the AP prolongs the AP (iv, the DAD in the trace is due to a second, smaller J_spon event occurring just after the AP). J_spon in systole can cause a late EAD (v), as in Fig. 4. J_spon in diastole just after the AP can cause a DAD that then triggers a new AP (vi).

3.3 “Late” EADs caused by high amplitude, short duration J_spon during systole

The AP model was modified to generate a high amplitude, short duration J_spon, as in [20] (see Methods and Tables 1 and 2). When paced at a rate of 160 ms, J_spon occurs during systole after approximately 1.6 s (see Fig. 3A, solid traces). Both an EAD and a Ca_i aftertransient occur in conjunction with the J_spon, as well as I_Ca,L reactivation. If the J_spon event is manually prevented during simulation, no EAD occurs (see Fig. 3A, dashed traces).

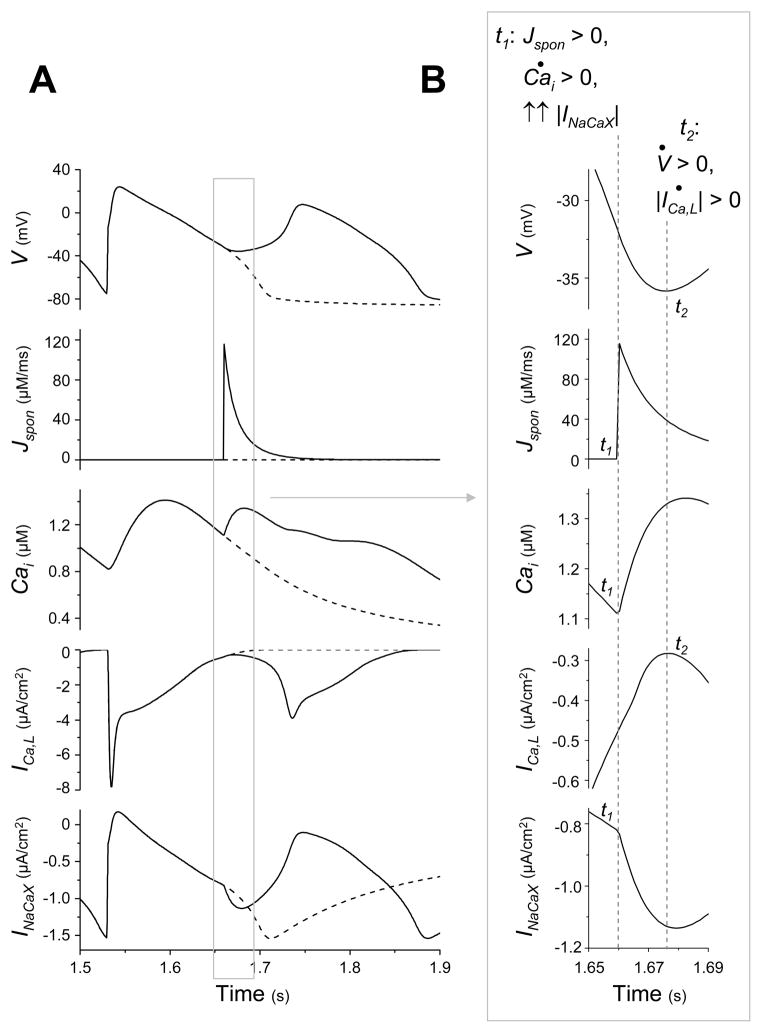
Fig. 3.

A high amplitude, short duration J_spon event during systole causes an I_ti-induced (“late”) EAD. (A) Traces of V, J_spon, Ca_i, I_Ca,L, and I_NaCaX in time during a tachycardia-induced EAD in an AP model with high amplitude, short duration J_spon (solid lines). After stimulating the AP model at a rate of 160 ms for approximately 1.5 s, a large J_spon activation occurs in systole, during the AP repolarization phase (approximately 1.66 s). An EAD, Ca_i aftertransient, I_Ca,L reactivation and sudden increase in I_NaCaX are observed in conjunction with the J_spon event. Dashed traces show the result of preventing the J_spon event by setting p_∞ = 0 just before it would otherwise occur. (B) Enlargement of the traces in (A) during EAD upstroke, illuminating the exact sequence of events. Time derivatives are denoted with dots (i.e., dV/dt = V̇). The large J_spon event occurs at time t₁, immediately causing a Ca_i aftertransient (indicated by d(Ca_i)/dt > 0). The increased Ca_i causes an immediate increase in reverse-mode I_NaCaX activity (and a similar increase in I_ns,Ca, not shown). This transient inward current, commonly termed I_ti, tips the balance of currents and reverses repolarization, inducing the EAD upstroke in V beginning at time t₂ (indicated by dV/dt > 0) and associated I_Ca,L current. Unlike the previous case, where the EAD upstroke in V drove the Ca_i aftertransient, here the Ca_i aftertransient drives the EAD upstroke in V.

To determine the mechanism by which J_spon causes the EAD, we examined the timing of the EAD closely (see Fig. 3B). At time t = 1.650 s, repolarization is proceeding normally. Then, at time t₁ = 1.660 s, J_spon occurs. The Ca_i aftertransient (d(Ca_i)/dt > 0) immediately begins, and the magnitude of I_NaCaX immediately begins to increase at an accelerated rate. Only later, at time t₂ = 1.676 s, do the EAD upstroke and I_Ca,L reactivation occur. In this case, the EAD is caused by I_NaCaX (as in late EADs) and I_Ca,L reactivation is a secondary effect.

Fig. 3 shows that the accelerated I_NaCaX increase is in response to the systolic J_spon, contributing to a transient inward current (I_ti). To determine what other currents may contribute to I_ti, we compare the rate of change of the membrane ionic currents immediately before the EAD upstroke to their rate of change during the same phase of repolarization of an AP without an EAD (see Table 4), in the same manner as we did in the previous case. Along with I_NaCaX, I_ns,Ca is the only other current (disregarding the strictly V-dependent currents) reducing repolarization reserve more in the EAD case than the non-EAD case.

Table 4.

Ionic currents responsible for a high amplitude, short duration J_spon-induced EAD upstroke. Three calculations of the average rate of change of membrane ionic currents, İ_i (μA/(cm² × s) ), over a 20 ms interval: immediately before the EAD upstroke (İ_i,EAD), during the same phase of repolarization of an AP without an EAD (İ_{i, noEAD}), and the difference between the first two cases (İ_i,EAD − İ_{i, noEAD}).

	İNa	İCa,L	İKr	İKs	İNaCaX	İns,Ca	İp(Ca)	İV
İi,EAD	0.0	13.2	−8.1	−10.6	−19.5	−43.6	2.6	30.9
İi, noEAD	0.0	12.9	−10.5	−13.7	−8.8	−18.6	−1.1	44.5
İi,EAD − İi, noEAD	0.0	0.3	2.5	3.1	−10.8	−25.0	3.7	−13.6

A high amplitude, short duration J_spon occurring during diastole after the final paced AP is capable of causing a DAD via the same I_ti-mediated mechanism. Depending on the size of J_spon, the DAD may exceed membrane excitation threshold and trigger a new AP. High amplitude, short duration J_spon occurring during diastole just before the final paced AP can cause neither an EAD nor DAD. There is not enough time for a DAD to occur, since the arrival of the next stimulus interrupts it and produces a full AP. I_Ca,L reactivation does not occur and cause an EAD on the ensuing AP, since the short duration of the J_spon prevents it from maintaining the potentiated Ca-sensitive inward currents through the repolarization phase.

A summary of the general findings for different J_spon formulations and timings of the J_spon onset in the AP cycle is presented in Fig. 4.

4. Discussion and Conclusions

EADs and DADs are widely believed to act as triggers in the initiation of tachyarrhythmias [16]. We have shown in our previous computer simulation studies how EADs may potentially sustain and exacerbate already established tachyarrhythmias [11–13]. Despite these important roles, the exact mechanism of EADs, particularly those occurring during tachyarrhythmias, is not known in detail. While spontaneous release is believed to cause EADs and DADs occurring at fast pacing rates [10], a lack of physiological data for the processes underlying spontaneous release prevents a full understanding of this mechanism. Mathematical modeling and computer simulation allow us to explore the effect of different predicted patterns of spontaneous release on tachycardia-induced EADs and delineate possible underlying cellular mechanisms. The results, discussed below, provide a framework for future experimental investigation to determine the physiological mechanisms relating spontaneous release characteristics to EADs, DADs, and triggered activity. Expanding our knowledge about mechanisms at the cellular level may help us better understand arrhythmias at the tissue-level (particularly ventricular fibrillation and defibrillation processes).

4.1 Two types of tachycardia-induced EADs: early and late

As described in [17, 18], spontaneous release in cardiac myocytes results from localized SR Ca release, originating in one or several regions of the cell due to Ca overload conditions, which then propagates via CICR as a Ca wave throughout the remainder of the cytoplasm. We replicate two spontaneous Ca wave morphologies suggested by existing AP models [19, 20]. These morphologies may phenomenologically represent possible types of propagating Ca waves in a cell. A low amplitude, long duration J_spon [19] may correspond to a Ca wave originating from a single site in the cell, that then propagates slowly (0.1–0.5 mm/s [24]) to the rest of the cell. A high amplitude, short duration J_spon [20] may correspond to a Ca wave originating near-simultaneously from multiple sites in the cell, that then more rapidly reaches the rest of the cell.

By adjusting the timing of these J_spon morphologies, we identified two distinct mechanisms for tachycardia-induced EADs (Fig. 4). In the first case, low amplitude, long duration J_spon starting during late diastole could cause an EAD on the ensuing AP. The EAD upstroke was caused by I_Ca,L reactivation and preceded the Ca_i aftertransient; these have been termed early EADs. To create an EAD, the late diastolic timing of this type of J_spon event was critical. If J_spon occurred earlier in diastole or during systole, it never caused a frank EAD, although it could influence APD. Moreover, the low peak amplitude of J_spon was insufficient to cause a measurable DAD. In the second case, high amplitude, short duration J_spon during systole could immediately cause an EAD on the same AP. The Ca_i aftertransient preceded the EAD upstroke, which was caused by I_ti; these have been termed late EADs. When this type of J_spon event occurred during diastole, it could cause a DAD via the same mechanism. Depending on the size of J_spon, the DAD could exceed cell membrane excitation threshold and trigger a new AP.

4.2 Role of repolarization reserve

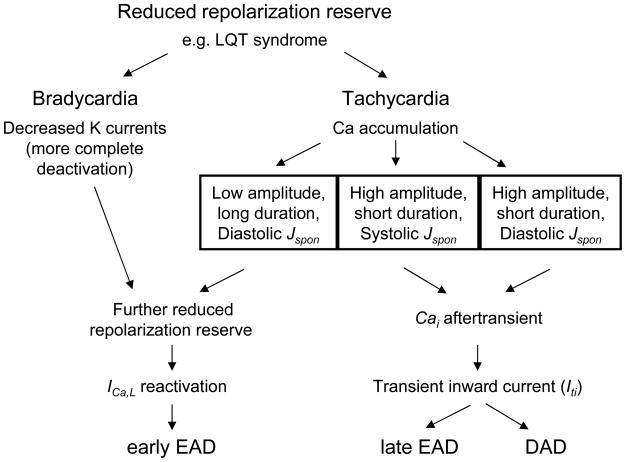
Fig. 5 presents a flowchart illustrating the similarities and differences between the mechanisms of bradycardia-induced EADs, DADs, and our two types of tachycardia-induced EADs. While EADs are known to occur under conditions of reduced repolarization reserve, such as the various LQT syndromes, they usually require further reduction of repolarization reserve via rate-dependent mechanisms. Under conditions of bradycardia, repolarization reserve is reduced by more complete deactivation of outward K currents during long diastolic intervals [29]. Under conditions of tachycardia, we found that repolarization reserve is reduced by larger Ca-sensitive inward currents during the AP plateau, which in this model is caused by a larger overall Ca_i transient when the J_spon-triggered release summated with the AP-triggered, I_CaL-gated CICR. It is possible that a smaller summated Ca_i transient, resulting from a differently timed pre-release of SR Ca by J_spon, could also reduce repolarization reserve during the subsequent AP by reducing Ca-induced inactivation of I_Ca,L and thereby cause an EAD. However, we did not simulate this case. In either the case of a larger or smaller overall Ca_i transient, the key element is that the J_spon induced alteration of the Ca_i transient causes a reduction in repolarization reserve during the subsequent AP, allowing I_Ca,L reactivation to induce an early EAD.

Fig. 5.

Flowchart illustrating the proposed mechanisms for bradycardia-induced EADs, tachycardia-induced EADs, and DADs.

In both the bradycardia- and tachycardia-induced cases, reduced repolarization reserve facilitates reactivation of I_Ca,L and appearance of an EAD. Both these bradycardia- and tachycardia-induced EADs can be considered early EADs, though the mechanisms causing reduced repolarization reserve are different.

If a high amplitude, short duration J_spon is delivered in late diastole, the diastolic peak does not persist long enough to amplify the Ca-sensitive currents during the repolarization phase of the ensuing AP, and an I_Ca,L reactivation-induced EAD cannot occur. However, as presented in Fig. 5, the large J_spon Ca flux can instantaneously produce a Ca_i aftertransient and I_ti that causes an afterdepolarization. Depending on the timing of the J_spon event, the afterdepolarization may be a late EAD (if occurring during systole) or a DAD (if occurring during diastole).

4.3 Spontaneous release generating paired DADs and EADs

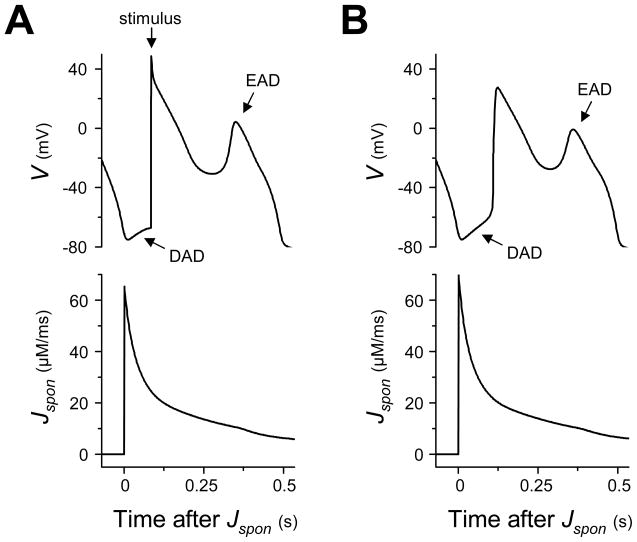
A shared spontaneous release-dependent mechanism for EADs and DADs has been suggested by both Priori et al. [30] and Volders et al. [14]. These groups found that the β-adrenergic agonist isoproterenol could induce both EADs and DADs in the same myocyte. In particular, they found that EADs and DADs could be associated with the same AP: a “late-coupled” DAD could occur just before (and often be interrupted by) the upstroke of a paced AP that then exhibited an EAD. An obvious mechanism would be two separate J_spon events, one J_spon peak occurring in diastole and the second in systole. However, our results suggest a more interesting alternative, which depends on an intermediate pattern of spontaneous release between the extremes of the low amplitude, long duration J_spon and the high amplitude, short duration J_spon. If we amplify the peak of the long duration J_spon to an intermediate value between our high and low amplitude cases, a J_spon event starting in late diastole is now sufficient to induce a DAD, and the elevation in Ca_i persists long enough to reduce repolarization reserve and cause an early EAD in the subsequent AP (Fig. 6A), reproducing late-coupled DADs similar to those observed in the physiological experiments [14, 30]. A single J_spon event starting in diastole explaining both the DAD and EAD may be more plausible, as two separate J_spon events occurring so temporally close to one another may be unlikely. Amplifying the J_spon peak further, but still considerably smaller than the high amplitude case, we observe a DAD that itself triggers an AP with an early EAD (Fig. 6B), reproducing another phenomenon observed in the data of Priori et al. [30]. Thus, our simulation results can reproduce (see Fig. 6) observed physiological phenomena [14, 30] and suggest alternative, more parsimonious explanations.

Fig. 6.

Amplified long duration J_spon can produce late-coupled DADs and DAD-triggered APs exhibiting EADs. (A) J_spon conductance is increased in the low amplitude, long duration case to produce a J_spon event with long duration and amplitude approximately 47% between the low and high amplitude cases. A single J_spon event starting in late diatole elicits an overt DAD that is interrupted by the subsequent paced AP (the pacing stimulus, applied 0.083 s after the J_spon onset, is delayed by 75 ms from the normal cycle length to make the DAD more evident). This J_spon event also produces an early EAD on the AP. (B) J_spon conductance increased further to produce a long duration J_spon event with amplitude approximately 52% between the low and high amplitude cases. A single J_spon event starting in late diastole elicits a suprathreshold DAD that triggers an AP. This J_spon event also produces an early EAD on the triggered AP.

4.5 Limitations and clinical implications

Although computer modeling is a powerful tool for predicting and identifying novel cardiac arrhythmia mechanisms, the relationship to real cardiac arrhythmias cannot be established without solid experimental confirmation. In particular, it will be especially important to establish direct relationships between Ca phenomena in spatially distributed cardiac cells and the phenomena observed with our spatially averaged AP model. However, it is encouraging that our simulations have replicated a number of experimentally observed afterdepolarization phenomena [14, 30]. Further work will be necessary to determine whether both EAD mechanisms are physiologically relevant. Until the development of required physiological imaging technology, our results based on previously introduced spontaneous release morphologies may be considered mathematical modeling predictions. In the mean time, as a preliminary speculation, it might hypothesized that when excitation-contraction features are relatively normal, such as in LQTS, spontaneous release may be more likely to occur in diastole when the luminal SR Ca content is highest and ryanodine receptor excitability is most recovered, favoring the early EAD mechanism. Conversely, when excitation-contraction coupling exhibits accelerated recovery of ryanodine receptor excitability, such as in CPVT syndromes and heart failure [31], spontaneous release during systole may become more likely, promoting the late EAD mechanism, especially if spontaneous release were initiated from multiple sites.

Arrhythmias in LQT1 are potentiated by sympathetic stimulation [32]. In our previous simulation studies we found that although EADs occurred during reentry in LQT1 tissue, they were not able to induce triggered activity unless paired with a moderate increase in sympathetic tone [12]. The increased sympathetic tone potentiates Ca cycling, acceleration Ca accumulation and leading to more powerful J_spon and consequently more powerful EADs [33].

In the present study we simulated LQT1, but our previous tissue simulations strongly suggest these results are generalizable to a number of physiologically relevant conditions. The appearance of tachycardia-induced early EADs during reentrant tachycardia was shown for both simulated LQT1 (caused by reduced I_Ks) and LQT2 (caused by reduced I_Kr), with qualitatively similar effects on wave propagation [12]. We would expect the same results in virtually any ionic model with reduced repolarization reserve and uninhibited Ca cycling, whether due to reduced K current (LQT1,2), incomplete Na current inactivation (LQT3), or increased sensitivity of inward repolarization currents to elevated Ca_i [13].

We have also shown in tissue studies that our results are generalizable to different cell types. The true myocardium is heterogeneous with respect to repolarization reserve and Ca cycling, both transmurally and base-to-apex [34–36]. We have shown in transmurally heterogeneous 3-dimensional tissue studies that regions of relatively reduced repolarization reserve (such as mid-myocardial M-cells) were more prone to our tachycardia-induced early EADs [33].

In our AP model, all ion channel gating processes were represented with a Hodgkin-Huxley type formulation of independent gating variables. A Markovian approach to gating processes introduces interdependent gate variables (channel state probabilities), allowing physiologically realistic representations of individual ion channel gating proteins and direct simulation of channel protein mutations. Markovian representations of several important cardiac ion channels have been introduced in previous studies [4, 37]. We chose not to use Markovian models because they require a significant increase in computational complexity. Furthermore, our experience has shown that introducing Markovian representations for single channels alters the quantitative results for the channel, but does not change the qualitative behaviors [38].

5. Summary

Early afterdepolarizations (EADs) are thought to be an important cause of ventricular arrhythmias in genetic channelopathies, drug reactions, and heart failure. Classically observed at slow heart rates, EADs can also be induced by rapid heart rates, exacerbated by conditions promoting Ca overload in the SR and cytoplasm, and subsequent spontaneous release. To explore possible underlying ionic mechanisms of these EADs, we performed computer simulations using a ventricular action potential mathematical model. We determined how changing model parameters, replicating patterns of spontaneous release amplitude and timing suggested by previous studies, affected EAD formation. We found that: 1) During tachycardia, spontaneous SR Ca release can generate both EADs and DADs. Depending on the morphology and timing of spontaneous release, EADs can be produced via two distinct mechanisms that previously have been termed early and late. 2) Early EADs are caused by low amplitude, long duration spontaneous release starting in late diastole just before the ensuing paced AP. The EAD upstroke is generated by reactivation of window I_Ca,L, mechanistically similar to bradycardia-induced EADs. 3) Late EADs are more likely to be caused by high amplitude, short duration spontaneous release occurring in systole. The EAD upstroke is generated by a spontaneous release-induced transient inward current (carried by I_NaCaX and I_ns,Ca), mechanistically similar to DADs. 4) A single medium amplitude, long duration spontaneous release starting in late diastole can produce both a DAD and an early EAD on the subsequent paced AP. Increasing spontaneous release amplitude slightly further can produce a DAD that triggers an AP that then exhibits an early EAD. These results coincide with experimental data and suggest a novel explanation.

Biographies

Ray B. Huffaker was born in Sacramento, CA, USA, in 1979. He received a B.S. in Biochemistry and a B.S. in Mathematics from Washington State University, USA, in 2002. He received an M.S. and Ph.D. in Computer Science from the University of California, Los Angeles, USA, in 2005 and 2008, respectively. His thesis concerned the mathematical modeling and computer simulation of cardiac tissue.

Richard Samade was born in Los Angeles, CA, USA, in 1982. He received a B.S. in Electrical Engineering, with a Biomedical Option, from the University of California, Los Angeles, USA, in 2006 and a M.S., from the same University, in 2006. Since 2006, he has been performing his Ph.D. research in the Biomedical Engineering Department of the same University, on the subject of mathematical modeling and computer simulation of defibrillation.

Dr. James N. Weiss was born in New Jersey, USA, in 1949. He received his AB degree from the Hamilton College in New York in 1971, and his MD degree from the University of Pennsylvania, Philadelphia, USA, in 1975, where he also completed his Internal Medicine Residency. He then completed a Cardiology Fellowship at UCLA School of Medicine in Los Angeles, CA, USA, in 1981, where he has since remained on the faculty. He is currently the Chief of Cardiology and Director of the Cardiovascular Research Laboratory. His research interests focus on arrhythmia and ischemia biology.

Dr. Boris Kogan was born in Kishinev, Moldavia, in 1914. He received his Masters Degree in Automatic Control Science in 1938 from the Electrical Engineering department of Kharkov Polytechnic, USSR, and his Ph.D. in automatic control in 1945 from the Institute of Automation and Telemechanics, Moscow Academy of Sciences, USSR. In 1962 he received the degree of Doctor of Engineering Sciences from the Air Force Military Academy in Moscow, USSR. From 1940 to 1981 he conducted research at the Institute of Control Science, USSR, where in 1956 he founded and directed the computer simulation laboratory. From 1948 to 1980, he was a full professor working part-time at the Moscow University for Physics and Engineering, USSR, in the Department of Radio-Physics. He arrived at the University of California, Los Angeles, USA, in 1987 as a visiting scholar and has since become an adjunct professor in the Computer Science and Biomedical Engineering Departments. In 2005, the IEEE Control Systems Society held a special history plenary session to honor Dr. Kogan’s life’s work. His current research interest is mathematical modeling and computer simulation of complex dynamical systems, particularly the application of massively parallel computer systems to simulation of cardiac electrophysiological problems.

Appendix

The implementation of Ca alternans was done in the same manner as in [26] and was based on the original investigation presented in [27], which involved the reformulation of CICR into a time-dependent process:

$$\frac{{dJ}_{\mathit{CICR}}}{dt}=g_{\mathit{CICR}}{P}_o{P}_v(Q({Ca}_{\mathit{jsr}})-{Ca}_i)-\frac{J_{\mathit{CICR}}}{{\tau }_{\mathit{CICR}}}$$ (Eq. 5)

with the initial condition J_CICR(t = 0) = 0. Here, J_CICR is the CICR flux from the JSR, g_CICR = 2.0 ms⁻¹ the conductance, and τ_CICR = 30 ms is the averaged time constant of Ca sparks throughout the myocyte. The open probability P_o reflects the dependence of CICR on Ca entry via I_Ca,L and the probability function P_v represents the voltage dependent nature of CICR. Expressions for both P_o and P_v can be found in the original Chudin model [19]. The term Q(Ca_jsr) is a function that reproduces the steep dependence of CICR on Ca concentration in the JSR. It is represented by the following piecewise-linear function:

$$Q({Ca}_{\mathit{jsr}})=\{\begin{array}{ll}0,\hfill & {Ca}_{\mathit{jsr}}<0.5mM\hfill \\ {Ca}_{\mathit{jsr}}-0.5,\hfill & 0.5mM\le {Ca}_{\mathit{jsr}}<0.9mM\hfill \\ \chi (u_{\mathit{rel}}{Ca}_{\mathit{jsr}}+b_{\mathit{rel}}),\hfill & {Ca}_{\mathit{jsr}}\ge 0.9mM\hfill \end{array}$$ (Eq. 6)

where u_rel = 11.0 ms⁻¹ is the gain of CICR at high JSR loads, b_rel = 10.0 mM/ms is the point of intersection between the second and third segments of Q(Ca_jsr), and χ is a parameter found in the original Chudin model [19] that prevents complete depletion of the SR during normal CICR.