Determination of Protein Complex Stoichiometry Through Multisignal Sedimentation Velocity Experiments

Abstract

Determination of the stoichiometry of macromolecular assemblies is fundamental to an understanding of how they function. Many different biophysical methodologies may be used to determine stoichiometry. In the past, both sedimentation equilibrium and sedimentation velocity analytical ultracentrifugation have been employed to determine component stoichiometries. Recently, a method of globally analyzing multisignal sedimentation velocity data was introduced by Schuck and colleagues. This global analysis removes some of the experimental inconveniences and inaccuracies that could occur in the previously used strategies. This method uses spectral differences between the macromolecular components to decompose the well-known c(s) distribution into component distributions c_k(s); i.e. each component k has its own c_k(s) distribution. Integration of these distributions allows for the calculation of the populations of each component in cosedimenting complexes, yielding their stoichiometry. In our laboratories, we have used this method extensively to determine the component stoichiometries of several protein-protein complexes involved in cytoskeletal remodeling, sugar metabolism, and host-pathogen interactions. The overall method is described in detail in this work, as well experimental examples and caveats.

Introduction

Almost from the beginning of modern biochemistry, it has been obvious that cells utilize large macromolecular complexes for critical and diverse functions. Protein synthesis, DNA replication, fatty acid synthesis, glucose metabolism, and a myriad of other processes are carried out on large, multicomponent complexes. As more genomes and proteomes are studied, more of such assemblies are discovered and characterized. In studying a macromolecular complex, a fundamental question always arises: what is the component stoichiometry? A host of different biophysical methods are available to address this question, e.g. X-ray crystallography, nuclear magnetic resonance, isothermal titration calorimetry (ITC), quantitative gel electrophoresis, and the scattering of neutrons and of light.

Recently, there have been significant advances in the analysis of analytical ultracentrifugation (AUC) sedimentation velocity (SV) data for interacting biological systems [1–6]. By the term “interacting systems,” we here refer to biological macromolecules that bind either to themselves (“self-association”) or to a binding partner(s) (“hetero-association”). Such systems may include the self- or hetero-associations of proteins or nucleic acids. Many of these advances are integrated into the software program SEDPHAT [1,3,4,6]. This program allows the user to model kinetic Lamm equation (LE) solutions to the SV data directly via a global analysis of SV experiments [4]. Although this approach is robust, it can be very computationally intensive. Alternatively, methods have been devised to use the information from the continuous distribution c(s) in order to obtain values from the SV data that may be fit to binding isotherms. For example, the c(s) distribution may be integrated to obtain a signal-average sedimentation coefficient of the interacting system. Proper conversion of these values using SEDPHAT allows for the determination of the equilibrium association constant (K_A) for a macromolecule or macromolecules exhibiting a self- or hetero-association, respectively [3,6]. In the case of fast (i.e. k_off > ~10⁻³ s⁻¹) hetero-associations, Gilbert-Jenkins theory can be applied to values obtained from the integration of the fast and slow sedimentation boundaries manifested as peaks in the c(s) distribution [3,7]. This treatment allows for the estimation of K_A and the sedimentation coefficient of the complex (s_complex). Although the above methods work well, they assume prior knowledge of a stoichiometry, and knowledge of that quantity is important in designing the experiments thus analyzed. Therefore, an experimental means of determining the stoichiometry before performing other analyses is often essential.

In addition to those techniques enumerated above, Schuck and colleagues have recently introduced the multi-signal SV (MSSV) technique [1]. This methodology allows the experimenter to globally model directly to multisignal SV data sets using convolutions of LE solutions with c_k(s) distributions, where c_k(s) represents a c(s)-type distribution to which only one macromolecular component, k, contributes. As a consequence, one may determine the concentrations of the components that comprise a co-sedimenting complex. In this way, the stoichiometry of the components in a hetero-associating complex may be derived.

In our laboratories, determining such stoichiometries has been of paramount concern. Our interest has been in characterizing protein-protein hetero-associations. We describe in this report three cases for which MSSV has been invaluable to determine the stoichiometries of the associations. The three systems are (a) human dihydrolipoamide dehydrogenase (hE3) binding to the hE3-binding domain (hE3BD) of human E3-binding protein (hE3BP), (b)Tp34 from Treponema pallidum binding to human lactoferrin (hLF), and (c) the binding of domains from the Wiskott-Aldrich Syndrome Protein (VCA) and cortactin (NtA) to a protein complex that initiates the branching of actin filaments (Arp2/3). Information on the physiological import and implications of these protein-protein interactions is detailed elsewhere [8–12].

In all cases delineated above, MSSV has performed well to report on the stoichiometry of the proteins in their respective complexes. In this paper, we detail, in a step-by-step fashion, how the MSSV method was used to confirm the stoichiometries of the respective protein assemblies. Features and caveats for the MSSV method are discussed.

Materials and Methods

Theoretical Underpinnings

The theoretical bases underlying the c(s) and MSSV methods have been discussed extensively in the literature [1,13,14]; they are only briefly recapitulated here. The observed signal from an SV experiment, a(r,t), may be represented as finite-element solutions to the Lamm equation (χ(s,D(s),r,t)) scaled by a continuous, differential concentration distribution called c(s) [14]:

$$a(r,t)\cong {\displaystyle {\int }_{s\text{min}}^{s\text{max}}c(s)\chi (s,D(s),r,t)ds,}$$ Eq. 1

where r is the radius from the center of revolution, t is time, s is the sedimentation coefficient, and D(s) is the diffusion coefficient as a function of s, calculated with the assumption of a single frictional ratio (i.e. the ratio of the species’ frictional coefficient, f, to the minimum frictional coefficient for a species of identical mass, f₀) for all sedimenting species.

If we consider an experiment in which there are K components (K > 1), and the SV data profiles are obtained at multiple signals (Λ = number of signals used), then the profiles at one signal, a_λ(r,t), may by analogy be described by the equation

$$a_{\lambda }(r,t)\cong {\displaystyle \sum _{k=1}^K{\epsilon }_{k\lambda }}{\displaystyle {\int }_{s_{\text{min},j}}^{s_{\text{max},j}}{c}_k(s)\chi (s,D_k(s),r,t)ds,}$$ Eq. 2

where c_k(s) represents the continuous distribution due to only one macromolecular component k, and ε _kλ is the molar signal increment of component k at wavelength λ [1]. Note that only Λ components can be distinguished with this method (i.e., K ≤ Λ). The “signals” may be absorbance (A_λ, where λ is the wavelength) detection at a given wavelength and data obtained using the Rayleigh interferometric (IF) system. For example, three solution components might be analyzed using A_280, A_250, and IF. Details on the practice of this methodology are given in the Results section (see below).

The sedimentation of discrete complexes of known stoichiometry presents the experimenter with the opportunity for a powerful constraint on the above analysis [1]. If we represent the number of subunits k in a complex κ as $S_k^{\kappa }$, a new signal increment of the complex may be defined:

$${\epsilon }_{\kappa \lambda }={\displaystyle \sum _k{S}_k^{\kappa }{\epsilon }_{k\lambda },}$$ Eq. 3

which leads to a new model

$$a_{\lambda }(r,t)\cong {\displaystyle \sum _j{\displaystyle \sum _{{\kappa }_j,k}{S}_k^{{\kappa }_j}{\epsilon }_{k\lambda }}{\displaystyle {\int }_{s_{\text{min},j}}^{s_{\text{max},j}}{c}_{\kappa }^{(j)}(s)\chi (s,D(s),r,t)ds.}}$$ Eq. 4

In this model, the continuous distribution is divided into j segments, and the $c_{\kappa }^{(j)}$ (s) distribution reports the abundance of only species with sedimentation coefficients between s_min,j and s_max,j and with the spectral composition of complex κ. This treatment allows the analysis of different expected complex stoichiometries in different segments of sedimentation coefficient space.

Protein Methods

The proteins used in this report were purified as described [8,9,11,15]. Iron-free (apo-) hLF was used in this study. The hLF/rTp34 experiments were undertaken in the presence of Zn²⁺, and there is evidence that both proteins bind to this cation [8,16]. The protein construct (XDD1) used to study the hE3-binding properties of hE3BD comprised residues 1–161 of hE3-binding protein. Bovine Arp2/3, purified from bovine thymus, had its native sequence, while residues 421–502 of the VCA domain of human Wiskott-Aldrich Syndrome Protein and residues 1–36 of the NtA domain of human cortactin were used.

For all SV experiments described in this paper, a Beckman XL-I (Beckman-Coulter) analytical ultracentrifuge was used. All experiments were performed in dual-sector charcoal-filled Epon centerpieces (sandwiched between two sapphire windows) that had been filled with 390 µl of sample in the sample sector and the same volume of buffer without proteins in the reference sector. Assembled centerpiece housings were placed in an An60Ti rotor or in an An50Ti rotor and centrifuged at 50,000 rpm until all components apparently had sedimented to the bottom of the cell. Data from multiple signals were collected simultaneously using the Beckman control software.

The hE3/XDD1 experiments were performed at 4°C in 50 mM Tris, pH 7.5. The samples were dialyzed against this buffer prior to their being loaded into the centrifugation cells. These proteins were mixed and loaded into the experimental apparatus, then allowed to equilibrate at the experimental temperature for six hours prior to centrifugation. The Zn-hLF/Zn-rTp34 experiments were performed in a buffer composed of 20 mM Tris-HCl pH 7.5, 20 mM NaCl, 300 µM Zn-acetate. Concentrated stocks of the proteins were diluted in this buffer just prior to cell loading; they were allowed to equilibrate to the experimental condition (20° C) for 2–4 hours before centrifugation was initiated. The experiments regarding Arp2/3, VCA, and NtA were carried out in a buffer comprising 5 mM HEPES pH 7.0, 50 mM KCl, 1 mM MgCl_2, and 1 mM ethylene glycol-bis(2-amino-ethylether)-N-N, N’,N’-tetra-acetic acid (EGTA). The samples were treated the same as the Zn-hLF/Zn-rTp34 samples.

Determination of Fixed Signal Increments

The MSSV experiment requires that the molar signal increments (these are functionally equivalent to extinction coefficients and are hereafter represented by the symbol “ε”) of all components be known and fixed during the analysis for at least one of the signals. In our experiments, we calculate or determine the ε values of all components for one signal. In cases where one of the signals is supplied by the Rayleigh interferometric system, we usually assume that the ε of a protein (ε_IF) is directly proportional to its molar mass, and thus may be easily calculated. The raw measurement of concentration of protein measured by the Beckman interferometer is expressed in units of “fringes displaced,” ΔJ, which can be expressed as:

$$\mathrm{\Delta }J=\mathrm{\Delta }nl/\lambda ,$$ Eq. 5

where Δn is the refractive index difference between the sample and reference sectors, l is the path length, and λ is the wavelength of the incident radiation [17]. The quantity Δn is related to the concentration of the protein by the relationship

$$\mathrm{\Delta }n=\raisebox{1ex}{$\mathrm{d}n$}\!\left/ \!\raisebox{-1ex}{$\mathrm{d}c$}\right.c_m,$$ Eq. 6

where c_m is the concentration of the protein (in mass units) and dn/dc is the specific refractive index increment of the protein. Assuming that proteins have a dn/dc of 1.86 × 10⁻⁴ L/g [17], and inserting the value for λ (the laser used in our Beckman XL-I has a wavelength of 6.75 × 10⁻⁵ cm), we obtain

$$\mathrm{\Delta }J\cong 2.75{\mathit{\text{lc}}}_m.$$ Eq. 7

In order to consider the concentration (c) in molar terms instead of mass terms, it is necessary to introduce the molar mass of the protein (M) into this equation:

$$\mathrm{\Delta }J\cong 2.75\mathit{\text{Mlc}}.$$ Eq. 8

By setting ε_IF = 2.75M and assigning it units of fringes·M⁻¹cm⁻¹, a formulation similar to the familiar Beer-Lambert equation is derived:

$$\mathrm{\Delta }J\cong {\epsilon }_{\text{IF}}lc.$$ Eq. 9

In practice, because the molar mass of the protein can usually be calculated from its amino-acid sequence, we use

$${\epsilon }_{\mathit{\text{II}}}^k=2.75M_c^k$$ Eq. 10

where $M_c^k$ is the calculated molar mass of component k. Therefore, in a typical multisignal experiment utilizing interferometry, the quantities ΔJ, l, and ${\epsilon }_{\mathit{\text{IF}}}^k$ are known; c is easily calculated.

The above treatment works well for most proteins, and it was used to determine ε_IF for hE3, XDD1, Arp2/3, VCA, and NtA (Table 1). However, the method assumes that the protein comprises only amino acids. If a significant percentage of the mass of the protein is derived from posttranslational modifications, e.g. glycosylation, the calculation of ε_IF is not as simple; accommodations for the different interferometric signal increments of the heterogeneous chemical moieties must be made. Among the proteins studied in this work, apo-hLF is known to be a glycoprotein. Therefore, in an earlier experiment [8], ${\epsilon }_{\text{IF}}^k$ was treated as an unknown for apo-hLF and, for consistency, for rTp34 as well. Instead of the above treatment, the ε’s for absorbance at 280 nm $({\epsilon }_{\text{ABS280}}^k)$ were determined using the method of Pace [18] for both proteins. In brief, this method entails (1) measuring the absorbance of chemically denatured protein, (2) determining the concentration of that protein using an extinction coefficient that is the weighted sum of the tabulated extinction coefficients of amino-acid chromophores, and (3) measuring the absorbance of the natively folded protein and calculating its extinction coefficient based on the known concentration of protein. The fixed ${\epsilon }_{\text{ABS280}}^k$ values derived from these analyses are shown in Table 1.

Table 1.

Fixed IF signal increments used in this study and empirically determined absorbance signal increments for rTp34 and hLF.

Protein	εIF (fringes/M·cm)	ε280 (AU/M·cm)
rTp34	65,276.3*	31,645†
hLF	226,612*	91,254†
XDD1	51,326‡	-
hE3 (homodimer)	289,759‡	-
Arp2/3	615,516‡	-
VCA	37.185.5‡	-
NtA	11,281.0‡	-

^*Refined in the MSSV experiment of reference [8].

^†Determined by Deka et al [8].

^‡Calculated using the known amino-acid composition and Eq. 10.

Data analysis

All data were analyzed using SEDPHAT version 7.22. By default, SEDPHAT corrects all s-values to standard conditions (s_20,w); it is these values that are reported below. Time-invariant noise (all data sets) and radially invariant noise (IF data sets) features were calculated and subtracted from all the data presented in this report [19]. All values for buffer densities (ρ), buffer viscosities (η), and partial specific volumes (ν̄)of the proteins were estimated using SEDNTERP [20]. In the calculation of, ν̄ for hLF, a glycoprotein, the sugar moieties were ignored. To provide estimates for the buffer parameters in the Arp2/3 experiments, EDTA was substituted for EGTA in the SEDNTERP calculations. For all c_k(s) distributions presented in this report, Tikhonov-Phillips regularization was applied with a confidence level of p = 0.7 [13]. In SEDPHAT, all SV data sets by default are assigned a “noise” level (σ_e) of 0.01. This value is used in the calculation of the overall reduced chi-squared $({\chi }_r^2)$ which is the goodness-of-fit statistic that the program uses (see http://www.analyticalultracentrifugation.com/sedphat/statistics.htm):

$${\chi }_r^2=\frac{1}{N_{\mathit{\text{tot}}}}{\displaystyle \sum _e{\displaystyle \sum _{i=1}^{N_e}\frac{{(a_{i,e}-f_{i,e})}^2}{{\sigma }_e^2},}}$$ Eq. 11

where N_tot is the total number of data points in all data sets, N_e is the number of data points in data set e, a_i,e is the i^th data point of data set e, and f_i,e is the corresponding fitted point. Theoretically, σ_e should be set to the expected error of data acquisition. Examination of Eq. 11 shows that data sets with a large number of data points will dominate the statistic and thus perhaps unduly influence parameter refinement. In our cases, N_e for the IF data is typically 3–4 times that in the absorbance data sets. We therefore compensated for this imbalance by dividing σ_e for the absorbance data sets by $~\sqrt{N_{\text{IF}}/N_e}$. The interested reader is referred to the above web site for an expanded discussion on this topic. The distributions were normalized such that the area under a peak yields its total concentration.

Results

The Methodology

Proteins are made up of 20 different amino acids, but only a small subset of these act as chromophores. The chromophoric amino acids are tryptophan, tyrosine, and phenylalanine; the disulfide linkage of a cystine also absorbs light in the UV range. With the exception of 100% identical homologs, each protein has a unique sequence of amino acids, and thus has the potential to possess a unique chromophoric signature. This phenomenon can manifest in several ways. For example, proteins often differ in the mass: chromophore ratios. A small protein with many tryptophan residues would have a much different mass-to-UV extinction ratio than a large protein with one tyrosine residue. Further, tyrosine and tryptophan have significantly different UV-absorption profiles. If we represent the signal increment at wavelength λ nm as ε_ABSλ (in units of signal·M⁻¹·cm⁻¹, which are assumed throughout the text) then proteins with different tryptophan-to-tyrosine ratios will have significantly different ε_ABS280: ε_ABS250 ratios. When necessary, unique absorption features can be introduced to proteins by modifying them with a chromophoric label. The signals measured by the Beckman XL-I are directly proportional to the protein concentration; the magnitude of the interference signal proportional to ε_IF, which is dependent on the protein’s molar mass (see Eqs. 5–10), and the magnitude of the absorbance signal is proportional to ε_λ, which is dependent on the number of chromophoric amino acids present in the protein.

The conventional c(s) distribution, as implemented in SEDFIT, has as its units signal per Svedberg (S). For example, an experiment carried out using IF would have a c(s) distribution with units of fringes/S. If only one component k were present, and its IF increment $({\epsilon }_{\text{IF}}^k)$ were known, it would be straightforward to convert these units to concentration/S. In the general sense, this distribution is termed a c_k(s) distribution for the single component k.

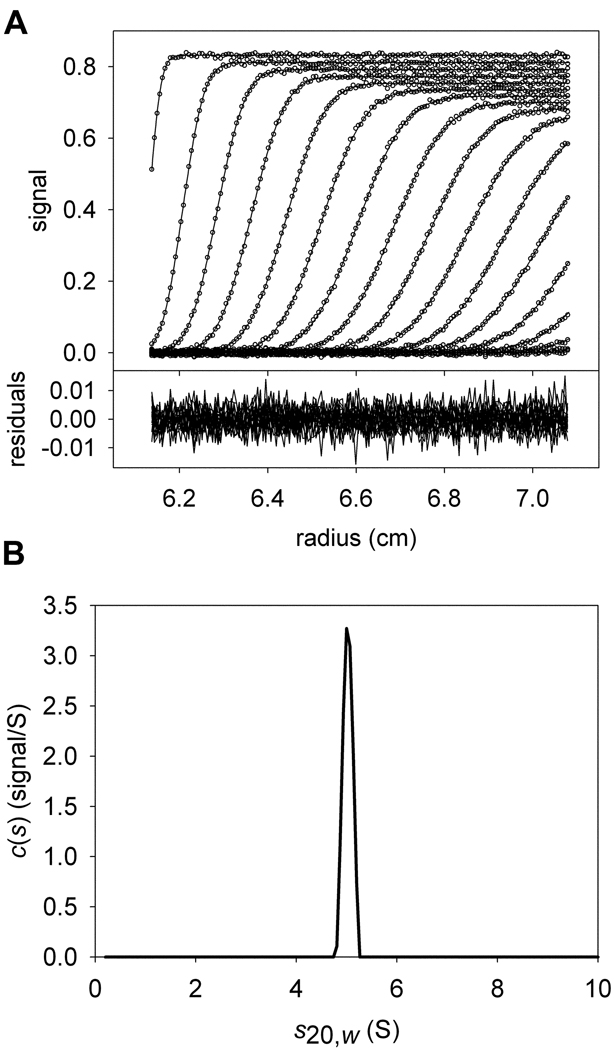
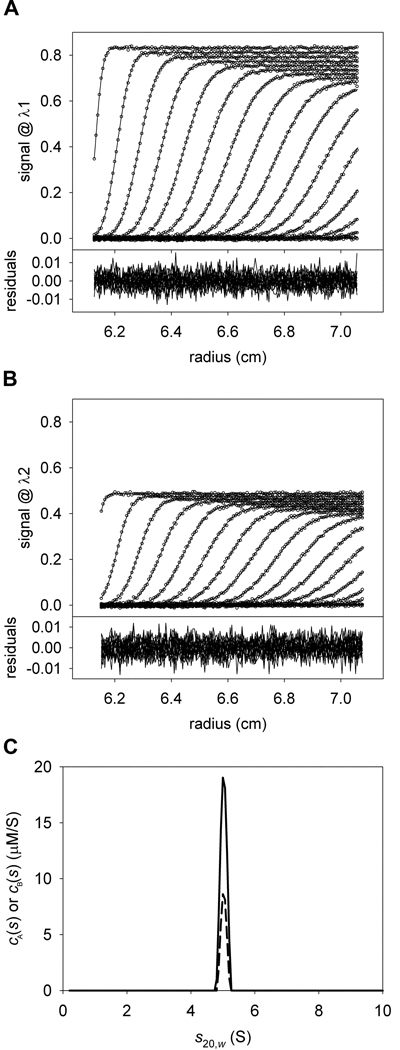
Consider now the case in which two components, A and B, are present, and have the same molar masses and sedimentation coefficients. If data using only one signal, λ1, were collected for an SV experiment containing these two components, there is no way to calculate the concentrations of the individual components present in the single c(s) or c_k(s) peak without additional information, even if ${\epsilon }_{\lambda 1}^{\mathrm{A}}\text{and}{\epsilon }_{\lambda 1}^{\mathrm{B}}$ were known (Fig. 1). However, if data from two signals, λ1 and λ2, were collected, and the ratios ${\epsilon }_{\lambda 1}^{\mathrm{A}}/{\epsilon }_{\lambda 2}^{\mathrm{A}}\text{and}{\epsilon }_{\lambda 1}^{\mathrm{B}}/{\epsilon }_{\lambda 2}^{\mathrm{B}}$ were significantly different, then the data could be analyzed globally to distinguish between the two cosedimenting proteins. Two overlapping distributions, c_A(s) and c_B(s) could be calculated simultaneously from such data (Fig. 2). In the c_A(s) distribution, the data are globally modeled using just the characteristic extinction properties (i.e. the spectral signature) of protein A. The c_B(s) distribution would do the same with the spectral signature of protein B. SEDPHAT is capable of simultaneously optimizing both the c_A(s) and c_B(s) distributions to the λ1 and λ2 data, allowing determination of the correct concentrations of the cosedimenting proteins (Fig. 2).

Figure 1. The conventional c(s) distribution.

Conventions established in this figure will hold for all other figures, except where noted. (A) Simulated sedimentation velocity data and fit thereto. In the upper part, the individual data points are represented as open circles; they form the characteristic sigmoid shape that describes one point in time (i.e. a “scan”) during the experiment. The inflection point of this feature moves from left to right as time progresses. The x-axis shows the radius from the center of rotation. The y-axis in the upper part shows the magnitude of the signal. For clarity, only every 6^th data point used in the data analysis is shown. Also, only every 3^rd scan used to analyze the data is shown. The fit to these data using the c(s) distribution in part B is shown as a solid line. The lower part of the figure shows the residuals as a function of radius, where the residual is equal to the y-value of a given data point minus the y-value of the fitted data point. The data were simulated using a single signal (λ1) to include two species (A and B) with identical hydrodynamic characteristics (5 S, 77081 Da), but different concentrations:[A] = 5 µM; [B] = 2 µM; ${\epsilon }_{\text{λ1}}^{\mathrm{A}}={\epsilon }_{\text{λ1}}^{\mathrm{B}}=\mathrm{100,000}$ M⁻¹cm⁻¹. (B) The c(s) distribution that best describes these data. On the x-axis is the s_20,w of the simulated species used for the fit, and on the y-axis is the normalized population of material present for each species. This distribution describes the data well, but no spectral discrimination between the two proteins is afforded.

Figure 2. A two-signal MSSV experiment.

For these simulated data, the signal increments for protein A were 100,000 M⁻¹cm⁻¹ and 50,000 M⁻¹cm⁻¹ for signals λ1 and λ2, respectively. For protein B, the increments were 100,000 M⁻¹cm⁻¹ and 80,000 M⁻¹cm⁻¹ for signals λ1 and λ2, respectively. (A) The data and global fit for signal λ1. (B) The data and global fit for signal λ2. The y-axis of the upper part was put on the same scale as that in Fig. 2A to emphasize the difference in the magnitude of the signals collected at the two different wavelengths. (C) The c_A(s) (solid line) and c_B(s) (dashed line) distributions that best describe the data in parts A & B. Integrating the peaks in these distributions returns the proper concentrations of the components,

$$\text{i.e.}{\displaystyle \underset{s\text{min}}{\overset{s\text{max}}{\int }}{c}_A(s)ds=5\mu \mathrm{M}\text{and}{\displaystyle \underset{s\text{min}}{\overset{s\text{max}}{\int }}{c}_B(s)ds=2\mu \mathrm{M}\text{.}}}$$

Experimental Considerations

As in all sedimentation experiments, the first concern is the experimental design. Many considerations, including rotor speed, buffer choice, and temperature are general for an SV experiment, and are addressed elsewhere [21]. Also, before the experiment begins, an assessment of its feasibility should be performed. For example, if researchers studying a two-component system plan to use both IF and A₂₈₀ as the two signals to monitor sedimentation, they should calculate the ratio of ε_IF to ε₂₈₀ for both components. The method is completely dependent on divergent signal-increment ratios for the spectral discrimination of the components. For this reason, as a rule-of-thumb, we suggest that the ratios be at least 20% different before proceeding (although even this may be insufficient, see below). The choice of wavelength is also important. To minimize the effect of the wavelength inaccuracy in the Beckman monochromator, wavelengths away from any steep slope in the macromolecule’s absorption spectrum should be chosen. Often, it is convenient to choose a wavelength near to an absorbance maximum or minimum, which fits the above criterion. Notably, not all proteins have an absorbance maximum at 280 nm; indeed, for hE3, studied below, there is an absorbance maximum at 274 nm.

The concentrations chosen for the components are critical. To obtain the proper stoichiometry, the complex must be fully occupied. For example, in a two-component system, it is advantageous to include one component at a large molar excess over the other, and well in excess of the dissociation constant; mass action will then favor a fully occupied complex. If the components are differently sized, it is convenient to include the smaller of the two in molar excess. This strategy allows the assumption that all of the faster-sedimenting material is complexed. There are limitations on the amount of molar excess that may be employed. It is undesirable for the signal due to the complex to be less than tenfold over the intrinsic noise of data acquisition, which is generally 0.005 signal units for both data acquisition systems. Further, the absorbance optical system is inaccurate above optical densities ranging from 1.0–1.5. Finally, very high protein concentrations may induce hydrodynamic non-ideality in the samples, compromising the quality of the data analysis. In practice, the concentration at which non-ideality becomes a hindrance to the analysis is difficult to predict; we avoid concentrations much greater than 1 mg/mL. The choices of concentrations therefore require a careful balance between mass action and physical and instrumentation limitations.

For a hetero-associating system with K components, at least K + 1 centrifugal cells must be prepared and centrifuged: one for each component, and at least one for the mixture of components. There are notable exceptions to this rule (see Arp2/3 below). Further, the centrifuge’s control software must be programmed to collect more than one signal from each cell. Currently, the control software for the Beckman-Coulter XL-I centrifuges is capable of collecting up to four signals per cell. One data set may come from the Rayleigh interferometer, and the other three may be absorbance data collected at three different wavelengths using the radially scanning spectrophotometer. At least as many signals as components must be collected (with a notable exception, see Arp2/3 below). It is essential that the reference buffers be identical to the sample buffers, and buffer components that absorb at the subject wavelengths should be avoided, if possible. The IF system is exquisitely sensitive to all buffer mismatches; because osmolytes like glycerol are difficult to match well, they are best avoided.

Finally, some information regarding the character of the interaction between the two proteins is desirable. In general, MSSV works best with proteins that associate tightly (i.e. K_A > 10⁵ M⁻¹ for a two-component hetero-association) and with a slow kinetic off rate (i.e. k_off < 10⁻³ s⁻¹). Associations that do not meet these criteria can be studied using MSSV, but they require a large molar excess of one or more of the components in order to fully populate the complex [1]. To obtain information concerning k_off, it is recommended that the experimenter study the interaction at various concentrations using SV and analyze the data using the c(s) distribution. The appearance of the distribution is diagnostic of the k_off [7,21]. For an A + B ↔ AB system, a slow k_off would yield three stationary c(s) peaks that change heights as the component concentrations change. For a fast k_off, two peaks would usually be observed, with one representing a free component and the other the reaction boundary [7]. The apparent position and height of the reaction-boundary peak would change based on the populations of complex and free components [7,22]. Simulations [1] have shown in the case of a fast k_off that, unless one of the components is present at a large molar excess, the observed molar ratio of the cosedimenting species is corresponds to the molar ratio of the reaction boundary, not the complex. For difficult cases, e.g. where the sedimentation coefficient of the complex (s_complex) is approximately equal to that of one (or both) of the components, we recommend using a large molar excess of one of the components, and at least two concentrations of the component in excess. We note that the method is not dependent on s_complex being the fastest-sedimenting species, but this is usually the case.

General features of the analysis

An MSSV analysis of a two-component hetero-associating system (e.g. A + B ↔ AB) usually comprises three steps. In the first step, a global SV analysis using at least two signals is performed on a sample that contains only component A. In this analysis, typically, for one of the signals (signal λ1 in the following notation), the signal increment of A $({\epsilon }_{\lambda 1}^A)$ is known, either through calculation (i.e. via Eq. 10 or a program like SEDNTERP) or through empirical determination (e.g. amino-acid analysis or absorption measurements under denaturing and native conditions [18])). The signal increments for A $({\epsilon }_{\lambda 2}^A,{\epsilon }_{\lambda 3}^A$ etc.) with respect to the other signals (signals λ2, λ3, etc.) are unknown; obtaining their best-fit values is the goal of this step. The value of ${\epsilon }_{\lambda 1}^A$ is held constant in the analysis, and the data from all signals are globally fit with a single c_A(s) distribution while concurrently allowing the unknown signal increments to refine to their optimal values. In essence, knowledge of ${\epsilon }_{\lambda 1}^A$ and the total amount of signal allows the program to calculate the concentration of A. Because all other signals come from the identical sample, [A] is known, and the unknown signal increments can be varied until the best global fit to the data is obtained. Once a satisfactory global fit to the data is reached, the refined values of ${\epsilon }_{\lambda 2}^A$ etc., are noted for future use. Contrary to traditional c(s), which has units of signal per Svedberg, c_A(s) (and, more generally, c_k(s)) has units of concentration per Svedberg. An important consequence of this difference is that the area beneath a peak in a c_A(s) distribution is equal to [A].

Step two in the analysis is similar to step one. The only difference is that the global analysis is carried out for the sedimentation of protein B alone, not protein A. Again, the refined values of ${\epsilon }_{\lambda 2}^B$ etc., are noted for use in step three.

In the third step, the fixed and refined increments are applied to the global analysis of sedimentation data obtained from a mixture of A and B. In this case, no signal increments are allowed to refine (hyper- or hypochromicity cannot be accommodated in this type of analysis). We always initially analyze such a system by fitting the data with two c_k(s) distributions, c_A(s) and c_B(s), which have the same range of s-values. In parts of the distribution that show co-sedimentation of the two components, the distributions are integrated to determine the molar concentrations of the respective components. The ratio of these molar concentrations is equal to the molar ratio of proteins in the complex. From the observed sedimentation coefficient of the complex, an estimate of the overall complex size can be made and the stoichiometry of the complex can be derived. Further analyses using assumed, fixed stoichiometries are possible, and are detailed below.

The MSSV analysis affords the experimenter the opportunity to test the statistical validity of constraints on the model. For example, if the data obtained as above point to a certain complex stoichiometry (e.g. 1:1), a stoichiometric constraint can be added to the analysis for pertinent s-value ranges. In essence, the following question is posed: given the quality of the data, the accuracy of the refined extinction coefficients, and the assumptions inherent in the c_k(s) model, does the addition of a stoichiometric constraint cause a statistically significant degradation of the quality of the fit? If this question is answered negatively, then we may say that the queried complex stoichiometry is consistent with the data given our statistical criterion. A positive answer should cause the experimenter to carefully evaluate whether the constraint can be considered correct or not.

All of the tools necessary for this test are present in SEDPHAT. The quality of the unconstrained fit (obtained in step 3) is assessed in SEDPHAT with a global reduced χ² $({\chi }_r^2)$ We call the ${\chi }_r^2$ arising from the best fit “${\chi }_b^2$”. Fits with a stoichiometric constraint in place result in a higher χ² value, called here the “test χ²”, or ${\chi }_t^2$. The answer to the question posed above depends on whether ${\chi }_t^2$ exceeds another χ² value, called the “critical χ²”, or ${\chi }_{c,1\sigma }^2$. The experimenter can determine ${\chi }_{c,1\sigma }^2$ using an F-statistics calculator available in SEDPHAT. To arrive at ${\chi }_{c,1\sigma }^2$, SEDPHAT uses the formula

$${\chi }_{c,1\sigma }^2={\chi }_b^2{F}_{\mu ,\nu }^{\alpha }$$ Eq. 12

where $F_{\mu ,\nu }^{\alpha }$ is the (1-α) one-sided F statistic with μ and ν degrees of freedom, and where μ = v=number of data points being fitted, and α = 0.683. Thus, our criterion for “statistical significance” is a change that that worsens the fit by over 1 σ. Constrained fits with ${\chi }_t^2$ less than or equal to ${\chi }_{c,1\sigma }^2$ are accepted as statistically indistinguishable from the best fit, and the answer to the above question is “no.” Conversely, constrained fits with ${\chi }_t^2\text{above}{\chi }_{c,1\sigma }^2$ are considered statistically worse; the answer to the above question is “yes.” In practice, the following steps are performed: (1) The experimenter makes note of ${\chi }_b^2$ for the best unconstrained fit. (2) The ${\chi }_{c,1\sigma }^2$ is calculated using SEDPHAT’s statistical calculator. (3) The stoichiometry of the components is constrained in relevant s-value ranges, which are typically greater than s_A or s_B. For example, components A and B can be constrained to be in 1:1 complexes in a given s-value range. (4) A new fit is performed in the presence of the constraint. (5) ${\chi }_t^2\text{is compared to}{\chi }_{c,1\sigma }^2$ and the question of statistical significance is answered using the criteria delineated above. We routinely use this method to check whether the derived stoichiometry is justified by the data.

A constrained fit with ${\chi }_t^2>{\chi }_{c,1\sigma }^2$ does not automatically invalidate the stoichiometric constraint. It is possible that the constraint is correct, but it causes a slightly “worse” fit. For cases where ${\chi }_t^2>{\chi }_{c,1\sigma }^2$ we suggest calculating a rejection χ², ${\chi }_{c,2\sigma }^2$. This value is calculated exactly as in Eq. 12, except α= 0.95. If ${\chi }_t^2>{\chi }_{c,2\sigma }^2$, then the stoichiometric constraint is unlikely to be correct. If ${\chi }_{c,1\sigma }^2<{\chi }_t^2<{\chi }_{c,2\sigma }^2$ then the constraint might be valid, but results in a statistically “worse” fit by our definition. In such a case, caveats should be acknowledged (e.g. deficits in the spectral resolution, the quality of refined extinction coefficients, or the degree of saturation of binding sites), and information from other experiments (e.g. repetitions of the experiment at different concentrations and stoichiometries derived from other biophysical methods) may come to bear on the validity of the constraint.

A straightforward example

To illustrate the steps outlined above, we re-analyzed one data set that, among others, was used to confirm the stoichiometry of a complex comprising human E3-binding domain (here called XDD1) and human dihydrolipoamide dehydrogenase (called hE3) [10]. Two crystal structures had established that the stoichiometry of the complex is 1:1 [11,12], but this finding was challenged in the literature [23,24].

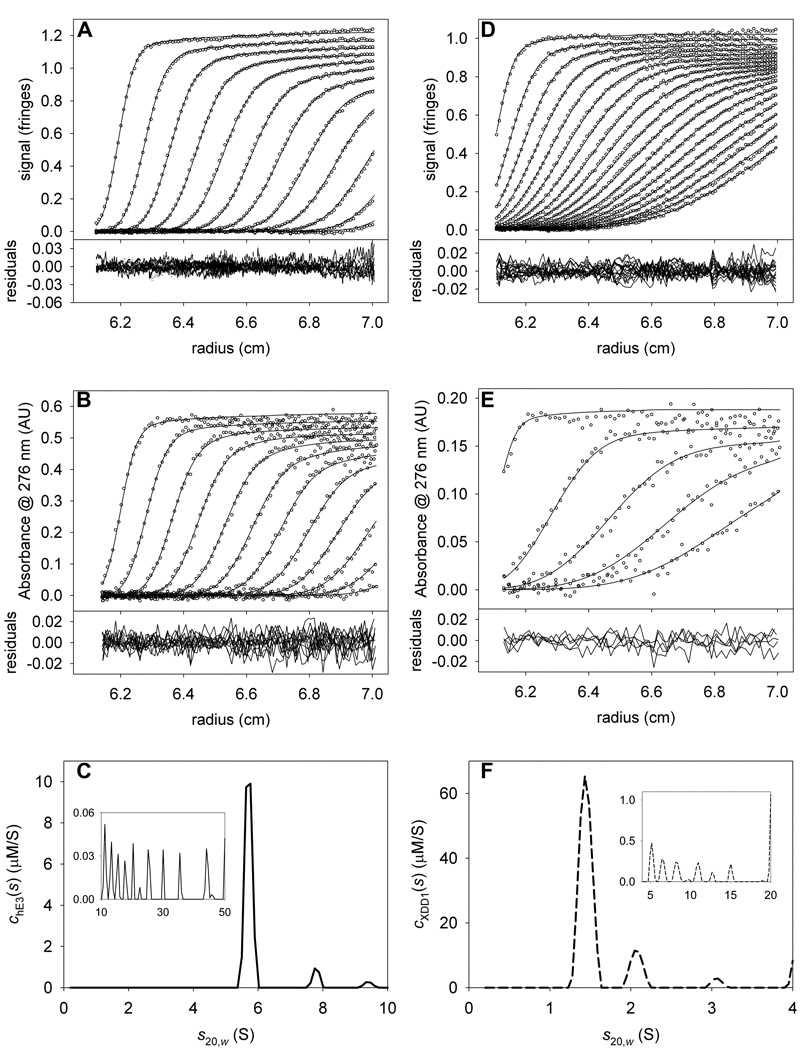
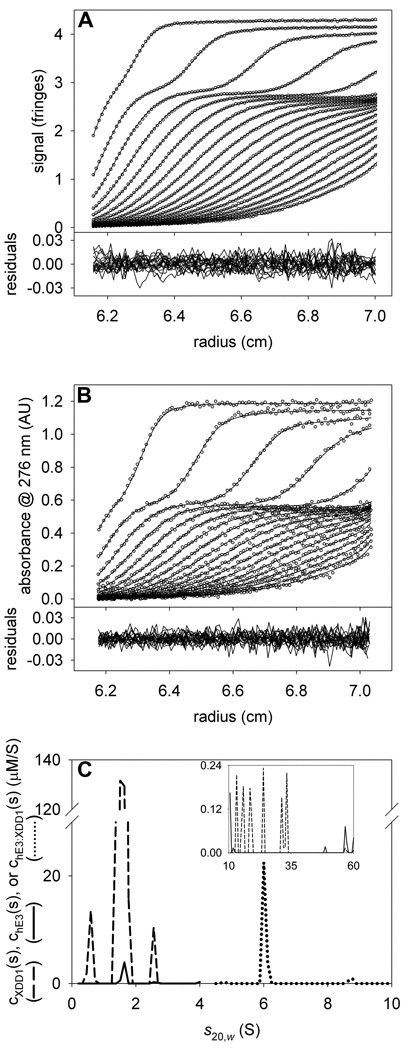
First, we analyzed the sedimentation of hE3 alone. This protein is a constitutive dimer; our construct had a calculated molar mass of 105,367 Da. The mass of FAD, which is noncovalently bound to hE3, was neglected in our calculations. Sedimentation data were acquired using both IF and absorbance optics (Figs. 3A and 3B, respectively). We chose 276 nm because it was near to an absorbance maximum for hE3 (274 nm) and a plateau in the absorbance of XDD1 (not shown). In our previous analysis of these data [10], we fixed the meniscus of the IF data because it tended to refine to unrealistic values. However, in the current work, we have removed this constraint. We find that refinement of the meniscus is more stable in newer versions of SEDPHAT. A small percentage (~9%) of the protein is present as higher-order aggregates. Previously, these were modeled with a few species having sedimentation coefficient near to 15 S. Here, we explicitly treat those aggregates as a continuous distribution of species sedimenting between 10.1 and 50 S (insets of Figs. 3C & 3F). Therefore, there are two “segments” of s-values considered: one from 0.2 S to 10 S, and a second from 10.1 S to 50 S. Each is allowed to have a separate overall frictional ratio (f_r). In our experience, the f_r’s refine to the same values obtained from a conventional c(s) analysis, and significant variance between the conventional and MSSV approach indicates a problem with the latter analysis. According to Eq. 10,${\epsilon }_{\text{IF}}^{\text{hE3}}=\mathrm{289,759}$ fringes·M⁻¹cm⁻¹. This value was fixed in the analysis. As a first substep in this analysis, we fixed the values of all nonlinear parameters except for that of ${\epsilon }_{\text{ABS276}}^{\text{hE3}}$ (e.g. the sample menisci, f_r’s, etc.). This methodology allowed the efficient approximate refinement of ${\epsilon }_{\text{ABS276}}^{\text{hE3}}$. Once this approximate value was obtained, the nonlinear parameters (except f_r of the 10.1–50 S segment) were also allowed to refine. The final value of ${\epsilon }_{\text{ABS276}}^{\text{hE3}}$ refined to 137,764 AU·M⁻¹cm⁻¹. The quality of the fits is good (Figs. 3A & 3B), with a root-mean-square deviation of the fitted line from the data (rmsd) of about 0.008 fringes for the IF data and about 0.008 AU for the A₂₇₆ data. For the optics on our centrifuge, we ordinarily expect rmsd values between 0.004 and 0.01. The c_hE3(s) distribution is shown in Fig. 3C. It has a dominant peak at 5.7 S. As noted before, there is also a minor peak having a sedimentation coefficient of 7.8 S [10,24]. This material is presumably an uncharacterized tetrameric form of hE3.

Figure 3. Data used to determine signal increments for hE3 and XDD1.

(A) IF data, fit, and residuals for hE3 alone. For this and all other IF data in this paper, only every 3^rd scan and every 12^th data point are shown. (B) A₂₇₆ data, fit, and residuals for the same sample as in A. For this and all other absorbance data in this paper, only every 3^rd scan and every 4^th data point are shown, except where noted. (C) The c_hE3(s) distribution used to model the data in parts (A) and (B). The inset in this part shows the distribution used to model the aggregates. Note the change in scale for the y-axis. (D) IF data, fit, and residuals for XDD1 alone. (E) A₂₇₆ data, fit, and residuals for the same sample as in C. Owing to the lower signal-to-noise ratio in this experiment, only every 6^th scan is shown for the sake of clarity. (F) The c_XDD1(s) distribution used to model the data in parts (D) and (E).

A similar analysis was performed for the sedimentation of XDD1 alone (Figs. 3D–F). In this case, the ${\epsilon }_{\text{IF}}^{\text{XDD1}}$ of the XDD1 monomer (18,664 Da) was calculated to be 51,326 fringes·M⁻¹cm⁻¹. Again, the menisci for both the IF and A₂₇₆ data sets were allowed to refine freely, and aggregation was modeled by species with s-values from 4.5 to 20 S. XDD1 sedimented mostly as a monomer with an s-value of 1.4 S (Figs. 3D–F). Other peaks in the c_XDD1(s) distribution occur at 2.1 and 3.1 S. These peaks could be dimeric and tetrameric forms of the protein, respectively. The value of ${\epsilon }_{\text{ABS276}}^{\text{XDD1}}$ refined to 9453.73 AU·M⁻¹cm⁻¹. Again, the overall quality of the fits is good, with rmsd’s of about 0.007 fringes and 0.007 AU for the IF and A₂₇₆ data, respectively. From the analysis to this point, we notice that the ε_IF-to-ε₂₇₆ ratios for the two proteins are significantly different (2.1 and 5.4 for hE3 and XDD1, respectively (Table 2)).

Table 2.

Refined signal increments for the hE3/XDDl experiments.

Protein	ε276 (AU/M·cm)	εIF (fringes/M·cm)	εIF/ε276
hE3	137,764	289,759‡	2.10
XDD1	9,453.73	51,326‡	5.43

^‡Fixed in this analysis. Calculated using the known amino-acid composition and Eq. 10.

With the refined values of ${\epsilon }_{\text{ABS276}}^{\text{hE3}}\text{and}{\epsilon }_{\text{ABS276}}^{\text{XDD1}}$ in hand (Table 2), we turned to the analysis of the mixture of the two proteins. For this exemplary analysis, we chose a sample that had large molar excess of XDD1 over hE3 (~13:1). The data (Figs. 4A & 4B) were modeled with two overlapping distributions: a c_hE3(s) distribution, which only reported the presence of hE3, and c_XDD1(s) distribution, which was specific for XDD1 (Fig 4C). Three segments of s-values were evaluated: 0.2–4 S, 4.5–10 S, and 10.5 to 60 S. The two most prominent peaks in the c_XDD1(s) distribution are at 1.5 S (free XDD1) and at 6.0 S (complexed XDD1). In the c_hE3(s) distribution, there is a single prominent peak at 6.0 S. By modeling the data with two c_k(s) distribution, we arrived at a high-quality fit (Figs. 4A & 4B); the rmsd’s of the IF and A₂₇₆ data sets were 0.008 fringes and 0.008 AU, respectively. We conclude that hE3 and XDD1 are cosedimenting in a complex that has a sedimentation coefficient of 6.0 S. To arrive at the stoichiometry of this complex, the distribution was integrated over the range of 5–7 S. The resulting concentrations, 2.9 µM for XDD1 and 3.3 µM for hE3, indicate that the ratio of XDD1 to hE3 in the XDD1:hE3 complex is about 0.9 to 1. This result suggests that equal numbers of XDD1 and hE3 molecules are present in the complex. Thus, possible stoichiometries are 1:1, 2:2, etc. However, a complex harboring 2 or more molecules of hE3 would have a sedimentation coefficient significantly greater than 6.0 S. As we concluded earlier [10], the most likely stoichiometry of the complex is therefore 1:1.

Figure 4. The stoichiometry of hE3 and XDD1.

(A) IF data, fit, and residuals for the mixture of XDD1 and hE3. (B) A₂₇₆ data, fit, and residuals for the same sample as in A. (C) The c_hE3(s) and c_XDD1(s) distributions used to model the data in parts (A) and (B). As in Figs. 3C and 3F, the c_hE3(s) distribution is represented by a solid line, while the c_XDD1(s) distribution is shown with a dashed line. The inset in this part shows the distribution used to model the aggregates. Note the change in scale for the y-axis.

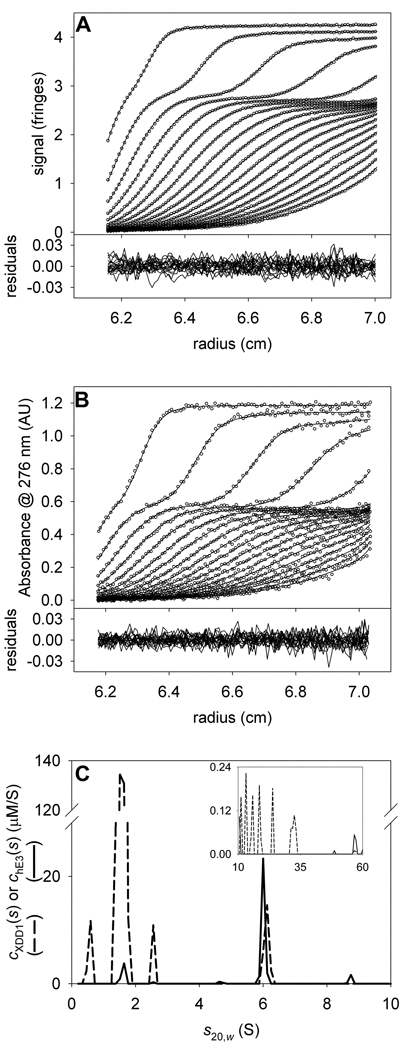
The concentrations of hE3 and XDD1 in the complex are very similar, and it is a reasonable hypothesis that all species sedimenting between 4.5 and 10 S are a 1:1 complex of the two proteins. To test this hypothesis, we fixed the stoichiometry of the two proteins to 1:1 in this range of s-values (see equation 4). Therefore, for this s-range, the data are modeled with a single c_XDD1:hE3(s) distribution with the built-in assumption of unitary stoichiometry (see Fig. 5 and “General Features,” above). Using a confidence level of 0.683 (one sigma), we find that the quality of the fit with the constrained 1:1 molar ratio in the range 5.1–10 S (${\chi }_t^2=1.206414$) is not statistically worse than the original, unconstrained fit (${\chi }_b^2=1.202899;{\chi }_{c\text{,1}\sigma }^2=1.206784$). Other researchers had concluded that the complex between a protein similar to XDD1 and hE3 was 2:1 [24]. We used the same methodology described above to constrain the ratio of XDD1 to hE3 to 2:1, but no optimization with this constraint arrived at a ${\chi }_t^2$ that was less than ${\chi }_{c,1\sigma }^2$. The best ${\chi }_t^2$ value we could obtain with this stoichiometric constraint was 1.451225. This value is well above ${\chi }_{c,2\sigma }^2$ (1.216374), indicating that the 2:1 stoichiometric constraint is not consistent with our data. These two results further buttress our contention that stoichiometry between the two proteins is 1:1.

Figure 5. Analyzing the hE3/XDD1 mixture data with a fixed stoichiometry.

(A) IF data, fit, and residuals for the mixture of hE3 and XDD1. (B) A₂₇₆ data, fit, and residuals for the same sample as in A. (C) The distributions used to model the data in parts A and B. At low and high (inset) s-values, c_hE3(s) and c_XDD1(s) distributions were used. But in the range 4.5 to 10 S, a c_hE3:XDD1(s) distribution (dotted line) was modeled, with a fixed stoichiometry of 1:1.

Ligand-induced extinction changes

In a preceding report, we established, using MSSV and isothermal titration calorimetry, that two molecules of the treponemal protein rTp34 could bind to the human mucosal protein apo-hLF [8]. In the same report, we demonstrated that divalent metal ions induce the dimerization of rTp34 in solution. Given these results, one may hypothesize that as many as four copies of rTp34 may bind to hLF in the presence of metal ions. To test this hypothesis, we studied these proteins in the presence of 300 µM Zn²⁺ using MSSV.

As noted above, because of the glycosylation on apo-hLF, we could not follow the method employed above, i.e. calculate ${\epsilon }_{\text{IF}}^{\text{apo-hLF}}$ from directly from the molar mass implied by its known amino-acid sequence. Instead, in our earlier work [8], we determined the ε_ABS280 for both apo-hLF and rTp34 using the method of Pace [18]. The ε_ABS280’s thus determined were fixed, and the ε_IF’s were refined [8]. Adding Zn²⁺ to a solution containing both rTp34 and apo-LF poses significant experimental challenges. The most relevant problem in the current context is that hLF binds to divalent cations, and often metal-bound hLF has a different ε_ABS280 than apo-hLF [25,26]. At the beginning of the experiment, we did not know the extent to which ${\epsilon }_{\text{ABS280}}^{\text{hLF}}$ would change in the presence of Zn²⁺. For this reason, we collected SV data using three different signals for this experiment: IF, A_280, and A₂₅₀. Previously, we had used just IF and A₂₈₀; it was surmised that the added signal could help if spectral resolution became difficult due to the addition of the cation.

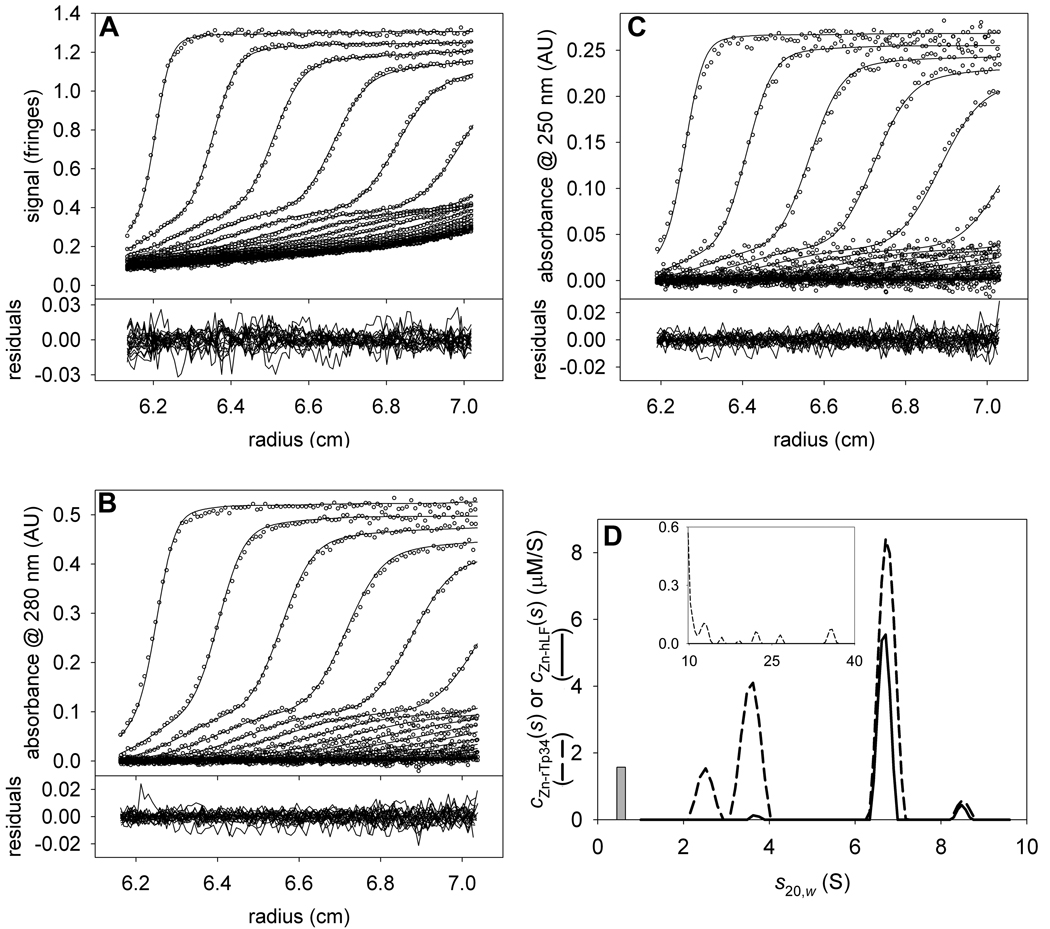
We started the current analysis with the naïve assumption that the ε_ABS280’s of Zn²⁺-bound hLF (Zn-hLF) and Zn²⁺-bound rTp34 (Zn-rTp34) were unaffected by the cation (Table 1). The ε_ABS280 ‘s were therefore fixed, and the ε_IF’s were allowed to refine to their optimal values. We obtained ${\epsilon }_{\text{IF}}^{\text{Zn-hLF}}=\mathrm{205,018}$ fringes·M⁻¹cm⁻¹ and ${\epsilon }_{\text{IF}}^{\text{Zn-rTp34}}=\mathrm{62,815.6}$ fringes·M⁻¹cm⁻¹. The latter value was about 4% less than that obtained previously, but the former value differed from ${\epsilon }_{\text{IF}}^{\text{apo-hLF}}$ by about 9% (Table 1). Moreover, these refined values resulted in signal-increment ratios that were very close to one another: ${\epsilon }_{\text{IF}}^{\text{Zn-hLF}}/{\epsilon }_{\text{ABS280}}^{\text{Zn-hLF}}=2.2,\text{and}{\epsilon }_{\text{IF}}^{\text{Zn-rTp34}}/{\epsilon }_{\text{ABS280}}^{\text{Zn-rTp34}}=2.0$ (Table 3). In our preceding report, these ratios had been 2.5 and 2.1, respectively. Finally, the cZn-hLF(s) and c_Zn-rTp34(s) distributions calculated using the refined signal increments appeared to be incorrect (Fig. 6). First, given the concentrations of both proteins derived from the experiments with the proteins alone, we expected a higher concentration of Zn-rTp34; the observed concentration was 5.5 µM, but the anticipated concentration was 7.5 µM. This error was quite large, even considering the pipetting errors that could have occurred. It is outside the range of concentration error that we usually observe (±10%, data not shown). Next, a significant amount of Zn-rTp34 was found to sediment at 8.4 S with no cosedimenting Zn-hLF; there was no precedent for uncomplexed Zn-rTp34 sedimenting that fast. Finally, the peak corresponding to the known sedimentation coefficient of dimeric Zn-rTp34 was contaminated with more signal for Zn-hLF than observed in this s-range with Zn-hLF alone (not shown). All of these observations indicate a lack of sufficient spectral discrimination between Zn-hLF and Zn-rTp34 for the two signals, IF and A₂₈₀.

Table 3.

Refined signal increments for the Zn-rTp34/Zn-hLF experiments.

Protein	ε280 (AU/M·cm)	ε250 (AU/M·cm)	εIF (fringes/M·cm)	εIF/ε280	εIF/ε250
Zn-hLF	101,218	72,006.8	226,612*	2.23	3.15
Zn-rTp34	32,844.6	11,292.6	65,276.3*	1.99	5.78

^*Fixed in this analysis. Refined by Deka et al [8].

Figure 6. Analysis of A₂₈₀ and IF data for rTp34 and hLF in the presence of Zn²⁺.

The dashed line depicts the c_rTp34(s) distribution, and the solid line represents the c_hLF(s) distribution. The bar shows the s-value and concentration of a discrete species that was also modeled in these data. Unlike the distributions, the unit of the height of the bar is µM. It is noteworthy that the true concentration is unknown; the quantity given in the chart is based on an arbitrary signal increment.

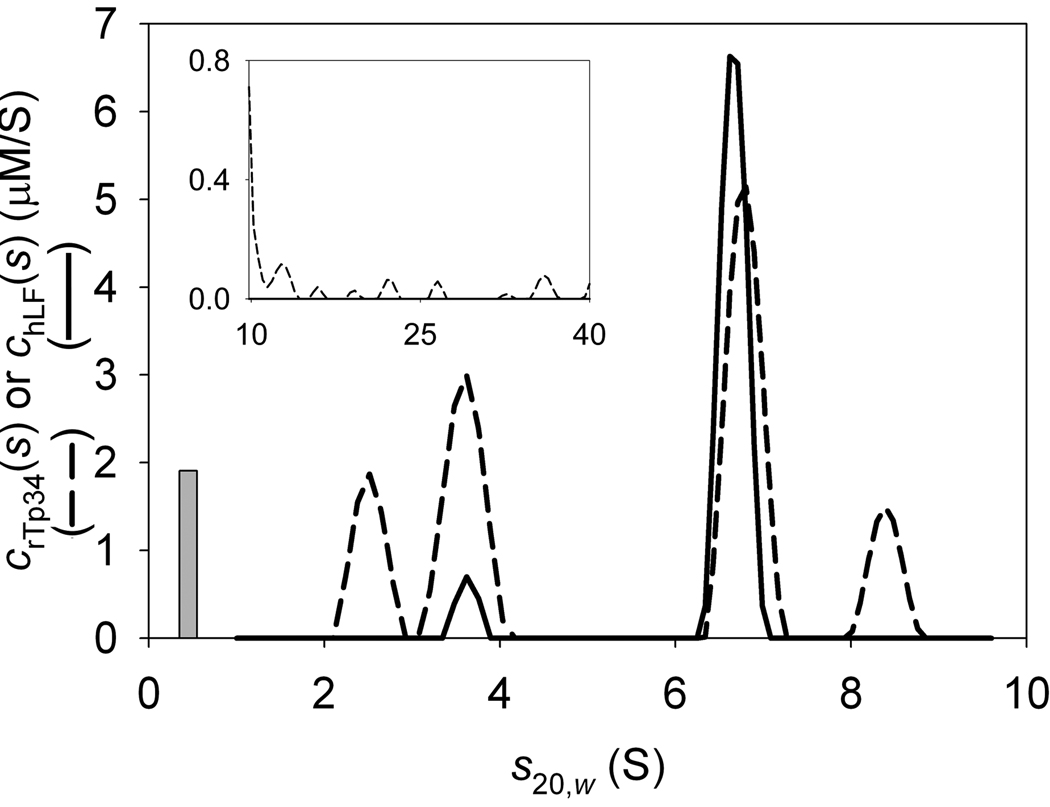
Gaining spectral resolution of the two zinc-bound proteins required a different strategy. It was clear that ${\epsilon }_{\text{ABS280}}^{\text{Zn-hLF}}$ had changed significantly from ${\epsilon }_{\text{ABS280}}^{\text{apo-hLF}}\text{and that}{\epsilon }_{\text{ABS280}}^{\text{Zn-rTp34}}$ could also have been altered. It seemed unlikely, however, that the IF signal increments for the two proteins would change greatly with the addition of a few bound zinc cations. We therefore elected to utilize the IF signal increments derived from the previous work [8] and fix them in our current analyses. Further, we used all three signals, IF, A₂₈₀, and A₂₅₀ in the analyses, allowing the ε_ABS280’s and ε_ABS250’s to refine to their optimal values. Finally, we noted that the IF system detected a small sedimenting species that was not present in the A₂₈₀ or A₂₅₀ data sets. It is very likely that this phenomenon was due to a buffer imbalance between the reference and sample sectors, and that this species was a non-UV-absorbing buffer salt. We modeled this sedimenting material as a discrete species with a high, arbitrary signal increment in the IF data set (100,000 fringes·M⁻¹cm⁻¹) and signal increments of 0 AU·M⁻¹cm⁻¹ in both the A₂₈₀ and A₂₅₀ data sets. This discrete species is shown as a bar in our distributions; its position on the x-axis represents its refined s-value and its height represents its refined “concentration” based on the arbitrary signal increment.

As a result of the above strategy, we were able to gain excellent spectral resolution between the two proteins (Fig. 7). We followed an identical strategy to that outlined above for XDD1 and hE3, except that three signals were used in this analysis. First, the signal increments were refined for an experiment containing only Zn-rTp34. The presence of Zn²⁺ in solution causes the protein to favor its dimeric form (3.5 S), although, under these conditions, there is also some monomer (2.2 S). It was not necessary to model aggregates for this protein. Second, the same type of analysis was performed for a sample containing only Zn-hLF. Three prominent peaks appear in this distribution, at 5.1, 6.7, and 8.1 S (Supplemental Fig. 1). The 5.1-S peak, which is dominant, is monomeric Zn-hLF; the 8.1-S peak is likely a dimer of hLF, and the 6.7-S species is probably a subpopulation of Zn-hLF dimer that has sedimented at a lower time-average s-value because some of it has dissociated during the SV experiment. There are also small species (2–3 S) that may be degradation products of hLF. A distribution of species from 10.1 to 40 S was used to model aggregates of Zn-hLF. The signal increments obtained by analyzing these first two experiments are found in Table 3. And third, the mixture of the two proteins was analyzed using the signal increments refined in the previous two steps. These data were modeled with one discrete species (0.54 S) and distributions spanning 1–5 S, 5.5–9.6 S, and 9.8–40 S. Excellent fits (Fig. 7, parts A–C) to the data are obtained in this analysis (local rmsd’s are 0.007 fringes, 0.004 AU, and 0.005 AU for IF, A₂₈₀, and A₂₅₀, respectively). Only two peaks are present in the 5.5–9.6 S range, indicating that the presence of Zn-rTp34 has slowed the off-rate of the Zn-hLF dimer such that little of the Zn-rT34-bound Zn-hLF dimer dissociates during the SV experiment. Also, the spectral resolution is superior to the two-signal Zn-hLF/Zn-rTp34 experiment described above (Fig. 7D). The observed concentrations are within ~10% of those expected, both proteins are found in the 8.6-S material, and very little Zn-hLF contaminates the peaks for the excess Zn-rTp34. Integrating the distributions at the dominant, 6.7-S peak shows that the molar ratio of Zn-rTp34 to Zn-hLF is approximately 2 ([Zn-Tp34] = 3.8 µM, [Zn-hLF] = 2.0 µM).

Figure 7. The three-signal analysis of the interaction of rTp34 and hLF in the presence of Zn²⁺.

(A) IF data, fit, and residuals for the mixture. (B) A₂₈₀ data, fit, and residuals for the same sample as in A. (C) A₂₅₀ data, fit, and residuals. (D) The distributions used to model the data in parts A–C. The dashed line denotes the c_Zn-rTp34(s) distribution, while the solid line describes the c_Zn-hLF(s) distribution.

The strategy delineated above for restricting certain s-ranges to hypothetical stoichiometries can also be used in this case. For this example, we modeled the material sedimenting at 5.5–9.6 S as 2:1 Zn-rTp34:Zn-hLF complexes. By comparing the ${\chi }_t^2$ of this fit to the data (0.573871) to the ${\chi }_{c,1\sigma }^2$ (0.575228), we conclude that the data are consistent with the 2:1 assumption.

Using labeled protein

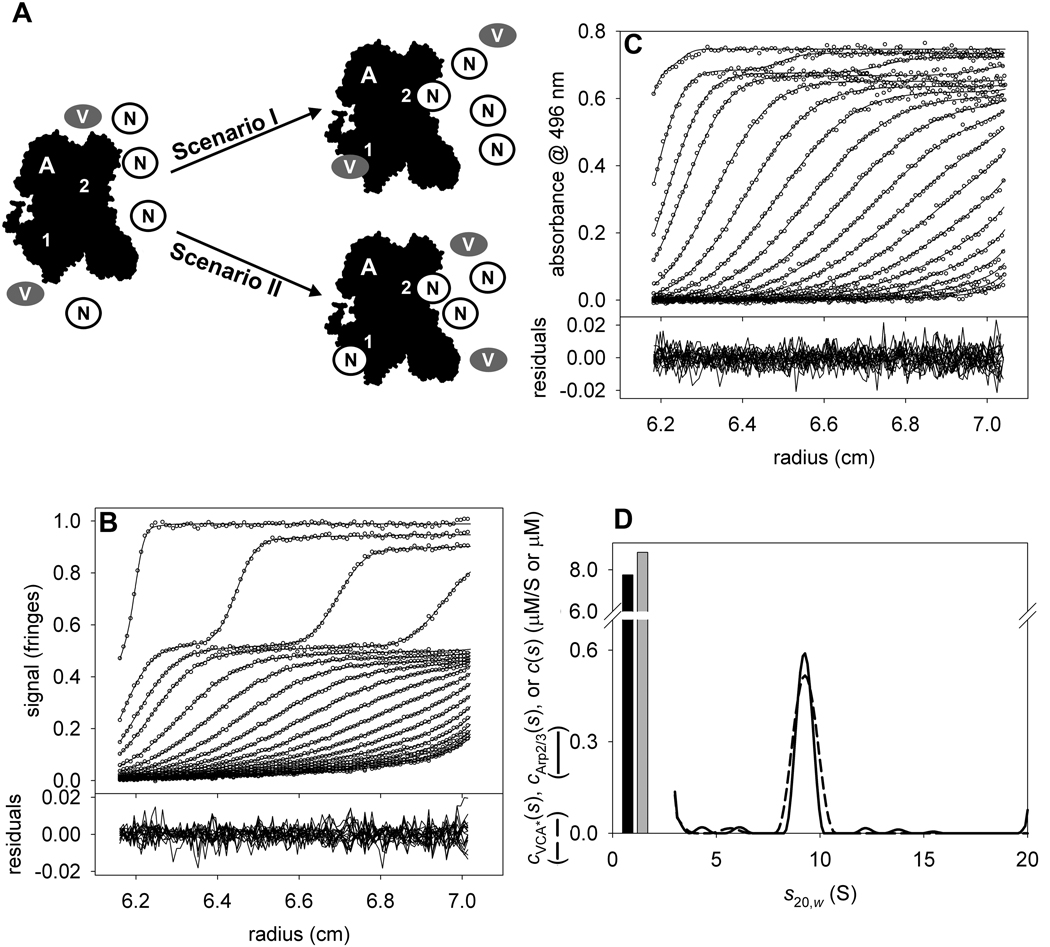
The heteroheptameric Arp2/3 complex binds to actin filaments and nucleates new filaments in a characteristic branched conformation. WASP family proteins are defined by a C-terminal VCA domain which binds to and activates the Arp2/3 complex. Previously, it had been assumed that only one VCA-containing protein could bind to Arp2/3 at a time [27–31]. However, recent evidence had suggested that two such proteins might bind simultaneously [9]. We used MSSV to address this issue.

The experimental approach was to study the interaction of a small, VCA-containing protein construct (called VCA hereafter) and bovine Arp2/3. The very large size difference between VCA and Arp2/3 complex posed a significant difficulty. The molar mass of VCA is about 13,500 Da, while that of Arp2/3 is approximately 224,000 Da. Given the calculated ε_ABS280’s of the proteins, we anticipated that the absorbance and mass changes in Arp2/3 upon VCA binding would be quite small, hampering accurate detection of VCA bound to Arp2/3. We therefore labeled VCA with the fluorophore Alexa-488, yielding VCA*. This expedient gave VCA* a unique absorption maximum at about 496 nm, well into the visible range of the spectrum. Further, the ε_ABS496 for VCA* was high, providing a strong signal for this small protein. We collected data sets from two signals: IF and A₄₉₆.

Unlike our above analyses, only two steps were required to assess the VCA*/Arp2/3 data. In step one, we held the calculated ${\epsilon }_{\text{IF}}^{\text{VCA*}}$ constant at 37,185.5 fringes·M⁻¹cm⁻¹, and refined ${\epsilon }_{\text{ABS496}}^{\text{VCA*}}$ (refined value = 64,629.9 AU·M⁻¹cm⁻¹). The fitted c_VCA*(s) distribution (not shown) describes the VCA*-alone data well, with local rmsd’s of 0.005 fringes and 0.005 AU for the IF and A₄₉₆ data sets, respectively. Ordinarily, there would in which ${\epsilon }_{\text{ABS496}}^{\text{Arp2/3}}$ was refined. However, ${\epsilon }_{\text{ABS496}}^{\text{Arp2/3}}$ was known to be 0, and ${\epsilon }_{\text{IF}}^{\text{Arp2/3}}$ (615,516 fringes·M⁻¹cm⁻¹) was calculated using Eq. 10; refinement was unnecessary. In the last step, the known and refined signal increments were used to analyze a mixture of the two proteins in which [VCA*] is approximately fifteen times [Arp2/3].

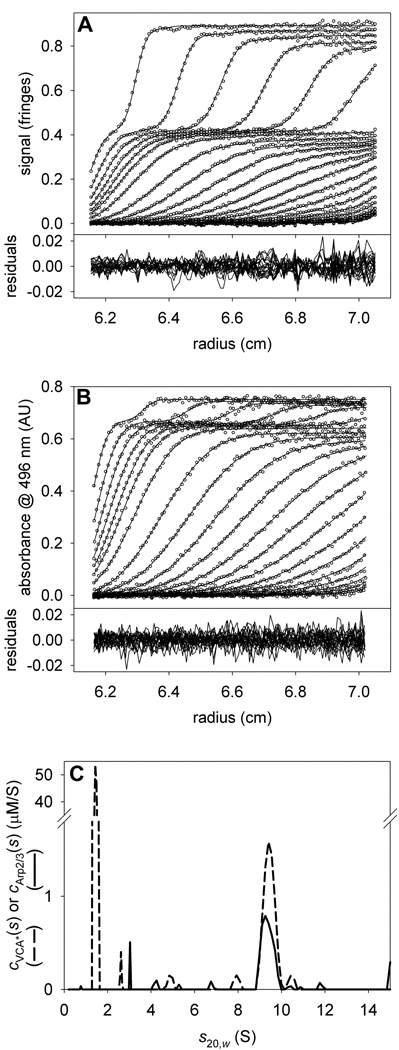
The results of this analysis are shown in Fig. 8. In the mixture analysis, excellent fits were achieved (Figs. 8A & 8B). Two segments of distributions were used to describe the data: one from 0.2 to 4 S, the other from 4.1–15 S; separate f_r’s were refined for each segment. The c_VCA*(s) distributions show two peaks: one at 1.4 S, the other at 9.4 S. The c_Arp2/3(s) distributions have only a single significant peak, at 9.4 S. Arp2/3 alone has a sedimentation coefficient of 9.0 S (not shown), indicating that complex formation with VCA causes a 0.4-S shift in the sedimentation of Arp2/3. Integrating the 9.4-S peaks in the distributions results in [VCA*] = 1.1 µM and [Arp2/3] = 0.5 µM. We therefore conclude that two copies of VCA* bind to a single Arp2/3 complex. This result has been replicated many times with differing molar excesses of VCA* (not shown). At very high molar excesses of VCA*, the absorbance at 496 nm fell out of the linear range of the on-board spectrophotometer. Instead, we capitalized on an absorption minimum of VCA* at 312 nm, which had roughly five-fold less absorbance than at 496 nm.

Figure 8. The interaction of VCA* with Arp2/3.

(A) IF data, fit, and residuals for the mixture of a large molar excess of VCA* with Arp2/3. (B) A₄₉₆ data, fit, and residuals for the same sample as in A. (C) The distributions used to model the data shown in parts A & B. The dashed and solid lines depict the c_VCA*(s) and c_Arp2/3(s) distributions, respectively.

Two signals, three proteins

In the VCA*/Arp2/3 system described above, it was of interest to introduce a third protein: the NtA domain of cortactin. This domain is known to compete with VCA domains for binding to the Arp2/3 complex [9,31], but it was unknown whether NtA domains compete with one or both VCA-binding sites on Arp2/3 (Fig. 9A). To explore this competition, we again turned to MSSV. We used the same materials as above, namely unlabeled Arp2/3 and VCA*. The NtA construct was unlabeled and consisted of residues 1–36 of human cortactin. Sedimentation was monitored using IF and A₄₉₆, as before.

Figure 9. The interaction of VCA* with Arp2/3 in the presence of NtA.

(A) A scheme of the competition of VCA* and NtA for binding to Arp2/3. Arp2/3 (black, labeled “A”) has two different binding sites (“1” & “2”). In this experiment, we added VCA* (gray ovals marked “V”) and NtA (white circles marked “N”) and allowed the system to come to equilibrium. It was known (Figure 8) that VCA could bind to both binding sites; the purpose of this experiment was to test whether NtA could effectively challenge VCA* for Arp2/3 binding at one or both of the sites. Two scenarios are considered. In Scenario I, shown in the upper part, a large excess of NtA will effectively compete for only one of the VCA* binding sites, and the limit of VCA:Arp2/3 stoichiometry at high [NtA] will be 1. In Scenario II, shown in the lower part, NtA effectively competes for both of the VCA* binding sites, and the limit of VCA:Arp2/3 stoichiometry at high [NtA] will be 0. (B) IF data, fit, and residuals for the VCA*/NtA/Arp2/3 mixture. (C) A₄₉₆ data, fit, and residuals for the same sample as in B. (D) Species and distributions used to model the data in parts B & C. Free VCA* and free NtA are modeled as single species corresponding to the gray and black bars, respectively. The c_VCA*(s) and cArp2/3(s) distributions are shown as dashed and solid lines, respectively.

Theoretically, to establish the stoichiometry of a three-component complex, at least three signals are needed. We monitored only two. However, our experiment was designed to track only the VCA*:Arp2/3 stoichiometry as NtA was titrated in. Two modifications to our VCA*/Arp2/3 strategy were therefore required. First, excess NtA was modeled as a discrete species with an ${\epsilon }_{\text{IF}}^{\text{NtA}}$ of 11,281 fringes·M⁻¹cm⁻¹ and a ${\epsilon }_{\text{ABS496}}^{\text{NtA}}$ of 0 AU·M⁻¹cm⁻¹. Second, the assumption was made that the binding of NtA to Arp2/3 did not alter ${\epsilon }_{\text{IF}}^{\text{Arp2/3}}$. In essence, the fact that NtA was binding to Arp2/3 was spectrally ignored. Using this assumption, we could calculate c_VCA*(s) and c_Arp2/3(s) distributions without accounting for the third protein. Strictly speaking, the assumption of unaltered ${\epsilon }_{\text{IF}}^{\text{Arp2/3}}$ cannot be true. The added mass of NtA will cause the signal increment of the NtA:Arp2/3 complex to be more than that of apo-Arp2/3. However, a single molecule of our NtA construct has only 1.8% of the molecular mass of Arp2/3. We therefore hypothesized that NtA binding to Arp2/3 would have a negligible effect on ${\epsilon }_{\text{IF}}^{\text{Arp2/3}}$, and thus that its binding could be ignored for the purposes of spectral discrimination.

We followed the same methodology as described above for VCA*/Arp2/3. The only difference is that a discrete species was added to model free NtA. The analysis was performed on five samples having the following concentrations of NtA: 0, 3.5, 7.7, 13.9, and 23.2 µM. The concentrations of Arp2/3 and VCA* were held constant at 0.5 and 9.6 µM, respectively.

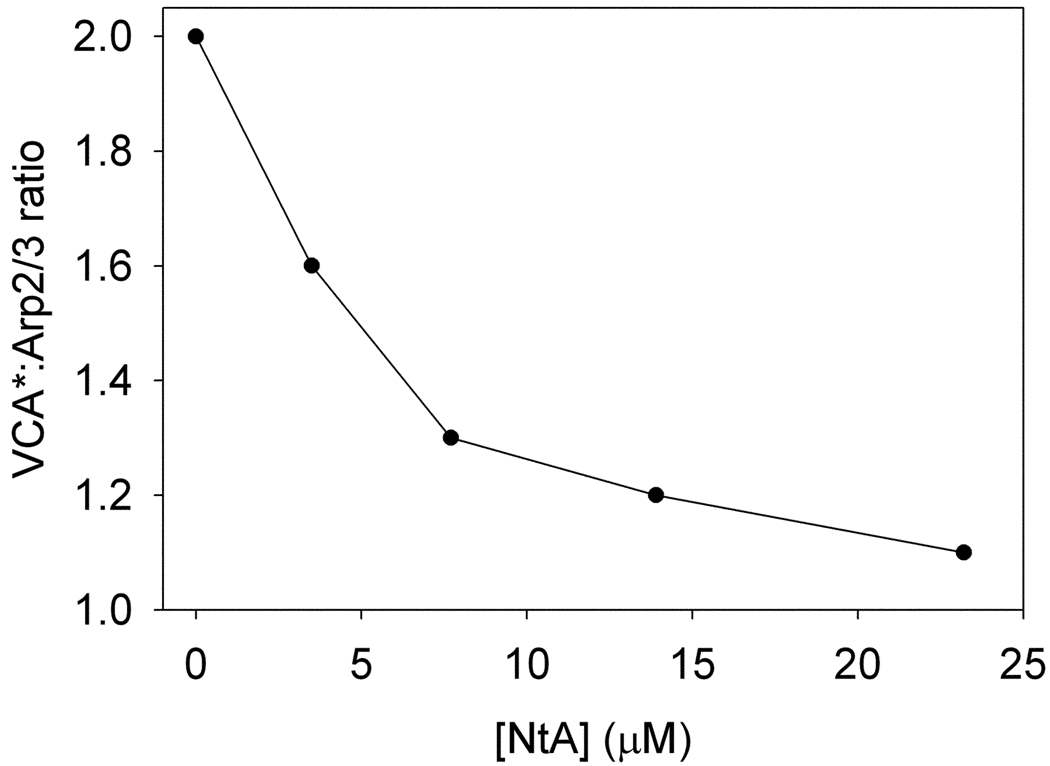
We present here the analysis of the sample with 7.7 µM NtA. Two discrete species (one for free VCA* and one for free NtA) and two c_k(s) distributions (ranging from 3–12 S) were used to globally model the two SV data sets. The data, resulting fits, and c_k(s) distributions resulting from this analysis are shown in Fig. 9. The quality of the fits was excellent; the rmsd’s were 0.004 fringes and 0.005 AU for the IF and A₄₉₆ data, respectively. We found that the concentrations of free VCA* and free NtA were 8.9 and 7.4 µM, respectively. Integrating the peaks at 9.2 S, we found that the 0.7 µM VCA* cosedimented with 0.5 µM Arp2/3, making the molar ratio of these two proteins 1.4 to 1. The presence of NtA has lowered the molar ratio, indicating that NtA effectively competes for at least one of the VCA*-binding sites on Arp2/3. The smaller sedimentation coefficient of the presumed Arp2/3:VCA*:NtA complex compared to the Arp2/3:VCA* complex is in keeping with its expected smaller size. In Fig. 10, we show the full results of the complete titration experiment. We found that even with a large molar excess of NtA over Arp2/3 (46:1), the molar ratio of VCA*: Arp2/3 was still greater than one. This result suggests that NtA only competes with VCA* for one of the two VCA*-binding sites on Arp2/3.

Figure 10. NtA titration.

The x-axis shows the total [NtA] calculated from the fitting session in SEDPHAT. The y-axis shows the ratio of VCA* to Arp2/3 in the cosedimenting complex.

Discussion

In all three of the experimental systems explored in this report, MSSV has proven to be a useful method for the determination of the stoichiometry of proteins that co-sediment as a complex in an SV experiment. In two of these cases (hE3/XDD1 and rTp34/hLF), the stoichiometry established here comports with that measured with another biophysical method, ITC, which is known for its ability to determine the stoichiometries of protein-protein associations [32].

In general, the MSSV method demands that at least as many signals be collected as there are proteins in the complex under study. The analyses presented above illustrated two interesting departures from this rule. First, the Zn-rTp34/Zn-hLF interaction was studied with one more signal than thought necessary. The inclusion of three signals (IF, A₂₈₀, A₂₅₀) in the analysis afforded spectral resolution whereas an analysis with just two of those signals (IF and A₂₈₀) failed (Figs. 6 & 7). Further analyses (not shown) demonstrate that two signals, IF and A₂₅₀, would have sufficed. As may be deduced from Tables 1 & 3, the IF:A₂₅₀ extinction ratios for the two proteins are significantly different. Most of the spectral discrimination, then, came from the difference in these ratios. However, the inclusion of the A₂₈₀ data likely added to the hydrodynamic resolution of the experiment, as exclusion of these data would have introduced time gaps wherein no information on the sedimentation of the several species was available. Obviously, if it were known beforehand that the A₂₈₀ signal would not contribute to the spectral discrimination, the optimal data collection strategy would be to collect only IF and A₂₅₀ signals.

The other exception to the “one signal per component” rule was in the VCA*/NtA/Arp2/3 study (Fig. 9). It is important to note that this method succeeded only because the molar mass of NtA was a small fraction of that of Arp2/3, and also because only the stoichiometry VCA* and Arp2/3 was monitored. These two conditions must be met before attempting an experiment of this type.

In principle, the MSSV experiment and analysis could accommodate more than the two-protein analyses described above. Given the current capabilities of the Beckman XL-I analytical ultracentrifuge, there is the possibility of spectrally distinguishing four cosedimenting components. One of the signals in such an experiment is necessarily IF. It is possible that the UV-absorbance of proteins would provide the second and third signals (A₂₈₀ and A₂₅₀). For most proteins, there is no other convenient peak of UV absorbance; the peptide chain absorbs too strongly in the far UV to be of general use. Consequently, a visible wavelength would be required for a four-signal experiment. Some proteins contain coenzymes that have peaks in the visible region of the spectrum, but most do not. Labeling at least one protein with a chromophore, as was accomplished for VCA in our example, would therefore be required. Importantly, the choices of chromophore and of the position at which to modify the protein are not trivial. If IF is to be used, the chromophore should not absorb the light emitted by that optical system’s laser. It signal increment should provide sufficient signal-to-noise, yet should not overwhelm the capabilities of the on-board spectrophotometer (see above). Further, the site of modification obviously should be distal from the protein’s interaction surface. Our choice of Alexa488 covalently attached to VCA at its amino terminus met all of these criteria.

Of course, there is no reason that only protein-protein interactions can be studied. Any interacting molecule with a measurable signal could be studied. Protein-nucleic-acid interactions seem particularly well suited to the method, as these macromolecules have distinctive UV-absorption signatures. The study of carbohydrates, e.g. in a protein/carbohydrate interaction, should be amenable as long as the size of the carbohydrate and the signal increments of the carbohydrate are known. In such a case, an experiment analogous to those of LeMaire, Salvay, et al. could be performed [33,34]. These researchers were concerned with the amount of detergent bound to their protein, but the same principal holds for protein/carbohydrate interactions.

Previously, other authors have used sedimentation equilibrium (SE) or multisignal sedimentation equilibrium (MSSE) to establish the stoichiometry of protein-protein or protein-nucleic acid interactions [35–39]. Two approaches are commonly employed. In the SE approach, several SE experiments are performed with different ratios of the interacting components. In this approach, it is helpful if one of the components dominates the data at one of the signals [37,38]. The radial concentration profiles in the centrifugation cells are monitored using a signal that is dominated by one of the components. The several experiments are analyzed individually, and a signal-average buoyant molar mass is derived for each one. A plot of this mass vs. the component ratio should reach a plateau at the buoyant molar mass of the maximal complex. This mass should coincide with the theoretical buoyant molar mass of a complex of a certain stoichiometry, thus establishing that quantity (e.g., see Ucci et al. [38]). In MSSE, a stoichiometry is assumed, and the data are fit to this experimental model. The goodness of the fit is taken as confirmation of the stoichiometry [35,36,39]. Often in such analyses, other information about the associating proteins is known. This information may be built into the analysis; for example, the buoyant molar masses of the components may be known, or the number of components and their approximate buoyant molar mass may be known from an SV experiment. MSSV represents a complementary approach to the problem with distinct advantages: (a) while an SE experiment generally takes days to perform, MSSV can be done in hours (overnight); (b) SE and MSSE do not give the experimenter information regarding the hydrodynamic properties (s_complex and f_r) of the complex, while MSSV does; (c) the data basis of the MSSV experiment is significantly larger than SE or MSSE, which may lead to better spectral resolution of species [1]; and (d) SE data analysis requires that an interaction model be imposed, while MSSV is model-free in that regard. It should be noted that short-column SE experiments may be performed in hours [37], mitigating point (a) above, at the expense of making the data basis of those experiments smaller. Therefore, SE, MSSE, or MSSV may be used to determine stoichiometry; for a quick, accurate determination of stoichiometry only, a single MSSV experiment should suffice.

As pointed out by Balbo et al. [1], MSSV is best suited to experimental systems that have a slow k_off relative to the time taken to perform an SV experiment (k_off < 10⁻³ s⁻¹). By simulating data for fast interactions, they found that they may be characterized by MSSV, but one of the components must be present at a large molar excess over the other. For the hE3/XDD1 and Zn-rTp34/Zn-hLF systems, the k_off’s are likely to be slow; they do not dissociate when subjected to size-exclusion chromatography (not shown). Further, the molar excesses used in these experiments ensure a high degree of occupation of the complex. The k_off of the VCA/Arp2/3 [9] interaction is fast by the above criterion, but the presence of large molar excesses of this protein ensures full occupation in our experiments.

In conclusion, MSSV has proved to be a dependable method to determine the stoichiometry of proteins in a hetero-associating complex. In addition to the experiments presented above, several other groups (e.g., see [1,40–43]) have successfully used this technique. The multisignal approach has also been used to characterize protein/detergent complexes [34]. MSSV adds a new tool to those already available to the biophysicist to answer one of the fundamental questions that arises from studying protein-protein interactions in detail, and should be applicable to a wide variety of experimental systems.

Supplementary Material

01. Supplemental Figure 1. The c_Zn-hLF(s) distribution in the absence of Zn-rTp34.

Shown is the distribution that best fits the Zn-hLF alone data. Both aggregates (inset) and a single discrete species (bar) were also modeled.