Abstract
It is well-known that muscle redundancy grants the CNS numerous options to perform a task. Does muscle redundancy, however, allow sufficient robustness to compensate for loss or dysfunction of even a single muscle? Are all muscles equally redundant? We combined experimental and computational approaches to establish the limits of motor robustness for static force production. In computer- controlled cadaveric index fingers, we find that only a small subset (<5%) of feasible forces is robust to loss of any one muscle. Importantly, the loss of certain muscles compromises force production significantly more than others. Further computational modeling of a multi-joint, multi-muscle leg demonstrates that this severe lack of robustness generalizes to whole limbs. These results provide a biomechanical basis to begin to explain why redundant motor systems can be vulnerable to even mild neuromuscular pathology.
1. Introduction
Muscle redundancy - having more muscles than mechanical degrees-of-freedom (DOFs) - has long been a central problem in biomechanics and neural control. At issue is how the central nervous system (CNS) selects muscle coordination patterns from a theoretically infinite set of possibilities (Bernstein, 1967). Little attention, however, has been given to the related critical clinical question of whether muscle redundancy grants the body robustness to dysfunction of even one muscle. Thus advancing motor systems research requires that we clarify the relationship between muscle redundancy and robustness to muscle dysfunction.
While muscle redundancy theoretically affords muscles infinitely many activation levels for a given submaximal task, the range of these valid activation levels has critical implications to robustness. For example, if muscle A can produce any force within a 10 N range for a particular task (i.e., an infinite number of possible activation levels), the implications to robustness are critically different if this range is 0–10 N or 5–15 N. If the former case, muscle A is redundant because the CNS can find valid coordination patterns even if it is lost (activation = 0). However, in the latter case, muscle A is necessary, because the CNS cannot adapt to its loss: there are no valid coordination patterns if muscle A is sufficiently weakened or lost. Here we present computational geometry methods that identify muscles that are necessary for specific tasks. By studying both human fingers and legs, we find that tendon-driven biomechanical systems exhibit surprisingly little robustness to dysfunction of even one muscle, and show how these computational methods open up numerous novel research avenues in biomechanics and neural control.
2. Methods
We studied the necessity of muscles by analyzing the static transmission from muscle force to endpoint output. For the human index finger, we measured that transmission experimentally by applying known tensions to its seven tendons in cadaveric hand specimens while recording the resulting fingertip forces. For the human leg, we used published data to construct a biomechanical model of the hip, knee, and ankle in the sagittal plane to predict the force vector produced at the foot by maximal activation of each muscle. In each case, we derived an action matrix A that maps a vector a 3 describing the activation in each muscle to the force output of the limb (Murray et al., 1994, Valero-Cuevas, 2005b). Such a linear transformation has been found to be valid for a fixed posture of a finger (Valero-Cuevas et al., 2000, 1998) and leg (Kuo and Zajac, 1993).
Action Matrix for Human Index Finger
We resected four fresh frozen cadaver arms at the mid-forearm level and dissected them to reveal the proximal end of the insertion tendons of all seven muscles controlling the index finger as in our prior work (Valero-Cuevas et al., 2000): flexor digitorum profundus (FDP), flexor digitorum superficialis (FDS), extensor indicis (EI), extensor digitorum communis (EDC), first lumbrical (LUM), first dorsal interosseous (FDI), and first palmar interosseous (FPI). We fixed the specimen rigidly to a tabletop using an external fixator (Agee-WristJack, Hand Biomechanics Lab, Inc., Sacramento, CA), and we tied and glued the proximal tendons to nylon cords attached to rotational motors. Motors were controlled using a real-time controller and custom-written software. Load cells measured the tension in each cord, which was fed back to the motor so that a desired amount of tension could be maintained on each tendon. The fingertip was rigidly attached to 6 DOF load cell (JR3, Woodland, CA).
We examined 5 different postures in 3 specimens, and 3 different postures in the final specimen. Each posture was neutral in add-abduction. The examined postures were chosen to cover the workspace and simulate those found in everyday tasks. After positioning the finger in a specific posture, we determined the action matrix for the finger: we applied 128 combinations of tendon tensions representing all possible combinations of 0 and 10 N across the seven tendons, and held each combination for 3 seconds. The fingertip forces resulting from each coordination pattern was determined by averaging the fingertip load cell readings across the hold period. Linear regression was performed on each fingertip force component using the tendon tensions as factors. In this way, the fingertip force vector generated by 1 N of tendon tension was determined for all muscles. The force vector generated by each muscle was scaled by an estimate for maximum muscle force (Valero-Cuevas et al., 2000) to generate the columns of the action matrix for each specimen and posture examined.
Action Matrix for Human Leg Model
We also studied the necessity of muscles for mechanical output for a simplified, but plausible, sagittal plane model of the human leg (hip, knee, and ankle joints). The model contained 14 muscles/muscle groups (Kuo and Zajac, 1993) (muscle/muscle group abbreviation in parentheses): medial and lateral gastrocnemius (gastroc), soleus (soleus), tibialis posterior (tibpost), per- oneous brevis (perbrev), tibialis anterior (tibant), semimembranoseus/semitendenosis/biceps femoris long head (hamstring), biceps femoris short head (bfsh), rectus femoris (rectfem), gluteus medialis/glueteus minimus (glmed/min), adductor longus (addlong), iliacus (iliacus), tensor facia lata (tensfl), gluteus maximus (glmax). Moment arms for hip flexion, knee flexion and ankle dorsiflexion for all of these muscles were obtained from a computer model of the lower limb (Arnold et al., 2010). When necessary, multiple muscles in were combined into the single muscle groups. We derived a 3 × 3 square Jacobian mapping changes in the hip, knee, and ankle angle to the foot position in the plane (2 components) and the orientation of the foot in space. This Jacobian matrix, inverted and transposed, was combined with the moment arms and maximal muscle forces to form the action matrix mapping muscle activation to forces and torques at the foot (Valero-Cuevas, 2005b), although our analysis of muscle redundancy was only performed with respect to the endpoint forces.
Analyzing the action matrix to determine muscle necessity
We used the action matrix to determine whether muscles are necessary for a given desired output force using standard tools in computational geometry. The muscle redundancy problem can be expressed as a set of linear inequalities (Chao and An, 1978, Spoor, 1983). These inequality constraints enforce that the activation for each muscle lie between 0 and 1, and that the actual output force is equal to the desired force. The inequality constraints define a region in muscle activation space called the task-specific activation set: any point inside that set will produce the desired output force (Kuo and Zajac, 1993, Valero-Cuevas, 2005b, Valero-Cuevas et al., 2000, 1998). We computed the vertices defining the task-specific activation set using a vertex enumeration algorithm (Avis and Fukuda, 1992). We then found the task-specific activation ranges to achieve the desired output force for each muscle by projecting all vertices onto the seven muscle coordinate axes to determine the minimum and maximum task-specific activations. While previous studies have used similar experimental (Valero-Cuevas et al., 2000) and computational (Valero-Cuevas et al., 1998) techniques, our study is novel in that it the first to demonstrate how computational geometry can be combined with experimental results to determine which muscles are required to achieve particular feasible outputs.
There are several metrics by which the importance of different muscles could be compared, including the area or volume reduction in the feasible force set subsequent to muscle dysfunction. In addition to computing volume reduction, we also examined a more conservative estimate of muscle necessity by calculating the worst deficit (WD) that would occur in any force direction if a particular muscle was lost. For example, if WDFPI = 0.95, there is some force direction in 95% of force producing capability would be lost if the FPI muscle dysfunctioned.
3. Results
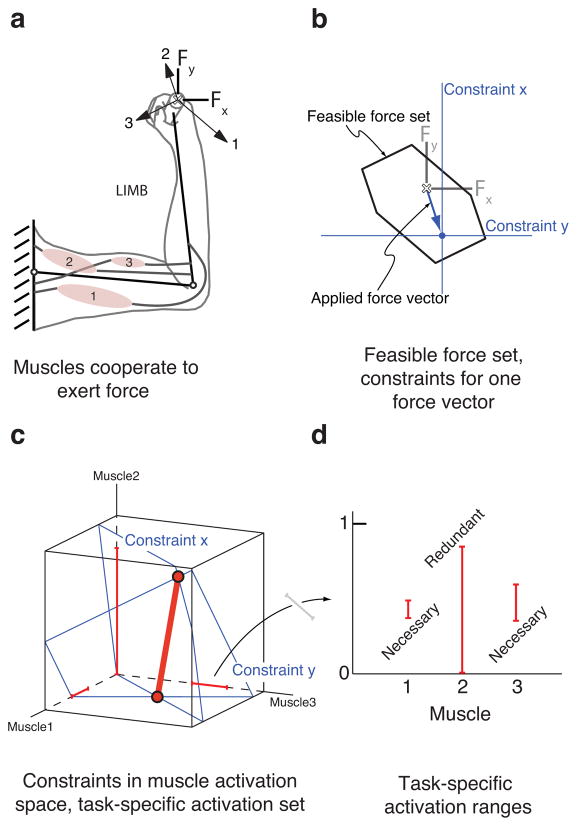
We use a ”schematic model” of a two-link arm with three idealized muscles (Figure 1a) to build intuition about our results without loss of generality. For the posture shown, muscle 1 extends both the shoulder and elbow, and exerts positive x and negative y force at the endpoint. Muscle 2 flexes both the shoulder and elbow, and exerts negative x and positive y force. Muscle 3 extends the shoulder and flexes the elbow, and exerts negative x and negative y force at the endpoint. The set of all possible forces that can be achieved with these three muscles is the feasible force set (Figure 1b, (Valero-Cuevas, 2005b)). Achieving a particular target force vector within the feasible force set can be viewed as achieving a particular target x-force and a target y-force (Figure 1b). The muscle activation patterns that produce the target x-force and the target y-force have the geometric interpretation of being planes in muscle activation space (Figure 1c). The intersection of these two planes that is within the unit cube (all activations between 0 and 1) is the task-specific activation set for the target force vector. Its extreme points are vertices (Figure 1c) that can readily be computed, and any feasible coordination pattern must lie between these vertices. Displaying the task-specific activation ranges for all muscles (Figure 1d) allows the easy visualization of muscles that are necessary and redundant for a given output: muscles whose minimum task-specific activation is zero are redundant for the given output (muscle 2 in this example), whereas muscles whose minimum task-specific activation range is greater than zero are necessary for the given output (muscles 1 and 3 in this example).
Figure 1.
Three muscle “schematic model” conceptually illustrates the necessity of muscles. a. Muscles can be functionally visualized as force vectors at the endpoint. b. A region of force space, the feasible force set, is achievable given this musculature. A particular target force vector can be decomposed into a target x-force and a target y-force. c. The valid coordination patterns for the x and y targets can also be viewed in muscle activation space as planes; the portion of the intersection of these two planes that is inside the unit cube is the task-specific activation set. Any point on the task-specific activation set will generate the same target force vector. d. The task-specific activation set can be projected onto the muscle coordinate axes, revealing the minimum and maximum activation in each muscle for the given applied force vector. The task-specific activation ranges can be constructed for each muscle, and reveal which muscles are necessary and which are redundant for a given target force vector.
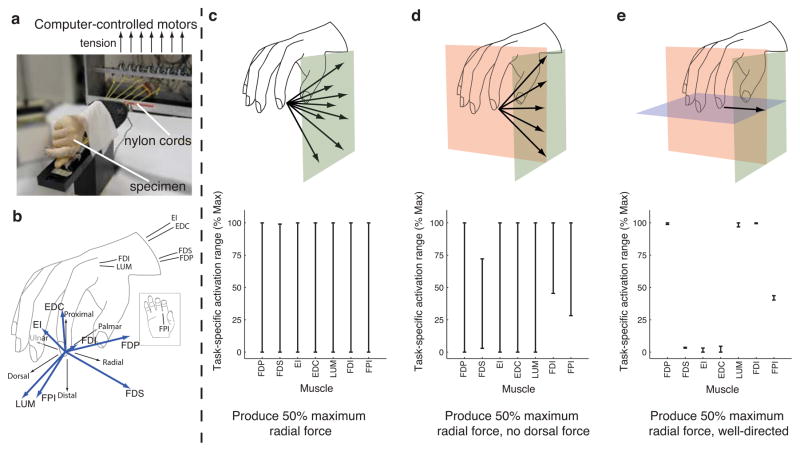
We find that whether a muscle is necessary for a particular static force can not be easily predicted from its anatomical layout, but arises from functional interactions among muscles, skeletal structure, and task constraints. For example, the human first dorsal interosseous (FDI) is widely believed to be the primary muscle used for abduction of the metacarpophalangeal joint (Flament et al., 1993, Infantolino and Challis, 2010); consequently, it would be not be surprising that this muscle would be required for abduction (radial force) tasks. In accord with experimental studies showing substantial activity from muscles other than the FDI during abduction (Kutch et al., 2008, Keenan et al., 2006), muscle necessity depends on the how tightly fingertip force direction was constrained. Using the same analysis as for the toy model, we find the 7-Dimensional task-specific activation set from data measured in a cadaveric index finger in a functionally- important precision pinch task (approximating “key pinch”) (Figure 2). When requiring 50% of maximum possible radial (abduction) force magnitude without specifying the exact direction of the force vector, no muscle is necessary (Figure 2c). However, if the force vector is limited to having no dorsal component, FDS, FDI, and FPI become necessary: if any one is lost there is no longer a feasible solution (Figure 2d). If the force vector direction is further constrained to a pure radial direction, several muscles became necessary with narrow task-specific activation ranges (Figure 2e).
Figure 2.
Muscle necessity depends on the nature of the task constraints. a. Experimental setup. Computer controlled motors produce specified amounts of tension to the tendons of all seven index finger muscles in a cadaver hand specimen, generating finger movement and/or fingertip force. b. The approximate anatomical location of these tendons is shown, along with the fingertip force vector produced by applying 1 N of tension to each tendon individually. c. The necessity of index finger muscles for a precision pinch task (approximating the index finger in “key pinch”) was analyzed for one representative specimen in the posture shown. When the task required 50% of the maximum possible radial force, no muscle was necessary as any could have zero activation for this task. d. However, when the task required the same amount of radial force but with zero dorsal force (more stringent task), the FDS, FDI and FPI became necessary. The CNS would not be able to adapt and find a coordination pattern satisfying these constraints if any of these three muscles were lost. e. The task constraints are particularly stringent when the same amount of radial force is required to be well-directed (zero dorsal and distal force). The FDP, FDS, LUM, FDI, and FPI are all necessary to achieve this task. Interestingly, the EI, EDC, and FDS muscles must be nearly inactive, suggesting that the CNS would not be able to adapt and achieve the task if either of these muscles was hyperactive.
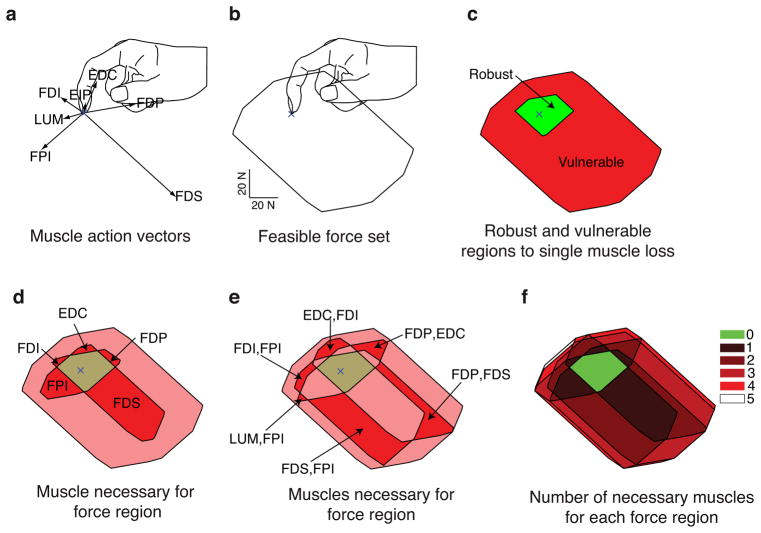
Muscle necessity generalizes to other fingertip force magnitudes and directions in the plane of finger flexion-extension (i.e., sagittal plane). The force vectors produced by each muscle are broadly distributed in this plane (Figure 3a), and their feasible force set shows the finger is stronger in flexion than extension, as expected from everyday experience (Figure 3b). We find a region of force magnitudes and directions surrounding the fingertip for which no muscle is necessary: i.e., it is robust to the loss of any one muscle (Figure 3c). Surprisingly, however, this region is quite small (8% of the 2D feasible force set area for this specimen and posture), as most of the feasible force set (92%) is vulnerable to the loss of any one muscle (Figure 3c). Across other specimens and postures studied, the 2D robust region ranged from 6 to 23% of the feasible force set (average 14%). Other regions are vulnerable to the loss of only 1 muscle (Figure 4d), or vulnerable to the loss of 2 muscles (Figure 3e). In general, the number of muscles to which a region is vulnerable increases with force magnitude because the solution space approaches uniqueness at the boundary of the feasible force set (Figure 3f (Valero-Cuevas, 2005b, Valero-Cuevas et al., 1998)).
Figure 3.
Muscles were necessary for most sub-maximal forces: one example specimen and posture. a. The action vectors of the 7 index finger muscles in the posture shown. b. The feasible force set, showing that the index finger is strongest in combinations of distal (downward) and palmar (rightward) force. c. The feasible force set decomposed into two regions: no particular muscle is necessary in the robust region, while particular muscles are required for all forces in the vulnerable region. d. The particular muscle vulnerabilities can be mapped out for single muscles. e. Regions that are vulnerable to dysfunction in either of a pair of muscles can also be mapped out. f. The number of muscles to which a region is vulnerable generally increases with increasing force magnitude.
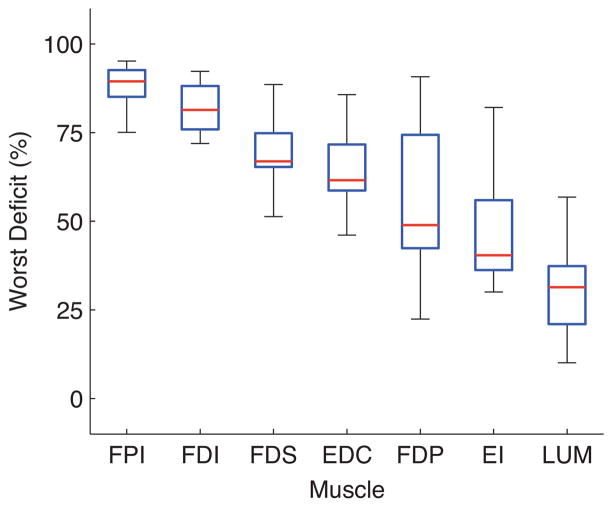
Figure 4.
The worst deficit (WD) metric rank orders muscles by necessity. The 3D fingertip force production deficit that would be incurred by the loss of each index finger muscle. Red lines show median, blue boxes show 25th and 75th percentiles, and the whiskers show the remainder of the data points. While muscles such as the FPI and FDI are clearly more necessary on average than muscles such as the EI and LUM, a specimen and posture could be found for every muscle for which WD value for that muscle was large.
We tested whether small robust regions resulted from the specific maximal force we assigned to each muscle - an assumption in our analysis - that were derived from estimates of physiological cross-sectional area (Valero-Cuevas et al., 2000). We performed a Monte Carlo simulation to calculate the robust region when varying the maximal muscle force estimate for each muscle stochastically by up to ±25% (Figure 5a, b). Upon convergence, we find that the robust region is consistently small for all specimens and postures examined never exceeding 27% of the 2D feasible force set. We extended our numerical analysis to the full 3D feasible force sets to calculate the volume of the robust region as a fraction of the total volume of feasible forces. We find even smaller robust regions in 3D than in the 2D sagittal plane analysis. The volume of the robust three-dimensional region was at most 5% of the feasible force set volume (95% was vulnerable to muscle loss), with an average of 2% across the specimens and postures examined.
Figure 5.
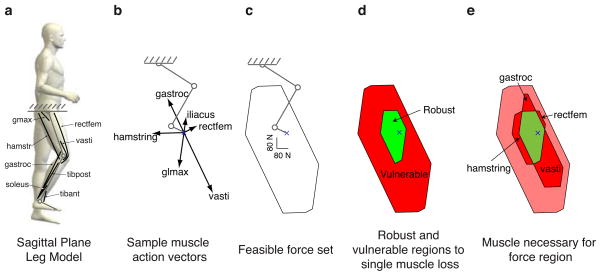
The ability of the leg to produce forces is also vulnerable to muscle loss. a. The leg model that we analyzed had 14 muscle groups, only 8 of which are shown for clarity. b. These muscles could also be visualized as action vectors in endpoint force space. Each muscle has an action vector, but only the dominant action vectors are shown for clarity. c. These action vectors generate a feasible force set, showing that the leg is particularly strong in generating downward force. d. The robust and vulnerable regions of the feasible force set were calculated: the robust region occupies 14% of the feasible force set area for this model. e. Similar to the human finger, the leg model predicts that certain regions of the feasible force set will be vulnerable to the loss of only one muscle. Regions also exist for the leg model in which only two muscles are necessary, etc., but are not shown for clarity.
There are clear differences among muscles in relative importance to force production (Figure 4). The FPI was found to be the most necessary muscle across specimens, postures, and force directions. For example in one specimen and posture, the loss of the FPI resulted in a 96% force deficit. While the LUM muscle was found to be the least necessary muscle on average, there was still a specimen and posture for which loss of the LUM muscle resulted in a 83% force deficit. Even a conservative non-parametric comparison across all specimens, postures, and force directions shows a clear rank ordering (Figure 4).
Analysis for a simulated planar human leg with 14 muscle groups in the sagittal plane (Figure 5) shows similar results. This model predicts that the region of robustness is approximately 16% of the feasible force set area (Figure 5d). As with the finger, there are regions of feasible force vulnerable to only one muscle/muscle group: hamstring, vasti, rectfem, and gastroc groups (Figure 5e).
4. Discussion
Muscle redundancy, as a problem of muscle coordination pattern selection, has been central to motor control for several decades. Our experimental and computational work clearly shows muscle redundancy affords very little robustness to muscle dysfunction in both fingers and limbs. Therefore, a thorough analysis of robustness should be part of testing theories of muscle coordination. After discussing clarifications and limitations, we point out areas in biomechanics and neural control for which this refined view of muscle redundancy provides insight.
We first note some clarifications and limitations. The tension applied to the cadaveric fingers remained less than 10 N to avoid tendon tearing. While this assumption could affect the quantitative predictions of our results at the extremes of feasible force, it is unlikely that potential nonlinear effects – such as bowing, stretching, or deformation of the tendons or ligaments, or seating of joints in response to changes in muscle force – would change the fundamental conclusion that mechanical interactions make some muscles necessary for low and high endpoint forces. One assumption we had to make is the relative strengths of the muscles. The specific maximal force a muscle can produce can only be approximated given the uncertainties in physiological cross sectional areas, pennation angles, etc. (Zajac, 1989), especially for hand muscles like the FDS (Agee et al., 1991). However, our Monte Carlo sensitivity analysis (Valero-Cuevas et al., 2009a) shows this assumption cannot undermine our results. Lastly, we assumed independence of muscle activation, and for the sake of brevity only present the analysis of muscle necessity to loss of single muscles. These two choices, in fact, lead to best-case, conservative estimates of robustness that strengthen our conclusions. Further reduction in force output due to simultaneous deficits in more than one muscle, or neural coupling between muscles, can only be equal or greater.
For the sake of simplicity, we primarily addressed robustness to complete muscle dysfunction in this article; limb force production will be more robust if muscles only become weaker, and do not dysfunction completely. However, our results already begin to address muscle weakness. For the index finger to produce 50% maximal radial force with no dorsal force (Figure 2d), both the FDS and FDI can not completely dysfunction. However, the FDS need only produce about 5% of its maximal force, whereas the FDI needs to produce nearly 50% of is maximal force. Therefore, this task is more robust to weakness in the FDS than the FDI. Our approach enables future studies that completely describe the robustness of different tasks to muscle weakness.
Another limitation of our work is that it currently applies only to the generation of static endpoint forces. However, our preliminary expectation is that future studies will find that individual muscles are also necessary for particular movement trajectories. The limb equations of motion relate the joint kinematics to the joint torques. Inverse dynamics would predict the joint torques given kinematics and external forces. If moment arm variation with posture could be estimated for the joints and muscles of interest, the computational geometry methods described in this paper would predict which muscles were necessary as a function of time along the kinematic trajectory. If a certain muscle became necessary at any point along the trajectory, that trajectory would no longer be feasible if that muscle were to dysfunction.
Synergistic patterns of muscle activation
The electrophysiological study of muscle activity has repeatedly shown that muscles are often coactivated in groups, generally called muscle synergies, that are interpreted as evidence of a neural strategy to simplify muscle control. These coactivation patterns can be seen over a range of tasks, as well as disappear for other tasks. For example, locomotor coactivation patterns among cat hindlimb muscles can change during such novel tasks as rapid ankle extension (Smith et al., 1980) and incline walking (Smith and Carlson-Kuhta, 1995). Our analysis of muscle necessity enables determining whether observed synergies arise from mechanical or neural constraints. In fact, we identify large regions of the feasible force set (i.e., a wide range of tasks) for which a specific pair of muscles is necessary to achieve the desired force output independently of any choice of neural control strategy (Figure 3e). For example, for the index finger in the sagittal plane, there is a region comprising approximately 20% of the feasible force in which the only necessary group of muscles is the FPI and FDS (note their very different actions: one an adductor, the other a flexor). Therefore, any valid choice of muscle coordination for those desired force tasks requires coactivation of the FPI and FDS, which could be interpreted as a neural muscle synergy that could “disappear” if the direction of the desired force output changes. By convention, a synergy of anatomical antagonists is called a “cocontraction” strategy that is traditionally interpreted as a choice the nervous system makes to stiffen joints and stabilize the limb. However, here we show that such cocontraction can arise simply due to the requirements of the task, in agreement with prior explanations of electromyograms based on model predictions (Buchanan et al., 1986, Kutch et al., 2008, Valero-Cuevas et al., 2009b). These findings, of course, do not in any way preclude the existence of synergies or cocontraction of neural origin, but do strongly emphasize that such interpretations must first rule out non-neural causes. While disambiguation of neural from non-neural sources of muscle synergies has been suggested previously (Valero-Cuevas,2005a), our improved computational capabilities now enable this disambiguation by explicitly describing the solution set available to the CNS.
Vulnerability of motor function
These results also help clarify the apparent and long-standing paradox between the concept of muscle redundancy and the clinical reality of motor development and dysfunction. If hand musculature is truly redundant, why does paralysis of a few muscles decimate force production and why is it so difficult to design tendon transfers to restore hand function (Hentz and Leclercq, 2008)? Why is manipulation so vulnerable to developmental problems (Forssberg et al., 1991), mild neurological pathologies, and aging (Schreuders et al., 2006)? This apparent paradox may arise simply because experiments and models had not explicitly described the control options available to the CNS, or identified muscles necessary for a wide range of tasks. This work complements recent studies (Venkadesan and Valero-Cuevas, 2008, Loeb, 2000, Keenan et al., 2009) showing that even ordinary manipulation tasks can push the motor system to its limits even for intact musculature, and enables further investigations into the robustness of natural behavior, and how development, aging, and mild pathology affect motor function.
Acknowledgments
We would like to thank hand surgeons VR Hentz, C Leclercq, N Lightdale, and I Fassola for assistance with cadaveric specimen preparation, and MU Kurse, and H Hoffmann for assistance performing the cadaveric experiments and helpful discussions. This material is based upon work supported by NSF Grants EFRI- COPN 0836042, and NIH Grants AR050520 & AR052345 to FVC.
Footnotes
Conflict of interest statement
We the authors have no real or perceived financial and personal relationships with other people or organizations that could inappropriately influence (bias) our work. Examples of potential conflicts of interest include employment, consultancies, stock ownership, honoraria, paid expert testimony, patent applications/registrations, and grants or other funding.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Agee J, Relton McCarroll H, Hollister A. The anatomy of the flexor digitorum superficialis relevant to tendon transfers. The Journal of Hand Surgery: Journal of the British Society for Surgery of the Hand. 1991;16(1):68–69. doi: 10.1016/0266-7681(91)90131-7. [DOI] [PubMed] [Google Scholar]
- Arnold EM, Ward SR, Lieber RL, Delp SL. A model of the lower limb for analysis of human movement. Annals of Biomedical Engineering. 2010:1–11. doi: 10.1007/s10439-009-9852-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Avis D, Fukuda K. A pivoting algorithm for convex hulls and vertex enumeration of arrangements and polyhedra. Discrete & Computational Geometry. 1992;8(3):295–313. [Google Scholar]
- Bernstein NA. The co-ordination and regulation of movements. Pergamon Press; Oxford: 1967. [Google Scholar]
- Buchanan TS, Almdale DPJ, Lewis JL, Rymer WZ. Characteristics of synergic relations during isometric contractions of human elbow muscles. Journal of Neurophysiology. 1986;56(5):1225–1241. doi: 10.1152/jn.1986.56.5.1225. [DOI] [PubMed] [Google Scholar]
- Chao EY, An KN. Graphical interpretation of solution to redundant problem in biomechanics. Journal of Biomechanical Engineering-Transactions of the Asme. 1978;100(3):159–167. [Google Scholar]
- Flament D, Goldsmith P, Buckley CJ, Lemon RN. Task dependence of responses in 1st dorsal interosseous muscle to magnetic brain-stimulation in man. Journal of Physiology-London. 1993;464:361–378. doi: 10.1113/jphysiol.1993.sp019639. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Forssberg H, Eliasson AC, Kinoshita H, Johansson RS, Westling G. Development of human precision grip i: Basic coordination of force. Experimental Brain Research. 1991;85(2):451–457. doi: 10.1007/BF00229422. [DOI] [PubMed] [Google Scholar]
- Hentz VR, Leclercq C. The management of the upper limb in incomplete lesions of the cervical spinal cord. Hand Clinics. 2008;24(2):175–184. doi: 10.1016/j.hcl.2008.01.003. [DOI] [PubMed] [Google Scholar]
- Infantolino BW, Challis JH. Architectural properties of the first dorsal interosseous muscle. Journal of Anatomy. 2010;216(4):463–469. doi: 10.1111/j.1469-7580.2009.01196.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keenan KG, McNamara RV, III, Backus SI, Schieber MH, Valero-Cuevas FJ. Neuroscience Meeting Planner. Society for Neuroscience; Atlanta, GA: 2006. Index finger abduction is a complex motor task. [Google Scholar]
- Keenan KG, Santos VJ, Venkadesan M, Valero-Cuevas FJ. Maximal voluntary fingertip force production is not limited by movement speed in combined motion and force tasks. Journal of Neuroscience. 2009;29(27):8784. doi: 10.1523/JNEUROSCI.0853-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuo AD, Zajac FE. Human standing posture - multijoint movement strategies based on biomechanical constraints. Progress in Brain Research. 1993;97:349–358. doi: 10.1016/s0079-6123(08)62294-3. [DOI] [PubMed] [Google Scholar]
- Kutch JJ, Kuo AD, Bloch AM, Rymer WZ. Endpoint force fluctuations reveal flexible rather than synergistic patterns of muscle cooperation. J Neurophysiol. 2008;100(5):2455–71. doi: 10.1152/jn.90274.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Loeb GE. Overcomplete musculature or underspecified tasks? Motor Control. 2000;4(1):81–3. doi: 10.1123/mcj.4.1.81. discussion 97–116. [DOI] [PubMed] [Google Scholar]
- Murray RM, Li Z, Sastry SS. A mathematical introduction to robotic manipulation. CRC; 1994. [Google Scholar]
- Schreuders TAR, Selles RW, Roebroeck ME, Stam HJ. Strength measurements of the intrinsic hand muscles: A review of the development and evaluation of the rotterdam intrinsic hand myometer. Journal of Hand Therapy. 2006;19(4):393–402. doi: 10.1197/j.jht.2006.07.024. [DOI] [PubMed] [Google Scholar]
- Smith JL, Carlson-Kuhta P. Unexpected motor patterns for hindlimb muscles during slope walking in the cat. Journal of Neurophysiology. 1995;74(5):2211. doi: 10.1152/jn.1995.74.5.2211. [DOI] [PubMed] [Google Scholar]
- Smith JL, Betts B, Edgerton VR, Zernicke RF. Rapid ankle extension during paw shakes: Selective recruitment of fast ankle extensors. Journal of Neurophysiology. 1980;43(3):612. doi: 10.1152/jn.1980.43.3.612. [DOI] [PubMed] [Google Scholar]
- Spoor CW. Balancing a force on the fingertip of a two-dimensional finger model without intrinsic muscles. J Biomech. 1983;16(7):497–504. doi: 10.1016/0021-9290(83)90064-7. [DOI] [PubMed] [Google Scholar]
- Valero-Cuevas FJ. An integrative approach to the biomechanical function and neuromuscular control of the fingers. J Biomech. 2005a;38(4):673–84. doi: 10.1016/j.jbiomech.2004.04.006. [DOI] [PubMed] [Google Scholar]
- Valero-Cuevas FJ. A mathematical approach to the mechanical capabilities of limbs and fingers. Progress in Motor Control. 2005b:619–633. doi: 10.1007/978-0-387-77064-2_33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Valero-Cuevas FJ, Zajac FE, Burgar CG. Large index-fingertip forces are produced by subject-independent patterns of muscle excitation. Journal of Biomechanics. 1998;31(8):693–703. doi: 10.1016/s0021-9290(98)00082-7. [DOI] [PubMed] [Google Scholar]
- Valero-Cuevas FJ, Towles JD, Hentz VR. Quantification of fingertip force reduction in the forefinger following simulated paralysis of extensor and intrinsic muscles. J Biomech. 2000;33(12):1601–9. doi: 10.1016/s0021-9290(00)00131-7. [DOI] [PubMed] [Google Scholar]
- Valero-Cuevas FJ, Hoffmann H, Kurse MU, Kutch JJ, Theodorou EA. Computational models for neuromuscular function. IEEE Reviews in Biomedical Engineering. 2009a;2:110–135. doi: 10.1109/RBME.2009.2034981. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Valero-Cuevas FJ, Venkadesan M, Todorov E. Structured variability of muscle activations supports the minimal intervention principle of motor control. Journal of Neurophysiology. 2009b;102(1):59. doi: 10.1152/jn.90324.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Venkadesan M, Valero-Cuevas FJ. Neural control of motion-to-force transitions with the fingertip. J Neurosci. 2008;28(6):1366–73. doi: 10.1523/JNEUROSCI.4993-07.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zajac FE. Muscle and tendon: Properties, models, scaling, and application to biomechanics and motor control. Critical reviews in biomedical engineering. 1989;17(4):359. [PubMed] [Google Scholar]