Abstract
Normal gastrointestinal (GI) motility results from the coordinated interplay of multiple cooperating mechanisms, both intrinsic and extrinsic to the GI tract. A fundamental component of this activity is an omnipresent electrical activity termed slow waves, which is generated and propagated by the interstitial cells of Cajal (ICCs). The role of ICC loss and network degradation in GI motility disorders is a significant area of ongoing research. This review examines recent progress in the multiscale modeling framework for effectively integrating a vast range of experimental data in GI electrophysiology, and outlines the prospect of how modeling can provide new insights into GI function in health and disease. The review begins with an overview of the GI tract and its electrophysiology, and then focuses on recent work on modeling GI electrical activity, spanning from cell to body biophysical scales. Mathematical cell models of the ICCs and smooth muscle cell are presented. The continuum framework of monodomain and bidomain models for tissue and organ models are then considered, and the forward techniques used to model the resultant body surface potential and magnetic field are discussed. The review then outlines recent progress in experimental support and validation of modeling, and concludes with a discussion on potential future research directions in this field.
Keywords: slow waves, cell models, continuum models, forward models, high-resolution mapping, EGG, ICCs, interstitial cells of Cajal
I. THE GASTROINTESTINAL TRACT
A. Introduction to the Structure and Function of the Gastrointestinal Tract
The gastrointestinal (GI) tract is a continuous tube comprising several distinct organs that runs over several meters in length from the mouth to the anus. While the compartment organs (e.g., the stomach and intestine) along GI tract are functionally discrete, their behavior is tightly coordinated and coregulated, affording a sophisticated overall level of integrated function that is tightly regulated by GI electrophysiology.
The integrated activity of the GI tract organs provides many essential bodily functions, i.e., storage, digestion, absorption, excretion, and protection. Digestion is the process by which ingested food is broken down into basic nutrients and water, ready for absorption and subsequent use in the functions, repair, and growth of bodily tissues. Digestion begins in the mouth, where food is first masticated (chewed) and mixed with saliva (which contains digestive enzymes). The resulting food bolus is then swallowed through the esophagus to reach the stomach, which is the most dilated part of the tract, acting as a storage reservoir. Digestion principally occurs in the stomach and small intestine, a process that involves both physical (e.g., mixing of food particle) and chemical (e.g., pH changes and enzymatic action) mechanisms. These digestive mechanisms break down food into a slurry of fine particles (termed chyme) and release chyme from the stomach into the small intestine at a controlled rate. Chyme is being continuously transported along the intestines, while absorption of nutrients and water takes place mainly via a densely folded (high surface area) small intestine wall. The large intestine is primarily concerned with desiccation and compaction of the waste products from the food and the GI tract, with storage in the sigmoid colon and rectum prior to excretion through the anus.
The structure of the GI wall consists of a number of distinct layers of tissues.1 Not all parts of the GI tract have the same composition, but the general structure is as follows. The mucosa is the innermost layer of the GI tract, and consists of epithelial tissues lining the lumen of the GI tract, underpinned by a thin layer of smooth muscle known as the muscularis mucosa. The next layer, deeper than the mucosa, is the submucosa, which consists largely of loose connective tissue, nerves, and blood vessels that support and supply the mucosa. Beyond the submucosa lies the muscularis externa, a thick muscular coat responsible for effecting the mixing and movement of digestive contents. In the stomach, the muscularis externa consists of smooth muscle arranged in three layers, i.e., the outer longitudinal, inner circular, and innermost oblique. The circular muscle layer contains smooth muscle fibers that are arranged in rings around the GI tract, while the longitudinal muscle layer contains smooth muscle fibers aligned in the direction along the tract. A rich plexus of nerves, the myenteric plexus, termed Auerbach's plexus, lies between these major muscle layers. The small intestine has only longitudinal and circular muscle layers, and in the human colon the longitudinal muscle is mostly coalesced into three bands termed the Tenia coli.2 The outermost layer of the GI tract is the serosa, which mainly consists of connective tissue, and serves as a structural outer coat.
Normal GI motility relies on the coordinated functions of structurally intact gut segments over both small and large scales of distance and time.3 Although normal motility is the end result of several cooperating mechanisms, including myenteric, neural, hormonal, and paracrine factors, this review will principally focus on the underlying electrophysiological mechanisms that initiate and coordinate motility. This is the area where the most sophisticated and detailed mathematical modeling of GI structure and function has been developed to date, and from which clinically meaningful results are beginning to be derived.
This review is organized in order of the principal scales of biological organization, i.e., cell, tissue, organ, and body scales. Recent advances in electrophysiology, modeling approaches, clinical implications, and validation methods are considered for each scale, and future research directions are considered last.
B. Electrophysiology of the Gastrointestinal Tract
In many parts of the gut, motility is wholly or partly initiated and coordinated by an underlying biological electrical activity, termed slow waves. This section examines the genesis of slow wave activity, the major cell types involved, its significance for motility, and its clinical importance.
1. The Role of Gastrointestinal Smooth Muscles
The smooth muscle cells (SMCs) in the GI tract are arranged in bundles, usually 2–5 μm in diameter and 20–500 μm in length.2 Bundles of SMCs and therefore smooth muscle layers contract in the direction of their fiber orientation. Like all cells, SMCs are enveloped by cellular membranes that act as semipermeable barriers, creating an intra-cellular niche known as the cytoplasm. The constituents of the cytoplasm include many chemicals and cellular organelles, of which most important to motility are charged particles known as ions, notably calcium ions (Ca2+), potassium ions (K+), and sodium ions (Na+).
There are a number of ion channels embedded in the membranes of SMCs that act as selective passageways for the entry and exit of ions across the cell membrane. As the concentrations of these ions differentiate between the inside and outside of SMCs, an electrical gradient develops across the cell membrane, known as the membrane potential (Vm). For a single ion species, there is a Vm at which the net flux due to the electrochemical gradient becomes zero. The Vm at this point is known as the Nernst potential of this ion species, usually donated as Ex, where x is the symbol of the ion species. In reality, a cell contains multiple types of ion species, and as each ion species influences the Vm toward its own Nernst potential, the Vm settles into a steady state where the Vm can be calculated under the assumption of electroneutrality. The Vm at this point is known as the resting membrane potential. The resting membrane potential of gastric SMCs is around −70 mV, however, there exist regional (−40 mV in the fundus to −65 in the antrum) as well as interspecies differences (−65 in guinea pig antrum and −69 in canine antrum).4,5
Preceding a contraction, the flux of ions across the cell membrane induces a depolarization event in the SMCs. This initial flux is induced by a change in Vm, caused by the cell-to-cell propagation of depolarizing events known as slow waves. The resultant influx of Ca2+ and Na+ rapidly depolarizes Vm toward −30 mV, and subsequently Na+ conductances inactivate and Ca2+ conductances remain open, maintaining Vm at a plateau phase.1 Smooth muscle contractions are triggered by the influx of Ca2+ during the depolarization and the plateau phases, leading to the activation of a series of cellular contractile reactions. Neural, hormonal, and paracrine influences also have a major bearing on the degree of contractile response,3 and without these additional modulating influences, the amplitude of the slow wave does not typically exceed a certain Vm threshold to enable significant contractions to occur. The subsequent inactivation of Ca2+ conductances and prolonged activation of K+ conductances repolarizes the Vm back to the resting membrane potential.
The manifestation of slow waves in SMCs is periodic, occurring at approximately three cycles per minute (cpm) in the human stomach, 10–12 cpm in the duodenum, and 8–9 cpm in the terminal ileum.1 The systematic propagation of slow waves in broad wave fronts over the GI tract organs at these frequencies confer a critical coordinating effect on GI motility patterns, which follow the slow wave pattern in much of the gut.
2. The Role of Interstitial Cells of Cajal
It was previously assumed that slow waves were autonomously generated and propagated within the GI smooth muscles. In the last two decades, this view has been overturned by the elucidation of the functions of the interstitial cells of Cajal (ICCs), which reside within and between the SMC layers.1 The ICCs were first described in 1911, as “nerve-like cells at ends of motor neurons in organs innervated by peripheral nerves” by the Spanish Nobel Prize laureate Santiago Ramón y Cajal.6 The close association between ICCs and nerve terminals throughout the musculature led to Cajal's original hypothesis that ICCs are involved in the neuromodulation of SMC contractions.
There is some ambiguity in the terms used to describe the slow waves. Due to historical reasons, slow waves were thought to only arise from gastric SMCs. However, with the identification of the role of ICCs in GI electrophysiology, the term “slow wave” is increasingly being used as a general term to encompass the electrical activity in both the SMC and ICC compartments. Previous studies have attempted to associate different terminologies of slow waves to the anatomical locations in which the slow waves are generated.7–9 In some instances, the slow waves generated by the ICCs have been referred to as pacemaker potentials. The terminology adopted by Sanders et al. is followed in this study, whereby the term slow wave applies to events registered in both the ICCs and SMCs1.
a. Classes and Functions of ICCs
The breakthrough in understanding that ICCs were essential for normal GI motility followed the serendipitous discovery that mice injected with a neutralizing antibody to Kit (a type III receptor tyrosine kinase prominent in ICCs) developed lethal hypomotility, accompanied by intestinal dilatation.10 Subsequently, it was documented that W/Wv mice, which have spontaneous Kit mutations, lacked both myenteric ICC and intestinal slow waves.11 Since these seminal studies, numerous investigations have confirmed that ICCs are critical for the generation and propagation of slow waves in the normal gut.1
Several different classes of ICC are now described, based on their anatomical site.1 The myenteric ICCs (ICC-MP or ICC-MY) surround the myenteric plexus and are the primary pacemakers of the gut. The intramuscular ICCs (ICC-IM) lie intermixed in the smooth muscle layers of the stomach and colon. The role of ICC-IM is primarily to act as a pacemaker of SMCs, although there is also a hypothesis that they may have the capacity to act as secondary pacemakers under certain circumstances such as with vagal neural stimulation.12 Other populations of ICCs lie near the deep muscular plexus at the submucosal surface of the small intestine's circular muscle coat (ICC-DMP); and a similar population in the colon are termed ICC-SMP. Another class of ICC line the septa between bundles of SMCs, termed ICC-SEP.
In combination, these ICC populations are now understood to play four essential roles in normal GI motility. A large number of studies have now confirmed that ICCs are responsible for generation of slow wave activity, through a coordinated system of intracellular events.1 First, slow waves conduct passively from ICCs to SMCs layers via gap junctions to electrically activate SMCs. Second, studies have also since confirmed a major role for ICCs in neuromodulation, and in mediating cholinergic and nitrergic neurotransmission in particular.13 Third, ICCs may also function as mechanoreceptors, as evidenced by their direct responses to stretch via mechanosensitive ion channels,14 and ultrastructural evidence showing their tight association with vagal afferents in the esophagus and gastric fundus.15 Finally, ICCs also set the gradient of resting membrane potential of smooth muscle layers via gas-mediated signaling, and particularly via the influence of carbon monoxide.16 The most pertinent function of ICCs to this review is their role in slow wave activity.
b. ICC Entrainment
In isolated cell cultures, ICCs generate slow waves at different intrinsic frequencies, but in an intact network, frequencies of the ICCs synchronize to the single frequency in the syncytium, in a process known as entrainment of slow wave activity. Entrainment occurs actively, in a manner such that the signal strength of slow waves does not dissipate as they propagate for distances of up to many centimeters in the stomach.17 The intestines also contain ICC networks, from which slow wave activity is entrained at a decreasing rate in a stepwise manner in the aboral direction.1 Without normal coherent entrainment, the slow wave activity of both the ICC network and smooth muscle layer becomes disorganized, and the resulting “dysrhythmia” is considered to be a contributing pathophysiological factor in many hypomotility disorders such as gastroparesis.18
The mechanism that leads to entrainment reamins an active area of ongoing research. Until recently, it was assumed by a number of investigators that the Ca2+-related ion conductances, e.g., the dihydropyridine-insensitive Ca2+ conductance (IVDDR) and the nonselective cation conductance (INSCC), in ICCs played a central role in initiating slow waves.17 The argument of the mechanism of entrainment currently focuses on how Ca2+ is released from the intracellular stores of Ca2+, namely, the mitochondria and the sarcoendoplasmic reticulum, in response to an extracellular voltage source. There are currently two main competing, but not mutually exclusive, views regarding Ca2+ activation. In the first view, the inositol 1,4,5-trisphosphate (IP3) voltage-dependent theory, the synthesis of the intracellular secondary messenger, IP3 is voltage dependent. Therefore, when the Vm is depolarized by an electrically coupled neighboring ICC, elevation of IP3 results in increased release of Ca2+ from the sarcoendoplasmic reticulum, leading to slow wave generation.17
The second hypothesis, known as the unitary potential theory, holds that entrainment of slow waves is dependent on a smaller and randomly occurring depolarization activity, termed unitary potentials, in theVm of ICCs.19 In this scenario, the depolarization of an ICC by an electrically coupled neighboring ICC would increase the chance of unitary potentials occurrence, which in turn results in an increased Ca2+ release from the sarcoendoplasmic reticulum via IP3 -receptors, via a T-type Ca2+ conductance expressed by ICCs.1 The mitochondria then responds to the elevated [Ca2+]i by rapidly uptaking the Ca2+ released by the sarcoendoplasmic reticulum, inducing a deficit of Ca2+, particularly near Ca2+ conductances such as IVDDR. The response of the Ca2+ conductances to a decrease in [Ca2+]i is an increased opening probability of their channel state, thereby inducing a slow wave activity.17,20
Recently, a new body of evidence has demonstrated that the Tmem16a gene product anoctamin 1 (“Ano 1”) is abundantly expressed in ICCs, and functions as a Ca2+-activated Cl− conductance.21–23 Further recent studies have shown that Cl− channel blockers effectively inhibit slow wave in multiple animal species, and that the Ca2+-activated Cl− conductance plays a fundamental role in the generation of ICC pacemaker activity and entrainment.22
C. The Clinical Significance of GI Electrophysiology
Given the importance of the roles of ICCs and SMCs in motility, it is not surprising that disorders of these cells play a major role in functional GI diseases. In particular, ICC loss and network degradation have now been documented in association with motility disorders in all segments of the GI tract.24,25 Likewise, therapeutic interventions seeking to prevent ICC loss, or restore their numbers and function, have become an important research focus.25,26
The association between ICC loss and dysmotility is best recognized in the conditions of gastroparesis and slow-transit constipation. Gastroparesis (typically defined as delayed gastric emptying in the absence of obstruction) is accompanied by symptoms including nausea, vomiting, bloating, and, in severe cases, malnutrition requiring invasive nutritional support. A principal contributor of gastroparesis is diabetes, with between 11 and 18% of long-term diabetics reporting symptoms consistent with the disease.27,28 The prevalence of gastroparesis is increasing, with hospital admissions in the United States having risen >150% in the last decade, partly due to the present epidemic of type II diabetes.27 ICC loss is now a recognized hallmark of diabetic gastroparesis, and is understood to result from disease influences that both promote ICC death, such as the inhibition of the protective enzyme heme oxygenase-1, and that reduce ICC survival or regeneration, such as inhibition of the ICC-promoting hormones, for example, insulin-like growth factor (ICF-1).29 However, the mechanisms by which ICC disruption impair GI motility remain under investigation.
Slow-transit constipation is a highly symptomatic condition in which there is a pathologically increased transit time of colonic contents. It is a difficult disease to manage clinically, since many patients are refractory to standard medical therapies such as increasing dietary fiber intake and laxative use. A decrease in ICC quantity in the colon has been identified as a striking histological feature in slow-transit constipation patients.30 However, again the patho-physiological relationship between ICC loss and increased colonic transit, and the means by which symptoms might result, remains uncertain.
II. MATHEMATICAL MODELS OF GASTROINTESTINAL ELECTRICAL ACTIVITY
Mathematical modeling of GI slow wave activity is gaining recognition as a significant research strategy in both basic science and clinical research. A validated mathematical model offers an alternative virtual medium in which hypotheses regarding normal and abnormal physiology can be exhaustively investigated, and the effects for treatment strategies predicted, without sole reliance on animal and human experimental models.31
Mathematical models of intestinal slow waves were formulated as early as the 1970s,32,33 and since that time the subsequent research and development of the mathematical models of GI slow waves have been steadily gaining complexity as more experimental evidence regarding the electrophysiological roles of the ICCs and SMCs have become known. State-of-the-art GI mathematical modeling has now been applied to represent the normal propagation of gastric slow waves, and to explain the effects of dysrhythmia of gastric slow waves in the form of electrical functional uncoupling in the human stomach.34–36
As the experimental understanding of GI electrophysiology continues to evolve across the major biological scales of subcellular, cell, tissue, organ, and whole body, a significant challenge lies in gaining a systematic understanding of the complex interactions between these activities at the different scales, which span vast spatial and temporal horizons. Multiscale modeling is ideally suited to this complex integrative task, and multiscale simulations are now at the forefront of advances in GI tract modeling. The concept for a multiscale framework to GI modeling has been adopted relatively recently compared to the cardiac field, yet significant progress has now been made to refine and adapt the established cardiac multiscale framework methods to modeling GI tract activities.36
This activity of multiscale modeling is broadly performed under the umbrella of the International Union of Physiological Sciences (IUPS) World Physiome Project (http://www.physiome.org.nz/), which aims to develop computational models of the entire human body in health and disease.37 One of the key aims envisaged by the Physiome project is to provide a comprehensive framework for modeling the human body using mathematical and computational modeling techniques that incorporate details of physiological relevance. With major developments in science and medicine occurring at the cellular or subcellular levels, and imaging and recording modalities such as MRI, CT, and ultrasound, electrical mapping occur at the organ levels, it becomes more important than ever to be able to integrate the understanding of this information across a multitude of biophysical scales. The scope of GI tract modeling has been variously termed the “digestive physiome” or the “GI-ome” by current investigators, although neither term is yet in widespread use. The key challenge of the Physiome project, in particular the aspect of the project dealing the digestive system, is the ability to bridge the gaps of knowledge in the current understanding of GI electrophysiology while relying on experimental validation to consolidate our knowledge of the digestive system. This section outlines the notable GI mathematical models and their modeling techniques at the cell, the tissue, the organ, and finally the whole-body scales.
A. Phenomenological Cell Models
Phenomenological models employ mathematical oscillators to simulate the periodic occurrences of slow waves, a concept that has been used to model the electrical events in different regions along the GI tract since the early 1970s.32,36,38 These early cell models also generally employed systems of mathematical equations that possess oscillatory behaviors with minor or no intra-cellular details that are based on experimental observation.36,39 The main reason for the lack of intracellular details in phenomenological models was due to the lack of understanding of the electrophysiology of the ICCs and SMCs in these early periods. Nevertheless, phenomenological models can be used to capture the basic biological characteristics efficiently, such as the frequency of slow waves. The amplitude of slow waves generated from phenomenological models is usually scaled to match the experimental data. However, the major drawback of phenomenological models is the lack of a physiological basis. Consequently, the phenomenological models are unable to simulate or provide predictions when the physiological effects of experimental protocols need to be evaluated.36
One of the earliest phenomenological GI models was a chain of coupled relaxation oscillators that was used to simulate intestinal slow waves,40 and during the early 1970s, a network of bidirectionally coupled relaxation oscillators was similarly used to simulate intestinal and gastric slow waves.32,33 Although the relaxation-oscillator models reproduced entrainment (referred to as “frequency pulling” in the original literature), the lack of a physiological basis strongly inhibited the application of these models as in silico hypothesis testing tools. Attempts have been made to develop phenomenological models with a stronger cellular basis.32,41 The following section outlines an example of a phenomenological GI cell model, the Aliev model.38
1. Aliev Model
The Aliev model is a phenomenological model that has been used to simulate gastric and intestinal slow waves.36,38 The mathematical model proposed by Aliev et al. was derived from the Fitzhugh-Nagumo model, and was originally intended to simulate the intestinal slow waves arranged in an idealized layered pipe structure.38,42,43 The Aliev model possesses a number of parameters that can be adjusted to fit the output of the cell model to experimental data. Furthermore, the Aliev model conceptually distinguishes slow waves as two interconnected electrical events generated from ICCs and SMCs. This was one of the first models that made such a distinction, and for this reason, the Aliev model was later selected to simulate the slow waves in anatomically based models of the small intestine and stomach.34–36
The basic expression of the Aliev model consists of a system of two first-order ordinary differential equations (ODEs) to describe the electrical activity in each tissue layer. Equations (1) and (2) possess an oscillatory two-variable system that simulates the periodic occurrence of slow waves, with no biophysically based components derived from experimental observations.39
| (1) |
| (2) |
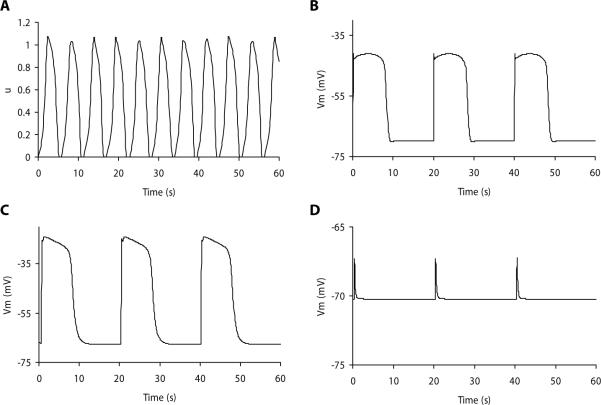
where u represents Vm of either SMC or ICC. There is a recovery parameter denoted by v, a rate constant denoted by k, a normalized threshold potential denoted by a, an excitability parameter denoted by ε, and rate constants denoted by γ and β that are used to shift the equilibrium of the Aliev model from an excitatory state in the SMCs to an oscillatory state in the ICCs.38 A trace of simulated intestinal slow waves (unscaled) is illustrated in Fig. 1A.
FIGURE 1.
Simulated gastrointestinal slow waves. (A) Simulated intestinal slow wave using the Aliev model. The dimensionless output, u, is a variable between 0 and 1, which can be scaled to match experimental recordings. (B) Simulated gastric smooth muscle cell slow wave using the Corrias and Buist smooth muscle cell model. (C) Simulated gastric interstitial cells of Cajal (ICC) slow wave using the Corrias and Buist ICC model. (D) Simulated unitary potentials using the Faville et al. ICC model. The simulated slow waves in B and C were generated using biophysically based cell models, and the simulated membrane potentials (Vm) provide a more accurate representation of experimental recordings than that of A.
B. Biophysical Cell Models
Recent understanding of the different types of ion conductances and intracellular processes that lead to the generation of slow waves have motivated the creation of a new generation of mathematical cell models that capture the intracellular processes in biophysical detail. In particular, the Hodgkin-Huxley-based approach to modeling individual ion conductances (see Appendix) has now been adopted to simulate the ion conductances in both SMCs and ICCs, allowing the simulation of slow waves to be related to the physiologically realistic parameters that govern the behavior of those ion conductances. Examples of recently published biophysically based GI cell models include the ICC model by Youm et al.44, the Corrias and Buist SMC and ICC models,45,46 and the ICC by Faville et al.19,20 The biophysically based cell models presented in further detail in this section are not the only GI cell models in the literature, but have been chosen on the basis of their thorough attempts to model the underlying cellular electrophysiology. Coding of all of the cell models introduced in this section can be downloaded from http://models.cellml.org/electrophysiology.
It is important to note that by current consensus, the ICC models described below are now understood to be incomplete, because they do not satisfactorily account for the new evidence describing a critical role for a Ca2+-activated Cl− conductance in slow wave generation. Renewed efforts will therefore now need to focus on updating these models to account for new experimental evidence.
1. Corrias and Buist Gastric Smooth Muscle Cell Model
The Corrias and Buist (C&B) SMC model is a biophysically based SMC model integrating the classical Hodgkin-Huxley gating equations to describe the Vm with eight ion conductances.45 A simulated trace of the Vm of gastric SMC using the C&B SMC model is illustrated in Fig. 1B.
The cell membrane equation of the C&B SMC model is
| (3) |
The C&B SMC model includes the following ion conductances. ICaL is the long type (long activation time) Ca2+ conductance in the SMC model. ILVA is a Ca2+ conductance that is activated by a small depolarization and is also fast inactivating. IKr is a commonly expressed K+ conductance in excitable cells. IKA is a fast inactivating K+ conductance. IBK serves as a mediator between the nervous system and its inhibitory signals to the digestive system. IKb is a background potassium conductance prescribed in order to yield a stable resting membrane potential. INa is the sodium current in SMCs. INSCC is the nonselective conductance, which means that it allows passage of all positively charged ions. One of the key features of this SMC model is the nonautonomous depolarization response to a slow wave current (IICC), without which the Vm would remain at the resting membrane potential of −68 mV.45
Because control of [Ca2+]i is one of the essential mediums through which SMCs regulate several types of ion conductances, in addition to the cell membrane equation the C&B SMC model also relates [Ca2+]i to Ca2+-related ion conductances using the following ODE:
| (4) |
where F is the Faraday's constant and Vc is the total cytoplasmic volume. Equation (4) relates the rate of change of [Ca2+]i to the rate of Ca2+ flux through the cell membrane via ICaL and ILVA and ICaExt. Here, ICaExt is an approximated and combined total rate of Ca2+ uptake by the endosarcoplasmic reticulum, the mitochondria and Ca2+ extrusion via a plasma membrane Ca2+ pump.
The success of external cardiac stimulation has provided a positive impetus for attempting GI electrical stimulation in an effort to restore normal motility and transit, and/or to improve symptoms in gastroparesis.47,48 Gastric electrical stimulation has also been employed with the aim of controllably disrupting normal slow wave activity in obese patients in order to induce delayed emptying and gastric distension, and thereby to reduce food intake. In an attempt to improve efficiency in gastric pacing research, the C&B SMC model has been adopted in a recent study to investigate the effects of gastric stimulation protocols, providing an example of its potential applications in in silico hypothesis testing.31 In that study, the C&B SMC model was parameterized to match theVm response of an initial set of recordings on the Vm of rodent gastric SMCs. Because the C&B SMC model carried parameters that represent realistic physical quantities, it was straightforward to update the values of different parameters in the cell model, such as Cm, to real experimental conditions. The remaining parameters that could not be directly identified experimentally were programmatically optimized to match an initial set of experimental recordings. The updated cell model was then used as a virtual platform to quantitatively determine the cellular responses of rodent gastric SMCs to a range of stimulation protocols (Fig. 2). The benefit of this approach was to exhaustively investigate the effects of a vast combination of possible electrical stimulation protocols (described above), without sole reliance on animal trials. Animal experiments were only performed at selected combinations to validate the simulated results, thereby significantly reducing the time and resources required.31 Coupled with experimental data, this study demonstrated the powerful analytical power of mathematical modeling.
FIGURE 2.
Simulated gastric electrical stimulation protocol using the Corrias and Buist gastric smooth muscle cell model. (A) The response of the simulated membrane potential (Vm) to an input stimulation protocol. (B) The stimulation protocol consists of a single electrical pulse of 200 pA amplitude and 1000 ms duration.
2. Corrias and Buist Interstitial Cell of Cajal Model
The C&B ICC model is a biophysically based cell model for simulating slow waves generated by the ICCs.49 Similar to the C&B SMC model, the C&B ICC model also adopts the Hodgkin-Huxley gating equations to represent individual ion conductances. A simulated trace of the Vm of gastric SMC using the C&B SMC model is illustrated in Fig. 1C.
The cell membrane equation of the C&B ICC model is
| (5) |
where IVDDR and IL-type are both Ca2+ conductances. Ikv11 is a K+ conductance, the name kv1.1 being a code name of a gene that has been identified in cell cultures of murine ICC. Ether-a-go-go (ERG) is another type of K+ conductance, which has been identified as an important contributor to ICC slow wave activity. The Ca2+-activated K+ conductance (BK), IBK, is a type of K+ conductance that is also [Ca2+]i dependent. IKb is the background potassium K+ conductance. INa is a sodium ion K+ conductance. INSCC is a nonselective ion K+ conductance that allows passage of all positive ions, its primary role being to allow influx of Ca2+ into the subspace compartment. ICl is a chloride ion K+ conductance. In addition to the nine ion channels, a Ca2+ extrusion mechanism (JPMCA) is also included in the model, allowing Ca2+ to be removed from the intracellular space.
The C&B ICC model adopted an extensive description of [Ca2+]i dynamics from a previously developed [Ca2+]i model by Fall et al.,50 because a detailed model of [Ca2+]i was required in order for the C&B ICC model to autonomously generate slow waves. The [Ca2+]i equation of the C&B ICC model is
| (6) |
where Jleak is the “link” between the subspace compartment, mitochondria, endosarcoplasmic reticulum, and the bulk cytoplasm in the C&B ICC model. As the Fall et al. [Ca2+]i model generates Ca2+ oscillations, the Ca2+ dynamics by the mitochondria and endosarcoplasmic reticulum induce changes of calcium concentration in the subspace compartment, from which Ca2+ leaks to the bulk cytoplasm through Jleak.50 This leads to a localized increase in [Ca2+]i, which in turn induces a cascade of events in the membrane ion conductances to generate slow waves.
3. Faville Interstitial Cell of the Cajal Model
The ICC model by Faville et al. simulates intestinal slow waves, and was formulated within the hypothesis that a nonselective cation conductance was fundamental to ICC pacemaker activity.19 Although the critical role of the Ca2+-actived Cl− conductance has now been elucidated,21,22 casting doubt on several assumptions inherent in the Faville et al model, this model nevertheless still holds merit in its multiple intracellular compartments approach, and its focus on describing the unitary potential phenomenon that has been hypothesized to be responsible for generating the whole-cell slow wave. This model is made up of two components: a unitary potential model,19 and a bulk cytoplasm model that incorporates the unitary potential model and a number of other types of ICC conductances.20
The hypothesis of unitary potentials states that a slow wave is initiated by the release of Ca2+ from IP3 receptor-operated stores that are in close physical proximity to the plasma membrane and to the mitochondria.19 The local increase in [Ca2+]i invokes a Ca2+ update mechanism in mitochondria that results in a transient reduction in [Ca2+]i in the localized space of a pacemaker unit. The reduction of [Ca2+]i in the micro-domain of the pacemaker unit activates the primary pacemaker conductance, which includes a Ca2+-inhibited, nonselective cation conductance, and a number of other types of ion conductances according to experiments on isolated ICCs.19 The first component of the model is a pacemaker unit (PU) model that simulates the unitary potential conductance pathway to simulate the unitary potentials that manifest as tiny fluctuations of Vm near the resting membrane potential.19 A simulated trace of unitary potentials of gastric ICC using the Faville ICC model is illustrated in Fig. 1D.
The equation of the PU model is
| (7) |
where ICa is an inward Ca2+ current, IPM is a plasma membrane Ca2+-ATPase, ISNCC is a nonselective cation conductance for Ca2+ and Na+, and INa is an outward Na+ conductance. The combined actions of those four types of ion conductances result in autonomous small fluctuations in the membrane potentials of ICCs.
The secondary component of the PU model is a whole-cell conductance equation that incorporates the unitary potential conductance pathway and other membrane conductances to simulate whole-cell slow wave activity.20 When the conductances in Eq. (7) are combined into a whole-cell model, the effect of n pacemaker units can then be combined into the bulk cytoplasm response as
| (8) |
where ICa(T) is the T-type Ca2+ conductance, ICa(Ext) is a plasma membrane Ca2+-ATPase, IK(ERG) is an ERG K+ conductance, IK(v1.1) is a voltage-dependent K+ conductance, IK(B) is a background K+ conductance, IL is the nonselective cation conductance; the sum of ICa(T), ICa(Ext), IK(ERG), IK(v1.1), IK(B), and IL represents the bulk cytoplasm conductance. The ICC model is “driven” by the summation of a number (nPU) of pacemaker unit currents [Iion(PU)], which is represented by the summation of the conductances in Eq. (7).
C. Multiscale Modeling of the GI Tract
As mentioned, our understanding of GI electrophysiology is beginning to integrate physiological processes across multiple biophysical scales. Consequently, the modeling techniques used to simulate slow waves are also beginning to take on a multiscale representation of the underlying electrophysiological processes that contribute to the generation of GI slow waves. A multiscale model of gastric slow waves includes mathematical models of ICCs and SMCs and their interactions and contributions at the tissue and the whole-body biophysical scales. At each scale, a particular approach may be required to relate the model to the other scales. At the cell level, both phenomenological and biophysical cell models are being used to simulate slow waves. Beyond the cell level, a continuum modeling approach is required.
There are a number of approaches to modeling electrical propagation using a continuum approach. These approaches can be classified according to the number of physical domains in which the conductance of slow waves is considered. In the monodo-main model, the conductance of slow wave events is restricted to one physical domain, which is usually the intracellular domain, including ion conductances and gap junctions.51 For example, in a network of ICCs, the Vm of one ICC has a passive effect on the Vm of another ICC, due to the passive conductance of current as a result of the slow wave generated within the ICC.52 The passive current will depolarize the Vm of neighboring ICCs slightly, which then induces an active response of the neighboring ICCs to regenerate slow waves, thereby carrying on the active propagation of slow waves. The passive current flow can be modeled as a diffusion-reaction process using a monodo-main equation [Eq. (9)],
| (9) |
where Am denotes the cell surface-to-volume ratio, and σ denotes the conductivity tensor of the tissue. The left-hand side of Eq. (9) contains the cellular description of slow waves [see Eqs. (3), (5), and (8)], whereas the terms on the right-hand side of Eq. (9) describe the rate of passive conduction as a diffusion process. The passive conduction of slow waves within the tissue is influenced by the magnitude of the components of σ.
The bidomain model is another continuum modeling approach that has previously been successfully employed to simulate the propagation of cardiac electrical events, and more recently adapted for slow wave simulations.36,51 The bidomain model conceptualizes two interpenetrating cellular domains that represent flow of electrical currents. The key advantage of the bidomain equations over the monodomain equation is that the bidomain considers the extracellular cellular potentials, which are often measured experimentally at the tissue and organ levels.36,53 The bidomain model that is used to simulate electrical propagation generally consists of a system of two equations. One of the equations describes the extracellular potentials. This equation is used to calculate the extracellular potential field that results from a given Vm distribution. The second equation is a reaction diffusion equation in terms of the Vm, where the sum of ionic currents from cell models provides the nonlinear reaction term.35 There are a number of ways to derive the bidomain equations. The derivation presented here is based on that of Henriquez, which was adopted by Pullan et al.51,54 The main advantage of this derivation is that it yields two equations that can be directly related to cell models in a continuum setting.
The derivation of the bidomain equations begins by taking the difference between the intracellular and extracellular potentials, ϕi and ϕe, which is equal to Vm
| (10) |
Ohm's law states that
| (11) |
where J is the current density, and E is the electric field strength. E is related to ϕ by
| (12) |
Substituting Eq. (12) into Eq. (11) for both intracellular and extracellular domains,
| (13) |
| (14) |
On the basis of the conservation of current, the current leaving domain i must enter the domain e in equal magnitude and opposite direction. This implies that
| (15) |
By combining Eqs. (13) and (14) with Eq. (15), the following expression is obtained:
| (16) |
Subtracting ▽ ·(σi▽ϕe) from both sides of Eq. (16) yields
| (17) |
Equation (17) can be further rearranged based on Eq. (10) to obtain the following expression:
| (18) |
Equation (18) is the first of the two equations in the bidomain model, and it is used calculate the extracellular potential field given a Vm distribution.
The second equation of the bidomain model can be derived from recognizing the fact that the conservation of current also implies that the changes in the intracellular ion flux must be equal to the ion flux across the cell membrane, i.e,
| (19) |
where Im is the total membrane current. The mathematical relationship between Vm, currents Iion and Im, and Cm, i.e., based on Eq. (A.1), can be expressed as
| (20) |
Based on Equation (19), the following equation is obtained:
| (21) |
Again, subtracting ▽ ·(σi▽ϕe) from both sides of Eq. (21) yields
| (22) |
Equation (22) can be rearranged using Eq. (10) as follows:
| (23) |
Equation (23) is the second of the two equations in the bidomain model and it is used to calculate the Vm when solved simultaneously with Eq. (18). Equation (23) can be related to the monodomain [Eq. (9)] by assuming equal anisotropy, i.e., σi = kσe, and the bidomain equations can be subsequently reduced to the monodomain equation.
In summary, the bidomain equations are
| (24) |
| (25) |
In cardiac electrical simulations, it is common to add a stimulus current to the left-hand side of Eqs. (24) and (25).51 The stimulus generally acts as a pacemaker activity to drive the onset of cardiac electrical propagations. However, in the bidomain equations [Eqs. (24) and (25)] used for simulating normal slow waves, the stimulus current terms are dropped to emphasis the autonomous basis of slow wave activity generated by the ICCs, as opposed to having an imposed physical stimulus to drive the activation of slow waves. However, for simulations of gastric electrical stimulation where an extraneous current is applied to the cell,55 the stimulus terms are required to represent extracellular stimulus current.
1. Grid-Based Finite Element Numerical Solution Technique
The rapid increase in high-performance computing power and applications of numerical solution techniques have seen an advent increase in both the scale and efficiency of simulations of biological processes. There are a number of numerical techniques that are used to solve the bidomain equations [Eqs (24) and (25)]. These methods include finite difference methods, finite volume methods, and the finite element methods. The finite different methods model the strong second derivative form of the bidomain equations, whereas the finite volume and finite element methods (FEMs) model the weak weighted integral of the bidomain equations.56 The approaches based on the weak form of the bidomain equations are more suitable for irregular and nonorthogonal computational meshes, whereas the finite difference methods are more suitable for regular and orthogonal meshes. Because of the irregular and curved surfaces of most GI organs, FEMs are generally employed to solve slow wave propagation problems.36
In particular, the GI mathematical models have benefited from the application of the grid-based FEM numerical solution technique. In biological simulations, the FEM is used to approximate the solutions of mathematical equations that represent physiological processes over a complicated physical domain, by discretizing the physical shape of a biological organ into smaller local elements. In GI simulations, the application of grid-based FEM is partly motivated by the large physical size of the GI organ, over which a numerically convergent solution of the propagation of slow waves needs to be simulated at fine spatial resolutions (typically < 1 mm).35,36 A stomach model may contain relatively few, e.g., 64 local geometric elements.35 Within each local geometric element, a number of solution points are allocated at high spatial resolutions, and the mathematical cell models, e.g., the Aliev model, are then solved at those solution points using numerical solution techniques such the Euler method.35,54
2. Tissue Models
The structural integrity of the network of ICCs in the GI tract is a quintessential feature for maintaining normal slow wave entrainment and motility. To date, simulations of GI slow waves at the tissue level involving a large physical network of ICCs and SMCs have largely adopted an idealized layered geometric structure of the gastric wall.35,36,52 With the recent development of many biophysically based cell models, incorporation of a physiologically realistic description of the tissue model has become a priority in order to enable multiscale simulations that provide informative outputs of realistic physiological data.
In a recent study, the C&B SMC model was adopted and incorporated into a tissue model to simulate the slow wave propagation in a porcine stomach.52 In this tissue model, the monodomain equation [Eq. (9)] was used to simulate the propagation of slow waves in a dual-layered structure comprising a layer of SMCs coupled to a regular network of ICCs. To simulate entrainment of slow waves in ICCs, an automata layer model [Eq. (26)] was used to reproduce the sequential activation of ICCs in an intact network.
| (26) |
where d and θ are the distance and angle (from a resting ICC) between the resting and depolarizing ICC, respectively, and Vc and Vl are the conduction velocities in the circular and longitudinal directions of the stomach, respectively. Equation (26) was used in conjunction with an algorithm that governed the propagation of slow waves in the ICC network.52 If all ICCs were entrained to the frequency of a single slow wave event, then the subsequent cascade of slow wave activations would generate active propagation of slow waves. The entrained slow waves then invoked a slow wave response in the SMC layer. A simulated propagation of slow waves across a regular 2D physical domain is illustrated in Fig. 3.
FIGURE 3.
A cellular-automata gastric tissue model showing simulated slow wave propagation across a 2D domain. The dimensions of the tissue model are 100 × 100 mm. The depolarization of gastric tissue occurred at a designated pacemaker site at 0 s and formed a broad wave front as it propagated across the tissue domain. Repolarization of the slow wave began at approximately 12 s, and the whole tissue domain returned to the resting membrane potential by 20 s, indicating the completion of a cycle of the gastric slow wave event.
The bidomain model [Eqs. (24) and (25)] has also previously been adopted to simulate the propagation of slow waves in a multilayered section of the gastric wall as shown in Fig. 4.35 Specifically represented are a longitudinal SMC layer and two circular smooth muscle layers. The SMC layers are separated by layers of ICCs (ICC-MP and ICC-SEP). The multilayered structure enabled a relatively realistic representation of the physical composition of the electrically active tissues in the gastric wall. At the cell level, the slow wave was simulated using the Aliev model.35 The simulated slow wave activation began in the ICC-MP and ICC-SEP layers, and subsequently activated the longitudinal and circular smooth muscle layers. The simulated activation further reinforces the concept of ICC slow waves initiating GI slow wave activity. Furthermore, the layered tissue model shown in Fig. 4 can be extended to represent the entire stomach, allowing simulations of whole-organ GI slow wave activity.35
FIGURE 4.
Simulations showing depolarization of an anatomically based gastric tissue model composed of five layers. The top of the tissue model represents the longitudinal muscle (LM) layer, the layer immediately below the LM layer represents the myenteric interstitial cells of Cajal (ICC-MP) layer, the next layer represents the thick circular muscle (CM) layer, and the layer within the CM layer represents the septa ICC (ICC-SEP) layer. The slow wave was simulated using the Aliev model. Propagation at the tissue and organ levels was simulated using the bidomain equations. Activations of the slow wave first began at approximately 2 s simultaneously within the ICC-MP and ICC-SEP layers. The subsequent activations of the LM and CM layers depolarized the tissue model. Repolarization of the tissue model began at approximately 14 s.
3. Organ Models
Until recently, an accurate representation of electrical activation in a whole-organ model of the GI tract remained an elusive goal, due to several significant technical challenges. First, the anatomical geometry of the GI tract organs could not be accurately and efficiently represented using conventional linear geometric descriptions. Second, biophysically based representations of gastric SMCs and ICCs were not available. Third, the experimental data regarding GI electrical propagation was derived mainly from sparse-electrode studies, whereby recordings were obtained from few distributed electrodes (typically ≤4).57–61 These sparse-electrode studies provide only a rough approximation of the global organ slow wave propagation, and therefore lack sufficient spatiotemporal detail to inform a reliable organ model description.36,53 However, recent experimental work has addressed and resolved most of these challenges, presenting the exciting opportunity to now make significant progress in GI organ-level modeling.62–64 In addition, these technical advances are now being applied to develop whole organ models of other segments of the GI tract, notably the small intestine and colon.65
To create an anatomically realistic geometry of the GI organs, finite element fitting techniques have been developed to fit a geometric mesh to a data cloud identifying the organ of interest outline, e.g., the stomach, from a high-resolution image set, such as the visible human data or from clinical imaging systems such as MRI or CT.35,66 The surface mesh of the organ is then created from the data cloud by an iterative linear fitting technique, and a volumetric mesh of the organ wall can be subsequently constructed in order to better represent known anatomical features. The wall of the organ can be further refined to incorporate the layered structure of the tissue model for more detailed multiscale representations. For longer GI organs, such as the small intestine, a 1D curve representing the centerline down the length of the small intestine has been digitized from the visible human data set. A tube of radius 10 mm was then extruded from the intestinal centerline to form a volumetric mesh.35,67,68
Slow wave activation over the whole-organ models is generally solved using techniques similar to the solution techniques for the tissue models. To date, the phenomenological Aliev model is the only cell model that has been integrated into a whole-organ model that is used to simulate slow wave activation.36 The results have generally shown a reasonable approximation of sequential activation of gastric or intestinal slow waves across the many layers of the organ models. For example, normal gastric slow waves have been simulated in the human stomach model and the simulated slow waves successfully matching the conduction velocity and entrained frequency observed from sparse-electrode experiments.35 The simulated slow waves originated from a pacemaker region located in the proximal corpus of the stomach model, and then formed a band of slow waves conducting in the aboral direction down the longitudinal axis of the stomach (Fig. 5A). Recent studies have also investigated the effects of functional uncoupling of slow waves, where the normal entrainment of slow waves in the different parts of stomach is lost, due to breakdown of the ICC network.34,35 To achieve this, the excitability parameter, ε, in the Aliev model was adjusted to produce a decoupled gastric antrum with independently entrained slow waves from the rest of the stomach.35 By altering the excitability profile of ICCs in the antrum, a condition that allows decoupled slow wave generation at the cellular level was imposed on the organ model under the multiscale framework. The simulated decoupled slow waves showed ectopic slow waves arising in the gastric antrum and conducting in the retrograde direction, and colliding with the normal propagation (Fig. 5B). In the intestinal model, normal conduction of individual slow waves along the parts of the small intestine has been demonstrated,35,36 while accounting for a decrease in entrainment frequency from 12 to 7 cpm in the aboral direction of the model.67
FIGURE 5.
Simulations of slow wave events in an anatomically realistic whole-stomach organ model. The Aliev model was used to simulate a slow wave at the cellular level. Propagation at the tissue and organ levels was simulated using the bidomain equations. (A) Simulated normal gastric slow waves propagated in the antegrade (aboral) direction of the stomach model. Up to two simultaneous wave fronts can be identified at 0 and 5 s. (B) Simulated slow waves in an abnormal stomach with a decoupled antral slow wave behavior. The decoupled slow waves in the antrum propagated in the retrograde direction, opposing the normal wave front in the antegrade direction. Up to three wave fronts could be identified at 0 s.
Finally, recent experimental advances in slow wave mapping have shown the potential to substantially improve the spatiotemporal resolution of slow wave propagation studies, including in humans, providing data that will support and improve organ-level modeling.53 This work is discussed in Section III.
4. Torso Models
At the body scale, the resulting potential and magnetic field on the torso surface from the underlying organ-level slow wave propagation is considered.36,51,69 Applications of torso model simulations include informing far-field techniques such as electrogastrography (EGG) and magnetogastrography (MGG) (see experimental validation section), by relating the underlying slow wave activity to the resultant torso surface electrical or magnetoactivities.36 Although these recording techniques have the advantages of being noninvasive, one of the key issues is that the recorded signals are difficult to interpret, partly due to the complex profile and relatively low signal-to-noise ratio of the transmitted slow waves.36 Therefore, a torso model can provide a virtual medium to help interpret the signals recorded from the far-field recordings in order to relate them to pathological states. The modeling problem that relates the simulated slow waves at the organ level to the resultant torso surface is known as the forward problem in GI modeling.
The calculation of the resultant torso surface potentials from simulated gastric slow waves is generally implemented as a secondary step from the simulation of the organ model, mainly due to computational requirements.51 The source models used in the forward GI modeling problem are typically comprised of a number of equivalent dipoles. The number of equivalent dipole sources can vary, the simplest being a single equivalent dipole to represent the overall electrical orientation of the whole organ at a moment in time.54 The first step in calculating the equivalent dipole is to deduce the local current density (Jcell) prescribed by the (continuum) cellular slow waves at each continuum cell (grid) level using the following expression:
| (27) |
The integration of Jcell over the active tissue in each geometric element and the summation of the individual local dipoles into an equivalent dipole (J) is achieved via a “weighted center” approach based on the following expressions69:
| (28) |
and
| (29) |
where and where J is the equivalent dipole source calculated from c (number of local dipoles), i.e., Jcell, and ∥.∥2 is the Euclidean norm.69 Equation (38) calculates C, the center of J through a weighted scheme of the local dipoles.
Each dipole source has a center and orientation that varies over time to describe the location, direction, and strength of the simulated slow wave activity in the organ model. These dipole sources are then used to compute the potential fields within the torso surface by solving the Poisson equation,
| (30) |
where the source term J is due to the equivalent dipole sources, and φ is the torso potential field. A typical solution then consists of three sets of calculations that must be performed at each time step. First, the cellular models are updated throughout the active stomach. Next, the Vm and ϕe are calculated from the organ model based on the activities of the cell models. The equivalent gastric dipolar sources are then created, and the passive torso volume conductor problem is then solved to calculate the potential field throughout the torso (Fig. 6). Using this equation set, activity within the cell can be related to the organ model, and then to activity on the torso surface, making a multiscale representation of slow wave activity possible through modeling (see Fig. 6).
FIGURE 6.
An instance of simulated body surface potential and magnetic field in an anatomically realistic human torso model. A current dipole (not shown) was calculated from the whole-organ model and then embedded within the torso model to solve for the electrical and magnetic activities at the torso surface. The electrical activity is displayed as a color-coded potential over the torso surface, and the magnetic activity is displayed in a virtual sensor array (yellow arrows) over the abdomen of the torso. (A) The anterior view. (B) The posterior view.
Simulations of the torso surface potential field can also be related to the magnetic field that accompanies the slow waves. All biological electrical fields have a corresponding magnetic field associated with them, which can be recorded via magnetometers (refer to Section III).70 The resultant magnetic field from slow waves is theoretically less attenuated by the layers tissue in the abdominal wall than the potential field, presenting a possible alternative way of studying the underlying slow wave propagation.36
The magnetic field (B) resulting from a dipole source is a conducting medium comprises two components as shown in Eq. (31).70
| (31) |
where Bd is the magnetic field due to the dipole source, and Bv is the magnetic field due to the volume current in the body. Commonly, Bd is also referred to as the primary source, and Bv is referred to as the secondary source.71 The calculation for the primary dipole source is expressed in the following equation:
| (32) |
where μ0 is the permittivity in free space, ρ is the dipole magnitude, R is the vector between the dipole center and the field at point rf, and r is the absolute distance of R.
To calculate Bv, the torso model can be used to explicitly determine the volume conductor effects via the following equation71:
| (33) |
where n is the total number of surfaces surrounding regions of different conductivity, j identifies a surface of a region with assumed constant conductivity σj and boundary defined by Ωj, and Φ(rd) is the potential on the torso surface due to a dipole located at rd. The magnetic field is generally computed in a secondary process from the dipole computation, with dipole sources embedded in the torso model and sampled over a virtual magnetometer sensor arrangement (the yellow arrows in Fig. 6). The direction and the magnitude of the magnetic field vectors could then be related to the underlying slow wave profile.
III. RECENT ADVANCES IN THE EXPERIMENTAL SUPPORT AND VALIDATION OF GASTROINTESTINAL ELECTROPHYSIOLOGICAL MODELING
The success of the conjoint modeling and experimental research paradigm in cardiac electrophysiology has provided strong motivations for applying the same concepts and principles to GI electrophysiology research.71 As the global infrastructure, such as the Physiome project and CellML language for model sharing and development, becomes more comprehensive, there will be an increase in the demand for mathematical models to be accurately informed and validated by experimental observations.37,72 To this end, the experimental methodology for evaluating GI electrophysiology is becoming a rapidly evolving area of research, with significant progress made in recent years. This is expected to further accelerate with the recent presentation of several promising experimental technical advances as outlined below.
A. Intracellular Slow Wave Recordings
A foremost limiting factor of SMC and ICC biophysically based modeling, and validation of the current models, is the lack of experimental data defining details of specific dynamics such as ion channel kinetics and intracellular ion concentrations.19,45,49 The precise mechanisms underlying slow wave rhythmicity are still debated, and a clear understanding of the ion conductances and intracellular messengers that contribute to the whole-cell slow wave event is yet to be consolidated. This section lists some of the current and emerging aspects of molecular and cellular research that may be of significance to GI cell modeling.
There remain two significant experimental challenges in GI slow wave recording. The first challenge is the variability between different animal models, and the second challenge is the limitations of the experimental preparations. An example of a significant experimental variation is the interspecies difference in the expressions of the mechanosensitive SCN5A-encoded Nav1.5 channel, which is consistently expressed in human and dog, variably expressed in mouse, but not expressed at all in pig and guinea pig.73 Such species differences need to be identified and accounted for when applying modeling studies to experimental contexts,31 and in future years, species-specific cell models may need be developed.
The second challenge is to develop robust in vitro means of recording slow waves at the cellular level. The critical role of the experimental preparation in determining experimental outcomes is highlighted by recent work investigating the Ca2+-activated Cl− conductance in ICCs. In the past, intracellular ICC electrophysiology studies have typically been performed in cell-culture preparations. However, the combination of the cell culturing and cell dissociation processes may have dramatic effects on the proteins and signal transduction pathways that are the focus of the experiments, including key features of the ICC phenotype such as Kit expression.23 This is true of the Cl− channel, which is prominent in in situ preparations, but that quickly recedes in cultured preparations.74 For these reasons, an active area of research focus has been the development of techniques for readily identifying dispersed ICCs in freshly dissected tissue, recently culminating in the presentation of a transgenic mouse strain that constitutively expresses a bright form of green fluorescent protein (copGFP) in ICCs.23 Development of this strain has already led to fundamental new insights into the role of the ICC Cl− conductance, and is expected to continue to drive significant experimental advances.23
Another promising emerging area of developing experimental work is the presentation of evidence that ICC channel abnormalities may be a cause of gastrointestinal symptoms. Mutations in the mechanosensitive SCN5A-encoded sodium channel have been found to be associated with generalized abdominal symptoms,75 and SCN5A has now been implicated as a candidate gene in irritible bowel syndrome.76 This avenue of experimental work provides fertile ground for complimentary multiscale modeling studies that seek to explore the integrated functional consequences of ion channelopathies, and that could potentially assist in the development of therapeutic targets in the future.
B. Tissue and Organ Slow Wave Recordings
1. High-Resolution Mapping
As detailed above, electrophysiological modeling at the tissue and organ levels depends on accurate and detailed experimental data on the characteristics of electrical propagation. The recent advent of high-resolution (HR) electrical mapping has been an important advance. This technique involves the placement of spatially dense arrays of many electrodes over the serosal surface along the GI tract in order to simultaneously record extracellular potentials from up to hundreds of electrodes as the slow waves propagate through the tissue beneath.53,65 Although related techniques have been widely employed in cardiac electrophysiology for many years, and are now routinely used clinically for cardiac dysrhythmia management, the strategy has only been adapted for GI research over the last 15 years, following the work of Lammers et al.62
The major advantage of HR mapping over previous sparse-electrode approaches is that the high spatial density of simultaneous sampling affords a detailed spatiotemporal understanding of the slow wave propagation. In particular, the slow wave activation times can be used to create activation time maps, graphical descriptions that accurately depict the slow wave propagation from cycle to cycle.53,62 Two recent studies highlight these benefits. In the first, HR mapping was used to define the mechanisms of gastric dysrhythmias for the first time, revealing complex focal activities and re-entrant behaviors that are similar to the events occurring in cardiac dysrhythmias.63 The presence, prevalence, and clinical significance of these events in motility disorders now await to be defined, and modeling strategies explored. In the second study, HR mapping was used to define the origin and propagation of slow wave activity in the canine stomach, providing new descriptions of a high-amplitude, high-velocity activity in association with the pacemaker site, and the presence of multiple simultaneously propagating wave fronts.64
The recent development of a flexible printed circuit board (PCB) electrode by Du et al. now promises to facilitate the HR mapping of the human GI tract.53 Flexible PCB electrodes are constructed of gold or silver contacts and copper wires in a polyimide ribbon base, and can be mass produced with high fidelity and low cost (Fig. 7A). Their ease of sterilization and potential disposability make them ideal for human use. Initial results from the first human GI mapping studies are beginning to appear,77 and these data are expected to provide a substantial advance in organ-level understanding of GI slow waves that will provide ideal material to inform and validate multiscale models.
FIGURE 7.
The electrode platforms used to record GI slow waves from the serosal surface of the GI tract. (A) PCB electrodes are manufactured on flexible base material (Polymide), with an array of 32 electrodes in a 4 × 8 configuration printed onto each PCB array. The PCB electrodes are used to record GI slow waves at high spatiotemporal resolutions. (B) Laparoscopic electrodes (the wand) that can be inserted through a port during keyhole surgery. A number of electrodes were embedded into the shaft of the recording device, which then made contact with the GI serosal surface to record slow wave activity. The wand electrode is minimally invasive and offers an efficient way to take snapshots of slow waves along the GI tract during surgery.
Current efforts to automate the analysis, interpretation, and visualization of HR mapping data will be critical to accelerate progress in this evolving research field, which is presently slow and inefficient.78 The recent presentation of an automated algorithm to determine slow wave activation times promises a 100-fold time saving compared to manually performing this task.79
2. Minimally Invasive Approaches
A major clinical limitation to the application of HR mapping is that it presently requires invasive surgical access. The highest-quality slow wave recordings must be taken from the serosal surface of the target organ, and ongoing experimental efforts have sought to achieve these recordings via less invasive strategies. One approach to eliminate incision during recording has been the targeted sparse-electrode recording of slow wave activity at endoscopy, usually via clipping or suctioning electrodes into position on the gastric mucosal surface for direct video vision.81 However, the high impedance of the mucosal surface has been one significant barrier to the development of more accurate HR endoscopic approaches.
An alternative minimally invasive approach is laparoscopy, facilitated by the recent presentation of a novel laparoscJ16opic device.82 This device contains a miniarray of electrodes on its tip, which is held in atraumatic contact with the GI serosa (Fig. 7B). An innovative aspect was to demonstrate that useful spatiotemporal detail can be achieved from as few as four electrodes, which can be used to generate a fair approximation of slow wave propagation direction and velocity. The laparoscopic approach is significantly more invasive than endoscopic recordings, since it requires general anesthesia and intraperitoneal access. However, this strategy will be useful for generating valuable experimental data in selected patients. Early work has also demonstrated the possibility of taking longer-term recordings in conscious subjects via implantable electrode platforms, which also contain a miniarray of electrodes.82
C. Noninvasive Body Surface Recordings
One of the key aims of both modeling and experimental studies is to devise means of noninvasively assessing GI electrophysiology from the body surface. Body surface recording strategies in cardiology, i.e., the electrocardiogram (ECG), have become routine diagnostic tools in hospitals around the world. This section outlines two of the current recording methods used to noninvasively record GI slow waves.
1. Electrogastrography
EGG involves the placement of electrodes on the body surface to record the distant electrical signals, in a similar manner to ECG. An EGG analysis is typically limited to frequency dynamics, aiming to identify periods of slow wave activity in which the frequency falls outside the normal range (~3–4 cpm). This approach has been attempted for many years; however, it is rarely used clinically because of the lack of consensus regarding its application, its poor specificity, and its poor correlation with other functional and symptom disease markers.83
It remains to be seen whether EGG can be advanced to improved clinical utility. One potential avenue of progress is to relate the sources of slow wave activation in the stomach to EGG, which is currently not certain, especially given the recent revelation of multiple propagating slow wave fronts in the human stomach.77 HR mapping information will also help to inform multiscale models that seek to solve the physical dispersion of slow wave currents over anatomically accurate torso geometries in order to better understand EGG sources and predict idealized EGG electrode placements.34 Improved electrode technology, such as multi-electrode body surface mapping approaches used in cardiology, and signaling processing advances could also prove valuable in seeking to categorically define the clinical potential of the EGG.
2. Superconducting Quantum Interference Device Magnetic Recordings
As previously mentioned, biological electrical fields have associated magnetic fields, and interpreting these fields has also been a focus of research for noninvasive GI electrophysiological diagnosis.84,85 Biomagnetic field detection is performed using devices called magnetometers, and in particular the highly sensitive superconducting quantum interference device (SQUID).84,85 GI SQUID devices were first developed with a view to improving the diagnosis of mesenteric ischemia,85 but have recently been applied to motility problems including gastric electrical disorders.84 One major theoretical advantage of SQUID over EGG recordings of GI electrical activity is that unlike electric fields, magnetic fields are not attenuated by the layers of the abdominal wall. However, interpreting magnetic data can be difficult, and further technological advances in SQUID design and signal processing advances are required to prove the potential of this approach. Because of these challenges, recent studies have proposed using multiscale computational simulations of magnetic fields, which are calculated from simulated GI electrical activity in order to aid in the interpretation of magnetic field recordings.69 This remains an active area of ongoing research.
IV. SUMMARY AND FUTURE DIRECTIONS
As research in GI electrophysiology is being improved through relating slow waves across multiple biological scales, there is a need to gain an integrated understanding of how the physiological processes at these scales interact in a biological system. Mathematical modeling and computational techniques have been proposed as a way to provide a virtual medium in which biophysically based components of GI slow waves can be investigated across multiple biophysical scales, under a general framework termed the multiscale modeling approach. Recent decades of research in cardiovascular electrophysiology have resulted in sophisticated multiscale mathematical models, which have been applied to successfully address complex clinical problems such as the mechanisms underlying atrial fibrillation.86 By comparison, the mathematical modeling of GI slow waves is still in its infancy, partly due to the historically limited understanding of the roles of ICCs and intracellular components that give rise to GI slow waves.
The key concept of the multiscale framework is to use a continuum modeling approach, in which either a monodomain or bidomain model is employed, to calculate propagation of slow waves in biophysical scales that are higher than the cellular scale, e.g., the whole-organ model. To date, most multiscale mathematical models of GI slow waves have relied on relatively simplistic phenomenological models such as the Aliev model, which cannot be applied to evaluate important intracellular physiological dynamics.36 Furthermore, whereas cardiac models have incorporated detailed microstructural tissue information to relate tissue structure to function, all previous tissue models simulating GI slow waves have employed idealizations of ICCs and smooth muscle layers that are relatively simplistic and lacking in realistic details. An area of interest would be to relate the structural information of ICC networks in wild-type and animal subjects with depleted ICC count, such as mouse with a germ line deletion of the 5-HT2B serotonin receptor. The 5-HT2B receptors are expressed on ICCs, and stimulation by serotonin induces proliferation of ICC populations and therefore are an important regulator of ICC network density.87 The functional output of the model will be based on realistic structural degradation of ICC networks.
A correct biophysically based representation of entrainment in ICC models is fundamental to the investigation of GI slow waves via mathematical modeling. Although the latest body of evidence on the role of Ano-1 (Ca2+-activated Cl− conductance21,22) has cast doubt on the current models of ICC pacemaker activity, the modeling techniques used in these models are still valuable for informing the creation of future models and for multiscale modeling.
The proposed 1,4,5-trisphosphate (IP3)–dependent mechanism of entrainment offers one potential direction for further refining the relevant components in the C&B ICC model.17 On the other hand, some researchers have also argued that the iso-forms of the IP3 receptors in certain types of ICCs may not be able to actively contribute to slow wave generation, and alternative ion conductance pathways have been proposed to be responsible for entrainment.88,89 One of the advantages of a virtual cell model is that both mechanisms of entrainment, i.e., IP3-dependent and ion conductance pathways, can be incorporated and virtually evaluated. The ICC model of Faville et al. could also serve as a potential virtual medium to test the different entrainment mechanisms.19,20 In this model, whole-cell slow wave activity would vary in accordance to the active contribution of the pacemaker units, which could be modified to display an entrainmentlike response to extracellular potential sources. A modified parameterization of the currents regulating the flow of Ca2+ into one of the subspace compartments in the ICC model by Faville et al. may also lead to a stable model of entrainment. In the future, these cell models would also benefit from the inclusion of mechanosensitivity modeling, since mechanosensitive ion channels have been shown to be significant in both ICCs and SMCs.14
With the ongoing development of biophysically based cell models, significant breakthroughs are also poised to occur in the area of tissue modeling. An attractive proposition is to relate the electrical events of the cells to realistic tissue structures within a multiscale framework, as has been performed in cardiac modeling research to define the normal and abnormal propagation of electrical events through complex tissue architectures.86,90 For example, anatomically realistic tissue structures containing the ICC network and SMCs could be obtained from human patients or animal models of dysmotility disorders, and biophysically based ICC models with the correct entrainment behavior could be integrated into those structures to investigate pathological differences in slow wave propagation. Early work has now begun in this direction.91
The advent of appropriate HR mapping tools for the accurate evaluation of human GI tract activity, and the flexible PCB electrodes in particular, will continue to guide more physiologically realistic modeling of GI motility.65 In related work, the flexible PCBs have already been applied to study the entrainment of slow waves following gastric pacing,92 providing an enhanced understanding of the effects of stimulation on slow wave activity, and enabling the validation of multiscale frameworks for simulating stimulation outcomes.52 With the advent of anatomically accurate organ models and biophysically based cell models, informed by HR electrical mapping, the path is now clear for substantial upgrades to the current generation of whole-organ models of GI slow wave activity.
Advanced simulations in cardiac electrophysiology research have produced mathematical techniques to relate torso surface recordings back to the electrical activity in the heart. This particular class of problem is known as the inverse modeling approach, which is a significantly more challenging problem than the corresponding forward problem due to the fact that it is highly ill posed.54 This means that in the presence of noise, the solution may not resemble the true activation sequence on the serosal surface. This is further complicated by the issue that there are multiple simultaneous wave fronts in the stomach at one time, a problem for which there are no effective generic algorithms.93 Furthermore, detailed spatiotemporal descriptions of GI slow waves are just beginning to emerge,62,64,65 and as a result there still lacks a detailed understanding of the characteristics underlying slow wave activity. This information, as well as detailed validated forward simulations, should be progressed before attempts are made at solving the inverse problem.94 However, given the theoretical advantage of being able to relate the noninvasive body surface recordings (e.g., EGG and SQUID recordings) to the underlying slow waves in the stomach and intestine, the inverse GI problem is becoming an active area of ongoing research.36,84
In conjunction with other cooperating mechanisms, GI slow waves ultimately manifest as physical contractions that break down and transport food particles.1,2 Mathematical models should also bridge the link between slow waves and mechanical contractions, and incorporate accurate biophysical descriptions of electromechanical coupling. This exciting future pathway whereby GI slow wave events are related to mechanical contractions, computational fluid dynamic studies, and pathological states within a multiscale framework will ultimately see GI tract electrophysiological modeling achieve its substantial clinical potential.
ACKNOWLEDGMENTS
The authors thank Dr. Rié Komuro for her technical assistance. This work and/or the authors are funded by the University of Auckland, the NZ Health Research Council, the NIH (Grant No. R01 DK64775), and the American Neurogastroenterology & Motility Society (ANMS).
APPENDIX
Hodgkin and Huxley Ion Gating Equations
One of the key bases for a biophysically based cell is the formulation of the ion channel descriptions that generally follow the classic Hodgkin-Huxley approach. The Hodgkin-Huxley approach states that the conductance of an ion channel is modulated by the product of a number of activation and inactivation gating variables.39,96 Activation gates represent the properties of a channel that allow ion passage, whereas inactivation gates cease ion passage. A channel may contain many activation gates, therefore involving a complex arrangement of gating kinetics to govern ion flow through the cell membrane.
The cell membrane can be modeled as a capacitor coupled to a resistor.39,51 The current flowing through the resistor represents the sum of all the ionic currents (Iion) through the ion channels. The relationship between voltage (Vm), current (Iion), and capacitance (Cm) is given by
| (A.1) |
where Iion consists of many ion conductances across the cell membrane. A generic expression of an ion conductance is
| (A.2) |
where Ix is the ionic current of an arbitrary ion species x, d is the activation gate, f is the inactivation gate, and Gx is the maximum conductance of the channel. The Nernst potential (Ex) of ion x is defined as
| (A.3) |
where R is the universal gas constant, F is the Faraday's constant, [x]e and [x]i are the extracellular and intracellular concentrations of ion x under homeostatic conditions. The Ex represents the electrochemical equilibrium of an ion species.2,39
The gating variables [variables d and f in Eq. (A.2)] that govern the ion conductance are in turn dependent on Vm and time (t). A single gating variable is assumed either to be in the open state or the close state. The transition from one state to the other can be written as a two-state reaction equation
| (A.4) |
where α is the rate at which the gate closes, and β is the rate at which the gate opens. Given that the probability, denoted by g, of a channel in the closed state lies between 0 and 1, Eq. (A.4) can be written in the form of an ODE as follows:
| (A.5) |
At steady state, the value of g can be expressed as a function of the rate constants α and β,
| (A.6) |
where g∞ is the steady state probability of the gating variable remaining in the closed state. Solving for g∞ gives
| (A.7) |
where τ∞ equals
| (A.8) |
Substituting expressions for α and β in Eqs. (A.6) and (A.8) back into Eq. (A.5) gives
| (A.9) |
Equation (A.9) relates the rate of change in Eq. (A.5) to two steady state variables τ∞ and g∞, both of which depend on Vm only. The expressions for τ∞ and g∞ are in turn described by mathematical expressions that can be obtained from fitting experimental data.39,45,49 The state of every gating variable for each ion current is solved using Eq. (A.9). Each gating variable has different functions for g∞ and τ∞ in terms of Vm and t. The states of the gating variables in turn govern the flow of ion conductance in accordance to Eq. (A.2). The sum of ion conductances is then used to relate to the change in Vm using Eq. (A.1).
REFERENCES
- 1.Sanders KM, Koh SD, Ward SM. Interstitial cells of Cajal as pacemakers in the gastrointestinal tract. Annu Rev Physiol. 2006;68:307–43. doi: 10.1146/annurev.physiol.68.040504.094718. [DOI] [PubMed] [Google Scholar]
- 2.Berne RM, Levy M,N, Koeppen BM, Stanton BA. The gastrointestinal system. In: Berne RM, Levy M,N, editors. Physiology. 4th ed. Mosby; St. Louis, Missouri: 1998. pp. 589–647. [Google Scholar]
- 3.Huizinga JD, Lammers WJEP. Gut peristalsis is coordinated by a multitude of cooperating mechanisms. Am J Physiol Gastrointest Liver Physiol. 2009;(296):1–8. doi: 10.1152/ajpgi.90380.2008. [DOI] [PubMed] [Google Scholar]
- 4.Bauer AJ, Reed JB, Sanders KM. Slow wave heterogeneity within the circular muscle of the canine gastric antrum. J Physiol. 1985 Sep;366:221–32. doi: 10.1113/jphysiol.1985.sp015793. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Hirst GD, Edwards FR. Electrical events underlying organized myogenic contractions of the guinea pig stomach. J Physiol. 2006 Nov 1;576(Pt 3):659–65. doi: 10.1113/jphysiol.2006.116491. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Cajal SR. Histologie du syst̀eme nerveux de l'homme et des vert̀ebr̀es. Maloine; Paris: 1911. pp. 891–942. [Google Scholar]
- 7.Dickens EJ, Hirst GD, Tomita T. Identification of rhythmically active cells in guinea-pig stomach. J Physiol. 1999 Jan 15;514(Pt 2):515–31. doi: 10.1111/j.1469-7793.1999.515ae.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Edwards FR, Hirst GD. An electrical analysis of slow wave propagation in the guinea-pig gastric antrum. J Physiol. 2006 Feb 15;571(Pt 1):179–89. doi: 10.1113/jphysiol.2005.100743. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Kito Y, Suzuki H. Properties of pacemaker potentials recorded from myenteric interstitial cells of Cajal distributed in the mouse small intestine. J Physiol. 2003 Dec 15;553(Pt 3):803–18. doi: 10.1113/jphysiol.2003.051334. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Maeda H, Yamagata A, Nishikawa S, Yoshinaga K, Kobayashi S, Nishi K, Nishikawa S. Requirement of c-kit for development of intestinal pacemaker system. Development. 1992;116(2):369–75. doi: 10.1242/dev.116.2.369. [DOI] [PubMed] [Google Scholar]
- 11.Huizinga JD, Thuneberg L, Kluppel M, Malysz J, Mikkelsen HB, Bernstein A. W/kit gene required for interstitial cells of Cajal and for intestinal pacemaker activity. Nature. 1995 Jan 26;373(6512):347–9. doi: 10.1038/373347a0. [DOI] [PubMed] [Google Scholar]
- 12.Hirst GD, Dickens EJ, Edwards FR. Pacemaker shift in the gastric antrum of guinea-pigs produced by excitatory vagal stimulation involves intramuscular interstitial cells. J Physiol. 2002;541(Pt 3):917–28. doi: 10.1113/jphysiol.2002.018614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Ward SM, Sanders KM. Involvement of intramuscular interstitial cells of Cajal in neuroeffector transmission in the gastrointestinal tract. J Physiol. 2006;576(Pt 3):675–82. doi: 10.1113/jphysiol.2006.117390. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Kraichely RE, Farrugia G. Mechanosensitive ion channels in interstitial cells of Cajal and smooth muscle of the gastrointestinal tract. Neurogastroenterol Motil. 2007 Apr;19(4):245–52. doi: 10.1111/j.1365-2982.2006.00880.x. [DOI] [PubMed] [Google Scholar]
- 15.Powley TL, Wang XY, Fox EA, Phillips RJ, Liu LW, Huizinga JD. Ultrastructural evidence for communication between intramuscular vagal mechanoreceptors and interstitial cells of Cajal in the rat fundus. Neurogastroenterol Motil. 2008;20(1):69–79. doi: 10.1111/j.1365-2982.2007.00990.x. [DOI] [PubMed] [Google Scholar]
- 16.Gibbons SJ, Farrugia G. The role of carbon monoxide in the gastrointestinal tract. J Physiol. 2004;556:325–36. doi: 10.1113/jphysiol.2003.056556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Koh SD, Ward SM, Ordog T, Sanders KM, Horowitz B. Conductances responsible for slow wave generation and propagation in interstitial cells of Cajal. Curr Opin Pharmacol. 2003 Dec;3(6):579–82. doi: 10.1016/j.coph.2003.09.002. [DOI] [PubMed] [Google Scholar]
- 18.Lin ZY, McCallum RW, Schirmer BD, Chen JD. Effects of pacing parameters on entrainment of gastric slow waves in patients with gastroparesis. Am J Physiol. 1998 Jan;274(1 Pt 1):G186–91. doi: 10.1152/ajpgi.1998.274.1.G186. [DOI] [PubMed] [Google Scholar]
- 19.Faville RA, Pullan AJ, Sanders KM, Smith NP. A biophysically based mathematical model of unitary potential activity in interstitial cells of Cajal. Biophys J. 2008 Jul;95(1):88–104. doi: 10.1529/biophysj.107.122507. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Faville RA, Pullan AJ, Sanders KM, Koh SD, Lloyd CM, Smith NP. Biophysically based mathematical modeling of interstitial cells of Cajal slow wave activity generated from a discrete unitary potential basis. Biophys J. 2009 Jun 17;96(12):4834–52. doi: 10.1016/j.bpj.2009.03.058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Gomez-Pinilla PJ, Gibbons SJ, Bardsley MR, Lorincz A, Pozo MJ, Pasricha PJ, Van de Rijn M, West RB, Sarr MG, Kendrick ML, Cima RR, Dozois EJ, Larson DW, Ordog T, Farrugia G. Ano1 is a selective marker of interstitial cells of Cajal in the human and mouse gastrointestinal tract. Am J Physiol Gastrointest Liver Physiol. 2009 Jun;296(6):G1370–81. doi: 10.1152/ajpgi.00074.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Hwang SJ, Blair PJ, Britton FC, O'Driscoll KE, Hennig G, Bayguinov YR, Rock JR, Harfe BD, Sanders KM, Ward SM. Expression of anoctamin 1/TMEM16A by interstitial cells of Cajal is fundamental for slow wave activity in gastrointestinal muscles. J Physiol. 2009;587(Pt 20):4887–904. doi: 10.1113/jphysiol.2009.176198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Zhu MH, Kim TW, Ro S, Yan W, Ward SM, Koh SD, Sanders KM. A Ca(2+)-activated Cl(−) conductance in interstitial cells of Cajal linked to slow wave currents and pacemaker activity. J Physiol. 2009 Oct 15;587(Pt 20):4905–18. doi: 10.1113/jphysiol.2009.176206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Farrugia G. Interstitial cells of Cajal in health and disease. Neurogastroenterol Motil. 2008 May;20(Suppl 1):54–63. doi: 10.1111/j.1365-2982.2008.01109.x. [DOI] [PubMed] [Google Scholar]
- 25.Huizinga JD, Zarate N, Farrugia G. Physiology, injury, and recovery of interstitial cells of Cajal: basic and clinical science. Gastroenterology. 2009 Nov;137(5):1548–56. doi: 10.1053/j.gastro.2009.09.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Sanders KM. Interstitial cells of Cajal at the clinical and scientific interface. J Physiol. 2006;576:683–7. doi: 10.1113/jphysiol.2006.116814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Wang YR, Fisher RS, Parkman HP. Gastroparesis-related hospitalizations in the United States: trends, characteristics, and outcomes, 1995–2004. Am J Gastroenterol. 2008 Feb;103(2):313–22. doi: 10.1111/j.1572-0241.2007.01658.x. [DOI] [PubMed] [Google Scholar]
- 28.Parkman HP, Hasler WL, Fisher RS. American Gastroenterological Association technical review on the diagnosis and treatment of gastroparesis. Gastroenterology. 2004 Nov;127(5):1592–622. doi: 10.1053/j.gastro.2004.09.055. [DOI] [PubMed] [Google Scholar]
- 29.Ordog T. Interstitial cells of Cajal in diabetic gastroenteropathy. Neurogastroenterol Motil. 2008 Jan;20(1):8–18. doi: 10.1111/j.1365-2982.2007.01056.x. [DOI] [PubMed] [Google Scholar]
- 30.Lyford GL, He CL, Soffer E, Hull TL, Strong SA, Senagore AJ, Burgart LJ, Young-Fadok T, Szurszewski JH, Farrugia G. Pan-colonic decrease in interstitial cells of Cajal in patients with slow transit constipation. Gut. 2002;51(4):496–501. doi: 10.1136/gut.51.4.496. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Du P, Li S, O'Grady G, Cheng LK, Pullan AJ, Chen JD. Effects of electrical stimulation on isolated rodent gastric smooth muscle cells evaluated via a joint computational simulation and experimental approach. Am J Physiol Gastrointest Liver Physiol. 2009 Aug 6;297(4):G672–80. doi: 10.1152/ajpgi.00149.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Sarna SK, Daniel EE, Kingma YJ. Simulation of slow-wave electrical activity of small intestine. Am J Physiol. 1971;221:166–75. doi: 10.1152/ajplegacy.1971.221.1.166. [DOI] [PubMed] [Google Scholar]
- 33.Sarna SK, Daniel EE, Kingma YJ. Effects of partial cuts on gastric electrical control activity and its computer model. Am J Physiol. 1972 Aug;223(2):332–40. doi: 10.1152/ajplegacy.1972.223.2.332. [DOI] [PubMed] [Google Scholar]
- 34.Buist ML, Cheng LK, Sanders KM, Pullan AJ. Multiscale modelling of human gastric electric activity: can the electrogastrogram detect functional electrical uncoupling? Exp Physiol. 2006 Mar;91(2):383–90. doi: 10.1113/expphysiol.2005.031021. [DOI] [PubMed] [Google Scholar]
- 35.Cheng LK, Komuro R, Austin TM, Buist ML, Pullan AJ. Anatomically realistic multiscale models of normal and abnormal gastrointestinal electrical activity. World J Gastroenterol. 2007 Mar 7;13(9):1378–83. doi: 10.3748/wjg.v13.i9.1378. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Cheng LK, O`Grady G, Du P, Egbuji J, Windsor JA, Pullan AJ. Gastrointestinal system. Wiley Interdiscip Rev Syst Biol Med. 2009;2(1):65–79. doi: 10.1002/wsbm.19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Hunter PJ, Borg TK. Integration from proteins to organs: the Physiome Project. Nat Rev Mol Cell Biol. 2003;4:237–43. doi: 10.1038/nrm1054. [DOI] [PubMed] [Google Scholar]
- 38.Aliev RR, Richards W, Wikswo JP. A simple nonlinear model of electrical activity in the intestine. J Theor Biol. 2000;204(1):21–8. doi: 10.1006/jtbi.2000.1069. [DOI] [PubMed] [Google Scholar]
- 39.Keener J, Sneyd J. In: Mathematical physiology. Marsden JE, Sirovich L, Wiggins S, editors. Springer; New York: 1998. pp. 116–153. [Google Scholar]
- 40.Nelsen TS, Becker JC. Simulation of the electrical and mechanical gradient of the small intestine. Am J Physiol. 1968;214:749–57. doi: 10.1152/ajplegacy.1968.214.4.749. [DOI] [PubMed] [Google Scholar]
- 41.Daniel EE, Bardakjian BL, Huizinga JD, Diamant NE. Relaxation oscillator and core conductor models are needed for understanding of GI electrical activities. Am J Physiol. 1994 Mar;266(3 Pt 1):G339–49. doi: 10.1152/ajpgi.1994.266.3.G339. [DOI] [PubMed] [Google Scholar]
- 42.Fitzhugh R. Impulses and physiological states in theoretical models of nerve membrane. Biophys J. 1961;1:445–65. doi: 10.1016/s0006-3495(61)86902-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Nagumo JS, Arimoto S, Yoshizawa S. An active pulse transmission line simulating nerve axon. Proc IRE. 1962;50:2061–71. [Google Scholar]
- 44.Youm T, Aharonoff G, Zuckerman JD, Koval KJ. Effect of previous cerebrovascular accident on outcome after hip fracture. J Orthop Trauma. 2000 Jun–Jul;14(5):329–34. doi: 10.1097/00005131-200006000-00004. [DOI] [PubMed] [Google Scholar]
- 45.Corrias A, Buist ML. A quantitative model of gastric smooth muscle cellular activation. Ann Biomed Eng. 2007;35(9):1595–607. doi: 10.1007/s10439-007-9324-8. [DOI] [PubMed] [Google Scholar]
- 46.Corrias A, Buist ML. Quantitative cellular description of gastric slow wave activity. Am J Physiol Gastrointest Liver Physiol. 2008 Apr;294(4):G989–95. doi: 10.1152/ajpgi.00528.2007. [DOI] [PubMed] [Google Scholar]
- 47.O'Grady G, Egbuji JU, Du P, Cheng LK, Pullan AJ, Windsor JA. High-frequency gastric electrical stimulation for the treatment of gastroparesis: a meta-analysis. World J Surg. 2009 Aug;33(8):1693–701. doi: 10.1007/s00268-009-0096-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.McCallum RW, Chen JD, Lin Z, Schirmer BD, Williams RD, Ross RA. Gastric pacing improves emptying and symptoms in patients with gastroparesis. Gastroenterology. 1998 Mar;114(3):456–61. doi: 10.1016/s0016-5085(98)70528-1. [DOI] [PubMed] [Google Scholar]
- 49.A quantitative cellular description of gastric slow wave activity. 2008 doi: 10.1152/ajpgi.00528.2007. database on the Internet. [DOI] [PubMed] [Google Scholar]
- 50.Fall CP, Keizer JE. Mitochondrial modulation of intracellular Ca(2+) signaling. J Theor Biol. 2001 May 21;210(2):151–65. doi: 10.1006/jtbi.2000.2292. [DOI] [PubMed] [Google Scholar]
- 51.Pullan AJ, Buist ML, Cheng LK. Mathematically modelling the electrical activity of the heart: from cell to body surface and back again. World Scientific; Singapore: 2005. [Google Scholar]
- 52.Du P, O'Grady G, Windsor JA, Cheng LK, Pullan AJ. A tissue framework for simulating the effects of gastric electrical stimulation and in-vivo validation. IEEE Trans Biomed Eng. 2009;56(12):2755–61. doi: 10.1109/TBME.2009.2027690. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Du P, O'Grady G, Egbuji JU, Lammers WJ, Budgett D, Nielsen P, Windsor JA, Pullan AJ, Cheng LK. High-resolution mapping of in vivo gastrointestinal slow wave activity using flexible printed circuit board electrodes: methodology and validation. Ann Biomed Eng. 2009 Apr;37(4):839–46. doi: 10.1007/s10439-009-9654-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Pullan AJ, Buist ML, Sands GB, Cheng LK, Smith NP. Cardiac electrical activity—from heart to body surface and back again. J Electrocardiol. 2003;36(Suppl):63–7. doi: 10.1016/j.jelectrocard.2003.09.016. [DOI] [PubMed] [Google Scholar]
- 55.Li S, Chen JD. Cellular Effects of Gastric ElectricalStimulation on Antral Smooth Muscle Cells in Rats. Am J Physiol Regul Integr Comp Physiol. 2010 Jun;298(6):R1580–7. doi: 10.1152/ajpregu.00024.2010. [DOI] [PubMed] [Google Scholar]
- 56.Trew ML, Smaill BH, Bullivant DP, Hunter PJ, Pullan AJ. A generalized finite difference method for modeling cardiac electrical activation on arbitrary, irregular computational meshes. Math Biosci. 2005;198:169–89. doi: 10.1016/j.mbs.2005.07.007. [DOI] [PubMed] [Google Scholar]
- 57.Yao SK, Ke MY, Wang ZF, Xu DB, Zhang YL. Visceral response to acute retrograde gastric electrical stimulation in healthy human. World J Gastroenterol. 2005 Aug 7;11(29):4541–6. doi: 10.3748/wjg.v11.i29.4541. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Bedi BS, Kelly KA, Holley KE. Pathways of propagation of the canine gastric pacesetter potential. Gastroenterology. 1972 Aug;63(2):288–96. [PubMed] [Google Scholar]
- 59.Song GQ, Chen JD. Synchronized gastric electrical stimulation improves delayed gastric emptying in nonobese mice with diabetic gastroparesis. J Appl Physiol. 2007 Nov;103(5):1560–4. doi: 10.1152/japplphysiol.00319.2007. [DOI] [PubMed] [Google Scholar]
- 60.Wilbur BG, Kelly KA. Effect of proximal gastric, complete gastric, and truncal vagotomy on canine gastric electric activity, motility, and emptying. Ann Surg. 1973 Sep;178(3):295–303. doi: 10.1097/00000658-197309000-00009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Wilbur BG, Kelly KA, Code CF. Effect of gastric fundectomy on canine gastric electrical and motor activity. Am J Physiol. 1974 Jun;226(6):1445–9. doi: 10.1152/ajplegacy.1974.226.6.1445. [DOI] [PubMed] [Google Scholar]
- 62.Lammers WJ, Stephen B, Arafat K, Manefield GW. High resolution electrical mapping in the gastrointestinal system: initial results. Neurogastroenterol Motil. 1996 Sep;8(3):207–16. doi: 10.1111/j.1365-2982.1996.tb00259.x. [DOI] [PubMed] [Google Scholar]
- 63.Lammers WJ, Ver Donck L, Stephen B, Smets D, Schuurkes JA. Focal activities and re-entrant propagations as mechanisms of gastric tachyarrhythmias. Gastroenterology. 2008 Nov;135(5):1601–11. doi: 10.1053/j.gastro.2008.07.020. [DOI] [PubMed] [Google Scholar]
- 64.Lammers WJ, Ver Donck L, Stephen B, Smets D, Schuurkes JA. Origin and propagation of the slow wave in the canine stomach: the outlines of a gastric conduction system. Am J Physiol Gastrointest Liver Physiol. 2009 Jun;296(6):G1200–10. doi: 10.1152/ajpgi.90581.2008. [DOI] [PubMed] [Google Scholar]
- 65.Lammers WJ, Stephen B. Origin and propagation of individual slow waves along the intact feline small intestine. Exp Physiol. 2008 Mar;93(3):334–46. doi: 10.1113/expphysiol.2007.039180. [DOI] [PubMed] [Google Scholar]
- 66.Spitzer V, Ackerman MJ, Scherzinger AL, Whitlock D. The visible human male: a technical report. J Am Med Inform Assoc. 1996;3:118–30. doi: 10.1136/jamia.1996.96236280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Lin AS-H, Buist ML, Smith NP, Pullan AJ. Modelling slow wave activity in the small intestine. J Theor Biol. 2006;242:356–62. doi: 10.1016/j.jtbi.2006.03.004. [DOI] [PubMed] [Google Scholar]
- 68.Lin AS, Buist ML, Cheng LK, Smith NP, Pullan AJ. Computational simulations of the human magneto- and electro-enterogram. Ann Biomed Eng. 2006 Aug;34(8):1322–31. doi: 10.1007/s10439-006-9142-4. [DOI] [PubMed] [Google Scholar]
- 69.Komuro R, Cheng LK, Pullan AJ. Comparison and analysis of inter-subject variability of simulated magnetic activity generated from gastric electrical activity. Ann Biomed Eng. 2008 Jun;36(6):1049–59. doi: 10.1007/s10439-008-9480-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Kim JH, Bradshaw LA, Pullan AJ, Cheng LK. Characterization of gastric electrical activity using magnetic field measurements: a simulation study. Ann Biomed Eng. 2010 Jan;38(1):177–86. doi: 10.1007/s10439-009-9804-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Bassingthwaighte J, Hunter P, Noble D. The Cardiac Physiome: perspectives for the future. Exp Physiol. 2009 May;94(5):597–605. doi: 10.1113/expphysiol.2008.044099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Lloyd CM, Halstead MD, Nielsen PF. CellML: its future, present and past. Prog Biophys Mol Biol. 2004;85:433–50. doi: 10.1016/j.pbiomolbio.2004.01.004. [DOI] [PubMed] [Google Scholar]
- 73.Strege PR, Mazzone A, Kraichely RE, Sha L, Holm AN, Ou Y, Lim I, Gibbons SJ, Sarr MG, Farrugia G. Species dependent expression of intestinal smooth muscle mechanosensitive sodium channels. Neurogastroenterol Motil. 2007 Feb;19(2):135–43. doi: 10.1111/j.1365-2982.2006.00844.x. [DOI] [PubMed] [Google Scholar]
- 74.Wang B, Kunze WA, Zhu Y, Huizinga JD. In situ recording from gut pacemaker cells. Pflugers Arch. 2008 Oct;457(1):243–51. doi: 10.1007/s00424-008-0513-6. [DOI] [PubMed] [Google Scholar]
- 75.Locke GR, 3rd, Ackerman MJ, Zinsmeister AR, Thapa P, Farrugia G. Gastrointestinal symptoms in families of patients with an SCN5A-encoded cardiac channelopathy: evidence of an intestinal channelopathy. Am J Gastroenterol. 2006 Jun;101(6):1299–304. doi: 10.1111/j.1572-0241.2006.00507.x. [DOI] [PubMed] [Google Scholar]
- 76.Saito YA, Strege PR, Tester DJ, Locke GR, 3rd, Talley NJ, Bernard CE, Rae JL, Makielski JC, Ackerman MJ, Farrugia G. Sodium channel mutation in irritable bowel syndrome: evidence for an ion channelopathy. Am J Physiol Gastrointest Liver Physiol. 2009 Feb;296(2):G211–8. doi: 10.1152/ajpgi.90571.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.O'Grady G, Du P, Egbuji J. High-resolution mapping of human gastric slow wave activity: initial results. Neurogastroenterol Motil. 2010 Sep;299(3):G585–92. doi: 10.1152/ajpgi.00125.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Du P, Qiao W, O'Grady G, Lammers WJ, Cheng LK, Pullan AJ, editors. IEEE Eng Med Biol Sci. 2009. Automated detection of gastric slow wave events and estimation of propagation velocity vector field from serosasl high-resolution mapping; pp. 2527–30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Erickson JC, O'Grady G, Du P, Obioha C, Qiao W, Richards WO, Bradshaw LA, Pullan AJ, Cheng LK. Falling-Edge, Variable Threshold (FEVT) Method for the automated detection of gastric slow wave events in high-resolution serosal electrode recordings. Ann Biomed Eng. 2010 Apr;38(4):1511–29. doi: 10.1007/s10439-009-9870-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Coleski R, Hasler WL. Directed endoscopic mucosal mapping of normal and dysrhythmic gastric slow waves in healthy humans. Neurogastroenterol Motil. 2004 Oct;16(5):557–65. doi: 10.1111/j.1365-2982.2004.00542.x. [DOI] [PubMed] [Google Scholar]
- 81.O'Grady G, Du P, Egbuji JU, Lammers WJ, Wahab A, Pullan AJ, Cheng LK, Windsor JA. A novel laparoscopic device for measuring gastrointestinal slow-wave activity. Surg Endosc. 2009 May;23(12):2842–48. doi: 10.1007/s00464-009-0515-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Ver Donck L, Lammers WJ, Moreaux B, Smets D, Voeten J, Vekemans J, Schuurkes JA, Coulie B. Mapping slow waves and spikes in chronically instrumented conscious dogs: implantation techniques and recordings. Med Biol Eng Comput. 2006 Mar;44(3):170–8. doi: 10.1007/s11517-005-0018-9. [DOI] [PubMed] [Google Scholar]
- 83.Abid S, Lindberg G. Electrogastrography: poor correlation with antro-duodenal manometry and doubtful clinical usefulness in adults. World J Gastroenterol. 2007 Oct 14;13(38):5101–7. doi: 10.3748/wjg.v13.i38.5101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Bradshaw LA, Irimia A, Sims JA, Richards WO. Bio-magnetic signatures of uncoupled gastric musculature. Neurogastroenterol Motil. 2009 Jul;21(7):778–e50. doi: 10.1111/j.1365-2982.2009.01265.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Richards WO, Garrard CL, Allos SH, Bradshaw LA, Staton DJ, Wikswo JP., Jr. Noninvasive diagnosis of mesenteric ischemia using a SQUID magnetometer. Ann Surg. 1995 Jun;221(6):696–704. doi: 10.1097/00000658-199506000-00009. discussion, 5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Zhao J, Trew ML, Legrice IJ, Smaill BH, Pullan AJ. A tissue-specific model of reentry in the right atrial appendage. J Cardiovasc Electrophysiol. 2009 Jun;20(6):675–84. doi: 10.1111/j.1540-8167.2008.01420.x. [DOI] [PubMed] [Google Scholar]
- 87.Tharayl VS, Wouters MM, Stanich JE, Roeder JL, Lei S, Beyder A, Gomez-Pinilla PJ, Gershon MD, Maroteaux L, Gibbons SJ, Farrugia G. Lack of serotonin 5-HT2B receptor alters proliferation and network volume of interstitial cells of Cajal in vivo. Neurogastroenterol Motil. 2010 Apr;22(4):462–9. e109–10. doi: 10.1111/j.1365-2982.2009.01435.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Mak DO, McBride S, Foskett JK. Regulation by Ca2+ and inositol 1,4,5-trisphosphate (InsP3) of single recombinant type 3 InsP3 receptor channels. Ca2+ activation uniquely distinguishes types 1 and 3 insp3 receptors. J Gen Physiol. 2001 May;117(5):435–46. doi: 10.1085/jgp.117.5.435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Suzuki H, Takano H, Yamamoto Y, Komuro T, Saito M, Kato K, Mikoshiba K. Properties of gastric smooth muscles obtained from mice which lack inositol trisphosphate receptor. J Physiol. 2000 May 15;525(Pt 1):105–11. doi: 10.1111/j.1469-7793.2000.00105.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.Trew ML, Caldwell BJ, Sands GB, Hooks DA, Tai DC, Austin TM, LeGrice IJ, Pullan AJ, Smaill BH. Cardiac electrophysiology and tissue structure: bridging the scale gap with a joint measurement and modelling paradigm. Exp Physiol. 2006 Mar;91(2):355–70. doi: 10.1113/expphysiol.2005.031054. [DOI] [PubMed] [Google Scholar]
- 91.Du P, O'Grady G, Gibbons SJ, Yassi R, Lees-Green R, Farrugia G, Cheng LK, Pullan AJ. Tissue-specific mathematical models of slow wave entrainment in wild-type and 5-HT(2B) knockout mice with altered interstitial cells of Cajal networks. Biophys J. 2010 May 19;98(9):1772–81. doi: 10.1016/j.bpj.2010.01.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.O'Grady G, Du P, Lammers WJ, Egbuji JU, Mithraratne P, Chen JD, Cheng LK, Windsor JA, Pullan AJ. Highresolution entrainment mapping of gastric pacing: a new analytic tool. Am J Physiol Gastrointest Liver Physiol. 2010 Feb;298(2):G314–21. doi: 10.1152/ajpgi.00389.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.Nash MP, Pullan AJ. Challenges facing validation of noninvasive electrical imaging of the heart. Ann Noninvasive Electrocardiol. 2005 Jan;10(1):73–82. doi: 10.1111/j.1542-474X.2005.00608.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94.Cheng LK, O'Grady G, Du P, Egbuji J, Windsor JA, Pullan AJ, editors. IEEE Eng Med Biol Sci. 2009. Detailed measurements of gastric electrical activity and their implications of inverse solutions. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95.Hodgkin AL, Huxley AF. A quantitative description of membrane current and its application to conduction and excitation in nerve. J Physiol. 1952 Aug;117(4):500–44. doi: 10.1113/jphysiol.1952.sp004764. [DOI] [PMC free article] [PubMed] [Google Scholar]