Stimulus Range and Discontinuity Effects on Information-Integration Category Learning and Generalization

Abstract

Two studies are reported that support the hypothesis that categories that require a multiple-unit representation, as opposed to a single-unit representation, lead to worse initial acquisition but better generalization. Based on the constraints imposed by the procedural-based learning system thought to mediate information-integration categorization, we argue that the need to train multiple units during initial category acquisition slows the procedural-based category learning process and adversely affects learning performance. However, we speculate that better generalization occurs because of the increased likelihood that a novel stimulus will activate at least one of the multiple units needed to represent the category. Relations to other findings in the literature and the implications of this work for training and clinical assessment are discussed.

INTRODUCTION

Understanding the experimental factors and psychological processes that facilitate acquisition and generalization has been the focus of psychological research since its inception. This has implications for education and training at all levels, from formal classroom training (e.g., reading, writing and arithmetic), to skill learning (e.g., driving, airline screening, medical diagnosis, radiology, etc.), to rehabilitation and interventions (e.g., to improve memory and attention, or to reduce drug relapse).

One cognitive skill for which acquisition and generalization processes are critical is information-integration perceptual classification (Ashby, Alfonso-Reese, Turken, & Waldron, 1998; Ashby & Maddox, 2010; Maddox & Ashby, 2004). These are classification problem for which there is no verbal analog to the optimal rule and for which learning is gradual and incremental. Some of the most important occupations in our society, such as airport screening, radiology or medical diagnosis, to name a few, involve classification, and we spend an enormous amount of time and money devoted to training individuals to perform these jobs. In a typical classification learning task, participants are presented with a stimulus and are asked to classify it into a single category. Once a response is made, participants are provided with corrective feedback. A common assumption in classification research (and other research areas) is that training regimens that lead to good initial acquisition when feedback is presented will also lead to good generalization to novel items within and outside the range of training items, even when corrective feedback is removed (for a review see Schmidt & Bjork, 1992; J. D. Smith, Redford, Washburn, & Taglialatela, 2005).

Early learning theorists, however, recognized that this assumption is often false and noted that experimental factors that improve initial acquisition can either lead to good or poor generalization once feedback is removed (Estes, 1955; Hull, 1943; Skinner, 1938; Tolman, 1932). Perhaps counter-intuitively, there is evidence in some domains that experimental factors that lead to worse initial acquisition actually lead to better generalization (Schmidt & Bjork, 1992). This pattern has been observed in the motor and verbal learning domains (Balota, Duchek, & Logan, 2007; Bjork, 1994; Bjork & Linn, 2006; Karpicke & Roediger, 2007, , 2008; Landauer & Bjork, 1978; Roediger & Karpicke, 2006). For example, in motor learning, spaced practice of motor movements leads to worse initial acquisition but better generalization, whereas massed practice of the same movements leads to better initial acquisition but worse generalization (e.g., Shea & Morgan, 1979).

Given the important role that classification plays in many real world skills, and given the fact that good acquisition training does not necessarily imply good generalization, it is critical to evaluate the efficacy of any training procedure by incorporating a transfer phase that includes novel items from within and outside the range of training items and for which feedback is not provided (Schmidt & Bjork, 1992). Although acquisition training usually involves presentation of a fixed set of items, the true test of generalization lies with one's ability to classify not only items that are similar to the training items (i.e., items from within the range of trained items), but also items that are dissimilar from the training items (i.e., items from outside the range of trained items) (M.A. Erickson & Kruschke, 1998; M. A. Erickson & Kruschke, 2002; J. D. Smith, Redford, Washburn, & Taglialatela, 2005). We take this approach in the current study.

In addition, we use a model based approach to determine how the different training regimens affect the types of processes people use to perform that task and how those affect the nature of generalization. To anticipate, the model based analysis turn out to be critical in the interpretation of the data.

Overview of the Current Study

The overriding aim of the current work is to examine the effects of category range and category discontinuity on acquisition and generalization to a broadly sampled set of stimuli. Category range is defined as the breadth of stimulus values along the stimulus dimensions [often referred to as category variance in the literature (Cohen, Nosofsky, & Zaki, 2001; Hahn, Bailey, & Elvin, 2005; Rips & Collins, 1993)]. Category discontinuity results when each category is composed of distinct sub-clusters of stimuli that are separated by unsampled portions of the stimulus space.

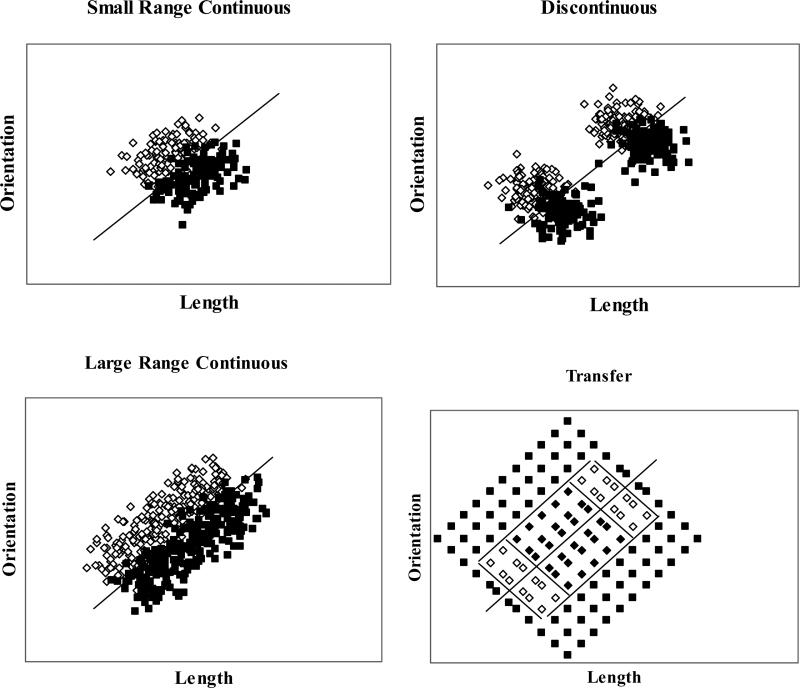
Category range and discontinuity effects have been examined in the literature but often the two factors are confounded making it difficult to determine their independent impact. For example, Maddox, Filoteo and Lauritzen (2007; for related work see Kornell & Bjork, 2008; Maddox, Filoteo, Lauritzen, Connally, & Hejl, 2005) examined the effects of continuous versus discontinuous category training on information-integration acquisition and generalization. Scatterplots of the exemplars from the (small range) continuous and discontinuous training conditions for the information-integration categories are displayed in Figure 1 (along with the transfer items). Maddox et al. (2007) found that for information-integration categories, acquisition was adversely affected by discontinuous category training, but that no-feedback transfer performance was better in the discontinuous training condition than in the continuous training condition. Unfortunately, discontinuity was confounded with range making it impossible to determine whether the increased range or category discontinuity led to the observed acquisition and generalization performance difference.

Figure 1.

Categorization conditions used for Experiment 1. The x axis denotes the line length in pixels and the y axis denotes the line orientation in degrees. Filled triangles denote stimuli from category A, open triangles denote stimuli from category B, open squares denote stimuli from category C, and filled squares denote category D. The solid lines that form an “x” in the small range continuous, discontinuous, and large range continuous conditions denote the optimal decision bound. Small range continuous condition: In the transfer stimulus plot, all items that lie within the small broken line parallelogram (filled diamonds) denote novel transfer items from within the range of training items, whereas all items outside this parallelogram (open diamonds and filled squares) denote novel transfer items from outside the range of training items. Large range continuous condition and discontinuous condition: All items that lie within the larger solid line parallelogram (filled and open diamonds) denote novel transfer items from within the range of training items, whereas all items outside this parallelogram (filled squares) denote novel transfer items from outside the range of training items.

Real world categories differ in their range and level of continuity. For example, members of the category “hand guns” (which an airline screener must learn) are highly similar and thus have a relatively small category range and are fairly cohesive (i.e., highly continuous). On the other hand, the category “weapon” is highly variable and contains items such as knives, bombs, guns, etc. which are highly discontinuous. The differences in continuity and range between these two categories could have implications for acquisition and generalization under various training conditions. Thus, it is important to disentangle category range and discontinuity to understand the affect these factors can independently have on acquisition and generalization in the real-world.

The current study provides an unconfounded test of the effects of category range and category discontinuity on information-integration acquisition and generalization across two experiments. Each study includes a small range continuous, a large range continuous, and a discontinuous acquisition training condition. Comparison of performance across the small and large range continuous conditions provides a test of the effects of increased category range on acquisition and generalization while holding discontinuity constant, whereas comparison of performance across the large range continuous and discontinuous conditions provides a test of the effects of category discontinuity on acquisition and generalization while holding category range constant.

A number of factors that are often left uncontrolled are held constant across our experimental conditions. These include the number of acquisition training trials, the nature of the optimal decision bound, and optimal accuracy. A no-feedback transfer phase is also included that tests performance for items from within the trained portion of the stimulus space and generalization to items outside the trained portion of the stimulus space.

As the results (presented below) suggest, one study supports the hypothesis that category discontinuity, and not category range, leads to poor initial acquisition but better generalization, whereas the other supports the hypothesis that category range, and not discontinuity, leads to poor initial acquisition but better generalization. Importantly, were we to focus our interpretation only on these empirical data, we would be left with a contradictory set of findings. However, by applying computational models, we offer a unified explanation of these findings that is consistent with the known processing characteristics of the procedural-based learning system thought to mediate information-integration classification acquisition (Ashby, Alfonso-Reese, Turken, & Waldron, 1998; Ashby & Ennis, 2006; Cincotta & Seger, 2007; Nomura et al., 2007). To do so, we apply a procedural-based learning model, called the Striatal Pattern Classifier (SPC; Ashby & Waldron, 1999), to the data. To anticipate, the model-based analyses suggest that neither increased category range, nor category discontinuity account for the results. Rather, the more direct mediator of performance appears to be whether a single-unit or multiple-units representation best represents each category. We now briefly outline the model based approach.

Model-Based Approach

The goal of the model-based approach is two-fold. First, we use the models to determine whether and when participants are using the task appropriate process—that is, a process consistent with the known characteristics of the procedural-based learning system—or an alternative process. We focus our analyses on those individuals who used the appropriate process as they are the ones who will be most telling in regard to the questions we ask. Second, we use the models to determine when participants use a multiple-unit representation and to determine whether these correspond to cases in which a multiple-unit representation is predicted. Although important for future research, we do not use this report to further develop the SPC as a formal model of procedural-based classification learning.

The model-based approach involves applying three models separately to the data from each participant (the details are provided in the Appendix). The first is the SPC that is a computational model whose processing is consistent with what is known about the neurobiology of the procedural-based category learning system thought to underlie information-integration classification performance (Ashby, Alfonso-Reese, Turken, & Waldron, 1998; Ashby & Ennis, 2006; Ashby & Waldron, 1999; Nomura et al., 2007; Seger & Cincotta, 2005). The second model is rule-based and instantiates hypothesis-testing strategies such as the application of uni-dimensional or conjunctive rules. These are verbalizable strategies that are sub-optimal in the present studies, but are often utilized by participants. The third model is a random responder model that assumes that the participant guesses on each trial. The model parameters will be estimated using maximum likelihood procedures (Ashby, 1992; Wickens, 1982). When the models are nested G² (likelihood ratio) tests will be applied to determine the best model. When models are not nested the goodness-of-fit statistic will be:

$$AIC=2r\text{-}2lnL,$$

where r is the number of free parameters and L is the likelihood of the model given the data (Akaike, 1974; Takane & Shibayama, 1992). The AIC statistic penalizes a model for extra free parameters in such a way that the smaller the AIC, the closer a model is to the “true model,” regardless of the number of free parameters (for a discussion of the complexities of model comparisons see Myung, 2000; Pitt, Myung, & Zhang, 2002).

Because the focus of this research is on information-integration learning and generalization, we describe the SPC in more detail. The SPC assumes that stimuli are represented perceptually in higher level visual areas, such as the inferotemporal cortex. Because of the massive many-to-one (approximately 10,000-to-1) convergence of afferents from the cortex to the striatum (Ashby & Ennis, 2006; Wilson, 1995), a low-resolution map of perceptual space is represented among the striatal units. During acquisition training, the striatal units become associated with one of the category labels, so that, after acquisition training is complete, a category response label is associated with each of a number of different regions of perceptual space. In effect, the striatum learns to associate a response with clumps of cells in the visual cortex. When all of the stimuli coming from a category are perceptually similar and form a coherent (or continuous) group, then the category can be represented by a small number of units. However, when the stimuli coming from a category are perceptually dissimilar and form a less coherent or even discontinuous group, then a multiple-unit representation will be needed.

It is important to be clear that the SPC is a computational model that is inspired by what is known about the neurobiology of the striatum. Because of this fact, the striatal “units” are hypothetical and could be interpreted within the language of other computational models (e.g., as “prototypes” in a multiple prototype model like SUSTAIN; Love, Medin, & Gureckis, 2004). In addition, we do not model learning in the SPC in the sense that we do not update association weights between units and category labels. Learning models have been proposed (Ashby, Paul, & Maddox, 2010), but because our focus is on asymptotic acquisition and generalization (see below) computational versions of the model are adequate to capture behavior at the end of learning.

Acquisition and Generalization Predictions

If we make the reasonable assumption that category learning is computationally and biologically more efficient when each category can be represented by fewer rather than more units, then it follows that the procedural-based learning system should be more efficient when stimuli coming from the same category form a coherent (or continuous) group because fewer units might be required. Alternatively it should be less efficient when stimuli coming from the same category are perceptually dissimilar and form a less coherent (or discontinuous) group because more units might be required to represent the categories. In line with this prediction, previous research suggests that initial acquisition is slower when more units are needed to represent each category, such as when the decision bound is nonlinear (Ashby & Maddox, 1990, , 1992; Ashby & Waldron, 1999; Maddox, Filoteo, & Lauritzen, 2007). In fact, Maddox et al. (2007) found that more units were needed to account for final block acquisition in their discontinuous condition than in their small range continuous condition.

Although initial acquisition might be slower when a multiple-unit representation is required, it is reasonable to hypothesize that a more distributed multiple-unit representation might lead to better generalization. This follows because novel stimuli presented during generalization would be more likely to activate one of the many units associated with a multiple-unit representation and would be less likely to activate the one unit associated with a single-unit representation. Importantly, this prediction holds in cluster models like SUSTAIN (Love, Medin, & Gureckis, 2004). Taken together this implies that the more striatal cells involved in representing a category the more difficult category acquisition will be, but the more likely it will be that a novel stimulus (e.g., stimuli presented during transfer), will be associated with that category. This leads to two predictions. First, multiple-unit SPC models should provide better model fits to data collected in generalization conditions for which a multiple-unit representation was needed during acquisition. Second, generalization accuracy rates should be higher in these conditions and should be especially high when a multiple-unit SPC model provides the best account of the data.

We turn now to the Experiments. For each study we will generate performance predictions based on the category structure and the models. We then use the models to help organize the results by breaking participants into groups based upon the best fitting model: SPC, rule-based or random-responder.

EXPERIMENT 1

Experiment 1 used stimuli that were lines that varied in length and orientation across trials. Scatter-plots of the training stimuli in the small range continuous, large range continuous, and discontinuous conditions are displayed in Figure 1, along with a scatter-plot of the transfer stimuli. The transfer block included test items from within and outside the trained portion of the stimulus space. Each point in Figure 1 denotes a unique stimulus, with each symbol denoting stimuli from different categories.

Maddox et al.(2007) found that the small range continuous condition required a single-unit representation for each category whereas the discontinuous condition require a multiple-unit (specifically, four-unit) representation. They reasoned that because the stimuli in each of the small range continuous categories were tightly packed around a single central prototype that a single-unit representation would suffice. They reasoned also that because the stimuli in each of the discontinuous categories were from discontinuous clusters of stimuli that a multiple-unit representation would be needed. In the large range continuous condition of Experiment 1, the stimuli are not tightly packed around a central prototype, but they are continuously sampled and more importantly are spread evenly around a central prototype. This makes a single-unit (or at the very least one strong central unit surrounded by other weaker units) representation likely in this condition. Thus, for Experiment 1, a single-unit representation is predicted in the two continuous conditions and a multiple-unit representation is predicted in the discontinuous condition. This implies that initial acquisition should be superior in the two continuous conditions but generalization should be superior in the discontinuous condition.

Methods

Participants

Ninety participants (30 per condition) completed the study and received course credit for their participation. All participants had normal or corrected to normal vision. Each participant served in only one condition. All participants met a learning criterion of 55% in the final acquisition training block.

Stimuli and Stimulus Generation

The stimuli are displayed in Figure 1, along with the optimal decision bounds. The category distribution parameters are outlined in Table 1 and optimal accuracy was 95%. In the small range continuous condition and in the discontinuous condition, each category was composed of four “sub-clusters” (16 total) with 30 stimuli being sampled randomly from each for a total of 480 stimuli. In the large range continuous condition, each category was composed of 9 “sub-clusters” (36 total) with 13 stimuli being sampled randomly from each and 3 additional stimuli being sampled randomly from each category for a total of 480 stimuli. The random samples were linearly transformed so that the sample mean vector and sample variance-covariance matrix equaled the population mean vector and variance-covariance matrix for each sub-cluster. Each random sample (x, y) was converted to a stimulus by deriving the length (in pixels) as l = x, and orientation (in degrees counterclockwise from horizontal) as o = 18y/50. These scaling factors were chosen to roughly equate the salience of each dimension. The resulting 480 stimuli were randomized and divided into five 96-trial blocks separately for each participant. These were presented during category acquisition training. One-hundred-forty-four stimuli (36 from each of the four response regions) were used during the no feedback transfer phase (see Figure 1).

Table 1.

Category Distribution Parameters from Experiment 1

	μ x	μ y
Small Range Continuous Condition
A	240	54
A	216	78
A	264	78
A	240	102
B	192	102
B	168	126
B	216	126
B	192	150
C	288	102
C	264	126
C	312	126
C	288	150
D	240	150
D	216	174
D	264	174
D	240	198

Large Range Continuous Condition
A	240	6
A	216	30
A	192	54
A	264	30
A	240	54
A	216	78
A	288	54
A	264	78
A	240	102
B	168	78
B	144	102
B	120	126
B	192	102
B	168	126
B	144	150
B	216	126
B	192	150
B	168	174
C	312	78
C	288	102
C	264	126
C	336	102
C	312	126
C	288	150
C	360	126
C	336	150
C	312	174
D	240	150
D	216	174
D	192	198
D	264	174
D	240	198
D	216	222
D	288	198
D	264	222
D	240	246

Discontinuous Condition
A	240	6
A	192	54
A	288	54
A	240	102
B	168	78
B	120	126
B	216	126
B	168	174
C	312	78
C	264	126
C	360	126
C	312	174
D	240	150
D	192	198
D	288	198
D	240	246

Note: The standard deviation along the x and y dimensions was 10 for all sub-clusters, and the covariance was zero.

Procedure

Each participant was run individually in a dimly lit testing room with an approximate viewing distance of 35cm. The participants were informed that there were four equally-likely categories. They were informed that perfect performance was impossible but that high levels of accuracy could be achieved. They were instructed to learn about the categories, to be as accurate as possible and not to worry about speed of responding. On each trial the stimulus appeared and remained on the screen until the participant generated a response by pressing one of two keys. The correct category label was then presented on the screen for 1 second along with the word “wrong” if their response was incorrect or “right” if their response was correct. Once feedback was given, the next trial was initiated. The procedure for the transfer trials was identical except that feedback was omitted.

Results

The results section is organized as follows. First, we apply the models to the final acquisition block and to the transfer block to determine whether each participant is using a procedural-based, rule-based or random process. Because of concerns with modeling aggregate data, each participant's data were fit separately (e.g., Ashby, Maddox, & Lee, 1994; Estes, 1956; Maddox, 1999; Maddox & Ashby, 1998; J.D. Smith & Minda, 1998). Four versions of the striatal pattern classifier (SPC) were fit to the data (SPC-1, SPC-2, SPC-4 and the optimal model). The SPC-1 assumed one unit per category, the SPC-2 assumed two units per category, and the SPC-4 assumed four units per category. Models with more units were not examined since, at most, a category contained four clusters of stimuli. The optimal model assumes that the optimal decision bounds were applied. Each of the SPC models assumes that, on each trial the participant determines which unit is closest to the perceptual effect and gives the associated response-- with the only difference among the models being the difference in the number of units. If one of these four models provided the best account of the data then the participant was classified as an “SPC-user”. A number of conjunctive and uni-dimensional hypothesis-testing models, as well as the random responder model were also applied to the data (see Appendix). If one of the hypothesis-testing models provided the best account of the data then the participant was classified as a “rule-based user”. If the random responder model provided the best account of the data then the participant was classified as a “random responder”.

Second, and because our main focus is on participants who use procedural-based learning strategies during the final acquisition block and during the transfer block, we display the learning curves and transfer performance for participants who were classified as SPC-users during both the final acquisition block and the transfer block. For these same participants, we also examine transfer performance in greater detail by examining transfer performance for items sampled from within the trained portion of the space separately from items sampled from outside the trained portion of the space. For completeness we also display the learning curves and transfer performance for those participants who do not use a procedural based learning strategy in the final acquisition block or in the transfer block. Finally, we examine the nature of strategy shifts across the final acquisition and transfer block and performance under various strategy shift conditions. The focus of this analysis is to compare and contrast performance for single- vs. multiple-unit SPC users.

Learning Curves and Transfer Performance for Participants Best Fit by the SPC in the Final Acquisition and Transfer Blocks

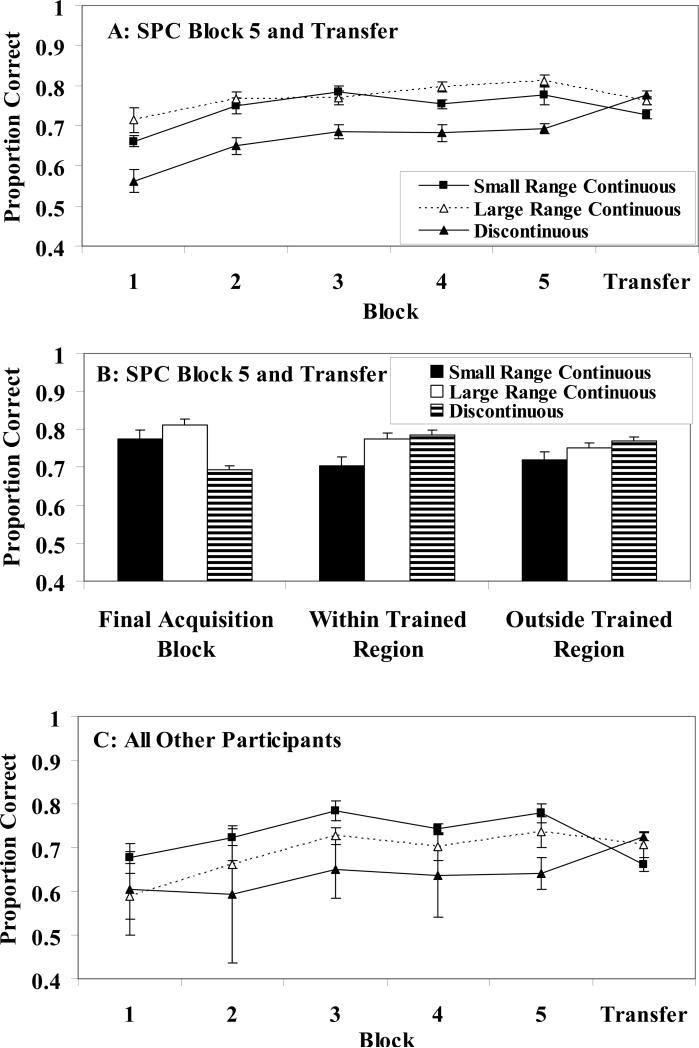
Figure 2A displays the average proportion correct for the small range continuous, large range continuous and discontinuous conditions for each of the 5 acquisition training blocks and the transfer block for only participants who were SPC-users (i.e., those best fit by the SPC-1, SPC-2, SPC-4 or the optimal model) in the final acquisition block and the transfer block. To reiterate, it is important to focus on these individuals because they are using the task appropriate process. This analysis includes 57%, 73%, and 93% of the participants from the small range continuous, large range continuous and discontinuous conditions, respectively. A 3 (small range continuous vs. large range continuous vs. discontinuous) condition × 5 acquisition block ANOVA was conducted. There was a significant effect of condition [F(2, 64) = 16.99, p < .001, η² = .347] that suggested worse acquisition in the discontinuous condition relative to the two continuous conditions (p's < .001 for both comparisons) with the latter two conditions showing no significant performance differences. There was a significant effect of block [F(4, 256) = 29.29, p < .001, ηΠ² = .314] suggesting that learning occurred, and the interaction was non-significant (F<1). Thus, category range had no effect on initial acquisition as suggested by a comparison of performance in the small and large range continuous condition, whereas category discontinuity had a large attenuating effect on initial acquisition as suggested by a comparison of performance in the large range continuous and discontinuous conditions.

Figure 2.

A. Proportion correct (averaged across participants) from the acquisition training and transfer phase of Experiment 1 for participants best fit by any of the SPC models in the final acquisition block and the transfer block. B. Absolute proportion correct for no feedback generalization transfer items from within the trained region of the space and from outside the trained region of the space from the same participants shown in panel A. C. Proportion correct (averaged across participants) from the acquisition training and transfer phase of Experiment 1 for all participants not included in panel A. Standard error bars included.

We also examined the change in performance from the final acquisition block to the transfer block. The performance drop was non-significant in the small range continuous condition but was significant in the large range continuous condition (p < .01). In the discontinuous condition there was a performance increase that was significant (p < .01).

Figure 2B displays the transfer performance for items from within and outside the trained region (along with performance in the final acquisition block) for the participants displayed in Figure 2A. The effect of condition was significant for the transfer items from within the trained region of the space [F(2, 64) = 6.39, p < .01, η² = .165] and was characterized by significantly worse performance in the small range continuous condition (.70) than in the large range continuous (.78) or discontinuous (.79) conditions (both p's <.01), with no performance difference emerging for the latter two conditions (ns). The effect of condition was nearly significant for the transfer items from outside the trained region of the space [F(2, 64) = 2.81, p =.068, η² = .081] and was characterized by significant performance difference between the small range continuous (.72) and discontinuous (.77) conditions (p < .05).

For completeness, Figure 2C displays the learning curves and transfer block performance for the remaining 43%, 27%, and 7% of the participants from the small range continuous, large range continuous and discontinuous conditions, respectively. These are the individuals whose final acquisition block or transfer block data was best fit by a rule-based model or the random responder model. Given the small sample size ANOVAs were not conducted.

Taken together, these data suggest that for SPC-users (those best fit by one of the SPC models in the final acquisition and transfer blocks), acquisition is worse but transfer is better in the discontinuous condition than in the two continuous conditions. This supports our initial claim that discontinuous categories should be more difficult to acquire but should lead to better transfer. What these data do not tell us is whether this performance pattern is due to the increased use of multiple-unit representations in the discontinuous condition. To answer this important question, we turn now to a more detailed analysis that examines performance separately for single-unit SPC users and multiple-unit SPC users. As outlined in the Introduction, we predict that a multiple-unit representation will be more likely to provide a better account of the data in the discontinuous than in the two continuous conditions.

Single- Versus Multiple-Unit SPC Analyses

The percentage of participants in each condition whose final acquisition block and transfer block of data was best fit by specific model pairings along with the proportion correct achieved by those participants is presented in Table 2. Five model pairings are examined. First, we examine performance for participants whose final acquisition block of data was best fit by the single-unit SPC (sSPC). These participants were divided into those whose transfer block was also fit by an SPC (SPC-1, SPC-2, SPC-4 or Optimal) model (sSPC-SPC) or by some other model (i.e., one of the hypothesis-testing models or the random responding model; SPC-Other). Next, we examine performance for participants whose final acquisition block of data was best fit by a multiple-unit SPC (mSPC; SPC-2, SPC-4 or Optimal). These participants were divided into those whose transfer block was also fit by an SPC (mSPC-SPC) or by some other model (SPC-Other). Finally, we examined performance for all participants whose final acquisition block of data was best fit by a rule-based model or the random responder model.

Table 2.

Model Results from Experiments 1 and 2 for the Final Acquisition Block and the No-Feedback Transfer Block (see text for details)

	Final Acquisition-Transfer Block Model	Percentage of Participants	Proportion Correct
Condition			Final Acquisition	Generalization
	Experiment 1
Small Range Continuous	sSPC-SPC	43	0.77	0.73
	SPC-Other	27	0.76	0.64
	mSPC-SPC	13	0.80	0.74
	mSPC-Other	10	0.80	0.67
	Rule Based or Random	7	0.86	0.74
Large Range Continuous	sSPC-SPC	53	0.79	0.75
	SPC-Other	10	0.74	0.66
	mSPC-SPC	20	0.86	0.81
	mSPC-Other	NA	NA	NA
	Rule Based or Random	17	0.73	0.74
Discontinuous	sSPC-SPC	47	0.67	0.76
	SPC-Other	3	0.68	0.74
	mSPC-SPC	47	0.72	0.79
	mSPC-Other	NA	NA	NA
	Rule Based or Random	3	0.60	0.72
	Experiment 2
Small Range Continuous	sSPC-SPC	4	0.84	0.90
	SPC-Other	NA	NA	NA
	mSPC-SPC	32	0.81	0.86
	mSPC-Other	14	0.78	0.79
	Rule Based or Random	50	0.75	0.78
Large Range Continuous	sSPC-SPC	NA	NA	NA
	SPC-Other	NA	NA	NA
	mSPC-SPC	88	0.72	0.84
	mSPC-Other	4	0.65	0.67
	Rule Based or Random	8	0.61	0.76
Discontinuous	sSPC-SPC	NA	NA	NA
	SPC-Other	NA	NA	NA
	mSPC-SPC	76	0.75	0.84
	mSPC-Other	8	0.75	0.82
	Rule Based or Random	16	0.66	0.80

Note: NA = non-applicable because no participants’ data was best fit by that model.

Several comments are in order. First, the proportion of mSPC-SPC participants was largest in the discontinuous condition (47%) and was smaller in the small range (13%) and large range (20%) continuous conditions. This supports our hypothesis that discontinuous training, relative to continuous training, is more likely to lead to a multiple-unit representation. Second, final acquisition block accuracy was higher for mSPC-SPC participant than for any other participant groups and this was especially salient in the discontinuous condition. Finally, transfer block accuracy was higher for mSPC-SPC participant than for any other participant groups and this also was especially salient in the discontinuous condition. .

Discussion

These data suggest that discontinuous category training leads to worse initial acquisition but an increase in performance from the final acquisition block to the transfer block, whereas continuous category training (even when the range of values is equated with that from the discontinuous categories) leads to better initial acquisition but a decrease in performance from the final acquisition block to the transfer block. The model-based analyses suggest that discontinuous categories, but not the continuous categories, are more likely to lead to a multiple-unit representation and that this might explain the finding of worse initial acquisition but better transfer in the discontinuous conditions. In Experiment 2, we test this hypothesis against the alternative hypothesis that category discontinuity alone drives the effect. To achieve this aim we compare discontinuous condition performance against performance in a continuous condition for which a multiple-unit representation is likely.

EXPERIMENT 2

Experiment 1 examined category range and discontinuity effects in a four-category information-integration task and found support for the hypothesis that discontinuous category training leads to worse initial acquisition but better generalization when category range is held constant. To our knowledge this is the first study to rigorously test these two hypotheses.

Notice from Figure 1, that the exemplars from each category in the discontinuous condition are sampled from four sub-clusters of stimuli. Many computational models of categorization would predict that under these conditions some sort of multiple-unit (e.g., SPC; Ashby & Waldron, 1999), multiple-prototype (e.g., rational model; Anderson, 1991) or multiple-cluster (e.g., SUSTAIN; Love, Medin, & Gureckis, 2004) representation would be required for learning. In other words, each of these sub-clusters of stimuli would be represented by a separate unit, prototype or cluster with each of these being assigned to a specific category. When presented with a new item the distance between the item and each unit is calculated and the item is assigned to the category associated with the nearest unit². Notice also that the exemplars from each category in the small range and large range continuous condition are sampled continuously from the space and are spread evenly around a central prototype. This makes a single-unit (or at the very least one strong central unit surrounded by other weaker units) representation likely in this condition. These observations, along with the finding that acquisition was worse but generalization was better in the discontinuous condition, support the hypothesis that the need for a multiple-unit representation impedes initial learning but results in better generalization.

In Experiment 2, we test the generalizability of these findings to a two-category case (Maddox, Filoteo, Lauritzen, Connally, & Hejl, 2005) for which multiple units would likely be required to represent the categories even though no discontinuity exists. Scatter-plots of the training stimuli in the small range continuous, large range continuous, and discontinuous conditions are displayed in Figure 3 along with a scatter-plot of the transfer stimuli. The transfer block included novel items from within and outside the range of training items to evaluate generalization. First, notice that each category of training items in the discontinuous condition is composed of two distinct and dissimilar clusters of items. Thus, a two-unit representation per category is likely required. Next notice that each category of training items in the large range condition, although not composed of discontinuous clusters, is composed of items that are “spread” out parallel along the decision bound. Using prototype terminology, there is no single prototype or central tendency that adequately describes the training stimuli. In this case, it is likely that a multiple-unit representation is also required. Finally, notice that each category of training items in the small range condition are tightly packed likely yielding a single-unit representation. If the large range continuous condition does, in fact, require a multiple-unit representation, then the performance pattern in that condition should be similar to that observed in the discontinuous condition, which should yielded poorer initial acquisition but better generalization relative to the small range continuous condition.

Figure 3.

Categorization conditions used for Experiment 2. The x axis denotes the line length in pixels and the y axis denotes the line orientation in degrees. Open diamonds denote stimuli from category A, and filled squares denote stimuli from category B. The solid line in the small range, large range, and discontinuous conditions denotes the optimal decision bound. Small range continuous condition: In the transfer stimulus plot, all items (denoted by filled diamonds) that lie within the small solid line parallelogram denote novel transfer items from within the range of training items, whereas all items outside this parallelogram denote novel transfer items from outside the range of training items (open diamonds and filled squares). Large range continuous condition and discontinuous condition: All items (denoted by filled diamonds and unfilled diamonds) that lie within the larger solid line parallelogram denote novel transfer items from within the range of training items, whereas all items outside this parallelogram (filled squares) denote novel transfer items from outside the range of training items.

Methods

Participants

Ninety participants (30 per condition) completed the study and received course credit for their participation. All participants had normal or corrected to normal vision. Each participant served in one condition. To ensure that only participants who showed some initial learning during the acquisition phase of the experiment were included in the analyses, a learning criterion of 55% correct during the final acquisition block was applied. All but 12 participants met the performance criterion (small range: N = 28; large range: N = 25; discontinuous: N = 25).

Stimuli and Stimulus Generation

The stimuli are displayed in Figure 3, along with the optimal decision bounds. The category distribution parameters are outlined in Table 3 and optimal accuracy was 90%. In the small range continuous and discontinuous conditions, each of the two training categories was composed of two “sub-clusters” (4 total) with 120 stimuli being sampled randomly from each for a total of 480 stimuli. In the large range continuous condition, each of the two categories was composed of four “sub-clusters” (8 total) with 60 stimuli being sampled randomly from each for a total of 480 stimuli. All other aspects of the acquisition training stimuli were identical to Experiment 1. One-hundred-thirty-two stimuli (66 from the A response region and 66 from the B response region) were used during the transfer phase and were randomized separately for each participant (see Figure 4).

Table 3.

Category Distribution Parameters from Experiment 2

	μ x	μ y
Small Range Continuous Condition
A	122	150
A	150	178
B	150	122
B	178	150

Large Range Continuous Condition
A	93	122
A	122	150
A	150	178
A	178	206
B	122	93
B	150	122
B	178	150
B	206	178

Discontinuous Condition
A	93	122
A	178	206
B	122	93
B	206	178

Note: The standard deviation along the x and y dimensions was 15 for all sub-clusters, and the covariance was zero.

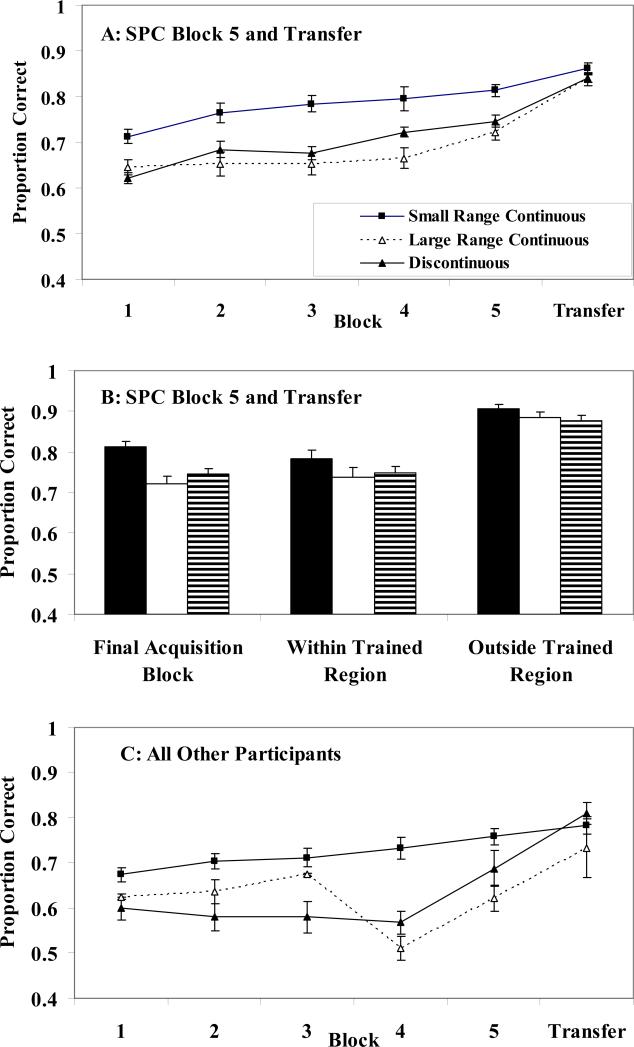
Figure 4.

A. Proportion correct (averaged across participants) from the acquisition training and transfer phase of Experiment 2 for participants best fit by the SPC in the final acquisition block and the transfer block. B. Absolute proportion correct for no feedback generalization transfer items from within the trained region of the space and from outside the trained region of the space from the same participants shown in panel A. C. Proportion correct (averaged across participants) from the acquisition training and transfer phase of Experiment 2 for all participants not included in panel A. Standard error bars included.

Procedure

The procedure was identical to that from Experiment 1 except that two response buttons were used instead of four.

Results

We follow the same data analytic approach in Experiment 2 that we used in Experiment 1. First, we fit the models to the final acquisition block and transfer block of data and characterize each participant as an SPC-user, rule-based user or a random responder. Next, we plot learning curves, overall transfer performance and transfer performance broken down by trained vs. untrained region for only those participants who were classified as SPC-users in the final acquisition and transfer blocks. For completeness we include learning curves for the remaining participants as well. Finally, we examine the nature of strategy shifts across the final acquisition and transfer block and performance under various strategy shift conditions. The focus of this analysis is to compare and contrast performance for single- vs. multiple-unit SPC users. The only caveat is that we do not fit the SPC-4 because at most a single category is composed of two sub-clusters of stimuli.

Learning Curves and Transfer Performance for Participants Best Fit by the SPC in the Final Acquisition and Transfer Blocks

The average proportion correct for the small range continuous, large range continuous and discontinuous conditions for each of the 5 acquisition training blocks and the transfer block for participants classified as SPC-users in the final acquisition block and the transfer block is displayed in Figure 4A. This includes 36%, 88%, and 76% of the participants from the small range continuous, large range continuous and discontinuous conditions, respectively. A 3 (small range continuous vs. large range continuous vs. discontinuous) condition × 5 acquisition block ANOVA was conducted. There was a significant effect of condition [F(2, 48) = 9.77, p < .001, η² = .289] that suggested better acquisition in the small range continuous condition relative to the large range continuous and discontinuous conditions (p's < .001 for both comparisons) with the latter two conditions showing no significant performance differences. There was a significant effect of block [F(4, 192) = 19.34, p < .001, η² = .2874] suggesting that learning occurred, and no interaction (F(8, 192) = 1.75, ns). Thus, category range had an effect on initial acquisition as suggested by a comparison of performance in the small range continuous condition with the large range continuous and discontinuous conditions, whereas category discontinuity did not have an effect as suggested by a comparison of performance in the large range continuous and discontinuous conditions.

We also examined the change in performance from the final acquisition block to the transfer block. There was a performance increase in all three conditions (all p's < .001). Even so, the increase was larger in the large range continuous and discontinuous conditions than in the small range continuous condition (both p's < .05).

Figure 4B displays the transfer performance for items from within and outside the trained region (along with performance in the final acquisition block) for the same participants. The effect of condition was non-significant for the transfer items from within the trained region of the space (F<1.0) and for the transfer items from outside the trained region of the space (F<1.0).

For completeness, we also plotted the learning curves and transfer block performance for the remaining 64%, 12%, and 24% of the participants from the small range continuous, large range continuous and discontinuous conditions, respectively. These data are plotted in Figure 4C. Given the small sample size ANOVAs were not conducted.

These data suggest that for SPC-users (those best fit by one of the SPC models in the final acquisition and transfer blocks), acquisition is worse but transfer is better in the large range continuous and discontinuous conditions relative to the small range continuous condition. This supports our initial claim that the two larger variance conditions (i.e., the large range continuous and discontinuous conditions) should be more difficult to acquire but should lead to better transfer. What these data do not tell us is whether this performance pattern is due to the increased use of multiple-unit representations in the large range continuous and discontinuous conditions. To answer this important question, we turn to a more detailed analysis that examines performance separately for single-unit SPC users and multiple-unit SPC users. As outlined in the Introduction, we predict that a multiple-unit representation will be more likely in the large range continuous and discontinuous conditions than in the small range continuous condition.

Single- Versus Multiple-Unit SPC Analyses

The percentage of participants in each condition whose final acquisition block and transfer block of data was best fit by the five model pairings outline in Experiment 1 is presented in Table 2. Two comments are in order. First, and as predicted, the proportion of mSPC-SPC participants was largest in the discontinuous (76%) and large range continuous conditions (88%) and was smaller in the small range continuous condition (32%). Second, final acquisition and transfer accuracy was higher for these participants then for other groups of participants.

Discussion

These data suggest that a large category range, regardless of discontinuity, leads to worse initial acquisition but an increase in performance from the final acquisition block to the transfer block, whereas a small category range leads to better initial acquisition but a smaller increase in performance from the final acquisition block to the transfer block. Based solely on accuracy, this finding appears in conflict with that from Experiment 1, but if one hypothesizes that the two large range conditions (large range continuous and discontinuous) require a multiple-unit representation, which is supported by the model-based analyses, then these data converge nicely with those from Experiment 1 in that both sets of results suggest that the pattern of acquisition and transfer observed is not related necessarily to the breadth or discontinuity of the category structures, but whether multiple units will provide a better representation of the category structures.

GENERAL DISCUSSION

Previous research suggests that discontinuous category training leads to worse initial acquisition, an increase in performance from acquisition to generalization blocks, and better overall generalization (Maddox, Filoteo, & Lauritzen, 2007). However, in this study discontinuity is confounded with an increase in the range of training items. In this article, two studies are reported that pit a discontinuity and range explanation of the results against the hypothesis that categories that require multiple-unit representations, as opposed to single-unit representations, lead to worse initial acquisition but better generalization. Taken together the data support the multiple-units hypothesis.

In the remainder of the discussion we address a number of relevant issues.

SPC vs. Other Non-Neuroscience Based Models

The multiple-unit hypothesis converges nicely with predictions from a number of computational models that share many properties with the SPC, including the grid model (Ashby & Maddox, 1989), the covering version of Kruschke's (1992) ALCOVE model, Anderson's (1991) rational model, and Love, Medin and Gureckis’ (2004) SUSTAIN model. Consider Love et al's SUSTAIN model as just one example. Although the exact behavior of the model is parameter dependent, across a wide range of parameter settings, SUSTAIN would predict a multiple-unit (called “clusters” in SUSTAIN) representation in the discontinuous condition from Experiment 1, and the large range and discontinuous conditions from Experiment 2. In addition, the model would predict a single-unit representation in the small and large range continuous conditions from Experiment 1 and the small range continuous condition from Experiment 2. The model would most likely predict the immediate generalization advantages mainly because the representation is spread out and thus the similarity between a trained unit and transfer items would be higher. Thus, the current findings are congruent with predictions from a popular computational model (SUSTAIN) as well the neurobiologically inspired SPC model.

Other Generalization Effects in Classification

Identifying training conditions that enhance learning and generalization is a fundamental problem facing learning theorists. The current study suggests that training on discontinuous clusters of stimuli can enhance generalization. Other studies have examined this topic and we briefly review two that are directly relevant. The first is a study by Spiering and Ashby (2008) who examined the effects of different training sequences on information-integration category acquisition using categories similar to those from Experiment 2 above. They compared a condition in which participants began by classifying easy stimuli (far from the decision bound), then classified intermediate difficulty stimuli (intermediate distance to the decision bound), then classified difficult stimuli (near the decision bound) (easy-to-hard) with a condition in which participants began by classifying difficult stimuli, then classified intermediate difficulty stimuli, then classified easy stimuli (hard-to-easy). This training was followed by a transfer block that required classification of all of the training items with feedback. With information-integration categories, they found that transfer performance was superior when difficult items were trained first as opposed to last. Interestingly, no effects emerged for rule-based categories. Future work should determine whether this effect holds when feedback is removed during transfer, as a true test of the permanence of the learning, and whether the effect holds across a broader sampling of stimuli that includes those from within and outside of the trained portion of the stimulus space.

In a related study, Kornell and Bjork (2008) examined the effects of spaced versus massed observational training on the learning of artist categories. Participants studied multiple paintings by different artists, with paintings from a given artist being presented sequentially along with the artist's name (massed training) or randomized with other artist's paintings (spaced training), with each being accompanied by the appropriate artist's name. A subsequent transfer test with new paintings from the same artists was administered. Participants viewed each new painting and were asked to give a categorization judgment followed by corrective feedback. Transfer was better for spaced as opposed to massed training. Although initial acquisition performance can not be assessed in this study because initial acquisition training was observational (i.e., the category label was presented along with the training stimulus), and thus no response was required, the transfer advantage for spaced observational training is interesting and is likely related in some sense to the multiple-unit training used in the current study. As with the Spiering and Ashby result future work should determine whether this effect holds when feedback is removed during transfer as a true test of the permanence of the learning. Thus, it appears that generalization advantages might emerge for other types of acquisition training and might not be constrained only to cases in which a multiple-unit representation is required. In fact, we deem this likely.

Training and Clinical Implications

The implications of this work for training, neurorehabilitation, and clinical assessment should not be overlooked. First, the procedural-based system is critically involved in acquisition and generalization for complex categorization problems such as the interpretation of medical imaging, the reading of sophisticated instrumentation, the diagnosis of complex illnesses, the identification of threats to security, etc, yet little is known about the effects of different training regimens. The current study takes a first step toward addressing these issues and suggests that categorization training that builds a multiple-unit representation facilitates generalization. As just one example, these data suggest that when training radiologists to identify benign versus malignant tumors it would be advantageous to select training samples that cluster into disparate subgroups, with x-rays within each subgroup being highly similar, but dissimilar from x-rays in the other subgroups. Second, measures of procedural-based categorization are largely absent from clinical assessment batteries, whereas one popular rule-based categorization task (the Wisconsin Card Sort Task; WCST) has been used extensively. The lack of procedural-based categorization measures exists despite the plethora of evidence that striatal functioning is impacted in Parkinson's Disease, Huntington's Disease, and normal aging (Ashby, Noble, Filoteo, Waldron, & Ell, 2003; Filoteo & Maddox, 1999, , 2004; Filoteo, Maddox, & Davis, 2001a, , 2001b; Filoteo, Maddox, Ing, Zizak, & Song, 2005; Filoteo, Maddox, Salmon, & Song, 2005; Filoteo et al., 2005; Maddox & Filoteo, 2001, , 2005, , 2007; Maddox, Filoteo, Delis, & Salmon, 1996; Maddox, Filoteo, & Huntington, 1998). In fact, in a recent study (Filoteo, Maddox, Salmon, & Song, 2007) we showed that performance in non-demented Parkinson's disease patients on an information-integration task that required a multiple unit representation was highly predictive of future cognitive decline, whereas the number of perseverative errors on the WCST (a rule-based task) was not predictive. In contrast, their performance on a task that required fewer SPC units was not predictive of cognitive decline. Finally, some neuropsychological disorders (e.g., Alzheimer's disease) do not impact the procedural-based system, which opens the possibility of rehabilitation approaches that emphasize the intact procedural-based learning system (Schacter, Rich, & Stampp, 1985). Thus, a deeper understanding of procedural-based acquisition and generalization could facilitate the success of neurorehabilitation by identifying the sub-processes that can replace damaged learning processes in various patient groups (Krakauer, 2006), and the optimal conditions under which procedural-based learning processes should be implemented. Taken together, these findings suggest that tasks that tap the procedural-based system might provide more useful clinical assessment tools than those that are currently used.

Conclusions

Two studies provided strong support for the hypothesis that the need for a multiple-unit, as opposed to a single-unit category representation lead to worse initial acquisition, a performance increase from acquisition to generalization, and better no feedback generalization. We argue that some category structures or more conducive to the need for a multiple-unit representation and that under these condition initial category acquisition is slowed but transfer is enhanced. In line with other models, such as SUSTAIN, we speculate that acquisition is slower because it is more taxing on the system to train multiple units, however during transfer a multiple-unit representation increases the likelihood that a novel stimulus would activate at least one of the multiple units needed to represent the category enhancing transfer performance.

Appendix

Procedural-Based Category Learning Models

The SPC-1, SPC-2, SPC-4, and the optimal model were applied to the data separately from each participant. The SPC-1 assumes that there is one striatal “unit” in the length-orientation space for each category, yielding a total of four striatal units in Experiment 1 and two striatal units in Experiment 2. The SPC-2 assumes that there are two striatal “units” in the length-orientation space for each category, yielding a total of eight striatal units in Experiment 1 and four striatal units in Experiment 2. The SPC-4 assumes that there are four striatal “units” in the length-orientation space for each category, yielding a total of sixteen striatal units in Experiment 1 and eight striatal units in Experiment 2. Because the location of one of the units can be fixed, and since a uniform expansion or contraction of the space will not affect the location of the resulting response region partitions, the SPC-1 contains six free parameters--5 that determine the location of the units, and one that represents the noise associated with the placement of the striatal units in Experiment 1 and three free parameters in Experiment 2. The noise parameter estimates the variability associated with the participant's responding, with large variability estimates being associated with less deterministic responding and small variability estimates being associated with more deterministic responding. The SPC-2 and SPC-4 models are the same as the SPC-1 model, except that the SPC-2 model assumes that each category has two striatal-category units (14 parameters in Experiment 1 and 6 parameters in Experiment 2), and the SPC-4 model assumes that each category has four striatal-category units (30 parameters in Experiment 1 and 14 parameters in Experiment 2). The optimal model assumes optimal placement of the decision bounds and contains only the single noise parameter.

Hypothesis-Testing Models

Three conjunctive hypothesis-testing models were applied to the data from Experiment 1. The conjunctive(1) model assumes that the participant makes one decision about the length of the line (short or long), a separate decision about the orientation of the line (shallow or steep), and then integrated this information post-decisionally (i.e., after deciding whether the line is short or long and after deciding whether the orientation is shallow or steep). The model assumes that the participant used the following decision rule: Respond A if the line length is short and the orientation is shallow, Respond B if the line length is short and the orientation is steep, Respond C if the line length is long and the orientation is shallow, and Respond D if the line length is long and the orientation is steep. This model has three free parameters--two decision criteria parameters and a noise parameter that estimates the variability associated the participant's trial by trial memory and application of the decision criteria. The conjunctive(2) model instantiates an “extreme values” type of decision rule. This model assumes that the participant sets two criteria along the length dimension that partitions the length dimension into three regions. The model assumes that the participant sets a criterion along the orientation dimension that is invoked only when the perceived length falls into the intermediate length region. The model assumes that the participant used the following rule: Respond B if the length is short, respond C if the length is long, if the length is intermediate then respond A if the orientation is shallow, and Respond D if the orientation is steep. The conjunctive(3) model is similar. This model assumes that the participant sets two criteria along the orientation dimension that partitions the orientation dimension into three regions. The model assumes that the participant sets a criterion along the length dimension that is invoked only when the perceived orientation falls into the intermediate orientation region. The model assumes that the participant used the following rule: Respond A if the orientation is shallow, respond D if the orientation is steep, if the orientation is intermediate then respond B if the line is short, and Respond C if the line is long. The conjunctive(2) and conjunctive(3) models contain four parameters--three criteria and the noise parameter.

Two conjunctive and two uni-dimensional hypothesis-testing models were applied to the data from Experiment 2. Both conjunctive models assume that the participant makes one decision about the length of the line (short or long), a separate decision about the orientation of the line (shallow or steep), and then integrated this information post-decisionally (i.e., after deciding whether the line is short or long and after deciding whether the orientation is shallow or steep). One version assumes that the participant responds A to all short, steep angle lines and B to all other lines, and the second version assumes that the participant responds B to all long, shallow angle lines and A to all other lines. Both models have three free parameters. The unidimensional length model assumes that the participant sets a criterion along length and ignores orientation and generates one response to short lines and the other response to long lines. The unidimensional orientation model assumes that the participant sets a criterion along orientation and ignores length and generates one response to shallow angle lines and the other response to steep angle lines. Both models have two free parameters.

The random responder model assumes a fixed probability of responding “A”, “B”, “C” and “D”. In Experiment 1 the model has 3 free parameters to denote the predicted probability of responding “A”, “B”, or “C” with the probability of responding “D” equal to one minus the sum for the other three categories. In Experiment 2 the model has one free parameter to denote the predicted probability of responding “A”.