A treatment planning methodology for sequentially combining radiopharmaceutical therapy (RPT) and external radiation therapy (XRT)

Abstract

Purpose

Effective cancer treatment generally requires combination therapy. The combination of external beam therapy (XRT) with radiopharmaceutical therapy (RPT) requires accurate 3-D dose calculations to avoid toxicity and evaluate efficacy. We have developed and tested a treatment planning methodology, using the patient-specific 3-dimensional dosimetry package 3D-RD, for sequentially combined RPT/XRT therapy designed to limit toxicity to organs at risk.

Methods

The biological effective dose (BED) was used to translate voxelized RPT absorbed dose (D_RPT) values into a normalized total dose (or equivalent two-Gray-fraction XRT absorbed dose), NTD_RPT map. The BED was calculated numerically using an algorithmic approach, which enabled a more accurate calculation of BED and NTD_RPT. A treatment plan from the combined Samarium-153 and external beam was designed which would deliver a tumoricidal dose while delivering no more than 50 Gy of NTD_sum to the spinal cord of a patient with a paraspinal tumor.

Results

The average voxel NTD_RPT to tumor from RPT was 22.6 Gy (1-85 Gy range); the maximum spinal cord voxel NTD_RPT from RPT was 6.8 Gy. The combined therapy NTD_sum to tumor was 71.5 Gy (40-135 Gy range) for a maximum voxel spinal cord NTD_sum equal to the maximum tolerated dose of 50 Gy.

Conclusions

A methodology which enables real time treatment planning of combined RPT-XRT has been developed. By implementing a more generalized conversion between the dose values from the two modalities and an activity-based treatment of partial volume effects, the reliability of combination therapy treatment planning has been expanded.

I. INTRODUCTION

Effective cancer treatment generally requires combination therapy. Combined external beam therapy (XRT) with radiopharmaceutical therapy (RPT) treatment for metastatic patients presents a possible advantage by providing localized high absorbed dose to the region of visible tumor, while at the same time enabling treatment of less-discernable distributed tumor sites. This treatment combination requires accurate 3-D dose calculations to avoid toxicity and evaluate efficacy. Using patient data from a phase I/II trial and the dosimetry software package, 3D-RD, we have developed and tested a methodology for sequentially combined RPT/XRT treatment planning focused on limiting toxicity to organs at risk.

The starting point for integrating RPT and XRT is recognizing that RPT and XRT absorbed doses are not Gray-for-Gray equivalent and can be expected to have different biological effects due to differing dose rates; each fraction of the XRT delivered dose being essentially instantaneous with multiple fractions being delivered over time, and the RPT dose delivered over an extended period of time as the activity distributes and decays. Using the biological effective dose (BED) formalism (1, 2), the RPT absorbed dose (D_RPT) can be converted to BED and then to XRT two-Gray-fraction-equivalent absorbed dose (NTD_RPT, where the RPT in the subscript indicates the origin of the dose, as opposed to D_XRT, absorbed dose from XRT; and NTD stands for normalized total dose, the conventional appellation of two-Gray-fractionated absorbed dose).

Previous studies (3, 4) have shown how absorbed doses from these two treatment modalities may be combined by converting absorbed dose values to BED values. The methodology presented here is based on this prior formalism, but has been extended to allow for a wider variability in pharmacokinetic input (i.e., dose-rate kinetics are not limited to a decreasing monoexponential function (5)) and for the conversion of results into an absorbed dose map that is radiobiologically consistent with that obtained from external beam. In radionuclide imaging, inherent limitations on the resolution of imaging devices lead to a smoothing of the true spatial activity distribution. In concentrated, high activity areas, this leads to a “spill-out” (or partial volume (PVE)) effect in which regions adjacent to the high activity region appear to have activity concentrations that exceed the true concentration. These effects are then propagated to the absorbed dose distribution, via the Monte Carlo simulation. Therefore an activity-based correction on the activity distribution is implemented (6, 7).

Treatment planning for external beam radiotherapy has a long and well-established history. In comparison, such methodologies have only recently been introduced for radionuclide therapy (8, 9). This study describes a first step towards an integrated treatment planning approach combining these two therapeutic modalities.

II. METHODS

¹⁵³Samarium

The active agent used in this study, Samarium-153 ethylenediaminetetramethylene phosphonic acid (¹⁵³Sm-EDTMP) is a bone-seeking radiopharmaceutical designed to selectively deliver radiation to osteoblastic skeletal metastases (10). The radioisotope ¹⁵³Sm emits an electron (β⁻ particle) with an average energy of 224 keV (approximate range of 0.5 mm), which is appropriate for targeted cytotoxicity. It has a half-life of 46.3 hours and its photon emissions include a 103 keV photon with 28.3% abundance, which was used for quantitative imaging. The use of ¹⁵³Sm-EDTMP for palliative treatment of bone metastases from a variety of carcinomas is well established and its therapeutic value for patients with osteosarcoma is being investigated (11, 12).

Procedure

The 3D-RD combination of RPT and XRT treatment planning is a multi-step process. The individual steps are described in detail below.

1. Data Acquisition

After administration of 16.7 GBq of ¹⁵³Sm, SPECT/CT images from two different time points (4h, 48h) were acquired. The SPECT images were reconstructed using the QSPECT method developed by He et al. (13), based on the iterative ordered-subsets expectation-maximization algorithm (30 iterations, 16 subsets per iteration) (14) with reconstruction-based compensation for attenuation, scatter, and the collimator-detector response function (CDRF). The attenuation was modeled using measured CT- based attenuation maps. Scatter compensation was performed using a fast implementation of the effective source scatter estimation method (15). Point sources at various distances from the face of the collimator were simulated to estimate the distance-dependent CDRF that included interactions and penetration of photons in the collimator and detector.

Camera saturation was accounted for by applying an exponential response function instead of a linear sensitivity value to the counts in each projection image:

$$C(A)=a{\mathit{Ae}}^{-bA}$$ (1)

The exact values for the response were obtained by imaging a flat phantom (16) used in the context of 2-dimensional imaging (a = 43060 cps/GBq, b = 0.715 GBq^-1, R² value > 0.99).

2. Co-registration

The reconstructed SPECT images were registered to each other across time by registering the CT portion of the SPECT/CT images on a HERMES (HERMES Medical Solutions; Stockholm, Sweden) workstation. The images were then loaded into the 3D-RD software (6, 17).

3. VOI determination

A co-registered CT image was loaded into the XRT treatment planning software, Philips Pinnacle³ Radiation Treatment Planning System (Koninklijke Philips Electronics; Eindhoven, Netherlands), where contours for the tumor VOI and the radiation sensitive dose limiting VOI, in this case the spinal column, were drawn by the radiation oncologist. A baseline intensity modulated radiation therapy (IMRT) treatment plan was also designed based on delivering a dose of 30 Gy to 90% of the tumor voxels, while minimizing the dose to the spinal column.

4. Spill-out (PVE) correction

The SPECT co-registered activity images and a co-registered CT image were imported into the 3D-RD software package and the VOI map was imported from Pinnacle. Clinical cases where target VOIs, generally tumors, and sensitive VOIs (in our case, the spinal cord) exist in close proximity to each other present a particular problem: the dose estimation can be skewed in sensitive regions due to high measured activity artificially created in the SPECT or PET emission images due to spill-out (PVE), miss-registration, and/or miss-identification of sensitive VOIs (3, 4). To first order, it can be assumed that all activity in excess of the background amount in the sensitive VOI is due to spill-out. Using an approach described earlier (6, 7), the activity in the spinal column voxels which are proximal to the tumor VOI are replaced with the background activity values taken from areas of the spinal column VOI not immediately adjacent to regions of high uptake.

5. 3D-RD Monte Carlo

A more complete description of 3D-RD has been given in detail elsewhere (6, 17, 18), briefly: using Electron Gamma Shower (EGS) Monte Carlo (MC) software, ten million events were run for the β^- and photon components of the ¹⁵³Sm decay spectra based on the SPECT images for each time point. The energy deposition distribution from the contributing components from MC were weighted for probability and activity and converted to absorbed dose rate for the VOIs (spectra probability distributions obtained from LBL/Lund web site (19)).

6. RPT absorbed dose calculations (D_RPT)

Using the dose rates calculated from the Monte Carlo output at the two time points, a functional fit was made for the VOIs as a whole and for the individual voxels. A monoexponential fit of the form:

$$\dot{D}(t)={\dot{D}}_0{e}^{-\lambda t}$$ (2)

was considered and the effective decay constant, λ, was calculated for each fit. If the decay constant was physical (λ > λ_φ, where λ_φ is the decay constant for ¹⁵³Sm equal to 0.01498 h^-1) the fit consisted of a linear fit between the origin and the first time point, followed by the monoexponential decay (see figure 1). If the decay constant was non-physical, a line was drawn between the two time points and an exponential tail with the ¹⁵³Sm physical decay constant, λ_φ, was implemented after the second time point. The resulting area under the curve was calculated as absorbed dose. The calculation was performed both on a voxel level, thereby accounting for density and kinetic differences amongst voxels, and also on a whole VOI level.

Figure 1.

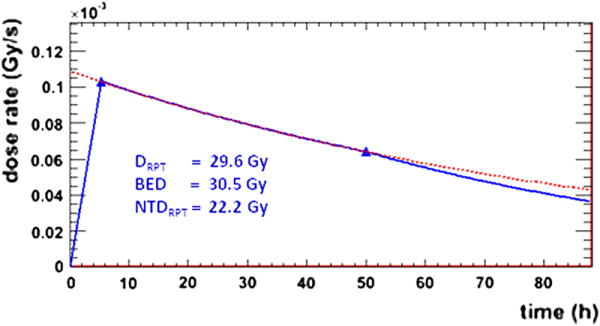
dose rate plots for the tumor VOI. The blue triangles show the calculated dose rates and the blue lines represent the fit used to calculate the D_RPT. The red dotted line shows the monoexponential fit. The resulting D_RPT, BED, and NTD_RPT values are also shown.

7. Absorbed dose conversion: NTD_RPT

The formula for the BED using RPT is (1, 2):

$$\mathit{BED}=D_{\mathit{RPT}}\left(1+\frac{G(\infty )}{\alpha /\beta }\cdot D_{\mathit{RPT}}\right)$$ (3)

Where α and β are the respective linear and quadratic radiosensitivity coefficients in the linear quadratic equation (20), and G(T) is the Lea-Catcheside G-factor (21, 22). The G-factor is a function of another radiobiological parameter, μ, the DNA repair rate, assumed exponential. The generalized expression of the G-factor is:

$$G(T)=\frac{2}{D_{\mathit{RPT}}^2}\cdot \underset{0}{\overset{T}{\int }}{\dot{D}}_{\mathit{RPT}}(t)dt\underset{0}{\overset{t}{\int }}{\dot{D}}_{\mathit{RPT}}(w)\cdot e^{-\mu (t-w)}\mathit{dw}$$ (4)

For a monoexponential fit to the dose rates, this factor reduces to the formula:

$$G(\infty )=\frac{\lambda }{\lambda +\mu }$$ (5)

A period of uptake is expected for most organs and tumors, resulting in kinetics curves that are not well-modeled by monoexponential decay. On a voxel basis the kinetics rarely satisfy a mono- or double exponential relationship. In these case, the BED is most easily obtained by numerical integration (5).

The values used for the radiobiological parameters were α/β = 5.4 Gy and μ = 1.73 Gy^-1 for osteosarcoma (23), and α/β = 3.33 Gy (24) and μ = 0.46 Gy^-1 for the spinal cord (3).

The BED formula for XRT is:

$$\mathit{BED}=D_{\mathit{XRT}}\left(1+\frac{D_{\mathit{XRT}}/N}{\alpha /\beta }\right)$$ (6)

where N is the number of fractions of dose d, in Gray, with D_XRT = Nd. By combining Equations (3) and (6), a conversion formula for D_RPT to ${\mathit{D}}_{\mathit{RPT}}^{\mathit{dGF}}$ is derived, where ${\mathit{D}}_{\mathit{RPT}}^{\mathit{dGF}}$, is the absorbed dose from RPT in values consistent with XRT delivered in d Gray fractions:

$$D_{\mathit{RPT}}^{\mathit{dGF}}=\frac{D_{\mathit{RPT}}(\alpha /\beta +G(\infty )\cdot D_{\mathit{RPT}})}{(\alpha /\beta +d)}$$ (7)

For different treatments, different d values are used; a value of d = 2 Gy for therapy is not uncommon and was the value used in this paper; consequently, the notation used will henceforth be NTD_RPT, where NTD stands for normalized standard dose.

8. Combination treatment planning

The NTD_RPT maps were imported into Pinnacle and added to the pre-established (step 3) external treatment plan (NTD_XRT) multiplied by a factor, k, such that the highest total voxel absorbed dose NTD_sum in the sensitive region is equal to the maximum tolerated dose (MTD) for that organ, in the present case equal to 50 Gy for the spinal cord. The mathematical formulation of this process is given by:

$$\{\begin{array}{l}{k}_i=\frac{\mathit{MTD}-{({\mathit{NTD}}_{\mathit{RPT}})}_i}{{({\mathit{NTD}}_{\mathit{XRT}})}_i}\\ k=\min \left\{k_i\right\}\end{array}$$ (8)

where for each voxel indexed by i, the scale factor k_i is calculated which delivers the MTD, given a baseline NTD_XRT value from XRT of (NTD_XRT)_i and a NTD_RPT value from RPT of (NTD_RPT)_i The smallest of all k_i values is taken as the definitive scale factor, k.

Note that this specific formulation is necessary for serial organs such as the spinal column, where the MTD limit is placed on each voxel. For parallel organs at risk, a single value k for the entire organ may be substituted. Second, should the MTD constraint be placed on BED rather than NTD_XRT, a simple conversion (Eq. 6) can be applied to the MTD to convert the value to an NTD_XRT equivalent MTD.

Finally, the total absorbed dose for each voxel is given by:

$${\mathit{NTD}}_{\mathit{sum}}={\mathit{NTD}}_{\mathit{RPT}}+{\mathit{kNTD}}_{\mathit{XRT}}$$ (9)

where the NTD_RPT component has already been delivered and NTD_XRT is the original baseline external beam absorbed dose component (from step 3). The total absorbed dose that will be delivered by external beam in this scenario is k NTD_XRT.

Clinical Case

The patient was a 21-year-old male with a four year history of osteogenic sarcoma. After multiple rounds of chemotherapy and surgery, including resection of two vertebrae, the patient was enrolled in a phase I trial of ¹⁵³Samarium (44.4 MBq/kg) in high risk osteogenic sarcoma (25), as well as in a high dose (222 MBq/kg) ¹⁵³Samarium protocol with peripheral blood stem cell support. Subsequently, the patient was considered for additional external beam radiotherapy, at which point the issue of potential toxicity to the spinal column from combined treatment was raised. However the patient elected palliative care closer to home and the XRT was not administered.

III. RESULTS

RPT absorbed dose calculations

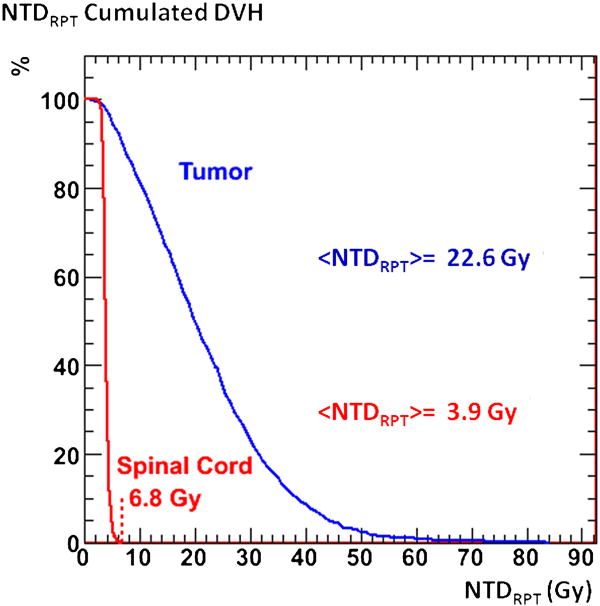
Figure 1 shows the dose rate kinetics curve from ¹⁵³Sm RPT for the tumor VOI considered as a single unit. The corresponding absorbed dose, D_RPT, to the tumor VOI is 29.6 Gy. The voxel-averaged absorbed dose, (D_RPT), is 29.2 Gy, the small difference reflecting the impact of density and kinetic variations within the tumor VOI. The spinal cord is not considered as a single unit since the toxicity is based on the highest dose to a single voxel. The voxel-averaged absorbed dose, (D_RPT), to the spinal cord is 5.8 Gy. Applying Equation (7) to the voxelized results gave average voxel normalized total doses, (NTD_RPT), from RPT, of 22.6 Gy and 3.9 Gy for the tumor and spinal column, respectively, with a maximum spinal cord voxel dose of 6.8 Gy. These results are illustrated in the form of cumulated dose volume histograms (DVHs) in Figure 2.

Figure 2.

cumulated dose volume histograms for the NTD_RPT values in the tumor and spinal cord calculated in 3D-RD from ¹⁵³Sm.

Combined treatment planning

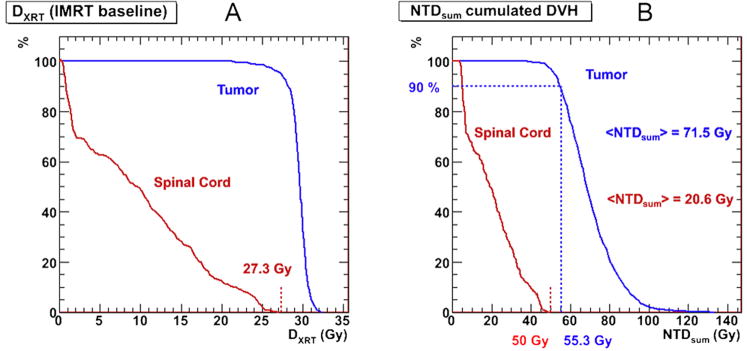
The voxelized NTD_RPT results are combined with the absorbed doses from the IMRT treatment plan, kNTD_XRT scaled to deliver a maximum of 50 Gy combined NTD_sum to the spinal cord by using Equation (8). Figure 3a shows the cumulated DVHs for the baseline IMRT treatment plan, while figure 3b shows the cumulated DVHs for the combined RPT plus scaled IMRT treatment plan. The value calculated for the k-factor for the combined plan was 1.64. Applying this factor to the baseline XRT plan and summing the two dose distributions resulted in average voxel (NTD_sum) values of 71.5 Gy and 20.6 Gy for the tumor and spinal column, respectively. Figure 4 shows the NTD_sum isodose contours as well as the VOIs as defined in Pinnacle and used in the 3D-RD calculation.

Figure 3.

cumulated dose volume histograms for the (a) baseline IMRT NTD_XRT values, and (b) the combined therapy NTD_sum, in the tumor and spinal cord. In figure 3b, the blue dotted lines show that 90% of the tumor VOI receives 55.3 Gy of combined dose.

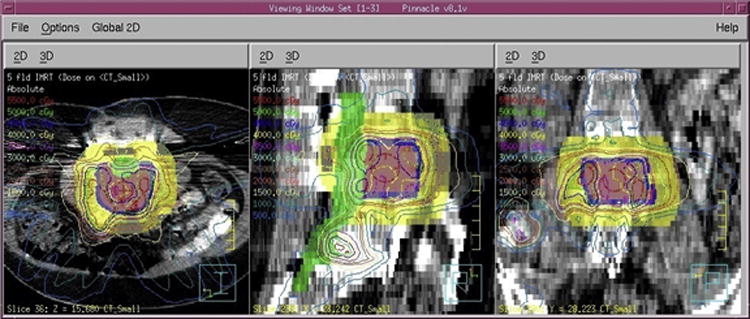
Figure 4.

Isodose contours in Pinnacle showing the combined therapy treatment plan. Pink is the planning tumor volume (PTV) and the volume used in the 3D-RD calculation, blue is the additional gross tumor volume (GTV), green is the contour identifying the spinal cord as the sensitive volume, and yellow an artificial VOI used to confine the D_XRT to the GTV, often called a “ring”.

IV. DISCUSSION

Sequence of treatments

In this case example, RPT has already been administered and dosimetry to scale the XRT plan is needed to limit the combined treatment toxicity. Other scenarios may be envisioned where the order is reversed, XRT having been implemented and an imaging/dosimetry tracer study of the radiopharmaceutical would be performed to determine the activity level for the RPT. In either scenario, for a clinical implementation, the methodology should include use of a fixation device or mold that would insure reproducible positioning of the patient and all images should be registered to the CT associated with the second treatment (i.e., either XRT or SPECT/CT for RPT).

The time frame for the sequence of treatments was intended to be 2-3 weeks between RPT and XRT, where the assumption is that of a worst case scenario where no long-term gross tissue repair to normal organs takes place in the time between treatment modalities. For longer intervals, this assumption may not be reasonable and a combined therapy model which incorporates gross tissue repair may be considered as preferable. Note also that the formula used for the BED and dose conversion does not account for proliferation and assumes that the RPT radiation is effective through complete decay. Revisions to the BED formulation that account for proliferation have been published (26, 27) and could be used as an alternative, although the spatial distribution of cell proliferation (i.e: at the voxel level) is unlikely to be uniform and this would not to be taken into account.

Activity spill-out

As figure 4 shows, the entire vertebral body was considered to be diseased; consequently a large interface between tumor VOI and sensitive VOI is present along with a very high potential for toxicity, both real and artificially perceived from activity spill-out. The estimation of absorbed dose to the spinal cord depends on the method of dealing with spill-out activity from the tumor region. Figure 5 shows the cumulated DVH for the tumor and spinal cord calculated in 3D-RD if no activity corrections are made, which results in NTD_RPT values that are close to the MTD in the spinal cord and if taken at face value would severely limit the amount of XRT available to the patient. However, not all of the dose to the spinal VOI can be attributed to erroneously located activity; consequently a simple cut on dose, i.e. eliminating the dose in the sensitive VOI, can seriously underestimate the amount of absorbed dose to the spinal column. Applying a correction at the level of activity rather than absorbed dose makes it possible to account for the dose to the sensitive volume arising from adjacent tumor activity (and spinal cord background activity).

Figure 5.

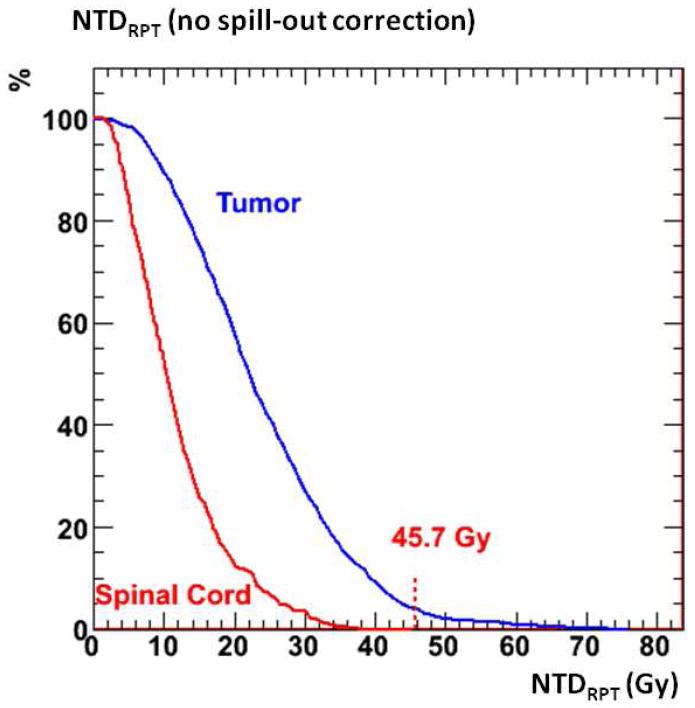
cumulated dose volume histograms for the NTD_RPT values in the tumor and spinal cord from a 3D-RD calculation with no activity spill-out correction.

For this particular isotope with a relatively low energy β particle and very low photon energy, the elimination of artificial spill-out activity within spinal cord resulted in a relatively low absorbed dose (< 8 Gy); for other isotopes this value could potentially increase quite considerably.

Superior methods of redistribution of activity from PVE are available (28), which relocate the spill-out activity to their source. However, such methods are not universal and their practical application carry other constraints such as an assumed homogeneity of tumor activity (clearly not the case for osteosarcoma (25)), or simple geometries of the tumor VOI (not the case here either).

Patient safety issues and potential adjustments

Because of the importance of limiting toxicity and the uncertainty associated with the radiobiological α/β value, a lower value for the spinal column (α/β= 2 Gy) is often used in XRT and could be considered here for combined therapy.

Similarly, the use of the average value of the non-proximal spinal column activity as a substitute for regions contaminated by spill-out could be altered to allow for greater local variability and thus create a larger safety margin. Alternate values could be: (a) the average background value plus the RMS value, or (b) an activity value in all voxels equal to the maximum voxel value in the sensitive volume not proximal to the tumor. In the present example, scenario (a) would results in an increase of 37% in the proximal activity, with a maximum voxel NTD_RPT of 5.0 Gy (127% of original method value), a k-factor of 1.60 (97.6%), and an average tumor (NTD_sum) of 70.3 Gy (98.3%). For the second option those values became: an increase of 109% in spinal activity, a maximum voxel NTD_RPT of 7.0 Gy (178% of original method value), a k-factor of 1.52 (92.9%), and an average tumor (NTD_sum) of 68.0 Gy (95.1%). In those cases in which the activity concentration in a particular normal organ differs from one part to another, when there is no evidence of disease, care should be taken in implementing this methodology;a possible approach would be to use scenario (b).

Voxel resolution

The figures shown in this paper (Figure 4) are not of superior resolution and visual quality. The CT image portion of the SPECT/CT is often acquired at a greater resolution (512×512 matrix) as opposed to the emission images (generally 128×128). Superimposing absorbed dose results on high resolution CT mages can create a false sense of the accuracy and resolution of the RPT data (and most often of the IMRT treatment plan) which can only be calculated at the emission data resolution with any pretense at accuracy. Even at this low resolution (4.4 mm per voxel side), uncertainties at the voxel level are important – from attenuation, scatter, patient motion, registration, and spill-out. It has been noted that for objects of size or distances between VOIs smaller than the SPECT resolution (6, 7), more accurate dosimetry may be obtained by modeling the uptake and energy deposition. Clearly this is the necessary direction for future combined treatment planning.

Anatomically, the spinal cord is surrounded by cerebrospinal fluid (CSF), which provides a cushion of protection. This CSF barrier is not present in the treatment plan (Figure 4), yet would be the anatomical feature closest to the tumor and diseased vertebra and consequently receive the most dose from tumor activity. Possibly, the spinal column receives less absorbed dose than calculated in this study, and the effects of the CSF would best be understood through modeling. However, because of the disease outgrowth, assuming a standard depth of CSF between vertebra and spinal cord may also be erroneous, as the disease impinges upon the column, reducing the CSF buffer significantly.

IMRT treatment comparison

For comparison, a simple IMRT treatment plan was calculated by scaling the baseline plan shown in Figure 3a to the spinal column MTD. The voxel-averaged absorbed dose values to the tumor and spinal column were 54.6 Gy and 18.6 Gy, respectively. These compare to 71.5 and 20.6 Gy for the combined plan (Fig 3b). The approximate 17-Gy increase in tumor absorbed dose obtained by combining RPT with XRT belies the relative contribution of RPT in a combined RPT/XRT treatment. Specifically, in XRT optimization methods, the tumor volume as drawn on CT (with some margin added) is traditionally used. This approach makes it difficult to consider the contribution of RPT in a combined treatment plan, since, in addition to targeting the measurable tumor, RPT is also treating systemic or sub-detectable disease that is not accounted for in the DVH, while simultaneously including healthy tissue not targeted by RPT, as in this particular instance where the whole vertebral body was designated as tumor, which lowers the apparent average dose to the VOI from RPT.

BED and dGF

Throughout the course of this study a value of d = 2 Gy for fractionated therapy was chosen. An equivalent procedure can be followed for any chosen d value. For example, a value of d = 3 Gy would result in average voxel 3-Gray-equivalent absorbed doses, $({\mathit{D}}_{\mathit{RPT}}^{\mathit{aGF}})$,of 19.9 Gy and 3.3 Gy for the tumor and spinal column, respectively, with a maximum spinal cord voxel dose of 5.7 Gy. The k-factor would have been 1.67 to deliver no more than the MTD of 50 Gy to the spinal cord. However, 50 Gy of 3-Gy fractionation is not biologically equivalent to 50 Gy of 2-Gy fractionated radiotherapy, and there would be a greater risk of toxicity to the spinal column in this case.

More than a bridge between different absorbed dose systems, the BED is the quantity that reflects the biological effects of the dose and is thus the absolute reference (29); any MTD in radiotherapy ultimately should be defined in BED and the necessary conversions made to and from that quantity. The BED – equivalent spinal column MTD for a 50 Gy NTD MTD would be 80.0 Gy and is only 42.1 Gy of D^3GF. Applying 50 Gy of D^3GF would be biologically equivalent to 59.4 Gy for the spinal cord of NTD and represents a BED of 95.0 Gy.

V. CONCLUSIONS

Important additions to the practical application of combined RPT-XRT treatment have been implemented within the framework of 3D-RD, potentially enabling effective sequential combination therapy.