Initial Status in Growth Curve Modeling for Randomized Trials

Abstract

The growth curve modeling (GCM) technique has been widely adopted in longitudinal studies to investigate progression over time. The simplest growth profile involves two growth factors, initial status (intercept) and growth trajectory (slope). Conventionally, all repeated measures of outcome are included as components of the growth profile, and the first measure is used to reflect the initial status. Selection of the initial status, however, can greatly influence study findings, especially for randomized trials. In this article, we propose an alternative GCM approach involving only post-intervention measures in the growth profile and treating the first wave after intervention as the initial status. We discuss and empirically illustrate how choices of initial status may influence study conclusions in addressing research questions in randomized trials using two longitudinal studies. Data from two randomized trials are used to illustrate that the alternative GCM approach proposed in this article offers better model fitting and more meaningful results.

Introduction

The growth curve model (GCM), or latent curve model (Meredith & Tisak, 1990), has been one of the most widely adopted statistical techniques in longitudinal studies to investigate progression over time (Bollen & Curran, 2005; Duncan, Duncan, & Strycker, 2006). The GCM is particularly instrumental in yielding insightful information on growth (progression or development over a specified period of time). Longitudinal data with repeated measurement of the same variable over a lengthy time interval is most adequate in reflecting growth patterns. Taking advantage of the growth information represented by the repeated measures of the outcome of interest, the GCM treats each of the repeated measures as a function of time to provide a better understanding of growth, or change, across time. The GCM approach is a special case of the mixed-effects (or random-effects, random-regression) model, which is considered a more powerful technique than the repeated-measures Analysis of Variance (ANOVA) or Analysis of Covariance (ANCOVA) (Gueorguieva & Krystal, 2004). More details on mixed-effect models can be found in Hedeker & Gibbons (2006), Gueorguieva & Krystal (2004), Laird & Ware (1982), and Ware (1985).

Conventional growth curve models include all repeated measures on an outcome of interest as the elements of the growth profile to reflect progression. The simplest GCM assumes a linear growth profile that can be represented by two growth factors: the initial status of the growth curve and the growth rate, or trajectory. It is of interest with GCMs to understand the variations of the initial status and growth rate and, furthermore, to identify factors that affect the variations of progression, or developmental pattern, over time. Evaluation of GCMs can be carried out with either the multilevel modeling (MLM) approach (Goldstein, 1987, 1995) or the latent curve analysis (LCA, Meredith & Tisak, 1990), which is also considered a structural equation model (SEM) approach. Both MLM and LCA conceptualize individual growth as a function of time. And both approaches have the capability of modeling systematic individual differences in the growth profile of each individual. The GCM can be considered as a special case of the mixed-effects model using the MLM approach.

In this study, the SEM approach was adopted since it has the advantage over the MLM in model testing and in having the more flexible model specifications needed for hypotheses testing (Chou, Bentler & Pentz, 1998). Relating latent variables to growth curves to investigate progression can be traced back to Rao (1958) and Tucker (1958) and was then further extended by Meredith and Tisak (1990). A major disadvantage of the GCM with SEM approach is that it only allows complete cases to be included in the analysis (Gueorguieva & Krystal, 2004). Dropping cases with missing data from the model may cause biased estimation of measures across time, including measures of the outcome of interest. More detailed information on GCM can be found in Bollen and Curran (2005), Duncan and colleagues (2006), Gueorguieva and Krystal (2004), Hedeker and Gibbons (2006), McArdle and Nesselroade (2003), and Mehta and West (2000). Packaged programs for structural equation modeling, such as AMOS (Arbuckle, 2003), EQS (Bentler, 2004), LISREL (Jöeskog & Söbom, 1993), and Mplus (Muthén & Muthén, 2007), can be used to conduct growth curve modeling.

Conventional application of the GCM treats the baseline data as the initial status of a growth profile. This practice can be less meaningful and even problematic in evaluating the effects of trials in which individuals are randomly assigned to program conditions. The baseline data is typically collected before the intervention. And it is usually expected that all the variables at the baseline, that is, before the implementation of the intervention program, are identical across the program conditions if randomization has been successfully conducted. Comparison on the initial status of growth profiles between program conditions with the conventional GCM approach then simply reflects if participants have been properly assigned to different program conditions. Therefore, including the pre-intervention measure as a part of a growth profile is not meaningful and can be problematic if the purpose is to evaluate program effects.

The purpose of this study is to propose an alternative GCM for randomized trials. To evaluate the effect of a randomized trial, the proposed GCM approach will treat only the post-intervention repeated measures of the outcome of interest as a complete piece of a growth profile, while controlling for the pre-intervention measure of outcome, or baseline response, as a covariate in the GCMs. Excluding pre-intervention measures as part of the growth curve may provide more precise information on changes or progression associated with the intervention and more appropriate parameter estimations for the evaluation of intervention effects. The appropriateness of the proposed alternative application of the GCM for randomized trials will be investigated using data from two longitudinal randomized trials.

Statistical Background

With repeated measures as the unit of analysis to reflect changes within individuals across time, the most fundamental growth curve model (GCM), assuming a linear trend of growth can be expressed as a regression model with the two growth factors the initial status and growth rate, η₀ and η₁, respectively, as predictors. Each repeated measure, y_it for individual i at time t, can be expressed as:

$$y_{it}={\lambda }_{0t}{\eta }_{0i}+{\lambda }_{1t}{\eta }_{1i}+{\epsilon }_{it},$$ (1)

Eq. (1), known as the Within-individual model, indicates that the outcome measure y_it is predicted by η_0i and η_1i; where η_0i and η_1i are the underlying growth factors representing the initial status and linear growth trajectory, respectively. Regression coefficients, λ_0t and λ_1t, are treated as fixed parameters with λ_0t = 1 for all the measurements of y, and λ_1t = t, the time point at which the outcome measure y_it was obtained. Subscript t usually takes the value of 0 to T, where 0 indicates baseline, or the initial observation time point, and time T indicates the T^th follow-up.

To identify factors that may account for the variations of the growth factors, η₀ and η₁, for all the individuals, the following Between-individual model can be specified:

$${\eta }_{0i}={\upsilon }_0+{\gamma }_{01}{\xi }_{1i}+{\gamma }_{02}{\xi }_{2i}+{\zeta }_{0i},$$ (2)

$${\eta }_{1i}={\upsilon }_1+{\gamma }_{11}{\xi }_{1i}+{\gamma }_{12}{\xi }_{2i}+{\zeta }_{1i}.$$ (3)

The η₀ and η₁ factors in Eqs (2) and (3) are the growth factors with means ν₀ and ν₁, respectively. Selected individual level variables, ξ_1i and ξ_2i, are used as predictors to account for the variations of η₀ and η₁ with residuals ζ_0i and ζ_1i, respectively. Variables ξ_1i and ξ_2i in Eqs. (2) and (3) are also known as time-invariant covariates that remain unchanged across all waves of measurement. The γ‘s in Eqs. (2) and (3) are regression weights reflecting the influences of the corresponding factors on the variations of η₀ and η₁.

In randomized trials, program condition, or group membership, is included as a time-invariant covariate in the between-individual models. Flitzmaurice, Laird, and Ware (2004), in discussing analysis of response profiles, which is similar to the GCM approach, suggested that group means on baseline responses should be assumed equal in a randomized trial. This assumption can be implemented in GCM by removing the group variable from the equation associated with η₀ (e.g., Eq. (2)). If ξ_1i is reserved as the group variable, it should be removed from Eq. (2).

The Within-individual model (see Eq. (1)) can be further developed to include time-variant covariates that are also measured repeatedly along with the outcome measure y. Including time-variant covariate, Eq. (1) becomes:

$$y_{it}={\lambda }_{0t}{\eta }_{0i}+{\lambda }_{1t}{\eta }_{1i}+{\beta }_i{x}_{it}+{\epsilon }_{it}$$ (4)

where x_it is the time-variant covariate of interest with β_i reflecting the impact of x on y. An equation similar to Eq. (3) can also be developed with β_i parameter as the dependent variable to investigate which time-invariant covariates are critical to account for its variation:

$${\beta }_i={\upsilon }_2+{\gamma }_{21}{\xi }_{1i}+{\gamma }_{22}{\xi }_{2i}+{\zeta }_{2i}.$$ (5)

The γ parameters: γ₂₁ and γ₂₂, represent the effects of cross-level interaction. While the conventional GCM approach involves all repeated measures of the outcome variable including pre-intervention measures (baseline measures) to represent an overall growth profile, the alternative GCM approach proposed for longitudinal randomized trials only uses post-intervention measures to reflect the growth profile. The equation for the within-individual model of the alternative GCM is the same as Eq. (1). However, the pre-intervention baseline measures are no longer considered as the measures of the outcome variables, y. In other words, there are fewer y_it measures in the alternative GCM. For example, it is typical in randomized trials that only one wave of pre-intervention baseline measures and T waves of post-intervention measures are collected. With the alternative GCM, the starting point of the growth profile (y_i0) is the measure at the first wave of post-intervention, or the first follow-up. And the end point of the outcome measures is y_i(T-1) with T being the final follow-up, the T^th wave.

With the baseline measure removed as one of the measures to reflect the growth profile, the alternative GCM can treat it as another time-invariant covariate and include it in Eqs. (2) and (3). More specifically, in the proposed alternative GCM, y_i0, not being part of the within-individual model (see Eq. (1)), is now treated as another time-invariant covariate in the between-individual models:

$${\eta }_{0i}={\upsilon }_0+{\gamma }_{01}{\xi }_{1i}+{\gamma }_{02}{\xi }_{2i}+{\gamma }_{03}{y}_{i0}+{\zeta }_{0i},$$ (6)

$${\eta }_{1i}={\upsilon }_1+{\gamma }_{11}{\xi }_{1i}+{\gamma }_{12}{\xi }_{2i}+{\gamma }_{13}{y}_{i0}+{\zeta }_{1i}.$$ (7)

The alternative GCM proposed in this study is analogous to the analysis of covariance (ANCOVA) approach (Flitzmaurice et al., 2004) since the baseline measure is considered as another time-invariant covariate. ANCOVA is usually a preferred analytical approach for randomized trials (e.g., Cohen, Cohen, West, & Aiken, 2003; Hays, 1994; Shadish, Cook, & Campbell, 2002; Tabachnick & Fidell, 1996). However, concerns have been raised when using ANCOVA in randomized trials, especially in psychosocial studies, in which pre-intervention group differences on covariates usually exist between program conditions (Miller & Chapman, 2001).

Using data from two empirical longitudinal randomized trials, this study compares the results of the conventional and the alternative GCM approaches. Several model fitting indices were used to evaluate the adequacy of the two competing GCM approaches for randomized trials. Although sensitive to the sample size, the goodness-of-fit χ² test statistic provides the most well-grounded statistical criterion. Comparative Fit Index (CFI) (Bentler, 1990) and Root Mean Square Error of Approximation (RMSEA) (Browne & Cudeck, 1993; Sugawara & MacCallum, 1993) offer more empirical standards on the appropriateness of the model. A CFI greater than .90 is considered a good fit, and CFI greater than 0.95 is considered a very good fit (Hu & Bentler, 1999). The RMSEA representing closeness of fit adjusting for sample size and the number of parameters should be less than .05 for a model to be considered to have a good fit (Browne & Cudeck, 1993; Sugawara & MacCallum, 1993).

Methods

Data Sources

Longitudinal data from two randomized trials were used in this study to illustrate the differences between two growth curve modeling conceptualizations. The two approaches basically conceptualize the initial status at a different time point. Both randomized trials only collected one wave of data before the intervention.

Prevention Trial Example (MPP)

The first longitudinal data set was obtained from a randomized prevention trial, the Midwestern Prevention Project (MPP), which involved a total of 57 middle or junior high schools in Indianapolis (Chou et al., 1998; Pentz et al., 1989). Baseline data were collected in the fall of 1987. School was the unit of intervention program assignment and each school was randomly assigned to either a health education program as the control group or a substance use prevention intervention program as the program group. As the primary purpose of the current study is to illustrate model comparisons of two GCM approaches, this paper excludes the 7 middle schools that started at the sixth grade and concentrates only on the 50 junior high schools that started at the seventh grade to simplify the models. The number of schools involved in the model comparisons includes 23 control and 27 program schools. There were more program schools than control schools because schools were randomly assigned to experimental conditions within the same school district, and more schools were assigned to the program group if a district had an odd number of schools. More detail on the MPP project can be found elsewhere (Chou, Montgomery, Pentz, & Rohrbach, 1998; Pentz et al., 1989).

A total of 2,779 seventh grade students were surveyed at the baseline wave. Four post-intervention follow-ups were conducted with the first being 6 months after baseline, and then 1 year apart for the other three follow-ups. At each of the five interviews, students were asked whether they had used cigarettes, alcohol, and marijuana in the past 30 days. School was used as the unit of analysis. Outcome measures considered in the GCMs were school prevalence rates of monthly use of cigarettes, alcohol, and marijuana, which are percentages of students reporting any monthly cigarette use, alcohol use, and marijuana use, respectively. Two school-level covariates were selected to investigate their impact on the progression of prevalence of monthly use of cigarettes, alcohol, and marijuana across time: program condition (PROGRAM=0 for control condition, and PROGRAM=1 for program condition), and school type (TYPE=0 for private school, and TYPE=1 for public school).

Treatment Trial Example (KPNC)

The second longitudinal data set was obtained from a randomized treatment trial of 744 adult individuals admitted to the day hospital versus traditional outpatient program for chemical dependency (CD) treatment within the Kaiser Permanente Northern California (KPNC) system. KPNC is a large, private, non-profit, group-model managed care health plan covering 40% of the commercially insured population of the region. There are approximately 3.4 million members; among them 88% are commercially insured, 10% insured through Medicare, and 2% through Medicaid. The membership is generally employed, middle class, and well educated, with 81% having at least some college education (Gordon, 2004). Both CD and psychiatric services are provided internally.

The study site was the KPNC Chemical Dependence Recovery Program (CDRP) in Sacramento, California. The CDRP provides traditional outpatient (OP) and day hospital (DH) treatment programs. Both are group-based with similar content, including supportive group therapy, education, relapse prevention, and family therapy with individual counseling available as needed, but the DH treatment program was structured to provide four times the intensity of the OP. Patients in the OP program attended a 1½-hour session 3 days a week for 8 weeks (a total of 24 sessions); DH patients attended the program daily for 6 hours during the first 3 weeks, and 4 days per week for 1½ hours per day for the next 5 weeks (a total of 104 sessions). Regular attendance at 12-step meetings off site was expected, and all patients received random breathalyzer and urine screens weekly during the first 4 weeks and monthly thereafter. Aftercare for both programs consisted of one 1½-hour group therapy meeting each week for 10 months, and all patients were encouraged to attend.

Research subjects were men and women aged 18 and older who met the criteria for alcohol or drug abuse or dependence and requested CD treatment at the study site between April 1994 and April 1996. Patients with dementia, mental retardation, or active psychosis were not eligible. Independent research staff conducted the baseline interview, explained the two treatment options, asked subjects to accept random assignment, and obtained informed consent. A total of 744 patients (33% women) agreed to the randomization, with 348 (47%) assigned to the DH arm and 396 (53%) to the OP arm. Interview data were collected at 6 months, 1 year, 5 years, 7 years, and 9 years after intake by telephone, with response rates of 79%, 85%, 78%, 71%, and 68%, respectively. Institutional review board approval has been continually obtained from the Kaiser Research Foundation Institute and the University of California, San Francisco. Detailed description of the programs and the study has been published elsewhere (Weisner et al., 2000; Weisner, Ray, Mertens, Satre, & Moore, 2003).

Measures

Prevention Trial (MPP)

Main outcome measures for the MPP intervention trial are the percentage of students reporting any cigarette, alcohol, or marijuana use in the past 30 days (or prevalence of monthly cigarette, alcohol, or marijuana use, respectively) in each school. Two school-level, or time-invariant, covariates were selected to investigate their impact on the progression of prevalence rates of monthly use of these three types of substance at the school level across time: group membership (PROGRAM=0 for control group and PROGRAM=1 for program group), and school type (TYPE=0 for private school and TYPE=1 for public school).

Treatment Trial (KPNC)

The main outcome measure of the KPNC treatment trial was the Addiction Severity Index (ASI), which is frequently used to assess severity of substance use and related problems. The ASI is a valid and reliable instrument (McLellan et al., 1992) that examines the type and severity of alcohol and drug use, as well as the severity of employment, medical, psychiatric, family/social, and legal problems. For each of the problem symptoms, it measures the number, frequency, and duration over the patient’s lifetime and within the past 30 days, and provides a composite score ranging from 0 to 1.00, with the higher scores indicating higher severity. ASI composite scores for drug use, alcohol use, and psychiatric problems were used in this study. To avoid the possibility of obtaining very small values of parameter estimates due to the narrow scale of the ASI, we multiplied the selected ASIs by 100 as the outcome measures to reflect the growth profiles of corresponding problems. We included two variables for the initial treatment episode in the GCMs: (1) treatment modality (0: OP and 1: DH), and (2) the length of stay for the treatment episode. For length of stay, we used data from the health plan’s automated database to measure the number of continuous weeks the patient stayed in treatment before dropping out of the treatment. Other time-invariant covariates included in the GCMs are: age (1: 18–29; 2: 30–39; 3: 40–49; 4: >=50), gender (0: man; 1: woman), employment (0: suspend/unemployed; 1: employed); and college education (0: <college; 1: >= college).

Results

Prevention Trial (MPP)

Prevalence rates of monthly cigarette, alcohol, and marijuana use in the MPP prevention trial across time by program condition are presented in Figure 1. The program and control groups had almost identical prevalence rates of all three types of substance at the baseline. Furthermore, there was no difference on the baseline prevalence rates of the three substances between the groups by school type (public vs. private). The prevalence rates of all three substances were lower for the program group after the intervention program, which was implemented between Time 0 (baseline) and Time 1 (6-month follow-up).

Figure 1.

Prevalence Rates of Cigarette, Alcohol, and Marijuana Monthly Use, the MPP Randomized Prevention Intervention Trial

Results of the application of the conventional GCM (Model A) and the alternative GCM (Model B) proposed in this study on the MPP intervention trial data are summarized in Table 1. With 50 schools and five waves of data for each school, the prevalence rates of monthly cigarette, alcohol, and marijuana use were treated as the outcomes. Estimates associated with growth factors, time-invariant covariates, model fitting information, such as goodness-of-fit test statistics, and comparative fit index (CFI) (Bentler, 1990) yielded by each of the two models for the three substances are presented in Table 1.

Table 1.

Comparison of Conventional GCM and Alternative GCM for the MPP Randomized Prevention Intervention Trial

	Cigarette		Alcohol		Marijuana
	Model A1	Model B1	Model A	Model B	Model A	Model B
Intercept
Mean	11.486 (1.231)**	15.001 (1.536)**	2.965 (.499)**	7.344 (1.024)**	1.960 (.365)**	4.498 (.750)**
PROGRAM	−.631 (2.173)	−3.729(2.134)†	−.719 (.942)	−3.109 (1.877)†	−1.012 (.689)	−2.258 (1.370)†
PUBLIC	7.856 (2.182)**	3.989 (2.143)†	2.030 (.946)*	.665 (1.885)	1.238 (.692)†	3.075 (1.375)*
Baseline as a covariate	N/A	.888 (.133)*	N/A	.651 (.274)*	N/A	.295 (.268)
Slope
Mean	2.370 (.212)**	2.060 (.315)**	3.250 (.196)**	2.962 (.223)**	1.404 (.165)**	1.122 (.192)**
PROGRAM	−.470 (.369)	.177 (.555)	−.582 (.372)	−.086 (.431)	−.415 (.312)	−.012 (.328)
PUBLIC	−1.338 (.371)**	−1.822 (.558)**	−.562 (.373)	−.519 (.432)	.576 (.314 )†	.021 (.329)
Baseline as a covariate	N/A	−.055 (.035)	N/A	−.072 (.063)	N/A	.266 (.064)**
Model fit
Chi-square	30.966	19.064	43.764	21.443	54.171	19.669
df	17	14	17	14	17	14
P-value	0.020	0.163	0.001	0.091	0.001	0.141
CFI	0.891	0.948	0.500	0.956	0.745	0.944
RMSEA	0.142	0.106	0.175	0.056	0.223	0.113

Notes. 1. Model A: GCM with baseline as the initial status; Model B: GCM with baseline as a time-invariant covariate.

^**significant at .01;

^*significant at 0.05;

^†significant at 0.10.

For prevalence of monthly cigarette use, Model A yielded a significant χ² goodness-of-fit test statistic indicating that the model cannot be considered as having an appropriate fit to the data. The alternative model (Model B) with three more parameters than Model A, on the other hand, yielded a nonsignificant χ² test statistic and a much improved CFI indicating a well-fitted model. The estimate of PROGRAM effect (−3.729 with STE of 2.134) on the Intercept (initial status) in the first panel of Table 1 also indicated that PROGRAM has a marginal (p < .10) effect in reducing the initial prevalence rate of monthly cigarette use immediately after the intervention program.

Defining each increment in time to be 6 months apart in the GCM (Model B), the progression of prevalence rate is at 2.060% every 6 months for the CONTROL group with the PROGRAM group having a slightly larger but nonsignificant increase of 0.177%. Model B also yielded better model fitting than Model A, with alcohol and marijuana prevalence rates as outcomes. PROGRAM also consistently showed marginally significant effects in reducing the prevalence rates of alcohol and marijuana use immediately following the intervention. Baseline prevalence rates demonstrated significant positive influence on the immediate post-intervention observation for cigarette and alcohol use (.888 and .651, respectively), but not marijuana use. Another effect of particular interest is the PROGRAM effect on Slope factor. The nonsignificant effects of PROGRAM on Slope indicated that the MPP prevention intervention did not demonstrate significant differential impact on the rate of progression of substance use by the fourth wave of post-intervention follow-up, although there was a trend for the intervention in reducing the rates of progression in alcohol and marijuana (but not cigarette) use.

Treatment Trial (KPNC)

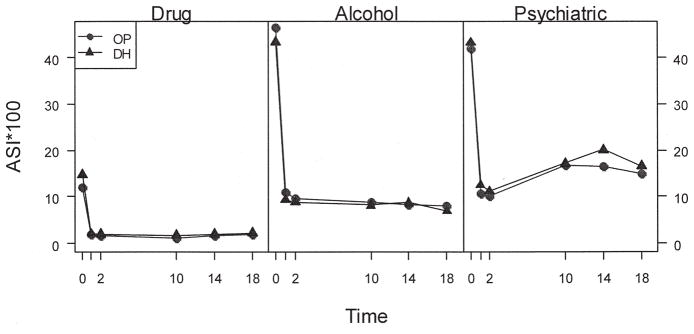
Six waves of repeated measures (baseline, 6-month follow-up, then 1-year, 5-year, 7-year and 9-year follow-ups) were collected in the KPNC randomized trial. The ASIs of drug, alcohol, and psychiatric problems were analyzed for model comparisons. Means of Addiction Severity Index (ASI) multiplied by 100 (ASI×100) for drug, alcohol, and psychiatric problems across time by treatment modality for the KPNC trial are presented in Figure 2. It is clearly demonstrated that the ASI×100 of each problem at the baseline was extremely high relative to the post-treatment measures. Evidently, the baseline measures before the treatment should not be considered in reflecting the progression of the ASI results, which dropped substantially immediately after the treatment. Repeated measures of the ASI of each problem except that of psychiatric problem were quite steady in general after the participants received treatments,. The three growth patterns provide a strong justification that repeated measures of ASIs are not suitable to be treated as a single piece of growth profile.

Figure 2.

Trend of Addiction Severity Indices (ASI) of Drug, Alcohol, and Psychiatric Problems, the KPNC Randomized Treatment Trial

To address the concerns of potential inadequate application of ANCOVA in randomized trials (Miller & Chapman, 2001), differences on covariates between the two program conditions were also examined before the GCMs were developed. Among the five common covariates, age, gender (female), employment, length of stay in treatment, and college education, only employment and college education were significantly different between the two treatment programs, with patients assigned to the outpatient modality having a higher percentage of being college educated and being employed. Among the three baseline ASI measures of drug, alcohol, and psychiatric problems, only the drug use ASI was significantly different between the two treatment programs. With patients being randomly assigned to either modality, the differences in covariates detected were likely to happen by chance. However, we calculated the propensity score and included it as another covariate in the statistical models to adjust for possible pre-existing differences between modalities (Miller & Chapman, 2001) and examined GCMs with and without the propensity score. The propensity score was created as a function of demographics (gender, race/ethnicity, age group, education, employment, income) and outcome measures at baseline. In each of the growth curve models evaluated, the propensity score as a time-invariant covariate did not have significant effects on either growth factor (initial status or growth rate), and results yielded by the models with or without the propensity score were consistent. Thus, only the results for the models without the propensity score are reported below.

Results obtained from the GCMs, which are summarized in Table 2, offered even more substantial contrast between Models A and B for each outcome. For the drug use ASIs across time, results of Model A with the conventional GCM approach yielded a poor model fitting with χ² of 405.639, which is significant at a=.05 level with degrees of freedom (df) of 40. Results from the proposed approach with Model B, however, offered a significantly improved model with χ² of 66.107 with a df of 31. The findings from model comparisons is consistent with the patterns observed in Figure 2, showing that the assumption of the linear trend for all the repeated ASI measurements of drug use starting from baseline, as in Model A, is not appropriate. On the other hand, it is more reasonable to assume that drug ASIs are linearly progressed after treatment. Although Model B is not considered well fitted based on the χ² test statistic, the substantial decrease in test statistic compared with Model A shows that Model B is a more adequate model. Furthermore, both the CFI and RMSEA empirical fit indices indicate that the alternative GCM (Model B) offers an adequate representation of the longitudinal data on drug use problems.

Table 2.

Comparison of Conventional GCM and Alternative GCM for the KPNC Randomized Treatment Trial

	DRUG ASI×100		Alcohol ASI×100		PSY AI×100
	Model A1	Model B1	Model A	Model B	Model A	Model B
Initial Status (intercept)
Mean	2.169 (.217)**	1.883 (.206)**	10.477(.747)**	9.483 (.719)**	14.653 (.843)**	11.873 (.850)**
Baseline	N/A	.117 (.019)**	N/A	.138 (.022)**	N/A	176 (.032)**
Treatment modality	0.680 (.428)	.155 (.393)	−2.913 (1.479)*	−1.937(1.356)	.153 (1.644)	1.060 (1.602)
Age group	−0.912 (.251)**	−.273 (.241)	.757 (.874)	−1.069 (.831)	−.068 (.966)	−.219 (.940)
Woman	.609 (.433)	.755 (.392)†	.226 (1.504)	.652 (1.375)	8.174 (1.667)**	6.374 (1.653)**
Employment	−.048 (.433)	.177 (.392)	.193 (1.497)	−.383 (1.368)	−4.072 (1.661)*	−1.531 (1.649)
Length of Stay	−.015 (.015)	−.016 (.013)	−.203 (.051)**	−.204 (.047)**	−.035 (.057)	−.022 (.055)
Education	.657 (.500)	1.112 (.457)*	.522 (1.732)	−.346 (1.585)	.339 (1.927)	1.783 (1.883)
Progression (Slope)
Mean	−.026 (.016)†	−.005 (.016)	−.148 (.050)**	−.088 (.051)†	.145 (.061)*	.358 (.064)**
Baseline	N/A	−.005 (.002)**	N/A	−.005 (.002)**	N/A	.000 (.003)
Treatment modality	−.009 (.032)	.015 (.032)	.106 (.101)	.073 (.101)	−.006 (.124)	−.032 (.130)
Age group	.046 (.019)*	.019 (.020)	−.152 (.060)*	−.085 (.062)	−.051 (.073)	−.048 (.076)
Woman	.000 (.032)	−.007 (.032)	.158 (.103)	−.182 (.102)†	.056 (.126)	.062 (.134)
Employment	.005 (.032)	−.006 (.032)	−.033 (.102)	−.011 (.102)	.089 (.126)	.044 (.133)
Length of Stay	−.001 (.001)	−.001 (.001)	.004 (.003)	.005 (.003)	−.001 (.004)	−.002 (.004)
Education	−.082 (.037)*	−.108 (.037)**	−.003 (.118)	0.032 (.118)	−0.138 (.146)	−0.182 (.152)
Model Fit
χ2	405.639	66.107	452.386	75.085	405.498	59.443
Df	40	31	40	31	40	31
CFI	0.699	0.955	0.687	0.932	0.814	0.989
RMSEA	0.113	0.049	0.124	0.066	0.095	0.027

Notes 1. Model A: GCM with baseline as the initial status: Model B: GCM with baseline as a time-invariant covariate.

^**significant at .01;

^*significant at 0.05;

^†significant at 0.10.

Estimates from Model B, which are summarized in the second column of Table 2, indicated that baseline drug use ASI has a significant impact (.117) on the initial status (intercept) of the post-treatment drug use ASI measures. Patients in the outpatient (OP) or the day hospital (DH) programs had similar severity of drug use problems immediately following treatment. However, being a woman or having a higher education level was positively associated with severity of drug problems at the 6-month follow-up. The progression of the degree of severity of drug problems decreases, although not significantly, across time at .005 units each 6 months. Results associated with the progression rate showed that drug problem severity at baseline may significantly decrease the progression of the severity of drug problems after receiving treatment. In addition, having some college education was negatively associated with the progression of drug problems after treatment.

Model comparisons on alcohol and psychiatric problems also consistently indicated that the alternative GCM approach (Model B) proposed in this study yielded considerably better fit to the data than the conventional GCM approach (Model A). For both alcohol and psychiatric problems, severity at baseline may significantly increase the corresponding problems 6 months after treatment. There was no significant difference in the severity of either alcohol or psychiatric problems between the OP and the DH treatments after treatment. Severity of alcohol problem at baseline also showed that it may lead to significant decrease on its progression after treatment. Results of Model B for ASI alcohol severity indicated that length of stay in treatment was negatively associated with alcohol problem severity at the 6-month follow-up, but not at later follow-ups. For psychiatric severity, women had significantly higher severity than men following the treatment program. However, no gender difference was found in the rate of progression of psychiatric problems after treatment. This is consistent with findings from prior research that women had greater substance-related and psychiatric severity at baseline, but equivalent psychiatric severity to men at follow-up (Galen, Brower, Gillespie, & Zucker, 2000).

Conclusion

Growth curve modeling as a variant of mixed-effects models (see e.g., Hedeker & Gibbons, 2006) has been one of the most frequently used statistical techniques in longitudinal studies (Bollen & Curran, 2005; Duncan et al., 2006; Meredith & Tisak, 1990). The conventional GCM approach assumes that all the repeated measures in longitudinal studies with multiple waves of follow-up constitute a complete piece of the growth profile. In this article, we proposed an alternative GCM approach for randomized longitudinal trials. The proposed approach suggests that the initial status as one of the growth factors needs to be meaningfully selected in order to accurately address the research question in randomized trials. In order to evaluate the effects of the intervention, the initial status should adequately reflect the beginning point of a progression with a well-defined and theoretically meaningful justification. We empirically illustrated and discussed how choices of initial status may influence study conclusions under randomized trials.

In order to more adequately investigate the effects of randomized trials, analyses usually concentrate on differences of the targeted outcomes across different treatment conditions. The alternative GCM approach we proposed suggests that the baseline measure(s) obtained prior to the implementation of intervention programs in randomized trials should not be considered as part of the growth profile to be evaluated for program effect. Instead, it is more meaningful in randomized trials to examine the growth profile, or progression, constituted by the outcome measures after the interventions have been delivered. Using longitudinal data from two randomized trials, one of a prevention intervention and the other of treatment, we found in our comparison that the alternative approach yielded a significantly better model fitting for both sets of data than the conventional approach. The poor fit of the conventional model may indicate that the linear growth assumption involving all the repeated measures before and after the trial is not appropriate for randomized trials’ longitudinal data since the pattern of natural development may be affected. The new approach, which considers only the post-intervention measures constituting the growth profile, yielded substantially better fit to the data and more reasonable results for evaluation than the conventional approach.

The parameters specified in the alternative approach are more appropriate for interpretation of the trial effects. The parameters associated with the program condition more directly reflect the effects of the trial. By separating longitudinal data in a randomized trial into pre-intervention and post-intervention measures, the proposed GCM is identical to the conceptualization of piecewise GCM, in which repeated measures are divided into several developmental periods (Chou, Yang, Pentz, & Hser, 2004).

It should be noted that the proposed alternative GCM approach, which includes only one wave of the baseline measure, can be considered a special case of piecewise GCM (Chou et al., 2004). The piecewise GCM approach divides all available repeated measures into several pieces, or segments, based on pre-determined developmental periods. With measures of variables of interest collected repeatedly before and after intervention, a two-piece GCM can be developed: one for the pre-intervention period and the other for the post-intervention period. The piecewise GCM can be used to address research questions regarding the relationships among the growth factors before and after interventions. Data from the two empirical longitudinal randomized trials presented in this article only contain one wave of pre-intervention measures; thus, the baseline measure, y, can be considered as the only measure for the first piece of growth profile.

Most research on clinical trials applies longitudinal designs, and recent advances in statistical theory, methodology, and software development enable more proper examination of the data and research questions. This paper proposes an alternative GCM approach that treats the baseline measures as one of the time-invariant covariates and examines the growth profile based on all post-baseline measurements. Researchers should pay special attention in utilizing the techniques and may consider model comparisons with different approaches.

Biographies

Dr. Chih-Ping Chou is a Professor at the Department of Preventive Medicine, Keck School of Medicine, University of Southern California. He has been conducting research in the development and application of statistical and methodological techniques in prevention research.

Ms. Felicia Chi is a senior analyst in the Drug and Alcohol Research Team (DART) at the Northern California Kaiser Permanente Division of Research.

Dr. Constance Weisner is an Investigator at the Northern California Kaiser Permanente Division of Research and a Professor at Department of Psychiatry, University of California, San Francisco.

Dr. MaryAnn Pentz is a Professor at the Department of Preventive Medicine, Keck School of Medicine, University of Southern California. She is also the director of the Institute for Prevention Research. For over 20 years, her research and program development have focused on community and policy approaches to preventing tobacco, alcohol, drug use, and violence in youth.

Dr. Yih-Ing Hser is a Professor-in-Residence at the UCLA Integrated Substance Abuse Programs, Semel Institute for Neuroscience and Human Behavior, David Geffen School of Medicine, University of California, Los Angeles. She has been conducting research in the field of substance abuse and its treatment since 1980. She is the director of the Center for Advancing Longitudinal Drug Abuse Research.