A Marginal Structural Modeling Approach to Assess the Cumulative Effect of Drug Treatment on the Later Drug Use Abstinence

Abstract

In this article, we applied a marginal structural model (MSM) to estimate the effect on later drug use of drug treatments occurring over 10 years following first use of the primary drug. The study was based on the longitudinal data that were collected in three projects among 421 subjects and covered 15 years since first use of their primary drug. The cumulative treatment effect was estimated by the inverse-probability of treatment weighted estimators of MSM as well as the traditional regression analysis. Contrary to the traditional regression analysis, results of the MSM showed that the cumulative treatment occurring over the 10 years significantly increased the likelihood of drug use abstinence in the subsequent 5-year period. From both the statistical and empirical point of view, MSM is a better approach to assessing cumulative treatment effects, considering its advantage of controlling for self-selection bias over time.

Introduction

Research on drug addiction reveals that drug treatment is rarely a one-time event. Instead, many drug-dependent individuals are involved in treatment multiple times over their addiction careers, with treatment episodes being of varying lengths of stay (Hser, Grella, Anglin, Longshore, & Prendergast, 1997). In addition to examining the effects of individual single treatment, researchers have also been interested in whether cumulative treatment effects exist, that is, if beneficial treatment effects result from the multiple treatments accumulated over time (Hser et al, 1997; Hser, Grella, Chou, & Anglin, 1998).

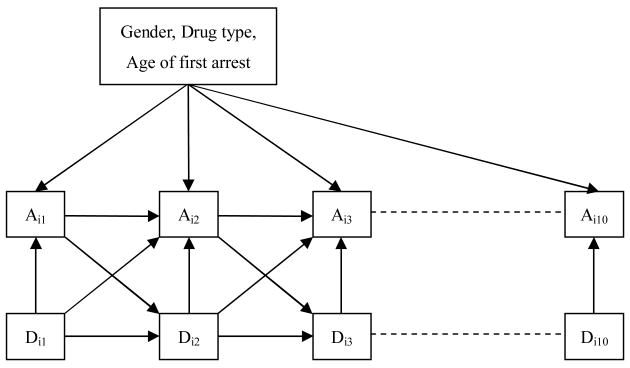
The challenge in assessing cumulative treatment effects in observational studies is that those multiple treatment episodes generally do not stand alone over the life course. Multiple treatments are often the result of drug use and related problems; even though a given treatment may reduce drug use, subsequent drug use may result in additional treatment. As a result, different treatment profiles of subjects may represent or be the result of different dynamic processes. We use Figure 1 to better illustrate this idea.

Figure 1.

Dynamic view on drug use and drug treatment over time points. A_i1, A_i2,…,A_i10 denote the amount of treatments received by the ith subject at each time point, while D_i1, D_i2,…,D_i10 denote the amount of drug use by the subject at each time point.

In Figure 1, A_i1, A_i2,…, A_i10 denote the amount of treatments received by the ith subject at each time point, while D_i1, D_i2,…, D_i10 denote the amount of drug use by the subject at each time point. Some studies have shown that treatment history is an important predictor of subsequent treatment entry (Hser, Maglione, Polinsky, & Anglin, 1998; Schutz, Rapiti, Vlahov, & Anthony, 1994). Other studies showed that drug use and treatment often intertwine with each other into a cyclic career (Hser et al., 1997). As illustrated by the arrows in Figure 1, for the ith subject, the probability of receiving treatments at any given time point (e.g., A_i2) may depend on treatments and drug use at the previous time points (e.g., A_i1, D_i2, D_i1), while drug use at a previous time point (e.g., D_i2) may depend on treatments and drug use at or before that time point (e.g., A_i1, D_i1). In addition, across time, the likelihood of receiving treatment at any given time point may also be influenced by some time-invariant variables, such as gender, primary drug type, or age of first arrest. As a result, the variables measured at baseline, as well as treatment and drug use at each time point, influence the likelihood of treatment involvement and form different treatment profiles of subjects observed in studies.

This dynamic process of drug use and treatment participation over the life course is a realistic reflection of typical addiction careers. However, it poses challenges in statistical methodology when assessing the cumulative effect of those past treatments on drug use outcome (e.g., abstinence) at a later time. One standard approach to this problem is to apply regression analysis to predict the mean of drug use outcome at a later stage as a function of those past treatments. Robins (1986, 1997) has shown that this standard approach may be biased, whether or not one further adjusts for past drug use history or covariates in the analysis, when:

• C1 – conditional on past treatments, a time-dependent variable is a predictor of the subsequent mean of the outcome and also a predictor of subsequent treatments;

• C2 – past treatments are independent predictors of the time-dependent variable.

In this article, we refer to variables satisfying C1 and C2 as time-dependent confounders. For example, for the case illustrated in Figure 1, drug use history (e.g., D_i2) is a time-dependent confounder for cumulative effect of treatments on drug use outcomes at a later stage since it predicts not only subsequent drug use outcomes (e.g., D_i3) but also subsequent treatments (e.g., A_i2, A_i3), and past treatments (e.g., A_i1) are independent predictors of D_i1. Thus, standard regression methods that predict the mean drug use outcome at a later stage using a summary of past treatments up to that stage may produce biased estimates of the causal effect of cumulative treatment whether or not one adjusts for drug use history in the analysis.

To overcome the limitations of this standard approach, Robins and his colleagues developed the marginal structural model (MSM; Robins, 1997, 1999; Robins, Hernan & Brumback, 2000). The advantage of MSM is that it can be adapted to unbiasedly estimate the causal effect of cumulative treatments on later drug use outcomes in the presence of time-dependent confounders that are themselves affected by past treatments (Robins, 1986, 1997; Robins et al., 2000).

Our article is organized as follows. We first review the definitions of causal effect and confounding based on counterfactual outcomes. Then the MSM framework will be introduced and applied to a 15-year longitudinal dataset. The results of MSM will be compared with results from traditional regression analysis and discussion will be presented at the end of the article.

Statistical Background of Marginal Structural Model

To better understand MSM models, we first present a formal definition of causal effect and no unmeasured confounding. Let $\overline{a_i}=(a_{i1},a_{i2},\dots ,a_{i10})$ and $\overline{A_i}=(A_{i1},A_{i2},\dots ,A_{i10})$ respectively denote the potential and observed treatment profiles by the ith subject where a_it and A_it respectively are the potential and observed amounts of treatment received by the ith subject at the tth time point in Figure 1. By this definition, the observed treatment profile $\overline{A_i}$ is the realization of $\overline{a_i}$ observed for the ith subject. Let Y_i denote the observed drug use outcome of the ith subject after the 10^th time point in Figure 1 and let $y_{\overline{a_i}}$ denote the potential or counterfactual drug use outcome of the ith subject with a treatment profile $\overline{a_i}$ after the 10^th time point. Then the subject’s observed outcome Y_i is the counterfactual drug use outcome $y_{\overline{a_i}}$ for the treatment profile $\overline{a_i}=\overline{A_i}$ that the ith subject did indeed receive (consistency assumption). The counterfactual outcome $y_{\overline{a_i}}$, even though generally unobserved, represents a subject’s outcome if the subject, possibly contrary to fact, had been treated with $\overline{a_i}$ rather than his or her observed treatment $\overline{A_i}$.

In statistical literature, the concept of counterfactual outcomes has been introduced and advocated for causal inference by many people (e.g., Neyman, 1923; Robins, 1986; Robins et al., 2000; Rubin, 1974). By this concept, treatment has a causal effect on a subject’s outcome if the counterfactual outcomes of the subject under two or more treatment profiles are different. For example, if treatment has no effect on the drug use outcome of the ith subject, then $y_{\overline{a_i}}=y_{\overline{0}}$ for all ā_i, where $y_{\overline{a_i}}$ is the outcome when the ith subject had been treated with profile ā_i, 0̄ denotes a specific treatment profile with no treatment involved at all and y_0̄ is the outcome when the subject had been assigned to that specific treatment profile 0̄. On the other hand, when treatment effect exists, the difference $y_{\overline{a_i}}=y_{\overline{0}}$ is the causal effect of treatment profile ā_i relative to 0̄. Similarly, $E(y_{\overline{a_i}}-y_{\overline{0}})=E(y_{\overline{a_i}})-E(y_{\overline{0}})$ is the average causal effect of treatment profile ā_i relative to 0̄ in the population. In addition, by the concept of counterfactual outcomes, no unmeasured confounding is defined as

$$y_{\overline{a_i}}\perp \overline{A_i}\mid F_{i0},F_{i1}$$

for all ā_i, where F_i0 denotes those covariates at baseline having the significant effect on treatment participation across time points, and F_i1 denotes all other available covariates at baseline not having such an effect. That is, prior treatment history is independent of the counterfactual outcome given a set of baseline covariates.

Given the definitions, suppose now we have such a model for the mean of $y_{\overline{a_i}}$

$$E(y_{\overline{a_i}})={\beta }_0+{\beta }_1\text{Cum}({\overline{a}}_i)+{\beta }_2{F}_{i0}+{\beta }_3{F}_{i1}$$ (1)

where $\text{Cum}({\overline{a}}_i)={\sum }_1^{10}{a}_{it}$, and β₀, β₁, β₂, and β₃ are the parameters for estimation. The model in (1) is our marginal structural model (MSM) adapted from Robins et al. (2000) and used for our analysis. It is a “marginal” model because it describes the effect of treatment profile ā_i on the marginal distribution of the corresponding counterfactual outcome $y_{\overline{a_i}}$ and is a “structural” model because models like (1) are called structural in the social and behavioral sciences (see Robins et al., 2000). By (1), we see that the average causal effect of treatment profile ā_i relative to 0̄ is $E(y_{\overline{a_i}}-y_{\overline{0}})=E(y_{\overline{a_i}})-E(y_{\overline{0}})$, which under our MSM model in (1) is β₁Cum(ā_i). Given that no other unmeasured confounding (as defined above) and model misspecification are present, the parameter β₁ has a causal interpretation as the mean change of later drug use outcome caused by the cumulative treatment.

Unlike the MSM model in (1), the traditional regression model for the investigation of cumulative treatment effect can be expressed as

$$E(y_{\overline{a_i}}\mid \overline{A_i})={\gamma }_0+{\gamma }_1\text{Cum}({\overline{a}}_i)+{\gamma }_2\text{Cum}(\overline{D_i})+{\gamma }_3{F}_{i0}+{\gamma }_4{F}_{i1}$$ (2)

where $\overline{D_i}=(D_{i1},D_{i2},\dots ,D_{i10})$ and $\text{Cum}(\overline{D_i})={\sum }_1^{10}{D}_{it}$. Notice that since the model in (2) is conditional on $\overline{A_i}$, it follows from the consistency assumption mentioned before that $y_{\overline{a_i}}=Y_i$. So a standard regression model is a model for the conditional mean of $y_{\overline{a_i}}$ given $\overline{a_i}=\overline{A_i}$. Robins et al. (2000) called the model in (2) “standard crude analysis” and pointed out that γ₁ in this analysis will generally not have a causal interpretation like β₁ in (1), even if the model in (2) is further adjusted by some other variables (e.g., drug use history and a set of baseline covariates in our case). This is because $\text{Cum}(\overline{a_i})$ depends on a subject’s entire treatment history including a_i1 = A_i1, and a_i1 = A_i1 may affect the time-dependent confounders, like D_i2, as defined by C1 and C2 before. Thus, given that the fitting model is correctly specified, the standard regression in (2) adjusted for covariates could provide an unbiased estimate of γ₁ but a biased estimate of the causal parameter β₁ because the outcome $y_{\overline{a_i}}$ is confounded with the past treatment history $\overline{A_i}$ in this “standard crude analysis” (see Robins et al., 2000).

Robins et al. (2000) provided the inverse-probability of treatment weighted (IPTW) estimators for β₁ in (1). Let $\text{P}(\overline{a_i}=\overline{A_i}\mid \overline{D_i},F_{i0})$ denote the probability of the ith subject’s treatment profile ( $\overline{a_i}=\overline{A_i}$), given the drug use profile at the same period ( $\overline{D_i}$) and some relevant covariates (F_i0). Let a weight w_i to be defined as

$$w_i=\frac{1}{\text{P}(\overline{a_i}=\overline{A_i}\mid \overline{D_i},F_{i0})}$$ (3)

for the ith subject. Robins et al. (2000) suggested that an unbiased estimation of β₁ can be obtained by using SAS Proc Genmod to fit the standard regression model in (2) with the weight specified as w_i in (3). By performing such model fitting, each subject was assigned a weight w_i equal to the inverse of the conditional probability of receiving his or her own treatment profile.

Robins et al. (2000) provided an intuitive explanation for the rationale of the adjustment described above. It was suggested that the effect of weighting in Proc Genmod is to create a pseudopopulation consisting of w_i copies of the ith subject. That is, if, for a given subject with w_i = 4, the subject contributes four copies of him or herself to the pseudopopulation. Thus this weighting will increase the number of replicates of the subject in the pseudopopulation when the subject has a lower probability of receiving his or her corresponding treatment profile and thus a larger w_i. On the other hand, the weighting will reduce the number of replicates of the subject in the pseudopopulation when the subject has a higher probability of receiving his or her corresponding treatment profile and thus a smaller w_i. Robins et al. (2000) argued that this new pseudopopulation has the following two important properties. First, in the pseudopopulation, unlike the actual population, $\overline{a_i}$ is unconfounded by the measured variables (e.g., $\overline{D_i}$ or F_i0). Second, the expectation $E(y_{\overline{a_i}})$ in the pseudopopulation is the same as in the true study population so that we can unbiasedly estimate the causal effect by a “standard crude analysis” in the pseudopopulation.

Although this explanation is intuitive, Robins et al. (2000) noticed that the weight w_i in (3) can lead to extreme weights that would result in estimates of β₁ with large variance and wider confidence intervals around estimates of β₁ in practice. With this instability, they suggested a stabilized weight sw_i, which was defined as

$${sw}_i=\frac{\text{P}(\overline{a_i}=\overline{A_i})}{P(\overline{a_i}=\overline{A_i}\mid \overline{D_i},F_{i0})}.$$ (4)

The numerator of the weight, which does not depend on the measured variables (e.g., $\overline{D_i}$ or F_i0), was added to minimize the difference between the numerator and denominator. Suppose $\overline{a_i}$ is not confounded by the measured variables (e.g., $\overline{D_i}$ or F_i0), the numerator and denominator will be equal to each other and sw_i = 1. Then each subject contributes the same weight. When $\overline{a_i}$ is confounded, sw_i would vary around the number 1 and tend to be less variable than w_i. As a result, the estimates of β₁ would have smaller variance and the confidence intervals of the estimates would become narrower.

In practice, to estimate sw_i, Robins et al. (2000) specified

$${sw}_i=\frac{\text{P}(\overline{a_i}=\overline{A_i})}{\text{P}(\overline{a_i}=\overline{A_i}\mid \overline{D_i},F_{i0})}=\frac{{\displaystyle \prod _t^{10}}\text{P}(a_{it}=A_{it}\mid A_{i(t-1)},A_{i(t-2)})}{{\displaystyle \prod _t^{10}}\text{P}(a_{it}=A_{it}\mid A_{i(t-1)},A_{i(t-2)},D_{it},D_{i(t-1)},D_{i1},F_{i0})}=\prod _t^{10}{sw}_{it}$$

where sw_it is the stabilized weight at the tth time point, P(a_it = A_it|A_i(t−1), A_i(t−2)) is the individual probability of a_it = A_it given A_i(t−1) and A_i(t−2), and P(a_it = A_it|A_i(t−1), A_i(t−2), D_it, D_i(t−1), D_i1, F_i0) is the individual probability of a_it = A_it given A_i(t−1), A_i(t−2), D_it, D_i(t−1), D_i1, and F_i0. Similarly, the non-stabilized weight w_i can also be expressed as the multiplication of w_it over time points. In practice, the individual probabilities above can be estimated from data by some parametric models (e.g., cumulative logit model). In this article, we followed Robins et al (2000) and adapted cumulative logit model to estimate these individual probabilities. Our cumulative logit models took the following forms

$$\text{Logit}\lfloor \text{P}(a_{it}\le A_{it}\mid A_{i(t-1)},A_{i(t-2)})\rfloor ={\alpha }_{0j}+{\alpha }_1{A}_{i(t-1)}+{\alpha }_2{A}_{i(t-2)}$$

and

$$\text{Logit}\left[\text{P}(a_{it}\le A_{it}\mid A_{i(t-1)},A_{i(t-2)},D_{it},D_{i(t-1)},D_{i1},F_{i0})\right]={\alpha }_{0j}^{\ast }+{\alpha }_1^{\ast }{A}_{i(t-1)}+{\alpha }_2^{\ast }{A}_{i(t-2)}+{\alpha }_3^{\ast }{D}_{it}+{\alpha }_4^{\ast }{D}_{i(t-1)}+{\alpha }_5^{\ast }{A}_{i(t-1)}{D}_{it}+{\alpha }_6^{\ast }{D}_{t1}+{\alpha }_7^{\ast }{F}_{i0}$$

where 1 ≤ j ≤ k_t − 1 and k_t is the total number of categories of A_it (see Appendix for the SAS syntax for these models). Then the individual probabilities can be estimated from the sample and used to calculate sw_it or w_it at each time point and the weights in (3) and (4).

Methods

Data Source

Analyses were conducted based on data from three studies that collected self-reported longitudinal information from substance abusers using the Natural History Instrument (NHI, described below). All studies were conducted in California. We relied on projects with the NHI data to maximize coverage of the drug use and treatment careers, and we selected from each study those subjects who were observed for 15 or more years since first use of their primary drug. Projects included the Methamphetamine Natural History Study (METH; N=155), the Treatment Process Study (TPROC; N=175), and the Treatment Utilization and Effectiveness study (TUE; N=117). The primary drug (i.e., the drug for which the subject was in treatment at the baseline assessment) was methamphetamine for the METH study. The TPROC and TUE studies included subjects recruited from non-treatment settings (emergency rooms, sexually transmitted disease clinics, and jails) and the primary drug type was self-identified. While many of these subjects reported use of drugs other than their primary drug, a separate analysis showed that use of other drugs was generally at a much lower level than the primary drug (Brecht, Huang, Evans, & Hser, 2008).

When data were pooled, 121 subjects (27%) entered treatment within 10 years following first use of their primary drug, while over the same time period, 326 subjects did not enter treatment at all (73%), constituting a total of 447 subjects. In addition, 26 subjects had missing values on the covariate, age at first arrest. When these subjects were omitted, a total of 421 subjects were included in the analysis.

Instruments

The NHI was adapted from instruments designed by Nurco and colleagues (Nurco, Bonito, Lerner, & Balter, 1975) and has been used with various drug-abusing populations. The instrument consists of a set of “static” and a set of “dynamic” forms that permit the capture of longitudinal, sequential data on drug use, drug treatment, employment, criminal involvement, and other behaviors over the life course of the subjects (see McGlothlin, Anglin, & Wilson, 1977, for detailed description). The static forms collect background information on the subject and are administered once during each interview. The dynamic forms are used to collect retrospective and current data on the drug-use history of the subjects as well as data on events that might have shaped or have been shaped by drug use (e.g., drug treatment, crime, incarceration, employment). The dynamic part of the interview consists of the repeated administration of these forms for as many life segments (defined by major changes in behaviors or life events being assessed) as necessary. The NHI has been shown to have generally high reliability; correlation coefficients of inter-variable relationships, based on 46 variables measured at two interviews 10 years apart, ranged as high as 0.86 and 0.90 (Chou, Hser, & Anglin, 1996; Hser, Anglin, & Chou, 1992).

Measures

Our longitudinal data provided a monthly record of primary drug use and treatment participation since age at first use of the primary drug. For our analyses, we aggregated by each year the number of months of primary drug use and drug treatment that were self-reported for the 10 years following first primary drug use to form the drug use and treatment profiles, $\overline{D_i}$ and $\overline{A_i}$ respectively, for each subject. Our outcome variable Y_i is the logarithmic transformed total drug use abstinence of the ith subject and $y_{\overline{a_i}}$ is its counterfactual counterpart. The total drug use abstinence here was defined as the total number of months of no primary drug use and no incarceration (incarceration may force abstinence, but is not an indicator for a voluntarily favorable outcome) between the 11^th and 15^th year of observation. We performed logarithmic transformation on it because of the nonnormality of raw data. To control baseline covariates, F_i0 in (1) and (2) included gender, primary drug type, and age at first arrest. Preliminary logistic regression showed that each of those covariates individually had a significant effect on treatment participation during the 10 years following first primary drug use. In addition, F_i1 for our analysis included other available covariates at baseline: project, race/ethnicity, employment status at baseline, education level at baseline, and age at first use of the primary drug.

Results

Throughout this article, we used .05 level of significance for testing any effect or parameter. Before applying the MSM model, we used our data to verify the time-dependent confounding of drug use over the first 10 years as specified in C1 and C2. First, the total number of months of primary drug use in each year (from the 2^nd to the 10^th year) was regressed on the total number of months of primary drug use and treatment in the previous year. In this regression with robust standard errors, the primary drug use in the previous year always significantly predicted the primary drug use in the next year. At the same time, the treatment participation in the first and second years significantly predicted the primary drug use in the next years. Second, the total number of months of treatment in each year (from the 2^nd to the 10^th year) was regressed by cumulative logit model on the total number of months of treatment in the previous year and the interaction between the total number of months of treatment and primary drug use in the previous year. In this logistic regression, the toal number of months of primary drug use in the second, fifth, and seventh years significantly interacted with the total number of months of treatment in these years to predict the treatment participation in the next years.

Using the unweighted GEE method with $y_{\overline{a_i}}$ specified as a normal variable and an independent working correlation matrix specified for robust standard errors, the estimate of the regression parameter γ₁ in (2) for cumulative treatment effect was .013 and the corresponding 95% confidence interval (CI) based on the robust or sandwich-type standard errors was (−.003, .029) when the covariates at intake, F_i0 and F_i1, were excluded from the standard regression model in (2). When F_i1 and F_i1 were included, they became .015 and (−.001, .031) respectively (see Table 1). Similarly, for our MSM model in (1) with a normal assumption of $y_{\overline{a_i}}$, the stabilized weights and an independent working correlation matrix specified for robust standard errors, our IPTW causal estimate of the parameter β₁ was .035 and the corresponding 95% robust CI was (.007, .063). When the non-stabilized weights were used, they became −.008 and (−.031, .015), respectively (see Table 1).

Table 1.

Estimates of the causal effect of cumulative drug treatment

Unweighted GEE method 1	Parameter	95 per cent robust CI
Unadjusted model	.013	−.003, .029
Model adjusted with covariates	.015	−.001, .031
MSM 2	Parameter	95 per cent robust CI
Stabilized weights	.035	.007, .063
Non-stabilized weights	−.008	−.031, .015

¹Non-causal models are shown for comparison purposes only. The unadjusted model includes only the total months of treatment $\text{Cum(}\overline{A_i})$ and the total months of drug use $\text{Cum}(\overline{D_i})$ accumulated in the ten years following first primary drug use. The model is further adjusted by intake variables, including gender, primary drug type, age at first arrest, project, race/ethnicity, employment at baseline, education at baseline, and age at first use of primary drug. For both models, the robust or sandwich-type standard error is used for the confidence interval calculation.

²Weights are estimated as described in the text using recent drug uses, recent drug treatments, and variables at intake including gender, primary drug type, and age at first arrest.

The point estimates, robust standard errors, and 95% robust CIs for each of the parameters of our final MSM are presented in Table 2 (see Appendix for the SAS syntax for our final MSM model). In Table 2, the parameter of the primary drug type (Heroin vs. Cocaine) was significant in addition to the cumulative treatment effect, while all others were not significant. To examine the effect of those nonsignificant covariates on the estimation precision of our final MSM model, we eliminated all covariates with p>.30 and re-estimated the model with stabilized weights (see Bodnar, Davidian, Siega-Riz, & Tsiatis, 2004). We found that the effects of treatment and primary drug type (Heroin vs. Cocaine) were still significant and in the same direction.

Table 2.

Final marginal structural model with stabilized weights.

Variables	Parameter estimates	Robust Standard error	95 per cent robust CI
$\text{Cum(}\overline{A_i})$ *	.035	.014	.007, .063
Gender (Female Y/N)	.239	.182	−.117, .596
Drug type 1 (Methamphetamine vs. Cocaine)	−.228	.322	−.858, .403
Drug 2 type (Heroin vs. Cocaine) *	−.859	.265	−1.378, −.339
Age at first arrest	.001	.012	−.022, .024
Project 1 (TUE vs. METH)	−.543	.328	−1.186, .100
Project 2 (TXPROC vs. METH)	−.269	.272	−.802, .264
Race 1 (White vs. Others)	−.316	.335	−.972, .341
Race 2 (Black vs. Others)	−.678	.366	−1.396, .040
Race 3 (Hispanic vs. Others)	.092	.368	−.630, .814
Employment at intake (Employed vs. Unemployed)	.416	.225	−.025, .856
Employment at intake (Not in labor force vs. Unemployed)	−.040	.222	−.475, .396
Education at intake (College or above vs. Less than high school)	.264	.210	−.147, .675
Education at intake (High school vs. Less than high school)	−.340	.233	−.797, .116
Age at first primary drug use	.000	.022	−.042, .043

^*p<.05

The outcome of our final model is the logarithmic transformed total drug use abstinence in the later five years. This implies that change of the value of covariates (e.g., cumulative treatment in first 10 years or the primary drug type) in the final model would predict a percent change for the total drug use abstinence (see Morris & Rolph, 1981, p. 98). For example, the cumulative treatment effect estimate by our MSM model with stabilized weights was .035. Given that e^.035 is equal to 1.036, an additional month of treatment in the first 10 years would predict a 3.6% increase in the total drug use abstinence in the later five years. Similarly, the parameter estimate for the primary drug type (Heroin vs. Cocaine) was −.859 in our model. Given e^−.859 is equal to .424, the total drug use abstinence of Heroin users in the later five years would be expected to be 57.6% less than that of Cocaine users.

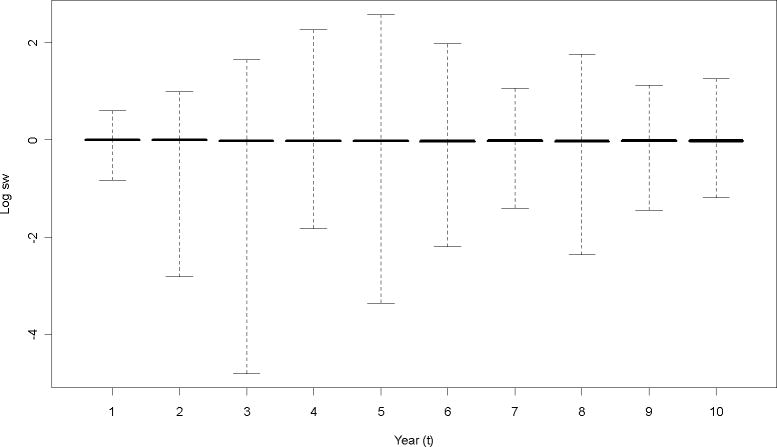
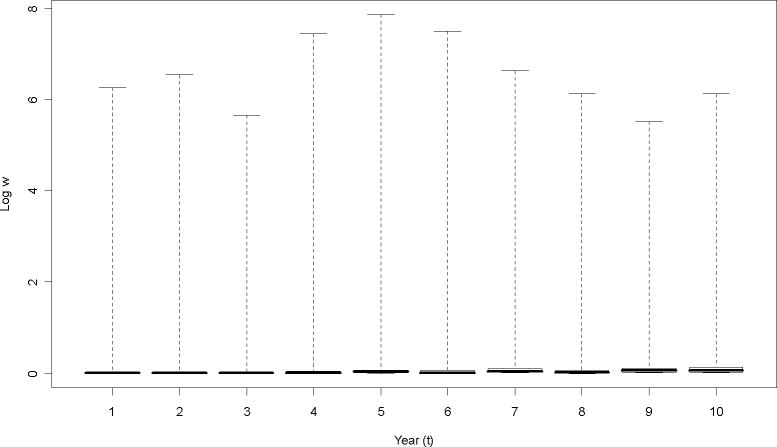
For comparison, the distribution of the stabilized weights sw_it and the non-stabilized weights w_it is presented in Figures 2 and 3, respectively (a logarithmic transformation was applied to weights for display purposes only). We also summarized the empirical distribution of sw_it and w_it at two arbitrary time points (the second and ninth years) in Table 3. From Table 3 and Figures 2 and 3, we found that the distribution of the non-stabilized weights w_it is more variable and skewed than that of sw_it.

Figure 2.

Distribution of stabilized weights sw_it by year. The box for each year shows the location of the mean, median and second and third quartiles. Vertical lines extend to the maximum and minimum values.

Figure 3.

Distribution of non-stabilized weights w_it by year.

Table 3.

Distribution of the estimated weight sw_it and w_it at the second and ninth year.

	Mean(SD)	Median (IQR)	Percentile 1	Percentile 99
Year 2
swit	1.00(0.12)	1.00(0.01)	0.81	1.47
wit	5.37(45.65)	1.02(0.01)	1.01	74.33
Year 9
swit	1.00(0.25)	0.98(0.06)	0.40	2.11
wit	6.55(25.91)	1.06(0.08)	1.01	145.00

Of course, sw_it could also have some extreme values so that the weights sw_i contain some “influential” individuals. For example, the minimum and maximum values of sw_i in our case were .00002 and 39.788, respectively. To examine the effect of those “influential” weights on our results, we conducted a sensitivity analysis. Specifically, the weights were truncated by resetting the value of sw_i greater than the 95^th percentile to the value of the 95^th percentile, which was equal to 2.0. At the same time, we also reset the value of sw_i lower than the 5^th percentile to the value of the 5^th percentile, which was equal to 0.127 (see Cole & Hernan, 2008). With this truncated sw_i, qualitative results of the final MSM were similar to those shown in Tables 1 and 2.

As mentioned before, we included drug use and some covariates at baseline to estimate the individual probabilities in the denominator of sw_i for our final MSM model. As a sensitivity analysis (see Bodnar et al., 2004), we re-estimated those individual probabilities using only variables with p<0.30 in the model and refitted the final MSM model. The results of the model did not change meaningfully.

In addition, note that we did not include some other time-dependent covariates, such as the number of months of incarceration or employment in each year during the first 10 years following first use of primary drug, to estimate the individual probabilities in the denominator of sw_i for our final MSM model. The exclusion of those covariates could have led to the presence of unmeasured confounders and incorrect estimation for cumulative treatment effect. To see the robustness of our results, we included both covariates into the estimation of sw_i in a similar manner to annual drug use in the first 10 years and re-estimated our final MSM model. The results of our final model after this sensitivity analysis were again similar to those shown in Tables 1 and 2.

Discussion

In this article, we described the causal inference of a marginal structural model (MSM) and applied it to investigate the effect of cumulative drug treatment occurring over 10 years on drug use abstinence over the subsequent five years. We used this method because standard unweighted regression analysis is not appropriate when time-dependent confounders, such as past drug use history (e.g., D_it in our analysis), exist in the observational studies (Robins, 1986, 1997; Robins et al., 2000).

Because of the presence of confounding, the unweighted GEE method gave nonsignificant regression estimates of γ₁ for cumulative treatment effect, whether or not the covariates at intake were adjusted. Conversely, the MSM with stabilized weights gave the significant estimate of β₁ for cumulative treatment. The difference between the unweighted and weighted estimates indicates a confounding effect by the time-dependent covariate D_it, which can be corrected by MSM to provide an unbiased estimate of causal effects. From our final model, we also found that the heroin users compared to users of other drugs would have a significantly shorter period of abstinence despite the cumulative treatment effect.

In drug abuse research, the cumulative effect of drug treatment has been investigated by methods such as structural equation models (e.g., Hser, Grella, et al., 1998). Although those methods may provide possibly significant estimates of cumulative treatment effects, they, like standard unweighted regression, are not based on the counterfactual outcomes and thus lack a causal interpretation for their estimates. In addition, the potential time-dependent confounding may not be eliminated by those methods.

Limitations

The longitudinal data for this study have been used in some of our previous studies (e.g., Hser, Evans, Huang, Brecht, & Li, 2008; Hser, Huang, Brecht, Li, & Evans, 2008). In this study, we aggregated the monthly records of the data into an annual dataset for analysis, and some loss of information may have resulted. Theoretically, the original monthly records could have been directly used for D_it or A_it in the analysis and the weighted MSM models could have handled this monthly data. However, our preliminary analysis of monthly data frequently encountered either complete separation or quasi-complete separation when the individual probabilities for the MSM weights were estimated by some parametric logistic models. The relatively low treatment participation in the months of the first 10 years following first use of primary drug could be a cause of the complete or quasi-complete separation. So, monthly records may not be appropriate for the MSM model in a drug abuse context. In our analysis, the complete or quasi-complete separation also happened when we included both F_i0 and F_i1 for the estimation of MSM weights. This is the reason that we selected F_i0 by a separate logistic regression and used it solely to estimate MSM weights.

Our results showed some degree of time-dependent confounding of drug use in the first 10 years, although this time-dependent confounding was not as strong as expected. For this article, we aggregated the longitudinal data in the first 10 years annually. Aggregation of the data based on every two or three years may provide stronger evidence for the time-dependent confounding of drug use and may be a better way of handling the data for the MSM model. Further exploration in this direction should be interesting.

For this article, we only selected the subjects who had 15 years of records for analysis and ignored the subjects who had a shorter history. Although MSM can handle the incomplete data due to the short history of subjects in some way (see Robins et al., 2000), it requires an assumption that the measured variables or covariates at each time point are sufficient to adjust for selection bias due to shorter history. Clearly, further investigation incorporating those subjects with a shorter history should be interesting.

Furthermore, we want to mention again that the validity of the causal inference of our MSM model depends on the correctness of our MSM model in (1) and weight specification. For example, the estimated causal effect and the conclusion of our MSM model here could be different once some unmeasured (time-dependent or time-independent) confounders are identified and added into the estimation. Although we conducted a sensitivity analysis to examine the robustness of our results by including some other time-dependent covariates such as incarceration and employment into the weight and final MSM model estimation, one difficulty is that further including some other (time-dependent or time-independent) covariates into the weight estimation could frequently lead to complete or quasi-complete separation. In addition, we assumed in this study that the cumulative logit models are correctly specified for drug treatment participation in the first 10 years following first use of primary drug. This assumption is vulnerable to model misspecification given the complexity of the dynamic process of drug use and treatment participation. Of course, this is not a problem unique to the MSM models—many advanced statistical models may suffer the same problem.

Implications

Despite some limitations, our study revealed findings of importance to the field by using a model that controls for self-selection due to time-dependent confounders. With the increased recognition of drug addiction as a chronic, relapsing condition, the need becomes apparent for developing long-term care or management appropriate for addressing the course of addiction. Many addicts may require multiple treatments before they show improvement through reduced drug use or begin a stable recovery including abstinence. The cumulative treatment effects found in this analysis support the need for planned multiple treatments by many addicts. Yet, most treatment programs in the current service delivery system appear disconnected. The multiple treatments patients received likely occurred as a result of relapse as opposed to planned continuing care. Previous studies have shown that multiple treatments in a continuing care arrangement produced more favorable outcomes than separate, discrete treatments (Hser, Huang, Teruya, & Anglin, 2004). Efforts to integrate treatment components to develop long-term care treatment should take these findings into consideration.

Previous to this study, marginal structural models have not been applied in drug abuse research. Drug abuse research often involves observational studies such as those included in the present analysis, in which self-selection effects often make the causal inference questionable. As demonstrated in the present study, MSM controlling for time-dependent confounders was able to demonstrate cumulative effects, whereas the traditional methods failed to do so. From both the statistical and empirical point of view, MSM is a better approach to assess cumulative treatment effects due to its advantages of controlling for self-selection bias over time.

Appendix

The SAS code (version 9.13) for obtaining our final MSM model is as follows:

proc genmod data=msmdata;
class id;
model abstinence=cumtx gender drugtype1 drugtype2 agefirstarrest
project1 project2 race1 race2 race3 emp1 emp2 edu1 edu2 agefirstuse/
dist=normal link=identity;
weight sweightyr;
repeated subject=id/type=ind;
run;

The SAS code (version 9.13) for the cumulative logit models to obtain the individual probabilities in each year for the stabilized weights is as follows:

proc logistic data=year&i;
/* the logistic model for the denominator of the stabilized weights; tx and primaryuse are the number of months of treatment and primary drug use in current year; txpre1 and primaryusepre1 are the number of months of treatment and primary drug use in the previous year; txpre2 is the number of months of treatment in the year before the previous year; primaryuse0 is the number of months of primary drug use in the first year; the new dataset yearapred&i would contain the individual probabilities for the denominator of the stabilized weights*/
 model tx=txpre1 txpre2 primaryuse primaryusepre1
   txpre1*primaryuse primaryuse0
   gender drugtype1 drugtype2 agefirstarrest;
  output out=yearapred&i predprobs=individual;
run;
/* the logistic model for the numerator of the stabilized weights; the new dataset yearbpred&i would contain the individual probabilities for the numerator of the stabilized weights*/
proc logistic data=year&i;
 model tx=txpre1 txpre2;
  output out=yearbpred&i predprobs=individual;
run;