Abstract
Multipole expansions offer a natural path to coarse-graining the electrostatic potential. However, the validity of the expansion is restricted to regions outside a spherical enclosure of the distribution of charge and, therefore, not suitable for most applications that demand accurate representation at arbitrary positions around the molecule. We propose and demonstrate a distributed multipole expansion approach that resolves this limitation. We also provide a practical algorithm for the computational implementation of this approach. The method allows the partitioning of the charge distribution into subsystems so that the multipole expansion of each component of the partition, and therefore of their superposition, is valid outside an enclosing surface of the molecule of arbitrary shape. The complexity of the resulting coarse-grained model of electrostatic potential is dictated by the area of the molecular surface and therefore, for a typical three-dimensional molecule, it scale as N2/3 with N, the number of charges in the system. This makes the method especially useful for coarse-grained studies of biological systems consisting of many large macromolecules provided that the configuration of the individual molecules can be approximated as fixed.
Keywords: Electrostatic potential, Coarse-graining, Molecular modeling, Multipole moments, Algorithms, Distributed multipole analysis
1. Introduction
Electrostatic interactions represent the major long-range component of the Hamiltonian that drives the dynamics of molecular systems. For example, full classical molecular simulations involve, typically, the computation of the electrostatic potential at a given point in space with a complexity of N, and of all pairwise atomic interactions with a complexity of N2 with respect to the charges and coordinates of the N atoms in the system. This quickly becomes the major bottleneck in such simulations when the number of atoms increases. Various algorithms have been developed to simplify the complexity of these calculations. In a most typical approach, the interaction between remote groups of charges are approximated by some collective representation of those groups. For example, in the fast multipole method (FMM) [1, 2, 3] the interaction between such groups of atoms are simplified by the use of a collective representation of their charges in terms of multipole moments. Various refinements of the FMM have been developed that take advantage of space division algorithms (octree algorithms in three dimensions) [4, 5, 6] to reduce the computational cost of the pairwise interaction to N log N, or even linear complexity.
The above approach is sufficient for many applications in material sciences and single-macromolecule biophysics where these techniques are often used. The rapid progress in biological sciences within the last few decades has, however, brought to the forefront of research, applications that far exceed this scale: studying processes at molecular, supramolecular and cellular levels of organization requires the modeling of systems consisting of large numbers of macromolecules (for example a virus may contain from tens to hundreds or thousands of protein molecules) of various shapes and physicochemical complexities. At this scale, even the linear complexity is too challenging. Unfortunately, further reduction of the complexity, by exact means, does not seem possible since N already represents the number of (three-dimensional) degrees of freedom of an atomic system. Therefore, the most efforts in overcoming this computational challenge have focused on development of approximate coarse-grained (CG) models [7, 8, 9].
The general underlying assumption of all CG models is that the biological processes of interest at this scale are robust with respect to certain detailed properties of the constituent molecules. This leads to various CG models depending on the type of details that are ignored. In many studies the configuration of individual macromolecular components of the system, or of big parts of such macromolecules, can be approximated as rigid. This results in a significant reduction in the dynamical degrees of freedom, and eliminates the computation of the internal interactions of rigid components. However, this is not automatically accompanied by a reduction in the complexity of the interaction between different rigid components. For example, the electrostatic interaction still requires the computation of all inter-component atomic pairwise interactions. To fully take advantage of the rigid-conformation approximation a CG model for the interaction itself is needed.
The purpose of this paper is to address this later aspect. More specifically, we present a method for automatic coarse-graining the electrostatic potential of a molecule at any level of accuracy demanded by an application. The CG potential is represented in the form of a superposition of multipole expansions corresponding to the components of a partition of the atomic system. In this sense, the approach resembles the distributed multipole analysis from theoretical chemistry [10]. However, that method serves a different purpose and relates to detailed chemical information about the molecular entity, which makes it only suitable for small molecules. By contrast, the partitioning of the system in our approach is done in such a way that convergence to the correct electrostatic potential is assured at any of a given set of “control” points. When the control points describe a closed surface enclosing the molecule, convergence at these points insures convergence anywhere outside this enclosing surface. The criterion used in our partitioning scheme can be applied in an automatic fashion, which is essential for the modeling of large molecular assemblies.
The structure of the paper is as follows. In the following Theory section we first introduce the contextual background on coarse-graining molecular systems, and describe how multipole expansions can provide an ideal framework for the modeling of their interactions. We also describe the main limitation that prevents their wide use for this purpose. Then, in the final subsection 2.3, we describe an approach that overcomes this limitation. Section 3 and the Appendix A provide the algorithm for the implementation of the proposed approach. Section 4 illustrates the performance of our approach on a specific application, coarse-graining the electrostatic potential of a large biological molecule. We summarize our results in the Conclusions section.
2. Theory
2.1. Coarse-graining molecular systems
Coarse-graining techniques should, in principle, address two problems: 1) defining the structural CG beads, a problem that consists in distributing the atoms of the molecules into separate subsystems whose internal state can be considered fixed for the purpose of the study under consideration and 2) deriving the functional form of the interaction (in the form of an effective Hamiltonian or potential) for the resulting CG beads.
The first aspect has been studied more extensively, even though there is no general prescription for choosing the CG beads and this process is usually strongly dependent on a priori knowledge about the properties of the physical system that is being modeled. Each of the present approaches to CG bead assignment is typically accompanied by a model or approximation for the interaction between CG beads. However, this second aspect has been addressed in a less systematic fashion except, perhaps, for some more recent approaches to multi-scale coarse-graining [11, 12, 8]. This is despite the fact that deriving a CG interaction should, at least in principle, be more amenable to solutions than the bead assignment step: once an atomic interaction model is known, deriving a CG Hamiltonian can be reduced to a transformation from atomic to collective coordinates (this may be more complicated if thermodynamic properties are to be captured; here, we are only concerned with coarse-graining the interaction Hamiltonian).
Deriving a collective coordinate representation of the Hamiltonian from the atomic interaction model is closely related to macroscopic averaging of the electromagnetic properties and, therefore, various techniques from this area can be used. In particular, for the electrostatic interaction, which forms our main interest, the multipole expansions provide an ideal candidate for the coarse-graining of the electrostatic potential of a three dimensional molecule. The advantages of this technique are: 1) it provides a systematic description of the electrostatic field in terms of a hierarchical set of multipoles describing features at various spatial scales (i.e., it is intrinsically a multi-scale approach); 2) the multipole moments are very effective in encoding directional properties of the interactions, properties that are essential when large and complex molecular entities are involved; 3) the multipole expansion techniques have been extensively studied – both as a core technique in theoretical physics (electromagnetism, nuclear physics, gravitational physics, astrophysics, for example) and from a practical perspective in the context of the FMM approach – and therefore many technical aspects are well understood. Despite all these advantages, the multipole expansions have been only applied on a limited scale to practical modeling of the molecular fields [13, 14, 15, 16]. This is due to major limitations in the accuracy of multipole expansions in the immediate vicinity of the surface of the molecule [17, 18], as discussed in the next section.
2.2. Multipole expansions and their limitations
The multipole expansions represent a systematic method for going from a microscopic to a “macroscopic” (or collective) representation of the electrostatic field of a system of charges. To understand the limitations of this technique in molecular modeling we briefly introduce here the derivation of these expansions. Since the algorithms presented here, as well as the applications (macromolecular modelling) that motivated them are discrete in nature, we adopt in this paper a point-charge model of the distribution of charge for purpose of presentation. However, the results can be directly extended to the continous case by an appropriate conversion, for example, to a discrete representation of the distribution of charge on a three-dimensional grid.
The Coulomb potential created by a point charge ei, located at point r⃗i is:
| (1) |
where r⃗ is the observation point, and ε is the permittivity of the medium. Eq. (1) can be expanded in a series in which the dependence on charge coordinates and observation point coordinates separates, in each term, into independent factors as follows [19]:
| (2) |
Here, ri and r are the lengths of the position vectors r⃗i and r⃗, and r̂i and r̂ are the unit vectors in the direction of those vectors. The unit vectors are specified in the last formula by their spherical angles θ and φ. The functions Pl are the Legendre polynomials, depending here only on the cosine function of the angle between the position vectors of the observation point and that of the charge. The Legendre polynomials satisfy the spherical harmonics addition theorem [19] which allows their factorization in terms of the Racahnomalised spherical harmonic functions as represented by the second summation (over index m) in the last formula.
The factorization in terms of spherical harmonics is essential because it is this property that allows the transition from the atomic (‘microscopic’) to a collective (‘macroscopic’ or molecular in the present context) representation, in terms of multipoles, of the electrostatic field of all charges in a molecule. Indeed, in the case of many charges, the superposition principle states that the total electrostatic potential is a sum over the potentials created by each individual particle. By grouping together the coefficients depending only on the charge coordinates, which is made possible by the above-mentioned factorization property, one arrives at the following multipole representation of the electrostatic potential:
| (3) |
The coefficients qlm are the multipole moments of the distribution of charge and are given by the expression:
| (4) |
where the summation runs over all N charges in the system. For a given l, the 2l + 1 components corresponding to different values of m form the multipole of order (or rank) l: the 0th order multipole is just the total charge, the 1st order is the dipole, the 2nd order is the quadrupole, etc.
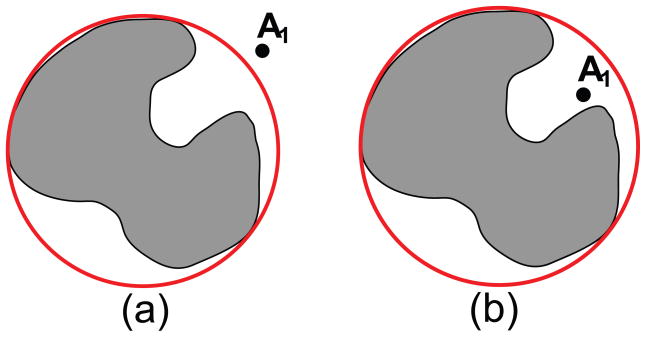
Note that in the series expansion of the Coulomb potential in Eq. (2) we tacitly made the critical assumption that r > ri, required for the series to converge. For a collection of charges, the convergence of the multipole expansion in Eq. (3) to the exact electrostatic potential requires this condition be satisfied, simultaneously, for all charged particles in the system. In geometrical terms, the condition states that the observation point must reside outside a spherical enclosure of the whole system of charges centered at the center of expansion, for example as shown in Fig. 1(a) for the smallest possible enclosing sphere.
Figure 1.
(a) For a point outside an enclosing sphere the multipole representation can be made arbitrarily precise by retaining a sufficient number of terms. (b) For points inside the sphere even a complete summation of all terms in the series will not converge to the correct value of the electrostatic potential.
Even if we place the origin such that the whole set of charges is enclosed in the smallest ball possible (the case illustrated in Fig. 1), for any non-spherical charge distributions there will be cavities where multipole methods can not accurately represent the real electrostatic potential, no matter how many terms in the series of Eq. (3) are retained (for example for points such as the one shown in Fig. 1(b)). As long as these regions are accessible to other molecules in the system, these regions cannot be ignored and the problem must be addressed.
The above restrictions in the immediate vicinity of molecules constitute the main limiting factor [17, 18] for the practical applications of multipole expansions in modeling molecular interactions. In most cases, their use for this purpose has been confined to small molecules such as water [15, 16], where other effects prevent molecules from exploring very close configurations anyway. Still, the effectiveness of multipole expansion in describing non-isotropic interactions (i.e., their directional variation) has motivated their usage for modeling of some larger molecules too [13, 14], despite these shortcomings.
Even though somewhat related, the problem defined above remains essentially distinct from another practical limitation of the classical multipole expansion: the dependence of their convergence rate on the location of the center of expansion, which makes choosing the center ambiguous. The ambiguity of the center of expansion can be removed by using a rankwise distributed multipole analysis as we have shown previously [20]. However, solving the ambiguity with respect to the center of expansion does not resolve the problem highlighted above, of limited accuracy near the distribution of charge.
2.3. Resolving the limitations of multipole expansions by partitioning
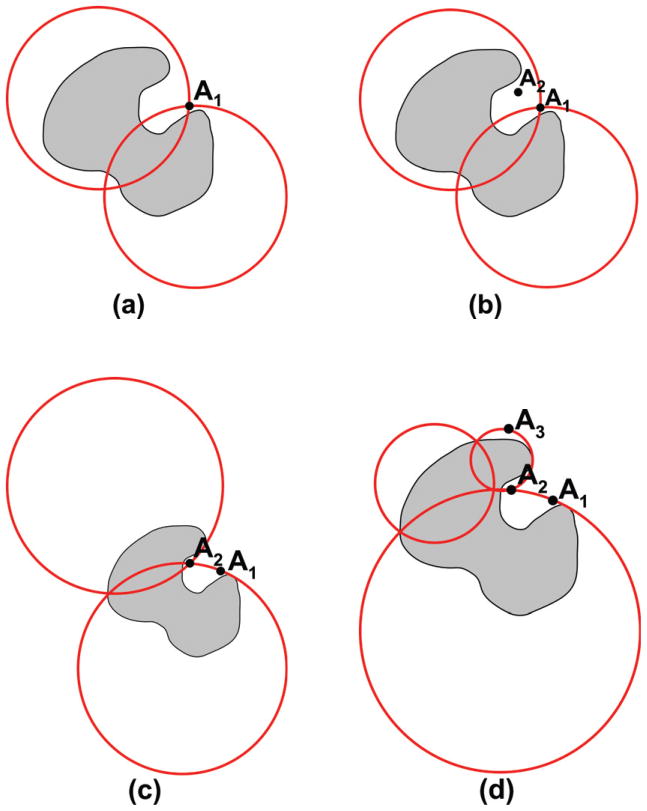
Let us assume that we are interested in an accurate representation of the electrostatic potential at point A1 located as shown in Fig. 1(b), and let us name such a point a “control point”. The multipole expansion of the total charge set is not convergent at that point. We choose to interpret this, in the context of a CG model, as signifying that our attempt to model the electrostatic potential of such a molecule by a single set of multipoles is too coarse. To refine the description, we will partition the distribution of charge into two parts, and represent the potential of the whole molecule as the superposition of the two potentials. We do this in effect by identifying two spheres such that 1) the union of the two spheres encloses all charges in the molecule, and 2) the control point A1 resides outside this union or, in the worst case, on its boundary. This can be achieved, for example, as shown in Fig. 2(a). Note that, unlike the illustration in Fig. 1, this time the spheres are not, typically, the smallest enclosing spheres, and, therefore, the surface of such a sphere resides outside the boundaries of a smaller sphere that can be fit inside. In other words, all the points of such a surface can be made, typically, points of convergence by choosing the center of the smaller sphere as center of expansion. Then, the potential at point A1 can be, typically, represented exactly as a superposition of convergent multipole expansions of the two distributions of charge corresponding to the two spheres of the geometric partitioning.
Figure 2.
Coarse-graining the electrostatic potential by geometric partitioning and superposition. The sequence of figures illustrate the process of building partitioning schemes that insure convergence at (a) 1, (b,c) 2, and (d) 3 specified control points.
The addition of another control point, A2 (Fig. 2(b)), imposes another constraint for the sphere coverage of the distribution of charge. This may be resolved without increasing the number of covering spheres, as is the case in Fig. 2(c), or may require a three-sphere coverage. The problem repeats itself with any additional point added to the set of control points. A further solution, for a three-point control set, is shown in Fig. 2(d). Obviously, if the added point is already outside of the coverage satisfying previous constraints, no further refinement is needed. The scenario described above can be formalized as the following problem:
Partitioning Problem
Given the set of charges
of a molecule, and a set of control points
, find a set of three-dimensional enclosing spheres
, and a partition of the charge set
with ΣNp = N, such that: a) the subset
is inside sphere
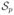 and b) none of the control points resides inside the union of the enclosing spheres.
and b) none of the control points resides inside the union of the enclosing spheres.
We will name a pair an “interaction CG bead”, to distinguish it from a regular structural CG bead. A solution of the partition problem consisting of a collection of N interaction beads constitutes an “N-bead CG partition model” of the interaction. Note that in the applications envisioned by our method a typical structural CG bead will consist of many interaction CG beads: a structural CG bead in such applications will often extend over large parts or even entire macromolecules, and retain their rigid conformation during a computational simulation.
Once a solution to the above problem is determined, the electrostatic potential surrounding the molecules can be coarse-grained as a superposition of multipole expansions of each of the interacting CG beads as follows:
| (5) |
The multipole moments are the moments of bead p of the partition with respect to the center of its enclosing sphere, and the unit vectors are the directions of the relative position vectors of the observation point with respect to that center.
For a rigid molecule, such as a structural CG bead, the inside of the molecule is not accessible to other molecules. In this case it is only useful to choose control points from regions located outside the molecule. The set of control points is arbitrary. However, the most obvious practical choice is a selection of control points from a closed surface enclosing the whole molecule. If the control points sample the surface densely enough, satisfying convergence at the control points will automatically ensure convergence at any point outside the surface. In other words, such a surface can be used to define the region of convergence of the CG model. Moreover, since the electrostatic potential outside the sampling surface satisfies Laplace’s equation, its value at any point is completely determined by its values on this surface. Therefore, the accuracy of the potential in the domain of convergence (outside the sampling surface) can be completely controlled by the accuracy of the potential over the set of control points.
The most complex scenario corresponds to control points located on the surface of the molecule [21]. The number of control points needed, and thus the size of the partition and the complexity of computation will then increase proportional to the surface of the molecule. Therefore, for a three-dimensional molecule, the complexity of the CG model of the interaction will scale as N2/3 with N atoms, for a given truncation order for the multipole expansions. The real complexity for a given molecule depends also on details of the spatial distribution of charges. In the simplest case of a spherical molecule with a uniform distribution of charge, the electrostatic field can be represented by the total charge only. On the other hand, in the more complex case of a deeply convoluted molecular surface, the CG model may require a much larger number of interaction CG beads and the complexity may exceed N2/3. This is because in this case the effective dimensionality of the space occupied by the molecule may be less than three – the dimensionality of the physical space. Our analysis applies only to three-dimensional molecules.
The above complexity of N2/3 in calculating the electrostatic potential at a given point is, asymptotically, the worst possible from a partitioning perspective. In practice, if the control points are selected from a more distant enclosing surface for example, the CG model may be significantly simpler. Therefore, since a full atomic representation has a computational complexity of N, a multipole CG model based on partitioning is assured to be more efficient against a full atomic representation for a sufficiently large molecule. The threshold size depends on details of implementation of the algorithms and, of course, the overall degree of accuracy required, since this determines the truncation order of the multipole expansions.
In many typical applications the pairwise interaction energy is also needed. In a naïve implementation, the complexity of such a calculation for a CG model obtained as described here would scale with the numbers N, M of atoms on the interacting molecules as N2/3M2/3. However, present techniques to reduce the complexity of electrostatic pairwise interaction can be used within the framework of our CG approach since the interaction CG beads plays the same role as the atomic charges in these methods. For example, one commonly used technique consists in precomputing the potential on a grid surrounding each molecule. With such an approach, the computation of the pairwise interaction energy can be linearized with respect to the number of interaction CG beads on each molecule.
3. The partitioning algorithm
As formulated, the partitioning problem does not, in general, have a unique solution: both the geometric partitioning into covering spheres and the way the charge is distributed among spheres in overlapping regions may admit multiple solutions. In particular, the problem always admits a trivial solution in which each charge is enclosed inside its own sphere. But even such a partitioning is not unique because the radius of the enclosing sphere is not strictly defined, unless additional constraints are imposed. This radius is irrelevant when the sphere is centered at the enclosed point charge since the multipole expansions converge in this case at all points, independent of the radius of enclosing sphere. In general, however, for an arbitrary placement of the center, the radius of the sphere has to be such that all control points, in particular the closest one to the center, reside outside the sphere, while the charge is contained inside. For the purpose of minimizing the size of the covering set of spheres for a more general solution, it is advantageous to choose the maximum possible radius, i.e. a radius equal to the distance to the closest control point. If the sphere is centered at the position of the enclosed charge, the radius then corresponds to the distance between that charge and the closest of the control points.
The solution described above in which each charge is enclosed in its own sphere centered at the position of that charge is equivalent to an all-atom Coulomb representation since, with this geometry, the multipole expansion reduces to the monopole Coulomb term only. This, of course, is the most detailed coarse-graining since complete accuracy of the electrostatic field can be achieved at any point in space. We will furthermore set the radius of the enclosing sphere of each charge to the distance to the closest control point, as discussed above, name the partition defined in this way an “atom-level partition”, and denote it by
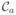 . The partition
. The partition
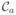 represents the starting point of the algorithm for deriving an optimal solution to the partitioning problem formulated in the previous section, i.e., for obtaining a CG partition of the distribution of charge and, therefore, a CG model for the electrostatic interaction.
represents the starting point of the algorithm for deriving an optimal solution to the partitioning problem formulated in the previous section, i.e., for obtaining a CG partition of the distribution of charge and, therefore, a CG model for the electrostatic interaction.
In general, a CG partition, in particular the atom-level partition
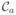 , is reducible in the sense that it contains pairs of interaction CG beads such that the whole set of charges of one of them is completely contained within the covering sphere of the other. That first member of such a CG bead pair can be “merged” into the other without losing the convergence of the multipole expansions. By recursively merging all reducible pairs of interaction CG beads one can reach an irreducible CG partition. By definition, we will consider optimal a solution of the partition problem that is an irreducible CG partition. A pseudo-code description of this algorithm is given in the Appendix.
, is reducible in the sense that it contains pairs of interaction CG beads such that the whole set of charges of one of them is completely contained within the covering sphere of the other. That first member of such a CG bead pair can be “merged” into the other without losing the convergence of the multipole expansions. By recursively merging all reducible pairs of interaction CG beads one can reach an irreducible CG partition. By definition, we will consider optimal a solution of the partition problem that is an irreducible CG partition. A pseudo-code description of this algorithm is given in the Appendix.
In a real application, the input partition is set initially to the atom-level partition
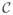 ←
←
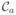 of the structural CG bead. The atom-level partition has to be precomputed in advance from the coordinates of the atoms in the molecule and their charges, and from the coordinates of the control points. From the definition, the calculation of the atom-level partition consists mainly in identifying the closest control point to each atom in the molecule and overall the computational complexity is proportional to the product between the number of atoms and the number of control points. Since the structural CG bead is rigid in the typical application of our method, this calculation needs to be done only once for each molecule, and therefore the complexity of this step is not important. However, tree methods can be used to reduce the complexity of the computation of the atom-level partition.
of the structural CG bead. The atom-level partition has to be precomputed in advance from the coordinates of the atoms in the molecule and their charges, and from the coordinates of the control points. From the definition, the calculation of the atom-level partition consists mainly in identifying the closest control point to each atom in the molecule and overall the computational complexity is proportional to the product between the number of atoms and the number of control points. Since the structural CG bead is rigid in the typical application of our method, this calculation needs to be done only once for each molecule, and therefore the complexity of this step is not important. However, tree methods can be used to reduce the complexity of the computation of the atom-level partition.
For the same reason, the CG interaction model only needs to be computed once at the beginning of the molecular simulation and, therefore, the complexity of the computation, which is quadratic in the worst case scenario, is not typically of concern. However, more efficient algorithms are possible and we will address this aspect elsewhere [22].
As an important note, we would emphasize again that the partitioning problem does not have a unique solution, even in an irreducible form. In the context of the coarse-graining algorithm presented above, this non-uniqueness manifests itself in the fact that the output of the algorithm depends on the order of the CG beads in the initial input partition. In particular, while the algorithm optimizes the CG interaction model by reducing the partition to a totally irreducible one, it does not necessarily produce the smallest CG partition. Additional optimization is possible with respect to the size of the CG model as well as the rate of convergence of each of the multipole expansions in the partition. This can be achieved, for example, by running the algorithm on randomized orderings of the interaction beads in the initial partition. However, this leads to combinatorial complexity. The main objective of the partitioning problem, however, is to insure convergence of the distributed multipole expansion. From this perspective, the objective is effectively achieved since any irreducible CG partition satisfies this requirement.
4. Illustration and performance of the partitioning CG approach
To evaluate our CG approach we now explore how well it performs by comparison to present multipole expansion techniques. In particular, we will analyze 1) how well it addresses the inaccuracies of multipole expansion near the distribution of charge; 2) the speed of convergence and 3) the reduction in computational complexity that it achieves.
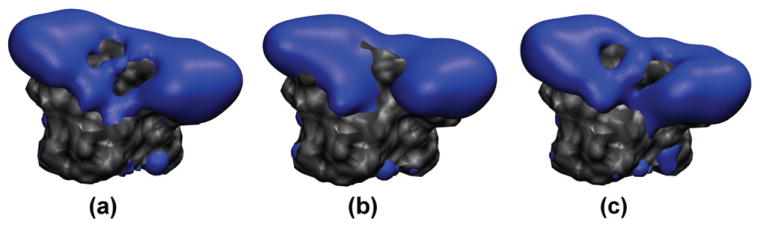
We illustrate these aspects with a concrete example: a CG model of the electrostatic potential of the Arc repressor, a DNA-binding protein [23] (PDB ID [24]: 1MYK). A graphical comparison of such a CG model with the exact calculation is shown in Fig. 3. The equipotential surface in Fig. 3(a) (shown in blue) is an exact calculation from Coulomb’s law. Figs. 3(b) and 3(c) represent the same isosurface as captured by a 70-bead CG model generated with our approach at the monopole and dipole truncation levels, respectively. For the generation of the 70-bead partition we used as control points the 2492 vertices describing a closed surface (not shown) shifted by 2Å outward, and parallel to the molecular surface (shown in black). The vertices, as well as the normal directions to the molecular surface were generated with a standard rolling-ball technique [25, 26] using the MSMS program [27]. The rolling ball radius and the vertex density were set to 2.0 Å and 0.25Å−2 respectively. The order of the initial atom-level partition used as input in the CG algorithm is the one in which the atoms are listed in the PDB file [24]. The molecule contains almost 1600 atoms for a total of about 6500 coordinate and charge parameters. At the dipole level (Fig. 3(c)) there are 490 parameters in this CG model, which amounts to a reduction in complexity by a factor of about 13. This is the reduction in complexity that would be expected in a simulation that uses this CG model instead of the exact calculation from Coulomb’s law.
Figure 3.
An isosurface of the electrostatic potential (0.5 e/Å) around the Arc repressor protein (PDB ID: 1MYK) from Coulomb’s potential (a), and from a 70-bead CG model in the monopole (Lmax = 0) (b) and dipole (Lmax = 1) order (c). The dark-grey surface represents the molecular surface generated with a rolling ball [25, 26, 27] of 2Å. About 2500 control points were selected from a closed surface shifted by 2Å in the outward direction from the molecular surface and used to generate the CG model as described in the text.
It is clear that the CG model captures quite well the features of the electrostatic potential at both levels of truncation (compare Figs 3(b) and 3(c) with 3(a)), with an obvious increase in the finesse of spatial details at the more accurate dipole level. To properly evaluate this, it is important to note that the equipotential surface chosen for illustration explores challenging regions around the molecule located in the immediate vicinity, above and below, the closed surface from where control points were sampled (surface that is not shown in the figure to avoid obstructing the view of the equipotential surface, but located just 2Å above the black molecular surface). Inevitably, when the isosurface crosses the sampled surface towards the molecular surface (and towards the interior of the distribution of charge) the convergence of the CG model fails, and this explains the small inaccuracies visible in the reentrant regions of the isosurface. This is particularly true for the fine features of the isosurface around the two central openings marking the DNA-binding regions in the three pictures (Fig. 3).
In Tables 1–3 we further illustrate the performance of the above CG model with quantitative results. Table 1 shows the root mean square deviation (RMSD) between the approximate electrostatic potential of our CG model and the exact Coulomb potential at the control points only. The regular single-center multipole expansion data, (“Single Center” row), highlights how inadequate this approach is: not only does this approach not converge to the correct field with the increase in the truncation order, but it actually rapidly worsens with every additional order retained in the multipole expansion. By contrast, the CG model obtained by partitioning the system of charges, (the “Partitioning” row), converges systematically with the increase in the order of expansion, as expected.
Table 1.
RMSD between the approximate and exact electrostatic potential at control points only (2492 points) (e/Å) for the Arc repressor protein model (“Partitioning” shows the data for the 70-bead CG model in Fig. 3).
| Order lmax | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| Partitioning | 0.080 | 0.060 | 0.041 | 0.024 | 0.021 |
| Single Center | 0.200 | 0.200 | 3.10 | 20.0 | 61.5 |
Table 3.
RMSD between approximate and exact electrostatic potential at grid points outside the enclosing sphere centered at the center of charge (278890 points) (e/Å) for the Arc repressor protein model (“Partitioning” shows the data for the 70-bead CG model in Fig. 3).
| Order lmax | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| Partitioning | 0.0049 | 0.0019 | 0.0010 | 0.0006 | 0.0003 |
| Single Center | 0.0110 | 0.0110 | 0.0061 | 0.0050 | 0.0045 |
In Table 2 we provide the same type of calculations, but this time we keep all points outside the region covered by the interaction CG-beads, not only the control points. This set of points includes about 42000 points located inside cavities of the molecule where the regular multipole expansions do not apply. As a result, the divergence of the regular single-center multipole expansion is even more dramatic in this analysis. The CG model converges again, as expected.
Table 2.
RMSD between the approximate and exact electrostatic potential at grid points outside the partition (320909 points) (e/Å) for the Arc repressor protein. (“Partitioning” shows the data for the 70-bead CG model in Fig. 3).
| Order lmax | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| Partitioning | 0.0110 | 0.0070 | 0.0045 | 0.0033 | 0.0028 |
| Single Center | 4.8 × 10−2 | 4.8 × 10−2 | 2.4 × 101 | 2.5 × 102 | 4.5 × 104 |
Finally, Table 3 shows the RMSD only for points ‘outside’ the molecule, i.e., outside a spherical enclosure where, according to theory, both approaches should converge. Reassuringly enough, both methods indeed converge. However, the CG model still converges much faster than the regular expansion.
The above data clearly illustrate the significance of the lack of convergence, and therefore the total inadequacy of the regular, single-center multi-pole expansion, for modeling the electrostatic potential in the regions close to the molecule. At the same time the results unambiguously show that the partitioning technique proposed here completely resolves this limitation, and provides a very efficient convergence of the CG field to the exact value within the domain exterior to the control point sampling surface.
The final aspect that we analyze is the complexity of our CG approach. As already mentioned, for a given multipole expansion order, the complexity of the resulting CG model is determined by the set of control points. While the control points can be chosen arbitrarily in general, the most practical scenario corresponds to their selection from a closed surface enclosing the molecule. Obviously, the closer this surface to the surface of the molecule, the stronger the convergence constraints they impose, and the larger the number of interaction CG beads required. On the other hand, for a surface sufficiently distant from the molecule, the CG model should comprise a single interaction CG bead since for the surface at infinity the classical single-center multipole expansion provides accurate convergence to the exact electrostatic potential.
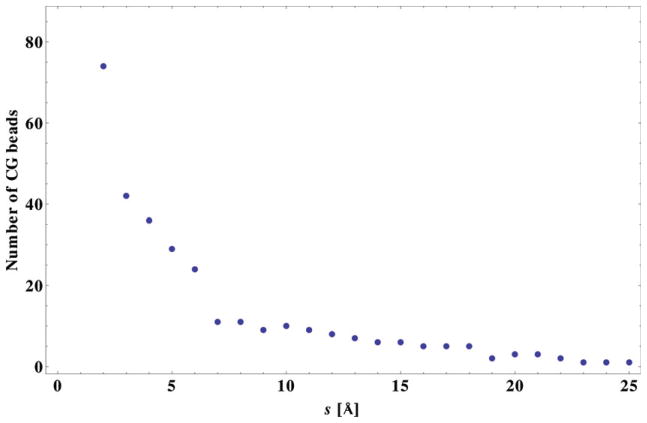
The model constructed above for the Arc repressor protein is rather refined and its complexity is, therefore, only about an order of magnitude lower than an atomic level model. Very often, simpler models are sought in practical applications. Such models can be obtained by imposing less stringent convergence requirements. One way to accomplish this is, for example, by selecting control points from a more distant surface. In Fig. 4 we provide a representation of the number of the CG beads of the model as a function of the offset distance of the sampled surface relative to the surface of the molecule. The sampled surfaces were generated by shifting the molecular surface, generated with the MSMS program [27], by various distances along the normal to the molecular surface. To prevent self-intersection of the shifted surface in regions of strong curvature (such as inside small cavities) we used a biger density of vertices (3.0Å−2 instead of 0.25 Å−2) and appropriately adjusted the rolling-ball radius [25, 26] of the reference molecular surface with the increase in the shift distance. The graph in Fig. 4 is typical for any three-dimensional molecule, and validates the expectations based on theoretical arguments for the computational complexity of the CG models generated with our approach.
Figure 4.
Size of the CG model (number of interaction CG beads) as a function of the offset distance s of the sampled surface relative to the surface of the molecule. Arc repressor protein data are used to generate this graph.
5. Conclusions
We have introduced a systematic approach for coarse-graining the electrostatic field created by large distributions of charge, such as those associated with biological molecules. The approach uses a geometric partitioning scheme to overcome the intrinsic limitations in accuracy of the regular multipole expansion in the immediate vicinity of the distribution of charge and, at the same time, to reduce the complexity in the computation of the intermolecular electrostatic interaction. We provide an algorithm for the implementation of the partitioning scheme and then illustrate it with a concrete example of a CG model for the electrostatic field of a biological molecule.
The analysis of the illustrative example confirms the performance expected on theoretical grounds: the approach resolves the convergence limitations of the regular multipole expansion techniques, and provides the possibility of adjusting the CG model with regard to degree of accuracy and computational efficiency. This later capability is enabled by two mechanisms: 1) the selection of control points defining the domain of convergence of the multipole expansions (which determines the number of interaction CG beads in the model – i.e., the granularity at which the distribution of charged is analyzed by the partitioning scheme), and 2) by the truncation order of these expansions, which allows the adjustment of accuracy.
In a typical application of our methods, the control points are chosen from a closed surface surrounding the molecule. Then, for a sufficiently dense sampling, the convergence of the resulting CG model is warranted anywhere outside that enclosing surface since the electrostatic potential satisfies Laplace’s equation in that domain. In other words, this mechanisms provides a practical path toward extending the applicability of multipole expansions from the exterior of a sphere to the exterior of a closed surface of arbitrary shape.
In the present form, the algorithms described here are appropriate for studies in which the coarse-grained molecular entities can be approximated as rigid. This limitation originates in the cost of calculating the initial CG model which is too complex to be applied repeatedly to a dynamically changing molecular configuration. It is possible however that updating an already computed CG model to configuration changes may be a simpler process. We are planning to address these aspects in future work.
Finally, we would like to emphasize that, while the development of the CG method described here was motivated by biological applications, the techniques involved are general and applicable to the modeling of the electrostatic field of any systems of charges. Therefore, they can be of interest for the computational simulation of other classes of physical systems.
Acknowledgments
We acknowledge support from NIH grant GM 078596 for the work reported in this paper.
Appendix A. Pseudo-code description of the partitioning algorithm
Here we provide a pseudo-code description of the algorithm for the partitioning of a distribution of charges into irreducible CG components. The elementary operations involved in constructing such an irreducible solution are represented by the functions IsIn(
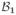 ,
,
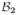 ) and MergeIn(
) and MergeIn(
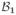 ,
,
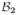 ) described below.
) described below.
IsIn(
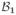 ,
,
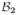 )
)
Input: An interaction CG bead pair
Output: True or False
| 1: | isin ← True | |
| 2: |
if e1i not inside S2 for any
|
|
| 3: | isin ← False | |
| 4: | end if | |
| 5: | return isin |
MergeIn(
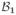 ,
,
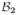 )
)
Input: An interaction CG bead pair
Output: A single interaction CG bead representing the first bead merged into the second
1: return
The function IsIn tests whether the set of charges belonging to the first bead are fully contained inside the covering sphere of the second bead (line 2) and returns False or T rue. Note, that testing for reducibility requires the application of the function in both directions. If both tests fail, then the pair of CG beads is irreducible already. If one of the tests succeeds, then the function MergeIn can be used to discard the redundant bead by incorporating all its charges into the other bead. In this way the size of the partition is reduced by one bead.
The algorithm described by the following Reduce function applies these two elementary operation repeatedly, in a recursive fashion, until an input partition
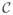 is reduced to an irreducible set of interaction CG beads. The CG partition is transformed in place in the steps 6–16 of a double loop over all pairs of CG beads. In each cycle, a pair is tested for reducibility and replaced by a merged bead if reducible (lines 7–9 and 11–12), or left alone if not. The program ends naturally when no reducible pair is left in the dynamically updated partition
is reduced to an irreducible set of interaction CG beads. The CG partition is transformed in place in the steps 6–16 of a double loop over all pairs of CG beads. In each cycle, a pair is tested for reducibility and replaced by a merged bead if reducible (lines 7–9 and 11–12), or left alone if not. The program ends naturally when no reducible pair is left in the dynamically updated partition
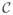 .
.
Reduce(
 )
)
Input: A CG partition (reducible, in general)
Output: An irreducible CG partition
| 1: | i ← 2 |
| 2: |
while i ≤ Length(
 ) do ) do
|
| 3: | im ← i − 1 |
| 4: | j ← i |
| 5: | while j ≤ Length(
 ) do ) do
|
| 6: | if IsIn(
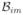 , ,
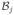 ) then ) then
|
| 7: | ReplacePart(
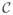 , ,
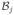 ← MergeIn( ← MergeIn(
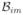 , ,
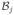 )) )) |
| 8: | j ← i |
| 9: | Drop(
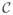 , ,
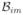 ) ) |
| 10: | else if IsIn(
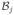 , ,
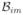 ) then ) then
|
| 11: | ReplacePart(
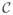 , ,
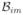 ← MergeIn( ← MergeIn(
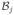 , ,
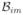 )) )) |
| 12: | Drop(
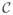 , ,
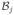 ) ) |
| 13: | else |
| 14: | Leave
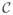 unchanged unchanged |
| 15: | j ← j + 1 |
| 16: | end if |
| 17: | end while |
| 18: | i ← i + 1 |
| 19: | end while |
| 20: |
return
|
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Greengard L, Rokhlin V. A fast algorithm for particle simulations. J Comput Phys. 1987;73:325. [Google Scholar]
- 2.Greengard L. The Rapid Evaluation of Potential Fields in Particle Systems. MIT Press; Cambridge, MA: 1988. [Google Scholar]
- 3.Greengard L, Rokhlin V. A new version of the fast multipole method for the laplace equation in three dimensions. Acta Numerica. 1997;6:229. [Google Scholar]
- 4.Appel A. An efficient program for many-body simulation. SIAM J Sci Stat Comput. 1985;6:85. [Google Scholar]
- 5.Barnes JE, Hut P. A hierarchical o(n log n) force-calculation algorithm. Nature. 1986;324:446. [Google Scholar]
- 6.Hernquist L. Hierarchical n-body methods. Comp Phys Comm. 1988;48:107. [Google Scholar]
- 7.Voth GA. Coarse-graining of condensed phase and biomolecular systems. 2008. [Google Scholar]
- 8.Chu JW, Izveko S, Voth GA. The multiscale challenge for biomolecular systems: coarse-grained modeling. Molecular Simulation. 2009;32:211–218. 3. [Google Scholar]
- 9.Klein ML, Shinoda W. Large-Scale molecular dynamics simulations of Self-Assembling systems. Science. 2008;321:798–800. 5890. doi: 10.1126/science.1157834. URL http://www.sciencemag.org/cgi/content/abstract/321/5890/798. [DOI] [PubMed]
- 10.Stone AJ. Distributed multipole analysis, or how to describe a molecular charge distribution. Chemical Physics Letters. 1981;83:233, 2. [Google Scholar]
- 11.Izvekov S, Voth GA. Multiscale coarse-graining of mixed Phospholipid/Cholesterol bilayer. J Chem Theory Comput. 2006;2:637. doi: 10.1021/ct050300c. [DOI] [PubMed] [Google Scholar]
- 12.Ayton GA, Noid WG, Voth GA. Multiscale modeling of biomolecular systems: in series and in parallel. Curr Opin Struct Biol. 2007;17:192. doi: 10.1016/j.sbi.2007.03.004. [DOI] [PubMed] [Google Scholar]
- 13.Golubkov PA, Ren P. Generalized coarse-grained model based on point multipole and Gay-Berne potentials. The Journal of Chemical Physics. 2006;125:064103, 6. doi: 10.1063/1.2244553. [DOI] [PubMed] [Google Scholar]
- 14.Nielsen SO, Lopez CF, Srinivas G, Klein ML. Coarse grain models and the computer simulation of soft materials. Journal of Physics: Condensed Matter. 2004;16:R481, 15. [Google Scholar]
- 15.Chowdhuri S, Tan M, Ichiye T. Dynamical properties of the soft sticky dipole-quadrupole-octupole water model: A molecular dynamics study. The Journal of Chemical Physics. 2006;125:144513, 14. doi: 10.1063/1.2357117. [DOI] [PubMed] [Google Scholar]
- 16.Ichiye T, Tan M. Soft sticky dipole-quadrupole-octupole potential energy function for liquid water: An approximate moment expansion. The Journal of Chemical Physics. 2006;124:134504, 13. doi: 10.1063/1.2161201. [DOI] [PubMed] [Google Scholar]
- 17.Sagui C, Pedersen LG, Darden TA. Towards an accurate representation of electrostatics in classical force fields: Efficient implementation of multipolar interactions in biomolecular simulations. The Journal of Chemical Physics. 2004;120:73, 1. doi: 10.1063/1.1630791. [DOI] [PubMed] [Google Scholar]
- 18.Wheatley R, Mitchell J. Gaussian multipoles in practice - electrostatic energies for intermolecular potentials. J Comput Chem. 1994;15:1187–1198. [Google Scholar]
- 19.Jackson JD. Classical Electrodynamics. John Wiley & Sons, Inc; New York: 1999. [Google Scholar]
- 20.Gramada A, Bourne PE. Resolving a distribution of charge into intrinsic multipole moments: A rankwise distributed multipole analysis. Phys Rev. 2008;E 78(6):066601. doi: 10.1103/PhysRevE.78.066601. [DOI] [PubMed] [Google Scholar]
- 21.Lee B, Richards F. The interpretation of protein structures: Estimation of static accessibility. Journal of Molecular Biology. 1971;55(3):379–400. IN3–IN4. doi: 10.1016/0022-2836(71)90324-X. [DOI] [PubMed] [Google Scholar]
- 22.Gramada A, Bourne PE. Efficient algorithm for computation of multipole CG models. To be published. [Google Scholar]
- 23.Schildbach JF, Milla ME, Jeffrey PD, Raumann BE, Sauer RT. Crystal structure, folding, and operator binding of the hyperstable arc repressor mutant PL8. Biochemistry. 1995;34:1405–12. 4. doi: 10.1021/bi00004a035. [DOI] [PubMed] [Google Scholar]
- 24.Berman HM, Westbrook J, Feng Z, Gilliland G, Bhat TN, Weissig H, Shindyalov IN, Bourne PE. The protein data bank. Nucleic Acids Res. 2000;28:235–42. 1. doi: 10.1093/nar/28.1.235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Connolly ML. Analytical molecular surface calculation. J Appl Cryst. 1983;16(5):548–558. [Google Scholar]
- 26.Richmond TJ. Solvent accessible surface area and excluded volume in proteins: Analytical equations for overlapping spheres and implications for the hydrophobic effect. Journal of Molecular Biology. 1984;178 (1):63–89. doi: 10.1016/0022-2836(84)90231–6.. [DOI] [PubMed] [Google Scholar]
- 27.Sanner MF, Olson AJ, Spehner JC. Reduced surface: an efficient way to compute molecular surfaces. Biopolymers. 1996;38:305–20. 3. doi: 10.1002/(SICI)1097-0282(199603)38:3%3C305::AID-BIP4%3E3.0.CO;2-Y. [DOI] [PubMed] [Google Scholar]