Abstract
Divergence measures provide a means to measure the pairwise dissimilarity between “objects,” e.g., vectors and probability density functions (pdfs). Kullback–Leibler (KL) divergence and the square loss (SL) function are two examples of commonly used dissimilarity measures which along with others belong to the family of Bregman divergences (BD). In this paper, we present a novel divergence dubbed the Total Bregman divergence (TBD), which is intrinsically robust to outliers, a very desirable property in many applications. Further, we derive the TBD center, called the t-center (using the ℓ1-norm), for a population of positive definite matrices in closed form and show that it is invariant to transformation from the special linear group. This t-center, which is also robust to outliers, is then used in tensor interpolation as well as in an active contour based piecewise constant segmentation of a diffusion tensor magnetic resonance image (DT-MRI). Additionally, we derive the piecewise smooth active contour model for segmentation of DT-MRI using the TBD and present several comparative results on real data.
Index Terms: Bregman divergence, diffusion tensor magnetic resonance image (DT-MRI), Karcher mean, robustness, segmentation, tensor interpolation
I. INTRODUCTION
In applications that involve measuring the dissimilarity between two objects (vectors, matrices, functions, images, and so on) the definition of a divergence/distance becomes necessary. A good divergence measure should be precise and statistically robust. The state of the art has many widely used divergences. The square loss function (SL) has been used widely for regression analysis; KL divergence [1], has been applied to compare the difference between two pdfs; and the Mahalanobis distance [2], is used to measure the dissimilarity between two random vectors of the same distribution. All the aforementioned divergences are special cases of the Bregman divergence which of late has been widely researched by many both from a theoretical and practical viewpoint, see [3]–[5] and references therein. At this juncture, it would be worth inquiring, why does one need yet another divergence? The answer would be that none of the existing divergences are statistically robust and one would need to use M-estimators from robust statistics literature to achieve robustness. This robustness however comes at a price, which is, computational cost and accuracy. Moreover, some of the divergences lack invariance to transformations such as similarity, affine, etc. Such invariance becomes important when dealing with for example, segmentation, it is desirable to achieve invariance to similarity or affine transformations that two different scans of the same patient might be related by.
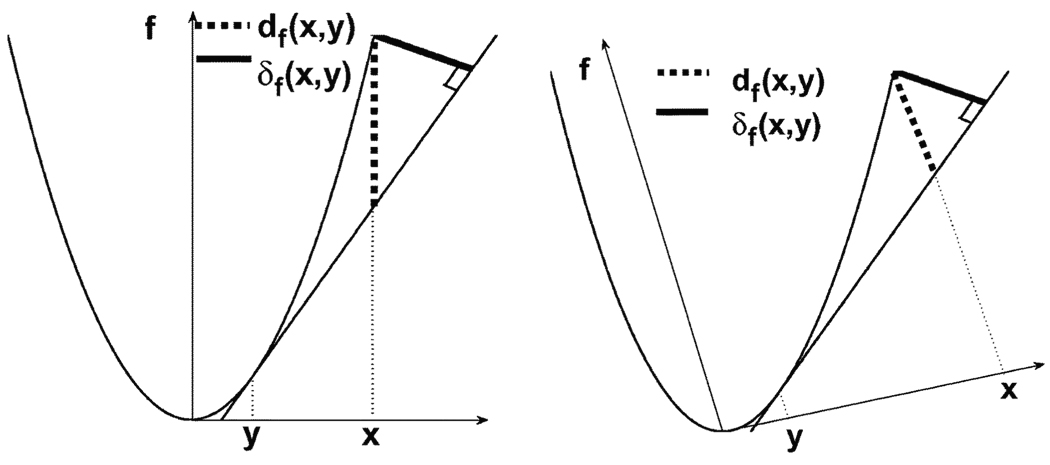
In this work, we propose a new class of divergences which measure the orthogonal distance (in contrast to the ordinal distance used in Bregman divergence) between the value of a differentiable convex function at the first argument and its tangent at the second argument. We dub this divergence the total Bregman divergence (TBD). A geometrical illustration of the difference between TBD and BD is given in Fig. 1. df(x, y) is the Bregman divergence between x and y based on a differentiable convex function f and δf(x, y) is the TBD between x and y based on the same differentiable convex function f. We can observe that df(x, y) will change if we apply a rotation to the graph (x, f(x)), while δf(x, y) does not.
Fig. 1.
In each figure, df(x, y) (dotted line) is BD, δf(x, y) (bold line) is TBD. Left figure shows df(x, y) and δf(x, y) before rotating the coordinate system. Right figure shows df(x, y) and δf(x, y) after rotating the coordinate system. df(x, y) changes with rotation while δf(x, y) is invariant with rotation.
Bregman divergence has been widely used in clustering, a ubiquitous task in machine learning applications. In clustering, cluster centers are defined using either a distance or a divergence. In this paper, we will define a cluster center using the TBD in conjunction with the ℓ1-norm that we dub the t-center. The t-center can be viewed as the cluster representative that minimizes the ℓ1-norm TBD between itself and the members of a given population. We derive an analytic expression for the t-center which gives it a major advantage over its rivals (for example, the Riemannian median for SPD tensors). Since, the TBD can be viewed as a weighted BD with the weight being inversely proportional to the magnitude gradient of the convex function, the t-center can thus be viewed as a weighted median of sorts. This weighting scheme makes t-center robust to noise and outliers, since it’s inversely dependent on the gradient of the convex function. We prove the robustness property theoretically in Section III and experimentally demonstrate it in the experiments section. Another salient feature of the t-center is that it can be computed very efficiently due to its closed form expression leading to efficient clustering algorithms, a topic of our continuing research.
To illustrate the robustness and computational efficiency properties of TBD, we applied our theory to the space of order-2 symmetric positive definite (SPD) tensors which are commonly encountered in applications such as diffusion tensor magnetic resonance imaging (DT-MRI) [6], [7], computer vision (structure tensors), elastography, etc. We prove that TBD between SPD tensors is invariant to transformations from the special linear group (SL(n)). Recall that, if A ∈ ℝn×n, then A ∈ SL(n) implies det A = 1. Given random variables X and Y, where X ~ 𝒩(x; P) and Y ~ 𝒩(y; Q), 𝒩(․; P) and 𝒩(․; Q) are Gaussian distributions with zero mean and covariances P and Q, respectively, we can define BD(X, Y) and generalize it to define TBD(X, Y). We can show that TBD(X, Y) is only related to P and Q, thus, TBD(P, Q) = TBD(X, Y). If x ↦ Ax, then P ↦ A′PA, TBD has the property of TBD(A′PA, A′QA) = TBD(P, Q), ∀A ∈ SL(n).We prove that the ℓ1 t-center, P*, for a population of SPD tensors {Qi} has an analytic form; furthermore, t-centers P* and P̂* corresponding to the original and transformed tensors is related by A and P̂* = A′P* A. This property makes t-center suitable for atlas construction applications in tensor field processing, which is very useful in DT-MRI [8]–[11]. Atlases are usually defined as representatives (most often as an average of sorts) of a population of images, shapes, etc. Atlas construction using t-center is efficient and robust to outliers, a property that is derived theoretically and demonstrated experimentally in Section IV. Further, we present quantitative comparisons between the proposed and other existing divergences, such as the Frobenius norm [12], Riemannian metric [9], [10], [13]–[15], symmetrized KL divergence [14], [16], [17] and the log-Euclidean distance [18]. Although some of these divergences are invariant to transformations in SL(n), none of them are statistically robust to outliers encountered in tensor field processing. When using the Riemannian metric to compute population statistics, neither the mean nor the median can be computed in closed form, which makes this metric computationally very expensive. Finally, we perform segmentation on synthetic tensor fields and real DTI images using TBD and compare the results with other divergences demonstrating the efficiency and robustness of TBD to outliers over its rivals.
The rest of this paper is organized as follows. In Section II we review the conventional Bregman divergence, followed by the definition of TBD and derivation of its properties. Section III introduces the t-center, which is derived from TBD, and delves into its better accuracy as a representative than centers obtained from other divergence measures or metrics. The detailed description of the experimental design and results with quantitative comparison with other divergence are presented in Section IV. Finally, we draw conclusions in Section VI.
II. TOTAL BREGMAN DIVERGENCE
In this section, we first recall the definition of conventional Bregman divergence [4] and then define the TBD. Both divergences are dependent on the corresponding convex and differentiable function that f : X ↦ ℝ that induces the divergence.
A. Definition of TBD and Examples
Definition II.1: The Bregman divergence d associated with a real valued strictly convex and differentiable function f defined on a convex set X between points x, y ∈ X is given by
| (1) |
where ∇f(y) is the gradient of f at y and 〈·, ·〉 is the inner product determined by the space on which the inner product is being taken.
For example, if f : ℝn ↦ ℝ, then 〈·, ·〉 is just the inner product of vectors in ℝn, and df(·, y) can be seen as the distance between the first order Taylor approximation to f at y and the function evaluated at x. Bregman divergence df is non-negative definite and does not satisfy the triangular inequality thus making it a divergence. As shown in Fig. 1, Bregman divergence measures the ordinate distance.
Definition II.2: The TBD δf associated with a real valued strictly convex and differentiable function f defined on a convex set X between points x, y ∈ X is defined as
| (2) |
〈·, ·〉 is inner product as in definition II.1, and ‖∇f(y)‖2 = 〈∇f(y), ∇f(y)〉 generally.
Consider the Bregman divergence df(η, ζ) = f(η) − f(ζ) − 〈η − ζ, ∇f(ζ)〉 obtained for strictly convex and differentiable generator f. Let x̂ denote the point (x, z = f(x)) of X × ℝ lying on the graph ℱ = {x̂ = (x, z = f(x))|x ∈ X}. We visualize the Bregman divergence as the z-vertical difference between the hyperplane Hζ tangent at ζ̂ and the hyperplane parallel to Hζ and passing through η̂
| (3) |
with Hζ(x) = f(ζ) + 〈x − ζ, ∇f(ζ)〉. If instead of taking the vertical distance, we choose the minimum distance between those two hyperplanes Hη and Hζ, we obtain the total Bregman divergence (by analogy to total least square fitting where the projection is orthogonal).
Since the distance between two parallel hyperplanes 〈x, a〉 + b1 = 0 and 〈x, a〉 + b2 = 0 is |b1 − b2|/‖a‖, letting a = (∇f(ζ), −1) and b1 = f(η) − 〈η, ∇f(ζ)〉, and b2 = f(ζ) − 〈ζ, ∇f(ζ)〉, we deduce that the total Bregman divergence is
| (4) |
As shown in Fig. 1, TBD measures the orthogonal distance. Compared to the BD, TBD contains a weight factor (the denominator) which complicates the computations. However, this structure brings up many new and interesting properties and makes TBD an “adaptive” divergence measure in many applications. Note that, in practice, X can be an interval, the Euclidean space, a d-simplex, the space of non-singular matrices or the space of functions [19]. For instance, in the application to SPD tensor interpolation, we let p and q be two pdfs, and f(p) ≔ ∫ p log p, then δf(p, q) becomes what we call the Total Kullback–Leibler divergence (tKL). Note that if q is a pdf or a probability mass function (pmf), then ‖∇f(q)‖2 = ∫(1+log q)2q. More on tKL later in Section IV. Table I lists some TBDs with various associated convex functions f.
TABLE I.
TBD δf Corresponding to f and the t-Center for a Set of Objects {xi}. ẋ = 1 − x, ẏ = 1 − y, x′ is the Transpose of x. Δd is d-Simplex. c is the Normalization Constant to Make it a pdf,
| X | f (x) | δf (x, y) | t-center | Remark | ||
|---|---|---|---|---|---|---|
| ℝ | x2 | (x−y)2 (1+4y2)−1/2 | ∑i wixi | total square loss (tSL) | ||
| ℝ − ℝ− | x log x |
|
∏i(xi)wi | |||
| [0, 1] | x log x + ẋ log ẋ |
|
|
total logistic loss | ||
| ℝ+ | − log x |
|
1/(∑i wi/xi) | total Itakura-Saito distance | ||
| ℝ | ex |
|
∑i wixi | |||
| ℝd | ‖x‖2 |
|
∑i wixi | total squared Euclidean distance | ||
| ℝd | x′ Ax |
|
∑i wixi | total Mahalanobis distance | ||
| Δd |
|
|
c∏i(xi)wi | total KL divergence (tKL) | ||
| ℂm × n |
|
|
∑i wixi | total squared Frobenius | ||
III. t-CENTER
In many applications of computer vision and machine learning such as image and shape retrieval, clustering, classification, etc., it is common to seek a representative for a set of objects having similar features. This representative normally is a cluster center of sorts, thus, it is desirable to seek a center that is robust to outliers and is efficient to compute. In this section, we use the TBD to derive an ℓ1-norm cluster center that we call the t-center, and explore its properties.
A. Definition
Let f : X ↦ ℝ be a convex and differentiable function and E = {x1, x2, ⋯, xn} be a set of n points in X, then, the TBD between a point x ∈ X and E associated with f and ℓp norm is defined as
| (5) |
The ℓp-norm center is defined as . These centers bear the name of median (p = 1), mean (p = 2) and circumcenter (p → ∞). In this paper, we call the median (p = 1) the t-center and will derive an analytic form for the t-center and focus on its applications. Before delving into the t-center, we define the circumcenter and the centroid (mean).
B. ℓ∞-Norm Circumcenter xc
In the limiting case, the circumcenter amounts to solving for
| (6) |
xc does not have a closed form, even though it can be solved to an arbitrarily fine approximation in Riemannian cases [5].
C. ℓ2-Norm Centroid xm
| (7) |
Like the ℓ∞-norm circumcenter, ℓ2-norm mean does not have a closed form in general and is hence expensive to compute.
D. The ℓ1-Norm t-Center
Given a set E, we can obtain the ℓ1-norm t-center x* of E by solving the minimization problem
| (8) |
Theorem III.1: The t-center of a population of objects (densities, vectors, etc.) with respect to a given divergence exists, and is unique.
Proof: To find x*, we take the derivative of with respect to x, and set it to 0, as in
| (9) |
Solving (9) yields
| (10) |
where wi = (1 + ‖∇f(xi)‖2)−1/2 is the weight that depends on ∇f(xi). Recall that TBD δf(·, y) is convex for any fixed y ∈ X, we know that is also convex as it is the sum of n convex functions. Hence, the solution to (9) exists and is indeed a minimizer of F(x). Furthermore, since f is convex, ∇f is monotonic, so x* is unique.
To obtain an explicit formula for x*, we will make use of the dual space. Suppose g is the legendre dual function of f in the space X, and the dual space is denoted as Y. Then ∀x ∈ X, ∃y ∈ Y
| (11) |
where x and y satisfy y = ∇f(x) and x = ∇g(y). Thus far, we know that the t-center x* satisfies (10), meaning that its legendre dual y* should satisfy , and x* = ∇g(y*).
Note that, in most cases, if f is given, then we can get the explicit form for x*, but x* does not have the same expression for all convex functions, instead, x* is dependent on the convex generator function for the chosen divergence. For a better illustration of theorem III.1, we provide three concrete examples of TBD with their t-centers in analytic form. The first is for the square loss function that we call total square loss (tSL), the second is for the exponential function and the third is the total Kullback–Leibler (tKL) as a measure of divergence between probability densities.
tSL: f(x) = x2, the t-center x* = (∑i wixi)/(∑i wi), where ;
Exponentials: f(x) = ex, the t-center x* = (∑i wixi)/(∑i wi), where wi = (1 + e2xi)−1/2;
- tKL: f(q) = ∫ q log qdx, which is the negative entropy [1], and E = {q1, q2, ⋯, qn} is a set of pdfs, the t-center
q* is obtained by solving the Euler–Lagrange equation of the minimization in (12), to obtain(12)
where c is a normalization constant such that ∫X q*(x)dx = 1. Furthermore, the t-centers for the most commonly used divergences can be derived in analytic form as shown in the Table I.
Theorem III.2: The t-center is statistically robust to outliers.
Proof: The robustness of t-center is analyzed by the influence function of an outlier y. Let x* be the t-center of E = {x1, ⋯, xn}. When ε% (ε small) of outlier y is mixed with E, x is influenced by the outliers, and the new center becomes to x̃* = x* + εz(y). We call z(y) the influence function. The center is robust when z(y) does not grow even when y is very large. The influence curve is given explicitly in the case of ℓ1-norm. x̃* is the minimizer of
| (13) |
Hence, by differentiating the above function, setting it equal to zero at x̃* = x* + εz and using the Taylor expansion, we have
| (14) |
where . Hence, the t-center is robust when z is bounded, i.e., ∀y, |z| < c, c is a constant
| (15) |
Since w(y) ≥ ‖∇f(y)‖ and w(y) ≥ 1, therefore
| (16) |
To make this proof more understandable, we give a simple example of the Euclidean case when f(x) = (1/2) ‖x‖2, x ∈ ℝd. Then
| (17) |
and , when ‖y‖ is large, this is approximated by z(y) = G−1(y/‖y‖), which implies z is bounded, and the t-center is robust for large ‖y‖.
Note that the influence function for the ordinary Bregman divergence is z = y, and hence is not robust.
Using the ℓ1-norm t-center x* has advantages over other centers resulting from the norms with p > 1 in the sense that x* has an analytic form and is robust to outliers. These advantages are explicitly evident in the experiments presented subsequently.
IV. TBD APPLICATIONS
We now develop the applications of the t-center in interpolating diffusion tensors in DT-MRI data and segmentation of tensor fields specifically DT-MRI.
A. SPD Tensor Interpolation Applications
We now define tKL, the total Kullback–Leibler divergence between symmetric positive definite (SPD) rank-2 tensors (SPD matrices), and show that it is invariant to transformations belonging to the special linear group SL(n). Further, we compute the t-center using tKL for SPD matrices, which has a closed form expression, as the weighted harmonic mean of the population of the tensors.
tKL between order two SPD tensors/matrices P and Q is derived using the negative entropy of the zero mean Gaussian density functions they correspond to. Note that order two SPD tensors can be seen as covariance matrices of zero mean Gaussian densities. Suppose
| (18) |
| (19) |
then
| (20) |
where c = (3n/4) + (n2 log 2π/2) + ((n log 2π)2/4). When an SL(n) transformation is applied on x, i.e., x ↦ Ax, then P ↦ A′PA and Q ↦ A′QA. It is easy to see that
| (21) |
which means that tKL between SPD tensors is invariant under the group action, when the group member belongs to SL(n). Given an SPD tensor set , its t-center P* can be obtained from (12) and
| (22) |
where . It can be seen that wi(Qi) = wi(A′QiA), ∀A ∈ SL(n). If a transformation A ∈ SL(n) is applied, the new t-center will be P̂* = (∑ wi(A′QiA)−1)−1 = A′P* A, which means that if are transformed by some member of SL(n), then the t-center will undergo the same transformation.
Also we can compute the tSL between P and Q from the density functions p, q and f(p) = ∫ p2dx, and the result is
also tSL(P, Q) = tSL(A′PA, A′QA), ∀A ∈ SL(n), which means that tSL is also invariant under SL(n) transformations. Similarly, we can also prove that the total Itakura-Saito distance and total squared Euclidean distance between SPD matrices are invariant under SL(n) transformations. For the rest of this paper, we will focus on tKL.
There are several ways to define the distance between SPD matrices, e.g. using the Frobenius norm [12], Riemannian metric [10], [13]–[15], symmetrized KL divergence [14], [16], [17] and the log-Euclidean distance [18], respectively, defined as
| (23) |
| (24) |
where λi, i = 1, ⋯, n, are eigenvalues of P−1Q
| (25) |
| (26) |
dF (․, ․) is not invariant to transformations in SL(n), dR(․, ․), KLs(․, ․) and LE(․, ․) are invariant to transformations in GL(n), but none of them are robust to outliers encountered in the data for e.g., in tensor interpolation. For dR(․, ․), neither its mean nor its median is in closed form, which makes it computationally very expensive as the population size and the dimensionality of the space increases. Here, the Karcher mean denoted by is defined as the minimizer of the sum of squared Riemannian distances and the median is minimizer of the sum of Riemannian distances [9]
For simplicity in notation, we denote by dM(P, Qi), and . Even though there are many algorithms (for example [8]–[10], [15]) to solve the geodesic mean and median, most of them adopt an iterative (gradient descent) method. Performing gradient descent on matrix manifolds can be tricky and rather complicated in the context of convergence issues (see [20]) and hence is not preferred over a closed form computation.
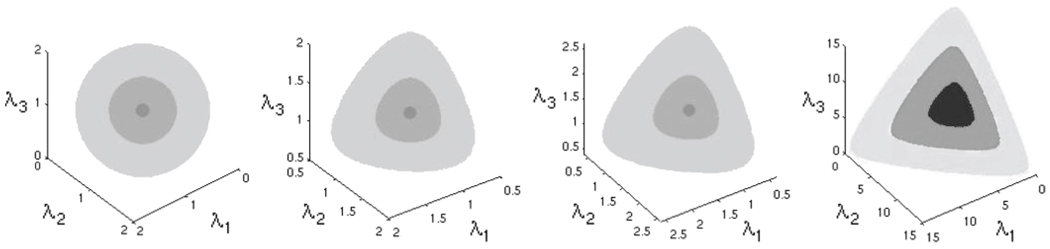
KLs in (25) has a closed form mean [14], [16], which is 𝒢(𝒜(Q1, ⋯, Qm), ℋ(Q1, ⋯, Qm), where 𝒜 is the arithmetic mean of , ℋ is the harmonic mean of , and 𝒢 is the geometric mean of 𝒜 and ℋ. However, it can be shown that the mean computed using sum of squared KLs divergences is not statistically robust since all tensors are treated equally. This is because, neither KLs nor the sum of squared KLss are robust functions. This is demonstrated in the experimental results to follow. First we will observe the visual difference between the aforementioned divergences/distances. Fig. 2 shows the isosurfaces centered at the identity matrix with radii r = 0.1, 0.5 and 1 respectively. From left to right are dF(P, I) = r, dR(P, I) = r, KLs(P, I) = r and tKL(P, I) = r. These figures indicate the degree of anisotropy in the divergences/distances.
Fig. 2.
The isosurfaces of dF (P, I) = r, dR (P, I) = r, KLs (P, I) = r and tKL (P, I) = r shown from left to right. The three axes are eigenvalues of P.
B. Piecewise Constant DTI Segmentation
Given a noisy diffusion tensor image (DTI) T0(x)—a field of positive definite matrices, our model for DTI segmentation is based on the Mumford–Shah functional [21]
| (27) |
where α and β are control parameters, δ is the tKL divergence same as (20). Ω is the region of the tensor field, T(x) is an approximation to T0(x), which can be discontinuous only along C. However, in a simplified segmentation model, a field T0(x) can be represented by piecewise constant regions [21], [22]. Therefore, we consider the following binary segmentation model for DTI:
| (28) |
T1 is the t-center of DTI for the region R inside the curve C and T2 is the t-center of the DTI for the region Rc outside C
| (29) |
| (30) |
The Euler Lagrange equation of (28) is
| (31) |
where κ is the curvature, κ = ∇ · (∇C/|∇C|), and N is the normal of C, N = ∇C. C can be updated iteratively according to the following equation:
| (32) |
At each iteration, we will fix C, update T1 and T2 according to (29) and (30), and then freeze T1 and T2 to update C.
In the level set formulation of the active contour [23], let ϕ be the signed distance function of C and choose it to be negative inside and positive outside. Then the curve evolution (32) can be reformulated using the level set framework
| (33) |
C. Piecewise Smooth DTI Segmentation
For complicated DTI images, the piecewise constant assumption does not hold. Therefore, we have to turn to the more general model, the piecewise smooth segmentation. In this paper, we follow Wang et al.’s [16] model but replace their divergence (KLs) with tKL, resulting in the following functional:
the third term measures the lack of smoothness of the field using the Dirichlet integral [24], giving us the following curve evolution equation:
where NR and NRc are the sets of x’s neighboring pixels inside and outside of the region R respectively. In the discrete case, one can use appropriate neighborhoods for 2-D and 3-D. We apply the two stage piecewise smooth segmentation algorithm in [16] to numerically solve this evolution.
V. EXPERIMENTAL RESULTS
We performed two sets of experiments here: 1) tensor interpolation and 2) tensor field segmentation. The experimental results are compared with those obtained by using other divergence measures discussed above.
A. Tensor Interpolation
SPD tensor interpolation is a crucial component of DT-MRI analysis involving segmentation, registration and atlas construction [25], where a robust distance/divergence measure is very desirable. First, we perform tensor interpolation on a set of tensors with noise and outliers. We fix an SPD tensor Ḡ as the ground truth tensor and generate noisy tensors G from it by using a the Monte Carlo simulation method as was done in [26], [27]. This entails, given a b-value (we used 1200 s/mm2) a zero gradient baseline image S̄0, and six vectors , the magnitude of the noise free complex-valued diffusion weighted signal is given by, . We add Gaussian distributed (mean zero and variance σ2 = 0.1) noise to the real and imaginary channels of this complex valued diffusion weighted signal and take its magnitude to get . Si then has a Rician distribution with parameters (σ, S̄i). G is obtained by fitting the using Log-Euclidean tensor fitting. To generate outliers, we first generate a 3 × 3 matrix Z, with each entry drawn from the normal distribution, and the outlier tensor G is given by G = exp(ZZ′). We compute the eigen-vectors U and eigen-values V of G, i.e. G = U diag (V)U′, and then rotate U by a rotation matrix r(α, β, γ) in 3-D, to get Uo, where α, β and γ are uniformly distributed in [0, π/2]. Then the outlier is given by . To generate an image, the same process is repeated at every randomly chosen voxel.
The tKL t-center, the geometric median, the geometric mean, the KLs mean and the log-Euclidean mean M for 21 SPD tensors along with 0, 5, 10, 15, and 20 outliers are then computed. The difference between the various means/medians, and the ground truth Ḡ are measured in four ways, using the Frobenius norm ‖Ḡ − M‖F, the ℓ∞ distance ‖Ḡ − M‖∞, angle between the principal eigenvectors of M and Ḡ, and the difference of fractional anisotropy index (FA) ([28], [29]) for M and Ḡ, i.e., |FA(M) − FA(Ḡ)|. The results are shown in Table II from left to right, top to bottom.
TABLE II.
Frobenius Norm Distance dF, ℓ∞ Distance, Angle Between the Principle Eigenvectors of the Ground Truth and the Eigenvector of the Mean/Median Found by the Divergences, and the Difference Between the FA of the Ground Truth and the Computed Mean/Median are Shown From Left to Right, Top to Bottom. There are 21 Original Tensors and the Number of Outliers is Shown in the Top Row of Each Table
| Errors in computed mean measured by Frobenius norm dF | Errors in computed mean measured by ℓ∞ | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| # of outliers | 0 | 5 | 10 | 15 | 20 | # of outliers | 0 | 5 | 10 | 15 | 20 | |
| tKL | 0.8857 | 1.0969 | 1.1962 | 1.3112 | 1.4455 | tKL | 0.6669 | 0.8687 | 1.0751 | 1.1994 | 1.5997 | |
| dR | 1.3657 | 1.4387 | 1.5348 | 1.6271 | 1.7277 | dR | 0.8816 | 1.3498 | 1.5647 | 1.8826 | 2.1904 | |
| dM | 1.4291 | 1.5671 | 1.8131 | 2.1560 | 2.5402 | dM | 1.3056 | 1.4160 | 1.6755 | 1.9390 | 2.5153 | |
| KLs | 3.4518 | 3.5744 | 3.7122 | 4.1040 | 4.3235 | KLs | 4.1738 | 4.3352 | 4.3463 | 4.3984 | 4.4897 | |
| LE | 1.0638 | 1.5721 | 1.6249 | 1.6701 | 1.8227 | LE | 0.8768 | 1.2843 | 1.6947 | 1.9418 | 2.2574 | |
| Errors in computed angle | Errors in computed FA | |||||||||||
| # of outliers | 0 | 5 | 10 | 15 | 20 | # of outliers | 0 | 5 | 10 | 15 | 20 | |
| tKL | 0.1270 | 0.3875 | 0.6324 | 1.8575 | 2.9572 | tKL | 0.0635 | 0.0738 | 0.0753 | 0.0792 | 0.0857 | |
| dR | 0.4218 | 0.9058 | 8.9649 | 17.4854 | 44.9157 | dR | 0.0983 | 0.1529 | 0.1857 | 0.1978 | 0.2147 | |
| dM | 0.8147 | 1.1985 | 10.1576 | 21.8003 | 43.7922 | dM | 0.1059 | 0.1976 | 0.2008 | 0.2193 | 0.2201 | |
| KLs | 0.8069 | 0.9134 | 14.9706 | 26.1419 | 44.9595 | KLs | 0.0855 | 0.1675 | 0.2005 | 0.2313 | 0.2434 | |
| LE | 0.6456 | 0.9373 | 8.9937 | 17.0636 | 44.7635 | LE | 0.0972 | 0.1513 | 0.1855 | 0.1968 | 0.2117 | |
From the tables, we can see that the t-center yields the best approximation to the ground truth, and faithfully represents the directionality and anisotropy. The robustness of t-center over others such as the Riemannian mean and median, KLs mean, and log-Euclidean mean is quite evident from this table. Even though geometric median seems to be competitive to the t-center obtained using tKL in the case of lower percentage of outliers, the geometric median computation however is much slower than that of t-center computation. This is because the t-center for tKL has a closed form while the geometric median does not. Table III shows the CPU time to find the tensor mean/median using different divergences. We use 1000 SPD tensors, along with 0, 10, 100, 500, and 800 outliers respectively. All tensors are generated in the same way as described in the first experiment. The time is averaged by repeating the experiment 10 times on a PC, with Intel Core 2 Duo CPU P7370, 2 GHz, 4 GB RAM, on 32-bit Windows Vista OS. Table II and III depict the superior robustness to outliers and the computational efficiency in estimating the tKL t-center for SPD tensor interpolation in comparison to its rivals.
TABLE III.
Time (Seconds) Spent in Finding the Mean/Median Using Different Divergences. There are 1000 Original Tensors and the Number of Outliers is Shown in the Top Row
| time | |||||
|---|---|---|---|---|---|
| Divergences\# of outliers | 0 | 10 | 100 | 500 | 800 |
| tKL | 0.02 | 0.02 | 0.02 | 0.03 | 0.03 |
| KLs | 0.03 | 0.03 | 0.03 | 0.04 | 0.04 |
| dR | 0.58 | 1.67 | 4.56 | 93.11 | 132.21 |
| dM | 0.46 | 1.42 | 3.13 | 72.74 | 118.05 |
| LE | 0.02 | 0.02 | 0.03 | 0.03 | 0.03 |
B. Tensor Field Segmentation
We now describe experiments on segmentation of synthetic and real DTI images.
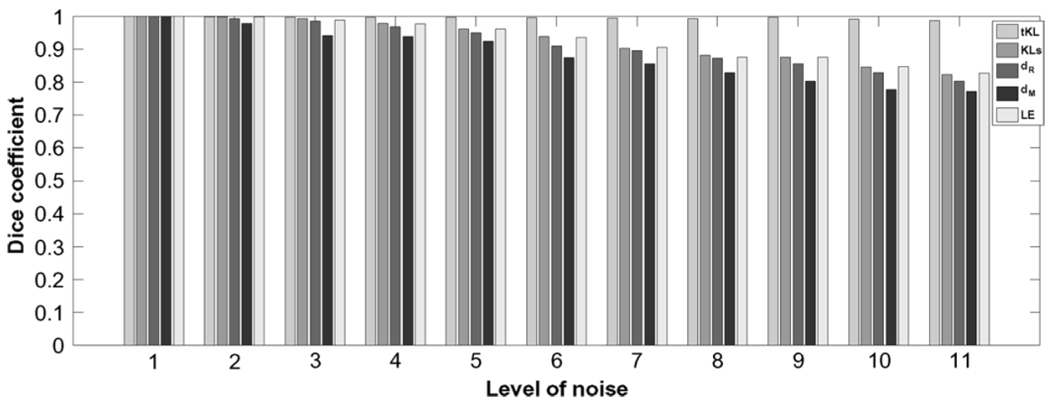
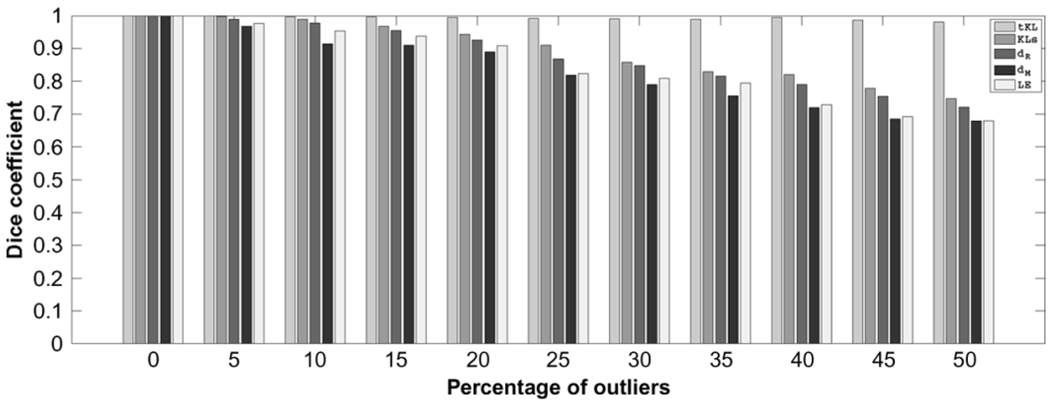
Segmentation of Synthetic Tensor Fields: The first synthetic tensor field is composed of two types of homogeneous tensors. Fig. 3 depicts the synthetic data and the segmentation results. We added different levels of noise to the tensor field using the method described in Section V-A, segmented it using the aforementioned divergences and compared the results using the dice coefficient [30]. We also added different percentages of outliers to the tensor fields and segmented the resulting tensor fields. Fig. 4 depicts the comparison of segmentation results from different methods using the dice coefficient, for varying noise levels with σ varying from 0, 0.02, 0.04, ⋯, 0.2). Fig. 5 displays the comparison of dice coefficient with different percentage (0, 5, 10, ⋯, 50) of outliers. The results show that even in the presence of large amounts of noise and outliers, tKL yields very good segmentation results in comparison to rivals. However, in our experiments, we observed that the segmentation accuracy is inversely proportional to the variance of the outlier distribution.
Segmentation of DTI Images: In this section, we present segmentation results on real DTI images from a rat spinal cord, an isolated rat hippocampus and a rat brain. The data were acquired using a PGSE with TR = 1.5 s, TE = 28.3 ms, bandwidth = 35 Khz, 21 diffusion weighted images with a b-value of 1250 s/mm2 were collected. A 3 × 3 diffusion tensor in each DTI image is illustrated as an ellipsoid [16], whose axes’ directions, and lengths correspond to its eigen-vectors, and eigen-values, respectively. The same initialization is used for each divergence based segmentation. We let all the divergence based methods run until convergence, record their time and compare the results.
Fig. 3.
From left to right are initialization, intermediate step, and final segmentation.
Fig. 4.
Dice coefficient comparison for tKL, KLs, dR, dM, and LE segmentation of synthetic tensor field with increasing level (x-axis) of noise.
Fig. 5.
Dice coefficient comparison for tKL, KLs, dR, dM, and LE segmentation of synthetic tensor field with increasing percentage (x-axis) of outliers.
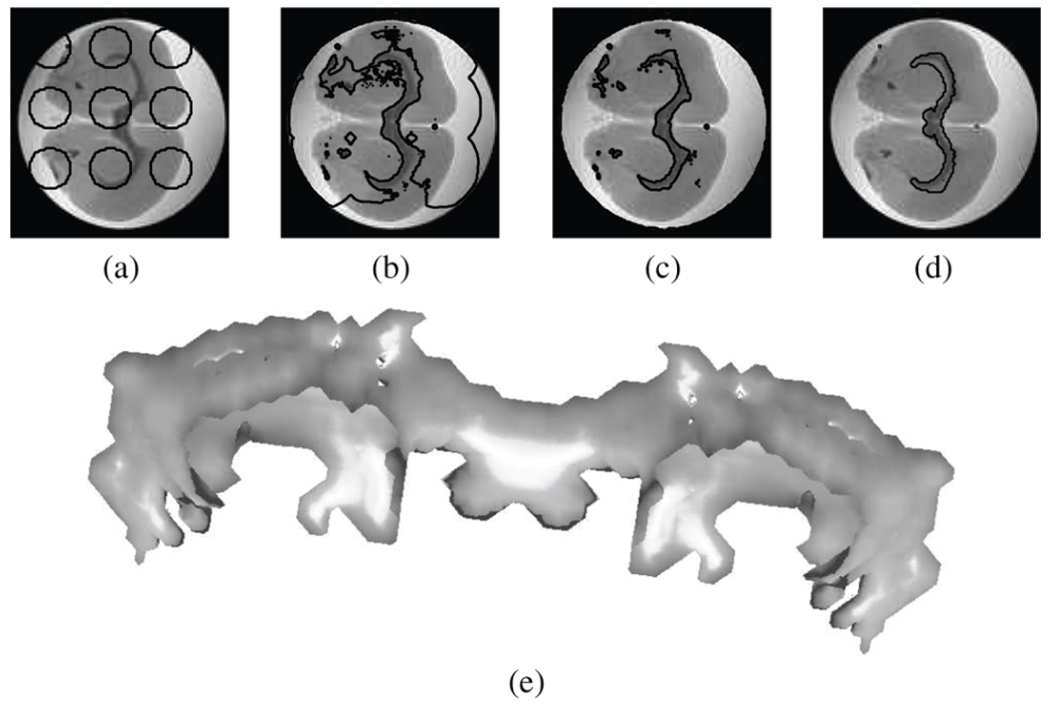
We apply the piecewise constant segmentation model on a single slice (108 × 108) of the rat spinal cord, and apply the piecewise smooth segmentation model on the molecular layer from single slices of size (114 × 108) for rat corpus callosum (CC) and (90 × 90) for the rat hippocampus, respectively. Fig. 6(a)–(c) shows the initialization, Fig. 6(d) shows the segmentation results, and Table IV records their execution time. The results confirm that when compared to other divergences, tKL yields a more accurate segmentation in a significantly shorter amount of CPU time.
Fig. 6.
(a)–(c) Initialization. (d) Segmentation results, from left to right, using tKL, KLs, dR, dM, and LE.
TABLE IV.
Time (Seconds) Comparison for Segmenting the Rat Spinal Cord, Corpus Callosum and Hippocampus Using Different Divergences
| Divergences | tKL | KLs | dR | dM | LE |
|---|---|---|---|---|---|
| Time for Cord | 33 | 68 | 72 | 81 | 67 |
| Time for CC | 87 | 183 | 218 | 252 | 190 |
| Time for hippocampus | 159 | 358 | 545 | 563 | 324 |
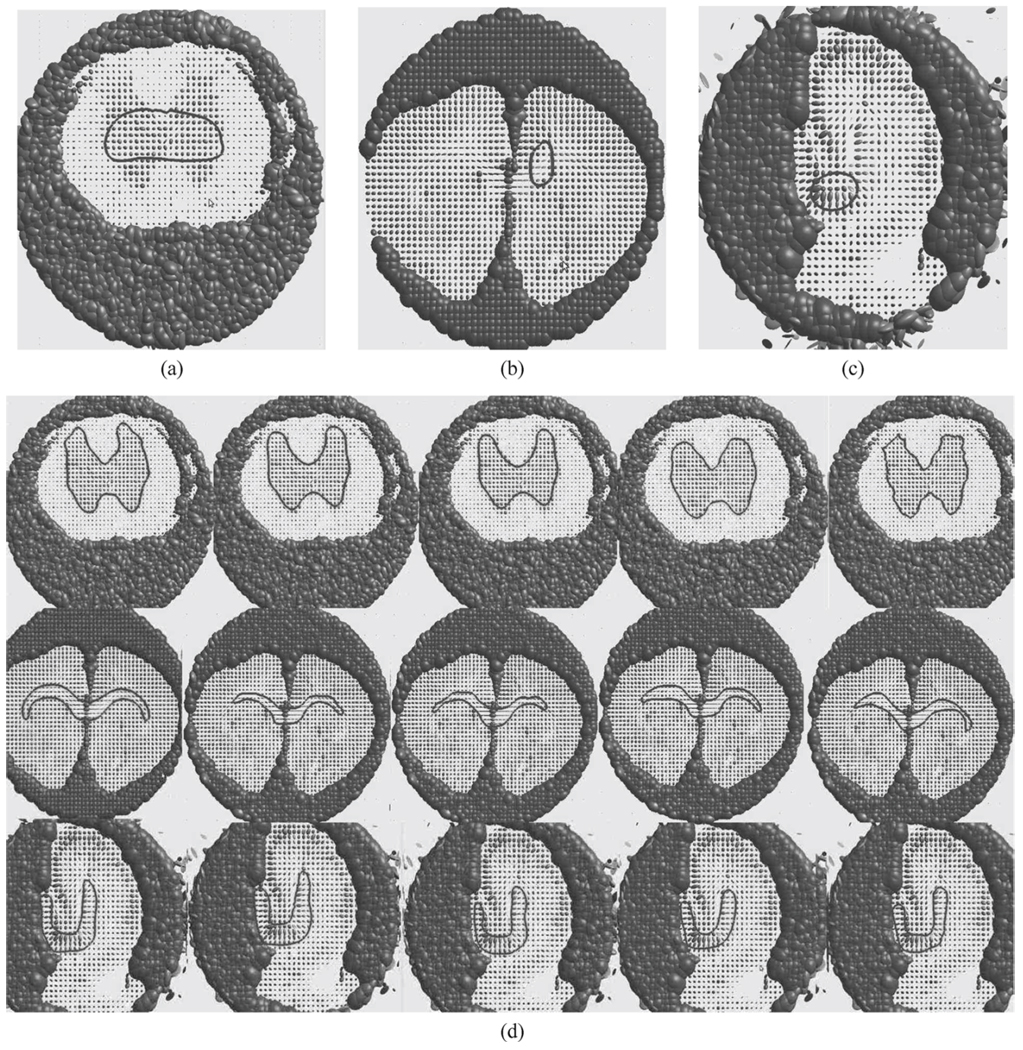
Apart from segmentation in 2-D slices, we also demonstrate 3-D DTI image segmentation using the proposed divergence. Fig. 7 depicts the process of segmenting rat corpus callosum (114 × 108 × 11) using the piecewise constant segmentation model. The result demonstrates that tKL can segment this white matter bundle quite well.
Fig. 7.
tKL segmentation of a 3-D rat corpus callosum. (a)–(d) A 2-D slice of the corresponding evolving surface, from left to right are initialization, intermediate steps and final segmentation. (e) A 3-D view of the segmentation result.
VI. CONCLUSION
In this paper, we developed a novel divergence dubbed the TBD, that is intrinsically robust to noise and outliers. The goal here was not simply to develop yet another divergence measure but to develop an intrinsically robust divergence. This was achieved via alteration of the basic notion of divergence which measures the ordinate distance between its convex generator and its tangent approximation to the orthogonal distance between the same. This basic idea parallels the relationship between least-squares and total least squares but the implications are far more significant in the field of information geometry and its applications since the entire class of the well known Bregman divergences have been redefined and some of their theoretical properties studied. Specifically, we derived an explicit formula for the t-center which is the TBD-based median, that is robust to outliers. In the case of SPD tensors, the t-center was shown to be SL(n) invariant. However, the story is not yet complete and further investigations are currently underway.
The robustness (to outliers) property of TBD was demonstrated here via applications to SPD tensor field interpolation and segmentation. The results favorably demonstrate the competitiveness of our newly defined divergence in comparison to existing methods not only in terms of robustness, but also in terms of computational efficiency and accuracy as well. Our future research will focus on applications of TBD to atlas construction, registration and other such tasks applied to DWMRI acquired from human brains.
Acknowledgments
The work of B. C. Vemuri was supported by the National Institutes of Health under the grants EB007082 and NS066340, respectively.
Contributor Information
Baba C. Vemuri, Department of Computer and Information Science and Engineering (CISE), The University of Florida, Gainesville, FL 32611 USA, (vemuri@cise.ufl.edu).
Meizhu Liu, Department of Computer and Information Science and Engineering (CISE), The University of Florida, Gainesville, FL 32611 USA.
Shun-Ichi Amari, Riken Brain Science Institute, Saitama 351-0198, Japan.
Frank Nielsen, Laboratoire d’Informatique (LIX), École Polytechnique, 91128 Palaiseau Cedex, France.
REFERENCES
- 1.Thomas JA, Cover TM. Elements of Information Theory. New York: Wiley; 1991. [Google Scholar]
- 2.Mahalanobis P. Proc. Nat. Inst. Sci. India: 1936. On the generalised distance in statistics; pp. 49–55. [Google Scholar]
- 3.Amari S. Differential-Geometrical Methods in Statistics. Heidelberg, Germany: Springer; 1985. [Google Scholar]
- 4.Banerjee A, Merugu S, Dhillon IS, Ghosh J. Clustering with Bregman divergences. J. Mach. Learn. Res. 2005;vol. 6:1705–1749. [Google Scholar]
- 5.Nielsen F, Nock R. On the smallest enclosing information disk. Inf. Process. Lett. 2008;vol. 105:93–97. [Google Scholar]
- 6.Basser PJ, Mattiello J, Lebihan D. Estimation of the effective self-diffusion tensor from NMR spin echo. J. Magn. Reson. 1994;vol. 103:247–254. doi: 10.1006/jmrb.1994.1037. [DOI] [PubMed] [Google Scholar]
- 7.Jian B, Vemuri BC. A unified computational framework for deconvolution to reconstruct multiple fibers from diffusion weighted MRI. IEEE Trans. Med. Imag. 2007 Nov;vol. 26(no. 11):1464–1471. doi: 10.1109/TMI.2007.907552. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Fletcher PT, Joshi S. Proc. CVAMIA. Prague: Czech Republic; 2004. Principal geodesic analysis on symmetric spaces: Statistics of diffusion tensors; pp. 87–98. [Google Scholar]
- 9.Fletcher PT, Venkatasubramanian S, Joshi S. The geometric median on Riemannian manifolds with application to robust atlas estimation. NeuroImage. 2008;vol. 45:143–152. doi: 10.1016/j.neuroimage.2008.10.052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Lenglet C, Rousson M, Deriche R. Proc. MICCAI. Saint-Malo, France: 2004. Segmentation of 3D probability density fields by surface evolution: Application to diffusion MRI; pp. 18–25. [Google Scholar]
- 11.Wang Z, Vemuri BC, Chen Y, Mareci TH. A constrained variational principle for direct estimation and smoothing of the diffusion tensor field from complex DWI. IEEE Trans. Med. Imag. 2004 Aug;vol. 23(no. 8):930–939. doi: 10.1109/TMI.2004.831218. [DOI] [PubMed] [Google Scholar]
- 12.Wang Z, Vemuri BC. Proc. ECCV. Prague: Czech Republic; 2004. Tensor-field segmentation using a region-based active contour model; pp. 304–315. [Google Scholar]
- 13.Karcher H. Riemannian center of mass and mollifier smoothing. Commun. Pure Appl. Math. 1977;vol. 30:509–541. [Google Scholar]
- 14.Moakher M, Batchelor PG. Visualization and Processing of Tensor Fields. New York: Springer; 2006. Symmetric positive-definite matrices: From geometry to applications and visualization. [Google Scholar]
- 15.Pennec X. Intrinsic statistics on Riemannian manifolds: Basic tools for geometric measurements. J. Math. Imag. Vis. 2006;vol. 25:127–154. [Google Scholar]
- 16.Wang Z, Vemuri B. DTI segmentation using an information theoretic tensor dissimilarity measure. IEEE Trans. Med. Imag. 2005 Oct;vol. 24(no. 10):1267–1277. doi: 10.1109/TMI.2005.854516. [DOI] [PubMed] [Google Scholar]
- 17.Nielsen F, Nock R. Sided and symmetrized Bregman centroids. IEEE Trans. Inf. Theory. 2009 Jun;vol. 55(no. 6):2882–2904. [Google Scholar]
- 18.Arsigny V, Fillard P, Pennec X, Ayache N. Log-Euclidean metrics for fast and simple calculus on diffusion tensors. Magn. Reson. Med. 2006;vol. 56:411–421. doi: 10.1002/mrm.20965. [DOI] [PubMed] [Google Scholar]
- 19.Frigyik BA, Srivastava S, Gupta MR. Functional Bregman divergence; IEEE Int. Symp. Inf. Theory; 2008. pp. 1681–1685. [Google Scholar]
- 20.Absil PA, Mahony R, Sepulchre R. 2008. Princeton, NJ: Princeton Univ. Press; Optimization Algorithms on Matrix Manifolds. [Google Scholar]
- 21.Mumford D, Shah J. Optimal approximations by piecewise smooth functions and associated variational-problems. Comm. Pure Appl. Math. 1989;vol. 42 [Google Scholar]
- 22.Chan TF, Vese LA. Active contours without edges. IEEE Trans. Image Process. 2001 Feb;vol. 10(no. 2):266–277. doi: 10.1109/83.902291. [DOI] [PubMed] [Google Scholar]
- 23.Malladi R, Sethian JA, Vemuri BC. Shape modeling with front propagation: A level set approach. IEEE Trans. Pattern Anal. Mach. Intell. 1995 Feb;vol. 17(no. 2):158–175. [Google Scholar]
- 24.Helein F. Harmonic Maps, Conservation Laws and Moving Frames. Cambridge, U.K: Cambridge Univ. Press; 2002. [Google Scholar]
- 25.Barmpoutis A, Vemuri BC, Shepherd TM, Forder JR. Tensor splines for interpolation and approximation of DT-MRI with applications to segmentation of isolated rat hippocampi. IEEE Trans. Med. Imag. 2007 Nov;vol. 26(no. 11):1537–1547. doi: 10.1109/TMI.2007.903195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Pasternak O, Sochen N, Basser PJ. The effect of metric selection on the analysis of diffusion tensor MRI data. NeuroImage. 2010;vol. 49:2190–2204. doi: 10.1016/j.neuroimage.2009.10.071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Pajevic S, Basser P. Parametric and non-parametric statistical analysis of DT-MRi data. J. Magn. Reson. 2003;vol. 161:1–14. doi: 10.1016/s1090-7807(02)00178-7. [DOI] [PubMed] [Google Scholar]
- 28.Papadakis NG, Xing D, Houston GC, Smith JM, Smith MI, James MF, Parsons AA, Huang CL, Hall LD, Carpenter TA. A study of rotationally invariant and symmetric indices of diffusion anisotropy. Magn. Reson. Imag. 1999;vol. 17:881–892. doi: 10.1016/s0730-725x(99)00029-6. [DOI] [PubMed] [Google Scholar]
- 29.Pierpaoli C, Basser P. Toward a quantitative assessment of diffusion anisotropy. Magn. Reson. Med. 1996;vol. 36:893–906. doi: 10.1002/mrm.1910360612. [DOI] [PubMed] [Google Scholar]
- 30.Morra JH, Tu Z, Apostolova LG, Green AE, Toga AW, Thompson PM. Comparison of adaboost and support vector machines for detecting alzheimers disease through automated hippocampal segmentation. IEEE Trans. Med. Imag. 2007;vol. 29:30–43. doi: 10.1109/TMI.2009.2021941. [DOI] [PMC free article] [PubMed] [Google Scholar]