Validation for 2D/3D registration I: A new gold standard data set

Abstract

Purpose

In this article, the authors propose a new gold standard data set for the validation of two-dimensional/three-dimensional (2D/3D) and 3D/3D image registration algorithms.

Methods

A gold standard data set was produced using a fresh cadaver pig head with attached fiducial markers. The authors used several imaging modalities common in diagnostic imaging or radiotherapy, which include 64-slice computed tomography (CT), magnetic resonance imaging using Tl, T2, and proton density sequences, and cone beam CT imaging data. Radiographic data were acquired using kilovoltage and megavoltage imaging techniques. The image information reflects both anatomy and reliable fiducial marker information and improves over existing data sets by the level of anatomical detail, image data quality, and soft-tissue content. The markers on the 3D and 2D image data were segmented using analyze 10.0 (AnalyzeDirect, Inc., Kansas City, KN) and an in-house software.

Results

The projection distance errors and the expected target registration errors over all the image data sets were found to be less than 2.71 and 1.88 mm, respectively.

Conclusions

The gold standard data set, obtained with state-of-the-art imaging technology, has the potential to improve the validation of 2D/3D and 3D/3D registration algorithms for image guided therapy.

I. INTRODUCTION

External beam radiotherapy is one of the major treatment options in oncology. Prior to radiotherapy, the treatment is planned using a three-dimensional (3D) data set from computed tomography (CT) or magnetic resonance (MR). The result of the treatment planning is a predicted radiation dose distribution in the target volume based on the simulation of the treatment device and the treatment geometry.^1,2 However, in practice, uncertainties exist in dose deposition, tumor delineation, and target localization due to intra- and interorgan motion.¹ An image guided radiation therapy (IGRT) aims to minimize the dose to critical structures (for instance, the spinal cord or the optical nerve) or can even enable radiotherapy treatment when the standard radiotherapy is impossible due to the risk to the nearby critical structures. Such an IGRT system should fulfill the following requirements: (i) Functionality in the treatment room, (ii) minimally invasive operation, (iii) sufficient speed in order not to significantly prolong the treatment time, (iv) geometric precision, and (v) the ability to differentiate soft tissue with sufficient spatial resolution to allow the desired margin reduction.³

Image registration is necessary to guide the radiotherapy treatment unit and its main application is the correction of the patient position in the treatment room.^1,2,4-10 More specifically, a registration algorithm is a tool to get the best match between two or more images by optimizing the image alignment criterion, which is usually a cost function or a similarity measure.¹¹ Two two-dimensional (2D) images, two 3D volumes, or a 3D volume to a 2D image can be registered. In the later case, the most common registration approach involves a projection of the 3D volume onto a 2D imaging plane and a comparison of the projected 2D image to the existing 2D image, for instance, a digitally rendered radiograph is derived from a CT volume and compared to an x-ray image obtained from the treatment device.^11-14

Since an IGRT system is a tool to ensure target localization during radiation delivery, it is mandatory that a painstaking validation process of individual components of the system is carried out in order to study how single errors in the IGRT system affect the overall accuracy.¹⁵ A prerequisite for an objective validation of an IGRT system component, like a 2D/3D registration algorithm, is the standardization of the validation process, which includes the design of validation data sets, the definition of corresponding ground truth and its accuracy, the validation protocol, and the design of a validation metric.^15-18

In Refs. ¹⁶ and ¹⁸, gold standard data sets and evaluation methods for 2D/3D registration are presented using a cadaver lumbar spine phantom embedded in polyurethane foam. The data sets are useful for validation of registration algorithms, but, in practice, problems become evident. Namely, the phantoms are symmetrical with respect to the midsagittal plane of the spinal column and consist of bony skeleton with virtually no soft tissue. Therefore, the effects of variable contrast and mobility of soft tissue cannot be assessed. Furthermore, they are rather small, therefore it is difficult to study the effects of perspective on 2D/3D registration. Finally, the 3D data are provided in 8 bit depth rather than in the usual 12 or 16 bit resolution. In this paper, we propose a new gold standard data set using a cadaver pig head with attached fiducial markers. The large amount of soft tissue, which shows considerable deformation in some of the data, should give a realistic idea of the problems encountered in clinical practice. Furthermore, the data set was acquired using the latest generation of medical imaging equipment for diagnostic radiology and IGRT.

II. MATERIALS AND METHODS

The pig head was supplied by the Department of Biomedical Research, Medical University of Vienna (MUV). Image acquisition took place within 24 h after the pig was sacrificed. The cups [Figs. 1(a) and 1(b)] for holding different types of fiducial markers were made in the workshop of the Center for Medical Physics and Biomedical Engineering at the MUV using fused decomposition modeling. The cups feature a thread that is identical to the thread of a surgical Schanz screw from an orthopaedic fixateur externe set. Using the screws, it was possible to tap threads in the bony skull of the pig. The replaceable spherical markers of 10 mm diameter were made of steel, aluminum, and polytetrafluoroethylene (PTFE). A plastic hollow sphere was filled with olive oil injection for MR-compatible markers [Fig. 1(c)].

Fig. 1.

The fiducial markers for establishing the ground truth.( a) shows three of the fiducial cups holding 10 mm spheres. Sphere 1 is made of plastic and was filled with olive oil, sphere 2 is made of PTFE, and sphere 3 is made of aluminum. (b) shows the fiducial cup in detail. The thread matches the thread of a surgical Schanz screw from an orthopedic fixateur externe set; this Schanz screw was used for tapping a thread into cortical bone. In (c), six out of seven fiducial markers in the final position are shown.

The spherical steel markers were used for kilovoltage (kV) x-ray imaging and megavoltage (MV) electronic portal imaging, while PTFE markers were used for the CT images. The aluminum markers were used for cone beam CT (CBCT) and olive oil markers were used for MR. The experiments were done at the University Clinics for Radiation Oncology and Radiology, both located at the MUV.

II.A. Image acquisition

The CT images were obtained by a 64-slice CT scanner (Philips Brilliance 64, Philips AG, Best, The Netherlands) at 120 kVp and 156 mA s with intraslice resolution of 0.4×0.4 mm² and 0.8 mm interslice distance (512×512×825 voxels; data size: 412.5 MB). For MR imaging, we used a Philips Achieva 3 T system. Tl, T2, and proton density (PD) sequences were used to acquire the images using a high-resolution head coil. The voxel size of the original data was 240×240×150 voxels with 1.0×1.0×2.0 mm³ (Tl-volume, size: 16.9 MB), 512×512×80 voxels with 0.43×0.43×2.00 mm³ (T2-volume, size: 40.2 MB), and 864×864×39 voxels with 0.45×0.45×4.40 mm³ (PD-volume, 55.6 MB).

The kV x-ray and MV images as well as the CBCT images were obtained with an Elekta Synergy linear accelerator, which is equipped with electronic portal imaging device (EPID) and a CBCT system. Both the EPID and the CBCT x-ray unit use a PerkinElmer XRD amorphous silicon detector with an active surface of 410×410 mm² and a resolution of 1024×1024 pixels. The detector panel for the CBCT and kV x-ray imaging is located 536 mm from the axis of rotation, while the distance between the EPID and the axis of rotation is 570 mm. The source is located at a distance of 1536 mm from the imaging panel for the kV and CBCT imaging and 1570 mm for MV imaging.

In the case of CBCT imaging, the images were captured at a fixed frame rate of 2.7 Hz. During the 360° rotation, the system acquired approximately 650 planar images, which were used to make a full 3D image. Two images with different fields of view (FOVs) (276 mm and 425 mm) were acquired. Imaging parameters were 120 kVp/1600 mA s for the small FOV (540×540×520 voxels of 0.5 mm³ in size; volume size of 290 MB) and 120 kVp/1000 mA s for the large FOV (410×410×264 voxels of 1.0 mm³ in size; volume size of 85 MB). For the registration experiments, data were interpolated to 1.0 mm cubic voxels; this resolution has proven to be a good compromise concerning the size of the data and the resolution required for successful 2D/3D registration in our experience. Since the volumes are isotropic, no additional scaling measures in the registration process are required. The complete data set, which is available from the corresponding author, however, also contains the original volumes and volumes interpolated to 0.5 mm³. Cubic interpolation was carried out using analyze 10.0 (AnalyzeDirect Inc., Kansas City, KN). The 2D kV x-ray and MV images were taken from the anterior posterior (AP) and lateral orientation. The kV x-ray images were acquired with the small FOV at 120 kVp/5 mA s, while the MV images were taken at 6 MV and 5 monitor units.

II.B. Centroids of the fiducial markers

Raw image data from several imaging modalities were extracted in the DICOM format and converted to AVW format using analyze 10.0 (AnalyzeDirect Inc., Kansas City, KN). The geometric center of the markers was determined by segmentation in each modality; first, an intensity threshold I₀ that separated the marker from the anatomical information was defined. This threshold had to be chosen manually for each marker type since, given the spherical nature of the markers, a considerable impact of the thresholding step on centroid estimation cannot be expected. The position of the marker centroid for 2D or 3D images c_m was then estimated with an intensity weighting method¹⁹ as

$${\mathbf{c}}_{\mathrm{m}}=\frac{{\Sigma }_{\mathbf{P}\in \Omega }(I\left(\mathbf{p}\right)-I_0)\mathbf{p}}{{\Sigma }_{\mathbf{P}\in \Omega }(I\left(\mathbf{p}\right)-I_0)},$$ (1)

where I(p) is the intensity of the pixel or voxel at position p and Ω is a small rectangular neighborhood around the segmented position of the fiducial.

II.C. Gold standard calculation

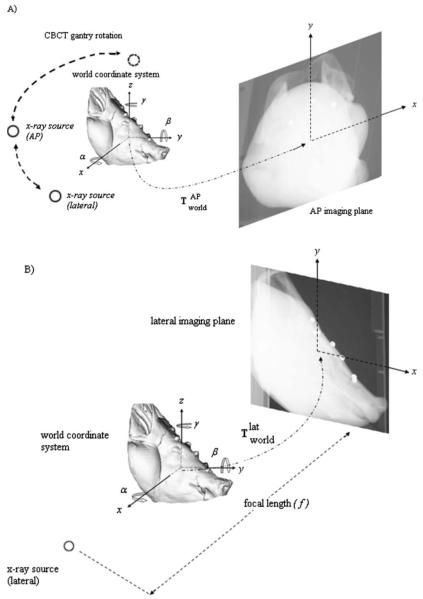
The imaging equipment of the Elekta Synergy is rotated around a fixed isocenter. The setup is regularly calibrated and does not require additional calibration of the acquisition setup. Therefore, the projection setup can be determined from the source to axis of rotation and source to flat panel distances. Using the geometrical setup, the projection matrices that map a 3D point of the volume to a 2D point of the flat panel are determined (Fig. 2).

Fig. 2.

Illustration of the perspective projection geometry for AP (a) and lateral (b) views, respectively. The origin of the camera coordinate system is located at the focal spot of the radiation source, whereas the world coordinate system is located at the center of the object volume. The focal length f is the distance between the x-ray source and the imaging plane (flat panel). The distance between x-ray source and the center of rotation is 1000 mm, whereas the distances of the center of rotation to imaging plane are 536 and 570 mm for kV x-ray and MV images, respectively.

Using homogeneous coordinates, the relation between a 2D point n in the x-ray image coordinate system and a 3D point w of the volume is given by

$$\mathbf{n}={\mathbf{P}}_{\text{camera}}^{\text{image}}{\mathbf{T}}_{\text{world}}^{\text{camera}}\mathbf{w},$$ (2)

where ${\mathbf{P}}_{\text{camera}}^{\text{image}}$ is a perspective projection matrix that defines the projection of any 3D point described in the coordinate system of the “camera” (in our case, either the AP or the lateral view) to the image plane and ${\mathbf{T}}_{\text{world}}^{\text{camera}}$ is a rigid transformation matrix that gives the transformation from the world coordinates to the coordinate system of the camera.

The perspective projection matrix ${\mathbf{P}}_{\text{camera}}^{\text{image}}$ is given by the following equation:

$${\mathbf{P}}_{\text{camera}}^{\text{image}}=\left[\begin{array}{cccc}\hfill 1\hfill & \hfill 0\hfill & 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill & 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \frac{-1}{f}\hfill & \hfill 1\hfill \end{array}\right],$$ (3)

where f is the focal length of the camera. With this setup, the origin of the camera coordinate system is placed on the image plane.

In our approach, the world coordinate system was defined as the coordinate system of the 3D volume (CT, CBCT, or MR). The transformation matrix from world coordinate system to the camera coordinate system ${\mathbf{T}}_{\text{world}}^{\text{camera}}$ is a rigid transformation matrix given by^20,21

$${\mathbf{T}}_{\text{world}}^{\text{camera}}=\left[\begin{array}{cccc}\hfill c_{\beta }{c}_{\gamma }\hfill & \hfill c_{\gamma }{s}_{\beta }{s}_{\alpha }-s_{\gamma }{c}_{\alpha }\hfill & \hfill c_{\gamma }{s}_{\beta }{c}_{\alpha }+s_{\alpha }{s}_{\gamma }\hfill & \hfill t_x\hfill \\ \hfill c_{\beta }{s}_{\gamma }\hfill & \hfill s_{\gamma }{s}_{\beta }s\alpha +c_{\gamma }{c}_{\alpha }\hfill & \hfill s_{\gamma }{s}_{\beta }{c}_{\alpha }-s_{\alpha }{c}_{\gamma }\hfill & \hfill t_y\hfill \\ \hfill -s_{\beta }\hfill & \hfill s_{\alpha }{c}_{\beta }\hfill & \hfill c_{\beta }{s}_{\alpha }\hfill & \hfill t_z\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right],$$ (4)

where c and s are the cosine and sine functions and α, β, and γ are the Euler angles of the Cartesian axes in the x, y, and z directions, respectively. The translation vector is indicated by T=(t_x, t_y, t_z)^T, while the 3×3 rotation matrix R is defined by the first three rows and columns and is calculated as

$$\mathbf{R}={\mathbf{R}}_z{\mathbf{R}}_y{\mathbf{R}}_x,$$ (5)

where R_z, R_y, and R_x, are 3×3 rotation matrices defining rotation around the z, y, and x axes, respectively.

For the 2D kV x-ray and MV images from the AP and lateral orientation used in the experiments, the following transformations were defined: Let ${\mathbf{T}}_{\text{world}}^{\mathrm{AP}}$ be a transformation matrix of the world coordinate system to the camera in the AP orientation and ${\mathbf{T}}_{\text{world}}^{\mathrm{lat}}$ be a transformation matrix of the world coordinate system to the camera in the lateral orientation. Then, we can use Eq. (2) to map the 3D position of a marker w_i in the volume to the corresponding 2D projection n_i in the image,

$${\mathbf{n}}_{i,a}={\mathbf{P}}_{\mathrm{AP}}^a{\mathbf{T}}_{\text{world}}^{\mathrm{AP}}{\mathbf{w}}_i,$$ (6a)

$${\mathbf{n}}_{i,l}={\mathbf{P}}_{\mathrm{lat}}^l{\mathbf{T}}_{\text{world}}^{\mathrm{lat}}{\mathbf{w}}_i,$$ (6b)

where ${\mathbf{P}}_{\mathrm{AP}}^a$ and ${\mathbf{P}}_{\mathrm{lat}}^l$ are perspective projection matrices for the AP and the lateral 2D images, respectively.

Since the camera system of the Elekta device is regularly calibrated, we introduce a new matrix ${\mathbf{T}}_{\mathrm{lat}}^{\mathrm{AP}}$, which is derived from the rotational geometry of the device and consists of a rotation matrix of −90° around the y component and two translations of 536 or 570 mm along the x and z components of lateral view coordinate system resulting in

$${\left({\mathbf{T}}_{\mathrm{lat}}^{\mathrm{AP}}\right)}_{\mathrm{kV}}=\left[\begin{array}{cccc}\hfill 0\hfill & \hfill 0\hfill & \hfill -0\hfill & \hfill 536\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 536\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right]$$ (7a)

and

$${\left({\mathbf{T}}_{\mathrm{lat}}^{\mathrm{AP}}\right)}_{\mathrm{MV}}=\left[\begin{array}{cccc}\hfill 0\hfill & \hfill 0\hfill & -1\hfill & 570\hfill \\ \hfill 0\hfill & \hfill 1\hfill & 0\hfill & 0\hfill \\ \hfill 1\hfill & \hfill 0\hfill & 0\hfill & 570\hfill \\ \hfill 0\hfill & \hfill 0\hfill & 0\hfill & 1\hfill \end{array}\right]$$ (7b)

for the kV and MV imaging systems, respectively.

Since the kV x-ray image and an orthogonal MV image are available on the Elekta Synergy linear accelerator without the need to rotate the imaging system, we also allow for the possibility to establish the 2D/3D registration by using the kV x-ray and the orthogonal portal MV image. Therefore, a separate gold standard for 2D/3D image registration is established using 2D image pairs of kV AP-MV lateral images and MV AP-kV lateral images.

We will refer to this setup as the kV-MV fusion setup. In this case, the matrices ${\mathbf{T}}_{\mathrm{lat}}^{\mathrm{AP}}$ were defined as

$${\left({\mathbf{T}}_{\mathrm{lat}}^{\mathrm{AP}}\right)}_{\mathrm{kV}\mathrm{AP}-\mathrm{MV}\mathrm{Lat}}=\left[\begin{array}{cccc}\hfill 0\hfill & \hfill 0\hfill & \hfill -1\hfill & \hfill 570\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 536\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right]$$ (8a)

and

$${\left({\mathbf{T}}_{\mathrm{lat}}^{\mathrm{AP}}\right)}_{\mathrm{MV}\mathrm{AP}-\mathrm{kV}\mathrm{Lat}}=\left[\begin{array}{cccc}\hfill 0\hfill & \hfill 0\hfill & \hfill -1\hfill & \hfill 536\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 570\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right]$$ (8b)

for MV AP-kV lateral [Eq. (8a)] and kV AP-MV lateral [Eq. (8b)] fusion setups, respectively.

Using the matrix ${\mathbf{T}}_{\mathrm{lat}}^{\mathrm{AP}}$ [Eqs. (7) and (8)], we can modify Eq. (6) to

$${\mathbf{n}}_{i,a}={\mathbf{P}}_{\mathrm{AP}}^a{\mathbf{T}}_{\mathrm{lat}}^{\mathrm{AP}}{\mathbf{T}}_{\text{world}}^{\mathrm{lat}}{\mathbf{w}}_i$$ (9a)

and

$${\mathbf{n}}_{i,l}={\mathbf{P}}_{\mathrm{lat}}^l{\mathbf{T}}_{\text{world}}^{\mathrm{lat}}{\mathbf{w}}_i.$$ (9b)

. Since ${\mathbf{P}}_{\mathrm{AP}}^a$, ${\mathbf{P}}_{\mathrm{lat}}^l$, and ${\mathbf{T}}_{\mathrm{lat}}^{\mathrm{AP}}$ are known from the geometrical setup parameters of the radiotherapy device, the only remaining unknown is the ${\mathbf{T}}_{\text{world}}^{\mathrm{lat}}$ transformation matrix. From Eqs. (9a) and (9b), this matrix is determined by minimizing the root mean square (RMS) distance $E\left({\mathbf{T}}_{\text{world}}^{\mathrm{lat}}\right)$, also referred to as the projection distance error (PDE), between the positions of the 3D markers projected to the 2D imaging plane and the centroid positions of segmented markers given as ${\mathbf{n}}_{i,l}^c$ or ${\mathbf{n}}_{i,a}^c$ in the lateral and AP 2D images as

$$E\left({\mathbf{T}}_{\text{world}}^{\mathrm{lat}}\right)=\sqrt{\frac{1}{2}\left(\sum _{i=1}^N\frac{1}{N}{\mid {\mathbf{n}}_{i,\mathrm{l}}^c-{\mathbf{P}}_{\mathrm{lat}}^l{\mathbf{T}}_{\text{world}}^{\mathrm{lat}}{\mathbf{w}}_i\mid }^2+\sum _{i=1}^N\frac{1}{N}{\mid {\mathbf{n}}_{i,\mathrm{a}}^c-{\mathbf{P}}_{\mathrm{AP}}^a{\mathbf{T}}_{\mathrm{lat}}^{\mathrm{AP}}{\mathbf{T}}_{\text{world}}^{\mathrm{lat}}{\mathbf{w}}_i\mid }^2\right)},$$ (10)

where N is the number of fiducial markers.

The minimization is carried out using the Levenberg–Marquardt optimizer in MATLAB 7.7 (MathWorks, Inc., Natick, MA).

Once the minimization is performed and the ${\mathbf{T}}_{\text{world}}^{\mathrm{lat}}$ matrix is determined, the ${\mathbf{T}}_{\text{world}}^{\mathrm{AP}}$ matrix can be calculated from the ${\mathbf{T}}_{\text{world}}^{\mathrm{lat}}$ and ${\mathbf{T}}_{\mathrm{lat}}^{\mathrm{AP}}$ matrices. The matrices ${\mathbf{T}}_{\text{world}}^{\mathrm{AP}}$ and ${\mathbf{T}}_{\text{world}}^{\mathrm{lat}}$ constitute the gold standard.

II.D. Reconstruction of the 3D markers and fiducial registration error (FRE) calculation

In this paper, the gold standard is established by minimization of the PDE, which represents the error in the imaging plane, i.e., a 2D error. In order to subsequently evaluate the 3D errors, FRE is determined. FRE is the error between the segmented 3D positions of the markers in the volume and the reconstructed positions of the markers, determined from the 2D positions in the image, the device geometry, and the known gold standard.

Having determined the gold standard registration, the 3D position ${\mathbf{w}}_i^r$ of the markers in the volumes can be reconstructed from the projection geometry. For one marker, ${\mathbf{w}}_i^r$ is given by the intersection of two imaginary lines, one line passing through the source of the x-ray and the 2D projection of the marker i in the AP direction and the second one passing through the source of the x-ray and the 2D projection of the marker i in the lateral direction. The equation of the lines is calculated in the world coordinate system. For that purpose, the position of the sources for the lateral and AP views and the position of the markers in the 2D images must also be given in the world coordinate system.

The position of the source in the AP view coordinate system is n_s,a=(0, 0, f₁, 1) and in the lateral view coordinate system n_s,l=(0, 0, f₂, 1) with f₁ and f₂ being the focal lengths of each view, respectively. The coordinates of the sources in the world system are then given by

$${\mathbf{w}}_{s,a}={\left[{\mathbf{T}}_{\text{world}}^{\mathrm{AP}}\right]}^{-1}{\mathbf{n}}_{s,a}$$ (11a)

and

$${\mathbf{w}}_{s,l}={\left[{\mathbf{T}}_{\text{world}}^{\text{lat}}\right]}^{-1}{\mathbf{n}}_{s,l}.$$ (11b)

Similarly, the coordinates of the 2D projection of the markers ${\mathbf{n}}_{i,a}^c$ and ${\mathbf{n}}_{i,l}^c$ in the world system are given by

$${\mathbf{w}}_{i,a}^{2\mathrm{D}}={\left[{\mathbf{T}}_{\text{world}}^{\mathrm{AP}}\right]}^{-1}{\mathbf{n}}_{i,a}^c$$ (12a)

and

$${\mathbf{w}}_{i,l}^{2\mathrm{D}}={\left[{\mathbf{T}}_{\text{world}}^{\text{lat}}\right]}^{-1}{\mathbf{n}}_{i,l}^c.$$ (12b)

For each view, the direction v_i of the imaginary line between the source and the 2D marker projection i is expressed in the world coordinate system by

$${\mathbf{v}}_{i,a}=\frac{{\mathbf{w}}_{s,a}-{\mathbf{w}}_{i,a}^{2\mathrm{D}}}{\mid {\mathbf{w}}_{s,a}-{\mathbf{w}}_{i,a}^{2\mathrm{D}}\mid },$$ (13a)

$${\mathbf{v}}_{i,l}=\frac{{\mathbf{w}}_{s,l}-{\mathbf{w}}_{i,l}^{2\mathrm{D}}}{\mid {\mathbf{w}}_{s,l}-{\mathbf{w}}_{i,l}^{2\mathrm{D}}\mid }.$$ (13b)

The reconstructed 3D positions of each marker ${\mathbf{w}}_i^r$ in the world coordinate system is determined by the intersection of the two imaginary lines with the respective directions v_i,a and v_i,l. However, due to the calibration errors, the two lines do not necessarily lie on the same plane. We consider then the reconstructed 3D position of each marker i as being the middle of the shortest distance between the two lines.

In order to calculate this position, the direction d_i of the shortest distance is given by

$${\mathbf{d}}_i=\frac{{\mathbf{v}}_{i,a}\mathrm{x}{\mathbf{v}}_{i,l}}{\mid {\mathbf{v}}_{i,a}\mathrm{x}{\mathbf{v}}_{i,l}\mid },$$ (14)

with x representing the cross product.

Let A_i be the intersection of the lines with direction v_i,a and d_i, and B_i be the intersection of the lines with direction v_i,l and d_i. The parametric equation of each line is given by

$$\begin{array}{cc}\hfill {\mathbf{A}}_i& ={\mathbf{w}}_{s,a}+{\lambda }_1{\mathbf{v}}_{i,a},\hfill \\ \hfill {\mathbf{B}}_i& ={\mathbf{w}}_{s,l}+{\lambda }_2{\mathbf{v}}_{i,l},\hfill \\ \hfill {\mathbf{B}}_i& ={\mathbf{A}}_i+{\lambda }_3{\mathbf{d}}_i.\hfill \end{array}$$ (15)

Solving the system of linear equations given in Eq. (15) allows to find the values of λ₁, λ₂, λ₃ and then the coordinates of A_i and B_i, retrospectively. The reconstructed 3D position ${\mathbf{w}}_i^r$ of the marker i is then given by

$${\mathbf{w}}_i^r=\frac{{\mathbf{A}}_i+{\mathbf{B}}_i}{2}.$$ (16)

Having determined ${\mathbf{w}}_i^r$, the FRE is the RMS distance between ${\mathbf{w}}_i^r$ and the segmented 3D position w_i.

II.E. Validation of the gold standard registration

To validate and assess the accuracy of the gold standard registration for positions of anatomical structures, target registration error (TRE) has become the metric of choice.^11,16 TRE can be derived from FRE. Sibson²² showed the variance of N markers to be (N−2)/N. He also demonstrated that FRE is, to a good approximation, independent of the shape of fiducial configuration and it depends only on the fiducial localization error (FLE) and the number of the fiducial markers (N) as

$${\mathrm{FLE}}^2=\frac{N}{N-2}{\mathrm{FRE}}^2.$$ (17)

In order to calculate the TRE, we used anatomical landmarks at the centers of various anatomical regions that are of interests as target points. In this work, target points were manually defined on the cervical C2 vertebra, the brain, the maxilla, and the mandible in CT, CBCT, and MR images using analyze 10.0 (AnalyzeDirect Inc., Kansas City, KN).We have chosen these anatomical landmarks as target points because these structures were easily segmented and do not deform with the soft tissue. Using Eq. (17) and the target point r, the TRE can be calculated as¹¹

$$\langle {\mathrm{TRE}}^2\left(\mathbf{r}\right)\rangle =\frac{\langle {\mathrm{FLE}}^2\rangle }{N}\left(1+\frac{1}{3}\sum _{k=1}^3\frac{d_k^2}{f_k^2}\right),$$ (18)

where f_k is the RMS distance of the fiducial markers to the principal axis k of the marker configuration and d_k is the RMS distance of the target point r to the principal axis k of the marker configuration.

For testing the quality of fiducial centroid extraction, a series of ten simulations with slightly varied values of localizations ${\mathbf{w}}_i^r$ was carried out using MATLAB 7.7 (MathWorks Inc.). Here, each fiducial position was changed by a random value of 1, 3, and 5 mm, and the point-based registration was carried out using these modified values. Subsequently, a set of 100 random target points distributed evenly in a sphere of 100 mm radius around the center of the volume data set was transformed using this new registration matrix. The effect on the projected target points was determined as the Euclidean difference in localization of the target points projected with the registration matrix found after fiducial centroid variation relative to the projected target positions when using the gold standard registration parameters. Given the fact that the anatomy of the pig left very little space to distribute the fiducial markers in a larger volume, this simulation should also shed some light on the overall quality of the registration. For additional validation, the FRE for 3D/3D registration using the seven fiducial markers was compared to the resulting TRE (computed from the fiducial marker centroids) of an intensity-based registration method. This second registration was carried out using the normalized mutual information method as implemented in analyze 10.0 (AnalyzeDirect Inc., Kansas City, KN).

III. RESULTS

III.A. Gold standard image data set

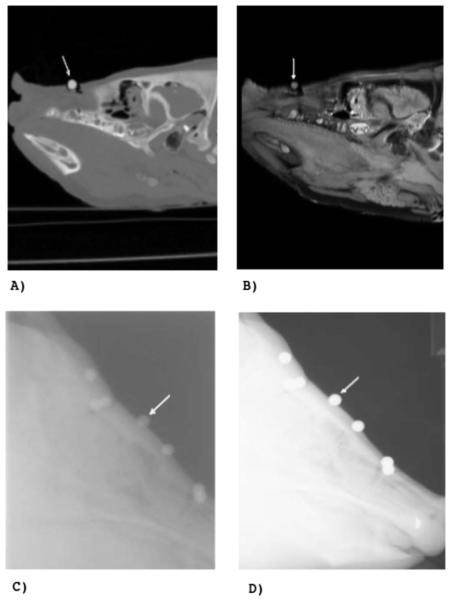
In order to establish a gold standard for all imaging modalities, the fiducial marker positions have to be identified in all 3D and 2D images. In Fig. 3, the markers are clearly visible, indicating that the PTFE, steel, and aluminum markers are appropriate for CT, kV x-ray, and MV imaging modalities [see arrow in Figs. 3(a)–3(d)], whereas the olive oil marker is applicable in MR [see arrows in Fig. 3(b)]. Moreover, the new data set provides anatomical structures with soft and hard tissue information in all of the imaging modalities. Therefore, the new data set is suitable for image guided radiotherapy applications since it facilitates the validation of the registration process in a realistic situation.

Fig. 3.

Sample images of the phantom. (a) shows a slice of the CT image, (b) a slice of the PD weighted MR image, (c) the lateral MV image, and (d) the lateral kV x-ray image. The arrow indicates one marker in each image.

III.B. Gold standard registration

Tables I and II show that error in the imaging plane (PDE) over all 3D modalities was in the range of 0.51–1.79 mm when using the kV x-ray images, whereas it was in the range of 1.33–2.03 mm when using the MV images. Additionally, for the kV-MV fusion setup, PDE over all the 3D modalities was in the range of 2.24–2.71 mm when using kV AP-MV lateral images, while it was in the range of 1.18–1.86 mm when using MV AP-kV lateral images. The highest accuracy of 0.51 mm was achieved for the projection of markers from the CT image to the kV x-ray images, while the lowest accuracy of 2.71 mm was observed when MR PD image and the kV-MV fusion setup of MV AP-kV lateral images was used. Figure 4 illustrates the position of the centroids of the markers obtained by the segmentation (dot) and by the geometrical setup calculation (circle) for both AP and lateral views.

Table I.

PDE given in mm for the projection of the positions of 3D fiducial markers to 2D kV x-ray and MV images for CT, CBCT with small (CBCTs) and big (CBCTb) FOV, and MR T1, T2, and PD weighted images.

	CT (mm)	CBCTs (mm)	CBCTb (mm)	MR T1 (mm)	MR T2 (mm)	MR PD (mm)
kV AP-kV Lat	0.51	0.66	0.67	0.76	1.79	1.58
MV AP-MV Lat	1.42	1.43	1.61	1.33	1.51	2.03

Table II.

PDE given in mm for the projection of the positions of 3D markers to the 2D kV x-ray and MV images of the fusion setup for CT, CBCT with small (CBCTs) and big (CBCTb) FOV, and MR Tl, T2, and PD weighted images.

	CT (mm)	CBCTs (mm)	CBCTb (mm)	MR T1 (mm)	MR T2 (mm)	MR PD (mm)
kV AP-MV lat	2.24	2.26	2.33	2.24	2.57	2.71
MV AP-kV lat	1.18	1.22	1.32	1.21	1.86	1.85

Fig. 4.

Illustration of the marker positions obtained by segmentation of the 2D images (dot) and by projection of the segmented markers from the CT image at the gold standard position (circle) for (a) the kV AP and (b) kV lateral views.

To further validate the gold standard, FRE was calculated using the marker positions segmented in the volumes and the 3D positions reconstructed from kV and MV images using the gold standard (Tables III and IV). FREs were in the range from 0.22 to 1.44 mm when using the kV x-ray images and from 0.81 to 1.45 mm when using the MV images for the marker reconstruction. For the fusion setup, FREs ranged from 0.53 to 1.31 mm and from 0.6 to 1.32 mm when the markers were reconstructed from the kV AP- MV lateral (RXMV) and MV AP- kV lateral (RMXV) setup, respectively. As for the PDE, the highest accuracy of 0.22 mm was reached with the CT volume and markers reconstructed from the two kV images. On the other hand, the lowest accuracy of 1.44 mm was observed when the MR T2 image was used with markers reconstructed from the two kV images.

Table III.

FREs of markers segmented from CT, CBCT with small (CBCTs) and big (CBCTb) FOV, and MR Tl, T2, and PD weighted images to reconstructed markers from kV x-ray and MV images. RXV denotes the reconstructed coordinates from kV x-ray and RMV denotes the reconstructed coordinates from MV images.

	CT (mm)	CBCTs (mm)	CBCTb (mm)	MR T1 (mm)	MR T2 (mm)	MR PD (mm)
RXV	0.22	0.43	0.45	0.54	1.44	1.21
RMV	0.90	0.94	1.11	0.81	1.03	1.45

Table IV.

FREs of markers segmented from CT, CBCT with small (CBCTs) and big (CBCTb) FOV, MR Tl, T2, and PD weighted images to reconstructed markers from the kV-MV fusion setup. RXMV denotes the reconstructed coordinates from kV AP-MV lateral 2D images and RMXV denotes the reconstructed coordinates from MV AP-kV lateral 2D images.

	CT (mm)	CBCTs (mm)	CBCTb (mm)	MR T1 (mm)	MR T2 (mm)	MR PD (mm)
RXMV	0.53	0.61	0.76	0.56	1.11	1.31
RMXV	0.60	0.68	0.80	0.64	1.32	1.28

We also calculated the expected TRE for cervical C2 vertebra, brain, maxilla, and mandible, which are given in Tables V and VI. The best accuracies were achieved with the gold standard computed from the two kV images and the CT, CBCT small and large FOV, and MR Tl volumes. In this case, all TREs were below 0.63 mm. For the same volumes (CT, CBCT small and large FOV, and MR-T1) with the two MV images, the TREs increased, with some values above 1 mm, whereas using the fusion setup, the TREs were still below 1 mm. The accuracy was worse with the MR T2 and MR PD volumes, with most of the TRE values above 1 mm.

Table V.

Expected TREs of the gold standard registration for the CT, CBCT, and MR images and, kV x-ray and MV images, respectively, for cervical C2 vertebra, brain, maxilla and mandible as target points, respectively. RXV notes the reconstructed coordinates from kV x-ray and RMV notes the reconstructed coordinates from MV images.

	RXV (mm)				RMV (mm)
	C2	Brain	Maxilla	Mandible	C2	Brain	Maxilla	Mandible
CT	0.27	0.17	0.22	0.23	1.09	0.70	0.90	0.91
CBCT small FOV	0.52	0.30	0.38	0.45	1.14	0.64	0.83	0.98
CBCT big FOV	0.52	0.30	0.42	0.45	1.30	0.76	1.06	1.13
MR T1	0.63	0.36	0.52	0.54	0.93	0.54	0.77	0.80
MR T2	1.86	1.26	2.05	–	1.33	0.90	1.46	–
MR PD	1.46	0.81	1.19	1.20	1.75	0.97	1.42	1.44

Table VI.

Expected TREs of the gold standard registration for the CT, CBCT, and MR images and the kV-MV fusion setup for cervical C2 vertebra, brain, maxilla and mandible as target points, respectively. RXMV denotes the reconstructed coordinates from kV AP-MV lateral 2D images and RMXV denotes the reconstructed coordinates from MV AP-kV lateral 2D images.

	RXMV (mm)				RMXV (mm)
	C2	Brain	Maxilla	Mandible	C2	Brain	Maxilla	Mandible
CT	0.64	0.41	0.53	0.54	0.73	0.47	0.60	0.61
CBCT small FOV	0.74	0.42	0.54	0.64	0.82	0.47	0.60	0.71
CBCT big FOV	0.89	0.52	0.72	0.77	0.93	0.54	0.76	0.81
MR T1	0.65	0.37	0.54	0.56	0.74	0.43	0.61	0.64
MR T2	1.43	0.97	1.58	–	1.71	1.16	1.88	–
MR PD	1.58	0.88	1.28	1.30	1.54	0.86	1.25	1.27

Finally, the comparison of FRE for point-based 3D/3D registration and the TRE computed from the fiducial markers when using the normalized mutual information algorithm as implemented in analyze AVW 10.0 showed a good correlation in the range of 0.63–3.85 mm. Detailed results can be found in Table VII.

Table VII.

The comparison of FRE for 3D/3D point-based registration and TRE for the fiducial centroids when using an intensity-based registration algorithm (normalized mutual information). FRE is given without parentheses, while TRE can be found in parentheses.

	CT (mm)	CBCT big FOV (mm)	CBCT small FOV (mm)	MR T1 (mm)	MR T2 (mm)	MR PD (mm)
CT	–	0.43 (1.14)	0.36 (0.63)	0.656 (0.79)	1.44 (1.70)	1.32 (3.85)
CBCT big FOV		–	0.52 (0.72)	0.62 (3.19)	1.55 (2.42)	1.25 (3.02)
CBCT small FOV			–	0.65 (1.13)	1.49 (2.29)	1.31 (3.42)
MR T1				–	1.26 (1.88)	1.16 (1.50)
MR T2					–	1.50 (2.31)
MR PD						–

III.C. Simulation results on fiducial localization error

Ten simulations of inaccurate fiducial localization by alterating the centroids ${\mathbf{w}}_i^r$ by a random value in the range of 1, 3, and 5 mm yielded an average difference in the projected target points of 3.7±0.5 mm for a 1 mm displacement and 41.5±10.5 mm for 3 mm displacements. An artificially introduced error of 5 mm gave no usable results. We conclude that accurate marker localization is crucial but was apparently carried out in a sufficient manner—also with respect to the placement of markers—in our experiment. A further simulation on the influence of x-ray calibration error with a range of up to 5 mm did not show an significant effect on TRE.

IV. DISCUSSION

Due to the invasiveness of marker implantation and some imaging modalities, it is difficult to obtain a gold standard data set with real patient data. Therefore, the three publicly available gold standard data sets for 3D/2D registration proposed by Tomaževič et al.,¹⁶ van de Kraats et al.,¹⁸ and by Markelj et al.²⁵ featured phantoms with mostly bone and little soft tissues^16,17 or simulated 2D images.²⁵ In this paper, we aimed to improve upon the existing publicly available gold standard data sets by presenting a new gold standard data set very close to a realistic clinical situation due to the fact that large amounts of soft tissue can be found in the cadaver; beyond that, the specimen extends in all three dimensions and therefore it is possible to study the influence of perspective on the registration process. Due to the soft-tissue deformations present, the data set also allows for studying the impact of patient positioning on registration outcome. While an additional nonrigid registration step was not included in this work, Part II of this paper presents strategies to cope with these problems. Since affine registration of volumes prior to the application of a deformation model is an inevitable step in nonrigid registration, the merit of the marker based rigid gold standard registration is evident. Application of deformation models on the data set presented is, however, an extension of the effort presented.

By minimizing the distance between the projected positions of markers from 3D images and the positions of markers in 2D images, an accurate gold standard was obtained, which is demonstrated by a good agreement of PDE and FRE values. For the results of different modalities and configurations, several observations can be made. First, as expected, the results show that the range of PDEs and FREs using the two kV x-ray images were always smaller than when using the two MV images. This is due to the different contrasts of the two imaging systems since the kV x-ray images offer significant performance advantages in terms of image contrast and signal-to-noise ratio per unit dose for visualization of soft-tissue structures than MV energies,³ enabling an easier and more accurate segmentation of the markers.

Since the CBCT and x-ray images were acquired using the same imaging system, we expected that the accuracy of fiducial based registration of CBCT images would be better than of the CT image. Surprisingly, the most accurate gold standard registration was obtained with the two kV X-ray images and the CT volume. This might be due to the lower image contrast of the CBCT system and thus less accurate determination of the centroid of the markers in those volumes. Furthermore, this may also be attributed to the fact that the aluminum markers used for the CBCT images exhibited some intensity inhomogeneities and could not be as clearly separated from the neighboring tissues as in the case of CT PTFE markers. On the other hand, the results confirmed that the cups were indeed rigidly attached to the skull and successfully endured the transfer between the acquisition devices.

Additionally, the comparison of PDE and FRE values obtained for the CBCT images showed that the accuracy of the gold standard for the CBCT image with a small FOV was higher than for the CBCT image with a large FOV; this is proportional to the resolution of the images before resampling. Among the MR images acquired with different protocols, the best accuracy of the gold standard was achieved for the MR Tl weighted image. More specifically, the best accuracy was achieved when the two MV images and MR Tl weighted image were used to obtain the gold standard registration. This is surprising since the localization of markers in MR images is hampered by nonrigid spatial distortions inherent to MR imaging. Although the obtained results are hard to explain, they might be a consequence of errors from different mutually excluding sources. FRE values of fiducial registrations using MR T2 weighted image were larger due to a reduced number of markers (six out of seven markers are presented in this volume),¹¹ while for the fiducial registration using the PD weighted MR image larger errors were due to the reduced image resolution.

Regarding the fusion setup, the FRE values were in the same range as for the regular setup (two kV images or two MV images). This means that our fusion setup gold standard is accurate and can be used to test algorithms for the 2D/3D registration of volumes to a pair constituted of a kV and a MV image; situation that can be found in a clinical environment.

Overall, the results show that PDE and FRE values are, in general, dependent on the variation in the intensities of markers in images, number of markers,¹¹ their configuration,^23,24 and positions.^23,24 Furthermore, the accuracy of registration is also dependent on the accuracy of marker localization in 2D and 3D images, and accuracy of 3D reconstruction.^11,16

For further validation of our gold standard registration, we chose one anatomical landmark as a target point in different anatomical regions of interest: The cervical C2 vertebra, brain, maxilla, and mandible and calculated the TRE. The low values of the TREs demonstrated that the gold standard is accurate and that our data set is suitable for evaluation of 2D/3D registration algorithms.

V. CONCLUSIONS

In this paper, a new gold standard data set obtained with the state-of-the-art imaging technology has been proposed. The proposed gold standard has the potential to improve the validation of 2D/3D registration algorithms for image guided therapy. The reported PDE values of the gold standard registrations were found to be less than 2.71 mm, while the expected TRE values for several anatomical target points were found to be less than 1.88 mm for all imaging modalities. The data set, together with the gold standard registration, is available from the corresponding author.