Abstract
A new computational approach to calculating binding energies and spatial positions of small molecules, peptides and proteins in the lipid bilayer has been developed. The method combines an anisotropic solvent representation of the lipid bilayer and universal solvation model, which predicts transfer energies of molecules from water to an arbitrary medium with defined polarity properties. The universal solvation model accounts for hydrophobic, van der Waals, hydrogen-bonding, and electrostatic solute-solvent interactions. The lipid bilayer is represented as a fluid anisotropic environment described by profiles of dielectric constant (ε), solvatochromic dipolarity parameter (π*), and hydrogen bonding acidity and basicity parameters (α and β). The polarity profiles were calculated using published distributions of quasi-molecular segments of lipids determined by neutron and X-ray scattering for DOPC bilayer and spin-labeling data that define concentration of water in the lipid acyl chain region. The model also accounts for the preferential solvation of charges and polar groups by water and includes the effect of the hydrophobic mismatch for transmembrane proteins. The method was tested on calculations of binding energies and preferential positions in membranes for small-molecules, peptides and peripheral membrane proteins that have been experimentally studied. The new theoretical approach was implemented in a new version (2.0) of our PPM program and applied for the large-scale calculations of spatial positions in membranes of more than 1000 peripheral and integral proteins. The results of calculations are deposited in the updated OPM database (http://opm.phar.umich.edu).
Keywords: transfer energy, water permeation, polarity profile, membrane protein, database, Arg-rich peptide, hydrophobicity scale
INTRODUCTION
Biological membranes separate cells from the environment and create intracellular compartments. Many vital functions are associated with membranes, such as biosynthesis, signaling, transport, communication and energy conversion. Interactions and reciprocal influence of major membrane components, proteins and lipids, define properties of membranes, including their size, thickness, shape, charge, polarity and density1–4. In particular, the presence of proteins affects the lipid order, lateral diffusion, surface tension, and lipid curvature3, 4. On the other hand, lipid environment organizes and directs folding and co-translational or post-translational insertion in membranes of transmembrane α-helical5–8 or β-barrel proteins9, membrane-associated peptides, toxins, and peripheral proteins10. Modulation of lipids influences spatial orientation, assembly, targeting, conformational transitions and function of membrane-embedded proteins2, 8, 11 and alter binding and distribution of small molecules, such as ligands, metabolites and drugs12.
To understand and describe these processes, it is important to have an adequate representation of complex physicochemical properties of the lipid bilayer, which markedly change over short distances along the membrane normal, and to properly describe the energetics of protein-lipid interactions. The lipid matrix can be represented either explicitly, or as a fluid milieu with defined characteristics. The later approach is much more computationally efficient and practical for simulation of large multi-protein complexes. However, even more advanced continuum solvent models, which account for both non-electrostatic and electrostatic protein-solvent interactions13, 14, usually apply a very simplistic approximation of the lipid bilayer by one or several hydrophobic slabs and implement arbitrary functions for describing the dielectric permittivity changes at the lipid-water interface1. Furthermore, these models focus mainly on the dielectric constant of solvent that defines the long-range electrostatics, but do not include the hydrogen bonding properties of the solvent that are known to be essential for describing interactions in the first solvation shell of polar molecules and ions15–18.
In the preceding paper we presented empirical separation and parameterization of long-range electrostatics and the first solvation shell effects that account for hydrophobic, van der Waals, and hydrogen-bonding solute-solvent interactions. We also found the minimal set of solvent parameters required to reproduce transfer energies of molecules from water to any solvent: hydrogen bonding acidity and basicity parameters (α and β), dielectric constant ε, and solvatochromic dipolarity/polarizability parameter π*.
In this study we extended this model to quantify the energetics of protein-lipid interactions in artificial lipid bilayers and natural biological membranes. We introduced an advanced implicit solvent representation of the lipid bilayer that describes its anisotropic properties by transbilayer profiles of parameters α, β, ε and π*. The profiles were calculated from experimental distributions of lipid segments along the bilayer normal as determined by X-ray scattering and neutron diffraction of dioleoylphosphatidylcholine (DOPC) bilayers19. We also included the distribution of water in the lipid bilayer assessed by spin probes20, preferential solvation of protein groups by water and lipid, and incorporated the lipid-protein hydrophobic matching condition21.
This advanced model was applied for calculation of transbilayer energy profiles of amino-acid residues incorporated in an α-helix or a β-barrel inserted in the lipid bilayer. These physical energy profiles were compared with statistical energy profiles derived from distributions along the membrane normal of solvent-exposed residues in three-dimensional (3D) structures of membrane proteins. This allowed us to refine the parameters of water distribution in the lipid acyl chain region of biological membranes.
The proposed anisotropic solvent model of the lipid bilayer was integrated in a new version (2.0) of our PPM (Positioning of Proteins in Membranes) program22. This computational method is aimed at prediction of energetically optimal orientations and binding energy of diverse molecules ranging from small organic compounds to multi-protein complexes in membranes. PPM 2.0 was thoroughly tested and subsequently applied for calculations of spatial positions in membrane of more than 1000 integral and peripheral membrane proteins and peptides that were deposited in the updated OPM (Orientations of Proteins in Membranes) database23 (http://opm.phar.umich.edu).
METHODS
Structure of the lipid bilayer
Volume probabilities (fractions) of different lipid segments along the DOPC bilayer, ϕm(z) were taken from the most recent X-ray and neutron scattering study19. The segments include CH=CH (CH), carbonyl+glycerol (CG), phosphate+choline (PCN), and methyl groups of choline (CholCH3). (m=1, 3, 4 and 5, respectively):
| (1) |
where A is the bilayer surface area per lipid molecule, Vm is the molecular volume of the fragment (in Å3), Zm and sm define the locations and widths of corresponding Gaussians, respectively, and the number (nm) is equal to 2 for CH(CH=CH) groups (there are two acyl chains in each lipid molecule) and to 1 for all other groups. The corresponding parameters are provided in Tables S1 and S2.
Volume fraction of total hydrocarbon (CH+CH2+CH3) was calculated using Gauss error function,
| (2) |
Volume fractions of CH2+CH3 groups and water were calculated as the differences:
| (3) |
| (4) |
According to Electron Spin Resonance (ESR) studies, lipid bilayers contain an appreciable amount of water that is not detected by scattering methods. The distribution of water in the fluid DOPC bilayer determined by ESR probes was described by sigmoid function:
| (5) |
where ϕW,outer=0.037 and ϕW,mid=0.07 are volume fractions of water in the outer (more ordered) region of lipid acyl chains near glycerol groups and in the center of membrane, respectively, λ=0.54 Å, and z0=8.2 Å20, 24. Molar water concentration can be defined as ϕW multiplied by bulk water concentration (55.5 M).
The concentration of water inside the membrane was taken as maximal of values determined from the X-ray and neutron scattering and ESR data because low concentrations of water are undetectable by the scattering (ϕWX-Ray=0 in the middle of membrane):
| (6) |
Mole fractions of components were calculated from the volume fractions:
| (7) |
where Vi is partial volume of group i (Table S1; the partial volume of aliphatic groups for calculating molar fractions was taken as for (CH2)4 segment, 108 Å3).
Calculation of polarity profiles
The bilayer was treated as a binary mixture of two weakly interacting solvents: (a) the hydrophilic (aqueous) solution of zwitterionic phosphatidylcholine groups in water and (b) the hydrophobic solution of lipid acyl chains including their glycerol groups. The preferential solvation occurs in the first solvation shell and includes the hydrophobic effect and direct hydrogen bonding with the solvent, as defined by parameters α and β. To describe this situation, we calculated six different profiles with α and β defined separately for the hydrophobic and aqueous components: αlip(z), βlip(z), αaq(z), βaq(z), πbil(z) or εbil(z) and concentration of water ϕaq(z).
Polarity profiles were calculated from volume fractions of lipid segments and water determined by X-ray and neutron scattering (equations (1–6)) and using contributions of the corresponding groups to parameters α, β, π*, and ε. The values of α, β, π*, and ε for different groups were taken as for solvents with similar chemical structure (Table S1). However, we made two additional simplifications which helped to improve performance of the model: (a) ε of charged lipid groups dissolved in water (PCN and CholCh3 segments) were taken the same as ε of the water (78.4) based on the general observation that aqueous solutions of zwitterions have dielectric constants only slightly different from that of water25; and (b) parameters α and β of PCN and choline methyl fragments were taken as for the whole phosphatidylcholine group (that is 0.82 and 1.74, respectively).
The π* values were defined from molar fractions of the corresponding components26, 27:
| (8) |
Dielectric constant of the non-protic lipid part was calculated as a harmonic mean of the lipid components27
| (9) |
where volume fractions reflect composition of only lipid components, excluding water
| (10) |
The subsequent averaging of dielectric constant for the mixture of lipid and water must be done in terms of mole fractions, since water is a protic solvent27:
| (11) |
where xW and εW are the molar fraction and dielectric constant of water, respectively, and the polynomial function F describes the non-linear behavior of ε using empirical coefficients ε0, ε1 and ε2 whose values depend on the specific co-solvent. These coefficients were determined for many different water-co-solvent pairs27. For co-solvents with dielectric constant lower than that of water, the εmix(xW) curves are usually convex because very low concentrations of water contribute little to the dielectric constant. Since the parameters for water-lipid mixtures are unknown, the convex curve (11) was approximated by a shifted linear dependence:
| (12) |
Hence the presence of very small amounts of water does not affect the dielectric constant of lipid bilyer (εbil=εlip at xW < δ=0.1), and εbil reaches the value of εW at xW=1.
Parameters α, β were calculated using mole fractions27:
| (13) |
| (14) |
| (15) |
| (16) |
where αm, βm, πm and εm are fragmental parameters of the corresponding lipid segments, CH(CH=CH), CH2/CH3, CG, PCN, and CholCH3 (m=1,2,3,4 and 5, respectively) and water (m=6) shown in Table S1. The corresponding mole fractions, ϕm were defined separately for the lipid acyl chain and aqueous mixtures:
| (17) |
| (18) |
Universal solvation model for anisotropic environment
The transfer energy of a solute molecule from water to an arbitrary position in the lipid bilayers was calculated using the universal solvation model developed in our previous work, but including the ionizable groups and dependence of solvation parameters σi and η on the atom position along the bilayer normal (zi):
| (19) |
where σi(zi) is solvation parameter that depends on type of atom and describes surface transfer energy (per Å2) of atom i from bulk water to the point zi, ASAi is a solvent-accessible surface area of atom i, η(zj) is an energy cost of transferring the dipole moment of 1D from water to point zj, μj is a dipole moment of group j, are energies of ionizable group k in ionized and neutral states, respectively, N is the number of atoms in the molecule (excluding atoms of ionizable groups), M is the number of group dipoles, L is the number of ionizable groups, and parameters d, ϕ and τ define spatial position of the molecule with respect to the lipid bilayer, as previously described22. Thus, each ionizable group was individually selected in a charged or uncharged state, whichever has a lower energy at the given depth in the membrane.
The transfer energy of ionizable group k in neutral state was calculated as a sum of ionization energy of the group and ASA-dependent transfer energies of the corresponding atoms in uncharged state:
| (20) |
where Lk is the number of atoms in ionizable group k, while the energy cost of deionization during transfer from water to nonpolar environment was defined by the Henderson-Hasselbalch equation:
| (21) |
The transfer energy in the ionized state was described by the following equation:
| (22) |
where σl,ion is solvation parameter of O or N atoms in charged state; eBorn is a weight factor of long-range electrostatic contribution to transfer energy; rk is an ionic radius. The dielectric function for ions was described by the Born equation modified by Abe28:
| (23) |
The electrostatic energy was corrected for charged groups involved in ion pairs as described in equation (40). To simplify the calculations, the energy of an ionizable group was evenly divided between all atoms of the group (two oxygens in acids and three nitrogens in guanidine group). Dipole moments of ionizable groups were taken as in unionized state (i.e. as in the middle of the lipid bilayer).
Atomic and solvation radii were chosen as described in our companion paper. Accessible surface areas were calculated using the program SOLVA from NACCESS with probe radius of water (1.4 Å).
According to our universal solvation model, the values of solvation parameters σi for different types of atoms (equation 19) depend on polarity parameters of the lipid-water mixture (α, β and ε) that change along the bilayer normal:
| (24) |
where αbil(z), βbil(z) and εbil(z) are transmembrane profiles of hydrogen bonding donor and acceptor capacities and dielectric constant of the lipid bilayer, respectively, αwat, βwat and εwat are the corresponding values in water, and the linear regression coefficients ei, ai and bi for different types of atoms (Table S3) were derived from water-solvent transfer energies of model compounds in the preceding publication. However, this equation was modified to describe the preferential solvation (see below).
Two alternative dielectric models were tested for describing the long-range dipolar contribution. This contribution was defined by parameter η that represents energy cost of transferring an electric dipole moment of 1D from water to the point of membrane with coordinate z. The first model was based on the use of solvatochromic dipolarity parameter, π*:
| (25) |
where π*bil(z) and π*wat are values of this parameter in bilayer and water, respectively.
An alternative model for the dipolar contribution was based on the Block-Walker dielectric function of the media, FBW(ε)29:
| (26) |
| (27) |
The required regression coefficients eBorn, σ0, ei, ai, bi, edip, π, and edip,BW (equations 22, 24–26) were taken from our accompanying paper (Table S3). The signs were chosen to describe transfer from water considered as the reference phase.
Treatment of preferential solvation
The universal solvation model (equations 19–27) was modified to account for the preferential solvation of protein groups by water. We used a simple model of preferential solvation that operates with local mole fractions of solvents in the first solvation shell of a solute27, 30. The lipid bilayer was treated as a binary mixture of two weakly interacting phases: an aqueous solution of charged phosphatidylcholine groups (Aq), and a nonpolar solution of acyl chains including glycerol groups of lipids (L).
| (28) |
where Aq is a molecule of an aqueous component (primarily water), and L is a segment of lipid that replaces the molecule of water. This equation was used for each individual atom, Si of the macromolecular solute.
The corresponding preferential solvation constant is then defined as follows27, 30:
| (29) |
where x are mole fractions of the corresponding species in the vicinity of solute group Si
| (30) |
and the free energy difference associated with Aq/L exchange is
| (31) |
where is an atomic solvation parameter describing transfer of protein atom i from aqueous to the lipid solution, and ASAAq is an area occupied by a molecule of an aqueous component at the surface of protein atom i. The average surface area occupied by a water molecule, ASAAq, was estimated 14 Å, based on the hydration numbers and ASA of ammonium, guanidine and carboxylete ions31–33.
Each atomic solvation parameter was described by an average value for the lipid-bound and aqueous solution-bound states, rather than simply using equation (24):
| (32) |
where mole fractions xAq and xSL were determined as follows:
| (33) |
| (34) |
and where xW, xPCN and xR are molar fractions of water, lipid phosphatidyl segment and choline group, respectively.
Transfer energies from bulk water to lipid acyl chain solvent were calculated using equation (24):
| (35) |
where εbil, αlip and βlip are calculated using equations (9–12), (13) and (14), respectively.
Transfer energies from bulk water to aqueous solution of phosphatidylcholine groups, were calculated similarly, but assuming no hydrophobic effect in this area and assuming dielectric constant to be the same as in water:
| (36) |
where αaq and βaq are calculated using equations (15) and (16), respectively.
The solvatochromic parameter π* and dielectric constant describe the long-range electrostatic component of the transfer energy. They depend only on the bulk dielectric properties of the mixture (as described by εbil or π*bil), but not on the direct binding of the solvent in the first shell. Therefore, they are not a part of the preferential solvation.
This approach takes into account only interactions of the solute group Si with both solvents, but it neglects the mutual interactions of the solvents Aq and L. It can be used because the aqueous and non-aqueous (acyl chain) solvents are poorly mixable. The phases could not be chosen as lipid and water because lipid phosphates are strongly hydrated.
Application of the model to proteins
The application of the method to proteins rather than to small molecules is facilitated by the existence of a limited number of standard amino acids, whose group dipole moments and ionization energies can be easily tabulated. The group dipole moments (1.8, 1.4 1.5, 3.7, 4.8 and 2.7 D for COOH, OH, SH, guanidine, imidazole and indole groups, respectively34–36) were assigned to the appropriate non-hydrogen atoms (Oη in Tyr, Nε of Trp, Oγ of Ser and Thr, Nε of Lys, and Nδ of Arg, Oδ of Asp and Asn, Oε of Glu and Gln, Nδ of Asn, Nε of Gln, Nδ and Nε of His). The dipole moments of the peptide groups were divided into contributions from NH and C=O groups (1.3 D and 2.3 D, respectively).
Many protein groups are buried from the solvent in the protein interior. They are not expected to significantly contribute to the transfer energy, because they remain in the same environment during transfer of the protein from water to the lipid bilayer. Hence, we took into account only the dipolar energy of groups exposed to the solvent. The individual dipolar contributions in (19) were smoothened to linearly decrease to zero when ASA of an atom associated with the dipole moment becomes smaller than the hydration area occupied by a single molecule of water (ASAAq ~ 14 Å, the same as in eq. (31)):
| (37) |
| (38) |
The smoothening of Born energy for ionized groups (equation (22)) was done similarly:
| (39) |
| (40) |
where coefficient fk=0.5 for groups involved in ion pairs, and fk=1 in all other cases. The value of 0.5 was chosen because an electrostatic self-energy of a dipole formed by an ionic pair is roughly of the same magnitude as the Born energy of a single individual ion37. The linear smoothing model should be improved in the future because it underestimates electrostatic energy of cationic groups with small ASA.
It has been evaluated that formation of the hydrogen bonds by OγH groups of sterically constrained Ser or Thr residues in nonpolar environments leads to an energy gain of ~−1.5 kcal/mol38. Hence we included contributions of these H-bonds normalized by the hydrogen bonding donor capacity α of the environment:
| (41) |
where E0 was chosen to provide −1.5 kcal/mol in the middle of membrane. The H-bonds were defined as pairs of non-hydrogen donor and acceptor atoms with distance smaller than 3.5 Å and valence angles A–B…X larger than 90°.
Hydrophobic matching condition for transmembrane proteins
The thickness of a fluid lipid bilayer can adjust to match the hydrophobic thickness of a transmembrane peptide or protein. The corresponding energy cost was described by the simplified expression21:
| (42) |
where d0 is intrinsic hydrophobic thickness of undisturbed bilayer, deq is the actual hydrophobic thickness of the protein and bilayer in the area of their direct contact, Nlip is the number of annular lipid molecules interacting with protein, and the constant Δedef =0.029 kcal/mol/Å was chosen based on experimental studies of hydrophobic mismatch (average value of Δgmis =0.08kBT nm−2 21).
The values of d0 were taken as average hydrophobic thicknesses of inner membranes and outer bacterial membranes: 30 and 23.6 Å, respectively, as estimated previously22. An additional ±1Å deviation from the d0 value was allowed without any energy penalty to account for a possible variation in the thickness of membranes in different organisms and cells. The numbers of annular lipids were estimated by calculating the transmembrane perimeter of a protein and dividing it by the width of an area occupied by a lipid molecule at the surface of the protein (it was found to be ~6 Å to reproduce the numbers of annular lipids for TM proteins21).
The equilibrium value of the thickness deq was determined for each individual transmembrane protein by minimizing total transfer energy of the protein (equation (19)) with added Elip. Incorporation of the hydrophobic mismatch did not significantly change the calculated hydrophobic thickness for a vast majority of TM proteins (the differences were usually within the ± deviations observed in energy interval of 1 kcal/mol, as provided in the OPM database). This could be expected because the additional energy penalty (equation 42) is relatively small: 0.3 kcal mol−1Å−1 for a single-helical protein (11 annular lipids) and 0.7 kcal mol−1Å−1 for the seven-helical protein, rhodopsin (25 annular lipids). Larger changes in the hydrophobic thickness (of ~2–4 Å) were observed for single-helical or double-helical peptides and a few poor quality structures with missing helix ends and loops.
Optimization of spatial positions of molecules in membrane
The original version of our PPM program was modified to optimize positions of molecules in the lipid bilayer with the new solvation model. The computation requires only energy functions and parameters described in equations (1–42) and Tables S1, S3, S4. A solute molecule was considered as a rigid body whose spatial position was defined by three independent variables: two rotation angles and one translation along the bilayer normal (φ, τ and d, respectively). Transfer energy (equation 19) was optimized by combining grid scan and Davidon-Fletcher-Powell method for local energy minimization. Derivatives of transfer energy with respect to rigid body variables of the molecule were analytically calculated, as described previously22. Derivatives of energy with respect to z were calculated as finite differences with step of 0.01 Å. The hydrophobic thickness of TM proteins was optimized by grid scan for location of the hydrocarbon boundary (ZHDC in eq. 2) with step of 0.05 Å. All other peaks of the lipid and water distributions were shifted accordingly during the optimization to remain at the same distance from the hydrocarbon boundary as in DOPC.
The program uses as input only a set of coordinate files in the PDB format. Unlike the previous version, it allows an automatic determination of transmembrane secondary structures without using any external software. The dipole moments and standard pKa values of different groups are included in the library of amino acid residues or directly in the PDB files for small molecules.
Calculation of energy profiles and interfacial scale for amino acid residues
The transbilayer energy profiles of amino acid residues were calculated by placing each amino-acid into the α-helix or β-barrel that was arranged perpendicularly to the membrane and moved along the membrane normal with step of 1 Å. The backbone structures of the α-helix or a β-barrel were taken from crystal structures of membrane proteins (1kzu and 1qjp PDB files, respectively). All residues surrounding the “probe” residue in α-helix or β-barrel were replaced by alanine. Side-chain conformers of the probe residue that are sterically allowed in α-helix or β-sheet were taken from a standard rotamer library and minimized with CHARMM implemented in Quanta (Accelrys Inc.). Conformers with the lowest transfer energy were automatically selected for each location along the bilayer normal during calculations of energy profiles. The conformers are not the same in different points of the profile due to “snorkeling” of polar residues to the regions with a higher concentration of water and preferential burial of nonpolar residues in the hydrocarbon core. Only side-chain atoms of the probe residue were included in the calculation of transfer energy. The locations of hydrocarbon core boundary ZHDC was adjusted to 30 and 23 Å, as corresponding to average hydrophobic thicknesses of α-helical and β-sheet proteins, respectively. The curves were symmetrized by averaging energies obtained for the positive and negative values of z because these energies are dependent on the overall (N- to C- terminus) orientation of the helix with respect to the membrane.
To make a comparison with the Wimley-White interfacial scale, the optimal water-membrane positions and transfer energy were calculated for N-methylacetamides of amino acids. The N-methylacetamides were taken in extended and folded conformations (φ= −120°, ψ=−120° and φ=−60°, ψ=−60°), with different side-chain conformers (χ1=±60 and 180°), and the conformation with the lowest transfer energy was selected after optimization of the molecule as a rigid body using OPM 2.1. The α-helical conformation of Arg-rich S4 peptide was taken from the corresponding X-ray structure (PDB ID: 2kyh, residues 113–130) and was modified to include residues 113–114 in the helix.
Calculation of statistical energy profiles of amino-acid residues
Statistical energies were derived from distributions along the membrane normal of solvent exposed residues in 3D structures of 119 α-helical and 53 β-barrel transmembrane proteins from the OPM database that were oriented relative to the membrane plane by PPM 1.022 (lists of proteins are provided in Supplementary materials). We did not include residues that are buried from the lipid in the protein interior, because the statistical preferences for such residues are dependent on the solid-state intra-protein van der Waals interactions and hydrogen bonds, rather than on protein-lipid interactions of interest. The number of transmembrane protein structures was relatively small because we use structures of only non-homologous or remotely homologous proteins (with sequence identity lower than 40%) to avoid a systematic statistical bias due to evolutionarily relatedness of the proteins. A majority of lipid-facing residues are replaced in homologous proteins with identity of ~40% because of the much higher sequence variability of solvent-exposed residues. We also excluded proteins whose hydrocarbon core boundaries were poorly defined, as followed from calculations with PPM 1.0.
Statistical energy of an amino-acid residue in a slice [z−δ; z+δ] was calculated by analogy to the partition coefficient, but using surface rather than volume concentrations of residues in structures of α-helical or β-sheet transmembrane proteins:
| (43) |
where Ci(z) is an average surface concentration of the lipid-facing residue type i in the slice with coordinate z ±0.5Å, and Ci,water is an average surface concentration of the residue type i facing the water, i.e. located beyond 25 Å distance from the membrane center. The sets of lipid-facing residues in transmembrane proteins (i.e. excluding water-facing residues in transmembrane channels and funnels) were calculated as previously described22.
The surface concentration of a residue in the slice was determined by averaging ASA of the residue (side-chain only) in a set of proteins:
| (44) |
where ASAi(z) is ASA of all side-chain atoms of residue in the slice, and ASAtotal(z) are total ASA of the slice, respectively, calculated for the set of proteins.
Reference surface concentration of the same residue in water was calculated similarly
| (45) |
Parameters of permeating water in biological membranes (ϕW,outer, ϕW,mid and λ in equation (5)) were optimized by minimizing the root mean square deviation of statistical and physical energy profiles calculated by PPM 2.0 for Tyr and Trp residues (all points from −30 to +30 Å with step of 1Å were taken simultaneously for both residues). Physical energy profiles were calculated for residues in individual α-helix moving across the membrane, as described above. These profiles were normalized to account for the difference in residue accessibility between polytopic proteins included in statistical analysis and an individual α-helix used for calculation of physical profiles, as explained in Results.
RESULTS
Polarity profiles of DOPC bilayer
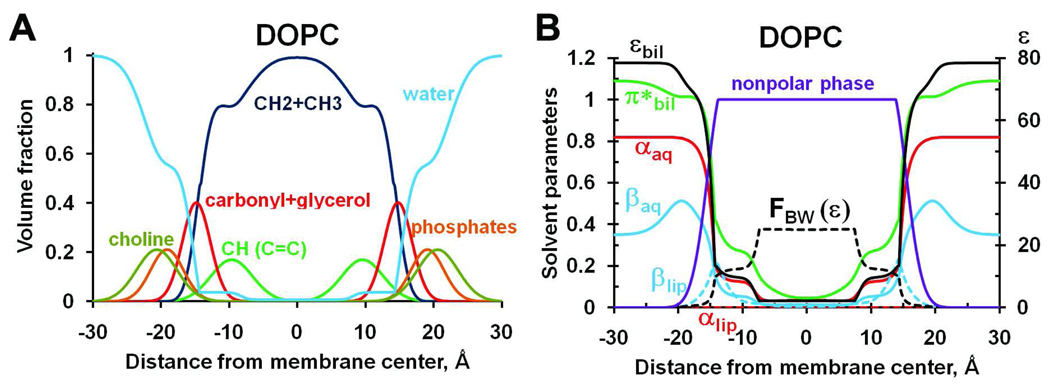
The lipid bilayer was considered as an anisotropic fluid whose physico-chemical properties change along the membrane normal (Figure 1). These properties are described by profiles of the commonly used polarity parameters that are required for the universal solvation model: hydrogen bonding donor (α) and acceptor (β) capacity, solvatochromic dipolarity parameter (π*), and Block-Walker dielectric function FBW(ε) for the lipid-water mixture. The profiles of these parameters (Figure 1B) were calculated for DOPC and DOPS bilayers from published experimental distributions of lipid fragments and water19, 39, 40 (Figure 1A) as described in Methods.
Figure 1.
(A) Volume fractions of lipid segments determined by X-ray and neutron scattering for fluid DOPC bilayer19. The volume fractions of individual lipid components are shown as colored solid lines for alkyl groups (CH2+CH3, purple), double bonds (CH, green), water (blue), carbonyls with glyceroles (CG, red), phosphate (orange), and choline (dark green) groups. (B) Profiles of hydrogen bonding donor (αaq and αlip) and acceptor (βaq and βlip) capacities, solvatochromic dipolarity parameter (π*lip), dielectric constant (εbil), Block-Walker dielectric function, FBW(ε), and volume fraction of nonpolar phase (CH+CH2+CH3+CG) calculated for DOPC bilayer.
According to the published ESR studies20, 39, the concentration of water quickly drops to 1–2.9 M in the carbonyl region (z=14.8 Å) and sharply decreases again to 0.1–0.4 M in the lipid double bond region (z0=8.2 Å) of the DOPC bilayer (Figure 1A), as described by equation (5). The middle point of z0=8.2 Å is close to the maximum of lipid double bond distribution (9.6 Å) that represents the natural boundary between the more ordered region with the higher concentration of defects for water and a more disordered, liquid-like region41.
To account for the preferential solvation, we treated the lipid bilayer as a binary mixture of polar aqueous and nonpolar lipid phases (see Methods). Polar phase represents aqueous solution of charged lipid segments including phosphate and choline groups. Nonpolar phase represents lipid acyl chains with glycerol/carbonyl segment (Figure 1B). Parameters α and β, which define solute-solvent interactions in the first shell were calculated separately for the phases (αaq, βaq and αlip, βlip, respectively, see equations 13–18). The dielectric parameters (π* and ε), which define long-range electrostatic interactions, were calculated for the whole mixture using equations (8–12).
The profiles of polarity parameters (αaq, βaq, πbil*, and εbil) and Block-Walker dielectric function FBW(εbil) demonstrate two sharp transition regions: one at the hydrocarbon core boundary (14.8 Ǻ from the interior), and another in the lipid double bond region (8.2 Ǻ from the interior). This behavior of polarity parameters follows the distribution of water inside the DOPC bilayer. Parameter βaq, which defines the hydrogen-bonding acceptor capacity of the aqueous phase, has an additional maximum at ~20 Ǻ from the membrane center, due to the presence of phosphate groups. Parameter βlip, which represents hydrogen-bonding acceptor capacity of the lipid phase, shows a maximum at the hydrocarbon core boundary due to the presence of lipid carbonyl groups. The shape of polarity profiles indicates the existence of three major regions: the polar head group region (i.e. ~15–30 Å from the interior), the “mid-polar”10 region (~8–15 Å from the interior) and the innermost nonpolar membrane core (0–8 Å).
Comparison of results for DOPC or DOPS bilayers shows that polarity parameters depend on the lipid composition. For example, DOPS is characterized by higher values of βaq (it is larger by ~20% at 20 Ǻ distance, see Figure S1) due to the presence of serine carboxyl groups in DOPS.
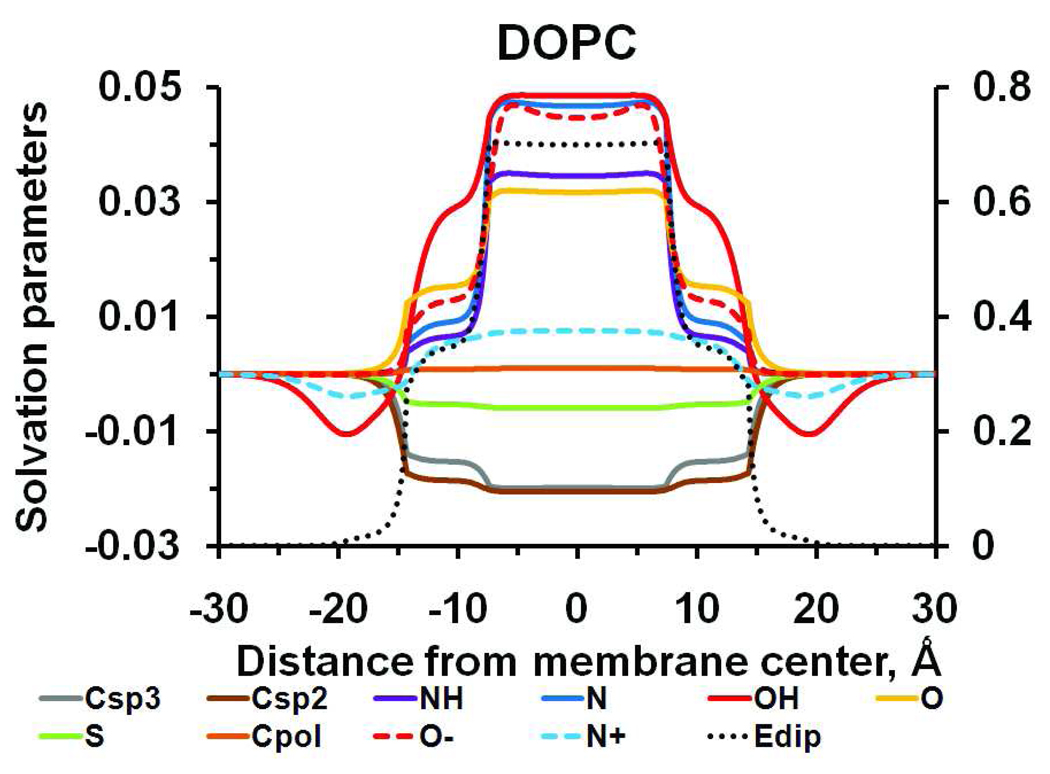
The profiles of hydrogen bonding capacities and dielectric functions (Figure 1B) were used to calculate atomic solvation parameters σi(z), which define transfer energy for each of ten atom types, and dipolar solvation parameter η(z), which defines the energy of transferring an electric dipole moment of 1D from water (Figure 2).
Figure 2.
Transbilayer profiles of atomic solvation parameters, σCsp3 (gray solid line), σCsp2 (brown solid line), σNH (purple solid), σOH (red solid line), σO, (yellow solid line), σS, (green solid line), σpol, (orange solid line), σCOO−, (red dashed line), σNH3+ (blue dashed line), and dipolar solvation parameter η for 1D dipole (black dotted line) calculated for DOPC bilayer.
Solvation parameter curves have two transition regions at ~15 Ǻ and ~8 Ǻ from the bilayer center. Further, parameters for OH and N+ groups show minima at ~20 Ǻ, due to the formation of H-bonds between these groups and lipid phosphate or carbonyl groups. Subsequent calculations of transfer energy (equation 19) are based on these profiles.
Energy profiles of amino-acid residues in DOPC bilayer
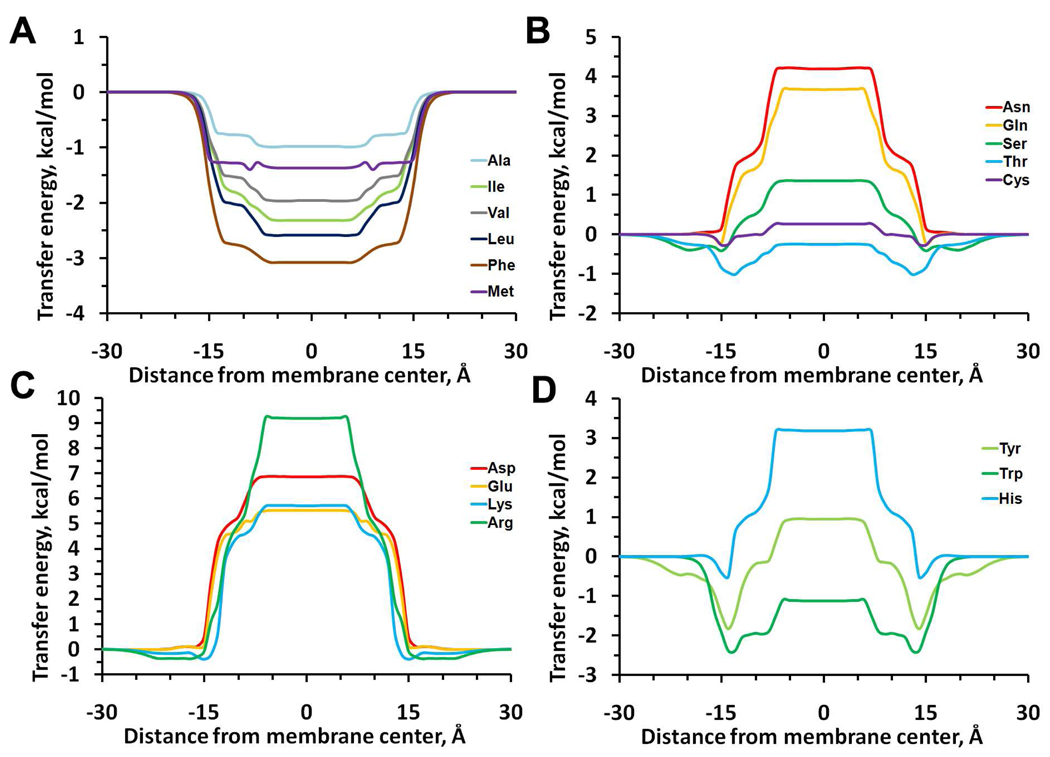
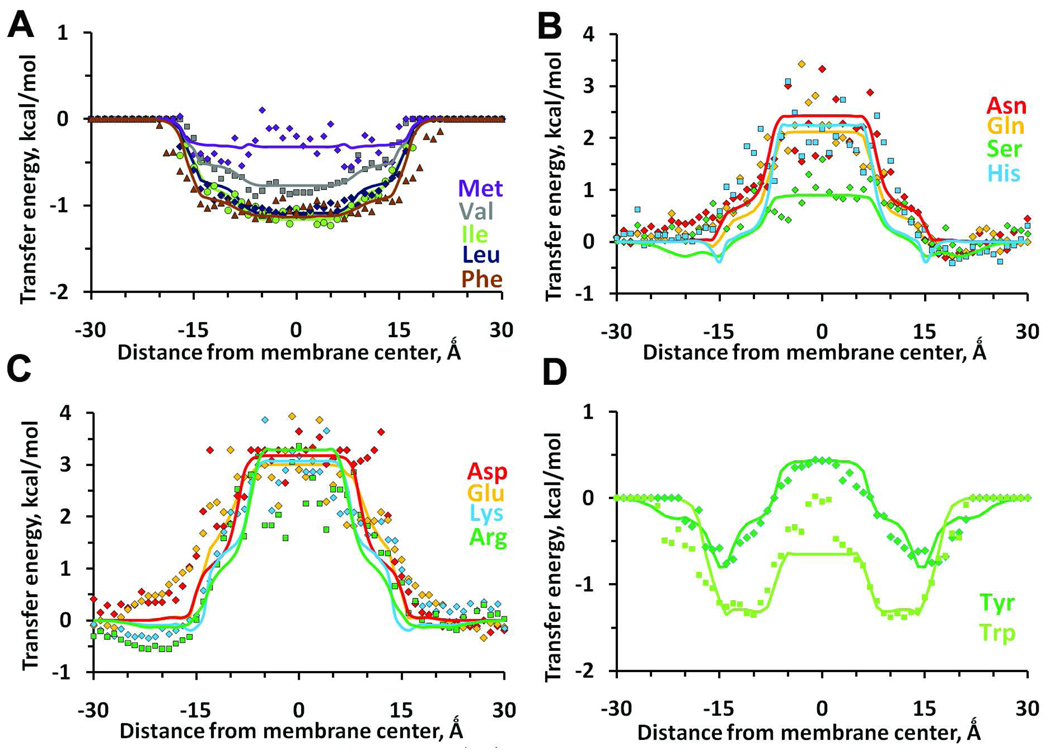
To verify the model, we calculated transfer energies of 18 residues (excluding Pro and Gly) incorporated into a poly-Ala α-helix moving along the membrane normal (Figures 3, 4). The profiles of calculated transfer (i.e. physical) energies were compared with statistical energies derived from distributions of corresponding residues in 3D structures of α-helical membrane proteins (Figure 5).
Figure 3.
Transfer energy profiles of 18 amino-acid residues incorporated into an α-helix moving across the DOPC bilayer, as calculated with PPM 2.0.
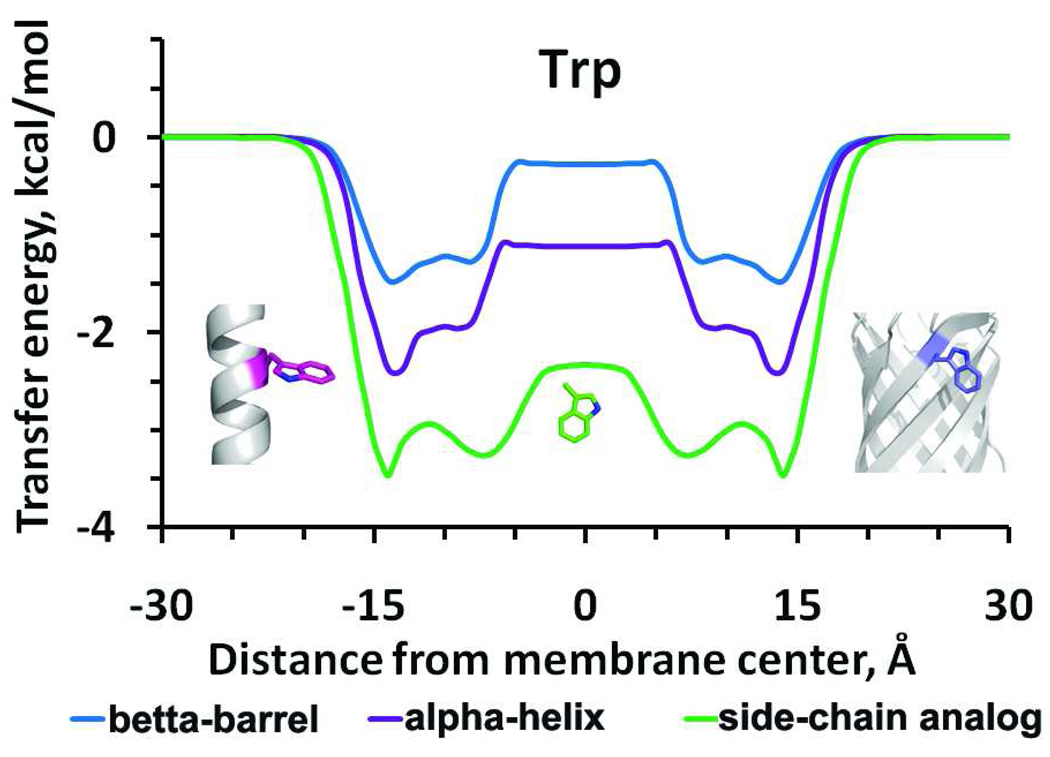
Figure 4.
Transfer energy profiles of Trp in the DOPC bilayer. Energy was calculated for Trp side chain analog, 3-methylindole (green), for Trp in a poly-Ala α-helix (purple), and Trp in a β-barrel (blue). The energies are roughly proportional to solvent-accessible surface area (ASA) of Trp in each environment: ASA = 293 Ǻ2 for Trp side chain analogue, ASA = 176 Ǻ2 for Trp in α-helix and ASA = 130 Ǻ2 for Trp in β-barrel.
Figure 5.
Comparison of transfer energies calculated for 15 amino acid residues in α-helix after optimization of parameters for water (solid lines) and statistical energies (squares, circles, triangles and diamonds) obtained for solvent-exposed residues in a set of 119 α-helical transmembrane proteins from bacterial, archaeal, and eukaryotic membranes from the OPM database. The calculated energies were normalized to account for the difference of ASA for the residue in the set of proteins and in isolated α-helix.
The analysis of energy profiles helped us to evaluate the role of permeating water in the ordered part of the lipid acyl chain region, the significance of the preferential solvation, and the performance of alternative dielectric models (Figure S2). Neglecting the presence of water in the lipid bilayer resulted in very narrow low-energy areas for Trp and Tyr in the “mid-polar” region, inconsistent with much wider statistical energy curves. Ignoring the preferential solvation led to a significant increase of transfer energies for polar and especially negatively charged residues, which also disagrees with statistical profiles. The Block-Walker dielectric model provided wider low-energy areas for Tyr and Trp residues than π*-based model, which is more consistent with statistical distributions. Therefore, we selected the Block-Walker dielectric model for describing electrostatic transfer energy of dipoles (equations 26, 27) and included the preferential solvation (equations 28–36) and water distribution parameters determined by spin probes (equation (5)) for all subsequent calculations.
Calculated energy profiles of nonpolar residues (Val, Leu, Ile, Phe, Ala, Met) (Figure 3A) have wide low-energy areas encompassing the whole lipid acyl chain region, while curves for polar (Cys, Ser, Thr, Asn, Gln, His), and charged (Lys, Arg, Asp, Glu) residues have wide plateaus in this region (Figure 3 B, C). All residues with significant dipole moments (His, Ser, Thr, Cys) have shoulders in the “mid-polar” region. Residues bearing OH and N+ groups (Ser, Thr, Tyr, Arg, Lys) have additional shallow minima in the lipid head group region due to their H-bonding with lipid phosphate and carbonyl groups.
Patterns for Tyr and Trp residues are more complex, with broad minima in the “mid-polar” region (Figure 3D) and maxima in the central bilayer region. More specifically, the curve for Tyr residues has well-pronounced minima (−1.83 kcal/mol) at 14 Ǻ, a shoulder at 8 Ǻ, and a wide area with positive transfer energy (+0.94 kcal/mol) in the middle (0–6 Ǻ from the interior). The curve for Trp residue has wider negative energy areas between 8 and 15 Ǻ from the bilayer center. The minima for Trp and Tyr are in agreement with experimental studies that show preferential location of these residues at the lipid-water interfaces42–44. These minima arise in part due to the presence of 1–2 M water in the "mid-polar" region.
Similar calculations were performed for residues in α-helix inserted into DOPS bilayer. Results for DOPS slightly deviate from those for DOPC. The most significant differences were obtained for residues bearing N+ (Lys, Arg) and OH-groups (Tyr, Ser) (Figure S3). Energy profiles for these residues show deeper minima in the head group region due to additional H-bonding interactions with carboxyls of phosphatidylserine in DOPS bilayer.
In order to better understand the influence of protein structural context on solvation energy, we compared the water-to-bilayer transfer energies of amino-acid residues in three different systems: (1) side-chain analogs; (2) amino-acid residues incorporated in a single transmembrane α-helix; (3) amino-acid residues incorporated in a hydrophobic β-barrel. Curves obtained for residues incorporated into the β-barrel are shown on Figures 4, S3, and S4.
Comparison of these three systems demonstrate that profiles of transfer energy for the same amino-acid residue follow a similar pattern, but show different absolute values of energies in each system (Figures 4, S4). The absolute values of transfer free energy depend on exposure of the corresponding residue to the solvent, which is different for isolated side chain analogs and residues in α-helix or in β-barrel. For example, the minimal absolute value of transfer energy of Trp side-chain analogue, 3-methylindole, was approximately 1.5 and 2.4 fold larger than for Trp residues in isolated α-helix and β-barrel, respectively, which is roughly proportional to their ASA of 293, 176 and 130 Ǻ2, respectively (Figure 4).
Comparison with statistical distributions of residues in transmembrane proteins
To further evaluate our model, we made a more detailed comparison of physical energy profiles, which were calculated for amino-acid residues in a transmembrane α-helix or a β-barrel, with statistical energies derived from distributions of solvent-exposed residues in α-helical and β-barrel transmembrane proteins, as described in Methods (Figures 5, 6 and S5).
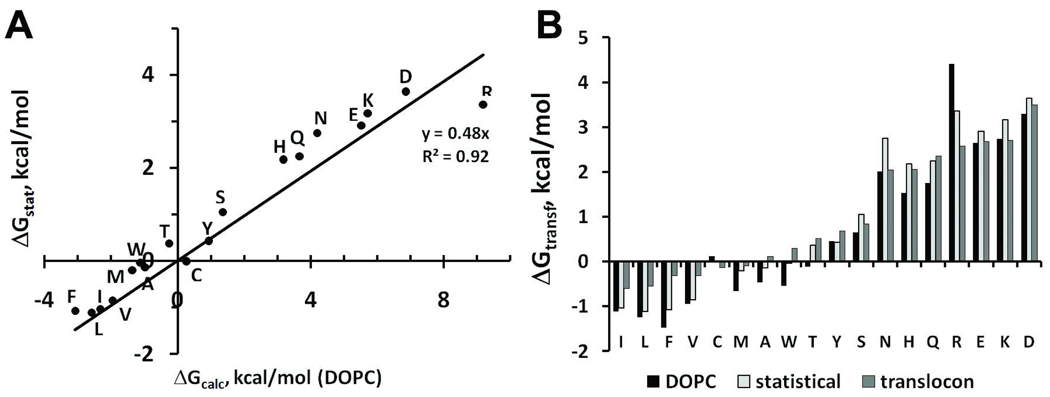
Figure 6.
Comparison of physical, statistical, and biological hydrophobicity scales of amino acid residues from α-helices in the middle of membrane. A. Correlation (R2=0.92) between statistical energies derived from distributions of surface residues in 119 α-helical transmembrane proteins (ΔGstat) and transfer energies calculated for residues from an α-helix in DOPC (ΔGcalc). The obtained slope (k=0.48) is likely related to the decreased accessibility of residues to lipid in polytopic membrane proteins in comparison to that in a single α-helix. B. Comparison of transfer energies: (a) calculated for the residues in an α-helix in DOPC after normalization by k=0.48 (black bars); (b) derived from statistical distributions of residues in transmembrane proteins (light gray bars); and (c) determined from translocon-mediated insertion experiments45 (dark gray bars).
The comparison of energy values in the middle of membrane shows that physical energies are approximately twice as large as statistical energies (Figure 6). This result may be attributed to the smaller accessibility of residues to solvent in polytopic proteins, compared to that in an isolated α-helix. To verify this, we calculated average lipid-accessible ASA for different types of residues in a set of 119 transmembrane α-helical proteins. Indeed, the average ASA of residues in proteins were between 30 and 50% of that in an isolated α-helix. Hence, in order to compare statistical and physical energies, the later must be adjusted by multiplying them by a normalizing coefficient of ~0.5 (k=0.48 in Figure 6A) that accounts for the difference in the lipid-exposed areas (similar to that in Figure 4). It is noteworthy that the obtained statistical and normalized physical scales are comparable to the biological hydrophobicity scale (Figure 6B) that was obtained using translocon-assisted insertion of hydrophobic peptides into endoplasmic reticulum membranes (see Discussion)45.
The normalized physical energy profiles reproduce the overall shape and the most important features of statistical energy profiles for the corresponding amino acids in α-helical and β-barrel proteins (Figures 5 and S5). These features include the negative transfer energies for nonpolar residues, the positive energies for polar and charged residues, the pronounced energy minima for Trp and Tyr in the “mid-polar” region, and the presence of two transition regions at ~15 and ~9 Å from the membrane center for amphiphilic and polar residues. The internal, ~9 Å transition appears as a shoulder in statistical energy profiles of uncharged polar residues (Figure 5B), which is less pronounced for charged residues (Figure 5C) in part due to insufficient statistics.
At the same time, the low-energy area of Tyr and Trp calculated in DOPC were narrower and more outwardly shifted than minima of statistical energy profiles. This could be due to the different lipid and protein compositions of biological membranes and the model DOPC bilayer. Hence, we attempted to refine the parameters of implicit solvation model for biological membranes by fitting the profiles of statistical and physical energies for Tyr and Trp residues. These residues were chosen as molecular probes for the following reasons: (1) shape of their curves is highly complex and, therefore, most informative; (2) their ASA are fairly constant along the bilayer normal; and (3) these residues are involved in all types of solute-solvent interactions, including hydrophobic and H-bonding interactions in the first solvation shell and long-range electrostatics of their dipoles.
We found that energy profiles for Tyr and Trp residues were sensitive to distribution of water inside the lipid bilayer (equation (5)). Fitting statistical and normalized physical energy profiles for residues in α-helices led to the following parameters in equation (5): ϕW,outer,=0.066, ϕW,mid,=0.010, zo,=9.0 Ǻ and λ=1.1 Ǻ, assuming that inner and outer leaflets of membrane are symmetric. The optimal parameters for transmembrane β-barrel proteins were slightly different, suggesting a higher water concentration in outer bacterial membrane (Table S4), although the fit was relatively poor (rmsd of 0.33 kcal/mol), as compared to α-helical proteins (rmsd 0.21 kcal/mol) due to smaller statistics for β-barrel proteins. The parameters of water distribution obtained by fitting for Tyr and Trp residues were used for calculation of energy profiles for the remaining residues.
The adjustment of energy profiles for Tyr and Trp residues indicates a higher concentration of water in biological membranes bearing α-helical proteins (3.66 M in the “mid-polar” region and 0.55 M in the central region) as compared to that in DOPC (2.05 M and 0.4 M, respectively) and more gradual changes of water concentration between the regions (λ=1.1 Ǻ in natural membranes versus λ=0.55 Ǻ DOPC). Dimensions of different bilayer regions in natural membranes and DOPC are rather similar: they have hydrophobic semi-thicknesses of 15 and 14.8 Å, respectively, with semi-widths of the central nonpolar region (z0) of 9 Å and 8.6, respectively, and widths of the “mid-polar” region of 6 and 6.2 Å, respectively (Table S4). The fitting shows that water concentration in outer bacterial membranes may be higher than in inner membranes (5.33 M in the “mid-polar” region and 0.55 M in the central region).
Further analysis shows that small differences of statistical and physical energies remain even after optimizing the concentration of water (Figure 5). These discrepancies are related to statistical biases not described by our model. Indeed, the statistical energies of Lys and Arg residues are lower and energies of Asp and Glu are higher than physical energies in the lipid head group region at the inner, but not at the outer side of membrane (Figure 5C). These differences reflect the increased amount of positively charged residues and the depletion of negatively charged residues in the inner leaflet of cellular membranes, known as the “positive inside” bias caused by topogenic signals and interactions of these residues with membrane lipids and the translocon machinery8, 46. The energy minima for aromatic residues (Phe, Tyr and Trp) are slightly wider on statistical energy curves than on physical energy curves in 15–20 Å region (Figure 5D). This might be due to stabilizing cation-πinteractions or other factors omitted in our model. For example, the calculations did not reproduce the higher occurrence of aromatic residues in β-barrel proteins in the inner leaflet of the outer membrane (Figure S5, A), which may be related to their participation in sequence motifs (e.g. YxF motif at C-terminus) essential for recognition of β-barrels by chaperones assisting translocation and membrane insertion47. However, all such energy preferences are dependent on the lipid composition and specific protein-protein interactions, which lies beyond the scope of the present work.
Binding and spatial locations of small molecules in phospholipid bilayers
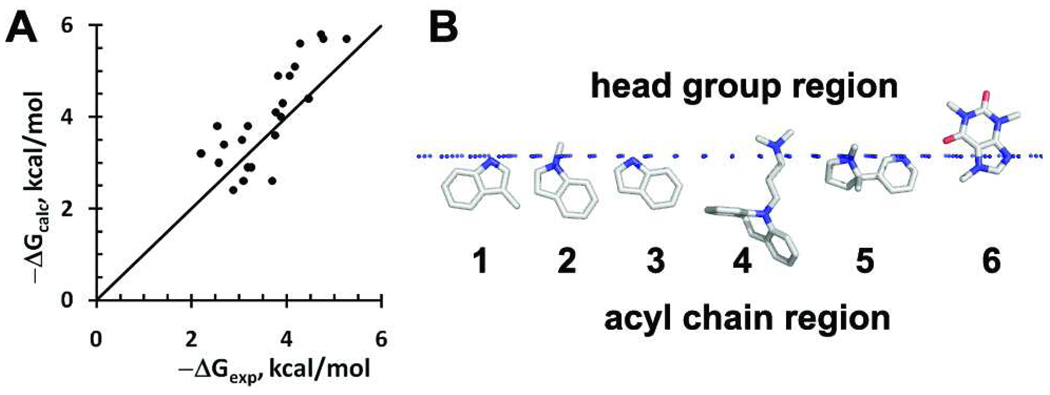
The proposed anisotropic solvent model of the lipid bilayer was integrated in a new version of our PPM program for calculation of membrane binding energy and spatial arrangement of proteins or small molecules in membranes. Such application is a sensitive test to identify the existing limitations and deficiencies of the method. Thus, we calculated binding energies and preferred localizations in a phospholipid bilayer for a diverse set of small molecules, including polar, nonpolar, neutral and charged compounds, whose partitioning between water and bilayers or positioning in membranes have been experimentally determined (Table S5). However, to avoid analysis of conformational equilibrium, we selected a set of conformationally rigid organic molecules composed of N, C, O, S, H atoms.
Experimental binding affinities of small molecules were reproduced with correlation coefficient R2=0.65 and rmse of 0.74 kcal/mol (Figure 7A). The performance of PPM 2.0 for small molecules should be further improved by additional parameterization and by including other factors that are currently missing in the model, such as immobilization energy, electrostatic components of ionic interactions, or steric factor48.
Figure 7.
Membrane binding of small drug-like molecules. A. Comparison of experimental and calculated transfer energies of small molecules from water to DOPC bilayer (data from Table S5; R2=0.65). B. Membrane-bound poses of small-molecules: 1: 3-methylindole; 2: N-methylindole; 3: indole; 4: imipramine; 5: nicotine; 6: caffeine. The hydrophobic boundary of the lipid bilayer (corresponding to location of lipid carbonyl groups) is shown by blue dots.
As an additional test, we calculated spatial positions and orientations in membrane for another set of amphiphils, including indole analogs and three drugs (imipramine, nicotine and caffeine), whose interactions with phopsholipid bicelles have been studied by NMR49–51. Our calculations show that all such molecules are located near the lipid carbonyl area, with nonpolar aromatic ring penetrating to the lipid acyl chain region and their positively charged groups interacting with lipid phosphates (Figure 7B). The overall orientations and positions of the molecules, including the penetration of imipramine and nicotine aromatic rings into the hydrophobic environment, and the weak insertion and binding of caffeine are consistent with NMR studies of these drugs in phospholipid bicelles50. The calculated locations of indole analogs in the “mid-polar”/glycerol region are consistent with one of the binding modes observed by 1H and 2H NMR49. However, we did not detect the second mode of indole binding near choline groups, as observed in a bimodal distribution found in NMR studies49. Such results indicate that our model can properly balance different nonspecific interactions that define locations of small molecules in the interfacial region of lipid bilayer, but the method should be improved by including the cation-π interaction52 to reproduce the second indole location49.
Comparison with interfacial energies of amino acid residues
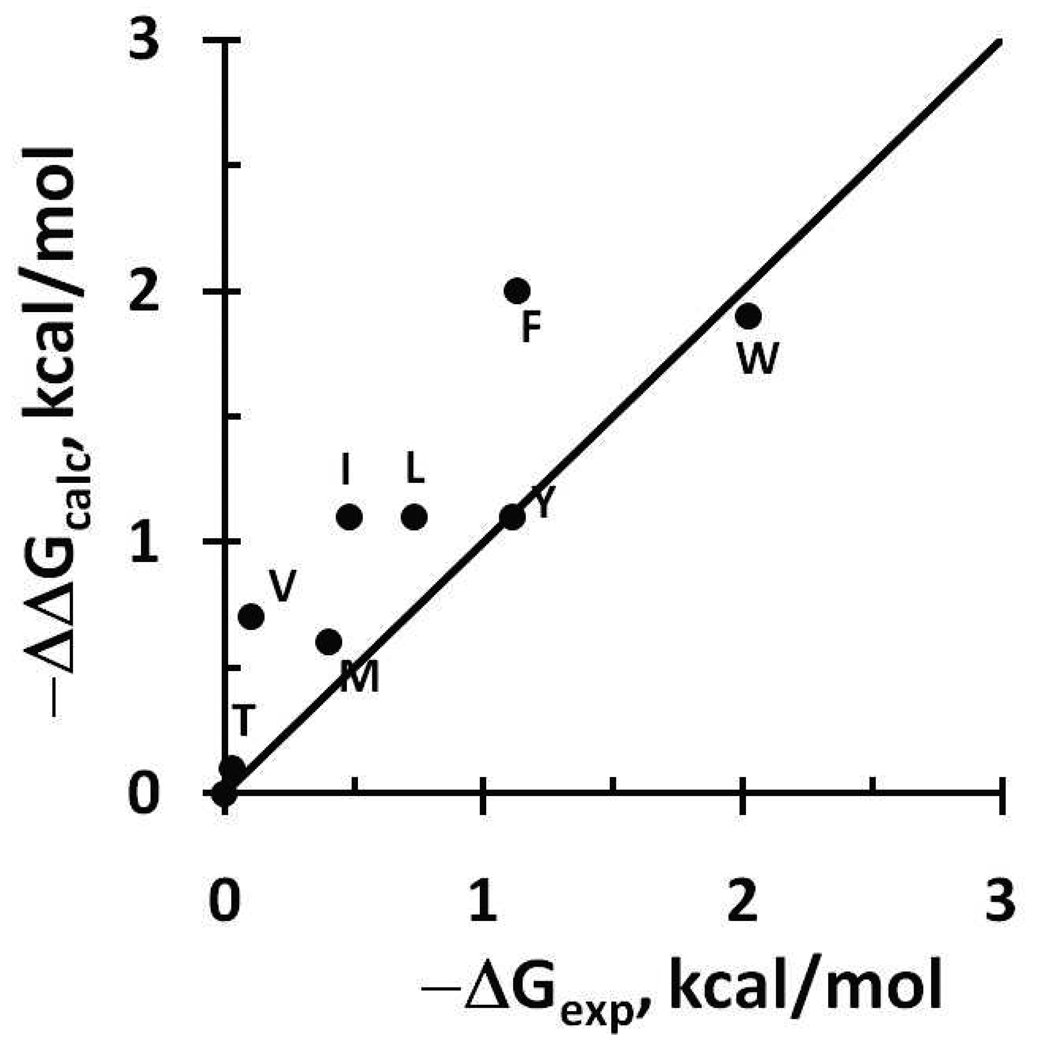
The method was tested by calculating spatial positions and transfer energies of N-methyl-acetamides of nonpolar amino acids, while N-methyl-acetamides of polar amino acids were predicted not to be bound. These energies were compared with membrane binding affinities that have been determined for the hydrophobic pentapeptide Ac-WL-X-LL and tripeptde AXA-O-t-Bu in the presence of POPC and DMPC bilayers, respectively53, 54. After subtraction of energy of the reference Ala residue, the relative binding energies of Tyr, Trp, Met, and Thr residues were reproduced with rmse of 0.5 kcal/mol and R2=0.6 (Table S6, Figure 8). However, calculated energies of strongly hydrophobic residues (Ile, Leu, Val, Phe) were overestimated as compared with data for pentapeptides. Better agreement was attained with experimental data for tripeptides. The discrepancy for strongly hydrophobic residues may be explained by a partial hydrophobic collapse of residues in the unfolded peptides in the membrane-bound state, which may be more pronounced for larger peptides. Indeed, NMR studies of the Ala-Phe-Ala-O-t-Bu demonstrated the presence of intramolecular NOEs between the aromatic ring of Phe2, Hβ of adjacent Ala and C-terminal tert-butyl group in membrane-bound tripeptide55.
Figure 8.
Comparison of calculated transfer energies of N-methyl acetamides of nonpolar residues and membrane binding energies of the corresponding residues included in host Ac-WL-X-LL pentapeptides53 (black circles; data from Table S6; R2=0.63). Energy of the reference peptide with Ala residue was subtracted.
Membrane binding affinities of peripheral proteins
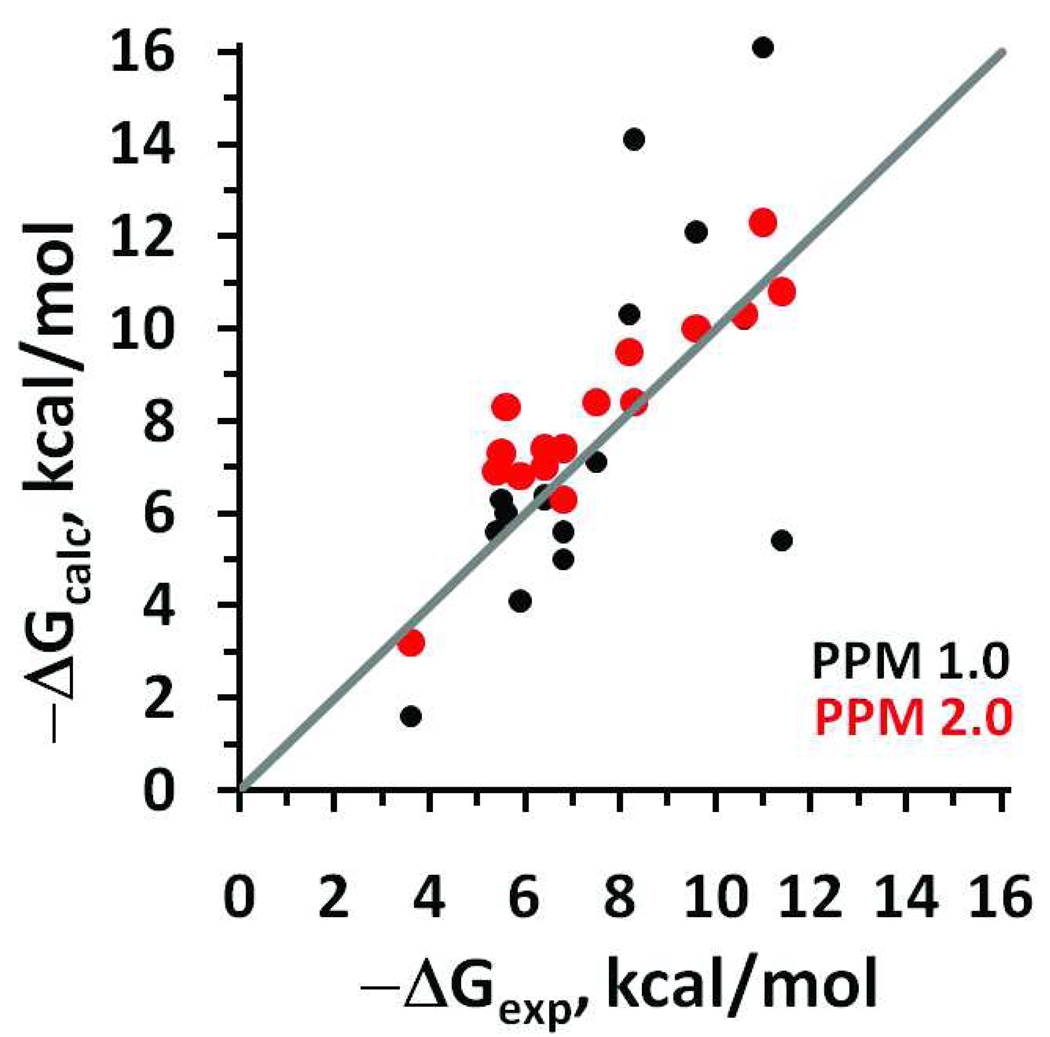
Our previous evaluation of the performance of the PPM1.0 indicated that even the simplified version of the method was able to predict the membrane binding free energies of peripheral proteins that are anchored to the membranes via patches of solvent-exposed hydrophobic residues. However, the correlation between experimental and PPM1.0-calculated values of transfer free energy was rather poor (R2=0.47 and rmse of 2.73 kcal/mol). The advanced PPM 2.0 method improved predictions of membrane binding energies (R2=0.78 and rmse of 1.13 kcal/mol) for the same set of 16 peripheral proteins (Figure 9, Table S7). The agreement between experimental and calculated values was better when calculations were performed with water distribution parameters obtained for natural membranes.
Figure 9.
Correlations of experimental (ΔGexp) and calculated (ΔGcalc) free energies of membrane insertion of 17 peripheral proteins (data from Table S7). Transfer energies were calculated by PPM 1.0 (black circles; R2=0.47) or PPM 2.0 (red circles; R2=0.78).
PPM2.0 has recently been applied for the prediction of the effects of mutations of water-exposed hydrophobic residues of human α-tocopherol transfer protein56. Good correlations (R2 from 0.83 to 0.89) were obtained between predicted changes in transfer free energy of mutant proteins and rates of protein binding to phospholipid bilayers, as well as with the relative rates of tocopherol delivery to PC vesicles.
Spatial positions in membrane of an Arg-rich peptide
We further evaluated our method on Arg-rich peptide 113LGLFRLVRLLRFLRILLI130 derived from the S4 helix of KvAP voltage sensor domain of the K-channel of archaebacteria Aeropyrum pernix,. Based on published studies, the energetic cost of burial of an Arg-residue in the nonpolar environment should be very high57, which would prevent insertion of S4-peptide with four arginines into the lipid bilayer. However, studies of isolated S4 peptide in model membranes by solid-state NMR58 demonstrated the transmembrane orientation of this peptide in α-helical conformation. This peptide also can be readily inserted into the membrane through the translocon machinery59. To reconcile the differences between theoretical expectations and the experiment, we calculated the spatial position of this peptide in the lipid bilayer.
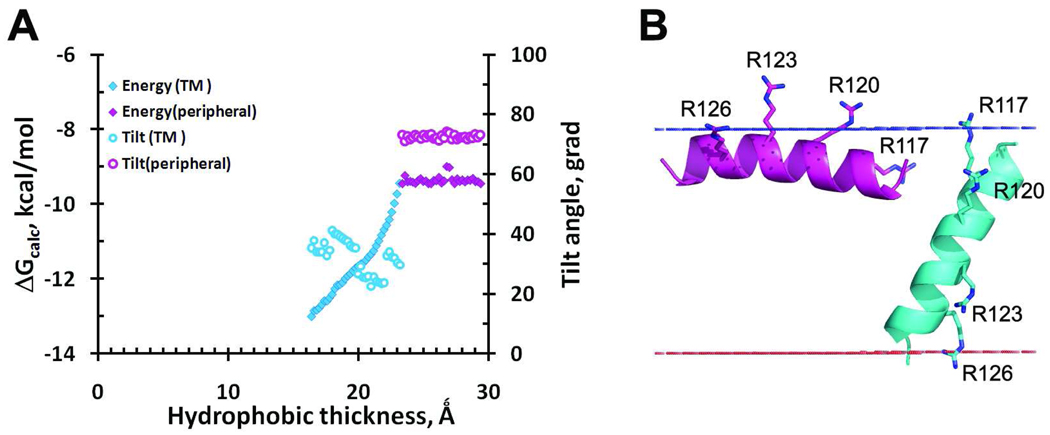
The results of calculations performed by PPM 2.0 indicate that S4 peptide can form α-helix and associate with the lipid bilayer either in a surface orientation (ΔGtransf equal to −9.5 kcal/mol) or in transmembane orientation (ΔGtransf from −9.5 to −14 kcal/mol), depending on the bilayer thickness (Figure 10A). The transmembrane orientation becomes energetically preferred only in a bilayer with hydrophobic thickness smaller than 23.5 Å. The tilt angle with respect to the membrane normal of the peptide in transmembrane orientation varies from 22 to 40° depending on the bilayer thickness, and it is ~73° in the alternative surface orientation.
Figure 10.
Transfer energies and tilt angles of S4-helix immersed in the lipid bilayer. A. Energies (diamonds) and tilt angles (open circles) calculated for different hydrophobic thicknesses of the bilayer for transmembrane (colored blue) and peripheral (colored purple) orientations of the S4 helix. ΔGcalc does not include the penalty for hydrophobic mismatch. B. Alternative orientations in the lipid bilayer of S4 peptide.
In the transmembrane orientation of S4 α-helix, the guanidinium groups of R120 and R123 "snorkel" to the “mid-polar” region of the lipid bilayer which has an increased water concentration (3.66 M, as evaluated for natural membranes). The preferential solvation of guanidinium groups by water in this region significantly reduces the energy penalty for transferring Arg residues to this generally hydrophobic environment. R117 and R126 residues are inserted in the lipid head group regions from the both sides of the bilayer, where they may form ionic bridges with lipid phosphates (Figure 10B).
Our observations agree with results of solid-state NMR studies, which demonstrated that S4 peptide can be inserted into a DMPC bilayer at 40° tilt angle producing local bilayer thinning of ~9 Ǻ58. Indeed, 9 Ǻ-thinning of the DMPC bilayer, whose average hydrophobic thickness in fully hydrated fluid state was estimated from X-ray scattering at 25.4 Ǻ60, would result in a bilayer with a hydrophobic thickness of 16.4 Ǻ. Our estimates indicate that S4 peptide would insert into the membrane at 40° tilt angle at this thickness. On the other hand, our calculations with the hydrophobic mishmatch penalty (see Methods) yield the optimal hydrophobic thickness of the peptide at 21±6.8 Ǻ. This thickness corresponds to the insertion of the S4 peptide at 22.5±11.4° tilt angle.
Thus, our results suggest that the relative proportion between two orientations depends on the membrane thickness: surface-bound S4-helices will be more abundant than transmembrane S4-helices for a hydrophobic thickness larger than 23.5 Ǻ and vice versa. This is in line with the small energy penalty (~0.5 kcal/mol) obtained for translocon-mediated insertion of S4-helix in endoplasmic reticulum membranes59, whose hydrophobic thickness was estimated at 27.5 Ǻ61.
Similar to recent MD simulations of the S4-helix62, our method was able to predict membrane thinning and to identify the most important interactions of S4 peptide with lipid bilayer components, such as hydration of R120 and R123 by water in the “mid-polar” region and hydrogen bonds of R117 and R126 with lipid phosphates. However, the significant advantage of our method is its high computational efficiency and its ability to operate directly with transfer free energies that can be easily compared with experimental data.
Application of PPM2.0 to membrane proteins from the OPM database
After the successful testing of the developed method for small molecules, peptides and peripheral proteins, we recalculated the spatial positions in membranes of ~1000 membrane-associated peptides and proteins deposited in our OPM database23. Membrane polarity profiles were essentially the same as in the DOPC bilayer (Figure 1B) except the increased concentration of permeating water in natural membranes (Table S4).
We compared the newly calculated spatial positions with experimental data for 24 transmembrane and 42 peripheral proteins that were previously used for verification of the PPM 1.0 method22, 63. The previously predicted and newly obtained orientations of these proteins in membrane were rather similar and almost equally consistent with experimental data, in part because such data are usually approximate or qualitative. A more detailed comparison with all relevant experimental studies of peptides and proteins is beyond the scope of this work, although the corresponding information is included in comments for individual proteins in the updated OPM database23.
The results of calculations were improved for proteins with incomplete 3D structures, transmembrane proteins with poorly defined hydrophobic boundaries and weakly bound peripheral proteins, but remained mostly unchanged in other cases. For example, recalculation of prostaglandin H2 synthase-1 dimer (PDB code 1q4g) resulted in a fully symmetric membrane binding mode, unlike the previously obtained slightly tilted orientation. For several transmembrane proteins, such as diacylglycerol kinase, ferrous-iron efflux pump and acid-sensitive ion channel (PDB codes 2kdc, 2qfi and 3hgc, respectively), PPM 2.0 determined positions of both hydrophobic boundaries, while PPM 1.0 erroneously predicted insertion from one side with penetration depth of more than 20 Å. The hydrophobic thicknesses of several transmembrane proteins, such as ClC-chloride channel and calcium ATPase, increased and became closer to 30 Å. Hydrophobic thicknesses of these proteins were probably underestimated previously. The incorporation of a hydrophobic mismatch penalty allowed us to improve calculations of single transmembrane α-helices, having small and therefore poorly defined hydrophobic boundaries. Furthermore, PPM2.0 was able to predict the experimentally suggested membrane binding modes for some proteins with incomplete 3D structures (outer membrane complex of type IV secretion system, 3jqo) or in closed conformation (oxysterol-binding protein homolog, 1zhx), where PPM 1.0 failed.
A significant progress was observed for positioning of peripheral proteins in membranes, whose binding energies were calculated more accurately with PPM 2.0 (Figure 9). Some proteins reduced their membrane penetration depths or slightly changed orientation due to explicit incorporation of electrostatic energy in a new model. This effect is more pronounced for peptides and proteins bound to membranes via nonregular hydrophobic loops whose main chain peptide groups are exposed to solvent. The stronger anchoring of Tyr and Trp residues also plays a role.
DISCUSSION
Main features of the proposed model
In this work we present the development, testing and application of our improved method for calculation of membrane binding affinities and spatial positions in biological membranes of diverse molecules, ranging from small drug-like compounds and peptides to peripheral and integral membrane proteins. In our approximation, a solute is regarded as a rigid body, and the lipid environment is represented as an anisotropic fluid. The underlying physical model describes only changes in solvation energy, assuming that the internal energy of a solute does not change upon its transfer from water to the lipid bilayer. This solvation model can be further applied for analysis of conformational changes and protein-protein association, when combined with molecular mechanics force fields for describing internal energy of the system38, 64, but this is beyond the scope of this work.
The underlying methodology includes two novel components: (a) an original universal solvation model for calculating transfer energy of molecules from water to an arbitrary isotropic or anisotropic environment with defined polarity parameters, (b) an anisotropic solvent representation of the lipid bilayer based on published experimental data.
According to the universal solvation model presented in the preceding paper, the transfer energy of a solute includes two terms: (1) an ASA-dependent term that accounts for van der Waals and H-bonding solvent-solute interactions and entropy of solvent molecules in the first solvation shell; and (2) an electrostatic term that describes solvation energy of dipoles and ions, ionic interactions, deionization penalty for charged groups in nonpolar environment. The universal solvation model was carefully parameterized to operate with free energy of solvation (as described in the accompanying paper). This allows us to make direct estimation of transfer free energies of membrane-associated peptides, proteins and small molecules that can be compared with their experimental membrane binding affinities.
The proposed anisotropic solvent model approximates complex properties of the lipid bilayer by profiles of polarity parameters (ε, π*, α and β) that are used in empirical solvation models developed for small molecules15, as well as for experimental characterization of membrane interfaces65, 66. The polarity profiles implemented in the current model (Figure 1B) are based on distributions of quasi-molecular segments of lipids in DOPC (Figure 1A) and DOPS, as determined from X-ray and neutron scattering data19, 40. The complex behavior of polarity parameters differs from that in hydrophobic slab models, where the water-lipid interface was characterized by the abrupt dielectric boundary with a smoothing length λ of 0.6 to 2 Å22, 67–69. Our new model also accounts for the permeation of water into the lipid bilayer, describes the preferential solvation in the lipid-water mixture, and includes the hydrophobic mismatch for transmembrane proteins21.
Comparison of polarity profiles calculated for DOPC and DOPS bilayers demonstrated that hydrogen bonding capacity parameters are sensitive to the nature of lipid head group. Dependence of polarity parameters on the lipid composition has been previously demonstrated by spin or fluorescent probes70, 71.
Properties of phospholipid bilayer
Observed changes of polarity parameters across the DOPC bilayer indicate the existence of three distinct regions: (1) the head group region formed by choline and phosphates (14.8 to 30 Ǻ from the center of membrane), where water concentration changes from 55.5 M to 30 M; (2) the “mid-polar” region (8.2 to 14.8 Ǻ) with octanol-like properties (ε~11) and intermediate water concentration (~1–3 M) that is formed by lipid carbonyls and ordered acyl chains including the double bonds; and (3) the internal hydrocarbon core region (within ~8 Ǻ from the membrane center) with cyclohexane-like properties (ε~2.5) and low water concentration (<0.5 M) that is formed by disordered acyl chains. The noticeable water concentration in the “mid-polar” region of the DOPC blayer was experimentally detected by spin probes20, 39, 72. The presence of water in the high density acyl tail/head group regions was supported by MD simulations of phospholipid bilayers73. Thus, the water concentration changes in a wide interfacial zone, which combines head groups of the lipids and the ordered part of their acyl chains. This aqueous gradient gives rise to transmembrane polarity profiles that can be detected by physical methods71, 72 or using statistical analysis of protein structures74. A similar structure of the lipid bilayer, with nonpolar, mid-polar and highly polar phosphatidylcholine regions was identified in MD simulations12.
The dielectric properties of phospholipid bilayers in our model generally agree with estimations based on EPR and fluorescence studies, especially for the lipid carbonyl and acyl chain regions 48, 71. At the same time, the dielectric constant was assumed to be about the same in the bulk water and in the lipid head group region but abruptly change at the hydrocarbon core boundary (Figure 1B), while the fluorescence data suggest a more gradual decrease of the dielectric constant from ε~60 to ε~30 over the entire lipid head group region48, 75. The relatively high dielectric field in the lipid head group area can be supported by the observation that aqueous solutions of zwitterions have dielectric constants slightly higher than water25. In general, the dielectric constant for the electrolyte solution may decrease or increase with rising electrolyte concentration due to the hydration of ions or formation of ion pairs, respectively76. Higher dielectric constant in the lipid head group region would facilitate penetration of charged groups inside this region. This agrees with the high occurrence of charged amino-acids in the lipid head group region, where they may form hydrogen bonds and ionic pairs with lipids.
Our evaluation of properties of biological membranes from the distribution of residues in structures of membrane proteins indicates that the hydrophobic thicknesses vary from ~28–30 Ǻ in membranes with α-helical proteins to ~22–24 Ǻ in outer bacterial membranes with β-barrel proteins. Accordingly, widths of the “mid-polar” regions vary from 6.0–6.2 Ǻ to 4–4.3 Ǻ in membranes with α-helical and β-barrel proteins, respectively.
The “mid-polar” region is composed of lipid acyl chains with double bonds including glycerol and carbonyl segments. It is also known as soft polymer region with a relatively high lipid order73. The abundance of acyl chains in this region provides hydrophobic interactions, while the 1–3 M of water is sufficient for the preferential hydrogen bonding with polar groups of the protein, which reduces their dehydration penalty in this region. This effect is most pronounced for the charged carboxylate groups of Asp and Glu residues. Furthermore, the electrostatic energy cost for transferring dipolar and ionized groups to this region is relatively small because Block-Walker and Abe dielectric functions reach only half of their maximal values (Figure 1B).
The distinct physicochemical properties of the “mid-polar” region favor the accumulation of Trp and Tyr residues, which was experimentally demonstrated for membrane proteins and amino acid analogues 42, 43, 49, 77. This can be understood by analyzing the relative contributions of hydrophobic, H-bonding and dipolar interactions of Trp and Tyr residues in different regions of the lipid bilayer (Figure S6). This analysis shows that energy minima of Tyr and Trp residues in the “mid-polar” region originate from the favorable hydrophobic interactions that are only slightly counterbalanced by electrostatic penalty for transferring their dipoles and by the cost of breaking hydrogen bonds between their polar groups and bulk water. The higher energy maximum in the membrane center for Tyr versus Trp residue can be attributed to the higher dehydration penalty of the Tyr OH group, which has a larger ASA than NH of the Trp indole.
Any molecule that combines a hydrophobic moiety with non-zero dipole moment is expected to be preferentially distributed in the “mid-polar” region. Indeed, we found that His, Cys and Thr residues have shallow energy minima in this area. The minima for Tyr, Thr and Ser residues are enforced by their hydrogen bonds with lipid carbonyls and phosphates. Amphiphilic drugs and drug-like compounds also tend to accumulate in the “mid-polar” region (Figure 7). This may explain the observed correlation between water-liposome partition coefficients of drugs and the corresponding water-octanol logP values48.
Intramembrane water distribution
Comparison of transfer energies calculated for residues in α-helix with statistical energies derived from analysis of protein structures (Figures 5, S5) allowed us to refine the distribution of water along the membrane normal. We assessed the water concentrations in the “mid-polar” and the central regions of different biological membranes by fitting the theoretically predicted and statistical energy profiles for Trp and Tyr residues in α-helical or β-barrel proteins. This estimate is rather approximate because we combined α-helical proteins from different types of membranes (archaeal, inner bacterial and eukaryotic) to increase the statistics, whereas β-barrel proteins were taken from outer membranes of different gram-negative bacteria.
The best fit for α-helical proteins was obtained with the average water concentration in the “mid-polar” region of 3.66 M, i.e. almost twice as much as the corresponding values obtained by spin probes for DOPC membrane (2.05 M)20. The increased water concentration in biological membranes may be attributed to the higher lipid heterogeneity and to the presence of proteins. Indeed, it was shown by spin probes that modifications of lipid composition or the addition of cholesterol increased the hydration level of spin probes in the region adjacent to the lipid head groups39, 72. The presence of peptides or proteins may also induce water permeation into the lipid bilayer, similar to the “dragging” of water by small polar molecules to nonpolar solvents78. Water distribution parameters, which we obtained for membranes bearing β-barrel proteins, indicated even higher water concentration inside outer bacterial membranes (5.33 M in the “mid-polar region and 0.55 M in the central region) (Table S4). This is consistent with neutron scattering studies of outer bacterial membranes of Pseudomonas aeruginosa, which found the presence of water in the entire length of the lipopolysaccharide bilayer, including the central core region, unlike that in DOPC bilayer79.
Whole-residue hydrophobicity scales
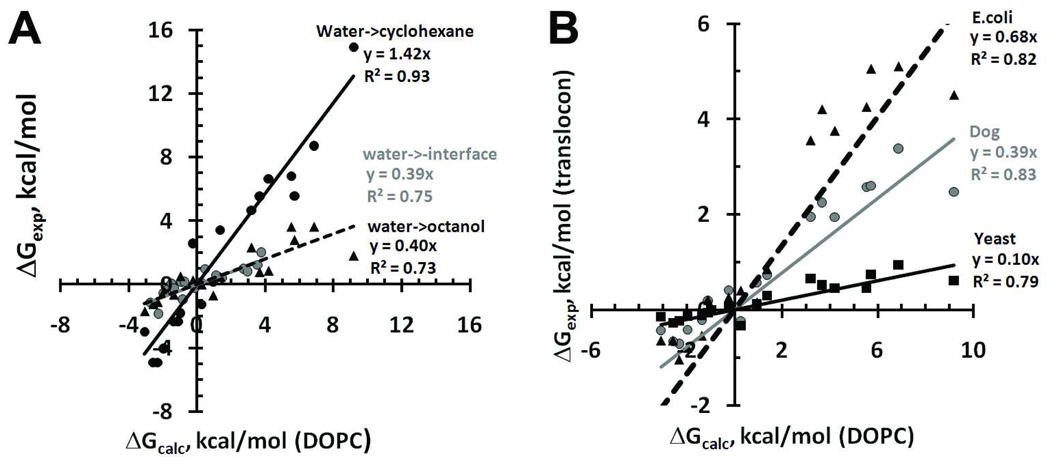
The physical and statistical energy profiles obtained in this work (Figures 5 and S5) can be regarded as whole-residue hydrophobicity scales of α-helical or β-barrel proteins defined for any location along the bilayer normal. Similar scales for residues in α-helical proteins have been developed using statistical analysis, MD simulations or in vivo experimental studies45, 80–83. In order to compare our energy profiles to experimentally-derived hydrophobicity scales45, 57, 84–86, we used transfer energy values for residues located in the membrane center. There is a good correlation between our physical and statistical scales for both α-helical and β-barrel proteins (R2 are equal to 0.92 and 0.91, respectively, Figure 6A). The physical scale correlates remarkably well with water/cyclohexane scale for amino acid side-chain analogues57 (R2 = 0.93), but shows only moderate correlation with Wimley-White (WW) water/octanol scale84 (R2 = 0.73, Figure 11A). This is expected because the central part of the lipid bilayer can be approximated well by a nonpolar aliphatic solvent, rather than by wet n-octanol solution87, 88, which dissolves up to 2.3 M of water89. On the other hand, n-octanol can mimic properties of the "mid-polar" region of the lipid bilayer. Indeed, the correlation between WW water/octanol scale84 and physical scale obtained for the “mid-polar” region (at 12 Ǻ distance from the interior) was much better (R2 = 0.82, slope 0.81; not shown).
Figure 11.
Correlations between theoretically predicted transfer energies of residues in α-helix from water to the middle of DOPC bilayer (ΔGcalc) and published whole-residue hydrophobicity scales. A. Comparison of ΔGcalc with experimental water/cyclohexane transfer energies of side chain analogues57 (black circles, black solid line, R2=0.92) and WW water/octanol scale84 (grey circles, gray solid line, R2=0.73). B. Correlations between physical scale and different biological scales obtained for mammalian45 (grey circles, grey solid line, R2=0.83), yeast85 (black squares, black solid line, R2=0.79) or bacterial86 (black triangles, black dashed line, R2=0.82) translocation systems.
A plot of the physical versus the statistical scale shows a slop factor of 0.48, while a plot of the physical scale versus the water-cyclohexane scale has slop factor of 1.42 (Figures 6A and 11A). The observed difference in slopes may reflect different accessibility of side chains in various systems: ~2 fold smaller ASA of residues in multi-spanning α-helical proteins than in an isolated α-helix and ~1.4 fold larger ASA of side chain analogues than of residues incorporated in an α-helix. Such dependence of transfer free energy of residues on their solvent exposure in different model systems was mentioned above (Figure 4).
We also compared transfer energies obtained in the present work with several biological scales recently developed for different in-vivo helix translocation systems: the translation of model proteins with a hydrophobic peptide by Sec61 machinery in mammalian45, 81 or yeast85 endoplasmic reticulum membranes, or insertion of an α-helical hairpin in inner membrane of E. coli by YidC machinery86 (Figure 11B). Correlation of the physical scale with different biological scales is reasonably good (R2 from 0.79 to 0.86), but the slopes vary significantly from 0.1 to 0.68, depending of the in-vivo translocation machinery. These differences in slopes may be related to the distinct local environment of the tested hydrophobic peptides inside the translocation systems and to the different interactions of the nascent helix with other transmembrane helices of the growing protein. However, the observed variations may also be related to the differences in data analysis45, 81.
The physical energy profiles obtained in the present work may be used for prediction of single-spanning (bitopic) α-helical proteins whose helices must be individually stable in the lipid bilayer without interactions with neighboring helices. Furthermore, the normalized physical scales or statistical scales from this work may also be used for prediction of transmembrane helices in polytopic proteins, just as the biological hydrophobicity scale derived from in vivo insertion of hydrophobic helixes mediated by translocon machinery45.
Although the whole-residue scales may be applied for the genome-wide prediction of transmembrane α-helices, the whole-residue approach is inadequate for the correct evaluation of lipid-protein interactions, because it does not account for significant variations of residue accessibilities on the surface of individual protein structures (Figure 4). In contrast, only all-atom representation of proteins and small molecules, as developed in this work, can accurately reproduce their interactions with surrounding water and anisotropic lipid environment.
Computational implementation and validation
The developed theoretical method was integrated in a new version of our program (PPM 2.0) that computes the energetically preferred spatial arrangements of molecules with respect to the lipid bilayer (see Methods). The new method was validated for peripheral proteins, peptides and small molecules whose membrane penetration depth, spatial orientation with respect to the lipid bilayer or membrane binding affinities have been experimentally studied. We found a much better accuracy of PPM 2.0 than PPM 1.0 in prediction of membrane binding energies of small molecules and peripheral proteins (R2 increased from 0.47 to 0.78 and rmse improved from 2.73 to 1.13 kcal/mol). An especially challenging test was prediction of the membrane binding mode for a short Arg-rich peptide, which requires a precise balance of the hydrophobic, electrostatic and other interactions in the “mid-polar” region of the bilayer that was provided only by the improved method. It is noteworthy that none of other published theoretical methods was validated against experimental membrane binding affinities of small molecules, peptides and proteins or for a large set of peripheral proteins with known spatial positions in membranes.
CONCLUSION
We improved our computational method (PPM 2.0) by developing a significantly more advanced anisotropic solvent model of the lipid bilayer. High efficiency, accuracy, and reliability of this method makes it a unique tool for large-scale computational analysis of binding and preferred spatial arrangement of integral and peripheral proteins, as well as small molecules, including peptides, organic compounds and drugs. Therefore, PPM 2.0 was applied for recalculation of spatial arrangement in membranes of ~1000 membrane-associated proteins and peptides from the OPM database23.
The current method operates with transverse properties of the lipid bialyer by calculating complex polarity profiles from the known distributions of lipid fragments and water along the membrane normal. However, increasing attention has recently been paid to the lateral structure of lipid bilayer: formation of protein clusters and lipid rafts. The impact of lateral pressure, curvature, charge, lipid order and the lipid domains on the insertion and orientation of proteins in membranes can be also included in the implicit solvent model of the lipid bilayer, but this will be the subject of future studies.
Supplementary Material
ACKNOWLEDGEMENT
This research was supported by grant 0849713 (A.L., I.P.) from the National Science Foundation (Division of Biological Infrastructure), Upjohn award from the College of Pharmacy of the University of Michigan (A.L.) and in part by the grant 5R01DA003910-23 (H.I.M.) from the National Institute of Health (National Institute Of Drug Abuse). We are thankful to Dr. Hubbard for the kindly provided NACCESS program.
ABBREVIATIONS
- DOPC
dioleoylphosphatidylcholine
- DOPS
dioleoylphosphatidylserine
- ASA
solvent accessible surface area
- rmse
root mean square error
- PPM
Positioning of Proteins in Membranes computational method
- OPM
Orientations of Proteins in Membranes database
Footnotes
Supporting Information Available: Supporting information includes parameters of lipid groups and water used for calculation of polarity profiles of DOPC and DOPS bilayers (Tables S1 and S2), linear regression coefficients applied for calculations of atomic solvation parameters (Table S3), water distribution parameters determined by fitting physical and statistical energies of Trp and Tyr residues (Table S4), comparison of calculated and experimental membrane binding free energies of small molecules (Table S5), comparison of calculated transfer energies of N-methyl acetamides of nonpolar amino acids with Wimley-White and Jacobs-White hydrophobicity scales (Table S6), comparison of experimental and calculated membrane binding affinities of 16 peripheral proteins (Table S7), lists of PDB codes of α-helical and β-barrel transmembrane proteins used for calculation of statistical energy profiles. It also includes figures with transbilayer profiles of hydrogen bonding donor and acceptor parameters in different model membranes (Figure S1), comparisons of transfer energy profiles calculated for Tyr and Trp residues in α-helix using different theoretical models (Figure S2) and in different bilayers (Figure S3), calculated transfer energy profiles of amino-acid residues in β-barrel (Figure S4), comparison of physical and statistical energy profiles for β-barrel residues (Figure S5), and different contributions to transfer energy of Trp and Tyr residues in α-helix (Figure S6). This material is available free of charge via the Internet at http://pubs.acs.org.
Contributor Information
Andrei L. Lomize, Email: almz@umich.edu.
Irina Pogozheva, Email: irinap@umich.edu.
Henry I Mosberg, Email: him@umich.edu.
REFERENCES AND NOTES
- 1.Grossfield A. Implicit modeling of membranes. In: Feller SE, editor. Curents Topics in Membranes. Computational Modeling of Membrane Bilayers. Vol. 60. Academic Press; 2008. pp. 131–157. [Google Scholar]
- 2.Marsh D. Protein modulation of lipids, and vice-versa, in membranes. BBA-Biomembranes. 2008;1778:1545–1575. doi: 10.1016/j.bbamem.2008.01.015. [DOI] [PubMed] [Google Scholar]
- 3.McMahon HT, Gallop JL. Membrane curvature and mechanisms of dynamic cell membrane remodelling. Nature (London) 2005;438:590–596. doi: 10.1038/nature04396. [DOI] [PubMed] [Google Scholar]
- 4.Zimmerberg J, Kozlov MM. How proteins produce cellular membrane curvature. Nat. Rev. Mol. Cell Bio. 2006;7:9–19. doi: 10.1038/nrm1784. [DOI] [PubMed] [Google Scholar]
- 5.Bogdanov M, Dowhan W. Lipid-assisted protein folding. J. Biol. Chem. 1999;274:36827–36830. doi: 10.1074/jbc.274.52.36827. [DOI] [PubMed] [Google Scholar]
- 6.Bogdanov M, Xie J, Dowhan W. Lipid-Protein Interactions Drive Membrane Protein Topogenesis in Accordance with the Positive Inside Rule. J. Biol. Chem. 2009;284:9637–9641. doi: 10.1074/jbc.R800081200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.White SH, von Heijne G. The machinery of membrane protein assembly. Curr. Opin. Struct. Biol. 2004;14:397–404. doi: 10.1016/j.sbi.2004.07.003. [DOI] [PubMed] [Google Scholar]
- 8.Dowhan W, Bogdanov M. Lipid-Dependent Membrane Protein Topogenesis. Ann. Rev. Biochem. 2009;78:515–540. doi: 10.1146/annurev.biochem.77.060806.091251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Bos MP, Robert V, Tommassen J. Biogenesis of the gram-negative bacterial outer membrane. Ann. Rev. Microbiol. 2007;61:191–214. doi: 10.1146/annurev.micro.61.080706.093245. [DOI] [PubMed] [Google Scholar]
- 10.Hanshaw RG, Stahelin RV, Smith BD. Noncovalent keystone interactions controlling biomembrane structure. Chem.-Eur. J. 2008;14:1690–1697. doi: 10.1002/chem.200701589. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.van Meer G, Voelker DR, Feigenson GW. Membrane lipids: where they are and how they behave. Nat. Rev. Mol. Cell Biol. 2008;9:112–124. doi: 10.1038/nrm2330. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.MacCallum JL, Tieleman DP. Interactions between small molecules and lipid bilayers. Computational Modeling of Membrane Bilayers. 2008;Vol. 60:227–256. [Google Scholar]
- 13.Im W, Feig M, Brooks CL. An implicit membrane generalized born theory for the study of structure, stability, and interactions of membrane proteins. Biophys. J. 2003;85:2900–2918. doi: 10.1016/S0006-3495(03)74712-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Feig M, Brooks CL. Recent advances in the development and application of implicit solvent models in biomolecule simulations. Curr. Opin. Struct. Biol. 2004;14:217–224. doi: 10.1016/j.sbi.2004.03.009. [DOI] [PubMed] [Google Scholar]
- 15.Cramer CJ, Truhlar DG. A universal approach to solvation modeling. Acc. Chem. Res. 2008;41:760–768. doi: 10.1021/ar800019z. [DOI] [PubMed] [Google Scholar]
- 16.Marcus Y. Some thermodynamic aspects of ion transfer. Electrochim. Acta. 1998;44:91–98. [Google Scholar]
- 17.Abraham MH, Zhao YH. Determination of solvation descriptors for ionic species: Hydrogen bond acidity and basicity. J. Org. Chem. 2004;69:4677–4685. doi: 10.1021/jo049766y. [DOI] [PubMed] [Google Scholar]
- 18.Reichardt C. Solvents and solvent effects: An introduction. Org. Process Res. Dev. 2007;11:105–113. [Google Scholar]
- 19.Kucerka N, Nagle JF, Sachs JN, Feller SE, Pencer J, Jackson A, Katsaras J. Lipid bilayer structure determined by the simultaneous analysis of neutron and x-ray scattering data. Biophys. J. 2008;95:2356–2367. doi: 10.1529/biophysj.108.132662. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Marsh D. Membrane water-penetration profiles from spin labels. Eur. Biophys. J. 2002;31:559–562. doi: 10.1007/s00249-002-0245-z. [DOI] [PubMed] [Google Scholar]
- 21.Marsh D. Energetics of hydrophobic matching in lipid-protein interactions. Biophys. J. 2008;94:3996–4013. doi: 10.1529/biophysj.107.121475. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Lomize AL, Pogozheva ID, Lomize MA, Mosberg HI. Positioning of proteins in membranes: A computational approach. Protein Sci. 2006;15:1318–1333. doi: 10.1110/ps.062126106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Lomize MA, Lomize AL, Pogozheva ID, Mosberg HI. OPM: Orientations of proteins in membranes database. Bioinformatics. 2006;22:623–625. doi: 10.1093/bioinformatics/btk023. [DOI] [PubMed] [Google Scholar]
- 24.Marsh D, Toniolo C. Polarity dependence of EPR parameters for TOAC and MTSSL spin labels: Correlation with DOXYL spin labels for membrane studies. J. Magn. Reson. 2008;190:211–221. doi: 10.1016/j.jmr.2007.11.005. [DOI] [PubMed] [Google Scholar]
- 25.Zhuo KL, Chen YJ, Kang L, Xu SJ, Wang JJ. Dielectric Constants for Binary Amino Acid-Water Solutions from (278.15 to 313.15) K. J. Chem. Eng. Data. 2009;54:137–141. [Google Scholar]
- 26.Marcus Y. The use of chemical probes for the characterization of solvent mixtures.2. Aqueous mixtures. J. Chem. Soc.-Perk. T. 2. 1994;8:1751–1758. [Google Scholar]
- 27.Marcus Y. Solvent Mixtures. Properties and Selective Solvation. New York, Basel: Marcel Dekker, Inc.; 2002. p. 259. [Google Scholar]
- 28.Abe T. A modification of the Born equation. J. Phys. Chem. 1986;90:713–715. [Google Scholar]
- 29.Block H, Walker SM. Modification of Onsager theory for a dielectric. Chem. Phys. Lett. 1973;19:363–364. [Google Scholar]
- 30.Marcus Y. On the preferential solvation of drugs and PAHs in binary solvent mixtures. J. Mol. Liq. 2008;140:61–67. [Google Scholar]
- 31.Jorgensen WL, Gao J. Monte-Carlo simulations of the hydration of ammonium and carboxylate ions. J. Phys. Chem. 1986;90:2174–2182. [Google Scholar]
- 32.Leung K, Rempe SB. Ab initio molecular dynamics study of formate ion hydration. J. Am. Chem. Soc. 2004;126:344–351. doi: 10.1021/ja036267q. [DOI] [PubMed] [Google Scholar]
- 33.Mason PE, Neilson GW, Enderby JE, Saboungi ML, Dempsey CE, MacKerell AD, Brady JW. The structure of aqueous guanidinium chloride solutions. J. Am. Chem. Soc. 2004;126:11462–11470. doi: 10.1021/ja040034x. [DOI] [PubMed] [Google Scholar]
- 34.Lien EJ, Guo ZR, Li RL, Su CT. Use of dipole-moment as a parameter in drug receptor interaction and quantitative structure activity relationship studies. J. Pharm. Sci. 1982;71:641–655. doi: 10.1002/jps.2600710611. [DOI] [PubMed] [Google Scholar]
- 35.Li WY, Guo ZR, Lien EJ. Examination of the interrelationship between aliphatic group dipole-moment and polar substituent constants. J. Pharm. Sci. 1984;73:553–558. doi: 10.1002/jps.2600730430. [DOI] [PubMed] [Google Scholar]
- 36.Spackman MA, Munshi P, Dittrich B. Dipole moment enhancement in molecular crystals from X-ray diffraction data. ChemPhysChem. 2007;8:2051–2063. doi: 10.1002/cphc.200700339. [DOI] [PubMed] [Google Scholar]
- 37.Israelachvili JN. Intermolecular and surface forces. London; Orlando, USA: Academic Press; 1992. p. 296. [Google Scholar]
- 38.Lomize AL, Reibarkh MY, Pogozheva ID. Interatomic potentials and solvation parameters from protein engineering data for buried residues. Protein Sci. 2002;11:1984–2000. doi: 10.1110/ps.0307002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Erilov DA, Bartucci R, Guzzi R, Shubin AA, Maryasov AG, Marsh D, Dzuba SA, Sportelli L. Water concentration profiles in membranes measured by ESEEM of spin-labeled lipids. J. Phys. Chem. B. 2005;109:12003–12013. doi: 10.1021/jp050886z. [DOI] [PubMed] [Google Scholar]
- 40.Petrache HI, Tristram-Nagle S, Gawrisch K, Harries D, Parsegian VA, Nagle JF. Structure and fluctuations of charged phosphatidylserine bilayers in the absence of salt. Biophys. J. 2004;86:1574–1586. doi: 10.1016/S0006-3495(04)74225-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Xiang TX, Xu YH, Anderson BD. The barrier domain for solute permeation varies with lipid bilayer phase structure. J. Membrane Biol. 1998;165:77–90. doi: 10.1007/s002329900422. [DOI] [PubMed] [Google Scholar]
- 42.Yau WM, Wimley WC, Gawrisch K, White SH. The preference of tryptophan for membrane interfaces. Biochemistry. 1998;37:14713–14718. doi: 10.1021/bi980809c. [DOI] [PubMed] [Google Scholar]
- 43.Liu W, Caffrey M. Interactions of tryptophan, tryptophan peptides, and tryptophan alkyl esters at curved membrane interfaces. Biochemistry. 2006;45:11713–11726. doi: 10.1021/bi0608414. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Killian JA, von Heijne G. How proteins adapt to a membrane-water interface. Trends Biochem. Sci. 2000;25:429–434. doi: 10.1016/s0968-0004(00)01626-1. [DOI] [PubMed] [Google Scholar]
- 45.Hessa T, Kim H, Bihlmaier K, Lundin C, Boekel J, Andersson H, Nilsson I, White SH, von Heijne G. Recognition of transmembrane helices by the endoplasmic reticulum translocon. Nature (London) 2005;433:377–381. doi: 10.1038/nature03216. [DOI] [PubMed] [Google Scholar]
- 46.Goder V, Junne T, Spiess M. Sec61p contributes to signal sequence orientation according to the positive-inside rule. Mol. Biol. Cell. 2004;15:1470–1478. doi: 10.1091/mbc.E03-08-0599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Jackups R, Cheng S, Liang J. Sequence motifs and antimotifs in beta-barrel membrane proteins from a genome-wide analysis: The Ala-Tyr dichotomy and chaperone binding motifs. J. Mol. Biol. 2006;363:611–623. doi: 10.1016/j.jmb.2006.07.095. [DOI] [PubMed] [Google Scholar]
- 48.Avdeef A. Absorption and Drug Development: Solubility, Permeability, and Charge State. NJ, USA: John Wiley & Sons; 2003. Partitioning into Liposomes; pp. 67–90. [Google Scholar]
- 49.Gaede HC, Yau WM, Gawrisch K. Electrostatic contributions to indole-lipid interactions. J. Phys. Chem. B. 2005;109:13014–13023. doi: 10.1021/jp0511000. [DOI] [PubMed] [Google Scholar]
- 50.Evanics F, Prosser RS. Discriminating binding and positioning of amphiphiles to lipid bilayers by H-1 NMR. Anal. Chim. Acta. 2005;534:21–29. [Google Scholar]
- 51.Al-Abdul-Wahid MS, Neale C, Pomes R, Prosser RS. A Solution NMR Approach to the Measurement of Amphiphile Immersion Depth and Orientation in Membrane Model Systems. J. Am. Chem. Soc. 2009;131:6452–6459. doi: 10.1021/ja808964e. [DOI] [PubMed] [Google Scholar]
- 52.Petersen FNR, Jensen MO, Nielsen CH. Interfacial tryptophan residues: A role for the cation-pi effect? Biophys. J. 2005;89:3985–3996. doi: 10.1529/biophysj.105.061804. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Wimley WC, White SH. Experimentally determined hydrophobicity scale for proteins at membrane interfaces. Nat. Struct. Biol. 1996;3:842–848. doi: 10.1038/nsb1096-842. [DOI] [PubMed] [Google Scholar]
- 54.Jacobs RE, White SH. The nature of the hydrophobic binding of small peptides at the bilayer interface - implications for the insertion of transbilayer helices. Biochemistry. 1989;28:3421–3437. doi: 10.1021/bi00434a042. [DOI] [PubMed] [Google Scholar]
- 55.Brown JW, Huestis WH. Structure and orientation of a bilayer-bound model tripeptide - a H-1-NMR study. J. Phys. Chem. 1993;97:2967–2973. [Google Scholar]
- 56.Zhang WX, Thakur V, Lomize A, Pogozheva I, Panagabko C, Cecchini M, Baptist M, Morley S, Manor D, Atkinson J. The Contribution of Surface Residues to Membrane Binding and Ligand Transfer by the α-Tocopherol Transfer Protein (alpha-TTP) J. Mol. Biol. 2011;405:972–988. doi: 10.1016/j.jmb.2010.11.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Radzicka A, Wolfenden R. Comparing the polarities of the amino-acids - side-chain distribution coefficients between the vapor-phase, cyclohexane, 1-octanol, and neutral aqueous-solution. Biochemistry. 1988;27:1664–1670. [Google Scholar]
- 58.Doherty T, Su YC, Hong M. High-Resolution Orientation and Depth of Insertion of the Voltage-Sensing S4 Helix of a Potassium Channel in Lipid Bilayers. J. Mol. Biol. 2010;401:642–652. doi: 10.1016/j.jmb.2010.06.048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Hessa T, White SH, von Heijne G. Membrane insertion of a potassium-channel voltage sensor. Science. 2005;307:1427–1427. doi: 10.1126/science.1109176. [DOI] [PubMed] [Google Scholar]
- 60.Kucerka N, Liu YF, Chu NJ, Petrache HI, Tristram-Nagle S, Nagle JF. Structure of fully hydrated fluid phase DMPC and DLPC lipid bilayers using X-ray scattering from oriented multilamellar arrays and from large unilamellar vesicles. Biophys. J. 2005;88:245A–245A. doi: 10.1529/biophysj.104.056606. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Mitra K, Ubarretxena-Belandia T, Taguchi T, Warren G, Engelman DM. Modulation of the bilayer thickness of exocytic pathway membranes by membrane proteins rather than cholesterol. Proc. Natl. Acad. Sci. U.S.A. 2004;101:4083–4088. doi: 10.1073/pnas.0307332101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Schow EV, Freites JA, Cheng P, Bernsel A, von Heijne G, White SH, Tobias DJ. Arginine in membranes: the connection between molecular dynamics simulations and translocon-mediated insertion experiments. J. Membr. Biol. 2010;239:35–48. doi: 10.1007/s00232-010-9330-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Lomize AL, Pogozheva ID, Lomize MA, Mosberg HI. The role of hydrophobic interactions in positioning of peripheral proteins in membranes. BMC Struct. Biol. 2007;7:44. doi: 10.1186/1472-6807-7-44. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Lomize AL, Pogozheva ID, Mosberg HI. Quantification of helix-helix binding affinities in micelles and lipid bilayers. Prot. Sci. 2004;13:2600–2612. doi: 10.1110/ps.04850804. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Fuguet E, Rafols C, Roses M. Characterization of the solvation properties of surfactants by solvatochromic indicators. Langmuir. 2003;19:6685–6692. [Google Scholar]
- 66.Carrozzino JM, Fuguet E, Helburn R, Khaledi MG. Characterization of small unilamellar vesicles using solvatochromic pi* indicators and particle sizing. J. Biochem. Bioph. Meth. 2004;60:97–115. doi: 10.1016/j.jbbm.2004.04.014. [DOI] [PubMed] [Google Scholar]
- 67.Efremov RG, Nolde DE, Vergoten G, Arseniev AS. A solvent model for simulations of peptides in bilayers. I. Membrane-promoting alpha-helix formation. Biophys. J. 1999;76:2448–2459. doi: 10.1016/S0006-3495(99)77400-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Lazaridis T, Mallik B, Chen Y. Implicit solvent simulations of DPC micelle formation. Journal of Physical Chemistry B. 2005;109:15098–15106. doi: 10.1021/jp0516801. [DOI] [PubMed] [Google Scholar]
- 69.Ulmschneider MB, Ulmschneider JP, Sansom MSP, Di Nola A. A generalized Born implicit-membrane representation compared to experimental insertion free energies. Biophys. J. 2007;92:2338–2349. doi: 10.1529/biophysj.106.081810. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Kurad D, Jeschke G, Marsh D. Lipid membrane polarity profiles by high-field EPR. Biophys. J. 2003;85:1025–1033. doi: 10.1016/S0006-3495(03)74541-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Koehorst RBM, Spruijt RB, Vergeldt FJ, Hemminga MA. Lipid bilayer topology of the transmembrane α-helix of M13 major coat protein and bilayer polarity profile by site-directed fluorescence spectroscopy. Biophys. J. 2004;87:1445–1455. doi: 10.1529/biophysj.104.043208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Subczynski WK, Widomska J, Feix JB. Physical properties of lipid bilayers from EPR spin labeling and their influence on chemical reactions in a membrane environment. Free Radical Bio. Med. 2009;46:707–718. doi: 10.1016/j.freeradbiomed.2008.11.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Marrink SJ, Berendsen HJC. Simulation of water transport through a lipid-membrane. J. Phys. Chem. B. 1994;98:4155–4168. [Google Scholar]
- 74.Chamberlain AK, Lee Y, Kim S, Bowie JU. Snorkeling preferences foster an amino acid composition bias in transmembrane helices. J. Mol. Biol. 2004;339:471–479. doi: 10.1016/j.jmb.2004.03.072. [DOI] [PubMed] [Google Scholar]
- 75.Voinov MA, Kirilyuk IA, Smirnov AI. Spin-Labeled pH-Sensitive Phospholipids for Interfacial pK(a) Determination: Synthesis and Characterization in Aqueous and Micellar Solutions. J. Phys. Chem. B. 2009;113:3453–3460. doi: 10.1021/jp810993s. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Wang PM, Anderko A. Computation of dielectric constants of solvent mixtures and electrolyte solutions. Fluid Phase Equilibr. 2001;186:103–122. [Google Scholar]
- 77.Hong HD, Park S, Jimenez RHF, Rinehart D, Tamm LK. Role of aromatic side chains in the folding and thermodynamic stability of integral membrane proteins. J. Am. Chem. Soc. 2007;129:8320–8327. doi: 10.1021/ja068849o. [DOI] [PubMed] [Google Scholar]
- 78.Tsai RS, Fan WZ, Eltayar N, Carrupt PA, Testa B, Kier LB. Solute water interactions in the organic-phase of a biphasic system.1. Structural influence of organic solutes on the water-dragging effect. J. Am. Chem. Soc. 1993;115:9632–9639. [Google Scholar]
- 79.Abraham T, Schooling SR, Nieh MP, Kucerka N, Beveridge TJ, Katsaras J. Neutron diffraction study of Pseudomonas aeruginosa lipopolysaccharide bilayers. J. Phys. Chem. B. 2007;111:2477–2483. doi: 10.1021/jp066012+. [DOI] [PubMed] [Google Scholar]
- 80.Ulmschneider MB, Sansom MSP, Di Nola A. Properties of integral membrane protein structures: Derivation of an implicit membrane potential. Proteins Struc. Func.Bioinf. 2005;59:252–265. doi: 10.1002/prot.20334. [DOI] [PubMed] [Google Scholar]
- 81.Hessa T, Meindl-Beinker NM, Bernsel A, Kim H, Sato Y, Lerch-Bader M, Nilsson I, White SH, von Heijne G. Molecular code for transmembrane-helix recognition by the Sec61 translocon. Nature (London) 2007;450:1026-U2. doi: 10.1038/nature06387. [DOI] [PubMed] [Google Scholar]
- 82.Senes A, Chadi DC, Law PB, Walters RFS, Nanda V, DeGrado WF. E-z, a depth-dependent potential for assessing the energies of insertion of amino acid side-chains into membranes: Derivation and applications to determining the orientation of transmembrane and interfacial helices. J. Mol. Biol. 2007;366:436–448. doi: 10.1016/j.jmb.2006.09.020. [DOI] [PubMed] [Google Scholar]
- 83.MacCallum JL, Bennett WFD, Tieleman DP. Partitioning of amino acid side chains into lipid bilayers: Results from computer simulations and comparison to experiment. J. Gen. Physiol. 2007;129:371–377. doi: 10.1085/jgp.200709745. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Wimley WC, Creamer TP, White SH. Solvation energies of amino acid side chains and backbone in a family of host-guest pentapeptides. Biochemistry. 1996;35:5109–5124. doi: 10.1021/bi9600153. [DOI] [PubMed] [Google Scholar]
- 85.Hessa T, Reithinger JH, von Heijne G, Kim H. Analysis of Transmembrane Helix Integration in the Endoplasmic Reticulum in S. cerevisiae. J. Mol. Biol. 2009;386:1222–1228. doi: 10.1016/j.jmb.2009.01.027. [DOI] [PubMed] [Google Scholar]
- 86.Xie K, Hessa T, Seppala S, Rapp M, von Heijne G, Dalbey RE. Features of transmembrane segments that promote the lateral release from the translocase into the lipid phase. Biochemistry. 2007;46:15153–15161. doi: 10.1021/bi701398y. [DOI] [PubMed] [Google Scholar]
- 87.Walter A, Gutknecht J. Permeability of small nonelectrolytes through lipid bilayer-membranes. J. Membane Biol. 1986;90:207–217. doi: 10.1007/BF01870127. [DOI] [PubMed] [Google Scholar]
- 88.Xiang TX, Anderson BD. The relationship between permeant size and permeability in lipid bilayer-membranes. J. Membrane Biol. 1994;140:111–122. doi: 10.1007/BF00232899. [DOI] [PubMed] [Google Scholar]
- 89.Leo A, Hansch C, Elkins D. Partition coefficients and their uses. Chem. Rev. 1971;71:525–616. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.