A Jackknife and Voting Classifier Approach to Feature Selection and Classification

Abstract

With technological advances now allowing measurement of thousands of genes, proteins and metabolites, researchers are using this information to develop diagnostic and prognostic tests and discern the biological pathways underlying diseases. Often, an investigator’s objective is to develop a classification rule to predict group membership of unknown samples based on a small set of features and that could ultimately be used in a clinical setting. While common classification methods such as random forest and support vector machines are effective at separating groups, they do not directly translate into a clinically-applicable classification rule based on a small number of features.We present a simple feature selection and classification method for biomarker detection that is intuitively understandable and can be directly extended for application to a clinical setting. We first use a jackknife procedure to identify important features and then, for classification, we use voting classifiers which are simple and easy to implement. We compared our method to random forest and support vector machines using three benchmark cancer ‘omics datasets with different characteristics. We found our jackknife procedure and voting classifier to perform comparably to these two methods in terms of accuracy. Further, the jackknife procedure yielded stable feature sets. Voting classifiers in combination with a robust feature selection method such as our jackknife procedure offer an effective, simple and intuitive approach to feature selection and classification with a clear extension to clinical applications.

Introduction

With technological advances now allowing measurement of thousands of genes, proteins and metabolites, researchers are using this information to develop diagnostic and prognostic tests and discern the biological pathways underlying diseases. Often, researchers initially seek to separate patients into biologically-relevant groups (e.g., cancer versus control) based on the full suite of gene expression, protein or metabolite profiles. Commonly though, the ultimate objective is to identify a small set of features contributing to this separation and to develop a classification rule to predict group membership of unknown samples (e.g., differentiate between patients with and without cancer or classify patients according to their likely response to a treatment).

A number of methods have been developed for feature selection and classification using gene expression, proteomics or metabolomics data. All methods share the two essential tasks of selecting features and constructing a classification rule, but differ in how these two tasks are accomplished. Methods can be categorized into three groups: filter, wrapper and embedded methods based on the relationship between the feature selection and classification tasks.¹ In filter methods, feature selection and classification are conducted independently. Typically, features are ranked based on their ability to discriminate between groups using a univariate statistic such as Wilcoxon, t-test, between-group to within-group sum of squares (BSS/WSS), and an arbitrary number of the top-ranking features are then used in a classifier. For wrapper methods, the feature selection step occurs in concert with classifier selection; features are evaluated for a specific classifier and in the context of other features. Lastly, with embedded techniques feature selection is fully integrated with classifier construction. Numerous methods within each category have been developed; Saeys et al¹ discuss the relative merits and weakness of these methods and their applications in bioinformatics.

Support vector machine (SVM)² and random forest³ are embedded methods that are two of the leading feature selection and classification methods commonly used in ‘omics research. Both methods have proved effective at separating groups using gene expression data^4–6 and proteomics^7–10 and recently SVM has been applied to metabolomics data.¹¹ However, while these methods demonstrate that groups can be differentiated based on gene expression or protein profiles, their extension to clinical applications is not readily apparent. For clinical applications, classifiers need to consist of a small number of features and to use a simple, predetermined and validated rule for prediction. In random forest, the classification rule is developed by repeatedly growing decision trees with final sample classification based on the majority vote of all trees. Although important features can be identified based on their relative contribution to classification accuracy, the method does not directly translate into a clinicially-meaningful classification rule. SVM are linear classifiers that seek to find the optimal (i.e., provides maximum margin) hyperplane separating groups using all measurements and thus does not accomplish the first task, that of feature selection. Several methods for identifying important features have been proposed^6,12 but as with random forest, the method does not yield classification rules relevant to a clinical setting. Further, SVM results can be very sensitive to tuning parameter values.

Voting classifiers are a simple, easy to understand classification strategy. In an unweighted voting classifier, each feature in the classifier “votes” for an unknown sample’s group membership according to which group the sample’s feature value is closest. The majority vote wins. Weighted voting can be used to give greater weight to votes of features with stronger evidence for membership in one of the groups. Voting classifiers have been sporadically used and evaluated for application to gene expression data.^13–16 Dudoit et al¹⁴ found Golub’s¹³ weighted voting classifier performed similarly to or better than several discriminant analysis methods (Fisher linear, diagonal and linear) and classification and regression tree based predictors, but slightly poorer than diagonal linear discriminant analysis and k-nearest neighbor. The weighted voting classifier also performed similarly to SVM and regularized least squares in Ancona et al¹⁵ study of gene expression from colon cancer tumors. These results suggest that voting classifiers can yield comparable results to other classifiers.

To be clinically-applicable, classification rules need to consist of a small number of features that will consistently and accurately predict group membership. Identifying a set of discriminatory features that is stable with respect to the specific samples in the training set is important for developing a broadly applicable classifier. In the traditional approach to classifier development, the data set is separated into a training set for classifier construction and a test set(s) for assessment of classifier performance. Using the training set, features are ranked according to some criterion and the top m features selected for inclusion in the classifier applied to the test set. By repeatedly separating the data into different training and test sets, Michelis et al¹⁷ showed that the features identified as predictors were unstable, varying considerably with the samples included in the training set. Baek et al¹⁸ compared feature set stability and classifier performance when features were selected using the traditional approach versus a frequency approach. In a frequency approach, the training set is repeatedly separated into training and test sets; feature selection and classifier development is conducted for each training set. A final list of predictive features is generated based on the frequency occurrence of features in the classifiers across all training:test pairs. They showed that frequency methods for identifying predictive features generated more stable feature sets and yielded classifiers with accuracies comparable to those constructed with traditional feature selection approaches.

Here we present a simple feature selection and classification method for biomarker detection that is intuitively understandable and can be directly extended for application to a clinical setting. We first use a jackknife procedure to identify important features based on a frequency approach. Then for classification, we use weighted or unweighted voting classifiers. We evaluate the performance of voting classifiers with varying numbers of features using leave-one-out cross validation (LOOCV) and multiple random validation (MRV). Three cancer ‘omics datasets with different characteristics are used for comparative study. We show our approach achieves classification accuracy comparable to random forest and SVM while yielding classifiers with clear clinical applicability.

Methods

Voting classifiers and feature selection

The simplest voting classifier is an unweighted classifier in which each feature “votes” for the group membership of an unknown sample according to which group mean the sample is closest. Let x_j(g) be the value of feature g in test sample j and consider two groups (0, 1). The vote of feature g for sample j is

$$v_j(g)=\{\begin{array}{c}1\hspace{0.17em}\mathit{\text{if}}\hspace{0.17em}|x_j(g)-{\mu }_1(g)|<|x_j(g)-{\mu }_0(g)|\\ 0\hspace{0.17em}\mathit{\text{if}}\hspace{0.17em}|x_j(g)-{\mu }_0(g)|<|x_j(g)-{\mu }_1(g)|\end{array}$$ (1)

where μ₁(g) and μ₀(g) are the means of feature g in the training set for group 1 and 0, respectively. Combining the votes of all features in the classifier (G), the predicted group membership (C_j) of sample j is determined by

$$C_j=\{\begin{array}{c}1\hspace{0.17em}\mathit{\text{if}}\hspace{0.17em}\sum _{G}I[v(g)=1]>\sum _{G}I[v(g)=0]\\ 0\hspace{0.17em}\mathit{\text{if}}\hspace{0.17em}\sum _{G}I[v(g)=0]>\sum _{G}I[v(g)=1]\end{array}$$ (2)

The unweighted voting classifier gives “equal” weight to all votes with no consideration of differences in the strength of the evidence for a classification vote by each feature. Alternatively, various methods for weighting votes are available. MacDonald et al¹⁶ weighted votes according to the deviation of each feature from the mean of the two classes, ie, W_j (g) = |x_j (g) − [μ₁ (g) + μ₀ (g) / 2]|. This approach gives greater weight to features with values farther from the overall mean and thus more strongly suggesting membership in one group. However, if features in the classifier have substantially different average values, this weighting strategy will disproportionately favor features with large average values. Golub et al¹³ proposed weighting each feature’s vote according to the feature’s signal-to-noise ratio a_g = [μ₁(g) − μ₂(g)]/[σ₁(g) + σ₂(g)]. In this approach, greater weight is given to features that best discriminate between the groups in the training set. While addressing differences in scale, this weighting strategy does not exploit information in the deviation of the test sample’s value from the mean as MacDonald et al’s¹⁶ method does.

We propose a novel weighted voting classifier that accounts for differences among features in terms of variance and mean values and incorporates the magnitude of a test sample’s deviation from the overall feature mean. In our weighting approach, the vote of feature g is weighted according to the strength of the evidence this feature provides for the classification of sample j, specifically.

$$w_j(g)=\frac{{\left(x_j(g)-\frac{{\mu }_1(g)+{\mu }_0(g)}{2}\right)}^2}{{\sum }_{i=1}^n\frac{{\left(x_i(g)-\frac{{\mu }_1(g)+{\mu }_0(g)}{2}\right)}^2}{n}}$$ (3)

where w_j(g) is the weight of feature g for test set sample j, x_j(g) is the value of feature g for test sample j, x_i(g) is the value of feature g for training sample i, n is the number of samples in the training set, and μ₁(g) and μ₀(g) are the grand means of feature g in the training set for group 1 and 0, respectively. This approach weights a feature’s vote according to how far the test set sample’s value is from the grand mean of the training set like MacDonalds et al’s¹⁶ but scales it according the feature’s variance to account for differences in magnitude of feature values. Test set samples are classified based on the sum of the weighted votes of each feature.

We used a jackknife procedure to select and rank features to include in the classifier (G = {1, 2, …, g, …, m}, where m<<n = number of all features in dataset). For this approach, data are separated into a training and test set. Using only the training set, each sample is sequentially removed and features are ranked based on the absolute value of the t-statistic calculated with the remaining samples. We then retained the top ranked 1% and 5% of features for each jackknife iteration. This step yielded a list of the most discriminating features for each jackknife iteration. Then the retained features were ranked according to their frequency occurrence across the jackknife iterations. Features with the same frequency of occurrence were further ranked according to the absolute value of their t-statistics. Using the frequency ranked list of features, we constructed voting classifiers with the top m most frequently occurring features (fixed up to m = 51 features in this study), adding features to the classifier in decreasing order of their frequency of occurrence and applied the classifier to the corresponding test set. In both the LOOCV and MRV procedures, we used this jackknife procedure to build and test classifiers; thus feature selection and classifier development occurred completely independently of the test set.

For clarification, our two-phase procedure is described by the following sequence:

Phase 1: Feature selection via jackknife and voting classifier construction

For each training:test set partition,

• 1.Select the m most frequently occurring features across the jackknife iterations using the training set for inclusion in the classifier (G), where G is the set of the m most frequently occurring features in descending order of frequency.
• 2.For each feature g selected in step 1, calculate the vote of feature g for test sample j using equation (1).
• 3.Repeat step 2 for all features in the classifier G.
• 4.Combine the votes of all features from step 3 and determine the group membership (C_j) of sample j using equation (2). For the weighted voting classifier, the vote of feature g is weighted according to equation (3).
• 5.Repeat steps 2–4 for all test samples in the test set.

Phase 2: Cross-validation

• 6.Repeat for all training:test set partitions.
• 7.Calculate the misclassification error rate to assess performance of the classifier.

Data sets

We used the following three publicly available data sets to evaluate our method and compare it to random forest and support vector machines.

Leukemia data set

This data set from Golub et al¹³ consists of gene expression levels for 3,051 genes from 38 patients, 11 with acute myeloid leukemia and 27 with acute lymphoblastic leukemia. An independent validation set was not available for this data set. The classification problem for this data set consists of distinguishing patients with acute myeloid leukemia from those with acute lymphoblastic leukemia.

Lung cancer data set

This data set from Gordon et al¹⁹ consists of expression levels of 12,533 genes in 181 tissue samples from patients with malignant pleural mesothelioma (31 samples) or adenocarcinoma (150 samples) of the lung. We randomly selected 32 samples, 16 from each group to create a learning set. The remaining 149 samples were used as an independent validation set. It was downloaded from http://datam.i2r.a-star.edu.sg/datasets/krbd/LungCancer/LungCancer-Harvard2.html.

Prostate cancer data set

Unlike the leukemia and lung cancer data sets, the prostate cancer data set is proteomics data set consisting of surface-enhanced laser desorption ionization time-of-flight (SELDI-TOF) mass spectrometry intensities of 15,154 proteins.²⁰ Data are available for 322 patients (253 controls and 69 with prostate cancer). We randomly selected 60 patients (30 controls and 30 cancer patients) to create a learning set and an independent validation set with 262 patients (223 controls and 39 cancer patients). The data were downloaded from http://home.ccr.cancer.gov/ncifdaproteomics/ppatterns.asp.

Performance assessment

To evaluate the performance of the voting classifiers, we used LOOCV and MRV. For MRV, we randomly partitioned each data set into training and test sets at a fixed ratio of 60:40 while maintaining the group distribution of the full data set. We generated 1,000 of these training:test set pairs. For each training:test set pair, we conducted feature selection and constructed classifiers using the training set and applied the classifier to the corresponding test set.

We compared the voting classifiers to random forest and support vector machines. The random forest procedure was implemented using the randomForest package version 4.5-34²¹ for R.²² Default values of the randomForest function were used. Support vector machines were generated using the svm function in the package e1071.²³ A radial kernel was assumed and 10-fold cross validation using only the training set was used to tune gamma and cost parameters for each training:test set pair. Gamma values ranging from 0.0001 to 2 and cost values of 1 to 20 were evaluated. As with the voting classifiers, random forest and SVM classifiers were developed using the training set of each training:test set pair within the LOOCV and MRV strategies and using features identified through the jackknife procedure rather than all features, ie, for a training:test set pair, all features that occurred in the top 1% or 5% of the features across the jackknife iterations were used in developing the classifiers.

Application to independent validation sets

The lung and prostate cancer data sets were large enough to create independent validation sets. For these data sets, we used the training sets to develop classifiers to apply to these sets. To identify features to include in the voting classifiers, we identified the m most frequently occurring features for each training:test set pair, with m equal to odd numbers from three to 51. For each m number of features, we ranked the features according to their frequency of occurrence across all the jackknife samples. Voting classifiers with three to 51 features were constructed using all of the training set samples and applied to the independent validation sets. Random forest and SVM classifiers were constructed using any feature that occurred at least once in the feature sets identified through the jackknife strategy procedure. We constructed classifiers using the top 1% and 5% features identified through the jackknife procedure for both validation strategies (LOOCV and MRV).

Results

Performance evaluation and comparison with random forest and support vector machines

We evaluated our method and compared it to random forest and SVM through application to three well-studied data sets from cancer studies (Table 1). Two of these data sets (leukemia¹³ and lung cancer)¹⁹ consist of gene expression data; the third (prostate cancer)²⁰ is proteomics data. We evaluated accuracy of the voting classifiers for each data set using the top 1% and 5% of features of the jackknife training sets for two validation strategies—LOOCV, and MRV using 1,000 randomly generated training:test set pairs.

Table 1.

Characteristics of data sets.

Data set	Ref	Data type	# features	Training set		Independent validation set
				# cases	# control
Leukemia	13	Gene expression	3,051	11a	27	No
Lung cancer	19	Gene expression	12,533	16	16	149 (15 controls, 134 cases)
Prostate cancer	20	Proteomics	15,154	30	30	262 (223 controls, 39 cases

Note:

^aPatients with acute myeloid leukemia were considered “cases” and those with acute lymphoblastic leukemia were used as “controls”.

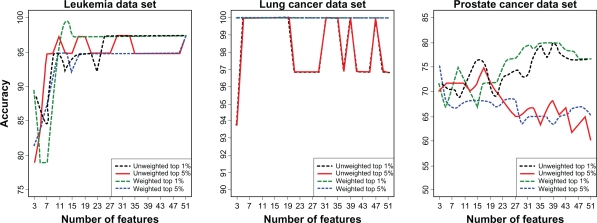
Accuracy of the two voting classifiers increased with the number of features included in the classifier (Figs. 1 and 2). However, the largest improvements in accuracy occurred as the number of features increased from 3 to about 11 after which further increases were small. In fact, accuracies within 5% of the maximum accuracy could be achieved with fewer than 13 features. The feature selection step influenced accuracy of the voting classifiers more strongly than the number of features included in the classifier. For both weighted and unweighted voting classifiers, accuracy was usually higher when the classifier was constructed based on the top 1% of features rather than the top 5% (Figs. 1 and 2), suggesting that a classifier with a small number of features could be developed. The weighted voting classifier generally yielded higher accuracy than the unweighted voting classifier; however, the differences tended to be small, within a few percentage points (Figs. 1 and 2).

Figure 1.

Multiple random validation results for voting classifiers. Mean accuracy for voting classifiers (unweighted and weighted) with varying numbers of features included in the classifier based on 1,000 random training:test set partitions of two gene expression data sets (leukemia, lung cancer) and a proteomics data set (prostate cancer). Features to include in the classifiers were identified through a jackknife procedure through which features were ranked according to their frequency of occurrence in the top 1% or 5% most significant features based on t-statistics across all jackknife samples.

Figure 2.

Leave-one-out cross validation (LOOCV) results for voting classifiers. Accuracy for voting classifiers (unweighted and weighted) with varying numbers of features included in the classifier based on LOOCV of two gene expression data sets (leukemia, lung cancer) and a proteomics data set (prostate cancer). Features to include in the classifiers were identified through a jackknife procedure through which features were ranked according to their frequency of occurrence in the top 1% or 5% most significant features based on t-statistics across all jackknife samples.

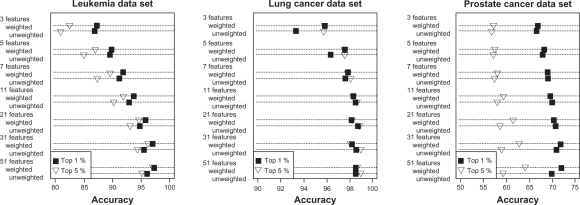
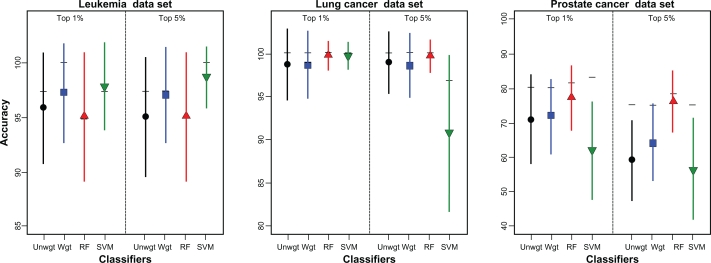
The voting classifiers performed similarly to random forest and SVM but classifier performance varied considerably for the three data sets evaluated (Fig. 3). All classifier methods performed well for the lung cancer data set with mean accuracies greater than 95%. Both the weighted and unweighted voting classifiers achieved greater than 90% accuracy with only three features and greater than 98% accuracy with only nine features. SVM yielded a relatively low accuracy based on the top 5% of features for the lung cancer data set (84.6%); accuracy potentially could be improved with more extensive parameter tuning. Classifier accuracy also was high for the leukemia data set with all classifiers achieving over 95% accuracy. The voting classifiers performed slightly better than random forest for this data set; SVM had the highest accuracy when the top 5% of features were used to construct the classifier. In contrast, for the prostate cancer data set, classifier accuracy was considerably lower and more variable than for the other data sets. Accuracy ranged from a low of 56.5% for SVM under MRV using the top 5% of features to a high of 83.3% for SVM using the top 1% in LOOCV. In general, though, random forest tended to produce the highest accuracies with the voting classifiers yielding intermediate performances.

Figure 3.

Comparison of voting classifiers, random forest and SVM. Accuracy (mean ± SE) for unweighted (Unwgt) and weighted (Wgt) voting classifiers, random forest (RF) and support vector machines (SVM) based on 1,000 random training:test set partitions of two gene expression data sets (leukemia, lung cancer) and a proteomics data set (prostate cancer). Features to include in the classifiers were identified through a jackknife procedure through which features were ranked according to their frequency of occurrence in the top 1% or 5% most significant features based on t-statistics across all jackknife samples. Horizontal bars show LOOCV results. Results presented for weighted and unweighted voting classifiers are based on the number of features yielding the highest mean accuracy. For the leukemia data set the 49 or 51 features yielded the highest accuracy for the voting classifiers in the MRV procedure while for LOOCV, the best numbers of features for the unweighted voting classifier were 17 and 11 using the top 1% and 5% of features, respectively and were 13 and 51, respectively for the weighted voting classifier. For the lung cancer data set, 3 and 5 features were best with LOOCV for the weighted and unweighted classifier. Under MRV, 51 features yielded the highest accuracy for the weighted voting classifier while 19 or 39 features needed for the unweighted voting classifier based on the top 1% and 5% of features, respectively. With the prostate cancer data set, the unweighted voting classifier used 31 and 49 features with MRV and 35 and 17 features with LOOCV based on the top 1% and 5% of features, respectively. For the weighted voting classifier, these numbers were 49, 51, 31 and 3, respectively. The number of features used in random forest and SVM varied across the training:test set partitions. Depending on the validation strategy and percentage of features retained in the jackknife procedure, the number of features ranged from 67 to 377 for the leukemia data set, from 233 to 2,692 for the prostate cancer set and from 247 to 1,498 for the lung cancer data set.

The poor performance of all classifiers for the prostate data set suggested greater heterogeneity in one of the groups. Control samples in this data set consisted of patients with normal prostates as well as patients with benign prostate hyperplasia (BPH). In Petricoin et al’s original analysis,²⁰ 26% of the men with BPH were classified as having cancer. They noted that some of these apparent misclassifications actually could be correct because over 20% of subjects identified as not having cancer based on an initial biopsy were later determined to have cancer. Thus, the poorer classification performance for the prostate data set could result from BPH patients having incorrectly been considered controls which led to increased within-group variation relative to between-groups variation.

We further analyzed the prostate cancer data set excluding BPH patients from the control group. The performance of all classifiers increased markedly with exclusion of BPH patients. For the LOOCV and MRV procedures, random forest and SVM achieved accuracies of 90% to 95% and the accuracy of the voting classifiers ranged from 76% to 98%. These values were 10% to 20% greater than with inclusion of the BPH samples (Table 2).

Table 2.

Accuracy of classifiers applied to prostate cancer data set excluding benign prostate hyperplasia samples.

	Classifier
	Unweighted	Weighted	Random forest	SVM
LOOCV
Top 1%	88.3a	93.3c	93.3h	95.0h
Top 5%	98.3b	96.7a	91.7i	95.0i
60:40 partitions
Top 1%	84.8 ± 10.2d	87.5 ± 8.6f	89.6 ± 7.3j	91.7 ± 6.8j
Top 5%	76.2 ± 11.4e	81.3 ± 10.3g	89.5 ± 7.3k	91.5 ± 6.4k

Notes: Accuracy of voting classifiers (unweighted and weighted), random forest and SVM applied to the prostate cancer data set excluding benign prostate hyperplasia samples from the control group. Features to include in the classifiers were derived using the top 1% or 5% of features based on t-statistics through a jackknife procedure using training sets in leave-one-out cross validation (LOOCV) or multiple random validation (60:40 partitions). Mean ± SD accuracy reported for 1,000 60:40 random partitions.

^aHighest accuracy achieved with 7 features in classifier;

^bHighest accuracy achieved with 9 features in classifier;

^cHighest accuracy achieved with 13 features in classifier;

^dHighest accuracy achieved with 21 features in classifier;

^eHighest accuracy achieved with 47 features in classifier;

^fHighest accuracy achieved with 23 features in classifier,

^gHighest accuracy achieved with 51 features in classifier. The number of features used in random forest and SVM varied across the training:test set partitions. The ranges were:

^h265–340 features;

ⁱ1,194–1,268 features;

^j212–533;

^k1,412–1,970 features.

Independent validation set evaluation

In cases where data sets are too small, overfitting can be a severe issue when assessing a large number of features. Therefore, it is very important to evaluate the accuracy of classifier performance with an independent validation set of samples that are not part of the development of a classifier. Hence, we constructed voting, random forest and SVM classifiers using only the training sets and applied them to independent validation sets from the lung cancer and prostate cancer data sets.

All classifiers had very high accuracies when applied to the lung cancer data set (Table 3). Sensitivity and the positive predictive value of the classifiers also were very high, 99% to 100%. The one exception was SVM with features selected through MRV which had considerably lower accuracies and sensitivities. The weighted voting classifier had 100% accuracy using 49 features. However, with just three features (37205_at, 38482_at and 32046_at), the unweighted voting classifiers had greater than 90% accuracy and the weighted more than 93% accuracy. These three features could easily form the basis of a diagnostic test for clinical application consisting of the mean and variances of these features in a large sample of patients with adenocarcinoma and mesothelioma.

Table 3.

Performance of classifiers applied to independent validation set of lung cancer data set.

	Unweighted	Weighted	Random forest	SVM
Accuracy
LOOCV
Top 1%	99.3a	100b	98.7e	100e
Top 5%	99.3a	100b	98.7f	100f
60:40 partitions
Top 1%	98.7c	100d	99.3g	94.6g
Top 5%	98.7c	100d	100h	84.6h
Sensitivity
LOOCV
Top 1%	100	100	99.2	100
Top 5%	100	100	99.2	100
60:40 partitions
Top 1%	99.2	100	100	94.0
Top 5%	99.2	100	100	82.8
Positive predictive value
LOOCV
Top 1%	99.3	100	99.2	100
Top 5%	99.3	100	99.2	100
60:40 partitions
Top 1%	99.2	100	99.3	100
Top 5%	99.2	100	100	100

Notes: Accuracy, sensitivity, and positive predictive value of voting classifiers (unweighted and weighted), random forest and SVM applied to independent data sets from the lung cancer data set. Features to include in the classifiers were derived using the top 1% or 5% of features based on t-statistics through a jackknife procedure using training sets in leave-one-out cross validation (LOOCV) or multiple random validation (60:40 partitions).

^aHighest accuracy achieved with 37 features in classifier;

^bHighest accuracy achieved with 23 features in classifier;

^cHighest accuracy achieved with 15 features in classifier;

^dHighest accuracy achieved with 49 features in classifier. The number of features used in developing SVM and random forest classifiers were:

^e452 features;

^f1,791 features;

^g4,172 features;

^h9,628 features.

Classifier performance was quite variable when applied to the prostate cancer validation data set. Accuracy was generally highest for the random forest classifier (Table 4). When features to use in the classifier were derived from the LOOCV procedure, the voting classifiers had relatively low accuracy (68.5% to 76.5%) while SVM and random forest had accuracies greater than 90%. Accuracy of the voting classifiers improved when features were derived through MRV and were within 5% of random forest and SVM. Sensitivity and positive predictive value were highest with random forest and similar between the voting classifiers and SVM. As seen in the LOOCV and MRV analyses, the performance of all classifiers increased when BPH samples were excluded from the control group. When applied to the independent validation set, the weighted voting classifier achieved accuracies of 93% to 99%; random forest and SVM were similar with accuracies of 97% to 99% and 89% to 99%, respectively.

Table 4.

Performance of classifiers applied to independent validation set of prostate cancer data set.

	Unweighted	Weighted	Random forest	SVM
Accuracy
LOOCV
Top 1%	68.5a	76.5b	92.7g	93.5g
Top 5%	74.5c	81.9c	91.6h	92.4h
60:40 Partitions
Top 1%	86.3d	88.2c	91.6i	89.7i
Top 5%	86.7e	89.9f	90.5j	86.6j
Sensitivity
LOOCV
Top 1%	74.4	76.9	87.2	84.6
Top 5%	89.7	79.5	87.2	74.4
60:40 Partitions
Top 1%	74.4	76.9	82.0	65.0
Top 5%	69.2	74.4	84.6	64.1
Positive predictive value
LOOCV
Top 1%	43.9	53.6	70.8	75.0
Top 5%	50.7	62.0	66.7	74.4
60:40 Partitions
Top 1%	52.7	57.7	68.1	66.7
Top 5%	54	61.7	63.5	54.3

Notes: Accuracy, sensitivity, and positive predictive value of voting classifiers (unweighted and weighted), random forest and SVM applied to independent data sets from the prostate cancer data set. Features to include in the classifiers were derived using the top 1% or 5% of features based on t-statistics through a jackknife procedure using training sets in leave-one-out cross validation (LOOCV) or multiple random validation (60:40 partitions).

^aHighest accuracy achieved with 37 features in classifier;

^bHighest accuracy achieved with 43 features in classifier;

^cHighest accuracy achieved with 45 features in classifier,

^dHighest accuracy achieved with 49 features in classifier;

^eHighest accuracy achieved with 47 features in classifier;

^fHighest accuracy achieved with 27 features in classifier. The number of features used in developing SVM and random forest classifiers were:

^g685 features;

^h2,553 features;

ⁱ9,890 features;

^j14,843 features.

Data set variability and classifier performance

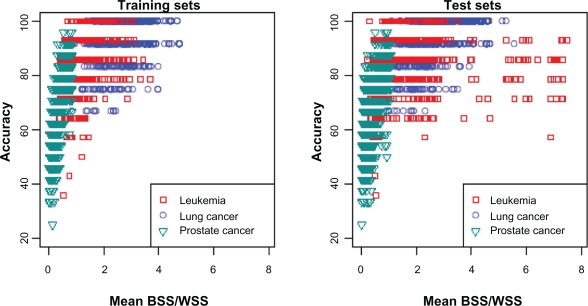
Classifier performance varied considerably among the three data sets. Accuracy was high for the leukemia and lung cancer data sets but lower for the prostate cancer data set. These differences likely reflect differences in the “signal-to-noise” ratio of features in these data sets. We used BSS/WSS to characterize the “signal-to-noise” ratio of each data set and investigated classifier performance in relation to BSS/WSS. First, we calculated BSS/WSS for each feature using all samples of the leukemia data set, and all learning set samples for the prostate and lung cancer data sets. Classifier accuracy was highest for the lung cancer data set and this data had the feature with the highest BSS/WSS of 3.50. Classifier accuracy was also high for the leukemia data set although slightly lower than for the lung cancer data set and accordingly the maximum BSS/WSS of features in this data set was smaller at 2.92. Finally, the maximum BSS/WSS for any feature in the prostate cancer data set was less than 1 (0.98) and classifier accuracy was lowest for this data set.

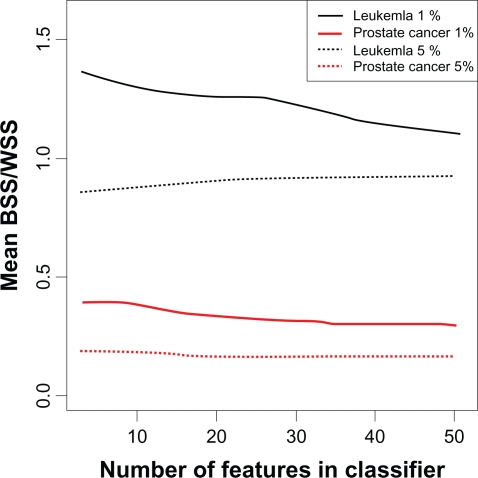
The “signal-to-noise” ratio of features in the classifier can also explain the better performance of classifiers constructed with the top 1% of the features as compared to the top 5%. For the prostate cancer and leukemia training sets, the mean BSS/WSS of features in the voting classifiers was always higher when the features were derived based on the top 1% than the top 5% (Fig. 4). By considering the top 5% of features for inclusion in the classifier, more noise was introduced and the predictive capability of the classifiers was reduced. SVM and random forest showed this effect as well (Fig. 3).

Figure 4.

Mean BSS/WSS of features in voting classifiers. Mean BSS/WSS of features included in the voting classifiers constructed from varying numbers of features for the leukemia and prostate cancer data sets. Mean values were calculated using the training sets from 1,000 random training: test set partitions. Features to include in the classifiers were identified through a jackknife procedure through which features were ranked according to their frequency of occurrence in the top 1% or 5% most significant features based on t-statistics across all jackknife samples.

We further evaluated the relationship between classifier performance and the BSS/WSS of features in the classifier using the weighted voting classifier with just the first three features in order of frequency of occurrence in MRV repetitions. Three features accounted for much of the classifier’s performance particularly for the lung cancer and leukemia data sets. Accuracy generally increased as the mean BSS/WSS of the three features included in the classifier increased in the training and test sets (Fig. 5). The lung cancer and leukemia data sets had the highest mean BSS/WSS values and also the highest accuracies while the lowest BSS/WSS values and accuracies occurred for the prostate cancer data set. Considering the test sets, when the mean BSS/WSS of these three features was greater than 1, the mean accuracy of the weighted vote classifier was greater than 80% for all data sets (Leukemia: 89%, Lung Cancer: 95%, Prostate Cancer: 81%) and was considerably lower when the mean BSS/WSS was less than 1 (Leukemia: 82%, Lung Cancer: 80%, Prostate Cancer: 66%).

Figure 5.

Mean accuracy of weigthed voting classifier versus mean BSS/WSS. Mean accuracy of the weighted voting classifier using three features versus the mean BSS/WSS of these features for two gene expression data sets (leukemia, lung cancer) and a proteomics data set (prostate cancer). Mean values were calculated across 1,000 random training:test set partitions. Features to include in the classifiers were identified through a jackknife procedure through which features were ranked according to their frequency of occurrence in the top 1% most significant features based on t-statistics across all jackknife samples. Mean BSS/WSS was calculated separately using the training and test set portions of each random partition.

Interestingly, accuracy was less than 70% for some partitions of the leukemia despite relatively high mean BSS/WSS values (>3) in the test set. These partitions tended to have one feature with a very high BSS/WSS (>10) resulting in a large mean BSS/WSS even though the other features had low values. Further, for these partitions, the mean values of the features in the test set for each group, particularly those with low BSS/WSS values, tended to be intermediate to those in the training set, resulting in ambiguous classification for some samples. Thus, even though the test set features of some partitions had a high mean BSS/WSS, the classification rule developed from the training set was not optimal. Overall, the results show that classification accuracy increases as the “signal-to-noise” ratio increases but even for data sets with a strong signal, some partitions of the data can yield low classification accuracies because of random variation in the training and test sets.

Feature frequency

An underlying goal of feature selection and classification methods is to identify a small, but sufficient, number of features that provide good classification with high sensitivity and specificity. Our jackknife procedure in combination with a validation strategy naturally yields a ranked list of discriminatory features. For each training:test set pair, features are ranked by their frequency of occurrence across the jackknife samples and the m most frequently occurring features used to build the classifier for that training:test set pair. Features used in the classifier for each training:test set pair can be pooled across all training:test set pairs and features ranked according to how frequently they occurred in classifiers. The features that occur most frequently will be the most stable and consistent features for discriminating between groups.

We compared the frequency of occurrence of features in the top 1% and 5% of features for the LOOCV and MRV validation strategies. LOOCV did not provide as clear of feature ranking as MRV. With LOOCV, many features occurred in the top percentages for all training:test set pairs, and thus were equally ranked in terms of frequency of occurrence. In contrast, few features occurred in the top percentages for all 1,000 training:test set pairs with MRV and thus, this procedure provided clearer rankings. Using the more liberal threshold of the top 5% resulted in more features occurring among the top candidates. As a result, more features were represented in the list of features compiled across the 1,000 training:test set pairs and their frequencies were lower. For example, for the leukemia data set, 31 features occurred in the top 5% of all 1,000 training:test set pairs while only two occurred in the top 1% of every pair.

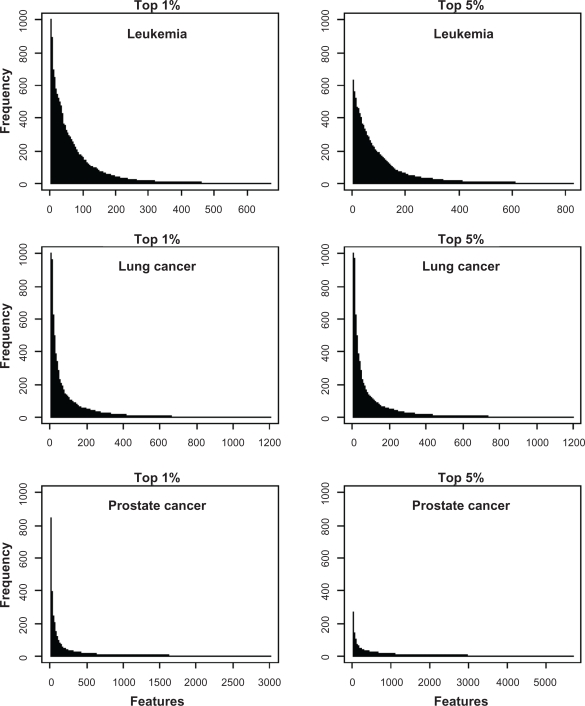
The frequency distributions of the features in the voting classifiers generated in the MRV strategy was indicative of the performance of the classifier for each data set. Considering the voting classifiers with 51 features, we tallied the frequency that each feature occurred in the classifier across the 1,000 training:test set pairs. All classifiers performed well for the lung cancer data set; the frequency distribution for this data set showed a small number of features occurring in all random partitions (Fig. 6). The leukemia data set had the next best classification accuracy. With the top 1% of features, this data set showed a small number of features occurring in every partition like the lung cancer data set but with using the top 5% of features, none of the features in the leukemia data set occurred in all partitions. In fact, the most frequently occurring feature occurred in only 600 of the training:test set pairs. Accordingly, classifier accuracy for the leukemia data set was lower using the top 5% features as compared to the top 1%. Finally, the prostate data set had the poorest classification accuracy and the frequency distribution of features differed substantially from the lung cancer and leukemia data sets. None of the features occurred in all random partitions and with a 5% threshold, the most frequently occurring features occurred in the classifier in only about 300 of the training:test set partitions. The best performance for the voting classifiers occurred when there were a small number of features that occurred in a large number of the classifiers constructed for each of the training:test set pairs.

Figure 6.

Frequency of occurrence of features in voting classifiers. Frequency of occurrence of features used in voting classifiers containing 51 features across 1,000 random training: test set partitions of two gene expression data sets (leukemia, lung cancer) and a proteomics data set (prostate cancer). Features to include in the classifiers were identified through a jackknife procedure through which features were ranked according to their frequency of occurrence in the top 1% or 5% most significant features based on t-statistics across all jackknife samples.

The instability of the most frequently occurring features for the prostate cancer data set could result in part from the BPH patients. While each training:test set partition had the same number of control and cancer patients, the relative number of BPH patients varied among partitions. Because of the variability within this group, the top features would be expected to be more variable across partitions than for the other data sets.

Discussion

In this study, we showed that voting classifiers performed comparably to random forest and SVM and in some cases performed better. For the three data sets we investigated, the voting classifier method yielded a small number of features that were similarly effective at classifying test set samples as random forest and SVM using a larger number of features. In addition to using a small set of features, voting classifiers offer some other distinct advantages. First, they accomplish the two essential tasks of selecting a small number of features and constructing a classification rule. Second, they are simple and intuitive, and hence they are easily adaptable by the clinical community. Third, there is a clear link between development of a voting classifier and potential application as a clinical test. In contrast, clinicians may not understand random forest and SVM such that the significance and applicability of results based on these methods may not be apparent. Further, demonstrating that these methods can accurately separate groups in an experimental setting does not clearly translate into a diagnostic test.

We used a frequency approach to identify important, discriminatory features at two levels. First, for each training:test set pair, we used a jackknife procedure to identify features to include in the classifier according to their frequency of occurrence. For the prostate and lung cancer data sets which had an independent validation set, we then selected features that occurred most frequently in classifiers to construct the final classifier applied to the independent validation set. The results from MRV were better for this step than LOOCV because the feature rankings were clearer under MRV. With LOOCV many features occurred in all classifiers and hence many features had the same frequency rank. In contrast, for MRV few features occurred in the classifiers of every random partition, resulting in a clearer ranking of features.

Our approach for feature selection differs from a standard LOOCV strategy in that we use a jackknife at each step in the LOOCV to build and test a classifier such that feature selection occurred completely independently of the test set. Baek et al¹⁸ followed a similar strategy but used V—fold cross validation rather than a jackknife with the training set to identify important features based on their frequency of occurrence. Efron²⁴ showed that V—fold cross validation has larger variability as compared to bootstrap methods, especially when a training set is very small. Because the jackknife is an approximation to the bootstrap, we elected to use a jackknife procedure in an attempt to identify stable feature sets.

In the jackknife procedure, we ranked features according the absolute value of t-statistics and retained the top 1% and 5% of features. Many other ranking methods have been used including BSS/WSS, Wilcoxon test, and correlation and our method easily adapts to other measures. Popovici et al²⁵ compared five features selection methods including t statistics, absolute difference of means and BSS/WSS and showed that classifier performance was similar for all feature-ranking methods. Thus, our feature selection and voting classifier method would be expected to perform similarly with other ranking methods. Of significance in our study was the performance differences between classifiers developed based on the top 1% and 5% of features. All classifiers (voting, random forest and SVM) generally had higher accuracy when they were constructed using the top 1% of the features as compared to those using the top 5%. Baker and Kramer²⁶ stated that the inclusion of additional features can worsen classifier performance if they are not predictive of the outcome. When the top 5% were used, more features were considered for inclusion in the classifier and the additional features were not as predictive of the outcome as features in the top 1% and thus tended to reduce accuracy. This effect was evident in the lower BSS/WSS values of features used in the voting classifiers identified based on the top 5% versus the top 1%. Thus, the criterion selected for determining which features to evaluate for inclusion in a classifier (eg, top 1% versus top 5% in our study) can affect identification of key features and classifier performance and should be carefully considered in classifier development.

To estimate the prediction error rate of a classifier, we used two validation strategies. Cross-validation systematically splits the given samples into a training set and a test set. The test set is the set of future samples for which class labels are to be determined. It is set aside until a specified classifier has been developed using only the training set. The process is repeated a number of times and the performance scores are averaged over all splits. It cross-validates all steps of feature selection and classifier construction in estimating the misclassification error. However, choosing what fraction of the data should be used for training and testing is still an open problem. Many researchers resort to using LOOCV procedure, in which the test set has only one sample and leave-one-out is carried out outside the feature selection process to estimate the performance of the classifier, even though it is known to give overly optimistic results, particularly when data are not identically distributed samples from the “true” distribution. Also, Michelis et al¹⁷ suggested that selection bias of training set for feature selection can be problematic. Their work demonstrated that the feature selection strongly depended on the selection of samples in the training set and every training set could lead to a totally different set of features. Hence, we also used 60:40 MRV partitions, not only to estimate the accuracy of a classifier but also to assess the “stability” of feature selection across the various random splits. In this study, we observed that LOOCV gave more optimistic results compared to MRV.

The proteomics data of prostate cancer patients was noisier than the gene expression data from leukemia and lung cancer patients as evidence by the lower BSS/WSS values and lower frequencies at which features occurred in the classifiers of the random partitions. For all classifiers, classification accuracy was lower for this data set than the gene expression data sets. For “noisy” data sets, studies with large sample sizes and independent validation sets will be critical to developing clinically useful tests.

Three benchmark ‘omics datasets with different characteristic were used for comparative study. Our empirical comparison of the feature selection methods demonstrated that none of the classifiers uniformly performed best for all data sets. Random forest tended to perform well for all data sets but did not yield the highest accuracy in all cases. Results for SVM were more variable and suggested its performance was quite sensitive to the tuning parameters. Its poor performances in some of our applications could potentially be improved with more extensive investigations into the best tuning parameters. The voting classifier performed comparably to these two methods and was particularly effective when applied to the leukemia and lung cancer data sets that had genes with strong signals. Thus, voting classifiers in combination with a robust feature selection method such as our jackknife procedure offer a simple and intuitive approach to feature selection and classification with a clear extension to clinical applications.