A Comparison of Methods for Data-Driven Cancer Outlier Discovery, and An Application Scheme to Semisupervised Predictive Biomarker Discovery

Abstract

A core component in translational cancer research is biomarker discovery using gene expression profiling for clinical tumors. This is often based on cell line experiments; one population is sampled for inference in another. We disclose a semisupervised workflow focusing on binary (switch-like, bimodal) informative genes that are likely cancer relevant, to mitigate this non-statistical problem. Outlier detection is a key enabling technology of the workflow, and aids in identifying the focus genes.

We compare outlier detection techniques MOST, LSOSS, COPA, ORT, OS, and t-test, using a publicly available NSCLC dataset. Removing genes with Gaussian distribution is computationally efficient and matches MOST particularly well, while also COPA and OS pick prognostically relevant genes in their top ranks. Also our stability assessment is in favour of both MOST and COPA; the latter does not pair well with prefiltering for non-Gaussianity, but can handle data sets lacking non-cancer cases.

We provide R code for replicating our approach or extending it.

Introduction

Despite the limitations of cancer cell lines, there is widespread and increasing interest in using cell lines in experimental models of anticancer drug sensitivity to predict human clinical tumor response on the basis of genetic or genomic variation. This poses numerous challenges for rigorous data analysis and relevant data interpretation.¹ These challenges are especially severe for novel agents in clinical development, where predictions are made, and potentially used, before any clinical response data is available.

Genes whose expression shows bimodality across multiple cancer data sets (this usually only happens within one tissue type or histology) have a strong potential to provide useful translatable biomarkers for predictive applications in diagnostics, prognostics, or predicted response to therapy. The bimodality provides a natural quantization, so that thresholding is obvious without generating a new training data set for each assay of interest, easing clinical assay or kit development as well as the use of additional (external, public domain) data sets. Further, the cancer relevance of such genes can stem from the on/off events—mutation, deletion or hypermethylation—that are commonly acknowledged as determinants of the molecular subtype. This has motivated assigning the name ‘Cancer Outlier Profile Analysis’ to the COPA algorithm² that we include in this study.

The usefulness and cancer (or more generally disease) importance of bimodality has been recognized in prior work, in particular by Ertel³ but also by others.^4,5 Shiraishi⁵ discusses other causes in addition to mutation, deletion or hypermethylation for such switch-like behavior between alternative steady states.

Semisupervised learning presumes that the background distribution of predictor variables is relevant to the supervised learning task at hand, since the unlabeled data can only inform us about the background distribution. Using bimodality as an indicator of cancer relevance matches this premise of semisupervised learning. Explicitly, detecting bimodality in tumor gene expression profiles suggests a gene is a prime candidate for predictive models in cell lines, for which we have the targeted output—the labels, such as resistance or sensitivity to a drug—determined experimentally. Not detecting bimodality in tumors suggests the gene has no relevance to cancer subtyping, and a predictive model using it (from supervised learning with cell line data) will not translate to tumors well. These thoughts provide the basis of the semisupervised workflow we share in this manuscript. Note that the published semisupervised approach COXEN⁶ does not consider this premise of semisupervised learning, and does in no way pursue cancer relevance in feature selection.

In small in vitro drug response studies focusing on a single histology, which typically employ on the order of 20 cell lines, being able to use additional tumor data is crucial for the discovery of useful and tumor relevant results. Even if the predictor were intended for use in only cell lines, the small number of cases relative to number of available variables is a recognized problem, easily incurring ‘false positives’ in feature selection. However, it is now known that cell lines often carry ‘in vitro specific aberrations’ not present in tumors,⁷ and these need to be eliminated in the feature selection to discover clinically useful biomarkers. These ideas are easily reduced to practice, as our workflow will show, so that the unlabeled tumor expression data provides a filtering scheme relevant for feature selection.

Despite such potential for translational research, exploiting bimodal expression is more of a curiosity than a common routine—instead of making use of a few genes with switch-like behavior, published signatures typically comprise tens or hundreds of mutually correlated genes, and use these genes to compute a single score to which a threshold is applied (think of the typical heatmaps showing a 2 by 2 checkerboard pattern). Considering multiple mechanisms in a redundant system, we would rather expect the need of logical AND or OR operations between inputs that do not correlate with each other. For such approaches, the binary nature of bimodal expression patterns provides a significant but underutilized opportunity.

To bridge the gap between needs and potential, we provide a practical data-driven assessment of several alternative computational approaches to detect bimodal genes. For this we include various methods to detect ‘outlier expression’; these are widely acknowledged as cancer relevant, and bimodal genes will also be detected as outliers by the characterizations used in (deriving) these methods.

We specifically use lung cancer expression data published by Bhattacharjee,⁸ which include multiple histologies of NSCLC as well as normal (non-cancer, control) samples. With the notable exception of COPA the actual methods compared require the availability of normal cases, as they are based on having two pre-labeled categories of cases (ie, cancer and normal).

We introduce the use of a generic test for normality (Gaussianity) as a fast pre-filter, and examine its relation to rankings from the other—much slower to compute—methods. To our knowledge this use of normality testing has not been reported previously. We report timings indicative of the computational cost of each method, though these are specific to the implementations that we also share in additional files.

The test for normality (Gaussian bell shape) of the distribution does not require non-cancer cases, while the actual outlier detection methods mostly do. If only cancer cases are available, the published bimodality index⁴ can be used, or simply fitting mixtures of Gaussians with any available (typically EM) routine remains an option, potentially supplementing results from COPA. This option will definitely be quite slow to compute, and pre-filtering by a test for normality becomes all the more important. We have not included these parametric methods that are restricted to seeking only mixtures of two Gaussian shapes; such assumption is very restrictive, and in practice some potentially useful genes seem trimodal etc., possibly due to copy number variation. However, the readers will be able to build on our shared code and extend this work as desired.

For a method to be useful it should be internally consistent, and the choice between methods may depend on ease of use (hampered by non-obvious parameters the user must choose) and costs of computation, implementation, and maintenance. The quality of the results—a list of top ranked probesets or genes—is in our case much more difficult to quantify or even assess qualitatively.

The methods are here assessed for their stability, ie, how strongly their top ranks are perturbed by subsampling, and for mutual concordance. If adding some experiments (cases) dramatically alters the results from a method, the user should have little reliance on results from small experimental data sets. Here we equate the internal consistency of a method to its stability, and instead of adding experiments we subsample multiple times the pool of cancer cases available. The mutual concordance might reveal that a costly method can be replaced by a cheaper one, or that one method can replace several others. Indeed, we find that both of these scenarios happen here.

Our results indicate that MOST⁹ alone recovers the extreme top ranked probesets selected by the other methods, while in these data LSOSS¹⁰ is for all practical purposes identical to the t-test but much less efficient to compute, when only viewed as a gene/feature selector. LSOSS does provide a split of the cancer cases between normal-like and outliers, while a t-test between non-cancer and cancer cases does not.

For the quality of the top ranked genes, we look for biological significance. We avoid pathway analysis on purpose, and instead resort to the available survival times in these data; we assess the prognostic relevance of some top ranked genes as individual predictors of survival. Pathway analysis relies on sets of genes representing the same pathway, and our practical experience is that strong bimodality—such that could lead to a useful biomarker with very clearly distinct states—is rare enough to not provide such gene sets. Also, multiple results from pathway analysis are difficult to compare quantitatively, so it would not (in its current state) provide interpretable comparisons between the methods.

The results of this single case study overall suggest that a good performer is found by combining fairly strict pre-filtering which removes genes showing normal distribution in cancer cases, and then applying MOST. This appears to provide cancer relevant probesets/genes that may support biomarker discovery or, more generally, cancer subtyping that could be informative for prognostics or drug response.

For datasets without non-cancer cases, COPA also provides relatively stable and cancer relevant ranking of features, comparable to MOST. We are unable to place these two methods in a rank order of preference, but note that MOST appears to include in its top ranks the probesets selected by COPA; whether MOST adds to sensitivity or COPA gives better selectivity remains undecided. However, the good match with ‘abnormality’ gives MOST a computational cost advantage when non-cancer cases are available.

While these results do suggest some preferences between the methods, we believe many readers will find that access to R implementations of these routines in attached material is particularly useful, enabling application to other data sets and exploration of the results.

To complete the picture, we briefly discuss a workflow, without showing results from its application, for semisupervised discovery of robust predictive biomarkers. By “robust” we mean that the expression clusters are widely separated from each other, allowing inaccuracy and noise, and that translation from pre-clinical (often in vitro) data to tumor applications is at least corroborated as feasible. It is the translation step that will most easily fail without a semisupervised approach, because one then tries to perform inference on tumors by only sampling cell lines—no statistical theory supports such transfer between different populations. For this reason, a practical semisupervised approach with the tools to make it work is one goal of this manuscript, and we hope others will find our approach useful as we have found in proprietary work that cannot be shared at this time. The reader need not rely on our anecdotal testimony, as trying out the methods is fully accessible with very low effort.

Materials and Methods

The expression data set

The Bhattacharjee⁸ data set includes 139 adenocarcinomas and 17 normal lung samples, among other histologies (squamous, carcinoid, and small cell). We focus on adenocarcinomas along with the normal cases, to demonstrate the use of bimodal expression indicators for subtyping within histology.

The downloaded expression data was MAS5 normalized and log2—transformed. The U95-Av2 arrays initially provide expression values for 12,651 probesets, to which we applied a median-absolute deviation (MAD) filter to remove low-variance genes. Selecting probesets with MAD > 0.7, we retained 5900 probesets.

Pre-filtering to remove normally distributed probesets

To remove normally distributed probesets, we applied the Anderson-Darling normality test from the package nortest in R. The statistic and P-value were kept for future analysis.

Implementations of algorithms used

The algorithms have been implemented in R, using available R packages when possible and otherwise by coding based on the publications in the references. The implementations, versions, and parameters used are explicit in the attached material, which allows similar applications to other data sets in a straightforward manner.

Stability analysis

The stability of a method is here assessed through changes in its results during subsampling.

We create a fixed set of 1,000 subsets of the cancer cases, while using all of the control cases (non-cancer normals) in each computation. Each subset comprises 80% of the cancer cases, and subsequently the statistics from all of the methods described earlier in this paper are computed. For each method the results from each computation are ranked, so that the most significant statistic gets rank 1. These ranks are averaged over the 1,000 samples, to generate a single average ranking of probesets for each method. Similarly for each method, the variance of the ranks of a single probeset is an indication of the stability of its rank across the 1,000 samples.

We expect the variance of the rank to depend on the average rank, and indeed a scatter plot on logarithmic scales of these variables gives a practically linear result for each of the methods. A less stable method will show a higher variance than a more stable method, at the same average rank.

Methods comparison for replaceability

The purpose of methods comparison is to show if some methods provide very similar average ranks for the top probesets, and also to potentially find some orderings between methods if possible. The analysis is exploratory in nature and done by visual assessment of plots of the average ranks. The workflow of this methods comparison is shown in the attached files as Supplementary Figure S1.

To compare such plots between different methods, each of which has its own top ranked probesets, we take top 100 probesets by average rank for each method, and the union across the methods. In this way the top ranked probesets for each method are included, and we can compare the average ranks between methods in scatter plots without any bias toward some ‘baseline method’.

Survival analysis

Kaplan Meier curves were plotted using the Survival Package in R. Logrank test P-values were computed between the cancer cases in the low expression and the high expression groups—one of these is designated normal-like and the other ‘outliers’. The distinction of these two groups was made based on the MOST algorithm which provides, for each probeset, the number of cases in the normal-like expression group (k-value in the attached code).

Results

Stability inspections

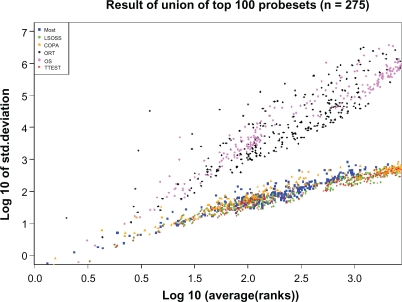
The stability of the methods is compared graphically in Figure 1. The top 100 probesets are included for each method, and log10 of the standard deviation is plotted against log10 of the average rank. ORT¹¹ and OS¹² consistently show a higher variance than the rest of the methods, so the other methods are preferred if stability is emphasized due to a small number of cases. Note that for some top ranked probesets, around average rank 10, ORT shows exceptionally high variances of the rank—this method appears, in this sense, worse performing than OS in these data.

Figure 1.

Stability of methods. At any given average rank, ORT and OS methods have similar variance of the probeset’s ranks across subsamples. The remaining methods cluster together at a lower variance, showing better stability across the subsamples.

Due to the population of subsamples being held constant, the different methods are fairly compared—superiority or inferiority does not stem from different subsamples between methods. Also, with 1,000 random subsamples, the numerical estimates of average rank and variance are not an artifact of the selection of subsamples. The consistent linear trends in Figure 1 corroborate that our analysis approach produces reasonable and consistent results.

The nearly linear relation in a log-log plot of variance to average rank suggests a power law dependence of variance on rank. The methods with a steeper slope have a higher exponent in the power law. Such an approximation of the variance could be useful for someone interested in deriving statistical confidence bounds or such by semi-analytic methods.

Correlations between different algorithms

The matrix of scatterplots in Figure 2 allows exploring the similarities and differences of the methods by visual exploration of the union of top 100 from each method.

Figure 2.

Pairs plot. The matrix of scatter plots illustrates dependencies between the different outlier measures. The scales of average ranks are again logarithmic, giving more relative emphasis to the top ranks. LSOSS is practically equivalent to t-test, providing for the top ranks exactly the same rank order. Note that a top rank from COPA implies a good rank also from MOST; the same goes for OS and t-test also, so MOST consolidates the sensitivity of several other methods.

The LSOSS and TTEST methods are almost identical; LSOSS is a variation of the t-test. Both COPA and OS methods appear to be strongly negatively correlated to the t-test (TTEST); COPA and OS seek outliers that subdivide the cancer cases to normal-like and normal-unlike, while t-test gives highest scores when all the cancer cases separate well from the non-cancer control cases. However, also t-test can rank highly some probesets that are useful for cancer vs. cancer subtyping, according to our practical analysis experience.

Interestingly, MOST appears to incorporate the sensitivities of the other outlier detection methods including also the t-test based methods. In other words, when any other method ranks a probeset among, say, the top 10, then the probeset is highly ranked also by MOST. Graphically, in the top row of Figure 2, points close to left edge are also close to the bottom of the scatterplots—the top left-hand-side corners are empty. Only the row with ORT—which was less stable—also shows empty top LHS corners, but it appears noisy in the correlations for the top ranked probesets.

Anderson-Darling normality filtering

This is a rather unusual prefiltering—we know of no prior report on removing normally distributed variables by pre-filtering—but here well motivated. Probesets showing an expression pattern with two or more peaks cannot possibly be well fit with a single normal distribution, therefore removing the cases with a good fit does no harm on seeking bimodals (with no requirement of mixing two Gaussians imposed). This provides the opportunity, while the motivation comes from the computational expense of several of the methods we compare, discussed in more detail later. As there is wide interest in the normality of a distribution of, say, the error residuals in statistical model fitting, we correctly expected that the available tests for Gaussian distribution would be well-developed and fast to compute. Particularly costly pre-filtering would make little sense.

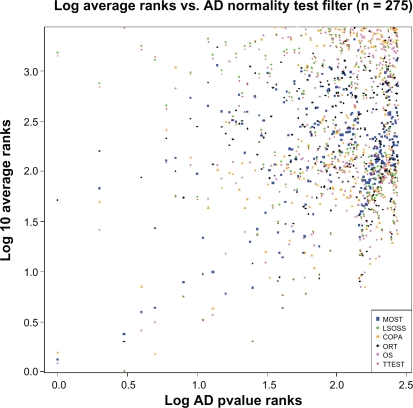
In Figure 3 the blue squares for MOST are bound below by a straight line, such that approximately x = y + 0.5 on the logarithmic scales shown. This means that if we want Y top probesets from MOST, we can pre-filter to keep only about 3*Y probesets with the fast AD normality score. Such a rule likely depends on the dataset, but the observation is encouraging and suggests that, for example, with some other given dataset, keeping only the top 500 probesets based on AD scores does little harm to finding the top about 150 probesets for MOST—and the most interesting top 20 are probably all retained. The effect on computational cost is significant, making fairly large problems feasible on a conventional laptop.

Figure 3.

Relation of outlier ranking to ranking of Gaussianity. The Anderson-Darling method provided a ranking of probesets, with the top ranks assigned to those whose expression distribution across cancer cases is least Gaussian. The ‘abnormally distributed’ probesets are to the left on the plot. For each of the outlier detection methods, the average rank is plotted on the vertical logarithmic scale. For example, the blue squares for MOST indicate that if we want average ranks up to 10 (1.0 on vertical scale), we can require AD rank better than 10^∧1.5 = 32 on the horizontal scale. This suggests that fairly strict filtering with the fast to compute AD scores can be used to speed up MOST computations.

The other methods do not allow as strict pre-filtering by AD scores—the lower bounding straight lines for these methods have lower slopes than the line for MOST. Therefore MOST seems to match prefiltering by AD normality score particularly well, possibly enabling very efficient computations for this general type of problems.

We have consciously avoided comparisons based on simulated datasets, whose clear advantage is that ‘everything is known’ about them, while they may be completely unrealistic. However, for the computation times we choose to use such data, and the code for generating it is included in case a reader wishes to pursue further comparisons with similar datasets.

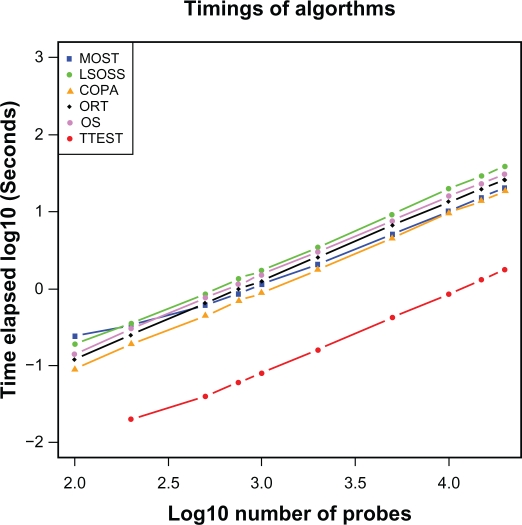
An artificial dataset of mixed Gaussian distributions was computationally generated to simulate 40 samples (20 normals, 20 cancer cases) and used to determine average computation times on a Windows Intel Notebook Machine with 2GB of RAM. The overall trends in Figure 4 show that the computation time versus number of probesets increases linearly. In general, these computations are fairly quick and can be conducted on a notebook. The largest Affymetrix mRNA platform (U133plus2) has about 55,000 probesets and at most 35,000 probesets remain after some mild conventional pre-filtering based on our experience. We estimate that the outlier computations should then take less than 1 minute on a Windows Machine. However with a larger number of cases, such as in the dataset by Bhattacharjee, both the memory and speed limitations will encourage the use of parallel processing.

Figure 4.

Computational costs. CPU times for computation across 20 cancer cases and 20 controls on a conventional business laptop of vintage 2009. Straight lines with slope 1 on the logarithmic plot show expected linear scaling with the number of probesets. T-test is roughly an order of magnitude faster than the other tests.

Survival analysis

The ultimate goal of selecting bimodal—or more generally outlier—genes is to find useful candidate biomarkers that are cancer relevant. We perform a data-driven evaluation, using the survival data provided by Bhattacharjee.

We collected the top 6 probesets identified by each method, to a total of 19 probesets. Only 3 of these meet the following criteria based on survival analysis: i) There are more than 2 samples in each arm of the Kaplan Meier plots ii) The Logrank P-value < 0.1 ensuring statistical significance.

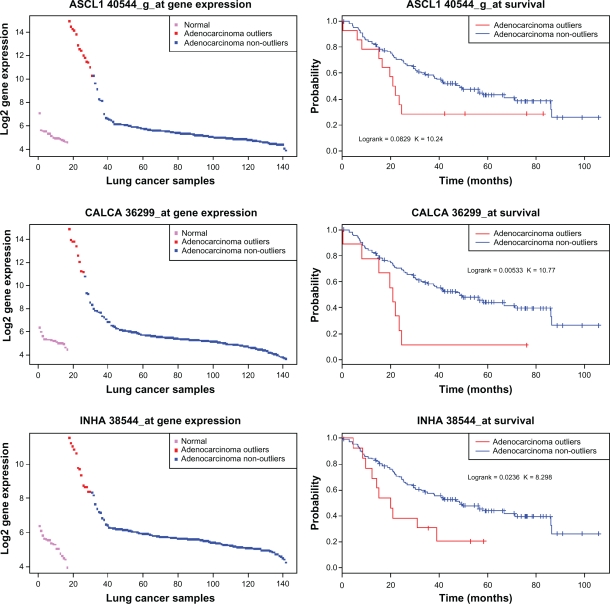
The Kaplan-Meier plots for these three probesets are shown in Figure 5. Note that the survival analysis used is somewhat naïve and basic, only assessing individual probesets and not their combinations. The results from this analysis do not allow quantitative comparison of the methods, but indicate relevance to cancer subtyping based on the top genes/probesets recovered.

Figure 5.

Top three markers for cancer subtyping having significance to survival. These three marker candidates satisfied a our survival significance criteria, while the other candidates collected from the top 6 of each method did not. For each of these, the normal-like cases have significantly better survival than the ‘outlier’ cases that differ from normals by expression.

ASCL1 and CALCA were identified in the top 6 genes as ranked by both MOST and COPA, while these genes and also INHA were identified among the top 6 by OS. Interestingly, the gene INHA was among the top 20 from both MOST and COPA.

ORT, LSOSS and TTEST had none of the above mentioned genes in the top 6—they were ranked many orders lower. So a simplistic survival analysis corroborates the cancer relevance of MOST, COPA and OS over the other methods tested, in these particular data.

The identified genes have strong survival significance by log rank test, and play important roles in cancer. ASCL1 is a pivotal member of the NOTCH pathway with known¹³ clinical relevance in prostate cancer. High expression of the gene inhibits the NOTCH signaling formation, allowing tumors to rapidly develop and progressively advance the disease.¹⁴ Similarly,¹⁵ high expression of Calcitonin-alpha (CALCA) results in high Ca²⁺ serum levels or hypercalcaemia, a condition which is strongly associated with tumor malignancy and poor 1-year survival rates of 10%–30%. Elevated levels of Inhibin drive prostate tumors into a pro-tumorigenic and pro-metastatic state¹⁶ and it is also a well-known marker¹⁷ for granulosa-cell tumors.

These three genes received average ranks of order 10^∧3 by LSOSS and TTEST (see Table 1), suggesting that these methods are possibly suitable for finding diagnostic markers of cancer, but not necessarily for finding markers to discover subtypes of cancer cases.

Table 1.

List of top 6 probesets from MOST and their average log ranks for all of the methods tested.

	MOST	LSOSS	COPA	ORT	OS	TTEST	genes	genenames
40544_g_at	0.119	3.181	0.192	1.711	0.087	3.147	ASCL1	achaete-scute complex homolog 1 (Drosophila)
37741_at	0.372	0.005	3.614	0.301	3.428	0.005	PYCR1	pyrroline-5-carboxylate reductase 1
36299_at	0.593	3.246	0.848	1.939	0.409	3.213	CALCA	calcitonin-related polypeptide alpha
37019_at	0.639	3.107	0.178	1.434	0.491	3.141	FGB	fibrinogen beta chain
39052_at	0.777	3.286	2.490	2.376	1.177	3.258	KRT14	keratin 14
34342_s_at	0.837	0.300	3.553	1.082	3.657	0.300	SPP1	secreted phosphoprotein 1

A semisupervised workflow for discovering robust translatable biomarkers

In the semisupervised setting for predicting clinical response we typically have labeled cell line data, with the label indicating eg, sensitivity or resistance, and basal (pre-treatment) mRNA expression values for these cell lines that we hope can predict the response to treatment. Unlabeled data is provided by basal expression values for clinical tumor samples, for which we usually have no information about sensitivity or resistance to the experimental drug under study (though survival under standard of care may be known). Our goal is to use both datasets to learn basal expression based predictors of sensitivity. The following steps seem to provide, at least on occasion, plausible candidate markers and predictors; although all of our results from this approach currently lack published clinical validation and are proprietary in nature.

The approach though has been published as a poster in Frontiers in Cancer Science, Singapore 2010, with a more detailed discussion than space allows here. Here we wish to share our approach, which strongly depends on the bimodality of biomarkers; it provides a natural application to outlier detection methods.

• 1.Use supervised training to select individually informative genes that allow robust thresholding, ie, slack in threshold location. The slack is calculated under constraining sensitivity and specificity limits. Most probesets do not satisfy these constraints at all, the remaining ones are ranked by the slack and a short ‘top ranked’ list is retained. A suitable Java software tool has been published,¹⁸ and we recommend requiring (sensitivity, selectivity) = (0.9, 0.4) and repeating the calculation with (0.4, 0.9). The two lists are joined, and the ‘margin’ from the Java program is typically required to exceed 1 or 2 in log2—transformed expression scale. Note that in particular bimodal genes allow moving the threshold between the two clusters, with little effect on the split of cases—the sensitivity and selectivity are then almost constant, so such genes/probesets will allow a large ‘margin’ and are picked by Pinese’s approach¹⁸ if they are informative.
• 2.Use an unsupervised check to refine this short list, picking genes that also in tumors show easy/robust thresholding (ie, cluster based quantization, or bimodal expression without any requirement for Gaussian shapes). This retains only genes relevant to the molecular subtyping of tumors, eliminating in vitro -specific aberrations.⁷ Now, predictors that take as inputs quantized (binary) values, learned from the labeled data, can be applied to the unlabeled data since similar quantization is enabled there.

The unlabeled data has contributed to feature selection, and if we had a list of its bimodal genes, we could only use these probesets in the supervised feature selection of step 1 and skip step 2. In our early applications, the short list from supervised feature selection was manually checked for bimodality in the unlabeled tumor data—often in multiple datasets.

• 3.Create predictor(s) from the labeled data using the binarized input features selected above.
• 4.Apply predictor(s) to unlabeled data, whether the same as used above or different, based on expression quantization from cluster patterns of expression. The cluster pattern for each gene should translate to a low/high binary value that is used as input to the predictor. Each application of a predictor gives an estimate of eg, responder prevalence.

Our approach nurtures the clinical tumor relevance of the biomarker candidates, ensures that in vitro specific aberrations are not used as predictors, and that prevalence estimates can be computed from available tumor data to assess the clinical need for biomarkers and predictors. Further, it leads to small predictors with few inputs that may use logical AND and OR operations with binarized (Boolean) inputs, and that facilitate use of other types of assays with the natural thresholding of expression patterns.

This approach addresses in a simple and doable way a problem that is not covered by statistics: sampling one population (cell lines) to perform inference in a different population (tumors), by making use of tumor relevant data before predictors are constructed. We suggest that on doing this type of inference with semisupervised tools, one should avoid giving confidence P-values with predictions, as they would suggest that the problem conforms to the requirements of statistical theory.

This brief discussion of semisupervised methodology serves as a significant motivation for the pursuit of outlier or bimodality analyses, and clearly links these tools to personalized medicine and translational oncology.

Conclusions

We have provided a reproducible comparison of a set of methods available for detecting outliers, including bimodal genes, with attached code that allows re-use also in other contexts. A single NSCLC data set which includes some non-cancer cases was used in the data-driven assessment.

The importance of this study may be less in the results, and more in supporting a wider use of bimodal genes in biomarker applications by sharing code, assessment methods, and a semisupervised workflow. Bimodality is an indication of cancer relevance, it provides natural thresholding and binarization that is robust against normalization and scaling effects, and can even carry over between different types of assay in a very convenient way.

As for the results, the timing and other results clearly indicate that pre-filtering with a score to remove probesets with (near) Gaussian expression distribution is numerically efficient and couples especially well with the MOST method for outlier detection. As MOST is also sensitive to top ranked genes by the other methods tested, it appears a useful overall performer. While our results from use of a single dataset can only be indicative, we consider such indications much more proper than those from simulated data. A typical flaw in such simulations is a ‘forced’ shape of distributions, eg, only creating mixtures of Gaussians—real expression data does not conform to such restrictions.

The stability results also favor MOST, positioned in the more stable cluster across all of the methods, while computational cost of MOST is on par with other outlier detection methods. We have also shown that a few of the top ranked probesets from MOST, in these data, include prognostically significant and therefore cancer relevant probesets. We have not evaluated the biological significance of the rankings by any other means.

Partly due to the fortunate interplay with filtering based on Gaussianity of the expression distribution across cancer cases, as well as the other observations above, our recommendation is to use MOST in combination with pre-filtering by the Anderson-Darling normality test, especially if speed of execution is essential. However, if time and other resources allow, the application of also other outlier detection methods will probably provide more comprehensive results—the other methods appear not compatible with strict pre-filtering by the normality test.

Aside from COPA, this comparison has not covered outlier detection or bimodality scoring methods that can be used with only cancer cases—the other methods we have covered require access to a set of non-cancer cases of the same tissue type. The current study could also be extended to cover more datasets, but we feel it serves its purpose by sharing a set of tools and instructing in their use.

Despite its simplicity and comparatively low computational cost on par with MOST (not taking into account prefiltering options), COPA is a good performer; it is comparatively stable and ranked highly the genes with prognostic value that we found among top ranks from any of the methods. Our assessment of survival also corroborated OS among the top performers to pick prognostic genes.

We included a simple but little known semisupervised approach that may be original and novel (aside from our prior publication as a poster) for predictive biomarker discovery from combined cell line and tumor expression data, with the labels (eg, resistant or sensitive) known only for cell lines. With our approach, relevance to tumors is favored and clinical assay development is facilitated by bimodal naturally thresholded expression patterns. This approach highlights the practical importance in translational oncology research of tools for detection of outliers and especially bimodality, and addresses the problem of sampling cell lines while doing inference in tumors; a type of problem outside the realm of statistical theories.

Supplementary Data

Figure S1

Workflow of methods comparison and stability analysis for expression outliers and bimodality.