Loss of Intrinsic Organization of Cerebellar Networks in Spinocerebellar Ataxia Type 1: Correlates with Disease Severity and Duration

Abstract

The spinocerebellar ataxias (SCAs) are a genetically heterogeneous group of cerebellar degenerative disorders, characterized by progressive gait unsteadiness, hand incoordination, and dysarthria. The mutational mechanism in SCA1, a dominantly inherited form of SCA, consists of an expanded trinucleotide CAG repeat. In SCA1, there is loss of Purkinje cells, neuronal loss in dentate nucleus, olives, and pontine nuclei. In the present study, we sought to apply intrinsic functional connectivity analysis combined with diffusion tensor imaging to define the state of cerebellar connectivity in SCA1. Our results on the intrinsic functional connectivity in lateral cerebellum and thalamus showed progressive organizational changes in SCA1 noted as a progressive increase in the absolute value of the correlation coefficients. In the lateral cerebellum, the anatomical organization of functional clusters seen as parasagittal bands in controls is lost, changing to a patchy appearance in SCA1. Lastly, only fractional anisotropy in the superior peduncle and changes in functional organization in thalamus showed a linear dependence to duration and severity of disease. The present pilot work represents an initial effort describing connectivity biomarkers of disease progression in SCA1. The functional changes detected with intrinsic functional analysis and diffusion tensor imaging suggest that disease progression can be analyzed as a disconnection syndrome.

Introduction

The spinocerebellar ataxias (SCAs) are a genetically heterogeneous group of cerebellar degenerative disorders, characterized by progressive gait unsteadiness, hand incoordination, and dysarthria due to degeneration of the cerebellum or its connections [1–4]. The pathological changes in the SCAs consist of degeneration of cerebellar Purkinje cells and, depending on the SCA type, of several other brainstem or deep brain nuclei. In particular, SCA1 has been described as a form of olivopontocerebellar atrophy [5–7].

Since the initial discovery in 1993 of the genetic cause of SCA1 [8], there has been an explosion of research progress elucidating the genetics and molecular basis of numerous genetic forms of SCA. However, while genetic advances have served as the staging platform for preclinical studies to develop therapy, they have radically outstripped our progress toward establishment of useful outcome measures to gauge the success of experimental therapies. A rating scale to estimate function in ataxia has recently been validated and shown to be sensitive to change, although, due to the slow rate of disease progression and large variance, its usefulness is limited to long studies and large sample sizes [9–11].

Comparable limitations in the study of other neurodegenerative diseases have inspired efforts to discover and validate structural, functional, or neurochemical biomarkers that are specific for the type or sensitive to stage of different neurodegenerative diseases [12]. Therefore, the identification and validation of surrogate measures of disease severity in SCA may enhance our ability to reproducibly gauge disease progression and facilitate the design of more efficient therapeutic trials.

In the present study, we hypothesize that graded changes in specific pathways and their associated brain regions may contain the key for a better characterization of the progression of illness in SCA1 [13]. To test this, we sought to apply functional MRI and diffusion tensor imaging to define the state of cerebellar connectivity. We then sought to test whether there are changes in connectivity in the SCA1 ataxia and whether the degree of these changes correlates with severity of ataxia.

Because of the complexity of cerebellar connectivity, it is not known which pathological changes can be used as biomarkers of disease progression and severity. With this study, we intend to provide some insight in two outstanding points: (a) Is there a specific cerebellar pathway linearly associated with disease progression in SCA1? (b) Is there a characteristic sequence and temporal progression of the pathological changes in regional involvement within cerebellum and elsewhere?

Methods

Six research volunteers were recruited from The University of Chicago Ataxia Center. In addition, eight control age-matched subjects were recruited from the local community. Individuals with preexisting severe psychiatric or other neurological illnesses were excluded. The diagnosis of SCA1 was established by genetic testing at a commercial gene testing laboratory according to standard methods (Athena Diagnostics, Wooster, MA, USA). The clinical disease severity was estimated by means of an internationally validated ataxia rating scale (SARAII) performed the same day of the imaging study by a single examiner (CMG) [14]. The age of onset of the five affected patients ranged from 32 to 59 years (mean = 43.2) and disease duration from 2 to 13 years (mean = 8.0). The SARA rating scale scores ranged from 7.5 to 13.0 (mean = 10.8). In addition, one subject, age 33, bore a pathological repeat expansion but was presymptomatic (SARA = 0). The demographics for all SCA1 subjects are listed in Table 1.

Table 1.

Demographic information for the SCA1 cohort included in the present results

Patient #	Age	Age at onset	Repeats	SARA
002a	43	34	32, 46	7.5
005	43	30	31, 46	9.0
008a	32	30	30, 52	13.0
009	33	–	35, 46	0.0
010a	59	49	31, 40	12.0
017	39	33	35, 46	12.5

^aThe cases shown in the result figures

This study and all procedures for recruitment and consent were approved by the Institutional Review Board of the University of Chicago.

Imaging

Scanning of subjects was performed on a clinical 3-T GE Signa MRI scanner (Waukesha, WI, USA) equipped with high-speed gradients.

The following sequences were used:

1. High-resolution anatomical images were acquired with a three-dimensional magnetization prepared rapid gradient echo (MPRAGE) sequence that used the following parameters: echo time (TE) = 3.2 ms, repetition time (TR) = 8 ms, preparation time = 725 ms, flip angle 6°, and field of view 24 cm for a resolution of 0.9375 × 0.9375 × 1.5 mm.

2. Diffusion tensor imaging (Turboprop-DTI): TR = 3,500 ms, eight spin echoes per TR (ETL = 8), and 5 k-space lines per spin echo (turbo-factor = 5); thus, each blade contained 8 × 5 = 40 lines, 16 k-space blades per image, field of view = 24 × 24 cm, 25 contiguous horizontal slices, and 2 × 2 × 3 mm voxel size. All images were reconstructed to a 256 × 256 matrix. DW images with b = 900 s/mm² were acquired for a set of 12 diffusion directions. Two b = 0 s/mm² images were acquired.

3. Proton density (PD) fast spin-echo sequence with two echo times. This provided PD and T₂-weighted images in the same slice locations as the Turboprop-DTI: TE₁ = 20 ms, TE₂ = 117 ms, TR = 7,000 ms, ETL = 16, field of view = 24 cm × 24 cm, 25 contiguous horizontal slices, 3 mm slice thickness, and 192 × 256 image matrix reconstructed to 256 × 256.

4. Functional imaging acquisition at rest used the spiral k-space method [15]. Thirty contiguous 5-mm axial slices were obtained starting from the vertex through the bottom of the cerebellum. A gradient echo spiral scan pulse sequence used a single spiral to provide 1.875 × 1.875 × 5-mm resolution over a 24-cm field of view. T₂*-weighted imaging was accomplished with a gradient TE of 25 ms and a TR of 2,000 ms with a flip angle of 80°.

Primary Analysis

Data analysis began with three-dimensional motion correction using weighted least squares alignment of three translational and three rotational parameters and a rigid-body three-dimensional registration of images to align the functional and anatomical datasets. The alignment parameters were computed by an iterative weighted least squares fit to a reference volume [16]. All images were spatially registered in three dimensions to a reference acquisition from the first fMRI run using the AFNI function 3dvolreg.

DTI

The diffusion tensors D, eigenvalues (λ₁, λ₂, λ₃), and eigenvectors (ε₁, ε₂, ε₃) of the tensors were estimated for all DTI acquisitions using our own script in C and the AFNI function 3dDWIto DT (images to tensor). From the eigenvalues of D, we estimated fractional anisotropy, which characterizes the anisotropy of diffusion in the tissue.

Functional Imaging

Preprocessing

Time series were bandpass filtered (0.01<f<0.08 Hz) and despiked with the respective AFNI functions 3dFourier and 3dDespike. Neither spatial nor temporal smoothing of data was performed.

In addition, time series were normalized (mean = 0) using the following algorithm:

$$X_{i,j}=X_{i,j}-\frac{1}{N}\times {\displaystyle \sum _{k=1}^N{X}_{k,j}}$$ (1)

where X_i,j is the jth time sample of the ith voxel.

Finally, the first three time points on the time series were discarded to avoid scanner instability.

Secondary Analysis

Multi-subject analysis was performed using an anatomical region-of-interest (ROI) approach, based on brain regions identified a priori on the basis of known functional anatomy of the cerebellar system (Fig. 1).

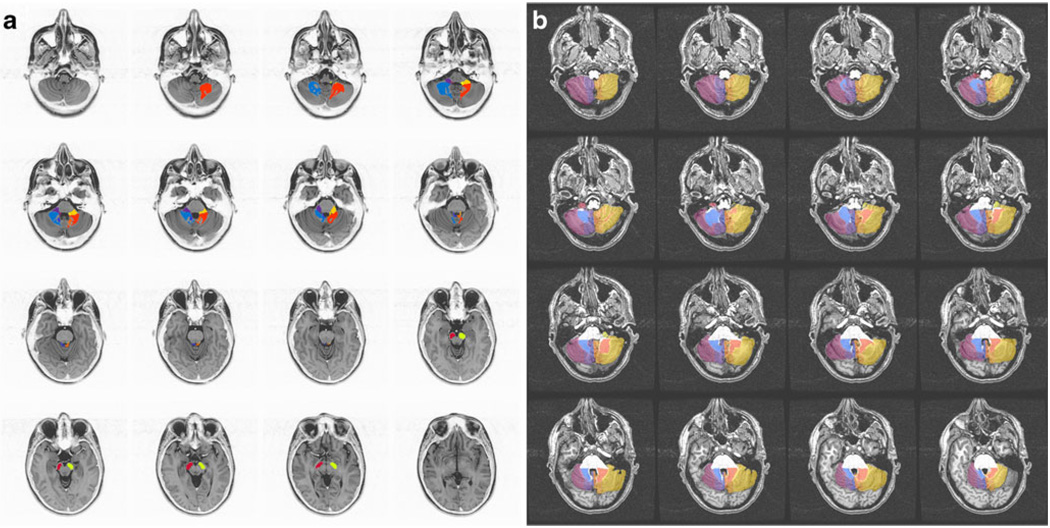
Fig. 1.

Horizontal sections depicting the location of the ROIs. a White matter ROIs drawn by hand in the original PD T2 files. The location of the dentate nucleus can be appreciated within the cerebellar white matter by the lack of a mask. Contrast on the PD images has been inverted to facilitate visualization of anatomy. b Subparcellation scheme of the cerebellar cortex [21] as done in the MPRAGE T1-weighted images. In each case, the different regions are color-coded. Note that structures in the right and the left sides of the brain were assessed independently

Pathways were manually outlined in the PD images and then used as masks on the DTI images for quantification of fractional anisotropy (FA) values. Gray matter regions were drawn in the MPRAGE images for determination of intrinsic functional connectivity in the functional data at rest. The white matter masks were resampled to fit the resolution of the DTI images, and the gray matter masks were resampled to the blood oxygen level-dependent resolution using the AFNI function 3dresample (using nearest neighbor interpolation). The brain areas included the following: white matter regions: (a) intracerebellar white matter; (b) superior, medial, and inferior cerebellar peduncles; and (c) the corticospinal pathway [17]; cerebellar peduncles were traced at the level of the fourth ventricle and within cerebellum. The medial cerebellar peduncle was drawn laterally to the hemispheres of lobules VI–VIII adjacent to the lateral border of the dentate nucleus. The inferior cerebellar peduncle was marked ventral to the superior cerebellar peduncle between the lateral wall of the fourth ventricle and the middle cerebellar peduncle. The superior cerebellar peduncle was found in the hilus of the dentate nucleus running in the dorsal aspect of the fourth ventricle toward the colliculi. The corticospinal pathway was marked at the cerebral peduncles in the midbrain, limited posteriorly by the substantia nigra [18]. The gray matter regions studied consisted of (d) the cerebellum, (e) red nuclei, (f) ventral medulla (olivary complex), (g) thalamus, and (h) globus pallidus–putamen. For the cerebellum, the anatomical parcellation was done based on connectivity patterns [19]: vermis (limited laterally by the paravermian sulcus [20]), paravermal region (located between the lateral paravermal fissure and a vertical imaginary line at the level of the lateral border of the intraculminate fissure [21]), lateral cerebellum¹ (limited medially by the same imaginary vertical line of the intraculminate fissure), flocculus–nodulus (limited by the posterolateral fissure), and dentate nucleus (defined in the DTI images since the resolution of the structural images did not have sufficient resolution). Because pontine nuclei are small and embedded within white matter fibers, our method for tertiary analysis could not be implemented.

The generation of DTI maps and functional connectivity measures as well as the generation of ROIs were performed blind to the clinical status of the subjects when possible.

Tertiary Analysis

Since the seminal report by Raichle et al. on functional connectivity at rest [22], numerous studies describing a variety of networks have followed (for review, see [23]). These studies have focused on the temporal coherence of signals among different brain regions under different conditions. Following their lead, our approach determines functional connectivity at rest. However, in contrast to previous studies [24–28], we determined the functional connectivity within brain regions. This approach allowed us to assess aspects of intrinsic organization. In order to facilitate the process, we built a software visualization package (Functional Holography Analysis). This analysis, developed from a previously reported approach applied to EEG signals [29, 30] and networks in culture [31], helped not only to reveal functional clusters within brain regions but also to determine their anatomical distribution. Details of the software can be accessed at http://sites.google.com/site/funcholoappl/. Taking preprocessed times series from individual voxels within each ROI (primary and secondary analyses), the functional holography analysis includes the following steps:

1. Calculation of the symmetric Pearson correlation matrix S in which the element on the ith row and jth column reflects the linear correlation between the recorded time series of ith and jth voxels [32]. The formula used was:

   $$S_{i,j}=\frac{{\displaystyle {\sum }_{k=1}^T(X_{i,k}-{\mu }_i)(X_{j,k}-{\mu }_j)}}{\sqrt{{\displaystyle {\sum }_{k=1}^T{(X_{i,k}-{\mu }_i)}^2}{\displaystyle {\sum }_{k=1}^T{(X_{j,k}-{\mu }_j)}^2}}}$$ (2)

   where X_i and X_j are the time series of voxels i and j, respectively, with the corresponding means:

   $${\mu }_i=\frac{1}{N}{\displaystyle \sum _{k=1}^T{X}_{i,k}\text{ and }{\mu }_j=\frac{1}{N}{\displaystyle \sum _{k=1}^T{X}_{j,k}}}$$ (3)

   and sample unbiased standard deviations:

   $$\begin{array}{c}{\sigma }_i={\left(\frac{1}{N}{\displaystyle \sum _{k=1}^T{(X_{i,k}-{\mu }_i)}^2}\right)}^{1/2}\text{and}\hfill \\ {\sigma }_i={\left(\frac{1}{N}{\displaystyle \sum _{k=1}^T{(X_{j,k}-{\mu }_j)}^2}\right)}^{1/2}\hfill \end{array}$$ (4)

   This matrix is then linearly shifted from the interval [−1,+1] into the [0,1] interval:

   $$C_{i,j}=0.5\times (S_{i,j}+1)$$ (5)

   Frequency histograms depicting the distribution of the normalized correlation coefficients are presented in the “Results” section.

2. Clustering algorithms are usually based on the implicit notion that the row/column vectors of the correlation matrices span a high-dimension “correlations space”—N-dimensional space for a network composed of N voxels. We implemented the matrix clustering using the K-means algorithm [33] which is based on an iterative process where the number of clusters has to be defined in advance as an input to the algorithm. After the algorithm is applied on the matrix, each voxel is attributed to a single correlation cluster. The correlation clusters are then color-coded as the voxels of each cluster are assigned with a unique color that can be visualized on different display domains described below.

3. We also performed Fourier transform using the FFT algorithm over the normalized data:

   $$W_{i,j}={\displaystyle \sum _{k=1}^T{X}_{i,k}^{\prime }\times e^{((-2\pi \times i)(k-1)(j-1))/T}}$$ (6)

   The Fourier Transform was performed separately for each of the voxel’s time series while each row in W is related to one voxel. However, since the number of voxels is too large to be displayed, the average from rows of voxels from the same correlation cluster is displayed.
4. Collective affinity transformation which generates the output affinity matrix A from the input normalized correlation matrix C. The main objective of this step is to perform a collective normalization of the correlations coefficients. For this, we first calculated the Euclidian distance between the locations of the voxels in the N-dimensional correlation space defined by the normalized correlation matrix C. The distance between voxel i and voxel j is defined by:

   $$D_{\mathit{\text{ij}}}=\Vert {\overrightarrow{C}}_i-{\overrightarrow{C}}_j\Vert =\sqrt{{\displaystyle \sum _k^N{(C_{\mathit{\text{ik}}}-C_{\mathit{\text{jk}}})}^2}}$$ (7)

   The affinity matrix A is then calculated using the following method:

   $$A_{i,j}\{\begin{array}{cc}\frac{C_{i,j}}{D_{i,j}}\hfill & i\ne j\hfill \\ A_0\hfill & i=j\hfill \end{array}$$ (8)

   Note that when the correlations are defined to be the Pearson’s correlations C_i,i = 1 while the Euclidian distance D_i,i = 0, the result is that the diagonal elements in the affinity matrix A_i,i are ill-defined. In order to overcome this problem, we estimated the noise using the standard deviation, defining A₀ as:

   $$A_0=1/\mathit{\text{STD}}\left({\overrightarrow{C}}_i\right)$$ (9)

   where C_i is the ith column or row.

5. Dimension reduction of the correlation matrices employing the principal component analysis (PCA) algorithm [34] that enables the extraction of maximum relevant information embedded in the matrices into a reduced space. Reduction to three dimensions extracts most of the relevant information, similarly applied for EEG activity [29] and fMRI [35, 36]. Therefore, we present the voxel correlations in a three-dimensional PCA space, whose axes are the three leading principal vectors computed by the PCA algorithm. Each voxel is placed in this PCA space according to its three eigenvalues for the three leading principal vectors. The nodes are color-coded with the same color as the original correlation cluster where the voxel belongs. Hence, two voxels that have high normalized correlations will be placed in close vicinity in the PCA space.

6. In order to quantify the distribution of voxels in the functional manifold (i.e., how compact or scattered they distribute in this functional space), we performed a radius of gyration measurement [34] for each correlation cluster. The radius of gyration is calculated using the following algorithm:

   $$R_g=\sqrt{\frac{1}{2N^2}{\displaystyle \sum _{i,j}\mathit{\text{dist}}{(i,j)}^2}}$$ (10)

   where dist(i,j) is the Euclidean distance between nodes i and j in the functional manifold. These values where then normalized with the number of voxels contained in each cluster. This provided a “density index” as described in the “Results” section.

Statistical Analysis

Group Comparisons

To assess group differences of ROI volumes and FA, we performed a Shapiro–Wilk test to determine multivariate normality for each measure. A Box’s M test was used to assess whether all groups had similar covariance matrices, and if so, a parametric multivariate Hotelling T² test was used. Otherwise, the nonparametric Cramer test was applied.

Kurtosis measured the “peakedness” relative to a normal distribution of correlation coefficients resulting from the functional connectivity analysis. It was calculated as the centralized fourth moment divided by the squared variance minus 3.

In the case of the density index and kurtosis measures, we used the Wilcoxon rank sum test to assess weather data from the two groups had the same distribution. Finally, in order to assess possible confounds with partial tissue volumes, we calculated Pearson’s correlation within groups, between FA values and volumes of white matter ROIs.

Regression Analysis

In order to determine the existence of linear relationships between dependent MRI-derived variables (FA and kurtosis) and clinical independent variables for the SCA1 individuals, a stepwise regression (forward and backward) was conducted. The independent variables were the SARA score, duration of the disease (Age minus age at onset), and the CAG repeat expansion size. During each step, a variable is added (dropped) based on Akaike information criteria until the model cannot be improved anymore. All statistical evaluations were done using SPSS 13.0 for Windows and R 2.1.1 software.

Results

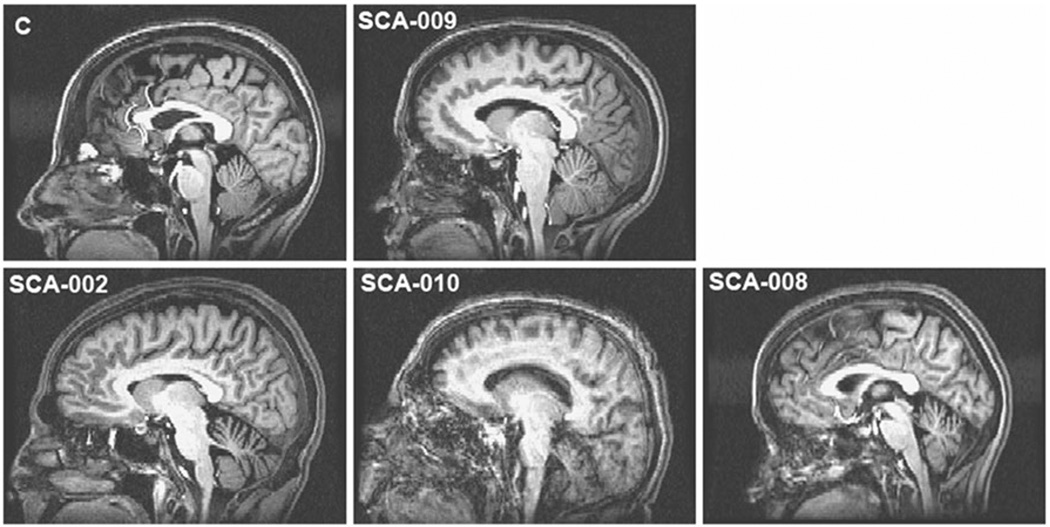
The SCA1 cohort included patients with different size CAG repeat expansions, different severity, and different duration of illness. The demographics for all SCA1 subjects are listed in Table 1. Likewise, the general degree of atrophy for selected SCA1 cases can be appreciated in the sagittal T₁-weighted images in Fig. 2.

Fig. 2.

Parasagittal sections depicting loss of cerebellar volumes as seen in MPRAGE MRI. a Cerebellum section in a healthy control subject; b case SCA-02; c case SCA-10; d case SCA-08; e case SCA-09 (presymptomatic). The cases are set according to severity of disease. Note that volume loss is not proportional to disease severity but rather with duration of illness

Group Analysis

The main goal of the present work was to determine if changes in any of the main cerebellar pathways were linearly related to clinical independent variables (size of CAG repeat expansion along severity and duration of illness). For this we first determined if there were statistical differences in the size or FA of the cerebellar pathways in SCA1 individuals compared to healthy controls. The nonparametric multivariate Cramer test (left and right brain sides) showed no significant difference in volumes of white matter between SCA1 and control groups even though their values in the SCA1 cases tended to be smaller (Table 2). In contrast, the superior cerebellar peduncles of SCA1 patients had lower FA values (p = 0.003) compared to controls (Fig. 3). Even when there was no difference with other pathways (inferior and middle cerebellar peduncles, cerebral peduncle, and cerebellar white matter), FA values in the ataxic group tended to be smaller (Table 3).

Table 2.

Average volumes (cubic millimeters) in white matter ROIs in healthy controls and SCA1 patients with their associated Cramer statistic and p values

ROI	Control		SCA1		Cramer statistic	p value
	Left	Right	Left	Right
CRB white matter	3,946	3,503	3,532	3,622	16.3	0.3
sCRB peduncle	619	617	493	515	10.1	0.4
mCRB peduncle	817	1009	543	620	15.1	0.2
iCRB peduncle	234	308	187	206	11.2	0.2
Cerebral peduncle	1,225	1,243	1,087	1,054	9.5	0.6

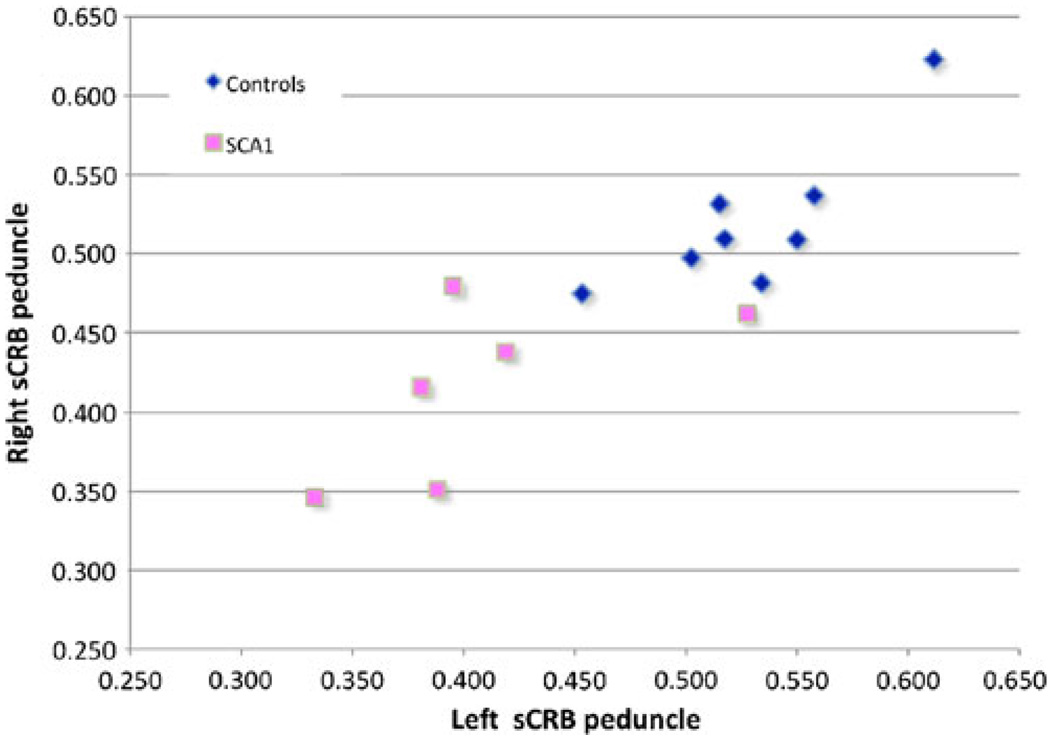
Fig. 3.

Graphic representation of distribution of FA values in the right and left superior cerebellar peduncles of all subjects. Note the large segregation in the distribution of these values between controls (blue diamonds) and SCA1 (pink squares) cases. Note, however, that there is one SCA1 case grouped with the control values. This is the case of the presymptomatic patient. The slope of both populations denote the similarity in the FA values for the right and left superior cerebellar peduncles

Table 3.

Average FA values in white matter ROIs in healthy controls and SCA1 patients with associated Cramer statistic and p values

ROI	Control		SCA1		Cramer statistics	p value
	Left	Right	Left	Right
CRB white matter	0.44	0.42	0.41	0.39	0.012	0.4
sCRB peduncle	0.53	0.52	0.41	0.41	0.153	0.003*
mCRB peduncle	0.58	0.54	0.60	0.54	0.003	0.7
iCRB peduncle	0.47	0.43	0.41	0.44	0.022	0.3
Cerebral peduncle	0.70	0.69	0.64	0.69	0.021	0.2

^*p≤0.01 for Bonferroni correction for multiple comparisons

Stepwise regression (forward and backward) analysis was conducted on the averaged FA values in the white matter pathways using the clinical independent variables. Average FA values in the superior cerebellar peduncle increased linearly with duration of the illness (p = 0.046) and decreased with SARA scores (p = 0.039) but not with the CAG repeat expansion. This linear relationship was not found in any other pathway. There was no significant correlation between age and mean FA values.

Functional Connectivity

Because FA values in the superior cerebellar peduncles had a linear relationship with disease severity and duration, next we determined if this observation was paralleled with changes in the intrinsic organization of brain regions associated with the pathway. The major component of the pathway is the output originating in dentate nucleus that projects to thalamus [37]. Because of sizable degeneration of the dentate nucleus in some ataxic cases, we could not perform statistics. Hence, instead of targeting this nucleus, in addition to thalamus, we assessed the intrinsic functional organization of its main input from lateral cerebellum.

Lateral Cerebellum

In healthy controls, functional clusters within lateral cerebellum had the following features:

• The mean value of the correlation coefficient was low (mean = 0.104), while their statistical distribution was normal in all cases. The mean value for kurtosis was 0.07 ± 0.34.

• The anatomical distribution of the functional clusters was not random. Rather, these were arranged in stripes or bands in the mediolateral plane (Fig. 4a).

• Similarly, functional clusters in the PCA space showed that their distribution was discrete with absence of inter-cluster correlations. The mean density index for all clusters was 20.77 (range 0.02–58.57).

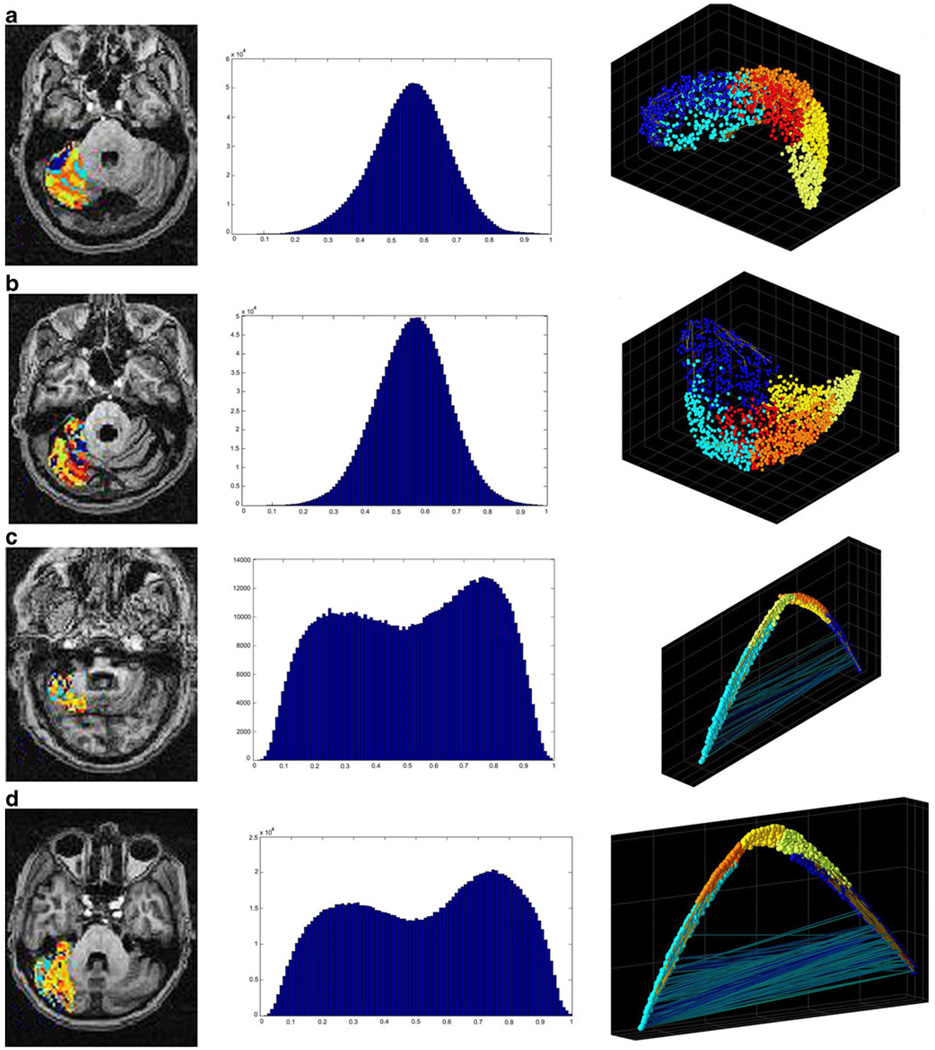
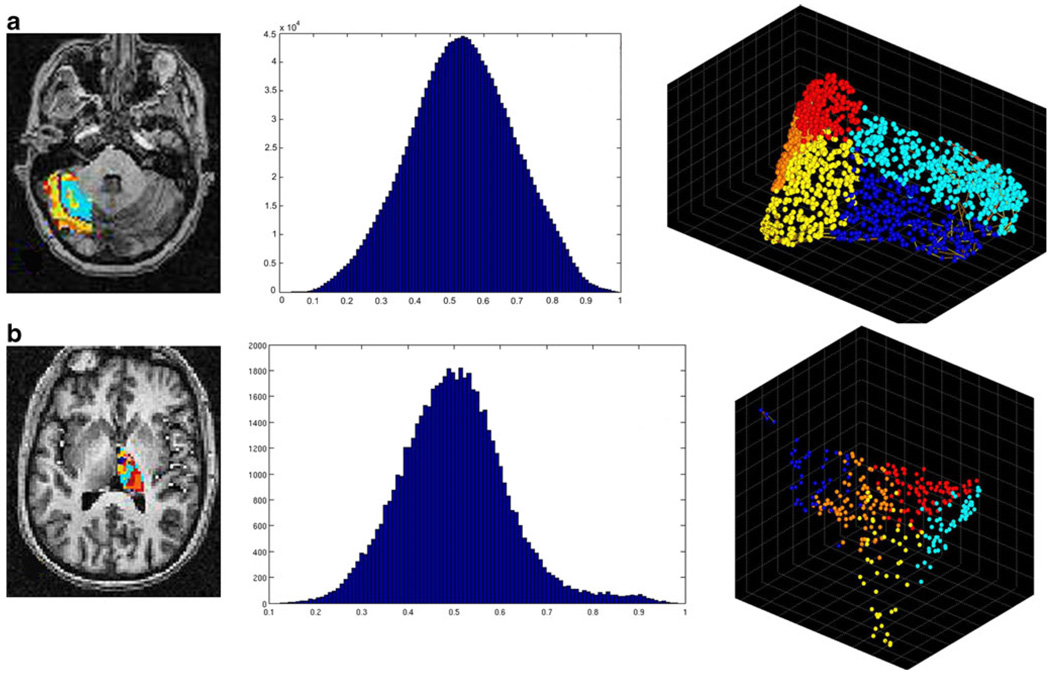
Fig. 4.

Graphical representation of the intrinsic functional organization in lateral cerebellum. Row a represents the holographic analysis in a healthy control subject. b The results for subject SCA-002, c for subject SCA-010, and d for subject SCA-008. Please refer to Table 1 for the specific clinical characteristics for each SCA patient. The first column shows the anatomical distribution of functional clusters found in lateral cerebellum. Note that the concentric arrangement seen in healthy subjects is progressively lost in the SCA1 subjects (including those with less severe disease). The second column shows the statistical distribution of the correlation coefficients in lateral cerebellum. In this case, the normality seen in all control subjects is progressively lost. The third column shows the functional manifold or magnitude reduction as seen by the first three principal components. In this case, not only the distribution changes, but in the most severe cases, it is apparent the presence of high negative correlations among clusters

In contrast to healthy controls, functional clusters in SCA1 cases presented the following features (Fig. 4b–d):

• Although the mean value of the correlation coefficients for all SCA1 subjects was low (mean = 0.071), their distribution was not normal. In most instances, distribution was bimodal (Fig. 4c–d). Mean kurtosis value was −0.52 ± 0.42. When these values were compared to those in controls, the Wilcoxon rank sum test showed a significant difference (w = 32; p = 0.03). Stepwise regression analysis did not detect a linear dependence between kurtosis with illness severity and duration nor with the size of the CAG repeat expansion.

• Remarkably, the anatomical distribution of the functional clusters was changed in symptomatic SCA1 cases. Instead of having a parasagittal distribution with segregated stripes, they presented a patchy appearance. This tendency tended to be more pronounced in the more severe cases.

• The PCA space showed two progressive changes. First, the distribution of the clusters became progressively denser and almost two-dimensional indicating the higher correlation values among voxels. The mean density index for all the SCA1 cases was 8.59 (range 0.02–17.63). This is an order of magnitude smaller than that of the healthy controls (w = 0; p = 0.004). In addition, it was apparent the presence of strong correlation (at least −0.94) among voxels from different functional clusters in SCA1 cases but not in controls.

• Observations in the presymptomatic SCA1 case (SARA = 0) showed changes in the density index (9.33; range 8.5–12.8) and in the distribution of correlation coefficients (kurtosis = −0.334) but not in the anatomical distribution of the functional bands (Fig. 6).

Fig. 6.

Intrinsic functional organization in a presymptomatic SCA1 case. Row a Holographic analysis results in the lateral cerebellum. First panel shows the anatomical distribution of functional clusters followed by the distribution of the correlation coefficients and the functional three-dimensional manifold. Row b Holographic analysis results in thalamus. The description of panels is similar to that in the lateral cerebellum

Thalamus

The intrinsic functional organization of the thalamus showed some parallels with those in lateral cerebellum (Fig. 5). The mean correlation coefficient was similar for the healthy controls and the SCA1 cases (mean = 0.12 ± 0.95 for the former and mean = 0.12 ± 0.94 for the latter). The distribution of correlation coefficients in all control cases was normal with a mean kurtosis value of 0.44 ± 0.71. In the SCA1 group, the mean kurtosis value was 0.02 ± 0.83. These ranged from similar values as in the controls in the less affected patients, to greatly diminished values in the more severe cases. With disease progression, the initial normal distribution was replaced by a progressive bimodality. Stepwise regression demonstrated a linear increase between kurtosis and severity of illness (p = 0.0003) and a linear decrease with duration of illness (p = 0.0002), but not with the size of the CAG repeat expansion.

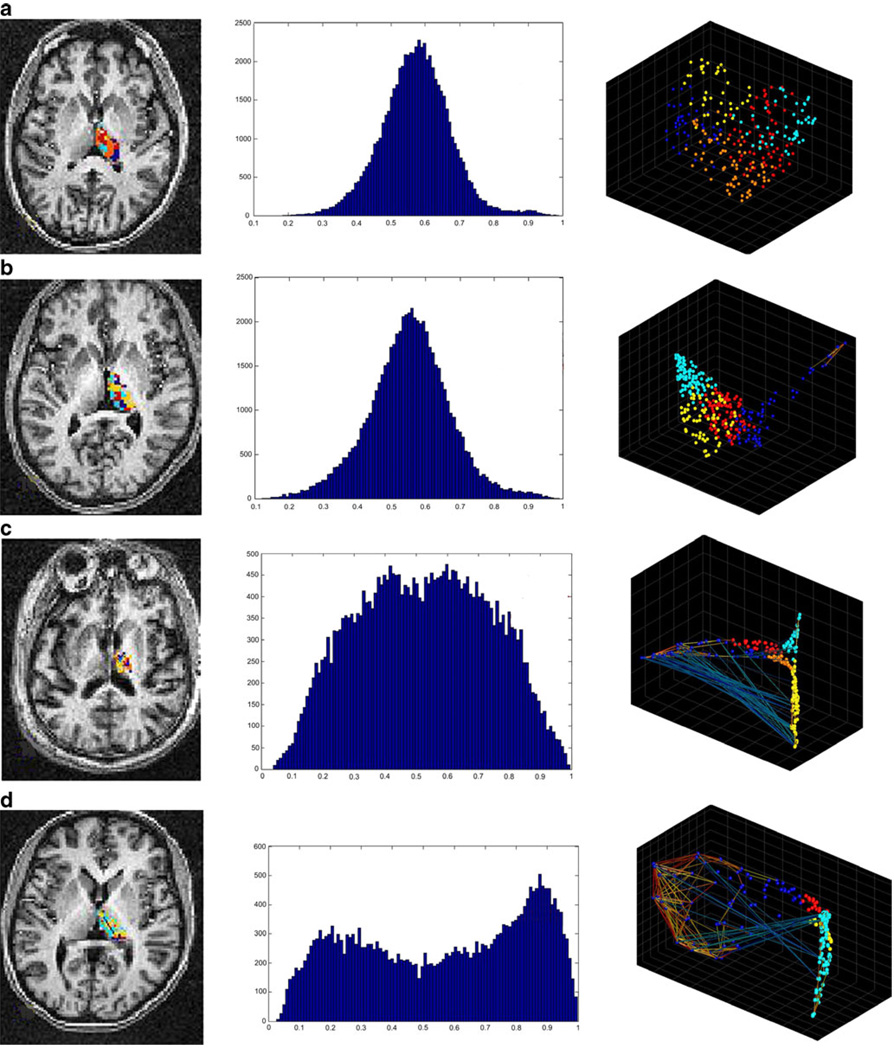
Fig. 5.

Graphical representation of the intrinsic functional organization in thalamus. Row a represents the holographic analysis in a healthy control subject. b The results for subject SCA-002, c for subject SCA-010, and d for subject SCA-008. Please refer to Table 1 for the specific clinical characteristics for each SCA patient. The first column shows the anatomical distribution of functional clusters found in thalamus. In this case, the anatomical distribution between healthy controls and SCA1 cases is not clearly different. The second column shows the statistical distribution of the correlation coefficients in thalamus. As in lateral cerebellum, the normality seen in all control subjects is progressively lost. This loss, however, is delayed with respect to the former region. The third column shows the functional manifold or magnitude reduction as seen by the first three principal components. In this case, not only the distribution changes, but in the most severe cases, it is apparent the presence of high negative correlations among clusters. In this brain region again, changes seem to be delayed when compared to those in the lateral cerebellum

With longer duration of disease, cluster distribution in the PCA space of SCA1 became denser and almost two-dimensional. However, as a group, there was no difference (w = 25; p = 0.3) in the density indexes between healthy controls (mean = 1.33; range 0.16–3.43) and SCA1 cases (mean = 1.82; range 0.21–7.1). In the most severe cases, strong negative correlation among voxels from different functional clusters started to be apparent.

Compared to controls, the presymptomatic SCA1 case did not present changes in the intrinsic organization of thalamus in terms of the statistical distribution of correlation coefficients (kurtosis = 0.58) and the absence of strong inter-cluster correlations (Fig. 6).

Spectral analysis (Fig. 7) showed a progressive shift to smaller frequencies of signals with the progression of disease. While in controls (and the presymptomatic SCA1), the proportion of frequencies had a more homogeneous distribution, in the symptomatic SCA1 cases there was a progressive shift toward lower frequencies, albeit at a later time compared to changes seen in lateral cerebellum.

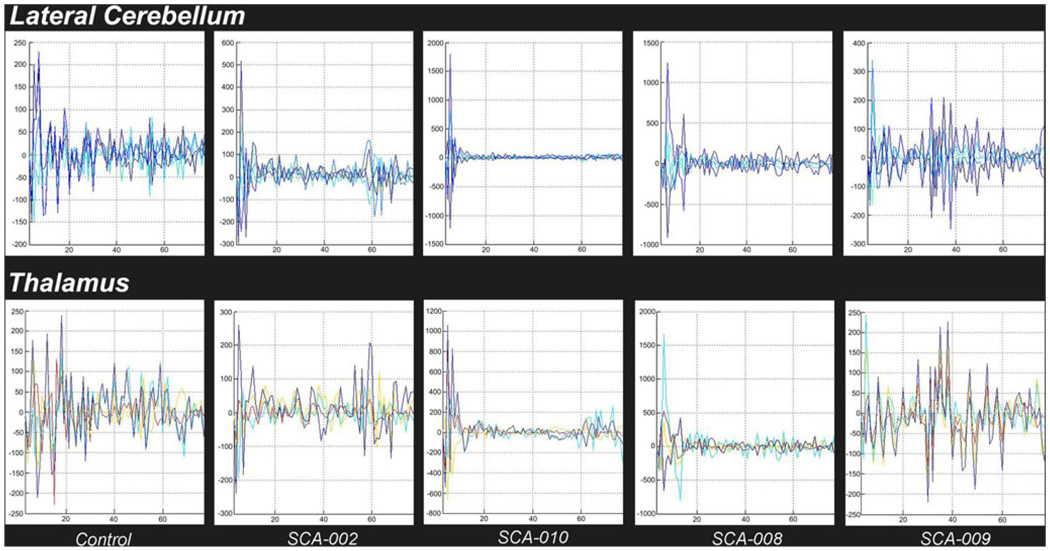
Fig. 7.

Graphical depiction of spectral analysis with FFT. Upper row: frequency distribution for clustered time series in the lateral cerebellum. Lower row: frequency distribution for clustered time series in contralateral thalamus. The first images on both rows represent the spectrum of a (typical) control case. Note the shift to the left in the distribution of frequencies for the SCA1 cases (SCA-002, 008, and 010) but not for the presymptomatic SCA-009 case. The shift seems to appear earlier in lateral cerebellum with respect to thalamus

Discussion

Anisotropy in the Superior Cerebellar Peduncles Is a Good Marker for Disease Progression

Even with a small cohort, our results showed that the FA associated with the superior cerebellar peduncle differed in controls and SCA1 subjects where it varied linearly with severity [38] and duration of disease, making it a suitable biomarker. Specifically, there was an inverse relationship between severity of disease and the integrity of the pathway and a direct relationship with duration of illness. The positive correlation between FA and duration of illness is counterintuitive and may be due to the rate of progression rather than the duration of disease per se since size of the repeat expansion gives rise to an earlier age of onset and ostensibly more severe disease [39].

The sensitivity of the superior cerebellar peduncle as biomarker for disease severity may be due to the fact that is the only peduncle with components influencing both cerebral cortex (via thalamus) and brainstem (attesting to the distributed nature of this disease).

Of note, although the changes were not statistically significant, decreased volumes were seen in all cerebellar peduncles and decreased FA values were seen in all but the middle cerebellar peduncle [38, 40]. The lack of statistical significance can be attributed to the inclusion of the presymptomatic case in the calculations.

Qualitative Changes in the Correlation Coefficients in Lateral Cerebellum Were the Earliest Changes Seen in SCA1 Patients

Whereas in controls the correlation coefficients from functional clusters in lateral cerebellum were low, in SCA1 these were significantly larger as quantified by kurtosis and density index measures. These were the only changes that the SCA1 presymptomatic case shared with the affected. Based on the spectral analysis, the immediate cause of this increase in the strength of the correlation coefficients can be attributed to a decrease in frequency in the signals.

Neuropathological changes described in SCA1 in humans [5, 6, 41–44] and animal models [45–49] show that Purkinje cells are especially vulnerable to the toxic effects of mutant ataxin-1. Thus, it is not surprising that early changes are seen in lateral cerebellum. The process of degeneration, however, passes through progressive changes ranging from subtle physiological alterations at the synaptic level to morphological changes in dendrites and ending with neuronal death [50–52]. In SCA1 transgenic mice, one of the first manifestations of disease is an alteration of synaptic transmission in glutamatergic signaling in Purkinje cells [50, 52]. These mild synaptic changes may lead to concomitant decrease in the frequency and the amplitude of signals such as those seen in our presymptomatic case. With disease progression, morphological changes and cell death will occur. From an imaging standpoint, these changes could be represented by further reduction in the signals consistent with overt ataxia.

Functional Intrinsic Organization of Lateral Cerebellum Reflects Cerebellar Compartmentalization

The functional clusters in lateral cerebellum in control subjects were organized into concentric bands or stripes arranged parasagittally reminiscent of the stripes specific to Purkinje cells seen with zebrinI/II (aldolase C) in several species including humans [53–60]. Interestingly, there is an anatomical coincidence between zebrinII stripes with the topology of the olivocerebellar climbing fibers [61–64]. Functionally, the olivocerebellar climbing fibers synchronize complex spike activity in Purkinje cells [65–72] plausible because of their electrical coupling that generates synchronic oscillations [66, 67, 73–75]. These patterns of synchrony produced in Purkinje neurons by the inferior olivary complex are not static, changing during motor behaviors and pharmacological manipulations [70, 71, 76, 77].

If the functional bands we detect in this study reflect this cerebellar compartmentalization [60], it is plausible that it is regulated by the climbing fiber system from the olivary complex. Support for this compartmentalization could potentially be based in the comparison of sizes of our stripes with those found with immunohistochemical techniques. Unfortunately, the single report on aldolase C bands in humans [60] albeit reporting their existence did not comment on their anatomical dimensions. Interestingly in other species, the zebrinII bands are not homogeneous, tending to be larger in lateral cerebellum [64].

Disruption of Functional Bands May Reflect Changes in the Olivocerebellar System

Disruption of Purkinje cell synchronization follows the decoupling of olivary neurons by carbenoxolone and in the connexin36 knockout mice [78, 79]. Consequently, it is tempting to think that disruption of functional bands in SCA1 is produced by the decoupling of inferior olivary neurons resulting from pathological changes. Degeneration of inferior olives with neuronal death and gliosis is one of the neuropathological hallmarks in SCA1 [5–7].

To assert if possible olivary degeneration is present in our SCA1 cohort, we computed the number of voxels in the olivary region in all subjects. Indeed, although numbers are not normalized by cranial volume, number of olivary voxels in SCA1 was smaller (mean = 9.5; range 7–14) than in controls (mean = 13.8; range 8–21). There are several potential mechanisms for olivary degeneration. On the one hand, it could be a direct effect from the mutated ataxin-1. Although there have been numerous studies reporting mouse genetic models of SCA1, there have not been opportunities to explore this issue [45–47, 49, 80]. However, these models have reported the presence of neuronal intranuclear inclusions in olivary neurons. These inclusions that have been related to a reaction of neurons to reduce the toxic effect of mutant proteins [49] have also been used as markers for vulnerable cells [42, 47, 81–83]. A second alternative for olivary degeneration is through an indirect path. Retrograde degeneration could be produced by loss of synaptic targets due to Purkinje cell death. This process, however, would require a significant amount of Purkinje cell death. The fact that changes were seen in early SCA1 cases argues against this possibility. Conversely, anterograde degeneration could result from loss of inputs from deep cerebellar nuclei. This alternative is perhaps less likely because an experimental lesion of the dentate nucleus with kainic acid in rats produces an increase of synchrony in Purkinje cells [84], the opposite effect of what we observed in the symptomatic SCA1 patients.

In summary, if we assume that decoupling of olivocerebellar neurons is causing loss of cerebellar compartmentalization in SCA1 cases, it becomes necessary to conclude that this process should be taking place after pathological changes in Purkinje cells initialized (since functional stripes were seen in the presymptomatic case) and before degeneration of the dentate nucleus occurs (since this produces an increase, not a decrease of synchrony).

The Progression of Changes in Thalamus as a Biomarker for SCA1

Changes in the functional organization of thalamus in SCA1 showed two characteristics: (a) The absolute values of correlation coefficients (kurtosis) increased linearly with disease severity and decreased linearly with disease duration. The functional organization in the presymptomatic SCA1 case did not differ from healthy controls. (b) Thalamic changes were delayed when compared to changes in the lateral cerebellum.

Although morphological changes in thalamus have not been typically associated with pathology of SCA1 [3, 44, 85, 86], functional changes have not been tested. In our results, functional changes not only were readily apparent but they also had a linear relationship with severity and duration of disease. The strong linear relationship could be the result, on the one hand, of the magnitude of the differences from the presymptomatic to the more severe cases. On the other hand, it could be due to the fact that changes in the most severe cases did not show a ceiling effect.

The linear dependence between variables in thalamus closely corresponds with a parallel linearity seen with FA values in the superior cerebellar peduncle highlighting the relevance of the connectivity between cerebellum and cerebral cortex via thalamus as described in macaques [87–92] and the possible development of cognitive changes with larger duration of disease [93, 94]. Kurtosis values were the better descriptors of disease severity and duration that could be explained by loss of input. FA values of the superior cerebellar peduncle not only are decreased [40, 85] and vary according to disease severity but also the origin of this pathway; the dentate nucleus also degenerates [43, 86, 95].

Hypothesis on the Progression of Disease Assessed with Connectivity Analysis

In summary, we propose an anatomical hypothesis on the temporal course of pathological functional changes in SCA1 that suggest this disease a “disconnection syndrome” [13]. Pathology initializes in Purkinje cells due to ataxin-1 toxicity reflected as functional downregulation of synaptic activity. Subsequently, pathological processes from ataxin-1 expand to the inferior olivary nucleus, decoupling olivary cells and producing de-synchronization of Purkinje cells. This accelerates disease progression in Purkinje cells producing morphological changes and disrupting efferent signals to the dentate nucleus. Once this happens, thalamic functional changes follow. The eventual Purkinje neuronal death will produce deafferentation and degeneration of output neurons in the dentate nucleus and input signals from inferior olives. At present, a larger number of SCA1 cases must be studied before definitive conclusions are reached. In addition, we plan to assess effective connectivity among the nodes detected in this study (such as olivary complex, thalamus in addition to red nucleus). Because this hypothesis could be tested experimentally, it can also assist in defining the efficacy of pharmacological agents to arrest the development of this devastating illness.