Stochastic Ensembles, Conformationally Adaptive Teamwork and Enzymatic Detoxification

Abstract

It has been appreciated for a long time that enzymes exist as conformational ensembles throughout multiple stages of the reactions they catalyze, but there is renewed interest in the functional implications. The energy landscape that results from conformationlly diverse poteins is a complex surface with an energetic topography in multiple dimensions, even at the transition state(s) leading to product formation, and this represents a new paradigm. Nearly simultaneous with the renewed interest in conformational ensembles, a new paradigm concerning enzyme function has grown, wherein catalytic promiscuity has clear biological advantages in some cases. ‘Useful’, or biologically functional, promiscuity or the related behavior of ‘multifunctionality’, can be found in the immune system, enzymatic detoxification, signal transduction, and in the evolution of new function from an existing pool of folded protein scaffolds. Experimental evidence supports the widely held assumption that conformational heterogeneity promotes functional promiscuity. The common link between these co-evolving paradigms is the inherent structural plasticity and conformational dynamics of proteins that, on one hand, leads to complex but evolutionarily selected energy landscapes, and on the other hand promotes functional promiscuity. Here we consider a logical extension of the overlap between these two nascent paradigms: functionally promiscuous and multifunctional enzymes such as detoxification enzymes are expected to have an ensemble landscape with a greater number of states accessible on multiple time scales than substrate specific enzymes. Two attributes of detoxification enzymes become important in the context of conformational ensembles: these enzymes metabolize multiple substrates, often in substrate mixtures, and they can form multiple products from a single substrate. These properties, combined with complex conformational landscapes, lead to the possibility of interesting time-dependent, or emergent, properties. Here we demonstrate these properties with kinetic simulations of non-equilibrium steady state (NESS) behavior resulting from energy landscapes expected for detoxification enzymes. Analogous scenarios with other promiscuous enzymes may be worthy of consideration.

Background

Conformational Dynamics and the New Enzymology

Proteins are inherently flexible, and they exhibit time-dependent fluctuation on a wide range of time scales. Slow times scales of fluctuation naturally imply greater energy barriers between states and more ‘rugged’ energy landscapes. Rapidly interconverting conformations of ligand-free enzymes are clearly described by many experimental techniques (1 - 3), and there is little doubt that ligand binding alters the energy landscape, and therefore the relative population of states and their rates of interconversion. These atomic level motions are consistent with two limiting cases for ligand-dependent conformational change: a) the classic concept of induced fit and b) the thermodynamically equivalent but kinetically different ‘conformational selection’ model for molecular recognition (4 - 9). Recently, however, it has become increasingly appreciated that such conformational changes may be sufficiently slow to occur on time scales similar to ligand binding and dissociation, and on time scales relevant to catalytic steps.

Whereas heterogeneity of ground state conformations of free enzymes and ligand-bound enzymes is a ‘certainty,’ with mature experimental support, the analogous heterogeneity at the level of the catalytically relevant enzymatic transition states has only recently been appreciated. Many recent studies based on computation, NMR, and single molecule methods suggest enzyme hetrerogeneity ‘during’ transition states associated with a single elementary reaction (9 - 15). These refinements in theory, together with the more detailed experimental measurements, result in an energy landscape for enzyme catalysis as schematized in Figure 1, as already suggested in (13, 14). According to the strict definition from the theory of chemical kinetics, “the” transition state is located at the global energy with the lowest barrier height among all possible paths connecting the reactant to the product. The transition state ensemble perspective, however, articulates the existence of multiple saddle points with nearly equal barrier heights. For the promiscuous enzymes that we highlight here, we refer to transition state ensembles that result from distinct transition states for different substrates, or different products from a single susbtrate, that are well separated by significant energy barriers. For these cases, the heterogeneity of transition states refers to distinct elementary reactions, in the classic sense and we do not imply that there is conformational flux between transition states (no arrows between TS's in Figure 1A, even though Figure 1B suggests that possibility).

Figure 1.

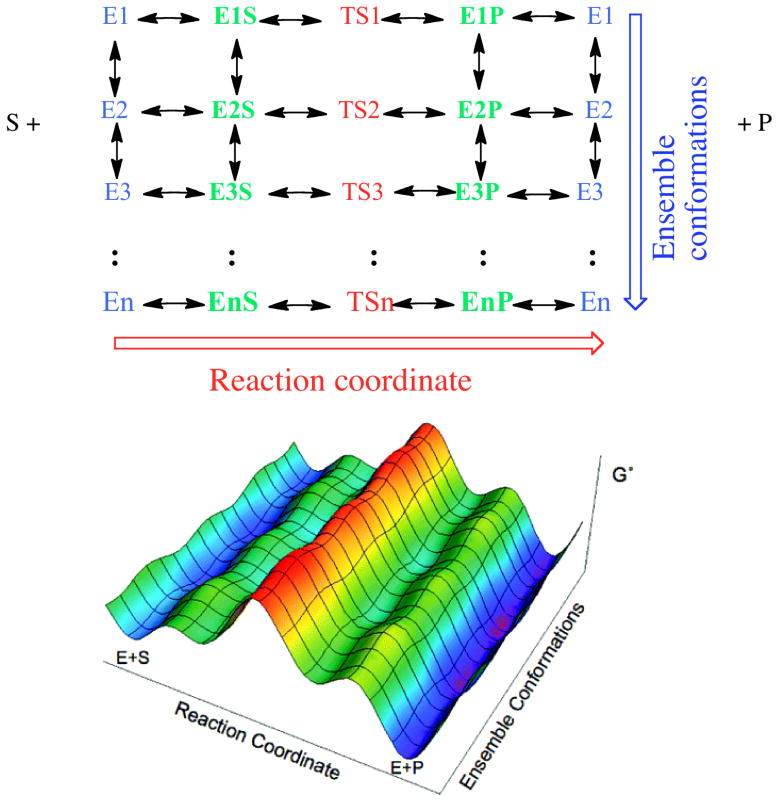
Top: Two-dimensional matrix of enzyme states reflecting ligand free forms (blue) on the left (E1 through EN), substrate complexes (green) with the corresponding states (E1S through ENS), Transition state complexes (red, TS1 through TSN), and product complexes (blue, E1P through ENP) for each state, with return to the initial ensemble of ligand free states. Note, in our model the transition state are not connected via arrows – we do not imply conformation rearrangement at the transition state ‘ridge’ (red). The multiple conformations present along this ridge are separated by significant barriers. Bottom: A three dimensional free energy (G′) landscape representation of the system, when the catalytic transition states (TS) are rate limiting, color coded to as the matrix above. The lower free energy surface is adapted from reference 13.

The specific case depicted in Figure 1 includes multiple rate limiting catalytic transition states, but conformational equilibria within the ensemble of the unbound enzyme may also include significant barriers. In short there are many populated ‘states’ for the ligand free enzyme (E1, E2, … En), various substrate complexes (E1S, E2S ‥ EnS), the transition state ensemble (TS1, TS2 ‥ TSn) and product complexes (E1P, E2P ‥ EnP). The extent to which these ground states equilibrate along the conformational axis on the time scale of flux through each transition state (the reaction coordinate) will have profound effects on the time-dependent behavior of the system. In general, if conformational sampling occurs on a time scale comparable with catalytic processes, then each successive round of catalysis for a single enzyme molecule can include participation from different states under certain conditions. The result could be a system that is highly heterogeneous and driven by probability and independent of its history at low turnover (stochastic), with increasingly deterministic behavior as it completes more catalytic cycles. Furthermore such a system can ‘relax’ back to its more stochastic state when not undergoing catalysis (15 - 16).

Transition State Ensembles and MultiFunctional Proteins

A related concept concerning enzyme function has recently developed, which acknowledges the utility of ‘promiscuity’ in biological function (18). Promiscuity is a functional property with distinct roles in: 1) protein interaction networks where ‘hub’ proteins regulate the function of multiple protein partners (19); 2) enzymatic detoxification by enzymes that metabolize an extraordinary range of structurally unrelated substrates (20); 3) the immune response, where promiscuous germline antibodies provide an efficient primary immune response (21); and 4) in maintaining a pool of structural scaffolds from which to evolve new enzymes (18, 22, 23). Tawfik and co-workers have attempted to articulate many aspects of ‘promiscuity’ and suggest the importance of distinguishing ‘promiscuous’ enzymes from ‘multifunctional’ enzymes, such as detoxification enzymes that have a clear function related to the metabolism of multiple substrates (18). Here, for convenience, we still use the terms interchangeably; the labels ‘promiscuity’ or ‘multifunctionality’ depend upon our knowledge of an enzyme's function. A presumed critical physical trait of promiscuous enzymes, or multifunctional ones, is flexibility, or the ability to sample a wide range of conformational space, and this may facilitate evolution of new function (18, 22, 23). In effect, functional promiscuity is likely to be correlated with structural plasticity (18, 22 - 24).

Merging Promiscuity with Conformational Ensembles; the Example of Detoxification Enzymes

Based on these nascent ideas about promiscuity, enzymatic conformational ensembles, and their common element of conformational dynamics, we have considered the possibility of time-dependent, emergent, properties of detoxification enzymes and transporters. Enzymes such as cytochrome P450s (CYPs), uridine diphosphate glucuronosyl transferases (UGTs), and transporters such as P-glycoprotein (P-gp) are known to be extraordinarily substrate promiscuous or ‘multifunctional’ and, as detoxification enzymes, they have evolved to decompose or transport a wide range of chemicals to which we are exposed. In the clinical realm, these enzymes dominate drug metabolism and thus are a critically important component of the therapeutic success or failure of drugs in development. We suggest that the energy landscapes of such enzymes lie near the limit of conformational breadth for transition state ensembles sampled by any enzymes.

The multi-conformational substate nature of detoxification enzymes, coupled with the possibility of multiple “elementary reactions” connecting mixtures of reactants and products, has fascinating consequences when considered within the context of their functional niche, which includes interactions with multiple drugs or toxins in a mixture. In this paper, our aim is to reconsider possible sources of complex kinetic behavior frequently observed with detoxification enzymes and to suggest that researchers who study them consider these scenarios when interpreting their data. An important task for us is to demonstrate the thermodynamic feasibility of time-dependent behavior, as it shares some of the essence of “conformational drift theory” which has been rigorously disputed on thermodynamic grounds (25, 26). Our analysis is similar to the kinetic proofreading mechanism (27) which involves free energy expenditure, where catalysis itself provides the chemical free energy required for such “drift”. Non-Michaelis-Menten (MM) kinetics are widely observed in detoxification enzyme reactions. One possible mechanism for the non-MM behavior comes from multiple substrates binding with allosterism, and we acknowledge that multiple binding is an established source of allosterism with these enzymes (28 - 32). In addition protein interactions between detoxification enzymes may contribute to complex kinetics (33). Another recently proposed possible mechanism of allosteric kinetics, with other enzymes, is dynamic cooperativity which is akin to the kinetic proofreading (27). The ideas summarized here, however, provide the essential reminder that such kinetics are possible even in the absence of multple ligand binding or protein-protein oligomerization.

Examples of Complex Kinetics

The steady state and pre-steady state effects of conformational fluctuation on kinetically relevant time scales have been discussed in theoretical examples (15, 16), and these effects have been demonstrated experimentally with several enzymes, including at least two broad specificity enzymes (34 - 37). Specifically, butylcholinesterase is thought to be a detoxification enzyme and an epoxide hydrolase (SteEH1) metabolizes a wide range of plant epoxides. Both are well described by kinetic models that include conformational sampling coupled with hysteresis (lag times) in transient kinetics or apparent cooperativity in steady state turnover. In addition, for the case of the epoxide hydrolase, with (1R, 2R) trans-2-methyl-styrene oxide as substrate, two diastereomeric hydrolysis products are formed. The generation of two products from a single substrate (product promiscuity), by definition, requires an energy landscape with more than one transition state. Furthermore, product promiscuity is a hallmark of detoxification enzymes, in addition to their well-appreciated substrate promiscuity. We acknowledge that, for these cases, there may be no actual flux along the transition state barrier, i.e. the saddle points corresponding to the two transition states may be separated by large energy barriers. The essential point is that multiple saddle points are accessible to the ground state substrate ensemble {[E1•S] … [En•S]} and to the ground state product ensemble {[E1•P] … [En•P]}. Depending on the landscape between states within the substrate and product ensembles, fascinating things can happen during catalytic turnoer. We provide some simple models to demonstrate the relevant parameters of interest.

Results

Models of time-dependent catalytic behavior

To demonstrate the kinetic principles, one can simply consider two equilibrating conformational substates of an enzyme E in the ligand free form, E₁ and E₂, where the catalytic efficiency of E₂ is significantly higher. There are many variations on this type of enzyme kinetic model based on the work of C. Frieden and others in the 1960s and 1970s (38), including recent studies by Min et al. (39). Here, we propose a variation on the theme: we consider the possibility that a catalytic cycle can push the enzyme from the E₁ conformation to the E₂ conformation, as shown in Fig. 2A. In Figure 2 k_cat/K_m for E₁ is k₁k₂/(k_-1 + k₂) = 10 and k_cat/K_m for E₂ = k₃k₄/(k_-3 + k₄) = 1000. That is E₂ is a much better catalyst than E₁. In Fig. 2A, we have deliberately neglected the direct fluctuations between E₁S and E₂S: This is to accentuate the idea of multiple pathways with multiple transition states. This emphasizes the lack of flux between structurally distinct complexes, which is possible for the reactions of detoxification enzymes, that yield different products or that start with very different substrates. The similar case of rapid equilibrium between E₁S and E₂S has been studied in (14).

Figure 2.

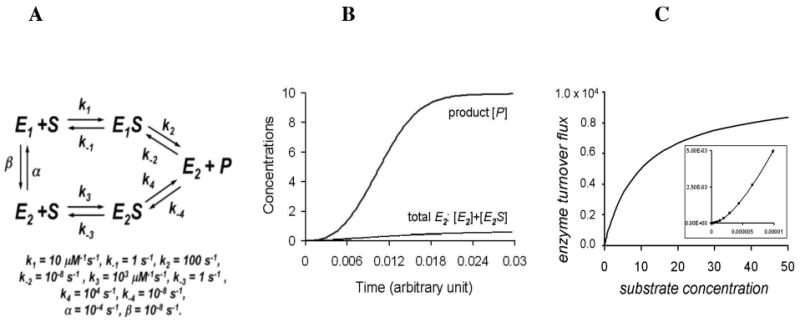
A. A variation of the general fluctuting enzyme kinetic model with two conformational substates E₁ and E₂, which yield the same product from a single substrate with different kinetic parameters. In this example, we specifically assume that E₂ is a better catalyst than E₁. The parameters used for the simulations are shown. In particular, we have assumed that the enzyme is inevitably in the state E₂ after accomplishing a catalysis step. B. The concentration of product (P) or all forms of E₂ ([E₂] + [E₂S]) as a function of time. There is marked hysteresis (lag) in the formation of product as the population of enzyme states shifts toward a greater fraction of E₂ with increasing turnover. C. The rate of product formation vs. [S]. The inset is a close up of the low [S] range, and demonstrates the sigmoidal dependence of rate on [S].

Because there is a continuous S to P catalytic cycle, the substates of the enzyme are not in equilibrium, but rather they are in a non-equilibrium steady state (NESS). The steady state ratio of [E₂]/[E₁] is

$$\frac{{[E_{\mathit{2}}]}^{\mathit{\text{ness}}}}{{[E_{\mathit{1}}]}^{\mathit{\text{ness}}}}=\frac{\widehat{a}(k_{-\mathit{1}}+k_{\mathit{2}})+k_{\mathit{1}}{k}_{\mathit{2}}[S]}{\acute{a}(k_{\mathit{2}}+k_{-\mathit{1}})+k_{-\mathit{1}}{k}_{-\mathit{2}}[P]}=\frac{{\mathit{10}}^{-\mathit{7}}+{\mathit{10}}^{\mathit{3}}[S]}{{\mathit{10}}^{-\mathit{2}}+{\mathit{10}}^{-\mathit{8}}[P]}.$$ (1)

We see this ratio is very different from the ratio of [E₂]/[E₁] in the absence of S or P, which is

$$\frac{{[E_{\mathit{2}}]}^{\mathit{\text{ness}}}}{{[E_{\mathit{1}}]}^{\mathit{\text{ness}}}}=\frac{\widehat{a}}{\acute{a}}=\frac{{\mathit{10}}^{-\mathit{7}}}{{\mathit{10}}^{-\mathit{2}}}.$$ (2)

Thus the ratio of E₂/E₁ is much greater in the presence of substrate than in its absence. The concentrations of free E₁ and E₂ differ from their equilibrium values when the enzyme is undergoing catalysis. Interestingly, however, for a reversible reaction the ratio of [E₂]/[E₁] will be the same in the presence and absence of S, when the ratio of [S]/[P] = (k₁k₂α)/(k₁k₂β) is equal to their chemical equilibrium ratio. In this case, the ratio [E₂]/[E₁] in equilibrium follows Boltzmann's law. It is determined by the internal energies of the E₁ and E₂ dictated by their molecular structures.

As long as [S]/[P] ≫ k_-1k_-2β/(k₁k₂α) = 10^-15, then the ratio in Eq. (1) ≫ β/α. So, the turnover of the enzyme with S keeps the ratio of [E₂]/[E₁] high and pushes the enzyme population toward the more active state. The interesting result of this situation is observed upon calculating the turnover flux of S to P (J^ness), which is

$$J^{\mathit{\text{ness}}}=\frac{(\mathit{1}+{\mathit{10}}^{\mathit{7}}[S]) ({\mathit{10}}^{\mathit{3}}[S]-{\mathit{10}}^{-\mathit{12}}[P])}{{\mathit{10}}^{\mathit{2}}+{\mathit{10}}^{\mathit{7}}[S]+{\mathit{10}}^{\mathit{6}}{[S]}^{\mathit{2}}+{\mathit{10}}^{-\mathit{3}}[S][P]+{\mathit{10}}^{-\mathit{14}}[P]}$$ (3)

Using this equation, the substrate concentration dependence of the flux (Figure 2 C) and the time-dependence of product formation (Figure 2B) with a given initial concentration of S can be simulated. As can be seen there is an apparent cooperativity at low [S] (Inset of Figure 2C), or a sigmoidal response in the concentration [S] vs. flux curves and the progress curve includes a marked lag in the formation of P, which reflects the changing concentration of ([E₂] + [E₂S]) with increased turnover. These well-appreciated properties of slowly exchanging enzyme conformations are not typically observed with classic ‘Michaelis-Menten enzymes.’ Interestingly, however sigmoidal plots of velocity vs. [S] are commonly observed with detoxification enzymes (28 - 32). There is ample evidence for many detoxification enzymes that the non-Michaelis-Menten kinetics include contributions from multiple substrate binding (40, 41), but the behavior described above may also contribute. In fact, this type of model describes the behavior of StEH and butylcholinesterase, as already noted (34 - 37).

The important reminder that comes from this model, as already appreciated (15 - 17), is that ground state heterogeneity of enzymes, with corresponding heterogeneity at the level of the transition state in the form or distinct elementary reactions, can yield emergent properties wherein the apparent kinetic properties of a population of enzymes change with time. Simultaneous heterogeneity in both the ground state and the transition state, which implies parallel paths for enzyme turnover, provides energy driven conformational drift of enzyme states.

It is interesting to consider enzymes that might exhibit these properties. For the reasons described above, wherein catalytic promiscuity or multifunctionality is likely to be due to conformational flexibility, detoxification enzymes are among those likely to exhibit such hysteresis. The possibility for such behavior with detoxification enzymes becomes significantly more intriguing when situations that are characteristic of detoxification catalysis are considered.

Case 1. Simultaneous Exposure to Multiple Substrates

An interesting implication of these ideas becomes obvious in the context of the functional promiscuity of detoxification enzymes. It is completely clear that a single isoform of, for example, a CYP can metabolize structurally unrelated drugs, including many that are simultaneously used in a single patient. This is a major source of drug-drug interactions. Extreme cases occur when one drug significantly inhibits the metabolism of another, but in many cases both drugs are metabolized efficiently. At the molecular level, however, simultaneous exposure to multiple drugs has fascinating consequences if the energy landscape has the properties we have considered above. We demonstrate this with the scheme in Figure 3A, which includes two substrates S₁ and S₂ that are converted to corresponding products P₁ and P₂, with differential kinetic properties for enzyme conformations E₁ and E₂.

Figure 3.

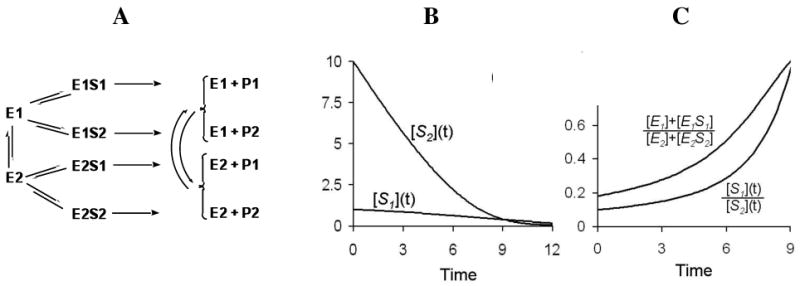
Dynamic adaptation of a stochastic enzyme ensemble in processing two different substrates S₁ and S₂, using “teamwork”. A. Minimal kinetic scheme with equilibrating E1 and E2, each contributing to clearance of both S₁ and S₂. However, as simulated, the two dynamically exchanging forms E₁ and E₂ have relative specificities for S₁ and S₂ respectively, and the reactions are assumed to be irreversible. The ratio of the two enzyme catalytic powers, θ = k_cat,1 K_m2/(k_cat,2 K_m1) = 0.3 in the simulations shown. In equilibrium in the absent of substrates, the ratio of the two enzyme forms is α/β = 1. The initial concentrations for [S₁]/K_m1 = 1 and [S₂] /K_m2 = 10. B. Concentrations of S₁ and S₂ vs. time. The enzyme ensemble immediately adjusts its distribution to 1:10 in order to process the dominant S₂. C. Ratios of E₁ and E₂ forms or S₁ and S₂ vs. time. With increasing time the ratio of [S₁](t) to [S₂](t) changes from 0.1 to 1, and the enzyme distribution ‘adapts’ accordingly.

In this case, the ratio of the rates of metabolism of S₁ and S₂ is a simple function of the dynamic ratio [S₁](t)/[S₂](t):

$$\frac{J_{S_1\to P_1}}{J_{S_1\to P_1}+J_{S_2\to P_2}}=\frac{\theta [S_1](t)}{\theta [S_1](t)+[S_2](t)},$$ 4

where θ = k_cat,1 K_m2/(k_cat,2 K_m1) is the ratio of the catalytic powers of the two states of the enzyme, for these respective substrates, and the J terms are the flux of S₁ to P₁ or S₂ to P₂ as denoted in the subscript. The Eq. (4) shows that if the ratio [S₂]/[S₁] increases, then the reaction flux that metabolizes S₂ will increases with respect to that of S₁. Therefore, there is an “adaptation” in the teamwork of the enzyme ensemble. At high concentrations of both S₁ and S₂, the enzyme population adjusts to convert both substrates simultaneously; after several catalytic cycles no individual enzyme molecule alternates between S₁ and S₂. Rather, the population has divided itself into two teams which each specialize in the metabolism of S₁ or S₂. Importantly, upon partial depletion of the substrate that is more quickly eliminated, the enzyme population readjusts to metabolize the other substrate more efficiently (Figure 3B). The enzyme molecules previously dedicated to clearance of S₂ adapt to aid in the clearance of S₁, and vice versa. Such nongenetic adaptation has not been documented experimentally, yet it represents a fascinating possibility predicted by the emerging view of enzyme ensembles and the increasing evidence that detoxification enzymes are conformationally heterogeneous.

In addition to Eq. (5), we also have

$$\frac{[E_1]+[E_1{S}_1]}{[E_2]+[E_2{S}_2]}=\left(\frac{\beta }{\alpha }\right)\frac{1+[S_1](t)/K_{m1}}{1+[S_2](t)/K_{m2}}.$$ (5)

We see that if both substrates are below their respective enzyme conformation K_m's, then the ratio of the two forms of the enzyme remains constant. However, if the concentration of one of the two substrates is greater than its corresponding K_m, then the enzyme population will shift toward the conformation needed to metabolize the remaining substrate. It is this dynamic adaption that “allocates” the enzyme to process the toxin at higher concentration relative to its K_M.

Dynamically, we also note that the S₂ really serves as a non-competitive inhibitor for the enzyme E₁, and S₁ is a noncompetitive inhibitor of E₂. That is, the two substrates will not yield competitive inhibition kinetics. If the rates of conversion of S₁ are monitored as a function of the concentration of S₂, then S₂ will not appear as a competitive inhibitor, but rather as a noncompetitive inhibitor of S₁. This is an important result in as much as many detoxification enzyme exposed simultaneously to multiple substrates in vitro, yield noncompetitive or mixed inhibition when analyzed by standard methods (42 - 45).

The striking result of the situation we consider here is that a population of equilibrating conformers, after exposure to multiple substrates, can distribute itself into ‘teams’ wherein one team specializes in the clearance of one substrate within the mixture, and other conformational team metabolizes other members of the substrate mixture. Such ‘conformational teamwork’, if it occurs, would represent a fascinating adaptability of the enzyme, ideally suited to perform its function of detoxification when faced with a mixture of toxins. In effect the ability of a single detoxification enzyme, as a single polypetide sequence, to metabolize a wide range of substrates simultaneously, without competition between substrates toward individual enzyme molecules, is enhanced by the teamwork achieved by discreet conformations.

Case 2: Formation of Multiple Products

In addition to their ability to metabolize multiple substrates, detoxification enzymes such as CYPs also frequently display product promiscuity, as noted above for StEH. That is, they can metabolize a single substrate to multiple products. With CYPs, the products formed from a single substrate often require dramatically different substrate orientations within the active site. Substantial rearrangement of the [E•S] complex would be required to convert the complex yielding one metabolite to the complex yielding the other metabolite.

This behavior also has interesting potential implications when the energy landscapes of the type we describe are operative. Specifically, for a single substrate being metabolized to multiple products via different conformations, after an initial pre-steady state period, at the level of the enzyme population, two ‘teams’ will emerge. For short time increments, or at saturating [S], one conformational team will generate exclusively one product and the other team will generate the second product, as long as each product leaves behind a conformation that is selective for the parent substrate orientation that yields that product, and as long as the conformational exchange among free enzyme states is sufficiently slow. However, the teams will redistribute in response to [S]. Thus, when [S] is high, a constant ratio of P2/P1 is formed, possibly to optimize clearance of total [S]. However, as [S] decreases the population shifts in favor of the conformation with higher affinity for S, with greater relative formation of the corresponding product (P₁).

A simple kinetic scheme to represent this scenario is shown in Fig. 4A in which the vertical transitions are sufficiently slow; thus each catalytic “pathway” essentially proceeds as an independent enzyme catalyzed reaction that produces different products P₁, P₂, ‥, Pn, with a slow conversion between the different forms of the enzyme.

Figure 4.

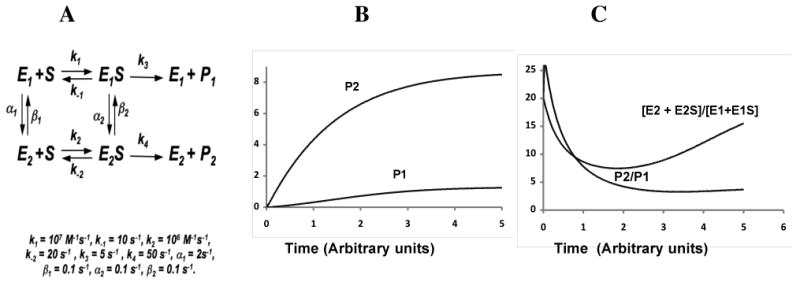
A. Minimal kinetic scheme for two enzyme conformations generating a multiple products from a single substrate. In the simulations E₂ is a more efficient catalyst than E₁. B. Rate of formation of P₁ and P₂. Note the hysteresis in the formation of P1. C. Ratios of all enzyme forms E₂ vs. E₁ ([E₂+E₂S]/[E₁+E₁S]) or the product ratio (P₂/P₁) vs. time. The enzyme forms ‘adapt’ from the initial preference for E₂ in the absence of substrate to a more ‘balanced’ ratio of all E₂ forms/all E₁ forms, and increases again as substrate is depleted.

Are there multiple interconverting ligand-dependent ground states and multiple transition states with detoxification enzymes?

Based on these speculative possibilities, which are supported by first principle simulations, it is important to seek or document experimental support for conformational exchange on relevant time scales for other detoxification enzymes. In addition to the examples of epoxide hydrolaase and butylcholinesterase mentioned above, other detoxification enzymes should be considered. Obviously, single molecule methods will be required to directly observe the behavior we postulate here. To date there are few published single molecule experiments with substrates binding to CYPs (46) or any other detoxification enzyme, and none that include catalytic turnover. However, we propose these methods could be an essential component of future work required to fully understand these enzymes. In the absence of direct experimental support from single molecule studies, it is useful to consider other recent work that may suggest these behaviors. Indeed, several spectroscopic and structural studies suggest the presence of conformational heterogeneity of CYPs (47 - 55), possibly with slow exchange between states. Other spectroscopic methods that suggest ground state conformational heterogeneity include CO flash photolysis studies that reveal multiple kinetic components (56), and steady state spectral experiments that indicate the simultaneous presence of different [E • S] complexes from a single substrate (57). Together, the results demonstrate that the CYP fold is capable of functionally relevant, in some cases large-scale, conformational changes among ground state complexes that may exchange on relevant time scales. In short, the roles of conformational change in CYP function have been appreciated and well documented, including the possible role of distinct conformations in complex CYP kinetics (58), but they have not been treated as a source of time-dependent adaptation.

The concept we expose here is generally applicable to any protein that interacts with multiple partners or substrates via different conformations, and is not limited to detoxification enzymes. A population of promiscuous enzymes or proteins may work in temporally distinct conformational teams if simultaneously exposed to multiple substrates, and the teams may adapt to changing substrate concentrations. That is, such enzymes may exhibit stochastic behavior upon initial exposure to a mixture of substrates or to a substrate from which multiple products are generated, but after some catalytic turnover each enzyme molecule may exhibit temporary deterministic behavior, until the substrate environment changes and the population of molecules ‘relaxes’ to the stochastic situation again. Similarly, for regulatory proteins that interact with multiple partners, the conformational distribution could change in response to altered expression of some binding partners, and there could be interesting and important time-dependence to these processes. The possibility of such fascinating behavior, exemplified by the detoxification enzymes considered here, warrants consideration.