RECONSTRUCTING DNA COPY NUMBER BY PENALIZED ESTIMATION AND IMPUTATION

Abstract

Recent advances in genomics have underscored the surprising ubiquity of DNA copy number variation (CNV). Fortunately, modern genotyping platforms also detect CNVs with fairly high reliability. Hidden Markov models and algorithms have played a dominant role in the interpretation of CNV data. Here we explore CNV reconstruction via estimation with a fused-lasso penalty as suggested by Tibshirani and Wang [Biostatistics 9 (2008) 18–29]. We mount a fresh attack on this difficult optimization problem by the following: (a) changing the penalty terms slightly by substituting a smooth approximation to the absolute value function, (b) designing and implementing a new MM (majorization-minimization) algorithm, and (c) applying a fast version of Newton's method to jointly update all model parameters. Together these changes enable us to minimize the fused-lasso criterion in a highly effective way.

We also reframe the reconstruction problem in terms of imputation via discrete optimization. This approach is easier and more accurate than parameter estimation because it relies on the fact that only a handful of possible copy number states exist at each SNP. The dynamic programming framework has the added bonus of exploiting information that the current fused-lasso approach ignores. The accuracy of our imputations is comparable to that of hidden Markov models at a substantially lower computational cost.

1. Introduction

New techniques of fine mapping have uncovered many regions of the human genome displaying copy number variants (CNVs) [Iafrate et al. (2004); Redon et al. (2006); Sebat et al. (2004)]. Variation is to be expected in cancer cells, but it also occurs in normal somatic cells subject to Mendelian inheritance. As awareness of the disease implications of CNVs has spread, geneticists have become more interested in screening their association study samples for copy number polymorphisms (CNPs) [Stefansson et al. (2008)]. Fortunately, the Illumina and the Affymetrix platforms used in high-density genotyping yield CNV information at no additional cost. Despite their obvious technical differences, the two platforms generate conceptually very similar CNV reconstruction problems.

Hidden Markov models and algorithms have dominated the field of CNV reconstruction [Colella et al. (2007); Korn et al. (2008); Scharpf et al. (2008); Wang et al. (2007, 2009)]. This statistical framework is flexible enough to accommodate several complications, including variable single nucleotide polymorphism (SNP) frequencies, variable distances between adjacent SNPs, linkage disequilibrium and relationships between study subjects. In the current paper we investigate the potential of penalized estimation for CNV reconstruction. Tibshirani and Wang (2008) introduced the fused-lasso penalty for the detection of CNVs based on generic considerations of smoothness and sparsity [Rudin, Osher and Fatemi (1992); Tibshirani et al. (2005)]. The application of the fused lasso to CNV detection is best motivated by a simplified model. Let the parameter vector β = (β₁,β₂, …, β_n) quantify DNA levels at n successive SNPs. These levels are normalized so that β_i = 0 corresponds to the standard copy number 2, where SNP i is represented once each on the maternal and paternal chromosomes. Variant regions are rare in the genome and typically involve multiple adjacent SNPs; CNVs range from a few thousand to several million base pairs in length. In high-density genotyping we query SNPs that are on average about five thousand base pairs apart. The true β is therefore expected to be piecewise constant, with the majority of values equal to 0 and a few segments with positive values (indicating duplication) and negative values (indicating deletion).

Tibshirani and Wang (2008) proposed the joint use of a lasso and a fused-lasso penalty $p\left(\beta \right)={\Sigma }_{i=2}^n\mid {\beta }_i-{\beta }_{i-1}\mid$ to enforce this piecewise constant structure. One then estimates β by minimizing the objective function l(β) + λ₁∥β∥_ℓ1 λ₂p(β), where l(β) is a goodness-of-fit criteria. The nondifferentiability of the objective function makes minimization challenging [Friedman et al. (2007)]. We mount a fresh attack on this difficult optimization problem by the following tactics: (a) changing penalty terms slightly by substituting a smooth approximation to the absolute value function, (b) majorizing the substitute penalties by quadratics and implementing a new MM (majorization–minimization) algorithm based on these substitutions, and (c) solving the minimization step of the MM algorithm by a fast version of Newton's method. When the loss function is quadratic, Newton's method takes a single step. More radically, we also reframe the reconstruction problem in terms of imputation via discrete optimization. Readers familiar with Viterbi's algorithm from hidden Markov models will immediately recognize the value of dynamic programming in this context. For the specific problem of detection of CNVs in DNA from normal cells, discrete imputation has the advantage of choosing among a handful of copy number states rather than estimating a continuous parameter. This fact renders discrete imputation easier to implement and more accurate than imputation via parameter estimation.

The remainder of the paper is organized as follows. In the methods section we briefly review the data generating mechanism for CNV problems. We then present our estimation approach to CNV reconstruction and the MM algorithm that implements it. Finally, we describe our new model and the dynamic programming algorithm for discrete imputation. In the results section we assess the statistical performance and computational speed of the proposed methods on simulated and real data sets.

2. Methods

2.1. Characteristics of the genotype data

When reconstructing CNV from genotype data, researchers rely not only on the final genotype calls but also on raw measurements obtained from the genotyping array. The character of these measurements varies slightly depending on the platform adopted. For definiteness, we focus on the data delivered by the Illumina platform at our disposal. A DNA sample from an individual is preprocessed, hybridized to a chip, and queried at n SNPs. For convenience, we will call the two alleles A and B at each SNP. The amount of DNA carried by each allele at a queried SNP is measured by recording the luminescence of specifically labeled hybridized DNA fragments. Transformations and normalizations of the luminescences lead to two noisy measurements for each SNP i: y_i (LogR) and x_i (BAF). The former quantifies the total DNA present at the SNP. After normalization, the average of y_i across individuals is 0. A large positive value suggests a duplication; a large negative value suggests a deletion. The variability y_i has been successfully described as a mixture of a Gaussian and a distribution to guard against contamination from outliers [Colella et al. (2007); Wang et al. (2007, 2009)].

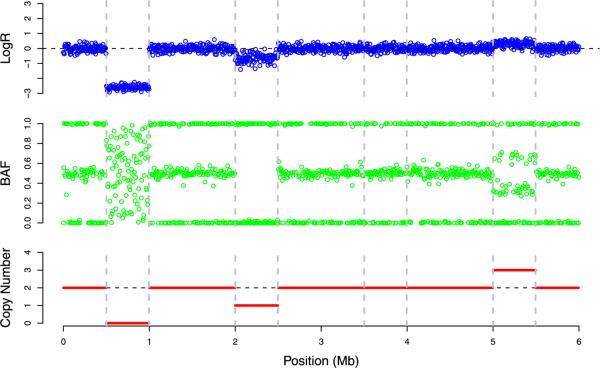
The B-allele frequency (BAF) represents the fraction of the total DNA attributable to allele B. The admissible values for x_i occur on the interval 0, 1]. When copy number equals 1, x_i takes on values close to 0 or 1, corresponding to the genotypes A and B. When copy number equals 2, x_i is expected to fluctuate around the three possible values 0, 1/2 and 1, corresponding to the three possible genotypes AA, AB and BB. When copy number equals 3, x_i varies around the four possible values 0, 1/3, 2/3, 1, corresponding to the genotypes AAA, AAB, ABB, BBB. When copy number equals 0, the value of x_i is entirely due to noise and appears to be distributed uniformly on [0, 1]. Figure 1 plots typical values of the pair (y_i, x_i) along a DNA segment that contains a homozygous deletion (copy number 0), a hemizygous deletion (copy number 1) and a duplication (copy number 3). Clearly both y_i and x_i convey information relevant to copy number.

Fig. 1.

Signal patterns for different DNA copy number scenarios organized by their physical locations along a simulated chromosome. The top panel displays in blue y_i (LogR), the middle panel displays in green x_i (BAF), and the bottom panel displays in red the true copy number.

2.2. Reconstructing a piecewise constant function

Consider first CNV reconstruction using signal intensities y_i and neglecting B-allele frequencies x_i. While this restriction overlooks important information, it has the benefit of recasting CNV reconstruction as a general problem of estimating a piecewise constant function from linearly ordered observations. In such regression problems, Tibshirani et al. (2005) and Tibshirani and Wang (2008) suggest minimizing the criterion

$$f\left(\beta \right)=\frac{1}{2}\sum _{i=1}^n{\left(y_i-\sum _{j=1}^p{z}_{ij}{\beta }_j\right)}^2+{\lambda }_1\sum _{j=1}^p\mid {\beta }_j\mid +{\lambda }_2\sum _{j=2}^p\mid {\beta }_j-{\beta }_{j-1}\mid .$$

Here y = (y_i)_n×1 is the response vector, Z = (z_ij)_n×p is the design matrix, β = (β_j)_n×1 is the parameter vector of regression coefficients, and λ₁ and λ₂ are tuning parameters that control the sparsity and smoothness of the model. The model is particularly suited to situations where the number of regression coefficients p is much larger than the number of cases n. For the special task of CNV detection, we take Z = I (i.e., p = n), reducing the objective function to

$$f\left(\beta \right)=\frac{1}{2}\sum _{i=1}^n{(y_i-{\beta }_i)}^2+{\lambda }_1\sum _{i=1}^n\mid {\beta }_i\mid +{\lambda }_2\sum _{i=2}^n\mid {\beta }_i-{\beta }_{i-1}\mid .$$ (1)

Notice that f(β) is strictly convex and coercive, so a unique minimum exists. When λ₂ = 0, the objective function can be decomposed into a sum of n terms, each depending only on one β_i. This makes it very easy to find its minimum using coordinate descent [Friedman et al. (2007); Wu and Lange (2008)]. Unfortunately, this is not the case with λ₂ ≠ 0 because the kinks in the objective function are no longer confined to the coordinate directions. This makes coordinate descent much less attractive [Friedman et al. (2007)]. Quadratic programming [Tibshirani et al. (2005); Tibshirani and Wang (2008)] is still available, but its computational demands do not scale well as p increases.

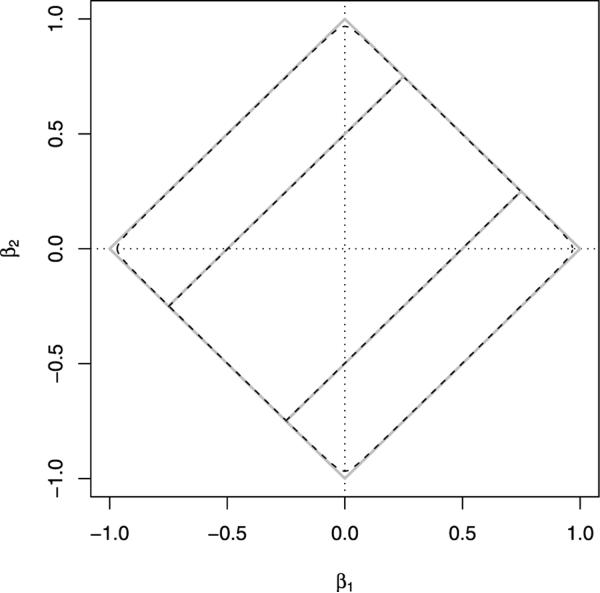
Inspired by the resolution of similar smoothing dilemmas in imaging [Bioucas-Diaa, Figueiredo and Oliveira (2006); Rudin, Osher and Fatemi (1992)], we simplify the problem by slightly modifying the penalty. The function

$${\parallel x\parallel }_{2,\epsilon }=\sqrt{x^2+\epsilon }$$

is both differentiable and strictly convex. For small ε >0 it is an excellent approximation to |x|. Figure 2 illustrates the quality of this approximation for the choice ε = 0.001. In practice, we set ε = 10⁻¹⁰. If we substitute ∥x∥_2,ε for |x|, then the CNV objective function becomes

$$f_{\epsilon }\left(\beta \right)=\frac{1}{2}\sum _{i=1}^n(y_i-{\beta }_i)+{\lambda }_1\sum _{i=1}^n{\parallel {\beta }_i\parallel }_{2,\epsilon }+{\lambda }_2\sum _{i=2}^n{\parallel {\beta }_i-{\beta }_{i-1}\parallel }_{2,\epsilon }.$$ (2)

As ε tends to 0, one can show that the unique minimum point of (2) tends to the unique minimum point of the original objective function.

Fig. 2.

Contours corresponding to different penalties. Solid gray line: |β₁| + |β₂| = 1 and $\mid {\beta }_1-{\beta }_2\mid =\frac{1}{2}$; Dashed line: ∥β₁∥_2,ε + ∥β₂∥_2,ε = 1 and ${\parallel {\beta }_1-{\beta }_2\parallel }_{2,\epsilon }=\frac{1}{2}$.

Another virtue of the substitute penalties is that they lend themselves to majorization by a quadratic function. Given the concavity of the function $t\mapsto \sqrt{t+\epsilon }$, it is geometrically obvious that

$${\parallel x\parallel }_{2,\epsilon }\le {\parallel z\parallel }_{2,\epsilon }+\frac{1}{2{\parallel z\parallel }_{2,\epsilon }}[x^2-z^2],$$

with equality holding if and only if x = z. This inequality enables a Majorization–Minimization (MM) [Lange (2004)] strategy that searches for the minimum of the objective function. Each step of this iterative approach requires the following: (a) majorizing the objective function by a surrogate equal to it at the current parameter vector and (b) minimizing the surrogate. The better-known EM algorithm is a special case of the MM algorithm. The MM algorithm generates a descent path guaranteed to lead to the optimal solution when one exists. More information can be found in Lange (2004). Returning to our problem, we can replace the objective function by the surrogate function

$$g_{\epsilon },m(\beta \mid {\beta }^{\left(m\right)})=\frac{1}{2}\sum _{i=1}^n{(y_i-{\beta }_i)}^2+\frac{{\lambda }_1}{2}\sum _{i=1}^n\frac{{\beta }_i^2}{{\parallel {\beta }_i^{\left(m\right)}\parallel }_{2,\epsilon }}+\frac{{\lambda }_2}{2}\sum _{i=2}^n\frac{{({\beta }_i-{\beta }_{i-1})}^2}{{\parallel {\beta }_i^{\left(m\right)}-{\beta }_{i-1}^{\left(m\right)}\parallel }_{2,\epsilon }}+c_m,$$

where m indicates iteration number and c_m is a constant unrelated to β. Minimization of g_ε,m(β | β^(m)) to obtain β^(m+1) drives the objective function f_ε(β) downhill. Although the MM algorithm entails iteration, it replaces the original problem by a sequence of simple quadratic minimizations. The descent property of the MM algorithm guarantees that progress is made every step along the way. This, coupled with the convexity of our problem, guarantees convergence to the global minimum.

Despite these gains in simplicity, the surrogate function still does not decompose into a sum of n terms, with each depending on only one β_i. The fact that the even numbered β_i do not interact given the odd numbered β_i (and vice versa) suggests alternating updates of the two blocks of even and odd numbered parameters. In practice, this block relaxation strategy converges too slowly to be competitive. Fixing β_i−1 and β_i+1 leaves too little room to move β_i. Fortunately, full minimization of the quadratic is less onerous than one might expect. The surrogate function can be written in a matrix form

$$g_{\epsilon },m(\beta \mid {\beta }^{\left(m\right)})=\frac{1}{2}{\beta }^T{\mathbf{A}}_m\beta -{\mathbf{b}}_m^T\beta +{\tilde{c}}_m,$$ (3)

where A_m is a tridiagonal symmetric matrix. In view of the strict convexity of the surrogate function, A_m is also positive definite. The nonzero entries of A_m and b_m are

$$a_{1,1}^{\left(m\right)}=1+\frac{{\lambda }_1}{{\parallel {\beta }_1^{\left(m\right)}\parallel }_{2,\epsilon }}+\frac{{\lambda }_2}{{\parallel {\beta }_2^{\left(m\right)}-{\beta }_1^{\left(m\right)}\parallel }_{2,\epsilon }}$$

$$a_{i,i}^{\left(m\right)}=1+\frac{{\lambda }_1}{{\parallel {\beta }_i^{\left(m\right)}\parallel }_{2,\epsilon }}+\frac{{\lambda }_2}{{\parallel {\beta }_i^{\left(m\right)}-{\beta }_{i-1}^{\left(m\right)}\parallel }_{2,\epsilon }}+\frac{{\lambda }_2}{{\parallel {\beta }_{i+1}^{\left(m\right)}-{\beta }_i^{\left(m\right)}\parallel }_{2,\epsilon }},i=2,\dots ,n-1;$$

$$a_{n,n}^{\left(m\right)}=1+\frac{{\lambda }_1}{{\parallel {\beta }_n^{\left(m\right)}\parallel }_{2,\epsilon }}+\frac{{\lambda }_2}{{\parallel {\beta }_n^{\left(m\right)}-{\beta }_{n-1}^{\left(m\right)}\parallel }_{2,\epsilon }};$$

$$a_{i,i+1}^{\left(m\right)}=-\frac{{\lambda }_2}{{\parallel {\beta }_{i+1}^{\left(m\right)}-{\beta }_i^{\left(m\right)}\parallel }_{2,\epsilon }},i=1,\dots ,n-1;$$

$$a_{i-1,i}^{\left(m\right)}=-\frac{{\lambda }_2}{{\parallel {\beta }_i^{\left(m\right)}-{\beta }_{i-1}^{\left(m\right)}\parallel }_{2,\epsilon }},i=2,\dots ,n;$$

$$b_i^{\left(m\right)}=y_i,i=1,\dots ,n.$$

The minimum of the quadratic occurs at the point $\beta ={\mathbf{A}}_m^{-1}{\mathbf{b}}_m$. Thanks to the simple form of A_m, there is a variant of Gaussian elimination known as the tridiagonal matrix algorithm (TDM) or Thomas's algorithm [Conte and deBoor (1972)] that solves the linear system A_mβ = b_m in just 9n floating point operations. Alternatively, one can exploit the fact that the Cholesky decomposition of a banded matrix is banded with the same number of bands. As illustrated in Section 3.5, Thomas's algorithm is a vast improvement over block relaxation.

A few comments on the outlined strategy are in order. By changing the penalty from ∥ · ∥_ℓ1 to ∥ · ∥_2,ε, we favor less sparse solutions. However, spareness is somewhat besides the point. What we really need are criteria for calling deletions and duplications. The lasso penalty is imposed in this problem because most chromo-some regions have a normal copy number where y_i hovers around 0. The same practical outcome can be achieved by imputing copy number 2 for regions where the estimated β_i value is close to 0. (See Section 3.1.) It is also relevant to compare our minimization strategy to that of Friedman et al. (2007). The fusion step of their algorithm has the advantage of linking coefficients that appear to be similar, but it has the disadvantage that once such links are forged, they cannot be removed. This permanent commitment may preclude finding the global minimum, a limitation that our MM algorithm does not share.

Perhaps more importantly, our strategy can be adapted to handle more general objective functions, as long as the resulting matrix A in (3) is banded, or, at least, sparse. For example, consider the inpainting problem in image reconstruction [Chan and Shen (2002)]. In this two dimensional problem, the intensity levels for certain pixels are lost. Let S be the set of pixels with known levels. The objective function

$$f\left(\beta \right)=\frac{1}{2}\sum _{(i,j)\in S}{(y_{ij}-{\beta }_{ij})}^2+\lambda \sum _{i=1}^n\sum _{j=2}^n{\parallel {\beta }_{ij}-{\beta }_{i,j-1}\parallel }_{2,\epsilon }+\lambda \sum _{i=2}^n\sum _{j=1}^n{\parallel {\beta }_{ij}-{\beta }_{i-1,j}\parallel }_{2,\epsilon }$$

represents a compromise between imputing unknown values and smoothing. If we majorize the penalties in this objective function by quadratics, then we generate a quadratic surrogate function. The corresponding Hessian of the surrogate is very sparse. (Actually, it is banded, but not in a useful fashion.) Although we can no longer invoke Thomas's algorithm, we can solve the requisite system of linear equations by a sparse conjugate gradient algorithm.

All of the algorithms mentioned so far rely on known values for the tuning constants. We will describe our operational choices for these constants after discussing the problem of imputing chromosome states from estimated parameters in the next section.

2.3. Reconstructing discrete copy number states

Imputation of copy number as just described has the drawbacks of neglecting relevant information and requiring the estimation of a large number of parameters. To overcome these limitations, we now bring in the BAF x_i and focus on a model with a finite number of states. This setting brings us much closer to the HMM framework, often used for CNV reconstruction. Such similarity will be evident also in the numerical strategy we will use for optimization. However, our approach avoids the distributional assumptions at the basis of an HMM.

We consider 10 possible genotypic states ϕ, A, B, AA, AB, BB, AAA, AAB, ABB and BBB at each SNP. Here ϕ is the null state with a copy number of 0. (Note that, in the interest of parsimony, we contemplate double deletions, but not double duplications. This has more to do with the strength of signal from duplications than their actual frequency, and it is an assumption that can be easily relaxed.) In the model the average signal intensity μ_c(s) for a state s depends only on its copy number c(s). Regardless of whether we estimate the μ_c or fix them, they provide a more parsimonious description of the data than the β_i, which could take on a different value for each SNP. Furthermore, while we still need to impute a state for each SNP i, selecting one possible value out of 10 is intrinsically easier than estimation of the continuously varying β_i. Table 1 lists the copy number c(s), the expected value of y_i and the approximate distribution of x_i for each genotype state s. To reconstruct the state vector s = (s₁,…,s_n), we recommend minimizing the generic objective function

$$f\left(\mathbf{s}\right)=\sum _{i=1}^n{L}_1(y_i,s_i)+\alpha \sum _{i=1}^n{L}_2(x_i,s_i)+{\lambda }_1\sum _{i=1}^n\mid {\mu }_{c\left(s_i\right)}\mid +{\lambda }_2\sum _{i=2}^n\mid {\mu }_{c\left(s_i\right)}-{{\mu }_c}_{\left(s_{i-1}\right)}\mid ,$$ (4)

which again is a linear combination of losses plus penalties. Here α, λ₁ and λ₂ are positive tuning constants controlling the relative influences of the various factors. The lasso penalty makes the states with copy number 2 privileged. The fused-lasso penalty discourages changes in state. Minimizing the objective function (4) is a discrete rather than a continuous optimization problem.

Table 1.

Genotype states, corresponding copy numbers, expected values of y_i and approximate distributions of x_i

Genotype state s	Copy number c(s)	Mean of yi	Distribution of xi
ϕ	0	μ0 (< μ1)	Uniform on [0, 1]
A	1	μ1 (< 0)	≈0
B	1	μ1 (< 0)	≈1
AA	2	μ2 (≈ 0)	≈0
AB	2	μ2 (≈ 0)	≈1/2
BB	2	μ2 (≈ 0)	≈1
AAA	3	μ3 (> 0)	≈0
AAB	3	μ3 (> 0)	≈1/3
ABB	3	μ3 (> 0)	≈2/3
BBB	3	μ3 (> 0)	≈1

Different loss functions may be appropriate in different circumstances. If the intensity values are approximately Gaussian around their means with a common variance, then the choice L₁(y, s) = [y − μ_c(s)]² is reasonable. For the BAF x_i, the choice L₂(x s) = (x − ν_s)² is also plausible. Here ν_s is the centering constant appearing in the fourth column of Table 1. For instance, L₂(x, ABB) = (x − 2/3)². For the null state ϕ, we would take

$$L_2(x,\varphi )={\int }_0^1{(x-u)}^2\mathit{du}=\frac{1}{3}[x^3+{(1-x)}^3].$$

Once the loss functions are set, one can employ dynamic programming to find the state vector s minimizing the objective function (4). If we define the partial solutions

$$g_i\left(j\right)=\underset{s_1,\dots ,s_{i-1}}{\text{min}}f(s_1,\dots ,s_{i-1},s_i=j)$$

for i = 1,…,n, then the optimal value of the objective function is min_j g_n(j). We evaluate the partial solutions g_i(j) recursively via the update

$$g_{i+1}\left(j\right)=\underset{k}{\text{min}}[g_i\left(k\right)+L_1(y_{i+1},j)+\alpha L_2(x_{i+1},j)+{\lambda }_1\mid {\mu }_{c\left(j\right)}\mid +{\lambda }_2\mid {\mu }_{c\left(j\right)}-{\mu }_{c\left(k\right)}\mid ],$$ (5)

with initial conditions

$$g_1\left(j\right)=L_1(y_1,j)+\alpha L_2(x_1,j)+{\lambda }_1\mid {\mu }_{c\left(j\right)}\mid .$$

The beauty of dynamic programming is that it applies to a variety of loss and penalty functions.

In fact, it is possible to construct an even more parsimonious model whose four states correspond to the four copy numbers 0, 1, 2 and 3. The loss function L₁(y, c) = (y − μ_c)² is still reasonable, but L₂(x, c) should reflect the collapsing of genotypes. Here c is the copy number. Two formulations are particularly persuasive. The first focuses on the minimal loss among the genotypes relevant to each copy number. This produces

$$L_2(x,c)=\{\begin{array}{cc}{\int }_0^1{(x-u)}^2\mathit{du}=\frac{1}{3}[x^3+{(1-x)}^3],\hfill & \hfill c=0,\hfill \\ \text{min}\{{(x-0)}^2,{(x-1)}^2\},\hfill & \hfill c=1,\hfill \\ \text{min}\{{(x-0)}^2,{(x-1∕2)}^2,{(x-1)}^2\},\hfill & \hfill c=2,\hfill \\ \text{min}\{{(x-0)}^2,{(x-1∕3)}^2,{(x-2∕3)}^2,{(x-1)}^2\}\hfill & \hfill c=3.\hfill \end{array}\phantom{\}}$$ (6)

The second formulation averages loss weighted by genotype frequency. There are other reasonable loss functions. Among these it is worth mentioning negative log-likelihood, Huber's function and the hinge loss function of machine learning.

Dynamic programming does require specification of the parameters characterizing the distribution of the intensities y_i and the BAF x_i. It may be possible to assign values to these parameters based on previous data analysis. If not, we suggest estimating them concurrently with assigning states. For example, if the parameters are the intensity means μ₀, μ₁, μ₂ and μ₃, then, in practice, we alternate two steps starting from plausible initial values for the μ_i. The first step reconstructs the state vector s. The second step re-estimates the μ_i conditional on these assignments. Thus, if G_i is the group of SNPs assigned copy number i, then we estimate μ_i by the mean of the y_i over G_i. Taking the median rather the mean makes the process robust to outliers. A few iterations of these two steps usually gives stable parameter estimates and state assignments. To further stabilize the process, we impose two constraints on the second step. If the number of SNPs assigned to G_i is less than a threshold, say, 5, we choose not to update μ_i and rather keep the estimate in the previous iteration. In each update we enforce the order of μ₀ <μ₁ <μ₂(≈ 0) < μ₃. In the following we will refer to the approach described in this section as dynamic programming imputation (DPI).

3. Results

3.1. Identification of deleted and duplicated segments by the fused lasso

In calling deletions and duplications with the fused lasso, we adopt the procedure of Tibshirani and Wang (2008). Originally designed for array-CGH platforms, this procedure aims to control false discovery rate (FDR). Fortunately, it can be readily applied to genotype data. The general idea is to formulate the problem as one of multiple hypothesis testing for nonoverlapping chromosome segments S₁ through S_K. For each segment S_k we define the test statistic

$${\widehat{z}}_k=\frac{{\Sigma }_{i∊S_k}{\widehat{\beta }}_i}{\sqrt{n_k}\widehat{\sigma }},$$

where n_k is the number of SNPs in segment S_k and $\widehat{\sigma }$ is a conservative estimate of standard deviation of the ${\widehat{\beta }}_i$ across all segments based on the y_i values between their 2.5 and 97.5 percentiles. The associated p-value for segment S_k is approximated by $p_k=2P(Z>\mid \widehat{z}k\mid )$ for Z ~ N(0, 1). For a given threshold q ∈ (0, 1), we estimate the FDR by

$$\widehat{\text{FDR}}\left(q\right)=\frac{K_q\cdot 1∕K{\Sigma }_{k=1}^K{n}_k}{{\Sigma }_{k=1}^K{n}_k{1}_{(p_k\le q)}}=\frac{q{\Sigma }_{k=1}^K{n}_k}{{\Sigma }_{k=1}^K{n}_k{1}_{(p_k\le q)}}.$$ (7)

Here the FDR is defined as the ratio between the number of SNPs in nominal CNV segments with true copy number 2 and the total number of SNPs claimed to be within CNV segments. In the FDR estimate (7), q is roughly regarded as the fraction of null (copy number 2) segments among all candidate CNV segments. In the numerator, $\frac{1}{K}{\Sigma }_{k=1}^K{n}_k$ counts the average SNP number within each segment, and Kq estimates the expected number of null segments. In the denominator, ${\Sigma }_{k=1}^K{n}_k{1}_{(p_k\le q)}$ counts the total number of SNPs claimed to be located in CNV segments. Thus, this approximation is desired according to the SNP-number-based definition.

Once we decide on an FDR level α, the threshold q is determined as the largest value satisfying $\widehat{\mathrm{FDR}}\left(q\right)\le \alpha$. We call a segment S_k a deletion if ${\widehat{z}}_k<0$ and p_k ≤ q and a duplication if ${\widehat{z}}_k>0$ and p_k ≤ q.

3.2. Choice of tuning constants

Choice of the tuning constants λ₁ and λ₂ is nontrivial. Because they control the sparsity and smoothness of the parameter vector β and therefore drive the process of imputation, it is crucial to make good choices. Both of the references Friedman et al. (2007) and Wu and Lange (2008) discuss the problem and suggest solutions in settings similar to ours. While explicit theoretical expressions for optimal λ₁ and λ₂ are currently unavailable, known results can inform practical choices.

Friedman et al. (2007) consider the optimal solution to the fused-lasso problem

$$\widehat{\beta }({\lambda }_1,{\lambda }_2)=\text{arg}\underset{\beta }{\text{min}}\frac{1}{2}\sum _{i=1}^n{(y_i-{\beta }_i)}^2+{\lambda }_1\sum _{i=1}^n\mid {\beta }_i\mid +{\lambda }_2\sum _{i=1}^n\mid {\beta }_i-{\beta }_{i-1}\mid .$$

They prove that $\widehat{\beta }({\lambda }_1,{\lambda }_2)$ for λ₁ > 0 is a soft-thresholding of $\widehat{\beta }(0,{\lambda }_2)$ when λ₁ = 0, namwly,

$${\widehat{\beta }}_i({\lambda }_1,{\lambda }_2)=\text{sign}\left({\widehat{\beta }}_i(0,{\lambda }_2)\right){(\mid {\widehat{\beta }}_i(0,{\lambda }_2)\mid -{\lambda }_1)}_{+},i=1,\dots ,n.$$ (8)

This implies that λ₁ > 0 will drive to 0 those segments of the piecewise constant solution $\widehat{\beta }(0,{\lambda }_2)$ whose absolute values are close to 0. It is also important to note that, since $\widehat{\beta }(0,{\lambda }_2)$ is piecewise constant, its effective dimension is much lower than n.

To understand how the optimal values of these tuning parameters depend on the dimension of the vector β, let us recall pertinent properties of the Lasso estimator in linear regression. In this setting

$$\widehat{\beta }=\text{arg}\underset{\beta }{\text{min}}\frac{1}{2}{\parallel \mathbf{y}-Z\beta \parallel }_{l_2}^2+\lambda {\parallel \beta \parallel }_{l_1},$$ (9)

where ${\mathbf{y}}_{n\times 1}~\mathcal{N}({\mathbf{Z}}_{n\times p}{\beta }_{p\times 1},{\sigma }^2{\mathbf{I}}_{n\times n})$, and ∥ · ∥_ℓ1 and ∥ · ∥_ℓ2 are the ℓ₁ and ℓ₂ norms. Candès and Plan (2009), Donoho and Johnstone (1994)and Negahban et al. (2009) show that a Lasso estimator with $\lambda =c\sigma \sqrt{\log p}$ for some constant c leads to an optimal upper bound on ${\parallel \mathbf{Z}\beta -\mathbf{Z}\widehat{\beta }\parallel }_{{\ell }_2}^2$. Our problem with λ₁ = 0 fits in this framework if we reparameterize via δ₁ = β₁ and δ_i = β_i − β_i−1 for i for i = 2, …,n. In the revised problem

$$\widehat{\delta }=\text{arg}\underset{\delta }{\text{min}}\frac{1}{2}\sum _{i=1}^n{\left(y_i-\sum _{j=1}^i{\delta }_j\right)}^2+{\lambda }_2\sum _{i=2}^n\mid {\delta }_i\mid ,$$ (10)

p = n, and the design matrix is lower-triangular with all nonzero entries equal to 1. This finding suggests that we scale λ₂ by $\sqrt{\log n}$

On the basis of these observations, we explored the choices

$${\lambda }_1={\rho }_1\sigma {\lambda }_2={\rho }_2\sigma \sqrt{\text{log}n},{\rho }_1,{\rho }_2>0.$$

Here σ relates the tuning parameters to the noise level. Because the effective dimension in (8) is much smaller than n, we assumed that λ₁ does not depend on n. Although ρ₁ and ρ₂ can be tuned more aggressively by cross-validation or criteria such as BIC, we chose the sensible and operational combination

$${\lambda }_1=\sigma ,{\lambda }_2=2\sigma \sqrt{\text{log}n}.$$ (11)

A small scale simulation study suggested that the performance of our methods does not vary substantially for values of ρ₁ and ρ₂ close to 1 and 2, respectively. One may also vary ρ₁ and/or ρ₂ mildly to achieve different combinations of sensitivity and specificity as defined in Section 3.4. (Data not shown.)

In practice, we do not know the value of σ. Here we estimated a different σ for each individual, using the standard deviation of y_i values between their 2.5 and 97.5 percentiles. We decided to use only data points within the 95%-interquantile range in order to exclude values of y_i corresponding to possible deletions and duplications. Other possible robust estimators are based on the median absolute deviation or the winsorized standard deviation. In a small-scale simulation we did not observe substantial differences between these estimators. (Data not shown.)

While most of the experiments in the paper used the values of λ₁ and λ₂ suggested in equation (11), we also designed and conducted a more general simulation study to find the optimal values of these tuning parameters; see Section 3.8 for details.

3.3. Simulated data with in silico CNVs

To illustrate the effectiveness of our algorithms, we tested them on simulated data. Real data with empirically validated CNVs would be ideal, but such a gold standard does not exist. Instead, we used data from male and female X chromosomes to construct in silico CNV. Since males are equipped with only one X chromosome, we can use their genotype data to approximate the signal generated by deletion regions. A patchwork of female and male data mimics what we expect from an ordinary pair of homologous chromosomes with occasional deletions. Our X chromosome data come from the schizophrenia study sample of Vrijenhoek et al. (2008) genotyped on the Illumina platform. We focus on the 307 male and 344 female controls.

To avoid artifacts, the data needed to be preprocessed. We identified SNP clusters on the X chromosome using the Beadstudio Illumina software on female controls. These clusters permit estimation of parameters typical of a diploid genome. We then normalized the corresponding male SNP signals relative to the corresponding female signals. Finally, to destroy the signature of possible CNVs in the female data, we permuted the order of the SNPs. This action breaks up the patterns expected within CNV regions and eliminates the smooth variation in the intensity signals [Diskin et al. (2008)].

After these preprocessing steps, we generated ordinary copy number regions from the female data and deleted regions from the male data. We also generated duplications by taking the weighted averages

$$y_{i,dup}=y_{i,f}+0.55\times \mid \text{median}\left(y_f\right)-\text{median}\left(y_m\right)\mid ,$$

$$x_{i,dup}=\frac{1}{3}{x}_{i,m}+\frac{2}{3}{x}_{i,f}$$

for the intensities and BAFs, where the f and m subscripts refer to females and males. Because duplications show a lesser increase in logR values than the deletions show a decrease, the factor 0.55 multiplies the absolute difference |median(y_f)−median(y_m)| between median female and male intensities.

We generated two different data sets to assess the operating characteristics of the proposed algorithms. In both data sets the number of deletions equals the number of duplications. Data set 1 consists of 3600 sequences, each 13,000 SNPs long, with either a deletion or a duplication in the central position. The CNVs had lengths evenly distributed over the 6 values 5, 10, 20, 30, 40 and 50 SNPs. Data set 2 consists of 300 sequences with variable numbers of SNPs and either a deletion or duplication in the central position. The sequence lengths were evenly distributed over the values 4000, 8000, 12,000, 16,000 and 20,000 SNPs; the CNV lengths followed the distribution of data set 1.

The sequence and CNV lengths in our simulations were chosen to roughly mimic values expected in real data. For the Illumina HumanHap550 BeadChip platform, the median number of SNPs per chromosome arm is 13,279, with a median absolute deviation of 8172. Current empirical data suggests that there is usually at most one CNV per chromosome arm [Wang et al. (2007)] and that the length of the typical CNV is usually less than 50 SNPs [Jakobsson et al. (2008)]. The sequences from data set 1 represent an average chromosome arm, while the sequences from data set 2 capture the diversity across all chromosome arms. Both data sets have useful lessons to teach.

3.4. Measures of accuracy and a benchmark algorithm

We will measure accuracy on a SNP by SNP basis, adopting the following indexes: true positive rate (TPR or sensitivity), false positive rate (FPR or 1-specificity), and false discovery rate (FDR). These are defined as the ratios

$$\text{TPR}=\frac{\text{TP}}{\mathrm{P}}=\frac{\text{TP}}{\text{TP}+\text{FN}},$$

$$\text{FPR}=\frac{\text{FP}}{\mathrm{N}}=\frac{\text{FP}}{\text{FP}+\text{TN}},$$

$$\text{FDR}=\frac{\text{FP}}{\text{TP}+\text{FP}},$$

where the capital letters T, F, P, N and R stand for true, false, positive, negative and rate, respectively. For example, the letter P by itself should be interpreted as the number of SNPs with true copy number equal to 0, 1 or 3; the pair of letters FN should be interpreted as the number of SNPs with true copy number 0, 1 or 3 but imputed copy number 2. We will also evaluate the number of iterations until convergence and the overall computational time required by each algorithm.

For benchmarking purposes, we will compare the performance of the proposed algorithms to that of PennCNV [Wang et al. (2007)], a state-of-the-art hidden Markov model for CNV discovery on Illumina data. PennCNV bases the geno-type call for SNP i on its y_i and x_i measurements and its major and minor allele frequencies. We expect PennCNV to perform well because it has been extensively tuned on real and simulated data. The main aim of our comparisons is simply to check whether the new algorithms suffer a substantial loss of accuracy relative to PennCNV.

3.5. Convergence of the MMTDM and MMB algorithms

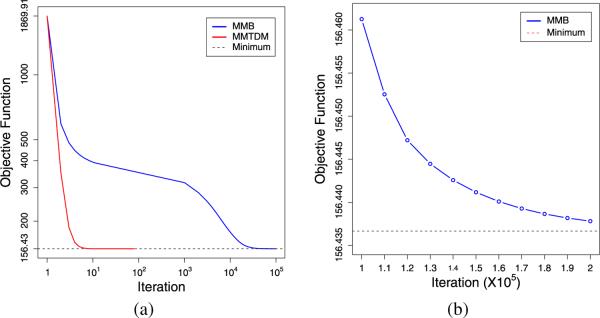
We first investigate two versions of the fused-lasso procedure. Both implement the MM algorithm on the objective function (2). The MMTDM algorithm solves the minimization step by the tridiagonal matrix algorithm. The MMB algorithm approximately solves the minimization step by one round of block relaxation. To assess the rate of convergence of MMTDM and MMB, we used data set 1 with 3600 sequences of 13,000 SNPs each. We declared convergence for a run when the difference between the objective function at two consecutive iterations fell below 10⁻. To limit the computational burden, we set the maximum number of iterations equal to 10,000. Both algorithms started with the values β_i = y_i. Each entry of Table 2 summarizes the results for a different CNV width. The table makes it abundantly clear that MMB is not competitive. Because MMB never converged in these trials, we took one sequence and ran it to convergence under the more stringent convergence criterion of 10⁻⁶. Figure 3 plots the value of the objective function under the two algorithms. Examination of these plots shows that MMTDM is on the order of 1000 times faster than MMB.

Table 2.

Number of iterations until convergence of MMTDM and MMB. For MMTDM, each entry summarizes the average number of iterations required for convergence; Standard errors appear in parentheses. MMB never converges within 10,000 iterations in this case

CNV size	5	10	20	30	40	50
MMB	>10,000	>10,000	>10,000	>10,000	>10,000	>10,000
MMTDM	33.1 (13.0)	33.3 (12.0)	34.5 (13.9)	33.3 (12.9)	33.7 (12.2)	33.9 (12.1)

Fig. 3.

Comparison of convergence rates for the two algorithms MMB and MMTDM for the fused lasso. (a) MMTDM converges much faster than MMB. Blue line: MMB; Red line: MMTDM; Black dashed line: minimum value of objective function; (b) After 10⁵ iterations, MMB converges with an accuracy of 0.01.

3.6. Effect of including BAF in discrete reconstruction

Data set 1 also illustrates the advantages of including BAF information in CNV reconstruction. Here we focus on dynamic programming imputation (DPI) based on the objective function (4). Note that this function does not incorporate prior knowledge of the frequency of deletions versus duplications. In running the dynamic programming algorithm, we rely on results from a previous study [Wang et al. (2009)] to initialize the intensity parameters μ_k. Because the μ_k are re-estimated after each round of imputation, we can safely ignore the slight differences between the genotyping platforms of the previous and current studies. Table 3 reports the various accuracy indexes as a function of the tuning constant α determining the relative influence of BAF. Although we already have acceptable reconstruction for α = 0, increasing it leads to substantial improvements. When α = 12, we reach an excellent balance between sensitivity and specificity. In the following we adopt the value α = 12 unless noted to the contrary.

Table 3.

TPR, FPR and FDR in DPI as α varies

α	TPR (%)	FPR (%)	FDR (%)	α	TPR (%)	FPR (%)	FDR (%)
0	87.56	0.0064	3.53	15	94.08	0.0010	0.53
1	89.55	0.0031	1.70	16	94.14	0.0010	0.53
2	90.68	0.0019	1.04	17	94.18	0.0010	0.54
3	91.57	0.0017	0.92	18	94.22	0.0011	0.57
4	92.14	0.0014	0.77	19	94.26	0.0011	0.57
5	92.55	0.0012	0.63	20	94.30	0.0012	0.63
6	92.80	0.0010	0.53	21	94.37	0.0012	0.65
7	93.06	0.0010	0.53	22	94.39	0.0013	0.68
8	93.27	0.0010	0.52	23	94.46	0.0015	0.77
9	93.50	0.0010	0.51	24	94.48	0.0015	0.81
10	93.58	0.0009	0.49	25	94.50	0.0016	0.83
11	93.66	0.0009	0.50	26	94.53	0.0016	0.86
12	93.83	0.0009	0.49	27	94.55	0.0018	0.93
13	93.94	0.0009	0.49	28	94.62	0.0018	0.95
14	94.02	0.0010	0.52	29	94.59	0.0019	1.02

3.7. Accuracy comparisons for various CNV sizes

Table 4 reports the values of the accuracy indices for various CNV sizes and types. Here we compare PennCNV, fused-lasso minimization under MMTDM and DPI on data set 1. To avoid overfitting and a false sense of accuracy, we used 3-fold cross-validation to choose α. The accuracy indices reported in the table represent averages over the left-out thirds. Although PennCNV falters a little with the shortest CNVs, it is clearly the best of the three methods. More surprising, DPI achieves comparable FPR and FDR to PennCNV as well as fairly good TPR. In particular, its FDR is uniformly low across CNV sizes and types. Overall, Table 4 demonstrates the promise of DPI. In contrast, the results for fused-lasso minimization are discouraging. Despite its post-processing to control FDR, it does poorly in this regard. Furthermore, it displays substantially worse TPR for duplications than PennCNV and DPI, particularly for duplications spanning only 5 SNPs. This behavior is to be expected given the poor ability of signal strength alone to separate duplications from normal chromosome regions. The performance of fused-lasso minimization underscores the advantages of explicitly modeling the discrete nature of the state space and taking BAF information into account. Nonetheless, it is important to keep in mind that the previous data sets are by design more favorable to PennCNV and DPI. The analysis of tumor samples with ambiguous copy numbers or signals from experimental devices, such as CGH arrays that lack allele-specific information, are bound to cast fused-lasso minimization in a kinder light.

Table 4.

Accuracy comparison of three methods for various CNV sizes. All accuracy indexes are listed as percentages. The average tuning parameters used in the fused lasso were λ₁ =0.13 (0.04) and λ₂ = 0.77 (0.22); standard deviations appear in parentheses. For DPI, the 3-fold cross-validation accuracy indexes are averages over the leftover thirds; initial values of average LogR for each copy number state: μ₀ = −5.5923, μ₁ = −0.6313, μ₂ = −0.0045, μ₃ = 0.3252

		PennCNV			Fused Lasso			DPI
CNV size	CNV type	TPR	FPR	FDR	TPR	FPR	FDR	TPR	FPR	FDR
5	Del	83.80	0.0017	4.92	76.67	0.0202	40.66	76.67	0.0006	1.88
	Dup	58.53	0.0011	4.67	00.33	0.0065	98.05	53.60	0.0003	1.28
10	Del	95.03	0.0011	1.45	94.23	0.0130	15.21	89.37	0.0005	0.77
	Dup	93.43	0.0006	0.78	26.00	0.0128	39.01	92.30	0.0006	0.89
20	Del	94.63	0.0008	0.58	96.97	0.0159	09.62	89.87	0.0016	1.15
	Dup	96.13	0.0014	0.92	74.93	0.0126	09.86	95.50	0.0011	0.76
30	Del	94.57	0.00130.62	0.28	96.76	0.0156	06.53	94.73	0.0013	0.62
	Dup	96.09	0.0001	0.05	85.84	0.0173	08.02	95.39	0.0012	0.55
40	Del	97.83	0.0018	0.59	98.33	0.0158	04.94	98.46	0.0006	0.19
	Dup	94.61	0.0014	0.46	87.88	0.0181	06.24	94.66	0.42	0.42
50	Del	94.33	0.0003	0.07	95.49	0.0162	04.21	93.82	0.0010	0.26
	Dup	94.50	0.0003	0.09	91.06	0.0121	03.33	95.03	0.0011	0.30
Overall		94.42	0.0009	0.49	88.00	0.0147	07.73	93.70	0.0009	0.50

3.8. Accuracy comparison for various SNP sequence lengths

Data set 2 allowed us to assess performance on longer sequences with less frequent SNPs and to gain insight into the impact of the tuning parameters λ₁ and λ₂. For the latter purpose we adopted two strategies: (a) define λ₁ and λ₂ by the values displayed in equation (11), and (b) adopt an “oracle” approach that relies on the knowledge of locations of deletions and duplications. Strategy (b) chooses constant values across the individuals to maximize TPR (sensitivity) while keeping FPR and FDR levels comparable to those under strategy (a). The oracle approach is not applicable to real data sets, where locations of deletions and duplications are unknown. We adopted it in this analysis to determine how optimal tuning parameters vary with sequence length.

Tables 5–7 summarize results for PennCNV, fused-lasso minimization and DPI, respectively. As with data set 1, PennCNV achieves the best sensitivity, followed by DPI. The best control of false positives occurs with DPI. The accuracy of the methods and the optimal values of λ₁ and λ₂ do not change with sequence length n. However, it is clear that the advantages of selecting individual-specific λ values outweigh the benefit of selecting constant λ values that maximize overall performance. In fact, the choice of the oracle λ is excessively influenced by some individuals with poor quality data; to control false discoveries in these subjects, one lowers performance in more favorable settings.

Table 5.

Accuracy of PennCNV for various SNP sequence lengths

Sequence length	TPR (%)	FDR (%)	FDR (%)
4000	95.54	0.0029	0.46
8000	95.43	0.0019	0.62
12,000	96.71	0.0038	1.77
16,000	96.46	0.0012	0.74
20,000	95.60	0.0007	0.59
Overall	95.95	0.0018	0.84

Table 7.

Accuracy of DPI for various SNP sequence lengths. For strategy (a), average values ofλ₁ and λ₂ specified for each individual are summarized for each SNP sequence length; Standard errors appear in parentheses

Sequence length	λ 1	λ 2	TPR (%)	FPR (%)	FDR (%)
(a) λ1 and λ2 specified for each individual according to equation (11)
4000	0.13 (0.04)	0.73 (0.23)	93.70	0.0013	0.22
8000	0.13 (0.04)	0.76 (0.24)	93.33	0.0007	0.22
12,000	0.12 (0.03)	0.76 (0.16)	95.78	0.0004	0.22
16,000	0.13 (0.04)	0.79 (0.22)	94.77	0.0009	0.56
20,000	0.13 (0.04)	0.80 (0.22)	92.32	0.0005	0.43
Overall	−	−	93.98	0.0007	0.33
(b) Oracle choice of λ1 and λ2: constant values across all individuals
4000	0.15	2.50	87.72	0.0013	0.22
8000	0.24	2.70	86.35	0.0007	0.25
12,000	0.12	0.0	94.43	0.0004	0.22
16,000	0.18	2.10	91.51	0.0009	0.60
20,000	0.16	20,00	90.18	0.0005	0.41
Overall	−	−	90.04	0.0007	0.34

3.9. Speed comparison of different methods for CNV detection

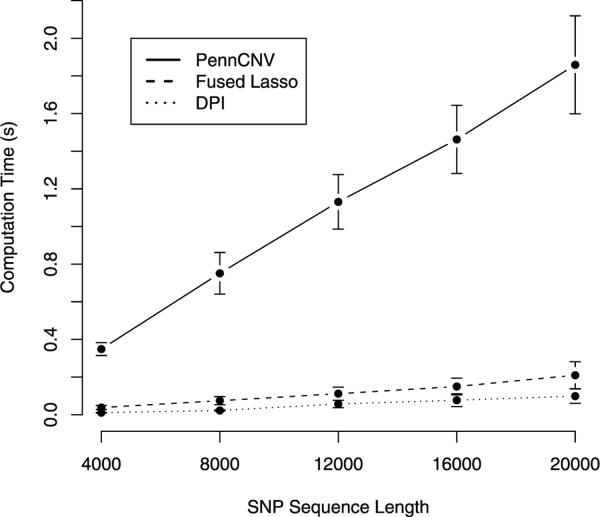
Finally, we compared the computational speeds of the three methods. Although the cost of each scales linearly with the number of SNPs, run times vary considerably in practice (see Figure 4). We base our comparisons on data set 2 run on an Intel Xeon 2.80 GHz processor operating under Linux. The PennCNV distributed software (2008, November 19 version) is a combination of C and Perl. We implemented DPI and the MMTDM algorithm for fused-lasso minimization in Fortran 95. The penalty tuning parameters were chosen according to equation (11). For DPI we set α = 12. Table 8 lists average run times for each sequence sample; standard errors appear in parentheses. As we anticipated, fused-lasso minimization and DPI require less computation per iteration and run much faster than PennCNV. DPI is 2 to 3 times faster than fused-lasso minimization.

Fig. 4.

Graphical comparison of computation speed as sequence length varies. Solid line: PennCNV; Dashed line: Fused Lasso; Dotted line: DPI.

Table 8.

Computation times for the three CNV imputation methods. The tuning constants in the fused lasso and DPI are noted in Section 3.8

Sequence length	PennCNV (s)	Fused Lasso (s)	DPI (s)
4000	0.349 (0.034)	0.038 (0.011)	0.011 (0.002)
8000	0.751 (0.111)	0.075 (0.022)	0.023 (0.003)
12,000	1.131 (0.145)	0.112 (0.035)	0.057 (0.020)
16,000	1.462 (0.181)	0.150 (0.045)	0.077 (0.034)
20,000	1.859 (0.260)	0.210 (0.072)	0.099 (0.038)

3.10. Analysis of four real samples

We tested the three methods on genome scan data on four schizophrenia patients from the study of Vrijenhoek et al. (2008). These patients were selected because they each exhibit one experimentally validated CNV (two deletions and two duplications). The four CNVs disrupt the genes MYT1L, CTNND2, NRXN1 and ASTN2, which play important roles in neuronal functioning and are associated with schizophrenia. This subset of the data is ideal for our purpose. The entire data set was collected as part of a genome-wide association study and consists of blood samples from unrelated individuals. It is expected that only a modest amount of CNV may be present; most CNVs probably represent inherited neutral polymorphisms rather de novo mutations. Unlike cancer cell lines, copy numbers should rarely exceed 3.

We analyzed the entire genomes of these four subjects, applying the three methods to each chromosome arm. In calling CNVs with fused-lasso minimization, we controlled FDR at the 0.05 level. The penalty tuning parameters were chosen according to equation (11). For dynamic programming, we set α 12. It took on average 113.8, 8.6 and 4.7 seconds for the three methods to run on the approximately 550k SNPs typed on each individual. The computational efficiency of DPI displayed here may be a decisive advantage in other data sets with thousands of participants. To focus on signals with a higher chance of being real, we eliminated all CNV calls involving fewer than 5 SNPs.

Table 9 reports the numbers of detected CNVs and their median sizes; median absolute deviations are listed in parentheses. PennCNV produced the largest number of CNVs calls, followed by fused-lasso minimization. The CNVs detected by PennCNV and DPI had similar sizes; those detected by fused-lasso minimization tended to be longer. Table 10 summarizes the overlap between the CNVs calls for the three methods. The vast majority of CNVs detected by DPI are also detected by PennCNV. There is a smaller overlap between PennCNV and the Fused Lasso.

Table 9.

CNVs detected by PennCNV, Fused Lasso and DPI for each patient

	PennCNV		Fused Lasso		DPI
Patient	#CNV	CNV size	#CNV	CNV size	#CNV	CNV size
1	34	8 (4)	18	17 (7)	16	10 (4)
2	12	7 (3)	13	11 (9)	7	7 (3)
3	19	8 (4)	14	18 (16)	22	7 (2)
4	85	8 (4)	20	19 (16)	18	9 (4)

Table 10.

Overlap of CNVs detected by PennCNV, Fused Lasso and DPI. The percentages listed in parentheses refer to the ratio of the number of overlapping CNVs to the total number of unique CNVs detected. For patient 1 DPI treated a large duplication region on the long arm of Chromosome 22 as two segments. Thus, the number of overlapping CNVs was increased by 1 compared to PennCNV vs Fused Lasso

Patient	PennCNV vs Fused Lasso	PennCNV vs DPI	Fused Lasso vs DPI	3 methods
1	7 (15.6%)	12 (31.6%)	9 (36.0%)	8 (16.7%)
2	7 (38.9%)	6 (46.2%)	7 (53.8%)	6 (33.3%)
3	10 (43.5%)	15 (57.7%)	8 (28.6%)	8 (26.7%)
4	8 (8.2%)	13 (14.4%)	8 (26.7%)	7 (6.9%)

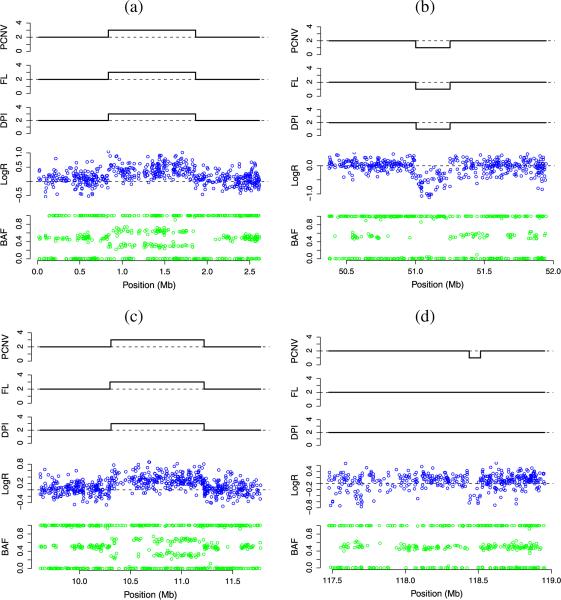
Three of the experimentally verified CNVs were detected by all three methods. The fourth, a deletion on 9q33.1 in patient 4, was detected only by PennCNV (see Figure 5). It is noteworthy that the quality of the data for this patient is poor. For example, it fails to pass the PennCNV quality control criterion requiring the standard deviation of LogR to be less than 0.2. In this sample the standard deviation is 0.26. It appears that the higher sensitivity of PennCNV comes at the price of allowing too many false positives. PennCNV calls an exceptionally high number (85) of CNVs for patient 4, with limited overlap with the other two methods.

Fig. 5.

PennCNV, fused-lasso minimization, and DPI detected experimentally verified CNVs in 4 schizophrenia patients:(a) A duplication on 2p25.3 of Patient 1; (b) A deletion on 2p16.3 of Patient 2; (c) A duplication on 5p15.2 of Patient 3; (d) A deletion on 9q33.1 of Patient 4. In each subplot from top to bottom, the first three panels display the CNV detected by PennCNV, fused-lasso minimization and DPI respectively, the fourth panel displays in blue y_i (LogR), and the fifth panel displays in green x_i (BAF).

4. Discussion

We have proposed two new methods for the reconstruction of CNV. Both methods are much faster than PennCNV, the current state-of-the-art method in CNV discovery. The greater accuracy of DPI versus fused-lasso minimization underscores the importance of using BAF measurements and capitalizing on the discrete nature of CNV imputation. DPI has the additional advantage of outputting the allelic copy numbers so helpful in refining the associations between CNVs and phenotypes. It is hardly surprising that DPI exhibits superior performance in the schizophrenia data where its underlying assumptions hold. By contrast in the analysis of tumor cells, it is much more difficult to fix a priori the number of copies. With its flexibility in fitting piecewise constant functions to LogR intensities, the fused lasso will shine in this less discrete setting.

We would like to emphasize that both proposed methods are rough compared to well-established algorithms like PennCNV. There is definitely room for further performance improvements by redefining the loss and penalty functions. As a concrete example, one could modify the fused-lasso penalties to reflect the distances between adjacent SNPs [Li and Zhu (2007)]. We suggest scaling the difference $\mid {\beta }_i-{\beta }_{i-1}\mid$ by the reciprocal of the physical distance $b_i-b_{i-1}$. Anyone wanting to use or modify our statistical procedures is welcome to our Fortran source code. Please contact the first author for a copy.

We can expect to see more applications of penalized estimation throughout genomics. In our view, penalized models are more parsimonious than hidden Markov models and achieve many of the same aims. Our redefinition of the fused-lasso penalty and application of the MM algorithm circumvent some of the toughest issues of penalized estimation in the CNV context and have important implications for other application areas such as time series analysis. For more traditional theoretical and numerical approaches to penalized estimation, we recommend the recent survey paper on ℓ₁ trend filtering [Kim et al. (2009)].

Table 6.

Accuracy of fused-lasso minimization for various SNP sequence lengths. For strategy (a), average values of λ₁ and λ₂ specified for each individual are summarized for each SNP sequence length; Standard errors appear in parentheses

Sequence length	λ 1	λ 2	TPR (%)	FPR (%)	FDR (%)
(a) λ1 and λ2 specified for each individual according to equation (11)
4000	0.13 (0.04)	0.73 (0.23)	88.40	0.0414	6.73
8000	0.13 (0.04)	0.76 (0.24)	89.54	0.0241	7.66
12,000	0.12 (0.03)	0.76 (0.16)	90.85	0.0148	7.00
16,000	0.13 (0.04)	0.79 (0.22)	87.63	0.0103	6.77
20,000	0.13 (0.04)	0.80 (0.22)	85.34	0.0084	7.07
Overall	−	−	88.35	0.0145	7.05
(b) Oracle choice of λ1 and λ2: constant values across all individuals
4000	0.16	0.80	83.70	0.0414	7.08
8000	0.19	0.80	77.46	0.0206	7.58
12,000	0.18	0.180	84.09	0.0141	7.20
16,000	0.17	0.90	81.12	0.0102	7.20
20,000	0.18	0.180	76.12	0.0077	7.26
Overall	−	−	80.50	0.0136	7.26