Stereoselectivity in Oxyallyl–Furan 4+3 Cycloadditions: Control of Intermediate Conformations and Dispersive Stabilisation with Evans’ Oxazolidinones

Abstract

Chiral oxazolidinones were previously thought to control cycloaddition stereoselectivity by steric crowding of one face of the substrate. We have discovered that in 4+3 cycloaddition reactions of oxallyls, the stereoinduction is caused instead by stabilising CH–π interactions that lead to reaction at the more crowded face of the oxazolidinone. Density functional theory calculations on the 4+3 cycloadditions of oxazolidinone-substituted oxyallyls with furans establish unexpected transition state conformations and a new explanation of selectivity.

Introduction

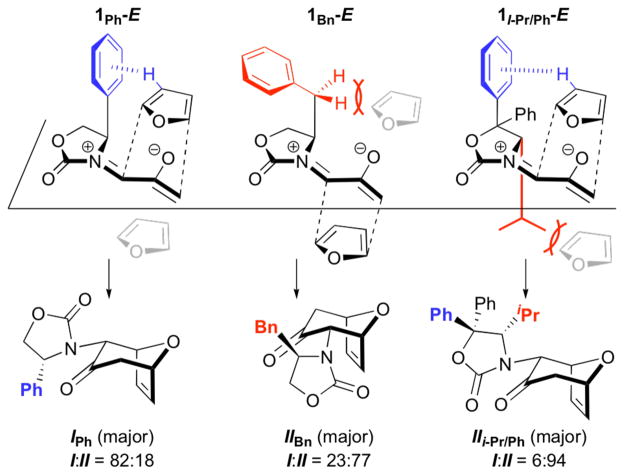
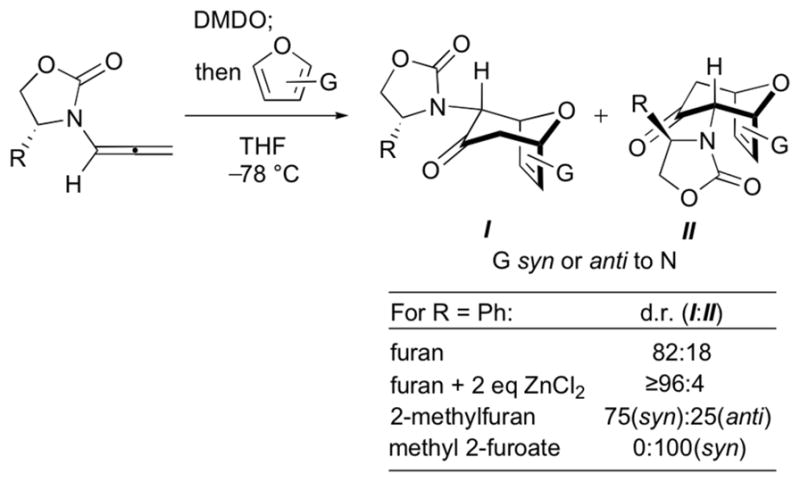
Amino acid-derived oxazolidinones are used extensively as chiral auxiliaries, following their introduction by Evans.¹ They have been applied to various cycloaddition reactions, including Diels–Alder^2–4 and 1,3-dipolar⁵ cycloadditions. We have found that they also provide useful stereoselectivities in the (4 + 3) cycloadditions of dienes with oxyallyls. These (4 + 3) cycloadditions are a key step in the transformation shown in Scheme 1. Oxidation of an allenamide with DMDO generates an oxyallyl, which is then trapped with a furan.^6,7 This sequence is a valuable synthetic procedure for formation of 7-membered carbocycles,^8,9 which had previously been achieved using various other chiral, donor-substituted oxyallyl cations.^10,11 Use of 4-phenyloxazolidinone as the auxiliary (R = Ph) provided the diastereomeric endo cycloadducts I and II in a ratio of 82:18,¹² and the ratio increased to ≥96:4 when ZnCl₂ was included in the reaction mixture.⁶

Scheme 1.

Oxazolidinone-directed asymmetric (4 + 3) cycloadditions of oxyallyls with furans.

The transformation shown in Scheme 1 is believed to involve the oxyallyl 1 (Scheme 2). The C_α–N bond in 1 is expected to have substantial double bond character, leading to the possibility of E and Z isomers.

Scheme 2.

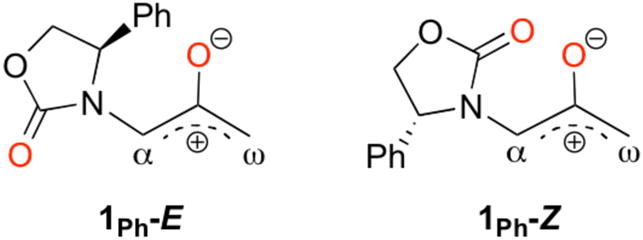
Isomers of the oxyallyl 1_Ph.

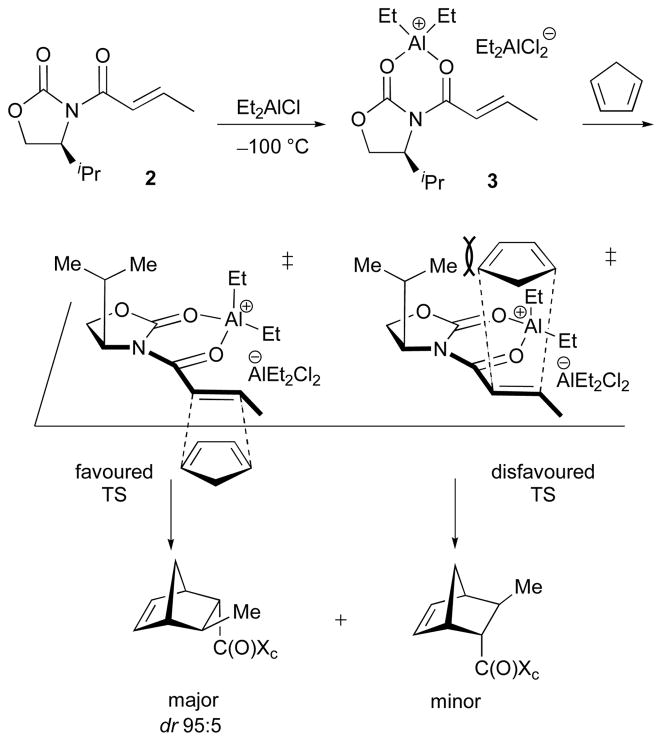
The mechanism by which oxazolidinones control cycloaddition stereoselectivity was examined by Evans during studies of Diels–Alder reactions (Scheme 3). These reactions were catalysed by ionisable aluminium-containing Lewis acids such as Et₂AlCl.² Evans showed that the stereoinduction arose through steric control. Chelation of the N-acyloxazolidinone 2 with AlEt₂⁺ was suggested to produce the active dienophile, 3, which is constrained to have a geometry in which the enone and the oxazolidinone ring lie within the same plane. Cycloaddition at the less-crowded face of 3, opposite the ⁱPr group, leads to the major product.

Scheme 3.

Evans’ oxazolidinone-directed asymmetric Diels–Alder reactions.

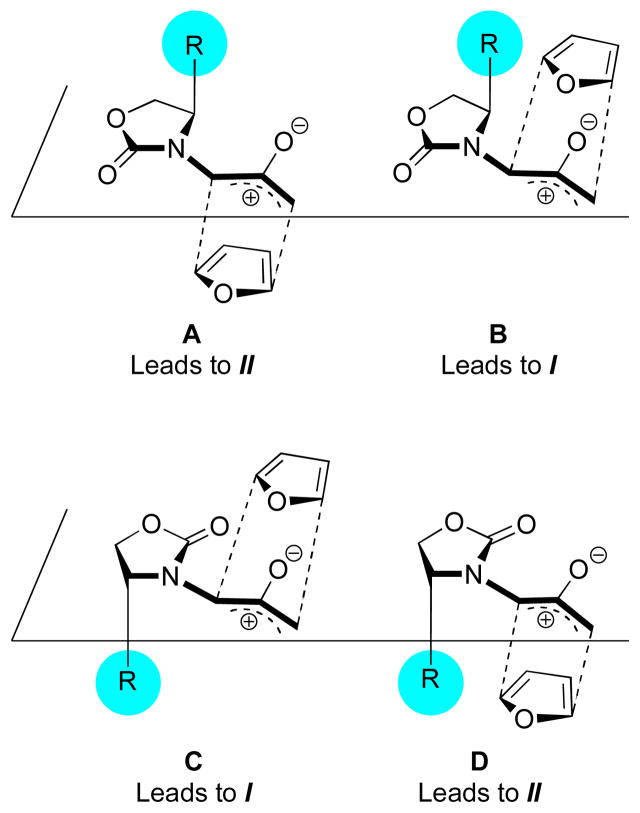
We originally supposed that a similar mode of stereocontrol was present in our oxyallyl–furan cycloadditions. Taking into account the E and Z isomers of 1, there are four plausible transition-state geometries. These are shown in Scheme 4. The less-crowded geometries, A and C, were presumed to be preferred over the more-crowded B and D. Out of A and C, geometry C was thought to be preferred, since it would lead to the major product observed experimentally. Moreover, C has a suitable geometry for forming a chelate with ZnCl₂, and the stereoselectivity was greater in the presence of ZnCl₂.

Scheme 4.

However, the cycloadditions of 1_Ph with substituted furans do not agree with this model. The reaction of 1_Ph with 2- methylfuran afforded the same major product as furan itself (I), but the reaction of 1_Ph with methyl 2-furoate provided the opposite diastereomer (II) as the sole cycloadduct.⁷ This reversal of stereoselectivity cannot easily be explained by the Evans-type mechanism.

We have undertaken a computational study, and report here that the factors that control stereoselectivity in oxallyl (4 + 3) cycloadditions are different from those established for Diels-Alder reactions involving the same oxazolidinone auxiliary. The cycloaddition of 1_Ph with furan is found to involve only the E conformer – i.e. geometries A and B shown in Scheme 4. This is the case even in the presence of ZnCl₂. The stereoselectivity is controlled not by steric repulsion between furan and the Ph group, but by “steric attraction”, where a stabilising CH–π interaction between furan and Ph favours cycloaddition at the more hindered π-face (geometry B). The sole involvement of 1-E, and the presence or absence of attractive CH–π interactions at the TS, correctly predict the stereoselectivities for other oxazolidinones. The reversal of stereoselectivity observed with methyl 2-furoate is also be explained by a mechanism involving only the E conformer of the oxallyl species.

Results and discussion

Electronic structure of donor-substituted oxyallyls

Density functional theory calculations were used to characterise the electronic structure of the oxazolidinone-substituted oxyallyls 1. The parent oxyallyl, 4 (Fig. 1), is a diradical, but is not an energy minimum. Highly-correlated calculations and photoelectron spectroscopy show it to have an open-shell singlet ground state, which lies 1.3 kcal mol⁻¹ below the triplet and undergoes a barrierless ring closure to cyclopropanone.^13,14 The diradical character of 4 is reflected quite well by B3LYP calculations.^15–18 At the B3LYP/6-311G(2d,p) level, the singlet diradical of 4 lies 10.8 kcal mol⁻¹ below the closed-shell singlet (which has one imaginary vibrational frequency). Although a DFT treatment is not ideal for the singlet diradical, and it predicts the singlet diradical to lie 0.8 kcal mol⁻¹ above the triplet, this error is relatively small.

Fig. 1.

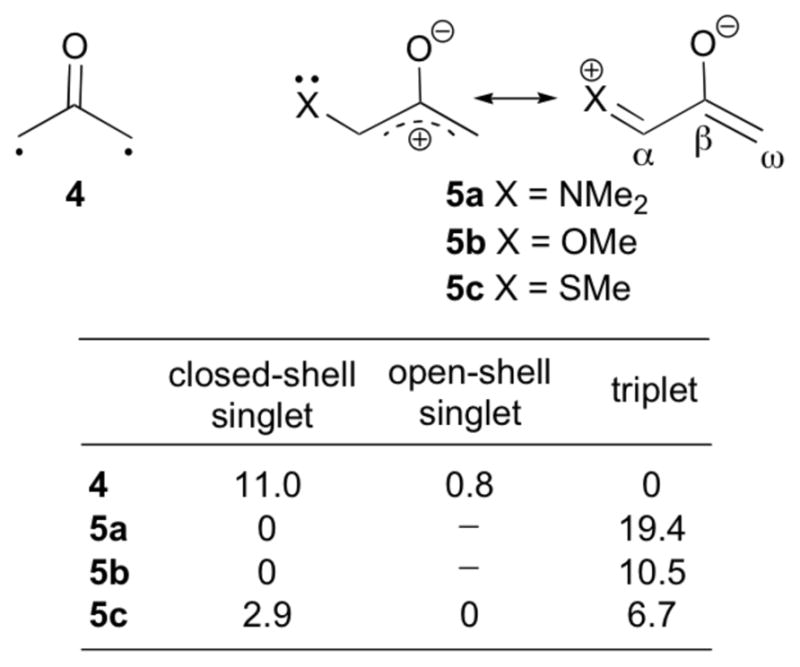
Energies of different electronic states of oxyallyls 4 and 5a–c [ΔE, kcal mol⁻¹, B3LYP/6-311G(2d,p)].

In the presence of a donor substituent, the closed-shell singlet of the oxyallyl (zwitterion) is stabilised. For both 5a (X = NMe₂) and 5b (X = OMe), B3LYP/6-311G(2d,p) calculations indicate a closed-shell ground state, which is stable with respect to an open-shell representation. The sulfur-substituted analogue 5c is more similar to 4 in retaining a singlet diradical ground state, but the closed-shell singlet lies only 2.9 kcal mol⁻¹ higher in energy.

The oxazolidinone-substituted oxyallyl 1_Ph has electronic properties similar to 5a and 5b. B3LYP/6-311G(2d,p) calculations indicate a negligible singlet instability (0.1 kcal mol⁻¹). The substituted structure, 1_Ph, is a local minimum on the B3LYP/6-31G(d) potential energy surface, but attempts to locate 1_Ph-Z led instead to the corresponding cyclopropanone. The cyclopropanone 1_Ph-E_cyc is 4.8 kcal mol⁻¹ more stable than 1_Ph-E (ΔH), and is the global minimum among all of the conformational and structural isomers of 1_Ph. Details of these related species are given in the ESI.

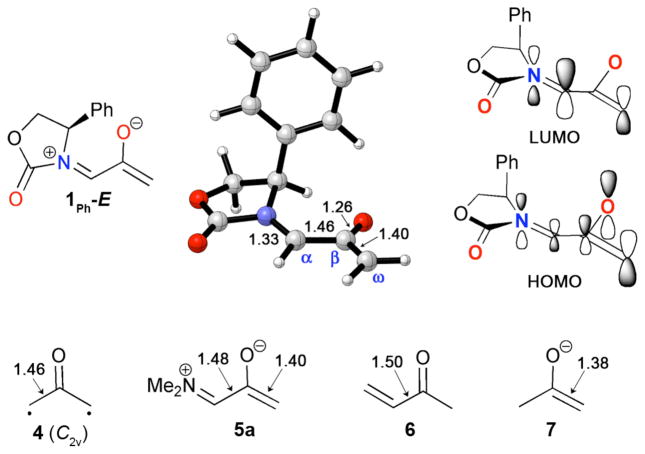
The geometry of 1_Ph-E is shown in Fig. 2. The CC bond lengths in 1_Ph-E are similar to those in 5a (also shown), and indicate that there is substantial electron delocalisation from nitrogen onto the allyl cation. The C_α–C_β distance (1.46 Å) is 0.04 Å shorter than the C_C=O–C_C=C bond in methyl vinyl ketone (6). The C_β–C_ω distance (1.40 Å) is only 0.02 Å longer than the C=C bond of acetone enolate (7). The C_α–N bond (1.33 Å) is intermediate in length between a C–N and a C=N bond.

Fig. 2.

Structure and molecular orbitals of 1_Ph-E, and related compounds [bond lengths in Å, B3LYP/6-31G(d)].

Fig. 2 also shows diagrams of the HOMO and LUMO of 1_Ph-E.¹⁹ The HOMO is enolate-like, and has a larger coefficient on C_ω than on C_α. The LUMO has both allyl cation and iminium π* character, with a larger coefficient on C_α than C_ω. All of these features indicate that 1_Ph-E is best regarded as an iminium enolate.

Transition states for (4 + 3) cycloadditions

Detailed earlier studies by Cramer²⁰ have revealed that the cycloadditions of oxyallyl cations with dienes can take place by several different mechanisms. For example, the highly electrophilic 2-hydroxyallyl cation was calculated to undergo (4 + 3) cycloaddition with furan by a two-step process. In comparison, the combination of enolate and iminium character in 1_Ph results in behaviour that is less markedly electrophilic. Transition states for the endo (4 + 3) cycloaddition of 1_Ph with furan are depicted in Fig. 3. The reaction is a concerted process, and bond development at the TS is more advanced at the nucleophilic carbon, C_ω.

Fig. 3.

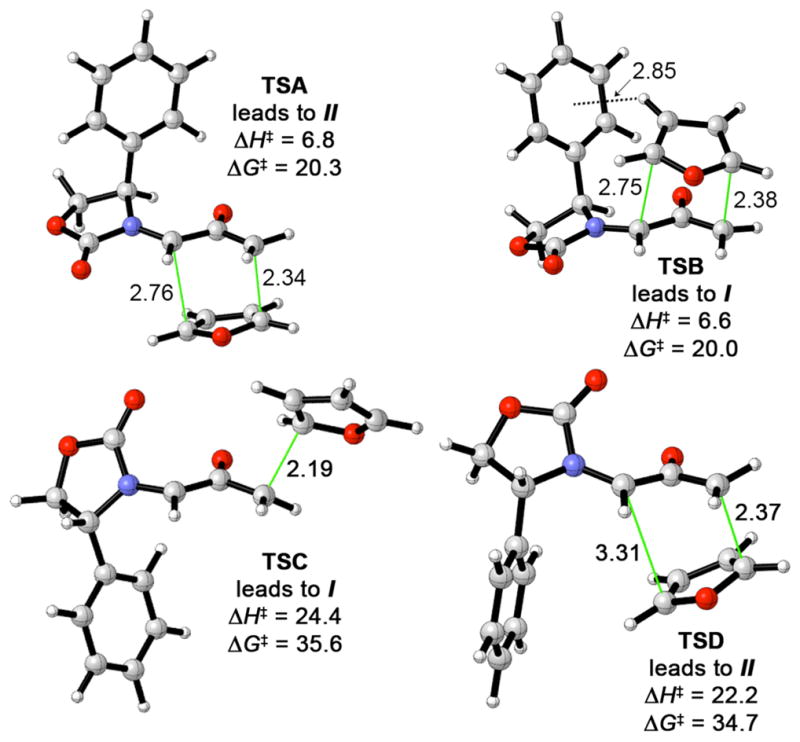
Transition structures and activation energies for the cycloaddition of 1_Ph with furan [298.15 K, B3LYP/6-31G(d)].

Although only the E isomer was located as an energy minimum for 1_Ph, cycloaddition transition states can be located for either the E or Z geometry. The latter are substantially higher in energy.²¹ For the E geometry, two concerted transition states were found—TSA and TSB—which lead to cycloadducts II and I, respectively. For the Z geometry, a concerted TS was located when furan adds to the more crowded π-face (TSD), but addition to the less crowded face is a stepwise process (TSC). Both TSC and TSD lie at high energies, due to electrostatic repulsion between the oxyallyl and carbonyl oxygens.

The Z transition states (C and D) are ≥14 kcal mol⁻¹ higher in energy than the E transition states (A and B); hence, cycloaddition takes place exclusively via 1_Ph-E. Unexpectedly, however, it is 0.2 kcal mol⁻¹ easier (ΔΔH^‡) for furan to add to the more crowded face of 1_Ph-E (TSB) than to the less crowded face (TSA). The corresponding free enegy difference is similar, ΔΔG^‡ = 0.3 kcal mol⁻¹. The small energy difference between TSA and TSB is in good qualitative agreement with the experimental stereoselectivity of 82:18 in favour of I.

Surprisingly, similar observations are made for the ZnCl₂-mediated cycloadditions of 1_Ph.²² Unlike Evans’ dienophile–AlEt₂⁺ complex, the ZnCl₂ complex of 1_Ph is 6.2 kcal mol⁻¹ more stable as the monodentate form, 1_Ph-E·ZnCl₂ (Scheme 5), than as the chelate 1_Ph-Z·ZnCl₂.²³ The cycloaddition transition structures for 1_Ph-E·ZnCl₂ and 1_Ph-Z·ZnCl₂ are analogous to those for uncomplexed 1_Ph, except more asynchronous (see ESI). Coordination to ZnCl₂ lowers the activation energies by as much as 18.8 kcal mol⁻¹, but the exclusive participation of the E geometry is maintained. TSs for 1_Ph-Z·ZnCl₂ lie ≥4.2 kcal mol⁻¹ above those for 1_Ph-E·ZnCl₂. Cycloaddition at the more crowded face is again preferred in 1_Ph-E·ZnCl₂, the selectivity being ΔΔH^‡ = 1.1 kcal mol⁻¹. This value is 0.9 kcal mol⁻¹ greater than in the thermal reaction, consistent with the higher experimental

Scheme 5.

Despite their quite different surface areas and dipole moments, the structures and energies of TSA and TSB are affected little by solvation, as modeled by CPCM calculations.²⁴ Free energies of solvation for TSA and TSB with B3LYP and several basis sets, and with additional solution-phase structure optimisations. The stereoselectivities for the thermal reactions in solution ranged from 0 to −0.4 kcal mol⁻¹ (ΔΔG^‡), compared with −0.3 kcal mol⁻¹ in the gas phase. Details are provided in the ESI.

The low energy of TSB appears to arise from an attractive interaction between furan and Ph. These two groups are suitably arranged for an edge-to-face CH–π interaction, with H-3 on the furan lying approximately 2.85 Å from the centre of the Ph ring. The interaction includes an electrostatic component, as indicated by a slightly (0.02e) more positive Mulliken charge on H-3 in TSB than in TSA, and is expected to include a dispersion component as in other aryl-aryl interactions.

Because the B3LYP functional does not generally model dispersion energies accurately,²⁵ we employed several other methods to quantify the role of dispersion in TSA/B. Grimme’s simple empirical formula (B3LYP-D, 2006), which sums the interatomic interactions in a pairwise fashion,²⁶ predicts that the total dispersion energy, E_disp, is 2.7 kcal mol⁻¹ larger (more stabilizing) in TSB than in TSA. The furan–Ph interaction is 4.3 kcal mol⁻¹ larger in TSB than in TSA.

The B3LYP-D dispersion correction strongly favours TSB, and indeed overestimates the stereoselectivity.²⁷ Grimme’s B97-D functional,²⁸ which is explicitly parameterised to provide a more sophisticated treatment of short- and long-range interactions, with the aug-cc-pVTZ basis set indicates a 2.2 kcal mol⁻¹ preference for TSB. A similar result is obtained with Truhlar’s M06-2X functional,²⁹ which includes attractive terms mimicking dispersion. The π-facial discrimination between TSA and TSB at the M06-2X/6-31G(d) level is ΔΔE^‡ = 1.4 kcal mol⁻¹, and this value increases to 2.2 kcal mol⁻¹ upon full geometry optimisation. Although these newer functionals have not been as extensively benchmarked for cycloaddition transition states as B3LYP, and indeed overestimate the stereoselectivity, they are consistent in their support for a stabilising CH–π interaction in TSB.

Stereoselectivities for other oxazolidinones

A combination of steric repulsion and attractive CH–π interactions determines the stereoselectivity induced by other oxazolidinones. We calculated transition states analogous to TSA and TSB for 4-Bn- and 4-ⁱPr-5,5-Ph₂-substituted oxazolidinones, and determined their experimental dr’s.³⁰ The predicted and observed selectivities are listed in Table 1.

Table 1.

Calculated and experimental stereoselectivities for (4 + 3) cycloadditions of oxazolidinone-substituted oxyallyls with furan

Oxazolidinone	Calcd ΔΔH‡ (TSA–TSB)b	Exptal dr (I:II)a
	0.2	82:18
	−0.1	23:77
	−2.3	6:94

^a298.15 K, kcal mol⁻¹, B3LYP/6-31G(d).

^bTHF, −40 to −50 °C.

When the 4-phenyl substituent on the oxazolidinone is replaced by a benzyl group, the possibility of a stabilising CH–π interaction is eliminated and replaced by a repulsive furan–alkyl interaction. This is illustrated in Fig. 4. The opposite stereoisomer is now favoured by 0.1 kcal mol⁻¹. Experimentally, II is indeed obtained as the major product, with a dr of 23:77 (I:II). An even higher selectivity in favour of II is obtained with the 4-ⁱPr-5,5-Ph₂-oxazolidinone. In this case, the favoured TS benefits from both the minimisation of repulsive interactions between furan and the ⁱPr group, and a stabilising CH–π interaction between furan and the C-5 Ph group trans to ⁱPr. The calculated selectivity of 2.3 kcal mol⁻¹ in favour of II agrees with the higher experimental selectivity for II (dr 6:94). In the absence of the two phenyl rings at C-5, the diastereoselectivity is only 45:55.⁶ These correlations accentuate the powerful impact that a non-bonding force such as CH–π interaction can exert on the stereochemical course of cycloadditions.

Fig. 4.

Control of stereoselectivity by a combination of stabilising furan–Ph interactions and destabilising furan–alkyl interactions for 1_Ph,1_Bn, and 1_i-Pr/Ph. Note: For 1_i-Pr/Ph, C-4 of the oxazolidinone has the S configuration, whereas 1_Ph and 1_Bn are R.

Reversal of stereoselectivity for methyl 2-furoate

The E-only mechanism predicts that the cycloadditions of 1_Ph with furan and methyl 2-furoate should give opposite stereoselectivities. The four stereo- and regioisomeric TSs for cycloaddition of 1_Ph-E with methyl 2-furoate are shown in Fig. 5. The TS leading to the experimental major product, syn-II (TSE), lies ≥1.9 kcal mol⁻¹ below the other three TSs. The syn regioselectivity is expected, as it is favoured by the reactants’ frontier orbital coefficients. The reversal of stereoselectivity can be ascribed to repulsive interactions between the Ph group and the 2-COOMe group. In TSG, H-3 on the furan lies only 0.05 Å further from the midpoint of the Ph ring than in TSB, but the electrostatic repulsion between the Ph π cloud and the carbonyl group at C-2 of the furan outweighs the stabilising effect of CH–π attraction. Cycloaddition therefore takes place preferentially through the less crowded syn TS.

Fig. 5.

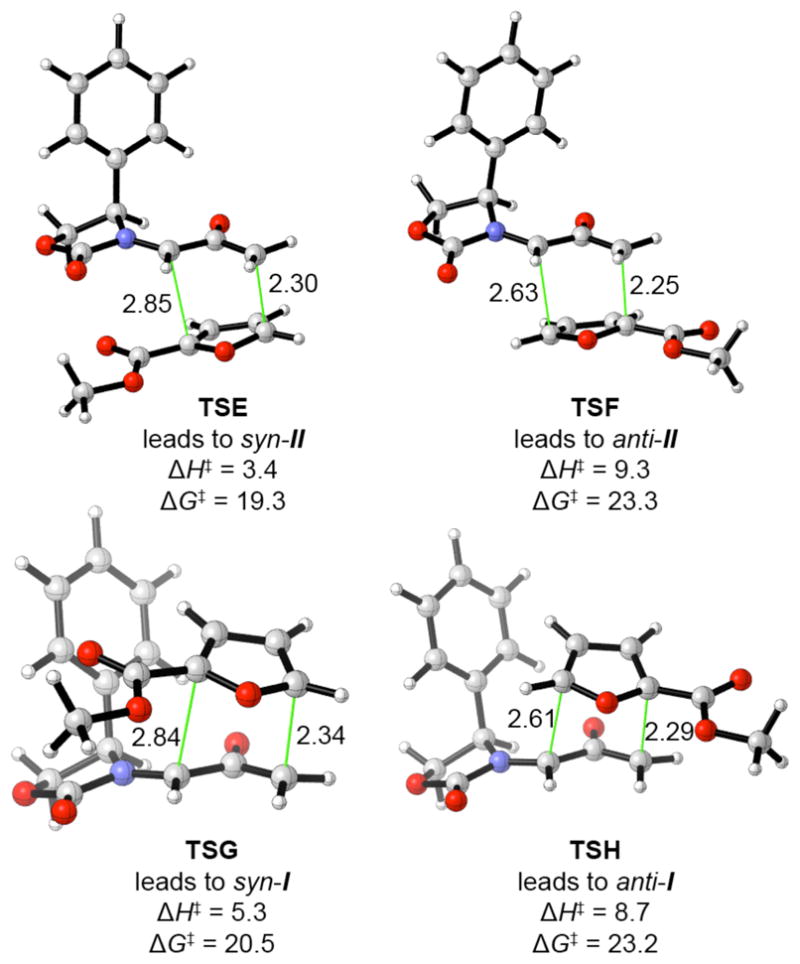
Transition structures and activation energies for the cycloaddition of 1_Ph with methyl 2-furoate [298.15 K, B3LYP/6-31G(d)].

Conclusions

Density functional theory calculations make it clear that only the E isomer of the oxyallyl 1 undergoes cycloaddition with furans. The Z isomer is subject to severe electrostatic repulsion between the oxyallyl and carbonyl oxygen atoms, and this destabilisation is not overcome even upon coordination to ZnCl₂. Santos et al. have recently reported related calculations on Evans’ Diels–Alder reactions (Scheme 2), and suggest that rather than taking place via the chelate, these reactions instead involve a complex of 2 in which the carbonyl groups are antiparallel (i.e. E), and each is bound to an AlEt₂Cl.³¹ They proposed that the stereoselectivity can then be traced to repulsive interactions between the Et groups on the Lewis acid and the ⁱPr group on the oxazolidinone. Antiparallel conformations of N-acyloxazolidinones have also been invoked in oxazolidinone-directed nitrile ylide cycloadditions⁵ and dynamic kinetic resolutions of α-haloketones.³² Santos’ calculations confirmed, however, that Evans’ original sterically-controlled mechanism of stereoinduction would still be valid within a stoichiometric regime where the chelate would exist.³¹

The origin of stereoinduction in the (4 + 3) cycloadditions of 1_Ph is quite distinct from these processes, and could be relevant to various other asymmetric reactions. CH–π interactions are well known to influence conformational equilbria, crystal packing, the structures of biological molecules, and molecular recognition.^33,34 Previous computational studies have shown that CH–π interactions are responsible for the endo selectivity of the Diels–Alder reaction of butadiene with cyclopropene³⁵ and the hetero-Diels–Alder reactions of ortho-xylylenes with benzaldehyde.³⁶ The calculated selectivities in these cases amounted to 1–2 kcal mol⁻¹.

CH–π interactions appear to be general design elements in asymmetric reactions. We recently discovered a similar example of this form of stereocontrol, in (4 + 3) cycloadditions of α-methylbenzyloxy-substituted siloxyallyl cations.³⁷ Like 1_Ph, these oxyallyl cations are relatively rigid species, and the aromatic group is held roughly perpendicular to the molecular plane. Furan was found to add to the aryl-containing face with a selectivity of approximately 1 kcal mol⁻¹. It is likely that further examples of stereocontrol via CH–π interactions will be reported in the future.

Experimental

Density functional theory were performed using the Gaussian 03³⁸ and Gaussian 09³⁹ packages. The nature of each stationary point was checked by means of frequency calculations, and transition states were further verified by IRC calculations.⁴⁰ Zero-point energy and thermal corrections were derived from the B3LYP or M06-2X frequencies, but not scaled. The effects of solvation were simulated by means of CPCM calculations²⁴ using UAKS radii (Gaussian 03).