Estimation of Myocardial Volume at Risk from CT Angiography

Abstract

The determination of myocardial volume at risk distal to coronary stenosis provides important information for prognosis and treatment of coronary artery disease. In this paper, we present a novel computational framework for estimating the myocardial volume at risk in computed tomography angiography (CTA) imagery. Initially, epicardial and endocardial surfaces, and coronary arteries are extracted using an active contour method. Then, the extracted coronary arteries are projected onto the epicardial surface, and each point on this surface is associated with its closest coronary artery using the geodesic distance measurement. The likely myocardial region at risk on the epicardial surface caused by a stenosis is approximated by the region in which all its inner points are associated with the sub-branches distal to the stenosis on the coronary artery tree. Finally, the likely myocardial volume at risk is approximated by the volume in between the region at risk on the epicardial surface and its projection on the endocardial surface, which is expected to yield computational savings over risk volume estimation using the entire image volume. Furthermore, we expect increased accuracy since, as compared to prior work using the Euclidean distance, we employ the geodesic distance in this work. The experimental results demonstrate the effectiveness of the proposed approach on pig heart CTA datasets.

1. INTRODUCTION

Prognosis and treatment of coronary artery disease frequently require the determination of the myocardial volume at risk caused by coronary stenosis. A previous study¹ shows that the regional myocardial mass at risk depends on the shape and content of myocardium distal to the coronary artery occlusion, which has been commonly used to estimate the myocardial area at risk. In one work², 3D models of the coronary artery tree are aligned with the 3D epicardial surface of the left ventricle (LV) built from perfusion SPECT to estimate the anatomic area at risk. Then, the mass at risk is obtained under the assumption that myocardium has a uniform thickness. In another work³, each tissue voxel is assigned to its nearest arterial branch to determine the dependent myocardial region using micro-CT images. In order to compute the coronary perfusion territories from CTA, Dijkstra’s algorithm is used to associate a region with its closest coronary over the LV epricardial surface segmented offline⁴.

However, much less work has been done for computing the myocardial volume at risk directly on the heart surfaces segmented from CAT imagery, rather than employing simplified models such as ellipsoids. The purpose of this study is to provide an efficient and general computational framework for estimating the myocardial volume at risk that can capture the individual myocardial variability. In this work, the relation between the myocardial mass at risk and the coronary artery occlusion is adopted as the basis for computation. In addition, a decomposition strategy is utilized to reduce the computational cost by first finding the regions at risk over the epicardial and endocardial surfaces, and then reconstructing the volume in between these regions as the approximation of the myocardial volume at risk.

2. METHODS

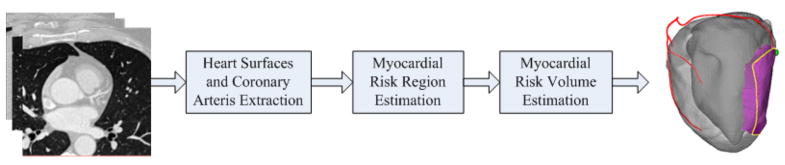
The overall procedure is shown in Figure 1, which includes the following steps: (1) heart surfaces and coronary arteries extraction; (2) myocardial risk region estimation; and (3) myocardial volume estimation. The first step is semi-automatic that requires only a few user interactions. The second and third steps are the key part of the overall framework, which are automatic. The details of each step are given in the following sections.

Figure 1.

The flowchart of the proposed framework.

2.1 Heart Surfaces Segmentation and Coronary Arteries Extraction

This is a preprocessing step. For heart surfaces segmentation, an interactive active contour method⁵ is applied with user specified seed points to extract the epicardial and endocardial surfaces. The segmented surfaces are triangulated and represented by triangle meshes.

Coronary arteries can be extracted using the same active contour method describe above by putting seed points at the distal branch of each coronary artery to avoid these seed points overgrow to aorta area. The centerline of each coronary artery is extracted using a Vascular Modeling Toolkit (VMTK)⁶. The extracted coronary arterial centerlines are represented by a tree structure. Given the location of a stenosis on the artery tree, we can classify all the points on the artery tree into two types based on whether the point is affected by the stenosis or not. Here, all the branch points distal to the stenosis are labeled as affected and assigned different index from that of unaffected points.

2.2 Estimation of Region at Risk on the Epicardial Surface

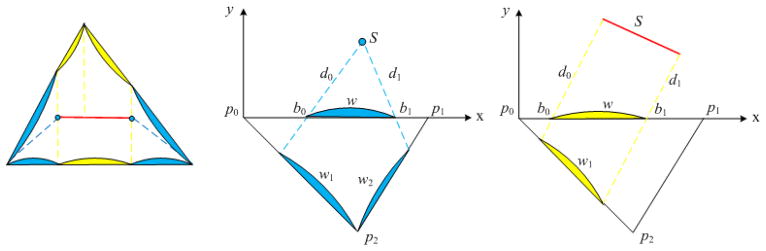
Since the extracted coronary centerlines do not lie exactly on the epicardial surface, projection is performed for each point on the centerlines by finding its closest point in terms of Euclidean distance on the epicardial mesh. Then, an efficient geodesic distance field computation method^7,8 is applied to the epicardial mesh using the projected arteries as source curves which define the zero set of the distance field. The key observation of this method is that the geodesic distance within a triangle on a mesh is a straight line, therefore we can virtually unfold these triangles in a common plane and propagate the distance field along straight lines through the so-called windows of each triangle edge. There are two types of sources, i.e. point source and line source that induce a set of windows on the edge of a triangle as shown in Figure 2. One advantage of this window formulation is that all computations can be done in the local coordinates defined by triangle p₀p₁p₂. Each window is described by a seven dimensional vector (type, id, b₀, b₁, d₀, d₁, dir), where type is either point or line source, id is the index of the source, b₀ and b₁ specify the endpoints of a window, d₀ and d₁ are the distance from a window endpoints to their closest source S, and dir shows from which side of x-axis that the source S propagates. Starting from the source curves, the distance information is propagated from one triangle to its neighbors in a Dijkstra-like manner (see^7,8 for details). A list of windows is maintained for each edge of a triangle to record the geodesic distance information for points in each window. After the distance field is computed over all triangles, each point on a triangle edge will be associated with its closest point on the source curves, i.e. coronary arteries. Then, the region at risk caused by a stenosis is defined as the region in which all its inner points associated with the affected artery points.

Figure 2.

Left: Windows induced by point sources (blue) and line source (yellow); Middle: Point source induced window propagation; Right: Line source induced window propagation.

2.3 Volume at Risk Estimation

Correspondingly, we can define the likely region at risk on the endocarial mesh as the projection of the risky region of the epicaridal mesh onto the endocardial mesh. Then, the likely volume at risk can be approximated by the volume defined in between those two regions. In order to reduce computational cost, we proposed an efficient method to find the volume at risk. The method consists of four steps: (a) extract the outer contour of the region at risk on the epicardial mesh; (b) project the contour onto the endocardial mesh; (c) find the region within the projected contour as the region at risk on then endocardial mesh; (d) construct the volume in between these two regions and compute its value.

Specifically, in step (a), a new contour extraction method is proposed to handle the challenges in processing noisy epicardial surface in which classical contour following methods may fail. This method formulates contour following as a distance propagation problem. First, for points on the epicardial mesh, the potential boundary points are selected as those that have the same geodesic distance to both affected and unaffected artery points. Moreover, the neighborhood is defined for each potential boundary point as the set of boundary points that lie on its adjacent triangles on the epicardial mesh. Then, from an initial point, e.g. a stenosis point, we can take one of its neighboring points each time as the second propagation point and propagate the distance field among all these potential boundary points using Dijkstra’s algorithm⁹. In each iteration, we can get one shortest path via backtracking the distance field from the farthest point to the start point. Finally, the longest shortest path is chosen as the contour for the region at risk. Ideally, a closed contour will be returned assuming the contour of the region at risk is not self-intersecting, which is a general case from our empirical observations. Unlike the classical contour following algorithms that need backtracking or even fail due to their local search characteristics for the next expansion direction, the proposed method has a global sense in that the shortest path is obtained only after the distance field has expanded through all the potential boundary points. A simulated example is given in Figure 3. There are three segments of simulated arteries, one of which is affected by a stenosis, denoted by S₀ in red color. The enlarged view of the mesh around S₀ is shown on the top left corner, where n₁ and n₂ are the neighbors of S₀. In this case, two iterations are needed, i.e. from direction $\overrightarrow{S_0{n}_1}$ or $\overrightarrow{S_0{n}_2}$. Two shortest path, c₁ and c₂, were returned by our method, and the longest one was selected as the final result, which is a directed curve.

Figure 3.

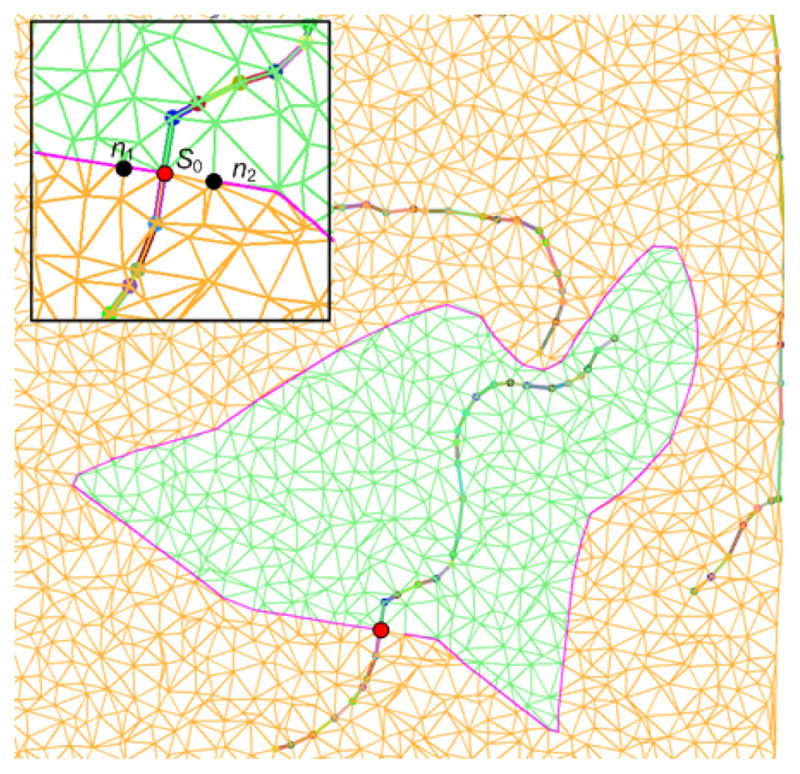
An example of extracting the contour of region at risk. The extracted contour is marked with pink color.

After obtaining the outer contour, projection is performed for each of the contour point by finding its closest point on the endocardial mesh in terms of Euclidean distance. If the projections of two adjacent points do not share a common triangle, then the contour between these two projected points is interpolated by searching for the shortest path between those two points using Dijkstra’s algorithm on the endocardial mesh. The classical flood fill algorithm is used to fill in the region within the projected contour defined in same the direction as the original contour.

Finally, the two regions at risk are linked by triangulating the area between the original and projected contours to form a closed volume which is taken as the approximation of the myocardial volume at risk. The triangle vertices of the risk volume are ordered so that the normal of each triangle is consistent with others and the value of this volume is computed as^10,11

$$V=\frac{1}{6}\sum _{k=1}^F{g}_k·N_k,$$

where F is the number of triangles of the constructed volume, $g_k=(x_k^1+x_k^2+x_k^3)/3$ and $N_k=\overrightarrow{x_k^1{x}_k^2}\wedge \overrightarrow{x_k^1{x}_k^3}$ for the kth triangle with its three vertices as $x_k^1,x_k^2,x_k^3$.

The four key steps for estimating the volume at risk are summarized are shown in Figure 4.

Figure 4.

An illustration of the process of estimating the myocardial volume at risk. (a) Contour of region at risk (yellow). (b) Projected contour on the endocardial mesh. (c) Region at risk on the endocardial mesh. (d) Approximated myocardial volume at risk.

2.4 Validation

Seven female pigs first underwent normal resting positron emission tomography (PET) Rb-82 imaging, and one week later underwent coronary catheterization and microembolization of either the distal left anterior descending (LAD) or left circumflex artery (LCx) coronary artery bed. A stent was placed at the site of microembolization as a marker that could be visualized in the CT. Pigs then underwent resting Rb-82 PET imaging and 64-slice dual-source CTCA using separate scanners. The CTCA were processed as described above, using the stent as the location of arterial “stenosis”. The PET scans were processed using a standard quantification program¹² to determine the mass of myocardium which was abnormal in the second study. This area is that which was supplied by the artery distal to the stent location, and thus, suffered embolization. We compared this mass at risk determined from PET to that computed from the CT anatomy alone. Both the absolute myocardial mass at risk and the percentage of mass at risk over the LV mass were compared.

3. EXPERIMENTAL RESULTS

The proposed approach has been validated with the pig CTA datasets described above. For our implementation, 3D Slicer3.6¹³ was used to segment heart surfaces and extract coronary arteries since it has integrated the methods described in section 2.1. Moreover, the extracted coronary centerlines were down-sampled with a uniform step to get a concise representation. Figure 5 shows one segmentation of the left ventricular epicardial surface, endocardial surface, and coronary arteries, superimposed with CTA volume. One example of the estimated volume at risk with LCx occlusion is shown in Figure 6 with two different views.

Figure 5.

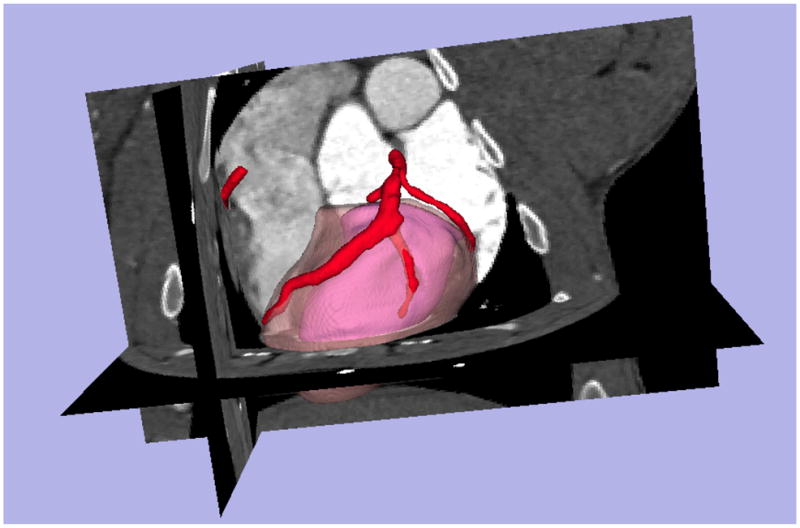
Segmentation of left ventricular epicardial and endocardial surfaces, and coronary arteries. The epicardial surface is shown in a transparent model for a better visual effect.

Figure 6.

Estimated myocardial volume at risk with LCx stenosis. Two views are shown, including the epicardial surface (light gray with transparency), endocardial surface (dark gray), coronary arteries centerlines (red), contour of regions at risk (yellow), and volume at risk (pink).

In order to evaluate the accuracy of the proposed approach, we compared the myocardial mass at risk estimated from seven pig CTA datasets with their corresponding values determined from PET. The myocardial mass is computed assuming a uniform gravity of myocardium as 1.05g/mL. Both the absolute myocardial mass at risk and the percentage of mass at risk over the LV mass were compared. Results are shown in Table 1. Overall, the average error for the estimated absolute myocardial mass at risk is −1.6 ± 4.1g, and the average error for the percentage of mass at risk over the LV mass is 2% ± 5.4%, which show that the estimation accuracy of our approach is very close to that obtained from the PET datasets.

Table 1.

Comparison of the myocardial mass estimated using our approach from CTA and that obtained from PET.

Pigs	Estimated Mass (g)	PET Mass (g)	Estimated %LV (%)	PET %LV (%)
Polly	14	16	23	19
Quinn	18	24	25	29
Ursula	12	16	17	19
Rosie	24	20	28	20
Tracy	20	16	25	16
Tammy	18	23	22	26
Velma	15	17	23	20

4. CONCLUSIONS AND FUTURE WORK

In this work, we propose a new computational framework for estimating the myocardial volume at risk caused by stenosis from CTA imagery using image processing and computational geometry techniques. We approximate the myocardial volume at risk as the volume in between the region at risk on the epicardial surface and its counterpart on the endocardial surface. This significantly reduces the computational complexity as compared to working on entire image volume directly. The experiments have shown good results and in future work, we will improve the accuracy of the heart surfaces segmentation, and make the overall framework works more automatically. Moreover, we will test our approach with human CTA and PET datasets to further evaluate its accuracy and potential application in actual human heart risk assessment.