Temporal presentation protocols in stereoscopic displays: Flicker visibility, perceived motion, and perceived depth

Abstract

Most stereoscopic displays rely on field-sequential presentation to present different images to the left and right eyes. With sequential presentation, images are delivered to each eye in alternation with dark intervals, and each eye receives its images in counter phase with the other eye. This type of presentation can exacerbate image artifacts including flicker, and the appearance of unsmooth motion. To address the flicker problem, some methods repeat images multiple times before updating to new ones. This greatly reduces flicker visibility, but makes motion appear less smooth. This paper describes an investigation of how different presentation methods affect the visibility of flicker, motion artifacts, and distortions in perceived depth. It begins with an examination of these methods in the spatio-temporal frequency domain. From this examination, it describes a series of predictions for how presentation rate, object speed, simultaneity of image delivery to the two eyes, and other properties ought to affect flicker, motion artifacts, and depth distortions, and reports a series of experiments that tested these predictions. The results confirmed essentially all of the predictions. The paper concludes with a summary and series of recommendations for the best approach to minimize these undesirable effects.

1 Introduction

Stereoscopic displays (abbreviated as “stereo”) are being increasingly adopted for cinema, television, gaming, scientific visualization, medical imaging, and more. Generally, these displays use one conventional 2-D display to present different images to the left and right eyes. Once the viewer fuses the images, they can gain a very compelling sensation of depth. Because stereo displays are so similar to conventional non-stereo displays, many of the standards, protocols, technical analyses, and artistic effects that have been developed for non-stereo displays also apply to stereo displays. There are, however, differences between non-stereo and stereo displays that produce artifacts unique to stereo presentation.

There are a variety of ways to present different images to the two eyes. The field-sequential approach, for example, presents images to the left and right eyes in temporal alternation (e.g., RealD, Dolby). Among field-sequential approaches, there are several ways to present the alternating images in time including multiple-flash methods. These different methods yield different artifacts. In addition to field-sequential approaches, one can present images to the two eyes simultaneously by using multiple projectors (IMAX), wavelength multiplexing techniques (Infitec and Anaglyph), or spatial multiplexing (micropol) on one 2-D display. Even with simultaneous presentation, different temporal presentation methods yield different artifacts.

In this paper, we examine how various temporal presentation methods affect the viewer’s perceptual experience with stereo displays. We first use an analysis in the spatio-temporal-frequency domain to examine how these methods ought to affect the visibility of flicker. We then describe an experiment on flicker visibility that generally confirms the expectations from that theory. The conditions that cause noticeable flicker in stereo displays are mostly the same as those that cause flicker in non-stereo displays. We then extend the frequency-domain analysis to examine how various temporal presentation methods ought to affect the visibility of motion artifacts for stimuli that move, but do not change disparity. After that, we describe an experiment that tests the predictions from that theoretical analysis; the experimental results generally confirm the predictions. Interestingly, the conditions that cause motion artifacts with stereo displays are essentially the same as those that cause artifacts with non-stereo displays. We next examine the visibility of motion artifacts for stimuli that are moving perpendicular to the display screen; i.e., stimuli that are changing in disparity. Here, we observe motion artifacts that are unique to stereo presentation. Finally, we examine how various temporal presentation methods create artifacts in the visual system’s estimate of disparity and show how they produce predictable distortions in the perceived depth of moving objects.

We find that some temporal presentation methods yield noticeable flicker, motion artifacts, or depth artifacts, and we describe how to minimize those undesirable outcomes.

2 Sampling theory

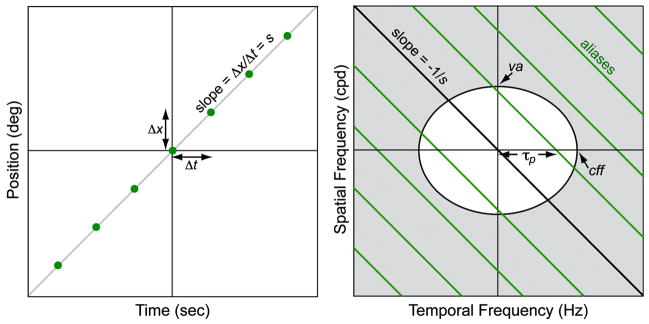
We begin by considering stroboscopic presentation of a moving object presented to one eye. Here, we follow the development by Watson and colleagues in 1986 for non-stereo displays¹. To create the appearance of a high-contrast vertical line moving smoothly at speed s, one presents a sequence of very brief views of the line at time intervals of Δt with each view displaced by Δx = sΔt. The temporal presentation rate τ_p is the reciprocal of the time between presentations: τ_p = 1/Δt.

We represent the smoothly moving real stimulus by

$$i(x,t)=\delta (x-st),$$ (1)

where i is the observed image and δ is the Dirac delta function. The stroboscopically presented stimulus is

$$i_s(x,t)=i(x,t)s(t),$$ (2)

where s(t) is the sampling function:

$$s(t)=\mathrm{\Delta }t\sum _{n=-\infty }^{\infty }\delta (t-n\mathrm{\Delta }t).$$ (3)

The sampling function has the effect of presenting the stimulus only at integral multiples of Δt. The left panel of Fig. 1 depicts the smoothly moving and stroboscopic stimuli.

FIGURE 1.

Properties of a smoothly moving stimulus and a stroboscopic stimulus. The gray diagonal line in the left panel represents the motion of a smoothly moving vertical line on axes of time and horizontal position. The green dots represent the stroboscopic version of that stimulus at integer multiples of Δt. The right panel shows the amplitude spectra of the smoothly moving and stroboscopic stimuli plotted on axes of temporal frequency (Hz) and spatial frequency (cpd). The black diagonal line represents the spectrum of the smoothly moving stimulus. The green lines are the additional spectra from the stroboscopic stimulus; they are temporal aliases separated by τ_p = 1/Δt. The ellipse contains combinations of temporal and spatial frequency that are visible to the visual system. The highest visible temporal frequency is indicated by cff and the highest visible spatial frequency by va. The shaded region contains combinations of temporal and spatial frequency that are invisible.

The Fourier transform for the smoothly moving stimulus is

$$I(\omega ,\tau )=\mathfrak{I}[i(x,t)]=\delta (\tau +s\omega ),$$

where ℑ indicates Fourier transformation, and ω and τ are the spatial and temporal frequency, respectively. The Fourier transform of the smoothly moving stimulus is the black line in the right panel of Fig. 1; it has a slope of −1/s. The Fourier transform for the stroboscopic stimulus is

$$I_s(\omega ,\tau )=\mathfrak{I}[i_s(x,t)]=\sum _{n=-\infty }^{\infty }\delta (\tau +s\omega -n{\tau }_p),$$ (4)

which is represented in the right panel of Fig. 1 by the black and green lines.^1,2 The green lines are aliases: artifacts created by the stroboscopic presentation. Their slopes are −1/s and they are separated horizontally by τ_p. Thus, the spectrum of the stroboscopic stimulus contains a signal component plus a series of aliases. As the speed of the stimulus (s) increases, the slope of the signal and aliases decreases. As the presentation rate (τ_p) increases, the separation between the aliases increases. We started with the analysis of stroboscopic sampling because such sampling determines the spatio-temporal frequencies of the aliases and those frequencies remain as we consider protocols that are actually used. Specifically, sample-and-hold and multi-flash protocols do not change the pattern of alias spectra; they only change the amplitudes of the aliases.

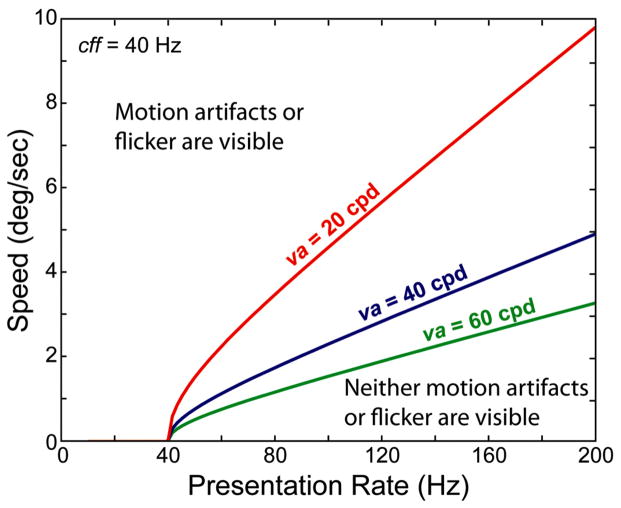
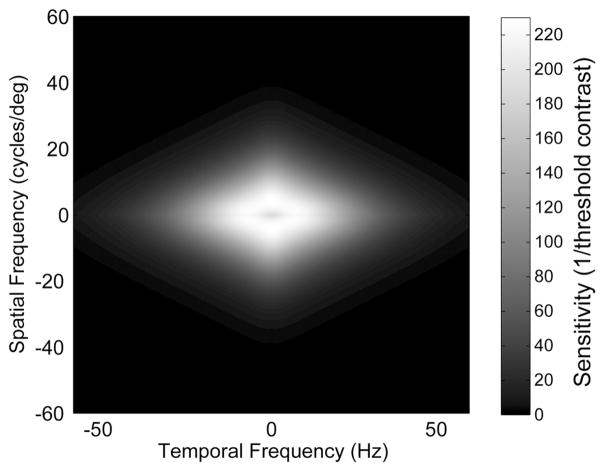
The visual system is not equally sensitive to contrast at all spatial and temporal frequencies. This differential sensitivity is described by the spatio-temporal contrast sensitivity function.^3,4 To understand which discretely presented moving stimuli will appear to move smoothly and which will appear to not move smoothly or will appear to flicker, we compare the spatio-temporal spectra of stroboscopic stimuli and smoothly moving stimuli to the contrast sensitivity function.^1,3,4,37 The function is represented in the right panel of Fig. 1 by the ellipse, which is a simplification of the actual sensitivity function. The dimensions of the ellipse’s principal axes are the highest visible temporal frequency – the critical flicker frequency (cff) – and the highest visible spatial frequency – the visual acuity (va). Spatio-temporal frequencies that lie outside the ellipse will be invisible; those lying inside the ellipse may or may not be visible depending on their contrasts. The region of visible components has been called the window of visibility.¹ The spectra of the smoothly moving and stroboscopic stimuli differ only by the aliases, so if the aliases were invisible, the two stimuli should appear identical. Said another way, the stroboscopic stimulus whose aliases all fall outside the window of visibility should appear to move smoothly without flicker. We can, therefore, calculate the combinations of speed and presentation rate that will just produce flicker or motion artifacts by determining when the aliases just encroach on the window of visibility. First, we consider how display protocols might change the perceptibility of flicker.

3 Theory for flicker visibility

We define visible flicker as perceived fluctuations in the brightness of the stimulus. We distinguish this from motion artifacts such as judder (unsmooth motion) and edge banding (more than one edge seen at the edge of a moving stimulus). We assume that flicker will be perceived when aliases such as those in the right panel of Fig. 1 encroach the window of visibility near a spatial frequency of zero (i.e., along the temporal-frequency axis).

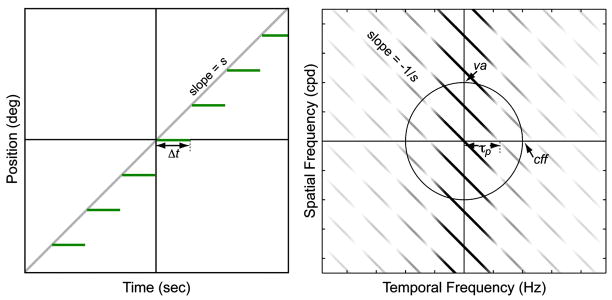
In many displays, most notably LCDs, the presentation is not stroboscopic; rather it lasts for nearly the entire interval between frames.⁵ This is sample and hold and is schematized in the left panel of Fig. 2. To derive the spatio-temporal spectrum for sample-and-hold presentation, one convolves the stroboscopic stimulus [Eq. (2)] with a temporal pulse function.¹ The moving stimulus is

FIGURE 2.

Properties of a sample-and-hold stimulus. The gray diagonal line in the left panel represents the motion of a smoothly moving vertical line on axes of time and horizontal position. The green line segments represent the sample-and-hold version of that stimulus. The right panel shows the amplitude spectra of the smoothly moving and sample-and-hold stimuli plotted as a function of temporal and spatial frequency. The black diagonal line repre sents the spectrum of the smoothly moving stimulus. The green lines are the aliases due to discrete presentation. The amplitudes of the aliases are attenuated by a sinc function in temporal frequency. After attenuation, the aliases are lower in amplitude than with the stroboscopic stimulus. Their amplitudes are zero at temporal frequencies of ±τ_p, ±2τ_p, ±3τ_p, etc.

$$\begin{array}{c}{i}_h(x,t)=i_s(x,t)\ast s_h(x,t),\\ s_h(x,t)=r\left(\frac{t}{\mathrm{\Delta }t}\right)\delta (x),\end{array}$$ (5)

where * represents convolution and r(t/Δt) is a rectangular pulse with width Δt = 1/τ_p. (Note that the width of the pulse is equal to the frame time.) The Fourier transform of this stimulus is

$$I_h(\omega ,\tau )=\mathfrak{I}[i_s(x,t)]\mathfrak{I}[s_h(x,t)].$$ (6)

The first term on the right is Eq. (4) and the second term is sin(πτ/τ_p)/(πτ/τ_p) (the sinc function) which has its first zero at a temporal frequency of τ_p. The resultant is the product of the spectrum in Fig. 1 and a sinc function in temporal frequency, which results in attenuation of higher temporal frequencies. This spectrum is illustrated in the right panel of Fig. 2. The amplitudes of the aliases in the sample-and-hold stimulus are lower than the amplitudes of the aliases in the stroboscopic stimulus, particularly at higher temporal frequencies. When the stimulus is not moving (s = 0), the aliases in Fig. 2 pivot to vertical, but they fall at zeros of the sinc function and would therefore have zero amplitude. Thus, with sample-and-hold stimuli, there should be no apparent flicker when the stimulus is not moving. When the stimulus is moving, the aliases rotate to a slope of −1/s thereby increasing the likelihood of perceiving unsmooth motion, but not increasing the likelihood of perceiving flicker. In summary, sample-and-hold displays produce little noticeable flicker.

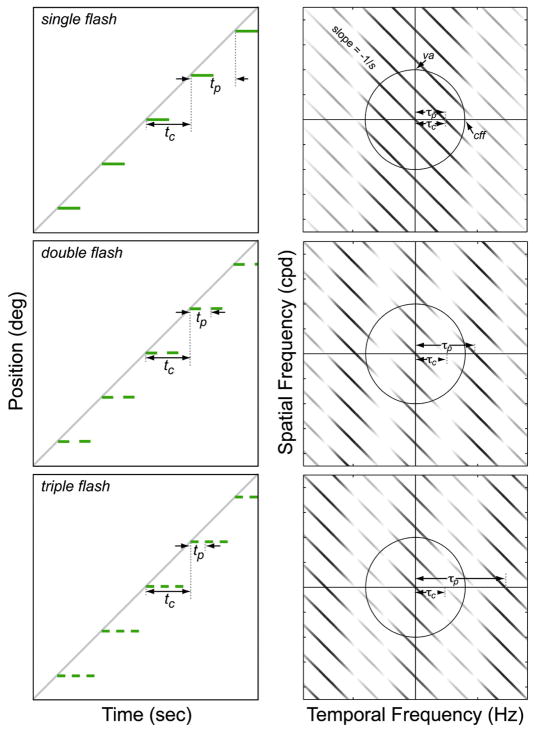
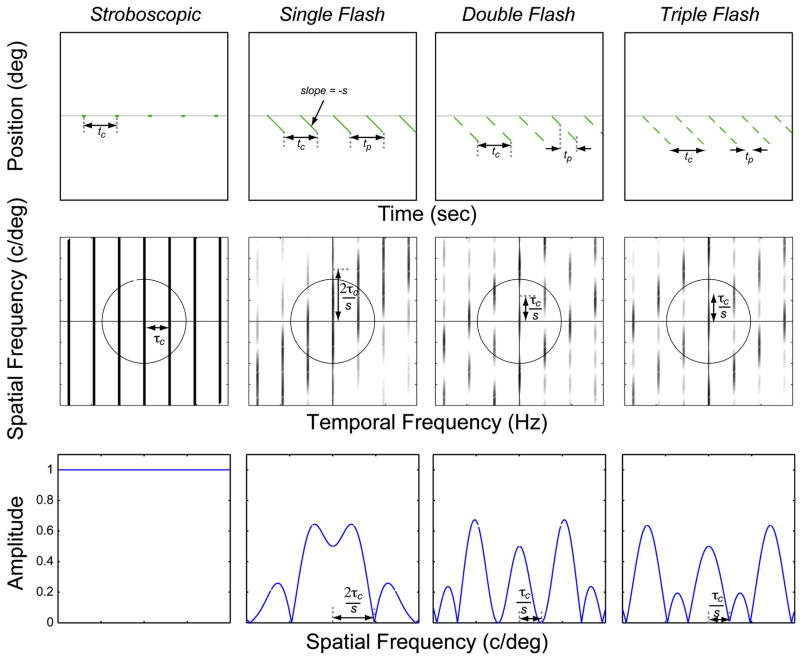
In many stereo displays (e.g., active shutter glasses or passive glasses with active switching in front of the projector), the images to the two eyes are presented field-sequentially: that is, to one eye and then the other, and so forth. The monocular images therefore consist of presentation intervals alternating with dark intervals of equal or shorter duration. In some cases, each presented image of the moving stimulus is a new one; we refer to this as a single-flash protocol; it is schematized in the upper left panel of Fig. 3. There is also a double-flash protocol in which the images are presented twice before updating and a triple-flash protocol in which they are presented three times before updating.⁶ We will use f to represent the number of such flashes in a protocol. Those protocols are also schematized in the left column of Fig. 3. Of course, multi-flashing is similar to the double and triple shuttering that is done with film-based movie projectors.³⁸ The double- and triple-flash protocols are used to reduce the visibility of flicker (RealD and Dolby use triple-flash, and IMAX uses field-simultaneous double-flash). We next examine why multi-flash protocols should indeed reduce flicker visibility.

FIGURE 3.

Properties of stimuli presented with multiple-flash protocols. The left panels schematize the single-, double-, and triple-flash protocols. In each case, the same images are presented during the interval t_c until updated images are presented in the next interval. In the multi-flash protocol, the duration of each image presentation t_p is t_c/f, where f is the number of flashes. Thus, t_p = t_c, t_c/2, and t_c/3 in single-, double-, and triple-flash protocols, respectively. The right panels show the corresponding amplitude spectra of the multi-flash stimuli plotted as a function of temporal and spatial frequency. The spectrum of a smoothly moving real stimulus would again be a diagonal line with slope −1/s. The presentation rate τ_p (or 1/t_p) is indicated by arrows. The aliases are separated by τ_c (1/t_c), which is also indicated by arrows. The circles represent the window of visibility defined by cff and va. The amplitudes of the aliases have been attenuated by ℑ[s_nf(x, t)], which is constant as a function of spatial frequency and oscillates as a function of temporal frequency.

We will refer to the rate at which new images are presented as the capture rate τ_c (or 1/t_c, where t_c is the time between image updating). We will refer to the rate at which images, updated or not, are delivered to an eye as the presentation rate τ_p (or 1/t_p). Note that τ_c = τ_p/f (or t_c = ft_p). Flash protocols are a form of sample-and-hold; in our implementation, the durations of dark frames and the hold interval are half the presentation time (t_p).

Now consider a moving stimulus presented with a single-, double-, or triple-flash protocol:

$$\begin{array}{l}{i}_{nf}(x,t)=i_s(x,t)\ast s_{nf}(x,t),\\ s_{nf}(x,t)=r\left(\frac{t}{t_c}\right)\left[\frac{1}{2}+\frac{1}{2}\mathit{sqr}\left(\frac{ft}{t_c}\right)\right]\delta (x),\end{array}$$ (7)

where sqr is a square wave that oscillates between −1 and 1 with a period of t_c/f, and f refers to the number of flashes. The Fourier transform of s_nf(x, t) is the sum of a series of sinc functions each with width 2τ_c, amplitudes of 1/2, 2/π, −2/3π, 2/5π, −2/7π…, and centered at temporal frequencies of 0, ±τ_c, ±3τ_c, ±5τ_c, ±7τ_c …:

$$\mathfrak{I}\left[s_{nf}(x,t)\right]=\frac{1}{2}\text{sinc}\left(\frac{\pi \tau }{{\tau }_c}\right)+\sum _{k=\pm 1}\left[\sum _{i=1}^{\infty }\left[\frac{{(-1)}^{(i+1)}}{2i-1}\text{sinc}\left(\frac{\pi }{{\tau }_c}(\tau -k(2i-1)f{\tau }_c)\right)\right]\right].$$ (8)

The stimulus spectrum for the multi-flash protocols is ℑ[s_nf(x, t)]ℑ[i_s(x, t)]. The spectrum for the single-flash protocol is shown in the upper right panel of Fig. 3. By comparing this spectrum to the one for sample-and-hold, we see that the insertion of dark frames yields less attenuation at τ_c. As a result, flicker should be much more visible with the single-flash protocol (in which the hold interval is half the frame duration) than with sample-and-hold (in which the hold interval is equal to the frame duration) whether the stimulus is moving or not.

The amplitude spectra for the double- and triple-flash protocols are also shown in the right column of Fig. 3. The frequencies of the aliases are the same in the single- and double-flash protocols, but their amplitudes go to zero at τ_c in double flash and at 2τ_c in single flash. In the triple-flash protocol, the aliases are again the same, but their amplitudes go to zero at τ_c and again at 2τ_c, remaining small in between. The first alias with non-zero amplitude along the temporal-frequency axis occurs at a temporal frequency of τ_p (1/t_p), which is the presentation rate. Thus, we predict that presentation rate will determine flicker visibility.

From these observations, we make the following predictions: (1) Presentation rate, not capture rate, should be the primary determinant of flicker visibility. (2) Because presentation rate should be the primary determinant, one should be able to reduce flicker visibility for a fixed capture rate by using multi-flash protocols. Specifically, flicker should be less visible in the triple-flash than in the double-flash protocol and less visible in the double-flash than in the single-flash protocol. (3) Because the temporal frequency of the first alias with non-zero amplitude along the temporal-frequency axis is determined by presentation rate only, flicker visibility should be unaffected by stimulus speed. (4) Stereo processing in the visual system is low pass in time and therefore the visual system should be less sensitive to rapidly changing disparities than to time-varying luminance signals,^3,7,8 so we predict little if any difference in flicker visibility between stereo and non-stereo presentations provided that the temporal protocols are the same. From this, it follows that matching capture and presentation synchrony should not affect flicker visibility; i.e., for simultaneous capture, simultaneous and alternating presentation should be equally likely to produce noticeable flicker.

We tested these four predictions in a psychophysical experiment.

4 Experiment 1: Flicker

4.1 Methods

Observers

Five UC Berkeley students 18–25 years of age participated. Two were authors (DMH and VIK); the others (AAB, DJW, and MST) were unaware of the experimental hypotheses. All were screened to assure that they had normal corrected visual acuity in both eyes and normal stereo acuity. If they usually wore an optical correction, they did so in the experiment.

Apparatus and stimulus

We used CRTs to emulate the properties of LCDs and DLPs. LCDs use sample and hold. DLPs use pulse-width modulation. CRTs have an impulse-like rise with an exponential decay. We used CRTs for our experiments because they offer the most robust dual-display synchronization and support for true refresh rates as high as 200 Hz. The displays were always set to at least double the presentation rate for the stimulus enabling us to blank the monitor for alternating presentation. To emulate a presentation of 1/4 or 1/6 of the monitor refresh rate, we doubled or tripled frames. Thus, to present 24-Hz field-sequential imagery with a refresh rate of 144 Hz, one display would present FFFDDDFFFDDD, while the other presented DDDFFFDDDFFF, where F represents an image frame and D a dark frame. This emulation of a low-frame-rate display has an alias structure that is nearly identical to a 24-Hz square wave at frequencies up to 72 Hz. Specifically, the low-frequency aliases are nearly identical to those for LCD and DLP; the differences only begin to emerge at temporal frequencies greater than half the CRT refresh rate (which was always greater than 120 Hz). Thus, conclusions drawn from these experiments are applicable to LCDs and DLP displays.

The apparatus was a mirror stereoscope with two CRTs (Iiyama HM204DT), one for each eye. The observer’s head was stabilized with a chin and headrest. The viewing distance was 116.5 cm. At that distance, the CRTs subtended 19° × 15°. The CRTs contained 800 × 600 pixels, so pixels subtended 1.5 arcmin at the observer’s eyes. Anti-aliasing was not used. The frame rate was set to 120–200 Hz depending on the presentation rate we were simulating.

The stimulus was a white 1° square that moved horizontally at constant speed across an otherwise dark background (Fig. 4). The time-average luminance of the square was 30 cd/m². The direction of motion was random. Speeds ranged from 1–4 deg/sec. We initially tried faster speeds, but found that observers had difficulty ignoring motion artifacts in that case. The stimulus moved from the starting position on the screen to the ending position in 2.5 sec. The motion path was centered on the screen. We used a moving stimulus in the flicker experiment so it would be the same as the stimulus in Experiment 2.

FIGURE 4.

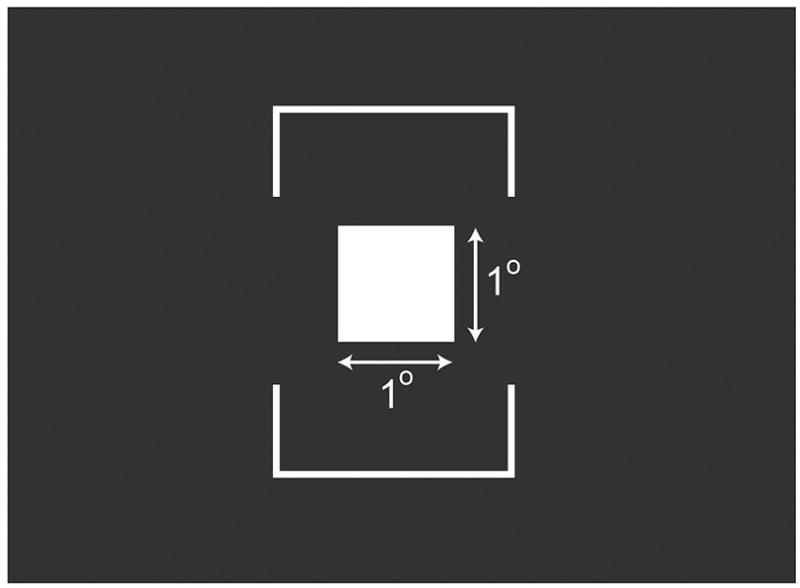
The stimulus. The white 1° × 1° square moved horizontally across the display screen. The background was black. The moving square had zero disparity with respect to the screen apart from disparities introduced by some temporal protocols.

Brackets above and below the center of the motion path provided a frame of reference. No fixation target or fixation instructions were provided.

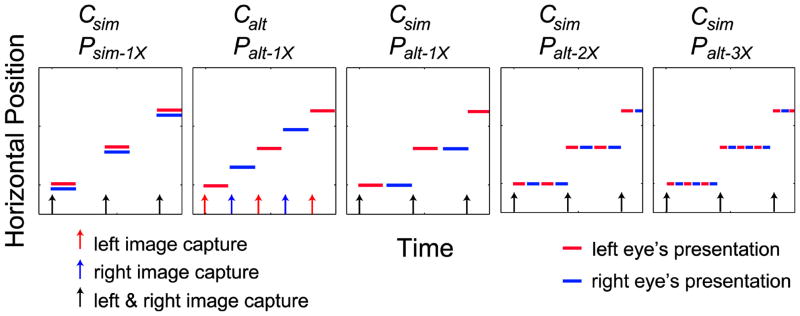
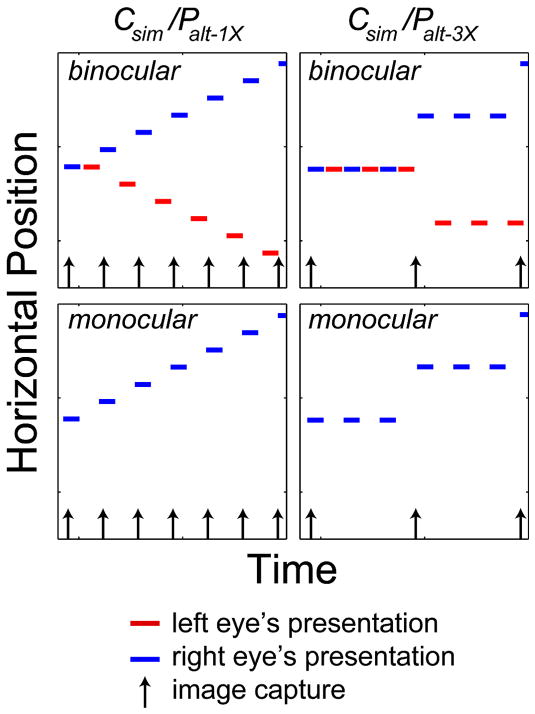
We represent the various capture and presentation protocols with abbreviations. C_sim and C_alt represent simultaneous and alternating capture of the left and right images, respectively. P_sim and P_alt represent simultaneous and alternating presentation to the two eyes. 1×, 2×, and 3× represent single-, double-, and triple-flash presentations, respectively. Thus, C_sim/P_alt–3X represents simultaneous capture and alternating, triple-flash presentation. We used the five protocols schematized in Fig. 5. Because the CRTs had a maximum frame rate of 200 Hz, we were restricted to capture rates lower than 50 and 33 Hz, respectively, for double- and triple-flash protocols.

FIGURE 5.

Temporal protocols in Experiments 1 and 2. The stimulus moved horizontally at constant speed. Its horizontal position is plotted as a function of time. Each panel represents a different temporal protocol. C refers to capture and P to presentation; sim refers to simultaneous and alt to alternating; 1×, 2×, and 3× refer to single-, double-, and triple-flash presentations, respectively. The arrows in each panel indicate the times at which the stimuli were captured (or computed). Black arrows indicate those times when the left and right images were captured simultaneously. Red and blue arrows indicate those times for the left and right images when they were captured at alternating times. The red and blue line segments represent the presentations of the images to the left and right eyes, respectively.

We set the CRT frame rate to a given value and then presented different protocols that were compatible with that rate (i.e., the presentation rate had to be an even multiple of the frame rate). Some protocols required a lower presentation rate than the frame rate, so we simulated this by presenting an image on multiple consecutive frames. For example, to present a 50-Hz C_sim/P_alt protocol with the frame rate set to 200 Hz, we presented the image sequence R1-R1-L1-L1-R2-R2-L2-L2… where R and L refer to the eyes being stimulated and 1 and 2 refer to the images. An image was always drawn on each CRT during half the display refreshes, so all protocols produced the same time-average luminance.

We presented a variety of speeds and capture rates, but concentrated on combinations that were near the flicker threshold. Each combination was presented 10 times.

Procedure

We explained the experiment to each observer. We told them that flicker is perceived as a fluctuation in the brightness of the square. We asked them to ignore motion artifacts such as unsmooth motion and edge banding. Observers viewed each stimulus presentation and then indicated whether or not they detected flicker.

We gave no instructions concerning eye movements, but we know from informal observation that observers usually tracked the stimulus.

Data analysis

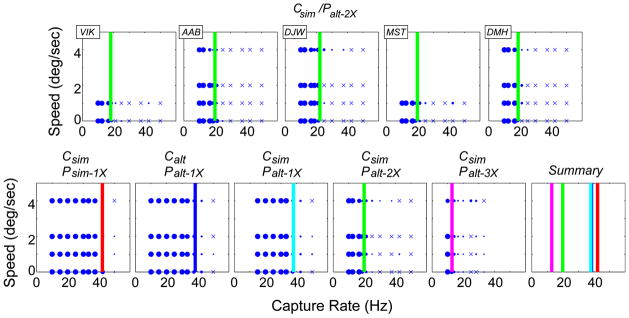
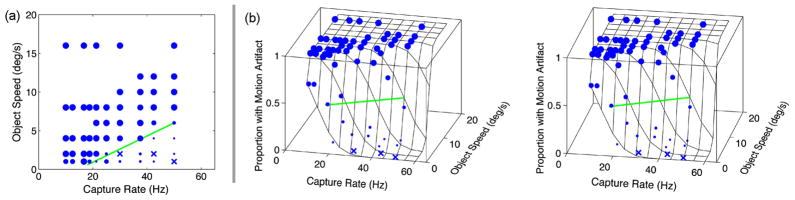
We computed the proportion of trials in which the observer reported flicker for each protocol condition. For each condition, we plotted the proportion of trials with reported flicker as a function of capture rate c and stimulus speed s. Those data are represented by the blue circles in Fig. 6. The proportion with reported flicker is indicated by the size of the circles. Cases in which flicker was never reported are indicated by small ×’s. We fit the data with a cumulative Gaussian function.^9,10

FIGURE 6.

Data and fits for all conditions in Experiment 1. Each panel plots the proportion of trials in which flicker was reported as a function of capture rate and stimulus speed. The proportion is indicated by the size of the data symbol. ×’s represent conditions in which flicker was never reported. The panels in the upper row show the data from the C_sim/P_alt–2X protocol for all five observers. The lower row shows the data averaged across observers for each protocol. We fit cumulative Gaussians to each observer’s data for each condition; the 0.5 point on each fitted function was the estimate of flicker threshold. Those thresholds across conditions were generally aligned vertically in plots like this figure (meaning that they were the same capture rate independent of speed). The color lines in each panel of the top row illustrate the similarity of our results across observers. To summarize the data, in the bottom row we averaged the raw data across observers and fit the vertical lines to the averaged data. The sixth panel in the bottom row plots the lines from the first five panels.

4.2 Results

The flicker data are shown in Fig. 6. The upper row shows data from individual observers for one protocol: C_sim/P_alt–2X. Each panel plots the proportion of trials with reported flicker as a function of speed and capture rate. The vertical lines represent the 0.5 points on the best-fitting cumulative Gaussians. As you can see, flicker visibility in this condition was not affected by speed.

The data were very similar across observers, so we averaged the data for each protocol across observers. The averaged data are shown in the lower row of Fig. 6; the rightmost panel summarizes all of the data. As predicted by the theory described above, there was essentially no effect of stimulus speed on flicker visibility. Also, as predicted by the theory, higher capture rates were required to eliminate visible flicker in single-flash protocols than in multi-flash protocols.

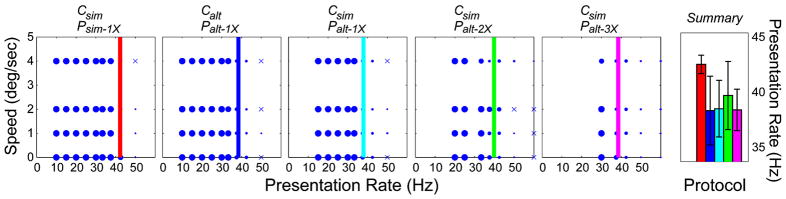
The theory also predicted that presentation rate, not capture rate, should be the primary determinant of whether a stimulus appears to flicker. We evaluate this prediction in Fig. 7 by re-plotting the data in the lower half of Fig. 6 as a function of speed and presentation rate. When the data are plotted this way, the boundary between visible and invisible flicker occurs in all protocols at a presentation rate of ~40 Hz. Thus, presentation rate is, as expected, the primary determinant of flicker visibility.

FIGURE 7.

Data and fits as a function of presentation rate. The five panels on the left plot the proportion of trials in which flicker was reported as a function of presentation rate and stimulus speed. The data were averaged across observers for each protocol. The lines are the 0.5 points in the best-fitting vertical cumulative Gaussians. The right-most panel summarizes the data from the other five panels. It plots the presentation rate that just produced visible flicker for each protocol averaged across observers. Different colors represent different protocols: red is C_sim/P_sim–1X, dark blue is C_alt/P_alt–1X, cyan is C_sim/P_alt–1X, green is C_sim/P_alt–2X, and purple is C_sim/P_alt–3X. Error bars represent standard deviations.

There was, however, a statistically significant difference with one protocol. A higher presentation rate (~10%) was required to eliminate noticeable flicker with simultaneous presentation than with the corresponding alternating presentation (C_sim/P_sim–1X vs. C_sim/P_alt–1X; p < 0.01, paired t-test). The temporal frequencies presented to the eyes are the same in these two protocols, but the illuminated frames are in the same phase in the two eyes in the simultaneous case and are in opposite phase in the two eyes in the alternating case. This means that some cancellation of flicker occurs in combining the two eyes’ images binocularly.¹¹ Thus, alternating presentation to the two eyes (e.g., shutter glasses) reduces flicker visibility compared to simultaneous presentation.

The right-most panel of Fig. 7 summarizes the data by plotting the presentation rate that produced flicker on half the trials for each protocol. The only consistent difference was between the simultaneous presentation, single-flash protocol (C_sim/P_sim–1X), and the other protocols, which again shows that temporal variations presented simultaneously to the two eyes are more likely to produce visible flicker than variations presented alternately. Otherwise, there was no consistent effect of protocol; only the presentation rate mattered.

It is important to relate these data to the standard protocols for stereo presentation. IMAX mostly uses simultaneous capture at 24 Hz with simultaneous double-flash presentation (C_sim/P_sim–2X) yielding a presentation rate of 48 Hz per eye. By using two projectors, IMAX does not have to insert dark frames, and thus IMAX uses a larger duty cycle, which reduces flicker visibility. RealD and Dolby use simultaneous capture at 24 Hz with alternating triple-flash presentation (C_sim/P_alt–3X) yielding a presentation rate of 72 Hz. Television content is, of course, recorded differently than cinematic content.¹² In the U.S., television cameras record images at an interleaved rate of 60 Hz (the even and odd rows are captured at 30 Hz in counterphase). This form requires de-interlacing before viewing on progressive displays like LCDs. Once de-interlaced, the typical stereo TV presentation protocol becomes C_sim/P_alt–1X with capture and presentation rates of 60 Hz. Our data show that these three standard protocols produce presentation rates that are high enough to eliminate perceived flicker.

5 Theory for visibility of motion artifacts

We now turn to the visibility of motion artifacts. These artifacts include judder (jerky or unsmooth motion appearance), edge banding (more than one edge seen at the edge of a moving stimulus), and motion blur (perceived blur at a moving edge). The analysis of motion artifacts is somewhat more complicated than the one for flicker because with a given capture rate, multi-flash protocols do not change the spatio-temporal frequency of the aliases. Instead they differentially attenuate the aliases at certain temporal frequencies. Thus, perceiving artifacts will be determined by the spatio-temporal frequencies and amplitudes of the aliases.

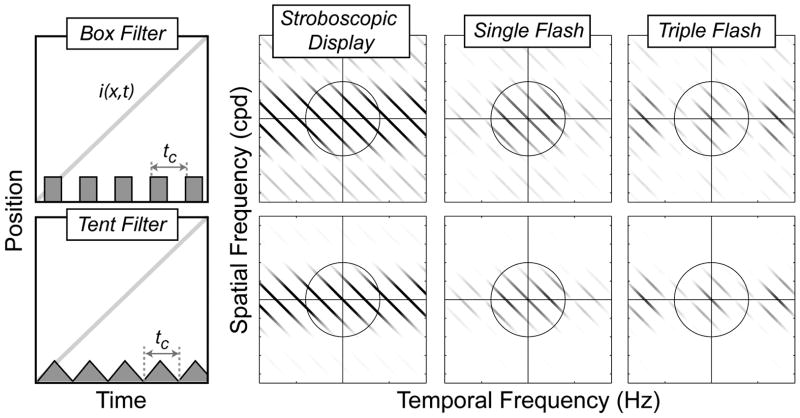
Observers typically track a moving stimulus with smooth-pursuit eye movements that keep the stimulus on the fovea, and this affects our analysis. Assuming the pursuit movement is accurate, the image of a smoothly moving stimulus becomes fixed on the retina; that is, for a real object moving smoothly at speed s relative to the observer, and an eye tracking at the same speed, the retinal speed of the stimulus s_retinal is 0. With a discrete stimulus moving at the same speed, the only temporally varying signal on the retina is created by the difference between smoothly moving and discretely moving images. These differences are shown in the top row of Fig. 8. Each image presentation of duration t_p displaces across the retina by Δx =−st_p. Thus, significant displacement can occur with high stimulus speeds and low frame rates thereby blurring the stimulus on the retina (“motion blur”). The amplitude spectra in retinal coordinates are displayed in the middle row. The signal and aliases are sheared parallel to the temporal-frequency axis such that they have a slope of−1/s_retinal; i.e., they become vertical. The zero crossings of the aliases on the temporal-frequency axis are unchanged because eye movements do not affect the rate at which images are delivered to the eyes. The envelope by which the signal and aliases are attenuated is sheared in the same fashion as the signal and aliases; it is now the sum of sinc functions centered on the line ω = τ/s. The amplitude spectra in the middle row are the sheared signal and aliases multiplied by the sheared envelope. The bottom row in the figure shows vertical cross-sections of those amplitude spectra along the retinal spatial-frequency axis (i.e., at τ = 0).

FIGURE 8.

Properties of multiple-flash stimuli with eye movements. From left to right, the columns depict stroboscopic, single-, double-, and triple-flash protocols with smooth eye movements. The top row shows the retinal position of the stimulus as a function of time for different protocols. The gray horizontal lines represent a smoothly moving stimulus. The green line segments represent discrete stimuli moving at the same speed. Each sample of the discrete stimulus shifts across the retina by Δx =−st_p. The middle row shows the amplitude spectra for each stimulus. The abscissa is temporal frequency and the ordinate is spatial frequency in retinal coordinates. The origin (τ = 0, ω = 0) is in the middle of each panel. Darker grays represent greater amplitude. The bottom row shows vertical cross sections of the amplitude spectra along the spatial-frequency axis (τ = 0). Again, spatial frequency is in retinal coordinates.

Imagine that the component along the spatial-frequency axis is the only visible component due to filtering by the window of visibility. The stroboscopic stimulus has a uniform spectrum along the spatial-frequency axis, so it should look like a vertical line that is stationary on the retina and would therefore be perceived to move smoothly as the eye rotates. The single-, double-, and triple-flash protocols have amplitude spectra along the spatial-frequency axis that are

$$\delta (\tau )\left\{\frac{1}{2}\text{sinc}\left(\frac{-\pi \omega s}{{\tau }_c}\right)+\sum _{k=\pm 1}\left[\sum _{i=1}^{\infty }\left[\frac{{(-1)}^{(i+1)}}{2i-1}\text{sinc}\left(\frac{\pi }{{\tau }_c}(-\omega s-k(2i-1)f{\tau }_c)\right)\right]\right]\right\},$$ (9)

where f is the number of flashes and ω is in retinal coordinates. The inverse Fourier transform of Eq. (9) is

$$r\left(\frac{x}{s/{\tau }_c}\right)\left[\frac{1}{2}+\frac{1}{2}\mathit{sqr}\left(\frac{x}{fs/{\tau }_c}\right)\right],$$ (10)

where s/fτ_c is the period of a square wave truncated by a pulse of width s/τ_c. Equation (10) describes the spatial stimulus in retinal coordinates. For single-flash presentation, the resultant is one spatial pulse of width s/2τ_c. For double flash, it is two pulses of width s/4τ_c separated by s/4τ_c. For triple-flash presentation, it is three pulses of width s/6t_c separated by s/6τ_c. This means that moving stimuli presented according to these three protocols should appear to have one, two, or three bands in regions of high contrast, and the widths of the bands should be proportional to speed. This is precisely what is observed.

We assume that motion artifacts will be perceived when either one or more of the aliases encroach on the window of visibility, or the amplitude of the central spectral component (the one going through the origin) deviates noticeably from the amplitude of that component with a smoothly moving stimulus.

It is interesting to note that Eq. (10) is similar for speeds and capture rates with a constant ratio (i.e., when s/τ_c is constant). We therefore predict that the visibility of motion artifacts, such as unsmooth motion and edge banding, will be roughly constant for all stimuli with a constant ratio s/τ_c.

Sample-and-hold and single-, double-, and triple-flash protocols generally produce spatial blur when the viewer tracks a moving stimulus.^2,13,14 The blur is caused by persistence in the temporal impulse response function of the display. With smooth tracking, sluggishness in time yields blur in space in a fashion very similar to the analysis above in which flashing in time yields banding in space.

From the analysis described here, we can make the following predictions: (1) The visibility of motion artifacts should increase with increasing stimulus speed and decrease with increasing capture rate. More specifically, combinations of speed and capture rate that yield a constant ratio (s/τ_c) should have approximately equivalent motion artifacts. (2) Although speed and capture rate should be the primary determinants of motion artifacts, we predict that using multi-flash protocols to increase the presentation rate for a fixed capture rate (τ_p = fτ_c) will cause some increase in the visibility of motion artifacts. This is quite different from flicker visibility where multi-flash protocols were very effective. (3) Edge banding should be determined by the number of flashes in multi-flash protocols: two bands being perceived with double-flash, three with triple-flash, etc. (4) The spatio-temporal filtering associated with stereo visual processing is lower pass than the filtering associated with monocular or binocular luminance processing, so we predict that motion artifacts will generally be equally visible with stereo and non-stereo presentation. It follows from this prediction that the visibility of motion artifacts should be unaffected by the match between capture and presentation; i.e., artifacts should be equally visible with simultaneous or alternating presentation and not depend on whether simultaneous or alternating capture was used.

We next tested these predictions in a psychophysical experiment.

6 Experiment 2: Motion artifacts

6.1 Methods

The observers, apparatus, stimuli, procedure, and manner of data analysis were the same as in Experiment 1 with a few exceptions that we note here. Stimulus speeds of 1–16 deg/sec were presented, which covers the range that is typically presented on television.¹⁵ The conditions were chosen following pilot experiments to concentrate measurements in the neighborhood of the thresholds. All of the conditions are shown in Fig. 10. Each condition was replicated 10 times. When the speed was 4 deg/sec or slower, the stimulus moved from the starting position on the screen to the ending position in 2.5 sec. The motion path was centered on the screen. When the speed was faster than 4 deg/sec, the square started off-screen and moved across the entire screen until it disappeared at the other side. In this case, the stimulus duration co-varied with speed. We told the observers to indicate after each trial whether they had seen motion artifacts or not. We told them that motion artifacts are discrete or unsmooth motion (judder), motion blur, or edge banding. They were told to ignore flicker.

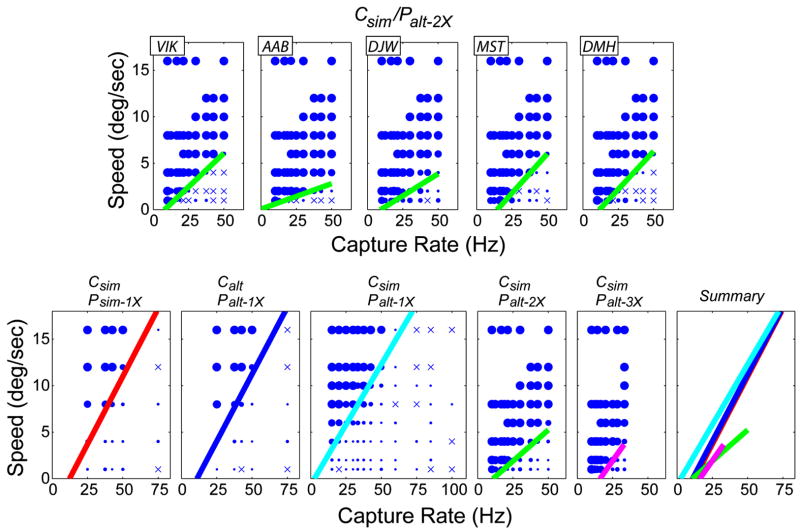
FIGURE 10.

Data and fits for all conditions in Experiment 2. Each panel plots the proportion of trials in which motion artifacts were reported as a function of capture rate and stimulus speed; proportion is indicated by the size of the data symbol. ×’s represent conditions in which artifacts were never reported. The upper row shows the data for one temporal protocol (C_sim/P_alt–2X) for all five observers. The lower row shows the data averaged across observers for five protocols. The lines are the 0.5 points in the best-fitting cumulative Gaussians to the full dataset [Eq. (11)]. The sixth panel plots the lines from the first five panels.

We then fit the data for each protocol with an oriented 3-D cumulative Gaussian:

$$P(j)=\mathit{normcdf}\left[\left(\frac{1}{\sqrt{1+{\phi }^2}}\right)(c-c_0)+s\left(\frac{\phi }{\sqrt{1+{\phi }^2}}\right),0,\sigma \right],$$ (11)

where P(j) is the proportion of trials with reported artifacts, c is capture rate, c₀ is the intercept on the abscissa, s is stimulus speed, φ is an orientation parameter, and σ is the standard deviation of the Gaussian. Figure 9 provides an example of the best-fitting function for one condition and observer. Figure 9(b) shows the data and best-fitting function as a stereogram; the green line indicates where the Gaussian has a value of 0.5. That line is reproduced in Fig. 9(a).

FIGURE 9.

Analysis of the motion-artifact data. (a) The proportion of trials in which motion artifacts were reported in the C_sim/P_alt–2X protocol is plotted as a function of capture rate and object speed. The proportion is indicated by the size of the data symbols, larger symbols for higher proportions. ×’s indicate conditions in which motion artifacts were never reported. (b) The same data are fit with a 3-D cumulative Gaussian and plotted as a stereogram. To see the figure in depth, cross-fuse (i.e., direct the right eye to the left panel and left eye to the right panel). The green line marks the positions on the fitted function where the observer reported artifacts on half the presentations.

6.2 Results

Figure 10 plots the proportion of trials with reported motion artifacts as a function of capture rate and stimulus speed. The top row shows the data from each observer from the C_sim/P_alt–2X protocol. The green lines represent the 0.5 points on the best-fitting cumulative Gaussians [Eq. (11) and Fig. 9]. Artifacts were frequently reported for capture-speed combinations in the upper left of each panel; those correspond to low capture rates and high stimulus speeds. Motion artifacts were not reported for combinations of high capture rate and low stimulus speed. There were no significant differences across the five observers.

The bottom row of Fig. 10 shows the artifact data averaged across observers for each of the five protocols along with the lines from the fitted function; the sixth panel shows the lines from each of the five protocols. The results were similar across protocols except that at a given capture rate, the double- and triple-flash protocols (C_sim/P_alt–2X and C_sim/P_alt–3X) produced artifacts at lower speeds than the corresponding single-flash protocol (C_sim/P_alt–1X).

To determine which differences between protocols were statistically reliable, we conducted single-factor paired-t significance tests on each observer’s data. Table 1 shows the results. The most reliable differences were between the triple-and single-flash protocols and between the double- and single-flash protocols; both multi-flash protocols required higher capture rates or lower speeds to eliminate motion artifacts than the single-flash protocol required.

TABLE 1.

Summary of Experiment 2 statistical results.

Comparison	Statistical Results
Csim/Psim-1X vs. Calt/Palt-1X	p < 0.05 for 1/5 observes
Csim/Psim-1X vs. Csim/Palt-1X	p < 0.05 for 2/5 observes
Calt/Palt-1X vs. Csim/Palt-1X	p < 0.05 for 1/5 observes
Csim/Palt-1X vs. Csim/Palt-2X	p < 0.05 for 5/5 observes
Csim/Palt-1X vs. Csim/Palt-3X	p < 0.01 for 5/5 observes
Csim/Palt-2X vs. Csim/Palt-3X	p < 0.05 for 0/5 observes

The theoretical analysis led to the expectation that speeds and capture rates with a constant ratio would yield constant artifact visibility. This prediction is largely borne out because s/τ_c is indeed roughly constant along the contours separating artifact and no-artifact regions. This is consistent with the first prediction above. It also appears that multi-flash protocols produced more visible artifacts at a given speed and capture rate than single-flash protocols. This is consistent with second prediction above. Although we did not formally measure perceived edge banding, our own observations revealed that once artifacts occurred, the number of bands seen at an edge was equal to the number of flashes in the protocol. This is consistent with third prediction above. There was no systematic effect of matching capture and presentation of the two eyes’ images; i.e., motion-artifact visibility was the same whether capture and presentation were matched (e.g., C_sim/P_sim or C_alt/P_alt) or unmatched (e.g., C_sim/P_alt). This is consistent with the fourth prediction above.

7 Experiment 2B

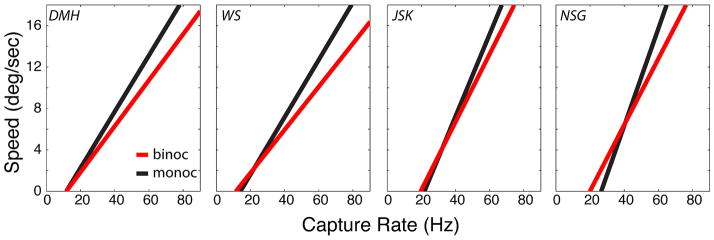
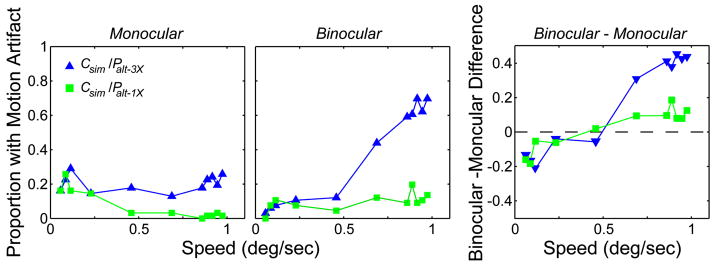
As we said earlier, the motion artifacts we observed may have little to do with binocular processing because the spatio-temporal contrast sensitivity function associated with monocular luminance processing extends to much higher spatial and temporal frequencies than the spatio-temporal sensitivity function associated with disparity estimation.^3,7,8 Therefore, we expected most if not all of the motion artifacts to be observable with monocular presentation. To test this, we ran an experiment in which we presented the C_sim/P_sim–1X protocol binocularly and monocularly (the latter by simply blocking the images being delivered to the left eye).

We tested four observers using the same apparatus and procedure as the main experiment. One of the observers was an author (DMH) and the others were unaware of the experimental hypotheses. All had normal or corrected-to-normal vision.

The results are shown in Fig. 11. Each panel plots the lines from the best-fitting cumulative Gaussians [Eq. (11)] that represent the combinations of stimulus speed and capture rate that produced motion artifacts on half the stimulus presentations. There was a small but statistically insignificant increase in artifact visibility with binocular viewing. The fact that binocular viewing did not yield significantly more artifacts is consistent with the fourth prediction above. The slight increase in the visibility of motion artifacts with binocular viewing is probably due to the increased luminance contrast sensitivity with binocular as opposed to monocular viewing.^16,17

FIGURE 11.

Motion artifacts with binocular and monocular presentation. Each panel shows the combination of speed and capture rate that yielded visible artifacts on half the stimulus presentations. The lines were determined by the fits of cumulative Gaussians [Eq. (11)] to the data as shown in Fig. 9. Red and black lines represent binocular and monocular presentation, respectively.

8 Summary of Experiments 1 and 2

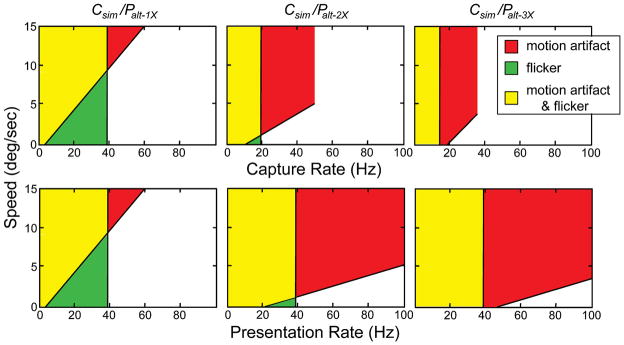
Thus far, we have considered how the presentation protocol and object speed influence flicker and motion artifacts separately by instructing the observers to report one artifact while ignoring the other. Now we consider the union of visible flicker and visible motion artifacts. Figure 12 summarizes the findings of Experiments 1 and 2. The columns represent the results with different protocols: C_sim/P_alt–1X, C_sim/P_alt–2X, and C_sim/P_alt–3X. The upper row shows the combinations of capture rate and stimulus speed that produced visible motion artifacts and/or flicker. The lower row shows the combinations of presentation rate and speed that produced visible artifacts and/or flicker. The combinations for which motion artifacts were perceived are shaded red, and the combinations for which flicker was perceived are shaded green. Combinations that produced both are shaded yellow. The figure makes clear that flicker visibility is determined by presentation rate. Specifically, flicker becomes visible in our apparatus when the presentation rate is less than 40 Hz. The fact that flicker visibility is independent of stimulus speed and predicted by presentation rate, not capture rate, is consistent with the theory presented earlier. Presentation rate is capture rate multiplied by the number of flashes (τ_p = fτ_c), so one can greatly reduce flicker visibility at a given capture rate by employing a multi-flash protocol; this is evident in the data in the upper row. The figure also makes clear that multi-flash protocols increase the visibility of motion artifacts: When employing a multi-flash protocol, one has to increase the capture rate or reduce the stimulus speed relative to what one has to do with a single-flash protocol. Interestingly, the visibility of motion artifacts is roughly constant for conditions in which the ratio of stimulus speed divided by capture rate is constant; that is, to first approximation, noticeable motion artifacts occur whenever s/τ_c exceeds 0.2°. This observation is also consistent with the theoretical analysis presented earlier. From the constant s/τ_c rule, one can make reasonable predictions about the visibility of motion artifacts for stimulus speeds higher than the range we presented.

FIGURE 12.

Summary of motion artifact and flicker data. The upper row summarizes the data when plotted with respect to capture rate and the lower row the same data when plotted with respect to presentation rate. The columns summarize the data from different protocols. The red regions represent combinations of stimulus speed and temporal rate that produced visible motion artifacts. The green regions represent combinations that produced visible flicker. The yellow regions represent combinations of speed and rate that produced both. The unshaded regions represent combinations that yielded smooth apparent motion without flicker. The colored regions in the middle and right panels of the upper row are clipped because we did not present capture rates greater than 50 and 33 Hz, respectively, with those protocols.

9 Experiment 3: Motion artifacts with motion in depth

In Experiment 2, we observed no systematic differences in the occurrence of motion artifacts with binocular and monocular presentations. This is perhaps not surprising because the stimulus motion was always horizontal in the plane of the display screen. Thus, the disparity was always zero, which means that the moving images presented to the two eyes were identical apart from differences in time. A stimulus moving in depth creates images that move in opposite directions in the two eyes. Such a stimulus is perhaps more likely to create the appearance of unsmooth motion with binocular than with monocular presentation. We next examined this possibility.

9.1 Methods

Seven observers, 18–25 years of age, participated. One was an author (DMH) and another was an assistant who was generally aware of the experimental hypotheses. The others were unaware of the hypotheses. They all had normal or corrected-to-normal visual acuity and stereoacuity and wore their optical corrections while performing the experiment.

We used the same stereoscope as in the previous experiments. The stimulus and procedure were the same as in Experiment 2 with a few exceptions. Instead of moving horizontally, the object moved directly toward the observer along the Z axis. The horizontal speeds of the square in the left and right eyes were s_L and s_R, respectively, where s_R =−s_L. Those speeds were constant over time, so the speed of the object specified in space was not constant. The square did not increase in size over time (i.e., it did not “loom”). We presented disparity speeds (s_R − s_L) of 0.1–2 deg/sec, so the speeds per eye were half those values. At stimulus onset, the disparity relative to the screen was 1.92° (uncrossed). It was then visible for 5 sec or until the disparity reached 2.55° (crossed). Each condition was repeated 10 times.

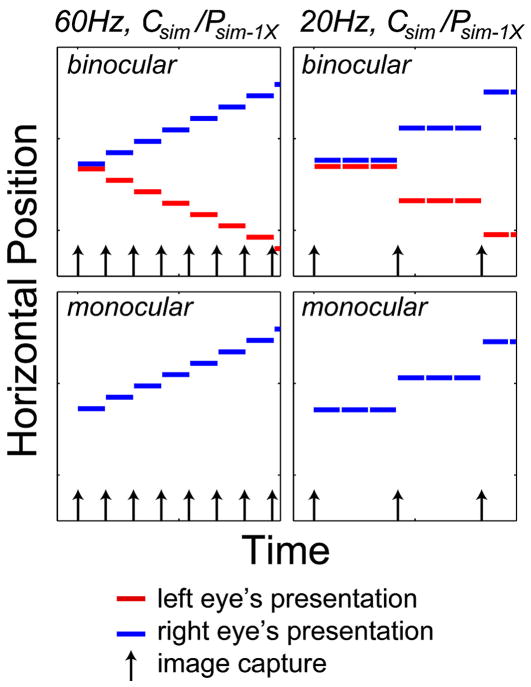
We conducted two sets of measurements. In the first set, we presented simultaneous, single-flash protocols (C_sim/P_sim–1X) at different presentation rates as schematized in Fig. 13. We set the resolution of the CRTs to 2048 × 768 such that pixels subtended 0.57 arcmin horizontally. We used this non-conventional resolution to present fine horizontal disparities. Anti-aliasing was employed. At the 2048 × 768 resolution, the CRT frame rate had to be set to 60 Hz, which restricted the temporal protocols we could present. The time-averaged luminance of the square stimulus was 59 cd/m². Because of the frame-rate restrictions, we only presented the C_sim/P_sim–1X protocol. Presentation rates were 5–60 Hz. To simulate rates lower than 60 Hz, we repeated frames as shown in the right column of Fig. 13. This is an approximation to sample and hold at 20 Hz. Note that there was no dark-frame insertion in these stimuli.

FIGURE 13.

Temporal protocols in the first set of measurements in Experiment 3. The stimulus moved in depth. Each panel plots the horizontal position of the stimulus presented to the eyes as a function of time. The temporal protocol was always C_sim/P_sim–1X. The columns represent different presentation rates: the left and right columns are 60 and 20 Hz, respectively. The upper row shows the protocols for binocular presentation and the lower row for monocular presentation. The arrows indicate the times at which the stimuli were captured (or computed). The red and blue line segments represent the presentations of the images to the left and right eyes, respectively.

In the second set of measurements, we presented alternating, multi-flash protocols (C_sim/P_alt), so dark frames were inserted as schematized in Fig. 14. The frame rate was set to 144Hz, which required a reduction in resolution to 800 × 600 (pixel size = 1.4 arcmin). Again anti-aliasing was employed. The luminance of the square also had to be reduced to 30 cd/m². The presentation rate was constant at 72 Hz per eye, so the single- and triple-flash protocols corresponded to capture rates of 72 and 24 Hz, respectively.

FIGURE 14.

Temporal protocols in the second set of measurements in Experiment 3. The stimulus again moved in depth. Panels plot the horizontal position of the stimulus presented to the eyes as a function of time. The left column represents the single-flash protocol C_sim/P_alt–1X and the right column the triple-flash protocol C_sim/P_alt–3X. The upper and lower rows schematize the stimuli for binocular and monocular presentation, respectively. The arrows indicate the times at which the stimuli were captured (or computed). The red and blue line segments represent the presentations of the images to the left and right eyes, respectively.

Observers viewed the stimuli binocularly in half the sessions and monocularly in the other half. After each presentation, they indicated whether they had detected motion artifacts or not. They were told to report artifacts whether the percept was unsmooth motion in depth or unsmooth horizontal motion.

9.2 Results

The left and middle panels of Fig. 15 display the data from the first set of measurements with the stimuli schematized in Fig. 13. There were no significant differences between the data from different observers, so we averaged across observers. The panels plot the proportion of trials with reported motion artifacts as a function of speed and capture rate: the left panel for monocular presentation and the middle one for binocular presentation. The green and red lines are the 0.5 points of the best-fitting cumulative Gaussians [Eq. (11)]. The right panel shows those lines on the same axes to facilitate comparison of the binocular and monocular data. As we found in Experiment 2, higher capture rates (which are equal to presentation rates in this experiment) allow one to display faster object speeds without visible judder. There was slightly more judder with monocular presentation at slow speeds and low capture rates and slightly more judder with binocular presentation at fast speeds and high capture rates. These differences were, however, small. The observation of no clear difference between motion artifacts with monocular and binocular presentation, coupled with a similar finding in Experiment 1, suggests that the predominant source of judder is not in the computation of disparity among binocular pathways.

FIGURE 15.

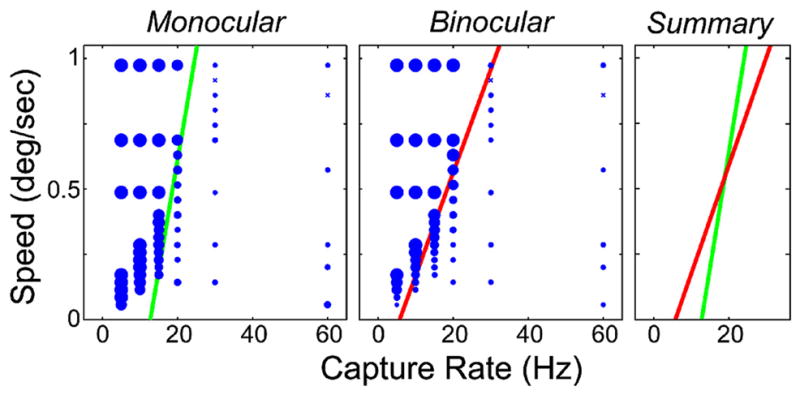
Results from first set of measurements in Experiment 3. The stimuli are schematized in Fig. 13. The left and middle panels show the data for monocular and binocular presentations, respectively, averaged across observers. Those panels plot the proportion of trials in which motion artifacts were reported as a function of speed and presentation rate, where speed is the horizontal speed of the stimulus in one eye and capture rate is the temporal frequency of the images delivered to the eyes. The proportion of reported judder is indicated by the size of the circles. ×’s indicate cases in which judder was never reported. The lines are the 0.5 points of the best-fitting cumulative Gaussians [Eq. (11)]. The right panel compares the best-fitting lines for the monocular (green) and binocular (red) data.

Figure 16 displays the data from the second set of measurements. All observers exhibited similar trends, so the figure shows average data. The left and middle panels plot the proportion of trials with reported judder as a function of object speed in one eye. The green squares and blue triangles represent single- and triple-flash protocols, respectively, with a presentation rate of 72 Hz (and therefore capture rates of 72 Hz for single flash and 24 Hz for triple flash). Motion artifacts were reported infrequently with monocular presentation and somewhat frequently with binocular presentation. The right panel plots the difference between the artifact proportions with binocular and monocular presentation. Differences greater than zero indicate that motion artifacts were more frequently seen with binocular than with monocular presentation. The triple-flash data reveal a clear increase in artifacts with binocular presentation at faster speeds. The single-flash data exhibit a similar trend, but they are affected by a floor effect (i.e., the proportion of reported artifacts is close to zero) so the trend in the data is attenuated. The difference plot reveals that slower object speeds produce more visible artifacts with monocular than with binocular presentation and that faster speeds produce more artifacts with binocular than with monocular presentation. This is similar to the pattern observed in the first set of measurements (Fig. 15). Thus, there is a purely binocular motion-artifact effect for motion in depth at faster speeds and particularly with triple-flash presentation.

FIGURE 16.

Results from second set of measurements in Experiment 3. The stimuli are schematized in Fig. 14. The left and middle panels show the data for monocular and binocular presentations, respectively, averaged across observers. Those panels plot the proportion of trials in which motion artifacts were reported as a function of object speed in one eye. The green squares represent the data for the single-flash protocol (C_sim/P_alt–1X) and the blue triangles the data for the triple-flash protocol (C_sim/P_alt–3X). The right panel plots the difference between the binocular and monocular data (the proportion of artifact trials with binocular presentation minus the proportion with monocular presentation).

10 Experiment 4: Depth distortion

In the Mach–Dvorak effect, a temporal delay to one eye’s input causes a moving object to appear displaced in depth.^18,19 Many of the presentation protocols we have considered here introduce such a delay to one eye, and that delay may alter the estimated disparity, which would in turn lead to distortion in the depth percept.²⁰ In the next experiment, we assessed the distortions in perceived depth associated with various protocols.

10.1 Methods

Observers

Four observers participated, ages 22–25 years. One (DMH) is an author, but the others were unaware of the experimental hypotheses. They all had normal or corrected-to-normal visual acuity and stereoacuity.

Apparatus and Stimuli

We used the same apparatus as in the previous experiments. The stimulus consisted of ten small circles in a circular arrangement [Fig. 17(a)]. The small circles had a diameter of 1° and a luminance of 30 cd/m². The circular arrangement had a diameter of 4.9°. A static vertical line was also presented with the same temporal protocol as the circles. The stimulus was otherwise dark. Stimulus speeds from −10 to 10 deg/sec were presented (positive values are counter-clockwise and negative are clockwise). Those speeds are the tangential speeds of the circles in degrees of visual angle. The horizontal speed varied, of course, with position along the path (maximum at the top and bottom, zero at the left and right). Our analysis of this task is based on only the horizontal-motion component because only that component affects the computation of horizontal disparity. The speeds were slow enough to avoid temporal aliasing that could have produced reversed apparent motion.²¹ Observers were given no instructions with respect to fixation and no feedback concerning the correctness of their responses.

FIGURE 17.

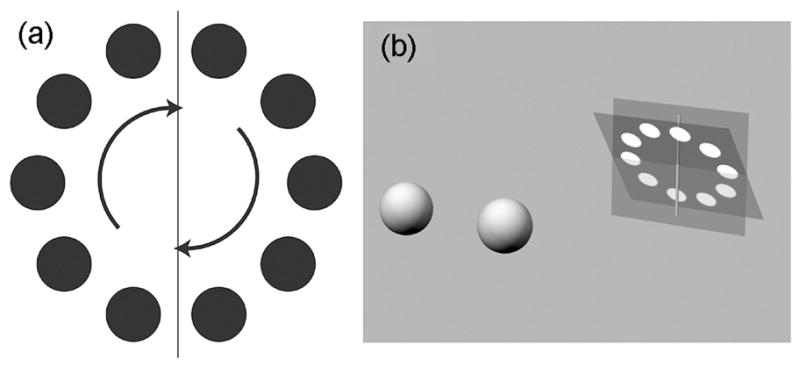
Stimulus for Experiment 4. (a) White circles moved at constant speed on a circular path on a dark background. The diameter of the white circles was 1°, and the diameter of the circular path was 4.9°. (b) Changes in apparent slant. The plane of white circles is represented by the dark square and the fronto-parallel plane by the gray square. The static vertical line was in the fronto-parallel plane. The rest of that plane was of course not visible. Observers indicated whether the plane of circles appeared to be pitched top forward or top back relative to the fronto-parallel plane.

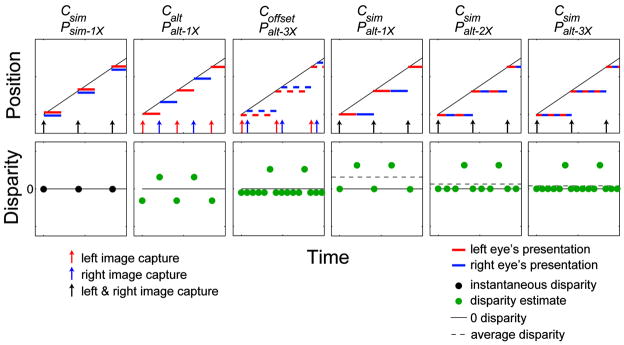
We presented several different temporal protocols, which are schematized in Fig. 18. All of the protocols were presented with a capture rate of 25 Hz (similar to the 24-Hz rate used in cinema), and some were also presented at capture rates of 37.5 or 75 Hz. The presentation rates varied depending on the specific protocol being presented. We also introduced a new triple-flash protocol, C_offset/P_alt–3X, in which the right eye capture was delayed by 1/6 of a frame so that the average disparity signal was correct.

FIGURE 18.

Temporal protocols in Experiment 4. The columns represent different temporal protocols. Upper row: Each panel plots the position of one of the white circles as a function of time. The red and blue line segments represent the presentations of the images to the left and right eyes, respectively. The arrows indicate the times at which the stimuli were captured (or computed). Black arrows indicate left and right images captured simultaneously. The red and blue arrows indicate left and right images captured in alternating fashion. The black diagonal lines represent the correct positions for the left and right images as a function of time. Lower row: Each panel plots disparity as a function of time. The black horizontal lines represent the correct disparities. The black dots represent the disparities when the two eyes’ images are presented simultaneously. The green dots represent the disparities that would be calculated if the left-eye image is matched to the successive right-eye image and the right-eye image is matched to the successive left-eye image. The dashed horizontal lines represent the time-average disparities that would be obtained by such matching. Wherever a horizontal line is not visible, the average disparity is the same as the correct disparity, so the two lines superimpose.

Procedure

On each trial, the circles travelled for 3 sec on a circular path at constant speed. The circles were extinguished at the end of the trial, and the observer indicated whether the plane in which the circles lay appeared pitched top forward or top back relative to the fronto-parallel plane [Fig. 17(b)]. A 1-up/1-down staircase procedure (an efficient psychophysical technique for finding the disparity gradient that makes the stimulus appear frontoparallel) adjusted the disparity gradient of the stimulus plane to find the value that made it appear fronto-parallel. We presented each protocol at least 100 times. The responses from each of those presentations were used to generate a set of psychometric data. We then fit those data with a cumulative Gaussian function using a maximum-likelihood criterion^9,10 and used the 0.5 point on that function as an estimate of the nulling disparity gradient. This is the gradient that made the plane of circles appear to be fronto-parallel.

10.2 Results

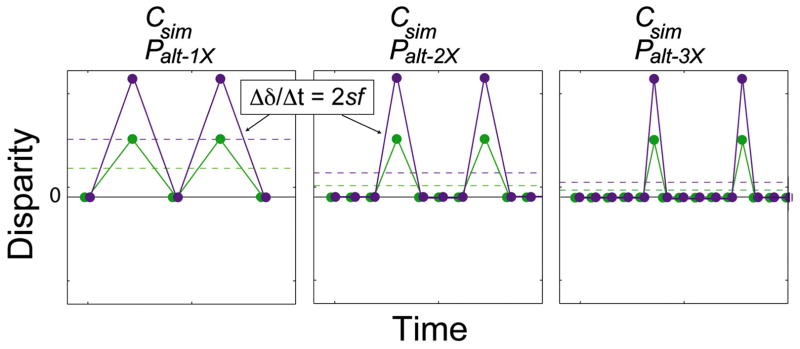
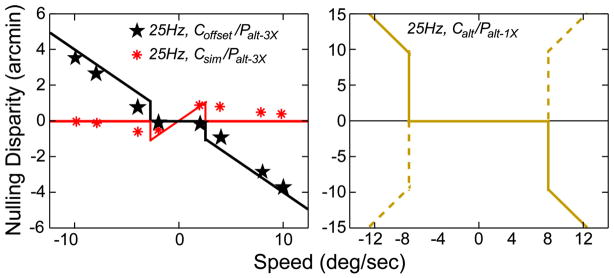
As we said earlier, time delays in the presentation of one eye’s image relative to the other eye’s image can plausibly lead to errors in the visual system’s estimate of the disparity. Consider, for example, the C_sim/P_alt–1X protocol (fourth column of Fig. 18). The solid horizontal line in the lower panel represents the correct disparity over time; i.e., the disparity that would occur with the presentation of a smoothly moving real object. To compute disparity, the visual system must match images in one eye with images in the other eye. But the images in this protocol are presented to the two eyes at different times, so non-simultaneous images must be matched. If each image in one eye is matched with the succeeding image in the other eye, the estimated disparities would be the green dots in the lower panel. For every two successive matches (three images), one disparity estimate is equal to the correct value and one is greater. As a result, the time-average disparity is biased relative to the correct value, and this should cause a change in perceived depth: a perceptual distortion. Notice that the difference between the time-average disparity and the correct disparity depends on the protocol: largest with single flash and smallest with triple flash. For this reason, the largest distortions should occur with single-flash protocols and the smallest with triple-flash protocols. The magnitude of the distortions should also depend on speed because the difference between the time-average disparity and the correct disparity is proportional to speed.

From this simple model of disparity estimation, the difference between the time-average disparity and the correct disparity (at the top of the stimulus) is

$$\mathrm{\Delta }=\left(\frac{s}{c}\right)\left(\frac{1}{2f}\right),$$ (12)

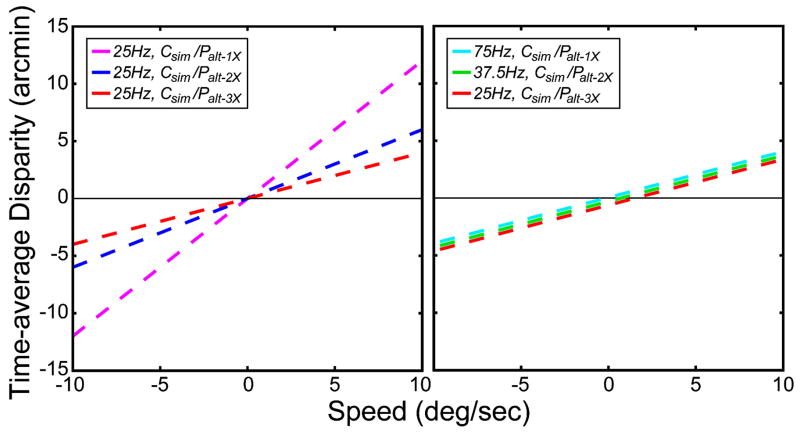
where s is speed in deg/sec, c is capture rate in Hz (cycles/sec), and f is the number of flashes associated with the alternating temporal protocol. Figure 19 shows the predictions plotted as Δ as a function of s for some example protocols.

FIGURE 19.

Predicted distortions for some of the temporal protocols. Time-average disparity is plotted as a function of stimulus speed. The predicted nulling disparity (the disparity between the top of the plane of circles and the fronto-parallel plane when the circle plane appears fronto-parallel) is equal to the time-average disparity. In the left panel, the purple, blue, and red dashed lines are the predictions for the single-flash (C_sim/P_alt–1X), double-flash (C_sim/P_alt–2X), and triple-flash (C_sim/P_alt–3X) protocols when the capture rate is 25 Hz. In the right panel, the cyan, green, and red dashed lines are the predictions for protocols with a 75-Hz presentation rate: single-flash (C_sim/P_alt–1X) with 75-Hz capture, double-flash (C_sim/P_alt–2X) with 37.5-Hz capture, and triple-flash (C_sim/P_alt–3X) with 25-Hz capture. The lines actually superimpose, but have been vertically separated for clarity.

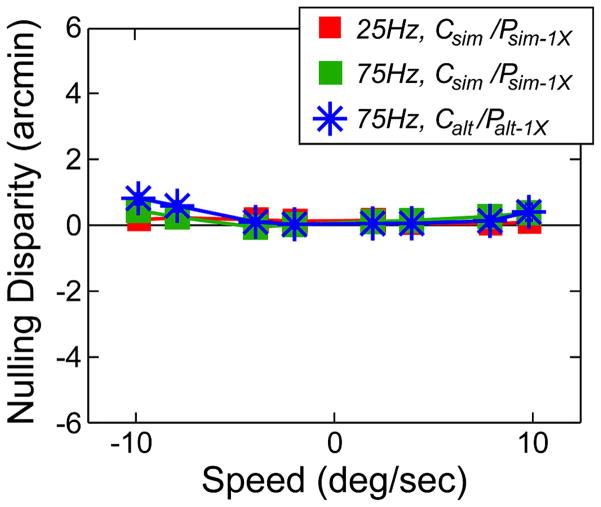
We next examined the experimental data and compare them to these predictions. The data from the different observers were very similar (with one exception that we highlight below), so we averaged across observers. We first look at the results for protocols in which the capture and presentation times are matched, so errors in disparity estimation should not occur. In Fig. 20, the protocols are C_sim/P_sim–1X and C_alt/P_alt–1X; in both cases, the two eyes’ presentations occur at the correct times, so the time-average disparity is equal to the correct disparity. The predicted disparity errors are zero, so the predictions are the horizontal line. The nulling disparity gradient was indeed close to zero at all speeds and in all conditions. Thus, matching the synchrony of presentation to the synchrony of capture yields essentially no distortion of perceived depth.

FIGURE 20.

Perceptual distortions with single-flash protocols in which the synchrony of capture and presentation are matched. Nulling disparity is plotted as a function of stimulus speed. The plotted value is the disparity between the top of the plane of circles and the objective fronto-parallel plane when the plane of circles appeared fronto-parallel. The red squares represent the data with the C_sim/P_sim-1X protocol with a capture rate of 25 Hz. The blue asterisks and green squares represent the data from the C_alt/P_alt–1X and C_sim/P_sim–1X protocols, respectively, with a capture rate of 75 Hz. The data have been averaged across observers. The 95% confidence intervals are smaller than the data-point symbols. The model expressed in Eq. (12) predicts no disparity error in these three conditions, so the prediction lines all correspond to the black horizontal line.

The most frequently used protocols employ simultaneous capture and alternating presentation. With such an arrangement, one eye’s image is delayed, so we expect to observe errors in disparity estimation and accompanying depth distortions. Figure 21 plots the predictions and data from the single-flash protocol with 25- and 75-Hz capture rates (and presentation rates). The predictions from Eq. (12) are the green and purple dashed lines. The experimental data are represented by the colored symbols. As predicted, the magnitude of perceptual distortion is greater at the slower capture and presentation rates because the right-eye’s image is more delayed at those rates. Also as expected, the size of the distortion increases as speed increases. With 75-Hz capture, the distortion increases up to the fastest speed tested. With 25-Hz capture, the distortion levels off at ~3 deg/sec and then decreases at yet higher speeds. We conclude that perceived depth distortions do occur, as predicted by the model in Eq. (12), when capture and presentation synchrony are not matched. The model’s predictions are accurate at slow speeds, but smaller distortions than predicted are observed at fast speeds.

FIGURE 21.

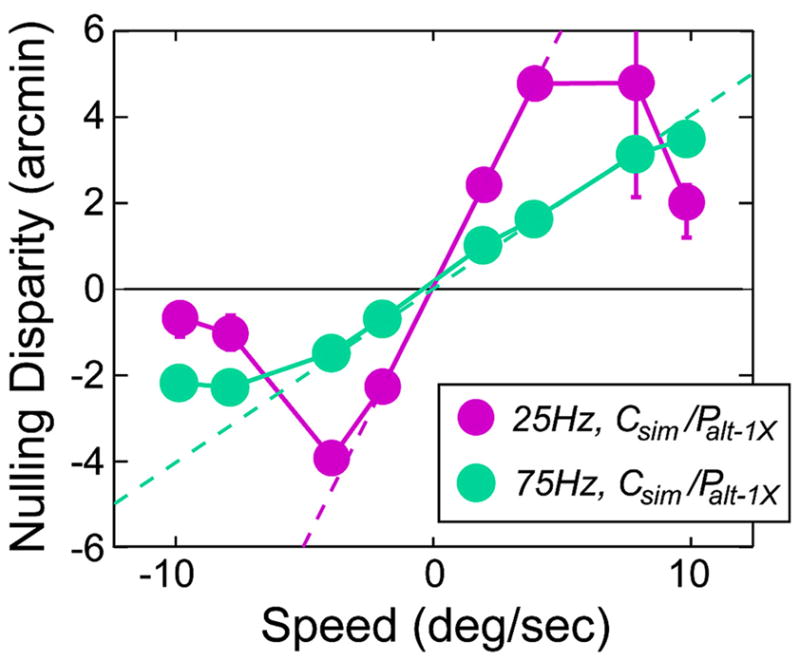
Perceptual distortions with single-flash protocols in which the synchrony of capture and presentation are not matched. Nulling disparity is plotted as a function of stimulus speed. The purple circles represent the data with the C_sim/P_alt–1X protocol with a capture rate of 25 Hz. Cyan circles represent the data from the C_sim/P_alt–1X protocol with a capture rate of 75 Hz. The data have been averaged across observers. Error bars are 95% confidence intervals. From Eq. (12), the prediction is the purple dashed line with 25-Hz capture and the cyan dashed line with 75-Hz capture.

The perceptual distortions manifest in Fig. 21 can be readily observed in stereo TV and cinema. For example, in stereo broadcasts of World Cup soccer in 2010, a ball kicked along the ground would appear to recede in depth when moving in one direction (paradoxically seeming to go beneath the playing field!) and would appear to come closer in depth when moving in the opposite direction. This speed-dependent effect can be quite disturbing, so it is clearly useful to understand what causes it and how one might minimize or eliminate it.

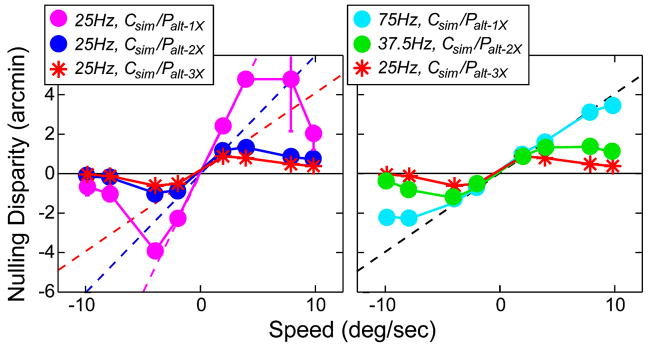
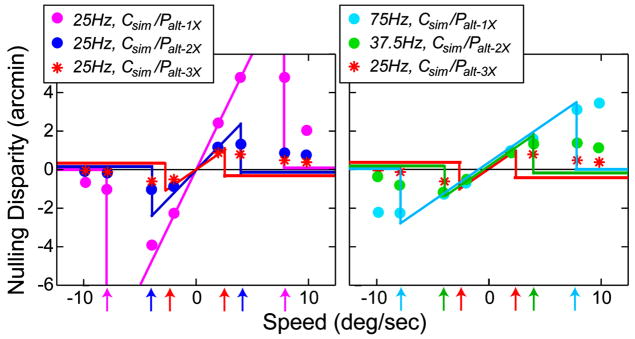
We have established that single-flash simultaneous-alternating protocols can produce large distortions in perceived depth, so we next examined whether multi-flash protocols reduce the magnitude of the distortions. Figure 22 shows the predictions and data from single-, double- and triple-flash protocols with simultaneous capture and alternating presentation (columns 4–6 in Fig. 18). The left panel plots the predictions and data when the capture rate was 25 Hz and presentation rates were 25, 50, and 75 Hz for the single-, double-, and triple-flash protocols, respectively. In those cases, the right-eye’s image was delayed relative to the left-eye’s image by 1/50, 1/100, and 1/150 sec, respectively, so the predicted distortions are larger in the single-flash protocol (purple dashed line) than in the multi-flash protocols (blue and red dashed lines). The data exhibited the predicted distortions at slow speeds in all three protocols; in particular, they were indeed smaller in the multi-flash protocols than in the single-flash protocol. The distortions then leveled off and declined with yet faster speeds. Thus, the predictions of the model were again accurate at slow, but not fast speeds. These data show that multi-flash presentation yields smaller perceptual distortions than single-flash presentation even when the capture rate is fixed, as predicted by the model in Eq. (12).

FIGURE 22.

Perceptual distortions with simultaneous capture and alternating presentation. Nulling disparity is plotted as a function of stimulus speed. The left panel shows the data from protocols with a 25-Hz capture rate. The purple circles represent the data with the single-flash protocol (C_sim/P_alt–1X); those data were also plotted in Fig. 21. The blue circles represent the data with the double-flash protocol (C_sim/P_alt–2X). The red asterisks represent the data from the triple-flash protocol (C_sim/P_alt–3X). Error bars are 95% confidence intervals. The predictions for the model in Eq. (12) are the dashed lines with the colors corresponding to the appropriate temporal protocol. The right panel shows the data from the same protocols, but with different capture rates. In each case, the presentation rate was 75 Hz, so the right-eye’s image was delayed relative to the left-eye’s image by 1/150 sec. The predictions for the model in Eq. (12) are the dashed line. The cyan circles, green circles, and red asterisks are the data from the single-, double-, and triple-flash protocols, respectively. The data have been averaged across observers. Error bars are 95% confidence intervals.

We next asked whether the time delay of one eye’s image is the only determinant of the perceptual distortions. The right panel of Fig. 22 plots the predictions and data for different capture rates (75, 37.5, and 25 Hz for single-, double-, and triple-flash, respectively) and a constant presentation rate of 75 Hz. In every case, the right-eye’s image stream is delayed by 1/150 sec relative to the left-eye’s image stream, so if the delay were the sole determinant of depth distortion, the data would be the same for the three protocols. The model predicts the same errors for the three protocols. As one can see, the observed distortions were indeed very similar at slow speeds for the three protocols, but became larger with single flash than with multi-flash at fast speeds. We conclude that the perceptual distortions for relatively slow speeds are determined by the time-average disparity, as expressed by the model. But distortions for fast speeds are minimized by use of multi-flash protocols, and this observation is not consistent with the model expressed by Eq. (12).

We next examined the effect of matching capture and presentation synchrony in the triple-flash protocol. The synchrony is not matched in the standard C_sim/P_alt–3X protocol, so the presentation of the right-eye’s image is delayed by 1/150 sec relative to the left-eye’s image, producing a small difference between the time-average and correct disparities (Fig. 18). The synchrony is matched in the C_offset/P_alt–3X protocol by delaying the capture of the right eye’s image by 1/150 sec, yielding no difference between the time-average and correct disparities (Fig. 18). As a consequence, one might expect smaller distortions in the C_offset/P_alt–3X than in the C_sim/P_alt–3X protocol. Figure 23 shows the predictions and data. The black horizontal and red dashed lines represent the predictions from Eq. (12). The black and red symbols represent the data. As you can see, the predictions were again quite accurate at slow speeds, but notably inaccurate at fast speeds. Interestingly, the distortions were greater at fast speeds when the capture and presentation synchrony was matched than when it was not. Notice that the direction of the depth distortion was the opposite of the direction observed in other conditions (Figs. 21 and 22). These data show that the model in Eq. (12) again predicts the data accurately at slow, but not fast speeds.

FIGURE 23.

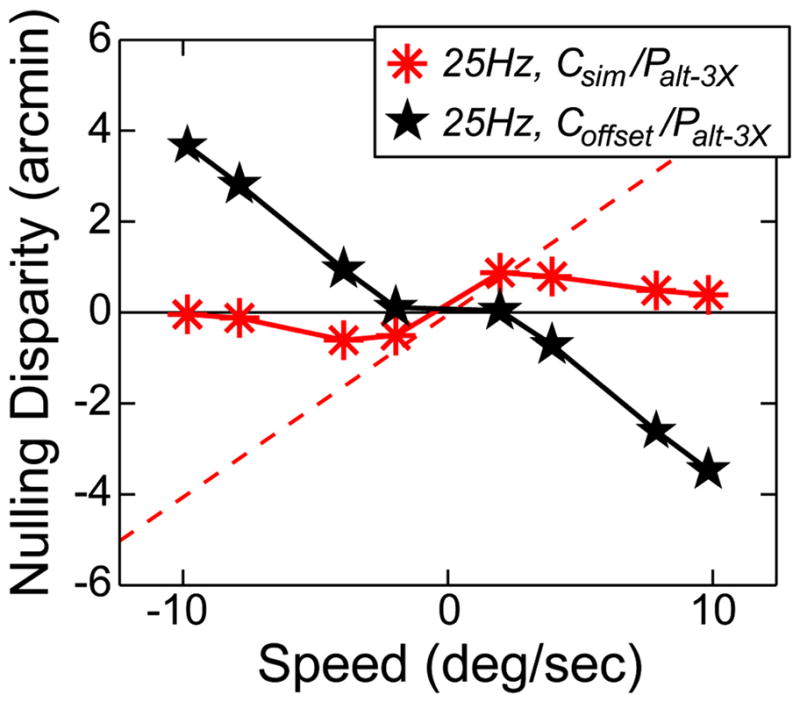
Perceptual distortions for triple-flash alternating presentation with simultaneous and offset capture. Nulling disparity is plotted as a function of speed. The capture rate is 25 Hz. Red asterisks represent the data from the C_sim/P_alt–3X protocol and black stars the data from the C_offset/P_alt–3X protocol. Error bars represent 95% confidence intervals and are smaller than the data symbols. The predictions for the model in Eq. (12) are the red dashed line for the C_sim/P_alt–3X protocol and the black horizontal line for the C_offset/P_alt–3X protocol.

We mentioned earlier that one protocol yielded significant between-observer differences. The predictions and data for that protocol – C_alt/P_alt–1X with a capture rate of 25 Hz – are plotted in Fig. 24. All four observers exhibited no distortion at slow speeds as predicted by the model. However, the observers behaved differently from the predictions and from one another at fast speeds.

FIGURE 24.

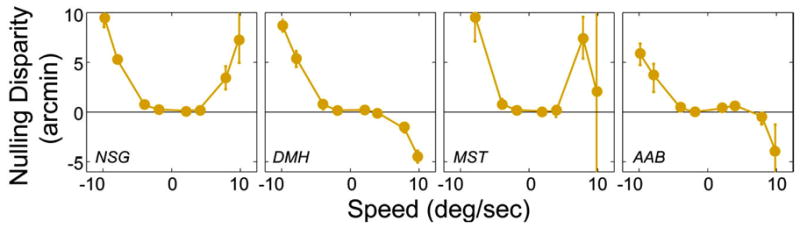
Individual observer data in the C_alt/P_alt–1X with a capture rate of 25 Hz. Each panel plots the data from a different observer. The nulling disparity is plotted as a function of speed. The model in Eq. (12) predicts no disparity error in this condition, so the horizontal black lines are the predictions. Error bars are 95% confidence intervals.

The model described by Eq. (12) predicts the observed distortions quite accurately at slow speeds for all the protocols, but not at all accurately at fast speeds. Why does the model fail at high speeds? It is well established that the visual system exhibits a spatial disparity-gradient limit. For example, Burt and Julesz²² found that when the disparity (Δδ) between two elements of a stereogram exceeded their angular separation (Δx), the perception of depth broke down. They argued that the limit to fusion is not disparity per se, as suggested by the notion of Panum’s fusional area.²³ Rather, the limit is a ratio: the disparity divided by the separation (Δδ/Δx). When the absolute value of the ratio exceeds ~1, fusion and disparity estimation fail. This is the spatial disparity-gradient limit. The consequences of the spatial disparity-gradient limit are also observed when the stimulus is a sinusoidal depth corrugation. Such a corrugation cannot be perceived when the product of corrugation spatial frequency and disparity amplitude exceeds a critical value^8,24 and that value is consistent with a disparity-gradient limit of ± 1.

The visual system also seems to have a temporal disparity-gradient limit. Specifically, it is unable to estimate disparity when the change in disparity per unit time (Δδ/Δt) becomes too large.²⁵ To our knowledge, the critical value of the temporal disparity-gradient limit has not yet been established. In our experiment,

$$\mathrm{\Delta }\delta /\mathrm{\Delta }t=\pm 2sf,$$

where s is object speed and f is the number of flashes in the protocol. Let C represent the critical value of |Δδ/Δt|, then the greatest speed before the disparity estimation fails would be

$$s=C/2f.$$ (13)

When disparity estimation fails, the visual system’s estimate of disparity over time would regress toward the disparities for which the temporal disparity gradient is low. Consider, for example, the middle panel of Fig. 25 where the double-flash protocol is depicted. When object speed is lower than the critical value specified by Eq. (13), the disparity estimate is the time average specified by Eq. (12) (represented by the dashed horizontal lines). However, when speed exceeds the critical value of Eq. (13), the disparity estimate regresses to the values for which the gradient is low. In the middle panel, it would regress toward the correct value (represented by the solid black line). As a consequence, the perceptual distortion associated with this multi-flash protocol would decrease with increasing speed.

FIGURE 25.

Temporal variations in disparity with different protocols and speeds. Each panel plots the temporal variation of disparity as a function of time. The green and purple dots represent the disparity estimates at specific times, the former when stimulus speed is s₁ and the latter when the speed is s₂ = 2s₁. The disparity gradients (Δδ/Δt) over time for the rising and falling parts of the disparity estimates are ±2sf, where f is the number of flashes in the protocol. The black horizontal line represents the correct disparity. The green and purple dashed lines represent the time-average disparities for speeds of s and 2s, respectively.

Now consider the predictions of this elaborated model. We found that a temporal disparity-gradient limit of 38 arcmin/40 msec (40 msec is 1/25 sec) provides the best fit to the data. We incorporated that critical value in the model and generated predictions. Figure 26 shows the predicted and observed distortions with protocols involving simultaneous capture and alternating presentation. The predictions are positively sloped lines for slow speeds until the gradient limit is exceeded and then the predictions become the horizontal lines at zero disparity. Obviously, the transition from one behavior (the positively sloped lines) to the other (the horizontal lines) would be smoother in a biological system, but we modeled it here as discontinuous. As you can see, the elaborated model of Eqs. (12) and (13) provides a reasonable fit to the data. Importantly, the model’s predictions are consistent with all of the main effects.

FIGURE 26.

Predicted and observed distortions with simultaneous capture and alternating presentation. Nulling disparity is plotted as a function of stimulus speed. The colored symbols are the data from Fig. 22. The predictions are represented by the colored lines. They are given by Eq. (12) until the temporal disparity-gradient limit is exceeded and then the predictions become the disparities with the lower disparity gradient. The arrows indicate the speeds at which the critical limit occurs. The left panel shows the predictions and data from protocols with a 25-Hz capture rate. The right panel shows the predictions and data from the same protocols, but with different capture rates.

We next examine the predicted and observed distortions in protocols involving simultaneous and alternating capture. The left panel of Fig. 27 plots the predictions and data with triple-flash protocols involving either offset capture and presentation or simultaneous capture and alternating presentation. As you can see, the elaborated model provides a reasonable fit to the data in both cases. Importantly, the model’s behavior is consistent with our observation that alternating capture and presentation can yield larger perceptual distortions than simultaneous capture and alternating presentation. The right panel of Fig. 27 plots the predictions and data with a single-flash protocol in which capture and presentation are both alternating. Recall that this is the one condition in which we observed inconsistent behavior across observers. When the disparity-gradient limit is exceeded in this condition, there is equivalent evidence for positive and negative disparities relative to the correct value. Thus, the model could produce the predictions represented by the solid lines or those represented by the dashed lines. The data in Fig. 24 show that all observers experienced distortions consistent with the solid-line prediction at negative speeds. Two of them experienced distortions consistent with the solid-line prediction at positive speeds and two experienced distortions consistent with the dashed-line prediction. Again, the elaborated model is reasonably consistent with this behavior.

FIGURE 27.

Predicted and observed distortions with either alternating capture and presentation or simultaneous capture and alternating presentation. Nulling disparity is plotted as a function of stimulus speed. The predictions are represented by the colored lines. They are given by Eq. (12) until the temporal disparity-gradient limit is exceeded and then the predictions become the disparities with the lower disparity gradient. The left panel shows the predictions and data from protocols with a 25-Hz capture rate and either offset capture with alternating presentation or simultaneous capture with alternating presentation. The colored symbols are the data from Fig. 23. The right panel shows the predictions and data for alternating capture and presentation with a 25-Hz capture rate. When the gradient limit is exceeded, the model predicts that either large errors of negative slope (solid line) or large errors of positive slope (dashed line).

In summary, we observed distortions in perceived depth that depended predictably on stimulus speed and the type of temporal protocol being used. We considered objects moving horizontally along paths that are roughly parallel to the display screen. At slow speeds, the disparity distortions were well predicted by Eq. (12). As speed increased, a critical temporal disparity-gradient limit of 38 arcmin/40 msec was reached after which the disparity estimate over time regressed to the base value (which for C_sim was the correct value). Substituting 38/40 into Eq. (13), we can estimate the critical speed at which the gradient limit is exceeded: s = 8/f. Therefore, the use of multi-flash methods can minimize depth distortions because the disparity-gradient limit is reached at slower speeds.

11 Discussion

11.1 Motion artifacts with non-tracked objects

In the earlier theoretical section on the visibility of motion artifacts, we assumed that the viewer was tracking the stimulus with a smooth-pursuit eye movement. We did so because observers tracked in our experiments. But in real applications, the viewer may maintain fixation on a static object while other objects move. We now consider how the various capture and presentation protocols ought to affect perceived artifacts with non-fixated moving objects. From the earlier analysis, we can calculate the combinations of speed and presentation rate that will just produce motion artifacts (or flicker) by determining when the aliases created by discrete presentation just encroach on the window of visibility.

For each combination of stimulus speed and temporal presentation interval, there is a line representing the alias of lowest frequency:

$$\tau =-s\omega +1/\mathrm{\Delta }t.$$ (14)

The window of visibility is represented by an ellipse with a horizontal dimension of 2cff and vertical dimension of 2va:

$$\frac{{\tau }^2}{{\mathit{cff}}^2}+\frac{{\omega }^2}{\upsilon a^2}=1.$$ (15)

Combining Eqs. (14) and (15) and representing the resultant in the form of the quadratic equation, we obtain:

$$\omega =\frac{s^2\upsilon a^2\pm (\mathit{cff})(s)(\upsilon a)\sqrt{({\mathit{cff}}^2\mathrm{\Delta }{t}^2+\upsilon a^2{s}^2\mathrm{\Delta }{t}^2-1)}}{\left({\mathit{cff}}^2+s^2\upsilon a^2\right)(s)\mathrm{\Delta }t}.$$ (16)

There are many cases in which the alias line intersects the ellipse in two points, which means that the alias should be visible. There are also many cases in which the alias does not intersect the ellipse, which means that it should not be visible. We seek cases in which there is only one intersection because that would represent combinations of speed and presentation interval that would just produce visible motion artifacts or flicker. For those cases, the quantity in the square root of Eq. (16) is zero. Given Δt, cff, and va, the value of s that yields zero for the square root is

$$s=\frac{1}{\upsilon a}\sqrt{{\left(\frac{1}{\mathrm{\Delta }t}\right)}^2-{\mathit{cff}}^2}.$$ (17)

This result is similar to Watson and colleagues¹ [their Eq. (6)] except that they assumed a rectangular window of visibility. Figure 28 plots the combinations of object speed and temporal presentation rate determined from Eq. (17). These combinations should just produce motion artifacts or flicker, given different assumptions about the window of visibility. In the figure, we assumed cff = 40 Hz and va = 20, 40, and 60 cpd (red, blue, and green curves, respectively). The resulting contours represent the speed and presentation rates that would just produce motion artifacts or flicker. Combinations above and to the left of the contours would produce noticeable artifacts or flicker while combinations below and to the right would not. The contours intersect the abscissa at cff. The slopes of the linear parts of the contours are roughly proportional to cff/va. These predictions are reasonably consistent with the data in Fig. 12, which suggests that eye movements do not substantially affect the visibility of motion artifacts or flicker. They do, however, affect what the artifacts look like (i.e., edge banding is more common with eye tracking).

FIGURE 28.

Combinations of object speed (s) and presentation rate (τ_p) that should just produce motion artifacts or flicker. From Eq. (17), we find cases in which the first alias of the stroboscopically presented stimulus would just intersect the window of visibility. We assume cff =40 Hz and that va = 20, 40, or 60 cpd (red, blue, and green curves, respectively). Everything above and to the left of a contour should yield motion artifacts or flicker while everything below and to the right should be perceived as smooth unflickering motion.

11.2 Human sensitivity

As we said earlier, the visual system is not equally sensitive to contrast at all spatial and temporal frequencies. This differential sensitivity is described by the spatio-temporal contrast sensitivity function.^3,4,37 This function was represented by an ellipse in Fig. 1. The dimensions of the principal axes were the highest detectable temporal frequency – the critical flicker frequency (cff) – and the highest detectable spatial frequency – the visual acuity (va).

The actual sensitivity function is of course more complicated. Figure 29 depicts that spatio-temporal contrast sensitivity function for a typical viewer.^3,4 Contrast sensitivity (the reciprocal of the contrast required to detect the stimulus) is plotted as a function of spatial and temporal frequency. Several viewing parameters affect this function. First, the viewer’s optical state has a significant effect on sensitivity at high spatial frequencies. If the eye is defocused (i.e., the viewer is not accommodated to the distance of the stimulus), the sensitivity roll-off at higher spatial frequencies becomes steeper.^16,26 The function in the figure was obtained with careful adjustment of the viewer’s optics to assure maximum performance at high spatial frequencies. Second, spatio-temporal contrast sensitivity is highly dependent on light level. With dim stimuli, the visual system needs to integrate light spatially and temporally to obtain a reliable signal. As a consequence, sensitivity at low luminance is reduced at high spatial and temporal frequencies. With bright stimuli, there is less need to integrate spatially and temporally, so sensitivity at high frequencies increases. The data in the figure were obtained with a retinal illumination of 300 trolands (~65 cd/m²), which corresponds to moderate daylight. The luminances in our experiments were only slightly lower than this, so Fig. 29 is a reasonable approximation of the effective contrast sensitivity function in our experiments. Third, the sensitivity function decreases monotonically at higher spatial and temporal frequencies, which means that the highest detectable frequencies are strongly dependent on stimulus contrast. In other words, cff and va increase with increasing contrast. Fourth, cff and particularly va vary with position in the visual field. cff is relatively low in central vision and increases a bit with greater retinal eccentricity up to ~30°; thus, flicker is somewhat more visible in peripheral than in central vision.^27,28 Visual acuity declines dramatically with increasing retinal eccentricity,²⁹ and this makes motion artifacts much more visible in central than in peripheral vision.

FIGURE 29.

The human spatio-temporal contrast sensitivity function. The sensitivity to a moving sinusoidal grating is plotted as a function of temporal frequency (abscissa) and spatial frequency (ordinate). Sensitivity is the reciprocal of the contrast required to detect the stimulus and is represented by gray scale. This figure is based on a fit to human contrast sensitivity data from Kelly (1979). The threshold contrast was measured for drifting gratings with different spatial and temporal frequencies. The data have been plotted on the linear axes. We clipped the low-frequency roll-off so that sensitivity did not go to zero when spatial or temporal frequency went to zero.

Because of these four properties of the visual system, the elliptical approximation to the window of visibility should grow and shrink depending on viewing conditions.³⁰ If the viewer is well-focused, and the stimulus is bright and high in contrast, the principal axes expand and the window incorporates a larger range of spatial and temporal frequencies. Larger windows allow more aliases to be seen, so flicker and motion artifacts become more noticeable. If the viewer is not well-focused, and the stimulus is dim and low in contrast, the principal axes shrink: Flicker and motion artifacts become less noticeable. If the viewer is looking at the stimulus (i.e., is viewing it in central vision), va is higher and cff is lower than when the viewer is not looking directly at the stimulus. Thus, placing the stimulus in central vision usually makes motion artifacts more noticeable, and flicker somewhat less noticeable.

The luminances for television and cinema viewing are 100–300 and 40–50 cd/m² (lower for stereo cinema), respectively. Thus, the contrast sensitivity function is a reasonable approximation for conventional cinema. The function would extend to somewhat higher spatial and temporal frequencies for television viewing, but flicker and motion artifacts might not be as visible as one would expect from the expansion of the window of visibility because contrast is often reduced by the presence of significant ambient illumination in the home. The contrast sensitivity function would shrink somewhat in stereo cinema making flicker and motion artifacts slightly less noticeable than one would expect from the function in Fig. 29.

11.3 Caveats on the disparity-estimation model

In the section on disparity distortions with various capture and presentation protocols, we presented a very simple model of disparity estimation based purely on computing the difference in spatial positions of successive presentations to the left and right eyes. The model ignores the time that elapses between the presentation of the left- and right-eye images, and thus does not fully incorporate the spatio-temporal filtering that occurs in the monocular pathways before disparity estimation in the visual system. In reality, the eyes’ optics, retinal sampling, and post-retinal neural processing filter the inputs to the disparity-estimation stage in space and time. However, the filtering that occurs before disparity estimation is not as severe as the filtering that occurs at the disparity-estimation stage. For example, the highest spatial frequency that can be detected in a luminance-varying stimulus (such as a sinusoidal grating) is 40–50 cpd,³ but the highest discernible spatial frequency for disparity variation (i.e., the finest depth corrugation one can see) is roughly 2–3 cpd, or ~20 times lower.^7,8 Likewise, the fastest variation in luminance one can detect (i.e., the highest flicker rate) is 60–70 Hz, while the fastest variation in disparity one can see is 8–10 Hz, which is nearly 10 times slower.^3,25 As a consequence, the limiting spatio-temporal filter in stereopsis is at the disparity-estimation stage and not in the inputs to this stage. It is reasonable, therefore, to ignore the spatio-temporal filtering that occurs before the input to this stage.

Our one-to-one method for disparity estimation also implicitly assumes that the rate at which disparity is estimated is equal to the presentation rate. By matching each left-eye image with a predecessor and a successor in the right eye, the disparity-estimation rate is 2τ_p. When the presentation rate is slow, this is a reasonable assumption. But many of the current protocols use presentation rates of 60 or even 72 Hz per eye and this makes the assumption of one-to-one matching in time less plausible. Rather, at high presentation rates, the neural representation of images will persist beyond the presentation time, and this will affect the disparity estimates in subsequent frames. Such filtering will reduce the likelihood of perceiving motion artifacts in a stimulus with changing disparity, and should therefore help make the appearance of motion in depth smooth.

11.4 Exposure during capture

So far we have considered only images that were captured with a very brief exposure. In practice, exposures must be longer in order to collect enough light or to accomplish mechanical transition of film from one exposure to the next. Conventionally, the exposure has been a box shutter in time whose duration is half of the time between exposures³¹: i.e., t_c/2 (upper left panel in Fig. 30). When capturing an object moving at speed s, the box shutter in time yields a box filter in space:

$$\frac{1}{{st}_c}r\left(\frac{x}{{st}_c/2}\right),$$

where r is a rectangular pulse with width st_c/2. The Fourier transform is

FIGURE 30.

Shutter functions, motion blur, and spatio-temporal aliases. Upper row: An object moving at speed s relative to the camera is captured with a box-filter shutter function as depicted in the upper left panel. The duration of each exposure is t_c/2, half the time between exposures. The left panel schematizes the stimulus motion and the capture. The second, third, and fourth panels show the amplitude spectra that result from a box-filter shutter with stroboscopic presentation, single-flash presentation, and triple-flash presentation, respectively. As before, the circle represents the window of visibility. Lower row: The moving object is captured with a tent-filter shutter function. The duration of each exposure is t_c. The three panels on the right show the spectra that result from a tent-filter shutter.

$$\frac{1}{2}\text{sinc}\left(\frac{\omega }{2/{st}_c}\right),$$ (18)

which has its first zero at a spatial frequency of 2/st_c. The attenuation in spatial frequency due to the shutter function in time is called motion blur. Note that there is no attenuation when the stimulus speed is zero and quite significant attenuation when the speed is high.

The amplitude spectrum of a moving stimulus is obtained by multiplying Eq. (18) with the spectrum associated with the presentation protocol (Figs. 1 and 3). The second, third, and fourth columns of Fig. 30 display the resulting spectra for one speed and for stroboscopic, single-flash, and triple-flash protocols, respectively. In all three cases, spatio-temporal aliases are attenuated by the shutter function. This increases the probability that motion will be perceived as smooth. The reduction in the likelihood of perceiving motion artifacts comes, however, at the cost of blurring the stimulus spatially. The trade-off between smoothing motion appearance while reducing spatial detail is generally advantageous because the visual system often perceives a moving blurred stimulus as sharper than the same spatial stimulus when it is not moving.³²

Other shutter functions can be used with computer-generated imagery. For example, tent filters are often used instead of box filters.³³ Capturing a moving stimulus with such a shutter function in time yields a triangular pulse in space:

$$\frac{1}{{st}_c}\mathit{tri}\left(\frac{x}{{st}_c/2}\right).$$

Its amplitude spectrum is

$$\frac{1}{2}{\text{sinc}}^{\text{2}}\left(\frac{\omega }{2/{st}_c}\right).$$ (19)

Like Eq. (18), this function has its first zero at 2/st_c, but at higher spatial frequencies, it tends toward zero more rapidly. As a result, the tent filter provides greater attenuation of spatio-temporal aliases without compromising brightness.

11.5 Frame interpolation strategies

One can reduce the visibility of judder and flicker by increasing the capture rate. But to increase capture rate, one needs a faster camera lens, brighter illumination, and so forth. Current work on vector-motion interpolation allows one to insert frames based on computed updated object positions and thereby to increase the frame rate without repeating frames.^34–36 The aim of such techniques is to reduce the visibility of motion artifacts without increasing spatial blur. As shown by our analysis in Experiment 4, the insertion of more frames may also increase the fidelity of depth perception, provided that the computed frames are high quality and do not produce their own disparity errors.

11.6 Spatial resolution of the display

The display’s spatial resolution also influences the visibility of motion artifacts. Consider a display with finite spatial resolution and infinite temporal resolution. The display has pixels at spatial intervals of x_p and the stimulus is an object moving at speed s. If the image is presented stroboscopically whenever the object has moved to a new pixel location, the temporal rate of presentation is t_p = x_p/s. The Fourier transform has aliases at intervals of 1/x_p along the spatial-frequency axis. The slope of the aliases is −1/s or −t_p/x_p. As stimulus speed changes, the aliases rotate about their intersections with the spatial-frequency axis. They tend toward vertical at slower speeds and toward horizontal at faster speeds. The aliases would therefore encroach on the window of visibility more and more as speed decreases. Thus, motion artifacts due to spatial limitations of the display should be most noticeable at slow speeds. Recall that motion artifacts due to temporal limitations are most noticeable at fast speeds. A thorough analysis of how the spatial and temporal resolution of a display affects perceived judder would consider the interplay between these two effects.

Pixel fill factor is the spatial proportion of a pixel that emits light. If the display has pixels centered at intervals of x_p and the fill factor p, the width of the light-emitting part of the pixel is px_p. A low fill factor yields pinpoints, so this is the spatial analog of stroboscopic presentation. A high fill factor yields block pixels and is analogous to sample and hold. We can understand the consequences of the pixel fill factor by considering Eqs. (4) and (5). The rectangular pulse r(t/Δt) that represents the hold time in the sample-and-hold protocol has a Fourier transform of sinc(τ/1/Δt). Thus, sample and hold in time attenuates higher temporal frequencies in the amplitude spectrum of the stimulus and thereby reduces the visibility of the aliases. The pixel fill factor would be represented by a spatial rectangular pulse r(x/px_p) in Eq. (5), which has a Fourier transform of sinc(ω/1/px_p). Thus, filling pixels yields attenuation of higher spatial frequencies and thereby also reduces the visibility of the aliases.

11.7 Real-time applications

With interactive applications, such as computer games, the delay can vary between when the user acts and when the result of the action appears on the screen. The results of Experiment 4 point to an interesting and potentially significant dilemma for interactive applications that employ stereo.

In non-stereo displays, the timing between image rendering and image display is dealt with by double buffering, which ensures that each display frame contains an image and that that image is as up to date as possible. In stereo displays, quad buffering is used to assure synchronization between the alternating fields presented to the two eyes. Two front buffers contain the left- and right-eye images that are being displayed alternately. The images in the left- and right-eye back buffers are not displayed until those images have both been fully rendered. If the rendering time exceeds the frame time, the system repeats the front-buffer images until the next images are ready. Thus, quad buffering maintains a constant presentation rate and assures image synchronization of the left- and right-eye images by dynamically adjusting the number of image repetitions before updated images are displayed to the two eyes. If the rendering time is short, the presentation protocol is single flash. If the rendering time is long, the protocol becomes multi-flash.

The results of Experiment 4 show that distortions in perceived depth depend on the type of protocol being used. With single-flash protocols, alternating capture and alternating presentation – C_alt/P_alt–1X (Fig. 20) – produces smaller perceptual distortions than simultaneous capture and alternating presentation – C_sim/P_alt–1X (Fig. 21). However, with multi-flash protocols, the situation reverses: Alternating capture and alternating presentation – e.g., C_offset/P_alt–3X – produces larger distortions than simultaneous capture and alternating presentation – C_sim/P_alt–3X (Fig. 23). The dilemma for interactive applications is that alternating capture and alternating presentation minimizes distortions when the rendering time is short, but exacerbates distortions when the rendering time is long. Thus, the designer should probably choose the protocol based on how frequently the rendering time will exceed the duration of a display frame.

12 Summary

The work described here adds to the theoretical and empirical foundation for determining what display parameters are likely to yield noticeable flicker, motion artifacts, and depth distortions. From this foundation, one can make effective decisions about how to minimize or even eliminate these undesirable effects. We reported several findings, but the following are the most important.

1. Flicker and motion artifacts are generally more prominent with stereo than with non-stereo displays, but the greater prominence is primarily due to the insertion of dark frames rather than something unique to stereo processing.

2. Flicker visibility is determined primarily by presentation rate.

3. The visibility of flicker is somewhat reduced with alternating as opposed to simultaneous presentation to the two eyes.

4. The visibility of motion artifacts increases with increasing stimulus speed and decreases with increasing capture rate. Thus, the ratio of speed divided by capture rate is a good predictor of the prominence of artifacts.

5. Motion artifacts for a fixed capture rate are somewhat more visible with multi-flash than with single-flash protocols.

6. Distortions of perceived depth occur with moving objects with some stereo presentation protocols because they delay the input to one eye relative to the other eye. Thus, objects moving in one direction can be perceived as closer than they are meant to be and objects moving in the opposite direction can be perceived as farther than they are meant to be.

Biographies

David M. Hoffman received his B.S. degree in bioengineering from the University of California, San Diego in 2005, and his Ph.D. degree in vision science from the University of California, Berkeley, in May 2010. He now works at MediaTek in San Jose, CA. His primary research interests are in optics, visual perception, electronic imaging, and the development of novel display technologies.

Vasiliy I. Karasev received his B.S. degree in electrical engineering from the University of California, Berkeley, in 2009. He is currently pursuing his Ph.D. degree in electrical engineering at the University of California, Los Angeles. After working with Hoffman and Banks on the stereoscopic sampling project as an undergraduate researcher, he has gone on to use Lidar to map urban environments and use volumetric signal processing to denoise magnetic-resonance images.

Martin S. Banks received his B.S. degree in psychology from Occidental College in 1970. After spending a year teaching in Germany, he entered graduate school and received an M.S. degree in experimental psychology from the UC San Diego in 1973. He then transferred to the University of Minnesota where he received his Ph.D. degree in developmental psychology in 1976. He became Assistant Professor of Psychology at the University of Texas at Austin later that year. He moved to the University of California, Berkeley, in 1985 where he is now Professor of Optometry, Vision Science, Psychology, and Neuroscience. He is known for his research on human-visual perception, particularly the perception of depth. He is also known for his work on the integration of information from different senses. He is a recipient of the McCandless Award for Early Scientific Contribution, the Gottsdanker and Howard Lectureships, the Koffka Award, and an Honorary Professorship of the University of Wales, Cardiff. He is also a Fellow of the American Association for the Advancement of Science and of the American Psychological Society, and a Holgate Fellow of Durham University.